Теорема косинусов. Видеоурок. Геометрия 9 Класс
Вспомним теорему Пифагора (рис. 1).
Рис. 1. Иллюстрация к теореме
К данному выражению прибавим и отнимем квадрат второго катета:
Но так как
,
то
Эту формулу мы получили для катетов в прямоугольном треугольнике, но оказывается, что аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника, это покажет нам теорема косинусов. Она звучит так:
Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Чтобы записать формулой данную теорему, принимаем стандартные значения.
Рис. 2. Иллюстрация к теореме
(рис. 2)
В доказательстве теоремы используем формулу длины отрезка в координатах. Рассмотрим данную формулу.
Рис. 3. Иллюстрация к теореме
Рис. 4. Иллюстрация к теореме
В доказательстве теоремы косинусов BC – это сторона треугольника АВС, обозначенная а (рис. 4). Вводим удобную систему координат и находим координаты нужных нам точек. У точки В координаты (с;0). А координаты точки С – (b, при
– основное тригонометрическое тождество.
Что и требовалось доказать.
Эта теорема справедлива для всех сторон треугольника (рис. 5), то есть:
Рис. 5. Иллюстрация к теореме
Таким образом, теорема косинусов обобщает теорему Пифагора, то есть используется для произвольного треугольника.
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Аналогично:
Теперь найдём углы.
Вспомним, что косинус угла из промежутка однозначно определяет угол (в отличие от синуса).
Рис. 6. Иллюстрация к теореме
Поясним это. Дана единичная полуокружность (рис. 6). Если нам задан , то нам задана точка на верхней полуокружносте и задан угол α. Следовательно, однозначно определяет точку М(), и однозначно определяется угол .
Рассмотрим пределы изменения синуса и косинуса α, если α – угол треугольника, то есть он лежит в пределах от 0.
Рис. 7. Иллюстрация к теореме
Предел изменения косинуса (рис. 7):
Предел изменения синуса (рис. 7):
Если , то
Если
Если
Теорема косинусов активно используется при решении задач, вот одна из них.
Рис. 8. Иллюстрация к задаче
Дано: Треугольник АВС. , АВ = 9, ВС = 3, , где М- точка на гипотенузе АВ (рис. 8).
Найти: СМ
Решение:
Так как АМ+МВ = 9, а , то АМ = 3, МВ = 6.
Из треугольника АВС найдём :
Из треугольника СМВ по теореме косинусов найдём СМ:
Дано: треугольник АВС, со сторонами – 5, 8, 10 (рис. 9).
Найти: остроугольный ли треугольник.
Решение:
Рис. 9. Иллюстрация к задаче
В треугольнике АВС наибольшая сторона ВС. Напротив наибольшей стороны находится наибольший угол, то есть следует сначала оценить его. .
По теореме косинусов:
Косинус угла α меньше 0, следовательно, тупой, поэтому данный треугольник АВС не остроугольный.
Дано: треугольник АВС, (рис. 10)
Доказать:тупой.
Доказательство:
Рис. 10. Иллюстрация к задаче
Для доказательства достаточно написать теорему косинусов для угла :
Данная задача показывает, что с помощью теоремы косинусов можно определить тупой угол или острый. Рисунки 10,11 и 12 иллюстрируют это.
Рис. 11. Иллюстрация к задаче
Если , то (рис. 11)
Рис. 12. Иллюстрация к задаче
Если , то острый (рис. 12).
На данном уроке мы рассмотрели и доказали теорему косинусов и решили задачи с её применением.
Список литературы
- Ат
interneturok.ru
Теорема косинусов для треугольника, формула и примеры
ТЕОРЕМА Для произвольного треугольника квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними. То есть для треугольника , изображенного на рисунке 1, имеют место следующие соотношения:
Следствие из теоремы косинусов
Косинус любого угла треугольника , при условии, что известны все его стороны, можно найти из соотношений
Примеры решения задач
ПРИМЕР 1| Задание | В треугольнике стороны см и см, угол между ними . Найти неизвестную сторону . |
| Решение | Запишем для неизвестной стороны теорему косинусов:
Подставляя известные значения сторон и угла, получим:
(см) |
| Ответ | см |
| Задание | Стороны треугольника равны соответственно 3, 7 и 8 см. Найти угол, лежащий против стороны длинной 7 см. |
| Решение | Обозначим стороны треугольника: ; а против стороны лежит . По следствию из теоремы косинусов, косинус выражается через стороны треугольника следующим образом:
Подставим известные значения длин сторон, получим
|
| Ответ |
ru.solverbook.com
калькулятор теорема косинусов
Вы искали калькулятор теорема косинусов? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и онлайн теорема косинусов, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «калькулятор теорема косинусов».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как калькулятор теорема косинусов,онлайн теорема косинусов,теорема косинусов калькулятор,теорема косинусов онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и калькулятор теорема косинусов. Просто введите задачу в окошко и нажмите «решить» здесь (например, теорема косинусов калькулятор).
Где можно решить любую задачу по математике, а так же калькулятор теорема косинусов Онлайн?
Решить задачу калькулятор теорема косинусов вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
www.pocketteacher.ru
Теорема косинусов для треугольника
При решении задач по геометрии из ЕГЭ и ОГЭ по математике довольно часто возникает необходимость, зная две стороны треугольника и угол между ними, найти третью сторону. Или же, зная все стороны треугольника, найти его углы. Для решение этих задач вам потребуется значение теоремы косинусов для треугольника. В данной статье репетитор по математике и физике рассказывает о том, как формулируется, доказывается и применяется на практике при решении задач данная теорема.
Формулировка теоремы косинусов для треугольника
Теорема косинусов для треугольника связывает две стороны треугольника и угол между ними со стороной, лежащей против этого угла. К примеру, обозначим буквами , и длины сторон треугольника ABC, лежащие соответственно против углов A, B и C.

Тогда имеет теорема косинусов для этого треугольника может быть записана в виде:
На рисунке для удобства дальнейших рассуждений угол
Понятно, что если бы вы выражали другую сторону треугольника, например, сторону , то в формуле нужно было бы брать косинус угла A, то есть лежащего против искомой стороны в треугольнике, а справа в уравнении на своих местах стояли бы стороны и . Выражение для квадрата стороны получается аналогично:
Доказательство теоремы косинусов для треугольника
Доказательство теоремы косинусов для треугольника проводят обычно следующим образом. Разбивают исходный треугольник на два прямоугольных треугольника высотой, а дальше играются со сторонами полученных треугольников и теоремой Пифагора. В результате после долгих нудных преобразований получаю нужный результат. Мне лично этот подход не по душе. И не только из-за громоздких вычислений, но ещё и потому что в этом случае приходится отдельно рассматривать случай, когда треугольник является тупоугольным. Слишком много трудностей.
Я предлагаю доказать эту теорему с помощью понятия «скалярного произведения векторов». Я сознательно иду на этот риск для себя, зная, что многие школьники предпочитают обходить эту тему стороной, считая, что она какая-то мутная и с ней лучше не иметь дела. Но нежелание возиться отдельно с тупоугольным треугольником во мне в
yourtutor.info
Теорема синусов и теорема косинусов — теория в ЕГЭ по математике онлайн
Теорема синусов
В любом треугольнике отношение стороны к синусу противолежащего угла не зависит от выбора стороны и равно диаметру описанной окружности.
Доказательство
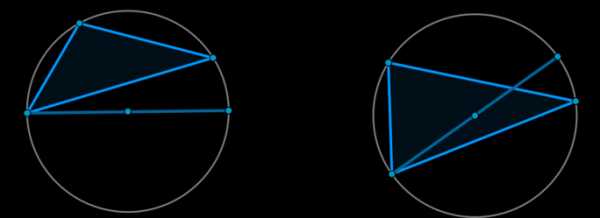
Пусть \(R\) – радиус окружности, описанной около треугольника \(ABC\). Проведём диаметр \(BA_1\) и рассмотрим треугольник \(A_1BC\) (случай, когда точки \(A_1\) и \(C\) совпадают, рассмотрите самостоятельно). Угол \(C\) этого треугольника прямой, поэтому \(BC = BA_1\cdot \sin\angle A_1\), но \(\sin\angle A = \sin\angle A_1\) так как углы \(A\) и \(A_1\) либо отличаются на угол, равный \(180^\circ\), либо совпадают.
Следовательно, \(BC = BA_1\cdot\sin\angle A\), то есть \(\dfrac{BC}{\sin\angle A} = 2R\). Так как в доказательстве мы не ограничивали общности, то равенства \(\dfrac{AC}{\sin\angle B} = 2R = \dfrac{AB}{\sin\angle C}\) показываются аналогично.
Теорема косинусов
В любом треугольнике квадрат стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Доказательство
Пусть в треугольнике \(ABC\) \(AB = c\), \(AC = b\), \(BC = a\), \(\angle C=\alpha\). Докажем, что \(c^2=a^2+b^2-2ab\cdot\cos\alpha\).
Проведем высоту \(BH=h\). Пусть она разбила сторону \(AC\) на отрезки длиной \(x\) и \(y\):
По теореме Пифагора из \(\triangle AHB: \ c^2=h^2+y^2\);
из \(\triangle CHB: \ a^2=x^2+h^2\).
Вычтем из первого равенства второе: \(c^2-a^2=y^2-x^2 \Rightarrow c^2=a^2+(y-x)(y+x)=a^2+b(y-x)\).
Заметим, что \(\cos\alpha=\dfrac xa \Rightarrow x=a\cos\alpha\). Тогда:
\[c^2=a^2+b(y+x-2x)=a^2+b(b-2x)=a^2+b(b-2a\cos\alpha)=a^2+b^2-2ab\cos\alpha\]
Замечание
С помощью данных теорем можно легко найти все элементы треугольника, если известны, например, две стороны и угол, угол и две стороны, три стороны и т.д.
Пример
Найти стороны и углы треугольника, если медиана \(BM\), проведенная к стороне \(AC=4\), равна \(2\sqrt3\), а угол треугольника \(\angle A=60^\circ\).
Решение. Рассмотрим данный треугольник:
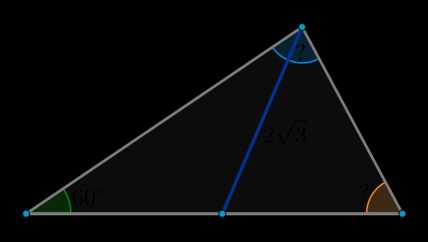
1) По теореме косинусов из \(\triangle ABM\):
\((2\sqrt3)^2=2^2+AB^2-2\cdot 2\cdot AB\cdot \cos60^\circ \Rightarrow
AB^2-2AB-8=0 \Rightarrow AB=4\)
2) \(\triangle ABC\) – равнобедренный (\(AB=AC=4\)), следовательно, \(\angle B=\angle C=\frac12\left(180^\circ-\angle A\right)=60^\circ\).
Значит, \(\triangle ABC\) – правильный, значит, \(BC=4\).
shkolkovo.net
Теорема косинусов
Теорема косинусов и теорема Пифагора. В этой статье мы рассмотрим теорему косинусов и как она используется для нахождения элементов треугольника. А так же разберём её взаимосвязь с теоремой Пифагора.

Знать эту теорему НЕОБХОДИМО. Что мы можем найти, используя её?
Если нам будут известны две стороны и угол между ними, мы без труда найдём третью сторону. Для этого нужно просто подставить в формулу известные величины. Для других сторон всё то же самое:
Можно ли использовать теорему косинусов для нахождения третьей стороны, если известны любые две стороны и угол, не лежащий между этими сторонами? Например, нам известны стороны a и b и угол альфа. Тогда из формулы
мы можем найти сторону «с». Приводим к виду:
То есть, мы получаем квадратное уравнение с переменной «с» (все остальные величины нам известны). Решив его, получим искомую сторону.
Мы можем найти любой угол, если нам известны все три стороны треугольника:
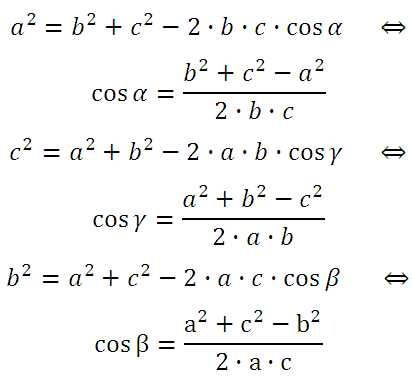
Разумеется, что учить все эти формулы не нужно, так как достаточно понимать сам смысл Теоремы косинусов. А косинус любого угла не трудно выразить используя простые алгебраические преобразования.
*Если вы вычисляете косинус тупого угла, то имейте ввиду, что должно получиться отрицательное значение, так как косинус угла от 90 до 180 градусов отрицателен. Если при решении в задачах получите положительное значение, то ищите ошибку.
Следующий вопрос: а если нам дана сторона и любые два угла, что делать? В этом случае теорема косинусов не используется, а на помощь приходит теорема синусов, её мы рассмотрим в одной из следующих статей, не пропустите!
Если вы будете в совершенстве владеть теоремами Пифагора, косинусов, синусов и свойствами подобия треугольников, то для вас не возникнет никаких сложностей с решением треугольников (в большинстве задач).
Следующий факт знают все, но всё же о взаимосвязи теоремы косинусов с теоремой Пифагора сказать стоит. Посмотрите на исходный рисунок, если угол альфа равен 90 градусов, то получим:
То есть, по сути, теорема Пифагора это как бы частный случай теоремы косинусов.
Рассмотрим прямоугольный треугольник. Покажем то же самое, но с другими обозначениями:

По теореме косинусов:
Так как угол С равен 90, то
Напомню, что зная любые две стороны в прямоугольном треугольнике, мы всегда можем найти третью. А далее без труда можем найти значение любой тригонометрической функции острого угла в нём. Можете изучить статью об этом.
Получить материал статьи в формате PDF
На этом всё. Успехов вам!!!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Теорема косинусов | Треугольники
Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Дано:
∆ ABC.
Доказать:
Доказательство:
I. Если треугольник ABC — остроугольный.
1) Опустим перпендикуляр CD на сторону AB.
2) Рассмотрим прямоугольный треугольник ADC.
По теореме Пифагора,
По определению косинуса острого угла в прямоугольном треугольнике,
следовательно,
3) Рассмотрим прямоугольный треугольник BDC.
По теореме Пифагора
Упрощаем
Откуда
II. Если треугольник ABC — тупоугольный.
1) Опускаем перпендикуляр CD на прямую, содержащую сторону AB.
2) Рассмотрим прямоугольный треугольник ADC.
По теореме Пифагора,
По определению косинуса,
Так как углы A и CAD — смежные, то ∠CAD=180º-∠A. По формуле приведения
3) Рассмотрим прямоугольный треугольник BDC.
Дальнейшая часть доказательства полностью повторяет рассуждения пункта I.
III. Если треугольник ABC — прямоугольный, где ∠A=90º, получаем теорему Пифагора (cos90º=0).
www.treugolniki.ru
