Формула нулевого х: Как найти икс нулевое 🚩 как находится x нулевое 🚩 Математика

Содержание

Проверка гипотез

Общий обзор

Определение нулевой и альтернативной гипотезы, уровня статистической значимости

Получение статистики критерия, определение критической области

Получение значения р (достигнутого уровня значимости)

Применение значения р

Проверка гипотез против доверительных интервалов

Общий обзор

Часто делают выборку, чтобы определить аргументы против гипотезы относительно популяции (генеральной совокупности). Этот процесс известен как проверка гипотез (проверка статистических гипотез или проверка значимости), он представляет количественную меру аргументов против определенной гипотезы.

Установлено 5 стадий при проверке гипотез:

Определение нулевой () и альтернативной гипотезы () при исследовании. Определение уровня значимости критерия.
Отбор необходимых данных из выборки.
Вычисление значения статистики критерия, отвечающей .
Вычисление критической области, проверка статистики критерия на предмет попадания в критическую область.
Интерпретация достигнутого уровня значимости р и результатов.

Определение нулевой и альтернативной гипотез, уровня статистической значимости

При проверке значимости гипотезу следует формулировать независимо от используемых при ее проверке данных (до проведения проверки). В таком случае можно получить действительно продуктивный результат.

Всегда проверяют нулевую гипотезу (), которая отвергает эффект (например, разница средних равняется нулю) в популяции.

Например, при сравнении показателей курения у мужчин и женщин в популяции нулевая гипотеза означала бы, что показатели курения одинаковые у женщин и мужчин в популяции.

Затем определяют альтернативную гипотезу (), которая принимается, если нулевая гипотеза неверна. Альтернативная гипотеза больше относится к той теории, которую собираются исследовать. Итак, на этом примере альтернативная гипотеза заключается в утверждении, что показатели курения различны у женщин и мужчин в популяции.

Разницу в показателях курения не уточнили, т.е. не установили, имеют ли в популяции мужчины более высокие или более низкие показатели, чем женщины. Такой подход известен как двусторонний критерий, потому что учитывают любую возможность, он рекомендуется постольку, поскольку редко есть уверенность заранее в направлении какого-либо различия, если таковое существует.

В некоторых случаях можно использовать односторонний критерий для гипотезы , в котором направление эффекта задано. Его можно применить, например, если рассматривать заболевание, от которого умерли все пациенты, не получившие лечения; новый препарат не мог бы ухудшить положение дел.

Уровень значимости. Важным этапом проверки статистических гипотез является определение уровня статистической значимости , т. е. максимально допускаемой исследователем вероятности ошибочного отклонения нулевой гипотезы.

Получение статистики критерия, определение критической области

После того как данные будут собраны, значения из выборки подставляют в формулу для вычисления статистики критерия (примеры различных статистик критериев см. ниже). Эта величина количественно отражает аргументы в наборе данных против нулевой гипотезы.

Критическая область. Для принятия решения об отклонении или не отклонении нулевой гипотезы необходимо также определить критическую область проверки гипотезы.

Выделяют 3 вида критических областей:

двусторонняя:

Рис. 1 Двусторонняя критическая область

левосторонняя:

Рис. 2 Левосторонняя критическая область

правосторонняя:

Рис. 3 Правосторонняя критическая область

— заданный исследователем уровень значимости.

Если наблюдаемое значение критерия (K) принадлежит критической области (K_кр, заштрихованная область на рис.1-3), гипотезу отвергают, если не принадлежит — не отвергают.

Для краткости можно записать и так:

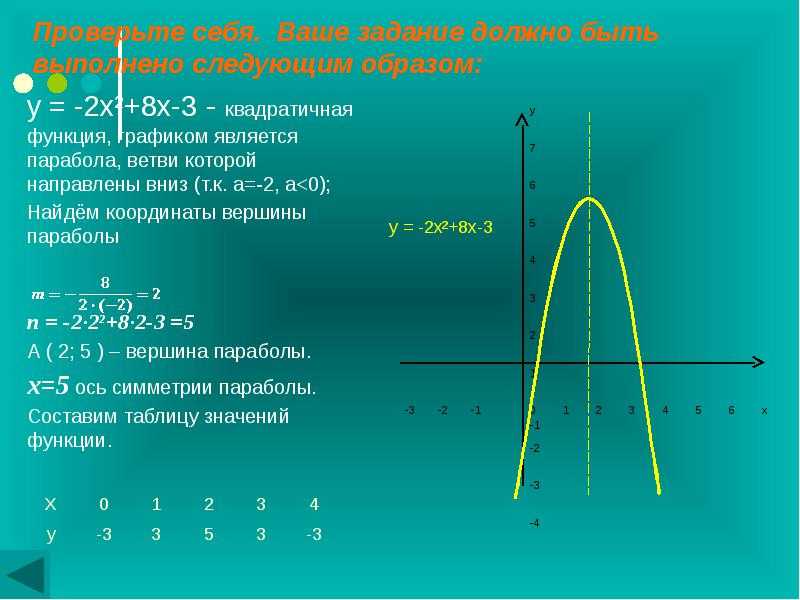
| K | > K_кр — отклоняем H

| K | < K_кр — не отклоняем H₀

Получение значения

Все статистики критерия подчиняются известным теоретическим распределениям вероятности. Значение статистики критерия, полученное из выборки, связывают с уже известным распределением, которому она подчиняется, чтобы получить значение р, площадь обоих «хвостов» (или одного «хвоста», в случае односторонней гипотезы) распределения вероятности.

Большинство компьютерных пакетов обеспечивают автоматическое вычисление двустороннего значения р.

Значение р — это вероятность получения нашего вычисленного значения критерия или его еще большего значения, если нулевая гипотеза верна.

Нулевая гипотеза всегда относится к популяции, представляющей больший интерес, нежели выборка. В рамках проверки гипотезы мы либо отвергаем нулевую гипотезу и принимаем альтернативу, либо не отвергаем нулевую гипотезу. Подробнее об ошибках при проверке гипотез

Применение значения

Следует решить, сколько аргументов позволят отвергнуть нулевую гипотезу в пользу альтернативной. Чем меньше значение р, тем сильнее аргументы против нулевой гипотезы.

Традиционно полагают, если р < 0,05, (=0,05) то аргументов достаточно, чтобы отвергнуть нулевую гипотезу, хотя есть небольшой шанс против этого. Тогда можно отвергнуть нулевую гипотезу и сказать, что результаты значимы на 5% уровне.
Напротив, если р > 0,05, то аргументов недостаточно, чтобы отвергнуть нулевую гипотезу. Не отвергая нулевую гипотезу, можно заявить, что результаты не значимы на 5% уровне. Данное заключение не означает, что нулевая гипотеза истинна, просто недостаточно аргументов (возможно, маленький объем выборки), чтобы ее отвергнуть.

Уровень значимости (т.е. выбранная «граница отсечки») 5% задается произвольно. На уровне 5% можно отвергнуть нулевую гипотезу, когда она верна. Если это может привести к серьезным последствиям, необходимо потребовать более веских аргументов, прежде чем отвергнуть нулевую гипотезу, например, выбрать значение = 0,01 (или 0,001).

Определение результата только как значимого на определенном уровне граничного значения (например 0, 05) может ввести в заблуждение. Например, если р = 0,04, то нулевую гипотезу отвергаем, но если р = 0,06, то ее не отвергли бы. Действительно ли они различны? Мы рекомендуем всегда указывать точное значение

Проверка гипотез против доверительных интервалов

Доверительные интервалы и проверка гипотез тесно связаны. Первоначальная цель проверки гипотезы состоит в том, чтобы принять решение и предоставить точное значение р.

Доверительный интервал (ДИ) количественно определяет изучаемый эффект (например, разницу в средних) и дает возможность оценить значение результатов. ДИ предоставляют интервал вероятных значений для истинного эффекта, поэтому его также можно использовать для принятия решения даже без точных значений р.

Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии

В начало

Содержание портала

Формула Тейлора с остаточным членом в форме Пеано

Допустим, мы знаем значение функции f в какой-то точке x0, а хотим узнать её значение в точке x.

21.1o-символика

21.1.1Определение o-малого

Пусть функцию f дифференцируема в точке x0. Тогда, как мы знаем, справедливо утверждение о линейном приближении:

f(x)=f(x0)+f′(x0)(x−x0)+α(x−x0)⋅(x−x0),(21.1)

f(x)=f(x0)+f′(x0)(x−x0)++α(x−x0)⋅(x−x0),(21.1)

где α(x−x0)→0 при x→x0. Иными словами, выражение α(x−x0)⋅(x−x0) не просто маленькое при x близком к x0, а оно маленькое по сравнению с разностью x−x0.

В дальнейшем нам пригодится более компактное обозначение для функций, которые являются маленькими по сравнению с какими-то другими функциями.

Определение 1. Говорят, что функция f является o-маленьким (или o-малым) от функции g при x→x0 если f и g определены в некоторой проколотой окрестности точки x0, g в этой окрестности не обращается в ноль и

limx→x0f(x)g(x)=0.(21.2)

Неформально это означает, что f(x) становится во сколько угодно раз меньше g(x) при x→x0.

Пример 1. Функция x2 является o-маленьким от x при x→0, поскольку

limx→0x2x=limx→0x=0.

Пример 2. Функция sin(1/x) является o-маленьким от функции 1/x при x→0, поскольку

limx→0sin(1/x)1/x=limx→0xsin1x=0.

Мы воспользовались тем, что произведение ограниченной функции и стремящейся к нулю стремится к нулю.

Пример 3. Функция sin(x) не является o-маленьким от функции x при x→0, поскольку

limx→0sin(x)x=1≠0.

(Это первый замечательный предел. )

Пример 4. Функция sin(1/x) не является o-маленьким от функции x при x→0, поскольку предел

limx→0sin(1/x)x

не существует.

Вопрос 1. Является ли функция x2 o-маленьким от функции x+x2 при x→0?

Да

Верный ответ. Действительно,

limx→0x2x+x2=limx→0x1+x=0.

Нет.

Неверный ответ. А если посчитать предел, что получается?

21.1.2Свойства o-малого

Можно сформулировать и доказать много разных утверждений про свойства o-малых, следующих из определения и свойств пределов. Например:

Утверждение 1. Пусть f(x)=o(g(x)) и h(x)=o(g(x)). Тогда f(x)+h(x)=o(g(x)). Это можно записать короче так:

o(g(x))+o(g(x))=o(g(x)).

В этом равенстве o-малые есть и справа и слева — на самом деле, правильно было бы записать так:

o(g(x))+o(g(x))⊂o(g(x)),

то есть для любого способа выбрать конкретные функции на место o(g(x)) в левой части найдётся функция справа, которая будет o(g(x)).

Доказательство. Проверим, что f(x)+h(x)=o(g(x)). Действительно:

limx→x0f(x)+h(x)g(x)=limx→x0(f(x)g(x)+h(x)g(x))=0

по теореме о пределе суммы.∎

Утверждение 2. Пусть f(x)=o(g(x)) и c≠0. Тогда f(x)=o(cg(x)).

Доказательство. Действительно,

limx→x0f(x)cg(x)=1climx→x0f(x)g(x)=0.

∎

На семинаре будут обсуждаться и другие свойства такого типа. Для тренировки можете придумать как можно больше верных свойств o-малых и доказать их.

21.2Приближение функций

21.2.1Непрерывность и дифференцируемость

Итак, пусть мы знаем значение функции f в точке x0, а нас интересует значение f в точке x. Будем считать, что x близко к x0.

Если мы знаем, что f непрерывна, это означает, что limx→x0f(x)=f(x0), то есть значения в близких точках близки к значению f(x0). Значит можно записать:

f(x)≈f(x0).

Если вы ничего не знаете про моделирование погоды и хотите узнать, какую погоду ждать завтра, самый лучший ответ, который вы можете дать — примерно такую же, как сегодня.

Знак приближенного равенства не имеет строгого смысла и не может использоваться в доказательствах. Однако, мы можем использовать o-символику, чтобы сформулировать аккуратное утверждение про непрерывность:

f(x)=f(x0)+o(1),(21.3)

где o(1) — это функция, являющаяся o-маленьким от 1 при x→x0. По определению, o(1) — это такая функция, которая при делении на единицу стремится к нулю, а поскольку деление на единицу ничего не меняет — она сама стремится к нулю. Иными словами, равенство (21.3) — это просто другой способ сказать, что функция f непрерывна в точке x0.

В общем, если мы знаем, что функция f непрерывна, и больше ничего, то лучшее, что мы можем сделать — это приблизить её константой, функцией y=f(x0).

Пусть теперь мы знаем, что f не только непрерывна в x0, но и дифференцируема, и, более того, мы знаем её производную в этой точке. Тогда справедливо равенство (21.1), которое может может быть записано в виде:

f(x)=f(x0)+f′(x0)(x−x0)+o(x−x0),(21.4)

f(x)=f(x0)+f′(x0)(x−x0)++o(x−x0),(21.4)

где o(x−x0) — это какая-то функция, являющаяся o-маленьким от (x−x0) при x→x0. Действительно, если поделить α(x−x0)⋅(x−x0) на (x−x0), получится α(x−x0), а про неё мы знаем, что она стремится к нулю при x→x0.

В приближении (21.4) мы заменяем функцию не на константу, как в (21.3), а на линейную функцию, и говорим, что разница между настоящей функцией и её линейным приближением будет не просто маленькой при x→x0 (это было верно и в (21.3)), но маленькой по сравнению с (x−x0). Иными словами, воспользовавшись дополнительной информацией (дифференцируемосью и знанием производной), мы получили лучшее приближение для функции.

Можем ли мы продолжить этот процесс? Оказывается, да.

21.2.2Многочлен Тейлора второй степени

Обозначим правые части равенств (21. 3) и (21.4) без o-малых через T0(x) и T1(x) соответственно: T0(x):=f(x0),T1(x):=f(x0)+f′(x0)(x−x0). Введённые нами функции T0 и T1 являются многочленами соответственно нулевой и первой степени. У T0 в точке x0 такое же значение, как у f, а у T1 не только такое же значение, но и такая же производная:

T1(x0)=f(x0),T′1(x0)=f′(x0).

Пусть теперь мы знаем, что функция f имеет не только первую, но и вторую производную в точке x0, и знаем эту производную. Хотим найти многочлен T2 второй степени, который бы имел в точке x0 такое же значение и такие же производные, как f, то есть хотим, чтобы выполнялись равенства

T2(x0)=f(x0),T′2(x0)=f′(x0),T′′2(x0)=f′′(x0).

Как этого добиться? Пусть

T2(x)=f(x0)+f′(x0)(x−x0)+q⋅(x−x0)2,

где q — какая-то константа. Видно, что каким бы ни было q, T2(x0)=f(x0) и

T′2(x)=f′(x0)+2q⋅(x−x0),

и значит T′2(x0)=f′(x0). Таким образом, первые два условия выполняются автоматически. Осталось выбрать такое q, чтобы выполнялось и третье условие:

T′′2(x)=2q=f′′(x0).

Значит q=f′′(x0)/2. Таким образом,

T2(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2(x−x0)2.

T2(x)=f(x0)+f′(x0)(x−x0)++f′′(x0)2(x−x0)2.

Пример 5. Пусть f(x)=2+lnx. Тогда f′(x)=1/x и f′′(x)=−1/x2. Пусть x0=1. Построим T0, T1 и T2:

T0(x)=f(1)=2T1(x)=f(1)+f′(1)⋅(x−1)=2+(x−1)T2(x)=f(1)+f′(1)⋅(x−1)+f′′(1)2⋅(x−1)2=2+1⋅(x−1)−12(x−1)2=2+(x−1)−(x−1)22.

T0(x)=f(1)=2T1(x)=f(1)+f′(1)⋅(x−1)=2+(x−1)T2(x)=f(1)+f′(1)⋅(x−1)++f′′(1)2⋅(x−1)2==2+1⋅(x−1)−12(x−1)2==2+(x−1)−(x−1)22.

Посмотрим на графики y=f(x) и y=T0(x), y=T1(x) и y=T2(x), см. рис. 21.1. График y=f(x) пересекается с горизонтальной прямой y=T0(x) в точке x=1 и касается прямой y=T1(x) в той же точке. Парабола y=T2(x) также касается графика y=f(x), причём ещё «плотнее», чем это делает y=T1(x) — в точках, близких к x0, она лучше приближает график нашей функции.

Рис. 21.1: Нулевое, первое и второе приближение логарифма

Построенные нами многочлены T0, T1 и T2 называются многочленами Тейлора. Как видно из построения и примера 5, многочлен Тейлора первой степени — это просто функция, задающая касательную, а многочлен Тейлора второй степени обобщает понятие касательной: вместо приближения графика прямой линией мы приближаем его параболой, и за счёт этого можем получить лучшую точность приближения.

21.2.3Тейлоровские многочлены в общем виде

Процесс построения многочленов Тейлора можно продолжать. Пусть функция f имеет n-ю производную в точке x0 (и, стало быть, все производные меньших порядков тоже).

Определение 2. Построим многочлен

Tn(x):=f(x0)+f′(x0)(x−x0)+f′′(x0)2(x−x0)2+f′′′(x0)3!(x−x0)3+…+f(n)(x0)n!(x−x0)n==n∑k=0f(k)(x0)k!(x−x0)k.

Tn(x):=f(x0)+f′(x0)(x−x0)++f′′(x0)2(x−x0)2++f′′′(x0)3!(x−x0)3+…++f(n)(x0)n!(x−x0)n==n∑k=0f(k)(x0)k!(x−x0)k.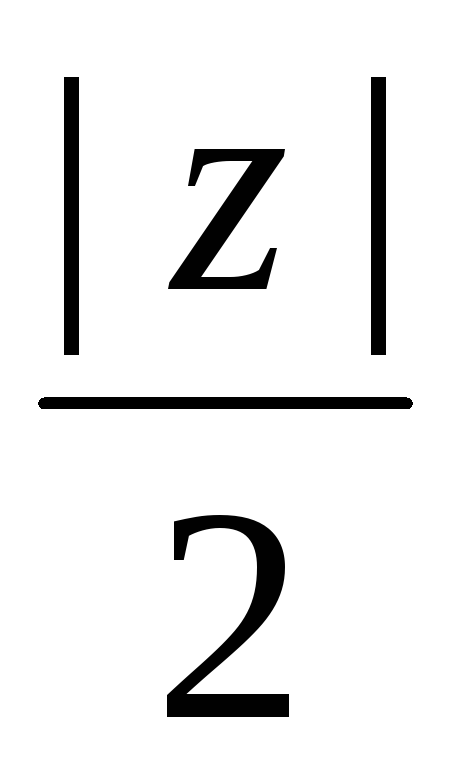

где f(k) — это k-я производная функции f, нулевая производная — это сама функция, 0!=1.

Этот многочлен называется многочленом Тейлора степени n для функции f в окрестности точки x0.

Утверждение 3. Для всех k=0,…,n:

T(k)n(x0)=f(k)(x0).

Доказательство. Утверждение проверяется непосредственно дифференцированием. Поскольку при каждом дифференцировании степень монома xl уменьшается на единицу, при k-кратном дифференцировании все слагаемые степени меньше k превращаются в ноль. Все слагаемые степени больше k будут иметь вид C(x−x0)m для каких-то чисел C и m∈N. При подстановке x=x0 они обнулятся. Значит, останется только слагаемое степени k. В результате каждого дифференцирования степень уменьшается на единицу и сносится коэффициентом рядом с соответствующим слагаемым. После k дифференцирований коэффициент будет равен k! и он сократится с k! в знаменателе. Останется f(k)(x0), что и требовалось получить. ∎

21.2.4Остаточный член в форме Пеано

До сих пор мы просто формально строили какие-то многочлены, ничего не говоря о том, как он будет соотноситься с исходной функцией f, по которой он строился. Настало время это исправить.

При построении каждого следующего тейлоровского многочлена мы используем всё больше и больше информации про функцию f: значение, производную, вторую производную, третью производную и т.д. Разумно ожидать, что многочлены больших степеней будут приближать нашу функцию всё лучше и лучше. Есть разные способы это формализовать. Сейчас мы сформулируем один из них.

Теорема 1. (Формула Тейлора с остаточным членом в форме Пеано) Пусть f имеет n производных в точке x0 и Tn — многочлен Тейлора для функции f в окрестности точки x0. Тогда

f(x)=Tn(x)+o((x−x0)n),x→x0.(21.5)

Доказательство. Для n=1 формула Тейлора совпадает с (21. 4) и была доказана ранее. Пусть n>1.

Нам нужно доказать, что f(x)−Tn(x) является o((x−x0)n) при x→x0, то есть доказать, что предел

limx→x0f(x)−Tn(x)(x−x0)n(21.6)

равен нулю.

Найдём этот предел явно. Поскольку f(x0)=Tn(x0), он является неопределенностью 0/0. Заметим, что числитель и знаменатель дифференцируемы в окрестности точки x0: поскольку у функции f есть n производных в точке x0, это означает, что (n−1)-я производная определена в некоторой окрестности точки x0, иначе производную от неё нельзя было определить; но тогда и (n−2)-я производная существует в окрестности и т.д. до первой производной; Tn является многочленом и дифференцируем сколько угодно раз где угодно, равно как и (x−x0)n в знаменателе. Производная знаменателя не обнуляется при x≠x0. Значит, можем применить правило Лопиталя и рассмотреть новый предел:

limx→x0f′(x)−T′n(x)n(x−x0)n−1.

Поскольку f′(x0)=T′n(x0), это снова неопределенность 0/0. Если n>2, вторая производная функции f существует в окрестности x0 и мы можем снова применить правило Лопиталя. Получится такой предел:

limx→x0f′′(x)−T′′n(x)n(n−1)(x−x0)n−2.

Так мы можем продолжать до тех пор, пока в числителе не появится производная порядка (n−1):

limx→x0f(n−1)(x)−T(n−1)n(x)n!(x−x0).(21.7)

Дальше использовать правило Лопиталя нельзя: нам известно, что n-я производная функции f существует к точке x0, но не факт, что она существует в окрестности этой точки. Значит, условия теоремы о правиле Лопиталя могут не выполняться. Однако, это не страшно. Заметим, что

T(n−1)n(x)=f(n−1)(x0)+f(n)(x0)(x−x0).

Проверьте, что это так (в частности, факториалы сократятся). Тогда предел (21.7) записывается в виде:

limx→x0f(n−1)(x)−f(n−1)(x0)−f(n)(x0)(x−x0)n!(x−x0)==1n!limx→x0(f(n−1)(x)−f(n−1)(x0)x−x0−f(n)(x0)).

limx→x01n!(x−x0)(f(n−1)(x)−−f(n−1)(x0)−f(n)(x0)(x−x0))==1n!limx→x0(f(n−1)(x)−f(n−1)(x0)x−x0−−f(n)(x0)).

Предел первого слагаемоего — это просто определение производной функции функции f(n−1) в точке x0. (Нужно приглядется к пределу и увидеть. Пригляделись? Ага, это оно.) А поскольку производная от (n−1)-й производной — это n-я производная, предел первого слагаемого равен f(n)(x0), а весь предел — нулю.

Теперь применение правила Лопиталя на каждом шаге обосновано и доказано, что исходный предел (21.6) тоже равен нулю. Что и требовалось!∎

21.3Применение формулы Тейлора

21.3.1Вычисление пределов

Пример 6. Найдём предел

limx→1ln(x)−x+1(x−1)2.

Это неопределенность 0/0 и в принципе её можно было бы раскрыть с помощью правила Лопиталя, но мы сделаем иначе. Разложим функцию ln(x) в ряд Тейлора с остаточным членом в форме Пеано в окрестности точки 1 до членов порядка 2 (ср. с примером 5 — разница только в константе). Получим:

lnx=(x−1)−(x−1)22+o((x−1)2).

Подставим это выражение в наш предел. Имеем:

limx→1ln(x)−x+1(x−1)2=limx→1(x−1)−(x−1)22+o((x−1)2)−x+1(x−1)2==limx→1−(x−1)22+o((x−1)2)(x−1)2=limx→1(−12+o((x−1)2)(x−1)2).

limx→1ln(x)−x+1(x−1)2==limx→1(x−1)−(x−1)22+o((x−1)2)−x+1(x−1)2==limx→1−(x−1)22+o((x−1)2)(x−1)2==limx→1(−12+o((x−1)2)(x−1)2).

Но по определению o-маленького, второе слагаемое стремится к нулю. (Какая бы функция не была написана вместо o((x−1)2), если её поделить на (x−1)2, частное будет стремиться к нулю.) Значит, предел равен −1/2.

21.3.2Достаточное условие экстремума

Теорема 2. Пусть функция f определена в окрестности x0, дважды дифференцируема в x0 и f′(x0)=0. Тогда если f′′(x0)>0, то в точке x0 строгий локальный минимум, а если f′′(x0)<0, то строгий локальный максимум.

Доказательство. Разложим функцию f в ряд Тейлора в точке x0 до членов порядка 2. Имеем:

f(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2(x−x0)2+o((x−x0)2).

f(x)=f(x0)+f′(x0)(x−x0)++f′′(x0)2(x−x0)2++o((x−x0)2).

Заметим, что f′(x0)=0, и второе слагаемое в формуле обнуляется. Заменим o((x−x0)2) на β(x−x0)(x−x0)2, где β(x−x0)→0 при x→x0. (Наличие такого представления эквивалентно определению o-малого.) Получаем такую штуку:

f(x)=f(x0)+(f′′(x0)2+β(x−x0))(x−x0)2.

f(x)=f(x0)++(f′′(x0)2+β(x−x0))(x−x0)2.

Поскольку β(x−x0)→0 при x→x0, в достаточно маленькой окрестности x0 знак выражения (f′′(x0)/2+β(x−x0)) совпадает со знаком f′′(x0), а (x−x0)2>0 при x≠0. Таким образом, если f′′(x0)>0, то второе слагаемое положительно, а f(x)>f(x0), а если f′′(x0)<0, то отрицательно, и f(x)<f(x0). Это и есть определения минимума и максимума соответственно.∎

21.4Заключение

Формула Тейлора с остаточным членом в форме Пеано — пожалуй, самый важный факт дифференциального исчисления. Это своего рода микроскоп, с помощью которого можно изучать сколь угодно тонкие локальные свойства функций. Однако, теорема 1 не говорит ничего про какую-то конкретную точку x. Она говорит, что если x приближается к x0, то тейлоровские многочлены быстро приближаются к значениям функции. Но что если мы будем делать наоборот — зафиксируем x и будем увеличивать n? Будет ли значение тейлоровских многочленов в точке x всё лучшим и лучшим приближением к f(x)? Оказывается, далеко не всегда. Однако во многих случаях — особенно важных с практической точки зрения — будет. Об этом — в следующей лекции.

← Предыдущая глава Следующая глава →

Нули функции – Объяснение и примеры

Одной из наиболее распространенных проблем, с которыми мы сталкиваемся на наших базовых и продвинутых занятиях по алгебре, является нахождение нулей определенных функций. нули функций.

Судя по названию, нули функции — это значения x, где f(x) равно нулю.

Мы встречаем нули на уроках математики и в повседневной жизни. Например, если мы хотим узнать сумму, которую нам нужно продать, чтобы выйти в ноль, мы в конечном итоге найдем нули в уравнении, которое мы составили. Это всего лишь один из многих примеров задач и моделей, где нам нужно найти нули f(x).

Широко применяя функции и их нули, мы должны научиться манипулировать различными выражениями и уравнениями, чтобы находить их нули. В этой статье мы научимся:

Знать, что представляет ноль функции.
Узнайте, как находить нули общих функций.
Определение нулей функции по ее графику.

Давайте продолжим и начнем с понимания основного определения нуля.

Что такое ноль функции?

Понимание того, что обозначают нули, может помочь нам узнать, когда находить нули функций по их выражениям, и научиться находить их по графику функции. В общем, нули функции — это значение x, когда сама функция становится нулевой .

Нули функции могут быть в разных формах — если они возвращают значение y, равное 0, мы будем считать это нулем функции.

Нули определения функции

Нули функции равны значения x, когда f(x) равно 0 . Отсюда и его название. Это означает, что когда f(x) = 0, x является нулем функции. Когда график проходит через x = a, говорят, что a является нулем функции. Следовательно, (a, 0) является нулем функции .

Функция f(x) = x + 3 имеет нуль при x = -3, поскольку f(-3) = 0.
Функция g(x) = x ² – 4 имеет два нуля: x = -4 и x = 4. Это означает, что f(-4) = 0 и f(4) = 0.
График h(x) проходит через (-5, 0), поэтому x = -5 равно ноль h(x) и h(-5) = 0,

Если задан график функции, ее действительные нули будут представлены точками пересечения x. Это имеет смысл, поскольку нули являются значениями x, когда y или f(x) равны 0.

Х-пересечения функции: ₃ , 0) и (х ₄ , 0). Это означает, что для графа, показанного выше, его действительные нули равны {x ₁, x ₂, x ₃, x ₄ } .

Однако бывают случаи, когда график не проходит через точку пересечения x. Это не означает, что у функции нет нулей, но вместо этого нули функций могут иметь сложную форму.

Как найти нули функции

Поиск нулей функции может быть таким же простым, как изолировать x в одной части уравнения, чтобы многократно манипулировать выражением, чтобы найти все нули уравнения.

В общем случае, если задана функция f(x), ее нули можно найти, установив функцию в ноль . Значения x, которые представляют заданное уравнение, являются нулями функции. Чтобы найти нули функции, найдите значения x, при которых f(x) = 0,9.0003

Как найти нули квадратичной функции?

Существует множество сложных уравнений, которые со временем можно свести к квадратным уравнениям. Вот почему на наших промежуточных занятиях по алгебре мы потратим много времени на изучение нулей квадратичных функций.

Чтобы найти нули квадратичной функции, мы приравниваем данную функцию к 0 и находим значения x, которые удовлетворяют уравнению. Вот несколько важных напоминаний при поиске нулей квадратичной функции:

Убедитесь, что квадратное уравнение имеет стандартную форму (ax ² + bx + c = 0).
По возможности множьте на множители, но не стесняйтесь использовать квадратную формулу.
Квадратичная функция может иметь не более двух нулей.

Мы узнали о различных стратегиях поиска нулей квадратичных функций в прошлом, поэтому вот руководство о том, как выбрать лучшую стратегию:

Как найти нули полиномиальной функции?

Тот же процесс применяется для полиномиальных функций – приравнять полиномиальную функцию к 0 и найти значения x, удовлетворяющие уравнению . Это руководство может помочь вам найти наилучшую стратегию при поиске нулей полиномиальных функций.

Нужен дополнительный обзор по решению полиномиальных уравнений? Не беспокойтесь, перейдите по этой ссылке здесь и освежите свои знания о решении полиномиальных уравнений.

Как найти нули рациональной функции?

Рациональные функции — это функции, которые имеют полиномиальное выражение как в числителе, так и в знаменателе. Применяя тот же принцип при нахождении нулей других функций, мы приравниваем рациональную функцию к 0,9.0003

Допустим, у нас есть рациональная функция f(x) с числителем p(x) и знаменателем q(x).

f(x) = p(x)/q(x)

Чтобы найти его ноль, приравняем рациональное выражение к нулю.

p(x)/q(x) = 0

Поскольку q(x) никогда не может быть равно нулю, мы упрощаем уравнение до p(x) = 0. Что это означает для всех рациональных функций?

При нахождении нуля рациональных функций мы приравниваем числитель к 0 и находим х .

Как найти нули других функций?

Как вы уже догадались, правило остается тем же для всевозможных функций . Получив уникальную функцию, не забудьте приравнять ее выражение к 0, чтобы найти ее нули.

Вот еще несколько функций, с которыми вы, возможно, уже столкнулись в прошлом:

Тип функции	Пример
. 0053 2 2x Узнайте здесь, как решать логарифмические уравнения.
Степенная функция	f(x) = 3x ^1/3 Здесь потренируйтесь решать уравнения, включающие степенные функции.
Exponential Function	f(x) = 2 ^{x + 1}
Trigonometric Function	f(x) = -3 sin x

The zeros from any of these functions will вернуть значения x, где функция равна нулю. Имея график этих функций, мы можем найти их действительные нули, проверив x-пересечения графика.

На приведенном выше графике показана зависимость f(x) = -3 sin x от -3π до 3π. Все точки пересечения x на графике являются нулями функции между интервалами. Следовательно, нули между данными интервалами равны: {- 3 π, -2 π , – π, 0, π, 2}.

Готовы применить то, что мы только что узнали? Давайте продолжим и попробуем решить некоторые из этих задач.

Пример 1

Функция f(x) имеет следующую таблицу значений, показанную ниже.

x	-3	-2	-1	0	1	2	3
f(x)	64	9	0	1	0	9	64

Основываясь на таблице, каковы нули f(x)?

Решение

Всегда возвращайтесь к тому факту, что нули функций — это значения x, когда значение функции равно нулю.

Мы видим, что когда x = -1, y = 0, а когда x = 1, y = 0. Следовательно, нули f(x) равны -1 и 1.

Пример 2

График f(x) показан ниже. Используя этот график, каковы нули f(x)?

Решение

График f(x) проходит через ось x в точках (-4, 0), (-1, 0), (1, 0) и (3, 0). Это x-перехваты и, следовательно, это действительные нули f (x).

Следовательно, нулей f(x) равны {-4, -1, 1, 3} .

Пример 3

Чему равны нули g(x) = –x ³ – 3x ² + x + 3?

Решение

Найдите ноль g(x), приравняв кубическое выражение к 0. и факторизовать выражение.

–х ³ + х – 3х ² + 3 = 0

-x(x ² – 1) – 3(x ² – 1) = 0

(-x-3)(x ² – 1) = 0

Применить свойство разности двух квадратов a ² – b ² = (a – b),(a + b) ко второму фактору.

(-x-3)(x – 1)(x + 1) = 0

Приравняйте каждый множитель к 0, чтобы найти x.

-x- 3 = 0

-x = 3

x = 3

x – 1 = 0

x = 1

x + 1 = 0

x = -1

Следовательно, нулей g(x) равны {-1, 1, 3}.

пример 4

Решение

Приравняйте выражение h(x) к 0, чтобы найти его нули. Это приведет к полиномиальному уравнению.

– 2x ⁴ – 2x ³ + 14x ² + 2x – 12 = 0

Разделите обе части уравнения на -2, чтобы упростить уравнение.

x ⁴ + x ³ – 7x ² – x + 6 = 0

Перечислите возможные рациональные множители выражения, используя теорему о рациональных нулях. Для нашего случая имеем p = 1 и q = 6.

Коэффициенты p	±1
Коэффициенты q	2 ±1392
Возможные нули (p/q)	± 1/6, ± 1/3, ± 1/2, ± 1 и x = -1 может удовлетворять уравнению. Это означает, что x = 1 является решением и h(x) можно переписать как -2(x – 1)(x ³ + 2x ² -5x – 6). Используйте кубическое выражение в следующем синтетическом делении и посмотрите, является ли x = -1 также решением. Следовательно, x = -1 является решением и (x + 1) является множителем h(x). Отсюда имеем h(x) = -2(x – 1)(x + 1)(x ² + х – 6). Чтобы найти два оставшихся нуля h(x), приравняйте квадратное выражение к 0.
х + 2 = 0 х = -2	х – 3 = 0 х = 3

^{0, следовательно, 1, 1, 3}.}

Пример 5

Чему равны нули g(x) = (x ⁴ -10x ² + 9)/(x ² – 4)?

Решение

Функция g(x) является рациональной функцией, поэтому, чтобы найти ее нуль, приравняйте числитель к 0.

x ⁴ -10x ² + 9 = 0 который удовлетворяет уравнению для нахождения нулей g(x).

Пусть a = x ² и сведем уравнение к квадратному уравнению.

(х ² ) ² – 10х ² + 9 = 0

a ² – 10a + 9 = 0

(a – 1)(a – 9) = 0

Приравняйте каждый множитель к 0, чтобы найти a, затем подставьте x ² обратно, чтобы найти возможные значения g (x) нули.

a – 1 =0

x ² – 1 = 0

x ² = 1

x = ± 1

a – 9 =0

x ² – 9 = 0

x ² = 9

x = ± 3

Следовательно, нули g(x) равны {-3, -1, 1, 3}.

F-Zero X (Игра) — Гигантская бомба
Обзор
F-Zero возвращается, теперь с новыми смертельными курсами!
F-Zero X — футуристическая научно-фантастическая гоночная игра, разработанная Nintendo EAD и изданная Nintendo для Nintendo 64 в Японии 14 июля 1998 г., в Северной Америке 26 октября 1998 г. и в Европе. 6 ноября 1998 года.
Продолжение гоночной игры для SNES F-Zero, F-Zero X обновляет оригинальную гоночную формулу с более быстрым темпом и полностью трехмерными трассами, позволяя создавать более уникальные трассы с холмами, штопорами, петлями, туннелями, и трубы. Кроме того, он изменяет формулу гонки, убирая ограничения на ускорение на основе круга (где ускорение теперь использует вместо этого датчик энергии транспортного средства), улучшая бой на основе столкновений (где игроки могут использовать боковые и вращательные атаки, чтобы повредить машины соперника) и убрать систему дисквалификации за круг. Вместо того, чтобы использовать обычных противников, в игре представлен полный список из 30 машин, каждая из которых имеет уникальные характеристики машины.
Наряду с традиционным режимом Гран-при (где теперь используется балльная система ранжирования, аналогичная той, что использовалась в серии Mario Kart), игра включает в себя обновленные режимы Практика и Атака на время (где можно использовать любой курс), сплит- экранный многопользовательский режим в VS Battle (одновременно участвуют до четырех игроков) и уникальный режим «Смертельная гонка» (где игроки пытаются уничтожить всех противников на специализированной трассе как можно быстрее). Игра включает в себя новый набор из 24 курсов, 18 из которых разблокированы с самого начала, а также разблокируемый процедурно-генерируемый курс.
Позже к игре было добавлено расширение в виде комплекта расширения F-Zero X, выпущенного исключительно в Японии для периферийного устройства дисковода 64DD 21 апреля 2000 года. Требуя наличия самой оригинальной игры, это расширение содержит дополнительные музыкальные треки, новые курсы, а также возможность создавать собственные машины, курсы и кубки.
Игра (без расширения) позже была переиздана в цифровом виде как название виртуальной консоли для Wii (в 2007 г.) и Wii U (в 2016-2017 гг.).
Геймплей
Grand Prix
Основной режим F-Zero X, в котором можно выбрать пять кубков (два из них должны быть разблокированы, как X Cup, кубок, заполненный случайно сгенерированными курсами). Также можно выбрать четыре сложности (Мастер, чтобы быть разблокированным). С большим количеством автомобилей на трассе (30, если быть точным), гонки становятся быстрыми и хаотичными, поскольку противоборствующие гонщики будут врезаться в машину игрока, а также в соперника-гонщика, которого игрок должен победить. Тот, кто наберет наибольшее количество очков, выигрывает кубок после пяти курсов. Как и у оригинального F-Zero, у автомобиля есть счетчик здоровья, и он потеряет одну жизнь, если затормозит (здоровье на нуле) или упадет со сцены. Также из оригинала бустер включается, как только начинается второй круг, так как его использование снимает часть здоровья автомобиля.
Атака на время
В этом режиме машина игрока и только его машина проходит определенный курс как можно быстрее.
Смертельная гонка
Цель этого режима — победить всех соперников как можно быстрее.
Versus
До четырех местных игроков могут соревноваться на любом из полей.
Машины
Наряду с четырьмя машинами из оригинальной игры (Синий сокол, Золотой лис, Дикий гусь и Огненный скат) в игре есть 26 новых машин на выбор. В отличие от предыдущей игры, где большинство противоборствующих машин являются копиями обычной машины, F-Zero X использует весь свой состав в каждой гонке. Большинство этих машин заблокированы с самого начала.
Каждая машина может быть точно настроена между ускорением и максимальной скоростью перед началом каждой гонки, и каждая машина имеет свой уникальный рейтинг, используя буквенную оценку от E (самая слабая) до A (самая сильная) в трех категориях:
Кузов , который оценивает прочность машины с точки зрения повреждений, которые она может выдержать от столкновений со стеной и конкурирующими гонщиками.
Ускорение , которое оценивает мощность ускорителя машины с точки зрения увеличения скорости и продолжительности.
Сцепление , который оценивает «сцепление» гусеницы машины с точки зрения сохранения контроля при поворотах.
Каждая машина также имеет несколько альтернативных цветовых схем.
С помощью дополнения F-Zero X Expansion Kit игроки могут создавать новые машины (используя готовые детали) и менять машины, используемые для каждого водителя в списке.
1-й ряд
Разблокирован с самого начала.
С комплектом расширения F-Zero X , игроки могут изменить Blue Falcon, Fire Stingray и White Cat на их обновленные версии «Super Falcon», «Super Stingray» и «Super Cat», каждая из которых имеет максимальные рейтинги во всех трех категориях и уникальные портреты водителей.

Machine Driver Body Boost Grip
Blue Falcon Captain Falcon B C B
Golden Fox Dr. Stewart D A D
Wild Goose Pico B B C
Fire Stingray Samurai Goroh A D B
Белая кошка Джоди Саммер C C A
Red Agazelle 7
Red Agazelle 7
Red Agazelle 7
7
. 0142
2-й ряд
Разблокируется после получения 3 отметок X.

Machine Driver Body Boost Grip
Iron Tiger Baba B D A
Deep Claw Octoman B B C
Crazy Bear Dr. Clash A B E
Great Star Mr. EAD E A D
Big Fang Bio Rex B D A
Mad Волк Билли B B C
3-й ряд
Разблокируется после получения 6 отметок X.
Машина Водитель Кузов Boost Grip
Night Thunder Silver Neelsen B A E
Twin Noritta Gomar & Shioh E A C
Wonder Wasp John Tanaka D A D
Queen Meteor Mrs. Arrow E B B
Blood Hawk Blood Falcon B A E
Astro Robin Jack Levin B D A
4th Row
Unlocked after obtaining 9 Х отметки.
Машина Водитель Кузов Буст Сцепление
Маленькая Вайверна
9 E B B
Death Anchor Zoda E A C
Wild Boar Michael Chain A C C
King Meteor Super Arrow E B B
Super Piranha Kate Alen B C B
Mighty Hurricane Роджер Бастер E B B
5-й ряд
Разблокируется после получения 12 отметок X.

Machine Driver Body Boost Grip
Space Angler Leon C C A
Mighty Typhoon Draq C А Г
Hyper Speeder Beastman C C A
Green Panther Antonio Guster A B D
Black Bull Black Shadow A E A
Sonic Phantom The Skull C A D
Circuits
The base game includes 24 courses (not including the special course used for the Death Race режим), только 18 из которых разблокированы с самого начала. Кроме того, игра включает в себя разблокируемый набор процедурно-генерируемых курсов.
Некоторые курсы имеют другие подзаголовки в японской версии.
Jack Cup
Mute City : Рисунок восемь / восемь дорог
Silence : Высокая скорость
Песочный океан : труба
Devil’s Forest : Corkscrew / Vill
Devil’s Forest : Corkscrew / Vill
9000 9000 Devil’s Forest : Corkscrew / Vill
9000 9000 9000 . Цилиндр
Портовый город : Прыжок в высоту
Кубок королевы
Сектор α : Перевернутая петля / Переворот
Красный Каньон : Многократный Прыжок / Прыжок, Прыжок
Лес Дьявола 2 : Вверх и Вниз / Вверх, Вниз
Mute City 2 : Техника / Техника
Большой Синий 820050
White Land : опасные шаги / подъемная дорога
King Cup
Огненное поле : Zig-Zag Jump
Silence 2 : Wavy Road / Wave Road
Сектор β : Double Road / Wave Road
. Сальто / Лунное сальто
Красный каньон 2 : Slim Line
Белая земля 2 : половина трубы
Морет город 3 : Прыжки с Doom / Clank, Clank
Кубок Joker
. Кубки в режиме GP на стандартной сложности (или выше).
Первая трасса, Rainbow Road, основана на трассе Rainbow Road из Mario Kart 64. Пятая трасса, Port Town 2, основана на трассе Port Town II из оригинальной F-Zero.
Rainbow Road : Психоделический опыт / Rainbow Road
Devil’s Forest 3 : Mirror Road
Space Plant : цилиндр и прыжок в высоту
Песочный океан 2 : волновый панинг
Sance Ocean 2 : волновый Panic
9999999999999999599005
Океан. : Snake Road
Big Hand : Deadly Curves / Big Hand
X-Cup
Разблокируется после того, как вы заняли первое место во всех четырех кубках в режиме GP на сложности Expert, X-Cup уникален тем, что все шесть Курсы генерируются процедурно.
Набор курсов расширения
В сочетании с набором расширения F-Zero X добавляется дополнительный набор из 12 курсов, а также возможность создавать пользовательские курсы и индивидуальные кубки.
DD-1 Cup
Silence 3 : Outside Loop
Sand Ocean 3 : Cylinder Loop
Devil’s Forest 4 : Diving
Port Town 3 : Zig-Zag Clank
Дьявольский лес 5 : X
Big Blue 3 : Япония
DD-2 Cup
Mute City 4 : Slim Half Pipe
Космос 2 : Прямой прыжок
Порт-Таун 4
: ловушка
Fire Field 2 : 180 Rolling
White Land 3 : Star
Big Foot : Big Foot
Edit Cup
Позволяет игрокам настраивать свой кубок из шести блюд как с включенными, так и с индивидуальными курсами.
No related posts.