Формула объем круга: Формула для вычисления объёма цилиндра

Элементарная математика

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) Оглавление ВВЕДЕНИЕ Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. 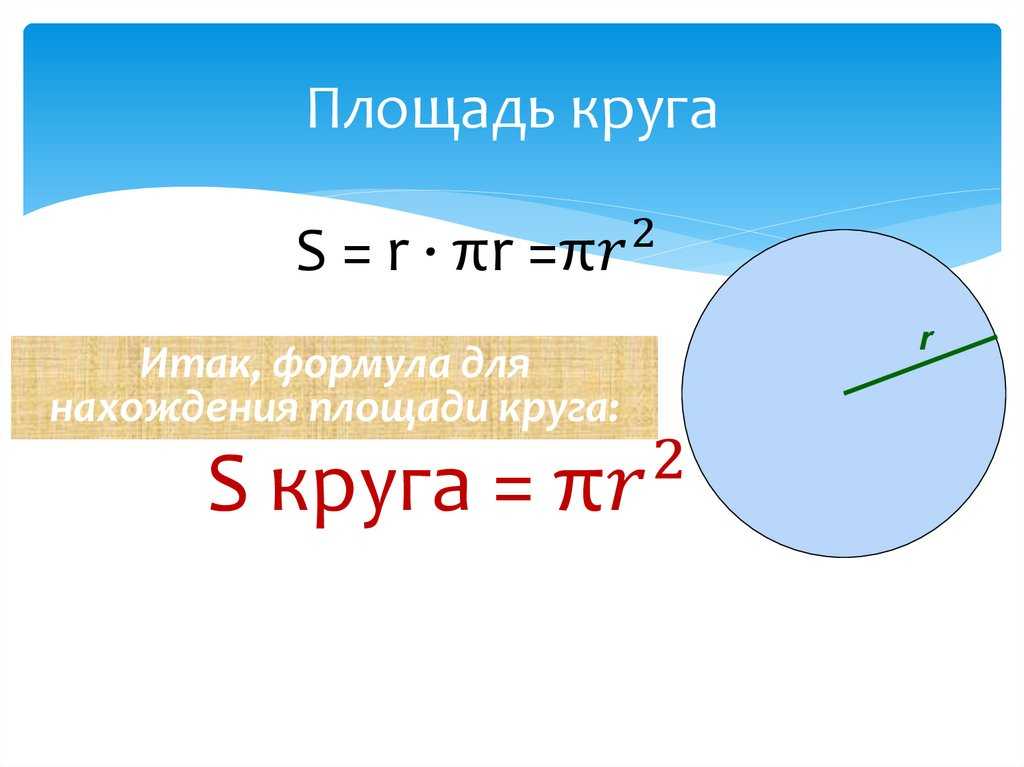Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 33. Элементарное исследование поведения функции. 34. Сложная функция. 35. Обратная функция. 36. n. 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства. Равносильные неравенства. 77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. Тригонометрические функции числового аргумента 108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 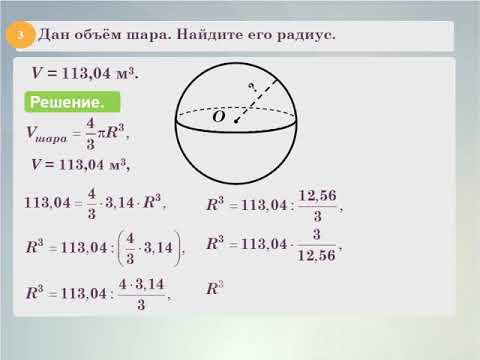121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. Функция у = arcsin (sin x). 138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. 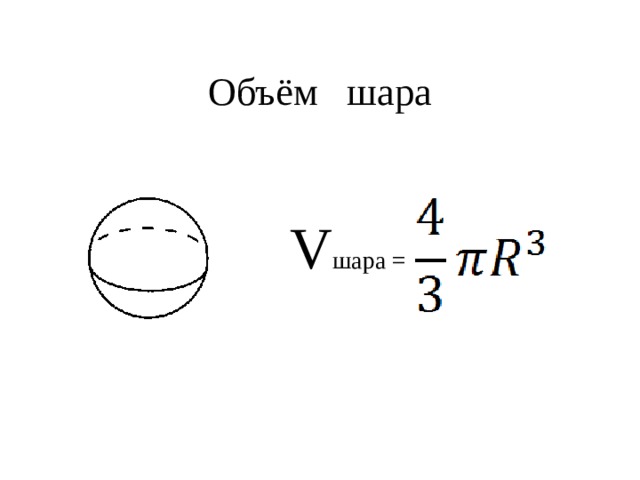§ 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. 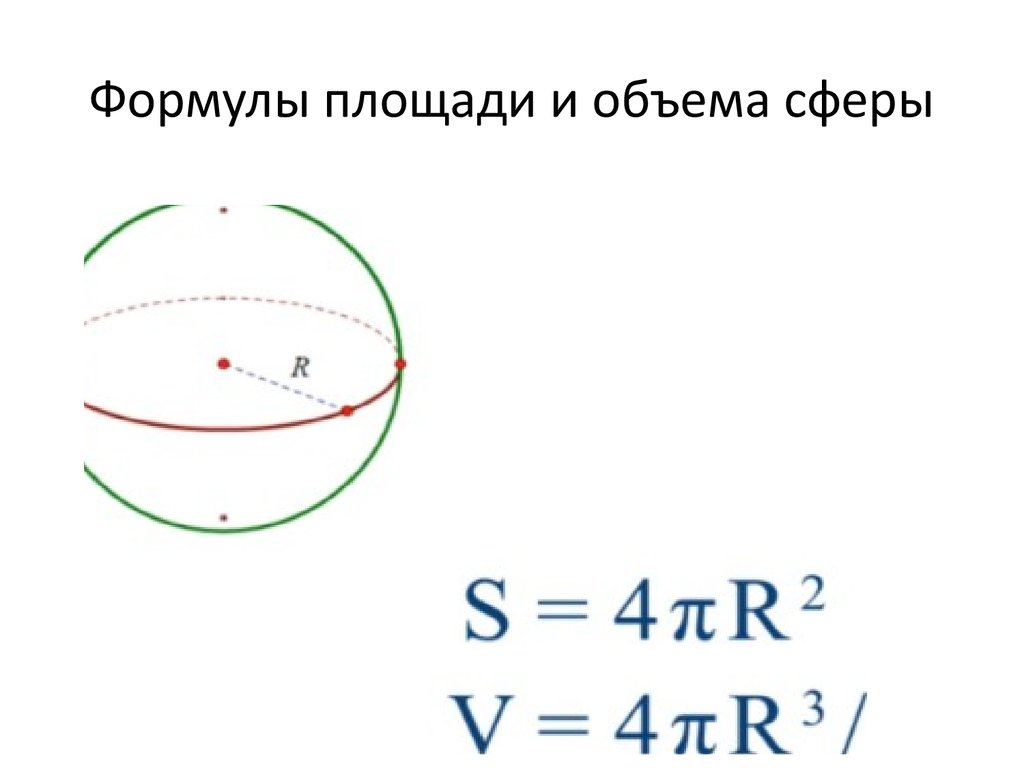Теорема Пифагора. 218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения

весы Архимеда / Этюды // Математические этюды

Объём шара: весы Архимеда / Этюды // Математические этюды

Математические этюды

К списку

Нахож­де­ние соот­ноше­ния между объёмами шара и опи­сан­ного около него цилин­дра Архимед (Архимед Сира­куз­ский, др.-греч. Ἀρχιμήδης, лат. Archimedes, 287 до н. э. — 212 до н. э.) счи­тал своим глав­нейшим матема­ти­че­ским открытием. Не слу­чайно на надгро­бии Архимеда были изоб­ражены шар и цилиндр.

Архимед Досифея при­вет­ствует! Неза­долго перед сим я препро­во­дил к тебе неко­то­рые пред­меты моих иcсле­до­ва­ний, вме­сте с най­ден­ными мною дока­за­тельствами […] Ныне я кон­чил и другие неко­то­рые мне на мысль при­шед­шие тео­ремы, из коих достопри­ме­ча­тель­нейшие суть сии: […] Цилиндр, имеющий осно­ва­нием наи­больший круг шара, а высоту, рав­ную попе­реч­нику оного, есть полу­тор­ный шара; и его поверх­ность есть полу­тор­ная же поверх­но­сти шара.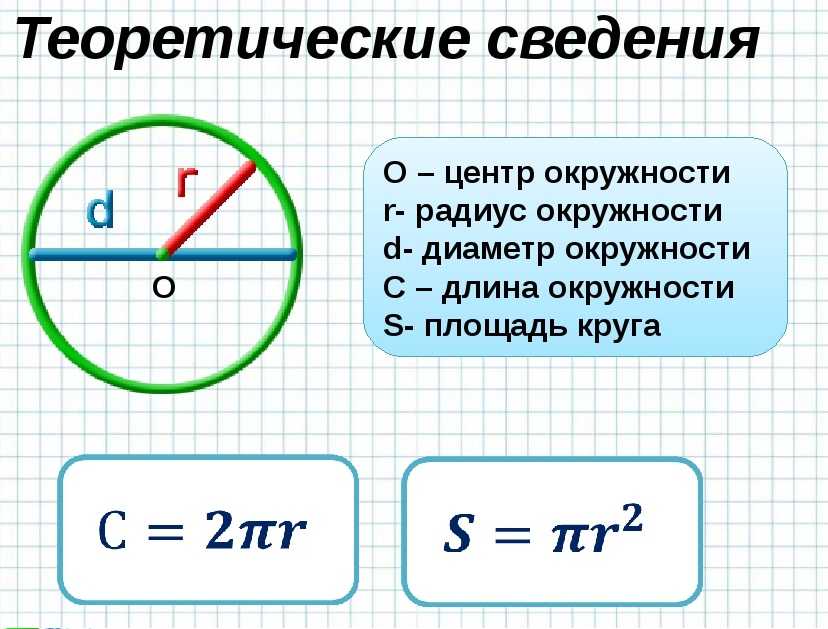 Свойства сии без сомне­ния суще­ство­вали в ска­зан­ных фигу­рах, но доселе не были ещё заме­чены никем из занимавшихся Геомет­рией…

Архимед. О шаре и цилин­дре.

Когда я был кве­сто­ром, я отыс­кал в Сира­ку­зах его <Архимеда> могилу, со всех сто­рон заросшую тер­нов­ни­ком, словно изго­ро­дью, потому что сира­ку­зяне совсем забыли о ней, словно ее и нет. Я знал несколько стиш­ков, сочи­нен­ных для его надгроб­ного памят­ника, где упоми­на­ется, что на вершине его постав­лены шар и цилиндр. И вот, осмат­ри­вая мест­ность близ Акрагант­ских ворот, где очень много гроб­ниц и могил, я при­ме­тил маленькую колонну, чуть–чуть воз­вышавшуюся из заро­с­лей, на кото­рой были очер­та­ния шара и цилин­дра. Тот­час я ска­зал сира­ку­зя­нам — со мной были пер­вейшие граж­дане города, — что этого–то, видимо, я и ищу. Они послали коса­рей и рас­чи­стили место. Когда доступ к нему открылся, мы подошли к осно­ва­нию памят­ника. Там была и надпись, но концы её стро­чек стёр­лись от времени почти напо­ло­вину. Вот до какой степени слав­нейший, а некогда и учё­нейший гре­че­ский город поза­был памят­ник умнейшему из своих граж­дан: пона­до­бился чело­век из Арпина, чтобы напом­нить о нём.

Цице­рон о могиле Архимеда в сочи­не­нии «Туску­лан­ские беседы». Пере­вод М. Гаспа­рова.

(Цит. по: Цице­рон Марк Тул­лий. Избран­ные сочи­не­ния. Пер. с латин. — М. : Худ. лит., 1975. — С. 342)

Рас­смот­рим рычаж­ные весы. Пред­ста­вим, что с одной сто­роны весов рас­по­ложен цилиндр, высо­той рав­ной ради­усу осно­ва­ния, а с дру­гой сто­роны, на том же рас­сто­я­нии от под­веса что и цилиндр, — конус и поло­вина шара. При­чём такие, что радиус осно­ва­ния конуса и высота равны ради­усу цилин­дра, радиус шара равен ради­усу цилин­дра.

Нач­нём послойно наби­рать эти фигуры так, чтобы высоты слоёв каж­дой из трёх фигур были оди­на­ковы. Ока­зы­ва­ется, при ука­зан­ных соот­ноше­ниях рычаж­ные весы все­гда будут при­хо­дить в рав­но­ве­сие. Когда фигуры будут пол­но­стью собраны, весы будут нахо­диться в рав­но­ве­сии. Зна­чит, объём цилин­дра равен сумме объёмов конуса и поло­вины шара, если ради­усы и высоты всех трёх фигур совпа­дают.

Уди­ви­тельно: с одной сто­роны весов про­стая фигура — прямой круго­вой цилиндр, с дру­гой сто­роны одна из фигур тоже отно­си­тельно про­стая — прямой круго­вой конус, а урав­но­веши­вающая весы фигура — шар.

Дело в том, что если про­ве­сти плос­кость, парал­лель­ную осно­ва­ниям фигур, то площадь круга, полу­чающегося в сече­нии цилин­дра равна сумме площа­дей кругов, полу­чающихся в сече­нии рас­смат­ри­ва­емых конуса и шара. Несложно (в наше время!) прямым вычис­ле­нием про­ве­рить, что равен­ство площа­дей будет выпол­няться для любого положе­ния секущей плос­ко­сти.

Из ука­зан­ного равен­ства площа­дей, как сей­час гово­рят, по принципу Кава­льери (итал. Bonaventura Francesco Cavalieri, лат. Cavalerius, 1598—1647), сле­дует равен­ство объёмов.

Отноше­ние объёмов цилин­дра и конуса было известно до Архимеда:

Таким обра­зом и Евдокс <Евдокс Книд­ский, др. -греч. Εὔδοξος, лат. Eudoxus, ок. 408 до н. э. — ок. 355 до н. э.> соб­ствен­ным рас­суж­де­нием открыл многое о телах, напри­мер: что вся­кая пирамида есть треть призмы, имеющей с пирами­дой то же осно­ва­ние и ту же высоту; что вся­кий конус есть треть цилин­дра, имеющего с кону­сом то же осно­ва­ние и ту же высоту.

Архимед. О шаре и цилин­дре.

Рав­но­ве­сие весов даёт возмож­ность выра­зить объём поло­вины шара через объём цилин­дра. Вычи­тая из объёма цилин­дра треть — объём конуса с теми же осно­ва­нием и высо­той, что и у цилин­дра, — полу­чаем, что объём поло­вины шара равен $2/3$ от объёма цилин­дра.

Тем самым, уста­нов­лено соот­ноше­ние, опи­сан­ное у Архимеда: объём шара, равен $2/3$ объёма опи­сан­ного около шара цилин­дра. Инте­ресно, что, как заме­тил Архимед, в том же отноше­нии нахо­дятся и площади их поверх­но­стей.

Из соот­ноше­ния Архимеда можно выве­сти явную формулу для объёма шара. В слу­чае цилин­дра, опи­сан­ного вокруг шара ради­уса $R$, площадь его осно­ва­ния равна $\pi R^2$, а высота равна $2R$.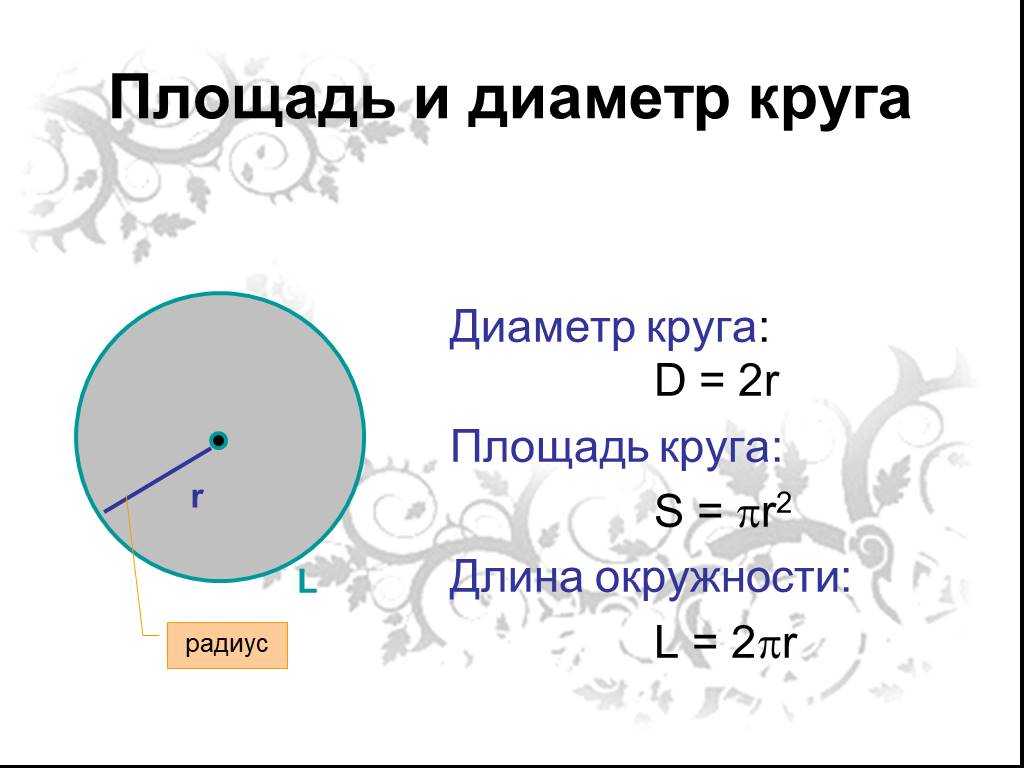 3$.

Впро­чем, остав­ляя всё сие на уваже­ние людей, могущих судить о тако­вых вещах, я с моей сто­роны желал бы выдать в свет сие сочи­не­ние при жизни ещё Конона <Конон Самос­ский, др.-греч. Κόνων, лат. Conon, ок. 280 до н.э. — ок. 220 до н. э.>, кото­рый весьма мог вник­нуть в оное, и назна­чить всему насто­ящую цену. Как бы то ни было, полагая что и другим занимающимся матема­ти­че­скими нау­ками не бес­по­лезно будет знать мои тео­ремы, я посылаю оные к тебе с над­лежащими дока­за­тельствами, дабы знающие сей пред­мет, рас­смот­рели оные.

Архимед. О шаре и цилин­дре.

Лите­ра­тура

Архимед. О шаре и цилин­дре. Книга I // Архимеда две книги о шаре и цилин­дре, изме­ре­ние круга и леммы / Пер. с греч. и лат. Ф. Пет­ру­шев­ского. — СПб., 1823.

Архимед. Сочи­не­ния / Пере­вод, вступи­тель­ная ста­тья и коммен­та­рии И. Н. Весе­лов­ского. — М. : ГИФМЛ, 1962.

Цице­рон Марк Тулий. Туску­лан­ские беседы // Цице­рон Марк Тул­лий. Избран­ные сочи­не­ния / Пер. с лат. М. Гаспа­рова. — М. : Художе­ствен­ная лите­ра­тура, 1975. — С. 342.

Смотри также

⁠⁠Взвеши­ва­ние цилин­дра и шара.

Другие этюды раздела «Площади и объёмы»

  Площади фигурОбновлено  Формула ПикаТеорема Пифагора: доказательство ЕвклидаОбновлено  Теорема Пифагора: интерактивная головоломка  Объём шара  Площадь на сфере: сферы, шапочки, кольца  Теорема о косточке  Сапог Шварца

Математические этюды

Нахождение объема и площади поверхности сферы

Результаты обучения

• Нахождение объема и площади поверхности сферы

Сфера имеет форму баскетбольного мяча, похожую на трехмерный круг. Как и в случае с кругом, размер сферы определяется ее радиусом, то есть расстоянием от центра сферы до любой точки на ее поверхности. Ниже приведены формулы объема и площади поверхности шара.

Показать, откуда берутся эти формулы, как мы это делали для прямоугольного тела, выходит за рамки этого курса.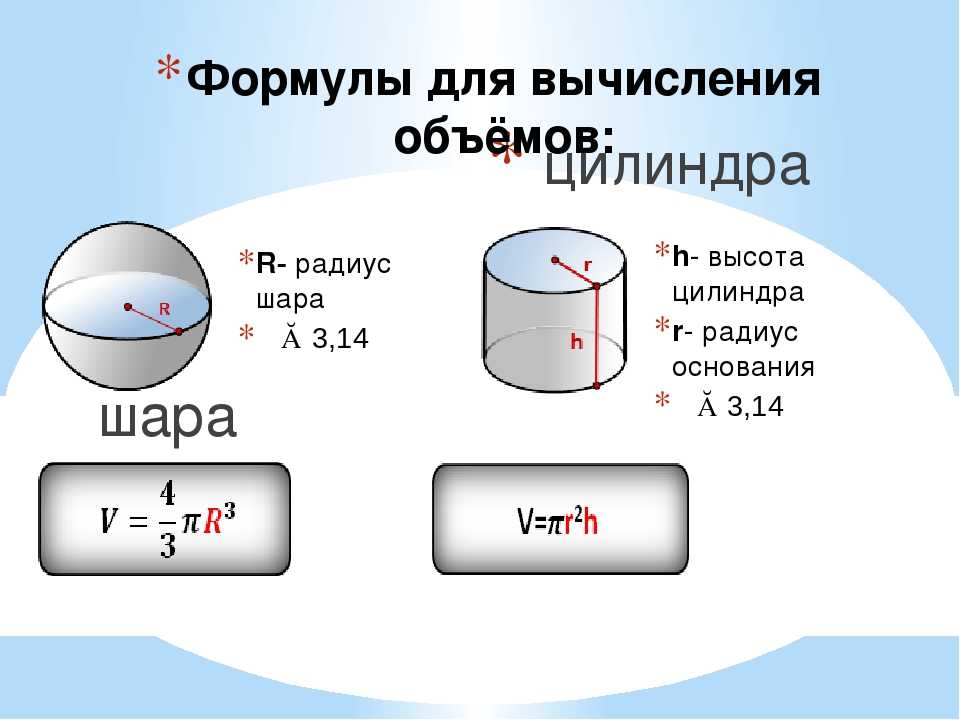 Мы аппроксимируем [латекс]\pi [/латекс] с [латекс]3,14[/латекс].

Объем и площадь поверхности сферы

Для сферы с радиусом [латекс]r\текст{:}[/латекс]

 

пример

Сфера имеет радиус [латекс]6[/латекс] дюймов . Найдите его 1. объем и 2. площадь поверхности.

Решение
Шаг 1 одинаков как для 1, так и для 2, поэтому мы покажем его только один раз.

Шаг 1. Прочтите проблему. Нарисуй рисунок и подпиши это с данной информацией.	9{3}[/латекс] [латекс]В\приблизительно 904,32\текст{куб.дюйм}[/латекс]
Шаг 6. Проверка: Дважды проверьте свои математические расчеты на калькуляторе.
Шаг 7. Ответьте на вопрос.	Объем приблизительно равен [латекс]904,32[/латекс] кубических дюймов.

2.
Шаг 2. Определите , что вы ищете.	площадь поверхности куба 9{2}[/латекс] [латекс]S\ок. 452,16[/латекс]
Шаг 6. Проверка: Дважды проверьте свои математические расчеты на калькуляторе
Шаг 7. Ответьте на вопрос.	Площадь поверхности составляет приблизительно [латекс]452,16[/латекс] квадратных дюймов.

 

попробуйте

 

пример

Земной шар имеет форму сферы с радиусом [латекс]14[/латекс] сантиметров. Найдите его 1. объем и 2. площадь поверхности. Округлите ответ до сотых.

Показать раствор

 

попробуйте

В следующем видео мы покажем пример того, как найти площадь поверхности сферы.

И в нашем финальном видео мы покажем пример того, как найти объем сферы, зная ее диаметр.

Объем сферы – формулы с выводами, примеры и диаграммы

Объем сферы – это пространство, которое она занимает в трехмерной плоскости. Это относится к объему твердого шара. Объем также является мерой емкости сферы или количества единичных кубов, которые могут в нее поместиться. Измеряется в кубических единицах, таких как м ³ , см ³ , мм ³ , фут ³ .

Давайте научимся находить объем твердого шара.

Формулы

С радиусом

Основная формула для расчета объема сферы:

Объем сферы

Теперь давайте узнаем, как вывести приведенную выше формулу.

Вывод

1. Использование интегрирования

Рассмотрим сферу, образованную несколькими тонкими круглыми дисками, расположенными друг над другом, как показано на рисунке ниже.

Получение объема сферы

Диаметры дисков постоянно меняются. Центр всех дисков лежит на одной прямой.

Теперь выберем любой диск с радиусом «x» и толщиной «dy». Диск находится на расстоянии y от оси x.

Таким образом, объем можно записать как:

Объем = Площадь круглого диска × Толщина круглого диска

Кроме того, радиус диска «x» можно выразить через вертикальный размер «y», применяя теорема Пифагора. 9{3}}$

2. Использование объема цилиндра и конуса

Как объяснил Архимед, цилиндр, конус и сфера с радиусом ‘r’ и одинаковой площадью поперечного сечения имеют свои объемы в соотношение 1:2:3.

Следовательно, соотношение между объемом шара, конуса и цилиндра равно:

Объем цилиндра = объем конуса + объем шара

Как мы знаем,

Объем цилиндра = объем конуса + объем сферы

∴Объем ( V ) шара = объем ( V ) цилиндра – объем ( V ) конуса
Как мы знаем,

V _{цилиндра 90994 8 πr 9091}

и,

V _Конус = 1/3 V _{Цилиндр} = (1/3) πr ² H
СЕЙЧАС,

V _SPEARE = V _{CYLINDE V Сфера = πr ² h – (1/3)πr ² h = (2/3)πr ² h
здесь высота цилиндра = диаметр сферы = 2r}

∴ V _Сфера = (2/3)πr ² × 2r

Объем ( V ) = (4/3) πr ³

Давайте решим пример с использованием приведенной выше формулы.

Найдите объем сферы с радиусом 6 см.

Решение:

Как известно,
Объем ( В )  = (4/3)π r ³ , here π = 22/7 = 3.141,  r  = 6 cm
∴ V = (4/3) × 3.141 × 6 ³
= 904.78 cm ³

Найдем объем шара, если радиус не задан напрямую.

Диаметр

Формула для нахождения объема сферы с использованием диаметра:

Объем сферы диаметром

Давайте решим пример с использованием приведенной выше формулы.

Найдите объем шара диаметром 10 см.

Решение:

Объем ( V ) = 1/6πd ³ , здесь π = 22/7 = 3,141, D = 10 CM 90220120 ∴ v = 10 CM 90220 ∴ ∴ . /6 × 3.141 × 10 ³
= 523. 5 cm ³

Finding the volume of a sphere when the SURFACE AREA is known

Find the volume of a sphere whose surface площадь 120 см 9{3/2}}{6\sqrt{\pi }}}$ , здесь SA = 120 см ² , π  = 22/7 = 3,141
= (120) ^3/2   ÷ ( 6 × √3,141)
= 123,60 см ³

Мы научились находить объем твердого шара. Теперь давайте выучим формулу, чтобы найти объем полого шара.

Объем полой сферы

Когда маленькая внутренняя сфера удаляется из твердой сферы, образуется сферическая полость. Полость создает вокруг себя равномерную толщину по отношению к твердой части сферы. Такая сфера является полой сферой. Полость имеет тот же центр, что и твердая сфера. Кокос чем-то похож на полую сферу, хотя это не идеальная сфера.

Теперь выведем формулу для нахождения объема полого шара.

Пусть,

Радиус внешней сферы = R

Радиус внутренней сферы = r

∴ R > r

Итак, объем такой сферы выражается как:

Объем полой сферы = Объем внешней сферы – Объем внутренней сферы

Объем внешней сферы = 4/3πR ³  

Объем внутренней сферы = 4/3πr ³  

Итак, формула приведена ниже:

Объем полой сферы

Давайте решим пример, включающий приведенную выше формулу.

No related posts.