Урок 32. объём прямоугольного параллелепипеда. единицы объёма — Математика — 5 класс
Математика
5 класс
Урок №32
Объём прямоугольного параллелепипеда. Единицы объёма
Перечень рассматриваемых вопросов:
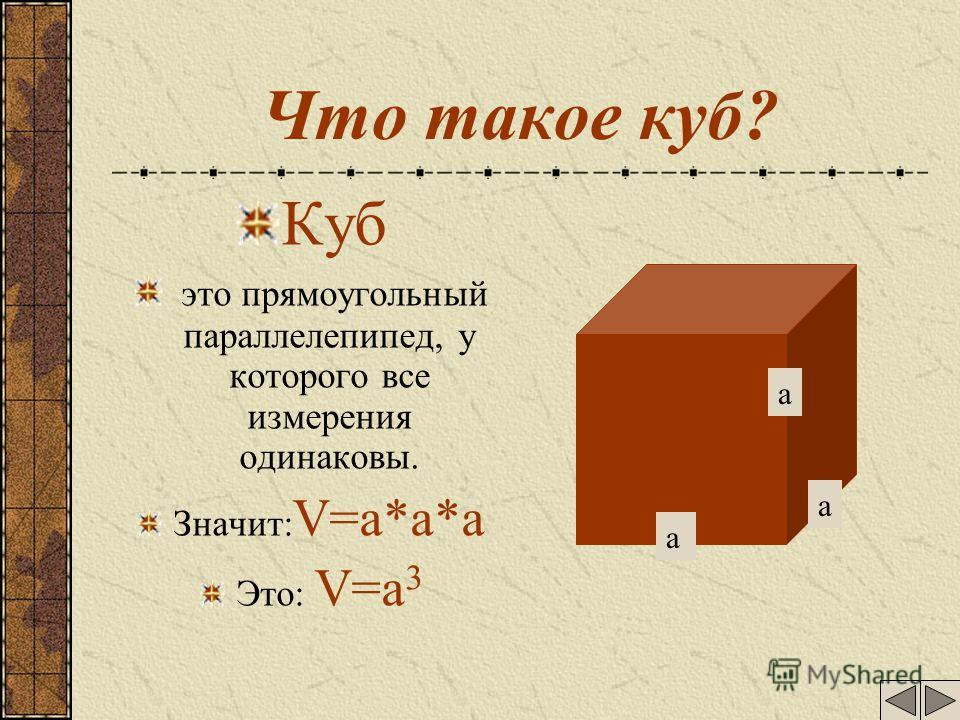
— куб;
— параллелепипед;
— элементы параллелепипеда;
— объём прямоугольного параллелепипеда, куба.
Тезаурус
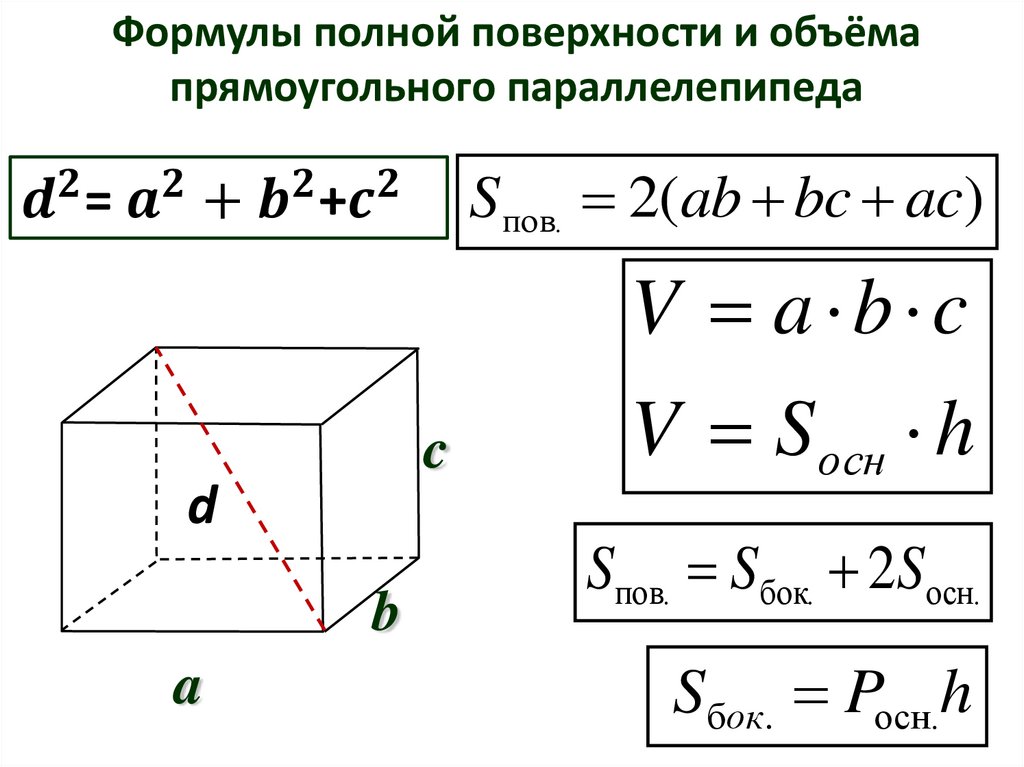
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками.
Высота, длина и ширина – это измерения прямоугольного параллелепипеда.
Единичный куб — куб, ребро которого равно линейной единице.
Обязательная литература
1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Как вы думаете, что больше занимает места– 1 кг ваты или 1 кг гвоздей? Чтобы ответить на этот вопрос, нужно знать величину, которая называется объём. В данной задаче ответ очевиден, так как мы можем представить предметы визуально. Но не всегда ответ может быть таким простым. Чаще всего нужно произвести определённые вычисления.
Сегодня мы рассмотрим объём прямоугольного параллелепипеда и научимся его находить.
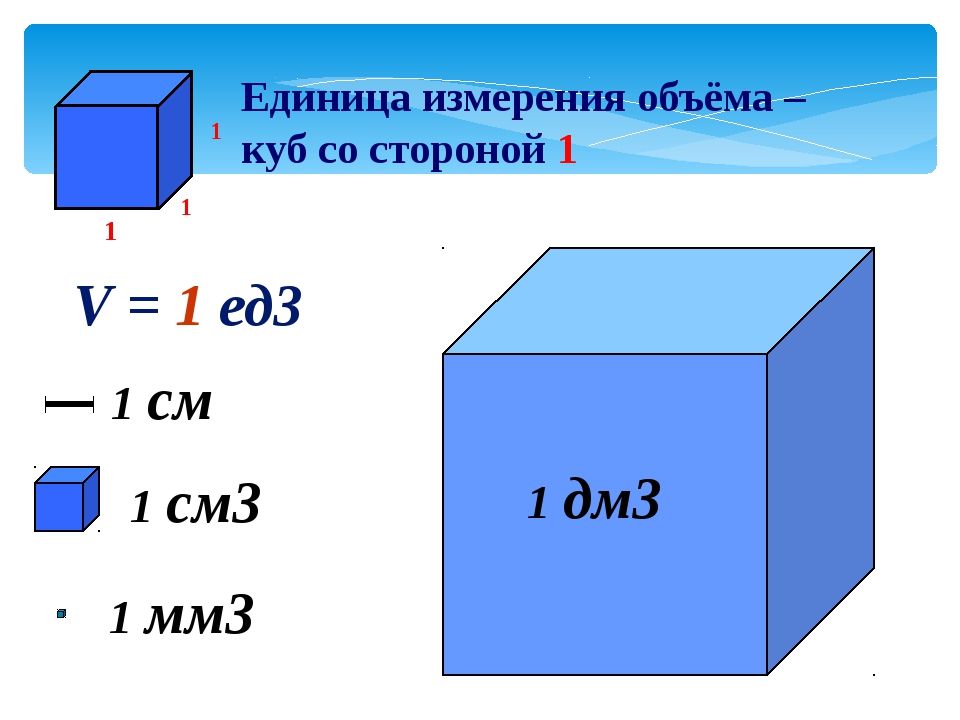
Объём можно измерить. Его измеряют в кубических миллиметрах, кубических сантиметрах, кубических метрах, литрах и т. д.
Найдём соотношение между единицами измерения объёма.
Так как 1 см = 10 дм, то 1 см3 = 1 000 мм3.
1 дм3 = 1000 см3 = 1 л
1 м3 = 1000 дм3
1 км3 = 1000000000 м3
В древности в разных частях планеты люди по-разному измеряли объём.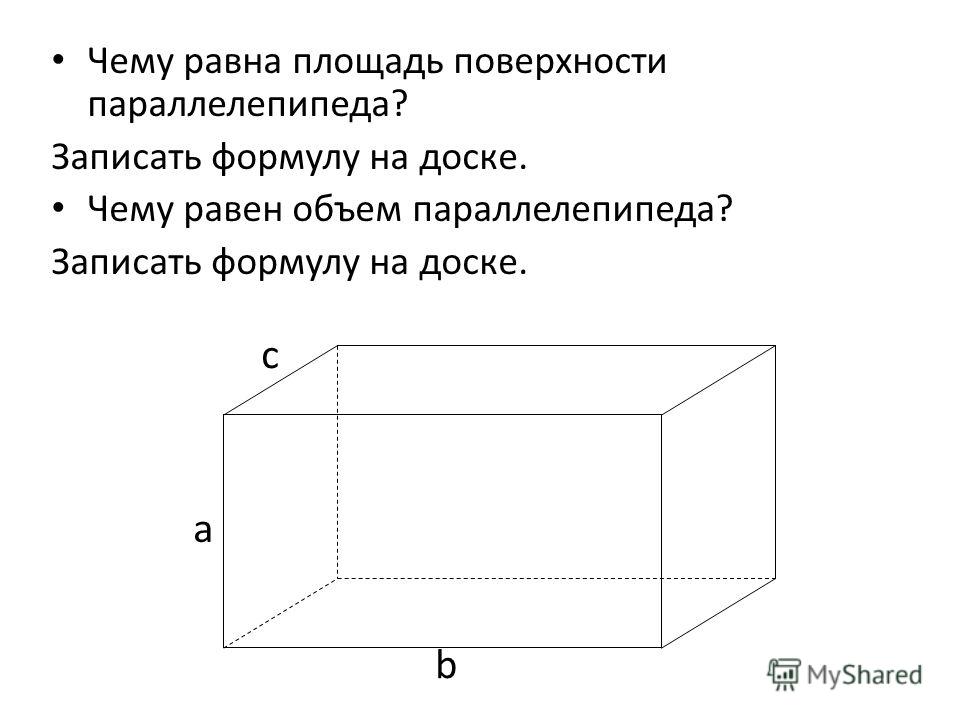 Например, в Древней Греции использовали глиняные мерные сосуды для зерна или жидкостей. Причём это были амфоры разного размера. Поэтому значение единицы объёма менялось от 2 до 26 литров.
Например, в Древней Греции использовали глиняные мерные сосуды для зерна или жидкостей. Причём это были амфоры разного размера. Поэтому значение единицы объёма менялось от 2 до 26 литров.
На Руси основной мерой жидкостей считалось ведро, в котором 10 кружек или 12 литров. Также для подсчётов объём ведра делили пополам, то есть на два полуведра, которые, в свою очередь, тоже можно было поделить пополам. Для торговли с иностранцами использовали меру объёма, называемую бочка, которая равнялась 40 вёдрам.
Дадим определение единичного куба – это куб, ребро которого равно линейной единице. Его тоже принимают за единицу объёма.
Если прямоугольный параллелепипед можно разрезать на К единичных кубов, то говорят, что его объём V равен К кубическим единицам.
Например, на рисунке объём параллелепипеда равен 24 кубическим единицам.
V = 24 куб. единиц
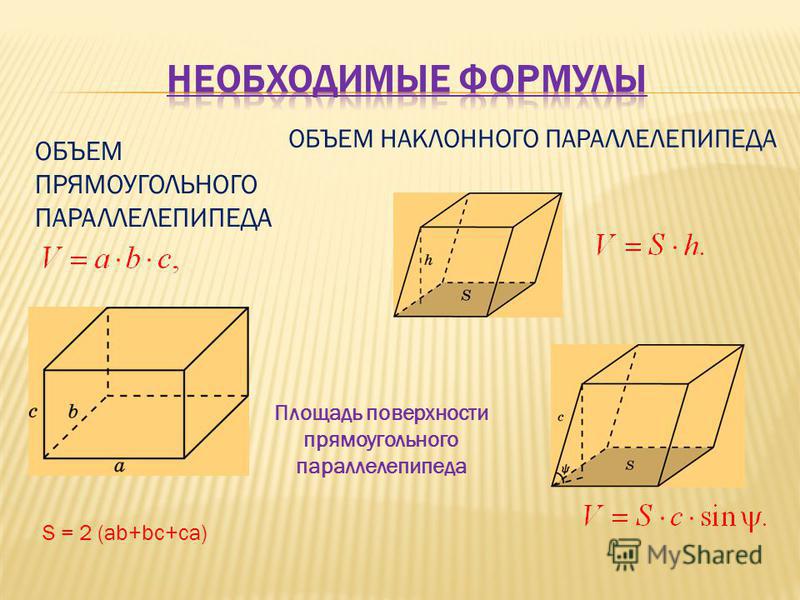
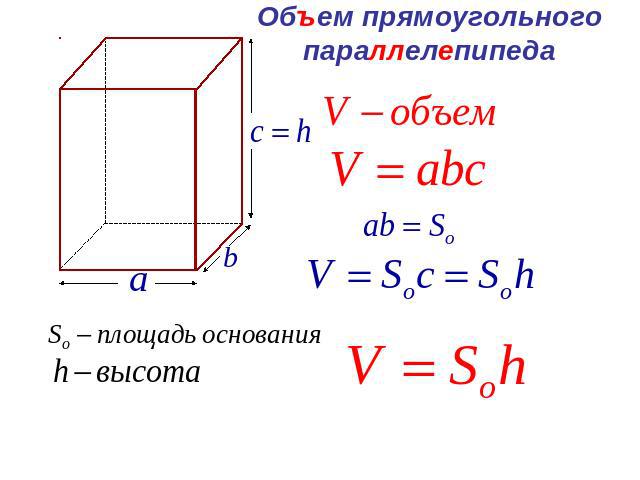
Введём формулу объёма прямоугольного параллелепипеда.
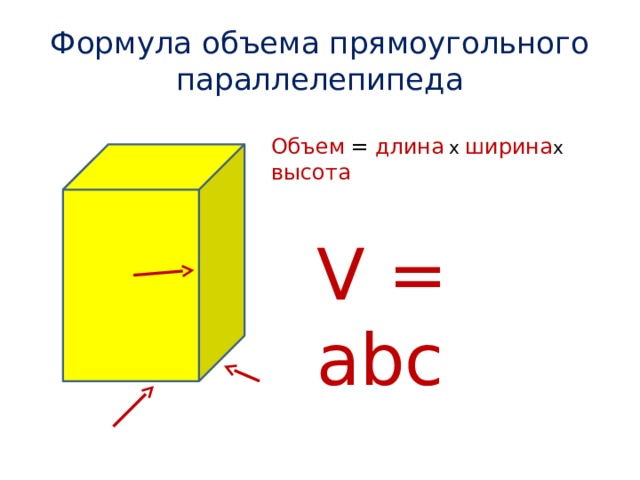
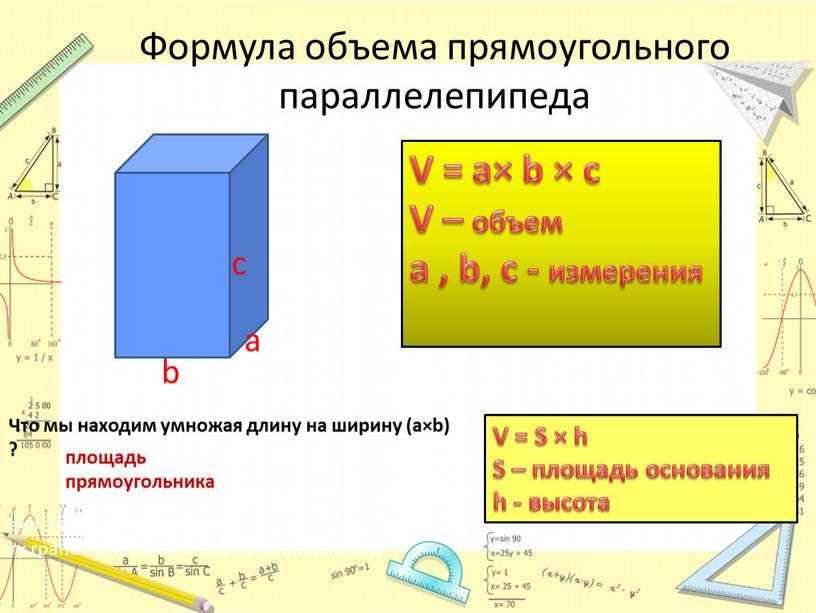
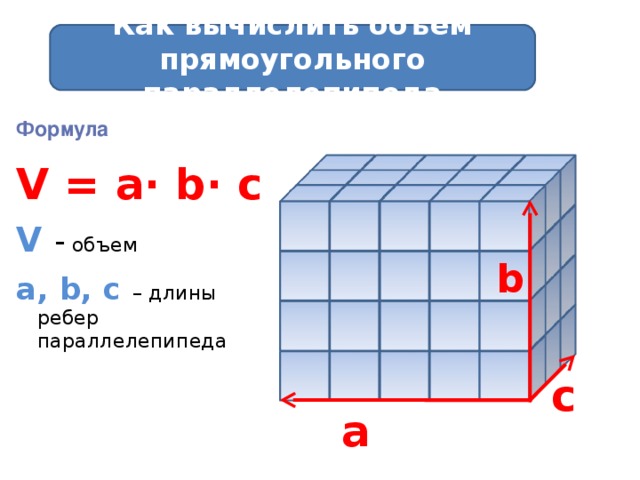
Объём прямоугольного параллелепипеда равен произведению трёх его измерений, то есть произведению длины а, ширины bи высоты c, или произведению площади основания S на высоту c.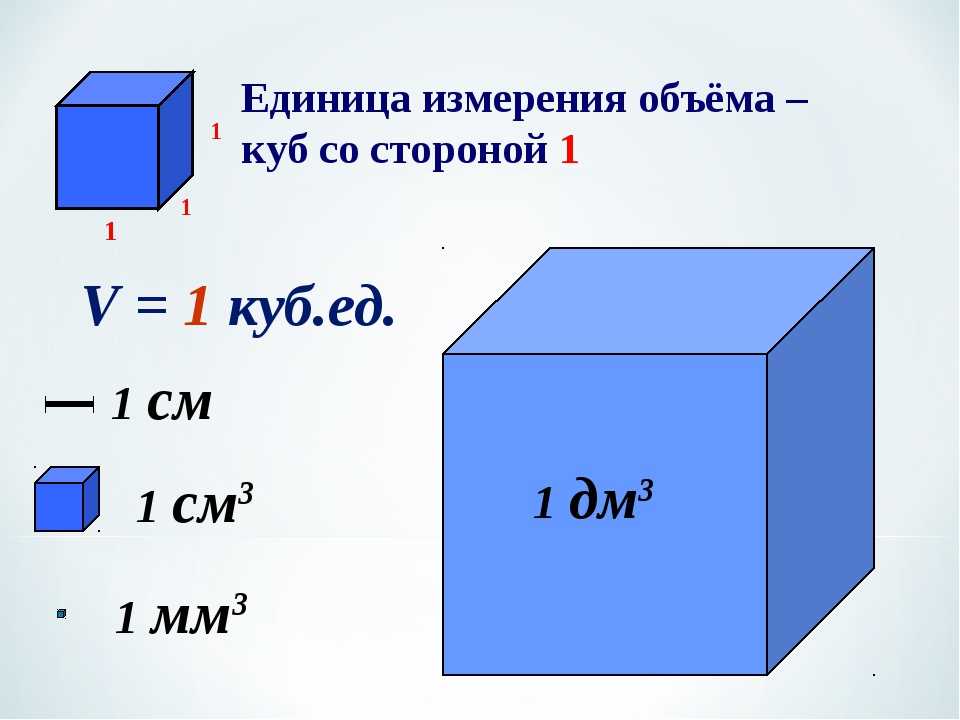
V = а · b · c = S · с
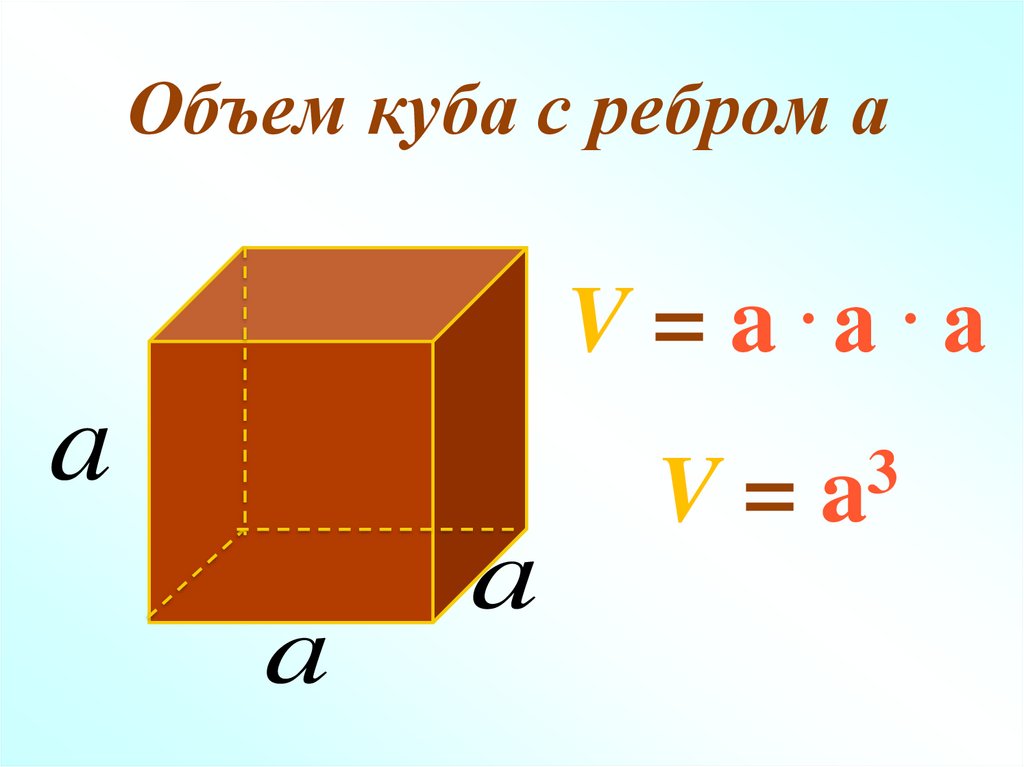
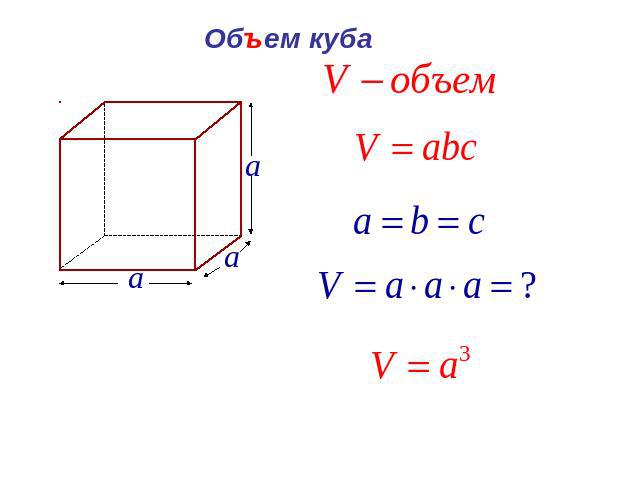
Так как куб является прямоугольным параллелепипедом, у которого все измерения равны, то его объём равен третьей степени длины его ребра а.
V = а3
Решим задачу.
Мальчик купил аквариум в форме прямоугольного параллелепипеда, который имеет площадь дна, равную 1400 см3, и высоту 6 дм. Какой объём воды он налил в аквариум, если уровень жидкости не доходил до края 5 см? Выразите ответ в кубических сантиметрах.
Чтобы решить эту задачу переведём единицы измерения длины в сантиметры.
6 дм = 60 см
Получается, что высота аквариума равна 60 см. Но по условию задачи требуется определить объём налитой жидкости, а её высота соответствует разности между высотой аквариума и уровнем жидкости, не доходящей до края:
с = 60 см – 5 см = 55 см
Получается, что высота жидкости в сосуде соответствует 55 см.
Теперь можно определить объём воды, которая налита в аквариум.
Для этого используем следующую формулу:
V = S · с = 1400 см2 · 55 см = 77000 см3
Ответ: мальчик налил в аквариум 77000 см3 воды.
Разбор решения заданий тренировочного модуля
№ 1. Чему равен объём куба, если длина его ребра равна 3 см?
Решение: для нахождения объёма куба нужно воспользоваться формулой.
V = а3 = (3 см)3 = 27 см3
Ответ: 27 см3.
№2. Как изменится объём прямоугольного параллелепипеда, если его длину увеличить в три раза. Подчеркните правильный ответ.
Решение: чтобы ответить на вопрос, нужно воспользоваться формулой для вычисления объёма прямоугольного параллелепипеда.
V = а · b · c, где а – длина прямоугольного параллелепипеда.
Если длина возрастет в три раза, то объём, соответственно, увеличится в три раза, так как, длина – это один из трёх множителей, входящих в формулу объёма прямоугольного параллелепипеда:
V = 3 · а · b · c
Ответ: объём увеличится в три раза.
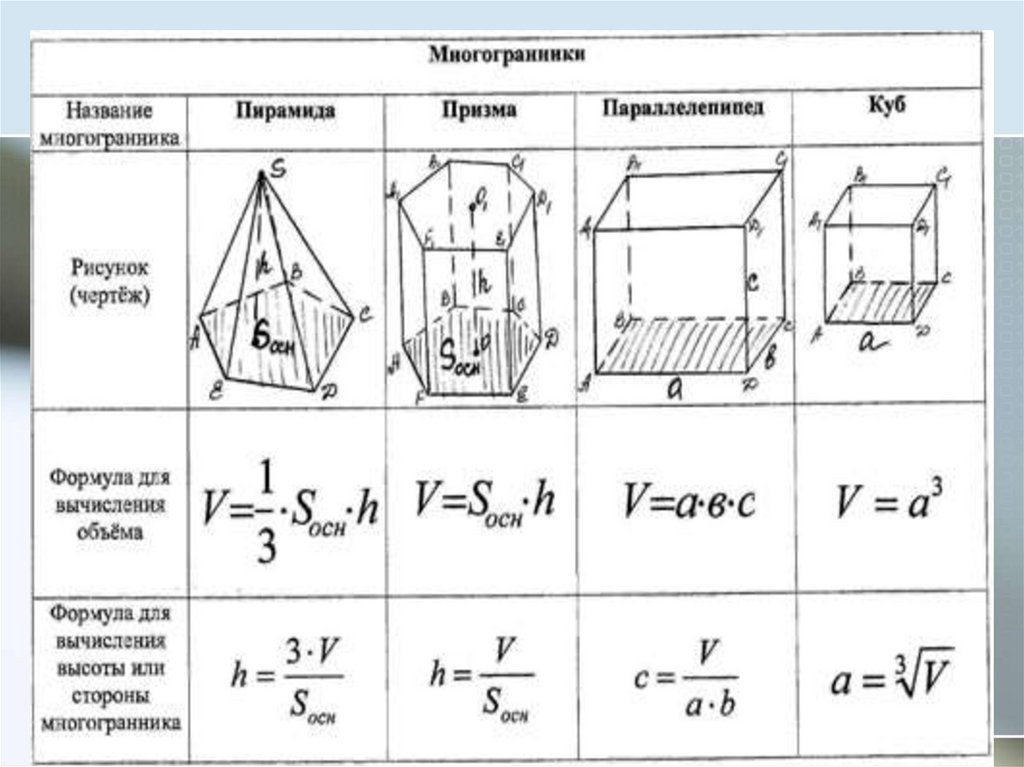
Объем геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. Навигация по странице: Формулы объема куба Формулы объема призмы Формулы объема параллелепипеда Формулы объема прямоугольного параллелепипеда Формулы объема пирамиды Формулы объема правильного тетраэдра Формулы объема цилиндра Формулы объема конуса Формулы объема шара Онлайн калькуляторы для вычисления объемов Объем кубаОбъем куба равен кубу длины его грани. Формула объема куба: V = a3 где V — объем куба, Смотрите также онлайн калькулятор для расчета объема куба Объем призмыФормула объема призмы: V = So h где V — объем призмы, Онлайн калькулятор для расчета объема призмы Формулы площади геометрических фигур для определения площади основания призмы Объем параллелепипедаОбъем параллелепипеда равен произведению площади основания на высоту. Формула объема параллелепипеда: V = So · h где V — объем параллелепипеда, Смотрите также онлайн калькулятор для расчета объема параллелепипеда Объем прямоугольного параллелепипедаОбъем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты. Формула объема прямоугольного параллелепипеда: V = a · b · h где V — объем прямоугольного параллелепипеда, Смотрите также онлайн калькулятор для расчета объема прямоугольного параллелепипеда Объем пирамидыОбъем пирамиды равен трети от произведения площади ее основания на высоту. Формула объема пирамиды:
где V — объем пирамиды, Онлайн калькулятор для расчета объема пирамиды Формулы площади геометрических фигур для определения площади основания пирамиды Объем правильного тетраэдра
где V — объем правильного тетраэдра, Смотрите также онлайн калькулятор для расчета объема правильного тетраэдра Объем цилиндраОбъем цилиндра равен произведению площади его основания на высоту. Формулы объема цилиндра:
где V — объем цилиндра, Смотрите также онлайн калькулятор для расчета объема цилиндра Объем конусаОбъем конуса равен трети от произведению площади его основания на высоту. Формулы объема конуса:
где V — объем конуса, Смотрите также онлайн калькулятор для расчета объема конуса Объем шараОбъем шара равен четырем третьим от его радиуса в кубе помноженного на число пи. Формула объема шара:
где V — объем шара, Смотрите также онлайн калькулятор для расчета объема шара Формулы по геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Формулы площади геометрических фигур Формулы периметра геометрических фигур Формулы объема геометрических фигур Формулы площади поверхности геометрических фигур Все таблицы и формулы Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! |
Объем прямоугольного параллелепипеда / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Объем прямоугольного параллелепипеда
Каждое из рассматриваемых нами тел имеет объём, который можно измерить с помощью выбранной единицы измерения объёмов. За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Такой куб называют единичным (смотри рисунок ниже).
За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Такой куб называют единичным (смотри рисунок ниже).
Единицы измерения объема:
| Ребро куба | Название объема куба | Запись объема |
| 1 мм | кубический миллиметр | 1 мм3 |
| 1 см | кубический сантиметр | 1 см3 |
| 1 дм | кубический дециметр | 1 дм3 |
| 1 м | кубический метр | 1 м3 |
| 1 км | кубический километр | 1 км3 |
При измерении объемов жидкостей или газов 1 дм3 называют литром, и записывают так: 1 л = 1 дм3.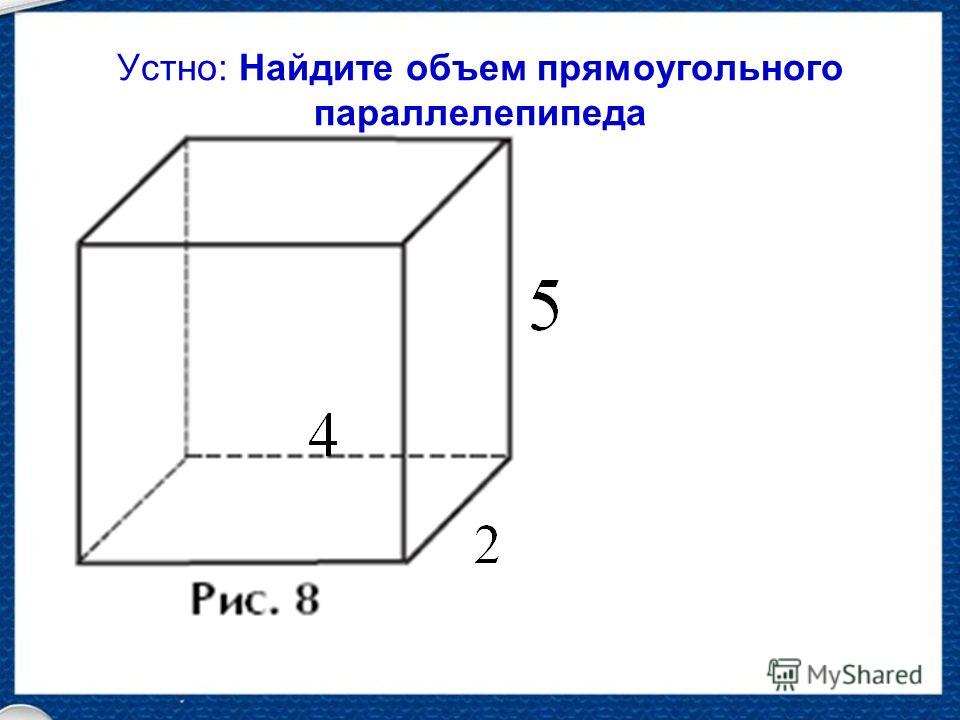
Обозначают объем буквой , т.е. если нам сказано, что объем фигуры равен 24 см3, то это можно записать так: = 24 см3.
| Измерить объем фигуры — значит подсчитать, сколько единичных кубов в ней помещается. |
Свойства объемов
1) Равные фигуры имеют равные объемы.
2) Объем фигуры равен сумме объемов фигур, из которых она состоит.
Формула для вычисления объема прямоугольного параллелепипеда
| Объем прямоугольного параллелепипеда равен произведению трех его измерений: длины, ширины и высоты. |
Если — длина параллелепипеда, — ширина параллелепипеда, — высота параллелепипеда, то объем такого параллелепипеда будет выражаться формулой: .
Пример:
Найдем объем параллелепипеда с ребрами 5 см, 2 см и 8 см:
= 528 = 80 (см3).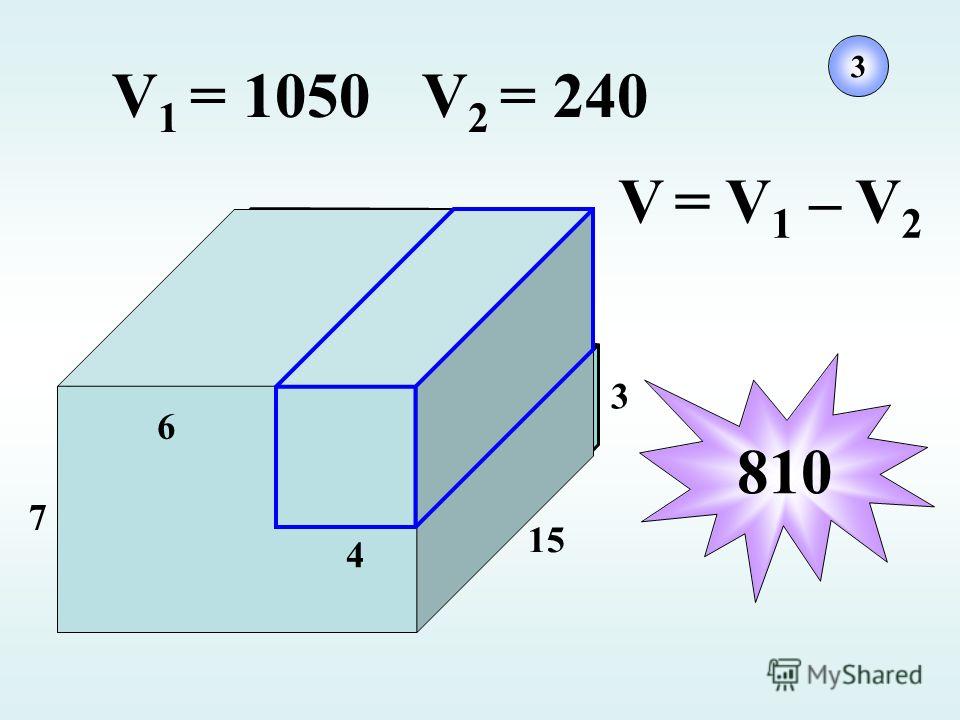
Связь объема параллелепипеда с площадью его основания
Если — длина прямоугольного параллелепипеда, — его ширина, то их произведение равно площади основания рассматриваемого параллелепипеда, т.к. основанием прямоугольного параллелепипеда является прямоугольник, т.е. (смотри рисунок ниже).
Если высоту данного прямоугольного параллелепипеда обозначить буквой , тогда объем данного параллелепипеда будет равен , откуда, учитывая то, что , получим: .
| Объем прямоугольного параллелепипеда равен произведению площади основания на высоту. |
Пример:
Найдем объем прямоугольного параллелепипеда, площадь основания которого равна 20 см
= 207 = 140 (см3).
Формула для вычисления объема куба
У куба все ребра равны, т.е. длина, ширина и высота совпадают, тогда, если ребро куба , его объем будет вычисляться по формуле: .
Пример:
Найдем объем куба с ребром 3 дм:
= 33 = 333 = 27 (дм3).
Связь между метрическими единицами объема
1 м3 = 1 000 дм3 = 103 дм3
1 дм3 = 1 000 см3 = 103 см3
1 см3 = 1 000 мм3 = 103 мм3
1 км3 = 1 000 м1 000 м1 000 = 109 м3.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Куб. Площадь поверхности куба
Куб.
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 828, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 844, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 865, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1099, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1646, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1789, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 606, Мерзляк, Полонский, Якир, Учебник
Номер 636, Мерзляк, Полонский, Якир, Учебник
Номер 996, Мерзляк, Полонский, Якир, Учебник
Номер 7, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 1, Мерзляк, Полонский, Якир, Учебник
Задание 156, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 495, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 782, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 833, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 834, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1036, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1041, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1413, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1493, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 230, Мерзляк, Полонский, Якир, Учебник
Номер 757, Мерзляк, Полонский, Якир, Учебник
Таблицы и формулы 2 — Познавательная математика
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба
V =
a
3
где
V
— объем куба,
a
— длина грани куба.
Смотрите также онлайн калькулятор для расчета объема куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы
V =
So h
где
V
— объем призмы,
So
— площадь основания призмы,
h
— высота призмы.
- Смотрите также
- онлайн калькулятор для расчета объема призмы.

- формулы площади геометрических фигур для определения площади основания призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда
V =
So · h
где
V
— объем параллелепипеда,
So
— площадь основания,
h
— длина высоты.
Смотрите также онлайн калькулятор для расчета объема параллелепипеда.
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда
V =
a · b · h
где
V
— объем прямоугольного параллелепипеда,
a
— длина,
b
— ширина,
h
— высота.
Смотрите также онлайн калькулятор для расчета объема прямоугольного параллелепипеда.
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды
So · hV = 1 3
где
V
— объем пирамиды,
So
— площадь основания пирамиды,
h
— длина высоты пирамиды.
- Смотрите также:
- онлайн калькулятор для расчета объема пирамиды,
- формулы площади геометрических фигур для определения площади основания пирамиды.
Объем правильного тетраэдра
Формула объема правильного тетраэдра
aV = 12
где
V
— объем правильного тетраэдра,
a
— длина ребра правильного тетраэдра.
Смотрите также онлайн калькулятор для расчета объема правильного тетраэдра.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
- Формулы объема цилиндра
- V =
π R
2h
- V =
So h
где
V
— объем цилиндра,
So
— площадь основания цилиндра,
R
— радиус цилиндра,
h
— высота цилиндра,
π = 3.141592
.
Смотрите также онлайн калькулятор для расчета Объем цилиндра.
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса
π R h So hV = 1 3 V = 1 3
где
V
— объем конуса,
So
— площадь основания конуса,
R
— радиус основания конуса,
h
— высота конуса,
π = 3.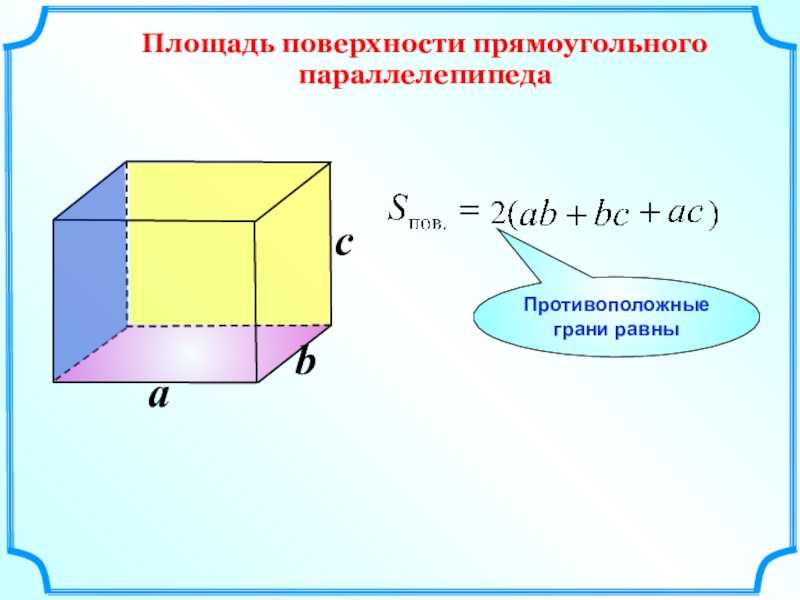 141592
141592
.
Смотрите также онлайн калькулятор для расчета объема конуса.
Объем шара
Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи.
Формула объема шара
π RV = 4 3
где
V
— объем шара,
R
— радиус шара,
π = 3.141592
.
Смотрите также онлайн калькулятор для расчета объема шара.
Площадь куба
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
Формула площади куба
S = 6
a
2
где
S
— площадь куба,
a
— длина грани куба.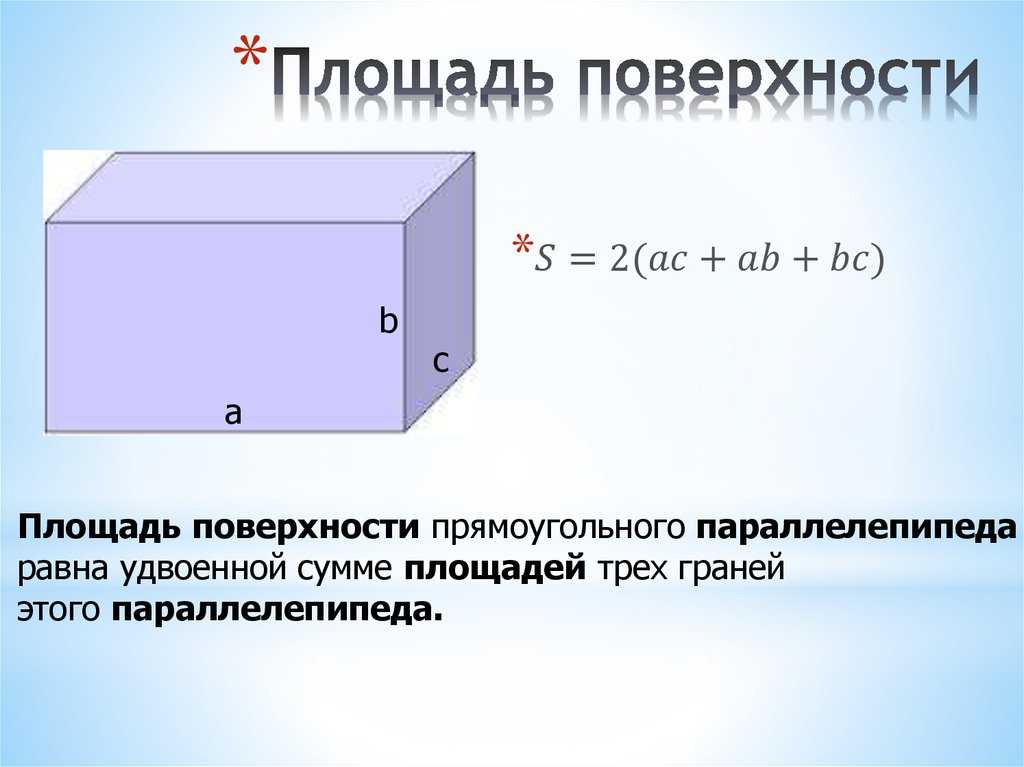
Смотрите также онлайн калькулятор для расчета площади куба.
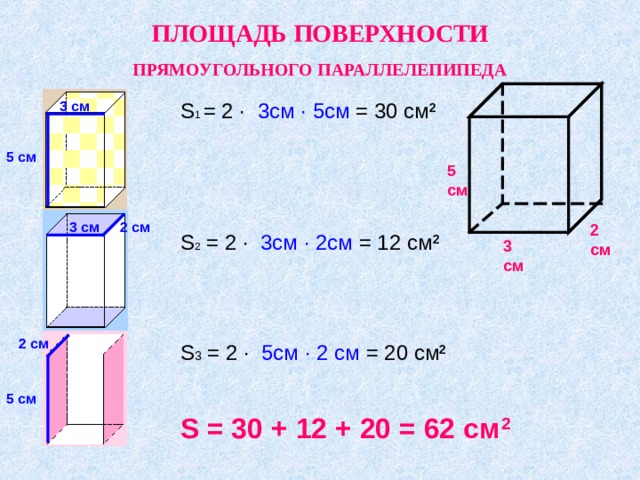
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда
S = 2(
a · b
+
a · h
+
b · h
)
где
S
— площадь прямоугольного параллелепипеда,
a
— длина,
b
— ширина,
h
— высота.
Смотрите также онлайн калькулятор для расчета площади прямоугольного параллелепипеда.
Площадь цилиндра
Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
Формула для вычисления площади боковой поверхности цилиндра
S = 2
π R h
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.
Формула для вычисления площади полной поверхности цилиндра
S = 2
π R h
+ 2
π R
2 = 2
π R
(
R
+
h
)
где
S
— площадь,
R
— радиус цилиндра,
h
— высота цилиндра,
π = 3.141592
.
Смотрите также онлайн калькулятор для расчета площади цилиндра.
Площадь конуса
Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число
π
.
Формула площади боковой поверхности конуса:
S =
π R l
Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.
Формула площади полной поверхности конуса:
S =
π R
2 +
π R l
=
π R
(
R
+
l
)
где
S
— площадь,
R
— радиус основания конуса,
l
— образующая конуса,
π = 3.141592
.
Смотрите также онлайн калькулятор для расчета площади конуса.
Площадь шара
Формулы площади шара
где
S
— площадь шара,
R
— радиус шара,
D
— диаметр шара,
π = 3.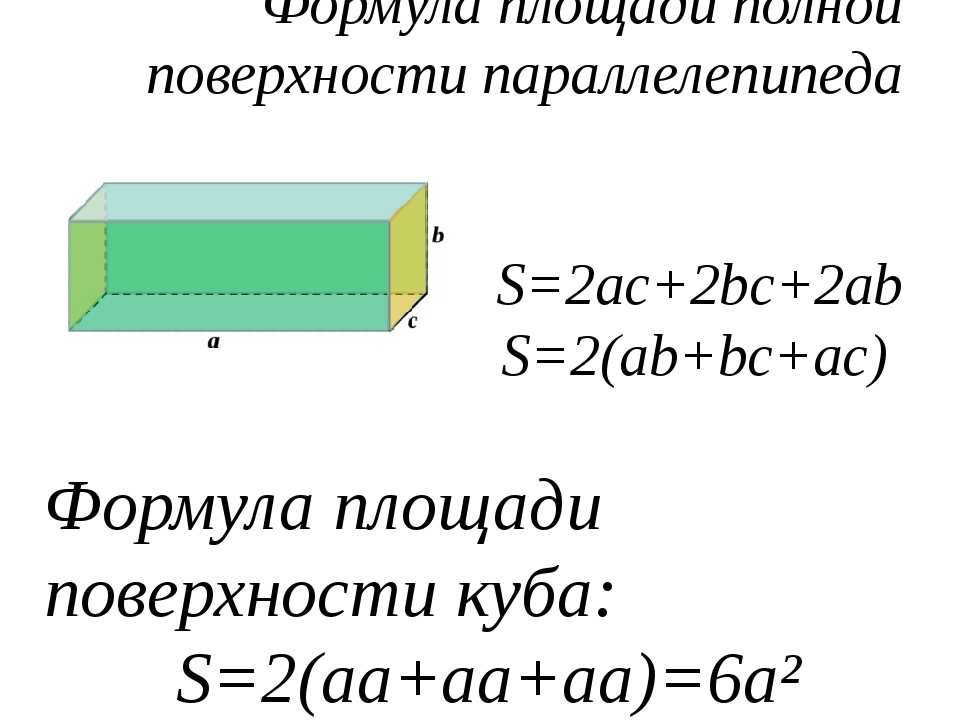 141592
141592
.
Смотрите также онлайн калькулятор для расчета площади шара.
Формулы объема фигур для школьников и студентов
Объем фигуры — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
- объём куба
- объём призмы
- объём параллелепипеда
- объём прямоугольного параллелепипеда
- объём пирамиды
- объём цилиндра
- объём конуса
- объём шара
Объём куба
Куб — правильный многогранник, каждая грань которого представляет собой квадрат.
Объём куба равен кубу длины его грани.
V=a3 ,
где V — объем куба,
a — длина грани куба.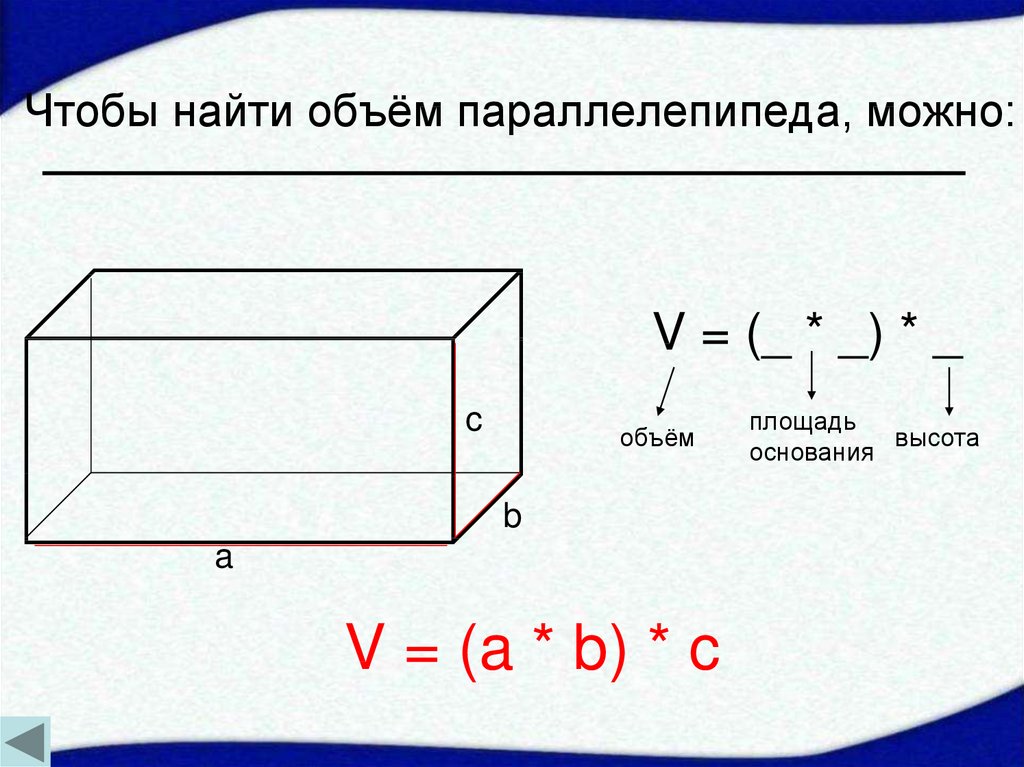
Объём призмы
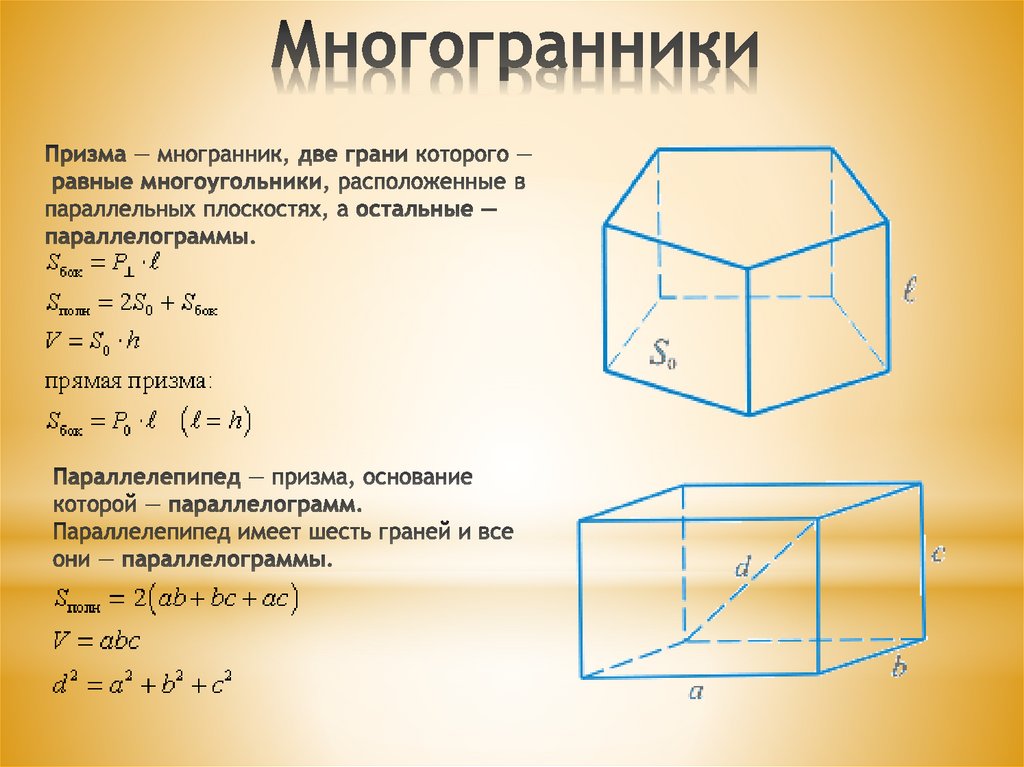
Призма — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.
Объем призмы равен произведению площади основания призмы, на высоту.
Если в основании:
- треугольник, то находите площадь треугольника,
- квадрат, то — квадрата,
- произвольная фигура, то найдите площадь произвольной фигуры.
V=Sо·h ,
где V — объем призмы,
Sо — площадь основания призмы,
h — высота призмы — расстояние между её основаниями. Для прямой призмы, у которой все рёбра перпендикулярны основаниям — это любое из рёбер.
Объём параллелепипеда
Параллелепипед — многогранник, у которого шесть граней и каждая из них параллелограмм.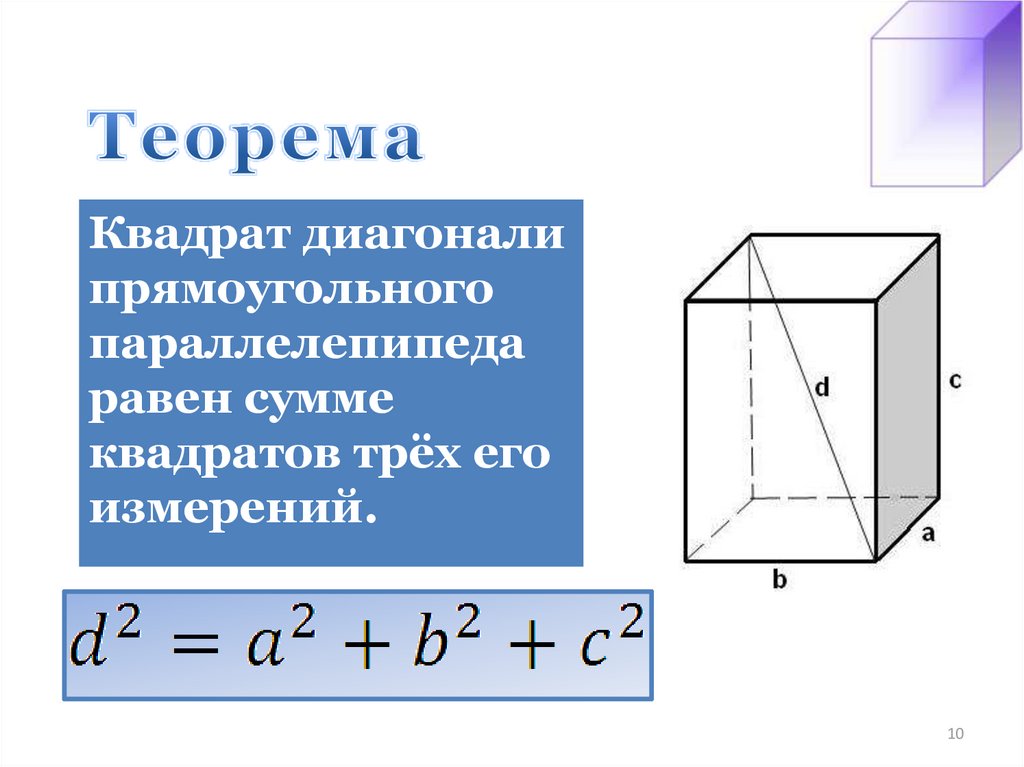
Объем параллелепипеда равен произведению площади основания параллелепипеда на высоту.
V=Sо·h ,
где V — объём параллелепипеда,
Sо — площадь основания параллелепипеда,
h — высота параллелепипеда — расстояние между его основаниями.
Объём прямоугольного параллелепипеда
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V=a·b·h ,
где V — объём прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Объём пирамиды
Пирамида — это многогранник, основанием которого является произвольный многоугольник, а все грани представляют собой треугольники с общей вершиной, являющейся вершиной пирамиды.
Объём пирамиды с произвольным основанием
Объём пирамиды равен одной трети произведения площади основания на высоту.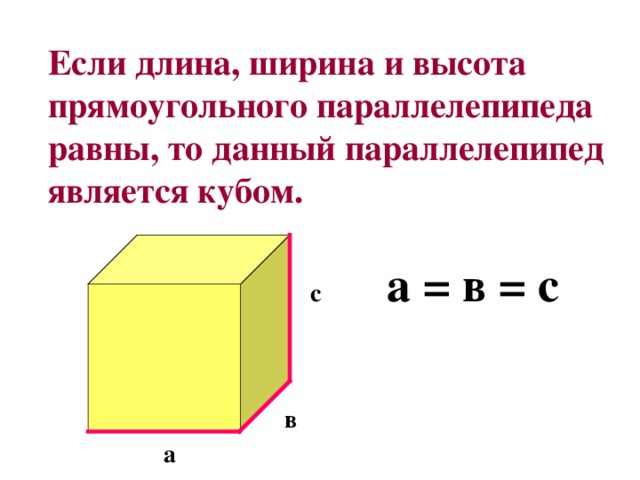
V=13·S·h ,
где V — объём пирамиды,
S — площадь основания пирамиды,
h — высота пирамиды.
Объём усечённой пирамиды
Усеченная пирамида — часть пирамиды между ее основанием и этим сечением. Сечение параллельное основанию пирамиды делит пирамиду на две части.
Объём усеченной пирамиды равен одной трети произведения высоты h на сумму площадей верхнего основания S1, нижнего основания усеченной пирамиды S2 и средней пропорциональной между ними.
V=13·h·S1+S1·S2+S2 ,
где V — объём усеченной пирамиды,
S1 — площадь верхнего основания усеченной пирамиды,
S2 — площадь нижнего основания усеченной пирамиды,
h — высота усеченной пирамиды.
Объём правильной пирамиды
Правильная пирамида — пирамида, в основани, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.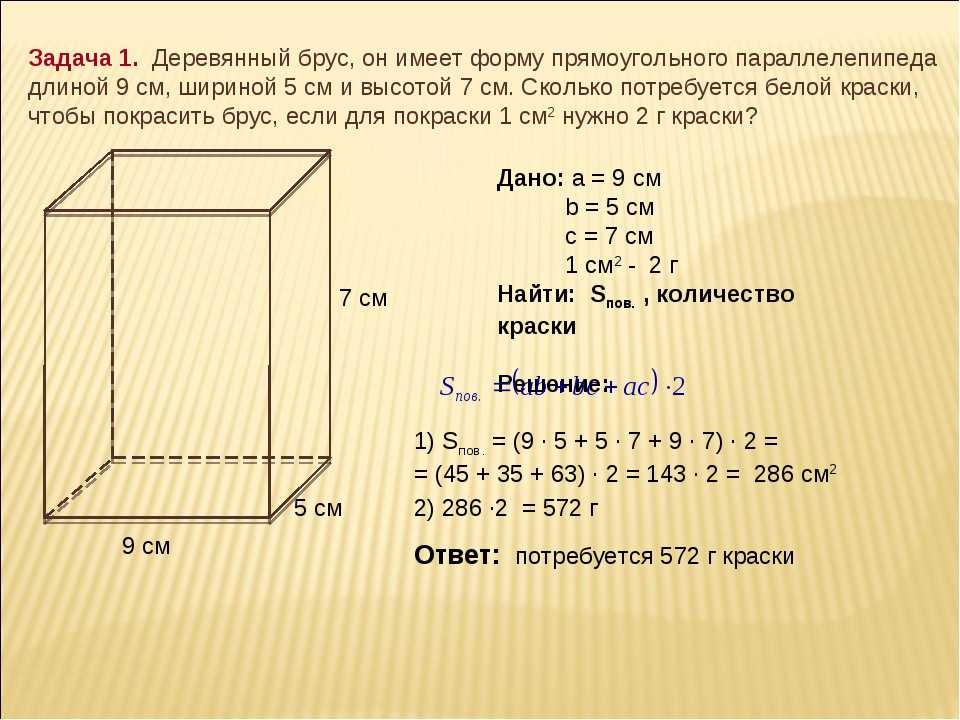
V=n·a2·h22·tg180°n ,
где V — объём пирамиды,
a — сторона основания пирамиды,
n — количество сторон многоугольника в основании,
h — высота правильной пирамиды.
Объём правильной треугольной пирамиды
Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани — равные равнобедренные треугольники.
V=h·a24·3 ,
где V — объём правильной треугольной пирамиды,
a — сторона основания пирамиды,
h — высота правильной треугольной пирамиды.
Объём правильной четырёхугольной пирамиды
Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани — равные равнобедренные треугольники.
Объём правильной четырёхугольной пирамиды равен одной трети произведения высоты пирамиды на куб стороны основания пирамиды.
V=h·a23 ,
где V — объём правильной четырёхугольной пирамиды,
a — сторона основания пирамиды,
h — высота правильной четырёхугольной пирамиды.
Объём тетраэдра
Тетраэдр — пирамида, у которой все грани — равносторонние треугольники.
Объем тетраэдра равен двенадцатой части произведения куба длины грани тетраэдра на квадратный корень из двух.
V=212·a3 ,
где V — объём тетраэдра,
a — любая из граней тетраэдра.
Объём цилиндра
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Объем цилиндра равен произведению площади его основания на высоту.
V=π·R2·h=S·h ,
где V — объём цилиндра,
S — площадь основания цилиндра,
R — радиус цилиндра,
π — число пи ≈ 3,14159265.
Объём конуса
Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Объем конуса равен трети от произведения площади его основания на высоту.
V=13·π·R2·h=13·S·h ,
где V — объём конуса,
S — площадь основания конуса,
R — радиус основания конуса,
π — число пи ≈ 3,14159265.
Объём шара
Шар — совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.
Объём шара равен четырём третьим от произведения числа пи на радиус шара в кубе.
V=43·π·R3 ,
где V — объём шара,
R — радиус шара,
π — число пи ≈ 3,14159265.
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
Формула объема куба
- Главная
- Справочник
- Геометрия
- Формулы объема
- Формула объема куба
- Объем куба
- Формула для расчета объема куба
- Калькулятор объёма куба
Куб или правильный гексаэдр — это правильный многогранник, у которого все грани это квадраты.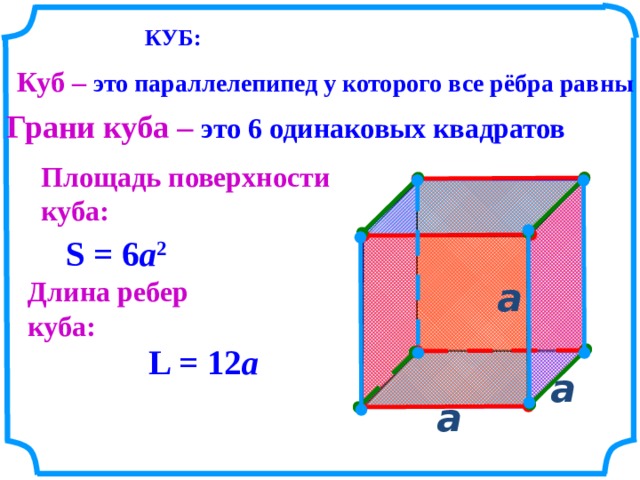 3 $$
3 $$
Уровень5 класс ПредметМатематика СложностьПростая
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Формула объема конуса
Объем конуса равен одной трети произведения площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема цилиндра
Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема пирамиды
Объем пирамиды равен одной трети произведения площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объёма параллелепипеда
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Что такое Ом
1 ом представляет собой электрическое сопротивление между двумя точками проводника, когда постоянная разность потенциалов 1 вольт, приложенная к этим точкам, создаёт в проводнике ток 1 ампер, а в проводнике не действует какая-либо электродвижущая сила.

Электротехника Формулы Физика Теория Электричество
Формула объема цилиндра
Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Треугольник Паскаля
Числа Калькулятор Расчёт Математика Формулы
Таблица мер измерения
Таблицы
Сколько километров в миле?
Морскую милю приравняли к 1862 метрам, сухопутная американская миля равна 1.609344 километра.
Размеры и расстояния Длина Формулы
Что такое дюйм? Чему равен 1 дюйм?
Дюйм — это длина, которая соответствует 2,54 сантиметра (приблизительно 25 миллиметров)
Размеры и расстояния Длина Формулы
Операции над числами
Числа Формулы Алгебра Числа
Сколько ягод в 1 литре?
Я́года — маленький сочный или мясистый плод, обычно кустарниковых или травянистых растений, который при употреблении в пищу не требуется откусывать или разрезать.

Площади и объемы Площадь Математика Формулы Геометрия
Параллелепипед – формулы, свойства, определение, примеры
Параллелепипед – это трехмерная фигура, образованная шестью параллелограммами. Слово «параллелепипед» происходит от греческого слова parallelepdon , что означает «тело, имеющее параллельные тела». Можно сказать, что параллелепипед относится к параллелограмму так же, как куб относится к квадрату. Параллелепипед имеет 6 граней в форме параллелограмма, 8 вершин и 12 ребер. Давайте разберемся со свойствами и различными формулами, связанными с площадью поверхности и объемом параллелепипеда, в следующих разделах.
| 1. | Что такое параллелепипед? |
| 2. | Свойства параллелепипеда |
| 3. | Площадь поверхности параллелепипеда |
| 4. | Объем параллелепипеда |
5. | Решенные примеры |
| 6. | Практические вопросы |
| 7. | Часто задаваемые вопросы о параллелепипеде |
Что такое параллелепипед?
Параллелепипед представляет собой трехмерную фигуру с шестью гранями, каждая из которых имеет форму параллелограмма. У него 6 граней, 8 вершин и 12 ребер. Куб, прямоугольный параллелепипед и ромбовидный — все это частные случаи параллелепипеда. Куб – это параллелепипед, все стороны которого имеют форму квадрата. Точно так же кубоид и ромбоид являются параллелепипедами с прямоугольной и ромбовидной гранями соответственно. На приведенном ниже рисунке мы можем наблюдать параллелепипед с длинами сторон «a», «b» и «c», а «h» — высотой параллелепипеда.
Свойства параллелепипеда
Существуют определенные свойства параллелепипеда, которые помогают нам отличить его от других трехмерных фигур. Эти свойства перечислены ниже:
- Параллелепипед представляет собой трехмерную твердую форму.

- Имеет 6 граней, 12 ребер и 8 вершин.
- Все грани параллелепипеда имеют форму параллелограмма.
- Параллелепипед имеет 2 диагонали на каждой грани, называемые диагоналями граней. Всего у него 12 диагоналей граней.
- Диагонали, соединяющие вершины, не лежащие на одной грани, называются телом или пространственной диагональю параллелепипеда.
- Параллелепипедом называется призма с основанием в форме параллелограмма.
- Каждая грань параллелепипеда является зеркальным отражением противоположной грани.
Площадь поверхности параллелепипеда
Площадь поверхности параллелепипеда определяется как общая площадь, занимаемая всеми поверхностями параллелепипеда. Площадь поверхности параллелепипеда выражается в квадратных единицах, например 9.0087 2 , см 2 , м 2 , фут 2 , ярд 2 и т. д. Площадь поверхности параллелепипеда может быть двух типов:
- Площадь боковой поверхности 9006
- Общая площадь поверхности
Площадь боковой поверхности параллелепипеда
Площадь боковой поверхности параллелепипеда определяется как площадь боковых или боковых граней параллелепипеда. Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями.
Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями.
Общая площадь поверхности параллелепипеда
Общая площадь поверхности параллелепипеда определяется как площадь всех граней параллелепипеда. Чтобы вычислить TSA параллелепипеда, нам нужно найти сумму площадей, покрытых 6 гранями.
Площадь поверхности параллелепипеда Формула
Формула для расчета площади боковой поверхности и общей площади поверхности параллелепипеда:
LSA параллелепипеда = P × H
TSA параллелепипеда = LSA + 2 × B = (P × H) + (2 × B)
где,
- B = Базовая площадь
- H = Высота параллелепипеда
- P = Периметр основания
Объем параллелепипеда
Объем параллелепипеда определяется как пространство, занимаемое фигурой в трехмерной плоскости. Объем параллелепипеда выражается в кубических единицах, например, 3 , см 3 , м 3 , фут 3 , ярд 3 и т. д.
д.
Объем параллелепипеда Формула
Объем параллелепипеда можно рассчитать, используя площадь основания и высоту. Формула для расчета объема параллелепипеда дается как,
В = В × Н
где
- B = Базовая площадь
- H = Высота параллелепипеда
Решенные примеры на параллелепипеде
Пример 1: Если базовая грань параллелепипеда имеет противоположные стороны размером 6 дюймов и 10 дюймов, а его высота равна 7 дюймам, найдите площадь боковой поверхности параллелепипеда.
Решение:
Используя формулу площади боковой поверхности параллелепипеда,
LSA = периметр основания × высота 90 115 ⇒ ЛСА = 2(6 + 10) × 7
= 224 в 3Ответ: Площадь боковой стороны данного параллелепипеда = 224 в 3.
Пример 2: Подарок упакован в прямоугольную коробку размером 10, 7 и 8 дюймов и должен быть обернут подарочной бумагой.
 Сколько подарочной бумаги требуется для упаковки подарочной коробки?
Сколько подарочной бумаги требуется для упаковки подарочной коробки?Решение:
Размеры данной подарочной коробки,
длина, l = 10 в
ширина, w = 7 в
высота, h = 8 inЧтобы найти необходимое количество подарочной бумаги, нам нужно найти общую площадь поверхности коробки. Поскольку форму коробки можно сравнить с прямоугольным параллелепипедом,
ВПС = 2 (дв + вх + вл)
= 2 (10 × 7 + 7 × 8 + 8 × 10)
= 2 (70 + 56 + 80)
= 412 в 2 .
Ответ: Площадь необходимой подарочной бумаги = 412 в 2 .
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Забронировать бесплатный пробный урок
Практические вопросы по параллелепипеду
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о параллелепипеде
Что такое параллелепипед?
Параллелепипед представляет собой трехмерную фигуру с 6 гранями в форме параллелограмма, 12 ребрами и 8 вершинами. Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно.
Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно.
Каков объем параллелепипеда?
Объем параллелепипеда – это емкость, форма или общее пространство, занимаемое в трехмерной плоскости. Объем параллелепипеда в кубических единицах, например, 3 , см 3 , фут 3 , 3 и т. д.
Какова общая площадь поверхности параллелепипеда?
Полная площадь поверхности параллелепипеда – это площадь, покрытая всеми гранями параллелепипеда. Выражается в квадратных единицах, например, в 2 , м 2 , см 2 , фут 2 и т. д.
Что такое площадь боковой поверхности параллелепипеда?
Площадь боковой поверхности параллелепипеда – это площадь или область, покрываемая всеми боковыми или боковыми гранями параллелепипеда. Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д.
Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д.
Что такое формулы параллелепипеда?
Формулы, связанные с параллелепипедом, даны как,
- LSA параллелепипеда = P × H
- TSA параллелепипеда = (P × H) + (2 × B)
- Объем параллелепипеда = B × H
где B — площадь основания, H — высота параллелепипеда, P — периметр основания.
Что такое прямоугольный параллелепипед?
Прямоугольный параллелепипед — тип параллелепипеда, все шесть граней которого имеют прямоугольную форму, а длины параллельных ребер равны.
Какой формы параллелепипед?
Параллелепипед — это трехмерная фигура, все стороны которой имеют форму параллелограмма. Противоположные грани параллелепипеда являются зеркальным отражением друг друга.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по фигурам
Определители и объемы
Цели
- Понимать связь между определителем матрицы и объемом параллелепипеда.

- Научитесь использовать определители для вычисления объемов параллелограммов и треугольников.
- Научитесь использовать определители для вычисления объема некоторых изогнутых фигур, таких как эллипсы.
- Картинки: параллелепипед, изображение криволинейной формы при линейном преобразовании.
- Теорема: определителя и объема.
- Словарное слово: параллелепипед .
В этом разделе мы даем геометрическую интерпретацию определителей в терминах томов. Это прольет свет на причину трех из четырех определяющих свойств определителя. Это также важный компонент формулы замены переменных в многомерном исчислении.
Определитель вычисляет объем геометрического объекта следующего типа.
Определение
параллелепипеда , определяемого n векторами v1,v2,…,vn в Rn, есть подмножество
P=Ca1x1+a2x2+···+anxnEE0≤a1,a2,…,an≤1D.
Другими словами, параллелепипед — это множество всех линейных комбинаций n векторов с коэффициентами в [0,1]. Мы можем нарисовать параллелепипеды, используя закон параллелограмма для сложения векторов.
Мы можем нарисовать параллелепипеды, используя закон параллелограмма для сложения векторов.
Пример (единичный куб)
Параллелепипед, заданный стандартными координатными векторами e1,e2,…,en, является единичным n-мерным кубом.
e2e1e1e2e3Пример (параллелограммы)
При n=2 параллелепипед — это просто параллелограмм в R2. Обратите внимание, что ребра идут параллельными парами.
Пример
При n=3 параллелепипед является разновидностью косого куба. Обратите внимание, что грани идут параллельными парами.
v1v2v3PКогда параллелепипед имеет нулевой объем? Это может произойти только в том случае, если параллелепипед плоский, т. е. сжат в более низкое измерение.
Pv1v2v1v2v3PЭто означает, что {v1,v2,…,vn} линейно зависима от , а , что согласно следствию из раздела 4.1 означает, что матрица со строками v1,v2,…,vn имеет нулевой определитель. Подводя итог:
Ключевое наблюдение, приведенное выше, — это только начало истории: объем параллелепипеда равен всегда определителя.
Теорема (Определители и объемы)
Пусть v1,v2,…,vn — векторы в Rn, P — параллелепипед, определяемый этими векторами, A — матрица со строками v1,v2,…,vn. Тогда абсолютное значение определителя A равно объему P:
|det(A)|=vol(P).
Доказательство
Поскольку четыре определяющих свойства характеризуют определитель, они также характеризуют абсолютное значение определителя. В явном виде |det| функция на квадратных матрицах, которая удовлетворяет следующим свойствам:
- Выполнение замены строки в A не меняет |det(A)|.
- Масштабирование строки A с помощью скаляра c умножает |det(A)| через |с|.
- Перестановка двух строк матрицы не меняет |det(A)|.
- Определитель единичной матрицы In равен 1.
Абсолютное значение определителя — это только такая функция: действительно, по этому рецепту из раздела 4.1, если вы выполните некоторое количество операций со строками над A, чтобы получить матрицу B в форме эшелона строк, тогда
|det(A)|=EEEE(произведение диагональных записей B)(произведение использованных коэффициентов масштабирования)EEEE.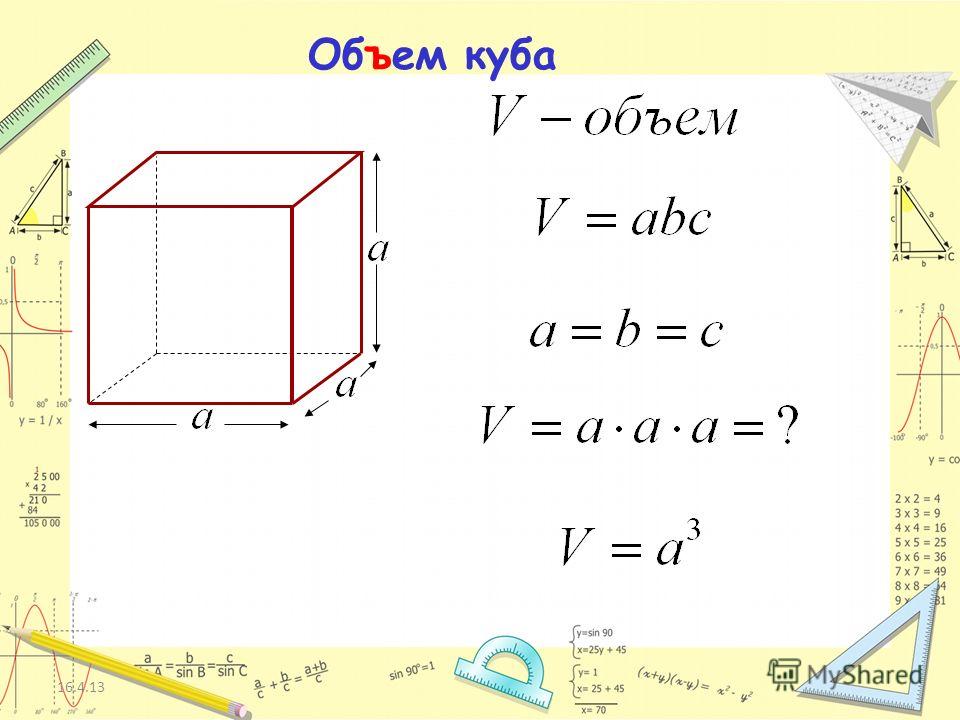
Для квадратной матрицы A мы злоупотребляем обозначениями и пусть vol(A) обозначает объем параллелепипеда, определяемый строками A. Тогда мы можем рассматривать vol как функцию от набора квадратных матриц к действительным числам. Мы покажем, что vol также удовлетворяет четырем указанным выше свойствам.
- Для простоты рассмотрим замену строки вида Rn=Rn+cRi. Объем параллелепипеда — это объем его основания, умноженный на его высоту: здесь «основание» — это параллелепипед, определяемый v1,v2,…,vn−1, а «высота» — это перпендикулярное расстояние vn от база. basev2v1heightbaseheightv1v2v3 Смещение vn на число, кратное vi, перемещает vn в направлении, параллельном основанию. Это не меняет ни основания, ни высоты! Таким образом, vol(A) не меняется при замене строк. basev2v1height—-→basev2v2-.5v1v1heightbaseheightv1v2v3—-→baseheightv1v2v3+.5v1v3
- Для простоты рассмотрим шкалу строк вида Rn=cRn. Это увеличивает длину vn в множителе |c|, что также увеличивает перпендикулярное расстояние vn от основания в множитель |c|.
 Таким образом, vol(A) масштабируется как |c|.basev2v1height—-→base34v2v134heightbaseheightv1v2v3—-→base43heightv1v243v3
Таким образом, vol(A) масштабируется как |c|.basev2v1height—-→base34v2v134heightbaseheightv1v2v3—-→base43heightv1v243v3 - Перестановка двух строк A просто переупорядочивает векторы v1,v2,…,vn и, следовательно, не влияет на параллелепипед, определяемый этими векторами. Таким образом, vol(A) не меняется при перестановке строк. v2v1—-→v1v2v1v3v2—-→v1v2v3
- Строки единичной матрицы In представляют собой стандартные векторы координат e1,e2,…,en. Ассоциированный параллелепипед — это единичный куб, объем которого равен 1. Таким образом, vol(In)=1.
Поскольку |det| — единственная функция, удовлетворяющая этим свойствам, у нас есть
объем(P)=объем(A)=|det(A)|.
Это завершает доказательство.
Поскольку det(A)=det(AT) по свойству транспонирования, абсолютное значение det(A) также равно объему параллелепипеда, определяемому столбцы также.
Пример (длина)
Матрица A 1×1 — это просто число AaB.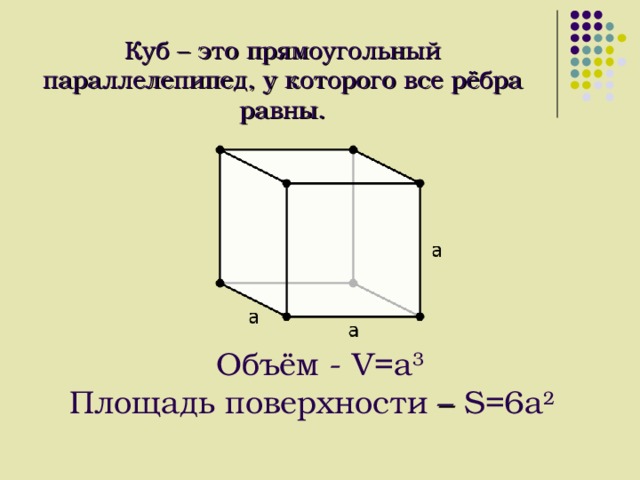 В этом случае параллелепипед P, определяемый одной своей строкой, представляет собой как раз отрезок [0,a] (или [a,0], если a<0). «Объем» области в R1=R — это просто ее длина, поэтому в данном случае ясно, что vol(P)=|a|.
В этом случае параллелепипед P, определяемый одной своей строкой, представляет собой как раз отрезок [0,a] (или [a,0], если a<0). «Объем» области в R1=R — это просто ее длина, поэтому в данном случае ясно, что vol(P)=|a|.
Пример (площадь)
Когда A является матрицей 2×2, ее строки определяют параллелограмм в R2. «Объем» области в R2 — это ее площадь, поэтому мы получаем формулу площади параллелограмма: это определитель матрицы, строки которой — векторы, образующие две смежные стороны параллелограмма.
HabIHcdIarea=EEEEdetHabcdIEEE=|ad-bc|Возможно, удивительно, что можно вычислить площадь параллелограмма без тригонометрии. Доказать эту формулу вручную — забавная задача по геометрии. [Подсказка: сначала подумайте о случае, когда первая строка A лежит на оси x.]
Пример
Пример
Пример (Площадь треугольника)
Вам может быть интересно: если абсолютное значение определителя является объемом, то каков геометрический смысл определителя без абсолютного значения? Следующее замечание объясняет, что мы можем думать об определителе как о подписанный том . Если вы прошли курс интегрального исчисления, вы, вероятно, вычисляли отрицательные площади под кривыми; идея здесь похожа.
Если вы прошли курс интегрального исчисления, вы, вероятно, вычисляли отрицательные площади под кривыми; идея здесь похожа.
Пусть A — матрица размера n×n со столбцами v1,v2,…,vn, и пусть T:Rn→Rn — ассоциированное матричное преобразование T(x)=Ax. Тогда T(e1)=v1 и T(e2)=v2, так что T переводит единичный куб C в параллелепипед P, определяемый v1,v2,…,vn:
Ce2e1TF||v1v2||Gv2v1PПоскольку единичный куб имеет объем 1, а его образ имеет объем |det(A)|, преобразование T масштабирует объем куба с коэффициентом |det(A)|. Перефразируя:
Если A — матрица размера n × n с соответствующим матричным преобразованием T: Rn→Rn, и если C — единичный куб в Rn, то объём T(C) равен |det(A)|.
Обозначение T(S) означает образ области S при преобразовании T. В обозначении построителя множеств это подмножество
T(S)=CT(x)|xinSD.
Фактически, T масштабирует объем любой области в Rn с тем же коэффициентом, даже для изогнутых областей.
Теорема
Пусть A — матрица размера n × n, и пусть T:Rn→Rn — ассоциированное матричное преобразование T(x)=Ax.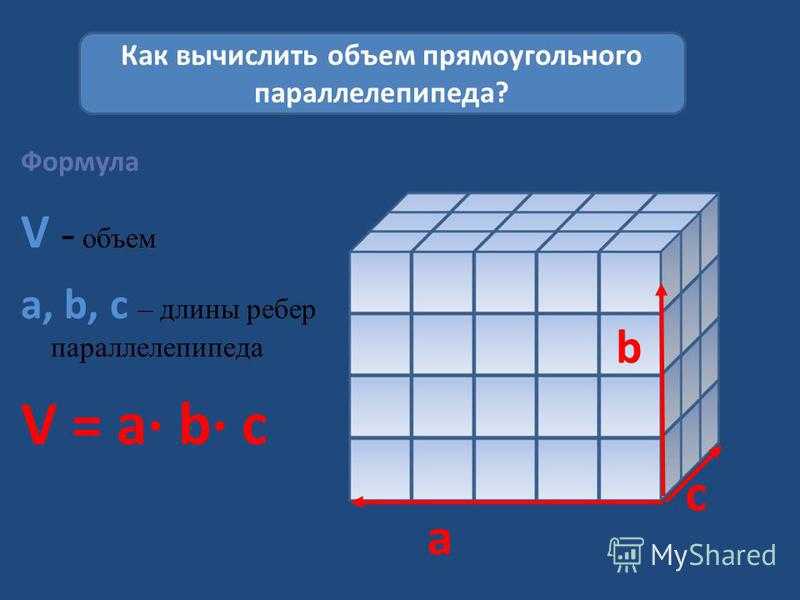 Если S — любая область в Rn, то
Если S — любая область в Rn, то
vol(T(S))=|det(A)|·vol(S).
Доказательство
Пусть C — единичный куб, пусть v1,v2,…,vn — столбцы A, и пусть P — параллелепипед, определяемый этими векторами, поэтому T(C)=P и vol(P)=|det (А)|. При A>0 обозначим через AC куб со сторонами A, т. е. параллелепипед, определяемый векторами Ae1,Ae2,…,Aen, и аналогично определим AP. По второму определяющему свойству T переводит AC в AP. Объем AC равен An (мы масштабировали каждый из n стандартных векторов с коэффициентом A), а объем AP равен An|det(A)| (по той же причине), поэтому мы показали, что T масштабирует объем AC на |det(A)|.
Ae2Ae1ACvol(AC)=AnTF||v1v2||GAv2Av1APvol(AP)=An|det(A)|По первому определяющему свойству образ перевода AC является переводом AP:
Т(х+АС)=Т(х)+АТ(С)=Т(х)+АР.
Поскольку перевод не изменяет объемы, это доказывает, что T масштабирует объем перевода AC на |det(A)|.
На этом этапе нам нужно использовать методы многомерного исчисления, поэтому мы даем только представление об остальной части доказательства. Любую область S можно аппроксимировать набором очень маленьких кубов вида x+AC. Затем образ T(S) аппроксимируется образом этого набора кубов, который представляет собой набор очень маленьких параллелепипедов вида T(x)+AP.
Любую область S можно аппроксимировать набором очень маленьких кубов вида x+AC. Затем образ T(S) аппроксимируется образом этого набора кубов, который представляет собой набор очень маленьких параллелепипедов вида T(x)+AP.
Объем S точно аппроксимируется суммой объемов кубов; на самом деле, когда A стремится к нулю, предел этой суммы в точности равен объему (S). Точно так же объем T(S) равен сумме объемов параллелепипедов, взятых в пределе при A→0. Ключевым моментом является то, что объем каждого куба масштабируется на |det(A)|. Следовательно, сумма объемов параллелепипедов равна |det(A)| умноженная на сумму объемов кубов. Это доказывает, что vol(T(S))=|det(A)|vol(S).
Пример
Пример (Площадь эллипса)
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
Изучите определения, формулы площади и объема здесь!
Объемная фигура с гранями в виде параллелограмма называется параллелепипедом.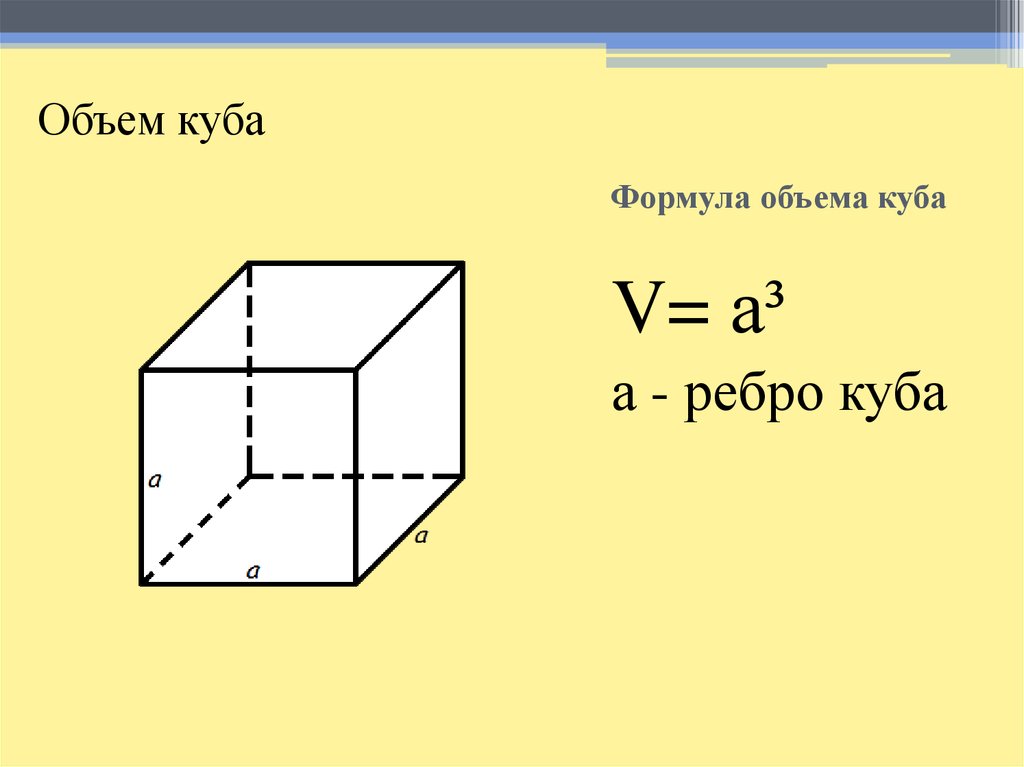 Оно происходит от греческой фразы «параллелепидон», означающей «объект, имеющий параллельную плоскость». По определению, это трехмерная фигура или призма с основанием в виде параллелограмма, образованным шестью сторонами параллелограмма. Трехмерные фигуры — это твердые формы или объекты, имеющие три измерения. Они измеряются по трем параметрам: длина, ширина и высота. В этой статье мы узнаем о конкретной трехмерной форме, называемой параллелепипедом, ее свойствах, формулах для общей площади, площади поверхности и объема, а также об уравнении прямоугольного параллелепипеда с решенными примерами.
Оно происходит от греческой фразы «параллелепидон», означающей «объект, имеющий параллельную плоскость». По определению, это трехмерная фигура или призма с основанием в виде параллелограмма, образованным шестью сторонами параллелограмма. Трехмерные фигуры — это твердые формы или объекты, имеющие три измерения. Они измеряются по трем параметрам: длина, ширина и высота. В этой статье мы узнаем о конкретной трехмерной форме, называемой параллелепипедом, ее свойствах, формулах для общей площади, площади поверхности и объема, а также об уравнении прямоугольного параллелепипеда с решенными примерами.
Параллелепипед Определение
В геометрии параллелепипед — это трехмерная фигура, образованная шестью параллелограммами. Его еще называют ромбовидным. По аналогии с 2D Shapes, он соотносится с параллелограммом так же, как куб соотносится с квадратом. Его можно определить как многогранник с шестью гранями, также называемый шестигранником, каждая грань которого представляет собой параллелограмм. Прямоугольный кубоид с шестью прямоугольными гранями, куб с шестью квадратными гранями и ромбоэдр с шестью ромбовидными гранями — все это частные случаи параллелепипеда.
Прямоугольный кубоид с шестью прямоугольными гранями, куб с шестью квадратными гранями и ромбоэдр с шестью ромбовидными гранями — все это частные случаи параллелепипеда.
О площади треугольника читайте здесь.
Объем параллелепипеда
Объем параллелепипеда — это количество пространства, которое содержит параллелепипед. Чтобы понять это, рассмотрим параллелепипед, наполненный водой. Объем воды, который помещается в параллелепипеде, является объемом параллелепипеда.
Объем параллелепипеда равен произведению площади основания на высоту. Из геометрического определения перекрестного произведения мы знаем, что его величина, ∥a×b∥, представляет собой площадь основания параллелограмма и что направление вектора a×b перпендикулярно основанию. Для описания параллелепипеда нам нужны три его смежные стороны и мера углов между ними, или три смежных вектора.
Формула объема параллелепипеда
Формула объема параллелепипеда, образованного векторами \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) с той же начальной точкой задается их скалярным тройным произведением:
\(V=∣(\vec{a}\times\vec{b})\cdot\vec{c}∣\).
V – Объем параллелепипеда, образованного тремя векторами; \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\)
Первый шаг вычисления объема параллелепипеда включает в себя нахождение векторного произведения или векторного произведения \((\vec{a}\times\vec{b})\). Вектор произведения перпендикулярен как \(\vec{a}\), так и \(\vec{b}\). Обратите внимание, что величина результирующего вектора \(\lvert\vec{a}\times\vec{b}\rvert\) равна площади параллелограмма, описываемого этими двумя векторами.
Последующее скалярное произведение между \((\vec{a}\times\vec{b})\) и \(\vec{c}\) обозначает проекцию \(\vec{a}\times\vec {b}\) на \(\vec{c}\). Другими словами, он перемещает базовый параллелограмм вдоль \(\vec{c}\), аналогично умножению базовой площади на высоту.
Формулу можно упростить и свести к одному определителю:
\(\begin{matrix}
(\vec{a}\times\vec{b})\cdot\vec{c}
&=
\left|
\begin{array}{cc}
a_2 & a_3\\
b_2 & b_3
\end{массив}
\right|
c_1
–
\левый|
\begin{array}{cc}
a_1 & a_3\\
b_1 & b_3
\end{array}
\right|
c_2
+
\левый|
\begin{array}{cc}
a_1 & a_2\\
b_1 & b_2
\end{array}
\right|
c_3
\\
&=
\влево|
\begin{array}{ccc}
c_1 & c_2 & c_3\\
a_1 & a_2 & a_3\\
b_1 & b_2 & b_3
\end{массив}
\right|.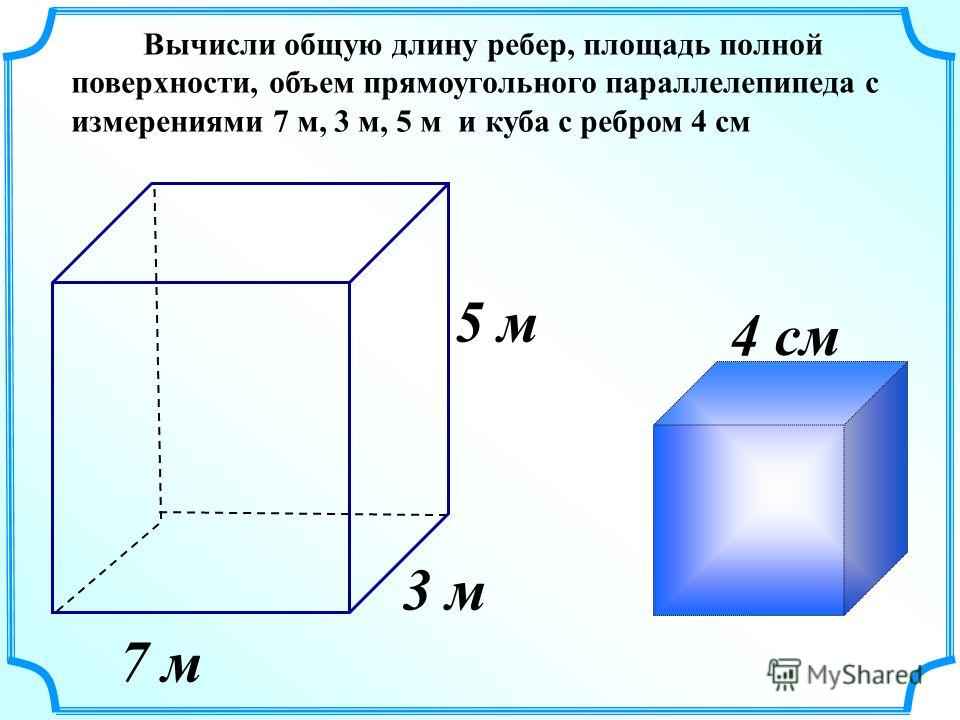
\end{matrix}\)
Это дает нам объем параллелепипеда, когда векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) известны.
Узнайте о Rhombus здесь.
Объем параллелепипеда с использованием вершин
Если мы знаем вершины параллелепипеда, мы можем найти его векторы, используя простую формулу расстояния. Если \(A < x_1, y_1, z_ 1 >, B < x_2, y_2, z_ 2 >\), \(C < x_3, y_3, z_ 3 >\) и \(D < x_4, y_4, z_ 4 > \) тогда мы можем найти векторы AB =a, AC=b и AD=c, имеющие одну и ту же начальную точку, и использовать их в качестве наших базисных векторов, образующих параллелепипед. AB будет задан как \( a =
Получив векторы a, b и c, выполните следующие простые шаги: Найдите векторное произведение между векторами \(\vec{a}\) и \(\vec{b}\), чтобы получить \(\ vec{a}\times\vec{b}\).
Вычислите скалярное произведение между векторами \(\vec{a}\times\vec{b}\) и \(\vec{c}\), чтобы получить скалярное значение \((\vec{a}\ раз\vec{b})\cdot\vec{c}\).
Определите объем параллелепипеда как абсолютное значение этого скаляра, заданного как \(∣(\vec{a}\times\vec{b})\cdot\vec{c}∣\).
Объем параллелепипеда с использованием сторон и углов 92({\gamma}))}\)
Где,
\(\alpha\) — угол между сторонами b и c;
\(\beta\) – Угол между сторонами а и с; и
\(\gamma\) – угол между сторонами a и b.
Площадь параллелепипеда
Площадь параллелепипеда равна сумме площадей всех его поверхностей. Это называется полной площадью поверхности параллелепипеда. Когда дело доходит до площади 3D-объектов, есть две важные площади поверхности:
- Общая площадь поверхности параллелепипеда
- Площадь боковой поверхности параллелепипеда
Давайте посмотрим, как мы можем их рассчитать.
О площади четырехугольника читайте здесь.
Площадь боковой поверхности параллелепипеда
Площадь боковой поверхности параллелепипеда определяется как сумма площадей его граней без учета основания и вершины. Площадь боковой поверхности (LSA) параллелепипеда равна произведению периметра основания на высоту параллелепипеда. Таким образом, формула площади боковой поверхности параллелепипеда имеет вид:
Площадь боковой поверхности (LSA) параллелепипеда равна произведению периметра основания на высоту параллелепипеда. Таким образом, формула площади боковой поверхности параллелепипеда имеет вид:
\(LSA= 2(a+b){\times}c\)
Общая площадь поверхности параллелепипеда
Общая площадь поверхности параллелепипеда определяется как общая площадь, покрытая всеми гранями формы . Общая площадь поверхности параллелепипеда определяется формулой
\(TSA=2(ab+bc+ac)\)
В векторной форме это можно записать как
\(A = 2{\times} (∣\vec{a}{\times}\vec{b}∣ + ∣\vec{b}{\times}\vec{c}∣ + ∣\vec{a}{\times}\vec{c} ∣)\)
Где,
\(∣\vec{a}{\times}\vec{b}|: Величина \; из \; \; перекрестное произведение \; между \; \vec{a}\) и \(\vec{ a}\)
\(∣\vec{b}{\times}\vec{c}|: Величина \; из \; \; перекрестное произведение \; между \; \vec{b}\) и \(\vec{c}\)
\(∣\vec{c}{\times}\vec{a}|: Величина \; of \; \; перекрестное произведение \; между \; \vec{ c}\) и \(\vec{b}\)
Узнайте больше о линиях здесь.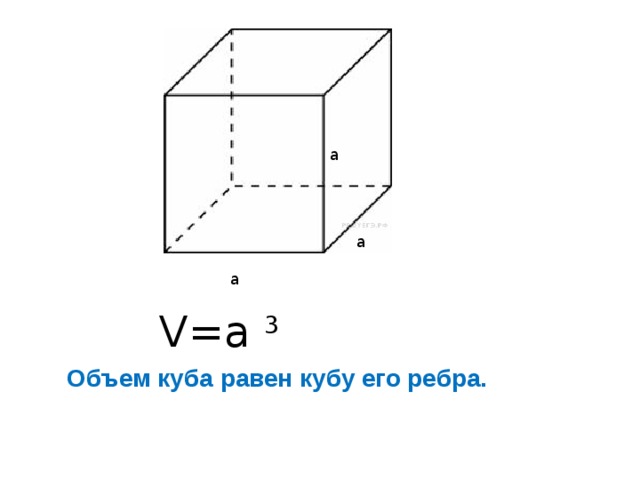
Площадь параллелепипеда с использованием сторон и углов
Существует альтернативный способ расчета площади параллелепипеда с использованием длин его сторон \(a\), \(b\) и углов. Он находится по формуле
\(A = 2\times(a{\cdot}b{\cdot}sin(\gamma) + b{\cdot}c{\cdot}sin(\alpha) + a{\cdot}c{\ cdot}sin(\beta))\), где:
\(\alpha\) – угол между b и c;
\(\beta\) – Угол между а и с; и
\(\gamma\) – Угол между a и b.
Прямоугольный параллелепипед
Прямоугольный параллелепипед представляет собой многогранник с шестью гранями, также известный как шестигранник. Это трехмерная структура в виде параллелепипеда, все шесть граней которой имеют прямоугольную форму, а длины параллельных ребер равны. Это частный случай параллелепипеда. Прямоугольный параллелепипед аналогичен двумерному прямоугольнику.
Узнайте о прямоугольниках здесь.
Формула прямоугольного параллелепипеда
Формула прямоугольного параллелепипеда включает в себя формулы площади его поверхности, объема и диагоналей. Давайте посмотрим, как мы можем это вычислить.
Давайте посмотрим, как мы можем это вычислить.
Площадь поверхности прямоугольного параллелепипеда
На фигуре прямоугольного параллелепипеда шесть прямоугольников. Мы должны вычислить площадь шести прямоугольников, чтобы определить площадь его поверхности (граней). Формула площади поверхности:
Площадь поверхности \(= 2(l{\times}h) + 2(l{\times}w) + 2(h{\times}w)\)
\(S = 2[(l{\ times}h) + (l{\times}w) + (h{\times}w)]\)
, где
\(l\), \(w\), \(h\) — длина, ширина, высота прямоугольного параллелепипеда соответственно.
Площадь боковой поверхности прямоугольного параллелепипеда
Произведение периметра основания и высоты называется площадью боковой поверхности. Каждая грань прямоугольного параллелепипеда представляет собой прямоугольник, поэтому периметр основания равен периметру прямоугольника. Ниже приведена формула для LSA (площадь боковой поверхности):
LSA = периметр основания × высота
Поскольку периметр основания равен 2 (длина + ширина)
= 2 (длина + ширина) × высота
\(LSA = 2lh + 2wh\)
где
\(l\), \(w\), \(h\) — длина, ширина и высота прямоугольного параллелепипеда соответственно.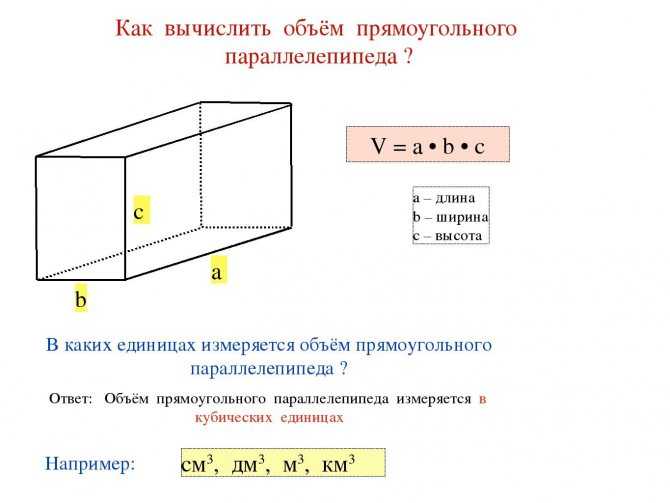
Объем прямоугольного параллелепипеда
Площадь основания, умноженная на высоту, дает объем прямоугольного параллелепипеда. Основание прямоугольного параллелепипеда — прямоугольник, как и каждая его грань, а его площадь равна произведению его длины на ширину. Формула объема следующая: 92}\)
Решенные примеры на параллелепипеде
Теперь давайте посмотрим несколько решенных примеров на параллелепипеде.
Решено Пример 1: Найдите площадь поверхности данного параллелепипеда, если его длина 13 см, ширина 12 см, высота 10 см.
Решение:
Мы знаем, что
Общая площадь поверхности (TSA) = 2(ab + bc + ac), здесь a = 13 см, b = 12 см, c = 10 см
= 2( 13 × 12 + 12 × 10 + 10 × 13 )
= 812 кв.см
Решено Пример 2: Рассмотрим параллелепипед ABCDEFGH с длинами ребер a = 7, b = 5 и c = 3. Если ∠DAE=45°, ∠BAD=63° и ∠BAE=50°, то что площадь поверхности параллелепипеда?
Решение:
Здесь
\(\alpha=∠BAD=63°\) – угол между b и c;
\(\beta=∠DAE=45°\) – Угол между а и с; и
\(\gamma=∠BAE=50°\) – угол между a и b.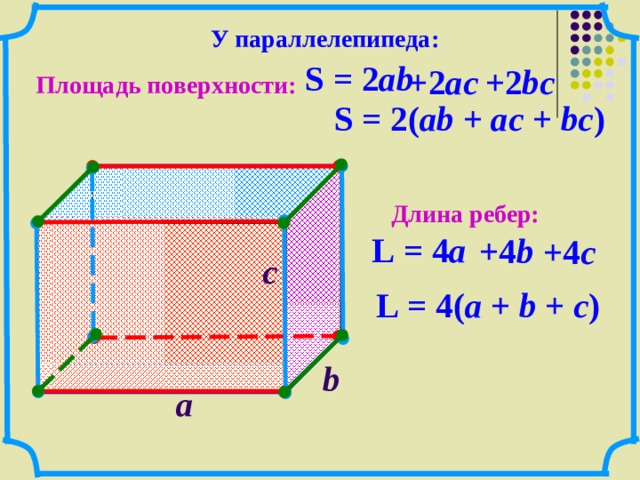
Площадь поверхности будет равна, будет равна
\(A = 2\times(a{\cdot}b{\cdot}sin(\gamma) + b{\cdot}c{\cdot}sin(\alpha) + a{\cdot}c{\ cdot} sin (\ beta)) \)
\ (A = 2 \ times (7 {\ cdot} 5 {\ cdot} sin (50) + 5 {\ cdot} 3 {\ cdot} sin (63) + 7 {\ cdot} 3 {\ cdot} sin (45)) \)
\ (A = 2 \ times (35 {\ cdot} sin (50) + 15 {\ cdot} sin (63) + 21 {\ cdot}sin(45))\)
\(A = 110,05\) кв. ед.
Решено Пример 3: Найти объем параллелепипеда с векторами a = (1, 1, 2), b = ( 2, 1, 3) и с = (3, 1, 2).
Решение:
Объем параллелепипеда определяется определителем матрицы:
\( V=
{\begin{bmatrix}
c_1 & c_2 & c_3\\
a_1 & a_2 & a_3\\
b_1 & b_2 & b_3
\end{bmatrix}}
\)
Подставляя значения получаем
\( V=
{\begin{bmatrix}
3 & 1 & 2\\
1 & 1 & 2\\
2 & 1 & 3
\end{bmatrix}}
\)
Нахождение определителя получаем,
\(V = |3(1\times3 – 2\times1) – 1(1\times3 – 2\times2) + 2(1\times1 – 1\times2)|\)
\(V = |3 \times1 – 1\times(-1) + 2\times(-1)|\)
\(V = 2 \) кубических единиц.
Надеюсь, эта статья о параллелепипеде была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о параллелепипеде
В.1 Как найти вершины параллелепипеда?
Ответ 1 Вершины параллелепипеда можно найти, используя длины ребер. Постройте параллелепипед по осям X, Y и Z и измерьте длины ребер, чтобы получить координаты вершин.
Q.2 В чем разница между кубоидом и прямоугольным параллелепипедом?
Ответ 2 Если мы ограничим определение прямоугольных граней, как это иногда делается, то прямоугольный параллелепипед и прямоугольный параллелепипед будут одним и тем же.
В.3 Как найти высоту параллелепипеда?
Ответ 3 Вы можете найти высоту параллелепипеда, если знаете его боковую или полную площадь. Просто используйте формулу площади поверхности и решите высоту.
Q.4 Как рассчитать площадь параллелепипеда?
Ответ 4 Формула площади боковой поверхности параллелепипеда: \(LSA= 2(a+b){\times}c\). Общая площадь поверхности параллелепипеда определяется по формуле \(TSA=ab+bc+ac\)
Q.5 Что является примером прямоугольного параллелепипеда?
Ответ 5 Пенал, обувная коробка, кирпичи, книги, матрацы — все это примеры прямоугольного параллелепипеда.
Скачать публикацию в формате PDF| Прямая и обратная пропорция: обучение с определением, формулой, примерами, символами, графиками и примерами решения Умножение здесь! |
| Антисимметричные отношения: вывод, график и примеры решения |
| Бета-функция: изучение формул, свойств, приложений с использованием примеров |
| Бензольные реакции: изучайте различные реакции, такие как сульфонация, нитрация и алкилирование |
Том параллелепипененный калькулятор
, созданный Кришной Нелатуром
. Проседанный Стивеном Вудинг
Проседанный Стивеном Вудинг
Last Advated: MAR 11, 2022 2
. оглавления:- Объем параллелепипеда формула
- Как рассчитать объем параллелепипеда?
- Как вычислить объем параллелепипеда по сторонам?
- Как рассчитать площадь поверхности параллелепипеда?
- Как использовать этот калькулятор объема параллелепипеда – И калькулятор площади параллелепипеда
- Часто задаваемые вопросы
Этот калькулятор объема параллелепипеда поможет вам вычислить объем параллелепипеда из его трех векторов , 90 167 вершин , или 90 166 длин ребер 90 167 . Кроме того, он также рассчитает площадь параллелепипеда. Вы задаетесь вопросом, как найти объем параллелепипеда , образованного тремя векторами ? Хотите узнать формулу для объема параллелепипеда с четырьмя вершинами ? Читайте дальше, чтобы узнать ответы на все эти и другие вопросы.
Объем параллелепипеда формула
Параллелепипед – это многогранник , у которого шесть граней являются параллелограммами . Для описания параллелепипеда нам понадобится его трех смежных сторон и их углов , или трех соседних векторов .
Три соначальных вектора в пространстве описывают параллелепипед.Формула для объема параллелепипеда определяется следующим образом: \vec{c}\, \rvertV=∣(a
×b
)⋅c
∣
где:
- VVV – Объем 6 параллелепипедов, образованных тремя
6 параллелепипедами0167 ; и
- a⃗\vec{a}a, b⃗\vec{b}b и c⃗\vec{c}c – Три вектора , описывающие три смежных (и уникальных) сторон параллелепипеда .

Используемое векторное умножение называется скалярным тройным произведением (или просто тройным произведением). Он включает в себя перекрестное произведение векторов a⃗\vec{a}a и b⃗\vec{b}b, в результате чего получается вектор a⃗×b⃗\vec{a}\times\vec{b}a×b перпендикулярно как на a⃗\vec{a}a, так и на b⃗\vec{b}b. Обратите внимание, что 90 166 величина 90 167 результирующего вектора, ∣a⃗×b⃗∣\lvert\vec{a} \times \vec{b}\rvert∣a×b∣, равна 90 166 площади параллелограмма 90 167, описанного формулой эти два вектора.
Последующее скалярное произведение между a⃗×b⃗\vec{a}\times\vec{b}a×b и c⃗\vec{c}c обозначает проекцию a⃗×b⃗\vec{a}\ раз\vec{b}a×b на c⃗\vec{c}c. Другими словами, он перемещает базовый параллелограмм вдоль c⃗\vec{c}c, аналогично умножению базовая область с высотой .
Формулу можно упростить и свести к одному определителю:
V=∣(a⃗×b⃗)⋅c⃗∣=∣ijka1a2a3b1b2b3∣⋅(c1i+c2j+c3k)⟹V=∣c1c2c3a1a2a3b1b2scriptbsize\begin\beginb2scriptb2 {выровнять*} V &= \lvert (\vec{a}\times\vec{b})\cdot\vec{c}\, \rvert\\\\ &= \begin{vmatrix} \bm{i} и \bm{j} и \bm{k}\\ а_1 и а_2 и а_3\\ б_1 и б_2 и б_3 \end{vmatrix}\cdot (c_1\bm{i} + c_2\bm{j} + c_3\bm{k})\\\\ \подразумевает V & = \begin{vmatrix} c_1 и c_2 и c_3\\ а_1 и а_2 и а_3\\ б_1 и б_2 и б_3 \end{vmatrix} \end{align*}V⟹V=∣(a
×b
)⋅c
∣=∣
∣ia1b1ja2b2ka3b3∣
∣⋅(c1i+c2j+c3 k)=∣
∣c1a1b1c2a2b2c3a3b3∣
∣
где:
- a1a_1a1, a2a_2a23, a3 – Компоненты a⃗\vec{\bm{a}}a;
- b1b_1b1, b2b_2b2, b3b_3b3 – Компоненты из b⃗\vec{\bm{b}}b;
- c1c_1c1, c2c_2c2, c3c_3c3 – Компоненты из c⃗\vec{\bm{c}}c; и
- i\bm{i}i, j\bm{j}j, k\bm{k}k – Единичные векторы вдоль координатных осей .

Теперь, когда вы знаете, как найти объем параллелепипеда с векторами, давайте узнаем, что делать, если единственными заданными значениями являются вершин параллелепипеда .
Зная вершины смежных сторон, мы можем определить векторы.Вы можете найти любой вектор между двумя точками, если знаете координаты этих точек. Как только вы определите векторы, вы можете рассчитать объем параллелепипеда, используя приведенную выше формулу.
Как рассчитать объем параллелепипеда?
To calculate the volume of a parallelepiped formed by the vectors a , b , and c , follow these simple steps:
- Find the cross -произведение между векторами
aиbдля полученияa × b.
- Вычислите скалярное произведение между векторами
a × bиc, чтобы получить скалярное значение(a × 7 6,6 91,3 c 91,3 c 9167). - Определите объем параллелепипеда как абсолютное значение этого скаляра, заданного как
∣(a × b) ∙ c∣.
Например, рассмотрим параллелепипед, образованный векторами a⃗=i+2j+3k\vec{\bm{a}} = \bm{i} + 2\bm{j} + 3\bm{k}a =i+2j+3k, b⃗=5i−4j+7k\vec{\bm{b}} = 5\bm{i} - 4\bm{j} + 7\bm{k}b=5i-4j+ 7k и c⃗=−5i+j+12k\vec{\bm{c}} = -5\bm{i} + \bm{j} + 12\bm{k}c=-5i+j+12k. Тогда объем параллелепипеда, описываемого этими векторами, будет равен
V=∣(a⃗×b⃗)⋅c⃗ ∣=∣−51121235−47∣V=290\begin{align*} V &= \lvert (\vec{a}\times\vec{b})\cdot\vec{c}\, \rvert\\\\ &= \begin{vmatrix} -5 и 1 и 12\\ 1 и 2 и 3\\ 5 и -4 и 7 \end{vmatrix}\\\\ V & = 290 \end{align*}VV=∣(a
×b
)⋅c
∣=∣
∣−51512−41237∣
∣=290 9003 вычислить объем параллелепипеда из его сторон?
Чтобы вычислить объем параллелепипед из его сторон (или длин ребер ), используйте формулу V = a∙b∙c∙√(1 + 2∙cos(α)∙cos(β)∙cos(γ) - cos² (α) - cos²(β) - cos²(γ)) , где:
-
V– Объем параллелепипеда; -
a,bиc– Три смежные стороны параллелепипеда; -
α– Уголок между сторонамиbиc; -
β– Уголок между сторонамиaиc; и -
γ– Уголок между сторонамиaиb.
Например, рассмотрим параллелепипед ABCDEFGH с длинами ребер a=5a = 5a=5, b=4b = 4b=4 и c=7c = 7c=7. Если ∠DAE=45°\угол \text{DAE} = 45\градус∠DAE=45°, ∠BAD=63°\угол \text{BAD} = 63\градус∠BAD=63° и ∠BAE=50 °\угол \text{ВАЕ} = 50\градус∠ВАЕ=50°, тогда объем параллелепипеда будет В = 5·4·7 √(1 + 2·cos(45)·cos(50)·cos(63) - cos²(45) - cos²(50) - cos²(63) = 75,83 .
Как do I calculate the surface area of a parallelepiped?
To calculate the surface area of a parallelepiped formed by the vectors a , b , and c , use the formula A = 2 × (∣a × b∣ + ∣b × c∣ + ∣a × c∣) , где:
-
∣a × b∣– Величина перекрестного произведения междуaиb; -
∣b × c∣– Величина перекрестного произведения междуbиc; и -
∣a × c∣– Величина перекрестного произведения междуaис.
В качестве альтернативы можно найти площадь поверхности из длин ребер a , b и c , используя формулу A = 2 × (a∙b∙sin(γ) + b∙c ∙sin(α) + a∙c∙sin(β)) , где:
-
α– Угол междуbиc; -
β– Угол междуaиc; и -
γ– Угол междуaиb.
Обратите внимание, что величина векторного произведения между двумя векторами a⃗\vec{a}a и b⃗\vec{b}b, заданная как ∣a⃗×b⃗∣\lvert \vec{a} \ раз \vec{b} \rvert∣a×b∣ равно площади параллелограмма , натянутого на эти векторы. Следовательно, складывая 90 166 величин 90 167 перекрестных произведений 90 166 трех векторов 90 167, описывающих 90 166 параллелепипедов и умножив его на два, получим площадь поверхности .
Например, рассмотрим параллелепипед ABCDEFGH с длинами ребер a=5a = 5a=5, b=4b = 4b=4 и c=7c = 7c=7. Если ∠DAE=45°\угол \text{DAE} = 45\градус∠DAE=45°, ∠BAD=63°\угол \text{BAD} = 63\градус∠BAD=63° и ∠BAE=50 °\угол \text{BAE} = 50\градус∠BAE=50°, тогда площадь поверхности будет равна
A= 2×(absin(α)+bcsin(β)+acsin(γ) )= 2×(5⋅4sin(63°)+4⋅7sin(45°)+5⋅7sin(50°))= 132,6\scriptsize \begin{align*} A =&\ 2 \times (ab\sin(α) + bc\sin(β) + ac\sin(γ))\\ =&\ 2 \times (5\cdot 4 \sin(63\степень) + 4\cdot7\sin(45\степень) \\ &+ 5\cdot 7 \sin(50 \степень))\\ =&\ 132,6 \end{align*}A=== 2×(absin(α)+bcsin(β)+acsin(γ)) 2×(5⋅4sin(63°)+4⋅7sin(45°)+5⋅ 7sin(50°)) 132,6
Как использовать этот объем калькулятора параллелепипеда – И калькулятор площади параллелепипеда
Этот объем калькулятора параллелепипеда является простым инструментом и легким в использовании. Он имеет три различных режима расчета, чтобы найти объем параллелепипеда с 3 векторами, 4 вершинами или с использованием длин ребер и углов:
Чтобы вычислить объем параллелепипеда по 3 векторам:
- Выберите опцию векторы aaa, bbb и ccc в поле Расчет с использованием поля .

- Введите значения компонентов каждого вектора.
- Этот объем калькулятора параллелепипеда будет отображать расчетный объем и площадь поверхности параллелепипеда в соответствующих полях в разделе Результаты .
- Выберите опцию векторы aaa, bbb и ccc в поле Расчет с использованием поля .
Чтобы вычислить объем параллелепипеда с 4 вершинами:
- Выберите опцию vertices p, q, r и s в поле Расчет с использованием поля .
- Введите координаты каждой вершины в соответствующее поле.
- Калькулятор отобразит вычисленные объем и площадь поверхности параллелепипеда в соответствующих полях раздела Результаты .
Чтобы вычислить объем параллелепипеда, используя длины ребер:
- Выберите опцию Длины и углы ребер в поле Расчет с использованием поля .
- Введите длины и углы ребер в соответствующие поля.

- Калькулятор отобразит вычисленные объем и площадь поверхности параллелепипеда в соответствующих полях раздела Результаты .
⚠️ Если ваш ввод равен , не принимается ни в одном из режимов расчета, это связано с тем, что вы ввели значения в другом режиме расчета, что делает невозможным обработку значений в текущем. Чтобы решить эту проблему, нажмите Перезагрузите кнопку в левом нижнем углу и снова введите значения, выбрав нужный режим расчета.
Часто задаваемые вопросы
Как определить, являются ли три вектора компланарными или коллинеарными?
If the volume of a parallelepiped described by the vectors
a,b, andcis equal to zero , then the vectors are coplanar . Другими словами, векторы
Другими словами, векторы a,bиcлежат в одной плоскости, еслиIf the surface area of a parallelepiped formed by the vectors
a,b, andcis equal to zero , then the vectors are collinear . Другими словами, векторыa,bиcколлинеарны, если2 × (∣a × b∣ + ∣b × c∣ = 0.
Сколько параллельных граней в параллелепипеде?
В параллелепипеде три пар параллельных граней. Попробуйте быстро произнести это предложение: Три пары параллельных параллелограммов в параллелепипеде!
Кришна Нелатуру
Рассчитайте с использованием . ..
..
Компоненты вектора 𝗮 (A₁𝗶 + A₂𝗷 + A₃𝗸)
Компоненты вектора 𝗯 (B₁𝗶 + B₂𝗷 + B₃𝗸)
Компоненты вектора 𝗰 (C₁𝗶 + C₃𝗸)
Результаты
Объем параллелепипеда
Площадь поверхности параллелепипеда
Посмотреть 38 похожих калькуляторов координатной геометрии 📈
Средняя скорость изменения Билинейная интерполяцияКатенарная кривая… Еще 35
Формулы объема для геометрических фигур.
Volume
— количество места, которое занимает объект; измеряется в кубических единицах.
Формулы объема геометрических фигур: Объем куба Объем призмы Объем параллелепипеда Объем прямоугольной призмы Объем пирамиды Объем тетраэдра Объем правильного кругового цилиндра Объем прямого кругового конуса Объем сферы
Онлайн-калькуляторы. Объемы геометрических фигур
Объем куба
Объем куба равен кубу длины его ребра.
Формула объема Куба:
V = a 3
где V - объем куба,
а - длина ребра.
См. также онлайн-калькулятор для расчета объема куба
Объем призмы
Объем призмы равен произведению площади основания на высоту призмы.
Формула объема призмы:
V = A b h
где V - объем призмы,
А б - площадь основания призмы,
h - высота призмы.
Онлайн-калькулятор для вычисления объема призмы
Формулы площади для вычисления площади основания призмы
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту параллелепипеда.
Формула объема параллелепипеда:
V = A b · h
где V - объем параллелепипеда,
А б - площадь основания параллелепипеда,
h - высота параллелепипеда.
См. также онлайн-калькулятор для расчета объема параллелепипеда
Объем прямоугольной призмы
Объем прямоугольной призмы равен произведению ее длины, ширины и высоты.
Формула объема прямоугольной призмы:
V = a · b · h
где V - объем прямоугольной призмы,
а - длина,
б - ширина,
ч - высота.
См. также онлайн-калькулятор для расчета объема прямоугольной призмы
Объем пирамиды
Объем пирамиды равен одной трети произведения площади ее основания на высоту.
Объемная формула пирамиды:
| V = | 1 | A B · H |
| 3 |
VOMID AR -VOMAM от A -VOLID OT VOMAMED OT VOMAM OF AR -VOMAM OF AR -VOMAM OF AR -VOMAM OF AR -VOMAM.
А б - площадь основания пирамиды,
h - высота пирамиды.
Онлайн-калькулятор для вычисления объема пирамиды
Формулы площади для вычисления площади основания пирамиды
Объем правильного круглого цилиндра
Объем правильного круглого цилиндра равен произведению площади его основания на высоту.
Формула объема прямого кругового цилиндра:
V = π R 2 h
V = A b h
900 объема цилиндра,А б - площадь основания,
R - радиус основания,
ч - высота,
π = 3,141592.
См. также онлайн-калькулятор для расчета объема цилиндра
Объем прямого круглого конуса
Объем прямого круглого конуса равен одной трети произведения площади его основания на высоту.
Объемная формула правого кругового конуса:
| V = | 1 | π R 2 H |
| 3 | ||
| 3 | ||
| 3 | ||
| 3 | ||
| 3 |
| V = | 1 | A B H |
| 3 |
, где V - Объем CONE,
, где V - объем CONE, CONE,.
А б - площадь основания,
R - радиус основания,
ч - высота,
π = 3,141592.
См. также онлайн-калькулятор для расчета объема конуса
Объем шара (тела)
Объем шара равен четырем третям куба радиуса, умноженному на число пи.
Объемная формула сферы (твердое вещество):
| V = | 4 | π R 3 |
| 3 | 0 | |
| 3 | 0 | |
| 3 |
R - радиус сферы,
π = 3,141592.
См. также онлайн-калькулятор для расчета объема шара
Формулы геометрии
Площадь. Формулы и свойства квадрата
Прямоугольник. Формулы и свойства прямоугольника
Параллелограмм.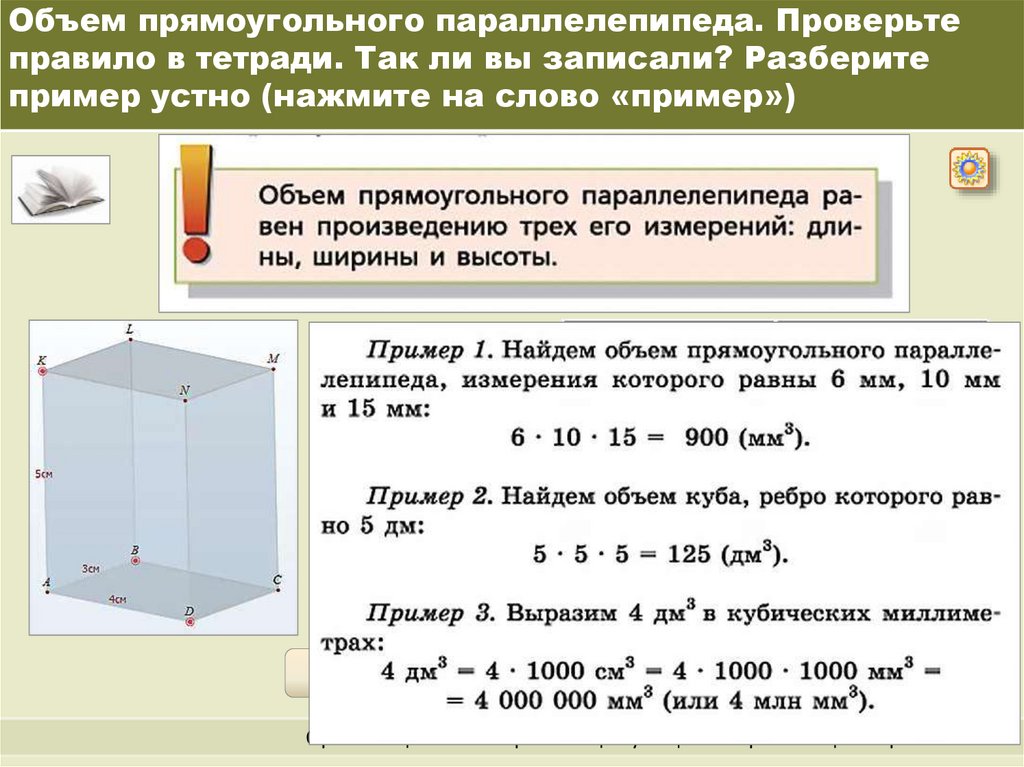 Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Круг, диск, сегмент, сектор. Формулы и свойства
Эллипс. Формулы и свойства эллипса
Цилиндр. Формулы и свойства цилиндра
Конус. Формулы, характеристики и свойства конуса
Область. Формулы площади
Периметр. Формулы периметра
Объем. Формулы объема
Формулы площади поверхности
Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Круг, диск, сегмент, сектор. Формулы и свойства
Эллипс. Формулы и свойства эллипса
Цилиндр. Формулы и свойства цилиндра
Конус. Формулы, характеристики и свойства конуса
Область. Формулы площади
Периметр. Формулы периметра
Объем. Формулы объема
Формулы площади поверхности
Все таблицы и формулы
Формула N-мерного объема - Джастин Скайчак
Используя эту форму, мы можем угадать формулу N-мерного объема:
Проверки работоспособности
Проверим эту формулу на простом примере: 4-мерный единичный куб, окруженный векторами $x_1 = \left< 1,0,0,0 \right>$, $x_2 = \left< 0,1,0,0 \right>$, $x_3 = \left< 0,0,1,0 \right>$ и $x_4 = \left< 0,0,0,1 \right> $.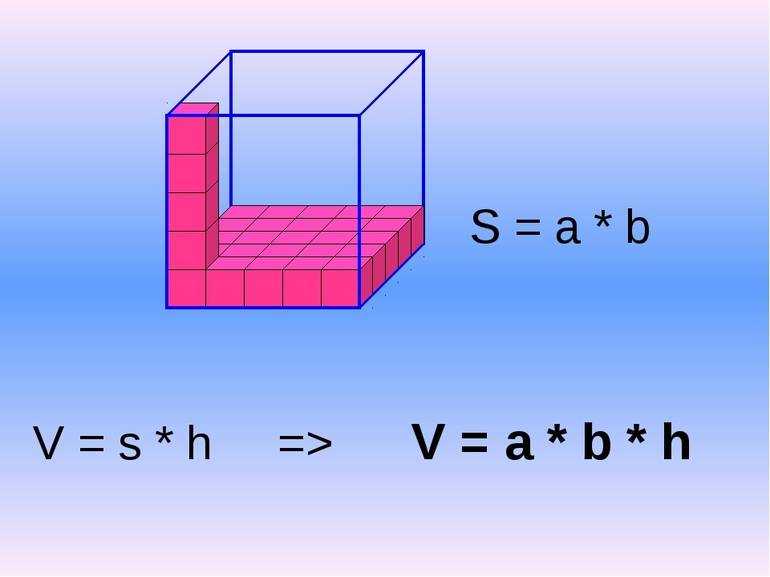
Теперь мы подошли к моменту, когда уже трудно «увидеть», что происходит.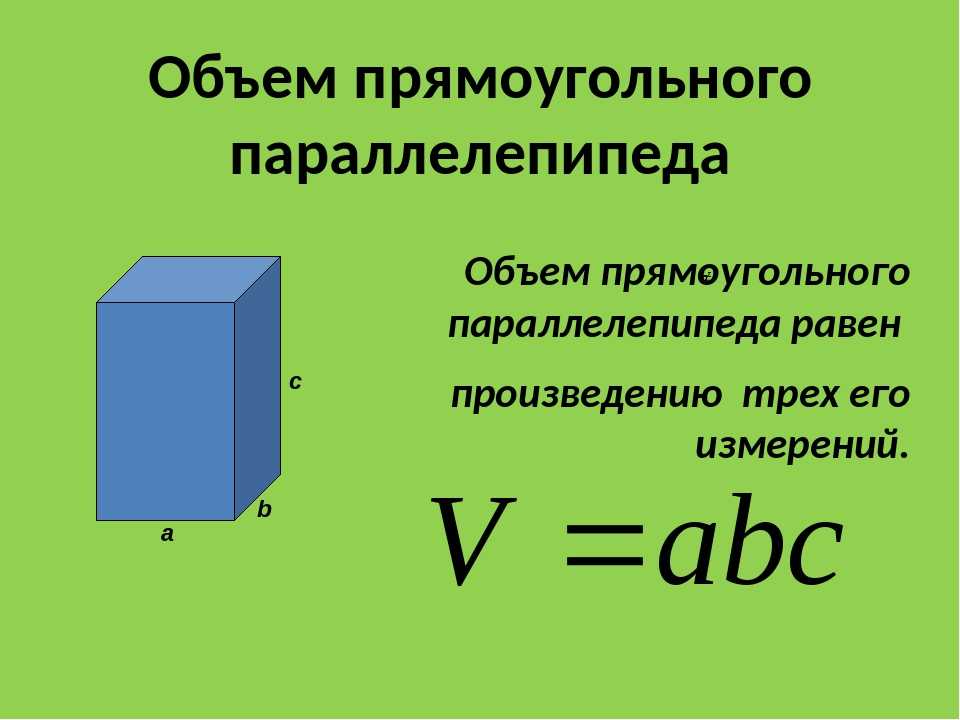 Но математика показывает нам закономерность, эта закономерность соответствует нашей интуиции в простом случае, и, учитывая, что трехмерный объем представляет собой сумму кратных двумерных объемов, кажется правдоподобным, что N-мерный объем может быть суммой кратных (N-1)-мерных объемов.
Но математика показывает нам закономерность, эта закономерность соответствует нашей интуиции в простом случае, и, учитывая, что трехмерный объем представляет собой сумму кратных двумерных объемов, кажется правдоподобным, что N-мерный объем может быть суммой кратных (N-1)-мерных объемов.
Более того, формула объема соответствует нашей интуиции, когда мы масштабируем вектор. Интуитивно, изменение масштаба вектора должно привести к изменению масштаба объема: например, если мы удвоим длину одной из сторон параллелограмма, площадь должна удвоиться.
Аналогично, если удвоить длину одной из сторон параллелепипеда, то объем должен удвоиться.
В более общем случае, если мы масштабируем отдельный вектор с коэффициентом $r$, то объем также должен быть масштабирован с коэффициентом $r$. Действительно, это относится к нашей формуле.
Конечно, мы только показали, что изменение масштаба первого вектора приводит к изменению масштаба объема.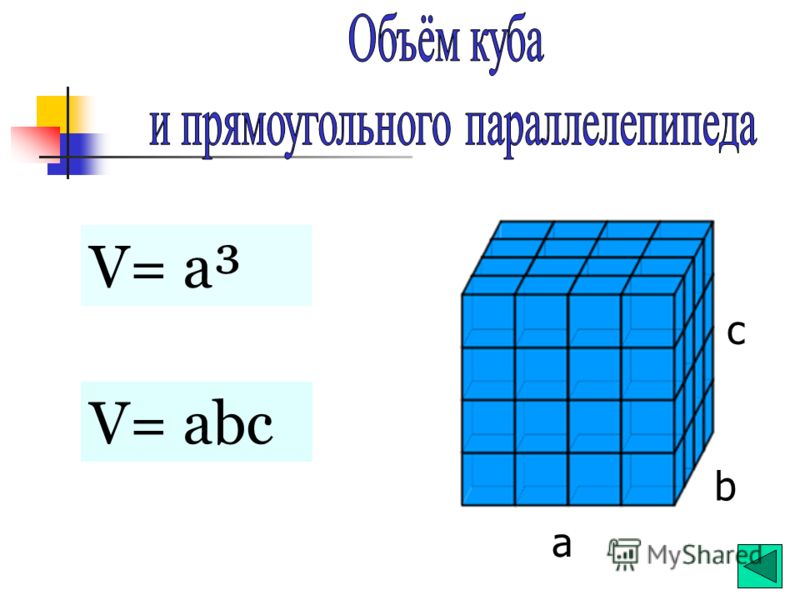 Однако мы можем использовать этот факт, чтобы показать, что изменение масштаба второго вектора также приводит к изменению масштаба объема.
Однако мы можем использовать этот факт, чтобы показать, что изменение масштаба второго вектора также приводит к изменению масштаба объема.
Мы могли бы продолжить, используя аналогичные аргументы, чтобы показать, что изменение масштаба 3-го, 4-го, так далее и N-го вектора имеет тот же эффект, что и изменение масштаба объема.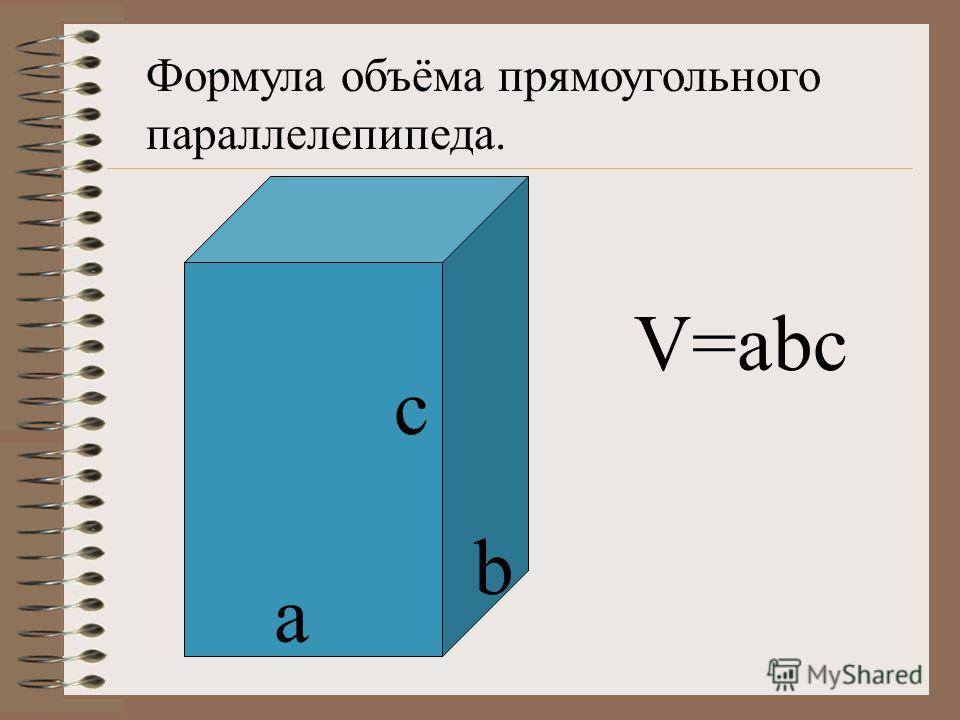
Заключительные замечания
К сожалению, эта формула объема неинтуитивна и громоздка для вычислений объема в многомерном пространстве.
Вскоре, однако, мы представим более интуитивную концепцию, называемую сдвигом , которая приведет нас к более простому и интуитивно понятному процессу вычисления многомерных объемов.
Формула объема, представленная в этой главе, по-прежнему заслуживает внимания, поскольку, хотя сдвиг дает нам процесс вычисления объема, он не дает нам формулы для вычисления объема.
Упражнения
Вычислить N-мерный беззнаковый объем $|V(x_1,x_2, \ldots,x_n)|$, заключенный в векторы $x_1,x_2, \ldots, x_n$. (Вы можете просмотреть решение, нажав на задачу.)
$\begin{align*} 1) \hspace{.5cm} x_1 &= \left< 1,0 \right> \\ x_2 &= \left< 0 ,2 \right> \end{align*}$Решение:
$\begin{align*} 2 \end{align*}$
$\begin{align*} 2) \hspace{.5cm} x_1 &= \left< 1,1 \right> \ \ x_2 &= \left< 1,2 \right> \end{align*}$
Решение:
$\begin{align*} 1 \end{align*}$
$\begin{align*} 3 ) \hspace{.
 5cm} x_1 &= \left< 3,4 \right> \\ x_2 &= \left< −1,2 \right> \end{align*}$
5cm} x_1 &= \left< 3,4 \right> \\ x_2 &= \left< −1,2 \right> \end{align*}$ Решение:
$\begin {align*} 10 \end{align*}$
$\begin{align*} 4) \hspace{.5cm} x_1 &= \left< 7,−3 \right> \\ x_2 &= \left< 2 ,−6 \right> \end{align*}$
Решение:
$\begin{align*} 36 \end{align*}$
$\begin{align*} 5) \hspace{.5cm} x_1 &= \left< 1,2,3 \right > \\ x_2 &= \left< 3,2,1 \right> \\ x_3 &= \left< 1,3,2 \right> \end{align*}$
Решение:
$\begin{ align*} 12 \end{align*}$
$\begin{align*} 6) \hspace{.5cm} x_1 &= \left< 2,0,−1 \right> \\ x_2 &= \left< 3,4,2 \right> \\ x_3 &= \left< 0,−1,2 \right> \end{align*}$
Решение:
$\begin{align*} 23 \end{align*}$
$\begin{align*} 7) \hspace{.5cm} x_1 &= \left< 1,5,7 \right> \\ x_2 &= \left< 3,2,1 \right> \\ x_3 &= \left< 0,1,2 \right> \end{align*}$
Решение:
$\begin{align*} 6 \end{align*}$
$\begin{align*} 8) \hspace{.5cm} x_1 &= \left< 4,0,−5 \right> \\ x_2 &= \left< −9, 1 , 7 \right> \\ x_3 &= \left< 2,−5,4 \right> \end{align*}$
Решение:
$\begin{align*} 59\end{align*}$
$\begin{align*} 9) \hspace{.

 Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Объём тела или вместимость сосуда определяется его формой и линейными размерами.
 141592.
141592.
 Сколько подарочной бумаги требуется для упаковки подарочной коробки?
Сколько подарочной бумаги требуется для упаковки подарочной коробки?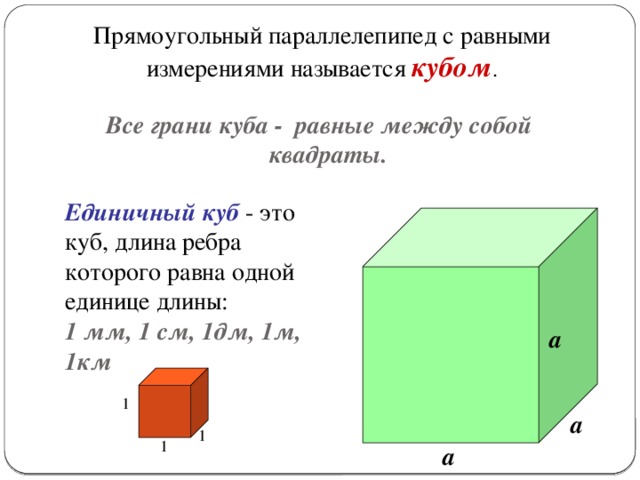
 Таким образом, vol(A) масштабируется как |c|.basev2v1height—-→base34v2v134heightbaseheightv1v2v3—-→base43heightv1v243v3
Таким образом, vol(A) масштабируется как |c|.basev2v1height—-→base34v2v134heightbaseheightv1v2v3—-→base43heightv1v243v3


 Другими словами, векторы
Другими словами, векторы