Y sin x график. График функции y=sin x
«Йошкар-Олинский техникум сервисных технологий»
Построение и исследование графика тригонометрической функции y=sinx в табличном процессоре MS Excel
/методическая разработка/
Йошкар – Ола
Тема . Построение и исследование графика тригонометрической функции y = sinx в табличном процессоре MS Excel
Тип урока – интегрированный (получение новых знаний)
Цели:
Дидактическая цель — исследовать поведение графиков тригонометрической функции y = sinx в зависимости от коэффициентов с помощью компьютера
Обучающие:
1. Выяснить изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов
2. Показать внедрение компьютерных технологий в обучение математике, интеграцию двух предметов: алгебры и информатики.
3. Формировать навыки использования компьютерных технологий на уроках математики
4. Закрепить навыки исследования функций и построения их графиков
Развивающие:
1. Развивать познавательный интерес учащихся к учебным дисциплинам и умение применять свои знания в практических ситуациях
2. Развивать умения анализировать, сравнивать, выделять главное
3. Способствовать повышению общего уровня развития студентов
Воспитывающие :
1. Воспитывать самостоятельность, аккуратность, трудолюбие
2. Воспитывать культуру диалога
Формы работы на уроке – комбинированная
Дидактическое оснащение и оборудование:
1. Компьютеры
2. Мультимедийный проектор
4. Раздаточный материал
5. Слайды презентации
Ход урока
I . Организация начала урока
· Приветствие студентов и гостей
· Настрой на урок
II . Целеполагание и актуализация темы
Для исследования функции и построения ее графика требуется много времени, приходится выполнять много громоздких вычислений, это не удобно, на помощь приходят компьютерные технологии.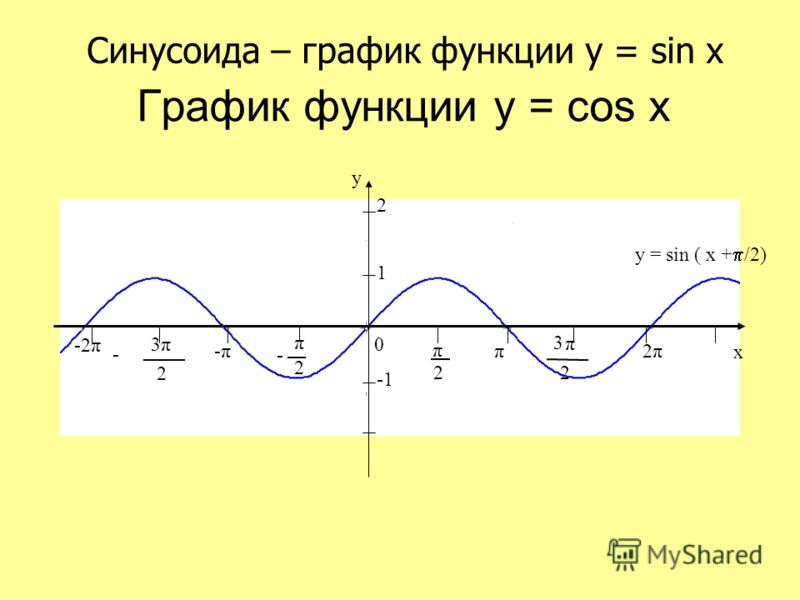
Сегодня мы научимся строить графики тригонометрических функций в среде табличного процессора MS Excel 2007.
Тема нашего занятия «Построение и исследование графика тригонометрической функцииy = sinx в табличном процессоре»
Из курса алгебры нам известна схема исследования функции и построения ее графика. Давайте вспомним как это сделать.
Слайд 2
Схема исследования функции
1. Область определения функции (D(f))
2. Область значения функции Е(f)
3. Определение четности
4. Периодичность
5. Нули функции (y=0)
6. Промежутки знакопостоянства (у>0, y
7. Промежутки монотонности
8. Экстремумы функции
III . Первичное усвоение нового учебного материала
Откройте программу MS Excel 2007.
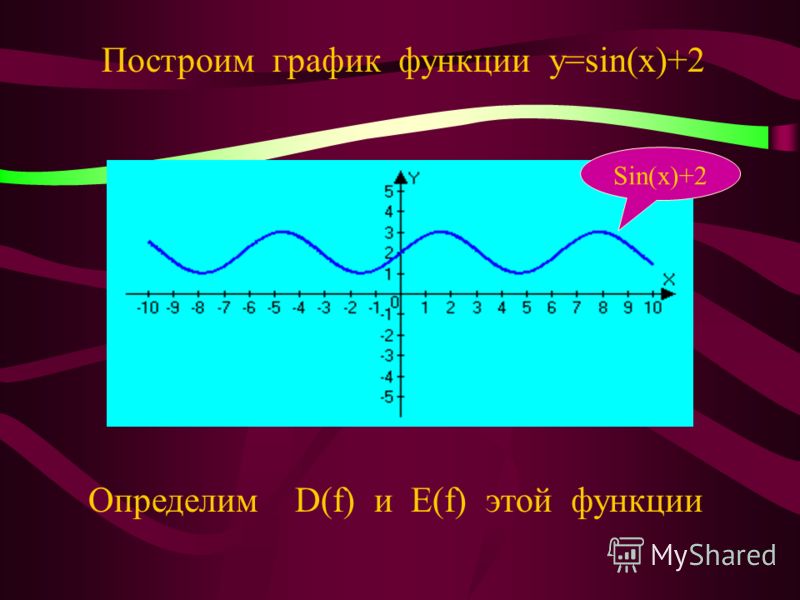
Построим график функции y=sinx
Построение графиков в табличном процессоре MS Excel 2007
График данной функции будем строить на отрезке x Є [-2π; 2π]
Значения аргумента будем брать с шагом, чтобы график получился более точным.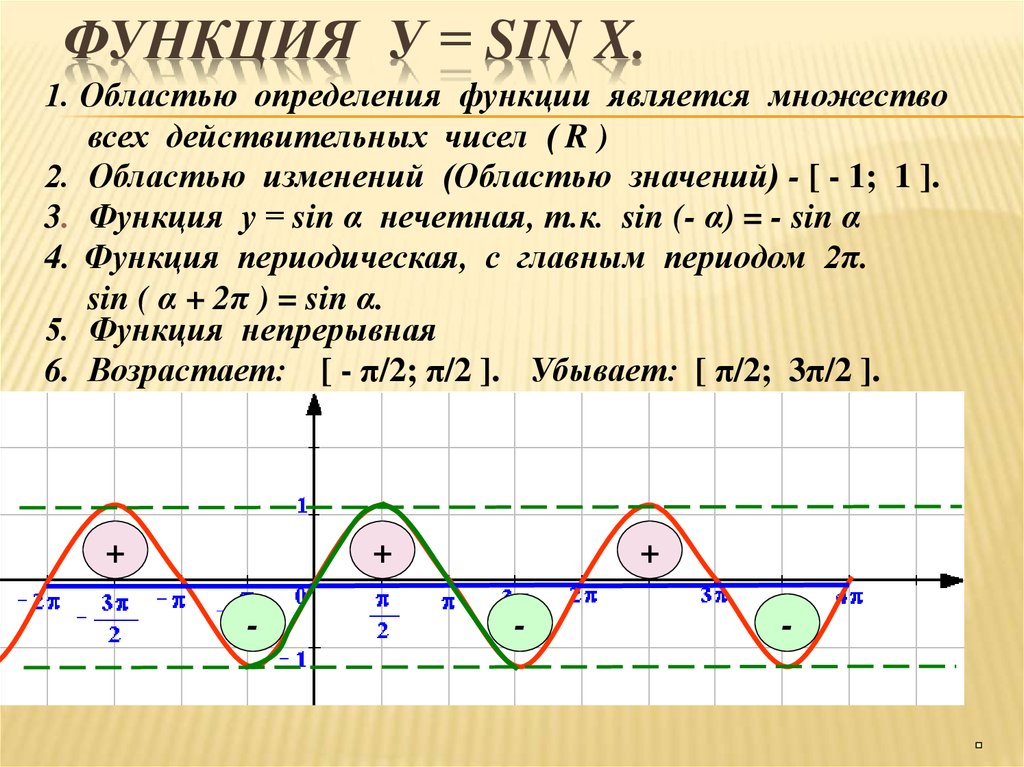
Т. к. редактор работает с числами, переведем радианы в числа, зная что П ≈ 3,14 . (таблица перевода в раздаточном материале).
1. Находим значение функции в точке х=-2П. Для остальных значение аргумента соответствующие значения функции редактор вычисляет автоматически.
2. Теперь у нас имеется таблица со значениями аргумента и функции. С помощью этих данных мы должны построить график этой функции с помощью мастера диаграмм.
3. Для построения графика надо выделить нужный диапазон данных, строки со значениями аргумента и функции
4..jpg»>
Выводы записываем в тетрадь (Слайд 5)
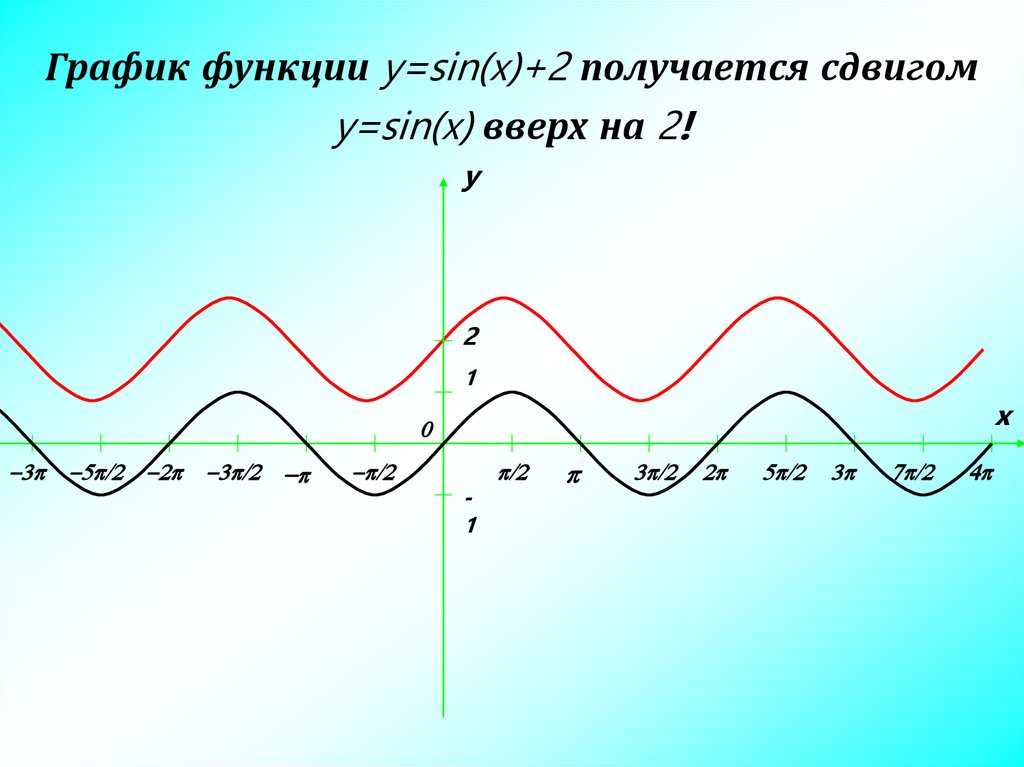
Вывод. График функции вида у=sinx+k получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОУ на k единиц
Если k >0, то график смещается вверх на k единиц
Если k
Построение и исследование функции вида у= k *sinx, k — const
Задание 2.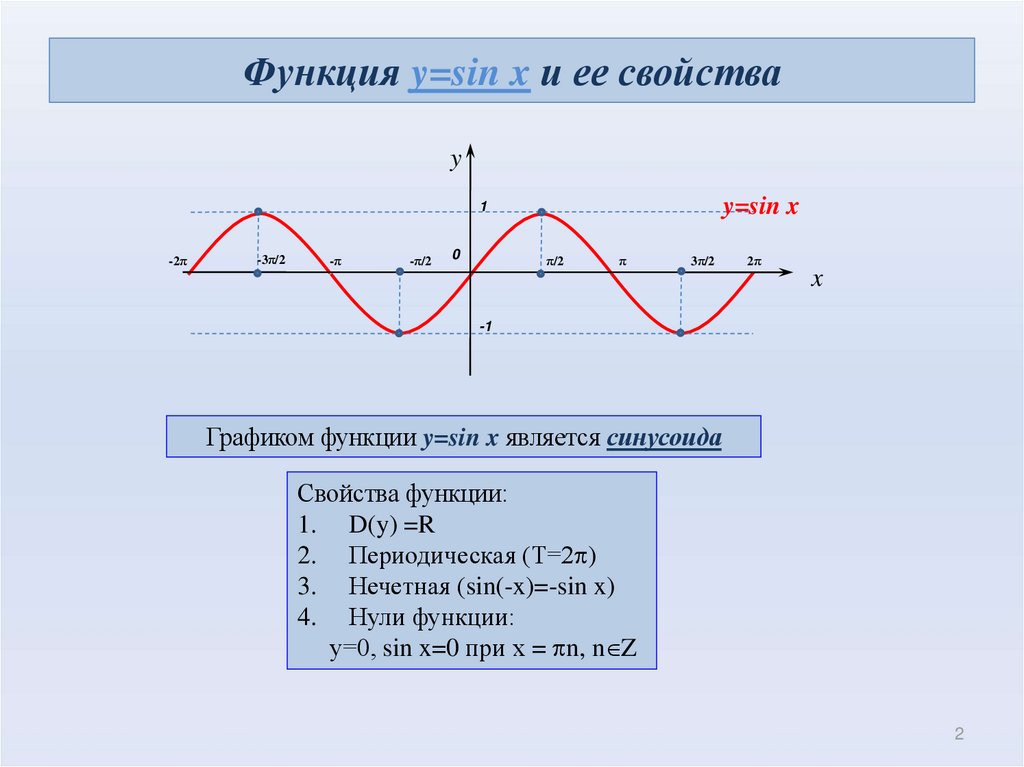 На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.
На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.
(Чтобы заново не задавать значение аргумента давайте скопируем имеющиеся значения. Теперь вам надо задать формулу, и по полученной таблице построить график.)
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
https://pandia.ru/text/78/510/images/image005_66.gif»>x , на интервале (-2π; 2π) и проследите как изменяется вид графика.
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 8)
https://pandia.ru/text/78/510/images/image008_35.jpg»>
Выводы записываем в тетрадь (Слайд 11)
Вывод. График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
Если k >1, то график смещается вправо вдоль оси ОХ
Если 0
IV . Первичное закрепление полученных знаний
Дифференцированные карточки с заданием на построение и исследование функции при помощи графика
Y=6 *sin(x) | Y= 1-2 sin х | Y= — sin (3х+ ) | |
1. Область определения | |||
2. Область значения | |||
3. | |||
4. Периодичность | |||
5. Промежутки знакопостоянства | |||
6. Промежутки монотонности | |||
Функция возрастает | |||
Функция убывает | |||
7. Экстремумы функции | |||
Минимум | |||
Максимум |
V . Организация домашнего задания
Организация домашнего задания
Построить график функции y=-2*sinх+1 , исследовать и проверить правильность построения в среде электронной таблицы Microsoft Excel. (Слайд 12)
VI . Рефлексия
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис.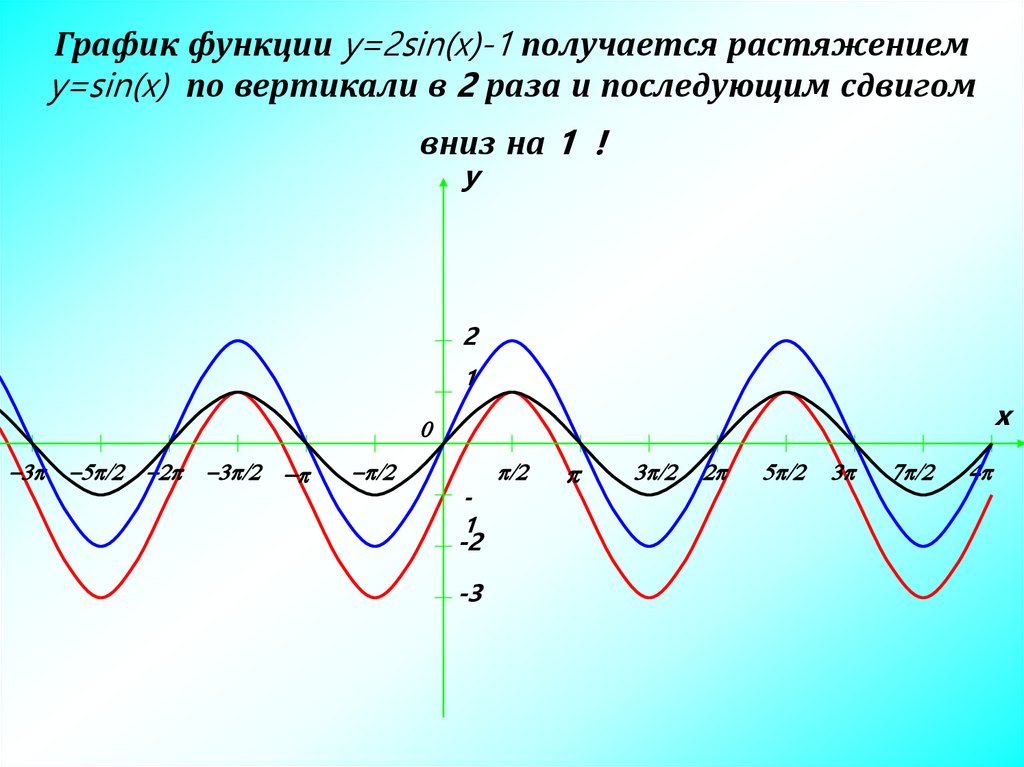 1).
1).
Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис. 2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график. Свойства неоднократно будут использоваться при решении задач.
Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
Х y O Единичная тригонометрическая окружность
3 =180 3,14 рад R R О Р М R Рассмотрим окружность радиуса R. Построим MOP: МР = R 1 радиан Величина МОР равна 1 радиан МР =1рад МОР 57 17= 1рад Радианная мера угла
4 Длина окружности выражается формулой C=2 R, где R – радиус окружности. 3, Окружность, радиус которой равен 1, называется … Точки М,Р,К,N – назовем узловыми.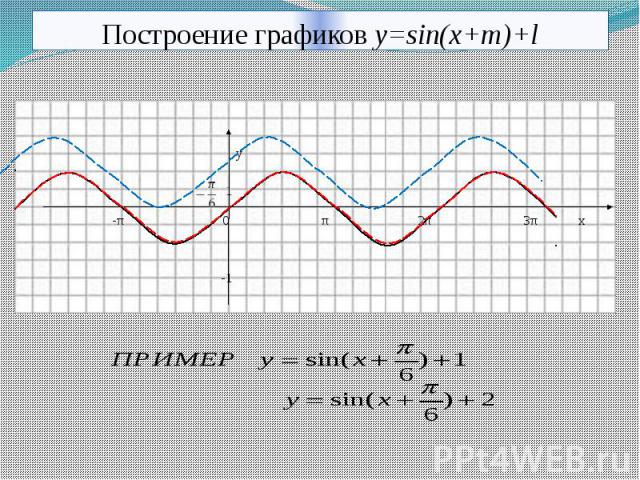 Отметим точки А,В,С. Длину единичной окружности удобно измерять в радианах. Если R=1, то С=2 рад! Наименование радиан обычно опускают. y х К Р С В А Длина дуги половины окружности равна рад. М N рад – четверть длины окружности рад – три четверти длины окружности О 1 единичной Радианная мера угла
uk-badge uk-margin-small-right»>
5 Градусная мера Радианная мера0 Итак, величину угла поворота точки, а также величину дуги единичной окружности, можно задавать: I четверть II четверть III четверть IV четверть О в градусной мере в радианной мере Радианная мера угла 0 2 I четверть II четверть III четверть IV четверть О 2
Отметим точки А,В,С. Длину единичной окружности удобно измерять в радианах. Если R=1, то С=2 рад! Наименование радиан обычно опускают. y х К Р С В А Длина дуги половины окружности равна рад. М N рад – четверть длины окружности рад – три четверти длины окружности О 1 единичной Радианная мера угла
uk-badge uk-margin-small-right»>
5 Градусная мера Радианная мера0 Итак, величину угла поворота точки, а также величину дуги единичной окружности, можно задавать: I четверть II четверть III четверть IV четверть О в градусной мере в радианной мере Радианная мера угла 0 2 I четверть II четверть III четверть IV четверть О 2
6 «Размотаем» окружность как нить на координатный луч с началом в точке 0 Установим соответствие между множеством действительных чисел на числовой прямой и точками единичной окружности. Такое «разматывание» можно продолжать бесконечно. 3,14 0 Построение графика х y=sin x
13 Преобразование графиков Функция Преобразование 1 y= f (x) + mПараллельный перенос вдоль оси OY на m единиц 2 y= f (x – n)Параллельный перенос вдоль оси OX на n единиц 3 y=А f (x) Растяжение вдоль оси OY относительно оси OX в А раз 4 y= f (k x)Сжатие вдоль оси OX относительно оси OY в k раз 5 y= – f (x) Симметричное отражение относительно оси OX 6 y= f (– x) Симметричное отражение относительно оси OY y = f (x)
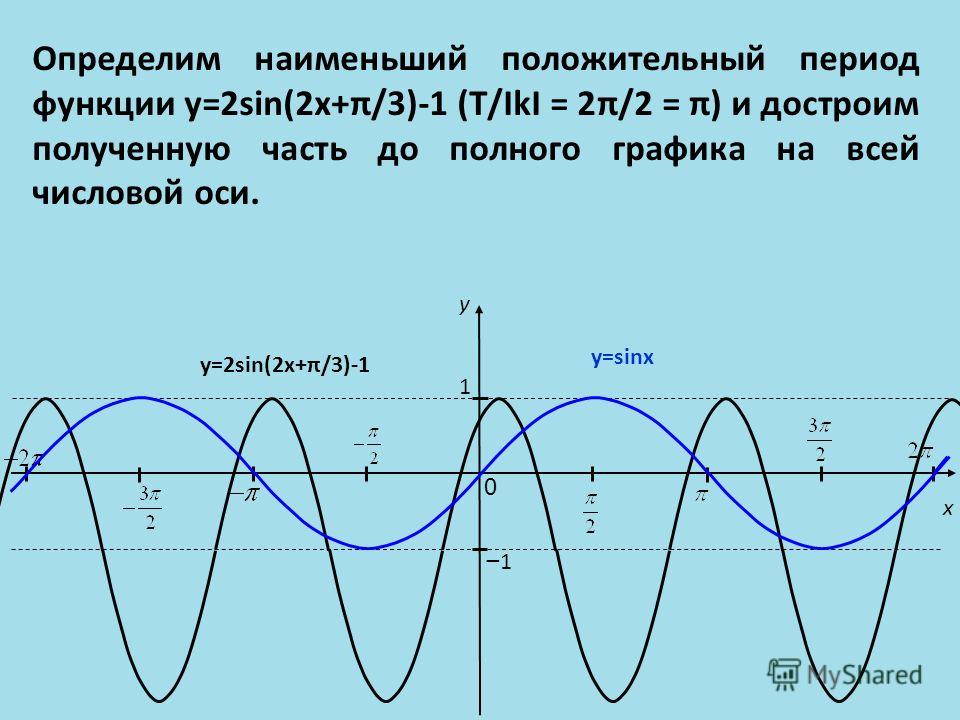
20 Построим график функции y= 3 sin(2x+ /3)–2 Этапы построения: 1.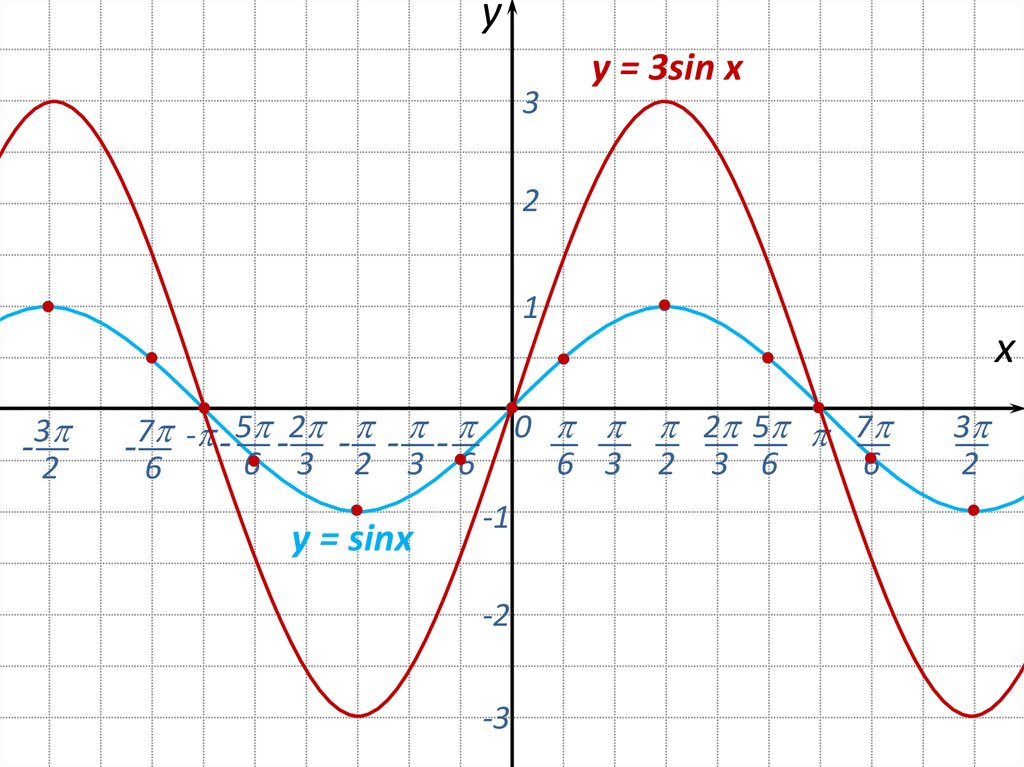 y= sin x – синусоида 3. y= sin(2x+ /3) – перенос на /3 единиц влево 4. y= 3 sin(2x+ /3) – растяжение в 3 раза вдоль оси Oy 2. y= sin 2x – сжатие в 2 раза вдоль оси Ох 5. y= 3 sin(2x+ /3)–2 – перенос на 2 единицы вниз
y= sin x – синусоида 3. y= sin(2x+ /3) – перенос на /3 единиц влево 4. y= 3 sin(2x+ /3) – растяжение в 3 раза вдоль оси Oy 2. y= sin 2x – сжатие в 2 раза вдоль оси Ох 5. y= 3 sin(2x+ /3)–2 – перенос на 2 единицы вниз
26 Преобразование графиков Функция Преобразование 1 y=sin(kx)Сжатие вдоль оси OX относительно оси OY в k раз 2 y=sin(x–m)Параллельный перенос вдоль оси OX на m единиц 3 y=А sin x Растяжение вдоль оси OY относительно оси OX в А раз 4 y=sin x+nПараллельный перенос вдоль оси OY на n единиц 5 y= – sin x Симметричное отражение относительно оси OX 6 y= sin (–x) Симметричное отражение относительно оси OY y = Asin(kx–n)+m
28 1.Функция y=sin x существует при всех действительных значениях x, причем, график ее является сплошной линией (без разрывов), т.е. функция непрерывна. 2.Функция y=sin x нечетная, ее график симметричен относительно начала координат 3.Наибольшие и наименьшие значения. Все возможные значения функции sinx ограничены неравенством -1 sinx 1, причем 4.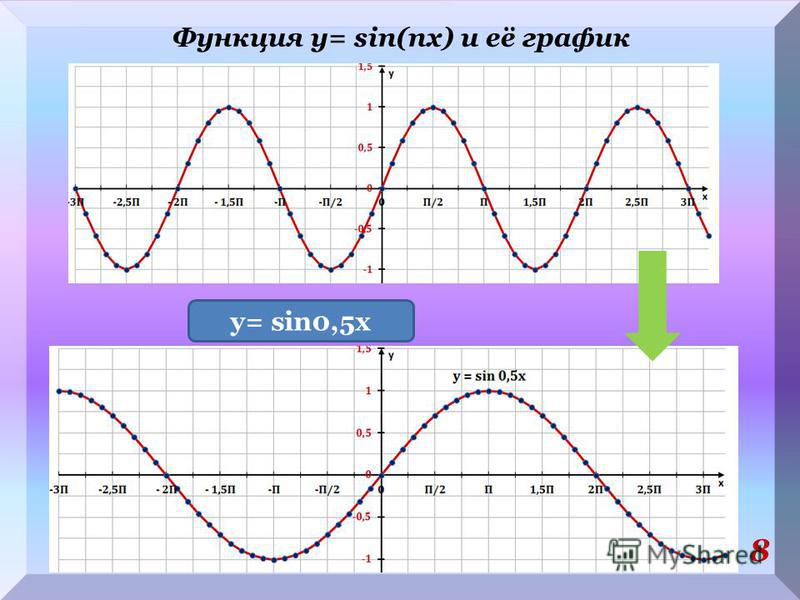 Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если
Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис.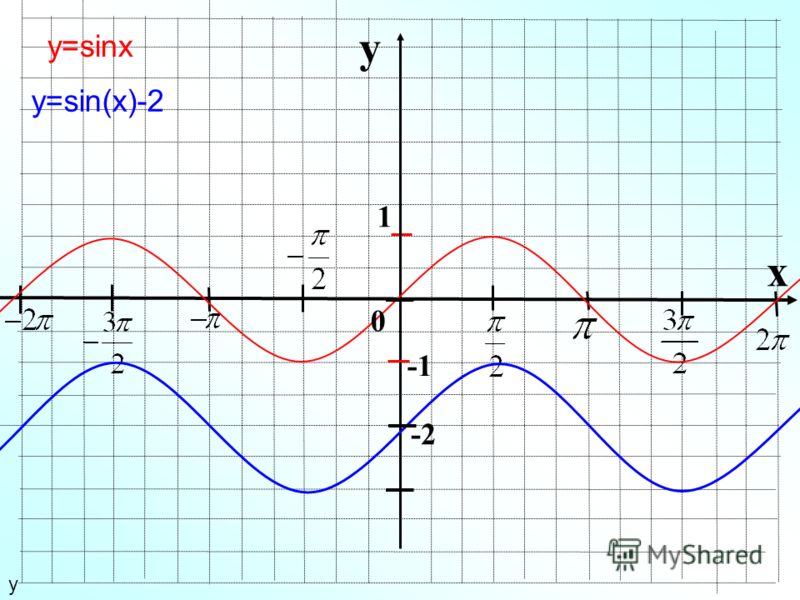 1).
1).
Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис. 2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график.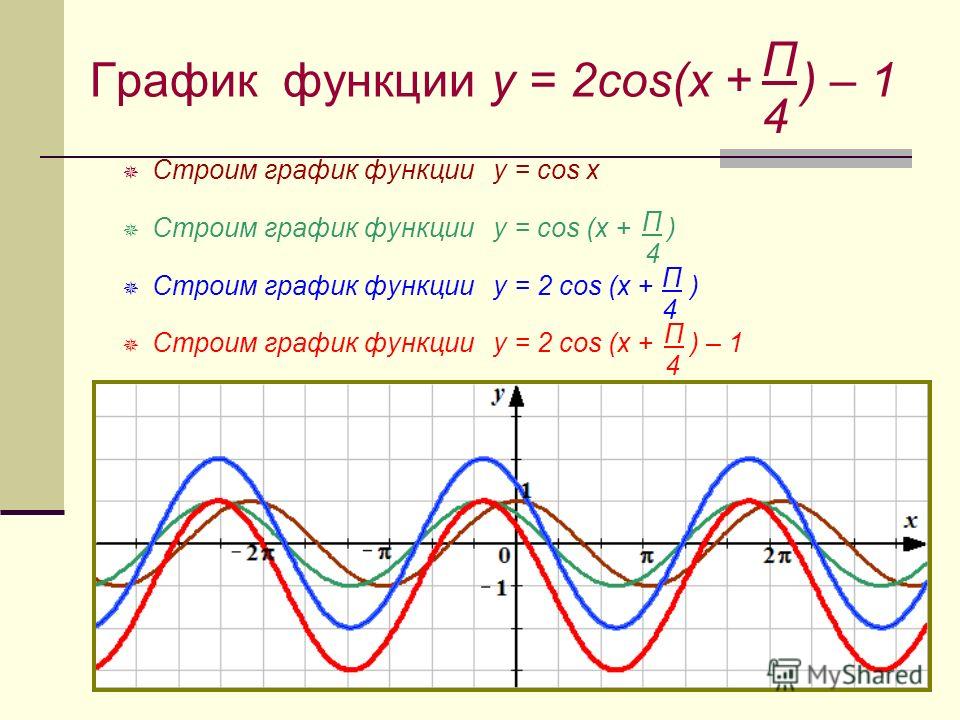 Свойства неоднократно будут использоваться при решении задач.
Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
Функция y = sin x
Графиком функции является синусоида.
Полную неповторяющуюся часть синусоиды называют волной синусоиды.
Половину волны синусоиды называют полуволной синусоиды (или аркой).
Свойства функции y = sin x :
3) Это нечетная функция. 4) Это непрерывная функция.
6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает. 7) На промежутках функция принимает положительные значения. 8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn]. 9) Точки минимума функции: -π/2 + 2πn. |
Для построения графика функции y = sin x удобно применять следующие масштабы:
На листе в клетку за единицу отрезка примем длину в две клетки.
На оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π.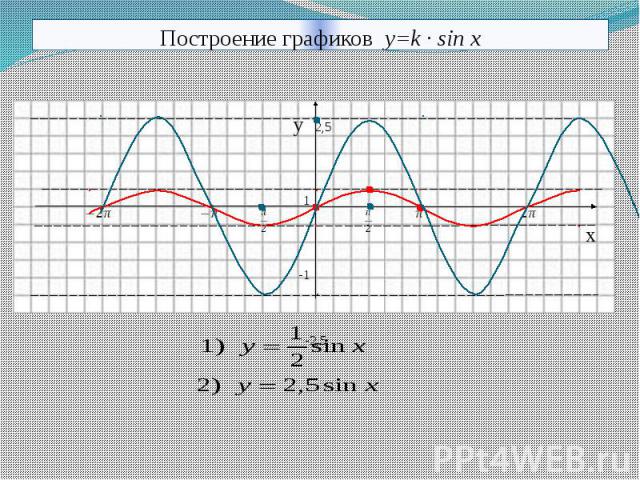 Это значения x .
Это значения x .
На оси y отметим 1, включающий две клетки.
Составим таблицу значений функции, применяя наши значения x :
√3 | √3 |
Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1). Это график функции y = sin x на отрезке . Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна.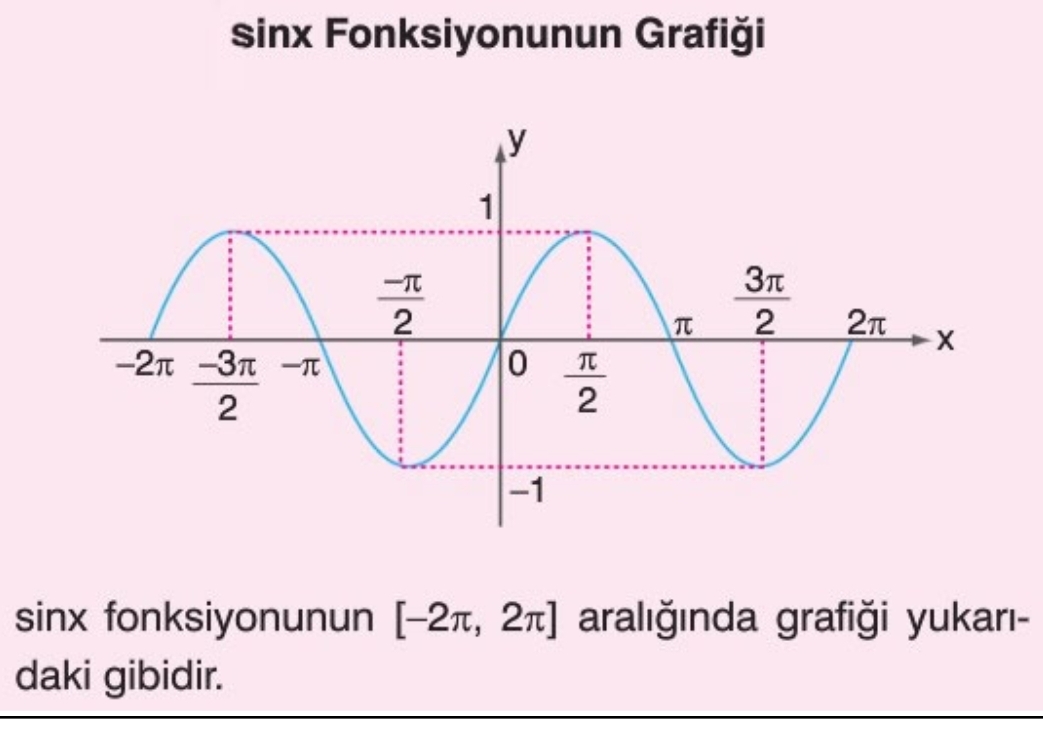 Это график функции y = sin x на отрезке [-π; π].
Это график функции y = sin x на отрезке [-π; π].
Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.
Функция y = cos x .
Графиком функции является синусоида (ее иногда называют косинусоидой).
Свойства функции y = cos x :
1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это четная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: 6) На отрезке функция убывает, на отрезке [π; 2π] – возрастает. 7) На промежутках [-π/2 + 2πn; π/2 + 2πn] функция принимает положительные значения. 8) Промежутки возрастания: [-π + 2πn; 2πn]. 9) Точки минимума функции: π + 2πn. 10) Функция ограничена сверху и снизу. Наименьшее значение функции –1, 11) Это периодическая функция с периодом 2π (Т = 2π) |
Функция y = mf (x ).
Возьмем предыдущую функцию y = cos x . Как вы уже знаете, ее графиком является синусоида. Если мы умножим косинус этой функции на определенное число m, то волна растянется от оси x (либо сожмется, в зависимости от величины m).
Эта новая волна и будет графиком функции y = mf(x), где m – любое действительное число.
Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m.
Если m x на коэффициент m. Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график.
Функция y = f (kx ).
Если функция y = mf (x ) приводит к растяжению синусоиды от оси x либо сжатию к оси x , то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y .
Причем k – любое действительное число.
При 0 k y на коэффициент k. Если k > 1, то синусоида сжимается к оси y на коэффициент k.
Составляя график этой функции, можно сначала построить одну полуволну синусоиды, а по ней достроить затем весь график.
Функция y = tg x .
Графиком функции y = tg x является тангенсоида.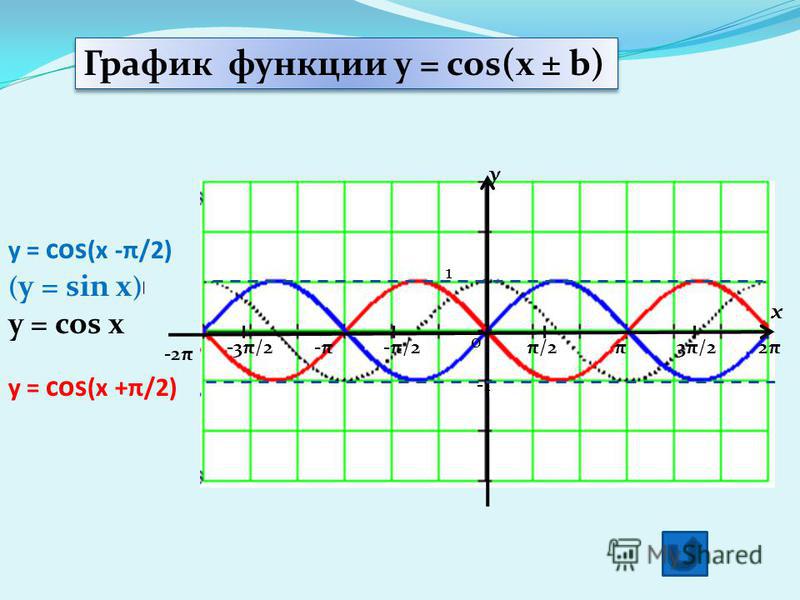
Достаточно построить часть графика на промежутке от 0 до π/2, а затем можно симметрично продолжить ее на промежутке от 0 до 3π/2.
Свойства функции y = tg x :
Функция y = ctg x
Графиком функции y = ctg x также является тангенсоида (ее иногда называют котангенсоидой).
Свойства функции y = ctg x :
Решить график синуса y sin x 3. Графики функций
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции.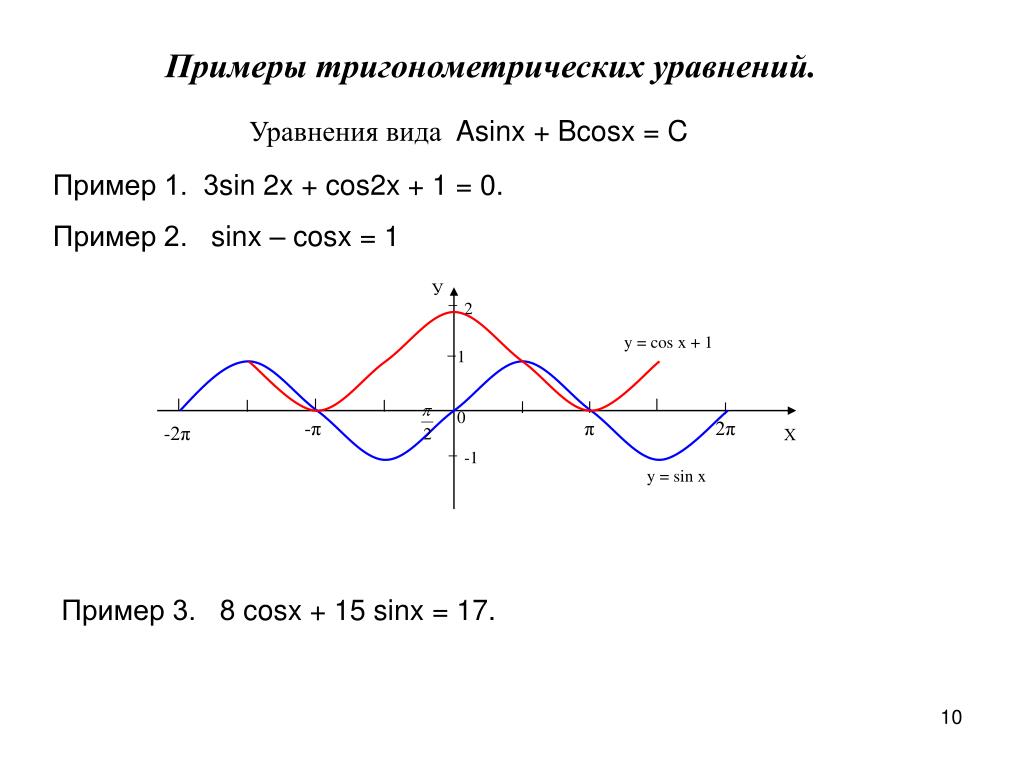 Этот закон соответствия и называется функцией.
Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).
Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис. 2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.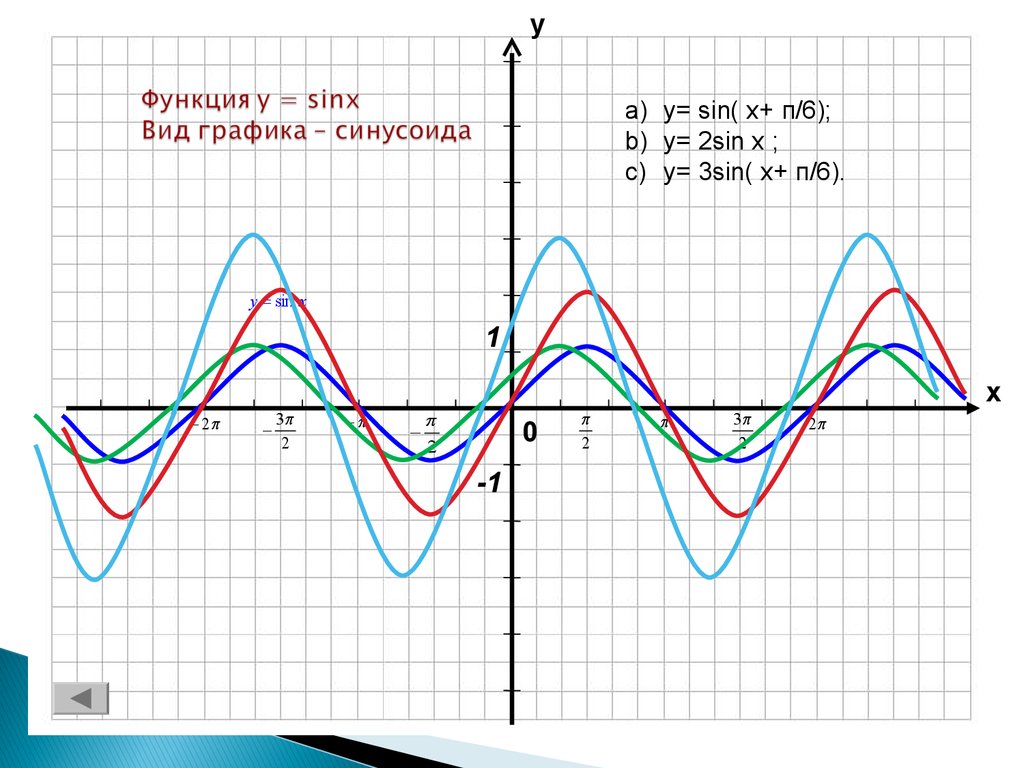
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график. Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях).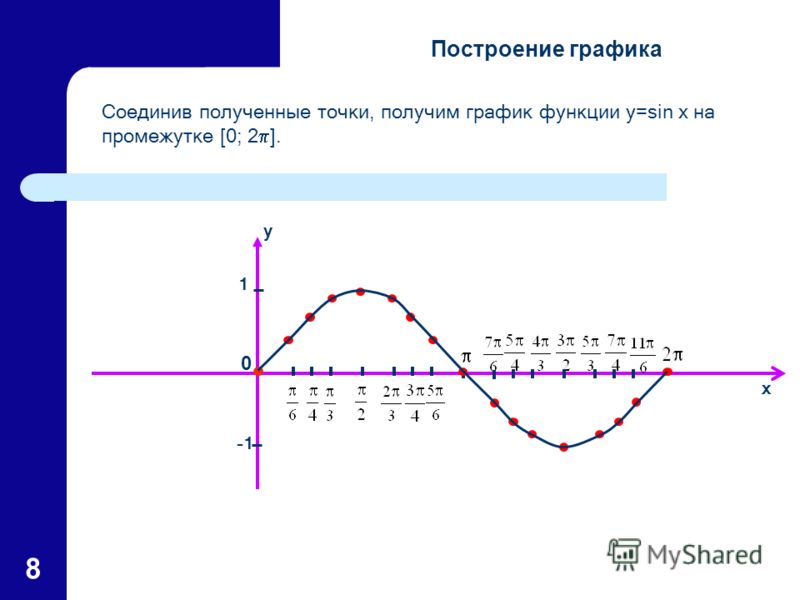 Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях).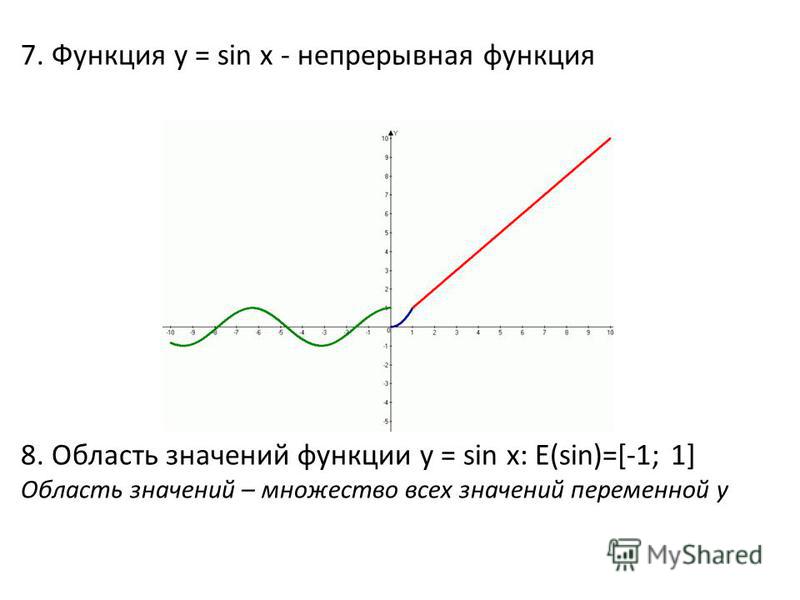 Задачник для общеобразовательных учреждений (профильный уровень) под ред.
Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
Х y O Единичная тригонометрическая окружность
3 =180 3,14 рад R R О Р М R Рассмотрим окружность радиуса R. Построим MOP: МР = R 1 радиан Величина МОР равна 1 радиан МР =1рад МОР 57 17= 1рад Радианная мера угла
4 Длина окружности выражается формулой C=2 R, где R – радиус окружности. 3, Окружность, радиус которой равен 1, называется … Точки М,Р,К,N – назовем узловыми. Отметим точки А,В,С. Длину единичной окружности удобно измерять в радианах. Если R=1, то С=2 рад! Наименование радиан обычно опускают. y х К Р С В А Длина дуги половины окружности равна рад. М N рад – четверть длины окружности рад – три четверти длины окружности О 1 единичной Радианная мера угла
uk-badge uk-margin-small-right»>
5 Градусная мера Радианная мера0 Итак, величину угла поворота точки, а также величину дуги единичной окружности, можно задавать: I четверть II четверть III четверть IV четверть О в градусной мере в радианной мере Радианная мера угла 0 2 I четверть II четверть III четверть IV четверть О 2
6 «Размотаем» окружность как нить на координатный луч с началом в точке 0 Установим соответствие между множеством действительных чисел на числовой прямой и точками единичной окружности. Такое «разматывание» можно продолжать бесконечно. 3,14 0 Построение графика х y=sin x
Такое «разматывание» можно продолжать бесконечно. 3,14 0 Построение графика х y=sin x
13 Преобразование графиков Функция Преобразование 1 y= f (x) + mПараллельный перенос вдоль оси OY на m единиц 2 y= f (x – n)Параллельный перенос вдоль оси OX на n единиц 3 y=А f (x) Растяжение вдоль оси OY относительно оси OX в А раз 4 y= f (k x)Сжатие вдоль оси OX относительно оси OY в k раз 5 y= – f (x) Симметричное отражение относительно оси OX 6 y= f (– x) Симметричное отражение относительно оси OY y = f (x)
20 Построим график функции y= 3 sin(2x+ /3)–2 Этапы построения: 1. y= sin x – синусоида 3. y= sin(2x+ /3) – перенос на /3 единиц влево 4. y= 3 sin(2x+ /3) – растяжение в 3 раза вдоль оси Oy 2. y= sin 2x – сжатие в 2 раза вдоль оси Ох 5. y= 3 sin(2x+ /3)–2 – перенос на 2 единицы вниз
26 Преобразование графиков Функция Преобразование 1 y=sin(kx)Сжатие вдоль оси OX относительно оси OY в k раз 2 y=sin(x–m)Параллельный перенос вдоль оси OX на m единиц 3 y=А sin x Растяжение вдоль оси OY относительно оси OX в А раз 4 y=sin x+nПараллельный перенос вдоль оси OY на n единиц 5 y= – sin x Симметричное отражение относительно оси OX 6 y= sin (–x) Симметричное отражение относительно оси OY y = Asin(kx–n)+m
28 1.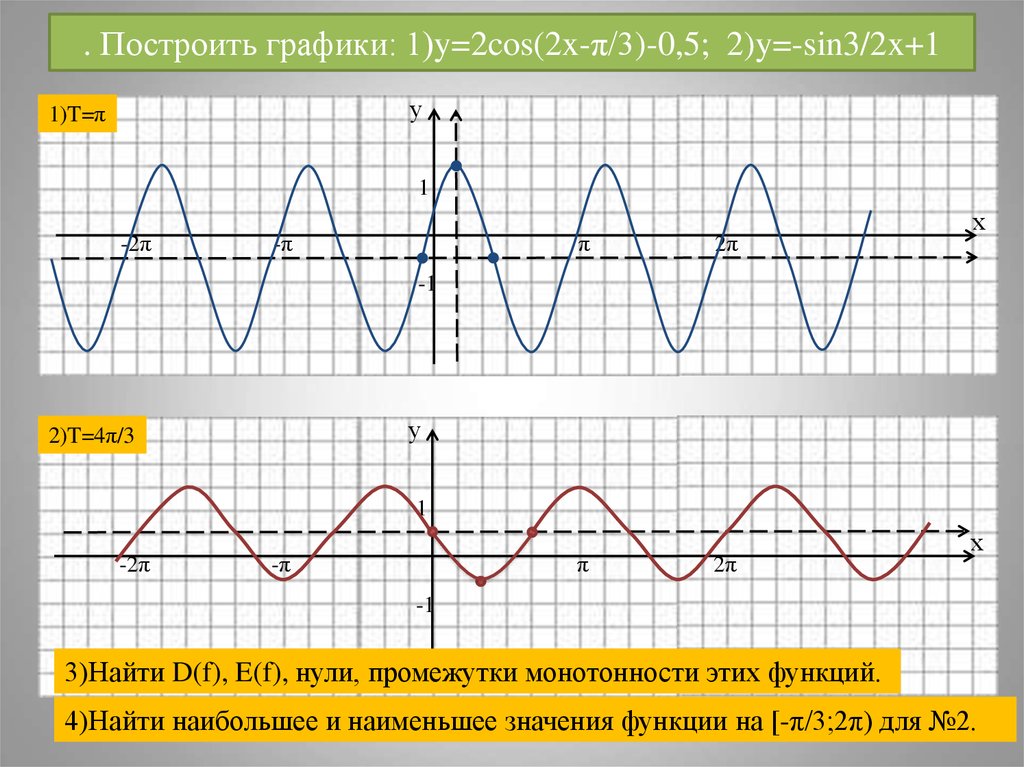 Функция y=sin x существует при всех действительных значениях x, причем, график ее является сплошной линией (без разрывов), т.е. функция непрерывна. 2.Функция y=sin x нечетная, ее график симметричен относительно начала координат 3.Наибольшие и наименьшие значения. Все возможные значения функции sinx ограничены неравенством -1 sinx 1, причем 4. Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если
Функция y=sin x существует при всех действительных значениях x, причем, график ее является сплошной линией (без разрывов), т.е. функция непрерывна. 2.Функция y=sin x нечетная, ее график симметричен относительно начала координат 3.Наибольшие и наименьшие значения. Все возможные значения функции sinx ограничены неравенством -1 sinx 1, причем 4. Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если
|BD| — длина дуги окружности с центром в точке A .
α — угол, выраженный в радианах.
Синус (sin
α
) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos
α
) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.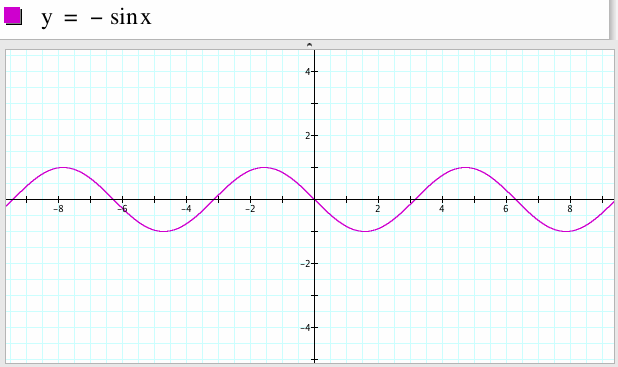
Принятые обозначения
;
;
.
;
;
.
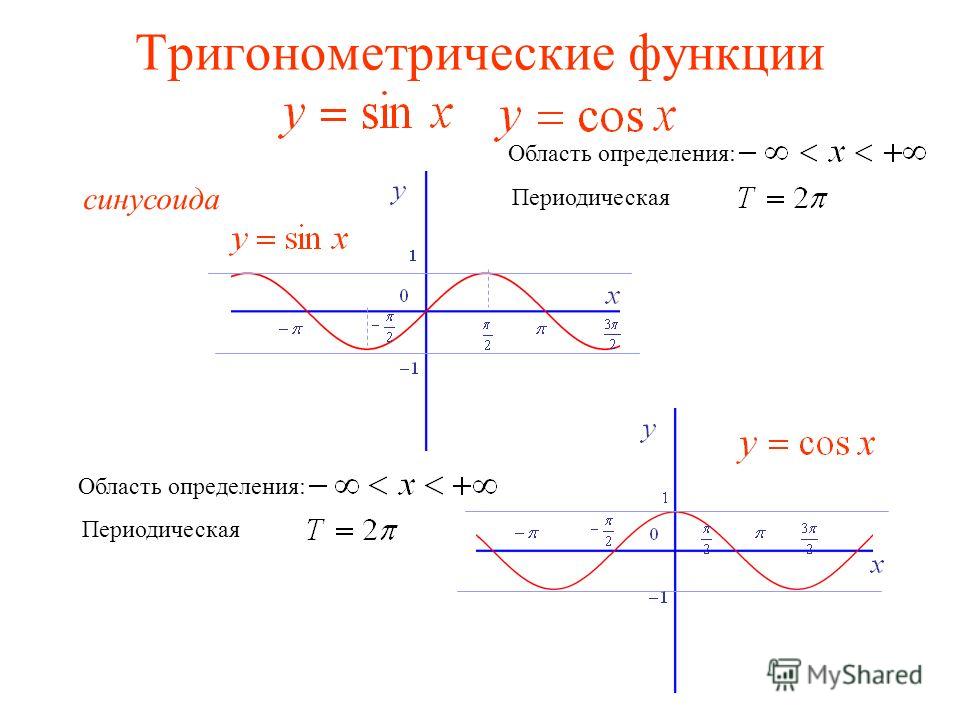
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
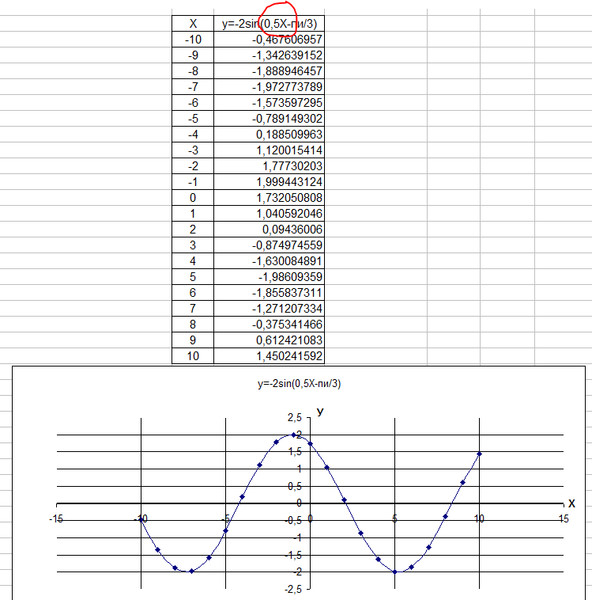
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
См. также:
ГРАФИКИ ФУНКЦИЙ
Функция синус
— множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная .
Функция нечетная: sin(−x)=−sin x для всех х ∈ R .
Функция периодическая
sin(x+2π· k) = sin x, где k ∈ Z для всех х ∈ R .
sin x = 0 при x = π·k , k ∈ Z .
sin x > 0 (положительная) для всех x ∈ (2π·k , π+2π·k ), k ∈ Z .
sin x (отрицательная) для всех x ∈ (π+2π·k , 2π+2π·k ), k ∈ Z .
Функция косинус
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная .
Функция четная: cos(−x)=cos x для всех х ∈ R .
Функция периодическая с наименьшим положительным периодом 2π :
cos(x+2π· k ) = cos x, где k ∈ Z для всех х ∈ R .
| cos x = 0 при | |
| cos x > 0 для всех | |
| cos x для всех | |
| Функция возрастает от −1 до 1 на промежутках: | |
| Функция убывает от −1 до 1 на промежутках: | |
| Наибольшее значение функции sin x = 1 в точках: | |
| Наименьшее значение функции sin x = −1 в точках: |
Множество значений функции — вся числовая прямая, т.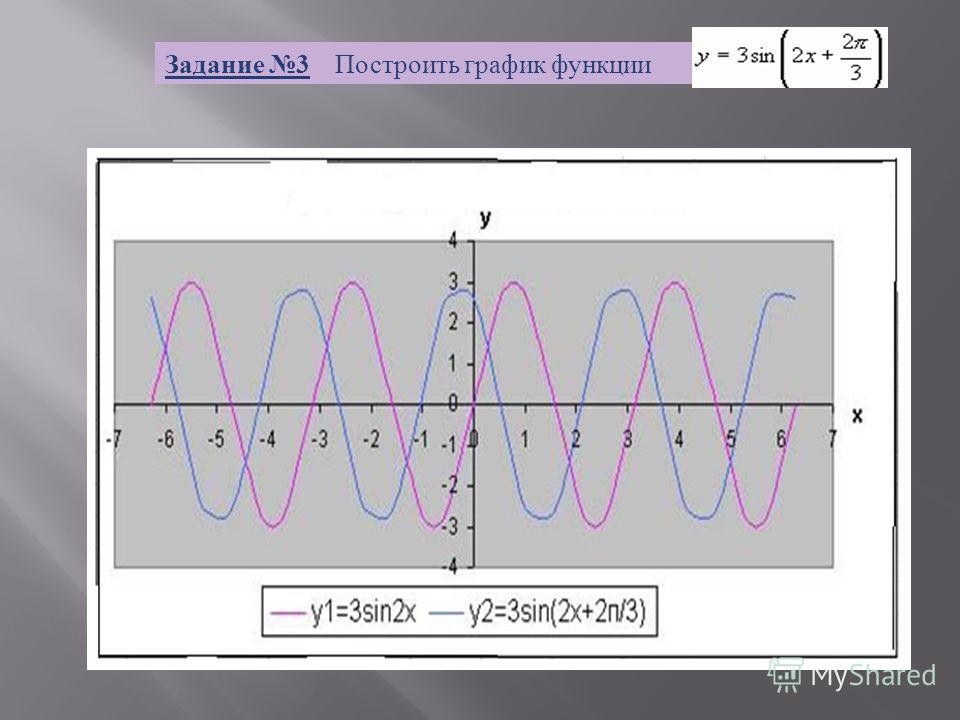 е. тангенс — функция неограниченная .
е. тангенс — функция неограниченная .
Функция нечетная: tg(−x)=−tg x
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом π , т.е. tg(x+π· k ) = tg x, k ∈ Z для всех х из области определения.
Функция котангенс
Множество значений функции — вся числовая прямая, т.е. котангенс — функция неограниченная .
Функция нечетная: ctg(−x)=−ctg x для всех х из области определения.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом π , т.е. ctg(x+π· k )=ctg x, k ∈ Z для всех х из области определения.
Функция арксинус
Область определения функции — отрезок [-1; 1]
Множество значений функции — отрезок -π
/2 arcsin x π
/2, т.е. арксинус — функция ограниченная .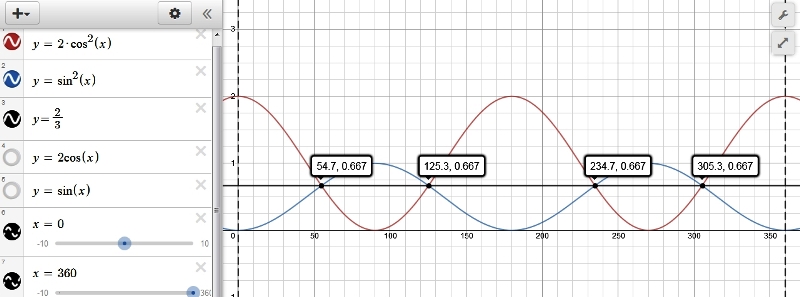
Функция нечетная: arcsin(−x)=−arcsin x для всех х ∈ R .
График функции симметричен относительно начала координат.
На всей области определения.
Функция арккосинус
Область определения функции — отрезок [-1; 1]
Множество значений функции — отрезок 0 arccos x π , т.е. арккосинус — функция ограниченная .
Функция является возрастающей на всей области определения.
Функция арктангенс
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок 0 π, т.е. арктангенс — функция ограниченная .
Функция нечетная: arctg(−x)=−arctg x для всех х ∈ R .
График функции симметричен относительно начала координат.
Функция является возрастающей на всей области определения.
Функция арккотангенс
Область определения функции — множество R всех действительных чисел.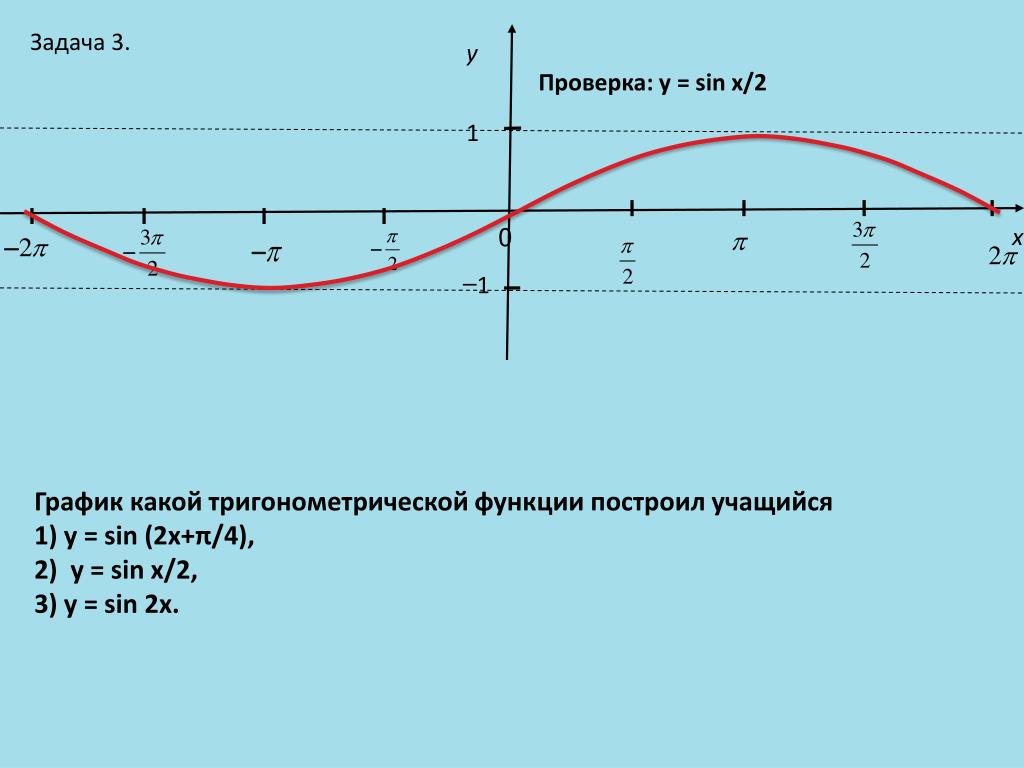
Множество значений функции — отрезок 0 π, т.е. арккотангенс — функция ограниченная .
Функция не является ни четной, ни нечетной.
График функции несимметричен ни относительно начала координат, ни относительно оси Оy.
Функция является убывающей на всей области определения.
, Конкурс «Презентация к уроку»
Презентация к уроку
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Железо ржавеет, не находя себе применения,
стоячая вода гниет или на холоде замерзает,
а ум человека, не находя себе применения, чахнет.
Леонардо да Винчи
Используемые технологии: проблемного
обучения, критического мышления,
коммуникативного общения.
Цели:
- Развитие познавательного интереса к обучению.
- Изучение свойств функции у = sin x.
- Формирование практических навыков построения графика функции у = sin x на основе изученного теоретического материала.
Задачи:
1. Использовать имеющийся потенциал знаний о свойствах функции у = sin x в конкретных ситуациях.
2. Применять осознанное установление связей между аналитической и геометрической моделями функции у = sin x.
Развивать инициативу, определенную готовность и интерес к поиску решения; умение принимать решения, не останавливаться на достигнутом, отстаивать свою точку зрения.
Воспитывать у учащихся познавательную активность, чувство ответственности, уважения друг к другу, взаимопонимания, взаимоподдержки, уверенности в себе; культуру общения.
Ход урока
1 этап. Актуализация опорных знаний, мотивация изучения нового материала
«Вход в урок».
На доске написаны 3 утверждения:
- Тригонометрическое уравнение sin t = a всегда
имеет решения.

- График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
- График тригонометрической функции можно построить, используя одну главную полуволну.
Учащиеся обсуждают в парах: верны ли утверждения? (1 минута). Затем результаты первоначального обсуждения (да, нет) вносятся в таблицу в столбец «До».
Учитель ставит цели и задачи урока.
2. Актуализация знаний (фронтально на модели тригонометрического круга ).
Мы уже познакомились с функцией s = sin t.
1) Какие значения может принимать переменная t. Какова область определения этой функции?
2) В каком промежутке заключены значения выражения sin t. Найти наибольшее и наименьшее значения функции s = sin t.
3) Решите уравнение sin t = 0.
4) Что происходит с ординатой точки при ее
движении по первой четверти? (ордината
увеличивается). Что происходит с ординатой точки
при ее движении по второй четверти? (ордината
постепенно уменьшается).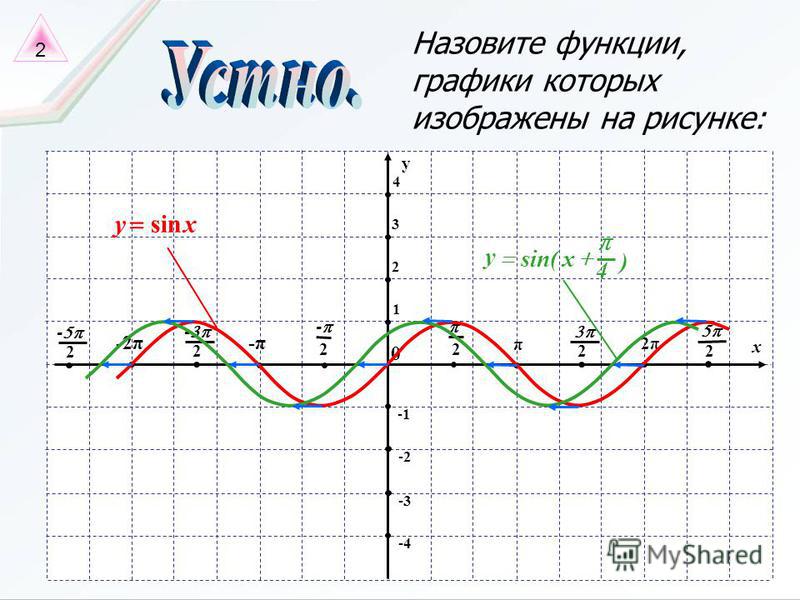 Как это связано с
монотонностью функции? (функция s = sin t возрастает
на отрезке и
убывает на отрезке ).
Как это связано с
монотонностью функции? (функция s = sin t возрастает
на отрезке и
убывает на отрезке ).
5) Запишем функцию s = sin t в привычном для нас виде у = sin x (строить будем в привычной системе координат хОу) и составим таблицу значений этой функции.
| х | 0 | ||||||
| у | 0 | 1 | 0 |
2 этап. Восприятие, осмысление, первичное закрепление, непроизвольное запоминание
4 этап. Первичная систематизация знаний и способов деятельности, их перенос и применение в новых ситуациях
6. № 10.18 (б,в)
№ 10.18 (б,в)
5 этап. Итоговый контроль, коррекция, оценка и самооценка
7. Возвращаемся к утверждениям (начало урока), обсуждаем, используя свойства тригонометрической функции у = sin x, и заполняем в таблице столбец «После».
8. Д/з: п.10, №№ 10.7(а), 10.8(б), 10.11(б), 10.16(а)
График функции y sin x 2. График функции y=sin x
«Йошкар-Олинский техникум сервисных технологий»
Построение и исследование графика тригонометрической функции y=sinx в табличном процессоре MS Excel
/методическая разработка/
Йошкар – Ола
Тема . Построение и исследование графика тригонометрической функции y = sinx в табличном процессоре MS Excel
Тип урока – интегрированный (получение новых знаний)
Цели:
Дидактическая цель — исследовать поведение графиков тригонометрической функции y = sinx в зависимости от коэффициентов с помощью компьютера
Обучающие:
1. Выяснить изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов
Выяснить изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов
2. Показать внедрение компьютерных технологий в обучение математике, интеграцию двух предметов: алгебры и информатики.
3. Формировать навыки использования компьютерных технологий на уроках математики
4. Закрепить навыки исследования функций и построения их графиков
Развивающие:
1. Развивать познавательный интерес учащихся к учебным дисциплинам и умение применять свои знания в практических ситуациях
2. Развивать умения анализировать, сравнивать, выделять главное
3. Способствовать повышению общего уровня развития студентов
Воспитывающие :
1. Воспитывать самостоятельность, аккуратность, трудолюбие
2. Воспитывать культуру диалога
Формы работы на уроке – комбинированная
Дидактическое оснащение и оборудование:
1. Компьютеры
2. Мультимедийный проектор
Мультимедийный проектор
4. Раздаточный материал
5. Слайды презентации
Ход урока
I . Организация начала урока
· Приветствие студентов и гостей
· Настрой на урок
II . Целеполагание и актуализация темы
Для исследования функции и построения ее графика требуется много времени, приходится выполнять много громоздких вычислений, это не удобно, на помощь приходят компьютерные технологии.
Сегодня мы научимся строить графики тригонометрических функций в среде табличного процессора MS Excel 2007.
Тема нашего занятия «Построение и исследование графика тригонометрической функцииy = sinx в табличном процессоре»
Из курса алгебры нам известна схема исследования функции и построения ее графика. Давайте вспомним как это сделать.
Слайд 2
Схема исследования функции
1. Область определения функции (D(f))
2. Область значения функции Е(f)
3. Определение четности
Определение четности
4. Периодичность
5. Нули функции (y=0)
6. Промежутки знакопостоянства (у>0, y
7. Промежутки монотонности
8. Экстремумы функции
III . Первичное усвоение нового учебного материала
Откройте программу MS Excel 2007.
Построим график функции y=sinx
Построение графиков в табличном процессоре MS Excel 2007
График данной функции будем строить на отрезке x Є [-2π; 2π]
Значения аргумента будем брать с шагом, чтобы график получился более точным.
Т. к. редактор работает с числами, переведем радианы в числа, зная что П ≈ 3,14 . (таблица перевода в раздаточном материале).
1. Находим значение функции в точке х=-2П. Для остальных значение аргумента соответствующие значения функции редактор вычисляет автоматически.
2. Теперь у нас имеется таблица со значениями аргумента и функции. С помощью этих данных мы должны построить график этой функции с помощью мастера диаграмм.
3. Для построения графика надо выделить нужный диапазон данных, строки со значениями аргумента и функции
4..jpg»>
Выводы записываем в тетрадь (Слайд 5)
Вывод. График функции вида у=sinx+k получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОУ на k единиц
Если k >0, то график смещается вверх на k единиц
Если k
Построение и исследование функции вида у= k *sinx, k — const
Задание 2. На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.
(Чтобы заново не задавать значение аргумента давайте скопируем имеющиеся значения. Теперь вам надо задать формулу, и по полученной таблице построить график.)
Сравниваем полученные графики.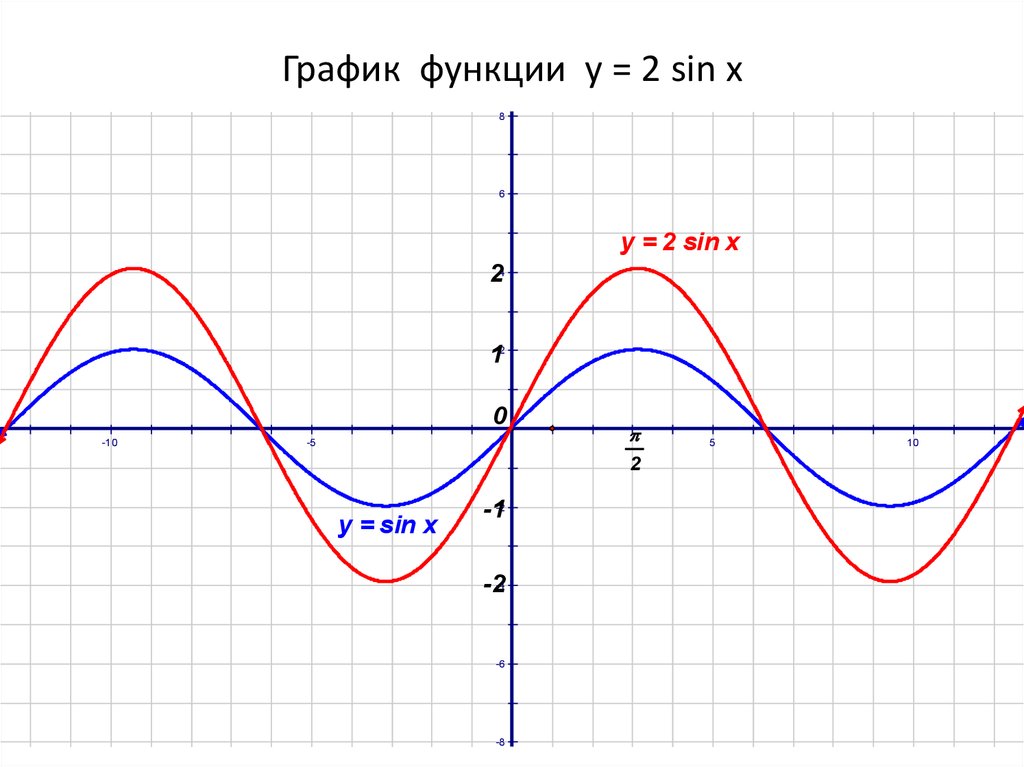 Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
https://pandia.ru/text/78/510/images/image005_66.gif»>x , на интервале (-2π; 2π) и проследите как изменяется вид графика.
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 8)
https://pandia.ru/text/78/510/images/image008_35.jpg»>
Выводы записываем в тетрадь (Слайд 11)
Вывод. График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
Если k >1, то график смещается вправо вдоль оси ОХ
Если 0
IV . Первичное закрепление полученных знаний
Дифференцированные карточки с заданием на построение и исследование функции при помощи графика
Y=6 *sin(x) | Y= 1-2 sin х | Y= — sin (3х+ ) | |
1. | |||
2. Область значения | |||
3. Четность | |||
4. Периодичность | |||
5. Промежутки знакопостоянства | |||
6. Промежутки монотонности | |||
Функция возрастает | |||
Функция убывает | |||
7. | |||
Минимум | |||
Максимум |
V . Организация домашнего задания
Построить график функции y=-2*sinх+1 , исследовать и проверить правильность построения в среде электронной таблицы Microsoft Excel. (Слайд 12)
VI . Рефлексия
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у = sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:
С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Функция y= sin x, её свойства и график .
МБОУ «СОШ №2 г.Щигры Курской области»
Петрищева Л.Д.
Пояснительная записка:
Изучение математики направлено на достижение, в первую очередь, целей интеллектуального развития школьников, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем.
В структуре изучаемой дисциплины «Математика» выделяется следующий раздел: «Тригонометрические функции». Содержание раздела «Тригонометрические функции » включает тему урока «Функция y= sin x, её свойства и график» .
В результате изучения данной темы обучающийся должен
Знать:
виды графиков тригонометрической функции y= sin x,ее свойства;
определение тригонометрических функций числового углового аргумента;
Уметь:
•вычислять значение функции по заданному значению аргумента при различных способах задания функции;
• определять основные свойства числовых функций, иллюстрировать их на графиках;
• строить графики изученных функций, иллюстрировать по графику свойства элементарных функций;
• использовать понятие функции для описания и анализа зависимостей величин;
Раздел «Тригонометрические функции».
Тема урока : Функция y= sin x, её свойства и график .
Тип урока :урок первоначальное формирование умений и навыков.
Цели урока:
1. Образовательная
-ввести понятие функции y= sin x , свойства графика;
-ввести схему построения функции y= sin x;
-закрепить понятия с помощью выполнения заданий.
2. Развивающая
-формировать понимание взаимосвязи между предметами Математика и черчение;
-развивать пространственное воображение.
3. Воспитывающая
-воспитывать внимание, аккуратность, бережное отношение к техническим средствам
-способствовать осознанию ценности коллективной мыслительной деятельности
-формировать представление о математике, как о части общечеловеческой культуры .
Задачи:
1. Использовать имеющийся потенциал знаний о свойствах функции у = sin x в конкретных ситуациях.
2. Применять осознанное установление связей между аналитической и геометрической моделями функции у = sin x.
Ход урока
1 этап. Актуализация опорных знаний, мотивация изучения нового материала
«Вход в урок».
Преподаватель: Здравствуйте ребята
На доске написаны 3 утверждения:
Тригонометрическое уравнение sin t = a всегда имеет решения.
График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
График тригонометрической функции можно построить, используя одну главную полуволну.
Верны ли утверждения? (1 минута). Затем результаты первоначального обсуждения (да, нет) вносятся в таблицу в столбец «До».
Утверждение | До | После |
1 |
|
|
2 |
|
|
3 |
|
|
Преподаватель ставит цели и задачи урока.
2. Актуализация знаний (фронтально на модели тригонометрического круга).
Самостоятельная работа (индивидуальные карточки задания)
Выполните следующие задания:
1 ) Выделите цветом ось синусов
2) Подпишите значения выделенных точек
3) Опустите перпендикуляры из точек на ось синусов
Ответ:
2 этап. Восприятие, осмысление, первичное закрепление, непроизвольное запоминание
Изучение нового материала .
Построение графика функции у = sin x и запись свойств функции в тетради.
1) D(y) =
2) E (y) =
3) функция ограничена и сверху, и снизу
4) унаиб = 1, унаим = -1
5) непрерывная функция
6) нечетная функция
7) возрастает на ; убывает на
Самостоятельная работа
Заполните таблицу значений и постройте график функции y=sin x
Ответ:
х | 0 | ||||||
у | 0 | 1 | 0 |
3 этап. Первичное обобщение, произвольное запоминание, применение знаний и способов деятельности в типичных ситуациях
Первичное обобщение, произвольное запоминание, применение знаний и способов деятельности в типичных ситуациях
4. Постройте график функции (самостоятельно с проверкой)
а) у = sin x + 2
б) у = sin x — 1
в) у = sin
г) у = sin
5. Решите графически уравнение sin x = .
4 этап. Первичная систематизация знаний и способов деятельности, их перенос и применение в новых ситуациях
5 этап. Оценка и самооценка
7. Возвращаемся к утверждениям (начало урока), обсуждаем, используя свойства тригонометрической функции у = sin x.
Самостоятельная работа:
1.Постройте в одной координатной плоскости графики функций:
y1 = sinx;
у2 = sinx + 2;
у3 = sinx — 2.
Ответ:
2.Найдите область значений функции:
3.Найдите значения других трёх основных тригонометрических функций, если:
4. Найдите числовое значение выражения:
Найдите числовое значение выражения:
Ответы: № 2
Преподаватель подводит итоги урока , анализирует уровень усвоения теоретического материала, задает задание на дом:
Список используемых материалов
1. А.Г.Мордкович и др., Алгебра и начала анализа: учебник для 10-11 кл. общеобразоват. учреждений (профильный уровень)– 7-е изд.стер. – М. : Мнемозина, 2010.
2. А.Г.Мордкович и др., Алгебра и начала анализа: задачник для 10-11 кл. общеобразоват. учреждений (профильный уровень)– 7-е изд. стер.– М. : Мнемозина, 2010.Учебник «Ал», Л.С. Атанасян и др., Москва ,Просвещение 2005
Справочник по математике А.А Рывкин и др, Москва, Высшая школа 2009
Математика. Справочные материалы В.А.Гусев, А.Г.Мордкович Москва, Просвещение 2009
www.ziimag.narod.ru — персональный сайт автора Мордковича А. Г. «Практика развивающего обучения».
www.math.ru -Интернет — поддержка учителей математики.
Вопрос: Постройте график y=sinx+sin п/3-x
y = sin модуль x
Просвет
График данной функции выглядит следующим образом:
Natasha1456
Всего 1 ответ. 3x
3x
Полезно сделать замену t=sin x и построить график на плоскости (t,y). На отрезке (0, pi/2) синус монотонно возрастает, и можно примерно состроить искомый график.
Гость3
Всего 1 ответ.
Постройте график y=sinx+sin п/3-x
заранее благодарюмарина дмитрук6На будущее: используйте адвансед графер. Даже для дипломов со сложными специальностями годится. Я использовал на факультете электроприводов и автоматики. Хорошая программа, и много разных функций модно изобразить. Там, кстати, роль запятой играет точка, а переменные ставятся в скобках при задании функции. Можно еще с табличными массивами графики задавать, и прочее, и прочее…
drwelder4
Всего 7 ответов.
Решите тригонометрические уравнения и обязательно нужны к ним чертежи!!! Прошу!!! Срочно!!! Люди добрые!! В пятницу сдавать!!
Кирилл Renault2Решение тригонометрических уровнений такое:
sint(sint-1)=0 sint=0⇒t=πn,n∈z sint=1⇒t=π/2+2πk, k∈z
4cos^2t-1=0 4cos^2t=1 cos^2t=1/4 1)cost=1/2 t=+-П/3 +2П*n, n принадлежит Z
2)cost=-1/2 t=+-2П/3+2П*n, n принадлежит Z2cos^2t-5cost+2=0 cost=а, tа1>=1
2a^2-5a+2=0 D=25-16=9, a=5+-3/4, a1=2 (не удовл. 2-5m+1=0
2-5m+1=0
D=25-24=1
m1,2=5t/12= m1=1/2, m2=1/3
cost=1/2 t=+-П/3+2Пn
cost=1/3 t=+-arccos1/3+2Пк
- sin(3*П/4-x)<√3/2
Sinx<√3/2 -3*П/4
sinx<П/√3
Ирина Г.1
Всего 1 ответ.
Начал смотреть Наруто. Стоит ли одновременно смотреть фильмы и аниме? Если да то в каком порядке?
Александр Парыгин21Порядок просмотра сериалов, фильмов и спин-оффов следующий:
1. Наруто [ТВ-1] – ТВ (220 эп.), первый сериал, адаптация манги, 2002-2007
2. Наруто OVA-1 – OVA (1 эп.), дополнение к сериалу, 2003 (смотреть после 19 серии ТВ-1).
3. Наруто OVA-2 – OVA (1 эп.), дополнение к сериалу, 2003 (смотреть после 52 серии ТВ-1).
4. Наруто (фильм первый) – п/ф, дополнение к сериалу, 2004 (смотреть после 101 серии ТВ-1).
5. Наруто: Спортивный фестиваль Конохи – к/ф, приложение к первому фильму, 2004 (смотреть после первого фильма).
6. Наруто (фильм второй) – п/ф, дополнение к сериалу, 2005 (смотреть после 141 серии ТВ-1).
7. Наруто OVA-3 – OVA (1 эп.), дополнение к сериалу, 2005 (смотреть после 143 серии ТВ-1).
8. Наруто (фильм третий) – п/ф, дополнение к сериалу, 2006 (смотреть после 147 серии ТВ-1).
9. Наруто [ТВ-2] – ТВ (500 эп.), второй сериал, адаптация манги, 2007 – 2017)
10. Наруто (фильм четвёртый) – п/ф, дополнение, 2007 (смотреть после 32 серии ТВ-2).
11. Наруто (фильм пятый) – п/ф, дополнение, 2008 (смотреть после 71 серии ТВ-2).
12 Наруто (фильм шестой) – п/ф, дополнение, 2009 (смотреть после 120 серии ТВ-2).
13 Naruto: The Cross Roads – к/ф, дополнение, 2009 (смотреть после 143 серии ТВ-2).
14. Наруто (фильм седьмой) – п/ф, дополнение, 2010 (смотреть после 175 серии ТВ-2).
15. Gekijouban Naruto Soyokazeden: Naruto to Mashin to Mitsu no Onegai Dattebayo!! – к/ф, дополнение к фильму, 2010 (смотреть после седьмого фильма).
16. Naruto x UT – музыкальное видео, дополнение, 2011 (6-минутный муз.клип, смотреть по желанию)
17. Наруто (фильм восьмой) – п/ф, дополнение, 2011 (смотреть после 260 серии ТВ-2).
18. Honoo no Chuunin Shiken! Naruto vs Konohamaru!! – к/ф, дополнение к фильму, 2011 (смотреть после восьмого фильма).
19. Наруто (фильм девятый) – п/ф, дополнение, 2012 (смотреть после 311 серии ТВ-2).
20. Naruto SD: Rock Lee no Seishun Full-Power Ninden – ТВ (51 эп.), ответвление сюжета, 2012-2013 (спинофф чиби-сериал, смотреть по желанию).
21. The Last: Naruto the Movie – п/ф, дополнение, 2014 (смотреть после 480 серии ТВ-2).
22. Boruto: Naruto the Movie – п/ф (1 эп. + 10-минутный спэшл Naruto ga Hokage ni Natta Hi), адаптация новой манги [новая эпоха], 2015 (смотреть желательно после того, как дочитаешь последнюю главу манги).
23. Boruto: Naruto Next Generations (>51 эп. ), 2017-2018 (смотреть можно после 500 эп. Наруто [ТВ-2] и фильма Boruto: Naruto the Movie).
), 2017-2018 (смотреть можно после 500 эп. Наруто [ТВ-2] и фильма Boruto: Naruto the Movie).
UPD: Последняя актуализация списка производилась 19.10.2017.
Блог: vk.com/animeshorts Твиттер: twitter.com/romor_on
Роман Корзинкин55
Всего 4 ответа.
Графики тригонометрических функций Функция у sin x
Графики тригонометрических функций Функция у = sin x, ее свойства Преобразование графиков тригонометрических функций путем параллельного переноса Преобразование графиков тригонометрических функций путем сжатия и расширения Для любознательных… тригонометрические функции
Графиком функции у = sin x является синусоида Свойства функции: 1. D(y) =R 2. Периодическая (Т=2 p) 3. Нечетная (sin(-x)=-sin x) 4. Нули функции: у=0, sin x=0 при х = pn, nÎZ тригонометрические функции y=sin x 2
Свойства функции у = sin x 5. Промежутки знакопостоянства: y = sin x У>0 при х Î (0+2 pn; p+2 pn), nÎZ У
Промежутки знакопостоянства: y = sin x У>0 при х Î (0+2 pn; p+2 pn), nÎZ У
Свойства функции у=sin x 6. Промежутки монотонности: функция возрастает на промежутках вида: [-p/2+2 pn; p/2+2 pn], nÎZ тригонометрические функции y = sin x 4
Свойства функции у=sin x Промежутки монотонности: функция убывает на промежутках вида: [p/2+2 pn; 3 p/2+2 pn], nÎZ тригонометрические функции y=sin x 5
Свойства функции у =sin x 7. Точки экстремума: Хмах= p/2 +2 pn, nÎZ Хмin= -p/2 +2 pn, nÎZ тригонометрические функции y=sin x 6
Свойства функции у =sin x 8. Область значений: Е(у) = [-1; 1] y = sin x тригонометрические функции 7
Преобразование графиков тригонометрических функций График функции у = f (x+в) получается из графика функции у = f(x) параллельным переносом на (-в) единиц вдоль оси абсцисс График функции у = f (x)+а получается из графика функции у = f(x) параллельным переносом на (а) единиц вдоль оси ординат тригонометрические функции 8
Преобразование графиков тригонометрических функций Постройте график Функции у =sin(x+p/4) тригонометрические функции вспомнить правила 9
Преобразование графиков тригонометрических функций Постройте график функции: y=sin (x — p/6) y =sin (x+ p/4) тригонометрические функции 10
Преобразование графиков тригонометрических функций Постройте график функции: y = sin x + p y =sin (x — p/6) тригонометрические функции 11
Преобразование графиков тригонометрических функций y= sin x +p Постройте график функции: y=sin (x + p/2) тригонометрические функции вспомнить правила 12
Графиком функции у = cos x является косинусоида sin(x+p/2)=cos x Перечислите свойства функции у = cos x тригонометрические функции 13
Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у =k f (x) получается из графика функции у = f(x) путем его растяжения в k раз (при k>1) вдоль оси ординат График функции у = k f (x) получается из графика функции у = f(x) путем его сжатия в k раз (при 0
Преобразование графиков тригонометрических функций путем сжатия и растяжения y=sin 4 x y=sin 2 x Y=sin 0. 5 x вспомнить правила тригонометрические функции 15
5 x вспомнить правила тригонометрические функции 15
Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у = f (kx) получается из графика функции у = f(x) путем его сжатия в k раз (при k>1) вдоль оси абсцисс График функции у = f (kx) получается из графика функции у = f(x) путем его растяжения в k раз (при 0
Преобразование графиков тригонометрических функций путем сжатия и растяжения y = cos 2 x y = cos 0. 5 x тригонометрические функции вспомнить правила 17
Преобразование графиков тригонометрических функций путем сжатия и растяжения Графики функций у = -f (kx) и у=-k f(x) получаются из графиков функций у = f(kx) и y= k f(x) соответственно путем их зеркального отображения относительно оси абсцисс синус – функция нечетная, поэтому sin(-kx) = — sin (kx) косинус –функция четная, значит cos(-kx) = cos(kx) тригонометрические функции 18
Преобразование графиков тригонометрических функций путем сжатия и растяжения y = -sin 3 x y = sin 3 x тригонометрические функции вспомнить правила 19
Преобразование графиков тригонометрических функций путем сжатия и растяжения y=2 cosx y=-2 cosx вспомнить правила тригонометрические функции 20
Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у = f (kx+b) получается из графика функции у = f(x) путем его параллельного переноса на (-в/k) единиц вдоль оси абсцисс и путем сжатия в k раз (при k>1) или растяжения в k раз ( при 0
Преобразование графиков тригонометрических функций путем сжатия и растяжения y= cos(2 x+p/3) y= cos(2(x+p/6)) y=cos(x+p/6) Y= cos(2 x+p/3) тригонометрические функции y=cos 2 x Y= cos(2 x+p/3) вспомнить правила 22
Для любознательных… Посмотрите как выглядят графики некоторых других триг. функций: y = 1 / cos x или y=sec x (читается секонс) тригонометрические функции y = cosec x или y= 1/ sin x читается косеконс 23
функций: y = 1 / cos x или y=sec x (читается секонс) тригонометрические функции y = cosec x или y= 1/ sin x читается косеконс 23
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус (-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Математическая сцена — Правила тригонометрии
Math Scene — Правила тригонометрии — Урок 3| 2008 Расмус Эф и Джанн Сак | Триггерные правила |
Урок 3
Уравнения типа a sin x + b cos x = c
На диаграмме показан график функции f(x)
= грех х + 2 потому что х.
Удивительно похоже на обычную синусоиду который был переведен в одну сторону и с амплитудой, превышающей что основной волны. Мы уже видели, что влияет на амплитуду и как можно увеличить амплитуду от значения 1 путем умножения на a константа больше 1. (см. триггерные функции, урок 3). Мы также видели, что график основного функцию можно перевести по горизонтали, добавив константу к углу. С это разум, мы должны быть в состоянии переписать наше уравнение в форме m sin (x + v), такой, что
г.м грех (х + v) = грех х + 2 потому что х
Теперь посмотрите на график g(x) = sin x − 2 потому что х.
Очевидно, это та же самая кривая, за исключением тот факт, что перевод теперь в направлении, противоположном предыдущему, сдвинута вправо на ту же длину, на которую была сдвинута предыдущая кривая Слева. В этом случае мы должны быть в состоянии составить эквивалентное уравнение.
м грех (х — v) = грех х — 2 потому что х
г.
Теперь перепишем эти выражения, используя формула сложения:
грех (x + v) = sin x cos v + cos x sin v
грех (x — v) = sin x cos v — cos x sin v
Умножая на m получаем:
м sin (x + v) = m sin x cos v + m cos x sin v
м грех (x — v) = m sin x cos v — m cos x sin v
Сравните результат с исходным уравнением.
м sin (x + v) = 1 sin x + 2 cos x
= m cos v sin x + m sin v cos x
м грех (х — v) = 1 грех х — 2 потому что х
= m cos v sin x − m sin v cos x
Мы видим, что в обоих случаях должно быть правда:
м потому что v = 1
м sin v = 2
Если мы разделим нижнее уравнение на верхнее, мы получить следующее:
г.загар v = 2 / 1
Что дает угол v = tan −1 (2) ≈ 63,4°.
Если мы нарисуем прямоугольный треугольник с более короткие стороны1 и 2, те же значения, что и в уравнении, то мы можем вычислить длину гипотенузы и увидеть, что:
cos v = 1 / и sin v = 2 /.
Использование уравнений
м потому что v = 1
m sin v = 2,
Дает нам это:
м1 / = 1
м =
Другими словами, мы можем переписать уравнение как:
Мы видим, что амплитуда волны в
функции
f (x) = sin x + 2, потому что x и g (x) = sin x — 2, потому что x есть .
Обобщение и использование a и b для констант
получаем следующее правило:
Угол v можно найти с помощью:
| тангенс v = б / а где а > 0, b > 0 и 0° < v°< 90° |
Пример 1
Найдите амплитуду функция f(x) = 3 sin x + 4 cos x.
Начнем с перезаписи функция.
Амплитуда равна 5.
Пример 2
График функции
f(x) = 3 sin x + 4 cos x — преобразованная синусоида. Рассчитать по
на сколько градусов и в каком направлении была переведена волна.
Рассчитать по
на сколько градусов и в каком направлении была переведена волна.
f(x) = 3 sin x + 4 cos x
= 5 sin (x + v)
v = tan −1 ( 4 / 3 ) ≈ 53,1°
Волна переведена
на 53,1° влево
г.
(f(x) ≈ 5 sin (x + 53,1°).
Пример 3
Учитывая функцию f(x) = 5 sin x + 12 cos x + 3. Найдите амплитуду, максимальную высоту и перевод волны.
Перепишите f(x).
загар −1 (12/5) ≈ 67,4°
f(x) = 13 sin (x + 67,4°) + 3
Амплитуда равна 13 , поэтому максимальная высота 13 + 3 = 16. Посмотрите на график.
г.Пример 4
Решите уравнение 3 sin x + 4 cos x = 5 на
интервал
0° x < 360°.
3 грех х + 4, потому что х = 5
= 5 sin (x + 53,1°)
sin (x + 53,1°) = 5 / 5 = 1
x + 53,1° = sin −1 1 = 90 + k360°
x = −53,1 + 90 + k360°
х = 36,9°
Это дает одно решение 36,9° в первом квадранте.
Интересно посмотреть на график. Мы видим другого решения на искомом интервале нет.
Пример 5
Найдите все решения уравнение грех х — 3 потому что х знак равно 1 .
Мы видим, что tan v = 3 и v = тангенс −1 (3) = / 3 (60°).
Итак, грех (x − / 3 ) =
| (x − / 3 ) = грех −1 () = / 6 + к2 | / 6 = 30 |
х = / 3 + / 6 + к2
знак равно / 2 + к2
Или второй вариант
(х – / 3 ) = — / 6 + к2
х = / 3 + — / 6 + к2
| х = 7 / 6 + k2 | 7 / 6 = 210 |
Попробуйте выполнить тест 1 по правилам тригонометрии.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Глава 11, ГРАФИК ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Видео Решения, Алгебра 2 и Тригонометрия
Раздел 1
График функции синуса
Выберите Раздел 11.1: График функции синуса 11.2: График функции косинуса 11.3: Амплитуда, период и фазовый сдвиг 11.4: Запись уравнения синуса или график косинуса 21.5: График функции тангенса 11.6: Графики обратных функций 11.7: Графики обратных тригонометрических функций 11.8: Набросок тригонометрических графиков
г.00:34
Проблема 1
Является ли график $y=\sin x$ симметричным относительно отражения в начале координат? Обосновать ответ.
Эрик С.
Преподаватель нумерейд
01:18
Проблема 2
Является ли график $y=\sin x$ симметричным относительно переноса $T_{-2 \pi, 0} ?$ Обоснуйте свой ответ.
Марта Р.
Преподаватель нумерейд
02:13
Проблема 3
Нарисуйте график $y=\sin x$ в интервале $0 \leq x \leq 4 \pi$
a. В интервале $0 \leq x \leq 4 \pi,$ при каких значениях $x$ график $y=\sin x$ возрастает?
б. В интервале $0 \leq x \leq 4 \pi$ , при каких значениях $x$ график $y=\sin x$ убывает?
г. Сколько циклов графика $y=\sin x$ находится в интервале $0 \leq x \leq 4 \pi ?$
Эрик С.
Преподаватель нумерадов
00:40
Проблема 4
Каково максимальное значение $y$ на графике $y=\sin x ?$
Марта Р.
Преподаватель Numerade
00:24
Проблема 5
Каково минимальное значение $y$ на графике $y=\sin x ?$
Erik S.
Numerade Educator
г.01:01
Проблема 6
Каков период функции синуса?
Марта Р.
Преподаватель нумерейд
00:22
Задача 7
Является ли синусоидальная функция взаимно однозначной? Обосновать ответ.
Эрик С.
Преподаватель нумерейд
03:10
Задача 8
а. Точка $P$ — точка на единичной окружности. $y$-координата точки $P$ равна $\sin \frac{\pi}{3} .$ Чему равна $x$-координата точки $P ?$
b. Точка $A$ — это точка на графике $y=\sin x .$ $y$-координата точки $A$ равна $\sin \frac{\pi}{3} .$ Что такое $x$- координата $A ?$
Марта Р.
Преподаватель нумерейд
Задача 9
Функция $\mathrm{f}$ нечетна тогда и только тогда, когда $\mathrm{f}(x)=-\mathrm{f}(-x)$ для всех $x$ в области определения функции. Обратите внимание, что функция нечетна, если она симметрична относительно начала координат. Другими словами, функция есть собственный образ при размышлении о происхождении.
Другими словами, функция есть собственный образ при размышлении о происхождении.
а. Нарисуйте единичную окружность и любой угол первого квадранта $R O P$ в стандартном положении с точкой $P$ на единичной окружности. Пусть $\mathrm{m} \angle R O P=\theta .$
b. На том же наборе осей нарисуйте в стандартном положении угол с мерой $-\theta .$ Какая связь между $\theta$ и $-\theta ?$ Между $\sin \theta$ и $\sin (- \тета) ?$
c. Повторите шаги a и b для углов второго, третьего и четвертого квадрантов. Соответствует ли $\sin \theta=\sin$ $(-\theta)$ для углов второго, третьего и четвертого квадрантов? Обосновать ответ. 9{\circ}$ .
а. Если $\theta$ представляет угол, который лестница образует с землей в радианах, то каков разумный набор значений для $\theta ?$ Объясните.
б. Выразите через $\theta,$ высоту $h$ точки, в которой лестница будет упираться в здание.
г. Постройте график функции из части b, используя набор значений $\theta$ из части a в качестве области определения функции.
д. Какова самая высокая точка, до которой может подниматься лестница?
Карсон М. 9{7}}{7 !}$ . Для каких значений $x$ $Y_{3}$ кажется хорошим приближением для $Y_{1} ?$
c. Используйте $Y_{2}$ и $Y_{3}$, чтобы найти приближения к значениям синусоидальной функции ниже. Какая функция дает лучшее приближение? Это то, что вы ожидали? Объяснять.
(1) $\sin \frac{\pi}{6}$ $\qquad$ (2) $\sin \frac{\pi}{4}$ $\qquad$ $(3) \sin \pi$
Заходите скорее!
Тригонометрия: тригонометрические функции
Амплитуда: Максимальное значение ординаты (y) на графике называется его «амплитудой».
Период: «Период» тригонометрической функции — это наименьшее +ve положительное число, которое при добавлении к исходной окружной мере угла дает то же самое значение функции.
Для синусоидальной функции вида: y = a sin bx
Амплитуда = | а |
Период = ` (2\pi)/ b `
Пример 1
Найдите амплитуду и период функции y = `2 sin( x /3)` y = 2 sin `(x/3)` = 2 sin `(1/3x)`
Амплитуда = | а | = 2
Период = `(2\pi)/b` = `(2\pi)/(( 1 )/3)` = 6`\pi`
Из графика функции косинуса показано выше,
Для y = cos x :
Амплитуда = 1
Период = 2`\pi`
Домен: -`\infty` Диапазон: -1 `\ leq` y `\leq` +1 На рисунке справа показан график зависимости y = cos x за один полный период. Для функции косинуса вида: y = a cos bx Амплитуда = | а | Период = `(2\pi)/b` Найдите амплитуду и период функции y = `( 1 )/2` cos 3x Решение: Для данного функция y = `( 1 )/2` cos 3x Амплитуда = | а | = `( 1 )/2` Период = `(2\pi)/b` = `(2pi)/3` График `y= tan x = (sin x)/cos x` был показан выше. Из определения функции видно, что значение касательной функции
не определено для всех значений x, для которых `cos x=0` (деление на ноль не определено). Следовательно, область определения касательной функции исключает
нечетные целые числа, кратные ` (\pi)/2 ` . Для всех этих значений x можно наблюдать вертикальные асимптоты. Примечание: Как видно из графика, тангенс функции имеет период пи (`\pi`). Из графика, показанного выше, Для y = tan x : Amplitude = none; для функции тангенса нет максимального значения. Период = `\pi` (функция касательной завершает один цикл между ` (-\pi)/2 и (\pi)/2) ` Домен: -`\infty` < x < +` \infty` , x`\neq((2n+1)\pi)/2` , n `\epsilon` Z Диапазон: -`\infty` На рисунке справа показан график зависимости y = tan x за один полный период. Для функции тангенса вида: y = a tan bx Period = ` \pi/b `
Пример 2:
 Это tan (`\pi`+ `\theta`)=`tan (\theta)`
Это tan (`\pi`+ `\theta`)=`tan (\theta)`
Пример 3:
tan 3x
Решение: Для заданной функции y = `( 1 )/2` tan 3x
Period = `\pi/3`
Пунктирные линии показывают вертикальные асимптоты, которые встречаются при
x = `\pi/6 \pm (n \pi)/3`, где n — целое число.
График y=cosec x = `( 1)/sin x ` был показан выше. Из определения функции видно, что значение cosec функция не определена для всех значений x, для которых `sin x=0` (деление на ноль не определено). Поэтому область определения функции cosec исключает целые кратные `\pi`. Вертикальные асимптоты существуют для всех этих значений x.
Из графика, показанного выше,
Для y = cosec x :
Амплитуда = нет; для функции cosec не существует максимального значения.
Период = `2\pi`
Домен: -`\infty` < x < +`\infty` , x`\ne n\pi` , n `\epsilon` Z
Диапазон: y `\le` -1 или y `\ge` 1
На рисунке справа показан график зависимости y = cosec x за один полный период.
Для функции COSEC формы:
Y = COSEC BX
ПЕРИОД = `(2 \ PI)/B Для данной функции y = cosec 2x
Period = `(2\pi)/2` = `\pi`
n\pi)/2`, где n — целое число.
График y=sec x = `( 1)/cos x` показан красным выше. Из определения функции видно, что значение y=sec x не определено для всех значений x, для которых `cos x=0` (деление на ноль не определено). Следовательно, область определения secx исключает нечетный интеграл кратно `(\pi)/2 ` . Вертикальные асимптоты существуют для всех этих значений x.
Из графика, показанного выше,
Для y = sec x :
Амплитуда = нет; для функции sec нет максимального значения.
Период = 2`\pi`
Домен: -`\infty` < x <+`\infty` , x`\ne` (2n+1) `\pi` )/2 , n `\epsilon` Z
Диапазон: y `\le` -1 или y `\ge` 1
На рисунке справа показан график зависимости y = sec x за один полный период.
Для секущей функции формы:
Y = Sec BX
Период = `(2 \ PI)/B`
Пример 5:
График y = sec 3x
55559 = секундо : Для заданной функции y = sec 3x
Period = ` (2\pi)/3 `
\pm (n\pi)/3`, где n — целое число.
График y=cot x = `( cos x )/sin x ` был показан выше. Из определения функции мы видим, что значение (y=cot x) функция не определена для всех значений x, для которых `sin x=0` (деление на ноль не определено). Поэтому область касательной функция исключает целые числа, кратные `\pi` . Для всех этих значений x можно наблюдать вертикальные асимптоты.
Примечание:
Функция раскладушки имеет период `пи` (`\pi`). Это кроватка (`\pi`+ `\theta`) = кроватка (`\theta`), что также видно из графика.
Для y = кроватка x :
Амплитуда = нет; для функции детской кроватки не существует максимального значения.
Период = `\pi` (Функция касательной завершает один цикл между `(-\pi )/2 и (\pi)/2)`
Домен: -`\infty` < x <+` \infty` , x`\ne`n`\pi` , n `\epsilon` Z
Диапазон: -`\infty` < y <+`\infty`
На рисунке справа показан график зависимости y = cot x за один полный период.
Для функции котангенса вида:
y = a cot bx
Период = `\pi/b`
Пример 6:
`Graph `
Решение: Для данной функции y = cot` ( x )/2`
Период = `(\pi)/(( 1)/2)` = `2\pi`
Тригонометрические функции
Тригонометрические функцииПроизвольные углы и единичная окружность
До сих пор мы использовали единичный круг для определения тригонометрических функций для острых углов. В следующем разделе, где мы рассмотрим косые треугольники, нам понадобятся не только острые углы. Некоторые косые треугольники тупые, и нам нужно знать синус и косинус тупых углов. Пока мы это делаем, мы также должны определить триггерные функции для углов, превышающих 180°, и для отрицательных углов. Во-первых, нам нужно понять, что такое такие углы. Древнегреческие геометры рассматривали только углы между 0° и 180°, и они не считали ни прямой угол 180°, ни вырожденный угол 0° углами. Полезно не только считать эти частные случаи углами, но также включать углы от 180° до 360°, иногда называемые «рефлекторными углами». С применением тригонометрии к предметам исчисления и дифференциальных уравнений также стали приняты углы за пределами 360 ° и отрицательные углы.
Полезно не только считать эти частные случаи углами, но также включать углы от 180° до 360°, иногда называемые «рефлекторными углами». С применением тригонометрии к предметам исчисления и дифференциальных уравнений также стали приняты углы за пределами 360 ° и отрицательные углы.
Рассмотрим единичный круг. Обозначим его центр (0,0) как O, , а точку (1,0) на нем как A. В качестве движущейся точки B движется по единичной окружности, начиная с A и двигаясь по против часовой стрелки, угол AOB как угол 0° и увеличивается. Когда B пройдет весь круг и вернется к A, , тогда угол AOB будет равен 360°. Конечно, это тот же угол, что и угол 0°, поэтому мы можем идентифицировать эти два угла. Как B продолжает второй раз по кругу, мы получаем углы от 360° до 720°. Это те же ракурсы, которые мы видели в первый раз, но у нас для них разные названия. Например, прямой угол называется либо 90°, либо 450°. Каждый раз по кругу мы получаем другое название угла. Таким образом, 90°, 450°, 810° и 1170° обозначают один и тот же угол.
Таким образом, 90°, 450°, 810° и 1170° обозначают один и тот же угол.
Если B начинается в той же точке A и движется по часовой стрелке, то мы получим отрицательные углы, а точнее имена в отрицательных градусах для тех же самых углов. Например, если вы пройдете четверть круга по часовой стрелке, угол г. AOB обозначен как –90°. Конечно, это то же самое, что угол 270°.
Таким образом, любой угол имеет бесконечное множество названий, но все они отличаются друг от друга на кратное 360°.
Синусы и косинусы произвольных углов
Теперь, когда мы задали произвольные углы, мы можем определить их синусы и косинусы. Пусть угол расположен так, что его вершина находится в центре единичной окружности O = (0,0), а первая сторона угла расположена вдоль x -ось. Пусть вторая сторона угла пересекает единичную окружность в точке B. Тогда угол равен углу AOB , где A равно (1,0). Мы используем координаты B для определения косинуса угла и синуса угла. В частности, координата x точки B является косинусом угла, а координата y точки B является синусом угла.
В частности, координата x точки B является косинусом угла, а координата y точки B является синусом угла.Свойства синусов и косинусов, вытекающие из этого определения
Есть несколько свойств, которые мы можем легко вывести из этого определения. Некоторые из них обобщают тождества, которые мы уже видели для острых углов.- Синус и косинус являются периодическими функциями периода 360°, то есть периода 2 π . Это потому, что синусы и косинусы определяются в терминах углов, и вы можете добавить числа, кратные 360°, или 2 π , и это не изменит угол. Таким образом, для любого угла θ ,
sin ( θ + 360°) = sin θ, и cos ( θ + 360°) = cos θ.
Многие из современных приложений тригонометрии вытекают из использования тригонометрического исчисления, особенно те приложения, которые имеют дело непосредственно с тригонометрическими функциями.
 Таким образом, мы должны использовать радианную меру, когда думаем о триггере с точки зрения триггерных функций. В радианах последняя пара уравнений читается как
Таким образом, мы должны использовать радианную меру, когда думаем о триггере с точки зрения триггерных функций. В радианах последняя пара уравнений читается какsin ( θ + 2 π ) = sin θ, и cos ( θ + 2 π ) 9 1 = 813 cos
- Синус и косинус дополняют друг друга:
cos θ = sin ( π /2 – θ ) sin θ = cos ( π / 2 – θ )
Мы видели это раньше, но теперь у нас есть это для любого угла θ. Это правда, потому что, когда вы отражаете плоскость через диагональную линию y = x, угол обменивается на его дополнение.
- Тождество Пифагора для синусов и косинусов следует непосредственно из определения. Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 =1.
 Но координаты косинус и синус, так что делаем вывод
Но координаты косинус и синус, так что делаем выводsin 2 θ + cos 2 θ = 1, Теперь мы готовы рассмотреть синус и косинус как функции.
- Синус — нечетная функция, а косинус — четная функция. Возможно, вы не встречали этих прилагательных «нечетный» и «четный» применительно к функциям, но знать их важно. Функция f называется нечетной функцией , если для любого числа x, f (– x ) = – f ( x ). Функция f называется функцией даже , если для любого числа x, f (– x ) = f ( x ). Большинство функций не являются ни нечетными, ни четными функциями, но некоторые из наиболее важных функций являются либо теми, либо другими. Любой полином только с нечетными степенями является нечетной функцией, например, f ( x ) = x 5 + 8 x 3 – 2 x.
 (Обратите внимание, что все степени числа x — нечетные числа.) Точно так же любой многочлен только с членами четной степени является четной функцией. Например, f ( x ) = x 4 – 3 x 2 – 5. (Константа 5 равна 5 x 0
(Обратите внимание, что все степени числа x — нечетные числа.) Точно так же любой многочлен только с членами четной степени является четной функцией. Например, f ( x ) = x 4 – 3 x 2 – 5. (Константа 5 равна 5 x 0 Синус — нечетная функция, а косинус — четная
sin (– θ ) = –sin θ, и cos (– θ ) = cos θ.
Эти факты следуют из симметрии единичного круга относительно оси x . Угол — х — это тот же угол, что и х , за исключением того, что он находится по другую сторону оси х . Переворот точки ( x,y ) на другую сторону оси x превращает ее в ( x,–y ), поэтому координата y инвертируется, то есть синус инвертируется , но x -координата остается прежней, то есть косинус не меняется.
- Очевидным свойством синусов и косинусов является то, что их значения лежат в диапазоне от –1 до 1.
 Каждая точка на единичной окружности находится на расстоянии 1 единицы от начала координат, поэтому координаты любой точки также находятся в пределах 1 от 0.
Каждая точка на единичной окружности находится на расстоянии 1 единицы от начала координат, поэтому координаты любой точки также находятся в пределах 1 от 0.
Графики функций синуса и косинуса
Возьмем t в качестве переменного угла. Вы можете думать о t и как об угле, и как о времени. Хороший способ для человека понять функцию — посмотреть на ее график. Начнем с графика sin т. Возьмите горизонтальную ось за ось t (а не ось x , как обычно), возьмите вертикальную ось за ось y и постройте уравнение y = sin t . Выглядит так. Во-первых, обратите внимание, что это периодический период 2 π . Геометрически это означает, что если вы возьмете кривую и сдвинете ее 2 π влево или вправо, то кривая вернется сама на себя. Во-вторых, обратите внимание, что график находится в пределах одной единицы т -ось. Мало что еще очевидно, за исключением того, где оно увеличивается и уменьшается. Например, sin t растет от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2.
Например, sin t растет от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2.
Далее давайте посмотрим на график косинуса. Снова возьмем горизонтальную ось за ось t , но теперь возьмем вертикальную ось за ось x и нарисуем уравнение 9.1813 x = cos 91 813 т.
Обратите внимание, что он выглядит точно так же, как график sin t , за исключением того, что он сдвинут влево на π /2. Это из-за тождества cos t = sin ( π /2 + t ). Хотя мы раньше не встречались с этим тождеством, оно легко следует из тех, что мы видели: π /2 + t ).
Графики функций тангенса и котангенса
График функции тангенса имеет вертикальную асимптоту при x = π /2. Это происходит потому, что тангенс стремится к бесконечности, когда t приближается к π /2. (На самом деле, оно приближается к минус бесконечности, поскольку t приближается к π /2 справа, как вы можете видеть на графике.

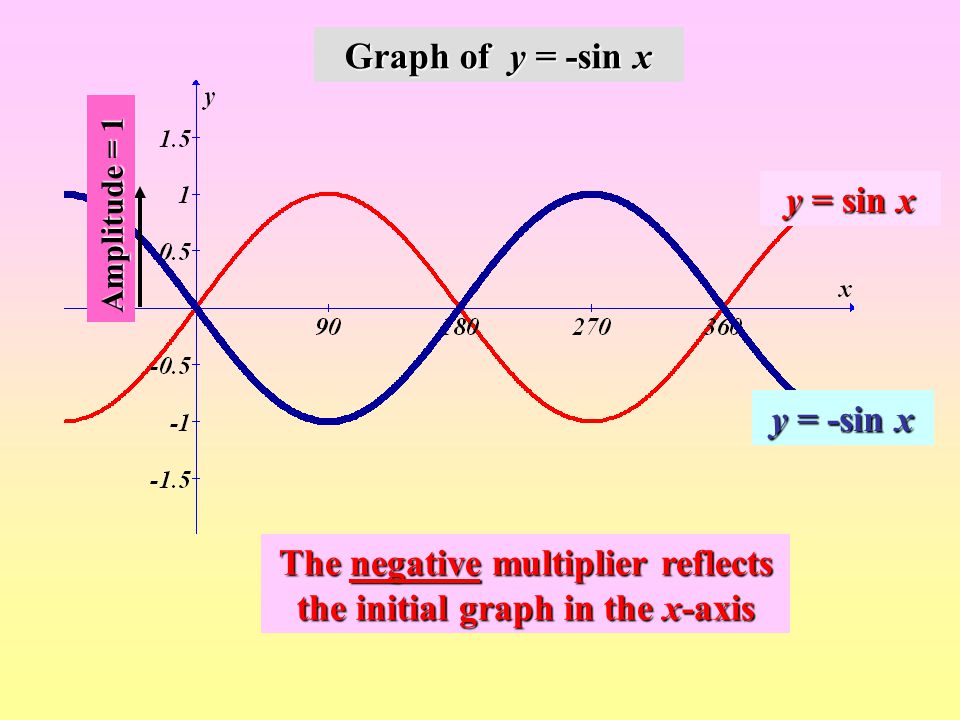
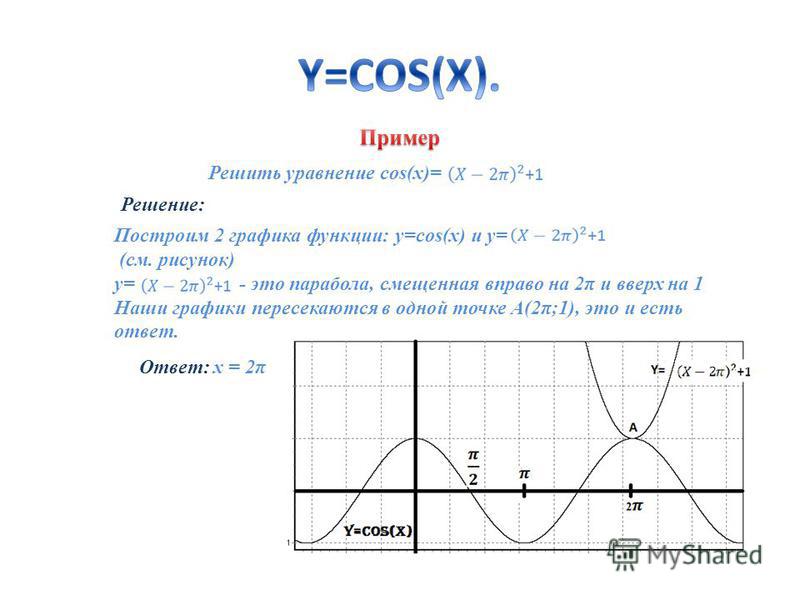
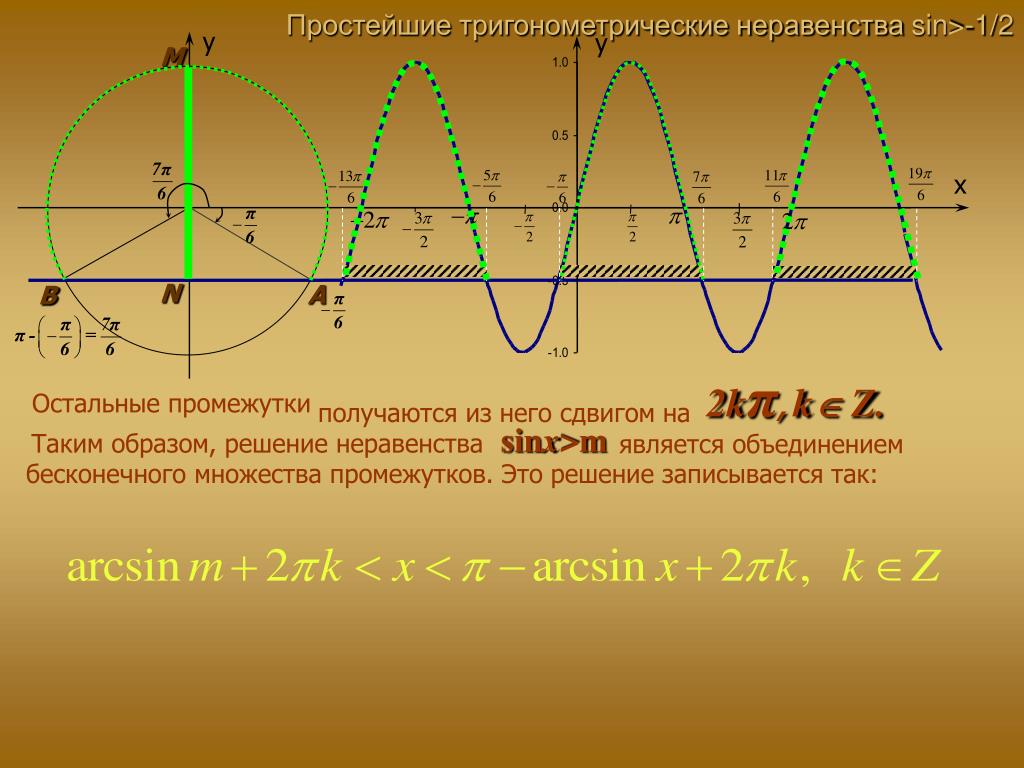
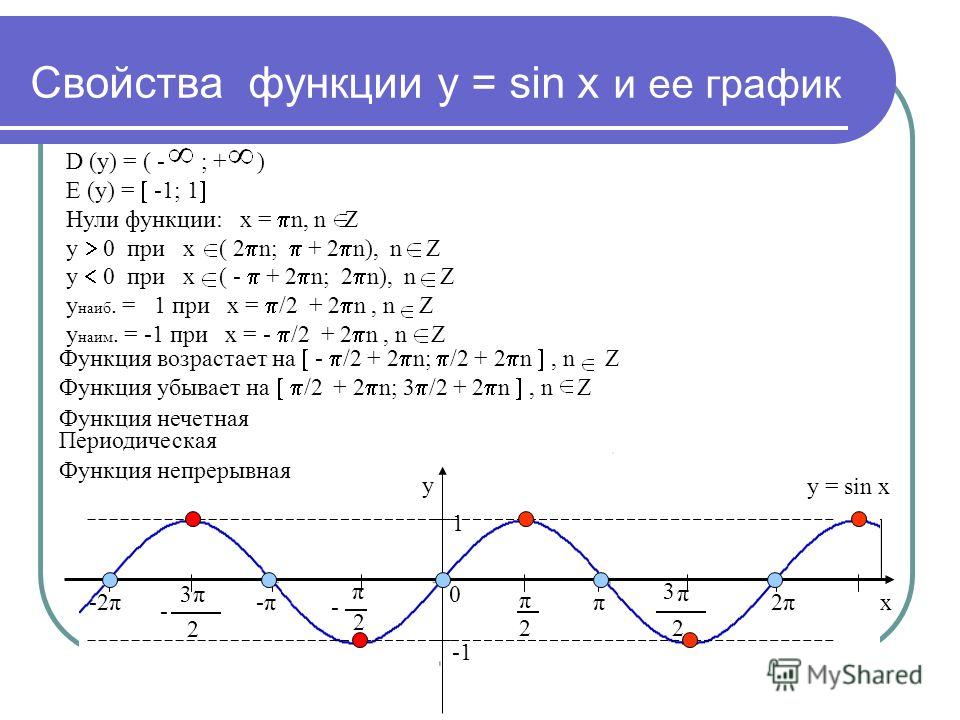
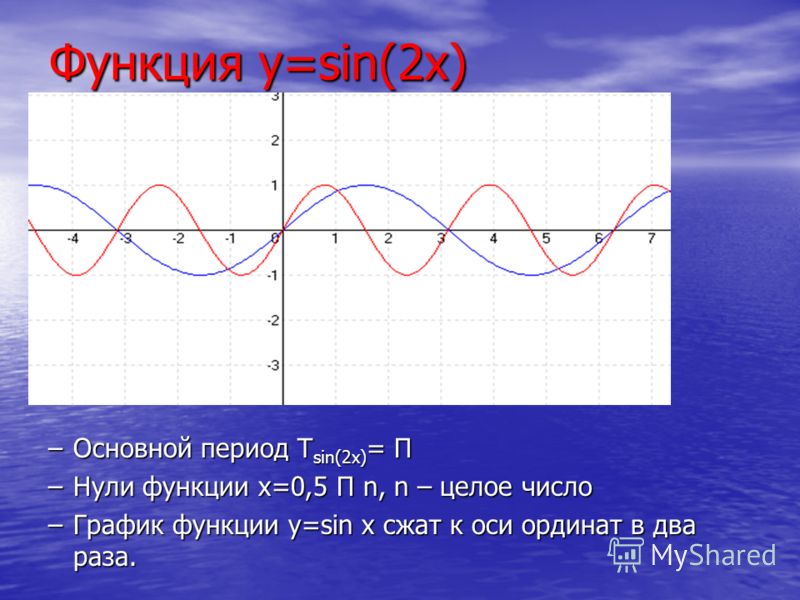 Область определения
Область определения