Формула объема тела: Если известны масса тела и его объем,можно ли определить плотность тела

41.4. Вычисление объема тела

Вычисление объема тела по известным площадям параллельных сечений

Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ох: S = S(x), а ≤ х ≤ b.

Применим схему II (метод дифференциала).

1. Через произвольную точку х є [a;b] проведем плоскость ∏, перпендикулярную оси Ох (см. рис. 188). Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении х. Через v(x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; х] величина v есть функция от х, т. е. v = v(x) (v(a) = 0, v(b) = V).

2. Находим дифференциал dV функции v = v(x). Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках х и х+Δх, который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx.

Поэтому дифференциал объема dV = S(x) dx.

3. Находим искомую величину V путем интегрирования dA в пределах от а до В:

Полученная формула называется формулой объема тела по площади параллельных сечений.

Пример 41.6. Найти объем эллипсоида

Решение: Рассекая эллипсоид плоскостью, параллельной плоскости Oyz и на расстоянии х от нее (-а≤х≤a), получим эллипс (см. рис. 189):

Площадь этого эллипса равна

Поэтому, по формуле (41.6), имеем

Объем тела вращения

Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = ƒ(х) 0, отрезком а ≤ x ≤ b и прямыми х = а и х = b (см. рис. 190). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (х Î [а; b]), есть круг с радиусом у= ƒ(х). Следовательно, S(x)=πy2.

Применяя формулу (41.6) объема тела по площади параллельных сечений, получаем

Если криволинейная трапеция ограничена графиком не прерывной функции х=φ(у) ≥ 0 и прямыми х = 0, у = с,

у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой (41.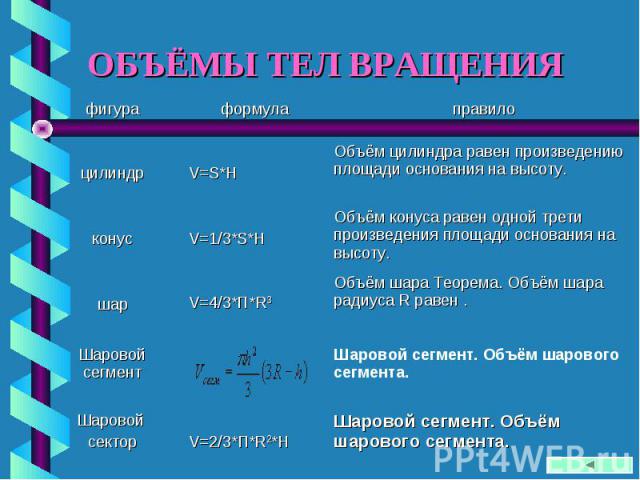 7), равен

Пример 41.7. Найти объем тела, образованного вращением фигуры, ограниченной линиямивокруг оси Оу (см. рис. 191).

Решение: По формуле (41.8) находим:

Пусть кривая АВ является графиком функции у = ƒ(х) ≥ 0, где х є [а;b], а функция у = ƒ(х) и ее производная у’=ƒ'(х) непрерывны на этом отрезке.

Найдем площадь S поверхности, образованной вращением кривой АВ вокруг оси Ох.

Применим схему II (метод дифференциала).

1. Через произвольную точку х є [а; b] проведем плоскость ∏, перпендикулярную оси Ох. Плоскость ∏ пересекает поверхность вращения по окружности с радиусом у = ƒ(х) (см. рис. 192). Величина S поверхности части фигуры вращения, лежащей левее плоскости, является функцией от х, т. е. s=s(x) (s(a)=0 и s(b)=S).

2. Дадим аргументу х приращение Δх = dx. Через точку х + dx є [а; b] также проведем плоскость, перпендикулярную оси Ох. Функция s=s(x) получит приращение Аз, изображенного на рисунке в виде «пояска».

Найдем дифференциал площади ds, заменяя образованную между сечениями фигуру усеченным конусом, образующая которого равна dl, а радиусы оснований рав ны у и у+dy. Площадь его боковой поверхности равна ds=π(у+у+dy)•dl=2πуdl + πdydl. Отбрасывая произведение dydl как бесконечно малую высшего порядка, чем ds, получаем ds=2πуdl, или, так как

3. Интегрируя полученное равенство в пределах от х = а до х = b, получаем

Если кривая АВ задана параметрическими уравнениями х = x(t),y=y(t), t1 ≤ t ≤ t2, то формула (41.9) для площади поверхности вращения принимает вид

Пример 41.8. Найти площадь поверхности шара радиуса R.

Решение: Можно считать, что поверхность шара образована вращением полуокружностивокруг оси Ох. По формуле (41.9) находим

Пример 41.9. Дана циклоида

Найти площадь поверхности, образованной вращением ее вокруг оси Ох.

Решение: При вращении половины дуги циклоиды вокруг оси Ох площадь поверхности вращения равна

Объём тела вращения с примерами решения

Содержание:

1. Понятие кубируемого тела
2. Примеры с решением
3. Пример 1.
4. Пример 2.
5. Пример 3.
6. Пример 4.
7. Пример 5.

Основные понятия и их определения в данном параграфе во многом аналогичны соответствующим понятиям и определениям параграфа (посвящённого площадям плоских фигур), являясь их обобщениями на случай трёхмерного пространства. Так, множество точек пространства будем называть ограниченны.и, если существует шар, содержащий все точки этого множества. Пространственной фигурой будем называть любое непустое ограниченное множество точек пространства.

Две пространственные фигуры называются равными, если существует взаимно однозначное соответствие, сохраняющее расстояния между точками, при котором фигура отображается на фигуру Договоримся называть пространственной точки множество точек пространства, расположенных внутри шара радиуса с центром в точке Точку пространственной фигуры назовём внутренней точкой этой фигуры, если найдется такое, что точки целиком принадлежит Точку назовём внешней точкой пространственной фигуры если найдётся такое что точки целиком не принадлежит Точку назовем граничной точкой фигуры если эта точка не является ни внутренней, ни внешней точкой фигуры Совокупность всех граничных точек фигуры называется границей этой фигуры.

Сформулируем определение того, что в школьном курсе элементарной стереометрии называют телом.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Телом называется ограниченная фигура в пространстве, обладающая двумя свойствами:

1. у нее есть внутренние точки, и любые две из них можно соединить линией (например, ломаной), целиком лежащей внутри фигуры;
2. фигура содержит свою границу, и сё граница совпадает с границей сё внутренней области.

Согласно первому условию, фигура является связной. Поэтому фигура, состоящая из объединения двух шаров, не имеющих общих точек, строго говоря, телом уже не считается.

Точно так же не считается телом фигура, состоящая из двух шаров, имеющих лишь одну общую точку.

Второе условие означает, что тело это замкнутое множество точек, граница тела принадлежит ему, так что шар без соответствующей сферы или даже шар без одной сё точки уже не тело. Кроме того, граница тела везде прилегает к его внутренней области, так что конус «со шпилем» или конус «с полями», как изображено на рисунке ниже, телами не считаются.

Граница тела называется также его поверхностью. В данном параграфе мы снимем ограничения на связность и замкнутость, и будем трактовать понятие тела в широком смысле, отождествляя его, по сути, с пространственной фигурой. Далее, тело, образованное при вращении плоской ограниченной замкнутой фигуры вокруг прямой, лежащей в плоскости этой фигуры и «с содержащей её внутренних точек, называется телом вращения. Прямая, вокруг которой осуществляется вращение, называется осью тела пращения.

Возможно вам будут полезны данные страницы:

Критерий Сильвестра

Найти частные производные

Разложение в ряд Тейлора

Матричные уравнения: пример решения

Граница тела вращения (его поверхность) образуется при вращении границы плоской фигуры (точки границы плоской фигуры, лежащие на оси вращения, являются внутренними точками тела вращения). Сечение тела (поверхности) вращения плоскостью, перпендикулярной оси этого тела (этой поверхности), называется перпендикулярным сечением тела (поверхности) вращения. Перпендикулярным сечением тела (поверхности) вращения может быть круг (окружность), точки или кольцо, ограниченное двумя концентрическими окружностями с центром на оси вращения. Сечение тела вращения плоскостью, проходящей через его ось, называется осевии сечением этого тела.

Поскольку поворот вокруг прямой на угол есть симметрия относительно этой прямой, то осевым сечением тела вращения является фигура, симметричная относительно его оси.

Многогранный телом в пространстве назовем множество, составленное из конечного числа ограниченных многогранников. Напомним, что многогранником называют тело, граница (поверхность) которого есть объединение конечного числа многоугольников, причём каждая сторона каждого такого многоугольника является стороной еще одного (и только одного) многоугольника. Такую поверхность называют замкнутой многогранной поверхностью. Многоугольники, составляющие поверхность многогранника, называются его гранями.

Уточним, что гранью многогранника следует считать только такой многоугольник на поверхности многогранника, который не содержится ни в каком другом многоугольнике, лежащем на поверхности многогранника (иначе он являегся лишь частью грани). Без учёта этого замечания можно было бы сказать, что грани куба, например, это двенадцать равнобедренных прямоугольных треугольников, поскольку они составляют границу куба.

Приведём общее определение цилиндра. Пусть даны две параллельные плоскости и на плоскости задана некоторая квадрируемая фигура Из всех точек фигуры проведём параллельные друг другу отрезки до плоскости Фигура, которую образуют эти отрезки, и называется цилиндром. Фигура при этом называется основанием цилиндра. Отрезки, образующие цилиндр, так н называются образующими. Концы образующих, лежащие на плоскости образуют ещё одно основание цилиндра. Таким образом, основания цилиндра равны друг другу и лежат в параллельных плоскостях.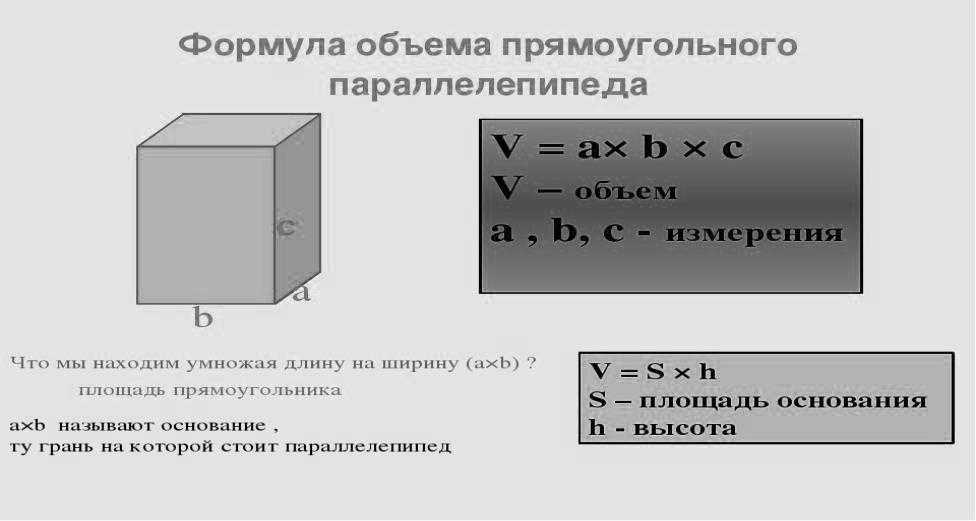

Иногда образующими называют только те из упомянутых выше отрезков, которые соединяют граничные точки оснований цилиндра. Существует и другой подход к определению цилиндра.

Цилиндрической поверхностью называется поверхность, производимая движением прямой линии сохраняющей одно и то же направление и пересекающей данную линию Прямая называется образующей, а линия направляющей (см. рис. ниже).

Бели за напривляющую цилиндрической поверхности взята окружность в некоторой плоскости, то такая поверхность называется круговой. Если плоскость, в которой лежит направляющая цилиндрической поверхности, перпендикулярна её образующей, то такая поверхность называется прямой. Тогда цияиндром называется тело, ограниченное цилиндрической поверхностью с замкнутой направляющей (начало линии совпадает с её концом) и двумя параллельными плоскостями, пересекающими образующие, Часть поверхности, заключенная между параллельными плоскостями, называется при этом боковой поверхностиьк> цилиндра, а части плоскостей, отсекаемые этой поверхкоегмо, основаниями цилиндра.

Расстояние между плоскостями оснований называется высотой цилиндра. Соответственно, если плоскости оснований цилиндра перпендикулярны образующим, то цилиндр называется пряиии. Если в основании прямого цилиндра лежит круг, то такой цилиндр имеет название прямого кругового цилиндра.

Отрезок, соединяющий центры его оснований, называется осью цилиндра. Прямой круговой цилиндр можно определить также как тело, образуемое при вращении прямоугольника вокруг прямой, содержащей его сторону. По этой причине второе название прямого кругового цилиндра цилиндр вращения.

В данном пособии под цилиндрическим телом будем понимать прямой цилиндр. Назовем ступенчатым телом объединение конечного числа цилиндрических тел. расположенных так. что верхнее основание каждого предыдущего из этих тел находится в одной плоскости с нижним основанием последующего. Определим теперь понятие гладкой поверхности. Пусть поверхность задастся параметрически при помощи уравнений где функции непрерывны вместе со своими частными производными в некоторой ограниченной замкнутой области на плоскости Непрерывную границу этой области будем считать состоящей из гладких кривых. Наконец, предположим, что поверхность не имеет ни кратных, ни других особых точек. Такая поверхность называется гладкой.

Понятие кубируемого тела

Объем тела в элементарной стереометрии было введено понятие объема для простейших пространственных тел, в том числе для многогранников. Отмечалось, что объем тела это неотрицательное число, поставленное в соответствие этому телу, которое обладает следующими свойствами. Г. (Инвариантность). Равные тела имеют равные объёмы. 2′. (Аддитивность).

Если тело является объединением конечного числа тел, любые два из которых не имеют общих внутренних точек, то объем данного тела равен сумме объёмов составляющих его тел. (Существование единицы объема). Объём куба, длина ребра которого равна единице измерения длин отрезков, равен одной кубической единице и принимается за единицу измерения объёмов. Гели, имеющие равные объемы, назывались равновеликими. Заметим, что аналогичными свойствами характеризуются и площади плоских фигур, и длины отрезков (дуг кривых).

Введём понятие объёма для произвольного тела в пространстве. Рассмотрим для этого всевозможные многогранные тела целиком содержащиеся многогранные тела целиком содержащие Тела будем называть вписанными в а тела описанными около . Числовое множество объёмов всех вписанных многогранных тел ограничено сверху, например, объёмом любого описанного многогранного тела

Поэтому это множество имеет конечную точную верхнюю грань которую будем называть нижним объёмом тела Если в тело нельзя вписать ни одного многогранника, то по определению полагается

Аналогично, числовое множество объёмов всех описанных около тела многогранных тел ограничено снизу, например, объёмом любого вписанного многогранного тела или нулём, и полому у него существует конечная точная нижняя грань называемая верхним объемом тела . Очевидно, что

Тело называется кубируемым (т.е. и.иеющим конечный объём), если Число называется при этом объёмом тела (поЖорлану). Будем говорить, что тело имеет объём, равный нулю, если это тело содержится в многогранном теле сколь угодно малого объёма.

Замечание.

Подчеркнём, что введённое таким образом определение объёма, допускающее существование фигур нулевого объёма, распространяет понятие объема на пространственную фигуру, не являющуюся телом в «школьном» понимании.

Например, поскольку объём сферы равен нулю, то объём шара, рассмотренного вмсстс с границей, и объём открытого шара (без границы), согласно введённому определению, существуют и равны. Дилее, если не оговорено противное, под термином «тело» будем понимать куби-русмос тело.

Понятие кубнрусмости допускает обобщение на случай неограниченных те.ч в пространстве. Пусть неограниченное пространственное тело и действительное число. Обозначим через тело, полученное при пересечении с шаром радиуса и с центром в начале координат:

Всегда можно выбрать такое достаточно большое чтобы Пусть, кроме того, для любого такого ограниченное тело кубируемо в смысле введённого выше определения. Если существует конечный предел то назовем тело кубируемым (в несобственном смысле), а число -его объёмом.

При вычислении объёмов таких тел с помощью определённых интегралов будем получать сходящиеся несобственные икгегрилы 1-го или 2-го рода (соответствующие примеры будут рассмотрены ниже пример 3 пункта 7.5.1).

Перечисленные свойства элементарных тел (неотрицательность, аддитивность, инвариантность, существование единицы) сохраняются и для произвольных кубируемых тел. Доказательство свойства аддитивности в случае, когда тела имеют общие граничные точки, аналогично соответствующему доказательству для плоского случая.

Подчеркнём, что свойство аддитивности выполняется для объединения любого конечного числа кубируемых тел без общих внутренних точек но уже объединение счётной совокупности кубируемых тел не является, вообще говоря, кубируемым телом. Замечание 5. Отметим также, что пересечение двух кубируемых тел есть кубируемое тело. 7.4.

Вычисление объёма тела по известным площадям поперечных сечений Рассмотрим в прямоугольной системе координат некоторое кубнруемое тело расположенное между плоскостями так, что при любом сечение данного тела плоскостью, проходящей через точку перпендикулярно оси непусто и киадрируемо, причём известна площадь этого сечения. Теорема I. Пусть площадь сечения курируемого тела как функция х непрерывна на сегменте Тогда объём тела вычисляется по формуле (1)

Доказательство. Произведём разбиение сегмента точками и разделим плоскостями всё тело на слои. Рассмотрим слой содержащийся между плоскостями Так канон кубируем (как часть кубируемого тела),тo существуют многогранные тела например, в вндс совокупностей прямоугольных параллелепипедов с ребрами, параллельными координатным осям, такие, что целиком содержится в a содержит внутри себя.

Проделав уго для каждого слоя, в результате построим два отвечающих данному разбиению многогранных тела первое из которых содержится в , а второе содержит в себе объёмы которых удовлетворяют неравенству причём разность можно сделать меньше любого наперед заданного положительного числа (при достаточно малом диаметре разбиения ). Так как к телам доказываемая формула, очевидно, применима, то, обозначив через площади их поперечных сечений, будем иметь

С другой стороны, так как то и Получили, что в силу объём тела и интеграл оба содержатся между одними и теми же числами разница между которыми меньше, чем можно выбрать произвольно малым, то отсюда и вытекает справедливость формулы (I).

Примеры с решением

Пример 1.

Вычислить объём цилиндрического отрезка (т.е. геометрического тела, отсекаемого от прямого кругового цилиндра плоскостью, проходящей через диаметр основания).

Решение:

Если в основании цилиндра лежит круг радиуса секущая плоскость проходит через диаметр и составляет угол с плоскостью основания. Решение. 1-й способ. Поместим начало координат в точку О центр круга, лежащего в основании цилиндра, и пустим ось абсцисс вдоль диаметра а ось ординат -перпендикулярно ей в плоскости круга.

Определим площадь сечения, перпендикулярного оси

Это представляет собой прямоугольный треугольник с основанием и высотой

Его площадь равна

Тогда по формуле (I) находим искомый обгём цилиндрического отрезка

2-й способ. Ту же величину объема можно было получить, рассекая тело плоскостями, перпендикулярными оси Найдем площадь поперечного сечения в этом случае. Очевидно. сечение представляет собой прямоугольник с основанием и высотой Поэтому площадь поперечного сечения равна Отсюда по формуле (1) находим объём 3-й способ. Можно было вычислить объем цилиндрического отрезка, рассматривая его сечения, перпендикулярные оси аппликат

Пример 2.

Найти объём тела, ограниченного поверхностью (эллипсоид), перпендикулярной оси

Решение:

Это эллипс Приведем его каноническому виду: Площадь этого сечения (т.е. площадь эллипса) равна Тогда, учитывая, что и интегрируя по формуле (1), находим искомый объём:

Заметим, что при решении задачи можно было аналогично рассматривать сечения эллипсоида плоскостями, перпендикулярными осям

Пример 3.

Найти объём тела, ограниченного поверхностями

Решение:

Объём тела вращения в декартовых координатах. Рассмотрим основные случаи вычисления объёмов тел вращения. Во всех случаях во избежание возникновения неопределенности будем считать, что вращаемая криволинейная трапеция не пересекает оси вращения. Криволинейная трапеция задана стандартно относительно оси и вращается вокруг оси Теорема 1.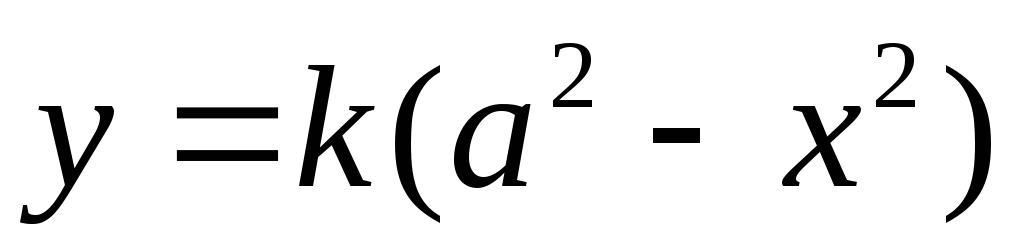 Пусть функция непрерывна на сегменте Тогда тело образованное вращением вокруг оси криволинейной трапеции кубируемо, и его объём может быть вычислен по формуле (1) Доказательство. Выполним произвольное разбиение сегмента н обозначим через соответственно точные нижнюю и верхнюю грани функции На каждом таком сегменте построим два прямоугольника у которых сегмент ,является основанием, а соответственно высотами. В результате получатся две ступенчатые фигуры, одна из которых содержится в криволинейном трапеции , а другая содержит ее. При вращении и этих ступенчатых фигур вокруг оси образуются тело и два ступенчатых тела, одно из которых содержится в а другое содержит в себе .

Пример 4.

Найти объём тела, полученного вращением вокруг оси плоской фигуры, ограниченной линиями

Решение:

Данная фигу ра является стандартной относительно оси следовательно,

Замечание 3 (случай произвольных а и Ь ). Отметим, что формула (1) остаётся справедливой для произвольных (любого знака и не обязательно конечных) действительных т.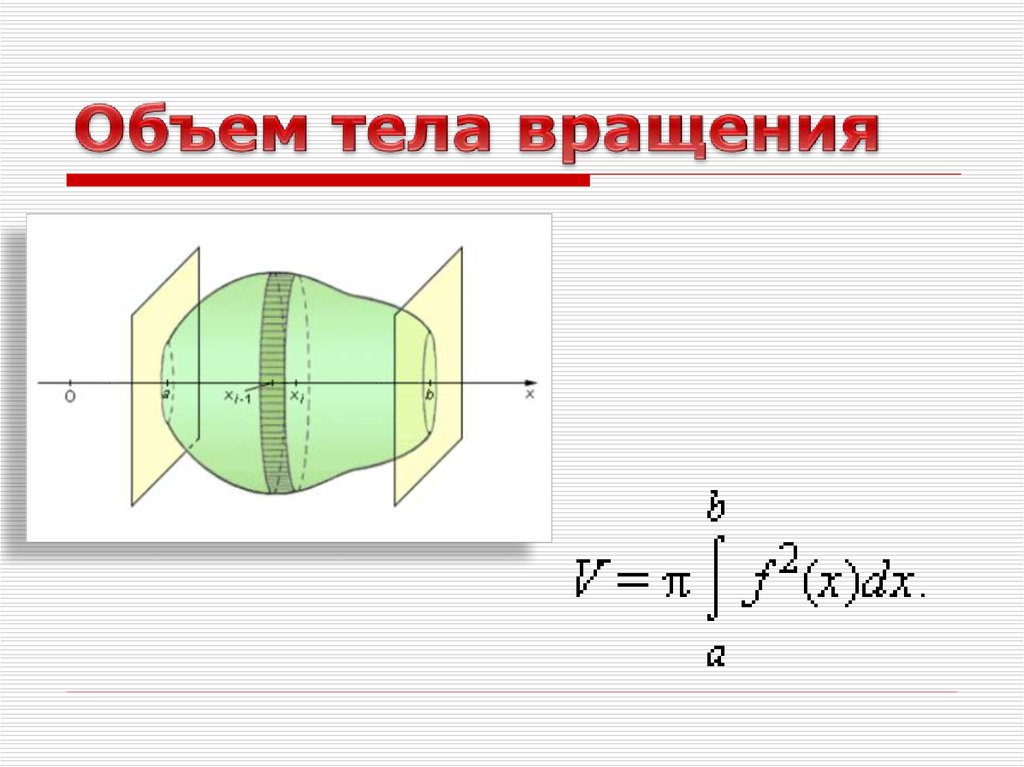 е. её можно использовать для вычисления объема тела, полученного вращением вокруг оси криволинейной трапеции

Пример 5.

Найти объём тела, полученного вращением вокруг оси Ох плоской фигуры, ограниченной кривыми

Решение:

Покажем, что в данном примере фигура вращения, являясь неограниченной, имеет, там не менее, конечный объем (получаемый по формуле (I) несобственный интеграл сходится). Так как при то

Сделаем в каждом из интегралов замену

Интегрируя по частям, находим

Вычисляя сумму вссх членов бесконечно убывающей геометрической прогрессии с первым членом и знаменателем

Пусть дана криволинейная трапеция, ограниченная сверху графиком непрерывной и неотрицательной на сегменте обращающейся на концах этого сегмента в нуль, и снизу отрезком оси

Пусть, кроме того, график функции допускает параметризацию с помощью уравнений окончательно, где функции непрерывно дифференцируемы на и при изменении параметра точка движется по кривой так, что криволинейная трапеция остаётся слева (т. е. в направлении от точки к точке,см. рисунок).

Перейдем в подынтегральном выражении в формуле (1) к переменной интегрирования и получим следующую формулу для вычисления объема тела вращения для этого случая: (3)

Как рассчитать объем человека

••• runna10/iStock/GettyImages

Обновлено 06 декабря 2020 г.

Автор: Chris Deziel

«Эврика!» — воскликнул древнегреческий философ и математик Архимед, когда нашел решение сложной задачи измерения объема царской короны. Царь хотел знать, сделана ли корона из чистого золота, и чтобы определить это, Архимеду нужно было знать ее плотность, что требует определения объема. Выйдя из ванны, он в восторге побежал по улицам, потому что только что понял, что количество воды, вытесненной им в ванне, равно объему его тела. Он мог использовать ту же процедуру для измерения объема короны.

Любой может использовать трюк Архимеда для измерения объема своего тела, но есть еще более простой способ. Все, что вам нужно сделать, это взвеситься, потому что плотность среднего человеческого тела является известной величиной.

Метод вытеснения воды

Если вы хотите подражать Архимеду и измерить объем воды, вытесняемый вашим телом в ванне, вам нужен точный способ измерения. Один из способов — наполнить ванну до краев, собрать воду, которая переливается, когда вы погружаетесь в воду, и перелить ее в мерный контейнер. Чтобы убедиться, что вы собрали всю воду, вам, вероятно, придется построить воронку или слив, который направляет воду в ведро, а не на пол.

Лучше начертить линию на боку ванны и наполнить ванну до этой линии. Убедитесь, что леска достаточно высока, чтобы вы могли погрузить все свое тело, включая голову. Когда вы находитесь под водой, попросите помощника отметить новый уровень воды. Расстояние между линиями — это глубина вытесненной вами воды, и если вы умножите это на длину и ширину ванны, вы получите объем воды — и вашего тела.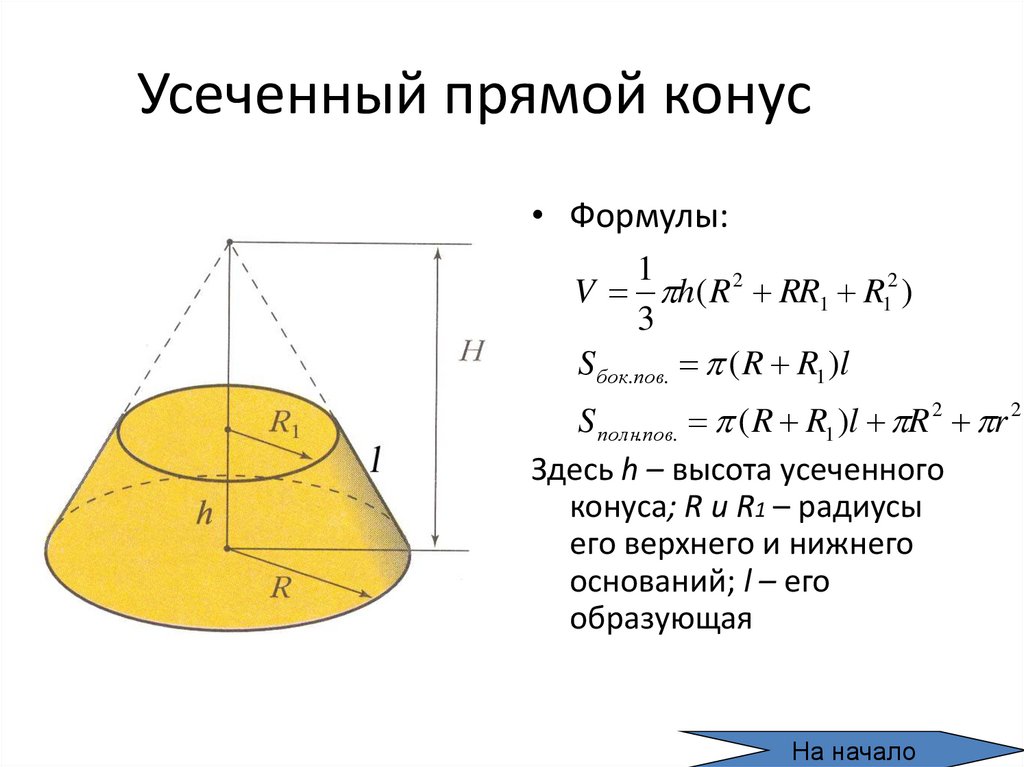

Весовой метод

Если вы обычный человек, плотность вашего тела составляет около 8,3 фунта/галлон (1010 кг/м ³ ), что немного меньше, чем у морской воды, но немного больше, чем у чистой воды. Вот почему вы плаваете в океане, а не в ванной. Вы можете использовать это значение плотности для расчета объема вашего тела, если вы знаете свой вес. Вот процедура:

Получите наиболее точные результаты, взвесившись перед тем, как одеться.

Плотность «d» определяется как масса «m», деленная на объем «V».

d=\frac{m}{V}

Решив V, мы находим, что:

V=\frac{m}{d}

Используйте один из следующих коэффициентов преобразования:

1 кубический метр = 264 Галлоны США = 1057 кварт = 33 814 унций = 35,31 кубических футов.

​ Пример: ​ Фил весит 155 фунтов. Чтобы рассчитать объем его тела, разделите его на среднюю плотность человеческого тела в фунтах на галлон:

Статьи по теме

Ссылки

• Плохая астрономия Фила Плейта: плавание в воде
• Обнаженные ученые: Архимед: первый обнаженный ученый
• Aqua-Calc: Плотность человеческого тела

Ресурсы

• Аргоннская национальная лаборатория: Человеческий объем

Об авторе степень бакалавра физики

и степень магистра гуманитарных наук. Он преподавал естественные науки, математику и английский язык в университете как в своей родной Канаде, так и в Японии. Он начал писать онлайн в 2010 году, предлагая информацию на научные, культурные и практические темы. Его работы охватывают науку, математику, обустройство дома и дизайн, а также религию и восточное искусство исцеления.

Расчетный объем крови

Лекарства и болезни > Калькуляторы

CalculatorAboutReferences

CalculatorAboutReferences

Вопросы

1.Вес?

2.Демографические (для определения среднего объема крови)?

О

Калькулятор приблизительного объема крови вычисляет аппроксимацию внутрисосудистого объема крови с учетом массы тела пациента и демографических данных. В частности, объем крови на килограмм варьируется в зависимости от пола и возраста, при этом средний показатель крови на килограмм у новорожденных детей выше, чем у взрослых. Эти значения были получены с помощью радиоизотопного мечения циркулирующей крови Nadler et al.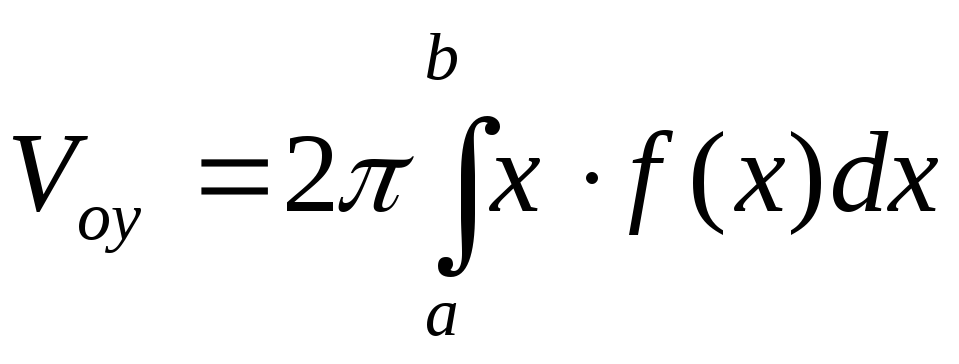 в 1962. В этом исследовании было получено прогностическое уравнение, основанное на поле пациента, площади поверхности и массе тела, которое с тех пор было упрощено до расчета на килограмм в зависимости от возраста и пола пациента.

С тех пор было получено множество других уравнений для оценки объема крови пациента на основе фундаментальной работы Надлера. Упрощенная формула, используемая в этом калькуляторе, обычно встречается в учебниках по анестезии и хирургии, включая Clinical Anesthesia , цитируемый здесь.

Калькулятор расчетного объема крови

Калькулятор вычисляет следующее уравнение:

• Средний объем крови = Вес пациента (кг) * (Средний объем крови в мл/кг)

При этом средний объем крови на демографическую группу (мл/кг)

• Взрослый мужчина = 75
• Взрослая женщина = 65 лет
• Младенцы = 80
• новорожденных = 85
• Недоношенные новорожденные = 95

Каталожные номера

Надлер С. Б., Идальго Дж.Х., Блох Т.

Прогноз объема крови у здоровых взрослых людей. Операция.

1962; 51(2):224-32.

Джон Ф. Баттерворт IV, Дэвид С. Макки, Джон Д. Васник.

Клиническая анестезиология Моргана и Михаила. 5-е издание. 2013.

Единицы по умолчанию

1. Вес?

Создано

О

Калькулятор расчетного объема крови приблизительно вычисляет внутрисосудистую кровь с учетом веса пациента и демографических данных. В частности, объем крови на килограмм варьируется в зависимости от пола и возраста, при этом средний показатель крови на килограмм у новорожденных детей выше, чем у взрослых. Эти значения были получены с помощью радиоизотопного мечения циркулирующей крови Nadler et al. в 1962. В этом исследовании было получено прогностическое уравнение, основанное на поле пациента, площади поверхности и массе тела, которое с тех пор было упрощено до расчета на килограмм в зависимости от возраста и пола пациента.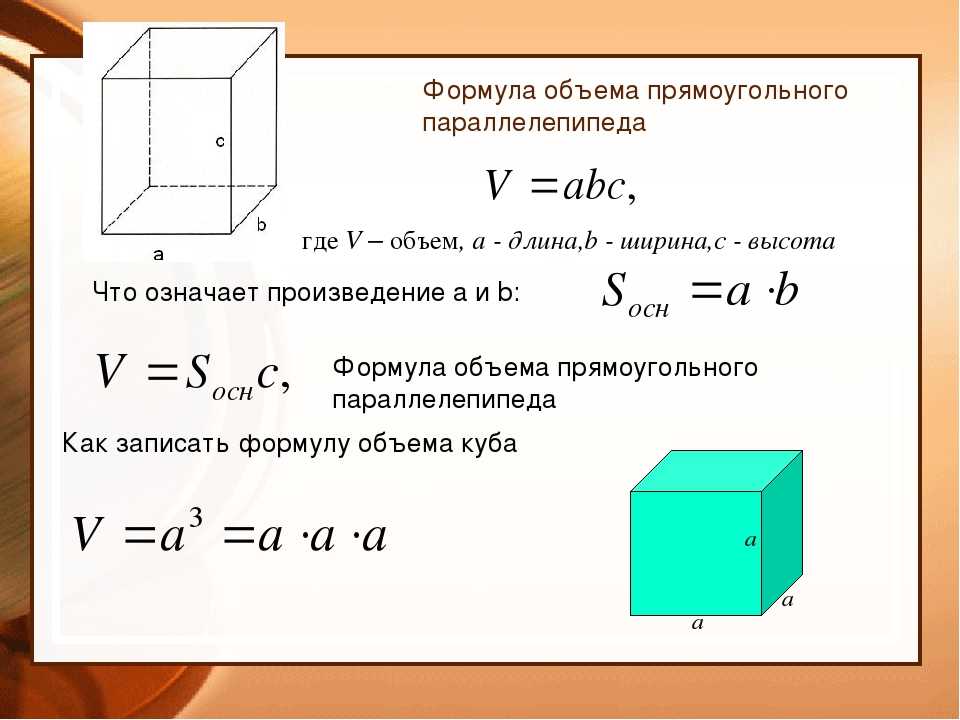

С тех пор было получено множество других уравнений для оценки объема крови пациента на основе фундаментальной работы Надлера. Упрощенная формула, используемая в этом калькуляторе, обычно встречается в учебниках по анестезии и хирургии, включая Clinical Anesthesia , цитируемый здесь.

Калькулятор расчетного объема крови

Калькулятор вычисляет следующее уравнение:

• Средний объем крови = Вес пациента (кг) * (Средний объем крови в мл/кг)

При этом средний объем крови на демографическую группу (мл/кг)

• Взрослый мужчина = 75
• Взрослая женщина = 65 лет
• Младенцы = 80
• новорожденных = 85
• Недоношенные новорожденные = 95

Каталожные номера

Надлер С.Б., Идальго Дж.Х., Блох Т.

Прогноз объема крови у здоровых взрослых людей. Операция.

1962; 51(2):224-32.