Система координат на плоскости. Функции. Окружность
6.
Система координат на плоскости. Функции. Окружность
6.1.
Система координат на плоскости
Графиком линейной функции является прямая y = kx + b, пересекающая ось 0y в точке, ордината которой равна b. Коэффициент k называется угловым коэффициентом прямой (рис. 6.1).
Две прямые y1 = k1 x + b1 и y2 = k2 x + b2 являются параллельными, если их угловые коэффициенты k1 и k2 равны и b 1 ≠ b 2. Например, прямые y = 6x — 5 и y = 6x — 7 параллельны.
Две прямые y1
= k1
x + b1
и y2
= k2
x + b2
являются пересекающимися, если их угловые коэффициенты k1
≠ k2
. Например, прямые y = 4x — 3 и y = 5x — 4 пересекаются. Две пересекающиеся прямые имеют одну общую точку, координаты которой удовлетворяют каждому из уравнений прямых.
Точка лежит на прямой, если ее координаты удовлетворяют уравнению этой прямой. Например, точка N (2; 7) лежит на прямой y = 5x — 3, так как координаты точки удовлетворяют уравнению прямой: 7 = 5 ∙ 2 – 3.
Если точка лежит на оси абсцисс (0x), то ее ордината равна нулю (y = 0).
Если точка лежит на оси ординат (0у), то ее абсцисса равна нулю (x = 0).
График квадратичной функции называется параболой (рис. 6.2). Уравнение y = ax2 + bx + c, где a, b, с — действительные числа и a ≠ 0, является уравнением параболы, пересекающей ось 0y в точке, ордината которой равна c. Коэффициент a называется старшим коэффициентом. Если a > 0, то ветви параболы направлены вниз.
Координаты вершины параболы (xв ; yв ) находят с помощью формул:
Координаты точек пересечения параболы с осями находят с помощью следующих рассуждений.
Абсцисса точки пересечения параболы с осью 0y равна нулю, а ордината точки пересечения равна c, т.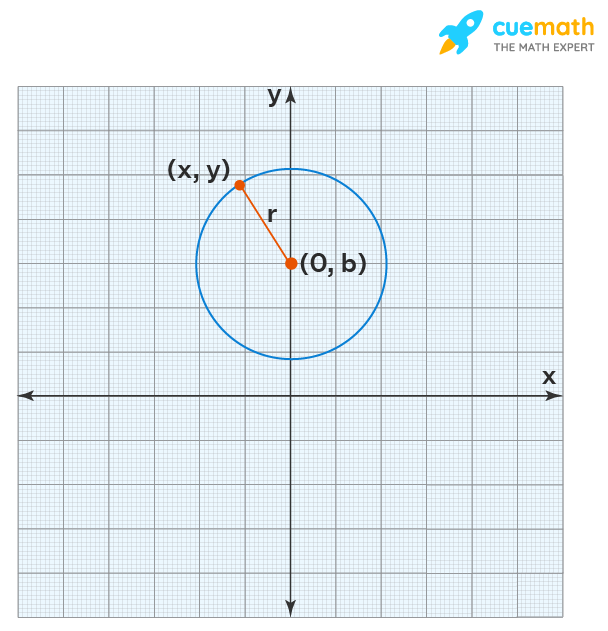
Ордината точки пересечения параболы с осью 0x равна нулю, а абсциссу точки пересечения можно найти, решив уравнение 0 = y = ax2 + bx + c.
На рисунке парабола пересекает ось 0y в точке C (0; 1), а ось 0x в точках A (-1; 0) и B (3; 0).
Парабола может иметь одну точку пересечения с осью 0x, может иметь две точки, и может не иметь точек пересечения. Определить количество точек пересечения параболы y = ax2 + bx + c с осью 0х можно с помощью результата дискриминанта квадратного уравнения ax2 + bx + c = 0:
1) если D > 0, то точек пересечения две;
2) если D < 0, то одна точка пересечения;
3) если D = 0, то точек пересечения нет.
Гипербола — — график обратной пропорциональности. Число k — коэффициент, k ≠ 0. В зависимости от знака коэффициента k гипербола будет располагаться либо в I и III квадранте, либо во II и IV (рис.
6.3).
6.2.
Функции
D(y) — область определения функции, y — множество, на котором задается функция. При графическом способе задания функции ее область определения может считываться по графику. Для нахождения области определения надо спроектировать все точки графика функции на ось 0x. Если функция задана формулой, и ее область определения не указана, то это означает, что функция задается на естественной области определения.
E(y) — множество значений функции y, которые она принимает при всех значениях аргумента из ее области определения. Проще всего находить множество значений, если задан ее график. Необходимо спроектировать все точки графика функции на оси 0y. Получившееся множество точек является множеством значений функции.
Нули функции для функции f(x), заданной графически, — это абсциссы точек, в которых график функции пересекает ось абсцисс или касается ее. Чтобы найти нули функции, заданной графически, нужно решить уравнение f(x) = 0.
Функция f(x) убывает на множестве Х, если для любых x1
и x2
из множества Х, таких, что x1
> x2
, выполняется неравенство f(x1
) > f (x2
).
Функция называется убывающей на множестве Х, если для любых двух значений аргумента из этого множества большему значению аргумента соответствует меньшее значение функции.
Функция f(x) возрастает на множестве Х, если для любых x1 и x2 из множества Х, таких, что x1
Функция y = f(x)называется четной, если для любого x из области определения функции выполняется равенство f(-x) = f(x). Свойство графика четной функции — симметричность относительно оси ординат.
Функция y = f(x)называется нечетной, если для любого x из области определения функции выполняется равенство f(-x) = -f(x). Свойство графика нечетной функции — симметричность относительно начала координат.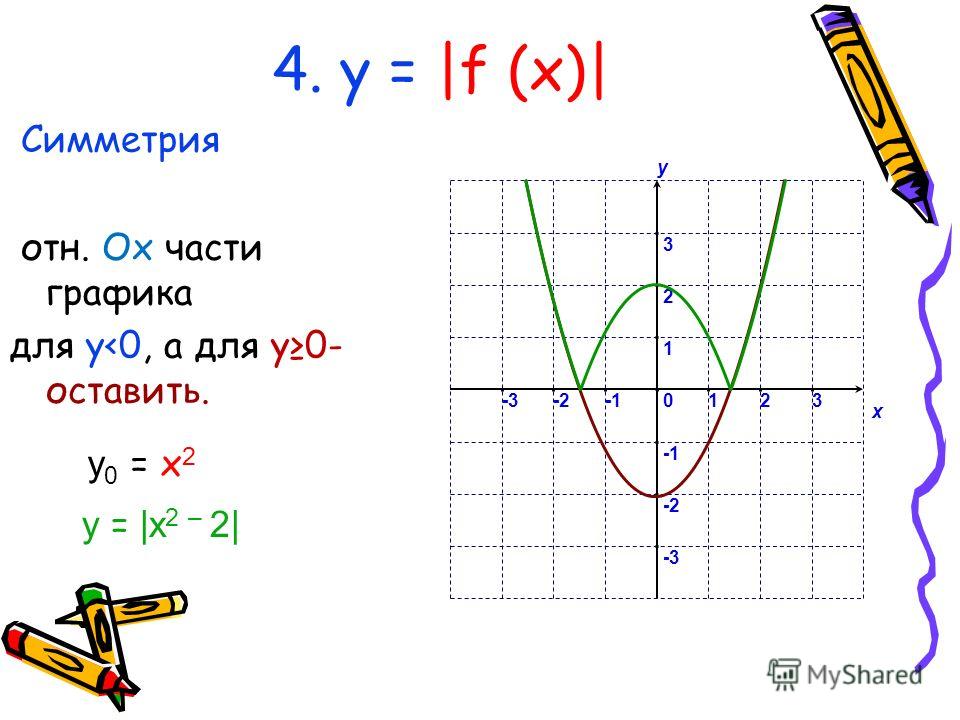
Свойства линейной функции
-
Область определения: .
-
Область значений:
-
, если k ≠ 0;
-
, если k = 0.
-
-
Монотонность:
-
если k > 0, то функция y возрастает на всей области определения;
-
если k < 0, то функция y убывает на всей области определения (рис. 6.4).
-
Свойства гиперболы
.
-
Область определения: .
-
Область значений: .
-
Монотонность:
-
если k > 0, то функция y убывает на промежутке и на промежутке ;
-
если k < 0, то функция y возрастает на промежутке .
и на промежутке (рис. 6.5).
-
-
Функция является нечетной.
и на промежутке (рис. 6.5).Свойства квадратичной функции
.
-
Область определения: .
-
График квадратного трехчлена — парабола с вершиной в точке с абсциссой:
-
направленная ветвями вверх, если a > 0;
-
направленная ветвями вниз, если a < 0.
-
-
Множество значений:
Свойства функции
-
Область определения.
-
Множество значений.
-
Монотонность: функция y возрастает на всей области определения (рис. 6.7).
6.3.
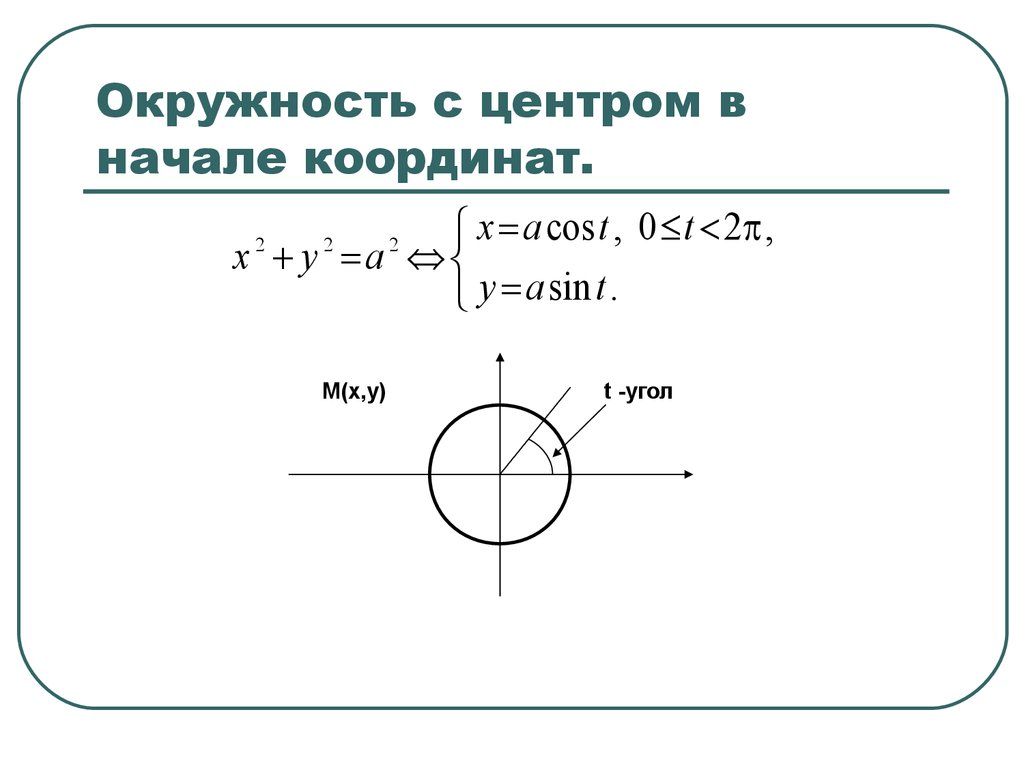
Уравнение окружности
Уравнение окружности с центром в начале координат О (0; 0) и радиусом R имеет вид:
x2
+ y2
= R2
.
Уравнение окружности с центром в точке A (a; b) и радиусом R имеет вид:
Пример 6.1
График показывает движение парусной яхты, которая первую часть пути прошла под парусом. Спустив парус, она продолжила движение.
-
Найдите скорость яхты под парусом и без паруса (выразив ее в км/ч).
-
На каком расстоянии от начала движения находилась яхта через 50 мин., через 2 часа?
-
Сколько времени потребуется яхте на обратный путь, если она будет двигаться с той же скоростью, что и на первом участке под парусом?
Решение
-
Под парусом яхта прошла 30 км за 60 мин., значит, ее скорость была . Без паруса яхта прошла 5 км за 60 мин., следовательно, ее скорость равна 5 км/ч.
Ответ: скорость яхты под парусом 30 км/ч, скорость яхты без паруса 5 км/ч.
-
На графике найдем точку с абсциссой, равной 50.
Найдем ординату этой точки. Она равна 25. Получили, что за 50 мин. яхта пройдет 25 км. Аналогично, за 120 мин. яхта пройдет 35 км.Ответ: за 50 мин. яхта пройдет 25 км, за 120 минут — 35 км.
-
Обратный путь составляет 35 км. Скорость яхты — 30 км/ч.
Найдем время обратного пути: , что составляет 1 час 10 мин.
Ответ: 1 ч 10 мин.
Найдем ординату этой точки. Она равна 25. Получили, что за 50 мин. яхта пройдет 25 км. Аналогично, за 120 мин. яхта пройдет 35 км.Примеры заданий с комментариями
Задание 1
Прямая x + y = c, где c — некоторое число, касается гиперболы в точке с положительными координатами. Найдите c.
Решение
Если графики функций касаются, то они имеют одну общую точку. Тогда:
Так как общая точка только одна, то дискриминант последнего квадратного уравнения D = 0.
.
При с = 2 уравнение x2
– 2x + 1 = 0 имеет единственный корень x = 1. Это означает, что абсцисса точки касания графиков положительна. При этом ордината точки касания также положительна.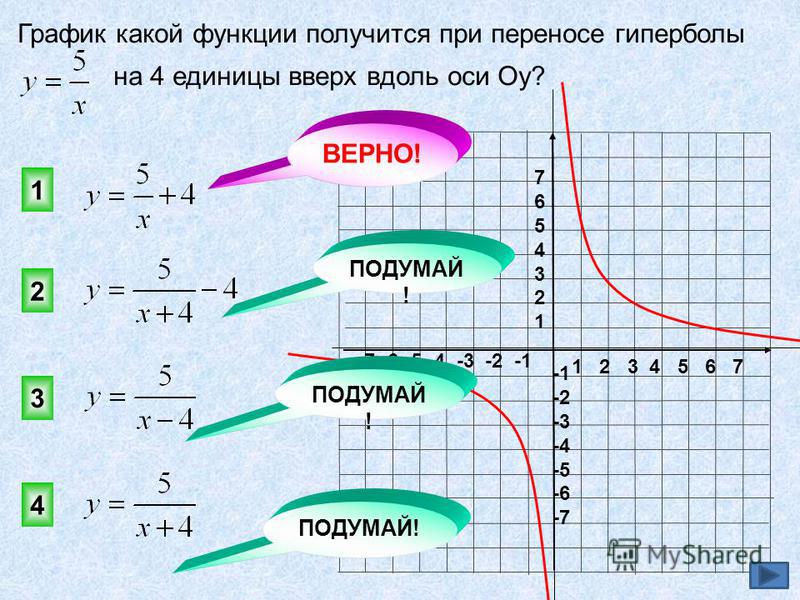
Следовательно, с = 2 удовлетворяет условию задачи.
Задание 2
Окружность, изображенная на рисунке, задана уравнением x2 + y2 = 16. Используя рисунок, определите, имеет ли система решение.
Решение
Система будет иметь решение в том случае, если прямая, построенная по второму уравнению системы, будет либо касаться окружности (в данном случае решение одно — точка касания), либо пересекать окружность в двух точках (решения два — точки пересечения). Чтобы проверить, имеет ли данная система решение, подставим во второе уравнение системы y = 1, получим, что x = 5 и x = 1, тогда y = 5. Получили две точки с координатами (5; 1) и (1; 5). Если данные точки нанести на представленной системе координат и соединить, то получим прямую, которая не касается и не пересекает нашу окружность. Таким образом, данная система решений не имеет.
Задание 3
На рисунке изображен график функции y = -x2
– 4x. Используя рисунок, решите неравенство -x2
≥ 4 x.
Решение
Чтобы решить неравенство, его необходимо преобразовать к виду заданной функции. Для этого 4 x перенесем влево. Получим:
-x2 – 4x ≥ 0.
По графику видно, что функция принимает значения большие или равные нулю выше оси абсцисс, т.е. на интервале [-4; 0]. Скобки квадратные, так как неравенство имеет не строгий знак.
Задание 4
Функция задана формулами:
1) ;
2) ;
3) ;
4) .
Найдите в этом перечне функции, графики которых проходят через начало координат.
Решение
Четвертая функция не подходит, так как это гипербола. Функция, проходящая через начало координат, имеет значения x = 0, y = 0. Таким образом, проверим все заданные функции на данное условие, подставив вместо x нуль. Получим, что первая и третья функции имеют значение y = 0. То есть первая и третья функции проходят через начало координат.
Задание 5
Запишите уравнение прямой, проходящей через точки A (-10; -7) и B (15; -2).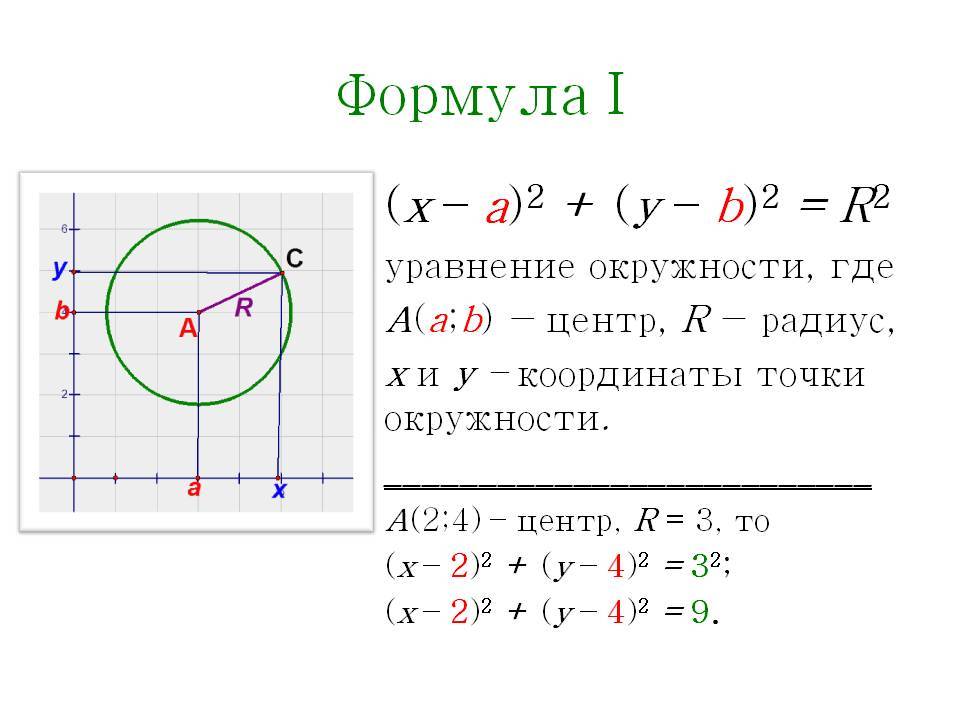
В какой точке эта прямая пересекает ось y?
Решение
Общий вид уравнения прямой y = kx + b. Подставим координаты данных точек в данное уравнение вместо xи y. Получим систему, состоящую из двух уравнений:
Решив данную систему, мы найдем значения k и b. Решить систему можно способом сложения. Для этого умножим первое уравнение на -1. Получим:
Сложив первое уравнение со вторым, получим:
Теперь, когда мы знаем значение k, найдем b, подставив k в любое из исходных уравнений системы, например, в первое, получим:
Теперь можно записать уравнение прямой, подставив значения k и b в общее уравнение прямой, получим:
.
Ответим на второй вопрос. Нам необходимо найти координаты точки пересечения прямой с осью y. Координата точки xв данном случае равна 0. Подставив в общее уравнение прямой вместо x нуль, найдем координаты точки y:
Таким образом, координаты точки пересечения прямой с осью y — (0; -5). Необходимо отметить, что если необходимо найти координаты точки пересечения прямой с осью x, y будет равен нулю.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |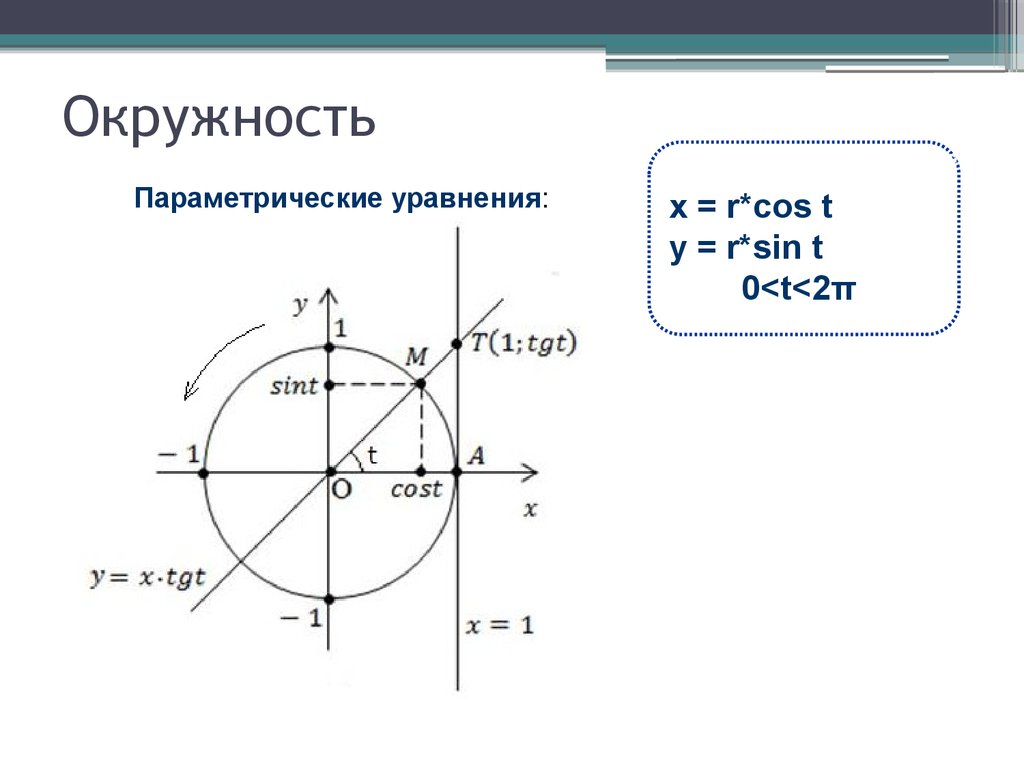
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |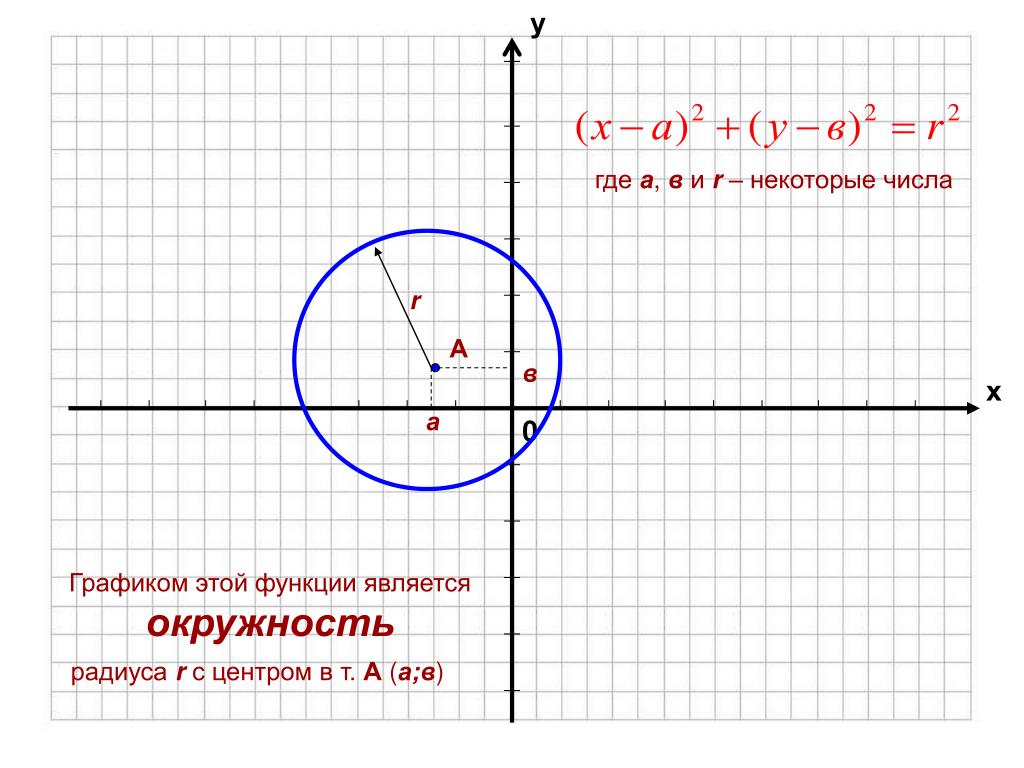
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Графические круговые функции — Алгебра II
Все ресурсы по Алгебре II
10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Алгебра II Помощь » Функции и графики » Квадратичные функции » Функции круга » Графические функции окружности
Определение графика уравнения
Возможные ответы:
Ellipse, центрированный на
Circle, в центре с Radius
Гипербола, центрированная на
Circle, в центре с Radius
Правильный ответ:
Circle, в центре с Radius с Radius с Radius.
Объяснение:
Стандартное уравнение окружности для:
Где центр и радиус окружности.
Деление на 4 обеих частей уравнения дает 9
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Пояснение:
Посмотрите на формулу уравнения окружности ниже.
Здесь центр и радиус. Обратите внимание, что вычитание в центре является частью формулы. Таким образом, глядя на наше уравнение, становится ясно, что центр равен , а квадрат радиуса равен . Извлекая корень из этого значения, мы получаем, что радиус должен быть равен .
Сообщить об ошибке
Определите уравнение окружности, центр которой лежит в точке и имеет радиус .
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение для окружности с центром и радиусом:
Центр нашей окружности с радиусом , поэтому уравнение для этой окружности:
Сообщить об ошибке
5 900 круга?
Возможные ответы:
Правильный ответ:
Объяснение:
Родительское уравнение окружности представлено .
Радиус окружности равен . Радиус круга .
Сообщить об ошибке
Что представляет собой центр круга, выраженный функцией ?
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение можно переписать так, чтобы оно выглядело как исходное уравнение для окружности . После завершения квадрата уравнение меняется с на . Оттуда это может быть выражено как . Следовательно, центр круга находится в .
Сообщить об ошибке
График уравнения
представляет собой окружность, радиус которой равен длине?
Возможные ответы:
Правильный ответ:
Объяснение:
Перепишите уравнение круга в стандартной форме
следующим образом:
С момента и, мы заполняем квадраты, добавив:
Стандартная форма уравнения.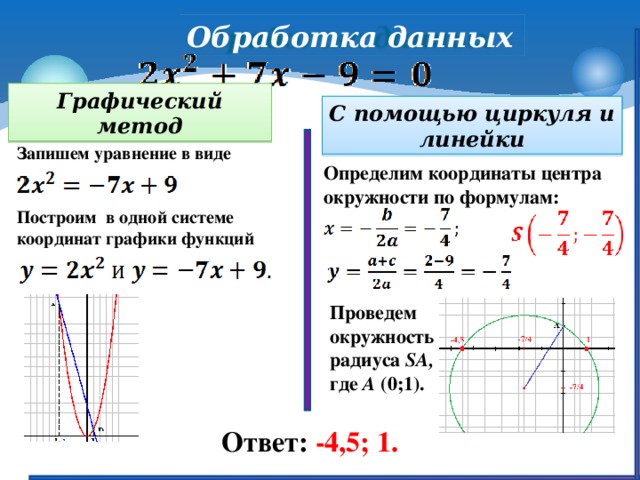
0005
,
поэтому радиус круга равен
Сообщить об ошибке
Каковы координаты центра круга с уравнением ?
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение окружности , в котором (h, k) — центр окружности. Чтобы получить центр окружности из ее уравнения, определите константы, следующие непосредственно за x и y, и поменяйте их знаки. В данном уравнении за x следует -1, а за y следует -6, поэтому координаты центра должны быть (1, 6).
Сообщить об ошибке
Каков радиус круга с уравнением ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы преобразовать данное уравнение в формат , завершите квадрат, прибавив к x-терминам и y-членам.
Квадратный корень из 4 равен 2, поэтому радиус круга равен 2.
Сообщить об ошибке
Каков радиус круга с уравнением ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы преобразовать данное уравнение в формат , завершите квадрат, прибавив к x-терминам и y-членам.
Квадратный корень из 25 равен 5, поэтому радиус круга равен 5,9.0005
Сообщить об ошибке
Какое уравнение представляет этот график?
Возможные ответы:
Правильный ответ:
Пояснение:
Уравнение окружности , в котором (h, k) — центр окружности, а r — ее радиус.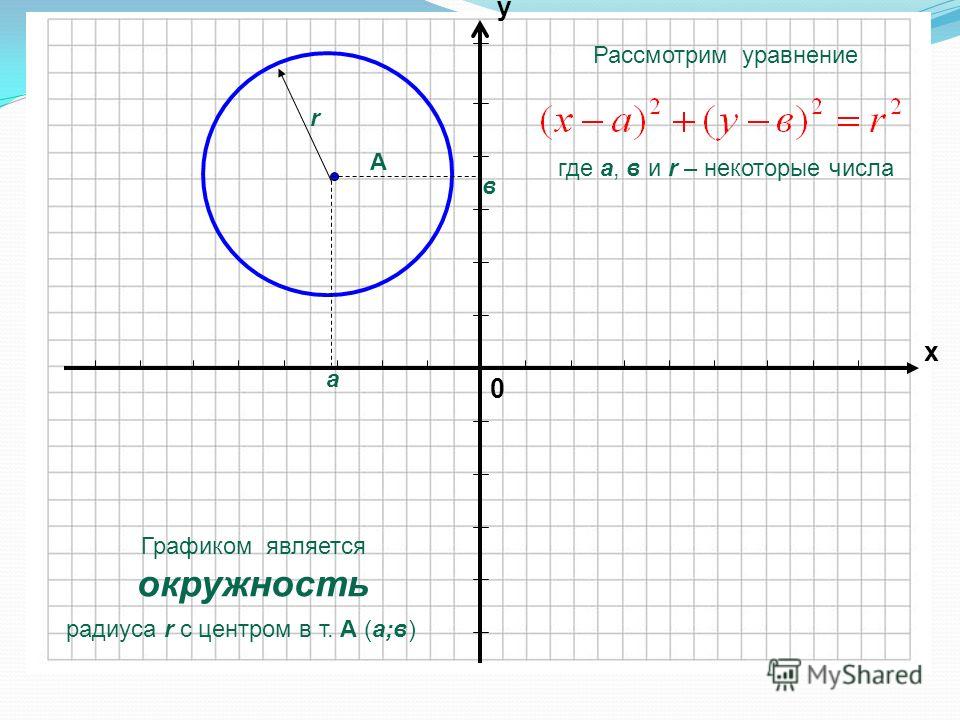
Поскольку график окружности центрирован в (0, 0), h и k оба равны 0. Поскольку радиус равен 3, правая часть уравнения равна 9..
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы Algebra II
10 Диагностические тесты 630 практических тестов Вопрос дня Карточки Learn by Concept
Как построить круг
Обновлено: 07-08-2021
Дифференциальные уравнения для чайников
Изучить книгу Купить на Amazon
Первое, что вам нужно знать, чтобы построить график уравнения круг — это место на плоскости, где расположен центр. Уравнение окружности выглядит как Это называется формой центр-радиус (или стандартной формой), потому что она дает вам обе части информации одновременно. h и v представляют центр круга в точке ( h , v ), а r обозначает радиус.
В частности, ч представляет горизонтальное смещение — насколько далеко влево или вправо центр круга падает от оси y . Переменная v представляет вертикальное смещение — насколько выше или ниже центр падает от оси x .
Можно отсчитать от центра до единиц (радиус) по горизонтали в обоих направлениях и по вертикали в обоих направлениях. Это даст вам четыре разные точки, равноудаленные от центра. Соедините эти четыре точки с лучшей кривой, которую вы можете нарисовать, чтобы получить график окружности.
Центр в начале координат
Самый простой круг для построения графика имеет центр в начале координат (0, 0). Потому что оба h и v равны нулю, они могут исчезнуть, и вы можете упростить стандартное уравнение окружности, чтобы оно выглядело как. Например, чтобы нарисовать окружность
, выполните следующие действия:
Осознайте, что центр окружности находится в начале координат (нет h и v ) и поместите эту точку туда.
Рассчитайте радиус, найдя r .
Установить r -квадрат = 16. В этом случае получится р = 4.
Нанесите точки радиуса на координатную плоскость.
Вы отсчитываете по 4 в каждом направлении от центра (0, 0): влево, вправо, вверх и вниз.
Соедините точки, чтобы нарисовать круг, используя плавную круглую кривую.
На этом рисунке показан этот круг на плоскости.
Центр от исходной точки
Начертить окружность в любом месте на координатной плоскости довольно просто, если ее уравнение представлено в форме центр-радиус. Все, что вам нужно сделать, это нанести центр круга на ( ч , к ), а затем отсчитываем от центра r единиц в четыре стороны (вверх, вниз, влево, вправо). Затем соедините эти четыре точки красивым круглым кругом. К сожалению, хотя гораздо проще рисовать круги в начале координат, очень немногие из них столь же прямолинейны и просты, как эти.
В pre-calc вы работаете с преобразованием графиков самых разных форм и размеров (для вас это не новость, верно?). К счастью, все эти графики следуют одной и той же схеме для горизонтального и вертикального смещения, так что вам не нужно запоминать множество правил.
Не забудьте поменять местами знак h и v внутри скобок в уравнении. Это необходимо, потому что h и v находятся внутри символов группировки, а это означает, что сдвиг происходит наоборот, чем вы думаете.
Например, для построения графика уравненияНайдите центр круга из уравнения ( ч , v ).
Поместите центр круга в (3, –1).
Рассчитайте радиус, найдя r .
Нанесите точки радиуса на координатную плоскость.
Считайте 5 единиц вверх, вниз, влево и вправо от центра (3, –1). Это означает, что у вас должны быть точки в точках (8, –1), (–2, –1), (3, –6) и (3, 4).
Соедините точки на графике круга с помощью круглой плавной кривой.
