Период колебаний нитяного и пружинного маятников
- Дворовенко Галина Валентиновна, учитель физики
Разделы: Физика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (7 МБ)
Цель урока: рассмотреть процесс колебаний на примере нитяного и пружинного маятников, выяснить зависимость периода колебаний от различных физический величин: длины нити, ускорения свободного падения, коэффициента жесткости и массы.
1. Проверка домашнего задания. (работа по формуле “Скажи ты…)
— Что называется амплитудой колебания; периодом колебания; частотой колебания; циклической частотой?
— Какой буквой обозначается циклическая частота?
— Какая математическая зависимость существует между периодом и частотой колебания?
Учащиеся в парах проверяют домашнюю работу:
упражнение №24.
2. Объяснение нового материала. Работа по теме урока.
Учитель. Как вы думаете, от каких величин может завесить период колебаний нитяного маятника?
Ученики. От длины нити и массы груза.
Учитель. Начнем с длины нити. Поставим опыт с двумя маятниками, имеющими разную длину нити, но одинаковую массу (эксперимент).
Ученики. С увеличением длины нити период колебаний увеличивается.
Учитель. А теперь посмотрим как зависит период колебаний от массы груза (эксперимент: маятники имеют одинаковую длину нити и разный вес грузов).
Учащиеся. Период не зависит от массы груза.
Учитель
. Но период колебания нитяного маятника зависит еще от одной физической величины. Это ускорение свободного падения. Проведем эксперимент и “поможем “ силе тяжести положив магнит.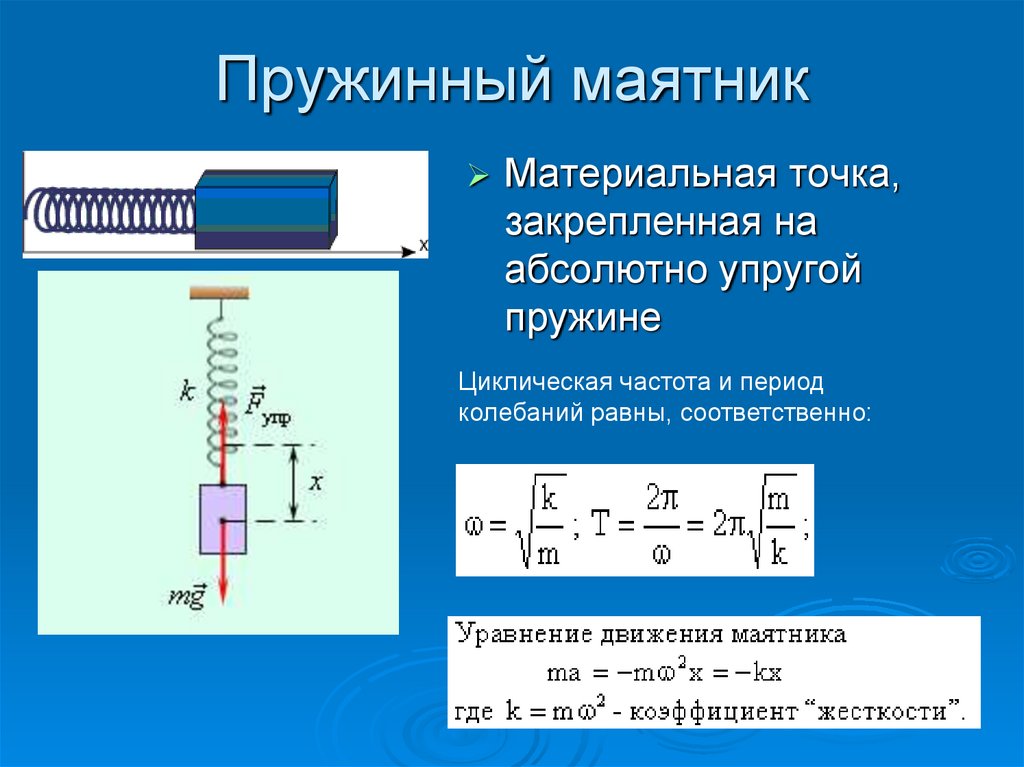 Теперь при той же массе груза
возвращающая сила будет больше.
Теперь при той же массе груза
возвращающая сила будет больше.Ученики. Период уменьшился, а частота увеличилась.
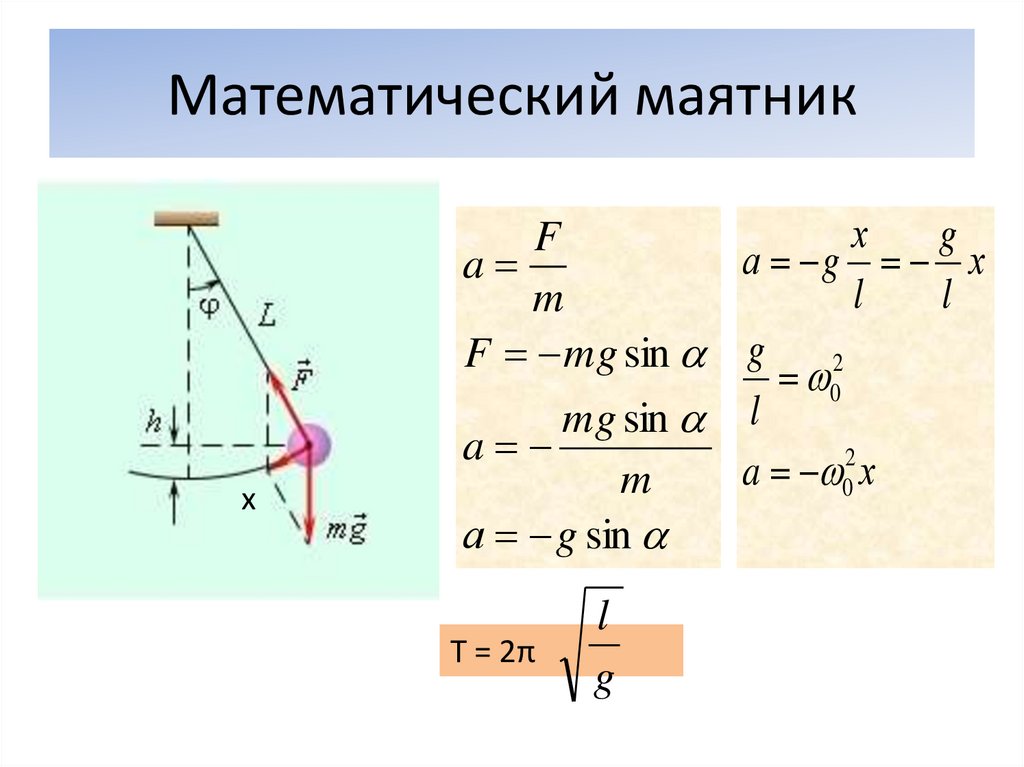
Учитель. А теперь выведем формулу для расчета периода колебания нитяного маятника.
формула Гюйгенса:
l – длина.
g – ускорение свободного падения.
Это очень важная формула и ее надо запомнить.
Учитель. От чего может зависеть период пружинного маятника?
Учитель. Сначала на опыте посмотрим зависимость периода колебаний и жесткости пружины.(эксперимент : две пружины разной жесткости, но одинаковой длины и одинаковой массой груза)
Ученики. Период меньше там, где
жесткость больше.
Учитель. А как вы думаете как зависит период от массы груза(эксперимент).
Ученики. Чем больше масса , тем больше и период.
Учитель. А теперь выведем формулу для расчета периода колебания пружинного маятника.
- возвращающая сила системы
— собственная частота системы.
Эту формулу так же запишите на обложку тетради и постарайтесь ее запомнить.
3. Закрепление материала
Решение задач Лукашик В.И.№ 873, 876.879
4.Домашнее задание. Лукашик В.И.№ 875, 877.880.
Список литературы:
1.Л.Э.Генденштейн,В.А.Орлов,Г.Г.Никифоров “Как
научить решать задачи по физике (основная школа ). Подготовка к ГИА.
Подготовка к ГИА.
2. С.Е.Полянский “Поурочные разработки по физике”.
3. Лукашик В.И. “Сборник задач по физике”.
4. Учебник физики Перышкин А.В. Физика 9
Колебания пружинного маятника • Игорь Иванов • Научно-популярные задачи на «Элементах» • Физика
Когда в школе проходят колебания, то их иллюстрируют двумя самыми простыми примерами: грузик на пружинке и математический маятник (то есть точечный грузик на нерастяжимой нити) в поле тяжести. В обоих случаях в колебаниях наблюдается важная закономерность: их период не зависит от амплитуды — по крайней мере до тех пор, пока эта амплитуда остается малой, — а определяется только механическими свойствами системы.
А теперь давайте совместим эти два примера и рассмотрим колебания грузика, подвешенного на растяжимой пружинке в поле тяжести (рис. 1).
Для простоты мы пренебрегаем третьим измерением и считаем, что этот пружинный маятник колеблется строго в плоскости рисунка. В этом случае грузик (который тоже считается точечным) может двигаться в вертикальной плоскости в произвольном направлении, а не только вверх-вниз или влево-вправо, как изображено на рис. 2. Но если опять ограничиться только малыми отклонениями от положения равновесия, то горизонтальные и вертикальные колебания совершаются практически независимо, со своими периодами Tx и Ty.
В этом случае грузик (который тоже считается точечным) может двигаться в вертикальной плоскости в произвольном направлении, а не только вверх-вниз или влево-вправо, как изображено на рис. 2. Но если опять ограничиться только малыми отклонениями от положения равновесия, то горизонтальные и вертикальные колебания совершаются практически независимо, со своими периодами Tx и Ty.
Казалось бы, раз эти колебания определяются совершенно разными силами и характеристиками системы, то их периоды могут быть совершенно произвольными, никак не связанными друг с другом. Оказывается — нет!
Подсказка
Задача может поначалу удивить тем, что в ней как будто ничего и не дано, а что-то при этом требуется доказать. Но ничего страшного тут нет. Когда задача формулируется таким образом, это означает, что вы можете для себя ввести какие-то обозначения, которые вам нужны, сосчитать с ними то, что требуется, а потом прийти к выводу, который уже не зависит от этих величин. Проделайте это для данной задачи. Возьмите формулы для периодов колебания, подумайте, что за величины в них входят, и сравните два периода друг с другом, поделив один на другой.
Проделайте это для данной задачи. Возьмите формулы для периодов колебания, подумайте, что за величины в них входят, и сравните два периода друг с другом, поделив один на другой.
Решение
Период колебания грузика массы m на пружинке жесткости k и длины L0 составляет
.
Эта формула не меняется и в том случае, если грузик подвешен в поле тяжести с ускорением свободного падения g. Конечно, положение равновесия грузика сместится вниз на высоту ΔL = mg/k — именно при таком удлинении пружинки сила упругости компенсирует силу тяжести. Но период вертикальных колебаний относительно этого нового положения равновесия с растянутой пружинкой останется тем же.
Период горизонтальных колебаний растянутого маятника выражается через ускорение свободного падения g и его полную длину L = L0 + ΔL:
.
Именно благодаря дополнительному растяжению в поле тяжести мы выясняем, что
Вот и всё решение.
Послесловие
Несмотря на свою кажущуюся простоту, маятник на пружинке — система, довольно богатая на явления. Это один из самых простых примеров симпатичного явления — резонанса Ферми. Заключается оно вот в чем. Вообще говоря, если грузик как-то оттянуть и отпустить, то он будет колебаться и по вертикали, и по горизонтали. Эти два типа колебания будут просто накладываться и не мешать друг другу. Но если периоды вертикальных и горизонтальных колебаний связаны соотношением
Выглядит это так: вы оттягиваете грузик вниз и отпускаете его. Он поначалу колеблется только вверх-вниз, затем сам по себе начинает раскачиваться в стороны, на какое-то мгновение колебание становится почти полностью горизонтальным, а потом снова возвращается к вертикальному.
Объяснение этого замечательного эффекта, а также магического соотношения Tx:Ty = 2:1, вот в чем. Обозначим через x и y отклонения грузика от положения равновесия (ось y направлена вверх). При таком отклонении потенциальная энергия вырастает на величину
Это — точная формула, она годится для любых отклонений, больших и маленьких. Но если x и y малы, существенно меньше L, то выражение приблизительно равно
плюс другие слагаемые, содержащие еще более высокие степени отклонений. Величины Uy и Ux — это обычные потенциальные энергии, из которых получаются вертикальные и горизонтальные колебания. А вот выделенная синим цветом величина Uxy — это особая добавка, которая порождает  Это становится совсем прозрачно, если провести вычисления дальше и написать уравнение колебаний по горизонтали и вертикали:
Это становится совсем прозрачно, если провести вычисления дальше и написать уравнение колебаний по горизонтали и вертикали:
где введены обозначения
Без синей добавки у нас были бы обычные независимые колебания по вертикали и горизонтали с частотами ωy и ωx. Эта добавка играет роль вынуждающей силы, дополнительно раскачивающей колебания. Если частоты ωy и ωx произвольны, то эта маленькая сила не приводит ни к какому существенному эффекту. Но если выполняется соотношение ωy = 2ωx, наступает резонанс: вынуждающая сила для обоих типов колебаний содержит компоненту с той же частотой, что и само колебание
. В результате эта сила медленно, но неуклонно раскачивает один тип колебаний и подавляет другой. Именно так горизонтальные и вертикальные колебания перетекают друг в друга.Дополнительные красоты возникают, если в этом примере по-честному учесть третье измерение. Будем считать, что грузик может сжимать-разжимать пружинку по вертикали и качаться, как маятник, в двух горизонтальных направлениях. Тогда, при выполнении условия резонанса, при взгляде сверху грузик выписывает звездчатую траекторию, как, например, на рис. 3. Так получается потому, что плоскость колебания не остается неподвижной, а поворачивается — но не плавно, а как бы скачками. Пока колебание идет из стороны в сторону, эта плоскость более-менее держится, а поворот происходит за тот короткий промежуток, когда колебание почти вертикально. Предлагаем читателям самостоятельно подумать, каковы причины этого поведения и от чего зависит угол поворота плоскости. А желающие окунуться с головой в эту довольно-таки глубокую задачу могут полистать статью Stepwise Precession of the Resonant Swinging Spring, в которой не только приведен подробный анализ задачи, но и рассказывается о ее истории и о связи этой задачи с другими разделами физики, в частности с атомной физикой.
Будем считать, что грузик может сжимать-разжимать пружинку по вертикали и качаться, как маятник, в двух горизонтальных направлениях. Тогда, при выполнении условия резонанса, при взгляде сверху грузик выписывает звездчатую траекторию, как, например, на рис. 3. Так получается потому, что плоскость колебания не остается неподвижной, а поворачивается — но не плавно, а как бы скачками. Пока колебание идет из стороны в сторону, эта плоскость более-менее держится, а поворот происходит за тот короткий промежуток, когда колебание почти вертикально. Предлагаем читателям самостоятельно подумать, каковы причины этого поведения и от чего зависит угол поворота плоскости. А желающие окунуться с головой в эту довольно-таки глубокую задачу могут полистать статью Stepwise Precession of the Resonant Swinging Spring, в которой не только приведен подробный анализ задачи, но и рассказывается о ее истории и о связи этой задачи с другими разделами физики, в частности с атомной физикой.
3
Показать комментарии (3)
Свернуть комментарии (3)
SwZ 15.
 02.2015 11:59
Ответить
02.2015 11:59
ОтветитьПри решении сделано допущение, что нулевая сила со стороны пружинки действует, когда её длина неотрицательна. Однако, я видел «напряжённые» пружинки которые в сокращённом состоянии сильно пытаются дальше сжаться, но им это не удаётся из-за того, что витки упираются друг в друга. Равновесная длина такой «напряжённой» пружинки может быть отрицательной. В этом случае период горизонтальных колебаний окажется меньше периода вертикальных колебаний.
Получить пружинку с отрицательным равновесным расстоянием довольно просто. Надо взять пружинку с положительным равновесным расстоянием и «вывернуть» её, протянув один конец внутри витков. Если при этом толщина проволоки существенно меньше диаметра пружины, то предел упругих деформаций не будет достигнут, и в результате получим пружинку с отрицательным равновесным расстоянием, равным по модулю исходному положительному равновесному расстоянию.Ответить
Игорь Иванов SwZ 16.
 02.2015 08:33
Ответить
02.2015 08:33
ОтветитьДа, конечно. Как и во всех школьных задачах на пружинки, тут подразумевается обычный закон Гука. Как ведет себя реальная пружинка с витками, это отдельная задача.
Ответить
Написать комментарий
ньютоновская механика — Почему период времени маятника с пружиной постоянной силы $k$ и грузом значительной массы $m$ на Луне такой же, как и на Земле?
Задавать вопрос
спросил
Изменено 2 года, 2 месяца назад
Просмотрено 365 раз 9\frac{1}{2}$$
$T$ в этом выражении не зависит от $g$. Таким образом, период времени нагруженной пружины на Луне будет таким же, как и на Земле.
Мои мысли
Я думаю, что значение $k$ для перевернутой пружины зависит от гравитационного притяжения. Из закона Гука получаем, что возвращающая сила пружины линейно зависит от перемещения.
$$ F(x) = -k(x) \\ k = \frac{-F(x)}{x} $$
Когда груз подвешен вертикально, $x$ зависит от гравитационного притяжения $g $. 9\frac{1}{4} $$
Таким образом, период времени на Луне будет немного больше, чем на Земле. Может ли кто-нибудь сказать мне, правильно ли я это сделал?
- ньютоновская механика
- ньютоновская гравитация
- гармонический осциллятор
- пружина
- осцилляторы
$\endgroup$
$\begingroup$
Обратите внимание, что масса $m$ и жесткость пружины $k$ на Земле такие же, как и на Луне. Следовательно, период времени пружины не зависит от разницы, вызванной ускорением силы тяжести. Следовательно, он не изменится, когда его доставят на Луну.
Следовательно, он не изменится, когда его доставят на Луну.
Я думаю, что значение 𝑘 для пружины, подвешенной вверх ногами, зависит от гравитационного притяжения
Нет. Это константа. Приведенный вами математический аргумент содержит много ошибок, но достаточно сказать, что период нагруженной пружины не будет отличаться.
Единственное, что будет отличаться, это положение равновесия массы, и в этом случае на Луне она будет выше.
$\endgroup$
$\begingroup$
Чтобы проиллюстрировать независимость величины гравитационного поля, можно установить систему пружинных масс на горизонтальном столе, и при отсутствии трения период колебаний все равно будет $2\pi \sqrt{\frac mk}$ при условии, что пружина может подвергаться как сжатию, так и растяжению.
Причина такой независимости в том, что восстанавливающая сила, $F$, зависит от смещения массы из положения равновесия, на нее не действует результирующая сила, которая не является функцией гравитационного поля и массы $m$ , также не зависит от гравитационного поля, поэтому ускорение массы $a=\frac Fm$ не зависит от гравитационного поля.
Соотношение $l$ и $g$, которое, по-видимому, показывает зависимость периода от силы гравитационного поля, не показывает этого, потому что $l$ и $g$ не независимы друг от друга и подобны уравнению $kl =mg$, так что $g$ увеличивается вместе с $l$ в той же пропорции.
$\endgroup$
$\begingroup$
… имеем, что возвращающая сила в пружине линейно зависит от смещения. $$F(x) = -k(x) \\ k = \frac{-F(x)}{x}$$
Этот расчет силы неверен.
Собственно сила ($F$) состоит из двух частей:
- Возвращающая сила пружины ($-kx$) который пропорционален текущему смещению ($x$). И константа пружины $k$ по-прежнему остается постоянной.
- Сила гравитации ($mg$) которое не зависит от текущего смещения ($x$)
Итак, у нас есть общая сила $$F=-kx+мг. \tag{1}$$
Согласно второму закону Ньютона ($m\ddot{x}=F$) получаем уравнение движения
$$m\ddot{x}=-kx+mg.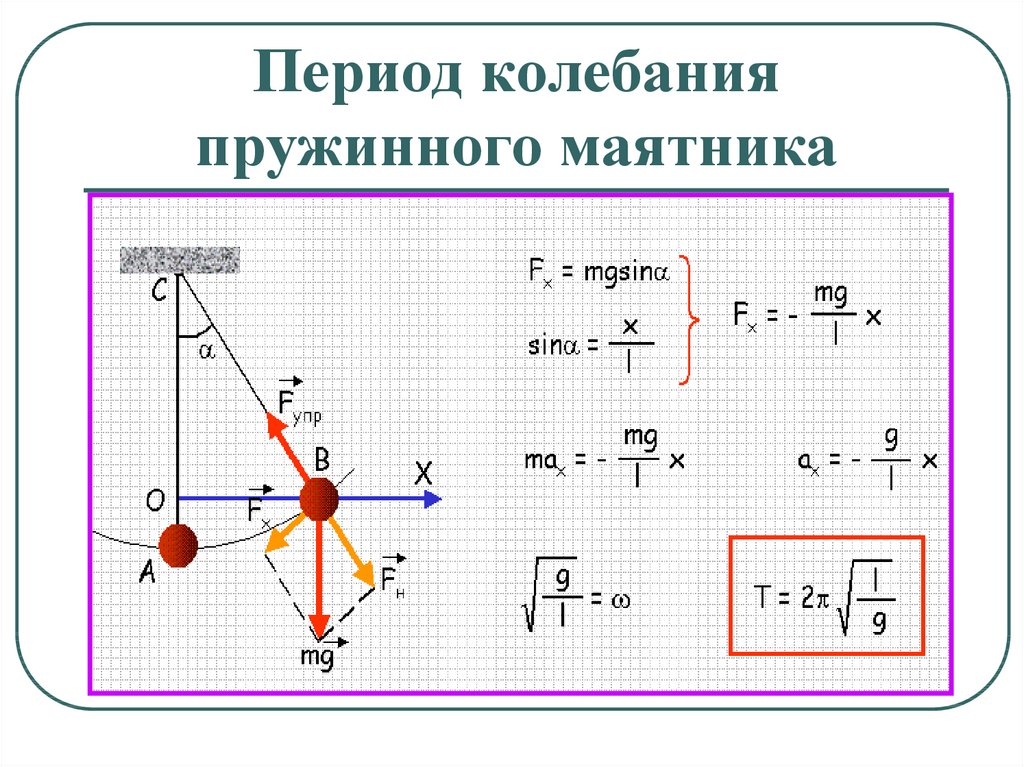 \tag{2}$$
\tag{2}$$
Наиболее общее решение (2) может быть найдено как $$x(t)=\frac{mg}{k}+A\sin\left(\sqrt{\frac{k}{m}}\ t+\phi\right) \tag{3}$$ где $A$ (амплитуда) и $\phi$ (начальная фаза) — произвольные константы. Вы можете проверить правильность этого решения, подставив его в дифференциальное уравнение (2).
В решении (3) вы видите две особенности.
- Период колебаний $T$ можно определить из $\frac{2\pi}{T}=\sqrt{\frac{k}{m}}$. Таким образом, $T$ не зависит от $g$.
- Равновесное перемещение равно $\frac{mg}{k}$. Таким образом, это зависит от $g$. На Луне он меньше, чем на Земле.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
5.
 5 Простое гармоническое движение — физика
5 Простое гармоническое движение — физикаРаздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать закон Гука и простое гармоническое движение
- Описать периодическое движение, колебания, амплитуду, частоту и период
- Решение задач на простое гармоническое движение с использованием пружин и маятников
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (7) Научные концепции. Учащийся знает характеристики и поведение волн. Ожидается, что студент:
- (A) исследуют и описывают колебательное движение и распространение волн в различных типах сред.
Кроме того, руководство по физике для средней школы обращается к содержанию этого раздела лабораторной работы под названием «Движение в двух измерениях», а также к следующим стандартам:
- (7) Научные концепции.
 Учащийся знает характеристики и поведение волн. Ожидается, что студент:
Учащийся знает характеристики и поведение волн. Ожидается, что студент:- (А) изучить и описать колебательное движение и распространение волн в различных типах сред.
Основные термины раздела
| амплитуда | деформация | положение равновесия | частота |
| Закон Гука | колебательный | период | периодическое движение |
| восстанавливающая сила | простое гармоническое движение | простой маятник |
Закон Гука и простое гармоническое движение
Представьте себе машину, припаркованную у стены. Если бульдозер втолкнет машину в стену, машина не сдвинется с места, но заметно изменит форму. Изменение формы из-за приложения силы является деформацией. Известно, что даже очень малые силы вызывают некоторую деформацию. При малых деформациях могут произойти две важные вещи. Во-первых, в отличие от примера с автомобилем и бульдозером, объект возвращается к своей первоначальной форме после прекращения действия силы. Во-вторых, размер деформации пропорционален силе. Это второе свойство известно как закон Гука. В форме уравнения закон Гука равен
Изменение формы из-за приложения силы является деформацией. Известно, что даже очень малые силы вызывают некоторую деформацию. При малых деформациях могут произойти две важные вещи. Во-первых, в отличие от примера с автомобилем и бульдозером, объект возвращается к своей первоначальной форме после прекращения действия силы. Во-вторых, размер деформации пропорционален силе. Это второе свойство известно как закон Гука. В форме уравнения закон Гука равен
F=−kx,F=−kx,
, где x – величина деформации (например, изменение длины), вызванная восстанавливающей силой F , а k – константа, зависящая от форму и состав предмета. Возвращающая сила — это сила, возвращающая объект в положение равновесия; знак минус стоит потому, что восстанавливающая сила действует в направлении, противоположном перемещению. Обратите внимание, что восстанавливающая сила пропорциональна деформации х . Деформацию также можно рассматривать как отклонение от равновесия. Это изменение положения под действием силы. В отсутствие силы объект находился бы в положении равновесия. Силовая постоянная k связана с жесткостью системы. Чем больше силовая постоянная, тем жестче система. Более жесткую систему труднее деформировать, и она требует большей восстанавливающей силы. Единицами k являются ньютоны на метр (Н/м). Одним из наиболее распространенных применений закона Гука является решение задач, связанных с пружинами и маятниками, которые мы рассмотрим в конце этого раздела.
Это изменение положения под действием силы. В отсутствие силы объект находился бы в положении равновесия. Силовая постоянная k связана с жесткостью системы. Чем больше силовая постоянная, тем жестче система. Более жесткую систему труднее деформировать, и она требует большей восстанавливающей силы. Единицами k являются ньютоны на метр (Н/м). Одним из наиболее распространенных применений закона Гука является решение задач, связанных с пружинами и маятниками, которые мы рассмотрим в конце этого раздела.
Поддержка учителей
Поддержка учителей
[BL] Повторите концепцию силы.
[BL][OL][AL] Ввести закон Гука и силовую постоянную пружины.
Колебания и периодическое движение
Что общего у океанского буя, ребенка на качелях, гитары и биения сердец? Все они колеблются. То есть они перемещаются туда и обратно между двумя точками, как линейка, показанная на рис.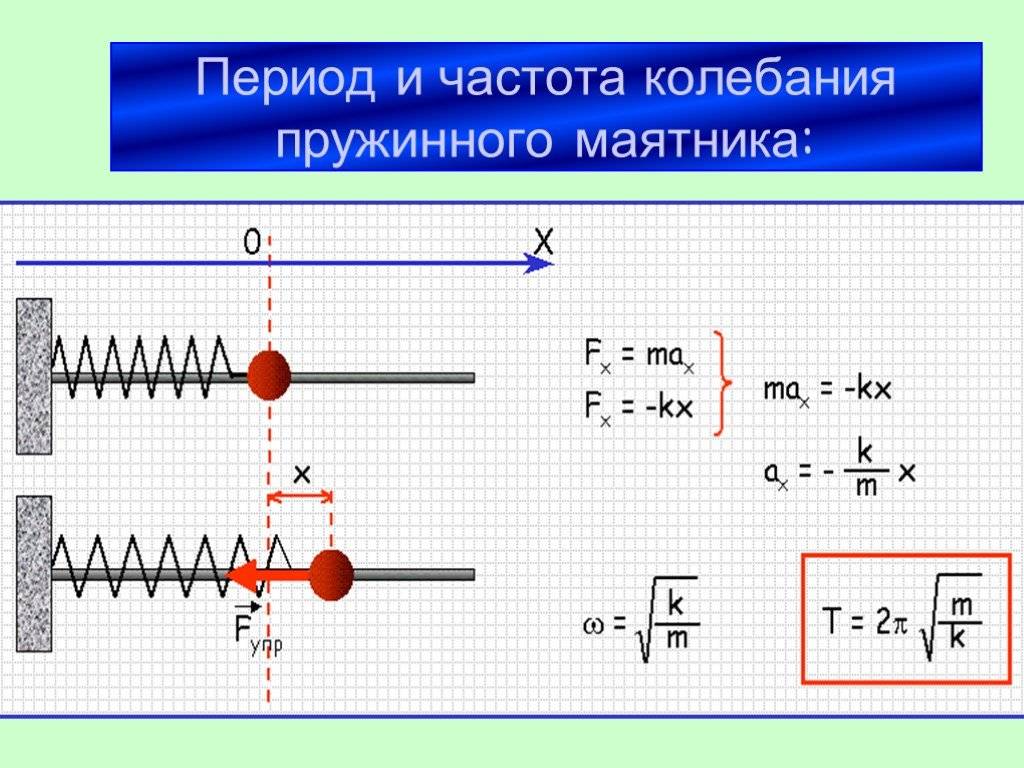 5.37. Все колебания связаны с силой. Например, вы толкаете ребенка на качелях, чтобы он начал движение.
5.37. Все колебания связаны с силой. Например, вы толкаете ребенка на качелях, чтобы он начал движение.
Рисунок 5,37 Линейка смещена из положения равновесия.
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Найдите пружины или резиновые ленты с различной степенью жесткости. Попросите учащихся прикрепить к ним грузы, чтобы построить осцилляторы. Познакомить с терминами «частота» и «период времени». Попросите учащихся понаблюдать, как жесткость пружины влияет на них. Как на них влияет масса системы? Как влияет на них начальная сила?
Первый закон Ньютона подразумевает, что объект, колеблющийся вперед и назад, испытывает силы. Без силы объект двигался бы по прямой линии с постоянной скоростью, а не колебался бы. Рассмотрим, например, выдергивание пластиковой линейки влево, как показано на рис. 5.38. Деформация линейки создает силу в противоположном направлении, известную как восстанавливающая сила. После освобождения восстанавливающая сила заставляет линейку вернуться к своему устойчивому положению равновесия, где результирующая сила, действующая на нее, равна нулю. Однако к тому времени, когда линейка туда попадает, она набирает обороты и продолжает двигаться вправо, вызывая противоположную деформацию. Затем его толкают влево, обратно через равновесие, и процесс повторяется до тех пор, пока он постепенно не потеряет всю свою энергию. Простейшие колебания возникают, когда возвращающая сила прямо пропорциональна смещению. Напомним, что закон Гука описывает эту ситуацию уравнением F = − кх . Следовательно, закон Гука описывает и применяется к простейшему случаю колебаний, известному как простое гармоническое движение.
После освобождения восстанавливающая сила заставляет линейку вернуться к своему устойчивому положению равновесия, где результирующая сила, действующая на нее, равна нулю. Однако к тому времени, когда линейка туда попадает, она набирает обороты и продолжает двигаться вправо, вызывая противоположную деформацию. Затем его толкают влево, обратно через равновесие, и процесс повторяется до тех пор, пока он постепенно не потеряет всю свою энергию. Простейшие колебания возникают, когда возвращающая сила прямо пропорциональна смещению. Напомним, что закон Гука описывает эту ситуацию уравнением F = − кх . Следовательно, закон Гука описывает и применяется к простейшему случаю колебаний, известному как простое гармоническое движение.
Рисунок
5,38
(а) Пластиковая линейка отпущена, и возвращающая сила возвращает линейку в положение равновесия. (b) Суммарная сила равна нулю в положении равновесия, но линейка имеет импульс и продолжает двигаться вправо. в) Возвращающая сила направлена в противоположную сторону. Он останавливает линейку и снова возвращает ее к равновесию. (d) Теперь импульс линейки направлен влево. д) При отсутствии демпфирования (вызванного силами трения) линейка достигает исходного положения. Оттуда движение будет повторяться.
в) Возвращающая сила направлена в противоположную сторону. Он останавливает линейку и снова возвращает ее к равновесию. (d) Теперь импульс линейки направлен влево. д) При отсутствии демпфирования (вызванного силами трения) линейка достигает исходного положения. Оттуда движение будет повторяться.
Когда вы дергаете гитарную струну, получаемый звук имеет устойчивый тон и длится долгое время. Каждое колебание струны занимает столько же времени, сколько и предыдущее. Периодическое движение — это движение, которое повторяется через равные промежутки времени, например, когда объект подпрыгивает вверх и вниз на пружине или маятник качается вперед и назад. Время совершения одного колебания (полного цикла движения) остается постоянным и называется периодом T . Его единицами обычно являются секунды.
Частота f — количество колебаний в единицу времени. Единицей частоты в системе СИ является герц (Гц), определяемый как количество колебаний в секунду. Отношение между частотой и периодом равно
Отношение между частотой и периодом равно
f= 1/T.f= 1/T.
Как видно из уравнения, частота и период — это разные способы выражения одного и того же понятия. Например, если вы получаете зарплату два раза в месяц, вы можете сказать, что частота выплат — две в месяц, или что период между чеками — полмесяца.
Если нет трения, замедляющего его, то объект в простом движении будет вечно колебаться с одинаковым смещением по обе стороны от положения равновесия. Положение равновесия — это положение, в котором объект естественным образом находился бы в отсутствие силы. Максимальное отклонение от равновесия называется амплитудой X . Единицы амплитуды и смещения одинаковы, но зависят от типа колебаний. Для объекта на пружине, показанного на рис. 5.39, единицами измерения амплитуды и перемещения являются метры.
Рисунок
5,39
Объект, прикрепленный к пружине, скользящей по поверхности без трения, представляет собой простой гармонический осциллятор. При выходе из равновесия объект совершает простое гармоническое движение с амплитудой X и периодом T . Максимальная скорость объекта возникает, когда он проходит через точку равновесия. Чем жестче пружина, тем меньше период T . Чем больше масса объекта, тем больше период T .
При выходе из равновесия объект совершает простое гармоническое движение с амплитудой X и периодом T . Максимальная скорость объекта возникает, когда он проходит через точку равновесия. Чем жестче пружина, тем меньше период T . Чем больше масса объекта, тем больше период T .
Масса m и силовая постоянная k являются единственными факторами, влияющими на период и частоту простого гармонического движения. Период простого гармонического осциллятора равен
T=2πmkT=2πmk
и, поскольку f = 1/ T , частота простого гармонического осциллятора равна
f=12πкм.f=12πкм.
Смотреть физику
Введение в гармоническое движение
В этом видеоролике показано, как построить график смещения пружины в направлении x с течением времени на основе периода. Посмотрите первые 10 минут видео (вы можете остановиться, когда рассказчик начнет освещать исчисление).
Посмотрите первые 10 минут видео (вы можете остановиться, когда рассказчик начнет освещать исчисление).
Если бы амплитуда смещения пружины была больше, как бы это повлияло на график смещения во времени? Что произошло бы с графиком, если бы период был больше?
Большая амплитуда приведет к более высоким пикам и впадинам, а более длинный период приведет к большему временному интервалу между пиками.
Большая амплитуда приведет к меньшим пикам и впадинам, а более длинный период приведет к большему расстоянию между пиками.
Большая амплитуда приведет к более высоким пикам и впадинам, а более длинный период приведет к более короткому расстоянию между пиками.

Большая амплитуда приведет к меньшим пикам и впадинам, а более длинный период приведет к более короткому расстоянию между пиками.
Решение задач о пружине и маятнике с помощью простого гармонического движения
Прежде чем решать задачи с пружинами и маятниками, важно сначала понять, как работает маятник. На рис. 5.40 представлена полезная иллюстрация простого маятника.
Рисунок
5.40
Простой маятник имеет груз небольшого диаметра и нить, которая имеет очень маленькую массу, но достаточно прочна, чтобы не растягиваться. Линейное смещение от равновесия равно s, длине дуги. Также показаны силы, воздействующие на груз, в результате чего результирующая сила равна − мг 9 .0278 sin θ в сторону положения равновесия, то есть восстанавливающая сила.
Поддержка учителей
Поддержка учителей
[BL] Обзор простого гармонического движения.
К повседневным маятникам относятся старомодные часы, детские качели или грузило на леске. При небольших смещениях менее 15 градусов маятник испытывает простые гармонические колебания, а это означает, что его возвращающая сила прямо пропорциональна его смещению. Маятник в простом гармоническом движении называется простым маятником. Маятник имеет объект с небольшой массой, также известный как маятник, который висит на тонкой проволоке или веревке. Положение равновесия маятника — это когда угол θθ равен нулю (то есть когда маятник висит прямо вниз). Вполне логично, что без приложения силы именно здесь будет лежать маятниковый груз.
Поддержка учителей
Поддержка учителей
[BL][OL][AL]Соберите простые маятники разной длины. Попросите студентов измерить их периоды времени или частоты.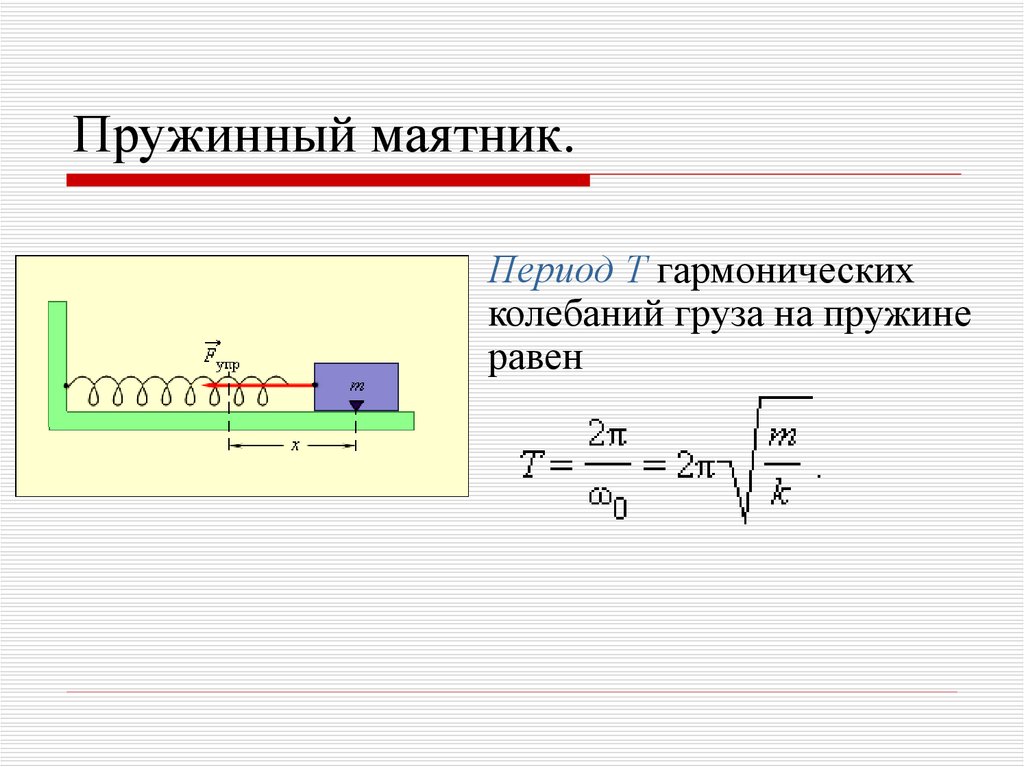 Постоянны ли они для данного маятника? Как масса влияет на частоту? Как на это влияет начальное смещение? Что произойдет, если слегка подтолкнуть маятник, чтобы он запустился? Это меняет частоту? Как длина влияет на частоту?
Постоянны ли они для данного маятника? Как масса влияет на частоту? Как на это влияет начальное смещение? Что произойдет, если слегка подтолкнуть маятник, чтобы он запустился? Это меняет частоту? Как длина влияет на частоту?
Перемещение маятника на длину дуги с . Вес м г имеет компоненты м г cos θθ вдоль струны и м г sin θθ по касательной к дуге. Натяжение струны точно компенсирует составляющую м г cos θθ, параллельную струне. Это оставляет чистую восстанавливающую силу обратно к положению равновесия, которая проходит по касательной к дуге и равна — м г sin θθ .
Для малоугловых колебаний простого маятника период равен T=2πLg.T=2πLg.
На период простого маятника влияют только его длина и ускорение свободного падения.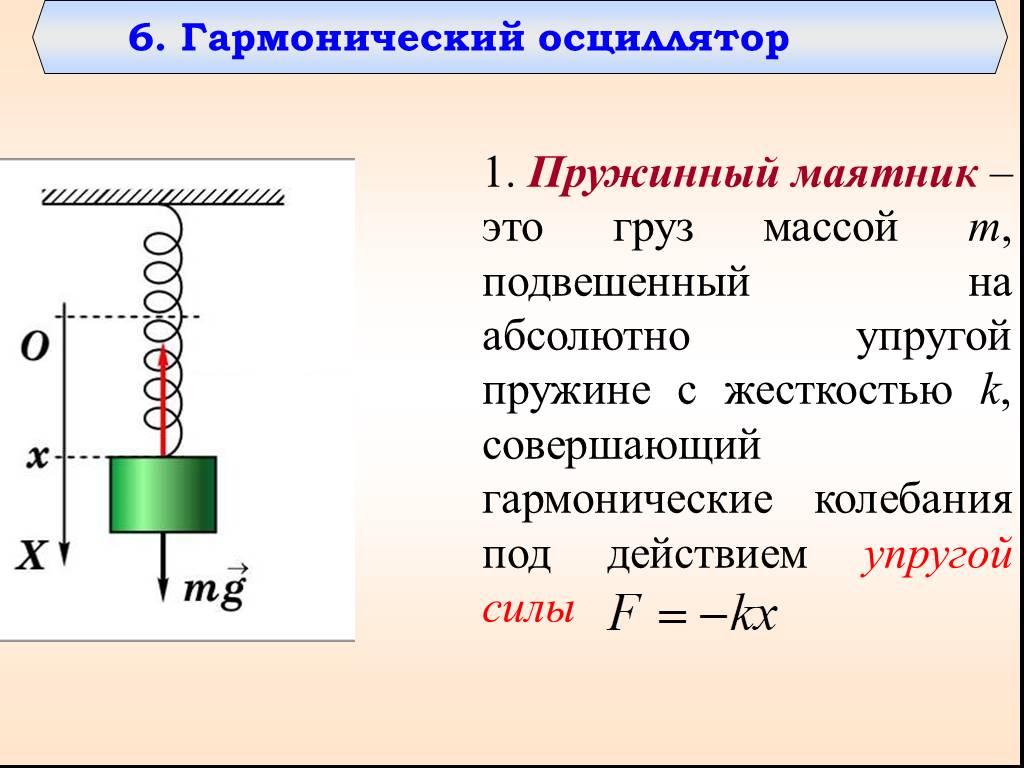 Период совершенно не зависит от других факторов, таких как масса или амплитуда. Однако обратите внимание, что T зависит от g . Это означает, что если мы знаем длину маятника, мы можем использовать его для измерения гравитации! Это пригодится в книге «Измерение ускорения под действием силы тяжести: период маятника».
Период совершенно не зависит от других факторов, таких как масса или амплитуда. Однако обратите внимание, что T зависит от g . Это означает, что если мы знаем длину маятника, мы можем использовать его для измерения гравитации! Это пригодится в книге «Измерение ускорения под действием силы тяжести: период маятника».
Советы для успеха
Напряжение представлено переменной T , а период представлен переменной T . Важно не путать их, поскольку напряжение — это сила, а период — это продолжительность времени.
Рабочий пример
Измерение ускорения свободного падения: период маятника
Каково ускорение свободного падения в области, где простой маятник длиной 75 000 см имеет период 1,7357 с?
Стратегия
Нас просят найти g , зная период T и длину L маятника. Мы можем решить T=2πLgT=2πLg для g , предполагая, что угол отклонения меньше 15 градусов. Напомним, что когда угол отклонения меньше 15 градусов, считается, что маятник находится в простом гармоническом движении, что позволяет нам использовать это уравнение.
Мы можем решить T=2πLgT=2πLg для g , предполагая, что угол отклонения меньше 15 градусов. Напомним, что когда угол отклонения меньше 15 градусов, считается, что маятник находится в простом гармоническом движении, что позволяет нам использовать это уравнение.
Решение
- Возведите в квадрат T=2πLgT=2πLg и найдите g .
г=4π2LT2g=4π2LT2
- Подставьте известные значения в новое уравнение.
g=4π20,75000 м(1,7357 с)2g=4π20,75000 м(1,7357 с)2
- Вычислите, чтобы найти г .
г = 9,8281 м/с2g = 9,8281 м/с2
Обсуждение
Этот метод определения г может быть очень точным. Вот почему в этом примере длина и период даны пятизначным числам.
Рабочий пример
Закон Гука: насколько жестки автомобильные пружины?
Чему равна постоянная силы системы подвески автомобиля, показанной на рис.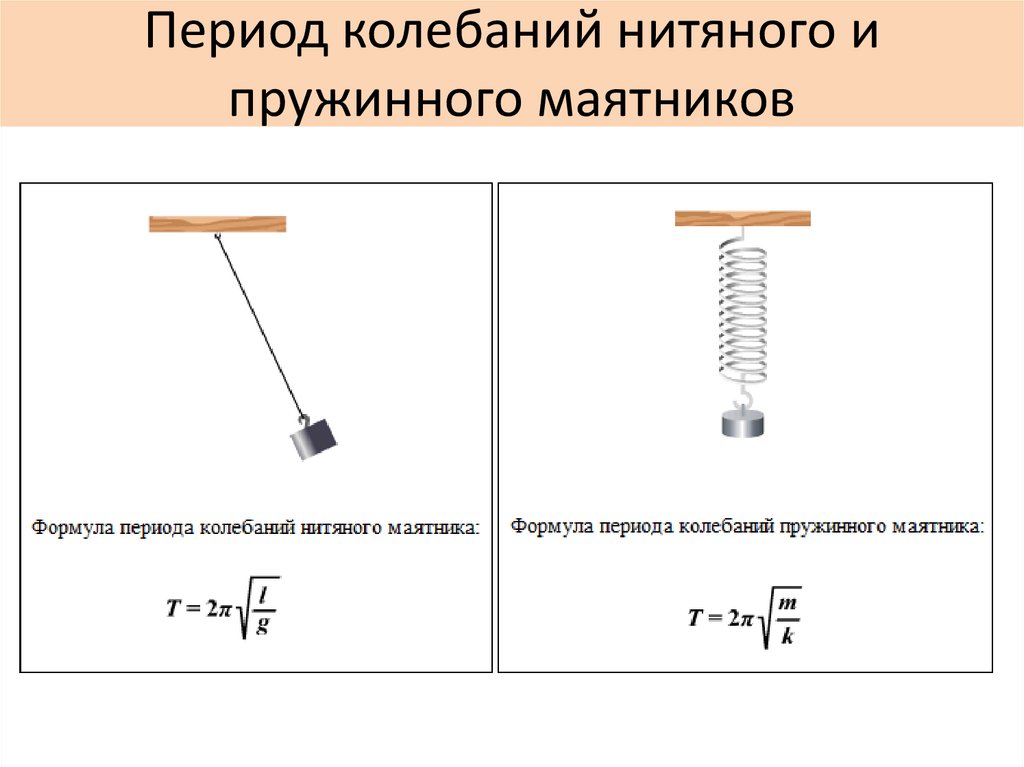 5.41, которая оседает на 1,20 см, когда в нее садится человек массой 80,0 кг?
5.41, которая оседает на 1,20 см, когда в нее садится человек массой 80,0 кг?
Рисунок 5.41 Автомобиль на стоянке. (exfordy, Flickr)
Стратегия
Считайте, что автомобиль находится в положении равновесия x = 0 до того, как в него сядет человек. Затем автомобиль опускается на 1,20 см, что означает, что он смещается в положение x = −1,20×10 −2 м.
В этой точке пружины создают восстанавливающую силу F , равную весу человека
w = м г = (80,0 кг)(9,80 м/с 2 90784) Мы принимаем эту силу равной F по закону Гука.
Зная F и x , мы можем найти силовую постоянную k .
Решение
Решить закон Гука, F = − kx , для k .
k=Fxk=Fx
Подставьте известные значения и найдите k .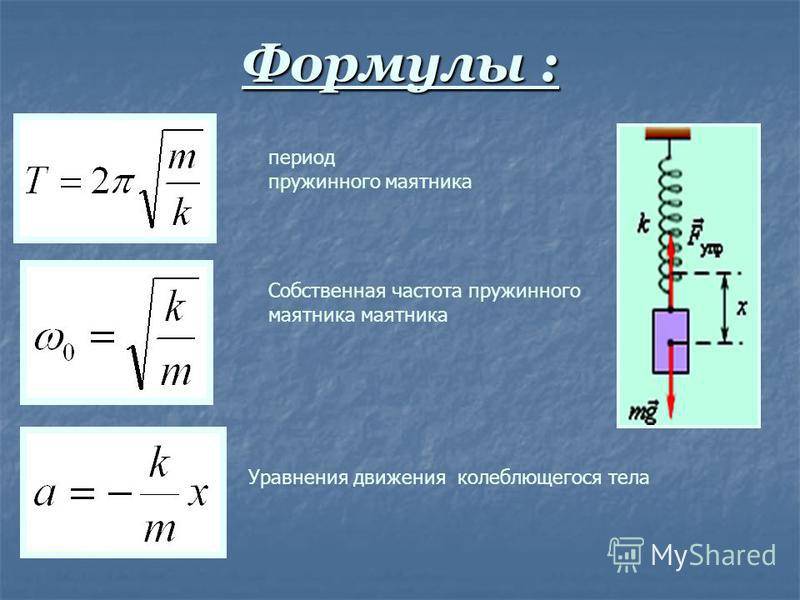
k=-784 Н-1,20×10-2 м=6,53×104 Н/мк=-784 Н-1,20×10-2 м=6,53×104 Н/м
Обсуждение
Обратите внимание, что F и x имеют противоположные знаки, потому что они направлены в противоположные стороны — восстанавливающая сила направлена вверх, а смещение — вниз. Также обратите внимание, что автомобиль будет раскачиваться вверх и вниз, когда человек садится в него, если бы не амортизаторы. Подпрыгивающие автомобили — верный признак плохих амортизаторов.
Практические задачи
20.
Сила в 70\,\text{Н}, приложенная к пружине, заставляет ее сместиться на 0,3\,\text{м}. Чему равна постоянная силы пружины?
{-233}\,\text{Н/м}
{-21}\,\text{Н/м}
21\,\text{Н/м}
91\,\text{Н/м}
Снап Лаборатория
Нахождение гравитации с помощью простого маятника
Используйте простой маятник, чтобы найти ускорение свободного падения g в вашем доме или классе.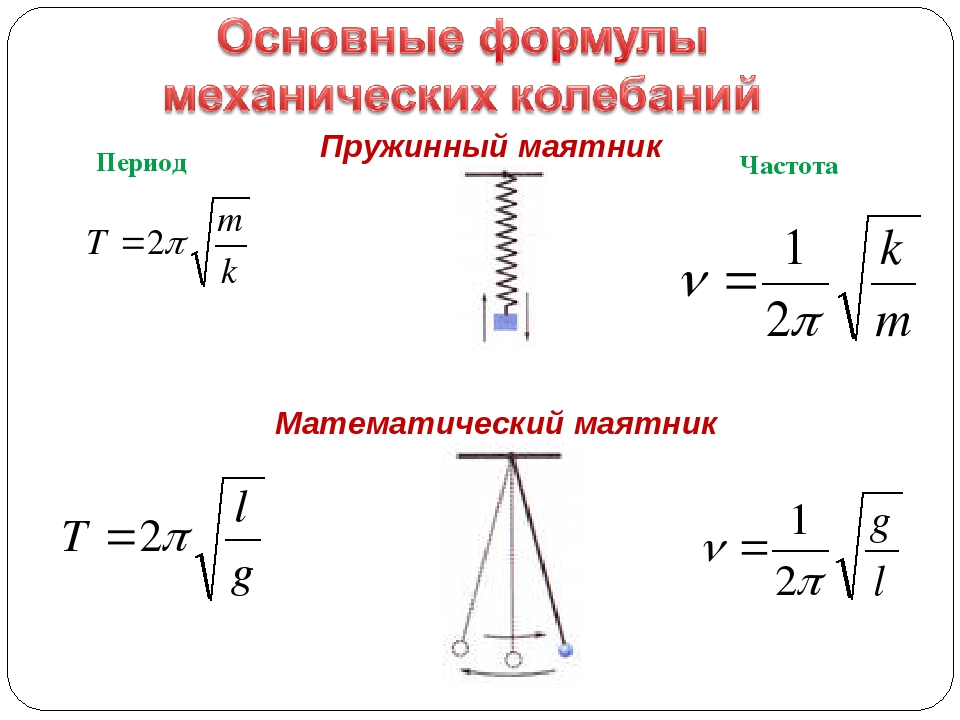
- 1 нить
- 1 секундомер
- 1 маленький плотный предмет
- Отрежьте кусок нити или зубной нити длиной около 1 м.
- Прикрепите к концу шнура небольшой предмет высокой плотности (например, металлическую гайку или ключ от машины).
- Начиная с угла менее 10 градусов, дайте маятнику раскачиваться и измерьте период маятника для 10 колебаний с помощью секундомера.
- Вычислить г .
Проверка захвата
Насколько точно это измерение для г ? Как это можно улучшить?
- Точность для значения г будет увеличиваться с увеличением массы плотного объекта.
- Точность для значения г будет увеличиваться с увеличением длины маятника.
- Значение г будет более точным, если угол отклонения больше 15°.

- Значение г будет более точным, если оно поддерживает простое гармоническое движение.
Проверьте свое понимание
22.
Что такое деформация?
Деформация – это величина восстанавливающей силы.
Деформация – это изменение формы из-за приложения силы.
Деформация — это максимальное усилие, которое можно приложить к пружине.
Деформация восстанавливает первоначальную форму после устранения внешней силы.

23.
Чему согласно закону Гука пропорциональна деформация?
- Сила
- Скорость
- Рабочий объем
- Постоянная силы
24.
Что такое колебания?
- Движение, приводящее к небольшим перемещениям
- Движение, которое периодически повторяется
- Периодическое повторяющееся движение между двумя точками
- движение, противоположное направлению возвращающей силы
25.
Верно или неверно — колебания могут происходить без приложения силы.
- Правда
- Ложь
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, достигают ли учащиеся целей обучения в этом разделе.

 02.2015 11:59
Ответить
02.2015 11:59
Ответить 02.2015 08:33
Ответить
02.2015 08:33
Ответить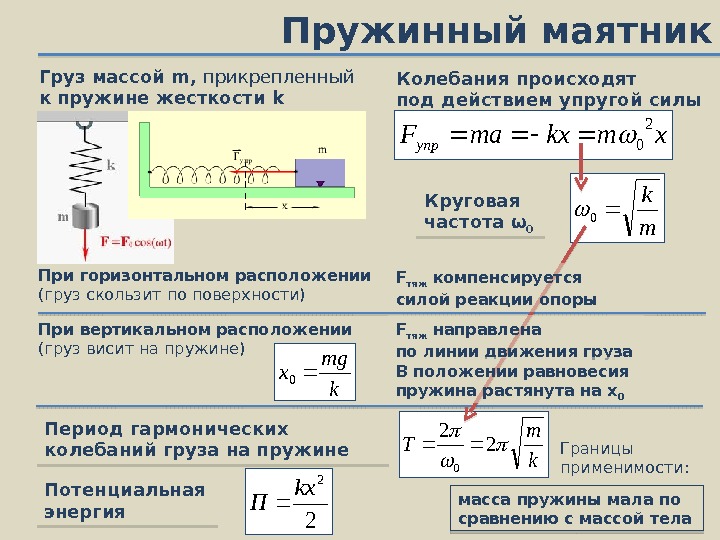 Учащийся знает характеристики и поведение волн. Ожидается, что студент:
Учащийся знает характеристики и поведение волн. Ожидается, что студент:

