Формула площадь квадрата 3 класс формула: Как найти площадь квадрата, формула

Как найти площадь треугольника. Формулы треугольника

Содержание статьи

1. Понятие площади

2. Как найти площадь треугольника через высоту и основание

3. Формула Герона

4. Площадь равностороннего треугольника

Понятие площади

Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.

Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.

Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.

Рассмотрим пример.

Пример 1

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Решение.

Очевидно, что одна из сторон треугольника является диагональю прямоугольника, у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется

$5\cdot 6=30$

Тогда площадь треугольника равняется

$30:2=15$

Ответ: $15$.

Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.

Как найти площадь треугольника через высоту и основание

Теорема 1

Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.

Математически это выглядит следующим образом

$S=\frac{1}{2}αh$

где $a$ — длина стороны, $h$ — высота, проведенная к ней.

Доказательство.

Рассмотрим треугольник $ABC$, в котором $AC=α$.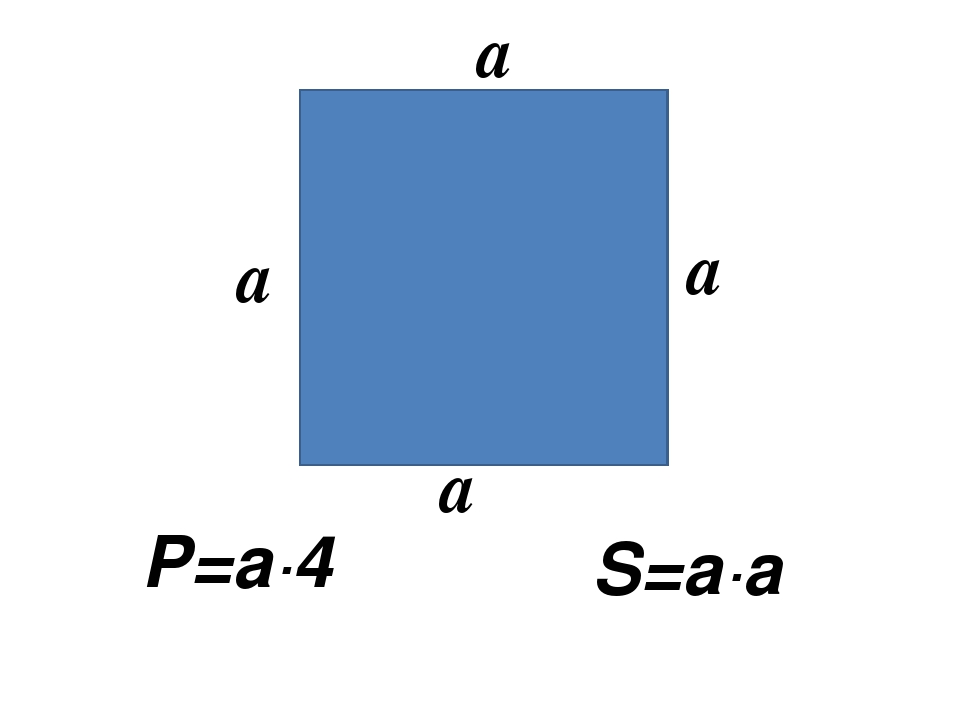 К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.

Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда

$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$

Следовательно, искомая площадь треугольника, по свойству 2, равняется

$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$

Теорема доказана.

Пример 2

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Решение.

Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим

$S=\frac{1}{2}\cdot 9\cdot 9=40,5$

Ответ: $40,5$.

Формула Герона

Теорема 2

Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом

$S=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

здесь $ρ$ означает полупериметр этого треугольника. 2\sqrt{3}}{4}$

Теорема доказана.

Пример 3

Найти площадь равностороннего треугольника, если его сторона равняется $2$.

Решение.

Используя теорему 3, получим

$S=\frac{4\sqrt{3}}{4}=\sqrt{3}$

Ответ: $\sqrt{3}$.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 07.07.2022

Выполнение любых типов работ по геометрии

Решение задач по геометрии Контрольная работа на тему теорема синусов и косинусов Реферат по геометрии Отчеты по практике по геометрии Курсовые работы по геометрии Контрольная работа по геометрии Дипломная работа по геометрии

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Площадь прямоугольника способы.

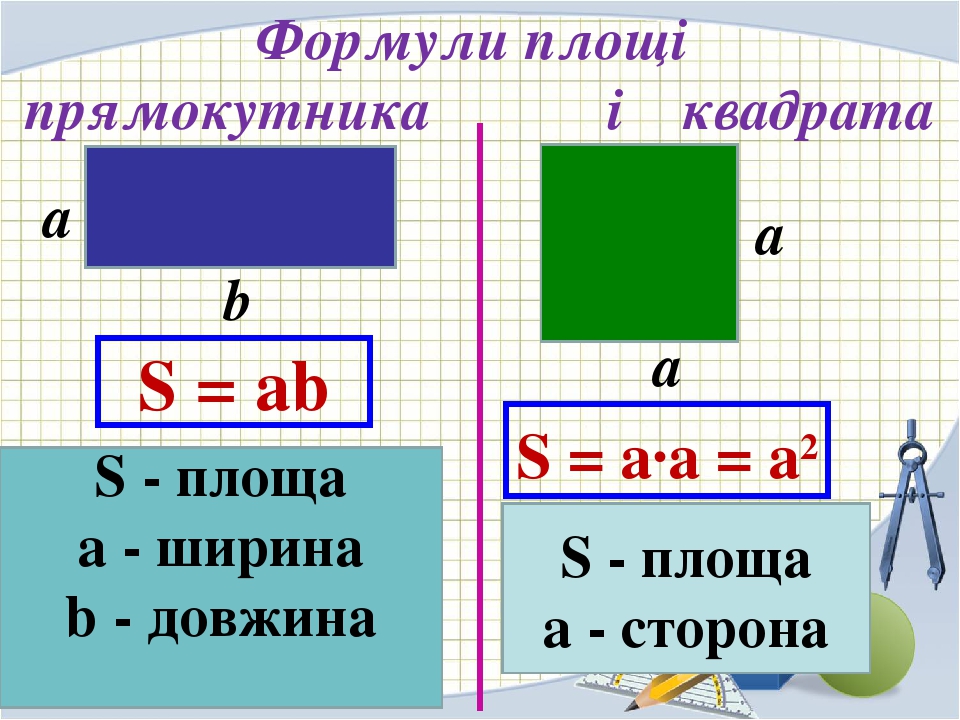Как узнать площадь прямоугольника

Для вычисления площади и периметра квадрата нужно разобраться в понятиях этих величин. Квадрат представляет собой прямоугольник только с четырьмя одинаковыми сторонам, которые имеют между собой угол в 90°. Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.

Площадь квадрата и как ее найти

Как было сказано выше, квадрат — это прямоугольник, имеющий 4 равные стороны, поэтому ответом на вопрос: «как найти площадь квадрата» является формула: S = a*a или S = a 2 , где а — сторона квадрата. Исходя из этой формулы, легко находится сторона квадрата, если известна площадь. Для этого необходимо извлечь квадрат из указанной величины.

Например, S = 121, следовательно, а = √121 = 11. Если заданное значение отсутствует в таблице квадратов, то можно воспользоваться калькулятором: S = 94, а = √94 = 9,7.

Как найти периметр квадрата

Периметр квадрата находится по легкой формуле: Р = 4а, где а — сторона квадрата.

Пример:

• сторона квадрата = 5, следовательно, P = 4*5 = 20
• сторона квадрата = 3, следовательно, Р = 4*3 = 12

Но существуют такие задачи, где заведомо обозначена площадь, а нужно найти периметр. При решении нужны формулы, которые представлены ранее.

Например: как найти периметр квадрата, если известна площадь, равная 144?

Шаги решения:

1. Выясняем длину одной стороны: а = √144 = 12
2. Находим периметр: Р = 4*12 = 48.

Нахождение периметра вписанного квадрата

Существуют еще несколько способов нахождения периметра квадрата. Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.

Алгоритм решения:

• так как на рассмотрении квадрат, формулу можно выразить таким образом: a 2 + a 2 = (2r) 2 ;
• затем следует уравнение сделать проще: 2a 2 = 4(r) 2 ;
• делим уравнение на 2: (a 2 ) = 2(r) 2 ;
• извлекаем корень: a = √(2r).

В итоге получаем последнюю формулу: а (сторона квадрата) = √(2r).

1. Найденная сторона квадрата умножается на 4, далее применяется стандартная формула по нахождению периметра: P = 4√(2r).

Задача:

Дан квадрат, который вписан в окружность, ее радиус равен 5. Значит, диагональ квадрата равняется 10. Применяем теорему Пифагора: 2(a 2 ) = 10 2 , то есть 2a 2 = 100. Делим полученное на два и в результате: a 2 = 50. Так как это не табличное значение, используем калькулятор: а = √50 = 7,07. Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!

Рассмотрим еще один вопрос

Часто в задачах встречается другое условие: как найти площадь квадрата, если известен периметр?

Мы уже рассмотрели все необходимые формулы, поэтому для решения задач подобного типа, необходимо умело их применять и связывать между собой. Перейдем сразу к наглядному примеру: Площадь квадрата равна 25 см 2 , найдите его периметр.

Шаги решения:

1. Находим сторону квадрата: а = √25 = 5.

1. Находим сам периметр: Р = 4*а = 4*5 = 20.

Подводя итог, важно напомнить, что такие легкие формулы применимы не только в учебной деятельности, но и повседневной жизни. Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.

Мы уже познакомились с понятием площадь фигуры , узнали одну из единиц измерения площади — квадратный сантиметр . На уроке мы выведем правило, как вычислить площадь прямоугольника.

Мы уже умеем находить площадь фигур, которые разделены на квадратные сантиметры.

Например:

Мы можем определить, что площадь первой фигуры 8 см 2 , площадь второй фигуры 7 см 2 .

Как найти площадь прямоугольника, длины сторон которого 3 см и 4 см?

Для решения задачи разобьём прямоугольник на 4 полоски по 3 см 2 каждая.

Тогда площадь прямоугольника будет равна 3*4=12 см 2 .

Этот же прямоугольник можно разбить на 3 полоски по 4 см 2 .

Тогда площадь прямоугольника будет равна 4*3=12 см 2 .

В обоих случаях для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника.

Найдем площадь каждого прямоугольника.

Рассмотрим прямоугольник АКМО.

В одной полоске 6 см 2 , а таких полосок в этом прямоугольнике 2. Значит, мы можем выполнить следующее действие:

Число 6 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Таким образом, мы перемножили стороны прямоугольника для того, чтобы найти площадь прямоугольника.

Рассмотрим прямоугольник KDCO.

В прямоугольнике KDCO в одной полоске 2см 2 , а таких полосок 3. Следовательно, мы можем выполнить действие

Число 3 обозначает длину прямоугольника, а 2 — ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.

Можно сделать вывод: чтобы найти площадь прямоугольника, не надо каждый раз разбивать фигуру на квадратные сантиметры.

Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (длины сторон прямоугольника должны быть выражены в одних и тех же единицах измерения), а потом вычислить произведение полученных чисел (площадь будет выражена в соответствующих единицах площади)

Обобщим: площадь прямоугольника равна произведению его длины и ширины.

Решите задачу.

Вычисли площадь прямоугольника, если длина прямоугольника 9см, а ширина — 2см.

Рассуждаем так. В данной задаче известны и длина и ширина прямоугольника. Поэтому действуем по правилу: площадь прямоугольника равна произведению его длины и ширины.

Запишем решение.

Ответ: площадь прямоугольника 18см 2

Как вы думаете, какими ещё могут быть длины сторон прямоугольника с такой площадью?

Можно рассуждать так. Поскольку площадь — это произведение длин сторон прямоугольника, поэтому надо вспомнить таблицу умножения.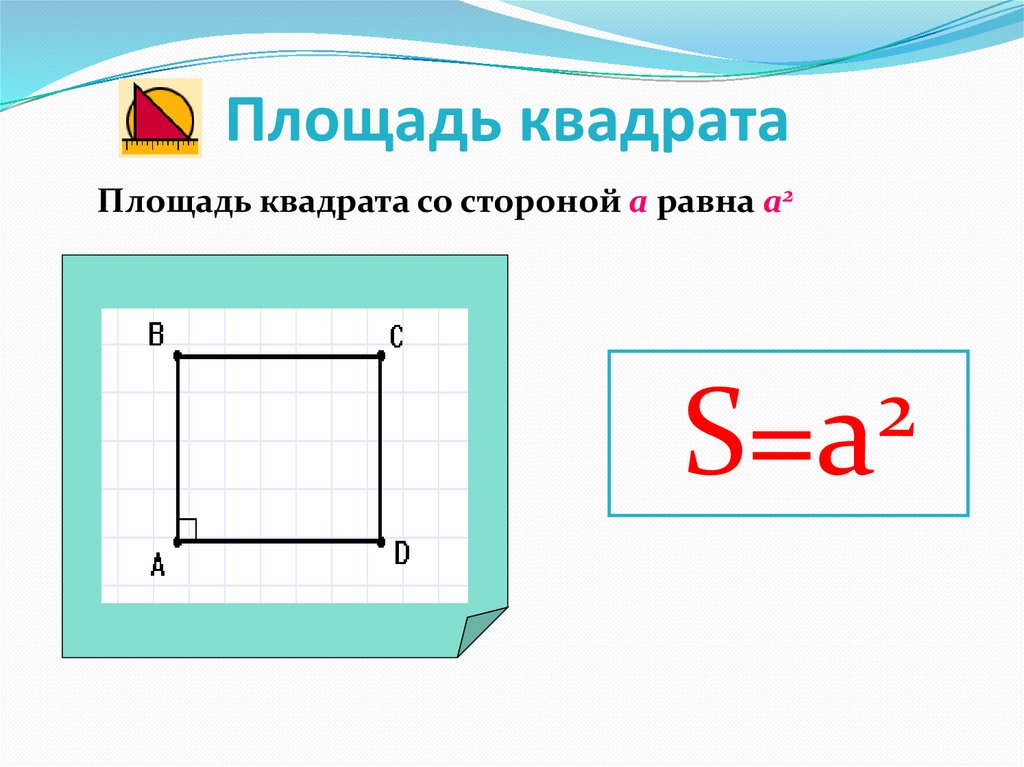 При умножении каких чисел получается ответ 18?

Правильно, при умножении 6 и 3 тоже получится 18. Значит, у прямоугольника могут быть стороны 6см и 3 см и его площадь тоже будет равна 18см 2 .

Решите задачу.

Длина прямоугольника 8см, а ширина 2см. Найди его площадь и периметр.

Нам известны длина и ширина прямоугольника. Необходимо вспомнить, что для нахождения площади необходимо найти произведение его длины и ширины, а для нахождения периметра нужно сумму длины и ширины умножить на два.

Запишем решение.

Ответ: площадь прямоугольника 16 см 2 , а периметр прямоугольника 20 см.

Решите задачу.

Длина прямоугольника 4см, а ширина — 3см. Чему равна площадь треугольника? (смотри рисунок)

Чтобы ответить на вопрос задачи, сначала надо найти площадь прямоугольника. Мы знаем, что для этого необходимо длину умножить на ширину.

Посмотрите на чертёж. Вы заметили, диагональ разделила прямоугольник на два равных треугольника? Следовательно, площадь одного треугольника в 2 раза меньше площади прямоугольника.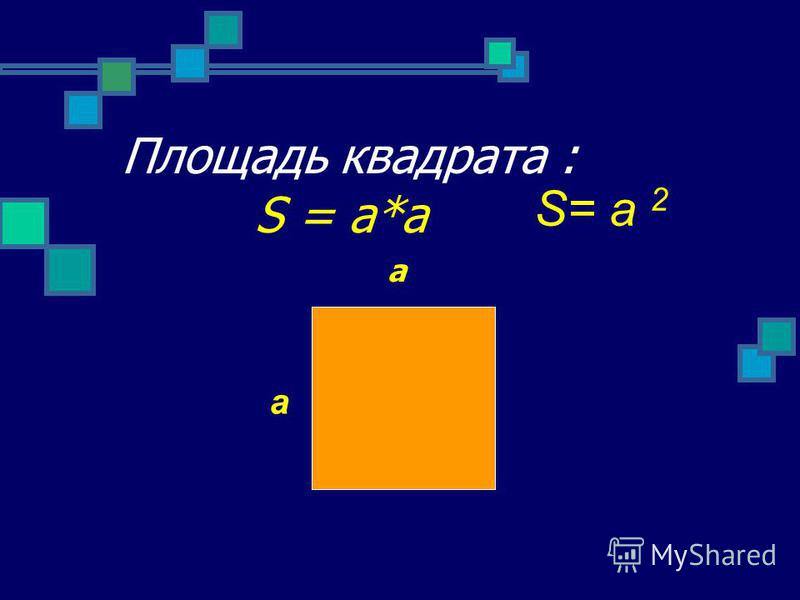

Значит, надо 12 уменьшить в 2 раза.

Ответ: площадь треугольника 6 см 2 .

Сегодня на уроке мы познакомились с правилом, как вычислить площадь прямоугольника и учились применять это правило при решении задач на нахождение площади прямоугольника.

1. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. М., «Просвещение», 2012 год.

2. М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. М., «Просвещение», 2012 год.

3. М.И.Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.

4. Нормативно-правовой документ. Контроль и оценка результатов обучения. М., «Просвещение», 2011 год.

5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.

6. С.И.Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.

7. В.Н.Рудницкая. Тесты. М., «Экзамен», 2012 (127с.)

2. Издательство «Просвещение» ()

1. Длина прямоугольника 7 см, ширина 4 см.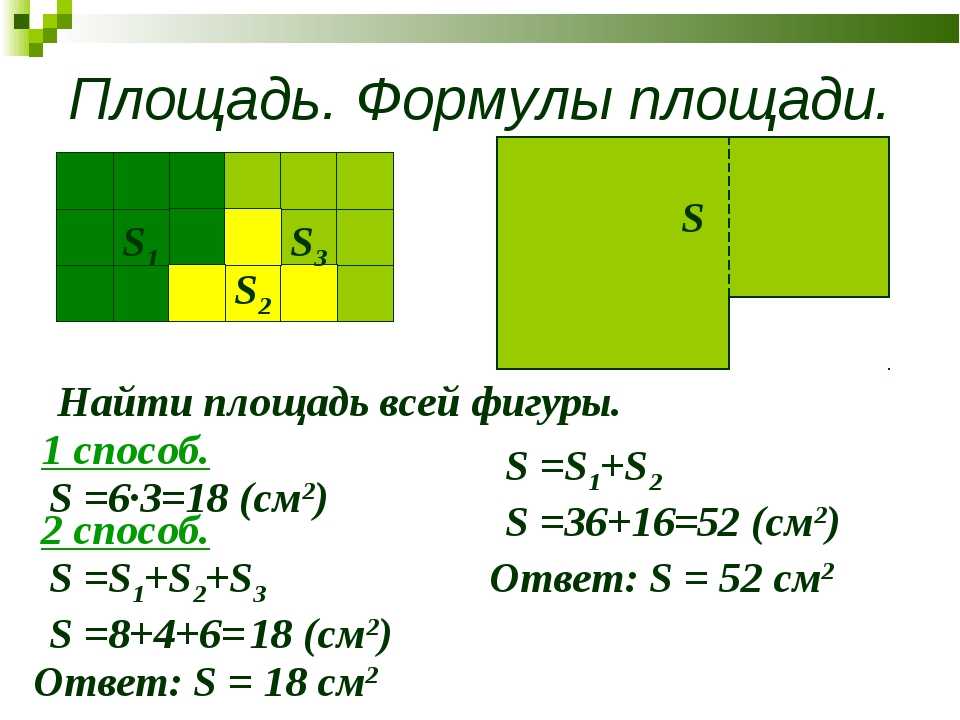 Найдите площадь прямоугольника.

2. Сторона квадрата 5 см. Найдите площадь квадрата.

3. Начертите возможные варианты прямоугольников, площадь которых 18 см 2 .

4. Составьте задание по теме урока для своих товарищей.

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами.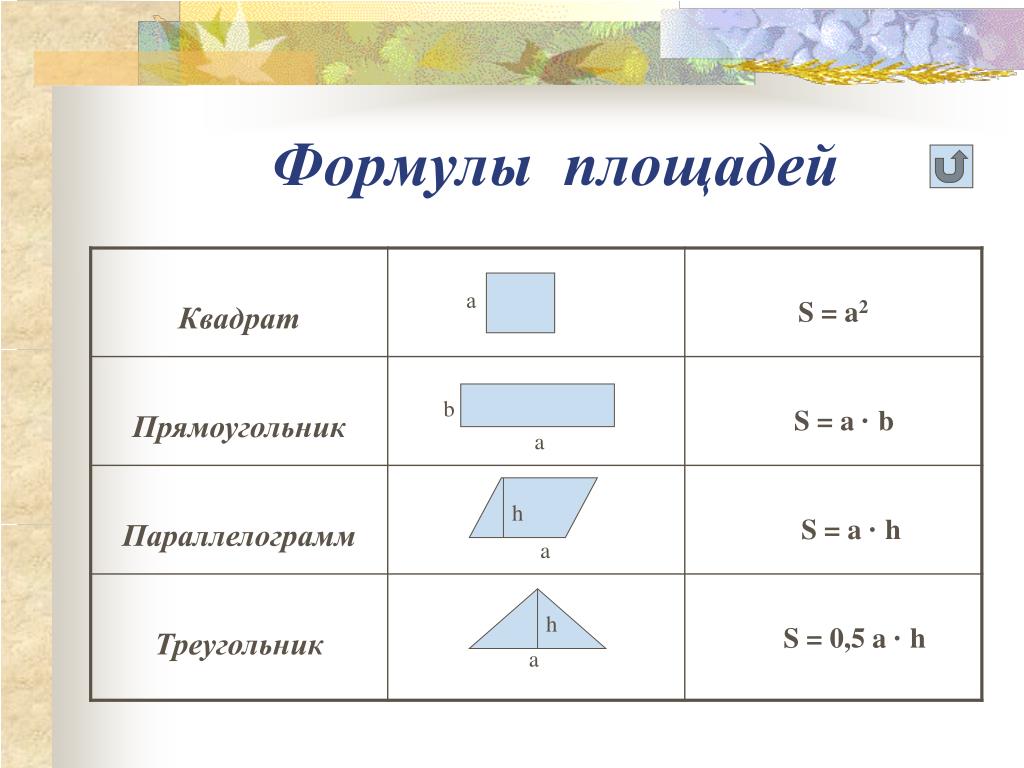 Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.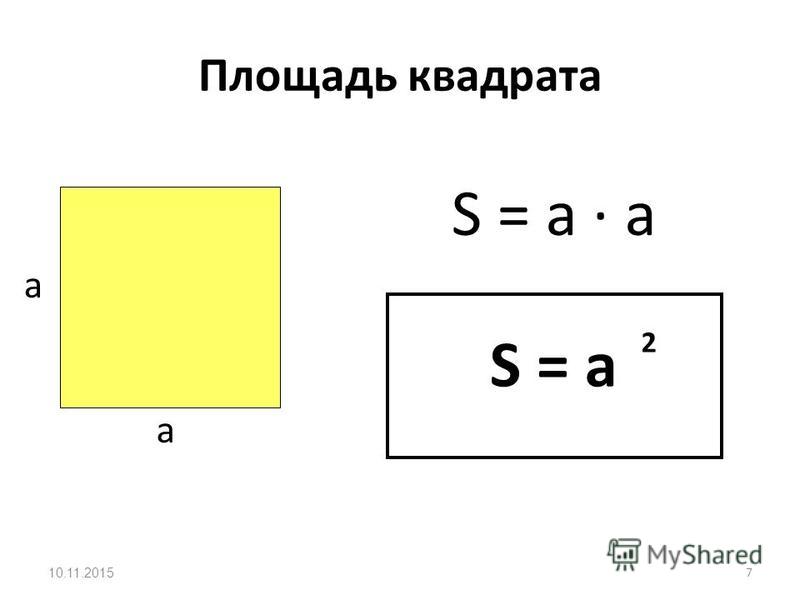
2. Напишем формулу для расчета периметра данного прямоугольника:

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1.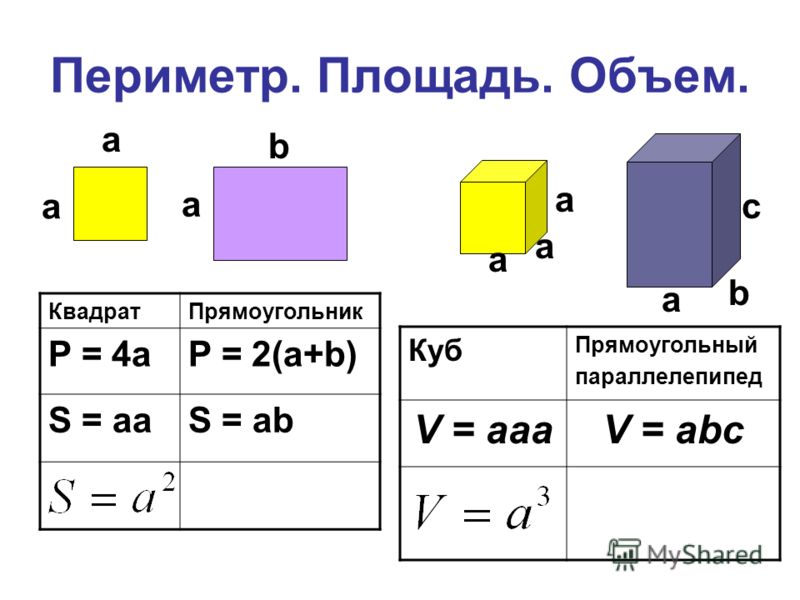 Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т. д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Прямоугольник – это частный случай четырехугольника. Это значит, что у прямоугольника четыре стороны. Его противоположные стороны равны: так например, если одна из его сторон равна 10 см, то противоположная ей будет так же равны 10 см. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.

Как узнать площадь прямоугольника по двум сторонам

Для того чтобы найти площадь прямоугольника, надо умножить его длину на ширину: Площадь = Длина × Ширина. В случае, указанном ниже: Площадь = AB × BC. 2$.

Диагонали разделяет прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.

Диагонали не является биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.

Что мы узнали?

Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также стоит не забывать, что если в задании разные единицы измерения сторон необходимо перевести их одну.

Тест по теме

Оценка статьи

Средняя оценка: 4.4 . Всего получено оценок: 292.

3 класс. Математика. Вычисление площади прямоугольника — Площадь прямоугольника

Комментарии преподавателя

Мы уже по­зна­ко­ми­лись с по­ня­ти­ем пло­щадь фи­гу­ры, узна­ли одну из еди­ниц из­ме­ре­ния пло­ща­ди – квад­рат­ный сан­ти­метр. На уроке мы вы­ве­дем пра­ви­ло, как вы­чис­лить пло­щадь пря­мо­уголь­ни­ка.

Мы уже умеем на­хо­дить пло­щадь фигур, ко­то­рые раз­де­ле­ны на квад­рат­ные сан­ти­мет­ры.

На­при­мер:

Мы можем опре­де­лить, что пло­щадь пер­вой фи­гу­ры 8 см2, пло­щадь вто­рой фи­гу­ры 7 см2.

Как найти пло­щадь пря­мо­уголь­ни­ка, длины сто­рон ко­то­ро­го 3 см и 4 см?

Для ре­ше­ния за­да­чи разо­бьём пря­мо­уголь­ник на 4 по­лос­ки по 3 см2 каж­дая.

Тогда пло­щадь пря­мо­уголь­ни­ка будет равна 3*4=12 см2.

Этот же пря­мо­уголь­ник  можно раз­бить на 3 по­лос­ки по 4 см2.

Тогда пло­щадь пря­мо­уголь­ни­ка будет равна 4*3=12 см2.

 

В обоих слу­ча­ях для на­хож­де­ния пло­ща­ди пря­мо­уголь­ни­ка пе­ре­мно­жа­ют­ся числа, вы­ра­жа­ю­щие длины сто­рон пря­мо­уголь­ни­ка.

Най­дем пло­щадь каж­до­го пря­мо­уголь­ни­ка.

Рас­смот­рим пря­мо­уголь­ник АКМО.

В одной по­лос­ке 6 см2, а таких по­ло­сок в этом пря­мо­уголь­ни­ке 2.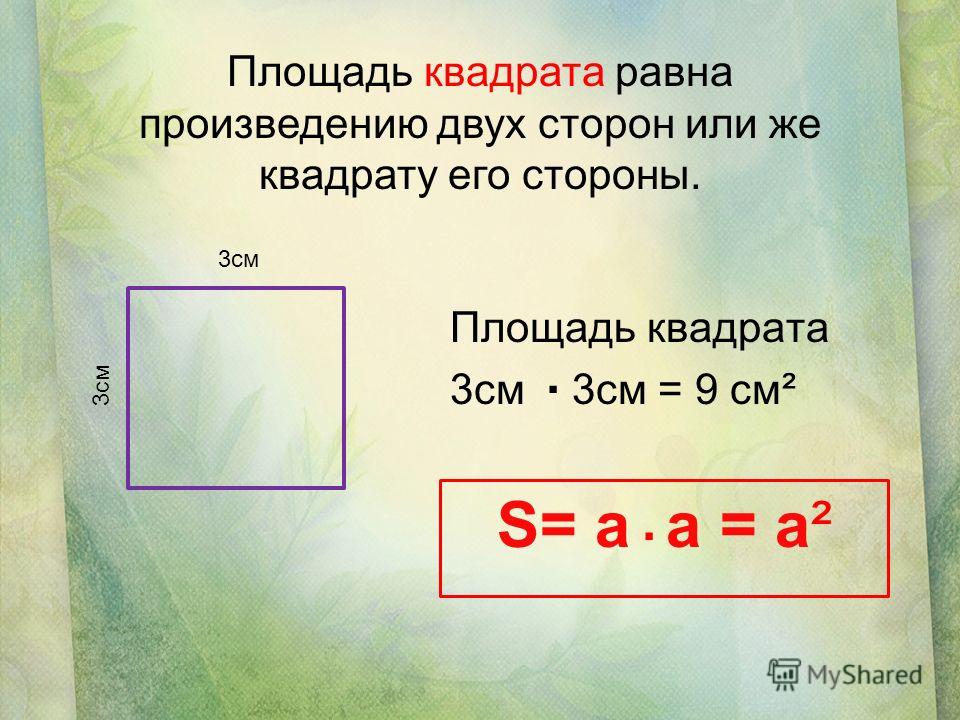 Зна­чит, мы можем вы­пол­нить сле­ду­ю­щее дей­ствие:

6*2=12 см2

Число 6 обо­зна­ча­ет длину пря­мо­уголь­ни­ка, а 2 – ши­ри­ну пря­мо­уголь­ни­ка. Таким об­ра­зом, мы пе­ре­мно­жи­ли сто­ро­ны пря­мо­уголь­ни­ка для того, чтобы найти пло­щадь пря­мо­уголь­ни­ка.

Рас­смот­рим пря­мо­уголь­ник KDCO.

В пря­мо­уголь­ни­ке KDCO  в одной по­лос­ке 2см2, а таких по­ло­сок 3. Сле­до­ва­тель­но, мы можем вы­пол­нить дей­ствие

2*3=6см2

Число 3 обо­зна­ча­ет длину пря­мо­уголь­ни­ка, а 2 – ши­ри­ну пря­мо­уголь­ни­ка. Мы их пе­ре­мно­жи­ли и узна­ли пло­щадь пря­мо­уголь­ни­ка.

 

Можно сде­лать вывод: чтобы найти пло­щадь пря­мо­уголь­ни­ка, не надо каж­дый раз раз­би­вать фи­гу­ру на квад­рат­ные сан­ти­мет­ры.

Чтобы вы­чис­лить пло­щадь пря­мо­уголь­ни­ка, нужно найти его длину и ши­ри­ну (длины сто­рон пря­мо­уголь­ни­ка долж­ны быть вы­ра­же­ны в одних и тех же еди­ни­цах из­ме­ре­ния), а потом вы­чис­лить про­из­ве­де­ние по­лу­чен­ных чисел (пло­щадь будет вы­ра­же­на в со­от­вет­ству­ю­щих еди­ни­цах пло­ща­ди)

Обоб­щим: пло­щадь пря­мо­уголь­ни­ка равна про­из­ве­де­нию его длины и ши­ри­ны.

 

Ре­ши­те за­да­чу.

Вы­чис­ли пло­щадь пря­мо­уголь­ни­ка, если длина пря­мо­уголь­ни­ка 9см, а ши­ри­на – 2см.

Рас­суж­да­ем так. В дан­ной за­да­че из­вест­ны и длина и ши­ри­на пря­мо­уголь­ни­ка. По­это­му дей­ству­ем по пра­ви­лу: пло­щадь пря­мо­уголь­ни­ка равна про­из­ве­де­нию его длины и ши­ри­ны.

За­пи­шем ре­ше­ние.

9*2=18см2

Ответ: пло­щадь пря­мо­уголь­ни­ка 18см2

 

Как вы ду­ма­е­те, ка­ки­ми ещё могут быть длины сто­рон пря­мо­уголь­ни­ка с такой пло­ща­дью?

Можно рас­суж­дать так. По­сколь­ку пло­щадь – это про­из­ве­де­ние длин сто­рон пря­мо­уголь­ни­ка, по­это­му надо вспом­нить таб­ли­цу умно­же­ния. При умно­же­нии каких чисел по­лу­ча­ет­ся ответ 18?

Пра­виль­но, при умно­же­нии 6 и 3 тоже по­лу­чит­ся 18. Зна­чит, у пря­мо­уголь­ни­ка могут быть сто­ро­ны 6см и 3 см и его пло­щадь тоже будет равна 18см2.

 

Ре­ши­те за­да­чу.

Длина пря­мо­уголь­ни­ка 8см, а ши­ри­на 2см.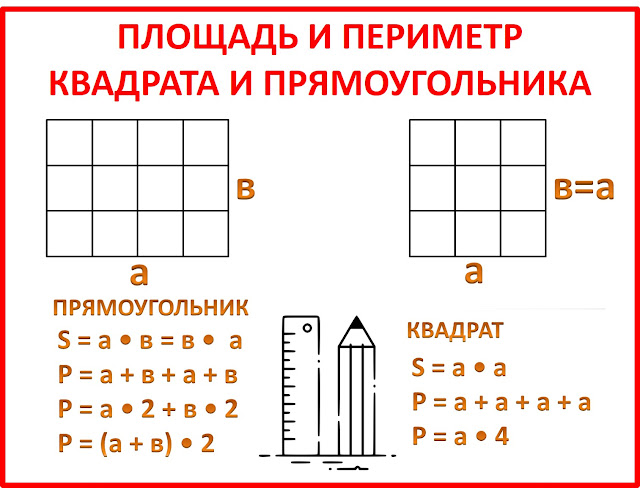 Найди его пло­щадь и пе­ри­метр.

Нам из­вест­ны длина и ши­ри­на пря­мо­уголь­ни­ка. Необ­хо­ди­мо вспом­нить, что для на­хож­де­ния пло­ща­ди необ­хо­ди­мо найти про­из­ве­де­ние его длины и ши­ри­ны, а для на­хож­де­ния пе­ри­мет­ра нужно сумму длины и ши­ри­ны умно­жить на два.

За­пи­шем ре­ше­ние.

8*2=16 см2

(8+2)*2=20 см

Ответ: пло­щадь пря­мо­уголь­ни­ка 16 см2, а пе­ри­метр пря­мо­уголь­ни­ка 20 см.

 

Ре­ши­те за­да­чу.

Длина пря­мо­уголь­ни­ка 4см, а ши­ри­на – 3см. Чему равна пло­щадь тре­уголь­ни­ка? (смот­ри ри­су­нок)

Чтобы от­ве­тить на во­прос за­да­чи, сна­ча­ла надо найти пло­щадь пря­мо­уголь­ни­ка. Мы знаем, что для этого необ­хо­ди­мо длину умно­жить на ши­ри­ну.

4*3=12 см2

По­смот­ри­те на чер­тёж. Вы за­ме­ти­ли, диа­го­наль раз­де­ли­ла пря­мо­уголь­ник на два рав­ных тре­уголь­ни­ка? Сле­до­ва­тель­но, пло­щадь од­но­го тре­уголь­ни­ка в 2 раза мень­ше пло­ща­ди пря­мо­уголь­ни­ка. Зна­чит, надо 12 умень­шить в 2 раза.

12:2=6 см2

Ответ: пло­щадь тре­уголь­ни­ка 6 см2.

 

Се­год­ня на уроке мы по­зна­ко­ми­лись с пра­ви­лом, как вы­чис­лить пло­щадь пря­мо­уголь­ни­ка и учи­лись при­ме­нять это пра­ви­ло при ре­ше­нии задач на на­хож­де­ние  пло­ща­ди пря­мо­уголь­ни­ка.

 

ИСТОЧНИКИ

http://interneturok.ru/ru/school/matematika/3-klass/tema/ploschad-pryamougolnika?seconds=0&chapter_id=1779

 

Площади прямоугольников и квадратов — Математика 3-го класса

Прямоугольники и квадраты — две наиболее распространенные формы.

Что такое прямоугольники?

Прямоугольники представляют собой плоские фигуры с 4 прямыми сторонами и 4 прямыми углами.

Вот несколько примеров прямоугольных объектов:

Совет : Квадратные углы также называются прямыми углами .

Что такое квадраты?

Квадраты — это прямоугольники, у которых все стороны имеют одинаковую длину .

Вот несколько квадратных объектов:

В этом уроке мы научимся находить площади прямоугольников и квадратов.

Что такое площадь?

Площадь — это количество места, которое занимает плоская фигура.

Этот зеленый прямоугольник занимает 6 квадратов.

Площадь 6 квадрат единиц .

Мы используем единицу из площадь , чтобы точно знать, насколько велика форма.

Например, если каждый квадрат равен 1 квадратному метру, то площадь зеленого прямоугольника равна 6 квадрата метра .

Совет: Мы можем записать 6 квадратных метров как 6 м² . Это читается как «6 квадратных метров » .

Площадь прямоугольника

Чтобы найти площадь из a прямоугольник , умножить ширину на высоту.

Ширина × Высота = Площадь

Этот прямоугольник имеет ширину 3 и высоту 2. 👇

Let’s Умножьте Ширина на высоту, чтобы найти область .

3 × 2 = 6 кв. шт.

Площадь 6 кв. шт. !

Такой же ответ мы получаем, подсчитывая каждый квадрат. 😃

Площадь квадрата

Чтобы найти площадь квадрат , умножьте длину любой стороны на себя.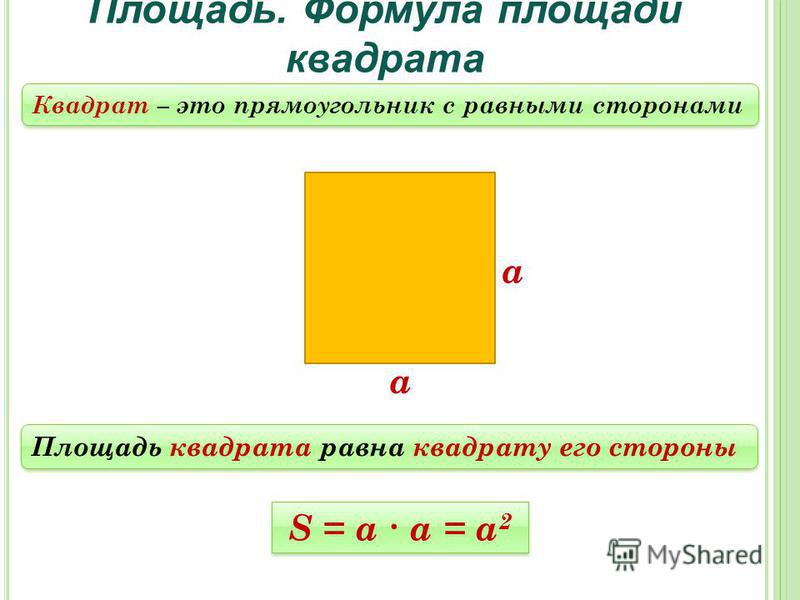

Длина каждой стороны равна 3. 

Итак, чтобы найти площадь, умножаем 3 на 3.

3 × 3 = 9

Итак, площадь квадрата равна 9 квадратных сантиметров.

Отличная работа! 😺

Давайте потренируемся на примерах!

Найдите площадь этого прямоугольника:

Просто умножьте длину на ширину.

10 × 6 = 60

Площадь этого прямоугольника составляет 60 квадрат дюйма (или 60 дюйма) . ✅ 

Убедитесь, что пишет блок из область после номера.

Какова площадь этого квадрата?

Длина каждой стороны 4 фута.

Давайте умножим то на себя.

4 FT × 4 FT = 16 квадрат

Площадь этого квадрата составляет 16 квадратных футов, или 16 FT². ✅

Отличная работа! 🥳

Теперь завершите практику. 😺 Вы узнаете больше и будете помнить дольше.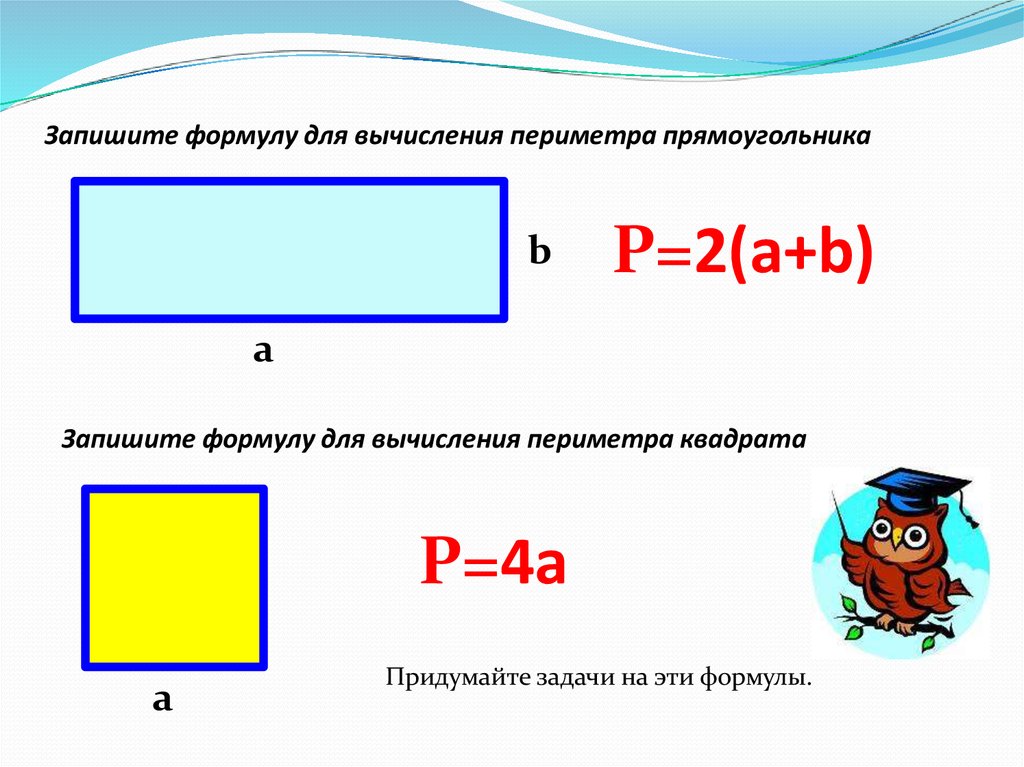

Формула площади квадрата — вывод и решенные вопросы

Когда мы говорим о некоторых плоских фигурах, мы думаем об их форме, области или границе. Мы сравниваем объекты по их размеру и площади. Мы все знаем, что нам нужны некоторые меры, чтобы сравнить их. И одним из таких показателей является его площадь. Все предметы, лежащие на плоскости, приобретают некоторый участок плоской поверхности. Мера поверхности, заключенной в замкнутую фигуру, называется ее площадью.

Существуют различные геометрические замкнутые формы, а именно квадрат, прямоугольник, треугольник, круг и т. д. В этой статье мы в основном сосредоточимся на понимании площади квадрата с некоторыми практическими примерами, ее расчетом, единицами измерения. Мы обсудим, что такое квадрат, разбираясь в формуле площади квадрата в этой статье. Давайте начнем!

Что такое Квадрат?

Давайте сначала разберемся, что такое квадрат, форма и структура квадрата.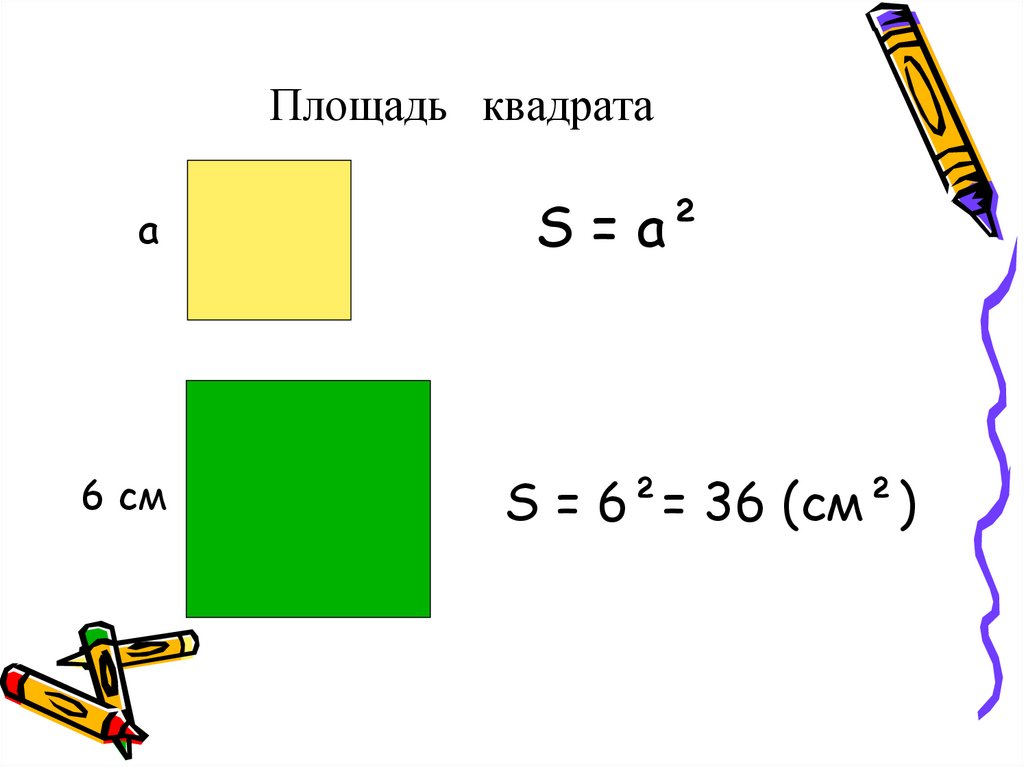 Квадрат – это четырехсторонняя прямоугольная замкнутая фигура на плоскости. Квадрат — это нормальный четырехугольник, у которого каждая из четырех сторон одинаковой длины, а каждая из четырех точек также эквивалентна. Объект, определяемый в двумерной геометрии, должен быть измерен по длине и ширине. Здесь, в случае квадрата, его длина и ширина равны.

Точки квадрата находятся в правой точке или эквивалентны 90 градусам. Точно так же диагонали квадрата сближаются и делят друг друга на 90 градусов.

Форма квадрата

Квадрат — это четырехсторонний многоугольник, все стороны которого имеют одинаковую длину, а пропорция точек составляет 90 градусов. Состояние квадрата, например, предполагает, что он рассечен плоскостью из середины, тогда в этой точке обе части уравновешены. Каждые 50% квадрата в этот момент напоминают квадрат с эквивалентными обратными сторонами.

Что такое площадь?

Площадь — это пространство, занимаемое объектом. Это область, занятая любой формой. Обычно площадь фигуры можно измерить в двумерной плоскости, где рассматривается только поверхность фигуры. Например, в случае квадрата мы учитываем только длину его стороны.

В математике область можно охарактеризовать как пространство, занимаемое формой уровня или внешним слоем предмета. Пространство фигуры — это количество единичных квадратов, покрывающих внешний слой закрытой фигуры. Область оценивается в квадратных единицах, например, в квадратных сантиметрах, квадратных футах, квадратных дюймах и т. д.

Область — это пространство, занимаемое элементом. Это район, вовлеченный в любую форму. Оценивая площадь квадрата, мы думаем только о длине его стороны. Каждая из сторон квадрата эквивалентна, и отныне его область эквивалентна квадрату стороны.

Квадрат стороны квадратной фигуры дает площадь, так как все стороны этой фигуры, являющейся квадратом, равны. Точно так же мы можем найти площадь других фигур, таких как прямоугольник, параллелограмм, треугольник или любой многоугольник, на основе его сторон. Только в случае любого изогнутого объекта или круга мы измеряем площадь на основе радиуса или расстояния его внешней линии от оси.

Какова площадь квадрата?

Площадь квадратной формулы в математике можно узнать по количеству места, занимаемого внутри квадрата. Ниже мы обсудим формулу для расчета площади квадрата. Он наиболее известен четырехугольниками в геометрии. Квадрат может быть просто частным случаем правильного многоугольника, но в данном случае с 4 равными сторонами. Все факты и свойства, описанные для правильных многоугольников, применимы и к квадрату.

Площадь квадрата характеризуется количеством квадратных единиц, которые должны заполнить квадрат. Как правило, область характеризуется как район, входящий в пределы статьи уровня или 2-й фигуры. 9{2} \]

Где — длина стороны квадрата.

Арифметически площадь квадрата можно найти, возведя в квадрат число, соответствующее пропорции стороны квадрата.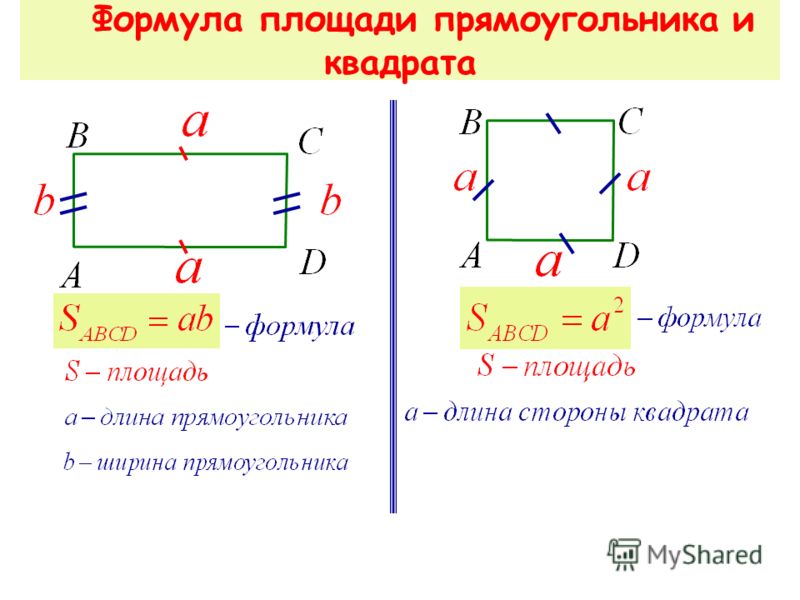 Теперь давайте воспользуемся этим уравнением, чтобы отследить площадь квадрата со стороной 7 см. Мы понимаем, что пространство a \[квадрат = сторона \times сторона\].

Вывод формулы площади квадрата

Чтобы лучше понять концепцию, давайте взглянем на вывод формулы площади квадрата в математике. Рассмотрим квадрат как прямоугольный объект, длина которого равна единице, а ширина равна единице. 9{2}}{2}\].

Дано, наклонная d = 4 фута. 

Площадь ковра \[= \frac{(4 \times 4)}{2} = \frac{16}{2} = 8 квадратных футов\].

Соответственно площадь напольного покрытия составляет 8 квадратных футов.

6. Какова площадь прямоугольного бассейна, одна сторона которого равна 8 м?

Ответ: Мы понимаем, что одна сторона бассейна равна 8 м, таким образом, 

мы будем использовать уравнение: 

\[\text{Площадь квадрата} = сторона \times side = 8 \times 8 = 64 м^{2} \].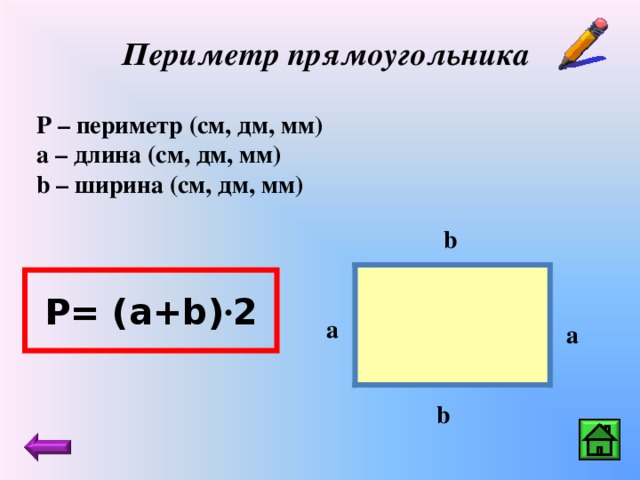

Соответственно площадь бассейна 64 кв.м.

19 Творческие способы изучения площади и периметра

Начиная примерно с третьего класса учащиеся переходят от изучения названий фигур к фактическим вычислениям с ними. Мы собрали наши любимые способы для области обучения и периметра для всех типов учащихся. Выберите свои любимые, чтобы реализовать их в классе.

1. Создайте якорную диаграмму площади и периметра

Начните с якорной диаграммы! Этот умный вариант показывает различия и сходства между измерениями площади и периметра.

Подробнее: Учить Создавать Мотивировать в Instagram

2. Украсить класс

Многие учащиеся с трудом запоминают разницу между площадью и периметром. Но если они каждый день будут проходить мимо этого дисплея, выходя из класса, они в конечном итоге получат его!

Подробнее: Математика = Любовь

3. Перекусывайте во время обучения

Квадратные закуски, такие как Cheez-Its, идеально подходят для практических занятий с площадью и периметром.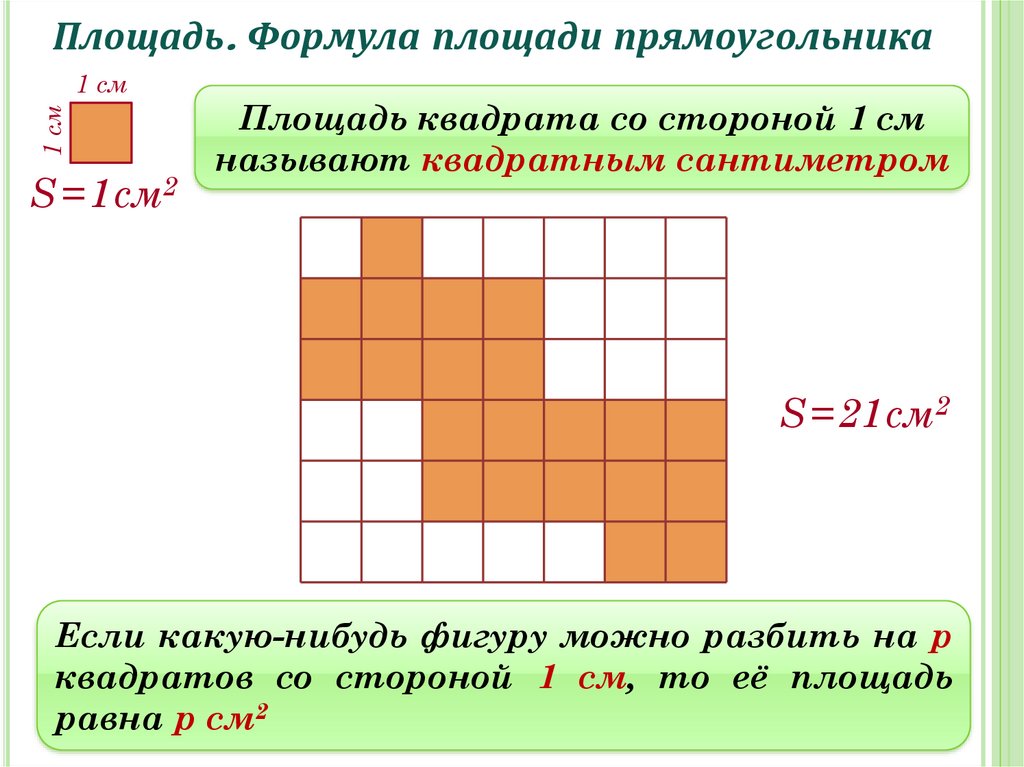 Конфеты Starburst тоже работают.

Подробнее: Плывем в секунду

4. Вытащите блоки шаблона

Это отличный способ ввести периметр, не вводя сразу фактические формулы. Студенты могут просто сосчитать стороны, что подготовит их к следующему шагу.

Узнайте больше: Образовательное путешествие Эшли

5. Прочтите

Спагетти и фрикадельки для всех!

В Спагетти и фрикадельки для всех! воссоединение семьи Комфорт становится более сложным, поскольку гости настаивают на перестановке схемы рассадки. Прочтите книгу и предложите учащимся нарисовать и рассчитать форму таблицы по ходу дела.

6. Нарисуйте человека по периметру

Предложите учащимся нарисовать себя на миллиметровой бумаге, а затем вычислить площадь и периметр. Такой милашка!

Узнать больше: Слово из третьего

7. Сложить математическую мозаику

Подобные проекты ставят пятерку в STEAM! Предложите учащимся использовать квадратные стикеры для создания мозаики с автопортретом или любой другой выбранной вами темы. Они могут писать в своих расчетах вокруг цифры.

Подробнее: Я хочу стать суперучителем

8. Исследуйте площадь и периметр с помощью кубиков LEGO

LEGO — идеальный учебный инструмент для изучения площади и периметра. Кроме того, они нравятся детям!

Узнать больше: Смех в начальной школе

9. Спой запоминающуюся песенку

Эта классная мелодия поможет учащимся запомнить, когда и как использовать вычисления площади и периметра.

10. Пишите имена печатными буквами

Учащиеся любят занятия, используя свои имена. Нарисуйте их печатными буквами, затем рассчитайте периметр и площадь. (Название слишком длинное? Вместо этого попробуйте инициалы. )

Подробнее: Снимки для старших классов

11. Используйте напольную плитку для определения площади и периметра

У вас есть квадратная напольная плитка? Используйте синюю малярную ленту (она легко отклеивается, мы обещаем), чтобы сделать фигуры, и пусть ваши ученики вычислят площади.

Подробнее: Быть женственной

12. Достать пентамино

Если вы играли в тетрис, вы узнаете блоки пентамино. Это отличный инструмент для решения различных математических задач, включая определение периметра и площади.

Подробнее: Преподавание с видом на горы

13. Возьмите свои геоборды

Геоборды — еще один потрясающий инструмент, который должен быть в каждом начальном классе. (Дополнительные способы их использования см. здесь.)

Подробнее: Triumphant Learning

14. Использование площади и периметра для обустройства комнаты

реальная жизнь?» Площадь и периметр на самом деле имеют множество реальных применений, например, этот проект, где студенты заполняют комнату мебелью, чтобы посмотреть, смогут ли они все это уместить.

Подробнее: Учитель-сова

15. Построй город

Одной комнаты мало? Построй город! Это классное занятие для студентов, которые тоже готовы перейти к объему.

Узнайте больше: Научите рядом со мной

16. Отправляйте их на поиски мусора по территории и периметру

Нужна быстрая и легкая деятельность? Раздайте учащимся линейки и отправьте их для измерения длины и ширины предметов. Затем на своих местах они могут вычислить периметр.

Подробнее: Образовательное путешествие Эшли

17. Изготовить пластину π

Работаете с площадью кругов? Сделай эти милые пи-тарелки!

Узнайте больше: Друзья по чтению

18. Играйте в «Покори территорию»

Возьмите миллиметровую бумагу и пару игральных костей, а затем сыграйте в эту классическую игру, в которой все зависит от периметра и площади.

Узнать больше: I Heart Teaching Elementary

19.