Формула площади полной поверхности цилиндра: Площадь поверхности цилиндра формула и калькулятор онлайн

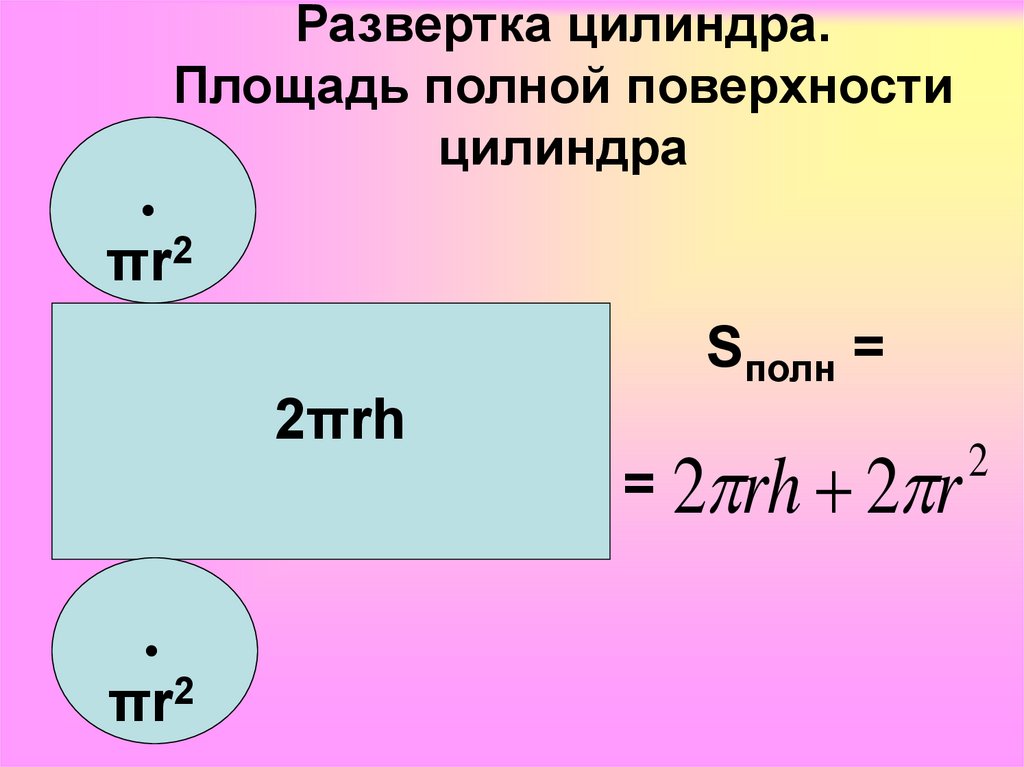
расчет боковой, полной поверхности цилиндра, формула нахождения

Математика

12.11.21

6 мин.

Как вычислить площадь поверхности цилиндра — тема данной статьи. В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.

Оглавление:

• Площадь поверхности цилиндра — онлайн калькулятор
• Площадь боковой поверхности цилиндра
• Площадь полной поверхности цилиндра
• Площадь цилиндра — формула через диаметр
• Примеры расчета площади цилиндра
• Заключение

Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.

Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.

Площадь поверхности цилиндра — онлайн калькулятор

Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.

Площадь боковой поверхности цилиндра

Сначала нужно представить, как выглядит развертка в двухмерном пространстве.

Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r, где r — радиус окружности. Другая сторона прямоугольника равна высоте h. Найти искомое не составит труда.

S_бок = 2π * r * h,

где число π = 3.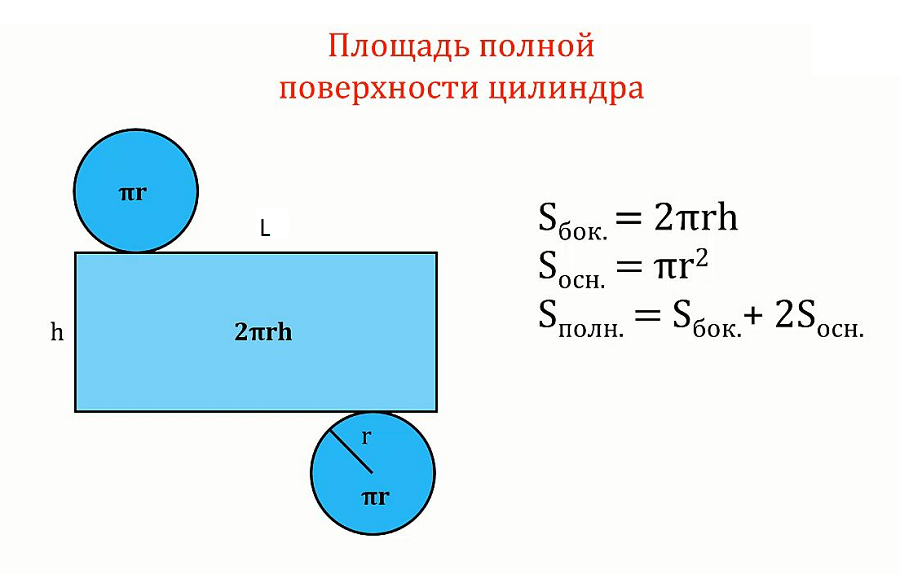 14.

Площадь полной поверхности цилиндра

Для нахождения полной площади цилиндра нужно к полученной S_бокдобавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле S_о = 2π * r².

Конечная формула выглядит следующим образом:

S_пол = 2π * r² + 2π * r * h.

Площадь цилиндра — формула через диаметр

Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.

Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.

Sпол = 2π * r² + 2π * r * h

= 2π * d²/4 + 2π * h * d/2 = π * d²/2 + π * d * h,

Вместо r в полную формулу нужно вставить значение r = d/2.

Примеры расчета площади цилиндра

Вооружившись знаниями, приступаем к практике.

Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.

Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:

S_пол = 2 * 3.14 * 24² + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм²).

Переводим в привычные м² и получаем 0,01868928, приблизительно 0.02 м².

Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.

Данные следующие: диаметр 0,2 м; высота 2 м. Используем формулу через диаметр:

S_пол = 3.14 * 0.2²/2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м².

Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.

Один момент, есть формула:

S_бок = 2 * 3.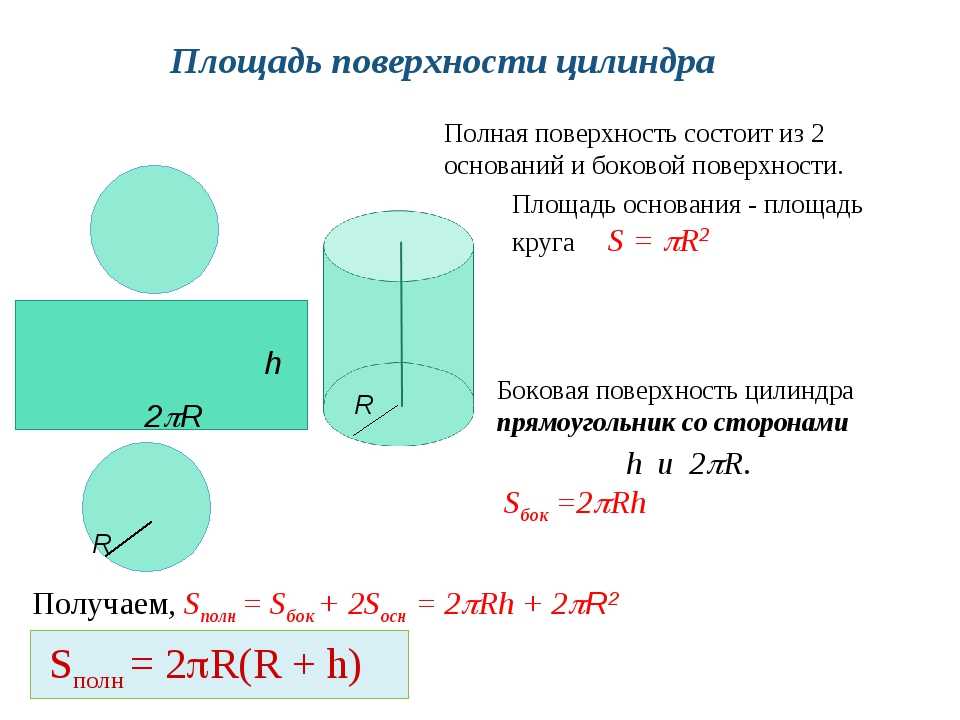 14 * 1 * 1 = 6.28 м².

Заключение

В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.

Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.

Не успеваете написать работу?

Заполните форму и узнайте стоимость

Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертация

Контактные данные — строго конфиденциальны!

Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.

* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности

Подтверждение

Ваша заявка принята.

Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.

Ошибка оформления заказа

Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.

Как найти площадь полной поверхности вписанного в цилиндр шара

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади поверхности вписанного в цилиндр шара

В данной публикации мы разберем варианты того, как можно вписать шар в цилиндр, а также, как исходя из этого определить его радиус (диаметр) и посчитать площадь поверхности.

• Формула расчета площади шара
• Способы вписать шар в цилиндр
• Примеры задач

Формула расчета площади шара

Для начала давайте вспомним общую формулу, по которой рассчитывается площадь поверхности шара:

S = 4 π R²
или S = 4 π (d/2)², где d = 2R.

• R – радиус шара;
• d – его диаметр;
• π – число, приближенное значение которого равняется 3,14.

Способы вписать шар в цилиндр

Теперь давайте разберемся, каким образом можно вписать шар в цилиндр. В данном случае возможно несколько вариантов:

1. Шар касается оснований и боковой поверхности цилиндра

• радиус (диаметр) цилиндра является, в том числе, и радиусом (диаметром) шара;
• высота цилиндра – это диаметр шара.

2. Шар касается только оснований цилиндра

Радиус шара равен половине высоты цилиндра, а диаметр – полной высоте.

3. Шар касается только боковой поверхности цилиндра

Радиус (диаметр) цилиндра – это и есть радиус (диаметр) шара.

Примечание: Выяснив радиус или диаметр шара далее остается только воспользоваться формулой для расчета площади его поверхности.

Примеры задач

Задание 1
Шар вписан в цилиндр радиусом 15 см таким образом, что соприкасается и с основанием, и с боковой поверхностью последнего. Найдите площадь поверхности шара.

Решение:
Исходя из условий задачи, мы имеем дело с первым из трех описанных вариантов выше. А это значит, что радиус шара, также, равняется 15 см. Следовательно, площадь составляет:
S = 4 ⋅ 3,14 ⋅ (15 см)² = 2826 см².

Задание 2
Площадь поверхности шара равняется 1519,76 см², и он вписан в цилиндр таким образом, что касается его оснований. Найдите высоту цилиндра.

Решение:
Для начала найдем радиус шара, которые равен:

Высота цилиндра равна двум радиусам шара или его диаметру (2-ой вариант, рассмотренный в разделе выше):
h = 2R = 2 ⋅ 11 см = 22 см.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Площадь поверхности цилиндра

Горячая математика

Поскольку цилиндр тесно связана с призма , формулы их площадь поверхности относятся к.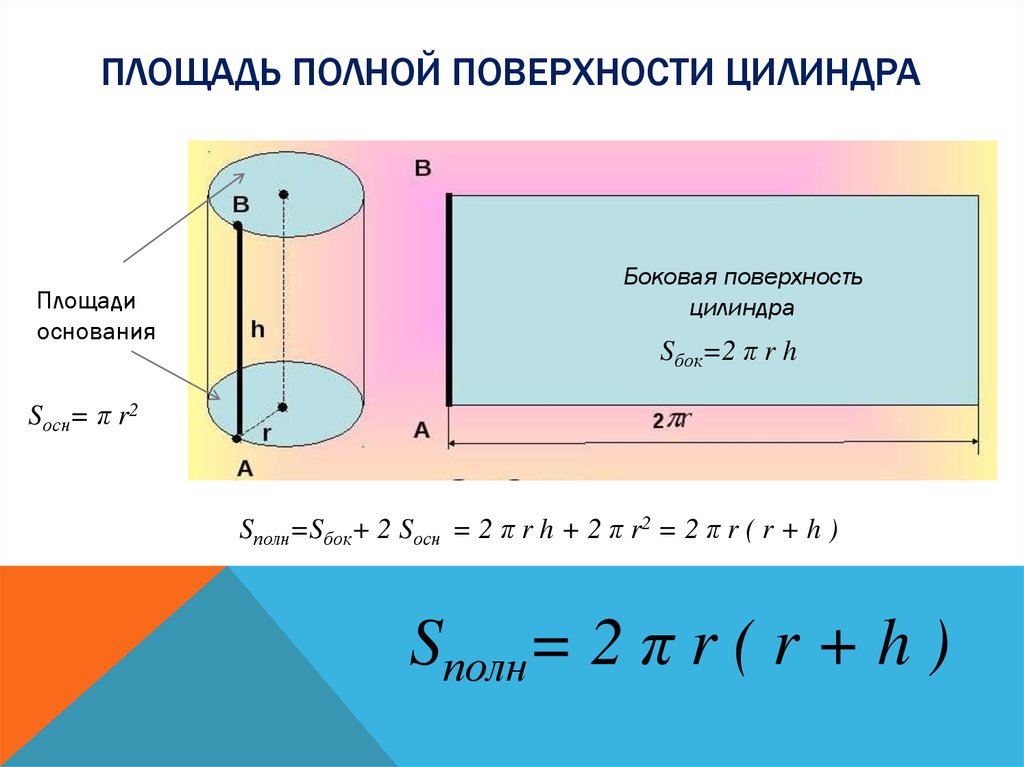

Вспомните формулу площади боковой поверхности призмы. п час а общая площадь поверхности п час + 2 Б . Поскольку основанием цилиндра является окружность, подставляем 2 π р за п а также π р 2 за Б куда р это радиус основания цилиндра.

Итак, формула для площадь боковой поверхности цилиндра л . С . А . знак равно 2 π р час .

Пример 1:

Найдите площадь боковой поверхности цилиндра с радиусом основания 3 дюймов и высотой 9дюймы.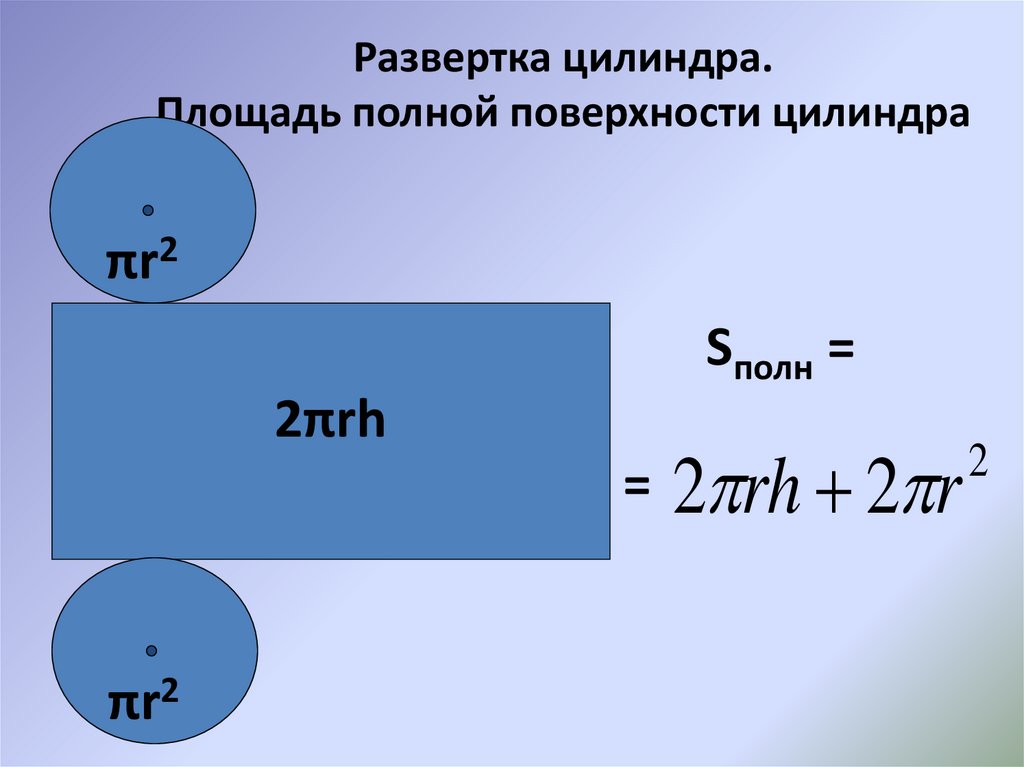

л . С . А . знак равно 2 π ( 3 ) ( 9 ) знак равно 54 π дюймы 2

≈ 169,64 дюймы 2

Общая формула для общая площадь поверхности цилиндра Т . С . А . знак равно 2 π р час + 2 π р 2 .

Пример 2:

Найдите площадь полной поверхности цилиндра с радиусом основания 5 дюймов и высотой 7 дюймы.

Т . С . А . знак равно 2 π ( 5 ) ( 7 ) + 2 π ( 5 ) 2 знак равно 120 π дюймы 2 ≈ 376,99 дюймы 2

Калькулятор круглого цилиндра

Форма круглого цилиндра

r = радиус
ч = высота
В = объем
L = площадь боковой поверхности
T = площадь верхней поверхности
B = площадь базовой поверхности

А = общая площадь поверхности
π = пи = 3,1415926535898
√ = квадратный корень

Калькулятор Использование

Этот онлайн-калькулятор рассчитает различные свойства цилиндра по двум известным значениям. Он также рассчитает эти свойства с точки зрения PI π. Это правильный круглый цилиндр, верхняя и нижняя поверхности которого параллельны, но его обычно называют «цилиндром».

Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты. Единицы используются для обозначения порядка результатов, таких как футы, футы ² или футы ³ . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты дадут V в мм ³ , L в мм ² , T в мм ² , B в мм ² и A в мм ² .

Ниже приведены стандартные формулы для цилиндра. Расчеты основаны на алгебраических манипуляциях с этими стандартными формулами.

Формулы цилиндра через r и h:

• Рассчитать объем цилиндра:
  • В = πr ² ч
• Рассчитайте площадь боковой поверхности цилиндра (только кривизну снаружи)**:
  • Д = 2πrh
• Рассчитайте площадь верхней и нижней поверхности цилиндра (2 круги):
  • Т = В = πr ²
• Общая площадь поверхности закрытого цилиндра:
  • A = L + T + B = 2πrh + 2(πr ² ) = 2πr(h+r)

** Расчетная площадь относится только к боковой поверхности внешней стенки цилиндра. Чтобы рассчитать общую площадь поверхности, вам нужно будет также рассчитать площадь верха и низа. Вы можете сделать это с помощью круговой калькулятор.

Цилиндр Расчеты:

Используйте следующие дополнительные формулы вместе с формулами выше.

• По заданным радиусу и высоте рассчитайте объем, площадь боковой поверхности и общую площадь поверхности.
  Вычислить V, L, A | Учитывая г, ч
  • используйте формулы выше
• По радиусу и объему рассчитайте высоту, площадь боковой поверхности и общую площадь поверхности.
  Вычислить h, L, A | Учитывая г, В
  • ч = В / πr ²
• По заданным радиусу и площади боковой поверхности рассчитайте высоту, объем и общую площадь поверхности.
  Рассчитать h, V, A | Учитывая г, L
  • ч = л/2πr
• Зная высоту и площадь боковой поверхности, рассчитайте радиус, объем и общую площадь поверхности.

  No related posts.