Формула площі ромба: Площадь ромба

Ромб. Формулы, признаки и свойства ромба

Ромб. Формулы, признаки и свойства ромба

Навигация по странице: Определение ромба Признаки ромба Основные свойства ромба Стороны ромба Диагонали ромба Периметр ромба Площадь ромба Окружность вписанная в ромб

Определение.

Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.

Ромбы отличаются между собой размером стороны и размером углов.

Рис.1		Рис.2

Признаки ромба

Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:

1. Две его смежные стороны равны (отсюда следует, что все стороны равны):

АВ = ВС = СD = AD

2.

Его диагонали пересекаются под прямым углом:

AC┴BD

3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:

∠BAC = ∠CAD или ∠BDA = ∠BDC

4. Если все высоты равны:

BN = DL = BM = DK

5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:

Δ ABO = Δ BCO = Δ CDO = Δ ADO

6. Если в параллелограмм можно вписать круг.

Основные свойства ромба

1. Имеет все свойства параллелограмма

2. Диагонали перпендикулярны:

AC┴BD

3. Диагонали являются биссектрисами его углов:

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:

AC² + BD² = 4AB²

5. Точка пересечения диагоналей называется центром симметрии ромба.

6. В любой ромб можно вписать окружность.

7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

a =	S
	ha

2. Формула стороны ромба через площадь и синус угла:

a =	√S
	√sinα

a =	√S
	√sinβ

3. Формула стороны ромба через площадь и радиус вписанной окружности:

a =	S
	2r

4. Формула стороны ромба через две диагонали:

a =	√d 12 + d22
	2

5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):

a =	d1
	√2 + 2 cosα

a =	d2
	√2 — 2 cosβ

6. Формула стороны ромба через большую диагональ и половинный угол:

a =	d1
	2cos(α/2)

a =	d1
	2sin(β/2)

7. Формула стороны ромба через малую диагональ и половинный угол:

a =	d2
	2cos(β/2)

a =	d2
	2sin(α/2)

8. Формула стороны ромба через периметр:

a =	Р
	4

Диагонали ромба

Определение.

Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.

Ромб имеет две диагонали — длинную d₁, и короткую — d₂

Формулы определения длины диагонали ромба:

1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)

d₁ = a√2 + 2 · cosα

d₁ = a√2 — 2 · cosβ

2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)

d₂ = a√2 + 2 · cosβ

d₂ = a√2 — 2 · cosα

3. Формулы большой диагонали ромба через сторону и половинный угол:

d₁ = 2a · cos(α/2)

d₁ = 2a · sin(β/2)

4. Формулы малой диагонали ромба через сторону и половинный угол:

d₂ = 2a · sin(α/2)

d₂ = 2a · cos(β/2)

5. Формулы диагоналей ромба через сторону и другую диагональ:

d₁ = √4a² — d₂²

d₂ = √4a² — d₁²

6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:

d₁ = d₂ · tg(β/2)

d₂ = d₁ · tg(α/2)

7. Формулы диагоналей через площадь и другую диагональ:

d1 =	2S
	d2

d2 =	2S
	d1

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

d1 =	2r
	sin(α/2)

d2 =	2r
	sin(β/2)

Периметр ромба

Определение.

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Формула периметра ромба через сторону ромба:

P = 4a

Площадь ромба

Определение.

Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.

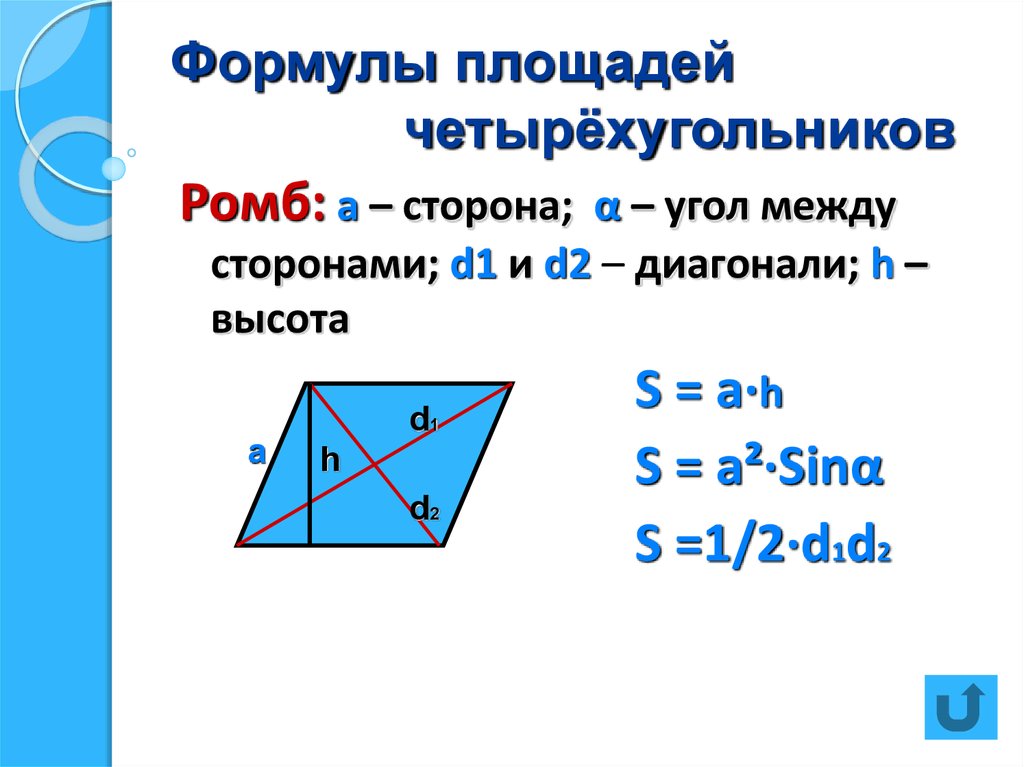
Формулы определения площади ромба:

1. Формула площади ромба через сторону и высоту:

S = a · h_a

2. Формула площади ромба через сторону и синус любого угла:

S = a² · sinα

3. Формула площади ромба через сторону и радиус:

S = 2a · r

4. Формула площади ромба через две диагонали:

S =	1	d1d2
	2

5. Формула площади ромба через синус угла и радиус вписанной окружности:

S =	4r2
	sinα

6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):

S =	1	d12 · tg(α/2)
	2

S =	1	d22 · tg(β/2)
	2

Окружность вписанная в ромб

Определение.

Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

r =	h
	2

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

r =	S
	2a

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

r =	√S · sinα
	2

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

r =	a · sinα
	2

r =	a · sinβ
	2

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

r =	d1 · sin(α/2)
	2

r =	d2 · sin(β/2)
	2

6. Формула радиуса круга вписанного в ромб через две диагонали:

r =	d1 · d2
	2√d12 + d22

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

r =	d1 · d2
	4a

Все таблицы и формулы

Площа ромба — всі формули як знайти площу ромба

Обчислити площу ромба, знаючи: (діагоналі) або (сторону і кут між ними) або (діагональ і кут між сторонами)

Зміст

1. Площа ромба формула
2. Знаходження площі ромба: формула і приклади
3. Формула обчислення площі
4. По довжині боку і висоті
5. По довжині боку і розі
6. За довжинами діагоналей
7. Приклади завдань
8. Площа проекції ромба
9. ПЛОЩА ПРОЕКЦІЇ ПЛОСКОЇ ФІГУРИ
10. Відео – як знайти площу ромба

Площа ромба формула

• a – сторона ромба

• D  – велика діагональ

• d – менша діагональ

• α – гострий кут

• β – тупий кут

Формули площі ромба через діагоналі і кути між сторонами ( S ):

• a  – сторона  ромба

• h – висота

• r – радіус вписаного кола

Формула площі ромба через висоту або радіус вписаного кола ( S ):

Знаходження площі ромба: формула і приклади

Ромб – це геометрична фігура; паралелограм, має 4 рівні сторони.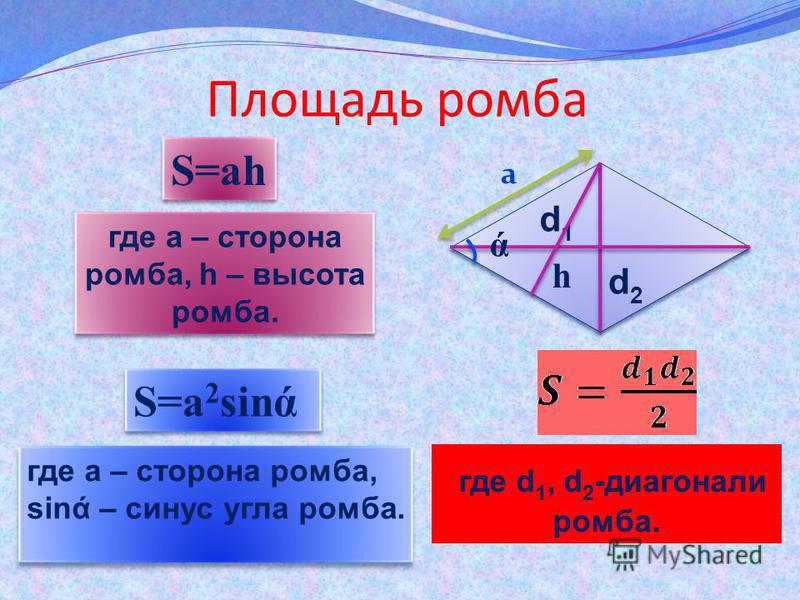

Формула обчислення площі

По довжині боку і висоті

Площа ромба (S) дорівнює добутку довжини його сторони і висоти, проведеної до неї:

S = a ⋅ h

По довжині боку і розі

Площа ромба дорівнює добутку квадрата довжини його сторони і синуса кута між сторонами:

S = a ² ⋅ sin α

За довжинами діагоналей

Площа ромба дорівнює одній другій твори його діагоналей.

S = ¹ / ₂ ⋅ d ₁ ⋅ d ₂

Приклади завдань

Завдання 1
Знайдіть площу ромба, якщо довжина його боку дорівнює 10 см, а висота, проведена до неї – 8 см.

Рішення:
Використовуємо першу формулу, яку розглянуто вище: S = 10 см ⋅ 8 см = 80 см ² .

Завдання 2
Знайдіть площу ромба, сторона якого дорівнює 6 см, а гострий кут – 30 °.

Рішення:
Застосуємо другу формулу, в якій використовуються відомі за умовами завдання величини: S = (6 см) ² ⋅ sin 30 ° = 36 см ² ⋅ 1/2 = 18 см ² .

Завдання 3
Знайдіть площу ромба, якщо його діагоналей рівні 4 і 8 см, відповідно.

Рішення:
Скористаємося третьої формулою, в якій використовуються довжини діагоналей: S = 1/2 ⋅ 4 см ⋅ 8 см = 16 см ² .

Площа проекції ромба

ПЛОЩА ПРОЕКЦІЇ ПЛОСКОЇ ФІГУРИ

Теорема : Площа проекції плоского багатокутника на деяку площину дорівнює площі проектованого багатокутника, помноженою на косинус кута між площиною багатокутника і площиною проекції.

1 етап: Проектована фігура – трикутник АВС, сторона якого АС лежить в площині проекції a (паралельна площині проекції a).

дано :

довести :

доказ :

По теоремі про три перпендикуляри 

ВD – висота

В ₁ D – висота

– лінійний кут двогранного кута

2 етап: Проектована фігура – трикутник АВС, жодна зі сторін якого не лежить в площині проекції a і не паралельна їй.

дано :

довести :

доказ :

3 етап: Проектована фігура – довільний багатокутник.

доказ :

Багатокутник розбивається діагоналями, проведеними з однієї вершини, на кінцеве число трикутників, для кожного з яких теорема вірна. Тому теорема буде вірна і для суми площ всіх трикутників, площини яких утворюють один і той же кут з площиною проекції.

Зауваження : Доведена теорема справедлива для будь-якої плоскої фігури, обмеженої замкнутою кривою.

вправи :

1. Знайти площу трикутника, площина якого нахилена до площини проекції під кутом , якщо проекція його – правильний трикутник зі стороною а.

2. Знайти площу трикутника, площина якого нахилена до площини проекції під кутом , якщо проекція його – трикутник з бічною стороною 10 см і підставою 12 см.

3. Знайти площу трикутника, площина якого нахилена до площини проекції під кутом , якщо проекція його – трикутник зі сторонами 9, 10 і 17 см.

4. Обчислити площу трапеції, площина якої нахилена до площини проекції під кутом , якщо проекція її – рівнобедрена трапеція, більше підставу якої 44 см, бічна сторона 17 см і діагональ 39 см.

5. Обчислити площу проекції правильного шестикутника зі стороною 8 см, площина якого нахилена до площини проекції під кутом .

6. Ромб зі стороною 12 см і гострим кутом утворює з цією площиною кут . Обчислити площу проекції ромба на цю площину.

7. Ромб зі стороною 20 см і діагоналлю 32 см утворює з цією площиною кут . Обчислити площу проекції ромба на цю площину.

8. Проекція навісу на горизонтальну площину є прямокутник зі сторонами і . Знайти площу навісу, якщо бічні грані – рівні прямокутники, нахилені до горизонтальної площини під кутом , а середня частина навісу – квадрат, паралельний площині проекції.

10. Вправи на тему «Прямі та площини в просторі»:

1. Сторони трикутника дорівнюють 20 см, 65 см, 75 см. З вершини більшого кута трикутника проведено до його площини перпендикуляр, рівний 60 см. Знайти відстань від кінців перпендикуляра до більшої сторони трикутника.

2. З точки, віддаленої від площини на відстані см, проведено дві похилі, які утворюють з площиною кути, рівні , а між собою – прямий кут. Знайти відстань між точками перетину похилих з площиною.

3. Сторона правильного трикутника дорівнює 12 см. Точка М обрана так, що відрізки, що з’єднують точку М з усіма вершинами трикутника, утворюють з його площиною кути . Знайти відстань від точки М до вершин і сторін трикутника.

4. Через сторону квадрата проведено площину під кутом до діагоналі квадрата. Знайти кути, під якими нахилені до площини дві сторони квадрата.

5. Катет рівнобедреного прямокутного трикутника нахилений до площини a, що проходить через гіпотенузу, під кутом .  Довести, що кут між площиною a і площиною трикутника дорівнює .

6. Двогранний кут між площинами трикутників АВС і DВС дорівнює . Знайти АD, якщо АВ = АС = 5 см, ВС = 6 см, ВD = DС = см.

Відео – як знайти площу ромба

Формула площади ромба с калькулятором

Формула площади ромба с калькулятором — Открытый справочник по математике

Открытый справочник по математике

Главная Контакт О Тематический указатель

Три разных способа вычисления площади ромба приведены ниже, с формулой для каждого.

Попробуйте это Перетащите оранжевые точки на каждую вершину изменить форму ромба. Площадь будет непрерывно рассчитываться с использованием метода «база умножается на высоту».

Ромб на самом деле просто особый тип параллелограмма.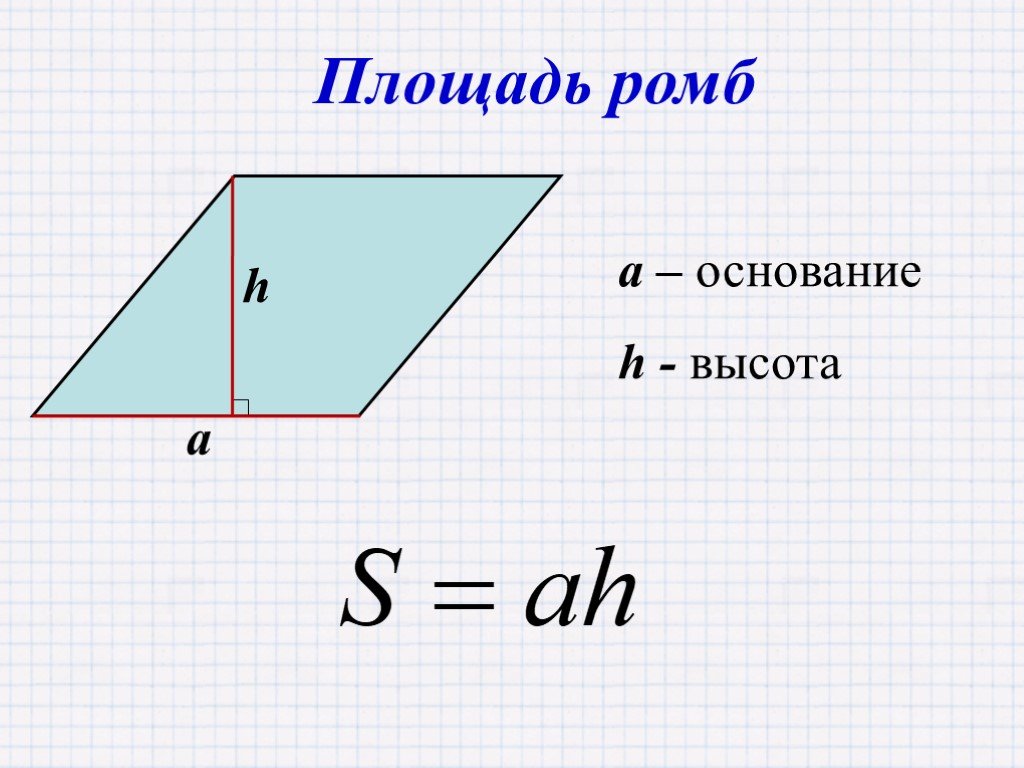 К ним также можно применить многие расчеты площади. Выберите формулу, основанную на значениях, которые вы знаете для начала.

1. Метод «база умножить на высоту»

Сначала выберите одну сторону, которая будет основой. Подойдет любой, они все одинаковой длины. Затем определите высоту – перпендикулярное расстояние от выбранного основания до противоположной стороны. Площадь является произведением этих двух или, как формула: где
b длина основания
a высота (высота).

Используйте приведенный ниже калькулятор, чтобы вычислить площадь ромба, зная длину основания (стороны) и высота (перпендикулярная высота).

Введите любые два значения, и будет рассчитано отсутствующее. Например, введите площадь и длину основания, и будет рассчитана высота, необходимая для получения этой площади.

Основание		прозрачный
Высота		прозрачный
Зона		прозрачный

2.

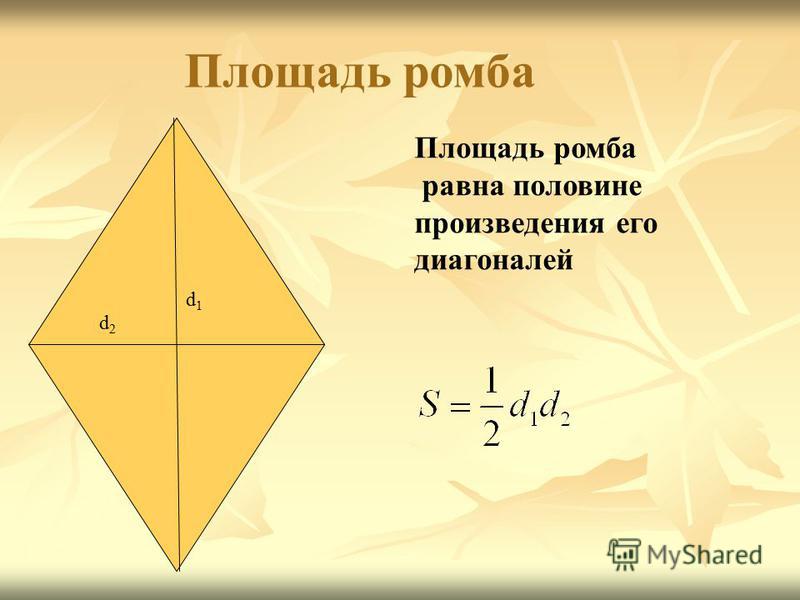Метод «диагоналей» Еще одна простая формула площади ромба, если известны длины диагоналей. Площадь равна половине произведения диагоналей. Как формула: где
d ₁ длина диагонали
d ₂ длина другой диагонали

3.90 Используя тригонометрию Если вы знакомы с тригонометрией, есть удобная формула, когда вы знаете длину стороны и любого угла: где

s — длина любой стороны
a — любой внутренний угол
sin — функция синуса
(см. Обзор тригонометрии)

Сначала может показаться странным, что вы можете использовать любой угол, поскольку не все они равны. Но углы либо равны, либо дополнительный, и дополнительные углы имеют один и тот же синус.

Другие полигональные темы

Общий

• Общее определение многоугольника
• Четырехугольник
• Правильный многоугольник
• Неправильный многоугольник
• Выпуклые многоугольники
• Вогнутые многоугольники
• Диагонали многоугольника
• Многоугольные треугольники
• Апофема правильного многоугольника
• Центр полигона
• Радиус правильного многоугольника
• Вписанная окружность правильного многоугольника
• В центре правильного многоугольника
• Окружность многоугольника
• Параллелограмм, вписанный в четырехугольник

Типы многоугольников

• Квадрат
• Диагонали квадрата
• Прямоугольник
• Диагонали прямоугольника
• Золотой прямоугольник
• Параллелограмм
• Ромб
• Трапеция
• Медиана трапеции
• Воздушный змей
• Вписанный (вписанный) четырехугольник
• Вписанные внутренние углы четырехугольника
• Площадь вписанного четырехугольника
• Диагонали вписанного четырехугольника

Площадь различных типов полигонов

• Площадь правильного многоугольника
• Область неправильного многоугольника
• Площадь ромба
• Кайт-площадка
• Область прямоугольника
• Площадь квадрата
• Трапециевидная площадка
• Область параллелограмма

Периметр различных типов полигонов

• Периметр многоугольника (правильного и неправильного)
• Периметр треугольника
• Периметр прямоугольника
• Периметр квадрата
• Периметр параллелограмма
• Периметр ромба
• Периметр трапеции
• Периметр воздушного змея

Углы, связанные с многоугольниками

• Внешние углы многоугольника
• Внутренние углы многоугольника
• Соотношение внутренних и внешних углов
• Центральный угол многоугольника

Именованные полигоны

• Четырехугольник, 4 стороны
• Пятиугольник, 5 сторон
• Шестигранник, 6 сторон
• Семиугольник, 7 сторон
• Октагон, 8 сторон
• Nonagon Эннеагон, 9 сторон
• Десятиугольник, 10 сторон
• Undecagon, 11 сторон
• Додекагон, 12 сторон

(C) 2011 Copyright Math Open Reference.
Все права защищены

Площадь ромба – объяснение и примеры

В статье о многоугольнике мы видели, что ромб представляет собой четырехугольник с четырьмя параллельными сторонами равной длины . Противоположные углы ромба также равны.

Аналогично диагонали ромба пересекаются под прямым углом, и их длины всегда равны . Квадрат — это разновидность ромба, у которого все 4 угла прямые. Иногда ромб называют ромбом, ромбом или ромбом.

В этой статье вы узнаете, как вычислить площадь ромба, используя формулы трех площадей ромба.

Как вычислить площадь ромба?

Площадь ромба – это область, ограниченная 4 сторонами ромба .

Есть три способа найти площадь ромба.

Один из способов — использование высоты и стороны ромба. Второй метод влечет за собой использование стороны и угла, а последний метод влечет за собой использование диагоналей.

Эти формулы для вычисления площади ромба известны под общим названием формулы площади ромба. Давайте взглянем.

Формула площади ромба

Площадь ромба можно найти несколькими способами. Мы увидим каждый из них один за другим ниже.

Площадь ромба с использованием высоты и основания

Когда известны высота или высота и длина сторон ромба, площадь определяется по формуле;

Площадь ромба = основание × высота

A = b × h

Поясним это на примере:

и высота 15 см.

Раствор

A = b × h

= (30 x 15) см ²

= 450 см ²

Следовательно, площадь ромба равна 450 см ² .

Пример 2

Вычислите площадь ромба, показанного ниже.

Решение

A = B × H

= (18 x 24) MM ²

Пример 3

Если высота и область ромбоба — 8 СМ и 72 C 9099 2

Если высота и область ромбоба — 8 см и 72 C 9099 2

. , соответственно, найти размеры ромба.

Решение

A = B × H

72 CM ² = 8 см x B

Разделите с обеих сторон на 8.

72 см ² /8 см = B

B = 90 см.

Следовательно, размеры ромба 9 см на 9 см.

Пример 4

Основание ромба в 3 раза больше высоты плюс на 1 больше. Если площадь ромба 10 м ² , найдите основание и высоту ромба.

Решение

Дайте высоту ромбы = x

и основание = 3x + 1

A = B × H

10 M ² = X (3x + 1)

10 = 3x ² = x (3x + 1)

10 = 3x ² + x

3x ² + x – 10 = 0

Решите квадратное уравнение.

⟹ 3x ² + x – 10 = 3x ² + 6x – 5x – 10

⟹ 3x (x + 2) – 5(x + 2)

+ ⟹ (3x – 2) (3x – 2) ) = 0

⟹ 3x – 5 = 0

⟹ x = 5/3

⟹ x + 2= 0

x = -2

Теперь подставьте значение x.

Высота = х = 5/3 м

Основание = 3х + 1 = 3(5/3) + 1 = 6 м

Итак, основание ромба 6 м, а высота 5/3 м .

Площадь ромба с использованием диагоналей

Учитывая длины диагоналей, площадь ромба равна половине произведения диагоналей.

A = ½ × d ₁  × d ₂

Где d ₁  и d ₂ — диагонали ромба.

Пример 5

Две диагонали ромба равны 12 см и 8 см. Вычислите площадь ромба.

Решение:

Пусть d ₁ = 12 см и d ₂ = 8 см.

A = ½ × d ₁  × d ₂

= (½ × 12 × 8) см ² .

= 48 см ² .

Пример 6

Рассчитайте длину стороны, если ее площадь равна 24 см ² , диагональ 8 см, высота 3 см.

Раствор

Пусть d ₁ = 8 см.

д ₂ =?

A = ½ × D ₁ × D ₂

24 CM ² = ½ × 8 × D ₂

24 CM ² = 4D ₂

Divide Divide Divide. чтобы получить,

6 = d ₂

Следовательно, другая диагональ равна 6 см.

Теперь вычислите длины сторон ромба.

A = b × h

24 см ² = 3 см x b

Обе стороны разделить на 3.

8 см = b.

Следовательно, длины сторон ромба равны 8 см.

Пример 7

Найдите диагонали показанного ниже ромба, если его площадь равна 3458 см ² .

Раствор

A = ½ × d ₁  × d ₂

3,458 см ² = ½ см * 8x 904, 03x 90Разделите обе стороны на 24.

x = -12 или 12.

Длина не может быть отрицательным числом; поэтому подставьте только x = 12 в уравнения диагоналей.

6x = 6 * 12 = 72 см

8x = 8 * 12 = 96 см

Следовательно, длины диагоналей 72 см и 96 см.

Пример 8

Предположим, стоимость полировки пола составляет 4 доллара за квадратный метр. Найдите стоимость полировки пола в форме ромба, каждая из его диагоналей равна 20 м и 12 м.

Решение

Чтобы узнать стоимость полировки пола, умножьте скорость полировки на площадь ромбовидного пола.

A = ½ × 20 м × 12 м

= 120 м ²

Стоимость покраски = 120 м ² x 4 $ за м.

= 480 долларов

Площадь ромба с использованием длины сторон и угла между ними.

Площадь ромба равна квадрату длины стороны произведения и синусу угла между двумя сторонами.

Площадь ромба = b ²  × Синус (A)

Где A = угол, образованный между двумя сторонами ромба.

Пример 9

Найдите площадь ромба, сторона которого равна 8 см, а угол между двумя сторонами равен 60 градусам.

Решение

A = b ²  × синус (A)

= 8 ² x синус (60)

= 55,43 см 1 2 .

Практические вопросы

1. Найдите длину диагонали ромба, если длина другой диагонали 5 единиц, а площадь ромба 30 квадратных единиц.

   No related posts.