Площа трапеції — формули як знайти площу трапеції
Зміст
- Прямокутна трапеція. Формули, ознаки та властивості прямокутної трапеції
- Ознаки прямокутної трапеції
- Основні властивості прямокутної трапеції
- Сторони прямокутної трапеції
- Середня лінія прямокутної трапеції
- Площа рівнобічної трапеції
- Ознаки рівнобедреної трапеції
- Основні властивості рівнобедреної трапеції
- Сторони рівнобедреної трапеції
- Формули довжин сторін рівнобедреної трапеції:
- Середня лінія рівнобедреної трапеції
- Формули довжини середньої лінії рівнобедреної трапеції:
- Висота рівнобедреної трапеції
- Формули визначення довжини висоти рівнобедреної трапеції:
- Діагоналі рівнобедреної трапеції
- Формули довжини діагоналей рівнобедреної трапеції:
- Площа рівнобедреної трапеції
- Формули площі рівнобедреної трапеції:
- Окружність описана навколо трапеції
- Формула визначення радіуса описаної навколо трапеції кола:
- Відео – як знайти площу трапеції
Прямокутна трапеція.
 Формули, ознаки та властивості прямокутної трапеції
Формули, ознаки та властивості прямокутної трапеціїВизначення. Прямокутна трапеція – це трапеція у якої одна з бічних сторін перпендикулярна основам.
Ознаки прямокутної трапеції
Трапеція буде прямокутною якщо виконується одна з цих умов:
1. У тапеціі є два суміжних прямих кута:∠BAD = 90 ° і ∠ABC = 90 °
2. Одна бічна сторона перпендикулярна основам:AB
┴ BC, AB
┴ AD
Основні властивості прямокутної трапеції
1. У трапеції є два суміжних прямих кута:∠BAD = ∠ABC = 90 °
2. Одна бічна сторона перпендикулярна основам:AB
┴ BC
┴ AD
3. Висота дорівнює меншій бічній стороні:h = AB
Сторони прямокутної трапеції
Формули довжин сторін прямокутної трапеції:
1. Формули довжини підстав через сторони і кут при нижньому підставі:a =
b +
d cos α =
b +
c ctg α =
b + √
d 2 –
c 2
b =
a –
d cos α =
a –
c ctg α =
a – √
d 2 –
c 2
2.Формули довжини підстав через сторони, діагоналі і кут між ними:
a =
d 1 d 2
· Sin γ –
b =
d 1 d 2
· Sin δ –
b
c
c
b =
d 1 d 2
· Sin γ –
a =
d 1 d 2
· Sin δ –
a
c
c
3. Формули довжини підстав трапеції через площу і інші сторони:a =
2S
–
b b =
2S
–
a
c
c
4. Формула збоку через інші сторони і кут при нижньому підставі:c = √
d 2 – (
a –
b )
2 = (
a –
b )
tg α =
d sin α
5. Формули збоку через основи, діагоналі і кут між ними:c =
d 1 d 2
· Sin γ =
d 1 d 2
· Sin δ
a +
b
a +
b
6. Формули збоку через площу, основи і кут при нижньому підставі:c =
S
=
2S
m
a +
b
d =
S
=
2S
m sin α
(
A +
b )
sin α
7.Формула збоку через інші сторони, висоту і кут при нижньому підставі:
d =
a –
b
=
c
=
h
= √
c 2 + (
a –
b )
2
cos α
sin α
sin α
Середня лінія прямокутної трапеції
Формули довжини середньої лінії прямокутної трапеції:
1. Формули середньої лінії через підставу, висоту (вона ж дорівнює стороні
c ) і кут α при нижньому підставі:
m =
a –
h ·
ctg α
=
b +
h ·
ctg α
2
2
2. Формули середньої лінії через підстави і бічні сторони сторону:m =
a –
√
d 2 –
c 2
=
b +
√
d 2 –
c 2
2
2
Площа рівнобічної трапеції
Визначення. Рівнобедрена трапеція – це трапеція у котрої бічні сторони рівні.
На цій сторінці представлені формули характерні рівнобедреної трапеції. Не забувайте, що для рівнобедреної трапеції виконуються всі формули і властивості трапеції.
Не забувайте, що для рівнобедреної трапеції виконуються всі формули і властивості трапеції.
Ознаки рівнобедреної трапеції
Трапеція буде рівнобедреної якщо виконується одна з цих умов:1. Кути при основі рівні:
∠ABC = ∠BCD і ∠BAD = ∠ADC2. Діагоналі рівні:
AC = BD3. Однакові кути між діагоналями і підставами:
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC4. Сума протилежних кутів дорівнює 180 °:
∠ABC + ∠ADC = 180 ° і ∠BAD + ∠BCD = 180 °5. Навколо трапеції можна описати коло
Основні властивості рівнобедреної трапеції
1. Сума кутів прилеглих до бічної сторони рівнобедреної трапеції дорівнює 180 °:
∠ABC + ∠BAD = 180 ° і ∠ADC + ∠BCD = 180 °2. Якщо в рівнобедрений трапецію можна вписати коло, то бічна сторона дорівнює середній лінії трапеції:
AB = CD = m3. Навколо рівнобедреної трапеції можна описати коло4. Якщо діагоналі взаємно перпендикулярні, то висота дорівнює напівсумі підстав (середньої лінії):
h = m5. Якщо діагоналі взаємно перпендикулярні, то площа трапеції дорівнює квадрату висоти:
S ABCD = h 26. Якщо в рівнобедрений трапецію можна вписати коло, то квадрат висоти дорівнює добутку основ трапеції:
Якщо в рівнобедрений трапецію можна вписати коло, то квадрат висоти дорівнює добутку основ трапеції:
h 2 = BC · AD7. Сума квадратів діагоналей дорівнює сумі квадратів бічних сторін плюс подвоєному добутку основ трапеції:
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD8. Пряма, що проходить через середини підстав, перпендикулярна підставах і є віссю симетрії трапеції:
HF ┴ BC, HF ┴ AD9. Висота (CP), опущена з вершини (C) на більше підставу (AD), ділить його на великий відрізок (AP), який дорівнює напівсумі підстав і менший (PD) – дорівнює полуразность підстав:
| AP = | BC + AD |
| 2 |
| PD = | AD – BC |
| 2 |
Сторони рівнобедреної трапеції
Формули довжин сторін рівнобедреної трапеції:
1. Формули довжини сторін через інші сторони, висоту і кут:
a = b + 2 h ctg α = b + 2 c cos α
b = a – 2 h ctg α = a – 2 c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2.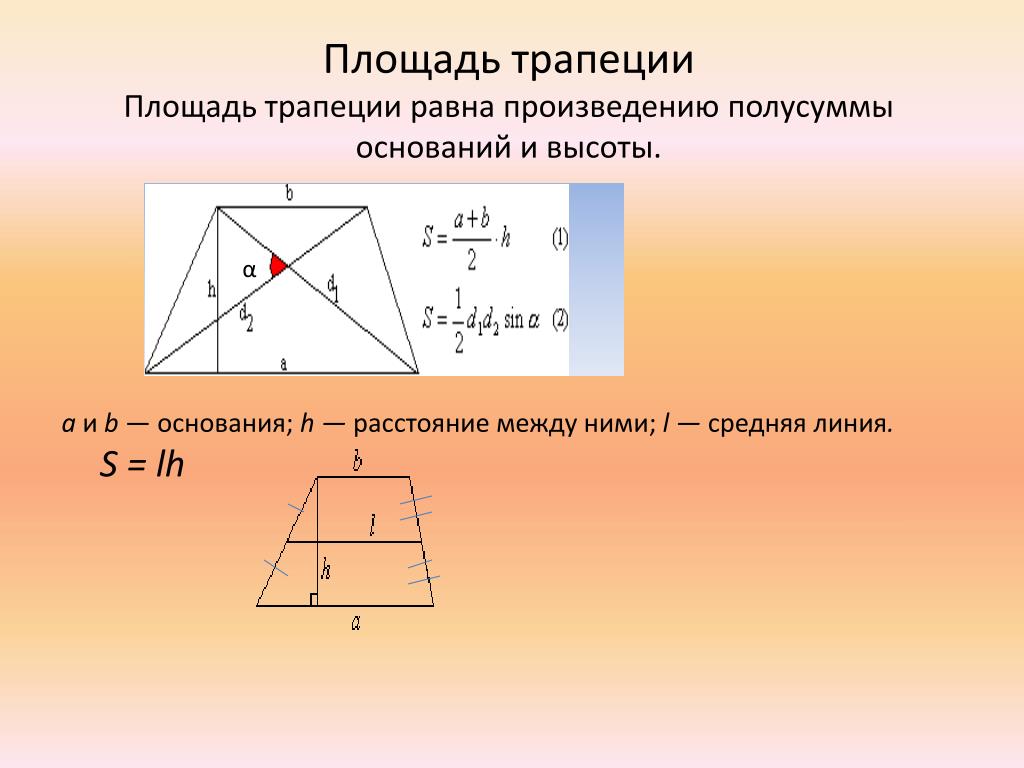 Формула довжини сторін трапеції через діагоналі і інші сторони:
Формула довжини сторін трапеції через діагоналі і інші сторони:
| a = | d 1 2 – c 2 | b = | d 1 2 – c 2 | c = √ d 1 2 – ab |
| b | a |
3. Формули довжини основ через площу, висоту і іншу основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формули довжини бічної сторони через площу, середню лінію і кут при основі:
| з = | S |
| m sin α |
5. Формули довжини бічної сторони через площу, підстави і кут при основі:
| з = | 2S |
| ( A + b ) sin α |
Середня лінія рівнобедреної трапеції
Формули довжини середньої лінії рівнобедреної трапеції:
1. Формула визначення довжини середньої лінії через підстави, висоту і кут при підставі:
Формула визначення довжини середньої лінії через підстави, висоту і кут при підставі:
m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 22. Формула середньої лінії трапеції через площу і сторону:
| m = | S |
| c sin α |
Висота рівнобедреної трапеції
Формули визначення довжини висоти рівнобедреної трапеції:
1. Формула висоти через сторони:
| h = | 1 | √ 4 c 2 – ( a – b ) 2 |
| 2 |
2. Формула висоти через сторони і кут прилеглий до основи:
| h = | a – b | tg β | = C sin β |
| 2 |
Діагоналі рівнобедреної трапеції
Діагоналі рівнобедреної трапеції рівні:
d 1 = d 2
Формули довжини діагоналей рівнобедреної трапеції:
1. Формула довжини діагоналі через сторони:
Формула довжини діагоналі через сторони:
d 1 = √ з 2 + ab2. Формули довжини діагоналі по теоремі косинусів:
d 1 = √ a 2 + c 2 – 2 ac cos α
d 1 = √ b 2 + c 2 – 2 bc cos β3. Формула довжини діагоналі через висоту і середню лінію:
d 1 = √ h 2 + m 24. Формула довжини діагоналі через висоту і підстави:
| d 1 = | 1 | √ 4 h 2 + ( a + b ) 2 |
| 2 |
Площа рівнобедреної трапеції
Формули площі рівнобедреної трапеції:
1. Формула площі через сторони:
| S = | a + b | √ 4 c 2 – ( a – b ) 2 |
| 4 |
2. Формула площі через сторони і кут:
S = ( b + c cos α ) c sin α = ( a – c cos α ) c sin α3. Формула площі через радіус вписаного кола і кут між основою і бічною стороною:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4.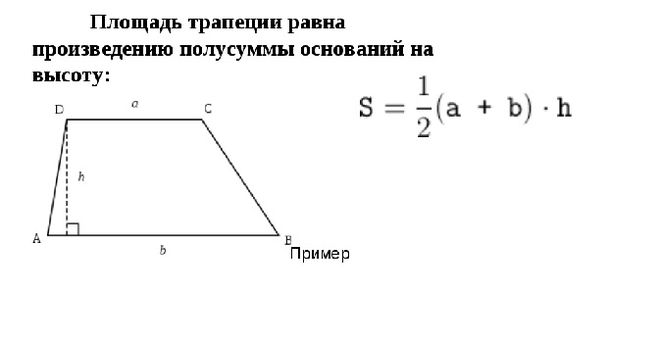 Формула площі через підстави і кут між основою і бічною стороною:
Формула площі через підстави і кут між основою і бічною стороною:
| S = | ab | = | ab |
| sin α | sin β |
5. Формула площі ранобедренной трапеції в яку можна вписати коло:
S = ( a + b ) · r = √ ab · c = √ ab · m6. Формула площі через діагоналі і кут між ними:
| S = | d 1 2 | · Sin γ | = | d 1 2 | · Sin δ |
| 2 | 2 |
7. Формула площі через середню лінію, бічну сторону і кут при підставі:
S = mc sin α = mc sin β8. Формула площі через підстави і висоту:
| S = | a + b | · h |
| 2 |
Окружність описана навколо трапеції
Окружність можна описати тільки навколо рівнобедреної трапеції !!!
Формула визначення радіуса описаної навколо трапеції кола:
1.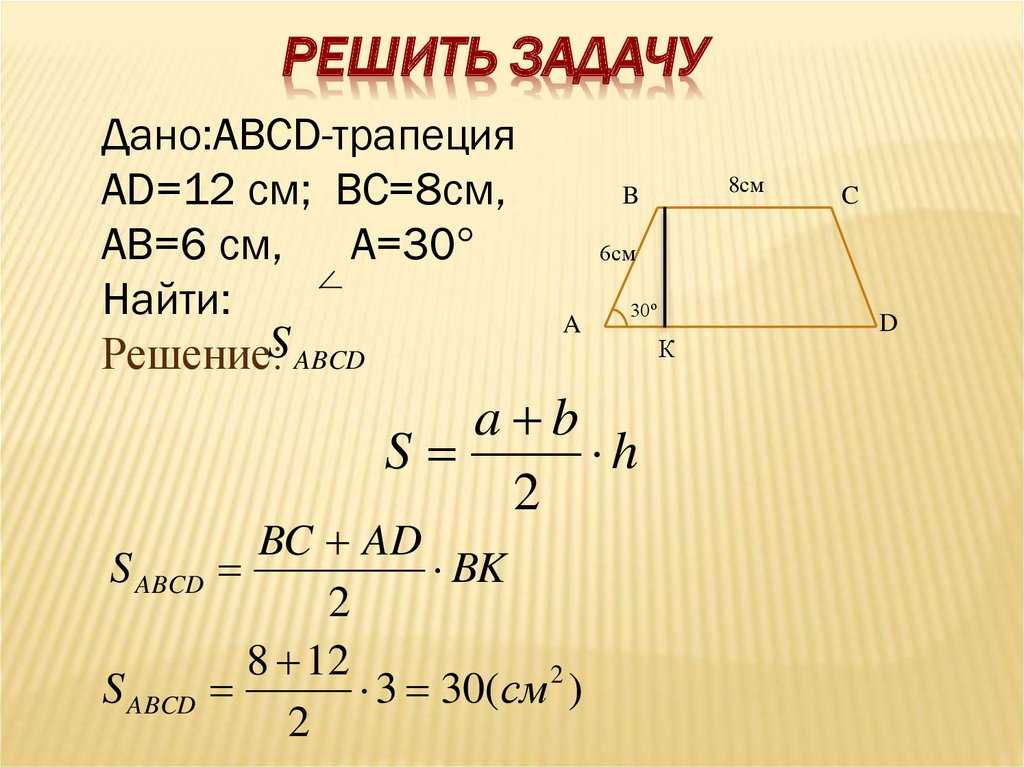 Формула радіусу через сторони і діагональ:
Формула радіусу через сторони і діагональ:
| R = | a · c · d 1 |
| 4√ p ( p – a ) ( p – c ) ( p – d 1 ) |
де
| p = | a + c + d 1 |
| 2 |
a – більше підставу
Відео – як знайти площу трапеції
Page not found – www.mathros.net.ua
Перейти до вмісту
Нічого не знайдено. Можливо, спробуйте пошук або одне з посилань нижче?
Archives
Archives Select Month April 2023 March 2023 February 2023 January 2023 December 2022 November 2022 October 2022 September 2022 August 2022 July 2022 June 2022 May 2022 April 2022 March 2022 February 2022 November 2021 October 2021 September 2021 August 2021 July 2021 June 2021 February 2021 December 2020 November 2020 October 2020 September 2020 August 2020 June 2020 May 2020 March 2020 February 2020 January 2020 December 2019 November 2019 October 2019 September 2019 May 2019 April 2019 March 2019 February 2019 January 2019 December 2018 November 2018 September 2018 August 2018 July 2018 June 2018 May 2018 April 2018 March 2018 February 2018 January 2018 December 2017 November 2017 October 2017 September 2017 August 2017 July 2017 June 2017 May 2017 April 2017 March 2017 February 2017 January 2017 December 2016 November 2016 October 2016 September 2016 August 2016 July 2016 June 2016 May 2016 April 2016 March 2016 February 2016 January 2016 December 2015 November 2015 October 2015 September 2015 August 2015 July 2015 June 2015 May 2015 April 2015 March 2015 February 2015 January 2015 December 2014 November 2014 October 2014 September 2014 August 2014 July 2014 June 2014 May 2014 April 2014 March 2014 February 2014 January 2014 December 2013 November 2013 October 2013 September 2013 August 2013 July 2013 September 2012 August 2012 July 2012Categories
CategoriesSelect CategorySQLІнформаційні системи на DelphiІрраціональні рівнянняАлгебра матрицьАлгоритми комп’ютерної графікиАлгоритми комп’ютерної графіки на delphiАрифметична прогресіяБагатокутникиБази данихВідрізокВектори і операції з нимиВступ до JavaГеометрична прогресіяДводольні графиДослідження операційЗадачі розміщенняЗадача дробово-лінійного програмуванняЗадача комівояжераЗадача про рюкзакЗнаходження власних значень і власних векторів матриціКвадратні кореніКвадратні рівнянняКоло і кругКомплексні числаКомпоненти зв’язності, кліки, точки сполученняЛінії другого порядкуЛінійні рівняння та їх системиЛінійне програмуванняЛінійне цілочисельне програмуванняМетоди наближення функційМетоди обходу графаМетоди розв’язування систем лiнiйних алгебраїчних рівняньМногогранникиМови програмуванняНаближене рішення систем нелінійних рівняньНелінійне програмуванняНерівностіОбчислення значень функціїОптимальні каркаси та шляхиПлоща і периметр фігурПлоща поверхні та об’єм геометричних фігурПодільність натуральних чиселПохідна і диференціалПошук екстремумів функційПрограми на Delphi (Дослідження операцій)Програми на Delphi (Методи обчислення)Пряма лінія на площиніРізнеРеалізація відомих алгоритмів на JavaРобота з базами даних в середовищі програмування DelphiРозфарбування графаТопологічне сортуванняТранспортна задача лінійного програмуванняТрикутникиЦиклиЧисельні методи розв’язання задач математичної фізикиЧисельні методи розв’язування звичайних диференцiальних рiвняньЧисельні методи розв’язування рівнянь з однією змінноюЧисельне диференціювання та інтегруванняЧто такое площадь трапеции | Работа с формулой и расчеты
В этой статье вы узнаете, что такое площадь трапеции и как ее вычислить. Также выучите формулу площади трапеции.
Также выучите формулу площади трапеции.
Что такое площадь трапеции?
Площадь трапеции относится к количеству пространства, занимаемого сторонами трапециевидной формы. Трапеция — это фигура с четырьмя ногами, имеющая пару параллельных сторон. Это четырехугольник, который представляет собой плоскость и замкнутую форму. Площадь, покрытая трапецией, может быть рассчитана с помощью формулы или путем разделения ее на более мелкие многоугольники, такие как треугольники и прямоугольники, а затем нахождение их площадей и добавление их, чтобы получить площадь трапеции.
Формула площади трапеции
Если A – площадь трапеции, h – высота, a и b – параллельные стороны, то формула площади трапеции:
Мы можем вычислить площадь трапеции, сложив параллельные основания трапеции вместе и умножив полученное значение на h, а затем разделив на 2.
Например, площадь данной трапеции можно рассчитать как:
основания данной трапеции:
B 1 = 8 см и B 1 = 6 см
, а высота или расстояние между основаниями:
H = 10 см
. $$ А \;=\; \frac{1}{2}(b_1 + b_2)h $$
$$ А \;=\; \frac{1}{2}(8 + 6) \times 10 $$
$$ А \;=\; \frac{1}{2}(140) $$
$$ А \;=\; 70см $$
$$ А \;=\; \frac{1}{2}(b_1 + b_2)h $$
$$ А \;=\; \frac{1}{2}(8 + 6) \times 10 $$
$$ А \;=\; \frac{1}{2}(140) $$
$$ А \;=\; 70см $$
Как вычислить площадь трапеции?
$$ А \;=\; \frac{1}{2}(a+b)h $$
См. следующие примеры, чтобы понять, как вычислить площадь трапеции.
Объем трапеции Формула
Объем трапеции – это общее пространство, занимаемое ею в трех измерениях. Его можно рассчитать, перемножив площадь и высоту трапеции. Формула для расчета объема трапеции:
V = площадь × высота
или
V = A × h
Итак, это формула объема трапеции для расчета объема трапеции. Давайте разберемся, как использовать эту формулу, чтобы понять понятия объема трапеции.
Например, чтобы рассчитать объем в приведенном выше примере 2, где
A=62,5 см и h=5 см
Тогда объем будет равен
V=62,55
см V=3 2Связанные формулы
- Площадь сектора Формула 92 $$
Где,
S = любая сторона квадрата - Площадь Пентагона Формула $$ А \;=\; \frac{1}{2} P \times A $$
- Формула окружности $$ С \;=\; 2 \pi г $$
Где
P = периметр
A = апофема
Где,
r = радиус окружности
Часто задаваемые вопросы (FAQ)
Какова формула площади трапеции?
Формула площади трапеции:
$$ А \;=\; \frac{1}{2}(a+b)h $$
Где a и b — длины параллельных сторон, а h — высота трапеции.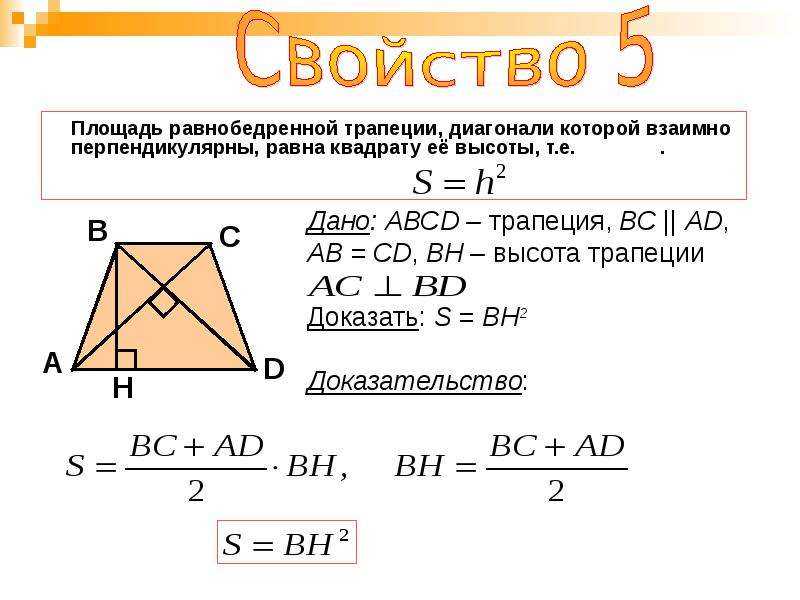
Что такое основания и стороны трапеции?
Основаниями трапеции являются ее параллельные стороны, а катетами — непараллельные стороны.
Простая формула для нахождения площади трапеции
Вот как найти площадь трапецииТрапеция — это двухмерная четырехсторонняя фигура, имеющая один набор параллельных сторон. Две другие стороны не параллельны. Параллельные стороны трапеции будут разной длины. Чтобы решить, как найти площадь трапеции, вы должны сложить две параллельные стороны, умножить эту сумму на высоту, а затем, наконец, разделить на два. Высота трапеции должна быть перпендикулярна основанию трапеции. При нахождении площади трапеции нельзя использовать стороны трапеции, потому что они не перпендикулярны основанию трапеции. Как правило, вы увидите пунктирную линию в трапеции, которая представляет высоту.
Стандарт общего ядра: 6.G.1
Связанные темы: Площадь треугольника, площадь параллелограммы, площадь составных рисунок
Возвращение к: Home, 6 -е класс
. Так как же все-таки найти площадь трапеции? Трапеция — это двумерная четырехсторонняя фигура, имеющая одну пару параллельных сторон. Другие противоположные стороны не параллельны. Параллельные стороны трапеции состоят из неравных длин. При ответе, как найти площадь трапеции, вы должны следовать формуле площади трапеции. Сначала вы находите сумму двух параллельных сторон, затем умножаете эту сумму на высоту трапеции и, наконец, делите на два. Высота трапеций будет 90 градусов с основанием. При нахождении площади трапеции нельзя использовать стороны трапеции, так как они не составляют 90 градусов с основанием трапеции. Обычно вы увидите пунктирную линию на трапеции, которая показывает высоту. Смотреть наш бесплатный видео на том, как найти область из Trapezoid . В этом видео показано, как решать задачи, представленные в нашем бесплатном листе «Площадь трапеции », который вы можете получить, отправив свое электронное письмо выше. Посмотрите бесплатное видео «Площадь трапеции» на YouTube здесь: «Площадь трапеции». Вы можете получить рабочий лист площади трапеции, используемый в этом видео, бесплатно, нажав на ссылку в описании ниже. Трапецией называется любая четырехсторонняя фигура, имеющая один набор параллельных сторон. Чтобы найти площадь трапеции, вы возьмете длину более длинного основания, которое, как мы собираемся сказать, равно b sub 1 плюс длина более короткого основания, которое равно b sub 2, деленное на 2, а затем умножив это на высоту. В данном примере длина основания равна 16, длина второго основания равна 8, а затем высота равна 12 футам. Основания — внешние ребра трапеции. Я знаю, что 16 будет более длинным основанием, потому что это большее основание из двух. 16 больше, чем восемь, поэтому я знаю, что это первое основание. Затем у нас есть второе основание, которое будет составлять восемь футов, потому что это меньшая длина двух оснований. И тогда я знаю, что 12 футов будут представлять высоту, потому что это расстояние между двумя параллельными сторонами. Мы знаем, что формула площади трапеции — это длинное основание плюс короткое основание, деленное на два, а затем умноженное на высоту. В нашем примере мы знаем, что длинная сторона равна 16. Мы собираемся сказать, что 16 плюс короткая сторона, которая в данном случае равна восьми, а затем мы делим на два, а затем умножаем на высоту, которая равна 12. в этом примере. Когда мы упрощаем для нашей площади трапеции, мы собираемся сделать 16 плюс 8, что 24 разделить на 2, а затем умножить на 12. Краткий обзор по нахождению площади трапеции
Краткий обзор по нахождению площади трапеции
Площадь проблем с трапециевидной практикой Quiz Посмотреть видео объяснение нашей области трапеции рабочего листа 


Давайте решим пару практических задач на нашей области листа трапеции. Первая задача о том, как площадь рабочего листа трапеции дает нам длины сторон 15 и 4 и высоту 8 дюймов. Чтобы показать вам, как найти площадь этой трапеции, мы собираемся использовать нашу формулу: площадь равна длинному основанию плюс короткое основание, деленное на два, а затем умножаемое на высоту. В случае с номером один я знаю, что длинная сторона равна 15 дюймам, а короткая — 4 дюймам. Высота должна быть 8 дюймов, потому что эта пунктирная линия представляет собой расстояние между двумя параллельными сторонами.
Вторая задача, показывающая, как найти площадь трапеции 6-й класс на нашем листе площади трапеции, который мы собираемся использовать, чтобы показать вам, как найти площадь трапеции, номер два. Мы знаем, что наша формула: площадь равна основанию длинной стороны плюс основание короткой стороны, деленному на два, а затем умноженному на высоту. В случае задачи 2 на нашей области рабочего листа трапеции мы знаем, что длинная сторона равна 20, потому что это внешний край трапеции, и это дает нам 20.

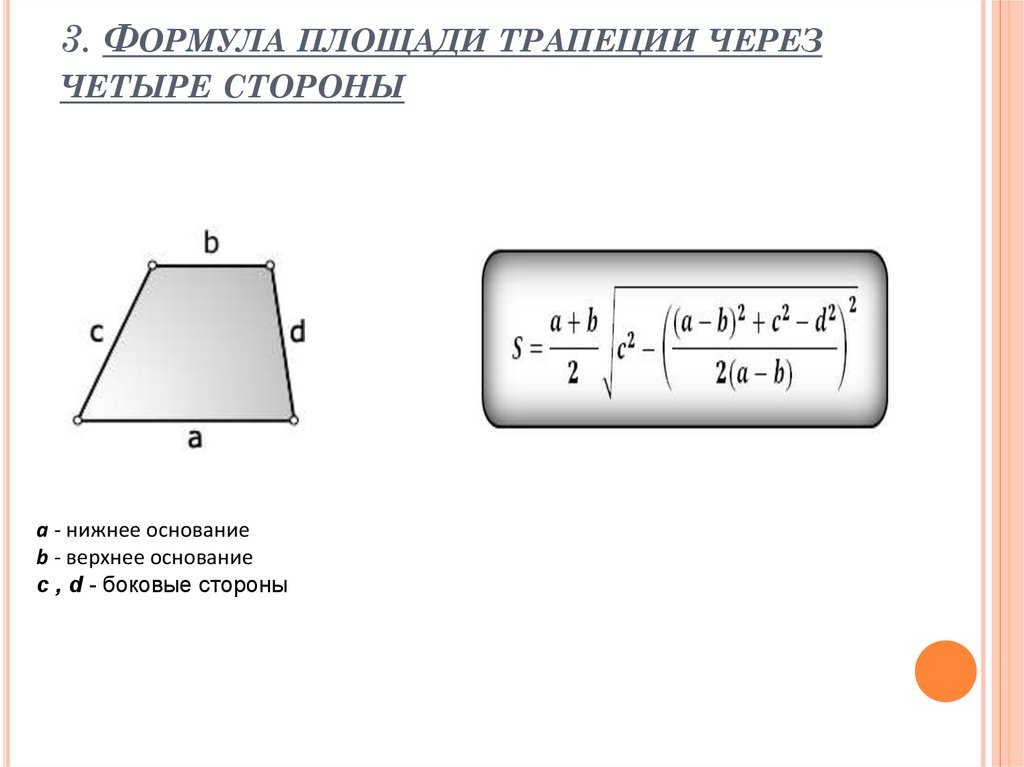 Формули довжини підстав через сторони, діагоналі і кут між ними:
Формули довжини підстав через сторони, діагоналі і кут між ними: Формула збоку через інші сторони, висоту і кут при нижньому підставі:
Формула збоку через інші сторони, висоту і кут при нижньому підставі: