| Развернуть структуру обучения | Свернуть структуру обучения |
| Формулы понижения степени тригонометрических функций sin cos tgПри решении тригонометрических уравнений часто необходимо понизить степень квадрата, куба функции sin cos tg. Иногда нужно понизить степень синуса, косинуса или тангенса даже четвертой степени. В таком случае можно воспользоваться следующими тригонометрическими тождествами, которые понижают степень тригонометрической функции до обычного синуса, косинуса или тангенса:Преобразования тригонометрических функций вида (α + a/bπ) и доказательство | Описание курса | Косинус двойного угла
|
| 1. | Формулы тригонометрии | 1 вид — рецептивный | лёгкое | 1 Б. | Даны различные тригонометрические формулы. Выбрать формулы понижения степени. |
| 2. | Применение формулы понижения степени (синус) | 1 вид — рецептивный | лёгкое | 1 Б. | Для выполнения данного задания необходимо применить формулу понижения степени. |
| 3. | Формула понижения степени (косинус) | 1 вид — рецептивный | лёгкое | 1 Б. | Необходимо воспользоваться формулой понижения степени (косинус). |
| 4. | 2 вид — интерпретация | лёгкое | 1 Б. | Для решения данного задания необходимо воспользоваться формулой понижения степени (косинус). | |
| 5. | Синус | 2 вид — интерпретация | среднее | 1 Б. | Упражнение выполняется, используя формулу понижения степени (синус). |
| 6. | Тангенс | 2 вид — интерпретация | среднее | 1 Б. | Применение формулы понижения степени (тангенс). |
| 7. | Использование тригонометрических формул | 3 вид — анализ | сложное | 1 Б. | Для решения данного задания необходимо воспользоваться основной тригонометрической формулой и формулой понижения степени. |
| 8. | Использование формул понижения степени | 3 вид — анализ | сложное | 1 Б. | Для решения данного задания необходимо воспользоваться двумя формулами понижения степени. |
| 9. | Вычисление значения выражения | 3 вид — анализ | сложное | 1 Б. | Вычисление значение выражения с использованием формулы понижения степени. |
Понижение степени
Определение 1
Тригонометрические формулы понижения степени — это формулы, используемые для того чтобы осуществлять перевод тригонометрического выражения, содержащего степень, в тождественное ему, содержащее меньшую степень.
Формулы понижения степени косинуса и синуса выводятся из формул двойного аргумента, выведем их для практики. Сделаем это сначала для синуса:
$\sin2x= \sin(x+x)$
К данному выражению можно применить формулу синуса суммы вида
$\sin(x+y) = \sin x \cos y + \cos x \cdot \sin y$, имеем:
$\sin2x = 2\sin x \cdot \cos x$ — данная формула называется формулой двойного аргумента для синуса.
Выразим также формулу двойного аргумента для косинуса:
$\cos2x= \cos(x+x)$
Применим к полученному выражению формулу косинуса суммы, она выглядит так — $\cos(x+y)= \cos x \cdot \cos y-\sin x \cdot \sin y$:
$\cos2x=\cos^2x-\sin^2x\left(1\right)$ — формула двойного аргумента для косинуса.
Теперь для того чтобы перейти к понижению степени, применим формулу двойного аргумента к выражению $\cos x$, получим:
Готовые работы на аналогичную тему
$\cos x= \cos^2(\frac{x}{2})-\sin^2(\frac{x}{2})\left(2\right)$
Воспользуемся основным тригонометрическим тождеством и выразим через него квадрат косинуса половинного угла:
$\cos(\frac{x}{2})=1-\sin(\frac{x}{2})\left(3\right)$
Подставим выражение $(3)$ в $(2)$ вместо квадрата косинуса половинного аргумента:
$\cos x= 1 – \sin^2(\frac{x}{2})- \sin^2(\frac{x}{2})$
$\cos x= 1 – 2\sin^2(\frac{x}{2})$
Выразим квадрат синуса:
$\sin^2(\frac{x}{2})=\frac{1-\cos x}{2}\left(4\right)$
Полученная формула называется формулой понижения степени синуса.
Сделаем тоже самое для косинуса, для этого выразим из тригонометрического тождества квадрат синуса половинного аргумента $\sin^2(\frac{x}{2})=1-\cos^2(\frac{x}{2})$ и затем подставим в выражение $(2)$, имеем:
$\cos x=\cos^2(\frac{x}{2})-1+\cos^2(\frac{x}{2})$
$\cos x=2\cos^2(\frac{x}{2})-1$
Теперь выразим квадрат косинуса половинного аргумента:
$\cos^2(\frac{x}{2})=\frac{\cos x+1}{2}\left(5\right)$
Данная формула носит название формулы понижения степени косинуса.
Формулы $(4)$ и $(5)$ также иногда называют формулами половинного аргумента. Используя их, можно вывести формулы понижения степени для квадратов тангенса и котангенса половинного аргумента:
$tg^2(\frac{x}{2})=\frac{\sin^2(\frac{x}{2})}{\cos^2(\frac{x}{2})}=\frac{1-\cos x}{1+\cos x}$;
$ctg^2\frac{x}{2}=\frac{\cos^2(\frac{x}{2}0}{\sin^2(\frac{x}{2})}=\frac{1+\cos x}{1-\cos x}$.
Замечание 1
В случае тангенса и котангенса стоит помнить о том, что данные записи имеют смысл лишь в том случае, если в знаменателе не получается нуль.
Пример 1
Докажите, что выражение верное:
$\sin^2(\frac{π}{4}+x)=\frac{1+\sin2x}{2}$
Применим к левой части равенства формулу понижения степени для синуса:
$\sin^2(\frac{π}{4}+x)=\frac{1-\cos(2 \cdot (\frac{π}{4}+x))}{2}$
Используем формулу разложения косинуса суммы к куску $\cos(2 \cdot (\frac{π}{4}+x)$:
$\cos(2 \cdot (\frac{π}{4}+x)=\cos (\frac{π}{2}+ 2x)=\cos\frac{π}{2} \cdot \cos2x — \sin\frac{π}{2} \cdot \sin2x =0-1 \cdot \sin2x= — \sin2x$
Используем полученное и подставим в наше равенство:
$\sin^2(\frac{π}{4}+x)=\frac{1+sin2x}{2}$
Равенство выполняется, что и требовалось доказать.
Тригонометрия — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Некоторые рекомендации к выполнению тригонометрических преобразований
К оглавлению…
При выполнении тригонометрических преобразований следуйте следующим советам:
- Не пытайтесь сразу придумать схему решения примера от начала до конца.
- Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
- Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
- Верьте, что всё будет хорошо.
Основные тригонометрические формулы
К оглавлению…
Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла. Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Дополнительные тригонометрические формулы
К оглавлению…
Тригонометрические формулы сложения. Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:
Разность синусов:

Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени. Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла. Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
К оглавлению…
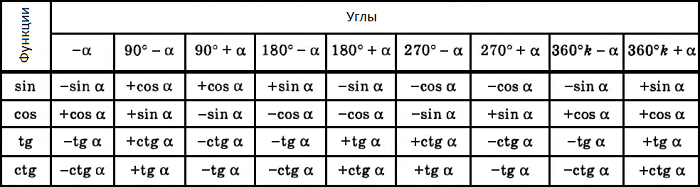
Функцию косинус называют кофункцией функции синус и наоборот. Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:
- Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
- Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
- При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т.е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
К оглавлению…
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:
- Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
- Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения, привести дроби к общему знаменателю и так далее.
- При решении тригонометрических уравнений можно применять метод группировки. При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали.
- Применяя метод замены переменной, как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
- Помните, что однородные уравнения часто встречаются и в тригонометрии.
- Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
- Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней). Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
?Тригонометрические формулы (более 100 шт.)
На этой странице вы найдете все основные тригонометрические формулы, которые помогут вам решать многие упражнения, значительно упростив само выражение.
Тригонометрические формулы — математические равенства для тригонометрических функций, которые выполняются при всех допустимых значениях аргумента.
Формулами задаются соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом, котангенсом.
Синус угла – это координата y точки (ордината) на единичной окружности. Косинус угла – это координата x точки (абсцисса).
Тангенс и котангенс – это, соответственно, соотношения синуса к косинусу и наоборот.
`sin \ \alpha, \ cos \ \alpha`
`tg \ \alpha=\frac{sin\ \alpha}{cos \ \alpha},` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac{cos\ \alpha}{sin\ \alpha},` ` \alpha\ne\pi+\pi n, \ n \in Z`
И две, которые используются реже – секанс, косеканс. Они обозначают соотношения 1 к косинусу и синусу.
`sec \ \alpha=\frac{1}{cos\ \alpha},` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac{1}{sin \ \alpha},` ` \alpha\ne\pi+\pi n,\ n \in Z`
Из определений тригонометрических функций видно, какие знаки они имеют в каждой четверти. Знак функции зависит только от того, в какой из четвертей располагается аргумент.

Содержание статьи:
Тригонометрические функции угла `(-\alpha)`
При изменении знака аргумента с «+» на «-» только функция косинус не меняет своего значения. Она называется четной. Ее график симметричен относительно оси ординат.
Остальные функции (синус, тангенс, котангенс) нечетные. При смене знака аргумента с «+» на «-» их значение также изменяется на отрицательное. Их графики симметричны относительно начала координат.
`sin(-\alpha)=-sin \ \alpha`
`cos(-\alpha)=cos \ \alpha`
`tg(-\alpha)=-tg \ \alpha`
`ctg(-\alpha)=-ctg \ \alpha`
Основные тригонометрические тождества
Основные тригонометрические тождества – это формулы, устанавливающие связь между тригонометрическими функциями одного угла (`sin \ \alpha, \ cos \ \alpha, \ tg \ \alpha, \ ctg \ \alpha`) и которые позволяют находить значение каждой из этих функций через любую известную другую.
`sin^2 \alpha+cos^2 \alpha=1`
`tg \ \alpha \cdot ctg \ \alpha=1, \ \alpha\ne\frac{\pi n} 2, \ n \in Z`
`1+tg^2 \alpha=\frac 1{cos^2 \alpha}=sec^2 \alpha,` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`1+ctg^2 \alpha=\frac 1{sin^2 \alpha}=cosec^2 \alpha,` ` \alpha\ne\pi n, \ n \in Z`
Формулы суммы и разности углов тригонометрических функций
Формулы сложения и вычитания аргументов выражают тригонометрические функции суммы или разности двух углов через тригонометрические функции этих углов.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac{tg \ \alpha+tg \ \beta}{1-tg \ \alpha\ tg \ \beta}`
`tg(\alpha-\beta)=\frac{tg \ \alpha-tg \ \beta}{1+tg \ \alpha \ tg \ \beta}`
`ctg(\alpha+\beta)=\frac{ctg \ \alpha \ ctg \ \beta-1}{ctg \ \beta+ctg \ \alpha}`
`ctg(\alpha-\beta)=\frac{ctg \ \alpha\ ctg \ \beta+1}{ctg \ \beta-ctg \ \alpha}`
Формулы двойного угла
`sin \ 2\alpha=2 \ sin \ \alpha \ cos \ \alpha=` `\frac {2 \ tg \ \alpha}{1+tg^2 \alpha}=\frac {2 \ ctg \ \alpha}{1+ctg^2 \alpha}=` `\frac 2{tg \ \alpha+ctg \ \alpha}`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \ sin^2 \alpha=2 \ cos^2 \alpha-1=` `\frac{1-tg^2\alpha}{1+tg^2\alpha}=\frac{ctg^2\alpha-1}{ctg^2\alpha+1}=` `\frac{ctg \ \alpha-tg \ \alpha}{ctg \ \alpha+tg \ \alpha}`
`tg \ 2\alpha=\frac{2 \ tg \ \alpha}{1-tg^2 \alpha}=` `\frac{2 \ ctg \ \alpha}{ctg^2 \alpha-1}=` `\frac 2{ \ ctg \ \alpha-tg \ \alpha}`
`ctg \ 2\alpha=\frac{ctg^2 \alpha-1}{2 \ ctg \ \alpha}=` `\frac { \ ctg \ \alpha-tg \ \alpha}2`
Формулы тройного угла
`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac{3 \ tg \ \alpha-tg^3 \alpha}{1-3 \ tg^2 \alpha}`
`ctg \ 3\alpha=\frac{ctg^3 \alpha-3 \ ctg \ \alpha}{3 \ ctg^2 \alpha-1}`
Формулы половинного угла
`sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`
`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`
`tg \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}=` `\frac {sin \ \alpha}{1+cos \ \alpha}=\frac {1-cos \ \alpha}{sin \ \alpha}`
`ctg \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}=` `\frac {sin \ \alpha}{1-cos \ \alpha}=\frac {1+cos \ \alpha}{sin \ \alpha}`
Формулы половинных, двойных и тройных аргументов выражают функции `sin, \ cos, \ tg, \ ctg` этих аргументов (`\frac{\alpha}2, \ 2\alpha, \ 3\alpha,… `) через эти ж функции аргумента `\alpha`.
Вывод их можно получить из предыдущей группы (сложения и вычитания аргументов). Например, тождества двойного угла легко получить, заменив `\beta` на `\alpha`.
Формулы понижения степени
Формулы квадратов (кубов и т. д.) тригонометрических функций позволяют перейти от 2,3,… степени к тригонометрическим функциям первой степени, но кратных углов (`\alpha, \ 3\alpha, \ …` или `2\alpha, \ 4\alpha, \ …`).
`sin^2 \alpha=\frac{1-cos \ 2\alpha}2,` ` (sin^2 \frac \alpha 2=\frac{1-cos \ \alpha}2)`
`cos^2 \alpha=\frac{1+cos \ 2\alpha}2,` ` (cos^2 \frac \alpha 2=\frac{1+cos \ \alpha}2)`
`sin^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}4`
`cos^3 \alpha=\frac{3cos \ \alpha+cos \ 3\alpha}4`
`sin^4 \alpha=\frac{3-4cos \ 2\alpha+cos \ 4\alpha}8`
`cos^4 \alpha=\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`
Формулы суммы и разности тригонометрических функций
Формулы являют собой преобразования суммы и разности тригонометрических функций разных аргументов в произведение.
`sin \ \alpha+sin \ \beta=` `2 \ sin \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`sin \ \alpha-sin \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2`
`cos \ \alpha+cos \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2=` `2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\beta-\alpha}2`
`tg \ \alpha \pm tg \ \beta=\frac{sin(\alpha \pm \beta)}{cos \ \alpha \ cos \ \beta}`
`ctg \ \alpha \pm ctg \ \beta=\frac{sin(\beta \pm \alpha)}{sin \ \alpha \ sin \ \beta}`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac{cos(\alpha \mp \beta)}{cos \ \alpha \ sin \ \beta}`
Здесь происходит преобразование сложения и вычитаний функций одного аргумента в произведение.
`cos \ \alpha+sin \ \alpha=\sqrt{2} \ cos (\frac{\pi}4-\alpha)`
`cos \ \alpha-sin \ \alpha=\sqrt{2} \ sin (\frac{\pi}4-\alpha)`
`tg \ \alpha+ctg \ \alpha=2 \ cosec \2\alpha;` `tg \ \alpha-ctg \ \alpha=-2 \ ctg \2\alpha`
Следующие формулы преобразовывают сумму и разность единицы и тригонометрической функции в произведение.
`1+cos \ \alpha=2 \ cos^2 \frac{\alpha}2`
`1-cos \ \alpha=2 \ sin^2 \frac{\alpha}2`
`1+sin \ \alpha=2 \ cos^2 (\frac {\pi} 4-\frac{\alpha}2)`
`1-sin \ \alpha=2 \ sin^2 (\frac {\pi} 4-\frac{\alpha}2)`
`1 \pm tg \ \alpha=\frac{sin(\frac{\pi}4 \pm \alpha)}{cos \frac{\pi}4 \ cos \ \alpha}=` `\frac{\sqrt{2} sin(\frac{\pi}4 \pm \alpha)}{cos \ \alpha}`
`1 \pm tg \ \alpha \ tg \ \beta=\frac{cos(\alpha \mp \beta)}{cos \ \alpha \ cos \ \beta};` ` \ ctg \ \alpha \ ctg \ \beta \pm 1=\frac{cos(\alpha \mp \beta)}{sin \ \alpha \ sin \ \beta}`
Формулы преобразования произведений функций
Формулы преобразования произведения тригонометрических функций с аргументами `\alpha` и `\beta` в сумму (разность) этих аргументов.
`sin \ \alpha \ sin \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}`
`sin\alpha \ cos\beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}`
`cos \ \alpha \ cos \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}`
`tg \ \alpha \ tg \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)} =` `\frac{tg \ \alpha + tg \ \beta}{ctg \ \alpha + ctg \ \beta}`
`ctg \ \alpha \ ctg \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)} =` `\frac{ctg \ \alpha + ctg \ \beta}{tg \ \alpha + tg \ \beta}`
`tg \ \alpha \ ctg \ \beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}`
Универсальная тригонометрическая подстановка
Эти формулы выражают тригонометрические функции через тангенс половинного угла.
`sin \ \alpha= \frac{2tg\frac{\alpha}{2}}{1 + tg^{2}\frac{\alpha}{2}},` ` \alpha\ne \pi +2\pi n, n \in Z`
`cos \ \alpha= \frac{1 — tg^{2}\frac{\alpha}{2}}{1 + tg^{2}\frac{\alpha}{2}},` ` \alpha \ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac{2tg\frac{\alpha}{2}}{1 — tg^{2}\frac{\alpha}{2}},` ` \alpha \ne \pi +2\pi n, n \in Z,` ` \alpha \ne \frac{\pi}{2}+ \pi n, n \in Z`
`ctg \ \alpha = \frac{1 — tg^{2}\frac{\alpha}{2}}{2tg\frac{\alpha}{2}},` ` \alpha \ne \pi n, n \in Z,` `\alpha \ne \pi + 2\pi n, n \in Z`
Формулы приведения
Формулы приведения можно получить, используя такие свойства тригонометрических функций, как периодичность, симметричность, свойство сдвига на данный угол. Они позволяют функции произвольного угла преобразовать в функции, угол которых находится в пределе между 0 и 90 градусами.
Для угла (`\frac {\pi}2 \pm \alpha`) или (`90^\circ \pm \alpha`):
`sin(\frac {\pi}2 — \alpha)=cos \ \alpha;` ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha`
`cos(\frac {\pi}2 — \alpha)=sin \ \alpha;` ` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`
`tg(\frac {\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):
`sin(\pi — \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi — \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi — \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi — \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
Для угла (`\frac {3\pi}2 \pm \alpha`) или (`270^\circ \pm \alpha`):
`sin(\frac {3\pi}2 — \alpha)=-cos \ \alpha;` ` sin(\frac {3\pi}2 + \alpha)=-cos \ \alpha`
`cos(\frac {3\pi}2 — \alpha)=-sin \ \alpha;` ` cos(\frac {3\pi}2 + \alpha)=sin \ \alpha`
`tg(\frac {3\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {3\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {3\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {3\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Выражение одних тригонометрических функций через другие
`sin \ \alpha=\pm \sqrt{1-cos^2 \alpha}=` `\frac{tg \ \alpha}{\pm \sqrt{1+tg^2 \alpha}}=\frac 1{\pm \sqrt{1+ctg^2 \alpha}}`
`cos \ \alpha=\pm \sqrt{1-sin^2 \alpha}=` `\frac 1{\pm \sqrt{1+tg^2 \alpha}}=\frac {ctg \ \alpha}{\pm \sqrt{1+ctg^2 \alpha}}`
`tg \ \alpha=\frac {sin \ \alpha}{\pm \sqrt{1-sin^2 \alpha}}=` `\frac {\pm \sqrt{1-cos^2 \alpha}}{cos \ \alpha}=\frac 1{ctg \ \alpha}`
`ctg \ \alpha=\frac {\pm \sqrt{1-sin^2 \alpha}}{sin \ \alpha}=` `\frac {cos \ \alpha}{\pm \sqrt{1-cos^2 \alpha}}=\frac 1{tg \ \alpha}`
Тригонометрия в буквальном смысле переводится, как «измерение треугольников». Она начинает изучаться еще в школе, и продолжается более детально в ВУЗах. Поэтому основные формулы по тригонометрии нужны, начиная еще с 10 класса, а также для сдачи ЕГЭ. Они обозначают связи между функциями, а поскольку этих связей много, то и самых формул есть немало. Запомнить их все нелегко, да и не надо – при необходимости их все можно вывести.
Тригонометрические формулы применяются в интегральном исчислении, а также при тригонометрических упрощениях, вычислениях, преобразованиях.
Материалы по теме:
Поделиться с друзьями:
 Загрузка…
Загрузка…Дополнительные идентификаторы
Фундаментальные (базовые) идентичности, обсуждаемые в предыдущем разделе, включают только одну переменную. Следующие тождества, включающие две переменные, называются тождествами тригонометрического сложения .

Эти четыре идентификатора иногда называют идентификатором суммы для синуса , идентификатором разности для синуса , идентификатором суммы для косинуса и идентификатором разности для косинуса соответственно.Проверка этих четырех тождеств следует из основных тождеств и формулы расстояния между точками в прямоугольной системе координат. Пояснения к каждому этапу доказательства будут даны только для первых нескольких следующих примеров.
Пример 1 : преобразовать sin 80 ° cos 130 ° + cos 80 ° sin 130 ° в тригонометрическую функцию в одной переменной (рисунок 1).
Рисунок 1
Чертеж для примера 1.

Дополнительные тождества могут быть получены из тождеств суммы и разности для косинуса и синуса.
Пример 2: Убедитесь, что cos (180 ° — x ) = — cos x

Пример 3: Убедитесь, что cos (180 ° + x ) = — cos x

Пример 4: Убедитесь, что cos (360 ° — x ) = cos x

Предыдущие три примера проверяют три формулы, известные как формулы редукции для косинуса .Эти формулы сокращения полезны при переписывании косинусов углов, превышающих 90 °, как функций острых углов.
Пример 5: Убедитесь, что sin (180 ° — x ) = sin x

Пример 6: Убедитесь, что sin (180 ° + x ) = — sin x

Пример 7: Убедитесь, что sin (360 ° — x ) = — sin x

Предыдущие три примера проверяют три формулы, известные как формулы редукции для синуса .Эти формулы сокращения полезны при переписывании синусов углов, превышающих 90 °, в зависимости от острых углов.
Напомним, что ниже приведены формулы сокращения (тождества) для синуса и косинуса. Они действительны как для градуса, так и для радиана.

Пример 8: Убедитесь, что sin 2 x = 2 sin x cos x .

Пример 9: Запишите cosβcos (α — β) — sinβsin (α — β) как функцию одной переменной.

Пример 10: Запишите cos 303 ° в форме sinβ, где 0 <β <90 °.

Пример 11: Запишите sin 234 ° в виде cos 0 <β <90 °.

Пример 12: Найдите sin (α + β), если sin (α + β), если sin α =  и α и β — углы четвертого квадранта.
и α и β — углы четвертого квадранта.
Сначала найдите cos α и sin β. В четвертом квадранте синус отрицательный, а косинус положительный.

Другие формы формулы двойного угла косинуса — Концепция
Формула двойного угла косинуса: cos (2theta) = cos2 (theta) — sin2 (theta). Комбинируя эту формулу с тождеством Пифагора, cos2 (theta) + sin2 (theta) = 1, появляются две другие формы: cos (2theta) = 2cos2 (theta) -1 и cos (2theta) = 1-2sin2 (theta). Их можно использовать для поиска формул снижения мощности, которые уменьшают триггерные функции второй степени или выше до первой степени. Эти формулы очень полезны в математическом анализе.
Я хочу поговорить о других формах тождеств двойного угла косинуса. Во-первых, давайте вспомним пифагорейскую идентичность и две другие ее формы. Косинус в квадрате плюс синус в квадрате равняется 1, также можно записать косинус в квадрате тета, равный 1 минус синус в квадрате тета или синус в квадрате тета, равный 1 минус косинус в квадрате тета. Теперь исходная формула двойного угла косинуса такова: косинус 2 тета равен квадрату косинуса тета минус синус квадрат тета, но я могу использовать свои пифагоровы тождества, чтобы переписать это, так что другой формой будет косинус ой косинус 2 тета равен альфа косинус тета I ‘ Я заменю его на 1 минус синус в квадрате тета минус синус тета синус в квадрате тета, и это 1 минус 2 синус в квадрате тета, так что это вторая форма, косинус 2 тета равен 1 минус 2 синус в квадрате тета, но мы также можем сделать косинус 2 тета равным и начать отсюда я могу заменить синус в квадрате на 1 минус косинус, поэтому я получаю косинус в квадрате тета минус 1 минус синус в квадрате тета и минус распределяется, я получаю минус 1, извините, это должен быть косинус, поехали, наш минус 1 распределяет мы получаем минус 1 и минус минус плюс косинус в квадрате тета, поэтому косинус в квадрате тета минус 1 плюс косинус в квадрате тета равен 2, косинус в квадрате тета минус 1, они очень похожи.Косинус 2 тета равен 1 минус 2, синус в квадрате тета, косинус 2 тета равен 2 косинусу в квадрате минус 1.
Чтобы запомнить, какой из них является, запомните исходную формулу двойного угла косинуса. в других формах синус остается отрицательным, а косинус — положительным.
Инструменты и ресурсы: Глоссарий по тригонометрии | Подготовка к экзамену
AAS ссылка на решение треугольника с учетом размера двух углов и длины не включенной стороны.абсолютное значение комплексного числа квадратный корень из суммы квадратов его действительного и мнимого коэффициентов.
алгебраический вектор упорядоченная пара чисел, представляющая конечную точку стандартного вектора.
амплитуда комплексного числа то же, что аргумент комплексного числа.
амплитуда вертикальный отрезок функции.
угол мера вращения.
угол наклона угол, измеренный ниже горизонтали.
угол возвышения угол, измеренный над горизонтом.
угловая скорость , определяемая через угол поворота и время.
аргумент комплексного числа угол, образованный между положительной осью x и отрезком линии между началом координат и числом.
ASA ссылка на решение треугольника с учетом меры двух углов и длины включенной стороны.
ASTC аббревиатура, обозначающая, какие тригонометрические функции положительны в квадрантах I, II, III и IV соответственно.
асимптоты строк, представляющих неопределенные значения для тригонометрических функций.
пеленг угол, измеренный по часовой стрелке от направления на север к вектору.
круговых функций функций, область значений которых — углы, измеренные в радианах, а диапазоны — значения, соответствующие аналогичным тригонометрическим функциям.
тождества функций фундаментальных тождества, которые включают основные триггерные функции дополнительных углов.
совместных функций пары тригонометрических функций дополнительных углов, тригонометрические отношения которых равны.
комплексная плоскость система координат для комплексных чисел.
составляющих вектора горизонтальных и вертикальных составляющих вектора данного вектора.
компоненты алгебраического вектора упорядоченная пара чисел, представляющая вектор.
компоненты отдельные векторы, которые объединяются для получения результирующего вектора.
условное уравнение уравнение, действительное для ограниченного числа значений переменной.
условные тригонометрические уравнения верны только для ограниченного числа значений замены.
Сопряжение комплексного числа то же, что и исходное, за исключением знака мнимой составляющей.
косеканс — величина, обратная синусоидальной функции.
косинус тригонометрическое отношение, равное смежной стороне, деленной на гипотенузу.
котангенс величина, обратная тангенциальной функции.
coterminal два угла в стандартном положении, которые имеют общую сторону вывода.
Теорема Де Муавра теорема о степенях комплексных чисел.
градуса единица измерения угла, равная 1/360 оборота.
разностных тождеств для касательных тождеств, включающих тангенсы разностей углов.
тождество разности для косинуса одно из тождеств тригонометрического сложения.
тождество разницы для синуса одно из тригонометрических тождеств сложения.
направленный линейный сегмент линейный сегмент заданной длины и заданного направления.
скалярное произведение процесс объединения двух векторов, дающий одно число.
двойные углы для тангенса полезны при написании триггерных функций, включающих двойные углы как функции одинарных чисел.
двойных углов полезно при написании триггерных функций, включающих двойные углы, как триггерные функции одинарных углов.
эквивалентных векторов два вектора одинаковой величины и направления.
четная функция функция даже если f (-x) = f (x).
общее решение решений, определенных для всего домена.
геометрический вектор величина, которая может быть представлена направленным отрезком линии.
Идентификаторы половинного угла для тангенса полезны при написании триггерных функций, включающих половинные углы как функции отдельных углов.
Идентификаторы полууглов полезны при написании триггерных функций, включающих половинные углы, как триггерные функции единичных углов.
Формула Герона формула для определения площади треугольника по длинам трех сторон.
тождества для негативов основных тождеств, включающих основные триггерные функции отрицательных углов.
тождество уравнение, составленное из тригонометрических функций угла, которое действительно для всех значений угла. Также называется тригонометрическим тождеством.
мнимая ось ось в комплексной плоскости.
начальная точка начальная точка вектора.
начальная сторона сторона угла, с которой начинается измерение угла.
функция обратного косеканса , определенная в терминах ограниченной синусоидальной функции.
функция обратного косинуса функция обратного ограниченного косинуса.
функция обратного котангенса , определенная в терминах ограниченной функции тангенса.
обратное обозначение обозначение, используемое для выражения угла через значение тригонометрических функций.
функция обратной секущей , определенная в терминах функции ограниченного косинуса.
обратная синусоидальная функция обратная синусоидальной функции с ограничениями.
функция обратной тангенса функция, обратная ограниченной касательной.
закон косинусов соотношение между длинами трех сторон треугольника и косинусом одного из углов.
закон синусов соотношение между соотношением синусов углов треугольника и стороны, противоположной этим углам.
линейная интерполяция метод аппроксимации значений в таблице с использованием значений соседних таблиц.
линейная скорость определяется длиной дуги и времени.
величина вектора длина линейного сегмента.
математическая индукция метод математического доказательства.
максимальное значение максимальное значение функции в заданном интервале.
минимальное значение наименьшее значение функции в заданном интервале.
минута измерение угла, равное 1/60 градуса.
модуль комплексного числа то же, что и модуль комплексного числа.
отрицательный угол получается при вращении по часовой стрелке.
норма другое название величины вектора.
Теорема о корне n-й степени — расширение теоремы Де Муавра, включающее корни комплексных чисел.
нечетная функция функция нечетная из f (-x) = -f (x).
нечетно-четных тождеств фундаментальных тождества, которые включают основные триггерные функции отрицательных углов. Также называется тождеством для негативов.
один к одному характеристика функций, в которых каждый элемент в домене является парами с одним и только одним элементом в диапазоне и наоборот.
ортогонально перпендикулярно.
правило параллелограмма процесс, используемый для сложения двух непараллельных векторов.
период наименьшее значение q такое, что f (x) = f (x + q), где f (x) — периодическая функция.
периодических функций тригонометрических функций, значения которых повторяются один раз за каждый период.
фазовый сдвиг горизонтальное смещение функции вправо или влево от вертикальной оси.
полярная ось луч, идущий от полюса в полярной системе координат.
полярная система координат система координат, использующая расстояние и угол для позиции.
полярные координаты упорядоченная пара, состоящая из радиуса и угла.
полюс фиксированный центр полярной системы координат.
вектор позиции другое имя стандартного вектора.
положительный угол получается в результате вращения против часовой стрелки.
основных решений решений, определенных в ограниченной области.
главный корень n-й степени унарный корень комплексного числа.
тождества произведения-суммы полезны при записи произведения триггерных функций как суммы и разности триггерных функций.
проекции другое название векторов компонентов, горизонтальных и вертикальных векторов компонентов данного вектора.
удостоверение личности подтверждение действительности одного удостоверения с использованием ранее известных фактов.
тождества Пифагора фундаментальных тождества, которые связывают функции синуса и косинуса и теорему Пифагора.
Угол квадранта Угол в стандартном положении с его конечной стороной на оси координат.
частных тождеств фундаментальных идентичностей, которые включают частное основных триггерных функций.
радиан мера угла с вершиной в центре окружности, которая образует дугу, равную радиусу окружности.
радиус-вектор другое название стандартного вектора, вектора в стандартной позиции.
действительная ось ось в комплексной плоскости.
взаимных идентификатора основных идентификатора, которые включают обратные значения базовых триггерных функций.
формулы редукции для косинуса , полезные при переписывании косинусов углов больше 90 ° как функций острых углов.
формулы приведения для синуса , полезные для переписывания синусов углов больше 90 ° как функций острых углов.
Формулы редукции для тангенса используются для переписывания касательных больше 90 ° как функций острых углов.
опорный угол острый угол, тригонометрические отношения которого совпадают (за исключением знака) с заданным углом.
результирующий вектор результат, полученный после обработки вектора.
SAS ссылка на решение треугольника с учетом длины двух сторон и меры включенного угла.
скалярное умножение изменение величины вектора без изменения его направления.
скалярное умножение алгебраических векторов процесс умножения компонент вектора.
скалярная величина значение скалярного произведения двух векторов.
секанс величина, обратная функции косинуса.
секунда измерение угла, равное 1/60 минуты.
сектор часть окружности, заключенная между центральным углом и прилегающей к нему дугой.
полупериметр половина периметра треугольника.
подобных треугольника два треугольника, угловые размеры которых совпадают.
простое гармоническое движение компонент равномерного кругового движения.
синус тригонометрическое отношение, равное противоположной стороне, деленной на гипотенузу.
решение треугольника процесс нахождения значений сторон и углов треугольника по значениям остальных сторон и углов.
SSA ссылка на решение треугольника с учетом длины двух сторон и меры невключенного угла.
SSS ссылка на решение треугольника с учетом длин трех сторон.
стандартное положение (угол) угол с его начальной стороной на положительной оси x и вершиной в начале координат.
стандартная позиция (вектор) вектор, который был переведен так, что его начальная точка находится в начале координат.
стандартный вектор вектор в стандартном положении.
статическое равновесие сумма всех векторов сил равна нулю.
тождеств сумм для касательных тождеств, содержащих касательные сумм углов.
тождество суммы для косинуса одно из тождеств тригонометрического сложения.
тождество суммы для синуса одно из тригонометрических тождеств сложения.
тождества сумма-произведение используется для записи суммы и разности триггерных функций как произведения триггерных функций.
касательная тригонометрическое отношение, равное делению противоположной стороны на соседнюю.
конечная точка конечная точка вектора.
сторона клеммы сторона угла, на которой заканчивается измерение угла.
правило кончика хвоста процесс сложения векторов.
тригонометрических сложения тождеств тождеств, включающих тригонометрические функции сумм и разностей углов.
тригонометрическая идентичность уравнение, составленное из тригонометрических функций угла, которое действительно для всех значений угла.
тригонометрические отношения отношения длины двух сторон прямоугольного треугольника.
равномерное круговое движение круговое движение вокруг точки с равномерной линейной и угловой скоростью.
единичный круг круг с радиусом в одну единицу.
сложение векторов процесс объединения двух векторов.
векторное количество количество, которое имеет размер и направление.
вектор скорости вектор, представляющий скорость и направление движущегося объекта.
вертикальное смещение вертикальное смещение функции выше или ниже горизонтальной оси.
нулевой алгебраический вектор алгебраический вектор, обе компоненты которого равны нулю.
нулевой вектор вектор с нулевой величиной и любым направлением.
,