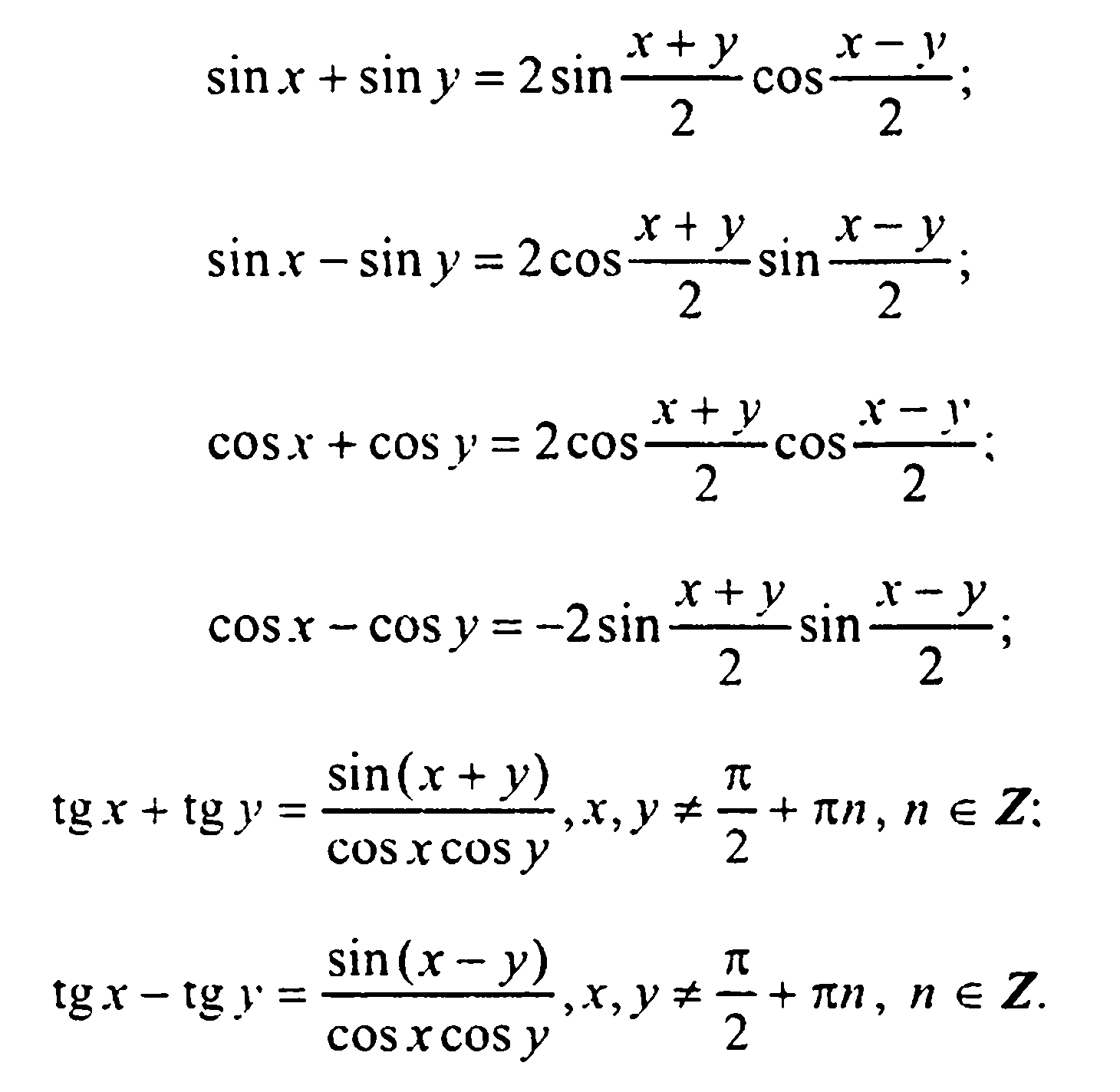Формула произведения тригонометрических функций.
Алгебра. 10 класс. Параграф 32. Тест 2.
Вариант I.
1. Упростить: sin75°sin15°.
А) 0,25; В) 0,5; С) 1; D) -0,5.
2. Упростить: cos40°cos20°.
3. Преобразовать в сумму: sin(30°+x) ∙ cos(30°- x).
4. Вычислить произведение: sin15°cos75°.
5. Вычислить: sin 45° ∙ cos 15°.
6. Записать в виде суммы произведение синусов:
7. Представить в виде суммы произведение косинусов:
8. Запишите в виде суммы произведение:
9. Вычислить: sin 15°cos 7° – cos 11°cos 79°.
A) sin 8°; B) 0,5sin 8°; C) cos 22°;
10. Упростить выражение: 2cos 20°cos 40° – cos 20°.
А) -0,5; B) 0; C) 0,5; D) -1.
11. Вычислить: sin 10° ∙ sin 50° ∙ sin 70°.
12. Упростить: 8cos 10° ∙ cos 20° ∙ cos 40°.
A) ctg10°; B) tg10°; C) –tg10°; D) –ctg10°.
Вариант II.
1. Упростить: cos15°cos75°.
А) -0,25; В) 0,25; С) 1; D) -0,5.
2. Упростить: sin70°sin10°.
A) 0,25-0,5cos80°; B) 0,25-0,5cos10°; C)
0,25cos80°; D) 0,25.3. Преобразовать в сумму: sin(15°-x) ∙ cos(15°+x).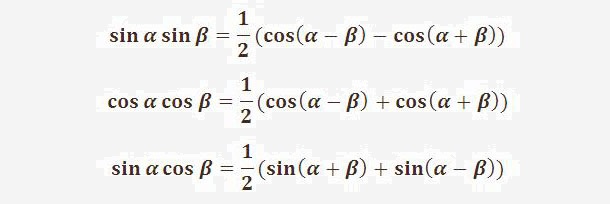
A) 0,25-0,5cos2x; B) 0,25-0,5sin2x; C) 0,25sin2x; D) 0,5.
4. Вычислить произведение: sin75°cos15°.
5. Вычислить: sin 15° ∙ cos 45°.
6. Записать в виде суммы произведение синусов:
7. Представить в виде суммы произведение косинусов:
A) 2; B) 1; C) 0; D) -1.
8. Запишите в виде суммы произведение:
A) 1; B) 0,5; C) 0; D) -0,5.
9. Вычислить: 2sin 16°cos 14° – 2sin 18°cos 12°.
10. Упростить выражение: 2cos 25°cos 35° – cos 10°.
А) -0,5; B) 0; C) 0,5; D) -1.
11. Вычислить: sin 10° ∙ cos 20° ∙ sin 50°.
12. Упростить: 8cos 20° ∙ cos 40° ∙ cos 80°.
A) 0,5; B) tg20°; C) tg10°; D) 1.
Сверить ответы.
Формулы преобразования произведения тригонометрических функций в сумму:
Формулы приведения:
1) cos(90° — α) = sinα; 2) sin(90° — α) = cosα;
3) cos(180° — α) = -cosα; 4) sin(180° — α) = sinα.
Формула синуса двойного аргумента:
sin2α = 2sinαcosα
В заданиях 11 и 12 используйте подходящую формулу приведения, а затем умножьте (и разделите, чтобы значение выражения не изменилось!) данное произведение на такое выражение, чтобы можно было применять формулу синуса двойного аргумента.
Поделиться новостью в соцсетях
Метки: алгебра 10 класс, тригонометрические формулы
Преобразование сумм тригонометрических функций в произведение (сумма и разность синусов) 10 класс онлайн-подготовка на
Введение.
Доказательство формулы суммы синусов
На уроке выводятся формулы суммы и разности синусов из формул синуса суммы аргументов и синуса разности аргументов, решается несколько примеров на использование этих формул. Также решается несколько примеров на преобразование суммтригонометрических функций в произведение.
Доказать:
Доказательство:
Складывая равенства, получим:
В полученной формуле вводятся удобные обозначения:
Выразим и через Складывая и вычитая равенства, получим
В новых обозначениях имеем:
Примеры на применение формулы суммы синусов
1. а)Упростить:
Решение:
Ответ:
б) Вычислить:
Решение:
1)
2)
Ответ:
Применение формулы при решении уравнений
2.
Решить уравнение: .
Решение:
Рис. 1. Рис. 2.
Решения второго уравнения (см. рис.2) содержатся в решении первого (см. рис.1), потому в ответ записываются только решения первого уравнения. Можно объяснить этот факт аналитически: формула уже содержит в себе , потому решения уравнения содержатся в решениях
Ответ:
Решение уравнения sinαx+sinβx=0 с помощью формулы суммы синусов
3. Решить уравнение:
Решение:
Ответ:
Доказательство формулы разности синусов
4. Доказать:
.
Доказательство:
Воспользуемся формулой суммы синусов и свойством нечетности синуса:
Применение формулы разности синусов
5. Упростить:
Решение:
Ответ:
6.
Вычислить:
Применение формулы разности синусов при решении уравнений
7. Решить уравнение:
Решение:
Рис. 1. Рис. 2.
Иллюстрацию расположения корней на единичной окружности смотри на рисунках 1-2.
Ответ:
Решение уравнений вида sinαx-sinβx=0
8. Решить уравнение:
Решение:
Ответ:
Итог урока
1)
2)
и
На уроке рассматривались формулы, по которым сумма и разность синусов преобразовывается в произведение, и решались некоторые задачи.
На следующем уроке будут рассмотрены формулы, по которым сумму и разность косинусов можно преобразовать в произведение.
Список рекомендованной литературы
1.
Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).
-М.: Дрофа, 2002.
8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics.ru (Источник).
2. Портал Естественных Наук (Источник).
3. Интернет-портал exponenta.ru (Источник).
Сделай дома
№№ 22.1(б, в), 22.3, 22.5(а) (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
комплексный анализ — Доказательство формулы произведения для функции синуса
спросил
Изменено 1 год, 8 месяцев назад
Просмотрено 981 раз
$\begingroup$
Я ищу простой способ доказать $$\frac{\sin\pi z}{\pi z}=\prod_{n=1}^\infty \left(1-\frac{z^2} {n^2}\right)$$, используя в основном тот факт, что вся функция имеет простые нули при $n=\pm 1, \pm 2,\cdots$.
и проинтегрируем обе части. Для доказательства этого уравнения рассмотрим функцию $f(z) = \frac{\cot z}{z(z — 1)}$, а затем воспользуемся исчислением остатков.
$\endgroup$
2
$\begingroup$
Для доказательства мы воспользуемся теоремой Хардамара о факторизации (см. https://en.wikipedia.org/wiki/Weierstrass_factorization_theorem#Hadamard_factorization_theorem). 92}\справа).$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.