Функция распределения вероятностей нормального закона: НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ • Большая российская энциклопедия

Теория вероятностей

Теория вероятностей

Вентцель Е.С. Теория вероятностей: Учеб. для вузов. — 6-е изд. стер. — М.: Высш. шк., 1999.— 576 c. Книга представляет собой один из наиболее известных учебников по теории вероятностей и предназначена для лиц, знакомых с высшей математикой и интересующихся техническими приложениями теории вероятностей. Она представляет также интерес для всех тех, кто применяет теорию вероятностей в своей практической деятельности. В книге уделено большое внимание различным приложениям теории вероятностей (теории вероятностных процессов, теории информации, теории массового обслуживания и др.). Оглавление Глава 1. Введение ПРЕДИСЛОВИЕ 1. 1. Предмет теории вероятностей Теория вероятностей: 1.2. Краткие исторические сведения Глава 2. Основные понятия теории вероятностей 2.1. Событие. Вероятность события 2.2. Непосредственный подсчет вероятностей 2.3. Частота, или статистическая вероятность, события 2.4. Случайная величина 2.5. Практически невозможные и практически достоверные события. Принцип практической универсальности Глава 3. Основные теоремы теории вероятностей 3.1. Назначение основных теорем. Сумма и произведение событий 3.2. Теорема сложения вероятностей 3.3. Теорема умножения вероятностей 3.4. Формула полной вероятности 3.5. Теорема гипотез (формула Бейеса) Глава 4. Повторение опытов 4.1. Частная теорема о повторении опытов 4.2. Общая теорема о повторении опытов Глава 5. Случайные величины и их законы распределения 5.1. Ряд распределения. Многоугольник распределения 5.2. Функция распределения 5.3. Вероятность попадания случайной величины на заданный участок 5. 4. Плотность распределения 5.5. Числовые характеристики случайных величин. Их роль и назначение 5.6. Характеристики положения (математическое ожидание, мода, медиана) 5.7. Моменты. Дисперсия. Среднее квадратичное отклонение 5.8. Закон равномерной плотности 5.9. Закон Пуассона Глава 6. Нормальный закон распределения 6.1. Нормальный закон распределения и его параметры 6.2. Моменты нормального распределения 6.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения 6.4. Вероятное (срединное) отклонение Глава 7. Определение законов распределения случайных величин на основе опытных данных 7.1. Основные задачи математической статистики 7.2. Простая статистическая совокупность. Статистическая функция распределения 7.3. Статистический ряд. Гистограмма 7.4 Числовые характеристики статистического распределения 7.5. Выравнивание статистических рядов 7.6. Критерии согласия Глава 8. Системы случайных величин 8.1. Понятие о системе случайных величин 8.2. Функция распределения системы двух случайных величин 8.3. Плотность распределения системы двух случайных величин 8.4. Законы распределения отдельных величин, входящих в систему. Условные законы распределения 8.5 Зависимые и независимые случайные величины 8.6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции 8.7. Система произвольного числа случайных величин 8.8. Числовые характеристики системы нескольких случайных величин Глава 9. Нормальный закон распределении дли системы случайных величин 9.1. Нормальный закон на плоскости 9.2 Эллипсы рассеивания. Приведение нормального закона к каноническому виду 9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания 9.4. Вероятность попадания в эллипс рассеивания 9.5. Вероятность попадания в область произвольной формы 9.6. Нормальный закон в пространстве трех измерений. Общая запись нормального закона для системы произвольного числа случайных величин Глава 10. Числовые характеристики функций случайных величин 10.1. Математическое ожидание функции. Дисперсия функции 10.2. Теоремы о числовых характеристиках 10.3. Применения теорем о числовых характеристиках Глава 11. Линеаризация функций 11.1. Метод линеаризации функций случайных аргументов 11.2. Линеаризация функции одного случайного аргумента 11.3. Линеаризация функции нескольких случайных аргументов 11.4. Уточнение результатов, полученных методом линеаризации Глава 12. Законы распределения функций случайных аргументов 12.1. Закон распределения монотонной функции одного случайного аргумента 12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону 12.3. Закон распределения немонотонной функции одного случайного аргумента 12.4. Закон распределения функции двух случайных величин 12.5. Закон распределения суммы двух случайных величин. Композиция законов распределения 12.6. Композиция нормальных законов 12.7. Линейные функции от нормально распределенных аргументов 12.8. Композиция нормальных законов на плоскости Глава 13. Предельные теоремы теории вероятностей 13.1. Закон больших чисел и центральная предельная теорема 13.2. Неравенство Чебышева 13.3. Закон больших чисел (теорема Чебышева) 13.4. Обобщенная теорема Чебышева. Теорема Маркова 13.5. Следствия закона больших чисел: теоремы Бернулли и Пуассона 13.6. Массовые случайные явления и центральная предельная теорема 13.7. Характеристические функции 13.8. Центральная предельная теорема для одинаково распределенных слагаемых 13.9. Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении Глава 14. Обработка опытов 14.1. Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения 14.2. Оценки для математического ожидания и дисперсии 14. 3. Доверительный интервал. Доверительная вероятность 14.4. Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону 14.5. Оценка вероятности по частоте 14.6. Оценки для числовых характеристик системы случайных величин 14.7. Обработка стрельб 14.8. Сглаживание экспериментальных зависимостей по методу наименьших квадратов Глава 15. Основные понятия теории случайных функций 15.1. Понятие о случайной функции 15.2. Понятие о случайной функции как расширение понятия о системе случайных величин. Закон распределения случайной функции 15.3. Характеристики случайных функций 15.4. Определение характеристик случайной функции из опыта 15.5. Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций 15.6. Линейные и нелинейные операторы. Оператор динамической системы 15.7. Линейные преобразования случайных функций 15.7.1. Интеграл от случайной функции 15. 7.2. Производная от случайной функции 15.8. Сложение случайных функций 15.9. Комплексные случайные функции Глава 16. Канонические разложения случайных функций 16.1. Идея метода канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций 16.2. Каноническое разложение случайной функции 16.3. Линейные преобразования случайных функций, заданных каноническими разложениями Глава 17. Стационарные случайные функции 17.1. Понятие о стационарном случайном процессе 17.2. Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий 17.3. Спектральное разложение стационарной случайной функции на бесконечном участке времени. Спектральная плотность стационарной случайной функции 17.4. Спектральное разложение случайной функции в комплексной форме 17.5. Преобразование стационарной случайной функции стационарной линейной системой 17.6. Применения теории стационарных случайных процессов к решению задач, связанных с анализом и синтезом динамических систем 17. 7. Эргодическое свойство стационарных случайных функций 17.8. Определение характеристик эргодической стационарной случайной функции по одной реализации Глава 18. Основные понятия теории информации 18.1. Предмет и задачи теории информации 18.2. Энтропия как мера степени неопределенности состояния физической системы 18.3. Энтропия сложной системы. Теорема сложения энтропий 18.4. Условная энтропия. Объединение зависимых систем 18.5. Энтропия и информация 18.6. Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии 18.7. Энтропия и информация для систем с непрерывным множеством состояний 18.8. Задачи кодирования сообщений. Код Шеннона-Фэно 18.9. Передача информации с искажениями. Пропускная способность канала с помехами Глава 19. Элементы теории массового обслуживания 19.1. Предмет теории массового обслуживания 19.2. Случайный процесс со счетным множеством состояний 19. 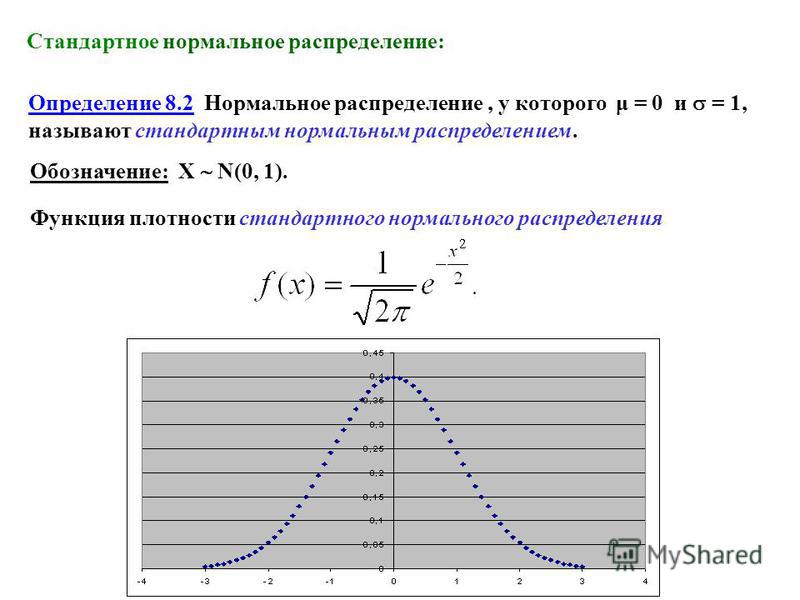3. Поток событий. Простейший поток и его свойства 19.4 Нестационарный пуассоновский поток 19.5. Поток с ограниченным последействием (поток Пальма) 19.6. Время обслуживания 19.7. Марковский случайный процесс 19.8. Система массового обслуживания с отказами. Уравнения Эрланга 19.9. Установившийся режим обслуживания. Формулы Эрланга 19.10. Система массового обслуживания с ожиданием 19.11. Система смешанного типа с ограничением по длине очереди Приложения Таблица 1 Значения нормальной функции распределения Таблица 2. Значения экспоненциальной функции Таблица 3. Значения нормальной функции Таблица 4. Значения “хи-квадрат” в зависимости от r и p Таблица 5. Значения удовлетворяющие равенству Таблица 6. Таблица двоичных логарифмов целых чисел от 1 до 100 Таблица 7. Таблица значений функции Таблица 8. Значения распределение Пуассона

Нормальный закон распределения непрерывной случайной величины

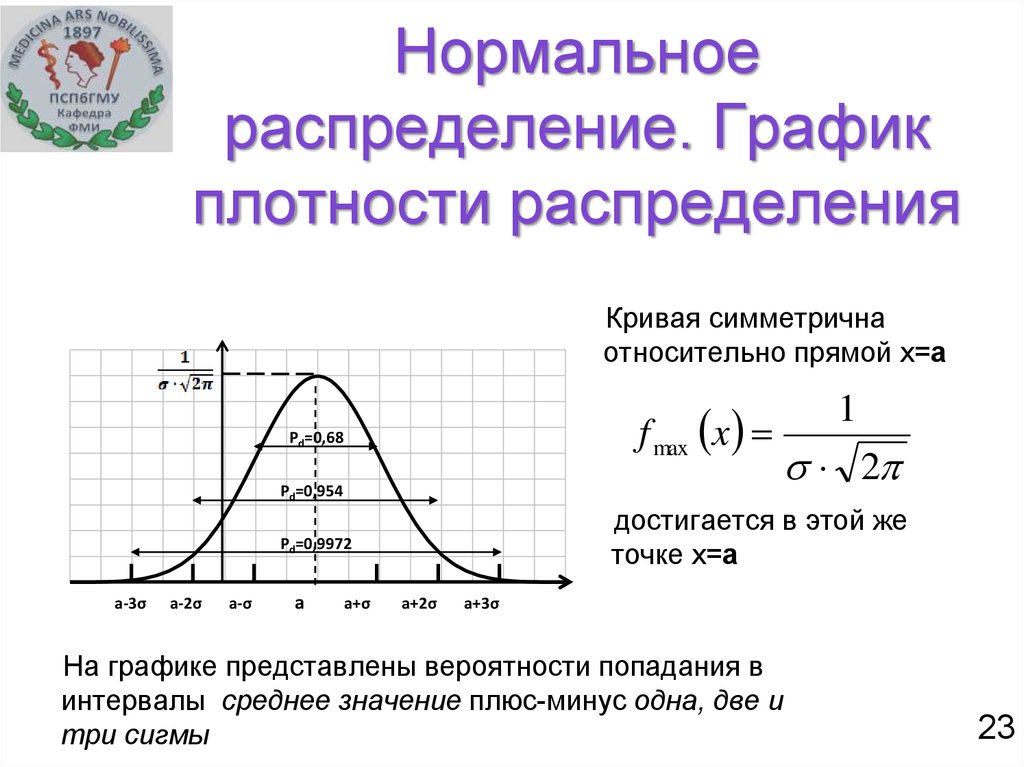
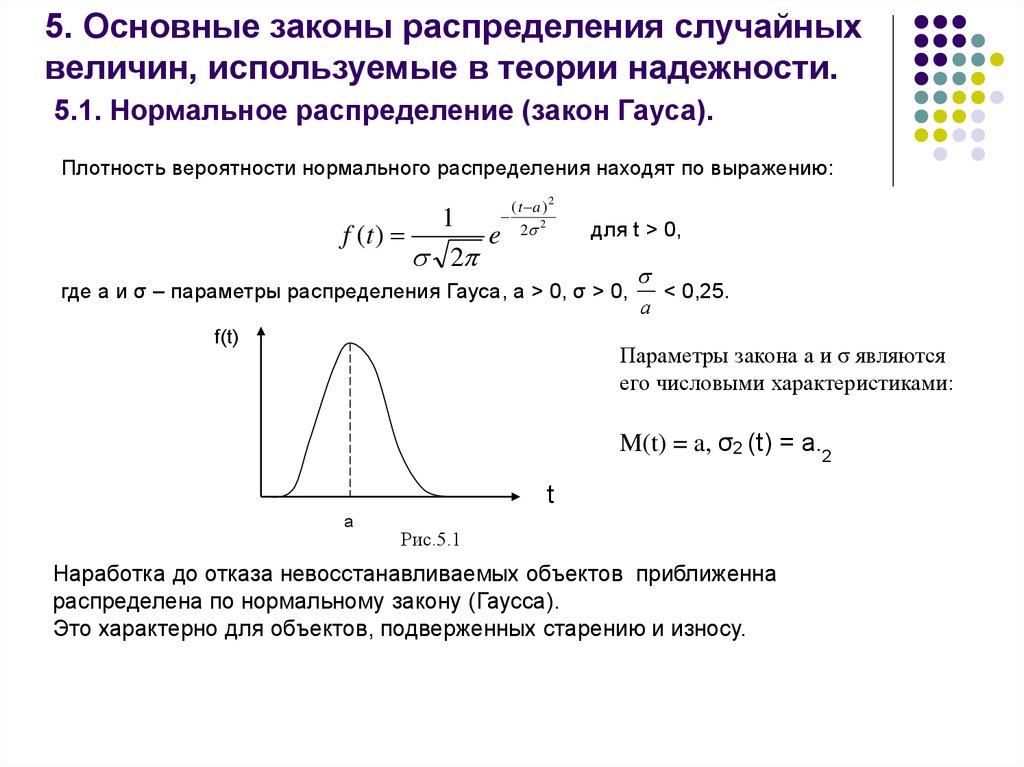
Как было сказано ранее, примерами распределений вероятностей непрерывной случайной величины Х являются: равномерное распределение вероятностей непрерывной случайной величины; показательное распределение вероятностей непрерывной случайной величины; нормальное распределение вероятностей непрерывной случайной величины. Дадим понятие нормального закона распределения, функции распределения такого закона, порядка вычисления вероятности попадания случайной величины Х в определенный интервал. № Показатель Нормальный закон распределения Примечание 1 Определение Нормальным называется распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид где mx – математическое ожидание случайной величины Х, σx – среднее квадратическое отклонение 2 Функция распределения 3 Вероятность попадания в интервал (а;b) — интегральная функция Лапласа 4 Вероятность того, что абсолютная величина отклонения меньше положительного числа δ при mx= 0 Пример решения задачи по теме «Нормальный закон распределения непрерывной случайной величины» Задача. Длина X некоторой детали представляет собой случайную величину, распределенную по нормальному закону распределения, и имеет среднее значение 20 мм и среднее квадратическое отклонение – 0,2 мм. Необходимо: а) записать выражение плотности распределения; б) найти вероятность того, что длина детали будет заключена между 19,7 и 20,3 мм; в) найти вероятность того, что величина отклонения не превышает 0,1 мм; г) определить, какой процент составляют детали, отклонение которых от среднего значения не превышает 0,1 мм; д) найти, каким должно быть задано отклонение, чтобы процент деталей, отклонение которых от среднего не превышает заданного, повысился до 54%; е) найти интервал, симметричный относительно среднего значения, в котором будет находиться X с вероятностью 0,95. Решение. а) Плотность вероятности случайной величины X, распределенной по нормальному закону находим по формуле 1: при условии, что mx=20, σ =0,2. б) Для нормального распределения случайной величины вероятность попасть в интервал (19,7; 20,3) определяется по формуле 3: Ф((20,3-20)/0,2) – Ф((19,7-20)/0,2) = Ф(0,3/0,2) – Ф(-0,3/0,2) = 2Ф(0,3/0,2) = 2Ф(1,5) = 2*0,4332 = 0,8664. Значение Ф(1,5) = 0,4332 мы нашли в приложениях, в таблице значений интегральной функции Лапласа Φ(x) (таблица 2) в) Вероятность того, что абсолютная величина отклонения меньше положительного числа 0,1 найдем по формуле 4: Р(|Х-20| < 0,1) = 2Ф(0,1/0,2) = 2Ф(0,5) = 2*0,1915 = 0,383. Значение Ф(0,5) = 0,1915 мы нашли в приложениях, в таблице значений интегральной функции Лапласа Φ(x) (таблица 2) г) Поскольку вероятность отклонения, меньшего 0,1 мм, равна 0,383, то отсюда следует, что в среднем 38,3 детали из 100 окажутся с таким отклонением, т.е. 38,3%. д) Поскольку процент деталей, отклонение которых от среднего не превышает заданного, повысился до 54%, то Р(|Х-20| < δ) = 0,54. Отсюда следует, что 2Ф(δ/σ) = 0,54, а значит Ф(δ/σ) = 0,27. Используя приложение (таблица 2), находим δ/σ = 0,74. Отсюда δ = 0,74*σ = 0,74*0,2 = 0,148 мм. е) Поскольку искомый интервал симметричен относительно среднего значения mx = 20, то его можно определить как множество значений X, удовлетворяющих неравенству 20 − δ < X < 20 + δ или |x − 20| < δ . По условию вероятность нахождения X в искомом интервале равна 0,95, значит P(|x − 20| < δ)= 0,95. С другой стороны P(|x − 20| < δ) = 2Ф(δ/σ), следовательно 2Ф(δ/σ) = 0,95, а значит Ф(δ/σ) = 0,475. Используя приложение (таблица 2), находим δ/σ = 1,96. Отсюда δ = 1,96*σ = 1,96*0,2 = 0,392. Искомый интервал: (20 – 0,392; 20 + 0,392) или (19,608; 20,392). Другие статьи по данной теме: назад: Равномерный и показательный законы распределения непрерывной случайной величины далее: Статистическая сводка и группировка. Статистический ряд распределения Список использованных источников Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004; Лисьев В.П. Теория вероятностей и математическая статистика: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006; Семёнычев В. К. Теория вероятности и математическая статистика: Лекции /Самара, 2007; Теория вероятностей: контрольные работы и метод. указания для студентов / сост. Л.В. Рудная и др. / УрГЭУ — Екатеринбург, 2008.

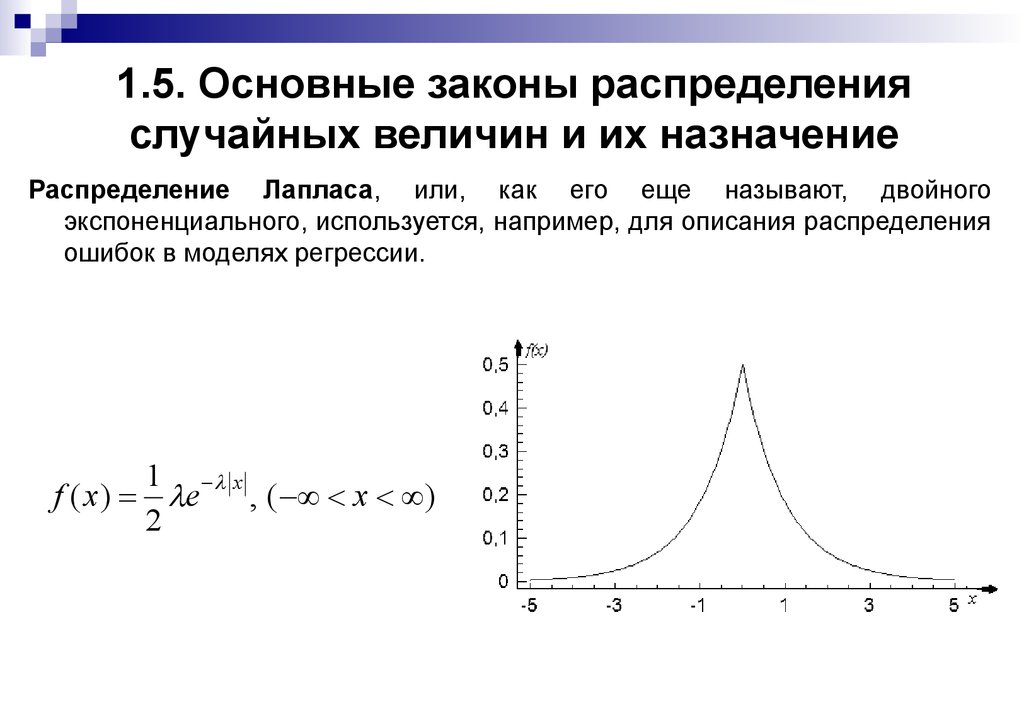
Стандартное нормальное распределение | Калькулятор, примеры и использование

Опубликован в 5 ноября 2020 г. от Прита Бхандари. Отредактировано 19 января 2023 г.

Стандартное нормальное распределение , также называемое z -распределением , является особым нормальным распределением, где среднее значение равно 0, а стандартное отклонение равно 1.

Любое нормальное распределение можно стандартизировать, преобразовав его значения в z баллов. Z-баллы говорят вам, сколько стандартных отклонений от среднего лежит в каждом значении.

Преобразование нормального распределения в распределение z позволяет рассчитать вероятность появления определенных значений и сравнить различные наборы данных.

Содержание

1. Калькулятор стандартного нормального распределения
2. Сравнение нормального распределения со стандартным нормальным распределением
3. Стандартизация нормального распределения
4. Использование стандартного нормального распределения для определения вероятности
5. Пошаговый пример использования z-распределения
6. Часто задаваемые вопросы о стандартном нормальном распределении

Калькулятор стандартного нормального распределения

Вы можете рассчитать стандартное нормальное распределение с помощью нашего калькулятора ниже.

Нормальное распределение по сравнению со стандартным нормальным распределением

Все нормальные распределения, как и стандартное нормальное распределение, являются одномодальными и симметрично распределяются по колоколообразной кривой. Однако нормальное распределение может принимать любое значение как среднее значение и стандартное отклонение. В стандартном нормальном распределении среднее значение и стандартное отклонение всегда фиксированы.

Каждое нормальное распределение представляет собой версию стандартного нормального распределения, которая была растянута или сжата и перемещена по горизонтали вправо или влево.

Среднее значение определяет центр кривой. Увеличение среднего значения сдвигает кривую вправо, а уменьшение — влево.

Стандартное отклонение растягивает или сжимает кривую. Небольшое стандартное отклонение приводит к узкой кривой, а большое стандартное отклонение приводит к широкой кривой.

Кривая	Положение или форма (относительно стандартного нормального распределения)
А ( М = 0, SD = 1)	Стандартное нормальное распределение
Б ( М = 0, SD = 0,5)	Сжато, потому что SD < 1
С ( M = 0, SD = 2)	Растянуто, потому что SD > 1
Д ( М = 1, SD = 1)	Сдвинут вправо, потому что M > 0
E ( M = –1, SD = 1)	Сдвинут влево, потому что M < 0

Предотвратите плагиат, запустите бесплатную проверку.

Попробуй бесплатно

Стандартизация нормального распределения

Когда вы стандартизируете нормальное распределение, среднее становится равным 0, а стандартное отклонение становится равным 1. Это позволяет легко рассчитать вероятность появления определенных значений в вашем распределении или сравнить наборы данных с разными средними значениями и стандартными отклонениями.

В то время как точки данных обозначаются как x в нормальном распределении, они называются z или z баллов в z 9Рассылка 0009. Оценка z — это стандартная оценка , которая говорит вам, сколько стандартных отклонений от среднего значения лежит отдельное значение ( x ):

• Положительная оценка z означает, что ваше значение x больше среднего.
• Отрицательная оценка z означает, что ваше значение x меньше среднего.
• Нулевой показатель z означает, что ваше значение x равно среднему значению.

Преобразование нормального распределения в стандартное нормальное распределение позволяет:

• Сравните результаты различных распределений с разными средними значениями и стандартными отклонениями.
• Нормализация оценок для принятия статистических решений (например, выставление оценок по кривой).
• Найти вероятность наблюдений в распределении выше или ниже заданного значения.
• Найдите вероятность того, что среднее значение выборки значительно отличается от известного среднего значения генеральной совокупности.

Как рассчитать балл

z

Чтобы стандартизировать значение из нормального распределения, преобразуйте отдельное значение в z -score:

1. Вычтите среднее значение из вашего индивидуального значения.
2. Разделите разницу на стандартное отклонение.

Z — формула оценки	Пояснение
	x = индивидуальное значение мк = среднее значение σ = стандартное отклонение

Пример: нахождение баллов z Вы собираете баллы SAT от учащихся на новом курсе подготовки к экзаменам. Данные подчиняются нормальному распределению со средним баллом ( M ) 1150 и стандартным отклонением ( SD ) 150. Вы хотите найти вероятность того, что баллы SAT в вашей выборке превысят 1380.

Чтобы стандартизировать ваши данные, сначала найдите число z для 1380. 9Счет 0008 z говорит вам, сколько стандартных отклонений от 1380 от среднего.

Шаг 1: Вычтите среднее из значения x .	x = 1380 M   = 1150 x – M = 1380 − 1150 = 230
Шаг 2: Разделите разницу на стандартное отклонение.	SD = 150 z = 230 ÷ 150 = 1,53

z оценка для значения 1380 равна 1,53 . Это означает, что 1380 — это 1,53 стандартных отклонения от среднего значения вашего распределения.

Затем мы можем найти вероятность этого результата, используя таблицу z .

Используйте стандартное нормальное распределение, чтобы найти вероятность

Стандартное нормальное распределение — это распределение вероятностей , поэтому площадь под кривой между двумя точками показывает вероятность того, что переменные принимают диапазон значений. Общая площадь под кривой равна 1 или 100%.

Каждая оценка z имеет связанное значение p , которое говорит вам о вероятности появления всех значений ниже или выше этой оценки z . Это площадь под кривой слева или справа от этой оценки z .

Z тесты и p значения

Оценка z — это тестовая статистика, используемая в тесте z . Тест z используется для сравнения средних значений двух групп или для сравнения среднего значения группы с заданным значением. Его нулевая гипотеза обычно предполагает отсутствие различий между группами.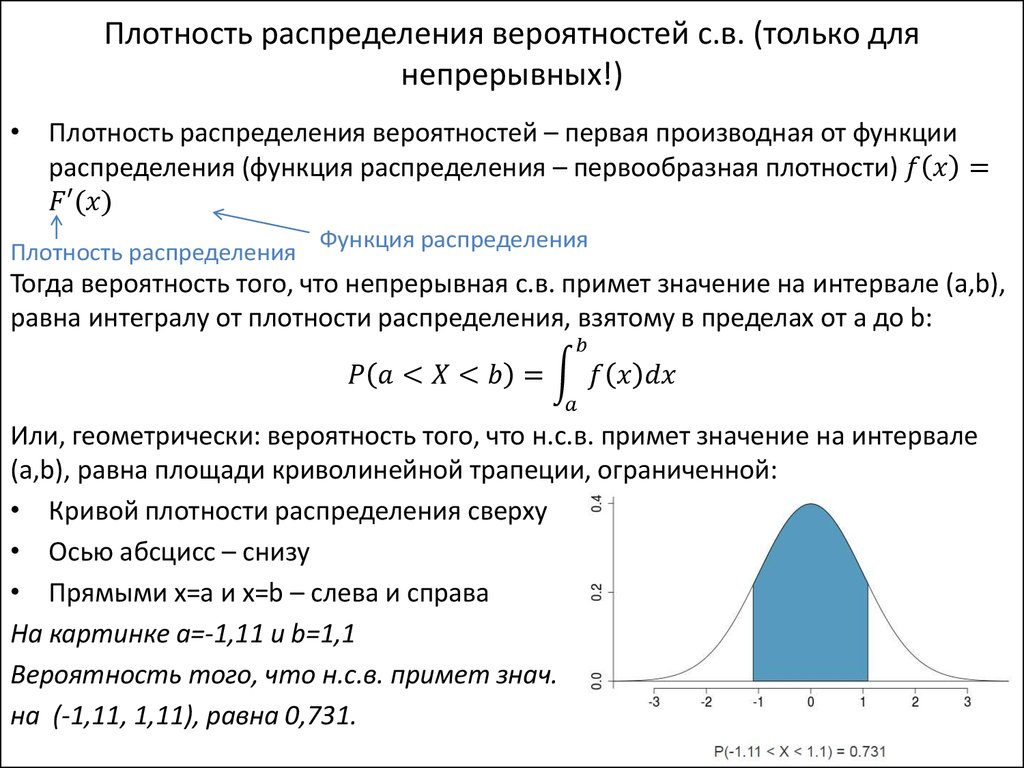

Площадь под кривой справа от значения z — это значение p , и это вероятность того, что ваше наблюдение произойдет, если нулевая гипотеза верна.

Обычно значение p 0,05 или меньше означает, что ваши результаты вряд ли возникли случайно; это указывает на статистически значимый эффект.

Преобразовав значение нормального распределения в оценку z , вы можете легко найти значение p для z тест.

Как пользоваться z-таблицей

Как только вы получите оценку z , вы можете посмотреть соответствующую вероятность в таблице z .

В таблице z площадь под кривой указывается для каждого значения z между -4 и 4 с интервалом 0,01.

Существует несколько различных форматов таблицы z . Здесь мы используем часть кумулятивной таблицы. В этой таблице указана общая площадь под кривой до заданного 9Оценка 0008 z — эта область равна вероятности появления значений ниже этой оценки z .

Первый столбец таблицы z содержит оценку z с точностью до первого десятичного знака. В верхней строке таблицы указан второй десятичный разряд.

Чтобы найти соответствующую площадь под кривой (вероятность) для z-показателя:

1. Перейдите к строке с первыми двумя цифрами вашего счета z .
2. Перейти к столбцу с той же третьей цифрой, что и ваша 9от 0008 до баллов.
3. Найдите значение на пересечении строки и столбца из предыдущих шагов.

Пример: использование распределения z для определения вероятности. Мы подсчитали, что балл SAT, равный 1380, соответствует баллу z , равному 1,53. Используя полную таблицу z , мы находим, что для z оценки 1,53 значение p составляет 0,937.

Это вероятность того, что баллы SAT будут равны 1380 или меньше (93,7%), и это область под кривой слева от заштрихованной области.

Чтобы найти заштрихованную площадь, нужно от 1 отнять 0,937, то есть общую площадь под кривой.

Вероятность x > 1380 = 1 − 0,937 = 0,063

Это означает, что, вероятно, только 6,3% баллов SAT в вашей выборке превышают 1380.

Пошаговый пример использования распределения

z

Давайте рассмотрим придуманный исследовательский пример, чтобы лучше понять, как работает стандартное нормальное распределение.

Вам как исследователю сна интересно узнать, как изменились привычки сна во время самоизоляции из-за COVID-19. Вы собираете данные о продолжительности сна из образца во время полной блокировки.

До введения режима самоизоляции в среднем население спало 6,5 часа. Среднее значение выборки блокировки составляет 7,62.

Чтобы оценить, значительно ли среднее значение вашей выборки отличается от среднего значения населения до изоляции, вы выполняете тест z :

.

1. Сначала вы вычисляете z баллов для выборочного среднего значения.
2. Затем вы находите значение p для вашего результата z , используя таблицу z .

Шаг 1: Рассчитайте

z -счет

Чтобы сравнить продолжительность сна во время и до блокировки, вы конвертируете среднее значение выборки блокировки в показатель z , используя среднее значение популяции до блокировки и стандартное отклонение.

Формула	Пояснение	Расчет
	x = выборочное среднее μ = среднее значение совокупности σ = стандартное отклонение совокупности

Оценка z , равная 2,24, означает, что среднее значение выборки на 2,24 стандартного отклонения больше, чем среднее значение генеральной совокупности.

Шаг 2. Найдите значение

p

Чтобы найти вероятность вашего выборочного среднего z со значением 2,24 или меньше, вы используете таблицу z , чтобы найти значение на пересечении строки 2,2 и столбца +0,04.

В таблице указано, что площадь под кривой до или ниже вашего значения z составляет 0,9874. Это означает, что средняя продолжительность сна в вашей выборке превышает примерно 98,74% средней продолжительности сна населения до изоляции.

Чтобы найти значение p для оценки того, отличается ли выборка от генеральной совокупности, вы вычисляете площадь под кривой выше или справа от вашего z-показателя. Поскольку общая площадь под кривой равна 1, вы вычитаете площадь под кривой ниже z оценка от 1.

Значение p менее 0,05 или 5% означает, что выборка значительно отличается от генеральной совокупности.

Вероятность z > 2,24 = 1 − 0,9874 = 0,0126 или 1,26%

При значении p менее 0,05 можно сделать вывод, что средняя продолжительность сна во время изоляции от COVID-19 была значительно выше, чем в среднем до блокировки.

Часто задаваемые вопросы о стандартном нормальном распределении

При нормальном распределении данные распределяются симметрично без перекоса. Большинство значений группируются вокруг центральной области, при этом значения сужаются по мере удаления от центра.

Меры центральной тенденции (среднее, мода и медиана) в нормальном распределении точно такие же.

Что такое эмпирическое правило?

Эмпирическое правило, или правило 68-95-99,7, говорит вам, где большинство значений находится в нормальном распределении:

• Около 68% значений находятся в пределах 1 стандартного отклонения от среднего.
• Около 95% значений находятся в пределах 2 стандартных отклонений от среднего значения.
• Около 99,7% значений находятся в пределах 3 стандартных отклонений от среднего значения.

Эмпирическое правило — это быстрый способ получить обзор ваших данных и проверить любые выбросы или экстремальные значения, которые не соответствуют этому шаблону.

Процитировать эту статью Scribbr

Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.

Бхандари, П. (2023, 19 января). Стандартное нормальное распределение | Калькулятор, примеры и использование. Скриббр. Проверено 25 января 2023 г., с https://www.scribbr.com/statistics/standard-normal-distribution/

Процитировать эту статью

Полезна ли эта статья?

Вы уже проголосовали. Спасибо 🙂 Ваш голос сохранен 🙂 Обработка вашего голоса…

Прита имеет академическое образование в области английского языка, психологии и когнитивной нейробиологии. Как междисциплинарный исследователь, она любит писать статьи, объясняющие сложные исследовательские концепции для студентов и ученых.

Асимметрия | Определение, примеры и формула

Опубликован в 10 мая 2022 г. от Шон Терни. Отредактировано 12 июля 2022 г.

Асимметрия — это мера асимметрии распределения. Распределение является асимметричным, если его левая и правая части не являются зеркальными отображениями.

Распределение может иметь правую (или положительную), левую (или отрицательную) или нулевую асимметрию. Правостороннее распределение длиннее с правой стороны своего пика, а левостороннее распределение длиннее с левой стороны своего пика:

Вы можете рассчитать асимметрию распределения до:

• Описать распределение переменной наряду с другими описательными статистическими данными
• Определите, нормально ли распределена переменная. Нормальное распределение имеет нулевую асимметрию и является допущением многих статистических процедур.

Содержание

1. Что такое нулевой перекос?
2. Что такое перекос вправо (положительный перекос)?
3. Что такое перекос влево (отрицательный перекос)?
4. Как рассчитать асимметрию
5. Что делать, если данные искажены
6. Практические вопросы
7. Часто задаваемые вопросы об асимметрии

Что такое нулевой перекос?

Когда распределение имеет нулевую асимметрию, оно симметрично. Его левая и правая стороны являются зеркальными отображениями.

Нормальные распределения имеют нулевую асимметрию, но они не единственные распределения с нулевой асимметрией. Любое симметричное распределение, такое как равномерное распределение или некоторые бимодальные (двухпиковые) распределения, также будет иметь нулевую асимметрию.

Самый простой способ проверить, имеет ли переменная асимметричное распределение, — нарисовать его на гистограмме.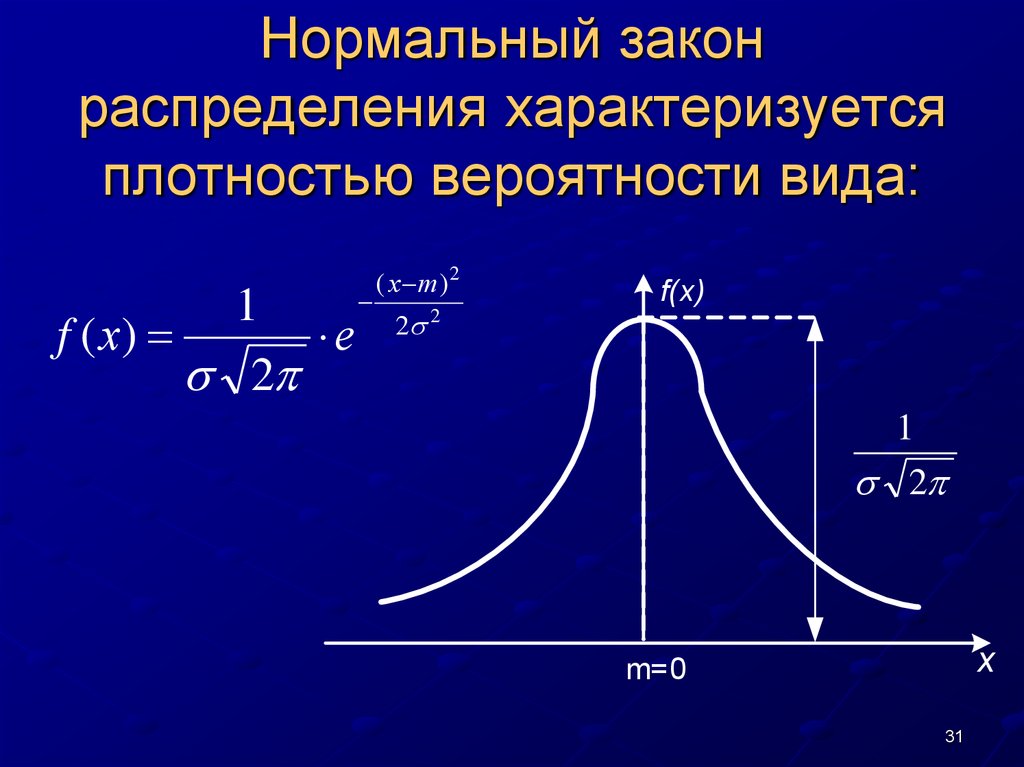 Например, на гистограмме ниже показан вес шестинедельных цыплят.

Распределение приблизительно симметрично, наблюдения распределены одинаково слева и справа от его пика. Таким образом, распределение имеет приблизительно нулевую асимметрию.

В распределении с нулевой асимметрией среднее значение и медиана равны.

Нулевая асимметрия: среднее = медиана

Например, средний вес цыпленка составляет 261,3 г, а медиана — 258 г. Среднее и медиана почти равны. Они не совсем равны, потому что выборочное распределение имеет очень маленькую асимметрию.

Хотя теоретическое распределение (например, распределение z ) может иметь нулевую асимметрию, реальные данные почти всегда имеют хотя бы небольшую асимметрию. Однако, если распределение близко к симметричному, обычно считается, что оно имеет нулевую асимметрию для практических целей, таких как проверка предположений модели.

Что такое перекос вправо (положительный перекос)?

Правостороннее распределение длиннее с правой стороны от пика, чем с левой. Правая асимметрия также называется положительной асимметрией.

Вы можете думать об асимметрии с точки зрения хвостов. Хвост — это длинный сужающийся конец распределения. Это указывает на то, что на одном из крайних концов распределения есть наблюдения, но они относительно редки. Правостороннее распределение имеет длинный хвост с правой стороны.

Количество солнечных пятен, наблюдаемых за год, показанное на гистограмме ниже, является примером распределения с асимметрией вправо. Солнечные пятна, представляющие собой темные, более прохладные области на поверхности Солнца, наблюдались астрономами в период с 1749 по 1983 год.

Распределение смещено вправо, поскольку оно длиннее справа от своего пика. Справа есть длинный хвост, означающий, что каждые несколько десятилетий наступает год, когда количество наблюдаемых солнечных пятен намного превышает среднее значение.

Среднее значение распределения с асимметрией вправо почти всегда больше, чем его медиана.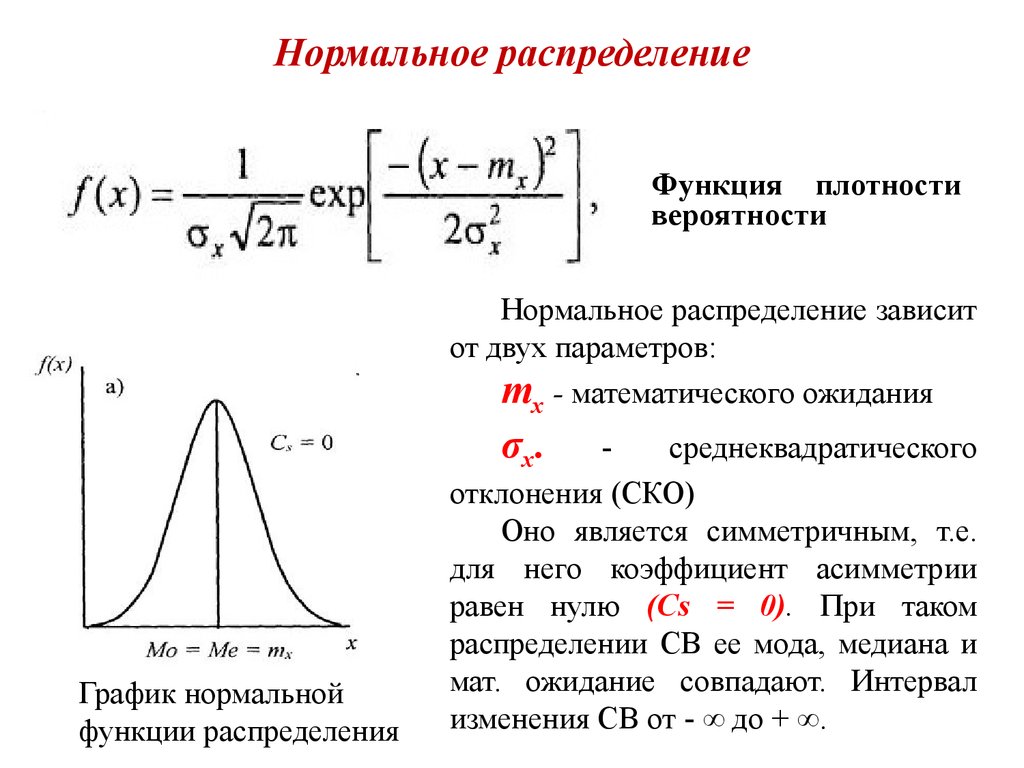 Это потому, что экстремальные значения (значения в хвосте) влияют на среднее значение больше, чем на медиану.

Искажение вправо: среднее > медиана

Например, среднее количество солнечных пятен, наблюдаемых за год, составляло 48,6, что больше медианы 39.

Предотвратите плагиат, запустите бесплатную проверку.

Попробуй бесплатно

Что такое перекос влево (отрицательный перекос)?

Распределение с асимметрией влево длиннее слева от своего пика, чем справа. Другими словами, асимметричное влево распределение имеет длинный хвост с левой стороны. Левый перекос также называют отрицательным перекосом.

Результаты тестов часто имеют левостороннее распределение: большинство учащихся показывают относительно хорошие результаты, а некоторые учащиеся показывают результаты намного ниже среднего. На приведенной ниже гистограмме показаны баллы по зоологической части стандартизированного теста, сдаваемого индийскими учащимися в конце средней школы.

Распределение смещено влево, поскольку оно длиннее слева от своего пика. Длинный хвост слева представляет небольшую часть учащихся, получивших очень низкие баллы.

Среднее значение распределения с асимметрией влево почти всегда меньше медианы.

Левая асимметрия: среднее < медианы

Например, средний балл теста по зоологии составил 53,7, что меньше медианы 55.

Как рассчитать асимметрию

Существует несколько формул для измерения асимметрии. Одним из самых простых является медианная асимметрия Пирсона. Он использует тот факт, что среднее значение и медиана не равны в асимметричном распределении.

Медианная асимметрия Пирсона =

Медианная асимметрия Пирсона говорит вам, сколько стандартных отклонений отделяет среднее значение от медианы.

Реальные наблюдения редко имеют медианную асимметрию Пирсона, равную точно 0. Если ваши данные имеют значение, близкое к 0, вы можете считать, что они имеют нулевую асимметрию. Не существует стандартного соглашения о том, что считается «достаточно близким» к 0 (хотя это исследование предполагает, что 0,4 и -0,4 являются разумными пороговыми значениями для больших выборок).

Пример: Расчет медианной асимметрии Пирсона Медианная асимметрия Пирсона числа солнечных пятен, наблюдаемых за год:

• Среднее = 48,6
• Медиана = 39
• Стандартное отклонение = 39,5

Расчет

Медианная асимметрия Пирсона =

Медианная асимметрия Пирсона =

Медианная асимметрия Пирсона  =

Что делать, если данные искажены

Одной из причин, по которой вы можете проверить, является ли распределение асимметричным, является проверка того, подходят ли ваши данные для определенной статистической процедуры. Многие статистические процедуры предполагают, что переменные или остатки имеют нормальное распределение. Перекос — это распространенный способ, которым распределение может отличаться от нормального распределения.

Обычно у вас есть три варианта, если ваша статистическая процедура требует нормального распределения, а ваши данные искажены:

1. Ничего не делать . Многие статистические тесты, включая тесты t , ANOVA и линейные регрессии, не очень чувствительны к искаженным данным. Особенно, если перекос легкий или умеренный, лучше его игнорировать.

2. Используйте другую модель . Вы можете выбрать модель, которая не предполагает нормального распределения. Для ваших данных больше подходят непараметрические тесты или обобщенные линейные модели.

3. Преобразование переменной . Другой вариант — преобразовать асимметричную переменную, чтобы она стала менее асимметричной. «Преобразование» означает применение одной и той же функции ко всем наблюдениям переменной.

Преобразования по типу перекоса

Тип перекоса	Интенсивность перекоса	Трансформация
Справа	Мягкий	Не трансформировать
	Умеренная	Квадратный корень
	Сильный	Натуральное бревно
	Очень прочный	Основание для бревен 10
Левый	Мягкий	Не трансформировать
	Умеренная	Отражение*, затем квадратный корень
	Сильный	Reflect*, затем натуральное бревно
	Очень прочный	Отразить*, затем логарифмировать по основанию 10

*В данном контексте «отражение» означает взять наибольшее наблюдение, K , а затем вычесть каждое наблюдение из K + 1. Имейте в виду, что отражение меняет направление переменной и ее отношения на противоположное. с другими переменными (т. е. положительные отношения становятся отрицательными).

Пример: Преобразование переменной с правым наклоном Представьте, что вы выполнили линейную регрессию, чтобы предсказать количество солнечных пятен, наблюдаемых за год, и обнаружили, что остатки не имеют нормального распределения.

Поскольку количество солнечных пятен, наблюдаемых за год, искажено вправо, вы можете попытаться решить эту проблему, преобразовав переменную. Вы также можете игнорировать асимметрию, поскольку линейная регрессия не очень чувствительна к асимметрии.

Начните с преобразования квадратного корня. Если этого недостаточно для исправления перекоса, вы можете перейти к следующему варианту преобразования.

Количество солнечных пятен в год	Sqrt(количество солнечных пятен в год)
5	2 236
11	3 317
16	4000
23	4 796
…	…

Когда вы наносите преобразованную переменную на гистограмму, вы можете видеть, что теперь она имеет близкую к нулю асимметрию.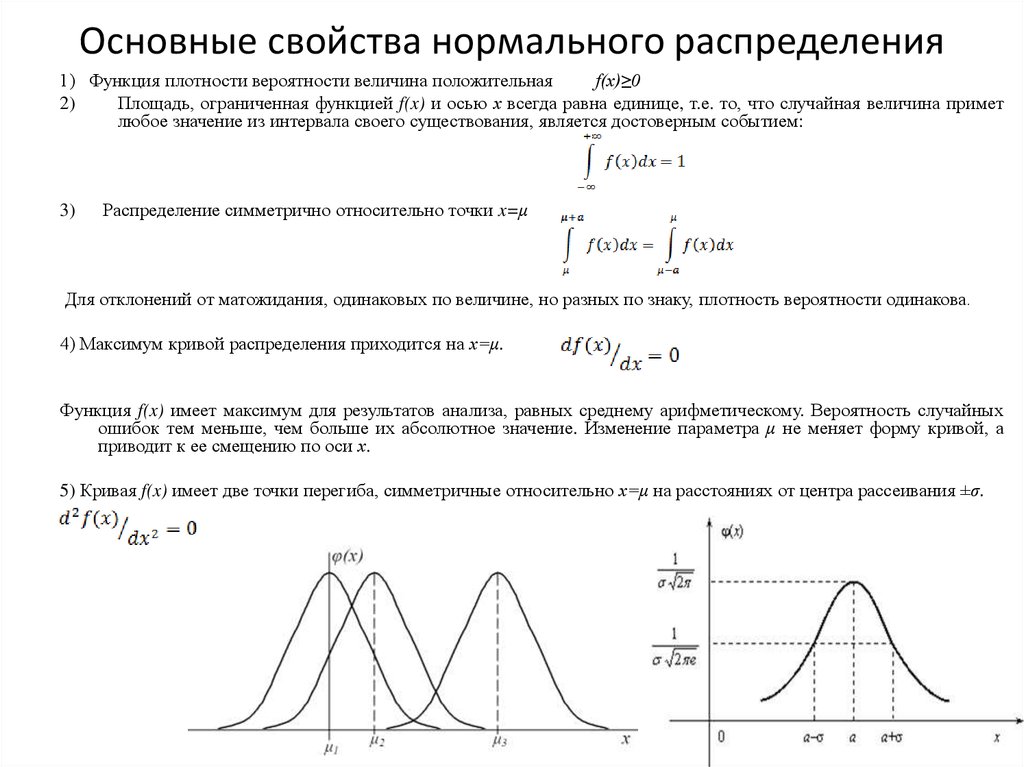 Вы можете заменить количество солнечных пятен в год преобразованной переменной в линейной регрессии. Вполне вероятно, что остатки линейной регрессии теперь будут нормально распределены.

Практические вопросы

на базе Typeform

Часто задаваемые вопросы об асимметрии

Каковы три типа асимметрии?

Существует три типа асимметрии:

• Правая асимметрия (также называемая положительной асимметрией ) . Распределение с перекосом вправо длиннее справа от пика, чем слева.
• Перекос влево (также называемый отрицательным перекосом). Распределение с асимметрией влево длиннее слева от пика, чем справа.
• Нулевой перекос. Он симметричен, его левая и правая стороны являются зеркальными отражениями.

Что такое нормальное распределение?

При нормальном распределении данные распределяются симметрично без перекоса. Большинство значений группируются вокруг центральной области, при этом значения сужаются по мере удаления от центра.

Меры центральной тенденции (среднее, мода и медиана) в нормальном распределении точно такие же.

Процитировать эту статью Scribbr

Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.

No related posts.