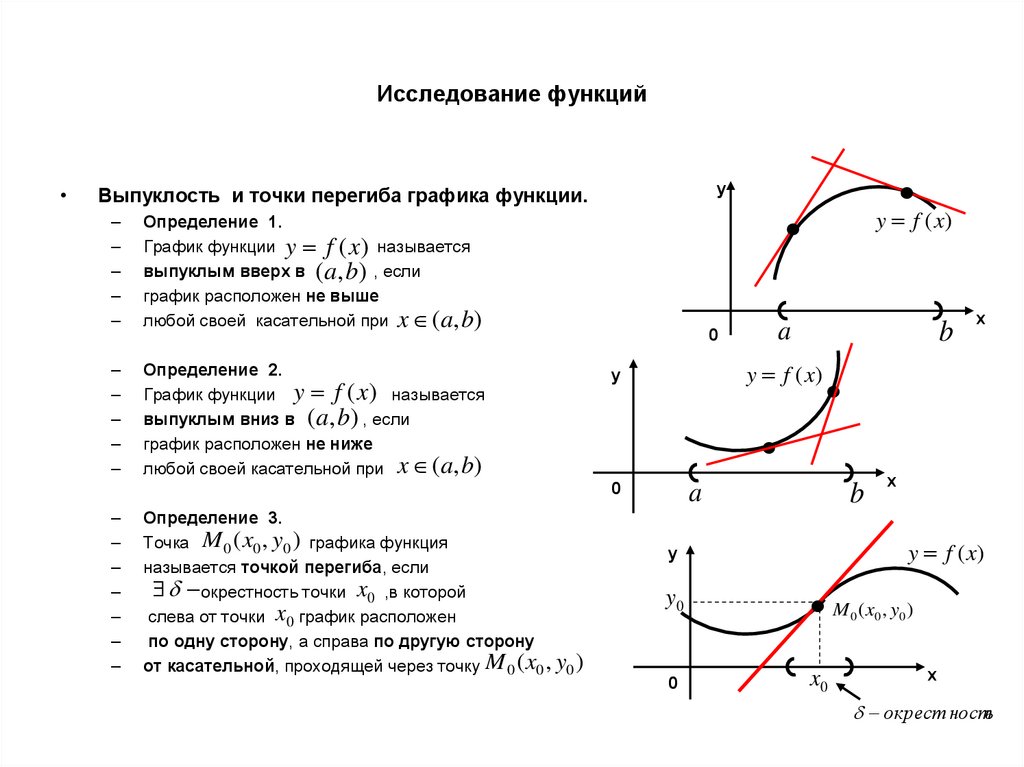
4.17. Общая схема исследования функции
Пусть – некоторая заданная функция. Требуется провести ее всестороннее (полное) исследование и построить ее график. Указанное полное исследование функции можно провести по следующей схеме.
1. Находим область определения функции. Заодно устанавливаем интервалы ее непрерывности и точки разрыва.
2. Исследуем функцию на четность-нечетность и тем самым устанавливаем возможную симметрию графика функции (относительно оси Oy или относительно начала координат). Для этого записываем выражение и сравниваем его с :
А) Если , то функция – четная. Ее график симметричен относительно оси Оу (рис. 4.16 (а)).
Б) Если , то функция – нечетная. Ее график симметричен относительно начала координат (рис. 4.16 (б)).
В) Если не имеет место ни вариант (а) ни вариант (б), то функция – общего вида (ее график симметрией (а) и (б) не обладает).
3. Исследуем функцию на периодичность (на повторяемость ее графика). Из элементарных функций это имеет смысл делать лишь для тригонометрических функций, ибо прочие функции заведомо не периодичны.
4. Исследуем поведение функции возле найденных в пункте 1 точек ее разрыва, а также возле границ области ее определения, учитывая при этом информацию, полученную в пунктах 2 и 3. Заодно устанавливаем (определяем) вертикальные и невертикальные асимптоты графика функции (см. § 3 главы 3).
5. Находим интервалы возрастания и убывания функции и точки ее экстремума (с помощью первой производной ). Заодно находим вершины и впадины графика функции и устанавливаем их тип (округлые; острые).
6. Находим интервалы выпуклости и интервалы вогнутости функции и точки ее перегиба (с помощью второй производной ). Заодно находим точки перегиба графика функции.
7. Находим точки пересечения графика функции с осями координат.
8. Строим график функции.
Пример 4. Провести полное исследование функции и построить ее график.
Решение.
Реализуем изложенную выше схему.
1. Область определения функции – любые X, кроме . То есть функция определена (а следовательно, и непрерывна) на всей числовой оси Ох, кроме точки , которая, таким образом, является единственной точкой разрыва функции.
2. Исследуем функцию на четность-нечетность. Имеем: ; тогда . Как видим, . Значит, наша функция – нечетная, ее график симметричен относительно начала координат. А значит, в дальнейшем достаточно исследовать функцию лишь для , ибо для можно будет учесть указанную выше симметрию.
3. Функция – алгебраическая (не тригонометрическая), а следовательно, не периодична.
4. Исследуем поведение функции возле точки ее разрыва (справа, при ), а также при (на правой границе области ее определения):
А) При функция
То есть
( при ).
А это значит, что вертикальная прямая с уравнением (ось
4.17 (А)):Б) При функция стремится, очевидно, к , ибо
.
При этом, очевидно, при функция стремится к эквивалентно функции , так как при . А это значит, что график нашей функции при стремится к прямой . То есть прямая – асимптота (наклонная асимптота) графика нашей функции. Причем график функции при стремится к прямой Сверху, ибо для всех (рис. 4.17 (Б)).
5. Найдем интервалы возрастания и убывания и точки экстремума функции (схема исследования изложена выше).
а) Находим производную :
;
Б) Найдем точки (значения X), подозрительные на экстремум:
.
не существует .
Точку исследовать не будем, так как она не входит в область определения функции. Не будем исследовать и отрицательную точку (см. пункт 2).
В) Нанесем оставшуюся подозрительную на экстремум точку на область определения функции (на ось Ох). При этом ограничимся рассмотрением лишь положительной полуоси :
В обоих получившихся интервалах найдем знак производной и отметим его.
Тем самым устанавливаем интервал возрастания и интервал убывания функции. Заодно устанавливаем, что – точка минимума функции.
Г) Найдем значение функции в точке минимума и тем самым определим впадину графика функции:
; точка – впадина графика функции (округлая, т. к. ).
6. Найдем интервалы выпуклости и интервалы вогнутости функции, а также точки перегиба функции и ее графика (схема исследования изложена выше).
А) Найдем :
;
Б) Найдем точки (значения X), подозрительные на перегиб:
таких X
не существует .
Но учитывать точку не будем, так как она не входит в область определения функции. Итак, рассматриваемая функция не имеет подозрительных на перегиб точек, а значит, точек перегиба у неё нет. И так как для , то для всех функция наша вогнутая.
7. Найдем точки пересечения графика функции с осями координат.
А) С осью Ох:
таких X нет.
Б) С осью Оу:
– не сущ.
Таким образом, ни с осью Ох, ни с осью Оу график нашей функции не пересекается.
8. Строим график функции – сначала для , а затем, по симметрии относительно начала координат, и для (рис. 4.18).
Упражнения
1. Провести полное исследование и построить графики функций:
А) ; б) ; в) .
Ответ:
| < Предыдущая | Следующая > |
|---|
2.14. Общая схема исследования функции
Пользуясь средствами дифференциального исчисления, можно провести глубокое и разностороннее изучение свойств функции и обосновать характерные её особенности. Для исследования функций и построения её графика удобно пользоваться следующей схемой:
Найти область определения функции.
Исследовать функцию на четность, периодичность.
Найти точки пересечения графика функции с осями координат.
Исследовать функцию на непрерывность, найти точки разрыва, определить их характер.
Найти асимптоты графика функции.
Найти интервалы монотонности функции, точки экстремума.
Найти интервалы выпуклости функции, точки перегиба.
Построение графика функции.
Пример. Провести полное исследование функции и построить её график.
Решение. Областью определения функции является промежуток .
Исследуем функцию на четность:
,
так как и , то функция ни четная, ни нечетная.
Функция не является периодической.
Определим координаты точек пересечения с осями координат:
.
Значит, координаты точек пересечения с Ох и Оу – (0 ; 0), (1; 0).
Функция
непрерывна и определена на всей числовой
оси, поэтому вертикальных асимптот нет.
Для определения промежутков монотонности найдем производную функции первого порядка:
.
Найдем стационарные точки:
.
Таким образом, разбивают числовую прямую на три промежутка , , .
Заполним таблицу
х |
|
||
Знак |
— |
+ |
— |
Поведение у |
убывает |
возрастает |
убывает |
Найдем значения функции в точках :
Для определения промежутков выпуклости найдем производную функции второго порядка:
.
.
Составим таблицу
|
|
|||
Знак |
+ |
— |
||
Направление выпуклости |
Найдем значение функции в точке :
.
Поскольку при переходе через точку с абсциссой вторая производная меняет знак, точка является точкой перегиба.
Используя результаты исследования, построим график функции
Пример.
Провести
полное исследование функции
и построить её график.
Решение. Областью определения функции является промежуток .
Функция ни четная, ни нечетная. Функция не является периодической.
.
Значит, функция пересекает ось Ох в точке (1; 0), с осью Оу пересечений нет, так как функция определена при .
Функция непрерывна и определена на промежутке , так как , поэтому вертикальная асимптота.
Наклонная асимптота графика функции имеет вид у = k x + b, определим параметры k и b:
,
(при нахождении предела использовали правило Лопиталя)
,
(при нахождении предела использовали правило Лопиталя),
Так
как
,
значит, функция
имеет горизонтальную асимптоту
.
Для определения промежутков монотонности найдем производную функции первого порядка:
.
Найдем стационарные точки:
.
Таким образом, разбивает числовую прямую на два промежутка , .
Заполним таблицу
Знак |
+ |
— |
||
Поведение у |
возрастает |
убывает |
Найдем значения функции в точке :
Для определения промежутков выпуклости найдем производную функции второго порядка:
.
Составим таблицу
х |
|
|
||
Знак |
— |
+ |
||
Направление выпуклости |
Найдем значения функции в точке :
.
Поскольку при переходе через точку с абсциссой вторая производная меняет знак, точка является точкой перегиба.
Используя результаты исследования, построим график функции
Пример.
Провести
полное исследование функции
и построить её график.
Решение. Функция определена при
,
Значит, областью определения функции является промежуток
.
Исследуем функцию на четность:
,
так как и , то функция нечетная, график функции симметричен относительно начала координат. Функция не является периодической.
Определим координаты точек пересечения с осями координат:
Значит, функция пересекает ось Ох и ось Оу в точке (0; 0) .
Функция непрерывна и определена на промежутке , так как , поэтому и вертикальные асимптоты.
Наклонная асимптота графика функции имеет вид у = k x + b, определим параметры k и b:
,
Так
как
,
значит, функция
имеет горизонтальную асимптоту
.
Для определения промежутков монотонности найдем производную функции первого порядка:
Стационарных точек нет, так как .
Критические точки разбивают числовую прямую на три промежутка , , .
Заполним таблицу
х |
|
( |
||||
Знак |
— |
— |
— |
|||
Поведение у |
убывает |
убывает |
убывает |
Для определения промежутков выпуклости найдем производную функции второго порядка:
Составим таблицу:
х |
|
|
|
|
Знак |
— |
— |
+ |
+ |
Направлене выпуклости |
Найдем значения функции в точке :
Поскольку
при переходе через точку
с абсциссой
,
в которой функция определена,
вторая производная меняет знак, точка
,
является
точкой перегиба.
Используя результаты исследования, построим график функции
Упражнения
Провести полное исследование функций и построить их график:
|
Определение функции и значение — Merriam-Webster
1 из 2функция ˈfəŋ(k)-shən
1
: профессиональная или служебная должность : род занятий
Его работа совмещает функции менеджера и рабочего.
2
: действие, для которого лицо или вещь специально приспособлены или используются или для которых существует вещь : цель действие
особенно : нормальный и специфический вклад частей тела в экономику живого организма
Функция сердца — перекачивать кровь по телу.
4
: официальная или формальная церемония или общественное собрание
Они побывали на нескольких мероприятиях во время встречи выпускников колледжа.
5
а
: математическое соответствие, которое ставит в соответствие ровно один элемент одного множества каждому элементу того же или другого множества
б
: переменная (такая как качество, черта или измерение), которая зависит от другой и изменяется вместе с ней
рост зависит от возраста
также : результат
болезни, являющиеся следствием стресса
6
: характерное поведение химического соединения из-за определенной реакционной единицы
также : функциональная группа
7
: компьютерная подпрограмма
конкретно
: тот, который выполняет вычисления с переменными (см.
запись переменных 2, смысл 1а), предоставленными программой, и предоставляет программе один результат
бесполезный
ˈfəŋ(k)-shən-ləs
имя прилагательное
функция
2 из 2
непереходный глагол
1
: иметь функцию : служить
атрибутивное существительное функционирует как прилагательное
2
: выполнять функцию или быть в действии : действовать
Синонимы
Существительное
- дело
- баш
- запой
- взрыв
- выброс
- до
- событие
- праздник
- праздник
- встреча
- вечеринка
- приемная
- вечеринка
глагол
- действие
- выполнять
- служить
- work
Просмотреть все синонимы и антонимы в тезаурусе
Примеры предложений
Существительное
Функция сердца заключается в перекачивании крови по телу.
Он считает, что истинная функция искусства — говорить правду.
Какие функции выполняют эти программы?
младенцы учатся управлять своим телом функции
Прибор в основном используется для измерения и регистрации функции сердца .
Дизайн представляет собой идеальное сочетание формы и функциональности .
Его работа сочетает в себе функции менеджера и рабочего.
Ее начальник 9Функция 0163 заключается в предоставлении квалифицированных юридических консультаций.
Они побывали на нескольких мероприятиях во время выходных, посвященных воссоединению колледжа.
Глагол
Новая машина хорошо работает с .
Его плохое здоровье не позволяло ему эффективно работать с в последние недели.
Ее сердце теперь, кажется, функционирует нормально.
Компьютерная сеть еще не полностью действующий .
Узнать больше
Последние примеры в Интернете
Компании Biogen и Eisai, тестирующие это лекарство, объявили в этом году, что леканемаб замедлил угасание мозга 9.0163 действует на при болезни Альцгеймера примерно на 27% по сравнению с плацебо.
Бренда Гудман, CNN , 14 ноября 2022 г.
Кроме того, помимо простого доказательства того, что красное мясо не связано с риском для здоровья, исследователи также создали более эффективное бремя доказательства риска функция .
Джошуа Хокинс, BGR , 14 ноября 2022 г.
Третье беспокойство сосредоточено на увеличении функция исследований, которые создают в лаборатории больше трансмиссивных или патогенных вирусов.
Диана Гитиг, Ars Technica , 29 октября 2022 г.
Потеря функции в нервных клетках головного мозга является естественным следствием старения, и те из нас, кто в возрасте, распознают сбои и ошибочную память, но те, у кого слабоумие, испытывают гораздо большие потери.
Брайант Стэмфорд, 9 лет0163 The Courier-Journal , 27 октября 2022 г.
БАС, часто называемый болезнью Лу Герига, в конечном итоге приводит к полной потере функции мышц .
Ян Кроуфорд, CBS News , 26 октября 2022 г.
Участники выполняли упражнения на беговой дорожке или велотренажере, а уровень кислорода контролировали вместе с измерениями функции сердца и легких 9.
0164 в течение трех месяцев после первоначального заражения COVID-19.
Алекса Михаил, Fortune , 12 октября 2022 г.
Однако тесты покажут ухудшение неврологической функции с течением времени.
Лиза Малкахи, Good Housekeeping , 5 октября 2022 г.
Поскольку это фактор затрат, ИТ-директор обычно считается частью финансового отдела выполняет функцию , иногда подчиняясь финансовому директору.
Клаус Джепсен, Forbes , 4 октября 2022 г.
Может быть, домохозяйство может выполняет функцию с одной машиной, а не с двумя.
WIRED , 17 ноября 2022 г.
У пациентов, принимающих диуретики при таких состояниях, как высокое кровяное давление, может возникнуть дефицит калия, минерала из класса электролитов, который помогает клеткам, мышцам и нервам 90–163 функционировать правильно 90–164.
Лора Ландро, WSJ , 13 ноября 2022 г.
Но полоски тоже функция , на мой взгляд, как своего рода моральный принцип.
Washington Post , 9 ноября 2022 г.
Потоки могут функционировать спорадически из-за условий.
Дэвид Шутц, Sun Sentinel , 9 ноября 2022 г.
Другими словами, последний месяц регулярного сезона будет функционировать как плей-офф для пяти из шести лучших команд.
Los Angeles Times , 1 ноября 2022 г.
То, что можно было бы назвать системой оповещения Ашанти, будет функционировать аналогично существующим оповещениям Amber, которые информируют общественность о пропавших детях.
Из отчетов Usa Today Network And Wire, USA TODAY , 28 октября 2022 г.
Проще говоря, без домашней работы эта страна не могла бы функционировать .
Кевин Л. Кларк, 9 лет0163 Сущность , 24 октября 2022 г.
Некоторые из выявленных механизмов могут функционировать для смягчения последствий изменения климата.
Джоан Майнерс, , Республика Аризона, , 6 октября 2022 г.
Узнать больше
Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «функция».
Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
История слов
Этимология
Существительное и глагол
Латинская функция-, функция производительность, от грибов выполнять; Вероятно, сродни санскриту Bhuṅkte . Он наслаждается
Перво известным использованием
Существительное
1533, по значению, определенному в смысле 2
Глагол
1856, по значению определено в смысле 1
Time Traveler
9000 2 9000 2
2
9 Первое известное использование функция была в 1533 г.
Другие слова того же года Фуншал
функция
функционер
Посмотреть другие записи поблизости
Процитировать эту запись0003
«Функция». Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/function. По состоянию на 26 ноября 2022 г.
Copy Citation
Kids Definition
function 1 из 2
функция ˈfəŋ(k)-shən
1
: профессиональная работа или обязанности : род занятий
2
а
: особая цель, для которой лицо или вещь специально приспособлены или используются или для которой существует вещь
функция ножа режущая
б
: естественное или правильное действие части тела в живом существе
функция сердца
3
: большая важная церемония или светское мероприятие
4
а
: математическое отношение, которое ставит в соответствие ровно один элемент одного набора каждому элементу того же или другого набора
б
: нечто (качество, черта или измерение), определяемое или основанное на чем-то другом
рост функция возраст у детей
бесполезный
-ləs
имя прилагательное
функция
2 из 2
: служить определенной цели : работа
Медицинское определение
функция 1 из 2
функция ˈfəŋ(k)-shən
: любое из группы связанных действий, способствующих более крупному действию
особенно : нормальный и специфический вклад частей тела в экономику живого организма
см.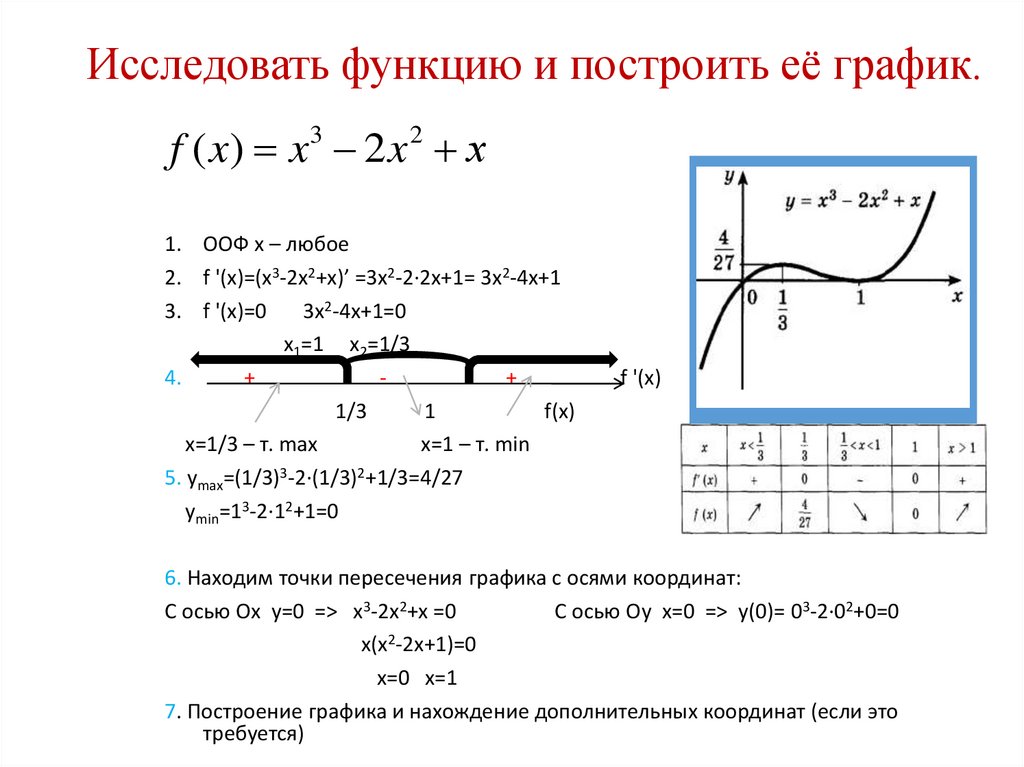
жизненная функция
бесполезный
-ləs
имя прилагательное
функция
2 из 2
: иметь функцию
функции дрожи для поддержания тепла тела
More from Merriam-Webster on
functionNglish: Translation of function for Spanish Speakers
Britannica English: Translation of function for Arabic Speakers
Britannica.com: Encyclopedia article about function
Последнее обновление: — Обновлены примеры предложений
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
Что такое исполнительная функция? | Понимание
Исполнительная функция – это набор умственных способностей, включающих рабочую память, гибкое мышление и самоконтроль.
Мы используем эти навыки каждый день, чтобы учиться, работать и управлять повседневной жизнью. Проблемы с исполнительной функцией могут затруднить концентрацию внимания, выполнение указаний и управление эмоциями, среди прочего.
Снимок: что такое исполнительная функция
Некоторые люди называют исполнительную функцию «системой управления мозга». Это потому, что необходимые навыки позволяют нам ставить цели, планировать и добиваться цели. Когда люди борются с исполнительной функцией, это сказывается на них дома, в школе и в жизни.
Существуют три основные области исполнительной функции. К ним относятся:
- Рабочая память
- Когнитивная гибкость (также называемая гибким мышлением)
- Ингибирующий контроль (включая самоконтроль)
Исполнительная функция отвечает за многие навыки, в том числе:
- Концентрация внимания
- Организация, планирование и расстановка приоритетов
- Начало задач и сосредоточение на них до завершения
- Понимание различных точек зрения
- Регулирование эмоций
- Самоконтроль (отслеживание того, что вы делаете)
Навыки управляющей функции обычно быстро развиваются в раннем детстве и в подростковом возрасте.
Но они продолжают развиваться до середины 20-х годов. Когда дети подрастают, некоторые из них могут на какое-то время отставать от сверстников. Однако по мере взросления у них может быть меньше проблем, как у подростков и молодых людей.
Погрузитесь глубже
- Узнайте больше о различных областях исполнительной функции.
- Узнайте об одном дне из жизни ребенка, у которого есть проблемы с этими навыками.
- Узнайте, что значит для детей самообладание.
Проблемы с исполнительной функцией могут по-разному влиять на людей. Трудности часто выглядят как признаки СДВГ. Это потому, что СДВГ — это проблема исполнительной функции.
Люди, испытывающие трудности с исполнительными навыками, могут:
- Имеют проблемы с началом и/или завершением задач
- Имеют трудности с расстановкой приоритетов задач
- Забывают то, что они только что услышали или прочитали
- Имеют проблемы с выполнением инструкций или последовательностью шагов
- Паника при изменении правил или процедур
- Имеют проблемы с переключением сосредотачиваться с одной задачи на другой
- Становятся чрезмерно эмоциональными и зацикливаются на вещах
- Имеют проблемы с организацией своих мыслей
- Имеют проблемы с учётом своих вещей
- Имеют проблемы с управлением своим временем
Проблемы с исполнительными функциями не являются диагнозом или неспособностью к обучению.
Но это характерно для людей, которые учатся и думают по-другому. У всех с СДВГ есть проблемы с этим. И многие люди с трудностями в обучении также борются с исполнительной функцией.
Эти трудности могут вызвать проблемы с обучением. Но они не означают, что люди ленивы или неразумны. Люди, которые борются с исполнительной функцией, так же умны и работают так же усердно, как и другие люди.
Погрузитесь глубже
- Узнайте о повседневных проблемах молодых людей, у которых проблемы с исполнительными функциями.
- Для семей: узнайте о поддержке в школе, которая может помочь детям, у которых проблемы с исполнительными функциями.
- Для преподавателей: получите основанную на фактах стратегию поведения, чтобы помочь учащимся, испытывающим затруднения.
Возможные причины проблем с исполнительными функциями
Было проведено множество исследований причин проблем с исполнительными функциями и СДВГ. Вот два основных фактора.
1. Различия в развитии мозга. Исследователи изучили исполнительную функцию мозга. Они обнаружили, что определенные области мозга развиваются медленнее у людей, которые борются с исполнительными навыками. Эти области отвечают за рабочую память и эмоциональный контроль.
2. Гены и наследственность. У людей, у которых есть проблемы с исполнительными функциями, часто есть члены семьи, у которых они тоже есть.
Кроме того, проблемы с исполнительной функцией часто возникают при проблемах с обучением.
Неспособность к обучению не всегда связана с нарушением исполнительной функции. Но дети с или , например, нередко также испытывают трудности с исполнительными навыками. Узнайте, как проблемы с исполнительной функцией могут повлиять на чтение и математику.
Низкая скорость обработки не является проблемой исполнительной функции. Но с ним могут возникнуть проблемы. Узнайте больше о медленной скорости обработки.
Нырнуть глубже
- Узнайте, как различия в мозге могут повлиять на исполнительную функцию и зрелость.
- Взгляните на СДВГ и мозг.
Диагностика и лечение нарушений исполнительной функции
Диагноза расстройства исполнительной функции не существует. Но есть специальные тесты, которые рассматривают широкий спектр исполнительных навыков. Эти навыки включают:
- Внимание
- Ингибирующий контроль
- Рабочая память
- Организация и планирование
- Формирование концепции
- Переключение набора (способность переключаться с одной задачи на другую)
- Генерация слов и идей
Тестирование должно проводиться как часть полной оценки, которая рассматривает многие области обучения и мышления. Эти оценки, которые школы проводят бесплатно, часто проводят психологи. Но есть и другие типы профессионалов, которые проводят этот тип тестирования.
Некоторые из этих специалистов предлагают такие методы лечения и подходы, как:
Поведенческая терапия и когнитивно-поведенческая терапия (КПТ).
Поведенческая терапия помогает людям заменить негативное поведение на позитивное. КПТ помогает детям справляться с мыслями и чувствами и управлять поведением.
Лекарства. Нет лекарств только для исполнительной функции, но есть лекарства от СДВГ.
Школьные услуги. Школьные психологи могут работать с детьми, чтобы разработать стратегии, которые помогут развить социальные навыки и управлять поведением. Учителя специального образования могут работать с детьми над развитием академических, социальных и организационных навыков. Они также могут работать над стратегиями управления поведением.
Организационный коучинг. Это консультанты, которых вы можете нанять. Они не репетиторы, которые помогают развивать академические навыки. Вместо этого они работают над формированием навыков организации и тайм-менеджмента. Они также могут работать над навыками обучения. Узнайте больше об организационных тренерах.
- Для семей: ознакомьтесь с нашим руководством по проблемам исполнительной функции у детей.
