Производная функции в точке (в картинках)
Приводятся определения, теоремы, свойства и методы вычислений производной функции в точке в сжатом виде – в виде изображений. Каждая картинка снабжена ссылкой на страницу с подробным изложением материала.
Далее приводятся главные картинки раздела «Производная функции в точке». На них изображены основные понятия и формулы дифференцирования. Каждое изображение снабжено заголовком, описанием и ссылкой на страницу с подробным изложением материала. Пройдя по этой ссылке можно посмотреть доказательство выбранного правила и примеры его применения. Также, просматривая картинки, можно освежить в памяти основные понятия, связанные с вычислением производных.
Определение производной и основные понятия
Производная функции в точке – определения, теоремы и свойства
Приводятся формулировки определений, теорем и свойств производной функции одной переменной в точке. Даны методы вычислений производных и формулы производных элементарных функций.
Рассмотрены производные и дифференциалы высших порядков.
Примеры решений производных
Страница содержит ссылки на 51 пример решений производных.
Физический смысл производной
На примере из механики показывается, что мгновенная скорость движения точки равна производной координаты этой точки по времени. Ускорение равно производной скорости по времени, или второй производной ее координаты по времени. Аналогичным образом, мгновенная скорость изменения любой физической величины равна производной этой величины по времени.
Определение производной функции в точке
Определение производной функции в точке. Примеры вычисления производных, используя определение. Односторонние производные справа и слева. Лемма об односторонних производных.
Дифференцируемые функции в точке – определение и свойства
Определение дифференцируемой функции одной переменной в точке. Важность понятия дифференцируемости для функций, зависящих от многих переменных. Доказательство теорем: об эквивалентности дифференцируемости и существованием производной; о непрерывности дифференцируемой функции.
Геометрический смысл производной
Проведен анализ геометрического смысла производной. Выявлено, что производная функции в точке связана с углом наклона касательной, проведенной к графику функции в рассматриваемой точке. Дано определение касательной, и получено ее уравнение. Рассмотрены случаи, когда производная равна бесконечности.
Касательная и нормаль к графику функции
Уравнения касательной и нормали к графику функции в точке. Определения, подкасательной и поднормали. Угол между двумя кривыми. Полезные формулы аналитической геометрии. Примеры решения задач на составления уравнений касательной и нормали, и на вычисление угла между кривыми.
Первый дифференциал функции в точке
Определение первого дифференциала функции, его суть и геометрический смысл. Доказательство арифметических свойств и инвариантности формы первого дифференциала.
Таблица производных элементарных функций
Представлена таблица производных элементарных функций для обучающихся студентов.
Приводится таблица производных сложных функций. Даны основные правила дифференцирования.
Методы вычисления производных
Правила дифференцирования — основные формулы вычисления производных
В кратком виде даны правила дифференцирования (формулы вычисления производных). Ссылки на страницы с подробным описанием выбранного правила.
Производная постоянной функции (константы)
Производная постоянной (константы). Вынесение постоянной за знак производной. Примеры вычисления производных. Пример вычисления производной от функции, составленной из корней.
Производная суммы и разности функций
Приведена формула производной суммы и разности функций. Приведено доказательство и подробно разобраны примеры применения этой формулы.
Производная произведения двух функций
Формула производной произведения двух функций. Доказательство и подробно разобранные примеры применения этой формулы.
Формула Лейбница для n-й производной произведения двух функций
Приводится формула Лейбница для вычисления n-й производной произведения двух функций.
Дано ее доказательство двумя способами. Рассмотрен пример вычисления производной n-го порядка.
Производная дроби из двух функций
Формула производной дроби из двух функций. Доказательство двумя способами. Подробно разобранные примеры дифференцирования частного.
Доказательство формулы производной сложной функции
Приводится доказательство формулы производной сложной функции. Подробно рассмотрены случаи, когда сложная функция зависит от одной и двух переменных. Производится обобщение на случай произвольного числа переменных.
Примеры применения формулы производной сложной функции
Приводятся примеры вычисления производных с применением формулы производной сложной функции.
Теорема о производной обратной функции
Приводится доказательство теоремы о производной обратной функции. Приводятся примеры применения этой теоремы.
Вычисление производных с помощью логарифмической производной
Приводятся примеры вычисления производных с помощью логарифмической производной.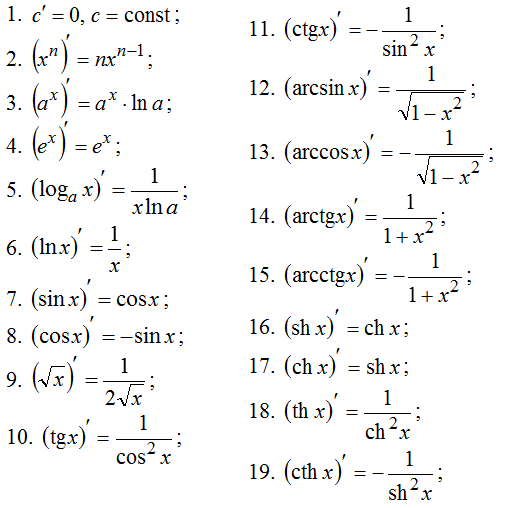
Вычисление производных степенно-показательных функций
Определение степенно-показательной функции. Вывод формулы для вычисления ее производной. Подробно разобраны примеры вычисления производных степенно-показательных функций.
Примеры вычисления производных высших порядков явных функций
Рассмотрены примеры вычисления производных высших порядков явных функций. Даны полезные формулы для вычисления производных n-го порядка.
Производная функции, заданной параметрическим способом
Формула производной функции, заданной параметрическим способом. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка.
Производная функции, заданной неявно
Формула производной функции, заданной неявно. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка.
Производные элементарных функций (вывод формул)
Производные основных элементарных функций и их вывод
Представлены производные основных элементарных функций и ссылки на страницы с их выводом.
nx. Формулы производных высших порядков.
Производная степенной функции (степени и корни)
Вывод формулы производной степенной функции (x в степени a). Рассмотрены производные от корней из x. Формула производной степенной функции высшего порядка. Примеры вычисления производных.
Производные тригонометрических функций
Представлены производные тригонометрических функций. Доказательство и вывод формул. Производные высшего порядка для синуса и косинуса.
Производная синуса: (sin x)′
Представлено доказательство и вывод формулы для производной синуса — sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка.
Производная косинуса: (cos x)′
Представлено доказательство и вывод формулы для производной косинуса — cos(x). Примеры вычисления производных от cos 2x, cos 3x, cos nx, косинуса в квадрате, в кубе и в степени n. Формула производной косинуса n-го порядка.
Производная тангенса: (tg x)′
Представлен вывод формулы для производной тангенса — tg(x).
Примеры вычисления производных от tg 2x, tg 3x и tg nx. Производная тангенса n-го порядка в виде многочлена по степеням tg(x).
Производная котангенса: (ctg x)′
Представлен вывод формулы для производной котангенса — ctg(x). Дана формула производной котангенса n-го порядка в виде многочлена по степеням ctg(x). Коэффициенты этого многочлена связаны рекуррентным соотношением.
Вывод производных обратных тригонометрических функций
Представлены производные обратных тригонометрических функций и вывод их формул. Также даны выражения производных высших порядков. Ссылки на страницы с более подробным изложением вывода формул.
Вывод производных арксинуса (arcsin x)′ и арккосинуса (arccos x)′
Представлен вывод производных первого порядка арксинуса (arcsin x)′ и арккосинуса (arccos x)′. Для каждой из функций, вывод дан двумя способами.
Вывод производных высших порядков арксинуса (arcsin x) и арккосинуса (arccos x)
Представлен вывод производных высших порядков арксинуса (arcsin x).
Формулы производных арксинуса второго, третьего, четвертого и пятого порядка. Производная n-го порядка выражается через многочлен и корень. Даны уравнения для многочленов и вывод значений их коэффициентов. Выражение производной n-го порядка арккосинуса через производную арксинуса.
Вывод производных арктангенса (arctg x)′ и арккотангенса (arcctg x)′
Представлен вывод производных первого порядка арктангенса (arctg x)′ и арккотангенса (arcctg x)′. Для каждой из функций, вывод дан двумя способами.
Вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x)
Представлен вывод производных высших порядков арктангенса (arctg x) и арккотангенса (arcctg x). Производные даны в двух видах — выраженные через независимую переменную x и через арктангенс (арккотангенс). Вычислены производные от второго до пятого порядка.
Производные высших порядков. Формула Тейлора
Содержание:
- Дифференциалы высших порядков
- Определение:
По этой ссылке вы найдёте полный курс лекций по математике:
| Решение задач по математике |
Пусть функция г = у) имеет частные производные и в каждой точке х области D.
Тогда эти производные будут функциями от х и у в области D, которые в свою очередь в точках области £ (во всех или в некоторых) могут иметь частные производные. Эти частные производные 01 и 5? (ее-™ они существуют) называются вторыми частными производными или частными производными второго порядка функции г = /(х,у).
Для функции 2 = /(х, у) двух независимых переменных х, у получаем четыре частные производные второго порядка, которые обозначаются так: Производные /Ц9 и называются смешанными: одна из них получается дифференцированием функции сначала по г, затем по у; другая, наоборот, дифференцированием сначала по у, затем по х. Аналогично определяются частные производные 3-го и т. д. порядков.
Пример. Найти частные производные 1-го и 2-го порядков от функции Обратим внимание на то, что смешанные производные z’iy и гЦх оказались тождественно равными. Это не случайно. Имеет место следующая теорема. Таорама 10 (о равенства смешанных производных). Пусть для функции Производные высших порядков Дифференциалы высших порядков формула Тейлора для функции нескольких переменных в некоторой окрестности точки М0(х о, У о) существуют производные пусть, кроме того, производные fxy и f,x в точке Afo(xo, Уо) непрерывны.
2 опыичаются между собой только порядком дифференцирования и непрерывны в некоторой точке, то они в этой точке имеют одно и то же значение. § 13.
Дифференциалы высших порядков
Пусть в области D задана функция z = /(ж, у) независимых переменных ж и у. Если эта функция дифференцируема в области D, то ее полный дифференциал в точке (ж, у) € D, соответствующий приращениям dx и dy независимых переменных ж, у, выражается формулой (здесь dx = Ax, dy = Ay — произвольные приращения независимых переменных, т. е. произвольныечисла, не зависящие от ж и у). Поэтому мы можем изменять х и у, оставляя dx и dy постоянными.
При фиксированных dx и dy полный дифференциал dz есть функция от ж и у, которая в свою очередь может оказаться дифференцируемой.
Определение:
Полный дифференциал от dz в точке (ж, у), соответствующий приращениям независимых переменных, равным прежним dx и dy, называется дифференциалом второго порядка функции z = /(ж, у) и обозначается символом d2z: Пусть функция z = /(ж, у) 6 C2(D), т.
Возможно вам будут полезны данные страницы:
| Задача сетевого планирования и управления (PERT) |
| Единицы измерения температуры давления объема |
| Интерполяция кусочно-полиномиальными функциями |
| Заказ №253440 готовое часть 2 |
Подобным же образом вводятся понятия дифференциалов 3-го, 4-го и т.д. порядков. Вообще, полный дифференциал n-го порядка dnz есть полный дифференциал от полного дифференциала (п — 1)-го порядка: Если функция , то у нее существует дифференциал n-го порядка.
Если х и у не являются независимыми переменными, а суть функции от ( и у, то, как и в случае функции одной переменной, уже второй дифференциал не обладает свойством инвариантности формы. В самом деле, пусть Тогда первый дифференциал может быть записан в прежнем виде но теперь сами есть функции и мог>т не быть постоянными.
| Поэтому так что инвариантностьформы вообше |
не имеет места. > . Формула Тейлора для функции нескольких переменных Пусть функция z = f(x, у) имеет непрерывные частные производные до n-го порядка включительно во всех точках (х, у) некоторой 6-окрестности точки (х0, уо) и пусть точка (х0 + Ах, уо + Ау) принадлежит этой окрестности (рис. 16). Положим где — новая независимая переменная.
Тогда так что величина г оказывается сложной функцией от t, определенной на отрезке [0,1] и имеющей там производные до порядка п включительно.
Поэтому можно представить формулой Тейлора по степеням t: Полагая t = 1, получим Выразим величины в правой части формулы (2) при помощи исходной функции f(x, у) и ее производных. Заметим, что аргументы х и у функции f(x,y) являются функциями от t, но имеют постоянные дифференциалы фиксированные числа).
Поэтомудля вычисления последовательныхдифференциалов функции z = /(х, у) применима формула откуда При * = 0 в силу соотношений (1) имеем У = Уо»и формула (3) принимает вид При t = 0 получаем Заметим еще, что . Подставляя выражения в равенство (2), получим, что Это — формула Тейлора для функции z = /(х, у) двух переменных, а — остаточный член этой формулы в форме Лагранжа.
Приведем сокращенную форму записи формулы Тейлора. Перенося первое слагаемое правой части формулы (7) в левую часть и обозначая разность через получаем, что Формулой (8) пользуются для приближенного вычисления приращения Д/ функции 2 = /(z, у) в точке Мо{хо,уо). При достаточно малых по модулю значениях Ах и Ду и при df Ф 0 за приращение функции Д/ приближенно можно принять дифференциал df.
Это означает, что в правой части формулы Тейлора (8) берется только одно первое слагаемое. Если приближенное равенство Д/ w df не дает требуемой точности, то для повышения точности можно воспользоваться дальнейшими членами формулы Тейлора (8). Пример. Разложить функцию Производные высших порядков Дифференциалы высших порядков формула Тейлора для функции нескольких переменных по формуле Маклорена с остаточным членом 3-го порядке.
•4 Формула Тейлора (7) с остаточным членом Я3 имеет вид Формула Маклорена получается из нее, если положить В данном случае Таким образом, формула Маклорена принимает вид Замечание 1. Нетрудно заметить, что формулу Маклорена можно записать так: однородный многочлен it-ой степени относительно
Высокая неотъемлемая производная формула — Русские Блоги
Высокая неотъемлемая производная формула
Теги: Высокий интеграл
Интегральная формула резюме
Формула искажения:
Директива и дифференциал
Есть два определения исчисления:
1, классическое прокаливание
Это интуитивное и удобное определение понимания.
Первые дифференциалы определяют небольшие вариации. Например, функция y = f (x) dx — это небольшое изменение количества x, то Dy — это небольшое изменение в Y dx. Производное также определено из него: это соотношение двухминутных переменных = DY / DX. Следовательно, производное также известно как микрофон. Это классическое определение, видно, что он очень легко понять.
2, основываясь на пределе исчисления.
Хотя классический исчислений интуитивно понятен, но не является строгим, изобретено новое определение исчисления, которое основано на пределе исчисления. Производное сначала строго определяется как предел:
Затем дифференциал определяется на основе производной: (от Wiki)
Как видно из определения, дифференциальный DY определяется как функция, эта функция Y True VariationΔyΔyЛинейное приближение.ΔyΔyс участиемΔxΔxЭто нелинейные отношения, но DY иΔxΔxЭто линейные отношения. Так что в точке х,ΔxΔxПри приближении 0, значение в линейной зависимости является производная функции в X.
F:
Видно, что DY также можно понять как небольшое изменение количества, такого как классическое значение исчисления, но только смысл больше
неопределенный интеграл
Определение неравития
Прежде всего, ясно, что необходимо различать интегралы и установить точки. Из концепции это совершенно другое.
Неопределенные моменты — это данная функция, ищая процесс оригинальной функции с постоянным сроком. Поэтому результат развехнутого интеграла является функцией. Напротив, результат, полученный фиксированной интеграцией, является значением.
Рассчитайте метод неупорядоченной интеграции:
1, базовая интеграция таблицы
2, нет очков не соответствуют добавке, безжалостно. (Две свойства линейной карты!)
3, первый метод изменения элемента
На этот раз временно рассматривается как неопределенный интеграл. Строго говоря, DX этот символ в интегральном выражении является частью общего и не представляет концепцию дифференциала. Однако, если DX используется в качестве дифференциала, согласно дифференциальному определению, изменение первого изменения модуля является разумным, поскольку этот процесс фактически заменен другим дифференцированным.
4, второй изменение элемента
Второй метод изменения изменений является противоположный процесс метода первого преобразования. Разложите DX, X можно рассматривать как функцию, однако X может быть преобразован в любую функцию, поэтому метод ингредиента второго изменения более гибкий и сложный.
5, метод отраслевого интеграла
Это метод умножения производной.
Интеллектуальная рекомендация
Четыре метода, прототипы и прототипные цепи JavaScript создают объекты
1. Создайте объекты: Все объекты в JavaScript создаются путем построения функций. Функции в JS также являются объектом, и это специальный объект 2. Прототип объект: 1. Если сам объект является функцие…
Рекомендовать Android обычно используемый плагин
Установка Android Studio Установка Plugquin-in: файл -> Настройки -> Плагины -> Просмотр репозиториев -> Введите плагин, который вы хотите установить 1. Color Manager: после установки ренд…
Imports Pycharm Импорт работает Советы по аннотации
Pycharm имеет красную ошибку при импорте пользовательского модуля, но время выполнения нормально, показывать сообщение об ошибке: No module named test1 less.
.. (Ctrl+F1) Inspection info: This in…
[SOGOU] Найти строку, содержащую наименьшую строку всех персонажей
Строка содержит N символов, где есть M разные символы, N >> m, найдите наименьшее время и пространство, чтобы найти кратчайшую строку, содержащую все M-символы, не учитывайте специальные символы…
Построение среды программирования Python (в системе Windows)
1 загрузка установочного пакета Python 2 Установите Python 3 О IDLE 4 Как запустить программу на Python 4.1 Интерактивное программирование на Python 4.2 Написание исходных файлов кода Python Поскольку…
Вам также может понравиться
Android Динамическое разрешение приложения
Android6.0 Динамические разрешения приложения Добавить связанные разрешения в файле инвентаризации Проверьте разрешение — Разрешения динамического приложения — Результаты Метод выполнения…
| Dijkstra Multi -Shortest Path | 1003 появление (25 баллов)
link…
Шаги перевода и компиляции языка C
Переведите Сначала изображение выше, изображение взято из C и указателя: Как видно на рисунке, исходная программа может состоять из одного или нескольких исходных файлов, которые преобразуются в соотв.
..
Oracle Create Table Space и пользователей
…
Общие модули и их работа
Справочник статей 1 модуль времени и даты и времени модуль времени модуль даты и времени 2 случайных модуля 3. ос модуль 4 повторный модуль 1 модуль времени и даты и времени модуль времени В питоне об…
производных формул | Superprof
Что такое производная?
Производная определяется как мгновенная скорость изменения функции в любой заданной точке. Эта мгновенная скорость изменения также известна как наклон. Общее обозначение производной функции дается следующей функцией:
Другими словами, мы можем сказать, что производная функции — это скорость изменения y по отношению к x. Интеграция функции обратна производной. Процесс вычисления производной известен как дифференцирование. В этой статье мы изучим некоторые производные правила или правила дифференцирования вместе с соответствующими примерами.
Лучшие репетиторы по математике
Поехали
Производная константы
Производная постоянной функции равна нулю.
Пример
Если a является константой, то следующая функция будет иметь нулевую производную:
Здесь мы представили производную функции через . Мы также можем представить производную функцию через . Оба обозначения используются для представления производной функции.
Производная постоянной, кратной
Если нам нужно найти производную функции, в которой константа умножается на функцию, то мы берем производную функции и умножаем на нее константу. Общие обозначения этого правила приведены ниже:
Если , то
Пример 1
Найдите производную функции .
Решение
В приведенной выше функции константа 7 умножается на переменную . Итак, сначала мы напишем 7 как есть, а в скобках возьмем производную от кубической переменной.
Чтобы получить производную кубической функции, мы использовали правило степени, которое гласит, что если , то .
Теперь умножьте 7 на член в скобках, чтобы получить окончательное значение .
Пример 2
Найдите производную функции .
Решение
Вы можете заметить, что в приведенной выше функции дробь умножается на квадрат переменной . Следовательно, мы можем записать функцию как произведение дроби и переменной следующим образом:
Теперь воспользуемся правилом степени производной, чтобы получить производную функции, заключенной в скобки:
Мы получим следующий окончательный ответ после упрощения приведенной выше производной:
Производная x
Производная равно 1, потому что, когда мы применим правило мощности, мы получим показатель степени 0 переменной . Поскольку , следовательно, как правило, мы можем сказать, что производная равна 1. Математически это можно записать как:
Если , то
Правило производной степени
Мы уже использовали это правило при дифференцировании функций в приведенных выше примерах. Степенное правило производной выражается как:
Если , то
Пример
Найдите производную функции .
Решение
Мы просто применим правило степени производной, чтобы найти производную приведенной выше функции. Поскольку в приведенной выше функции значение n равно 10, следовательно, производная функции будет записана следующим образом, используя это значение n:
Производная корня
Правило производной корня объясняется ниже математически:
Если , то
Вышеприведенная формула для производной функции, которая включает квадратный корень. Если вам нужно найти производную функции корня, отличной от квадратного корня, то следует использовать следующую формулу:
Если , то
Поясним вышеприведенное правило на следующих примерах.
Пример 1
Найдите производную функции
Решение
Производная члена внутри корневого символа равна 6. Используя формулу квадратного корня производной, мы запишем окончательный ответ следующим образом:
Чтобы упростить приведенный выше ответ , мы просто разделим числитель и знаменатель на 2:
Пример 2
Найдите производную функции
Решение
Чтобы найти производную указанной выше функции, используйте формулу .
Можно также записать как:
Производная суммы или разности
Производная суммы или разности двух чисел равна производной отдельных членов. Если m и n два слагаемых, то их производная будет вычисляться следующим образом:
Если , то
Пример 1
Найдите производную функции .
Решение
Чтобы найти производную вышеприведенной функции, мы воспользуемся правилом сумм производных, которое работает путем нахождения производной отдельных членов, участвующих в ней. Производная от 2x вычисляется по степенному правилу, а производная от 4x равна 4. Следовательно, производная всей функции приведена ниже:
Пример 2
Найдите производную функции .
Решение
Найдите производные отдельных членов функции. Производная от is и производная от 5x равна 5.
Правило производного произведения
Математическая запись правила производного произведения приведена ниже:
Если , то
Приведенное выше правило поясняется следующим примером.
Пример
Найдите производную функции .
Решение
Найдите производную отдельных факторов, входящих в указанную выше функцию. Производная is и производная 5x равна 5. Следовательно, используя формулу , тогда , мы запишем производную всей функции следующим образом: выражается математически как:
Если , то
Пример
Найдите производную функции .
Решение
Производная члена равна 18x, а производная члена 2x равна 2. Мы подставим эти значения в формулу производной в частном, которая говорит, что если , то :
Производное правило взаимности
Производное правило взаимности математически обозначается следующим образом:
Если , то
Пример
Найдите производную функции
Решение
Так как приведенная выше функция имеет обратную форму, поэтому мы будем использовать формулу производной, чтобы найти производную. Производная функции равна .
Подставьте это значение в формулу, чтобы получить производную:
Разделите члены в числителе и знаменателе на — 8x:
Производная экспоненциальной функции
Производная экспоненциальной функции математически обозначается как :
Если , то
Пример
Найдите производную показательной функции .
Решение
Мы найдем производную вышеприведенной функции в четыре шага:
Шаг 1 — Сначала запишем функцию как она есть
Шаг 2 — Найдите производную функции в степени. Производная функции в показателе степени представляет собой линейное уравнение. Мы знаем, что производная линейной функции равна ее наклону, поэтому ее производная будет равна 6,9.0005
Шаг 3 — Найдите логарифм основания. База в приведенной выше функции равна 5, поэтому ее журнал будет записан как .
Шаг 4 — Мы получим производную всей функции путем умножения членов, полученных в шагах 1, 2 и 3:
Производная логарифмической функции
Математическая запись производной логарифмической функции приведен ниже:
Если , то
Пример
Найдите производную логарифмической функции .
Решение
Сначала найдите производную от 7x. Производная от 7x равна 7. Подставьте это значение в формулу.
Производная функции синуса
Математическое обозначение этого правила производной приведено ниже:
Если , то
Пример
Найдите производную функции
4 Подставьте это значение в формулу.
Производная функции косинуса
Производная функции косинуса математически обозначается следующим образом:
Если , то
Пример
Найдите производную функции
Решение
Производная члена равна 7. Подставляя это значение в формулу, мы получится:
Производная функции тангенса
Производная функции тангенса математически обозначается следующим образом:
Если , то
В приведенной выше формуле cos представляет функцию косинуса, а sec представляет функцию секанса.
Пример
Найдите производную функции тангенса.
Решение
Производная члена 3x равна 3. Подставьте это значение в формулу тангенса, чтобы получить следующий ответ: . Мы используем правило цепочки производных, когда у нас есть функция внутри другой функции. Математически правило производной цепи обозначается следующим образом:
Если есть , то его производная равна
Пример
Найдите производную функции .
Решение
Мы не можем решить приведенную выше функцию, используя любое из приведенных выше правил дифференцирования, кроме цепного правила, потому что это составная функция. Есть функция внутри другой функции. Сначала у нас есть функция, а затем мы берем куб всей функции. Можно сказать и так. Когда мы напишем функцию в виде , мы получим функцию .
Используя правило цепочки производных, мы запишем производную функции следующим образом:
После упрощения мы можем переписать ее следующим образом:
Производная по первому принципу | Brilliant Math & Science Wiki
Содержание
- Производная по первому принципу
- Односторонняя производная
- Решение проблем
Производная — это просто мера скорости изменения.
Это может быть скорость изменения расстояния по отношению ко времени или температуры по отношению к расстоянию. Мы хотим измерить скорость изменения функции y=f(x) y = f(x) y=f(x) относительно ее переменной x x x.
Общее понятие скорости изменения величины y y y по отношению к xxx представляет собой изменение yyy, деленное на изменение xxx относительно точки aaa. Это описывает
f(x)−f(a)x−a. \frac{f(x) — f(a)} {x — a}. х-аф(х)-f(а).
Чтобы найти мгновенную скорость изменения, мы берем предельное значение, когда xx x приближается к aaa. Чтобы упростить это, мы устанавливаем x=a+h x = a + h x=a+h и хотим взять предельное значение, когда h h h приближается к 0. Таким образом, мы имеем
limh→0f(a+h)− ф(а)ч. \lim_{h \rightarrow 0 } \frac{f(a+h) — f(a)} {h}. h→0limhf(a+h)−f(a).
(Обратите внимание на двусторонние пределы.) Если этот предел существует и конечен, то мы говорим, что 9{n-1}.
\ _\квадрат
\конец{массив}
dxdf(x)=limh→0hf(2+h)−f(2)=limh→0h(2+h)n−(2)n=limh→0h3n+(1n )2n−1⋅h+(2n)2n−2⋅h3+⋯+hn−2n=limh→0h(1n)2n−1⋅h+(2n)2n−2⋅h3+⋯+hn =limh→0[(1n)2n−1+(2n)2n−2⋅h+⋯+hn−1]=n2n−1. □
Оцените производную от sinx\sin x sinx при x=a x=ax=a, используя первый принцип, где a∈R a \in \mathbb{R} a∈R.
Здесь f(x)=sinxf(x) = \sin xf(x)=sinx и c=ac=ac=a. Используя первый принцип, мы можем написатьddxf(x)=limh→0f(a+h)−f(a)h=limh→0sin(a+h)−sin(a)h=limh→0sinacos h+cosasinh−sinah=limh→0[sina(cosh−1h)+cosa(sinhh)]=sinalimh→0(cosh −1h)+cosalimh→0(sinhh)=sina⋅(0)+cosa⋅(1)=cosa. □\begin{массив}{л л} \frac{\text{d}}{\text{d}x} f(x) & = \lim_{h \to 0} \frac{f(a + h) — f(a)}{h} \ \ & = \lim_{h \to 0} \frac{ \sin (a + h) — \sin (a)} }{h} \\ & = \lim_{h \to 0} \frac{ \sin a \cos h + \cos a \sin h — \sin a }{h} \\ & = \lim_{h \to 0}\left[ \sin a \bigg( \frac{\cos h-1}}{h} \bigg) + \cos a \bigg(\frac{\sin h}}{h } \bigg)\справа] \\ & = \sin a \lim_{h \to 0} \bigg( \frac{\cos h-1}}{h} \bigg) + \cos a \lim_{h \to 0} \bigg( \frac{\ sin ч {ч} \bigg) \\ & = \sin a\cdot (0) + \cos a \cdot (1) \\ & = \cos a.
\ _\квадрат \end{массив}dxdf(x)=limh→0hf(a+h)−f(a)=limh→0hsin(a+h)−sin(a)=limh→0 hsinacosh+cosasinh−sina=limh→0[sina(hcosh−1)+cosa(hsinh)]=sinalimh→0(hcosh−1)+cosalimh→0(hsinh)=sina⋅ (0)+коса⋅(1)=коза. □ 9nxn и sinx,\sin x,sinx, вы могли бы просто понять, что полученные выше значения являются просто значениями производных при x=2x=2x=2 и x=a,x=a,x=a, соответственно. Фактически, все стандартные производные и правила выведены с использованием первого принципа. Вы можете попытаться вывести те, используя принцип для дальнейшего упражнения, чтобы познакомиться с оценкой производной через предел.
Рассмотрим функцию f:[a,b]→R,f : [a,b] \rightarrow \mathbb{R}, f:[a,b]→R, где a,b∈R a, b \ в \mathbb{R} a,b∈R. Как правило, производная определяется только для значений в интервале (a,b) (a,b) (a,b). Пусть c∈(a,b) c \in (a,b) c∈(a,b) число, при котором измеряется скорость изменения.
Сначала рассмотрим интервал (c,c+ϵ), (c, c+ \epsilon ),(c,c+ϵ), где ϵ \epsilon ϵ число, сколь угодно близкое к нулю.
Скорость изменения (m)(m)(m) определяется выражением f(x2)−f(x1)x2−x1 \frac{f(x_2) — f(x_1)}{x_2 — x_1} x2− x1f(x2)−f(x1). Таким образом, для заданного значения δ \delta δ скорость перехода от c cc к c+δ c + \delta c+δ может быть определена как
m=f(c+δ)−f(c)(c+ δ)−c. m = \frac{ f(c + \delta) — f(c) }{(c+ \delta ) — c}.m=(c+δ)−cf(c+δ)−f(c). 9-} \frac{ f(c + h) — f(c) }{h}.m−=h→0−limhf(c+h)−f(c).
Функция fff называется производной в ccc, если m+=m− m_+ = m_- m+=m−. Равное значение называется производной от fff при ccc.
Предел limh→0f(c+h)−f(c)h \lim_{h \to 0} \frac{ f(c + h) — f(c) }{h} limh→0 hf(c+h)−f(c), если она существует (согласно вышеприведенным условиям), является производной fff в точке ccc, и метод нахождения производной по такому пределу называется производной по первому принципу .
Часто предел также выражается как ddxf(x)=limx→cf(x)−f(c)x−c\frac{\text{d}}{\text{d}x} f( x) = \lim_{x \to c} \frac{ f(x) — f(c) }{x-c} dxdf(x)=limx→cx−cf(x)−f(c) .
Производная по первому принципу часто используется в тех случаях, когда необходимо определить пределы, включающие неизвестную функцию, а иногда и саму функцию.
Функция удовлетворяет следующему уравнению:
limh→0f(4h)+f(2h)+f(h)+f(h3)+f(h5)+f(h8)+⋯h=64. \lim_{h \to 0} \frac{ f(4h) + f(2h) + f(h) + f\big(\frac{h}{2}\big) + f\big(\frac{h }{4}\big) + f\big(\frac{h}{8}\big) + \cdots}{h} = 64. h→0limhf(4h)+f(2h)+f(h )+f(2h)+f(4h)+f(8h)+⋯=64.
Учитывая, что f(0)=0 f(0) = 0 f(0)=0 и что f′(0) f’(0) f′(0) существует, определить f′(0) f’(0 ) f′(0).
На первый взгляд кажется, что вопрос вообще не касается первого принципа, а просто касается свойств пределов.
Что ж, на самом деле это связано с простым свойством пределов, но суть заключается в применении первого принципа. Может быть, сейчас это не так ясно, но просто запишем производную от fff в 000 по первому принципу:
f′(0)=limh→0f(0+h)−f(0)h=limh→0f(h)−(0)h=limh→0f(h)h.
Это несколько общая схема терминов в данном пределе. Это намекает на то, что может быть какая-то связь с каждым из членов данного уравнения с f′(0). f'(0).f'(0). Рассмотрим предел limh→0f(nh)h \lim_{h \to 0}\frac{f(nh)}{h} limh→0hf(nh), где n∈R. п \in \mathbb{R}. n∈R. Это довольно просто. Пусть t=nh t=nh t=nh. Тогда при h→0,t→0 h \to 0 , t \to 0 h→0,t→0, и поэтому заданный предел принимает вид limt→0nf(t)t=nlimt→0f(t) t, \lim_{t \to 0}\frac{nf(t)}{t} = n \lim_{t \to 0}\frac{f(t)}{t},limt→0tnf(t )=nlimt→0tf(t), что есть не что иное, как nf′(0) n f’(0) nf′(0). Теперь это, вероятно, делает следующие шаги не только очевидными, но и простыми:
limh→0f(4h)+f(2h)+f(h)+f(h3)+f(h5)+f(h8)+⋯h=limh→0f(4h)h+f( 2h)h+f(h)h+f(h3)h+⋯=4f′(0)+2f′(0)+f′(0)+12f′(0)+⋯=f′(0)(4 +2+1+12+14+⋯ )=f′(0)×8=64.
Учитывая, что f′(1)=c f'(1) = c f′(1)=c (существует и является конечным), найдите нетривиальное решение для f(x)f(x) f(x).
Предыдущий вопрос дает нам необходимое опережение:f′(1)=limh→0f(1+h)−f(1)h=p (назовем это p).\displaystyle f'(1) =\lim_{h \to 0}\frac{ f(1+h) — f(1)}{h} = p \ (\text{назовем это}p).f′(1)=h→0limhf(1+h)−f(1) =p (назовем это p).
Проанализируем данное уравнение. Для m=1, m=1,m=1 уравнение принимает вид f(n)=f(1)+f(n) ⟹ f(1)=0 f(n) = f(1) +f(n ) \ подразумевает, что f (1) = 0 f (n) = f (1) + f (n) ⟹ f (1) = 0. Более того, чтобы найти функцию, нам нужно правильно использовать данную информацию. Выражение, включающее производную при x=1 x=1 x=1, скорее всего, получится, когда мы продифференцируем данное выражение и приравняем одну из переменных к единице.
Но подождите, мы на самом деле не знаем дифференцируемость функции. Либо мы должны это доказать, либо установить соотношение, подобное f′(1) f’(1) f′(1) из данного соотношения. Это означает, что в любом случае мы должны использовать первый принцип!
Пусть m=x m =x m=x и n=1+hx, n = 1 + \frac{h}{x}, n=1+xh, где xxx и hhh — действительные числа. Тогда у нас есть
f(x(1+hx))=f(x)+f(1+hx) ⟹ f(x+h)−f(x)=f(1+hx). f\Bigg( x\left(1+\frac{h}{x} \right) \Bigg) = f(x) + f\left( 1+ \frac{h}{x} \right) \ подразумевает f (x+h) — f(x) = f\left( 1+ \frac{h}{x} \right).
Разделить обе части на hhh и приблизить hhh к 000:
limh→0f(x+h)−f(x)h=limh→0f(1+hx)h. \lim_{h \to 0}\frac{f(x+h) — f(x)}{h} = \lim_{h \to 0} \frac{f\left( 1+ \frac{h}{ х} \справа) {ч}. h→0limhf(x+h)−f(x)=h→0limhf(1+xh).
Левая часть уравнения представляет f′(x),f’(x), f′(x), и если правый предел существует, то должен существовать и левый предел, и, следовательно, мы сможет оценить f′(x)f’(x) f′(x). Рассмотрим правую часть уравнения:
limh→0f(1+hx)h=limh→0f(1+hx)−0h=1xlimh→0f(1+hx)−f(1)hx. \lim_{ h \to 0} \frac{ f\Big( 1+ \frac{h}{x} \Big) }{h} = \lim_{ h \to 0} \frac{ f\Big( 1+ \frac{h}{x} \Big) — 0 }{h} = \frac{1}{x} \lim_{ h \to 0} \frac{ f\Big( 1+ \frac{h}{x } \Big) -f(1) }{\frac{h}{x}}. h→0limhf(1+xh)=h→0limhf(1+xh)−0=x1h→0limxhf(1+xh)−f(1).
Окончательное выражение равно 1x\frac{1}{x} x1, умноженному на производную в точке 1 (\big((с помощью замены t=hx) t = \frac{h}{x}\big) t= xh), который считается существующим, подразумевая, что f′(x) f’(x) f′(x) существует.
Это стандартное дифференциальное уравнение, решение которого выходит за рамки этой вики. Поскольку f(1)=0 f(1) = 0 f(1)=0 (((положим m=n=1 m=n=1 m=n=1 в данном уравнении),),), функция есть f(x)= ln x. \displaystyle \boxed{f(x) = \text{ln}x}. f(x)= ln x. □_\квадрат□
Примечание. Если бы нам не было известно, что функция дифференцируема в 0, то мы не можем заключить, что f(x)=cxf(x) = cx f(x)=cx. (См. Функциональные уравнения.)
Рассмотрим кусочную функцию 9+} \frac{ \sin (0 + h) — (0) }{h} \\ & = \lim_{h \to 0} \frac{ \sin h}{h} \\ & = \в коробке{1}. \end{выровнено}m+=h→0+limhf(0+h)−f(0)=h→0+limhsin(0+h)−(0)=h→0lim hsin=1.
Для f(0+h) f(0+h) f(0+h), где h h h — небольшое положительное число, мы будем использовать функцию, определенную для x>0 x > 0 x>0, поскольку hhh положительно и, следовательно, уравнение.
Аналогично имеем
m−=limh→0−f(0+h)−f(0)h=limh→0−(0+h)2−(0)h=limh→0h3h=0.
Теперь для f(0+h) f(0+h) f(0+h), где h h h — небольшое отрицательное число, мы будем использовать функцию, определенную для x<0 x < 0 x<0, поскольку hhh отрицательно и, следовательно, уравнение.
Но подождите, m+≠m− m_+ \neq m_- m+=m−!! Это означает, что производная функции в точке 000 вообще не существует!!
Так что на самом деле этот пример был выбран, чтобы показать, что первый принцип также используется для проверки «дифференцируемости» такой кусочной функции, которая подробно обсуждается в другой вики. Такие функции необходимо проверять сначала на непрерывность, а затем на дифференцируемость. Кроме того, если бы мы знали, что функция дифференцируема, на самом деле нет необходимости вычислять как m+ m_+ m+, так и m− m_-m−, потому что оба должны быть равны и конечны, и, следовательно, должен оцениваться только один из них. легче вычислить производную.
Итак, ответ таков, что f′(0) f’(0) f′(0) не существует. □_\square□
Цитировать как: Производная по первому принципу. Brilliant.org . Извлекаются из https://brilliant.org/wiki/derivative-by-first-principle/
Формулы производных — объяснение, правила, примеры решений и часто задаваемые вопросы
Производные — один из фундаментальных инструментов, широко используемых для решения различных задач на исчисление и дифференциальные уравнения. Это одна из важных тем исчисления. Вопросы, основанные на производных, задают не только в школе, но и на конкурсных экзаменах, таких как JEE Main, JEE advance и т. д. Даже концепции производных используются для решения различных реальных задач, таких как расчет прибыли и убытков бизнеса. , проверка изменения температуры, определение скорости или пройденного расстояния, например километров в час, миль в час и т.
Следовательно, учащиеся должны хорошо разбираться в формулах производных и правилах производных. Здесь вы найдете список всех формул производных, а также правила производных, которые помогут вам решать различные задачи на дифференцирование.
Производная в математике
В математике производная — это метод, показывающий мгновенную скорость изменения, то есть величину, на которую функция изменяется в данный момент времени. Производные часто представляются как $\dfrac{dy}{dx}$ (пишется как $dy$ над $dx$, что означает, что разница в $y$ делится на разницу в $x$). $d$ в $\dfrac{dy}{dx}$ не является переменной и не может быть отменено. Другим распространенным представлением производной является $f’(x)$, означающее производную функции $f$ в точке $x$.
Определение производной
Пусть $f(y)$ — функция, область определения которой включает открытый интервал относительно некоторой точки $y_0$. Тогда, поскольку функция $f(y)$ считается дифференцируемой в точке $y_0$, а производная от $f(y)$ в точке $y_0$ задается как:
$f'(y_0)= \underset{y \to 0}{lim} \dfrac{\Delta x}{\Delta y} = \underset{y \to 0}{lim} \dfrac{f(y_0 + \Delta y) — f(y_0)}{\ Delta y}$
Список всех формул производных
Найдите список всех формул производных:
Общие производные формулы
Функции
$ $ \ DFRAC a Alans $ $ $ \ DFRAC a Alans $ $ $ \ DFAC a Alans $ $ $ \ DFAC a Almy $ $ vmal.
$\dfrac{d}{dx} (x) = 1$
$\dfrac{d}{dx} \sqrt{x} = \dfrac{1}{2\sqrt{x} } $
$\dfrac{d}{dx}\sqrt{f(x)}=\dfrac{1}{2\sqrt{f(x)}}\dfrac{d}{dx} f(x)= \dfrac{1}{\sqrt{2f(x)}}f'(x)$
$\dfrac{d}{dx} k \cdot f(x) = k\dfrac{d}{dx} f(x) = k \cdot f'(x)$
Derivatives of Logarithmic Function
Functions
Derivatives
$\dfrac{d}{dx} In x$
$\dfrac{1} {x}$
$\dfrac{d}{dx} log_a x$
$\dfrac{1}{x In a}$
$\dfrac{d}{dx} In f(x)$
$\dfrac{f'(x)}{f (x)}$
$\9054 dfrac{d}{dx} log_a f(x)$
$\dfrac{1}{f(x) In a} \dfrac{d}{dx}f(x)$
Производные формулы экспоненциальной функции
Функции
$
91 $1 $74444441 $.Derivatives of Trigonometric Functions Formulas
Functions
Derivatives
$\dfrac{d }{dx} (sin(x))$
$cos (x)$
$\dfrac{d}{dx} (cos(x))$
$-sin (x)$
$\dfrac{d}{dx} (tan(x))$
92}$Derivatives of Hyperbolic Functions
Function
Derivative
$\dfrac{d}{dx} (sinh x ) $
$ cosh x $
$ \ dfrac {D} {DX} (COSH x) $
70572$ SINH X $
$ SINH X $
$
$
$
$
$
$
.
\ _\квадрат
\end{массив}dxdf(x)=limh→0hf(a+h)−f(a)=limh→0hsin(a+h)−sin(a)=limh→0 hsinacosh+cosasinh−sina=limh→0[sina(hcosh−1)+cosa(hsinh)]=sinalimh→0(hcosh−1)+cosalimh→0(hsinh)=sina⋅ (0)+коса⋅(1)=коза. □
9nxn и sinx,\sin x,sinx, вы могли бы просто понять, что полученные выше значения являются просто значениями производных при x=2x=2x=2 и x=a,x=a,x=a, соответственно. Фактически, все стандартные производные и правила выведены с использованием первого принципа. Вы можете попытаться вывести те, используя принцип для дальнейшего упражнения, чтобы познакомиться с оценкой производной через предел.
Пусть 0<δ<ϵ 0 < \delta < \epsilon 0<δ<ϵ .
\begin {выровнено}
f'(0) & = \lim_{h \to 0} \frac{f(0 + h) — f(0)}{h} \\
& = \lim_{h \to 0} \frac{f(h) — (0)}{h} \\
& = \lim_{h \to 0} \frac{ f(h)}{h}.
\end{align}f′(0)=h→0limhf(0+h)−f(0)=h→0limhf(h)−(0)=h→0limhf(h ).
\begin{выровнено}
\lim_{h \to 0} \frac{ f(4h) + f(2h) + f(h) + f\big(\frac{h}{2}\big) + f\big(\frac{h }{4}\big) + f\big(\frac{h}{8}\big) + \cdots }{h}
= & \lim_{h \to 0} \frac{f(4h)}{h} + \frac{f(2h)}{h} + \frac{f(h)}{h} + \frac{f \big(\frac{h}{2}\big)}{h} + \cdots \\
= & 4 f'(0) + 2 f'(0) + f'(0) + \frac{1}{2} f'(0) + \cdots \\
= & f'(0) \left( 4+2+1+\frac{1}{2} + \frac{1}{4} + \cdots \right) \\
= & f'(0) \times 8\\
= &64.
\end{выровнено} h→0limhf(4h)+f(2h)+f(h)+f(2h)+f(4h)+f(8h)+⋯===== h→0limhf(4h)+hf(2h)+hf(h)+hf(2h)+⋯4f′(0)+2f′(0)+f′(0)+21 f′(0)+⋯f′(0)(4+2+1+21+41+⋯)f′(0)×864. 9{+} .f(mn)=f(m)+f(n)∀m,n∈R+.
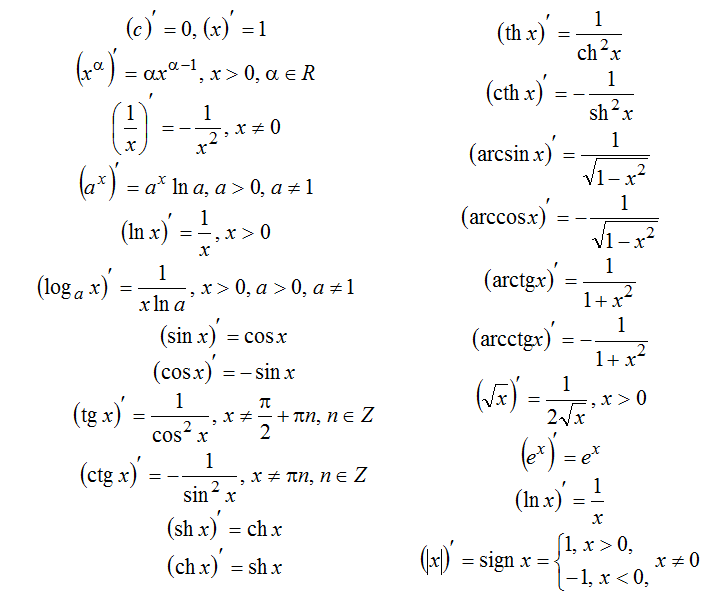f(x(1+xh))=f(x)+f(1+xh)⟹f(x+h)−f(x)=f(1+xh).
Следовательно, f′(x)=px f'(x) = \frac{p}{x} f′(x)=xp.
2}{h} \\
& = \в коробке{0}.
\end{выровнено}m−=h→0−limhf(0+h)−f(0)=h→0−limh(0+h)2−(0)=h→ 0limhh3=0.
д.
{f(x)}In af(x)$