Теория вероятностей
Теория вероятностей
ОглавлениеГлава 1. ВведениеПРЕДИСЛОВИЕ 1.  Теория вероятностей: 1.2. Краткие исторические сведения Глава 2. Основные понятия теории вероятностей 2.1. Событие. Вероятность события 2.2. Непосредственный подсчет вероятностей 2.3. Частота, или статистическая вероятность, события 2.4. Случайная величина 2.5. Практически невозможные и практически достоверные события. Принцип практической универсальности Глава 3. Основные теоремы теории вероятностей 3.1. Назначение основных теорем. Сумма и произведение событий 3.2. Теорема сложения вероятностей 3.3. Теорема умножения вероятностей 3.4. Формула полной вероятности 3.5. Теорема гипотез (формула Бейеса) Глава 4. Повторение опытов 4.1. Частная теорема о повторении опытов 4.2. Общая теорема о повторении опытов Глава 5. Случайные величины и их законы распределения 5.1. Ряд распределения. Многоугольник распределения 5.2. Функция распределения 5.3. Вероятность попадания случайной величины на заданный участок 5.  4. Плотность распределения 4. Плотность распределения5.5. Числовые характеристики случайных величин. Их роль и назначение 5.6. Характеристики положения (математическое ожидание, мода, медиана) 5.7. Моменты. Дисперсия. Среднее квадратичное отклонение 5.8. Закон равномерной плотности 5.9. Закон Пуассона Глава 6. Нормальный закон распределения 6.1. Нормальный закон распределения и его параметры 6.2. Моменты нормального распределения 6.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения 6.4. Вероятное (срединное) отклонение Глава 7. Определение законов распределения случайных величин на основе опытных данных 7.1. Основные задачи математической статистики 7.2. Простая статистическая совокупность. Статистическая функция распределения 7.4 Числовые характеристики статистического распределения 7.5. Выравнивание статистических рядов 7.6. Критерии согласия Глава 8.  Системы случайных величин Системы случайных величин8.1. Понятие о системе случайных величин 8.2. Функция распределения системы двух случайных величин 8.3. Плотность распределения системы двух случайных величин 8.4. Законы распределения отдельных величин, входящих в систему. Условные законы распределения 8.5 Зависимые и независимые случайные величины 8.6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции 8.7. Система произвольного числа случайных величин 8.8. Числовые характеристики системы нескольких случайных величин Глава 9. Нормальный закон распределении дли системы случайных величин 9.1. Нормальный закон на плоскости 9.2 Эллипсы рассеивания. Приведение нормального закона к каноническому виду 9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания 9.4. Вероятность попадания в эллипс рассеивания 9.5. Вероятность попадания в область произвольной формы 9.6. Нормальный закон в пространстве трех измерений.  Общая запись нормального закона для системы произвольного числа случайных величин Общая запись нормального закона для системы произвольного числа случайных величинГлава 10. Числовые характеристики функций случайных величин 10.1. Математическое ожидание функции. Дисперсия функции 10.2. Теоремы о числовых характеристиках 10.3. Применения теорем о числовых характеристиках Глава 11. Линеаризация функций 11.1. Метод линеаризации функций случайных аргументов 11.2. Линеаризация функции одного случайного аргумента 11.3. Линеаризация функции нескольких случайных аргументов Глава 12. Законы распределения функций случайных аргументов 12.1. Закон распределения монотонной функции одного случайного аргумента 12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону 12.3. Закон распределения немонотонной функции одного случайного аргумента 12.4. Закон распределения функции двух случайных величин 12.5. Закон распределения суммы двух случайных величин.  Композиция законов распределения Композиция законов распределения12.6. Композиция нормальных законов 12.7. Линейные функции от нормально распределенных аргументов 12.8. Композиция нормальных законов на плоскости Глава 13. Предельные теоремы теории вероятностей 13.1. Закон больших чисел и центральная предельная теорема 13.2. Неравенство Чебышева 13.3. Закон больших чисел (теорема Чебышева) 13.4. Обобщенная теорема Чебышева. Теорема Маркова 13.5. Следствия закона больших чисел: теоремы Бернулли и Пуассона 13.6. Массовые случайные явления и центральная предельная теорема 13.7. Характеристические функции 13.8. Центральная предельная теорема для одинаково распределенных слагаемых 13.9. Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении Глава 14. Обработка опытов 14.1. Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения 14.2. Оценки для математического ожидания и дисперсии 14.  3. Доверительный интервал. Доверительная вероятность 3. Доверительный интервал. Доверительная вероятность14.4. Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону 14.5. Оценка вероятности по частоте 14.6. Оценки для числовых характеристик системы случайных величин 14.8. Сглаживание экспериментальных зависимостей по методу наименьших квадратов Глава 15. Основные понятия теории случайных функций 15.1. Понятие о случайной функции 15.2. Понятие о случайной функции как расширение понятия о системе случайных величин. Закон распределения случайной функции 15.3. Характеристики случайных функций 15.4. Определение характеристик случайной функции из опыта 15.5. Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций 15.6. Линейные и нелинейные операторы. Оператор динамической системы 15.7. Линейные преобразования случайных функций 15.7.1. Интеграл от случайной функции 15.  7.2. Производная от случайной функции 7.2. Производная от случайной функции15.8. Сложение случайных функций 15.9. Комплексные случайные функции Глава 16. Канонические разложения случайных функций 16.1. Идея метода канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций 16.2. Каноническое разложение случайной функции 16.3. Линейные преобразования случайных функций, заданных каноническими разложениями Глава 17. Стационарные случайные функции 17.1. Понятие о стационарном случайном процессе 17.2. Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий 17.3. Спектральное разложение стационарной случайной функции на бесконечном участке времени. Спектральная плотность стационарной случайной функции 17.4. Спектральное разложение случайной функции в комплексной форме 17.5. Преобразование стационарной случайной функции стационарной линейной системой 17.6. Применения теории стационарных случайных процессов к решению задач, связанных с анализом и синтезом динамических систем 17.  17.8. Определение характеристик эргодической стационарной случайной функции по одной реализации Глава 18. Основные понятия теории информации 18.1. Предмет и задачи теории информации 18.2. Энтропия как мера степени неопределенности состояния физической системы 18.3. Энтропия сложной системы. Теорема сложения энтропий 18.4. Условная энтропия. Объединение зависимых систем 18.5. Энтропия и информация 18.6. Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии 18.7. Энтропия и информация для систем с непрерывным множеством состояний 18.8. Задачи кодирования сообщений. Код Шеннона-Фэно 18.9. Передача информации с искажениями. Пропускная способность канала с помехами Глава 19. Элементы теории массового обслуживания 19.1. Предмет теории массового обслуживания 19.2. Случайный процесс со счетным множеством состояний 19. 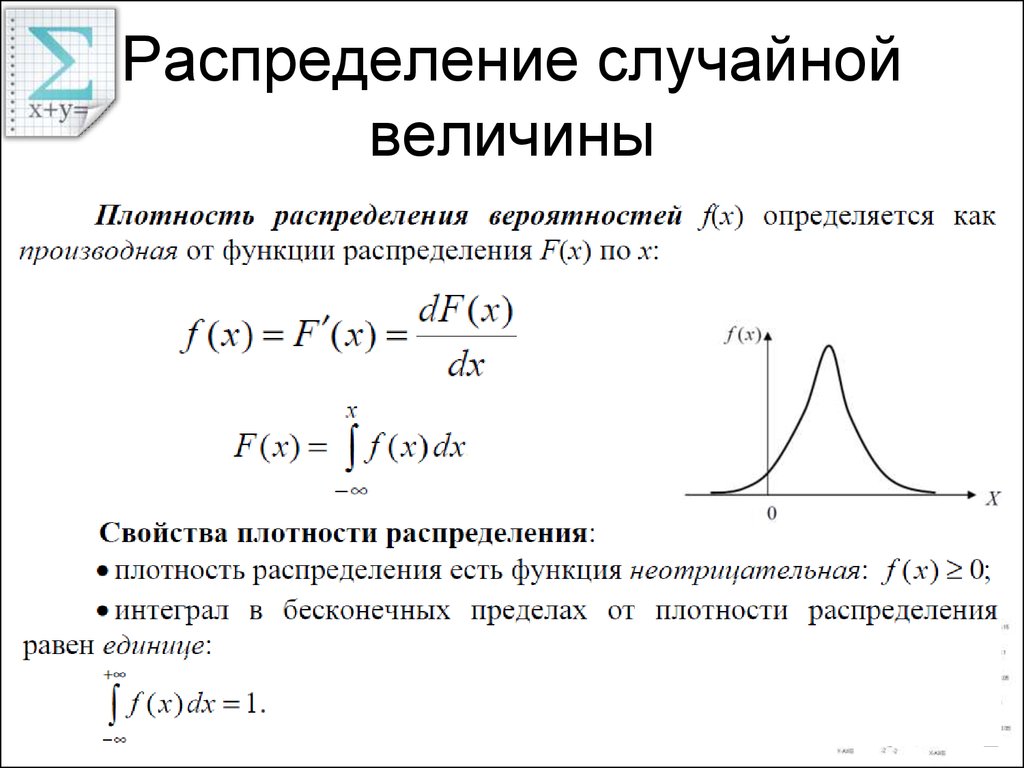 3. Поток событий. Простейший поток и его свойства 3. Поток событий. Простейший поток и его свойства19.4 Нестационарный пуассоновский поток 19.5. Поток с ограниченным последействием (поток Пальма) 19.6. Время обслуживания 19.7. Марковский случайный процесс 19.8. Система массового обслуживания с отказами. Уравнения Эрланга 19.9. Установившийся режим обслуживания. Формулы Эрланга 19.10. Система массового обслуживания с ожиданием 19.11. Система смешанного типа с ограничением по длине очереди Приложения Таблица 1 Значения нормальной функции распределения Таблица 2. Значения экспоненциальной функции Таблица 3. Значения нормальной функции Таблица 4. Значения “хи-квадрат” в зависимости от r и p Таблица 5. Значения удовлетворяющие равенству Таблица 6. Таблица двоичных логарифмов целых чисел от 1 до 100 Таблица 8. Значения распределение Пуассона |
Функция НОРМ.РАСП — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще. ..Меньше
..Меньше
Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция очень широко применяется в статистике, в том числе при проверке гипотез.
Синтаксис
НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
Аргументы функции НОРМ.РАСП описаны ниже.
-
X Обязательный. Значение, для которого строится распределение.
-
Среднее Обязательный. Среднее арифметическое распределения.
-
Стандартное_откл Обязательный.
 Стандартное отклонение распределения.
Стандартное отклонение распределения. -
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если имеется истина, норм. Функция DIST возвращает накопительную функцию распределения; Если этот ложь, возвращается функция плотности вероятности.
Замечания
-
Если число или standard_dev не является числом, то норм. DIST возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если standard_dev ≤ 0, норм. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
org/ListItem»>
-
Уравнение для плотности нормального распределения (аргумент «интегральная» содержит значение ЛОЖЬ) имеет следующий вид:
-
Если аргумент «интегральная» имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x.
Если значение «среднее» = 0, «стандартное_откл» = 1 и «интегральная» = ИСТИНА, то функция НОРМ.РАСП возвращает стандартное нормальное распределение, как функция НОРМ.СТ.РАСП.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД.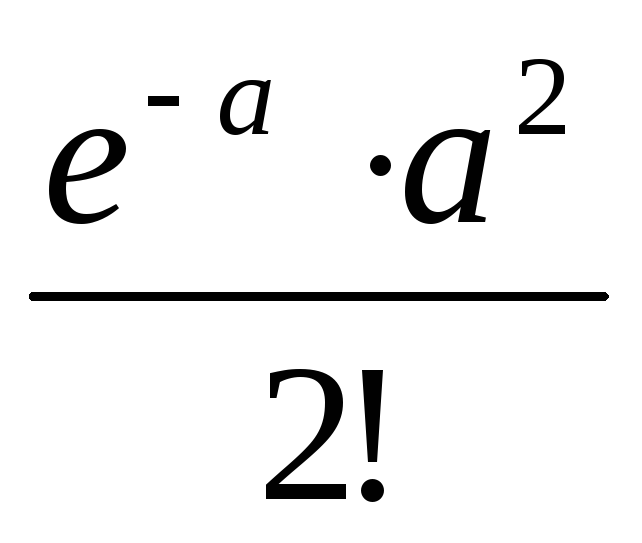 При необходимости измените ширину столбцов, чтобы видеть все данные.
При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
42 |
Значение, для которого нужно вычислить распределение |
|
|
40 |
Среднее арифметическое распределения |
|
|
1,5 |
Стандартное отклонение распределения |
|
|
Формула |
Описание |
Результат |
|
=НОРМ. |
Интегральная функция распределения для приведенных выше условий |
0,9087888 |
|
=НОРМ.РАСП(A2;A3;A4;ЛОЖЬ) |
Функция плотности распределения для приведенных выше условий |
0,10934 |
Распределение вероятностей — определение, формулы, примеры
Распределение вероятностей — это функция, которая дает относительную вероятность возникновения всех возможных исходов эксперимента. Есть две важные функции, которые используются для описания распределения вероятностей. Это функция плотности вероятности или функция массы вероятности и кумулятивная функция распределения.
В статистике могут быть два типа данных, а именно дискретные и непрерывные. Исходя из этого, распределение вероятностей можно разделить на дискретное распределение вероятностей и непрерывное распределение вероятностей. В этой статье мы узнаем больше о распределении вероятностей и различных аспектах, которые с ним связаны.
| 1. | Что такое распределение вероятностей? |
| 2. | Функция распределения вероятностей |
| 3. | Формулы распределения вероятностей |
| 4. | График распределения вероятностей |
| 5. | Функция распределения вероятностей и функция плотности вероятностей |
| 6. | Часто задаваемые вопросы о распределении вероятностей |
Что такое распределение вероятностей?
Распределение вероятностей — это функция, которая используется для определения вероятности всех возможных значений, которые может принимать случайная величина. Дискретное распределение вероятностей может быть описано функцией распределения вероятностей и функцией массы вероятностей. Точно так же функция распределения вероятностей и функция плотности вероятности используются для описания непрерывного распределения вероятностей. Биномиальное, Бернуллиевское, нормальное и геометрическое распределения являются примерами вероятностных распределений.
Дискретное распределение вероятностей может быть описано функцией распределения вероятностей и функцией массы вероятностей. Точно так же функция распределения вероятностей и функция плотности вероятности используются для описания непрерывного распределения вероятностей. Биномиальное, Бернуллиевское, нормальное и геометрическое распределения являются примерами вероятностных распределений.
Функция распределения вероятностей
Функция распределения вероятностей также известна как кумулятивная функция распределения (CDF). Если имеется случайная величина X, и ее значение оценивается в точке x, то функция распределения вероятностей дает вероятность того, что X примет значение, меньшее или равное x. Его можно записать как F(x) = P (X ≤ x). Кроме того, если существует полузамкнутый интервал, заданный (a, b], то функция распределения вероятностей задается формулой P (a < X ≤ b) = F (b) - F (a). Функция распределения вероятностей случайной величины всегда лежит между 0 и 1. Это неубывающая функция.0003
Это неубывающая функция.0003
Формулы распределения вероятностей
Распределение вероятностей случайной величины может быть описано функцией распределения вероятностей (CDF) и функцией массы вероятности (для дискретных случайных величин) или функцией плотности вероятности (для непрерывных случайных величин). В зависимости от типа распределения, за которым следует случайная величина, могут быть разные формулы для распределения вероятностей.
Вероятностное распределение случайной величины
Случайная величина может быть описана как переменная, которая может принимать возможные значения результата эксперимента. Случайные величины могут быть двух типов, а именно дискретные и непрерывные случайные величины. Ниже приведены различные формулы распределения вероятностей случайной величины.
Вероятностное распределение дискретной случайной величины
Дискретная случайная величина может быть определена как переменная, которая может принимать исчисляемые различные значения, такие как 0, 1, 2, 3. .. Формулы для функции распределения вероятностей и функции массы вероятности для дискретной случайной величины приведены ниже:
.. Формулы для функции распределения вероятностей и функции массы вероятности для дискретной случайной величины приведены ниже:
- Функция распределения вероятностей: F(x) = P (X ≤ x)
- Функция массы вероятности: p(x) = P(X = x)
Вероятностное распределение непрерывной случайной величины
Непрерывная случайная величина может быть определена как переменная, которая может принимать бесконечно много значений. Поскольку вероятность того, что непрерывная случайная величина примет точное значение, равна 0, следовательно, мы не можем использовать функцию массы вероятности (pmf) для описания такого распределения. Мы используем функцию плотности вероятности вместо pmf. Формулы распределения вероятностей непрерывной случайной величины приведены ниже: 9{2}}}\)
Распределение вероятностей геометрического распределения
Геометрическое распределение — это тип дискретного распределения вероятностей, где случайная величина X представляет количество испытаний Бернулли, необходимых для получения первого успеха. Исходом каждого испытания может быть либо успех (p), либо неудача (1 — p). Ниже приведены формулы распределения вероятностей геометрического распределения.
Исходом каждого испытания может быть либо успех (p), либо неудача (1 — p). Ниже приведены формулы распределения вероятностей геометрического распределения.
- Функция распределения вероятностей: F(x) = P (X ≤ x) = 1 — (1 — p) х
- Функция массы вероятности: P(X = x) = (1 — p) x — 1 p
Распределение вероятностей биномиального распределения
Биномиальное распределение — это еще один тип дискретного распределения вероятностей, который дает число успехов при проведении последовательности из n независимых экспериментов. Результатом каждого эксперимента может быть как успех, так и неудача. Обозначается как \(X\sim Bin(n,p)\) Формулы для распределения вероятностей биномиального распределения приведены ниже: 9{п — х}\)
График распределения вероятностей
График распределения вероятностей помогает наглядно представить распределение, которому следует данная случайная величина. Для непрерывных распределений площадь под кривой распределения вероятностей всегда должна быть равна единице. Это аналогично дискретным распределениям, где сумма всех вероятностей должна быть равна 1.
Это аналогично дискретным распределениям, где сумма всех вероятностей должна быть равна 1.
Для непрерывной случайной величины X функция плотности вероятности используется для получения графика распределения вероятностей. Предположим, что X лежит между a и b, тогда график распределения вероятностей задается следующим образом:
Если дискретная случайная величина подчиняется распределению вероятностей, такому как распределение Бернулли, то график распределения вероятностей имеет следующий вид:
Результат испытания Бернулли может быть равен 0 или 1. переменная X может принимать только значения 0 или 1, как показано на графике.
Функция распределения вероятностей и функция плотности вероятности
Для описания распределения вероятностей используются как функция распределения вероятности, так и функция плотности вероятности. Функция распределения вероятностей используется для суммирования распределения вероятностей случайной величины. Такая функция хорошо определена как для непрерывного, так и для дискретного распределения вероятностей. С другой стороны, функция плотности вероятности (PDF) может использоваться только для непрерывных распределений. Его можно определить как вероятность того, что непрерывная случайная величина X примет значение, лежащее между заданным диапазоном значений. Для дискретных распределений используется функция массы вероятности (pmf), аналогичная функции плотности вероятности. Эта функция дает вероятность того, что случайная величина точно примет определенное значение. Мы используем PDF вместо PMF для непрерывных распределений, поскольку вероятность того, что непрерывная случайная величина примет точное значение, равна 0,9.0003
Такая функция хорошо определена как для непрерывного, так и для дискретного распределения вероятностей. С другой стороны, функция плотности вероятности (PDF) может использоваться только для непрерывных распределений. Его можно определить как вероятность того, что непрерывная случайная величина X примет значение, лежащее между заданным диапазоном значений. Для дискретных распределений используется функция массы вероятности (pmf), аналогичная функции плотности вероятности. Эта функция дает вероятность того, что случайная величина точно примет определенное значение. Мы используем PDF вместо PMF для непрерывных распределений, поскольку вероятность того, что непрерывная случайная величина примет точное значение, равна 0,9.0003
Статьи по теме:
- Вероятность и статистика
- Экспериментальная вероятность
- Вероятностные правила
Важные замечания по распределению вероятностей
- Распределение вероятностей используется для описания всех возможных значений случайной величины и соответствующих им вероятностей появления.

- Может быть два типа распределения вероятностей. Это непрерывное распределение вероятностей (например, нормальное распределение) и дискретное распределение вероятностей (например, распределение Бернулли).
- Функция распределения вероятностей и функция плотности вероятности (PDF) могут использоваться для описания характеристик непрерывного распределения.
- Дискретное распределение может быть определено функцией массы вероятности (pmf) и функцией распределения вероятности.
Примеры распределения вероятностей
Пример 1: Если бросить две игральные кости, то каково будет распределение вероятностей суммы костей?
Решение: Возможные суммы, которые могут быть получены (2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12).
Предположим, что на первом кубике выпадает 1, а на втором кубике — 1. Тогда сумма будет равна 2. Поскольку никакая другая комбинация чисел не даст такой же суммы, следовательно, вероятность получения суммы 2 = 1/36. {n — x}\) 9{15 — 5}\) = 0,165
{n — x}\) 9{15 — 5}\) = 0,165
Ответ: Вероятность того, что вы попадете в яблочко ровно 5 раз, равна 0,165.Пример 3: Предположим, что игральная кость подбрасывается несколько раз. Какова вероятность того, что на кубике выпадет число меньше 6?
Решение: P(X < 6) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)
P(X < 6) = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 5/6
перейти к слайдуперейти к слайдуперейти к слайду
Разложите сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по распределению вероятностей
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о распределении вероятностей
Что подразумевается под распределением вероятностей?
Распределение вероятностей — это статистическая функция, которая связывает все возможные исходы эксперимента с соответствующими вероятностями.
Какова формула распределения вероятностей?
Существует два типа функций, которые используются для описания распределения вероятностей. Это функция распределения вероятностей и функция массы вероятности (дискретная случайная величина) или функция плотности вероятности (непрерывная случайная величина). Формулы для этих функций приведены ниже: 9{х}f(u)du\). Здесь f(u) — функция плотности вероятности.
Что такое распределение вероятностей случайной величины?
Распределение вероятностей случайной величины описывает, как вероятности результатов эксперимента распределяются по значениям случайной величины.
Что такое функция распределения вероятностей и кумулятивная функция распределения?
Функция распределения вероятностей и кумулятивная функция распределения совпадают. Он используется для описания распределения как непрерывной, так и дискретной случайной величины.
Что такое функция распределения вероятностей и функция плотности вероятности?
Функция плотности вероятности применима только к непрерывным случайным величинам. Это дает вероятность того, что значение случайной величины попадет в указанный интервал. Функция распределения вероятностей дает вероятность того, что значение случайной величины будет меньше или равно заданному результату.
Это дает вероятность того, что значение случайной величины попадет в указанный интервал. Функция распределения вероятностей дает вероятность того, что значение случайной величины будет меньше или равно заданному результату.
Для чего используется распределение вероятностей?
Распределение вероятностей широко используется при определении доверительных интервалов и вычислении критических областей для проверки гипотез (например, p-значения). Это используется в нескольких отраслях, которые ориентированы на науку о данных.
Скачать БЕСПЛАТНЫЕ учебные материалы
Таблица распределения вероятностей
Распределение вероятностей
Распределение вероятностей представляет собой таблицу или уравнение который связывает каждое возможное значение, которое случайная величина может принять с вероятностью его возникновения.
Примечание: Ваш браузер не поддерживает видео HTML5. Если вы просматриваете эту веб-страницу в другом браузере
(например, последняя версия Edge, Chrome, Firefox или Opera), вы можете посмотреть видеообработку этого урока.
Если вы просматриваете эту веб-страницу в другом браузере
(например, последняя версия Edge, Chrome, Firefox или Opera), вы можете посмотреть видеообработку этого урока.
Дискретные распределения вероятностей
Распределение вероятностей дискретный случайная величина всегда может быть представлена таблицей. Например, предположим, что вы подбрасываете монету два раза. Это просто упражнение может иметь четыре возможных результата: HH, HT, TH и TT. Теперь пусть переменная X представляет собой количество орлов, выпавших в результате броски монет. Переменная X может принимать значения 0, 1 или 2; и X — дискретная случайная величина.
В таблице ниже показаны вероятности, связанные с каждым возможное значение X. Вероятность выпадения 0 решек 0,25; 1 головка, 0,50; и 2 головы, 0,25. Таким образом, таблица пример распределения вероятностей для дискретной случайной величины.
| Количество головок, х | Вероятность, Р(х) |
|---|---|
| 0 | 0,25 |
| 1 | 0,50 |
| 2 | 0,25 |
Примечание: Учитывая распределение вероятности, вы можете найти
кумулятивные вероятности. Например,
вероятность выпадения 1 или менее решек [ P(X < 1) ] равна
P(X = 0) + P(X = 1), что равно 0,25 + 0,50 или 0,75.
Например,
вероятность выпадения 1 или менее решек [ P(X < 1) ] равна
P(X = 0) + P(X = 1), что равно 0,25 + 0,50 или 0,75.
Непрерывные распределения вероятностей
Распределение вероятностей непрерывный случайная величина представлена уравнением, называется Функция плотности вероятности (pdf). Все функции плотности вероятности удовлетворяют следующему условия:
- Суммарная площадь под кривой функции равна единице.
На приведенных ниже диаграммах показаны два непрерывных распределения вероятностей.
На первом графике показана функция плотности вероятности
описывается уравнением y = 1 в диапазоне от 0 до 1 и y = 0
в другом месте.
На втором графике показана функция плотности вероятности
описывается уравнением y = 1 — 0,5x в диапазоне от 0 до 2 и y = 0
в другом месте. Площадь под кривой равна 1 для
оба графика.
y = 1
y = 1 — 0,5x
Вероятность того, что непрерывная случайная величина попадет в интервал между a и b равен площадь под кривой PDF между a и b . Например, на первой диаграмме выше заштрихованная область показывает вероятность того, что случайная величина X будет падает между 0,6 и 1,0. Эта вероятность равна 0,40. А на втором графике заштрихованная область показывает вероятность падения между 1,0 и 2,0. Эта вероятность равна 0,25.
Примечание: При непрерывном распределении существует бесконечное количество
количество значений между любыми двумя точками данных. Как результат,
вероятность того, что непрерывная случайная величина примет
конкретное значение всегда равно нулю. Например, в обоих вышеперечисленных
диаграммы, вероятность того, что переменная X будет равна ровно 0,4 это ноль.
Реклама
Проверьте свои знания
Задача 1
Число взрослых, проживающих в домах на случайно выбранном городской квартал описывается следующей вероятностью распределение.
| Количество взрослых, х | Вероятность, P(x) |
|---|---|
| 1 | 0,25 |
| 2 | 0,50 |
| 3 | 0,15 |
| 4 или более | ??? |
Какова вероятность того, что 4 или более взрослых проживают в случайно выбранный дом?
(А) 0,10
(Б) 0,15
(С) 0,25
(Д) 0,50
(Э) 0,90
Решение
Правильный ответ А. Сумма всех вероятностей равна
к 1. Следовательно, вероятность того, что четыре или более взрослых
проживание в доме равно 1 — (0,25 + 0,50 + 0,15) или 0,10.

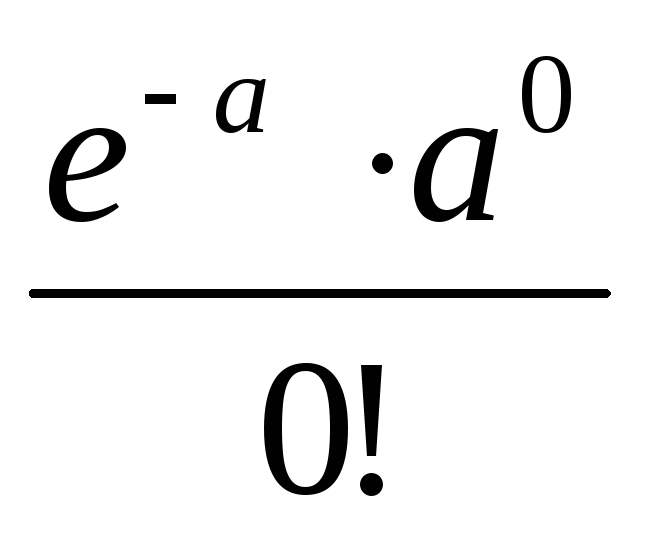 Стандартное отклонение распределения.
Стандартное отклонение распределения. РАСП(A2;A3;A4;ИСТИНА)
РАСП(A2;A3;A4;ИСТИНА)
 {n — x}\) 9{15 — 5}\) = 0,165
{n — x}\) 9{15 — 5}\) = 0,165