Комбинаторика — математика и искусство
- Математический анализ
- Математическая логика
- Комбинаторика
- Вероятность и статистика
- Тригонометрия
Другие разделы
Число, место и комбинация — три взаимно перекрещивающиеся, но отличные сферы мыщления, к которым можно отнести все математические идеи.
Д.Сильвестр.
КОМБИНАТОРИКА, раздел математики, в котором изучаются простейшие «соединения».
Перестановки — соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок
Размещения — соединения, содержащие по m предметов из числа n данных, различающиеся либо порядком предметов, либо самими предметами
Сочетания — соединения, содержащие по m предметов из n, различающиеся друг от друга, по крайней мере, одним предметом
Слово «комбинаторика» происходит от латинского combina — сочетать, соединять.
Это раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисление элементов) и отношения на них.
Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций.
Наиболее употребляемые комбинаторные конфигурации
Число размещений. Число упорядоченных различных k элементов некоторого n-элементного множества. Обозначается A nk, и вычисляется по формуле: A nk = n! / (n — k)!
Здесь и далее символ n! (читается n факториал) обозначает произведение всех натуральных чисел от 1 до n включительно. Считается, что 0!=1!=1.
Число перестановок. Число различных способов, которыми может быть упорядочено n-элементное множество. Обозначается P n, и вычисляется по формуле: P n=n!.
Зависимость между числом размещений, перестановок и сочетаний выражается формулой A nk=C nkP k.
Существует два основных правила, используемые при решение задач комбинаторики.
Правило суммы: пусть объект A можно выбрать m способами, а объект B — n способами, и существует k общих способов выбора объектов A и B одновременно, тогда один из объектов A или B можно выбрать (m + n — k) способами.
Правило произведения: пусть объект A можно выбрать m способами, а объект B — n способами, причем выбор B не зависит от выбора A, тогда пару объектов A и B можно выбрать m * n способами.
Комбинаторика развивалась параллельно с другими математическими теория, такими как алгебра, теория чисел, теория вероятно, с которыми комбинаторика тесно связана. Еще во 2 веке до нашей эры математикам Индии были известны формулы вычисляющие число сочетаний. Рождение комбинаторики как математического раздела связано с работами Блеза Паскаля и Пьера Ферма, положившими основу теории вероятности. Эти труды содержали принципы определения числа комбинаций элементов конечного множества, тем самым устанавливая связь комбинаторики с теорией вероятности.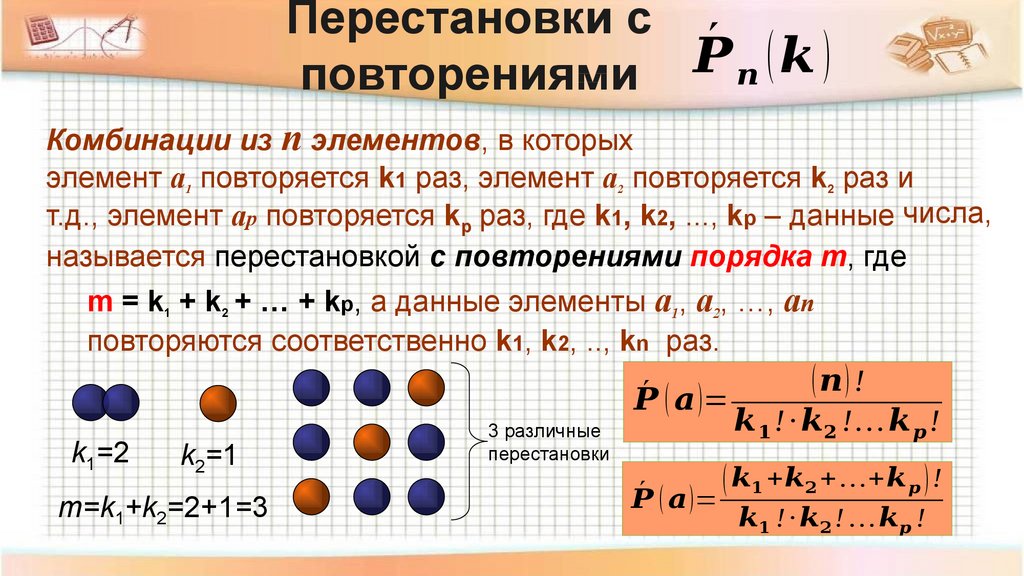
Понятие «комбинаторика» было введено Г. Лейбницем в 1666 году в работе «Рассуждения о комбинаторном искусстве», в которой так же приводится научное объяснение теории сочетаний и перестановок. Большой вклад в развитии комбинаторики имели работы Я. Бернулли, посвященные теории вероятности, в которых изложены некоторые комбинаторные понятия и указаны их применения к вычислению вероятностей. Бернулли так же впервые занимался изучение числа размещений.
В середине 20 века возрождается интерес к комбинаторике в связи с развитием дискретной математики и кибернетики, а так же в связи с широким использованием компьютеров.
Комбинаторика — один из разделов дискретной математики, который приобрел большое значение в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной технике, кибернетике. Так же она находит приложения во многих других областях наук: в биологии, где она занимается изучением состава белков и ДНК, в химии, физики, экономики, механике сложных сооружений и т.
д.
/БДЭМатематика/
Статья из журнала «Наука и жизнь»( рубрика Математические досуги)
БИНОМ НЬЮТОНА И ТРЕУГОЛЬНИК ПАСКАЛЯ
Сегодня, как и лет тридцать-сорок назад, абитуриенты на вступительных экзаменах в вуз традиционно опасаются вытянуть билет с вопросом о биноме Ньютона. (Автор формулы — великий английский физик, математик, астроном и философ сэр Исаак Ньютон.) Дело не только в том, что формула кажется сложной. Изучение её то включали в программу средней школы, то выводили за рамки основного курса, но в серьёзных вузах экзаменаторы спрашивали и продолжают спрашивать о биноме Ньютона.
На самом деле бояться тут особенно нечего. Бином Ньютона — формула разложения произвольной натуральной степени двучлена в многочлен. Каждый из нас знает наизусть формулы «квадрата суммы» (a+b)² и «куба суммы» (a+b)³, но при увеличении показателя степени с определением коэффициентов при членах многочлена начинаются трудности. Чтобы не совершить ошибку и применяется формула бинома Ньютона:
В более общем виде формула коэффициентов в биноме записывается так:
где k — порядковый номер слагаемого в многочлене.
n с коэффициентами 1. Ясно также, что всякий иной член многочлена выглядит как произведение определённых степеней каждого из слагаемых двучлена причём сумма степеней всегда равна n. Например, в выражении (a+b)³=а³+За²Ь+ЗаЬ²+Ь³ сумма степеней сомножителей во всех членах равна трём (3, 2+1,1+2,3). То же самое справедливо и для любой другой степени. Вопрос лишь втом, какие коэффициенты следует ставить при членах.
Видимо, для того чтобы облегчить труд школяров и студентов, великий французский математик и физик Блез Паскаль триста пятьдесят лет назад придумал специальный инструмент для определения этих самых коэффициентов — «треугольник Паскаля».
Строится он следующим образом. В вершине треугольника пишем 1. Единица соответствует выражению (a+b)⁰, поскольку любое число, возведённое в нулевую степень, даёт единицу. Достраивая треугольник, ниже пишем ещё по единице. Это коэффициенты разложения того же двучлена, возведённого в первую степень: (a+b)¹=a+b. Идём дальше. Стороны треугольника образуют единицы, а между ними — сумма двух единичек, находящихся сверху, то есть 2.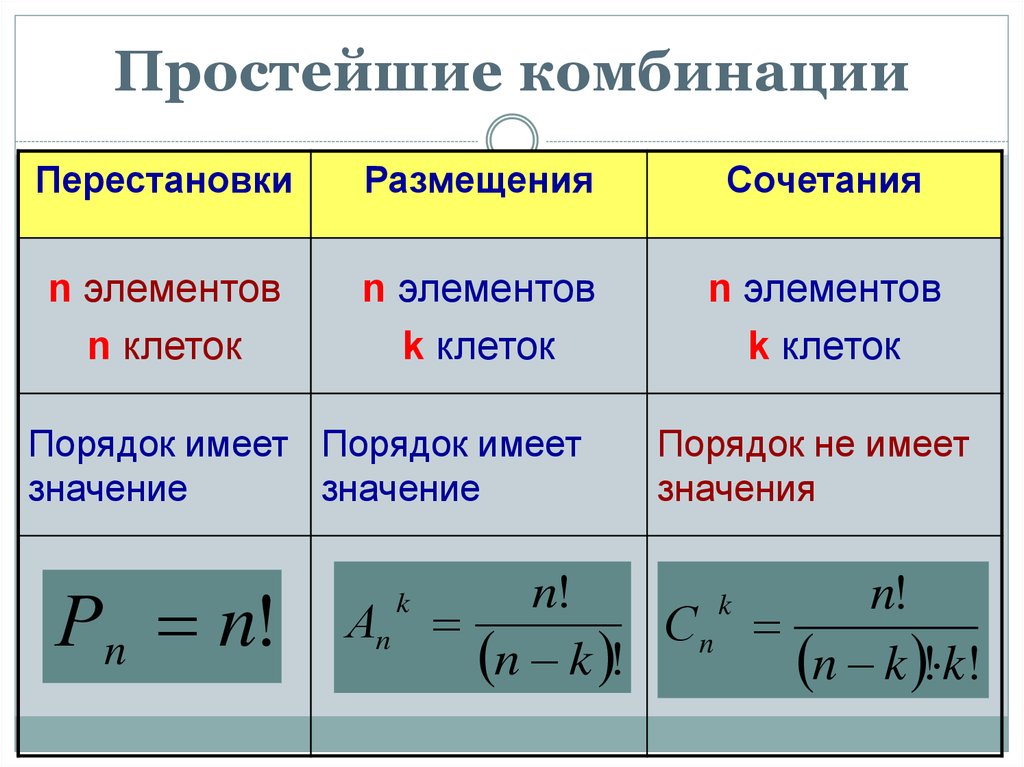
Следующий ряд, как и предыдущий, начинается и заканчивается единицами, а между ними — суммы цифр, находящихся сверху: 1, 3, 3, 1. Мы получили коэффициенты разложения « куба суммы ». Ряд коэффициентов двучлена четвёртой степени составят 1, 4, 6, 4, 1 и так далее.
Для примера с помощью треугольника Паскаля разложим в многочлен сумму двучленов в шестой степени:
(a+b)⁶=а⁶+6а⁵ Ь + 15а⁴ Ь² +20а³Ь³+ 15а² Ь⁴+6аЬ⁵+Ь⁶.
Всё очень несложно и запоминается на всю жизнь. Кстати, самостоятельно вспомнить и вывести формулу бинома Ньютона, нарисовав на черновике треугольник Паскаля, тоже намного проще.
Некоторые историки науки приписывают Блезу Паскалю авторство не только треугольника, позволяющего находить биномиальные коэффициенты, но и самой формулы бинома. Они считают, что Паскаль вывел её несколько раньше Ньютона, а тот лишь обобщил формулу для разных показателей степеней.
Главная | Алгебра | Геометрия | Математика | Другие разделы | Искусство | Галерея | Биографии | Цитаты | К уроку рисования | Разное | Главная Карта Сайта
расстройств
расстройство
Университет штата Иллинойс, математический факультет
MAT 305: Темы комбинаторики для K-8 Учителя |
Психозы | |||
Здесь мы применяем принцип включения-исключения к проблема расстройств :В жилом комплексе с к почтовыми ящиками, сколько способов может ли почтальон разослать k писем, одно из которых адресовано каждого почтового ящика, так что письмо не помещается в правильная коробка? Каждое из них называется расстройством .
Будем обращаться к письму по номеру и к почтовому ящику по номеру. Наша задача — определить количество способов спаривания букв и коробок так, чтобы никакие номера букв не совпадали с номерами ящиков. Если k = 1, то нет способы расстроить букву, ибо есть одна буква, которую нужно поместить в одну коробка. Если k = 2, мы можем поместить букву № 2 в коробку № 1 и букву № 1 в коробку. # 2, это единственное расстройство.
Когда у нас три буквы, получается 3! = всего 6 способов распространять их. Теперь пишем номера букв в том порядке, в котором они доставлены, например 1 3 2, указывая на то, что буква № 1 доставлена ящик №1, письмо №3 доставляется в ящик №2, письмо №2 доставляется в ящик №3. 6 возможных распределений для 3 букв:
.1 2 3 | 1 3 2 |
2 1 3 | 2 3 1 |
3 1 2 | 3 2 1 |
Схемы 2 3 1 и 3 1 2 являются единственными нарушениями трех
письма.
Суммируя наши результаты, используя D(n) для представления количество нарушений n букв, имеем D(1) = 0, D(2) = 1 и D(3) = 2. Есть предположения относительно D(4)? Давайте узнаем, что это такое.
Мы знаем, что их 4! = 24 способа распределить 4 буквы. Скорее
чем перечислить 24 случая, давайте рассмотрим, как включение-исключение
Принцип может помочь нам. Мы ищем количество способов разместить
числа в наборе {1,2,3,4} в строке так, что ни одно значение не встречается в его
естественное положение. Пусть X(1) представляет свойство, состоящее в том, что 1 встречается в
его естественное положение при перестановке 1,2,3,4. Тогда |Х(1)| = (1)*3!.
1 представляет 1 способ поместить 1 в ее естественное положение и
3! показывает количество способов переставить оставшиеся 3 значения.
Обратите внимание, что мы не рассматриваем, попадут ли какие-либо из 2,3,4 в
соответствующие им естественные положения. Точно так же мы могли бы утверждать, что
|Х(2)| = |Х(3)| = |Х(4)|. Поэтому есть 4*3! пути для ценности
находиться в своем естественном положении.
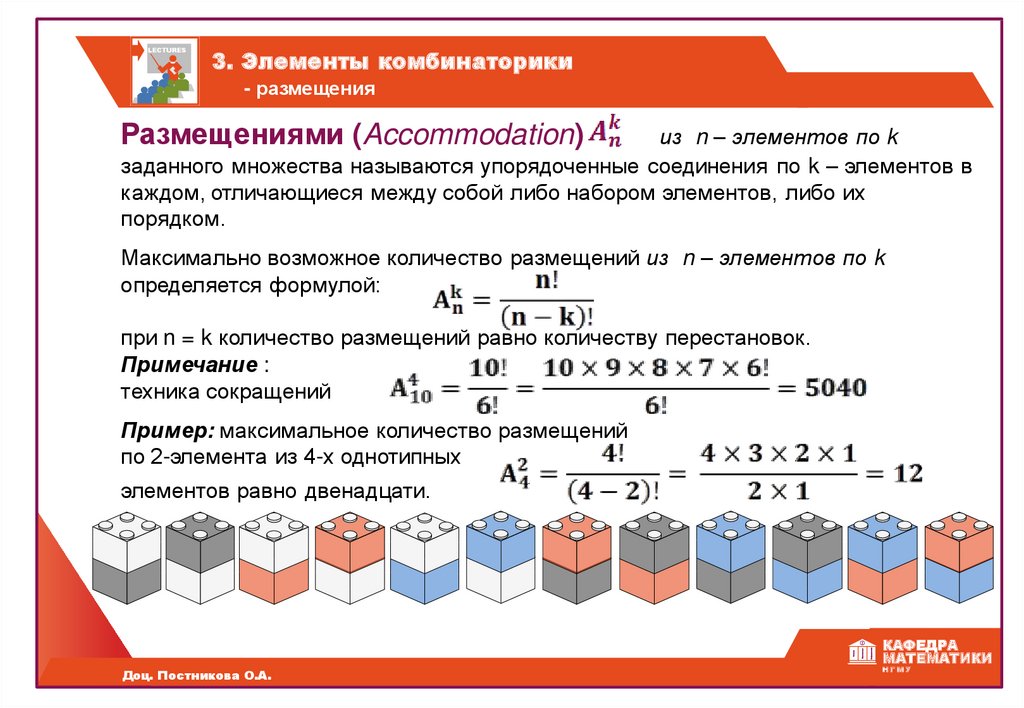9Х(4)| = 4! — 4(3!) + 6(2!) — 4(1!) + 1 =
9. На словах, используя И-ЭП, мы предлагаем определить
количество нарушений значений 1,2,3,4, сначала рассчитайте
количество перестановок этих значений (4!), вычесть количество
способы сохранить хотя бы один элемент в его естественном положении, добавить обратно
количество способов сохранить по крайней мере два значения в их естественном
позиции, вычтите количество способов сохранить не менее трех значений
в их естественном положении, и, наконец, прибавьте количество способов
сохранить все значения в их естественном положении.
Мы можем переписать правую часть приведенного выше уравнения, чтобы лучше выразить общий результат:
Если мы начнем с n объектов, а не с 4, мы сможем рассуждать в аналогично
определяет количество неисправностей n предметов.
Рекурсивное определение расстройств
Теперь мы будем рассматривать расстройства рекурсивно. То есть, зная несколько легко вычисляемых значений для нарушений небольшого числа объектов, можем ли мы определить закономерность количества расстройств большее количество элементов?
Предположим, мы хотим определить количество нарушений n
целые числа 1,2,.
..,n для n больше 2. Давайте сосредоточимся на k и переместим его
в первую позицию. Таким образом, мы начали расстройство, ибо 1 есть
не в естественном положении. Где можно поставить 1? Есть два
случаи, которые мы могли бы рассмотреть: либо 1 равно в позиции k, либо 1 равно
не в позиции k.
Если 1 равно в позиции k, вот что мы знаем: Целые числа 1 и k просто торговали позициями.
 .. | |||||||||
Обозначено вопросительными знаками, осталось (n-2) целых чисел, которые нужно сходить с ума. Это можно сделать D(n-2) способами.
Если 1 не равно в позиции k, мы не так много знаем. Обратите внимание, что
мы дважды показали 1 как запрещенное значение. Это требуется для
этом случае, потому что у нас не может быть 1 в первой позиции (это
естественное положение) и 1 не может стоять в положении k.
 .. |
Обозначено вопросительными знаками, теперь осталось (n-1) целых чисел сходить с ума. Это можно сделать D(n-1) способами.
Собрав это вместе, мы имеем D(n-1) + D(n-2) возможных расстройства, когда k находится в первой позиции. Сколько разных целые числа мы могли бы поставить в позицию 1 и выполнить этот процесс? Все целые числа, кроме 1. то есть (n-1) различных целых чисел.
Это дает рекурсивную формулу D(n) = (n-1)[D(n-1) + D(n-2)]. Поскольку мы знаем, что D(1) = 0 и D(2) = 1, мы можем генерировать последующие значения для D(n).
Понимание комбинаторики: количество путей в сетке | by Branislav Holländer
Photo by Jens Lelie on Unsplash Базовая комбинаторика — незаменимый инструмент в распоряжении любого человека, занимающегося программированием, будь то разработчик, эксперт по искусственному интеллекту или специалист по данным.
В этой статье мы решим простую комбинаторную задачу: подсчитаем количество путей из одного угла общей сетки ШхВ в другой.
Давайте начнем с сетки 3×3:
Предположим, мы хотим перейти от оранжевого квадрата к зеленому. Каждый шаг мы можем двигаться вправо или вниз. Обозначим движение вправо на через R и движение вниз на через D . Нас интересует количество различных путей, по которым мы можем пойти. Пронумеруем пути вручную:
- RRDD
- DDRR
- RDRD
- DRDR
- RDDR
- DRRD
Мы можем заключить, что в этой сетке имеется
Если вы попытаетесь подсчитать количество путей в этой сетке, это займет у вас довольно много времени. Нам понадобится более разумный, математический подход. Во-первых, обратите внимание, что количество шагов, которые мы должны сделать, не зависит от пройденного пути.
Расстояние, измеряемое в шагах, всегда одинаково.
Это расстояние также называют расстоянием L1, расстоянием городского квартала или расстоянием Манхэттена из-за квадратных кварталов в центре Нью-Йорка.
С другой стороны, мы замечаем, что на квадратной сетке количество ходов R должно равняться количеству ходов D из-за симметрии. Кроме того, нам нужно 7 + 7 = 14 шагов на каждом пути (это легко сделать, двигаясь вдоль границы сетки). Эти два требования позволяют переопределить задачу для сетки 8×8 следующим образом:
Найдите количество различных перестановок строки RRRRRRRDDDDDDD.
Теперь количество перестановок в общем случае определяется N! или N*(N-1)*(N-2)*…*2 , также известный как факториал . Таким образом, N — это длина строки. В нашем случае 14! = 87178291200. Однако мы должны учитывать тот факт, что порядок R и D не имеет значения; они одинаковые.
Количество различных перестановок обоих равно 7! = 5040. Мы должны посчитать это число дважды, так как буквы R и D неотличимы друг от друга. Другими словами, мы делим 14! на 7!*7!. Это дает нам 3432, что является правильным ответом.
Чтобы обобщить нашу формулу для любой сетки NxN, мы можем написать:
Кстати, есть более простой способ записать это: число D = N! / (K! * (N-K)!) также называется биномиальным коэффициентом, и мы можем написать (N выбрать K) . Это число обозначает количество способов, которыми мы можем выбрать K объектов из пакета с N объектами, независимо от порядка выбора. Следовательно, мы также можем записать нашу формулу как:
А как насчет более общей сетки ШхВ? В этом случае количество шагов равно (W-1) * (H-1), и мы должны выбрать (W-1) R ходов (вы можете проверить это сами). Следовательно, формула принимает вид:
Легко, правда? Теперь обратите внимание, что вместо выбора (W-1) R ходов мы могли бы выбрать (H-1) D ходов.