Сумма и разность синусов (sin) и косинусов (cos): вывод формул, примеры, объяснение
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α+β2 и α-β2. Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусовsinα+sinβ=2sinα+β2cosα-β2sinα-sinβ=2sinα-β2cosα+β2
Формулы суммы и разности для косинусовcosα+cosβ=2cosα+β2cosα-β2cosα-cosβ=-2sinα+β2cosα-β2, cosα-cosβ=2sinα+β2·β-α2
Данные формулы справедливы для любых углов α и β. Углы α+β2 и α-β2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin(α+β)=sinα·cosβ+cosα·sinβsin(α-β)=sinα·cosβ-cosα·sinβcos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβ
Также представим сами углы в виде суммы полусумм и полуразностей.
α=α+β2+α-β2=α2+β2+α2-β2β=α+β2-α-β2=α2+β2-α2+β2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sinα+sinβ заменим α и β на выражения для этих углов, приведенные выше. Получим
sinα+sinβ=sinα+β2+α-β2+sinα+β2-α-β2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sinα+β2+α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2sinα+β2-α-β2=sinα+β2cosα-β2-cosα+β2sinα-β2sinα+β2+α-β2+sinα+β2-α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2+sinα+β2cosα-β2-cosα+β2sinα-β2Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sinα+β2cosα-β2+cosα+β2sinα-β2+sinα+β2cosα-β2-cosα+β2sinα-β2==2sinα+β2cosα-β2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sinα-sinβ=sinα+β2+α-β2-sinα+β2-α-β2sinα+β2+α-β2-sinα+β2-α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2-sinα+β2cosα-β2-cosα+β2sinα-β2==2sinα-β2cosα+β2
Вывод формулы суммы косинусов
cosα+cosβ=cosα+β2+α-β2+cosα+β2-α-β2cosα+β2+α-β2+cosα+β2-α-β2=cosα+β2cosα-β2-sinα+β2sinα-β2+cosα+β2cosα-β2+sinα+β2sinα-β2==2cosα+β2cosα-β2
Вывод формулы разности косинусов
cosα-cosβ=cosα+β2+α-β2-cosα+β2-α-β2cosα+β2+α-β2-cosα+β2-α-β2=cosα+β2cosα-β2-sinα+β2sinα-β2-cosα+β2cosα-β2+sinα+β2sinα-β2==-2sinα+β2sinα-β2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов.
Пусть α=π2, β=π6. Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
α=π2, β=π6sinπ2+sinπ6=1+12=32sinπ2+sinπ6=2sinπ2+π62cosπ2-π62=2sinπ3cosπ6=2·32·32=32
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α=165°, β=75°. Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусовα=165°, β=75°sinα-sinβ=sin165°-sin75°sin165-sin75=2·sin165°-75°2cos165°+75°2==2·sin45°·cos120°=2·22·-12=22
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Сумма и разность синусов (sin) и косинусов (cos): вывод формул, примеры, объяснение
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α+β2 и α-β2. Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.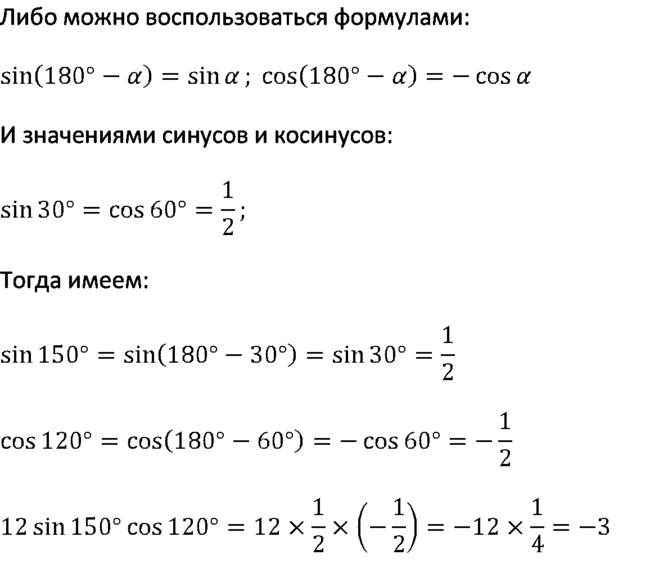
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусовsinα+sinβ=2sinα+β2cosα-β2sinα-sinβ=2sinα-β2cosα+β2
Формулы суммы и разности для косинусовcosα+cosβ=2cosα+β2cosα-β2cosα-cosβ=-2sinα+β2cosα-β2, cosα-cosβ=2sinα+β2·β-α2
Данные формулы справедливы для любых углов α и β. Углы α+β2 и α-β2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусовСумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin(α+β)=sinα·cosβ+cosα·sinβsin(α-β)=sinα·cosβ-cosα·sinβcos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβ
Также представим сами углы в виде суммы полусумм и полуразностей.
α=α+β2+α-β2=α2+β2+α2-β2β=α+β2-α-β2=α2+β2-α2+β2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sinα+sinβ заменим α и β на выражения для этих углов, приведенные выше. Получим
sinα+sinβ=sinα+β2+α-β2+sinα+β2-α-β2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sinα+β2+α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2sinα+β2-α-β2=sinα+β2cosα-β2-cosα+β2sinα-β2sinα+β2+α-β2+sinα+β2-α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2+sinα+β2cosα-β2-cosα+β2sinα-β2Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sinα+β2cosα-β2+cosα+β2sinα-β2+sinα+β2cosα-β2-cosα+β2sinα-β2==2sinα+β2cosα-β2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sinα-sinβ=sinα+β2+α-β2-sinα+β2-α-β2sinα+β2+α-β2-sinα+β2-α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2-sinα+β2cosα-β2-cosα+β2sinα-β2==2sinα-β2cosα+β2
Вывод формулы суммы косинусов
cosα+cosβ=cosα+β2+α-β2+cosα+β2-α-β2cosα+β2+α-β2+cosα+β2-α-β2=cosα+β2cosα-β2-sinα+β2sinα-β2+cosα+β2cosα-β2+sinα+β2sinα-β2==2cosα+β2cosα-β2
Вывод формулы разности косинусов
cosα-cosβ=cosα+β2+α-β2-cosα+β2-α-β2cosα+β2+α-β2-cosα+β2-α-β2=cosα+β2cosα-β2-sinα+β2sinα-β2-cosα+β2cosα-β2+sinα+β2sinα-β2==-2sinα+β2sinα-β2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α=π2, β=π6. Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух угловα=π2, β=π6sinπ2+sinπ6=1+12=32sinπ2+sinπ6=2sinπ2+π62cosπ2-π62=2sinπ3cosπ6=2·32·32=32
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице.
α=165°, β=75°sinα-sinβ=sin165°-sin75°sin165-sin75=2·sin165°-75°2cos165°+75°2==2·sin45°·cos120°=2·22·-12=22
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Сумма и разность синусов (sin) и косинусов (cos): вывод формул, примеры, объяснение
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α+β2 и α-β2.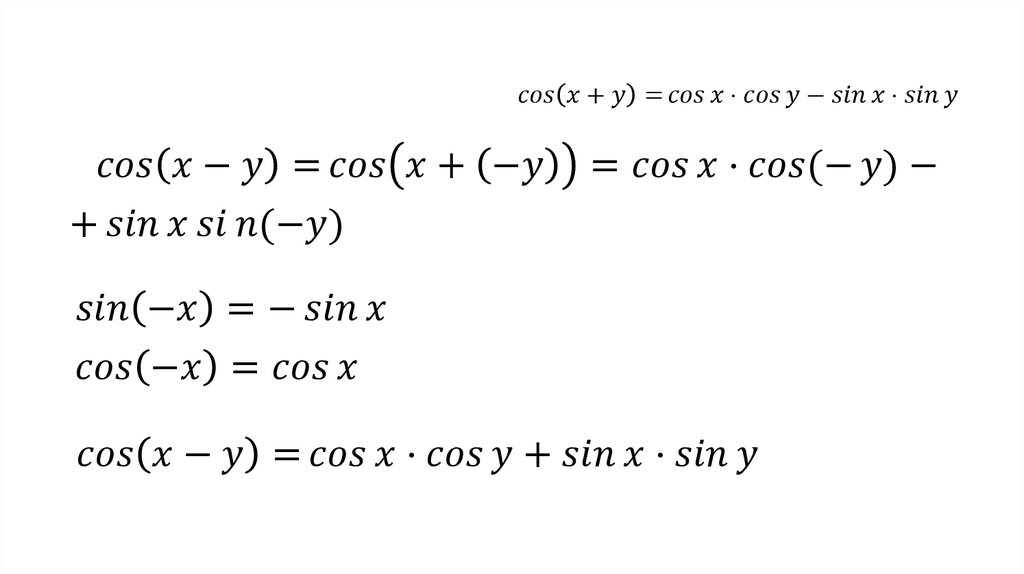
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусовsinα+sinβ=2sinα+β2cosα-β2sinα-sinβ=2sinα-β2cosα+β2
Формулы суммы и разности для косинусовcosα+cosβ=2cosα+β2cosα-β2cosα-cosβ=-2sinα+β2cosα-β2, cosα-cosβ=2sinα+β2·β-α2
Данные формулы справедливы для любых углов α и β. Углы α+β2 и α-β2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin(α+β)=sinα·cosβ+cosα·sinβsin(α-β)=sinα·cosβ-cosα·sinβcos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβ
Также представим сами углы в виде суммы полусумм и полуразностей.
α=α+β2+α-β2=α2+β2+α2-β2β=α+β2-α-β2=α2+β2-α2+β2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sinα+sinβ заменим α и β на выражения для этих углов, приведенные выше. Получим
sinα+sinβ=sinα+β2+α-β2+sinα+β2-α-β2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см.
формулы выше)
sinα+β2+α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2sinα+β2-α-β2=sinα+β2cosα-β2-cosα+β2sinα-β2sinα+β2+α-β2+sinα+β2-α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2+sinα+β2cosα-β2-cosα+β2sinα-β2Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sinα+β2cosα-β2+cosα+β2sinα-β2+sinα+β2cosα-β2-cosα+β2sinα-β2==2sinα+β2cosα-β2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sinα-sinβ=sinα+β2+α-β2-sinα+β2-α-β2sinα+β2+α-β2-sinα+β2-α-β2=sinα+β2cosα-β2+cosα+β2sinα-β2-sinα+β2cosα-β2-cosα+β2sinα-β2==2sinα-β2cosα+β2
Вывод формулы суммы косинусов
cosα+cosβ=cosα+β2+α-β2+cosα+β2-α-β2cosα+β2+α-β2+cosα+β2-α-β2=cosα+β2cosα-β2-sinα+β2sinα-β2+cosα+β2cosα-β2+sinα+β2sinα-β2==2cosα+β2cosα-β2
Вывод формулы разности косинусов
cosα-cosβ=cosα+β2+α-β2-cosα+β2-α-β2cosα+β2+α-β2-cosα+β2-α-β2=cosα+β2cosα-β2-sinα+β2sinα-β2-cosα+β2cosα-β2+sinα+β2sinα-β2==-2sinα+β2sinα-β2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов.
α=π2, β=π6sinπ2+sinπ6=1+12=32sinπ2+sinπ6=2sinπ2+π62cosπ2-π62=2sinπ3cosπ6=2·32·32=32
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α=165°, β=75°. Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусовα=165°, β=75°sinα-sinβ=sin165°-sin75°sin165-sin75=2·sin165°-75°2cos165°+75°2==2·sin45°·cos120°=2·22·-12=22
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.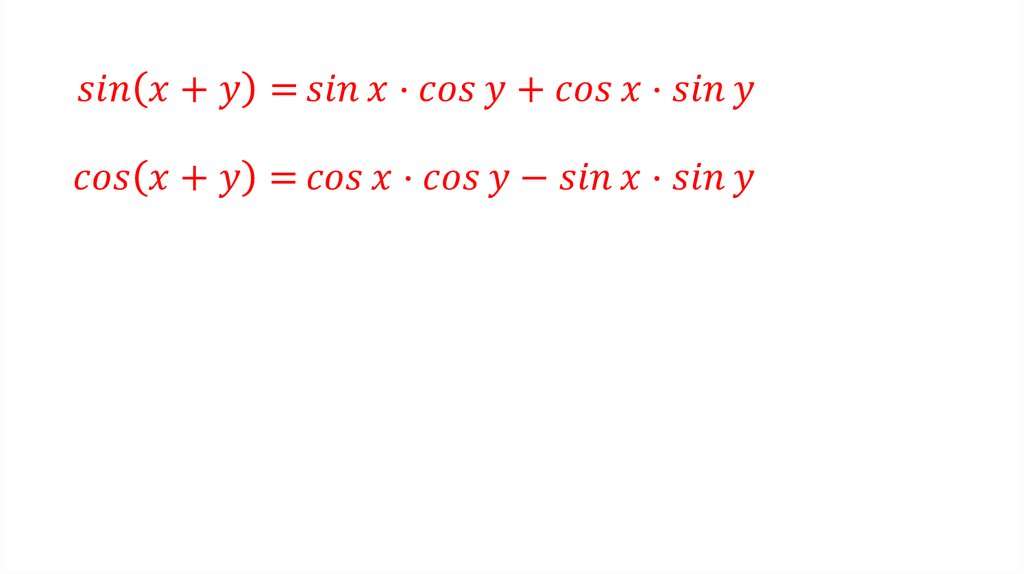
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Формула синуса суммы аргументов. Сумма и разность синусов и косинусов: вывод формул, примеры
Данный электронный ресурс является отличным материалом для проведения интерактивного обучения в современных школах. Он составлен грамотно, обладает четкой структурой и соответствует школьному плану. Благодаря подробным объяснениям, тема, которая представлена в видеоуроке станет понятна как можно большему количеству учеников в классе. Учителя должны помнить, что не все ученики имеют одинаковую степень восприятия, быстроты понимания, базу.
Справиться с трудностями и догнать своих сверстников, исправить успеваемость, помогут подобные материалы. С помощью них в домашней спокойной обстановке, самостоятельно либо вместе с репетитором, ученик может разобраться в той или иной теме, изучить теорию и просмотреть примеры практического применения той или иной формулы и т.д.
Данный видеоурок посвящен теме «Синус и косинус разности аргументов». Подразумевается, что ученики уже изучили основы тригонометрии, ознакомлены с основными функциями и их свойствами, формулами привидения и таблицами тригонометрических значений.
Также, до того, как перейти к изучению данной темы, необходимо иметь понятие о синусе и косинусе суммы аргументов, знать две основные формулы и уметь ими пользоваться.
Вначале видеоурока диктор напоминает школьникам эти две формулы. Далее демонстрируется первая формула — синус разности аргументов. Помимо того, как выводится сама формула, показывается каким образом она получается от другой. Таким образом, школьнику не придется зазубривать новую формулу без понимания, что является частой ошибкой.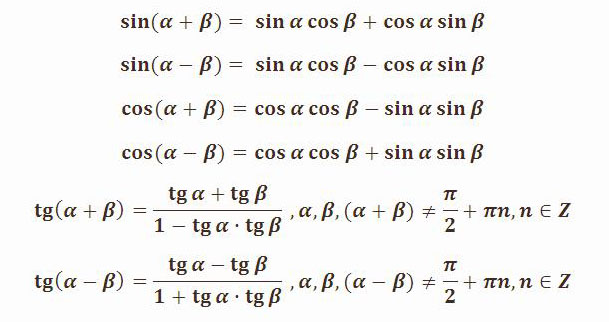
Это очень важно для учеников в этом классе. Нужно всегда помнить, что перед знаком минуса всего можно добавить знак +, а минуса на знак плюс в итоге превратится в минус. С помощью такого нехитрого шага, можно воспользоваться формулой синуса суммы и получить формулу синуса разности аргументов.
Аналогичным образом выводится формула косинуса разности из формулы косинуса суммы аргументов.
Диктор пошагово все объясняет, а в результате выводится общая формула косинуса суммы и разности аргументов и синуса, аналогично.
Первый пример из практической части данного видеоурока предлагает найти косинус Пи/12. Предлагается представить данное значение в виде некоторой разности, при котором уменьшаемое и вычитаемое будут являться табличными значениями. Далее применятся формула косинуса разности аргументов. Заменив выражение, можно подставить полученные значения и получить ответ. Диктор зачитывает ответ, который выводится в конце примера.
Второй пример представляет собой уравнение.
И в правой, и в левой сторонах мы видим косинусы разностей аргументов. Диктор напоминает формулы приведений, которые используются для замены и упрощения этих выражения. Эти формулы записываются с правой стороны, чтобы школьники могли понять, откуда появляются те или иные изменения.
Еще один пример, третий, представляет собой некоторую дробь, где и в числителе и в знаменателе имеем тригонометрические выражения, а именно, разности произведений.
Здесь также при решении используются формулы приведений. Таким образом, школьники могут убедиться, что пропустив одну тему в тригонометрии, понять остальные будет все сложнее.
И, наконец, четвертый пример. Это также уравнение, при решении которых необходимо использовать новые изученные и старые формулы.
Примеры, которые приводятся в видеоуроке, можно рассмотреть более подробно и попробовать решить самостоятельно. Их можно задать в качестве домашнего задания школьникам.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тема занятия «Синус и косинус разности аргументов».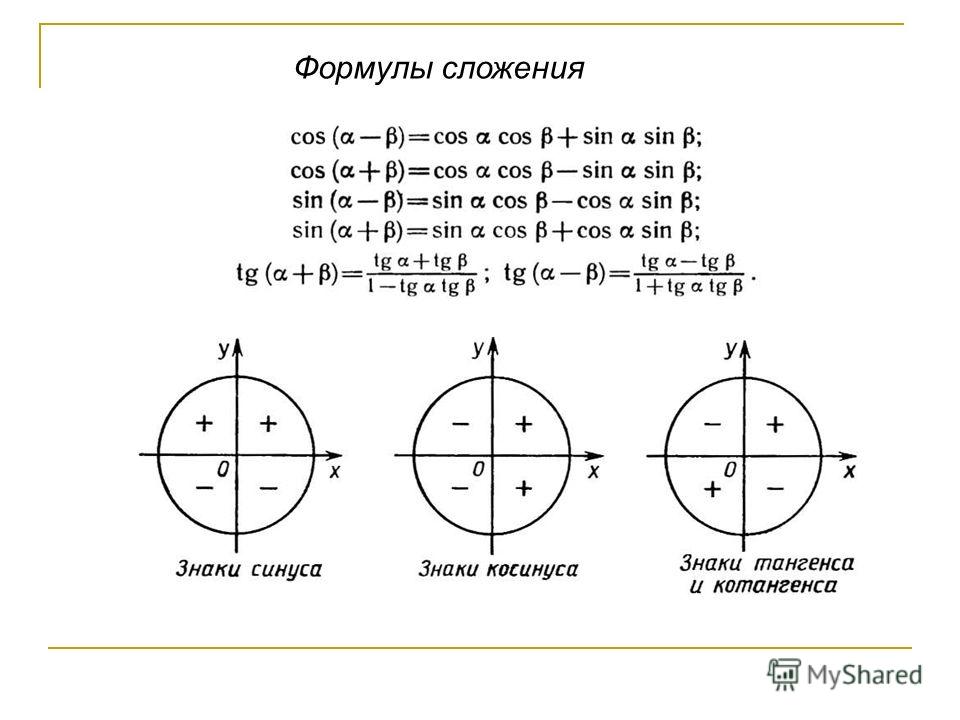
На предыдущем курсе мы познакомились с двумя тригонометрическими формулами синус и косинус суммы аргументов.
sin(x + y) = sin x cos y + cos x sin y,
cos (x + y) = cos x cos y — sin x sin y.
синус суммы двух углов равен сумме между произведением синуса первого угла и косинусом второго угла и произведением косинуса первого угла и синуса второго угла;
косинус суммы двух углов равен разности между произведением косинусов этих углов и произведением суммы этих углов.
При помощи этих формул выведем формулы Синус и косинус разности аргументов.
Синус разности аргументов sin(x- y)
Две формулы (синус суммы и синус разности) можно записать в виде:
sin(x y) = sin x cos y cos x sin y.
Аналогично выведем формулу косинуса разности:
Косинус разности аргументов перепишем в виде суммы и применим уже известную формулу косинуса суммы: cos (x + y) = cosxcosy — sinxsiny.
только для аргументов х и -y. Подставив данные аргументы в формулу, получим cosxcos(- y) — sinxsin(- y).
sin(- y)= — siny). и получим окончательное выражение cosxcosy + sinxsiny.
cos (x — y) = cos (x +(- y)) =cos xcos(- y) — sin x sin(- y)= cosx cos y + sin xsin y.
Значит, cos (x — y) = cosxcos y + sin xsin y.
косинус разности двух углов равен сумме между произведением косинусов этих углов и произведением синусов этих углов.
Объединяя две формулы (косинус суммы и косинус разности) в одну, запишем
cos (x y) = cosxcos y sin xsin y.
Запомним, что формулы на практике можно применять как слева направо, так и наоборот.
Рассмотрим примеры.
ПРИМЕР 1. Вычислить cos (косинус пи, деленное на двенадцать).
Решение. Запишем пи, деленное на двенадцать, как разность пи на три и пи, деленное на четыре: = — .
Подставим значения в формулу косинуса разности: cos (x — y) = cosxcosy + sinxsiny, таким образом cos = cos (-) = cos cos + sin sin
Нам известно, что cos = , cos = sin= , sin = . Показать таблицу значений.
Заменим значение синуса и косинуса числовыми значениями и получим ∙ + ∙ при умножении дробь на дробь числители и знаменатели перемножаем, получаем
cos = cos (-) = cos cos + sin sin = ∙ + ∙ = = =.
Ответ: cos =.
ПРИМЕР 2. Решить уравнение cos(2π — 5х) = cos(- 5х) (косинус два пи минус пять икс равно косинусу от пи на два минус пять икс).
Решение. К левой и правой частям уравнения применим формулы приведения cos(2π — cos (косинус два пи минус альфа равен косинусу альфа) и cos(- = sin (косинус пи на два минус альфа равно синусу альфа), получим cos 5х = sin 5х, приведем его к виду однородного уравнения первой степени и получим cos 5х — sin 5х = 0. Это однородное уравнение первой степени. Разделим почленно обе части уравнения на cos 5х. Имеем:
cos 5х: cos 5х — sin 5х: cos 5х = 0, т.к. cos 5х: cos 5х =1, а sin 5х: cos 5х= tg 5x, то получим:
Так как мы уже знаем, что уравнение tgt = а имеет решение t = arctgа + πn, а так как у нас t=5х, а =1, то получим
5x = arctg 1 + πn,
а значение arctg 1, тогда tg 1= Показать таблицу
подставим значение в уравнение и решим его:
Ответ: х = + .
ПРИМЕР 3. Найти значение дроби. (в числителе разность произведения косинусов семидесяти пяти градусов и шестидесяти пяти градусов и произведения синусов семидесяти пяти градусов и шестидесяти пяти градусов, а в знаменателе разность произведения синуса восьмидесяти пяти градусов и косинуса тридцати пяти градусов и произведения косинуса восьмидесяти пяти градусов и синуса тридцати пяти градусов).
Решение. В числителе данной дроби разность можно «свернуть» в косинус суммы аргументов 75° и 65°, а в знаменателе — разность «свернем» в синус разности аргументов 85° и 35°. Получим
Ответ: — 1.
ПРИМЕР 4. Решить уравнение: cos(-х) + sin(-х) = 1(косинус разности пи на четыре и икс плюс синус разности пи на четыре и икс равно одному).
Решение. Применим формулы косинус разности и синус разности.
Показать общую формулу косинуса разности
Тогда cos (-х) = cos cos х + sinsinх
Показать общую формулу синуса разности
а sin (-х)= sin cosх — cos sinх
Подставим данные выражения в уравнение cos(-х) + sin(-х) = 1 и получим:
cos cos х + sinsin х + sin cos х — cos sin х = 1,
Так как cos= и sin= Показать таблицу значение синуса и косинуса
Получим ∙ cos х + ∙ sinх + ∙ cos х — ∙ sinх = 1,
второе и четвертое слагаемые противоположны, поэтому взаимно уничтожаются, остается:
∙ cos + ∙ cos = 1,
Решим данное уравнение и получим, что
2∙ ∙ cos x= 1,
Так ка мы уже знаем, что уравнение cos = а имеет решение t = arcos a + 2π k , а так как у нас t=x, а =, то получим
х = arccos + 2πn,
а так как значение arccos, тогда cos =
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 .
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Yandex.RTB R-A-339285-1
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению.
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Разность косинусов формула. Сумма и разность синусов и косинусов: вывод формул, примеры
Косинус суммы и разности двух углов
В этом параграфе будут доказаны следующие две формулы:
cos (α + β) = cos α cos β — sin α sin β, (1)
cos (α — β) = cos α cos β + sin α sin β. (2)
Косинус суммы (разности) двух углов равен произведению косинусов этих углов минус (плюс) произведение синусов этих углов.
Нам удобнее будет начать с доказательства формулы (2). Для простоты изложения предположим сначала, что углы α и β удовлетворяют следующим условиям:
1) каждый из этих углов неотрицателен и меньше 2π :
0 α 2π, 0 β
2) α > β .
Пусть положительная часть оси 0х является общей начальной стороной углов α и β .
Конечные стороны этих углов обозначим соответственно через 0А и 0В. Очевидно, что угол α — β можно рассматривать как такой угол, на который нужно повернуть луч 0В вокруг точки 0 против часовой стрелки, чтобы его направление совпало с направлением луча 0А.
На лучах 0А и 0В отметим точки М и N, отстоящие от начала координат 0 на расстоянии 1, так что 0М = 0N = 1.
В системе координат х0у точка М имеет координаты (cos α, sin α ), а точка N — координаты (cos β , sin β ). Поэтому квадрат расстояния между ними равен:
d 1 2 = (cos α — cos β) 2 + (sin α — sin β) 2 = cos 2 α — 2 cos α cos β +
+ cos 2 β + sin 2 α — 2sin α sin β + sin 2 β = .
При вычислениях мы воспользовались тождеством
sin 2 φ + cos 2 φ = 1 .
Теперь рассмотрим другую систему координат В0С, которая получается путем поворота осей 0х и 0у вокруг точки 0 против часовой стрелки на угол β .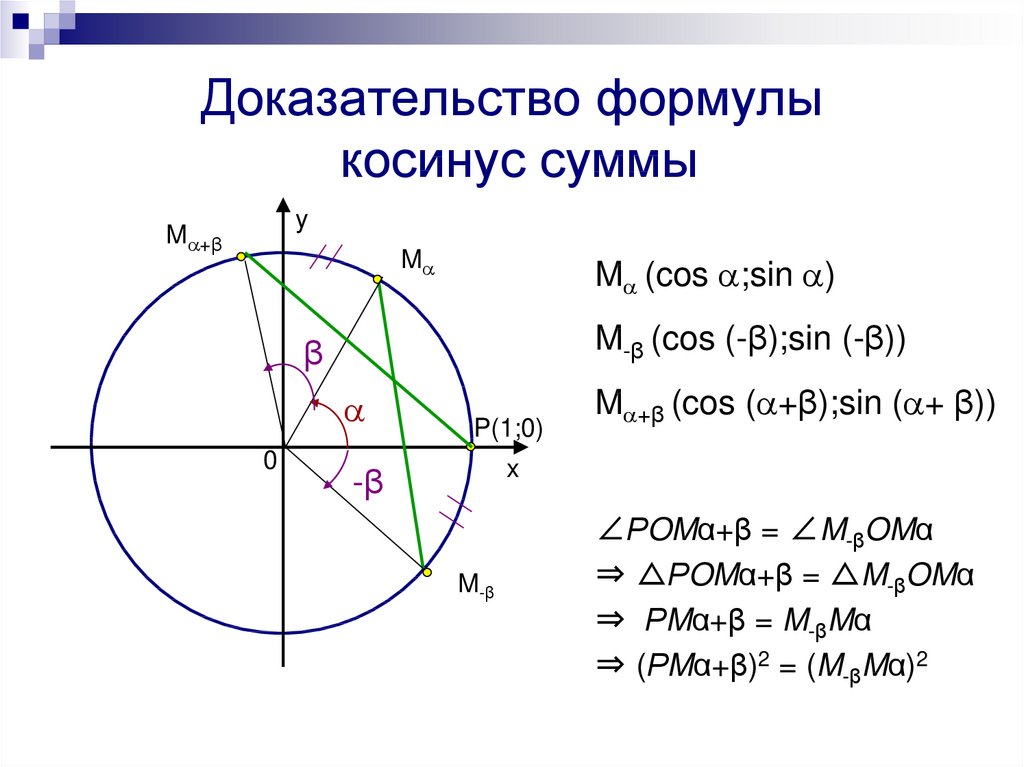
В этой системе координат точка М имеет координаты (cos (α — β ), sin (α — β )), а точка N -координаты (1,0). Поэтому квадрат расстояния между ними равен:
d 2 2 = 2 + 2 = cos 2 (α — β) — 2 cos (α — β) + 1 +
+ sin 2 (α — β) = 2 .
Но расстояние между точками М и N не зависит от того, относительно какой системы координат мы рассматриваем эти точки. Поэтому
d 1 2 = d 2 2
2 (1 — cos α cos β — sin α sin β) = 2 .
Отсюда и вытекает формула (2).
Теперь следует вспомнить о тех двух ограничениях, которые мы наложили для простоты изложения на углы α и β .
Требование, чтобы каждый из углов α и β был неотрицательным, на самом деле не существенно. Ведь к любому из этих углов можно прибавить угол, кратный 2я, что никак не отразится на справедливости формулы (2). Точно так же от каждого из данных углов можно вычесть угол, кратный 2π .
Поэтому можно считать, что 0 α
2π
, 0 β
2π
.
Не существенным оказывается и условие α > β . Действительно, если α β , то β >α ; поэтому, учитывая четность функции cos х , получаем:
cos (α — β) = cos (β — α) = cos β cos α + sin β sin α,
что по существу совпадает с формулой (2). Таким образом, формула
cos (α — β) = cos α cos β + sin α sin β
верна для любых углов α и β . В частности, заменяя в ней β на —β и учитывая, что функция cos х является четной, а функция sin х нечетной, получаем:
cos (α + β) = cos [α — (- β)] =cos α cos (-β) + sin α sin (-β) =
= cos α cos β — sin α sin β,
что доказывает формулу (1).
Итак, формулы (1) и (2) доказаны.
Примеры.
1) cos 75° = cos (30° + 45°) = cos 30° cos 45°-sin 30°-sin 45° =
2) cos 15° = cos (45° — 30°) = cos 45° cos 30° + sin 45° sin 30° =
Упражнения
1 .
Вычислить, не пользуясь тригонометрическими таблицами:
a) cos 17° cos 43° — sin 17° sin 43°;
б) sin 3° sin 42° — cos 39° cos 42°;
в) cos 29° cos 74° + sin 29° sin 74°;
г) sin 97° sin 37° + cos 37° cos 97°;
д) cos 3π / 8 cos π / 8 + sin 3π / 8 sin π / 8 ;
e) sin 3π / 5 sin 7π / 5 — cos 3π / 5 cos 7π / 5 .
2.Упростить выражения:
a). cos (α + π / 3 ) + cos (π / 3 — α ) .
б). cos (36° + α ) cos (24° — α ) + sin (36° + α ) sin (α — 24°).
в). sin (π / 4 — α ) sin (π / 4 + α ) — cos (π / 4 + α ) cos (π / 4 — α )
г) cos 2α + tg α sin 2α .
3 . Вычислить :
a) cos (α — β) , если
cos α = — 2 / 5 , sin β = — 5 / 13 ;
90° α β
б) cos (α + π / 6), если cos α = 0,6;
3π / 2 α
4 . Найти cos (α + β) и cos (α — β) ,если известно, что sin α = 7 / 25 , cos β = — 5 / 13 и оба угла (α и β ) оканчиваются в одной и той же четверти.
5 .Вычислить:
а). cos [ arcsin 1 / 3 + arccos 2 / 3 ]
б). cos [ arcsin 1 / 3 — arccos (- 2 / 3)] .
в). cos [ arctg 1 / 2 + arccos (- 2) ]
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники.
Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов.
Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов.
Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы.
Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице.
Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники.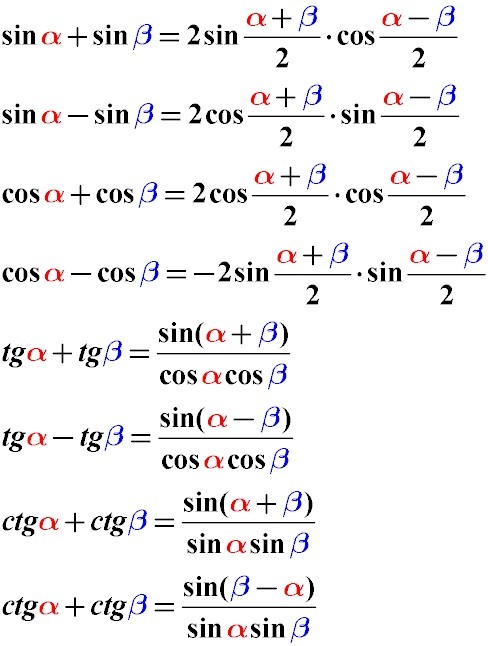
Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу.
То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету.
Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Yandex.RTB R-A-339285-1
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Разность косинусов. Сумма и разность синусов и косинусов, вывод формул, примеры. Вывод формул суммы и разности синусов и косинусов
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — 75 ° 2 cos 165 ° + 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
). Эти формулы позволяют от суммы или разности синусов и косинусов углов и перейти к произведению синусов и/или косинусов углов и . В этой статье мы сначала перечислим эти формулы, дальше покажем их вывод, а в заключение рассмотрим несколько примеров их применения.
Навигация по странице.
Список формул
Запишем формулы суммы и разности синусов и косинусов. Как Вы понимаете, их четыре штуки: две для синусов и две для косинусов.
Теперь дадим их формулировки. При формулировании формул суммы и разности синусов и косинусов угол называют полусуммой углов и , а угол — полуразностью. Итак,
Стоит отметить, что формулы суммы и разности синусов и косинусов справедливы для любых углов и .
Вывод формул
Для вывода формул суммы и разности синусов можно использовать формулы сложения , в частности, формулы
синуса суммы ,
синуса разности ,
косинуса суммы и
косинуса разности .
Также нам потребуется представление углов и в виде и . Такое представление правомерно, так как и для любых углов и .
Теперь подробно разберем вывод формулы суммы синусов двух углов вида .
Сначала в сумме заменяем на , а на , при этом получаем . Теперь к применяем формулу синуса суммы, а к — формулу синуса разности:
После приведения подобных слагаемых получаем . В итоге имеем формулу суммы синусов вида .
Для вывода остальных формул нужно лишь проделать аналогичные действия. Приведем вывод формул разности синусов, а также суммы и разности косинусов:
Для разности косинусов мы привели формулы двух видов или . Они эквивалентны, так как , что следует из свойств синусов противоположных углов .
Итак, мы разобрали доказательство всех формул суммы и разности синусов и косинусов.
Примеры использования
Разберем несколько примеров использования формул суммы синусов и косинусов, а также разности синусов и косинусов.
Для примера проверим справедливость формулы суммы синусов вида , взяв и . Чтобы это сделать, вычислим значения левой и правой частей формулы для данных углов. Так как и (при необходимости смотрите таблицу основных значений синусов и косинусов), то . При и имеем и , тогда . Таким образом, значения левой и правой частей формулы суммы синусов для и совпадают, что подтверждает справедливость этой формулы.
В некоторых случаях использование формул суммы и разности синусов и косинусов позволяет вычислять значения тригонометрических выражений, когда углы отличны от основных углов (). Приведем решение примера, подтверждающего эту мысль.
Пример.
Вычислите точное значение разности синусов 165 и 75 градусов.
Решение.
Точных значений синусов 165
и 75
градусов мы не знаем, поэтому непосредственно вычислить значение заданной разности мы не можем. Но ответить на вопрос задачи нам позволяет формула разности синусов . Действительно, полусумма углов 165
и 75
градусов равна 120
, а полуразность равна 45
, а точные значения синуса 45
градусов и косинуса 120
градусов известны.
Таким образом, имеем
Ответ:
.
Несомненно, главная ценность формул суммы и разности синусов и косинусов заключается в том, что они позволяют перейти от суммы и разности к произведению тригонометрических функций (по этой причине эти формулы часто называют формулами перехода от суммы к произведению тригонометрических функций). А это в свою очередь может быть полезно, например, при преобразовании тригонометрических выражений или при решении тригонометрический уравнений . Но эти темы требуют отдельного разговора.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб.
для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3. - Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Формулы приведения
Формулы приведения дают возможность находить значения тригонометрических функций для любых углов (а не только острых). С их помощью можно совершать преобразования, упрощающие вид тригонометрических выражений.
Рисунок 1.
Кроме формул приведения при решении задач используются следующие основные формулы.
1) Формулы одного угла:
2) Выражение одних тригонометрических функций через другие:
Замечание
В этих формулах перед знаком радикала должен быть поставлен знак $»+»$ или $»-«$ в зависимости от того, в какой четверти находится угол.
Сумма и разность синусов, сумма и разность косинусов
Формулы суммы и разности функций:
Кроме формул суммы и разности функций, при решении задач бывают полезны формулы произведения функций:
Основные соотношения между элементами косоугольных треугольников
Обозначения:
$a$, $b$, $c$ — стороны треугольника;
$A$, $B$, $C$ — противолежащие перечисленным сторонам углы;
$p=\frac{a+b+c}{2} $ — полупериметр;
$S$ — площадь;
$R$ — радиус описанной окружности;
$r$ — радиус вписанной окружности. \circ -\left(A+B\right)$.
Тема урока. Сумма и разность синусов. Сумма и разность косинусов.
(Урок усвоения новых знаний.)
Цели урока.
Дидактические :
вывести формулы суммы синусов и суммы косинусов и способствовать их усвоению в ходе решения задач;
продолжить формирование умений и навыков по применению тригонометрических формул;
проконтролировать степень усвоения материала по теме.
Развивающие:
способствовать развитию навыка самостоятельного применения знаний;
развивать навыки самоконтроля и взаимоконтроля;
продолжить работу по развитию логического мышления и устной математической речи при поиске решения поставленной проблемы.
Воспитательные:
приучать к умению общаться и выслушивать других;
воспитывать внимательность и наблюдательность;
стимулировать мотивацию и интерес к изучению тригонометрии.
Оборудование: презентация, интерактивная доска, формулы.
Ход урока:
Организационный момент. — 2 мин.
Актуализация опорных знаний. Повторение. – 12 мин.
Целеполагание. – 1 мин.
Восприятие и осмысливание новых знаний. – 3 мин.
Применение приобретённых знаний. – 20 мин.
Анализ достижений и коррекция деятельности. – 5 мин.
Рефлексия. — 1мин.
Домашнее задание. – 1 мин.
1. Организационный момент. (слайд 1)
– Здравствуйте! Тригонометрия – один из интереснейших разделов математики, но почему-то большинство учащихся считают его самым трудным. Объяснить это, скорее всего можно тем, что в этом разделе формул больше, чем в любом другом. Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Многие формулы уже изучены, но оказывается, не все. Поэтому девизом этого урока станет изречение Пифагора «Дорогу осилит идущий, а математику – мыслящий». Давайте мыслить!
2. Актуализация опорных знаний. Повторение.
1) математический диктант с взаимопроверкой (слайды 2-5)
Первое задание. Используя изученные формулы вычислить:
1 вариант
2 вариант
sin 390 0
cos 420 0
1 – cos 2 30 0
1 – sin 2 60 0
сos 120 0 ∙cos 30 0 + sin 120 0 ∙sin 30 0
sin 30 0 ∙cos 150 0 + cos 30 0 ∙sin 150 0
Ответы: ; 1 ; -; ; — ; — 1 ; 1 ; ; ; 0 ; ; 3 . – взаимопроверка.
Критерии оценок: (работы сдаются учителю)
«4» — 10 – 11
2) задача проблемного характера (слайд 6) – доклад учащегося.
Упростить выражение, используя тригонометрические формулы:
А можно ли эту задачу решить иначе? (Да, с помощью новых формул.)
3. Целеполагание (слайд 7)
Тема урока:
Сумма и разность синусов. Сумма и разность косинусов. – запись в тетради
Цели урока:
вывести формулы суммы и разности синусов, суммы и разность косинусов;
4. Восприятие и осмысливание новых знаний. (слайд 8-9)
Выведем формулу суммы синусов: — учитель
Аналогично доказываются остальные формулы: (формулы преобразования суммы в произведение)
Правила запоминания!
В доказательстве каких ещё тригонометрических формул использовались формулы сложения?
5. Применение приобретённых знаний. (слайды 10-11)
С помощью новых формул:
1)Вычислить: (у доски) – Что будет ответом? (число)
Под диктовку с учителем
6. Анализ достижений и коррекция деятельности. (слайд 13)
Дифференцированная самостоятельная работа с самопроверкой
Вычислить:
7. Рефлексия. (слайд 14)
Удовлетворены ли вы своей работой на уроке?
Какую оценку вы поставили бы себе за весь урок?
Какой момент наиболее интересен был на уроке?
Где вам пришлось больше всего сконцентрироваться?
8. Домашнее задание: выучить формулы, индивидуальные задания на карточках.
Преобразование суммы (разности) косинусов двух углов в произведение
Для суммы и разности косинусов двух углов верны следующие формулы:
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы на косинус полуразности этих углов.
Разность косинусов двух углов равна минус удвоенному произведению синуса полусуммы на синус полуразности этих углов.
Примеры
Формулы (1) и (2) могут быть получены многими способами. Докажем, например, формулу (1).
cos α cos β = 1 / 2 .
Полагая в ней (α + β) = х , (α — β) = у , мы и приходим к формуле (1). Этот способ аналогичен тому, с помощью которого в предыдущем параграфе была получена формула для суммы синусов двух углов.
2-й способ. В предыдущем параграфе была доказана формула
Полагая в ней α = х + π / 2 , β = у + π / 2 , получаем:
Но по формулам приведения sin (х + π / 2) == cos x , sin (у + π / 2) = cos у ;
Следовательно,
что и требовалось доказать.
Формулу (2) мы предлагаем учащимся доказать самостоятельно. Попробуйте найти не менее двух различных способов доказательства!
Упражнения
1. Вычислить без таблиц, используя формулы для суммы и разности косинусов двух углов:
а). cos 105° + cos 75°. г). cos 11π / 12 — cos 5π / 12 ..
б). cos 105° — cos 75°. д). cos 15° -sin 15°.
в). cos 11π / 12 + cos 5π / 12 .. е). sin π / 12 + cos 11π / 12 .
2 . Упростить данные выражения:
а). cos ( π / 3 + α ) + cos ( π / 3 — α ).
б). cos ( π / 3 + α ) — cos ( π / 3 — α ).
3. Каждое из тождеств
sin α + cos α = \/ 2 sin (α + π / 4 )
sin α — cos α = \/ 2 sin (α — π / 4 )
доказать не менее чем двумя различными способами.
4. Данные выражения представить в виде произведений:
а). \/ 2 + 2cos α . в). sin x + cos y.
б). \/
3 — 2 cos α . г). sin x — cos y .
5 . Упростить выражение sin 2 (α — π / 8 ) — cos 2 (α + π / 8 ) .
6 .Разложить на множители данные выражения (№ 1156-1159):
а). 1 + sin α — cos α
б). sin α + sin (α + β) + sin β .
в). cos α + cos 2α + cos 3α
г). 1 + sin α + cos α
7. Доказать данные тождества
8. Доказать, что косинусы углов α и β равны тогда и только тогда, когда
α = ± β + 2 nπ,
где n — некоторое целое число.
Формулы суммы и разницы | Brilliant Math & Science Wiki
Содержание
- Синус — формулы суммы и разности
- Косинус — формулы суммы и разности
- Тангенс — формулы суммы и разности
- Тригонометрические формулы суммы и разности — решение задач
Формулы суммы и разности утверждают, что
sin(a+b)=sinacosb+cosasinbsin(a−b)=sinacosb−cosasinb\begin {выровнено} \sin(a+b) &= \sin a \cos b + \cos a \sin b \\ \sin(a-b) &= \sin a \cos b — \cos a \sin b \end{выровнено}sin(a+b)sin(a−b)=sinacosb+cosasinb=sinacosb-cosasinb
и что
cos(a+b)=cosacosb−sinasin bcos(a−b)=cosacosb+sinasinb. \begin{выровнено}
\cos(a+b) &= \cos a \cos b — \sin a \sin b \\
\cos(a-b) &= \cos a \cos b + \sin a \sin b.
\end{align}cos(a+b)cos(a−b)=cosacosb-sinasinb=cosacosb+sinasinb. 9{я(а+б)}
&= \cos(a+b) + i\sin(a+b)\\
&=\cos a \cos b — \sin a \sin b + i(\sin a \cos b + \sin b \cos a).
\end{aligned}ei(a+b)=cos(a+b)+isin(a+b)=cosacosb−sinasinb+i(sinacosb+sinbcosa).
Но так как cos \cos cos и sin \sin sin являются вещественнозначными функциями, должно быть верно, что
cos(a+b)=cosacosb−sinasinbisin(a+b)=i(sinacosb+sinbcosa),\begin{выровнено} \cos(a+b) &= \cos a \cos b — \sin a \sin b \\ i\sin(a+b) &= i(\sin a \cos b + \sin b \cos a), \end{выравнивание} cos(a+b)isin(a+b)=cosacosb−sinasinb=i(sinacosb+sinbcosa),
что подразумевает
cos(a+b)=cosacosb−sinasinbsin(a+b)=sinacosb+sinbcosa. □\begin{выровнено}
\cos(a+b) &= \cos a\cos b — \sin a \sin b \\
\sin(a+b) &= \sin a \cos b + \sin b \cos a. \ _\площадь
\end{выравнивание}cos(a+b)sin(a+b)=cosacosb−sinasinb=sinacosb+sinbcosa. □
Пусть на диаграмме точка AAA обращается к точкам BBB и C,C,C, а углы α\alphaα и β\betaβ определяются следующим образом:
∠AOB=α,∠BOC=β. \угол AOB = \alpha, \quad \угол BOC = \beta. ∠AOB=α,∠BOC=β.
Пусть и CD‾\overline{CD}CD, и FG‾\overline{FG}FG перпендикулярны OA‾,\overline{OA},OA, и пусть EEE — точка на CD‾\overline{CD }CD такой, что ∣ED‾∣=∣FG‾∣.\lvert \overline{ED}\rvert=\lvert\overline{FG}\rvert.∣ED∣=∣FG∣.
Тогда формула для суммы косинусов cos(α+β), \cos (\alpha+\beta) ,cos(α+β), которая равна ∣OD‾∣∣OC‾∣, \frac{\lvert \ overline{OD}\rvert}{\lvert \overline{OC}\rvert} ,∣OC∣∣OD∣, можно получить следующим образом:
cos(α+β)=∣OD‾∣∣OC‾∣=∣OG‾∣∣OC‾∣−∣EF‾∣∣OC‾∣=∣OG‾∣∣OF‾∣⋅∣OF‾∣ ∣OC‾∣−∣EF‾∣∣CF‾∣⋅∣CF‾∣∣OC‾∣(поскольку ∣OD‾∣=∣OG‾∣−∣EF‾∣)=cosα⋅cosβ−sin α⋅sinβ. \begin{выровнено}
\cos (\alpha + \beta) &= \frac{\lvert \overline{OD}\rvert}{\lvert \overline{OC}\rvert} \\
&= \frac{\lvert \overline{OG}\rvert}{\lvert \overline{OC}\rvert} — \frac{\lvert \overline{EF}\rvert}{\lvert \overline{OC}\rvert } \\
&= \frac{\lvert \overline{OG}\rvert}{\lvert \overline{OF}\rvert} \cdot \frac{\lvert \overline{OF}\rvert}{\lvert \overline{OC}\ rvert} — \frac{\lvert \overline{EF}\rvert}{\lvert \overline{CF}\rvert} \cdot \frac{\lvert \overline{CF}\rvert}{\lvert \overline{OC} \rvert} \qquad \left(\text{так как} \lvert \overline{OD}\rvert = \lvert \overline{OG}\rvert-\lvert \overline{EF}\rvert\right)\\
&= \cos\alpha\cdot\cos\beta — \sin\alpha\cdot\sin\beta. \end{выровнено} cos(α+β)=∣OC∣∣OD∣=∣OC∣∣OG∣−∣OC∣∣EF∣=∣OF∣∣OG∣⋅∣OC∣∣OF ∣−∣CF∣∣EF∣⋅∣OC∣∣CF∣(поскольку ∣OD∣=∣OG∣−∣EF∣)=cosα⋅cosβ−sinα⋅sinβ.
Формула косинус-разности может быть получена из формулы суммы косинусов путем замены β\betaβ на −β, — \beta,−β и использования cos(−β)=cosβ\cos(-\beta ) = \cos\betacos(-β)=cosβ и sin(-β)=-sinβ:\sin(-\beta) = -\sin \beta:sin(-β)=-sinβ:
cos(α+β)=cosα⋅cosβ−sinα⋅sinβ⇒cos(α−β)=cosα⋅cos(−β)−sinα⋅sin( −β)=cosα⋅cosβ+sinα⋅sinβ. \begin{выровнено} \cos(\alpha + \beta) &= \cos \alpha \cdot \cos \beta — \sin \alpha \cdot \sin \beta \\ \стрелка вправо \cos(\alpha — \beta) &= \cos \alpha \cdot \cos (-\beta) — \sin \alpha \cdot \sin (-\beta) \\ &= \cos\alpha\cdot\cos\beta+\sin\alpha\cdot\sin\beta. \end{выровнено} cos(α+β)⇒cos(α−β)=cosα⋅cosβ−sinα⋅sinβ=cosα⋅cos(−β)−sinα⋅sin(−β)=cosα⋅cosβ+sinα⋅ sinβ.
Таким образом, у нас есть следующие две формулы суммы косинуса и разности косинуса:
формула суммы косинуса : cos(α+β)=cosα⋅cosβ−sinα⋅sinβ,\cos(\alpha + \beta)= \cos\alpha\cdot\cos\beta — \sin\alpha\ cdot \sin \beta ,cos(α+β)=cosα⋅cosβ−sinα⋅sinβ,
Формула косинус-разности :
cos(α−β)=cosα⋅cosβ+sinα⋅sinβ. \cos(\alpha — \beta) = \cos\alpha\cdot\cos\beta+\sin\alpha\ cdot \sin \beta .cos(α−β)=cosα⋅cosβ+sinα⋅sinβ.
92}} = \frac{5\sqrt{3}}{14}. \end{выравнивание} cosαcosβ=1−sin2α=1−142132=1433,=1−sin2β=1−142112=1453Таким образом, из формулы суммы косинусов имеем
cos(α+β)=cosα⋅cosβ−sinα⋅sinβ=3314×5314−1314×1114=−12. \begin{выровнено} \cos (\alpha + \beta) &= \cos \alpha \cdot \cos \beta — \sin \alpha \cdot \sin \beta \\ &= \frac{3\sqrt{3}}{14} \times \frac{5\sqrt{3}}{14} — \frac{13}{14} \times \frac{11}{14} \ \ &= -\фракция{1}{2}. \end{выровнено} cos(α+β)=cosα⋅cosβ−sinα⋅sinβ=1433×1453−1413×1411=−21.
Следовательно, поскольку 0<α+β<π, 0< \alpha + \beta < \pi ,0<α+β<π, мы можем получить α+β \alpha + \beta α+β следующим образом:
, потому что(α+β)=−12⇒α+β=23π. □ \begin{выровнено} \cos (\alpha + \beta) &= -\frac{1}{2} \\ \Rightarrow \alpha + \beta &= \frac{2}{3} \pi. \ _\площадь \end{выровнено} cos(α+β)⇒α+β=−21=32π. □
Формулы тангенса суммы и разности:
АтанБ. \begin{выровнено}
\tan(A+B) &= \dfrac{\tan A + \tan B}{1 — \tan A \tan B} \\\\
\tan(AB) &= \dfrac{\tan A — \tan B}{1 + \tan A \tan B}.
\end{aligned} tan(A+B)tan(A−B)=1−tanAtanBtanA+tanB=1+tanAtanBtanA−tanB.
Выведите формулу касательной суммы.
Мы знаем, что
sin(a+b)=sinacosb+cosasinb(1)cos(a+b)=cosacosb−sinasinb.(2)\begin{выровнено } \sin(a+b) &= \sin a \cos b + \cos a \sin b &\qquad (1) \\ \cos(a+b) &= \cos a \cos b — \sin a \sin b. &\qquad (2) \end{align}sin(a+b)cos(a+b)=sinacosb+cosasinb=cosacosb−sinasinb.(1)(2)
Деление (1)(1)(1) на (2)(2)(2) дает
sin(a+b)cos(a+b)=sinacosb+cosasinbcosacosb−sinasinb.\dfrac{\sin(a+b)}{ \cos(a+b)} = \dfrac{ \sin a \cos b + \cos a \sin b}{\cos a \cos b — \sin a \sin b}.cos(a+b)sin( a+b)=cosacosb−sinasinbsinacosb+cosasinb.
Деление правой части на cosacosb \cos a \cos b cosacosb дает
tan(a+b)=sinacosbcosacosb+cosasinbcosacosbcosacosbcosacosb−sinasinbcosacosb=tana +tanb1−tanatanb,\tan(a+b) знак равно \dfrac{\dfrac{\sin a \cos b}{\cos a \cos b} + \dfrac{\cos a \sin b}}{\cos a \cos b}}{\dfrac{\cos a \ cos b}{\cos a \cos b} — \dfrac{\sin a \sin b}{\cos a \cos b}} = \dfrac{\tan a + \tan b}{1 — \tan a \tan b}, tan(a+b)=cosacosbcosacosb −cosacosbsinasinb cosacosbsinacosb+cosacosbcosasinb=1−tanatanbtana+tanb,
, что является формулой суммы.
Вывести формулу разности тангенсов.
Мы знаем, что
загар(-а)=-загара. \tan(-a) = -\tan a .tan(-a)=-tana.
Подставив b=−b b = -b b=−b в формулу суммы тангенсов, мы получим
загар(а+(-b))=загар(а)+загар(-b)1-загаратан(-b)загар(а-b)=загара-загарb1+загар атанб. □\begin{выровнено} \tan\big(a+(-b)\big) &= \dfrac{\tan(a) + \tan(-b)}{1 — \tan a \tan(-b)} \\ \tan(a-b) &= \dfrac{\tan a — \tan b}{1 + \tan a \tan b}. \ _\площадь \end{выровнено} tan(a+(-b))tan(a-b)=1-tanatan(-b)tan(a)+tan(-b)=1+tanatanbtana-tanb. □ 9{\circ})} = \dfrac{11}{2}tan(x−30∘)tan(x+120∘)=211
Если xxx является решением приведенного выше уравнения, а cos(4x) =ab,\cos(4x) = \dfrac{a}{b},cos(4x)=ba, где aaa и bbb — взаимно простые положительные целые числа, затем найдите a+b.a + b.a+b.
Найдите сумму
tan(a)tan(2a)+tan(2a)tan(3a)+⋯+tan(8a)tan(9a),\tan (a) \tan ( 2a) + \tan(2a) \tan(3a) +\cdots+ \tan(8a) \tan(9a),tan(a)tan(2a)+tan(2a)tan(3a)+⋯+tan(8a) )tan(9a),
, где a=π5.
Приведенное выше уравнение верно для целых положительных чисел a,b,a,b,a,b и c.c.c. Каково значение a+b+c?a+b+c?a+b+c?
Цитировать как: Формулы суммы и разности. Brilliant.org . Извлекаются из https://brilliant.org/wiki/sum-and-difference-formulas/
2. Sin, Cos и Tan суммы и разности двух углов
М. Борна
Синус суммы и разности двух углов выглядит следующим образом:
На этой странице…
Тангенс суммы и разности двух углов
sin( α + β ) = sin α cos β + cos α sin β
sin( α − β ) = sin α cos β − cos α sin β
Косинус суммы и разности двух углов выглядит следующим образом:
cos( α + β ) = cos α cos β − sin α sin β
cos( α − β ) = cos α cos β + sin α sin β
Доказательства синуса и косинуса сумм и разностей двух углов
Мы можем доказать эти тождества разными способами.
Вот относительно простое доказательство с использованием единичного круга:
Доказательство 1
Доказательство 1. Использование единичной окружности
Начнем с единичной окружности (что означает, что она имеет радиус 1) с центром O.
Построим углы `BOA = alpha` и `AOP = beta`, как показано.
Затем мы опускаем перпендикуляр из точки P на ось x в точке T. Точка C является пересечением OA и PT.
Затем мы строим линию PR перпендикулярно OA.
Наконец, мы опускаем перпендикуляр из R на x — ось в S, а другая от R до PT в Q, как показано.
Отметим следующее:
(1) `/_TPR = alpha`, так как треугольники OTC и PRC подобны. (`/_OTC = /_PRC = 90°` и `/_OCT = /_PCR = 90°-альфа`.)
(2) Длина |QT| = |РС|
(3) sin (α + β) = |PT| = |PQ| + |QT| = |PQ| + |РС|
(4) |PR| = sin (β)
(5) В треугольнике PQR |PQ| = |PR| cos (α)
(6) Итак, из (4) и (5) |PQ| = sin (β) cos (α).
(7) |ИЛИ| = cos (β)
(8) В треугольнике OSR |RS| = |ИЛИ| sin (α)
(9) Итак, из (7) и (8) |RS| = cos (β) sin (α)
(10) Таким образом, из (3), (6) и (9) мы доказали:
sin (α + β) = sin (β) cos (α) + cos (β) sin (α)
Перестановка дает:
sin (α + β) = sin (α) cos (β) + cos (α) sin (β)
(11) Из четных и нечетных функций имеем: cos (− β ) = cos( β) и sin (− β ) = −sin(β)
(12) Таким образом, заменив β на (− β ), тождество в (10) станет
sin ( α − β ) = sin α cos β − cos α sin β
[Спасибо Дэвиду Макинтошу за схему приведенного выше доказательства.]
Доказательства косинуса
Теперь нам нужно доказать
, потому что ( α + β ) = потому что α cos β − sin α sin β
(13) |ОТ| = cos ( α + β )
(14) В треугольнике ORS имеем: `cos alpha = |OS|/|OR|`.
(15) cos (β) = |ИЛИ|, из (7) выше.
(16) Из (14) и (15) получаем `cos alpha cos beta= |OS|/|OR|xx|OR| = |ОС|`.
(17) В треугольнике QPR имеем `sin alpha = |QR|/|PR|`.
(18) sin (β) = |PR|, из (4) выше.
(19) Из (17) и (18) получаем `sin alpha sin beta= |QR|/|PR|xx|PR| = |QR|`.
(20) Сейчас |ОС| − |QR| = |ОТ|.
(21) Итак, `cos alpha cos beta — sin alpha sin beta` `= cos(alpha+beta)`.
(22) Переставляем, имеем:
cos ( α + β ) = cos α cos β − sin α sin β
(23) Снова заменяем β на (− β ), и тождество в (22) принимает вид:
cos ( α − β ) = cos α cos β + sin α sin β
Следующее доказательство — стандартное, которое можно найти в большинстве учебников. В нем также используется единичный круг, но оно не такое простое, как первое доказательство.
Доказательство 2
Доказательство 2 — Использование единичного круга
Сначала мы докажем тождество косинуса суммы двух углов, а затем покажем, что этот результат можно распространить на все другие приведенные тождества.
cos (α+β) = cos α cos β − sin α sin β
Рисуем окружность радиусом 1 единица с точкой P на окружности в точке (1, 0).
Проведем угол α из центра с конечной точкой Q в (cos α, sin α), как показано. [ Q равно (cos α, sin α), потому что гипотенуза равна 1 единице.]
Мы расширяем эту идею, рисуя:
a. Угол β с конечными точками Q (cos α, sin α) и R (cos (α + β), sin (α + β))
б. Угол −β с конечной точкой S (cos (−β), sin (−β))
c. Строки PR и QS , которые эквивалентны по длине.
Теперь, используя формулу расстояния из Аналитической геометрии, мы имеем:
PR 2 = (cos (α + β) − 1) 2 + sin 2 (α + β)
= cos 2 (α + β) − 2 cos (α + β) + 1 + sin 2 (α + β)
= 2 − 2cos (α + β)
[так как sin 2 (α + β) + cos 2 (α + β) = 1]
Теперь используем формула расстояния на расстоянии QS :
QS 2 = (cos α − cos (−β)) 2 + (sin α − sin (−β)) 2
6s4 = 2 α − 2 потому что α потому что (−β) + потому что 2 (−β) + sin 2 α − 2sin α sin(−β) + sin 2 (−β)
= 2 − 2cos α cos(−β) − 2sin α sin(−β)
[начиная с
sin 2 α + cos 2 α = 1 и
sin 2 (−β) + cos 2 (−2αs 4 s cos 4 s −β s = 2 s cos 4 s −β 1 cos = 1] 900 900 β + 2sin α sin β
[поскольку
cos(−β) = cos β (косинус — четная функция) и
sin(−β) = −sinβ (синус — нечетная функция — см.
Так как PR = QS , мы можем приравнять два расстояния, которые мы только что нашли:
2 − 2cos (α + β) = 2 − 2cos α cos β + 2sin α sin β и деля на -2, получаем:
cos (α + β) = cos α cos β − sin α sin β
Если мы заменим β на (−β), это тождество примет следующий вид: β) = cos α cos β + sin α sin β
[поскольку cos(−β) = cos β и sin(−β) = −sinβ]
Синус суммы двух углов
Мы стремимся доказать, что
sin (α + β) = sin α cos β + cos α sin β
Напомним, что (см. фазовый сдвиг)
sin ( θ ) = cos (π/2− θ )
Если θ = α + β, то имеем:
sin (α + β)
= потому что [π/2 — (α + β)]
= потому что [π/2 — α — β)]
Затем мы перегруппируем углы внутри косинуса, так как это нам нужно для остальной части доказательства:
cos [π/2 − α − β)] = cos [(π/2 − α) − β]
Используя косинус разности двух углов, который мы только что нашли выше [который сказал
cos ( α − β) = cos α cos β + sin α sin β],
имеем:
cos [(π/2 − α) − β]
= cos (π/2 − α) cos (β) + sin (π/2 − α) sin (β)
= sin α cos β + cos α sin β
[Поскольку cos (π/2 − α) = sin α; и sin (π/2 − α) = cos α]
Следовательно:
sin (α + β) = sin α cos β + cos α sin β
Заменив β на (−β), это тождество станет (из-за четных и нечетных функций):
sin (α − β) = sin α cos β − cos α sin β
и косинус суммы и разности двух углов.
Итог:
sin (α + β) = sin α cos β + cos α sin β
sin (α − β) = sin α cos β − cos α sin β
cos (α+β) = cos α cos β − sin α sin β
cos (α − β) = cos α cos β + sin α sin β
Наконец, вот более простое доказательство тождеств с использованием комплексных чисел :
Доказательство 3
Доказательство 3. Использование комплексных чисел
Экспоненциальная и полярная формы комплексного числа обеспечивают простой способ доказательства фундаментальных тригонометрических тождеств.
Предположим, у нас есть 2 комплексных числа, которые мы записываем как:
.r 1 e jα = r 1 (cos α + j sin α)
и
r 2 e jβ = r 2 (cos β + j sin β)
Перемножаем эти комплексные числа.
Умножение левых частей:
r 1 e jα × r 2 e jβ = r 1 r 2 e j(α+β)
We can write this answer as:
r 1 r 2 e j(α+β) = r 1 r 2 (cos ( α+β) + j sin (α+β)) … (1)
Умножая правые части:
r 1 (cos α + j sin α) × r 2 (cos β + j SIN β)
= R 1 R 2 (COS α COS β + J COS β β + J j COS α β + J j COS α β + J J SIN α α α α α α α α J J α α j J J J J J J J J .
[начиная с j 2 = −1]
Теперь приравняем (1) и (2) и разделим обе части на r 1 r 2 :
cos (α+β) + j sin (α+β) = cos α cos β − sin α sin β + j β sin (cos α cos β + sin α cos β)
Приравнивание действительных частей дает:
cos (α+β) = cos α cos β − sin α sin β
Приравнивание мнимых частей дает:
sin (α+β) = sin α cos β + cos α sin β
Затем мы заменим β на (−β), как и раньше, чтобы получить тождества для sin (α − β) и cos (α − β).
Имеем следующие тождества для тангенса суммы и разности двух углов:
`тангенс(альфа+бета)=(тангенс альфа+тангенс бета)/(1-тангенс альфа\ тангенс бета)`
и
`тангенс (альфа-бета)=(тангенс альфа-тангенс бета)/(1+тангенс альфа\ тангенс бета)`
Доказательство тангенса суммы и разности двух углов
Наше доказательство для них использует тригонометрическое тождество для tan, с которым мы уже встречались.
Доказательство
Случай: `tan(альфа+бета)`
Напомним, что
`tan theta=(sin theta)/(cos theta)`
Итак, полагая θ = α + β и расширяя с помощью наших новых тождеств синуса и косинуса, мы имеем:
`tan(alpha+beta)` `=(sin(alpha+beta))/(cos( alpha+beta))` `=(sin alpha cos beta+cos alpha sin beta)/(cos alpha cos beta-sin alpha sin beta)`
Деление числителя и знаменателя на cos α cos β:
`=(sin alpha cos beta+cos alpha sin beta)/(cos alpha cos beta-sin alpha sin beta)` `-:(cos alpha cos beta)/(cos alpha cos beta`
Упрощение дает нам:
`tan(alpha+beta)=` `(tan alpha+tan beta)/(1-tan alpha\ tan beta)`
Случай: `tan(alpha-beta)`
Замена β на (−β) дает нам
`tan(alpha-beta)=` `(tan alpha-tan beta)/(1+tan alpha\ tan beta)`
[Функция тангенса нечетная, поэтому tan (−β) = − tan β]
Мы доказали тождества двух тангенсов суммы и разности двух углов:
`tan(alpha+beta)=` `(tan alpha+tan beta)/(1- загар альфа\ загар бета)` 9(«o»)`
`=sqrt3/2(1)/sqrt2-1/2(1)/sqrt2`
`=(sqrt3-1)/(2sqrt2)`
Это точное значение для cos 75 o .
Пример 2
Если «sin α = 4/5» (в квадранте I) и «cos β = -12/13» (в квадранте II), вычислите «sin(α − β)».
Ответить
Мы используем
sin( α − β ) = sin α cos β − cos α sin β
Сначала нам нужно найти `cos α` и `sin β`.
Если `sin α = 4/5`, то мы можем нарисовать треугольник и найти значение неизвестной стороны по теореме Пифагора (в данном случае 3):
345αОткрыть изображение на новой странице3-4- 5 прямоугольный треугольник
Проделываем то же самое для `cos β = 12/13` и получаем следующий треугольник.
12513βОткрыть изображение на новой странице5-12-13 прямоугольный треугольник
Примечание 1: Мы используем положительное значение «12/13» для расчета требуемого опорного угла относительно «бета».
Примечание 2: Коэффициент синусов положителен как в квадранте I, так и в квадранте II.
Примечание 3: Мы воспользовались теоремой Пифагора, чтобы найти неизвестную сторону, 5.
Теперь о неизвестных соотношениях в вопросе: )
`sin β = 5/13`
(положительно, потому что в квадранте II)
Теперь мы готовы найти требуемое значение sin( α − β ):
`sin(alpha-beta)=` `sin alpha\ cos beta-cos alpha\ sin beta`
`=4/5(-12/13)-3/5(5/13)`
` =(-48-15)/65`
`=(-63)/65`
Это точное значение для sin( α − β ).
Упражнения
1. Найдите точное значение cos 15 o , используя 15 o = 60 o − 45 o
Ответить
Снова используем 30 или -60 9(«o»)`
`=1/2(1)/sqrt2+sqrt3/2(1)/sqrt2`
`=(1+sqrt3)/(2sqrt2)`
2. Если `sin α = 4/5` (в квадранте I) и `cos β = -12/13` (в квадранте II) оценивают `cos(β − α)].`
[Это не то же самое, что пример 2 выше. На этот раз нам нужно найти косинус разности.
Ответить
В этом случае для косинуса разности двух углов имеем:
`cos(beta-alpha)=` `cos beta cos alpha+sin beta sin alpha`
`=((-12)/13)3/5+(5/13)4/5`
`=(-36+20)/65`
`=(-16)/65`
3. Сократите следующее до одного термина. Не расширяйтесь.
cos( x + y )cos y + sin( x + y )sin y
Ответить
Мы распознаем это выражение как правую часть:
cos( α − β ) = cos α cos β + cos α соз β ,
с α = х + у и β = у.
Теперь мы можем написать это в терминах COS ( α — β ) следующим образом:
COS ( x + Y ) COS Y + SIN + 1 ( y 1 ( y 1 ( y ( y ( y ( y ( y y y .
= потому что [( х + у ) — ( у )]
= потому что х 9″o»\ sin x`
`=sqrt3/2 cos x-1/2sin x`
`=(sqrt3\ cos x-sin x)/2`
`=»RHS»`
LHS = RHS, мы доказали тождество.
Нахождение фазового сдвига синуса или косинуса
Нахождение фазового сдвига синуса или косинуса — предварительный расчет—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы Precalculus
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Учитесь по концепции
Справка по предварительному исчислению » Графики и обратные тригонометрические функции » График функций синуса и косинуса » Найдите фазовый сдвиг функции синуса или косинуса
Найдите фазовый сдвиг функции .
Возможные ответы:
Правильный ответ:
Объяснение:
В формуле
.
представляет фазовый сдвиг.
Включение того, что мы знаем, дает нам:
.
Упрощенно, тогда фаза .
Сообщить об ошибке
Пожалуйста, выберите лучший ответ из следующих вариантов.
Опишите фазовый сдвиг следующей функции:
Возможные ответы:
Сдвиг вниз на радианы.
Сдвиг влево на радиан.
Вертикальное растяжение в радианах.
Сдвиг вверх на радианы.
Правильный ответ:
Сдвиг влево на радиан.
Объяснение:
Так как добавляется внутри скобок, произойдет сдвиг по горизонтали.
Сообщить об ошибке
Какое уравнение даст этот график?
Возможные ответы:
Правильный ответ:
Пояснение:
Это график синуса, но сдвинутый вправо на единицы. Чтобы отразить этот сдвиг, следует вычесть из x.
Таким образом получается
.
Сообщить об ошибке
Какое уравнение даст этот синусоидальный график?
Возможные ответы:
Правильный ответ:
Объяснение:
Амплитуда графика равна 2, но он сдвинут вниз на 1:
С точки зрения уравнения это ставит 2 перед грехом и -1 в конце.
Это облегчает понимание того, что график начинается [находится в 0], где .
Фазовый сдвиг вправо или .
Сообщить об ошибке
Напишите уравнение синусоидального графика с максимумом в и минимумом в .
Возможные ответы:
Правильный ответ:
Пояснение:
Для написания этого уравнения полезно начертить график:
Указав точки максимума и минимума, мы видим, что этот график сдвинут вверх на 1, а его амплитуда равна 2,9.0015
Расстояние от точки максимума до точки минимума равно половине длины волны. В этом случае длина волны равна . Это означает, что полная длина волны равна , а частота равна 1.
На этом рисунке показано, что график начинается слева от оси Y. Чтобы выяснить, где именно, вычтите из максимальной координаты x :
.
Наше уравнение будет иметь вид, где A — амплитуда, f — частота, h — сдвиг по горизонтали, а k — сдвиг по вертикали.
Этот график имеет уравнение
.
Сообщить об ошибке
Напишите уравнение для графика косинуса с максимумом в и минимумом в .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы написать это уравнение, полезно начертить график:
Пунктирная линия находится в точке , где достигается максимум и, следовательно, где начинается график. Это означает, что график сдвинут вправо.
Расстояние от максимума до минимума составляет половину всей длины волны. Вот .
Поскольку половина длины волны равна , это означает, что полная длина волны равна , поэтому частота равна всего 1.
Амплитуда равна 3, потому что график идет симметрично от -3 до 3.
Уравнение будет иметь вид где A амплитуда, f — частота, h — сдвиг по горизонтали, а k — сдвиг по вертикали.
Это уравнение
.
Сообщить об ошибке
Напишите уравнение синусоидальной функции с максимумом в точке и минимумом в точке .
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение будет иметь вид, где A — амплитуда, f — частота, h — сдвиг по горизонтали, а k — сдвиг по вертикали.
Чтобы написать уравнение, полезно начертить график:
Из построения максимума и минимума видно, что график находится в центре с амплитудой 3,
Расстояние от максимума до минимума равно половине длины волны. Для этого графика это расстояние равно .
Это означает, что общая длина волны равна 1, а частота равна 1.
График начинается за точкой максимума. Чтобы определить это значение x, вычтите из x-координаты максимума:
Наше уравнение:
.
Сообщить об ошибке
Уведомление об авторских правах
Посмотреть репетиторов Pre-Calculus
Анна
Сертифицированный репетиторКолледж Маунт-Холиок, бакалавр биологических наук, общий.
View Pre-Calculus Tutors
George
Сертифицированный преподавательГосударственный колледж Пенсаколы, бакалавр искусств, математика.
Посмотреть репетиторов по математике
Кеннет
Сертифицированный репетиторУниверситет Мэри Вашингтон, бакалавр наук, математика. Колледж Худ, магистр наук, компьютерных и информационных наук…
Все ресурсы Precalculus Resources
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Учитесь по концепции
Интуитивное понимание синусоидальных волн – BetterExplained
Синусоидальные волны меня смутили. Да, я могу бормотать «SOH CAH TOA» и рисовать линии внутри треугольников.
Я застрял на мысли, что синус нужно извлекать из других форм. Быстрая аналогия:
Вы: Геометрия — это фигуры, линии и так далее.
Чужой: О? Можете ли вы показать мне линию?
Вы (оглядываясь): Э… видишь вон тот кирпич? Линия — это один край этого кирпича.
Инопланетянин: Значит, линии являются частью фигуры?
Вы: Вроде того. Да, в большинстве фигур есть линии. Но линия сама по себе является базовым понятием: луч света, маршрут на карте или даже…
Чужой: У кирпичей есть линии. Линии идут из кирпичей. Кирпичи кирпичи кирпичи.
Большинство уроков математики проходят именно так. «У кругов есть синус. Синус получается из кругов. Круги круги круги».
Арх! Нет — круги один пример синуса. В предложении: Синус — это естественное колебание, воплощение гладкости: он делает круги «круглыми» точно так же, как линии делают квадраты «квадратными».
Давайте построим нашу интуицию, рассматривая синус как его собственную форму, и , а затем поймем, как он вписывается в круги и тому подобное. Вперед!
Синус против линий
Не забудьте отделить идею от примера : квадраты равны примеров строк. Синус щелкнул, когда он стал собственной идеей, а не «частью круга».
Посмотрим синус в симуляторе:
Хьюберт проведет экскурсию:
- Нажми старт . Иди, Хьюберт, иди! Заметили это плавное движение вперед и назад? Это Хьюберт, но что более важно (извините, Хьюберт), это синус! Это естественно, как пружины подпрыгивают, маятники качаются, струны вибрируют… и многие вещи движутся.
- Изменить «вертикальный» на «линейный» . Большая разница — видите, как движение становится постоянным и роботизированным, как игра в понг?
Давайте рассмотрим различия с помощью видео:
youtube.com/embed/iUz4OLQi_uw?start=45″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Линейное движение постоянно: мы движемся с заданной скоростью и мгновенно разворачиваемся. Это неестественное движение в танце робота (обратите внимание на линейный отскок без замедления по сравнению со стробирующим эффектом).
Синус меняет свою скорость: начинает быстро, замедляется, останавливается и снова ускоряется. Это чарующая плавность плавного танца (человеческая синусоида и естественный отскок).
К сожалению, в учебниках синус с анимацией или танцами не показан. Нет, они предпочитают вводить синус с временной шкалой (попробуйте установить «горизонтальную» на «временную шкалу»):
(источник)
Эгадс. Это схематическая диаграмма, которую нам всегда показывали. Это дает вам ощущение синуса? Не больше, чем скелет изображает ловкость кошки.
Неизбежный круг
Круги имеют синус. Да. Но увидеть синус внутри круга — это все равно, что достать яйца из омлета. Это все смешано!
Давайте помедленнее. В симуляции установите для Хьюберта значение vertical:none и horizontal: sine*. Видишь, как он извивается вбок? Это движение синуса. Есть небольшая поправка: обычно синусоидальный цикл начинается с нейтральной средней точки и достигает максимума. На этот раз мы начинаем с максимума и опускаемся к середине. Синус, который «начинается с максимума», называется косинусом, и это просто версия синуса (например, горизонтальная линия — это версия вертикальной линии).
Хорошо. Время для обеих синусоид: укажите вертикальную как «синус» и горизонтальную как «синус*». И… у нас есть круг!
Горизонтальная и вертикальная «пружины» вместе создают круговое движение. Большинство учебников рисуют круг и пытаются извлечь синус, но я предпочитаю наращивать: начинать с чистого горизонтального или вертикального движения и добавлять другое.
Быстрые вопросы и ответы
Несколько идей, которые я упустил при первом изучении синуса:
Синус действительно является одномерным
Синус колеблется в одном измерении. Действительно. Мы часто рисуем график синуса с течением времени (чтобы не писать поверх себя), и иногда «вещь», производящая синус, тоже движется, но это необязательно! Пружина в одном измерении — это совершенно счастливая синусоида.
(Источник: Википедия, постарайтесь не поддаваться гипнозу.)
Окружности пример двух синусоид
Окружности и квадраты представляют собой комбинацию основных компонентов (синусов и линий). Круг состоит из двух связанных одномерных волн, каждая из которых движется в горизонтальном и вертикальном направлениях.
(Источник http://1ucasvb.tumblr.com/)
Но помните, круги не являются началом синусов, так же как квадраты не являются началом линий.
Что означают значения синуса?
Синусоидальный цикл между -1 и 1. Он начинается с 0, увеличивается до 1,0 (макс.), опускается до -1,0 (мин.) и возвращается в нейтральное положение. Я также вижу синус как процент от 100% (полный ход вперед) до -100% (полный отход).
Что такое ввод ‘x’ в sin(x)?
Каверзный вопрос. Синус — это цикл, а x, вход, равен , как далеко мы продвинулись в цикле .
Посмотрим на строки:
- Вы едете по квадрату. Каждая сторона занимает 10 секунд.
- Через 1 секунду вы готовы на 10% на этой стороне
- Через 5 секунд вы готовы на 50%
- Через 10 секунд вы закончили борт
В линейном движении мало сюрпризов. Теперь для синуса (сосредоточившись на цикле «от 0 до максимума»):
- Мы путешествуем по синусоиде от 0 (нейтраль) до 1,0 (максимум).
- Через 5 секунд мы… на 70% готовы! Синус вылетает из ворот и замедляется. Большая часть выигрыша приходится на первые 5 секунд
- Требуется еще 5 секунд, чтобы перейти от 70% к 100%. А переход с 98% на 100% занимает почти целую секунду!
Несмотря на нашу начальную скорость, синус замедляется, поэтому мы осторожно целуем максимальное значение, прежде чем развернуться. Эта плавность делает синус, синус.
Для гиков: Нажмите «показать статистику» в симуляции. Вы увидите процент завершения всего цикла, мини-цикла (от 0 до 1,0) и достигнутое значение. Остановитесь, пройдите и переключитесь между линейным и синусоидальным движением, чтобы увидеть значения.
Быстрый тест: что дальше, 10% линейного цикла или 10% синусоидального цикла? Синус. Помните, он вылетает из ворот на максимальной скорости. К тому времени, когда синус достигает 50% цикла, он движется со средней скоростью линейного цикла, а за пределами этого он движется медленнее (пока не достигнет максимума и не развернется).
Итак, x — это «количество вашего цикла». Какой цикл?
Зависит от контекста.
- Базовый триггер: «x» — градусы, а полный цикл — 360 градусов
- Расширенный триггер: ‘x’ — это радианы (они более естественны!), и полный цикл проходит по единичному кругу (2*пи радиан)
Поиграйте со значениями x здесь:
Но опять же, циклы зависят от кругов! Можем ли мы избежать их тирании?
Пи без картинок
Представьте себе слепого инопланетянина, который замечает только оттенки света и тьмы. Не могли бы вы описать число пи? Трудно представить себе длину окружности, верно?
Вернемся немного назад. Синус — это повторяющийся узор, а это значит, что он должен… повторяться! Он идет от 0 до 1, до 0, до -1, до 0 и так далее.
Определим число пи как время, которое требуется синусу от 0 до 1 и обратно до 0. Ого! Теперь мы используем пи и без круга! Пи — это концепция, в которой просто случайно появляется в кругах:
- Синус — это мягкое раскачивание вперед-назад
- Pi — время от нейтрального до максимального и обратно
- n * Пи (0 * Пи, 1 * Пи, 2 * Пи и т.
- 2 * пи, 4 * пи, 6 * пи и т. д. являются полными циклами
Ага! Вот почему число Пи появляется во многих формулах! Пи не «принадлежит» к окружностям больше, чем 0 и 1 — пи примерно равно синусу, возвращающемуся к центру ! Окружность — это пример формы, которая повторяется и возвращается в центр каждые 2*пи. Но пружины, вибрации и т.д. возвращаются в центр после пи тоже!
Вопрос: Если пи — это половина естественного цикла, то почему это не простое число?
Ответим вопросом на вопрос. Почему квадрат 1×1 имеет длину диагонали $\sqrt{2} = 1,414…$ (иррациональное число)?
Философски неудобно, когда природа не совпадает с нашей системой счисления. У меня нет хорошей интуиции. Я подозреваю, что простые правила (квадрат 1×1 + теорема Пифагора) могут привести к сложным результатам.
Какова скорость синуса?
Я был хитрым.
- sin(x) — стандартная синусоидальная волна по умолчанию , которая действительно требует пи единиц времени от 0 до максимума до 0 (или 2*пи для полного цикла)
- sin(2x) — волна, которая движется в два раза быстрее
- sin(0.5x) — волна, которая движется в два раза медленнее
Итак, мы используем sin(n*x), чтобы синусоида зацикливалась так быстро, как нам нужно. Часто фраза «синусоида» относится к общей форме, а не к конкретной скорости.
Часть 2: Понимание определений синуса
Это очень умно — сделайте перерыв, если вам это нужно. Будем надеяться, что синус становится самостоятельным паттерном. Теперь давайте разовьем нашу интуицию, увидев, как связаны общие определения синуса.
Определение 1: Высота треугольника / круга!
Синус впервые был найден в треугольниках.
- SOH: синус противоположен / гипотенуза
- CAH: косинус смежный/гипотенуза
- TOA: Тангенс противоположен/смежен
Для прямоугольного треугольника с углом x sin(x) — это длина противоположной стороны, деленная на гипотенузу. Если мы сделаем гипотенузу 1, мы можем упростить до:
- Синус = Противоположный
- Косинус = Смежный
И с большим умом мы можем нарисовать наши треугольники с гипотенузой 1 в круге с радиусом 1:
Вуаля! Круг, содержащий все возможные прямоугольные треугольники (поскольку их можно увеличить, используя сходство). Например:
- sin(45) = 0,707
- Положите 10-футовый шест и поднимите его на 45 градусов. 10 * sin(45) = 7,07 фута от земли
- 8-футовый шест будет равен 8 * sin(45) = 5,65 фута
Эти прямые манипуляции отлично подходят для построения (пирамиды сами себя не вычислят).
На самом деле, для решения многих задач мы переходим в «режим геометрии» и начинаем думать «синус = высота», чтобы ускорить решение задач. Это нормально — просто не застрять там.
Определение 2: бесконечный ряд
Я избежал слона в комнате: как, черт возьми, мы вычисляем синус!? Мой калькулятор рисует круг и измеряет его?
Рад вас разозлить. Вот секрет синуса без круга:
Синус — это ускорение, противоположное вашему текущему положению
Используя нашу метафору банковского счета: представьте себе извращенного босса, который дает вам повышение на против вашего текущего банковского счета! Если у вас есть 50 долларов в банке, то ваша надбавка на следующей неделе составит 50 долларов. Конечно, ваш доход может составлять $75 в неделю, так что вы все равно будете зарабатывать $75-$50 за эту неделю), но в конечном итоге ваш баланс уменьшится, так как «повышения» превысят ваш доход.
Но не бойся! Как только ваш счет станет отрицательным (скажем, вы на 50 долларов), тогда ваш босс даст законную прибавку в 50 долларов в неделю. Опять же, ваш доход может быть отрицательным, но в конечном итоге повышение превысит его.
Это постоянное притяжение к центру поддерживает цикл: когда вы поднимаетесь вверх, «притяжение» снова втягивает вас внутрь. Это также объясняет, почему нейтральная максимальная скорость для синуса: если вы находитесь на максимальной скорости, вы начинаете падать и накапливать все больше и больше «отрицательных подъемов» по мере падения. Когда вы проходите через нейтральную точку, вы чувствуете все возможные отрицательные подъемы (как только вы пересекаете их, вы начинаете получать положительные подъемы и замедляетесь).
Кстати: поскольку синус — это ускорение, противоположное вашему текущему положению, а окружность состоит из горизонтального и вертикального синуса… вы поняли! Круговое движение можно описать как «постоянное притяжение, противоположное вашему текущему положению, к вашему горизонтальному и вертикальному центру».
Знакомство с исчислением
Давайте опишем синус с помощью исчисления. Как и e, мы можем разбить синус на более мелкие эффекты:
- Начать с 0 и увеличивать с единичной скоростью
- В каждое мгновение отталкиваться отрицательным ускорением
Как мы должны думать об этом? Посмотрите, как каждый эффект выше изменяет наше расстояние от центра:
- Наш начальный удар увеличивает расстояние линейно: y (расстояние от центра) = x (затраченное время)
- В любой момент мы чувствуем возвращающую силу -х. Мы дважды интегрируем, чтобы превратить отрицательное ускорение в расстояние:
Наблюдать за тем, как ускорение влияет на расстояние, все равно, что наблюдать, как повышение зарплаты бьет по вашему банковскому счету. «Повышение» должно изменить ваш доход, а ваш доход меняет ваш банковский счет (два интеграла «вверх по цепочке»). 97/7! что создает восстанавливающую силу удара…
Как и e, синус можно описать бесконечным рядом:
Я много раз видел эту формулу, но она сработала только тогда, когда я увидел синус как комбинацию начального импульса и восстанавливающих сил .
Несколько забавных заметок:
- Рассмотрим «возвращающую силу», например «положительный или отрицательный процент». Это облегчает понимание связи синус/е в формуле Эйлера. Синус похож на e, за исключением того, что иногда он приносит отрицательный процент. Здесь есть чему поучиться :).
- Для очень малых углов «y = x» является хорошим предположением для синуса. Мы просто принимаем первоначальный импульс и игнорируем любые восстанавливающие силы.
Вычисление косинуса
Косинус — это просто сдвинутый синус, и это весело (да!) теперь, когда мы понимаем синус: 92/2!. Но это запускает другую восстанавливающую силу, которая запускает другую, и прежде чем вы это узнаете:
Определение 3: Дифференциальное уравнение
Мы описали поведение синуса с помощью конкретных уравнений.
Эта красота говорит:
- Наша текущая позиция y
- Наше ускорение (2-я производная или y») противоположно нашему текущему положению (-y)
И синус, и косинус подтверждают это. Сначала я ненавидел это определение; это так далеко от визуализации. Я не знал, что это описывает сущность синуса, «ускорение против вашего положения». 9x можно описать (уравнением):
То же уравнение с положительным знаком («ускорение равно вашему положению»)! Когда синус — это «высота круга», очень сложно установить связь с e.
Одно из моих самых больших математических сожалений — это то, что я не выучил дифференциальные уравнения. Но я хочу, и я подозреваю, что наличие интуиции для синуса и е будет иметь решающее значение.
Подводя итоги
Цель состоит в том, чтобы перевести синус из некоторой математической мелочи («части круга») в его собственную форму:
- Синус — это плавное колебательное движение между минимумом (-1) и максимумом (1).
- Синус появляется в кругах и треугольниках (и пружины, маятники, вибрации, звук…).
- Pi — это время от нейтрального до нейтрального в sin(x). Точно так же число «пи» не «принадлежит» кругам, оно просто появляется там.
Позвольте синусу войти в ваш умственный набор инструментов ( Хм, мне нужна формула для плавных изменений… ). В конце концов, мы интуитивно поймем основы (е, пи, радианы, мнимые числа, синус…), и их можно смешать в восхитительный математический салат. Наслаждаться!
Приложение
Используя этот подход, Алистер Макдональд создал отличный учебник с кодом для создания собственных функций синуса и косинуса.
Другие сообщения из этой серии
- Наглядное интуитивное руководство по воображаемым числам
- Интуитивная арифметика с комплексными числами
- Понимание того, почему сложное умножение работает
- Интуитивное руководство по углам, градусам и радианам
- Интуитивное понимание формулы Эйлера
- Интерактивное руководство по преобразованию Фурье
- Интуитивное руководство по свертке
- Интуитивное понимание синусоидальных волн
- Интуитивное руководство по линейной алгебре
- Интуиция программиста для умножения матриц
- Мнимое умножение против мнимых показателей
- Интуитивное руководство по гиперболическим функциям
Математическая сцена — Правила тригонометрии
Математическая сцена — Правила тригонометрии — Урок 2
2008 Расмус ehf и Jhann sak
Урок 2
- Формула сложения
- Формулы для двойного углы
Формулы синусов, косинусов и тангенсов суммы или разности двух углов может быть очень полезным.
Треугольник OPQ на диаграмме имеет вершины P, Q и O, центр системы координат. Будем называть угол между ось x и OQ u, а также угол между осью x и OP v. Следовательно, угол POQ равен u − v. Точка Q имеет координаты (cos u, sin u), а точка P имеет координаты (cos v, sin v). Расстояние между П и Q можно записать как |PQ| . Теперь воспользуемся формулой расстояния между двумя точек, чтобы найти это расстояние.
|PQ| 2 = (cos u − cos v) 2 + (sin u − sin v) 2 = cos 2 u − 2 cos u cos v + cos 2 v
+ грех 2 у − 2 sin u sin v + sin 2 v
= 1 − 2 cos u cos v − 2 sin u грех v + 1
= 2 − 2 cos u cos v − 2 sin u sin v
(расстояние) 2 =
(x 2 −x 1 ) 2 + (y 2 −y 1 ) 2
Умножить за скобки и упростить.
Теперь находим |PQ| используя правило косинусов.
|PQ| 2 = 1 2 + 1 2 — 2×1×1×cos (и — v)
= 2 − 2×cos (u − v)
Приравнивая эти два выражения получаем:
2 − 2×cos (u − v) = 2 − 2 cos u cos v − 2 sin u sin v
− 2×cos (u − v) = − 2 cos u cos v − 2 sin u грех v
Если мы разделим все на −2, мы получим следующая формула:
cos (u − v) = cos u cos v + sin u sin v Из этой формулы мы получаем вторую, полагая −v в формуле вместо v:
потому что (u − (−v)) = cos u cos (−v) + sin u sin (−v)
Используя правила, которые мы нашли из единичного круга, cos (−v) = cos v и sin (−v) = − sin v мы можем переписать это выражение как:
cos (u + v) = cos u × cos v − sin u × sin v На диаграмме ниже мы нарисовали два треугольника.
Эти конгруэнтные треугольники приводят к следующему правила:
потому что v = sin (90 − v) и sin v = cos (90 − v)
Теперь подставляем 90 вместо u и (u + v) вместо v в эти правила получить две формулы для синусов.
грех (и + v) = потому что (90 — (и + v))
= cos ((90 − u) − v)
= cos (90 − u) cos v + грех (90 — и) грех v
= sin u cos v + cos u sin v
Таким образом мы нашли формула для греха (u + v):
sin (u+v) = sin u cos v + cos u sin v Мы используем правило cos(u-v) = cos u cos v+sin u sinv и тогда sin v = cos (90 − v) и cos v = грех (90 — v). Если мы теперь подставим (−v) вместо v в этом формулы, получаем следующее:
sin (u − v) = sin (u + (−v)) = sin u cos (−v) + cos u sin (−v)
= sin u, потому что v − cos u sin v
Таким образом мы нашли формула для греха (u − v):
sin (u-v) = sin u × cos v — cos u × sin v Путем замены v на u в формулах sin (u + v) и cos (u + v) получаем формулы для sin (u + u) и cos (u + u), называемые формулами двойного угла. Это может быть написано:
sin 2u = 2 sin u × cos u cos 2u = cos 2 u − sin 2 u
Правило для cos 2u можно записать еще двумя способами, используя правило cos 2 u + sin 2 u = 1.
Сначала мы заменим cos 2 u на cos 2 u = 1 − sin 2 u а затем sin 2 u, используя sin 2 u = 1 − cos 2 у, дающие формулы:
cos 2u = 2 cos 2 u − 1 cos 2u = 1 − 2 sin 2 u
Пример 1
Используйте приведенные выше формулы для найти точные значения для sin 15
и cos 15.Мы уже нашли, что cos 45 = 2 / 2 , sin 45 = 2 / 2 ,
cos 60 = и sin 60 = 3 / 2 . Используя формулу для
cos(u — v) получаем следующее:cos 15 = cos (60 − 45)
= cos 60 × cos 45 + sin 60 × sin 45
= × 2 / 2 + 3 / 2 × 2 / 2
= 2 / 4 + 3× 2 / 4
= 2× (1 + 3) / 4
Используя формулу для sin(u — v) получаем следующее:
грех 15 = грех (60 — 45)
= sin 60 × cos 45 − cos 60 × sin 45
= 3 / 2 × 2 / 2 − × 2 / 2
= 3× 2 / 4 − 2 / 4
= 2× ( 3 − 1)/ 4
Пример 2
Упростите выражение sin (270 — v).
Используем правило sin (u — v) = sin u × cos v — cos u × sin v.
sin (270 − v) = sin 270 × cos v − cos 270 × sin v = −1× cos v − 0× sin v
= − cos v
sin 270 = −1
cos 270 = 0
Пример 3
Найдите формулу для cos 3x который использует только sin x и cos x.
Используем формулу cos (u + v) = cos u × cos v − sin u × sin v и заменить u
в 2 раза и v на х.
cos (2x + x) = cos 2x × cos x − sin 2x × sin x кос 2x = cos 2 x − sin 2 x sin 2x = 2 sin x × cos x = (cos 2 x − sin 2 x)×cos х — (2 грех х × потому что х) × грех х
= cos 3 x − sin 2 х × cos х − 2 sin 2 х × cos х
= cos 3 x − 3 sin 2 x × cos x
Пример 4
Решите уравнение sin 2x + 2 sin x = 0 на интервале
0 х < 2.
грех 2x + 2 sin x = 0
2 sin x cos x + 2 грех х = 0
2 sin x (cos x + 1) = 0
sin x = 0 og cos x = — 1,Используйте sin 2x = 2 sin x cos x.
Одно решение sin x = 0
х = 0 или (0 или 180)
Другим решением является cos x = −1
.х = (180)
Таким образом, решения равны 0 и .
Пример 5
Решить уравнение 7 cos 2 x + 5 sin 2 х + 6 sin 2x = 0
Сначала используем формулу sin 2x = 2 sin x × cos x.
7 cos 2 х + 5 sin 2 x + 12 sin x × cos х = 0
Уравнение такого типа, с двумя множителями sin или cos в каждом члене можно решить, разделив на cos 2 x и преобразование уравнения в уравнение тангенса.
Это квадратное уравнение при a = 5, b = 12 и c = 7,
tan x = −1 дает x = −/4 + k× (−45 + k×180)
tan x = −7/5 не укажите угол, который является точной пропорцией .
х ≈ −0,95 + k× (54,5 + k×180)
Попробуйте выполнить тест 1 по правилам тригонометрии.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Sin Theta — определение, формулы, значения и примеры
Функция синуса «или» Sin Theta — одна из трех наиболее распространенных тригонометрических функций наряду с косинусом и тангенсом. В прямоугольной тригонометрии функция синуса определяется как отношение противолежащего катета к гипотенузе.
Математическое обозначение функции синуса:
\(\sin(\theta) = \frac{\text{Противоположная сторона}}{\text{Сторона гипотенузы}}\)
Подробнее о Sin Theta
Формула Sin theta также может быть рассчитана путем произведения тангенса угла на косинус угла.
\(\sin(\theta) = \tan(\theta) \times \cos(\theta)\)
Производная \(\sin(\theta)\) в исчислении равна \(\cos( \theta)\), а интеграл от него равен \(-\cos(\theta)\).
График тета-функции синусаНиже приведена таблица значений тета-синуса для различных градусов и радиан.
Радианы Градусы Значение тангенса 0 0° 0 \(\frac{\pi}{6}\) 30° \(\frac{1}{5}\)
(\frac{\pi}{4}\)
45° \(\frac{1}{\sqrt{2}}\) \(\frac{\pi}{3}\ ) 60° \(\frac{\sqrt{3}}{2}\) \(\frac{\pi}{2}\) 90° 1 5
5
\(\pi\) 180° 0 \(\frac{3\pi}{2}\) 92}\\
& = \frac{5/4}{89/64}\\
\sin(x) & = \frac{80}{89}\\
\end{align}
\)Вопрос 3.
Раствор. Дано, угол между лестницей и землей \(\theta = 60\) и гипотенуза = 44 фута
Как мы знаем,
\(\sin(\theta) = \frac{\text{Опровержение}}{\text{Гипотенуза}}\)
\(\sin(60°) = \frac{\ text{Напротив}}{44}\)
\(\frac{\sqrt{3}}{2} = \frac{\text{Напротив}}{44}\)
\(\text{Напротив} = 22 \sqrt{3}\)
∴ Высота стены составляет \(22 \sqrt{3}\) футов.
Часто задаваемые вопросыОбъясните, как sin(-x) = -sin(x ).
Как известно, угол (-x) лежит в 4-м квадранте графика, и синус в этом квадранте отрицателен. Следовательно, это показывает, что sin(-x) = -sin(x).
Что такое грех тета ?
Синус тета прямоугольного треугольника равен отношению длины противоположной стороны к длине гипотенузы.