Угол между прямой и плоскостью: определение, примеры нахождения
Статья начинается с определение угла между прямой и плоскостью. В данной статье будет показано нахождение угла между прямой и плоскостью методом координат. Подробно будут рассмотрены решение примеров и задач.
Угол между прямой и плоскостью – определение
Предварительно необходимо повторить понятие о прямой линии в пространстве и понятие плоскости. Для определения угла между прямой и плоскостью необходимый несколько вспомогательных определений. Рассмотрим эти определения подробно.
Определение 1Прямая и плоскость пересекаются в том случае, когда они имеют одну общую точку, то есть она является точкой пересечения прямой и плоскости.
Прямая, пересекающая плоскость, может являться перпендикулярной относительно плоскости.
Определение 2Прямая является перпендикулярной к плоскости, когда она перпендикулярна любой прямой, находящейся в этой плоскости.
Определение 3Проекция точки M на плоскость γ является сама точка, если она лежит в заданной плоскости, либо является точкой пересечения плоскости с прямой, перпендикулярной плоскости γ, проходящей через точку M, при условии, что она не принадлежит плоскости γ.
Проекция прямой а на плоскость
Отсюда получаем, что перпендикулярная к плоскости γ проекция прямой имеет точку пересечения. Получаем, что проекция прямой a – это прямая, принадлежащая плоскости γ и проходящая через точку пересечения прямой a и плоскости. Рассмотрим на рисунке, приведенном ниже.
На данный момент имеем все необходимые сведения и данные для формулировки определения угла между прямой и плоскостью
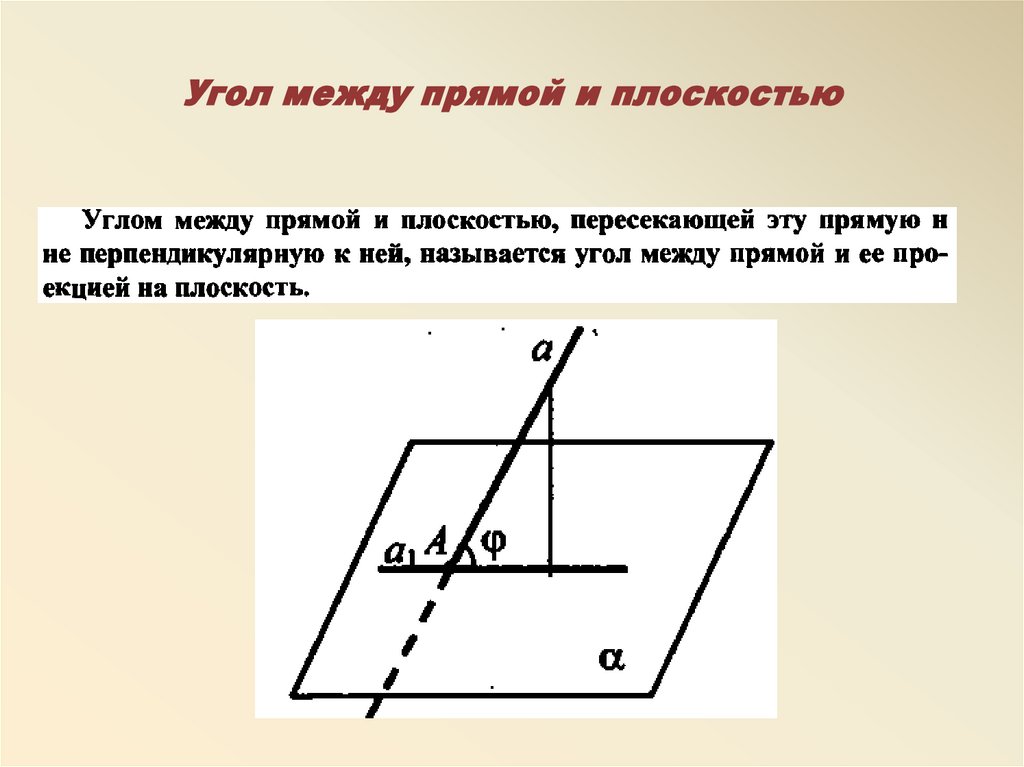
Определение 5Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая не перпендикулярна к ней.
Определение угла, приведенное выше, помогает прийти к выводу о том, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми, то есть заданной прямой вместе с ее проекцией на плоскость. Значит, угол между ними всегда будет острым. Рассмотрим на картинке, приведенной ниже.
Угол, расположенный между прямой и плоскостью, считается прямым, то есть равным 90 градусов, а угол, расположенный между параллельными прямыми, не определяется. Бывают случаи, когда его значение берется равным нулю.
Нахождение угла между прямой и плоскостью
Задачи, где необходимо найти угол между прямой и плоскостью, имеет множество вариация решения. Ход самого решения зависит от имеющихся данных по условию. Частыми спутниками решения являются признаки подобия или равенства фигур, косинусы, синусы, тангенсы углов. Нахождение угла возможно при помощи метода координат. Рассмотрим его более детально.
Если в трехмерном пространстве вводится прямоугольная система координат Охуz, тогда в ней задается прямая a, пересекающая плоскость γ в точке M, причем она не перпендикулярна плоскости. Необходимо найти угол α, находящийся между заданной прямой и плоскостью.
Для начала необходимо применить определение угла между прямой и плоскостью методом координат. Тогда получим следующее.
В системе координат Охуz задается прямая a, которой соответствуют уравнения прямой в пространстве и направляющий вектор прямой пространства, для плоскости γ соответствует уравнение плоскости и нормальный вектор плоскости. Тогда a→=(ax, ay, az) является направляющим вектором заданной прямой a, а n→(nx, ny, nz) — нормальным вектором для плоскости γ. Если представить, что у нас имеются координаты направляющего вектора прямой a и нормального вектора плоскости γ, тогда известны их уравнения, то есть заданы по условию, тогда есть возможность определения векторов a→ и n→, исходя из уравнения.
Для вычисления угла необходимо преобразовать формулу, позволяющую получить значение этого угла при помощи имеющихся координат направляющего вектора прямой и нормального вектора.
Необходимо отложить векторы a→ и n→, начиная от точки пересечения прямой a с плоскостью γ. Существуют 4 варианта расположения этих векторов относительно заданных прямых и плоскости. Рассмотри рисунок, приведенный ниже, на котором имеются все 4 вариации.
Нахождение косинуса при известном синусе позволительно, применив основное тригонометрическое тождество. Пересечение прямой и плоскости образует острый угол. Это говорит о том, что его значение будет являться положительным числом, а его вычисление производится из формулы cos α=1-sin α.
Выполним решение нескольких подобных примеров для закрепления материала.
Пример 1Найти угол, синус, косинус угла, образованного прямой x3=y+1-2=z-116 и плоскостью 2x+z-1=0.
Решение
Для получения координат направляющего вектора необходимо рассмотреть канонические уравнения прямой в пространстве. Тогда получим, что a→=(3, -2, 6) является направляющим вектором прямой x3=y+1-2=z-116.
Для нахождения координат нормального вектора необходимо рассмотреть общее уравнение плоскости, так как их наличие определяется коэффициентами, имеющимися перед переменными уравнения. Тогда получим, что для плоскости 2x+z-1=0 нормальный вектор имеет вид n→=(2, 0, 1). a→·n→=ax·nx+ay·ny+az·nzax2+ay2+az2·nx2+ny2+nz2==3·2+(-2)·0+6·132+(-2)2+62·22+02+12=1275
a→·n→=ax·nx+ay·ny+az·nzax2+ay2+az2·nx2+ny2+nz2==3·2+(-2)·0+6·132+(-2)2+62·22+02+12=1275
Отсюда найдем значение косинуса и значение самого угла. Получим:
cos α=1-sin α=1-12752=10175
Ответ: sin α=1275, cos α=10175, α=arccos10175=arcsin1275.
Пример 2Имеется пирамида, построенная при помощи значений векторов AB→=1, 0, 2, AC→=(-1, 3, 0), AD→=4, 1, 1. Найти угол между прямой AD и плоскостью АВС.
Решение
Для вычисления искомого угла, необходимо иметь значения координат направляющего вектора прямой и нормального вектора плоскости. для прямой AD направляющий вектор имеет координаты AD→=4, 1, 1.
Нормальный вектор n→, принадлежащий плоскости АВС, является перпендикулярным вектору AB→ и AC→. Это подразумевает то, что нормальным вектором плоскости АВС можно считать векторное произведение векторов AB→ и AC→. Вычислим это по формуле и получим:
n→=AB→×AC→=i→j→k→102-130=-6·i→-2·j→+3·k→⇔n→=(-6, -2, 3)
Необходимо произвести подстановку координат векторов для вычисления искомого угла, образованного пересечением прямой и плоскости. AD→·n→=arcsin4·-6+1·-2+1·342+12+12·-62+-22+32=arcsin23212
AD→·n→=arcsin4·-6+1·-2+1·342+12+12·-62+-22+32=arcsin23212
Ответ: arcsin23212.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Геометрия Угол между прямой и плоскостью
Материалы к уроку
Конспект урока
Тема видеоурока: «Угол между прямой и плоскостью».
|
Тема урока: «Угол между прямой и плоскостью».
Сегодня мы введем несколько новых понятий, определим , что называется «углом между прямой и плоскостью», научимся делать рисунок пространственной модели наклонной и плоскости, решим некоторые стереометрические задачи, приведем пример из открытого банка заданий ФИПИ по теме. |
Текст: «Угол между прямой и плоскостью».
— Что называют углом между прямой и плоскостью? — Как изображают наклонную и плоскость на рисунке? — Каковы приемы решения стереометрических задач? — Как это поможет успешно сдать ЕГЭ? |
|
Ранее мы уже определили понятия перпендикуляра, проведенного из точки к плоскости; основания перпендикуляра; наклонной и ее проекции. Проведем наклонную a. На рисунке она изображена в виде прямой, пересекающей плоскость в точке А. Условно закрытая плоскостью часть наклонной изображена пунктирной линией. Из любой точки М наклонной проведем перпендикуляр к плоскости α. Основание перпендикуляра обозначим точкой В. Назовем точку В проекцией точки М на плоскость . Определим вновь введенное понятие: «Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости». Соединим точку А (точку пересечения прямой и плоскости) и точку В (проекцию точки М на плоскость), Отрезок АВ является проекцией наклонной АМ на плоскость А, это мы определили ранее. Небольшая иллюстрация проекции прямой на плоскость при помощи луча дает понимание того, что проекцией прямой на плоскость является прямая. Но утверждать это можно только с помощью доказательства.
Теорема: Проекцией прямой на плоскость, не перпендикулярную к этой прямой, является прямая. Используем имеющийся рисунок. Проведем через точки М, А и В плоскость β. Получим прямую а1 пересечения плоскостей. Докажем, что эта прямая является проекцией прямой а на плоскость α. Возьмем произвольную точку М1 на прямой а. Проведем прямую М1Р параллельно МВ. Получим некоторую точку Н пересечения прямой а1 и прямой М1Р и точку Н1 пересечения прямой М1Р и плоскости α (проекции точки М1 на плоскость α). Докажем, что точки Н и Н1 совпадают. Действительно, отрезок М1Н перпендикулярен прямой а1 (это следует из того, что он параллелен МВ, а отрезок МВ перпендикулярен прямой а1) Отрезок М1Н1 перпендикулярен прямой а1 (это следует из того, что отрезок М1Н1 перпендикулярен плоскости α, следовательно перпендикулярен любой прямой в плоскости в том числе прямой а1. Из одной точки можно провести только одну прямую, перпендикулярную данной прямой, отсюда следует, что точки Н и Н1 совпадают, а проекция точки М1 лежит на прямой а1. Представим прямую а как множество точек. Проекции этих точек принадлежат прямой а1. Из этого следует, что проекцией прямой на плоскость, не перпендикулярную к этой прямой является прямая.
Используя известные математические термины, составим определение: Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
Если прямая пересекает плоскость перпендикулярно, ее проекцией будет точка пересечения этой прямой и плоскости. В таком случае величина угла между прямой и плоскостью считается равной 900. |
а – наклонная, АВ – проекция наклонной ВМ – перпендикуляр из М на , В – основание перпендикуляра, В проекция М на .
Определение: «Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости».
Текст: Теорема: Проекцией прямой на плоскость, не перпендикулярную к этой прямой, является прямая.
Добавить к рисунку плоскость β Добавить прямую a1 пересечения плоскостей.
Провести в плоскости β прямую М1Р параллельно МВ Доказать что а1проекция а Доказательство: Провели : М, А и В . М1а, М1Р || МВ, Н= М1Ра, Н1=М1Р, Покажем, что Н=Н1, М1На1, т.к. М1Р || МВ, М1Н1а1, т. Получаем а1 проекция а. ч.т.д.
Текст: Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость. Картинка
Текст АМВ–угол между а и
Если прямая пересекает плоскость перпендикулярно, ее проекцией будет точка пересечения этой прямой и плоскости. В таком случае величина угла между прямой и плоскостью считается равной 900. |
|
Некоторые полезные выводы: — Проекцией прямой на плоскость, не перпендикулярной к плоскости, является прямая; — Проекцией отрезка на плоскость, не перпендикулярного к плоскости, является отрезок, концами которого являются проекции концов отрезка; — Проекцией прямой и отрезка на плоскость, перпендикулярных к плоскости является точка; — Угол между наклонной и плоскостью (между наклонной и ее проекцией) является наименьшим из всех углов, образованных этой наклонной с любой прямой принадлежащей плоскости; — Угол между перпендикуляром к плоскости и самой плоскостью Равен 900. -Если данная прямая параллельна плоскости, то ее проекцией на плоскость является прямая, параллельная данной. В таком случае угол между параллельными прямой и плоскостью считают равным 0. Чтобы построить проекцию какой-нибудь фигуры F на плоскость, надо построить проекции всех ее точек на данную плоскость. |
Текст: выводы: — Проекцией прямой на плоскость, не перпендикулярной к плоскости, является прямая; — Проекцией отрезка на плоскость, не перпендикулярного к плоскости, является отрезок, концами которого являются проекции концов отрезка; — Проекцией прямой и отрезка на плоскость, перпендикулярных к плоскости является точка; — Угол между наклонной и плоскостью (между наклонной и ее проекцией) является наименьшим из всех углов, образованных этой наклонной с любой прямой принадлежащей плоскости;
— Угол между перпендикуляром к плоскости и самой плоскостью Равен 900.
— Чтобы построить проекцию какой-нибудь фигуры F на плоскость, надо построить проекции всех ее точек на данную плоскость
|
|
Задача 1: Дан куб ABCDA1B1C1D1. Решение: Отрезок B1B – перпендикулярен плоскости ABC. Соединим основание перпендикуляра точку В и точку пересечения прямой B1D с плоскостью АВС, получим отрезок BD, проекцию наклонной B1D. Найти угол BDB1. Треугольник BB1D прямоугольный. Найдем тангенс угла BDB1. Он равен отношению B1B к BD. Все ребра куба равны, значит B1B=1, а BD2=В1В2+BD2= 12+12 (по теореме Пифагора) BD получили табличное значение тангенса угла, тогда, угол BDB1 равен 450. |
Текст: Задача 1 Дан куб ABCDA1B1C1D1. Сторона АВ равна 1дм.
Дано: ABCDA1B1C1D1,– куб, АВ = 1дм Найти: угол между B1D и ABC. Решение: ΔBB1D–прямоугольный, по определению куба.
Ответ: угол между B1D и ABC равен 45º.
|
|
В ЕГЭ эта тема представлена задачами подобного содержания: В правильной четырёхугольной пирамиде SABCD с вершиной S точка O – центр основания, SO=35, SD=37. Найдите длину отрезка BD. Решение: Отрезок OD – проекция наклонной SD на плоскость АВС равна половине отрезка ВD. Треугольник SOD прямоугольный. Применим теорему Пифагора: OD2+352=372; OD2=372-352; OD2=1369-1225=144; OD=12 12х2=24 Ответ: 24 |
Комментарий: необходимо больше уделить внимание оформлению того текста что должно быть на экране, теоретического материала и задач, так как всегда при изложении материала должны быть записи его сопровождающие.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Угол между прямой и плоскостью
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Понятие проекции фигуры на плоскость
2. Понятие угла между прямой и плоскостью
3. Примеры задач
Понятие проекции фигуры на плоскость
Для введения понятия угла между прямой и плоскостью вначале необходимо разобраться в таком понятии, как проекция произвольной фигуры на плоскость.
Определение 1
Пусть нам дана произвольная точка $A$. Точка $A_1$ называется проекцией точки $A$ на плоскость $\alpha $, если она является основанием перпендикуляра, проведенного из точки $A$ на плоскость $\alpha $ (рис. 1).
Рисунок 1. Проекция точки на плоскость
Определение 2
Пусть нам дана произвольная фигура $F$. Фигура $F_1$ называется проекцией фигуры $F$ на плоскость $\alpha $, составленная из проекций всех точек фигуры $F$ на плоскость $\alpha $ (рис. 2).
Рисунок 2. Проекция фигуры на плоскость
Теорема 1
Проекция не перпендикулярной плоскости прямой является прямая.
Доказательство.
Пусть нам дана плоскость $\alpha $ и пересекающая ее прямая $d$, не перпендикулярная ей. Выберем на прямой $d$ точку $M$ и проведем её проекцию $H$ на плоскость $\alpha $. Через прямую $(MH)$ проведем плоскость $\beta $. Очевидно, что эта плоскость будет перпендикулярна плоскости $\alpha $. Пусть они пересекаются по прямой $m$. Рассмотрим произвольную точку $M_1$ прямой $d$ и проведем через нее прямую $(M_1H_1$) параллельно прямой $(MH)$ (рис. 3).
Пусть они пересекаются по прямой $m$. Рассмотрим произвольную точку $M_1$ прямой $d$ и проведем через нее прямую $(M_1H_1$) параллельно прямой $(MH)$ (рис. 3).
Рисунок 3.
Так как плоскость $\beta $ перпендикулярна плоскости $\alpha $, то $M_1H_1$ перпендикулярно прямой $m$, то есть точка $H_1$ — проекция точки $M_1$ на плоскость $\alpha $. В силу произвольности выбора точки $M_1$ все точки прямой $d$ проецируются на прямую $m$.
Рассуждая аналогично. В обратном порядке, будем получать, что каждая точка прямой $m$ является проекцией какой-либо точки прямой $d$.
Значит, прямая $d$ проецируется на прямую $m$.
Теорема доказана.
Понятие угла между прямой и плоскостью
Определение 3
Угол между прямой, пересекающей плоскость и её проекцией на эту плоскость, называется углом между прямой и плоскостью (рис. 4).
Рисунок 4. Угол между прямой и плоскостью
Отметим здесь несколько замечаний. 0$.
0$.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 27.04.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Угол между прямой и плоскостью
Угол между прямой и плоскостьюУгол — фигура образованная парой лучей из одной точки, которая называется вершиной угла.
Мера угла определяется сравнением двух углов. Сравнение выполняется выбором начальных сторон углов и определением направления отсчёта угловой меры. Совмещением вершин углов и начальных сторон определяется меньший угол, чья вторая сторона оказывается внутри другого угла.
В задачах по начертательной геометрии рассматриваются углы между: прямыми в одной плоскости, двумя плоскостями (угол при ребре), скрещивающимися прямыми и между прямой и плоскостью.
Угол между скрещивающимися прямыми определяется по углу между проекциями прямых на плоскость параллельную этим прямым.
- Угол между плоскостями
- Угол между прямыми
- Найти угол между плоскостями
- Угол наклона плоскости
- Угол между прямой и плоскостью
- Найти угол между прямыми
- Угол между двумя плоскостями
- Найти угол между прямой и плоскостью
- Угол между плоскостью и основанием
- Угол между точкой и плоскостью
- Угол между наклонной и плоскостью
- Угол между ребром и плоскостью
- Найти угол между плоскостью и точкой
- Найти угол между двумя плоскостями
- Найти угол между ребром и плоскостью
- Угол наклона плоскости к горизонту
- Найти угол между прямыми в плоскости
- Угол между стороной и плоскостью
- Определить угол между плоскостями
- Угол между прямыми на плоскости
- Угол между плоскостями треугольников
- Пирамида и угол между плоскостью
- Угол между перпендикулярными плоскостями
- Угол наклона прямых
- Найти угол между плоскостями пирамиды
- Угол между плоскостями призмы
- Угол между гранью и плоскостью
- Как находить угол между плоскостями
- Угол между сечением и плоскостью
- Угол между ребром и плоскостью основания
- Угол между образующей конуса и плоскостью
- Угол между скрещивающимися прямыми
- Перпендикуляр, наклонная и угол между плоскостями
- Угол между образующей конуса и плоскостью основания
- Параллелепипед угол между плоскостями
- Найти угол между ребром и плоскостью пирамиды
- Угол между плоскостью сечения и плоскостью основания
- Найти угол между сечением и плоскостью
- Угол между параллельными плоскостями
- Найти угол между наклонной и плоскостью
- Угол между боковым ребром и плоскостью основания
- Угол наклона плоскости к плоскостям проекций
- Угол наклона грани
- Угол между ребром и плоскостью в пирамиде
- Угол между плоскостью и плоскостью проекции
- Угол наклона между плоскостями
- Угол между ребром и плоскостью основания пирамиды
- Найти угол между плоскостями в кубе
- Угол между отрезком и плоскостью
- Угол между диагональю и плоскостью основания
- Угол между прямой и плоскостью призмы
- Угол между плоскостями презентация
- Найти угол между плоскостью проходящей через точки
- Угол наклона пирамиды
- Угол между плоскостями рисунок
- Угол между прямой и плоскостью презентация
- Угол между прямой AB и плоскостью
- Презентация угол между прямыми и плоскостями
- Определите угол наклона плоскости к горизонту
- Угол между боковым ребром пирамиды и плоскостью
- Тема углы между плоскостями
- Угол между боковой гранью и плоскостью основания
- Углы между прямыми и плоскостями задачи
- Угол наклона прямой к плоскости
- Двугранный угол и угол между плоскостями
- Угол между плоскостями в пространстве
- Как находить угол между прямой и плоскостью
- Построить угол между плоскостями
- Угол наклона плоскости к грани
- Угол наклона к горизонтальной плоскости
- Определить углы наклона плоскости к плоскостям проекций
- Угол наклона двух плоскостей
- Решение задач об углах между плоскостями
- Определение угла между плоскостями
- Угол наклона отрезка к плоскости
- Найти угол наклона прямой
- Определить угол между двумя плоскостями
- Угол между прямой и плоскостью в пространстве
- Угол между двумя прямыми на плоскости
- Угол наклона ребра к плоскости
- Найти угол наклона плоскости к грани
- Угол между плоскостями в треугольной призме
- Найти двугранный угол между плоскостями
- Нахождение угла между плоскостями
- Угол наклона к плоскости П1
- Угол наклона боковой грани
- Угол между прямой и плоскостью в пирамиде
- Определить угол между прямой и плоскостью
- Определить угол наклона прямой
- Угол между прямой и плоскостью является
- Угол наклона треугольника к плоскости
- Угол наклона прямой к оси
- Определение угла между прямой и плоскостью
- Угол наклона боковых граней пирамид
- Угол наклона прямой к плоскости проекций
- Угол наклона боковой грани к основанию
- Определить угол наклона плоскости к плоскости П1
- Угол наклона отрезка к плоскостям проекций
- Угол между скрещивающимися плоскостями
- Угол наклона ребра к грани
- Определить угол наклона прямой к плоскости
- Угол наклона стороны пирамиды
- Найти угол наклона прямой к плоскости
- Определение угла наклона плоскости
- Угол наклона ребра к основанию пирамиды
- Угол наклона к фронтальной плоскости
- Определить угол наклона треугольника к плоскости
- Угол между плоскостью и линией пересечения плоскостей
- Угол между линиями на плоскости
- Угол наклона боковой грани к плоскости
- Как определить угол наклона плоскости
- Определить угол наклона плоскости к плоскости П2
- Угол наклона боковой грани к плоскости основания
- Найти угол между главными плоскостями
- Найти угол наклона основания пирамиды к плоскости
- Угол наклона бокового ребра пирамиды к основанию
- Угол наклона бокового ребра к плоскости основания
- Угол между прямой и плоскостью двугранный угол
- Угол между плоскостями начертательная геометрия
- Самостоятельная работа угол между прямой и плоскостью
- Определить углы наклона прямой к плоскостям проекций
- Определить угол наклона отрезка к плоскостям проекций
- Угол наклона ребра пирамиды к плоскости основания
- Определение угла наклона плоскости к плоскости проекции
- Углы наклона треугольника к плоскостям проекций
- Угол наклона к фронтальной плоскости проекций
- Найдите угол наклона грани пирамиды к основанию
- Найти угол между двумя прямыми на плоскости
- Как найти угол наклона плоскости
- Определить угол наклона треугольника к плоскостям проекций
- Угол наклона треугольника к плоскости П1
- Определение угла наклона прямой к плоскости проекции
- Угол наклона плоскости на П2
- Определить угол наклона прямой к плоскости П1
- Угол наклона прямой к плоскости треугольника
- Угол наклона прямой к плоскости П2
- Найти угол наклона прямой к оси ох
- Угол наклона прямой к оси Х
- Определить угол наклона грани к плоскости
- Угол наклона отрезка АВ к фронтальной плоскости
- Начертательная геометрия угол наклона плоскости
- Определить угол наклона отрезка к горизонтальной плоскости
- Угол наибольшего наклона плоскости к плоскостям проекций
- Определить угол наклона прямой АВ к П1
- Определение угла наклона плоскости к плоскости П1
- Определить угол наклона прямой к плоскости треугольника
- Определить угол наклона альфа к плоскости П1
- Как найти угол наклона плоскости к горизонту
Решение задач по начертательной геометрии.
Угол между прямой и плоскостью. Упражнения презентация, доклад
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Углом между наклонной и плоскостью называется угол между этой наклонной и ее ортогональной проекцией на данную плоскость.
Считают также, что прямая, перпендикулярная плоскости, образует с этой плоскостью прямой угол.
Теорема
Угол между наклонной и плоскостью является наименьшим из всевозможных углов между этой наклонной и прямыми, лежащими в данной плоскости.
Упражнение 1
Прямые a и b образуют с плоскостью α равные углы. Будут ли эти прямые параллельны?
Ответ: Нет.
Упражнение 2
Две плоскости образуют с данной прямой равные углы. Как расположены плоскости относительно друг друга?
Ответ: Параллельны или пересекаются.
Упражнение 3
Под каким углом к плоскости нужно провести отрезок, чтобы его ортогональная проекция на эту плоскость была вдвое меньше самого отрезка?
Ответ: 60о.
Упражнение 4
Может ли катет равнобедренного прямоугольного треугольника образовать с плоскостью, проходящей через гипотенузу, угол в 60°? Каков наибольший угол между катетом и этой плоскостью?
Ответ: Нет, 45о.
Упражнение 5
Одна из двух скрещивающихся прямых пересекает плоскость под углом 60°, а другая перпендикулярна этой плоскости. Найдите угол между данными скрещивающимися прямыми.
Ответ: 30о.
Упражнение 6
Будут ли в пирамиде боковые ребра равны, если они образуют равные углы с плоскостью основания?
Ответ: Да.
Упражнение 7
Через сторону квадрата проведена плоскость, составляющая с диагональю квадрата угол 30°. Найдите углы, которые образуют с плоскостью стороны квадрата, наклонные к ней.
Ответ: 45о.
Упражнение 8
Основание равнобедренного треугольника лежит в плоскости π (плоскость треугольника не совпадает с плоскостью π). Какой из углов больше: угол наклона боковой стороны к плоскости π или угол наклона высоты, опущенной на основание треугольника, к плоскости π?
Ответ: Угол наклона высоты.
Упражнение 9
Из вершины A квадрата ABCD перпендикулярно его плоскости проведен отрезок AK, равный 3. Из точки K опущены перпендикуляры на стороны BC и CD. Перпендикуляр из точки K к стороне BC равен 6. Найдите углы, которые образуют эти перпендикуляры с плоскостью квадрата.
Ответ: 30о.
В кубе A…D1 найдите угол между прямой AA1 и плоскостью ABC.
Ответ: 90o.
Куб 1
В кубе A…D1 найдите угол между прямой AA1 и плоскостью AB1C1.
Ответ: 45o.
Куб 2
В кубе A…D1 найдите тангенс угла между прямой AA1 и плоскостью BC1D.
Куб 3
В кубе A…D1 найдите угол между прямой AB1 и плоскостью ABC.
Ответ: 45o.
Куб 4
В кубе A…D1 найдите угол между прямой AB1 и плоскостью BCC1.
Ответ: 45o.
Куб 5
В кубе A…D1 найдите угол между прямой AB1 и плоскостью ABC1.
Ответ: 30o.
Куб 6
В кубе A…D1 найдите угол между прямой AB1 и плоскостью BB1D1.
Ответ: 30o.
Куб 7
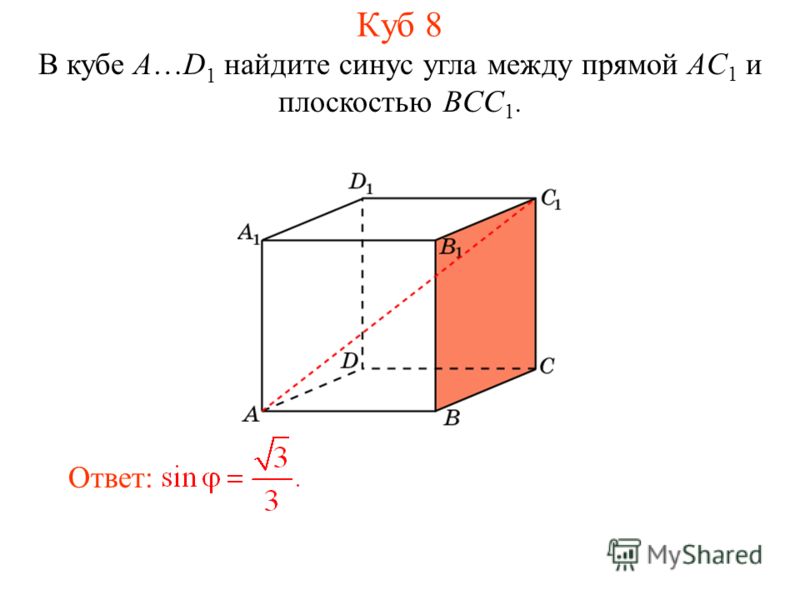
В кубе A…D1 найдите синус угла между прямой AC1 и плоскостью BCC1.
Куб 8
В кубе A…D1 найдите синус угла между прямой AC1 и плоскостью BB1D1.
Куб 9
В кубе A…D1 найдите угол между прямой AC1 и плоскостью BA1D.
Ответ: 90o.
Куб 10
В правильном тетраэдре ABCD точка E – середина ребра CD. Найдите угол между прямой AD и плоскостью ABE.
Ответ: 30о.
Пирамида 1
В правильном тетраэдре ABCD найдите косинус угла между прямой AD и плоскостью ABC.
Пирамида 2
В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол между прямой SA и плоскостью ABC.
Пирамида 3
В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол между прямой SA и плоскостью SBD.
Пирамида 4
В правильной пирамиде SABCD, все ребра которой равны 1, найдите косинус угла между прямой AB и плоскостью SAD.
Пирамида 5
В правильной 6-ой пирамиде SA…F, боковые ребра которой равны 2, а стороны основания – 1, найдите угол между прямой SA и плоскостью ABC.
Пирамида 6
В правильной 6-ой пирамиде SA…F, боковые ребра которой равны 2, а стороны основания – 1, точка G – середина ребра SB. Найдите угол между прямой AG и плоскостью ABC.
Найдите угол между прямой AG и плоскостью ABC.
Пирамида 7
В правильной 6-ой пирамиде SA…F, боковые ребра которой равны 2, а стороны основания – 1, найдите косинус угла между прямой AC и плоскостью SAF.
Пирамида 8
В правильной 6-ой пирамиде SA…F, боковые ребра которой равны 2, а стороны основания – 1, найдите косинус угла между прямой AB и плоскостью SAF.
Пирамида 9*
В правильной 6-ой пирамиде SA…F, боковые ребра которой равны 2, а стороны основания – 1, найдите косинус угла между прямой BC и плоскостью SAF.
Пирамида 10*
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите тангенс угла между прямой AA1 и плоскостью AB1C1.
Призма 1
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите тангенс угла между прямой AA1 и плоскостью ABC1.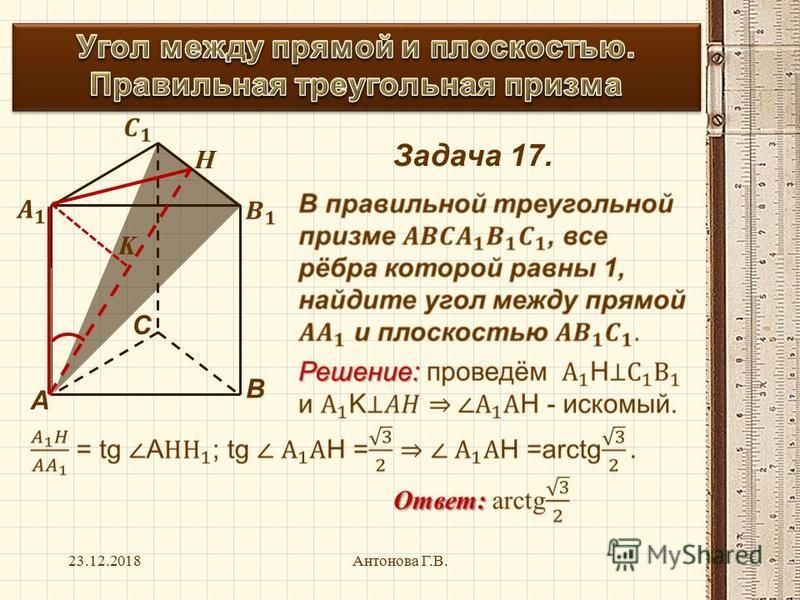
Призма 2
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между прямой AB и плоскостью BB1C1.
Ответ: 60o.
Призма 3
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите синус угла между прямой AB1 и плоскостью BB1C1.
Призма 4
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите синус угла между прямой AB и плоскостью A1BC1.
Призма 5*
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите синус угла между прямой AB1 и плоскостью и ABC1.
Призма 6*
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямой AA1 и плоскостью ABC.
Ответ: 90о.
Призма 7
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямой AB1 и плоскостью ABC.
Ответ: 45о.
Призма 8
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямой AC1 и плоскостью ABC.
Призма 9
В правильной 6-й призме A…F1, ребра которой равны 1, найдите тангенс угла между прямой AD1 и плоскостью ABC.
Призма 10
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямой AA1 и плоскостью ABD1.
Призма 11
В правильной 6-й призме A…F1, ребра которой равны 1, найдите тангенс угла между прямой AA1 и плоскостью ABC1.
Призма 12
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямой AA1 и плоскостью ACD1.
Призма 13
В правильной 6-й призме A…F1, ребра которой равны 1, найдите тангенс между прямой AA1 и плоскостью ACE1.
Призма 14
В правильной 6-й призме A…F1, ребра которой равны 1, найдите тангенс угла между прямой AA1 и плоскостью ADE1.
Призма 15
В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус угла между прямой AB1 и плоскостью ABD1.
Призма 16*
В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус угла между прямой AB1 и плоскостью ABС1.
Призма 17*
В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус угла между прямой BC1 и плоскостью BDE1.
Призма 18*
В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус угла между прямой AB1 и плоскостью ACE1.
Призма 19*
В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус угла между прямой AB1 и плоскостью ADE1.
Призма 20*
В правильной 6-й призме A…F1, ребра которой равны 1, найдите синус угла между прямой AC1 и плоскостью ADE1.
Призма 21*
Скачать презентацию
определение, как найти, свойства, формула и примеры
Определение понятия угла между прямой и плоскостью в пространстве
Для начала введем несколько определений из геометрии.
Определение 1Проекцией точки на плоскость называется точка пересечения плоскости и перпендикуляра, проведенного через заданную точку к плоскости.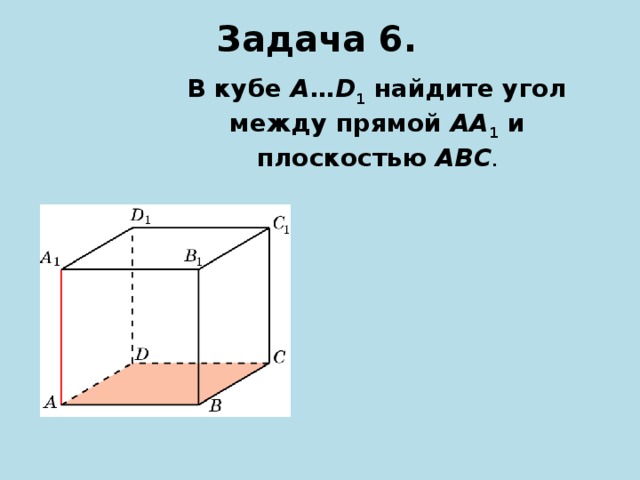 =α.
=α.
Как найти угол между прямой и плоскостью в пространстве
При решении задач используют один и следующих методов определения угла между прямой и плоскостью:
- геометрический;
- аналитический, также известный как алгебраический.
Рассмотрим алгоритм решения каждого из методов.
Суть геометрического способа ясна из его названия и заключается в построении чертежа, с помощью которого находят искомый угол. В трехмерной системе координат строят плоскость и заданную прямую. Из двух произвольно выбранных точек на прямой опускают перпендикуляры на плоскость. По точкам пересечения перпендикуляров с поверхностью проводят проекцию прямой. Допускается опускать перпендикуляр из одной точки прямой. В этом случае проекцию строят по точкам пересечения перпендикуляра и прямой с плоскостью.
После того как построена проекция прямой, решение задачи переходит в область планиметрии. Искомый угол находят через синус или косинус угла прямоугольного треугольника.
В аналитическом способе для вычисления искомого угла используют уравнения прямой и плоскости. Из уравнения прямой находят координаты ее направляющего вектора s→(x1, y1, z1), а из уравнения плоскости – координаты нормального вектора n→(x2, y2, z2). Тогда углом между плоскостью и прямой считают угол между векторами s→ и n→.
Косинус угла β можно найти через скалярное произведение векторов по формуле:
cosβ=s→·n→s→·n→
Угол β=π2-α. Подставим выражение для β в формулу косинуса, получим: cosβ=cos(π2-α)=sinα.
Тогда синус искомого угла α можно определить следующим образом:
Формулаsinα=s→·n→s→·n→=x1·x2+y1·y2+z1·z2x12+y12+z12·x22+y22+z22
Свойства угла между прямой и плоскостью в пространстве
Приведем основные свойства угла между прямой и плоскостью:
- Из точки пересечения прямой и плоскости построим перпендикуляр к плоскости. Так как прямая, ее проекция и перпендикуляр лежат в одной плоскости, можно утверждать, что угол между прямой и плоскостью дополняет до 90° угол между перпендикуляром и прямой.

- Если угол между прямой и плоскостью равен 0º, то прямая параллельна плоскости. Если угол между прямой и плоскостью равен 90º, прямая является перпендикуляром к плоскости.
- Перпендикуляр к плоскости всегда меньше по величине чем наклонная, проведенная из той же плоскости.
- Проекции двух равных наклонных, проведенных из одной точки, также равны между собой.
К свойствам угла между прямой и плоскостью можно отнести свойства линий, образующих данный угол: наклонной, проекции.
Сформулируем теорему о трех перпендикулярах и докажем ее.
ТеоремаЕсли прямая, проведенная через точку пересечения наклонной и плоскости, перпендикулярна проекции, то она также перпендикулярна наклонной.
Доказательство
Через точку пересечения наклонной MK и плоскости φ проведем прямую f. Теперь построим отрезок LK так, что LK||MN. Отрезок LK⊥f, так как перпендикулярен плоскости, в которой лежит f. По двум параллельным отрезкам LK и MN построим плоскость ω⊥φ. Тогда f перпендикулярна NK и LK, а значит, и плоскости ω. Прямая, перпендикулярная плоскости, перпендикулярна любой прямой, принадлежащей этой плоскости, то есть f⊥MK, что и требовалось доказать.
Тогда f перпендикулярна NK и LK, а значит, и плоскости ω. Прямая, перпендикулярная плоскости, перпендикулярна любой прямой, принадлежащей этой плоскости, то есть f⊥MK, что и требовалось доказать.
Примеры решения задач
В дополнении рассмотрим примеры задач для самостоятельной подготовки. Для решения будем пользоваться геометрическим и аналитическим способами.
Пример 1Дана пирамида MNKLP. Известно, что ребро LP=6. Из вершины P проведена высота PH=3. Найти угол между боковым ребром LP и основанием пирамиды MNKL.
Решение.
Угол между отрезком LP и основанием MNKL есть угол между наклонной LP и плоскостью, образованной вершинами основания.
Высота PH — перпендикуляр к плоскости MNKL.
Соединим точки L и H, получившийся отрезок LH является проекцией прямой LP.
Искомый угол найдем как угол между гипотенузой LP и катетом LH прямоугольного треугольника LPH.
sin(∠PLH)=PHLP=36=12
Тогда угол между ребром LP и основанием пирамиды равен 30°.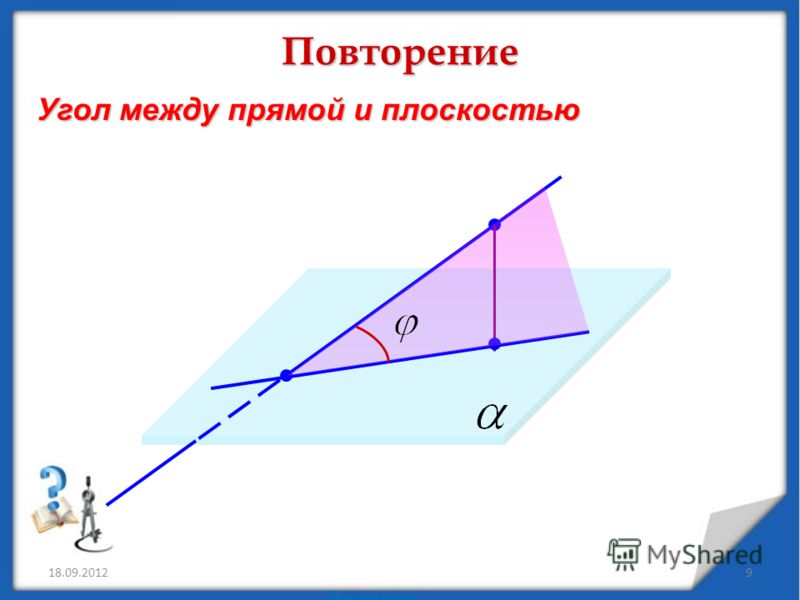
Ответ: 30°.
Пример 2Дан параллелепипед MNKLDEFG. Известно, что ребра MD=NE=KF=LG=6. Угол между ребром MD и диагональю нижнего основания MK равен 30°. Найти расстояние между верхним и нижним основаниями.
Решение.
Из вершины D опустим перпендикуляр к плоскости MNKL, полученный отрезок обозначим DH.
Расстояние между двумя поверхностями есть их общий перпендикуляр, то есть отрезок DH.
Длину DH найдем из выражения для угла DMK прямоугольного треугольника DHM.
sin(∠DMK)=DHMD ⇒ DH=MD·sin(∠DMK)=6·32=33
Расстояние между основаниями равно 33.
Ответ: 33.
Пример 3Дана плоскость, заданная уравнением 2x+3y-z+5=0, и прямая, заданная уравнением x-22=y4=z+11. Найти угол между прямой и плоскостью.
Решение.
Сначала определим координаты направляющего и нормального векторов. Для заданной плоскости нормальный вектор задается координатами n→ (2; 3; -1). Направляющим вектором для прямой является вектор s→ (2; 4; 1). Теперь решение задачи сводится к нахождению угла между s→ и n→. =s→·n→s→·n→=2·2+3·4+(-1)·14+9+1·4+16+1=15294
=s→·n→s→·n→=2·2+3·4+(-1)·14+9+1·4+16+1=15294
Тогда искомый угол между прямой и плоскостью равен ≈61°.
Ответ: ≈61°.
Угол между линией и плоскостью
В этой статье мы подробно обсудим понятие угла между линией и плоскостью. Прежде чем приступить к обсуждению этой концепции, сначала давайте посмотрим, что такое прямая и плоскость.
Что такое прямая линия?
Прямая линия, также известная как прямая в геометрии, представляет собой двухмерную фигуру, в которой бесконечное число точек простирается в любом направлении. Прямая линия является частью 2D-геометрии и не имеет ширины или высоты. Длина прямой линии бесконечна.
Лучшие репетиторы по математике
Поехали
Что такое самолет?
Плоскость — это плоская поверхность, образованная бесконечным числом точек, простирающихся без ограничений в любом направлении. Это также фигура 2-D , потому что, как и прямая линия, она не имеет толщины, а имеет только длину и ширину. Например, если вы рисуете что-то на плоской бумаге, то это значит, что вы рисуете что-то на плоскости.
Например, если вы рисуете что-то на плоской бумаге, то это значит, что вы рисуете что-то на плоскости.
Угол между линией и плоскостью
Угол между линией и плоскостью образуется, когда линия наклонена к плоскости и к плоскости проведена нормаль из точки, где ее касается линия. Этот угол между прямой и плоскостью равен дополнению угла между нормалью и прямой.
Могут быть следующие три сценария, когда прямая и плоскость могут существовать вместе:
- Прямая может быть на плоскости
- Прямая может быть параллельна плоскости
- Линия может быть секущей
Угол между плоскостью и прямой будет разным в каждом из трех вышеприведенных обстоятельств.
- Если прямая присутствует на плоскости или параллельна ей, то угол, образованный между прямой и плоскостью, будет равен 0 градусов.
- Если линия является секущей плоскости, то угол, образованный между ними, обозначается . Этот угол, который образуется между линией и плоскостью, на самом деле является углом, образованным прямой линией с ее ортогональная проекция на плоскость.

Другими словами, можно сказать, что угол между прямой и плоскостью — это угол, образованный между прямой и ее ортогональной проекцией на плоскость.
Это явление показано на рисунке ниже, поскольку он показывает угол между линией r и плоскостью.
Угол между линией и плоскостью
Если у нас есть информация о следующих элементах, то мы можем определить угол между линией и плоскостью, используя следующую формулу:
- Плана
- Прямая линия
- Руководящий вектор
- Нормальный вектор плоскости
IF LINE, R 9, и плоскость
, если линия, R , и плоскость
, если линия R , и плоскость
, если линия R , а также плоскость
, если линейка
. π , перпендикулярны, вектор направления прямой и вектор нормали к плоскости имеют одинаковое направление и поэтому его компоненты пропорциональны:
Теперь давайте перейдем к следующим примерам, в которых мы будем использовать приведенную выше формулу для определения угла между прямой и плоскостью.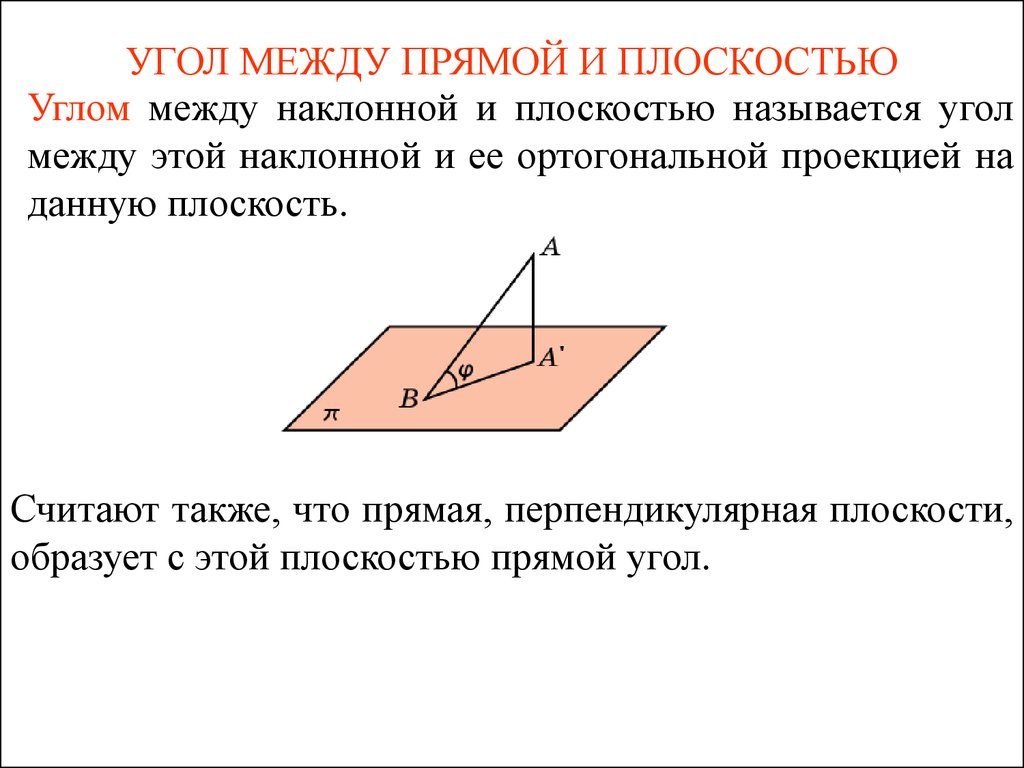
Пример 1
Определить угол между прямой и плоскостью.
Решение
Из уравнений плоскости и прямой линии мы можем найти:
Управляющий вектор прямой =
Вектор нормали к плоскости =
Подставьте эти значения в следующую формулу, чтобы получить угол :
Следовательно, угол между прямой и плоскостью примерно равен 45 градусам.
Пример 2
Определить угол между прямой и плоскостью .
Решение
Из уравнений плоскости и прямой можно найти:
Вектор направления прямой =
Вектор нормали к плоскости =
Подставьте эти значения в следующую формулу, чтобы получить угол:
Следовательно, угол между прямой и плоскостью приблизительно равен 67,09 градуса. Пример 3 линии:
Вектор нормали плоскости:
Подставьте эти значения в приведенную ниже формулу, чтобы получить угол:
Следовательно, угол между прямой и плоскостью примерно равен 30 градусам.
Пример 4
Найдите угол между следующей линией и плоскостью: строка =
Нормальный вектор плоскости =
Подставьте эти значения в следующую формулу, чтобы получить угол: 0,960 градуса.
Найдите различные курсы по математике на сайте Superprof.
Угол между линией и плоскостью
LearnPracticeDownload
В классической математике и аналитической геометрии угол между линией и плоскостью равен дополнению угла между линией и нормалью. В этой теме двумерной геометрии давайте сначала определим прямую линию и плоскость, а также то, как определяется угол между линией и плоскостью.
| 1. | Что такое прямая линия? |
| 2. | Что такое самолет? |
| 3 | Угол между линией и плоскостью |
| 4. | Решенные примеры |
| 5. | Практические вопросы |
6. | Часто задаваемые вопросы |
Что такое прямая линия?
Где в реальной жизни встречаются прямые линии? Карандаш, перо, прямая дорога; край линейки, здание, стрелки часов и т. д. — вот несколько примеров этого. Прямая линия – это простая двухмерная геометрическая фигура с набором точек, не имеющих ширины. Он простирается в обоих направлениях без конечных точек и имеет только длину. Таким образом, длина линии бесконечна, и у нее нет ни высоты, ни ширины, что делает ее частью двумерной геометрии.
Линии могут быть параллельными, перпендикулярными, пересекающимися или параллельными.
Что такое самолет?
Плоскость также является двухмерной геометрической поверхностью, которая не имеет толщины, а имеет только длину и ширину. Плоскость образуется, когда бесконечное число точек простирается бесконечно в любом направлении, образуя плоскую поверхность.
В геометрии плоскость получается, когда набор прямых расположен рядом друг с другом. Если мы что-то рисуем на плоской бумаге, то это значит, что мы рисуем что-то на плоскости.
Если мы что-то рисуем на плоской бумаге, то это значит, что мы рисуем что-то на плоскости.
Угол между линией и плоскостью
В то время как плоскость представляет собой двумерную поверхность, измеренную по длине и ширине, прямая линия имеет одно измерение, которое измеряется по длине. Линия образует угол с плоскостью в точке касания, когда эта линия падает на плоскость, которая называется углом между линией и плоскостью. Проще говоря, его можно определить как угол между линией и ее проекцией на эту плоскость.
9{2}}}}\)Важные примечания
- Угол между плоскостью и линией можно определить как угол между линией и ее проекцией на плоскость.
- Прямые линии могут быть параллельными, перпендикулярными или пересекающимися
Пример 1:
Если угол \(\theta\) между линией \(\frac{x+1}{1}=\frac{y-1}{2}=\frac{z-2 {2}\) и плоскость \(2 x-y+\sqrt{\lambda} z+4=0\) такая
что \(\sin \theta=\frac{1}{3}\), затем найдите значение \(\lambda\).
Решение:
Дано: Симметрические уравнения линии = \(\frac{x+1}{1}=\frac{y-1}{2}=\frac{z-2}{2} \)
Сравнивая его с уравнением \(\frac{x+x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}\)Следовательно, для линии 〈 л; м ; n〉 = 〈 1 ; 2; 2〉
Угол между линией и плоскостью:
\(\begin{align}&\sin \left(\theta\right)=\frac{2-2+2 \sqrt{\lambda}}{3 \times \sqrt{5+\lambda}}, \text { где } \theta \text { угол между прямой и плоскостью }\\
&\Стрелка вправо\sin\theta=\frac{2\sqrt{\lambda}}{3\sqrt{5+\lambda}}=\frac{1}{3}\\
&\стрелка вправо 4 \лямбда=5+\лямбда\\
&\стрелка вправо \лямбда=\фракция{5}{3}
\конец{выровнено}\)Пример 2: Найти угол между плоскостями \(\overrightarrow{\mathrm{r}} .(\hat{\mathrm{i}}-2 \hat{\mathbf{j}}+3 \ шляпа {\ mathrm {k}}) = 5 \) и линия \ (\ overrightarrow {\ mathrm {r}} = (\ шляпа {\ mathrm {i}} + \ шляпа {\ mathbf {j}} — \ шляпа {\ mathrm {к}}) +
\lambda(\hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}})\)Решение:
Дано уравнение плоскости: \ (\overrightarrow{\mathrm{r}} .
 {-1} \frac{\sqrt{42}}{7}\end{выровнено}\) 9{\circ}\end{выровнено}\)
{-1} \frac{\sqrt{42}}{7}\end{выровнено}\) 9{\circ}\end{выровнено}\)
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы об угле между линией и плоскостью
Может ли точка быть линией?
Точка обозначается точкой. Линия может быть определена как набор точек, бесконечно простирающихся от обоих концов. У него есть одно измерение — длина. Точки, лежащие на одной прямой, называются коллинеарными.
Что означает линия?
Линия может быть определена как прямая одномерная фигура, не имеющая толщины и бесконечно простирающаяся в обоих направлениях.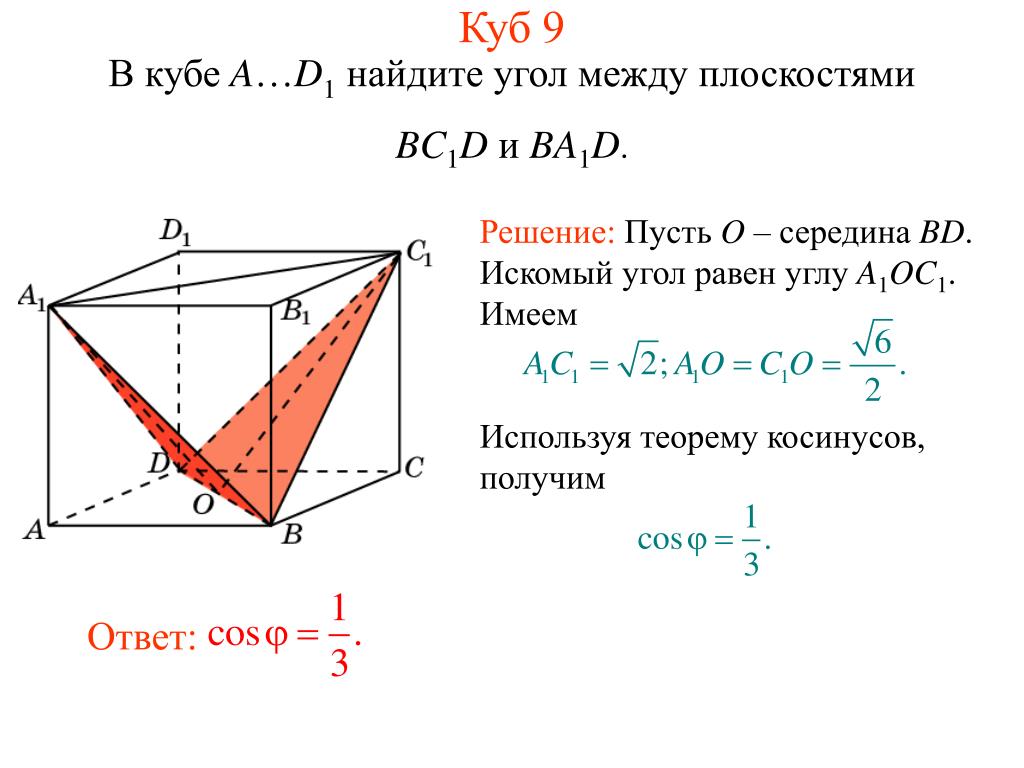 И это чаще всего описывается как кратчайшее расстояние между любыми двумя точками.
И это чаще всего описывается как кратчайшее расстояние между любыми двумя точками.
Какие существуют две классификации прямых линий?
Прямые линии подразделяются на горизонтальные и вертикальные. Типы линий также включают параллельные линии, пересекающиеся линии и перпендикулярные линии.
Может ли угол быть прямой?
Прямой угол – это угол, равный 180 градусам, а прямой угол также называют плоским углом. Поскольку на самом деле он выглядит как прямая линия, его называют прямым углом.
Сколько измерений имеет плоскость?
Самолеты двумерны, но могут существовать и в трехмерном пространстве.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по углам
Рабочие листы по математике и наглядный учебный план
Объяснение урока: Угол между двумя плоскостями и между плоскостью и прямой
В этом объяснении мы научимся находить меру угла
между двумя плоскостями или между линией и плоскостью.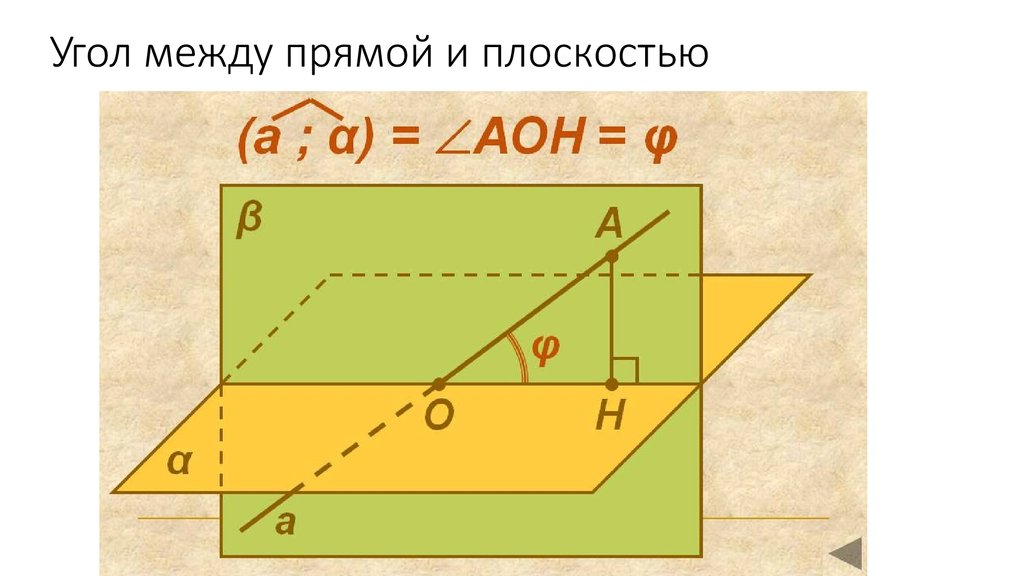
Рассмотрим две пересекающиеся плоскости 𝑃 и 𝑄.
Угол между ними можно визуализировать в плоскости, перпендикулярной линия их пересечения. Мы видим, что, как и для двух пересекающихся прямых, между ними два угла, 𝜃 и 𝜃, с 𝜃+𝜃=180∘.
Теперь рисуем две пары возможных векторов нормалей к двум плоскостям, мы видим, что либо 𝜃, либо 𝜃 угол между векторами нормалей в зависимости от направления нормальные векторы.
Если мы определим угол 𝜃 между двумя плоскостями 𝑃 и 𝑄 как острый угол между ними, то есть, 0≤𝜃≤90∘, то мы можем написать cos𝜃=||⃑𝑛⋅⃑𝑛||‖‖⃑𝑛‖‖‖‖⃑𝑛‖‖, поскольку скалярное произведение с ⃑𝑛 и ⃑𝑛 есть ⠀ и |𝜃|=|𝜃|coscos (потому что 𝜃=180−𝜃∘).
Определение: угол между двумя плоскостями
Угол 𝜃 между двумя плоскостями 𝑃
и 𝑄 с нормальными векторами
⃑𝑛 и
⃑𝑛 это
определяется как острый угол между ними; следовательно,
0≤𝜃≤90∘, и мы имеем
cos𝜃=||⃑𝑛⋅⃑𝑛||‖‖⃑𝑛‖‖‖‖⃑𝑛‖‖.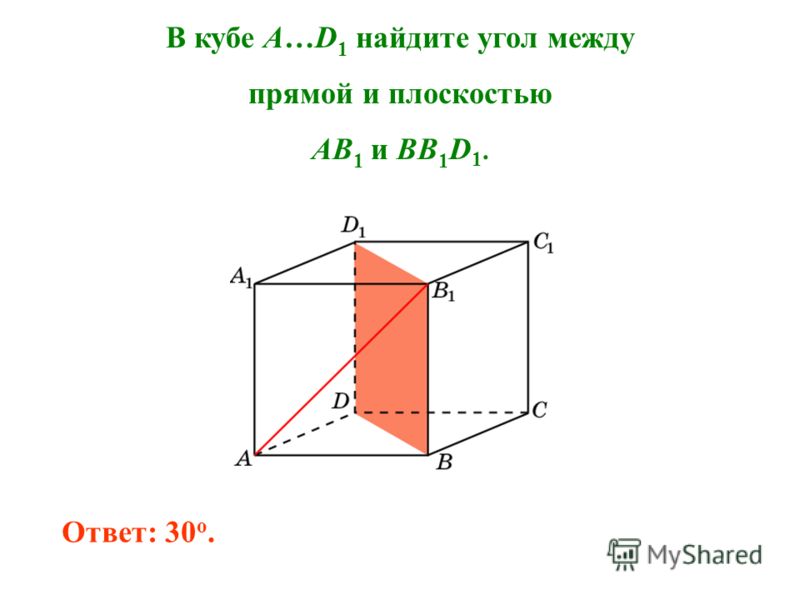
Давайте посмотрим на первый пример.
Пример 1. Нахождение угла между двумя плоскостями по их общим уравнениям
Найдите с точностью до секунды меру угла между двумя плоскостями. плоскости −9𝑥−6𝑦+5𝑧=−8 и 2𝑥+2𝑦+7𝑧=−8.
Ответ
Чтобы найти угол между плоскостями, нам нужны векторы нормалей два самолета. Зная, что общие уравнения плоскости форма 𝑎𝑥+𝑏𝑦+𝑐𝑧=𝑑, с (𝑎,𝑏,𝑐) будучи компонентами нормального вектора плоскости, мы находим, что компоненты нормальных векторов двух плоскостей равны (−9,−6,5) и (2,2,7). Угол 𝜃 между двумя плоскостями таков, что cos𝜃=||⃑𝑛⋅⃑𝑛||‖‖⃑𝑛‖‖‖‖⃑𝑛‖‖, где ⃑𝑛 и ⃑𝑛 — два вектора нормалей к двум плоскостям.
У нас есть cos𝜃=|−9×2+(−6)×2+5×7|√81+36+25×√4+4+49=5√142√57.
Чтобы найти 𝜃, мы используем обратную функцию нашего калькулятора: 𝜃=5√142√57=86.81408006….cos∘
Нам нужно задать угол с точностью до секунды. Помните, что один градус равен 60 минутам.
(1=60′)∘ и
одна минута равна 60 секундам (1′=60′′).
Помните, что один градус равен 60 минутам.
(1=60′)∘ и
одна минута равна 60 секундам (1′=60′′).
Следовательно, 0,81408006=(0,81408006×60)′=48,84480343…′,∘ а также 0,84480343′=(0,84480343×60)′′=50,68820581…≈51′′.
Угол между плоскостями 8648′51∘.
Найдем теперь угол между двумя плоскостями, когда уравнение одной из плоскостей является общим уравнением, а другой векторным уравнением.
Пример 2. Нахождение угла между двумя плоскостями по стандартным и векторным уравнениям
Найдите с точностью до градуса угол между двумя плоскостями. плоскости 2(𝑥−1)+3(𝑦−4)+4(𝑧+5)=0 и ⃑𝑟⋅(1,−2,5)=16.
Ответ
Чтобы найти угол между плоскостями, нам нужны векторы нормалей
два самолета. Коэффициенты 𝑥, 𝑦 и
𝑧 в общем уравнении — это 𝑥-,
𝑦- и 𝑧-компоненты вектора нормали
самолет. В приведенном уравнении мы видим, что при раскрытии скобок каждый
время дает термин в 𝑥, 𝑦 или 𝑧 и константу. Коэффициенты 𝑥, 𝑦 и 𝑧 равны
поэтому дается коэффициентом перед каждой скобкой. Итак, нормальный вектор
первой плоскости (2,3,4).
Коэффициенты 𝑥, 𝑦 и 𝑧 равны
поэтому дается коэффициентом перед каждой скобкой. Итак, нормальный вектор
первой плоскости (2,3,4).
Уравнение другой плоскости задается в векторной форме, где (1,−2,5) — вектор нормали к плоскости.
Угол 𝜃 между двумя плоскостями таков что cos𝜃=||⃑𝑛⋅⃑𝑛||‖‖⃑𝑛‖‖‖‖⃑𝑛‖‖, где ⃑𝑛 и ⃑𝑛 — два вектора нормали к двум плоскостям. Следовательно, cos𝜃=|(2,3,4)⋅(1,−2,5)|√2+3+41+(−2)+5=|2−6+20|√29√30=16√ 870, а также 𝜃=16√870=57,14936803…≈57,.стоит ближайшее целое число
Угол между двумя плоскостями с точностью до градуса равен 57∘.
Теперь рассмотрим прямую 𝑙, пересекающую плоскость 𝑃.
Угол между линией 𝑙 и плоскостью 𝑃
определяется как наименьший возможный угол между линией 𝑙 и любым
прямая в плоскости 𝑃, пересекающая 𝑙
(т. е. проходит через точку пересечения 𝑙
с 𝑃).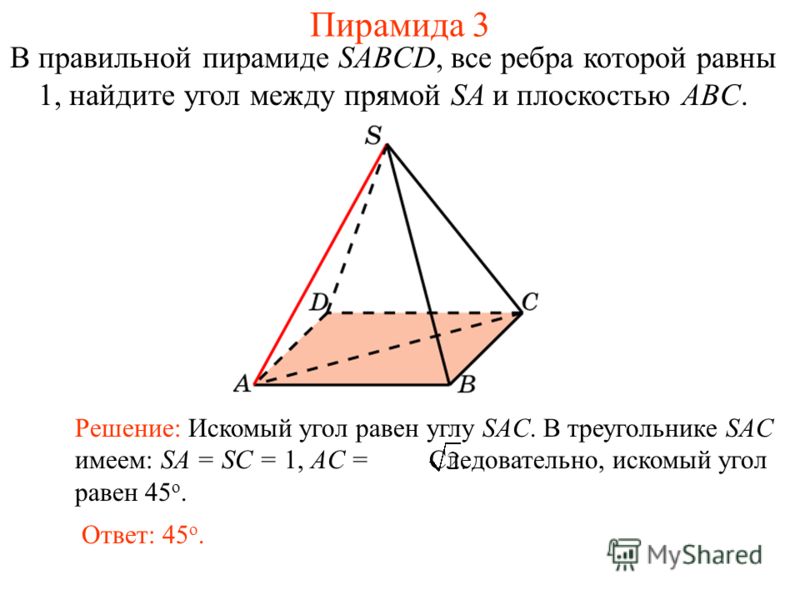 Следовательно, это острый угол между прямой
𝑙 и линией пересечения 𝑙 между
плоскость 𝑃 и плоскость 𝑁, которая является плоскостью
перпендикулярно 𝑃, содержащему 𝑙. Поэтому он определяется как дополнительный угол к наименьшему
возможный угол между линией 𝑙 и нормалью к плоскости
𝑃, как мы можем визуализировать на плоскости 𝑁 показано
на следующем рисунке.
Следовательно, это острый угол между прямой
𝑙 и линией пересечения 𝑙 между
плоскость 𝑃 и плоскость 𝑁, которая является плоскостью
перпендикулярно 𝑃, содержащему 𝑙. Поэтому он определяется как дополнительный угол к наименьшему
возможный угол между линией 𝑙 и нормалью к плоскости
𝑃, как мы можем визуализировать на плоскости 𝑁 показано
на следующем рисунке.
Вектор направления ⃑𝑑 вектора 𝑙 и обычный вектор ⃑𝑛 из 𝑃 также представлены. Вектор, обозначенный пунктирная линия представляет собой вектор нормали к 𝑃 с направлением, противоположным что из ⃑𝑛.
Находим, что угол 𝜃 между прямой 𝑙 и плоскостью
𝑃 равно 90−𝜃∘ или 𝜃−90∘, где
𝜃 и 𝜃 — два возможных угла между
⃑𝑑 и ⃑𝑛,
в зависимости от их соответствующих направлений. (Обратите внимание, что мы найдем угол 𝜃 между ⃑𝑛, как показано здесь, и
вектор направления 𝑙 в направлении, противоположном ⃑𝑑, как показано на
диаграмме.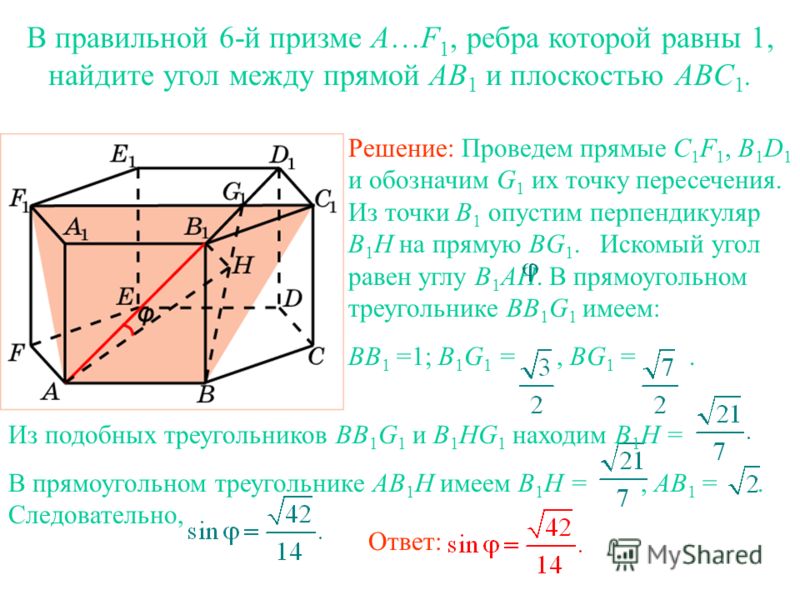 ) Однако, что касается угла между двумя плоскостями, мы
знать, что cos||⃑𝑑⋅⃑𝑛||‖‖⃑𝑑‖‖‖‖⃑𝑛‖‖ даст острый угол
(здесь 𝜃), так как cos𝜃
и cos𝜃 имеют один и тот же абсолют
значение, но cos𝜃 отрицательно, а
cos𝜃 положителен.
) Однако, что касается угла между двумя плоскостями, мы
знать, что cos||⃑𝑑⋅⃑𝑛||‖‖⃑𝑑‖‖‖‖⃑𝑛‖‖ даст острый угол
(здесь 𝜃), так как cos𝜃
и cos𝜃 имеют один и тот же абсолют
значение, но cos𝜃 отрицательно, а
cos𝜃 положителен.
Следовательно, угол 𝜃 между прямой 𝑙 и плоскостью 𝑃 дополняет 𝜃(𝜃+𝜃=90)∘, с cos𝜃=||⃑𝑑⋅⃑𝑛||‖‖⃑𝑑‖‖‖‖⃑𝑛‖‖.
Поскольку косинус(90−𝜃)=𝜃∘, отсюда следует, что sin𝜃=||⃑𝑑⋅⃑𝑛||‖‖⃑𝑑‖‖‖‖⃑𝑛‖‖.
Определение: Угол между прямой и плоскостью
Угол 𝜃 между плоскостью 𝑃 с вектором нормали ⃑𝑛 и линия 𝑙 с вектором направления ⃑𝑑 есть определяется как дополнительный угол к наименьшему возможному углу между линией 𝑙 и нормалью плоскости 𝑃.
Это так, что sin𝜃=||⃑𝑑⋅⃑𝑛||‖‖⃑𝑑‖‖‖‖⃑𝑛‖‖.
В прямоугольном треугольнике легко увидеть, почему, если 𝜃+𝜃=90∘, тогда sincos𝜃=𝜃.
Однако обратите внимание, что косинус(90−𝜃)=𝜃∘ и
sincos(90−𝜃)=𝜃∘ — истинные равенства за пределами
случае прямоугольных треугольников (т. е. также для углов
≥90∘) из-за
симметрии функций синуса и косинуса,
как показано здесь с единичными кругами. Точка 𝑃 связана
с углом 90−𝜃∘ является
отражение в линии 𝑦=𝑥 точки 𝑃
связанный с углом 𝜃,
это означает, что 𝑦=𝑥 и
𝑥=𝑦; следовательно,
синкос(90−𝜃)=𝜃∘ и
коссин(90−𝜃)=𝜃∘.
е. также для углов
≥90∘) из-за
симметрии функций синуса и косинуса,
как показано здесь с единичными кругами. Точка 𝑃 связана
с углом 90−𝜃∘ является
отражение в линии 𝑦=𝑥 точки 𝑃
связанный с углом 𝜃,
это означает, что 𝑦=𝑥 и
𝑥=𝑦; следовательно,
синкос(90−𝜃)=𝜃∘ и
коссин(90−𝜃)=𝜃∘.
Давайте посмотрим в следующем примере, как найти угол между плоскостью и линия, заданная их векторными уравнениями.
Пример 3. Нахождение угла между плоскостью и прямой по их векторным уравнениям
Что из следующего является меньшим углом между прямая ⃑𝑟=−7⃑𝑖−⃑𝑗−9⃑𝑘+𝑡2⃑𝑖+⃑𝑗−⃑𝑘 и самолет ⃑𝑟⋅9⃑𝑖−9⃑𝑗+2⃑𝑘=13?
- cos7√249498
- cos7√4386
- sin7√249498
- sin7√4386
Ответ
Чтобы найти угол между прямой и плоскостью, нам нужно знать
компоненты вектора направления линии и вектора нормали
самолета. В векторном уравнении прямой вектор направления
это вектор, который умножается на 𝑡. Здесь ⃑𝑑=2⃑𝑖+⃑𝑗−⃑𝑘;
поэтому его компоненты
(2,1,−1).
В векторном уравнении прямой вектор направления
это вектор, который умножается на 𝑡. Здесь ⃑𝑑=2⃑𝑖+⃑𝑗−⃑𝑘;
поэтому его компоненты
(2,1,−1).
Векторное уравнение плоскости имеет вид ⃑𝑟⋅⃑𝑛=c, где с — константа. Здесь нормальный вектор плоскости равен ⃑𝑛=9⃑𝑖−9⃑𝑗+2⃑𝑘; его компоненты (9,−9,2).
Угол 𝜃 между плоскостью 𝑃 с нормалью вектор ⃑𝑛 и прямая 𝑙 с направляющим вектором ⃑𝑑 такова, что sin𝜃 = || ⃑𝑑⋅⃑𝑛 || ‖⃑𝑑⃑𝑑⃑𝑑‖‖‖⃑𝑛⃑𝑛. ||⃑𝑑⋅⃑𝑛||‖‖⃑𝑑‖‖‖‖⃑𝑛‖‖=|2×9+1×(−9)+(−1)×2|2+1+(−1)9+( −9)+2=7√996=72√249=7√249498.
Значение 7√249498 есть значение грех𝜃; следовательно, 𝜃=7√249498sin. Правильный ответ: С.
Применим ту же идею к последним двум примерам, но с разными типами линейных уравнений.
Пример 4. Нахождение угла между плоскостью и прямой по их общему и параметрическому уравнениям
Найдите с точностью до секунды меру угла между
прямая 𝑥=3𝑡−1,
𝑦=−2𝑡+4,
𝑧=5 и плоскость 3𝑥−4𝑦+𝑧=2.
Ответ
Чтобы найти угол между прямой и плоскостью, нам нужно знать компоненты вектора направления линии и вектора нормали самолета. В параметрических уравнениях линии 𝑥-, 𝑦- и 𝑧-компоненты вектор направления — коэффициент 𝑡 в уравнении для 𝑥, 𝑦 и 𝑧 соответственно. Находим, что компоненты направляющего вектора данной прямой равны (3,−2,0).
Общее уравнение плоскости имеет вид 𝑎𝑥+𝑏𝑦+𝑐𝑧=𝑑, с (𝑎,𝑏,𝑐) будучи компоненты нормального вектора плоскости. Следовательно, компоненты вектора нормали к плоскости здесь равны (3,−4,1).
Угол 𝜃 между плоскостями 𝑃 с вектором нормали ⃑𝑛 и линией 𝑙 с вектор направления ⃑𝑑 таков, что sin𝜃 = || ⃑𝑑⋅⃑𝑛 || ‖⃑𝑑⃑𝑑⃑𝑑‖‖‖⃑𝑛⃑𝑛. ||⃑𝑑⋅⃑𝑛||‖‖⃑𝑑‖‖‖‖⃑𝑛‖‖=|3×3+(−2)×(−4)+0×1|3+(−2)+03+( −4)+1=17√13×26=1713√2.
Чтобы найти значение 𝜃, мы используем на нашем калькуляторе
обратная функция синуса:
𝜃=1713√2𝜃=67. 61986495….sin∘
61986495….sin∘
Нам нужно задать угол с точностью до секунды. Помните, что один градус равен 60 минутам. (1=60′)∘ и одна минута равна 60 секундам (1′=60′′).
Следовательно, 0,61986495=(0,61986495×60)′=37,19189688…′,∘ а также 0,19189688′=(0,19189688×60)′′=11,51381295…≈12′′.
Угол между плоскостью и прямой равен 6737′12∘.
Пример 5: Нахождение угла между плоскостью и прямой по их общему и декартовому уравнениям
Найдите с точностью до секунды меру меньшего угол между прямой 𝑥−77=𝑦−7−5=𝑧−41 и плоскость 6𝑥−8𝑦−5𝑧−17=0.
Ответ
Чтобы найти угол между прямой и плоскостью, нам нужно
знать компоненты вектора направления прямой и
нормальный вектор плоскости. Декартово уравнение прямой
имеет форму
𝑥−𝑥𝑙=𝑦−𝑦𝑚=𝑧−𝑧𝑛,
где (𝑥,𝑦,𝑧) —
координаты точки, лежащей на
линия и (𝑙,𝑚,𝑛) является
вектор направления линии. Следовательно
компоненты вектора направления данной прямой равны
(7,−5,1).
Следовательно
компоненты вектора направления данной прямой равны
(7,−5,1).
Общее уравнение плоскости имеет вид 𝑎𝑥+𝑏𝑦+𝑐𝑧=𝑑, где (𝑎,𝑏,𝑐) — компоненты нормального вектора плоскости. Следовательно, компоненты вектора нормали к плоскости здесь равны (6,−8,−5).
Угол 𝜃 между плоскостью 𝑃 с вектором нормали ⃑𝑛 и линия 𝑙 с направляющим вектором ⃑𝑑 такова, что sin𝜃 = || ⃑𝑑⋅⃑𝑛 || ‖⃑𝑑⃑𝑑⃑𝑑‖‖‖⃑𝑛⃑𝑛. ||⃑𝑑⋅⃑𝑛||‖‖⃑𝑑‖‖‖‖⃑𝑛‖‖=|7×6+(−5)×(−8)+1×(−5)|7+(−5)+1 6+(−8)+(−5)=77√75×125=77√25×3×25×5=7725√15.
Чтобы найти значение 𝜃, мы используем на нашем калькуляторе обратную функцию синуса: 𝜃=7725√15𝜃=52.67
1….sin∘
Нам нужно задать угол с точностью до секунды. Помните, что один градус 60 минут (1=60′)∘ и одна минута составляет 60 секунд (1′=60′′).
Следовательно, 0,67
1=(0,67
1×60)′=40,74714076…′,∘
а также
0,74714076′=(0,74714076×60)′′=44,82844578…≈45′′.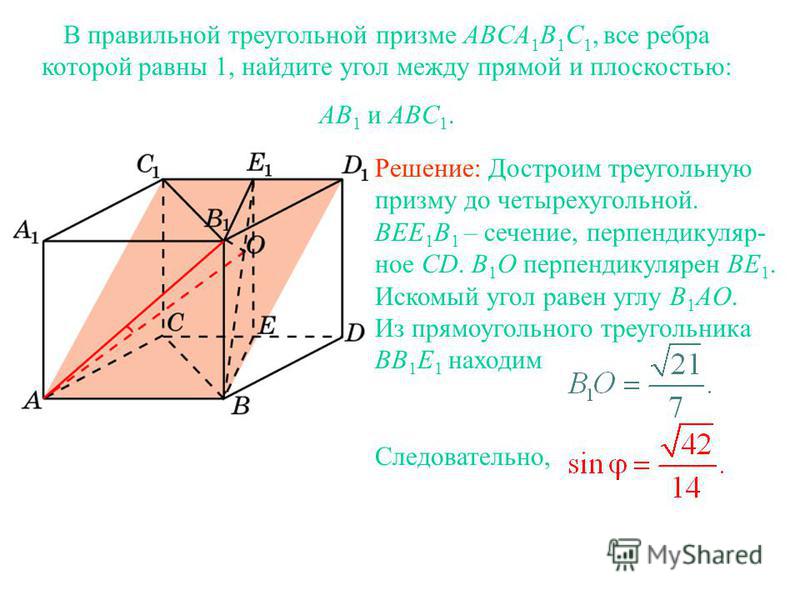
Угол между плоскостью и линией равен 5240′45∘.
Ключевые точки
- Угол 𝜃 между двумя плоскостями 𝑃 и 𝑄 с нормальными векторами ⃑𝑛 и ⃑𝑛 определяется как острый угол между ними; следовательно, 0≤𝜃≤90∘, и мы имеем cos𝜃=||⃑𝑛⋅⃑𝑛||‖‖⃑𝑛‖‖‖‖⃑𝑛‖‖.
- Угол 𝜃 между плоскостью 𝑃 и вектор нормали ⃑𝑛 а прямая 𝑙 с направляющим вектором ⃑𝑑 такова, что sin𝜃=||⃑𝑑⋅⃑𝑛||‖‖⃑𝑑‖‖‖‖⃑𝑛‖‖.
Угол между прямой и плоскостью: формулы и примеры решений
Геометрию часто называют одним из важнейших разделов математики. Среди них трехмерная геометрия, где мы изучаем свойства линии и плоскости, образующих угол друг с другом. Он имеет вес 14 баллов, что составляет 17% от общего количества баллов по предмету. В статье будут объяснены уравнения прямых и плоскостей относительно угла между прямой и плоскостью в векторной, но и декартовой форме. В этой статье мы также изучим направляющие косинусы и отношения направлений прямой, соединяющей две точки.
Также читайте: Трехмерная геометрия
Таблица содержимого
|
Ключевые термины: Трехмерная плоская плоскость, векторы, уловка, уловка, уловка, уловка, уловка, уловка, уловка, уловка, уловка, уловка, уловка. .
Что означает «линия» и «плоскость»?
[Щелкните здесь, чтобы просмотреть примеры вопросов]
Линия — это одномерная фигура, которая имеет длину, но не имеет ширины.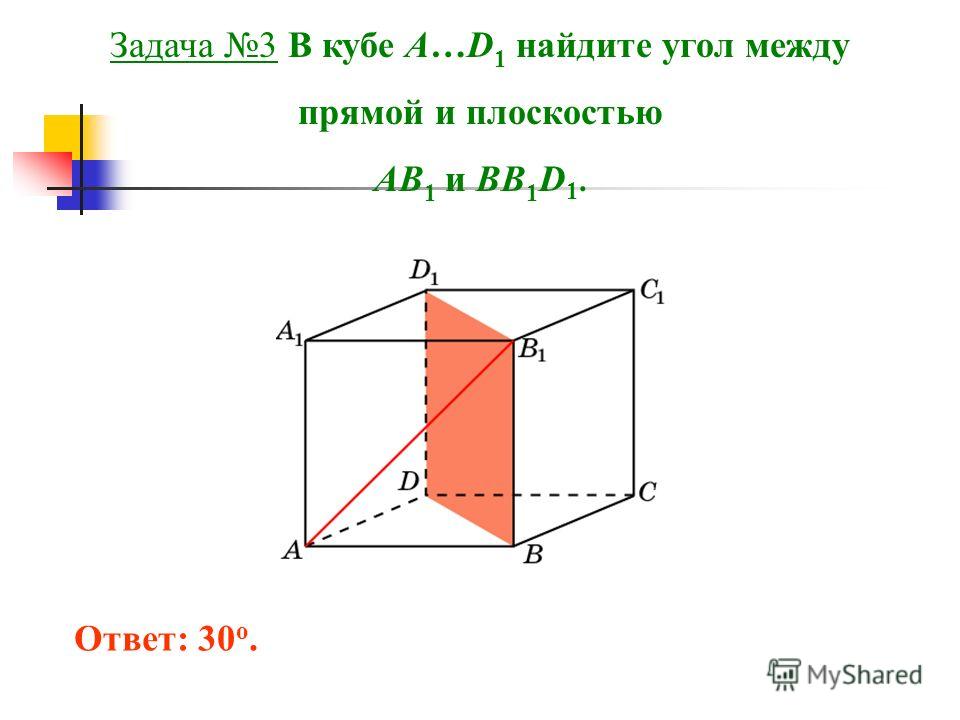 Линия состоит из множества точек, бесконечно продолженных в противоположных направлениях.
Линия состоит из множества точек, бесконечно продолженных в противоположных направлениях.
Точно так же, когда бесконечное количество точек простирается бесконечно в любом направлении, образуя плоскую поверхность, это называется плоскостью. Получается набор линий, расположенных рядом друг с другом на плоскости. Плоскость — это двумерная геометрическая фигура, которую можно измерить по длине и ширине.
Читайте также: Сложение векторов
Что означает угол между прямой и плоскостью?
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Дополнение угла между прямой, примыкающей к плоскости, и нормалью к плоскости называется углом между прямой и плоскостью.
Угол между прямой и плоскостью
Векторное уравнение любой жизни задается формулой —
линия и нормаль равнины. Тогда
Теперь пусть линия наклонена под углом µ к плоскости.
По определению, µ является дополнением угла.
И , sin 90°-θ =sin µ =cosθ .
Таким образом, это можно записать:
или,
Читать также: CO Планраровые векторы
Cosines и Riemer Ratios of Line
Cosines и Riemer Ratios of Line
.
Направленные углы: Углы, образованные линией с положительными направлениями осей X, Y и Z, называются направленными углами.
Направленные косинусы: Если α, β и γ являются направленными углами направленной прямой L, то cosα,cosβ и cosγ называются направленными косинусами прямой.
Directional cosines
Direction ratio of the line joining two points A(x 1 ,y 1 ,z 1 ) and B(x 2 ,y 2 ,z 2 ) определяется как
(x 2 −x 1 ,y 2 −y 1 ,z 2 −z 1 )
Если вектор задан как A=pi+qj+rk, то его отношения направлений задаются (p,q,r)
Читайте также: Координатная геометрия
Связь между направляющими косинусами и отношениями направлений
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Если l, m ,n – направляющие косинусы прямой, то a, b, c – ее отношения направлений, такие, что:
и l 2 +m 2 +n 2 =1
- Декартовы формы прямой и плоскости
(x – x 1 )/ a = (y – y 1 )/ b = (z – z 1 )/ c — декартова форма линии.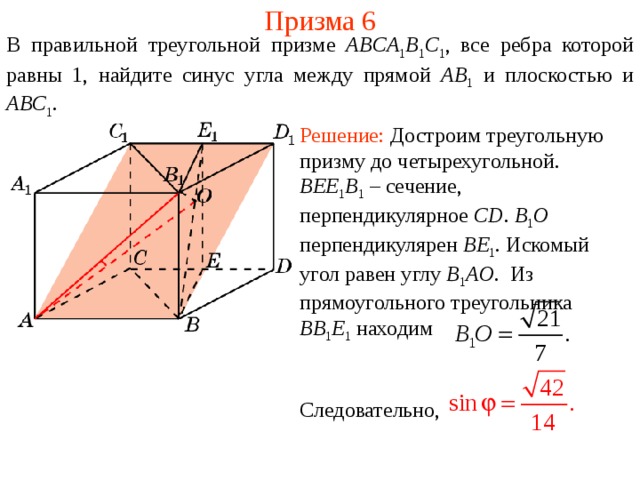
a 2 x + b 2 y + c 2 z + d 2 = 0 – декартова форма плоскости.
Следовательно, угол между прямой и плоскостью определяется как:
Подробнее: Уравнение плоскости в трехмерном пространстве
Решенные примеры
Q1) Найдите угол между прямой
и плоскостью 2x+y-3z+4=0.
Ответ: Здесь,
Уравнение прямой :
Уравнение плоскости: 2x+y-3z+4=0
Мы знаем,
Q2) Найдите угол между плоскостью 10x + 2y — 11z = 3 и прямой (x + 1)/ 2 =y/ 3 = (z — 3)/ 6.
Ответ: Угол можно рассчитать с помощью декартовой формы, например,
Sinθ = | 10 х 2 + 2 х 3 + (-11) х 6 | / 10 2 +2 2 + (-11) 2 ). ( 2 2 + 3 2 + 6 2 )
Sinθ = | 20 + 6 — 66 | / (100 + 4 + 121).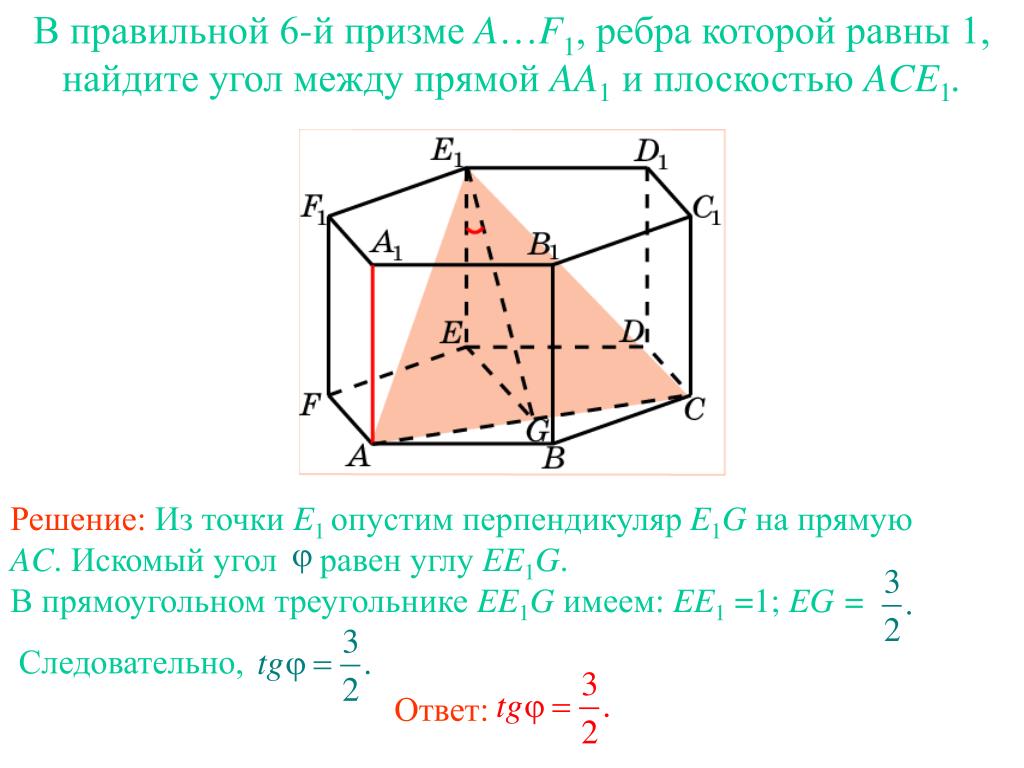 ( 4 + 9 + 36)
( 4 + 9 + 36)
Sinθ = | -40 | / ( 15 x 7)
Sinθ = 8/ 21
θ = Sin -1 (8/21) — угол между плоскостью и прямой.
Примеры вопросов
Вопрос: Какие существуют типы линий? (5 баллов)
Ответ : В геометрии есть четыре типа линий. Это не:
- Горизонтальные линии: Когда линия движется слева направо в прямом направлении, это горизонтальная линия
- Вертикальные линии: прямое направление, это вертикальная линия.
- Параллельные линии : Если две прямые линии не встречаются и не пересекаются ни в одной точке, даже в бесконечности, то они параллельны друг другу.
Предположим, две прямые PQ и RS параллельны, тогда это представляется как PQ||RS.
- Перпендикулярные линии: Когда две линии встречаются или пересекаются под углом 90 градусов или под прямым углом, они перпендикулярны друг другу.

Если PQ и RS две прямые, перпендикулярные друг другу, то это представляется как PQ ⊥ RS.
Вопрос:- В чем разница между 2D и 3D геометрией? (2 балла)
Ответ: Геометрия – это наука о формах и фигурах. Плоская геометрия или 2D-геометрия — это тип геометрии, в котором есть только 2 измерения, а именно длина и ширина, тогда как 3D-геометрия — это тот, в котором формы занимают пространство и имеют 3 измерения, а именно длину, ширину и высоту.
Вопрос:- Что означает перпендикулярная линия? (1 балл)
Ответ: Перпендикулярные линии определяются как две линии, которые встречаются или пересекаются друг с другом под прямым углом (90°).
Вопрос:- Какова формула расстояния? (1 mark)
Ans : d =
Here , d= distance between two points (x 1 ,y 1 ) and (x 2 ,y 2 )
Вопрос:- Каково кратчайшее расстояние между двумя линиями? (1 балл)
Ответ : Кратчайшее расстояние между любыми двумя данными линиями может быть выражено как:
Расстояние между двумя линиями вида l 1 = a 1 + q b 1 909 6 9 и l = a 2 + p b 2 определяется по формуле:
Вопросы прошлых лет (решенные)
Вопросы. Найдите уравнение плоскости, проходящей через точки (3, 4, 1) и (0, 1, 0) и параллельной прямой . (CBSE Delhi 2008) (6 баллов)
Найдите уравнение плоскости, проходящей через точки (3, 4, 1) и (0, 1, 0) и параллельной прямой . (CBSE Delhi 2008) (6 баллов)
Ответ: Уравнение, проходящее через (3,4,1), будет: a(x-3) + b(y-4) + c(z-1). ) = 0 —————(1)
Так как он также проходит через (0,1,0) : -3a – 3b – c = 0 ——- ——(2)
Далее, параллельно данной прямой. Следовательно,
a.2 + b.7 + c.5 = 0 ————————-(3)
Исключая a, b и c из уравнения (2) и (3),
Помещение приведенных выше значений в (1),
-9k(x – 3) – 17k(y-4) – 23k(z-1) = 0
Следовательно, 9x + 17y + 23z = 20
– искомое уравнение.
Вопросы. Найдите уравнение плоскости через линию пересечения плоскостей 2x + y -z = 3 и 5x — 3y + 4z +9=0 и параллельную прямой:
(CBSE AI 2011) (6 баллов)
Ответ: Уравнение плоскости, проходящей через линию пересечения плоскостей 2x + y -z = 3 и 5x-3y + 4z +9 = 0 равно
(2x+y-z-3)+λ(5x-3y + 4z + 9) = 0
x(2 +5λ) + y(1-3λ) + z(4λ-1) +9λ-3=0 . ..(i)
..(i)
Поскольку плоскость (i) параллельна прямой
2(2 +5λ) + 4(1-3λ) + 5(4λ-1) +9λ-3=0
λ = -1/6
Подставляя значение λ в (i), получаем
⇒ 7x+9y-10z — 27 = 0
Это уравнение искомой плоскости.
Вопросы. Найдите координаты точки, в которой линия, проходящая через точки A(3, 4, 1) и B(5, 1,6), пересекает плоскость XY. (CBSE AI 2012) (4 балла)
Ответ: Уравнение прямой, проходящей через A(3, 4, 1) и B(5, 1, 6), имеет вид
Ques. Найти координаты точки, в которой прямая через точки (3, -4, -5) и (2, -3, 1) пересекает плоскость, проходящую через точки (2, 2, 1), (3, 0, 1) ) и (4, -1,0). (CBSE Delhi 2013) (4 балла)
Ответ: Пусть A(2, 2, 1), B(3, 0, 1) и C(4, -1,0).
Любая плоскость, проходящая через A, определяется выражением a(x-2) + b(y-2) + c(z − 1) = 0 …..(i)
Так как B и C также лежат на нем, то
a-2b +0 c = 0
2a — 3b — c = 0
Из (i) уравнение плоскости равно
2(x- 2) + (y-2) + (z — 1) = 0
2x+y+z-7=0
Вопросы.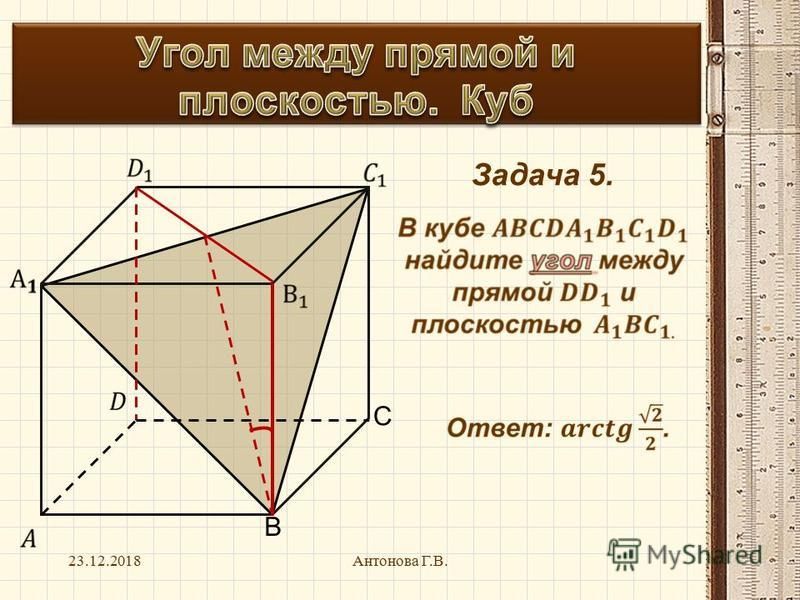 Найдите уравнение плоскости, проходящей через точку (3, 2, 0) и содержащей прямую . (Иностранный 2015)(6 баллов)
Найдите уравнение плоскости, проходящей через точку (3, 2, 0) и содержащей прямую . (Иностранный 2015)(6 баллов)
Ответ: Уравнение плоскости, проходящей через (3, 2, 0), равно
a(x-3) + b(y-2) + c(z — 0) = 0………..(i)
Данная линия:
Так как плоскость содержит линию, то
a(3-3) + b(6-2) + c(4-0) = 0
0a + 4b + 4c =0 ………..(ii)
и a(1) + b(5) + c(4) = 0
a + 5b + 4c=0 ………..(iii)
Решение ( ii) & (iii), мы получаем
a = −4λ, b = 4λ, c = −4λ
Подставляя значения a, b, c в (i), мы получаем -4λ(x-3) + 4λ(y-2) — 4λ(z — 0) = 0
-4x+12+ 4y — 8-4z = 0
⇒x-y+z-1=0 искомое уравнение плоскости 9\circ$$.
Чтобы вычислить угол между обеими плоскостями, мы определим угол между векторами нормалей каждой плоскости.
Удобно помнить, что для плоскости $$\pi$$ с уравнением $$\pi: Ax + by + cz + D = 0$$ перпендикулярный вектор (вектор нормали к плоскости) есть $$\ vec{n}=(A, B, C)$$
Следовательно, если мы имеем:
- плоскость $$\pi_1$$ с управляющим вектором $$\vec{n}_1$$.
- плоскостей $$\pi_2$$ с управляющим вектором $$\vec{n}_2$$.
Тогда: $$$\cos(\widehat{\pi_1 \\pi_2})=\cos\alpha= |\cos(\widehat{\vec{n}_1 \\vec{n}_2})|= \Big| \dfrac{\vec{n}_1\cdot\vec{n}_2}{|\vec{n}_1||\vec{n}_2|}\Big|= \dfrac{|\vec{n}_1\cdot\vec{n}_2|}{|\vec{n}_1||\vec{n}_2|}$$$
Следовательно, $$$ \alpha =\arccos\Big(\dfrac{|\vec{n}_1\cdot\vec{n}_2|} {|\vec{n}_1||\vec{n}_2|} \Big) \qquad \alpha \in [0,\dfrac{\pi}{2}]$$$ 92}}$$$
Примечание. Важно помнить, что если у нас есть плоскость в векторной или параметрической форме, мы можем получить вектор нормали, выполнив векторное произведение управляющих векторов плоскости.
Также замечательно, что мы можем полностью определить одну плоскость с помощью вектора нормали и одной точки. Для этого воспользуемся общим уравнением, в котором неизвестным является только $$D$$, и которое мы найдем, заменив точку и решив.
Для этого воспользуемся общим уравнением, в котором неизвестным является только $$D$$, и которое мы найдем, заменив точку и решив.
С учетом самолетов: $$$ \pi_1: 3x-y+2z+1=0 \qquad \pi_2: 2x+y-5z-1=0$$$ 9\circ$$.
Обратите внимание, что, определяя угол между прямой линией и плоскостью как угол между прямой и ее ортогональной проекцией на плоскость, мы можем узнать угол из определяющего вектора прямой линии и вектора нормали к плоскости. Это связано с тем, что 3 вектора (прямая, проекция и нормаль к плоскости) компланарны — они лежат в одной плоскости — а также угол между вектором нормали и управляющим вектором проекции прямой и постоянный. Следовательно, если у нас есть:
- $$\pi$$: плоскость.
- $$r$$: прямая.
- $$s$$: перпендикулярная линия (перпендикулярная плоскости).
 \circ \end{массив}$$$
\circ \end{массив}$$$12.5 Линии и плоскости
Линии и плоскости, пожалуй, самые простые из кривых и поверхностей в трехмерное пространство. Они также окажутся важными, поскольку мы стремимся понимать более сложные кривые и поверхности.
Уравнение линии в двух измерениях: $ax+by=c$; это разумно ожидать, что линия в трех измерениях задается $ax + by +cz = d$; разумно, но неправильно — оказывается, что это уравнение плоскости.
У плоскости нет очевидного «направления», как у линии. можно связать плоскость с направлением очень полезным способом, однако: есть ровно два направления, перпендикулярные самолет. Любой вектор с одним из этих двух направлений называется нормальный к самолету. Таким образом, хотя векторов нормали к данной плоскости много, все они параллельны или антипараллельны друг другу.
Предположим, две точки $\ds (v_1,v_2,v_3)$ и $\ds (w_1,w_2,w_3)$ лежат в плоскости; тогда вектор $\ds\langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$ параллелен к самолету; в частности, если этот вектор положить хвостом в $\ds (v_1,v_2,v_3)$, то его головка находится в точке $\ds (w_1,w_2,w_3)$ и лежит в самолет.
 В результате любой вектор, перпендикулярный плоскости,
перпендикулярно $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$. На самом деле, это
Легко видеть, что плоскость состоит из ровно тех точек
$\ds (w_1,w_2,w_3)$, для которых $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$ равно
перпендикулярно нормали к плоскости, как показано на
рисунок 12.5.1. То есть предположим
мы знаем, что $\langle a,b,c\rangle$ нормальна к плоскости, содержащей
точка $\ds (v_1,v_2,v_3)$. Тогда $(x,y,z)$ лежит в плоскости тогда и только тогда
если $\langle a,b,c\rangle$ перпендикулярно $\ds \langle
x-v_1,y-v_2,z-v_3\rangle$. В свою очередь, мы знаем, что это правда
именно тогда, когда $\ds \langle a,b,c\rangle\cdot\langle
x-v_1,y-v_2,z-v_3\rangle=0$. Таким образом, $(x,y,z)$ лежит в плоскости, если и
только если
$$\выравнивание{
\langle a,b,c\rangle\cdot\langle x-v_1,y-v_2,z-v_3\rangle&=0\cr
a(x-v_1)+b(y-v_2)+c(z-v_3)&=0\cr
топор+by+cz-av_1-bv_2-cv_3&=0\cr
топор+by+cz&=av_1+bv_2+cv_3.\cr
}$$
Работая в обратном направлении, обратите внимание, что если $(x,y,z)$ — точка, удовлетворяющая
$ax+by+cz=d$ тогда
$$\выравнивание{
топор+by+cz&=d\cr
топор+by+cz-d&=0\cr
a(x-d/a)+b(y-0)+c(z-0)&=0\cr
\langle a,b,c\rangle\cdot\langle x-d/a,y,z\rangle&=0.
В результате любой вектор, перпендикулярный плоскости,
перпендикулярно $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$. На самом деле, это
Легко видеть, что плоскость состоит из ровно тех точек
$\ds (w_1,w_2,w_3)$, для которых $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$ равно
перпендикулярно нормали к плоскости, как показано на
рисунок 12.5.1. То есть предположим
мы знаем, что $\langle a,b,c\rangle$ нормальна к плоскости, содержащей
точка $\ds (v_1,v_2,v_3)$. Тогда $(x,y,z)$ лежит в плоскости тогда и только тогда
если $\langle a,b,c\rangle$ перпендикулярно $\ds \langle
x-v_1,y-v_2,z-v_3\rangle$. В свою очередь, мы знаем, что это правда
именно тогда, когда $\ds \langle a,b,c\rangle\cdot\langle
x-v_1,y-v_2,z-v_3\rangle=0$. Таким образом, $(x,y,z)$ лежит в плоскости, если и
только если
$$\выравнивание{
\langle a,b,c\rangle\cdot\langle x-v_1,y-v_2,z-v_3\rangle&=0\cr
a(x-v_1)+b(y-v_2)+c(z-v_3)&=0\cr
топор+by+cz-av_1-bv_2-cv_3&=0\cr
топор+by+cz&=av_1+bv_2+cv_3.\cr
}$$
Работая в обратном направлении, обратите внимание, что если $(x,y,z)$ — точка, удовлетворяющая
$ax+by+cz=d$ тогда
$$\выравнивание{
топор+by+cz&=d\cr
топор+by+cz-d&=0\cr
a(x-d/a)+b(y-0)+c(z-0)&=0\cr
\langle a,b,c\rangle\cdot\langle x-d/a,y,z\rangle&=0. \cr
}$$
А именно, $\langle a,b,c\rangle$ перпендикулярен вектору с
хвост в $(d/a,0,0)$ и голова в $(x,y,z)$. Это означает, что точки
$(x,y,z)$, удовлетворяющие уравнению $ax+by+cz=d$, образуют плоскость
перпендикулярно $\langle a,b,c\rangle$. (Это не
работать, если $a=0$, но в этом случае мы можем использовать $b$ или $c$ в роли
$а$. То есть либо $a(x-0)+b(y-d/b)+c(z-0)=0$, либо
$a(x-0)+b(y-0)+c(z-d/c)=0$.)
\cr
}$$
А именно, $\langle a,b,c\rangle$ перпендикулярен вектору с
хвост в $(d/a,0,0)$ и голова в $(x,y,z)$. Это означает, что точки
$(x,y,z)$, удовлетворяющие уравнению $ax+by+cz=d$, образуют плоскость
перпендикулярно $\langle a,b,c\rangle$. (Это не
работать, если $a=0$, но в этом случае мы можем использовать $b$ или $c$ в роли
$а$. То есть либо $a(x-0)+b(y-d/b)+c(z-0)=0$, либо
$a(x-0)+b(y-0)+c(z-d/c)=0$.)Рисунок 12.5.1. Плоскость, определяемая векторами, перпендикулярными нормали.
Таким образом, для вектора $\langle a,b,c\rangle$ мы знаем, что все плоскости перпендикулярные этому вектору, имеют вид $ax+by+cz=d$, и любая поверхность этой формы является плоскостью, перпендикулярной $\langle a,b,c\rangle$.
Пример 12.5.1 Найдите уравнение для плоскости, перпендикулярной $\langle 1,2,3\rangle$ и содержащий точку $(5,0,7)$.
Используя приведенный выше вывод, плоскость равна $1x+2y+3z=1\cdot5+2\cdot0+3\cdot7=26$. Поочередно, мы знаем, что плоскость равна $x+2y+3z=d$, и чтобы найти $d$, можно подставить известную точку на плоскости, чтобы получить $5+2\cdot0+3\cdot7=d$, поэтому $d=26$.
 Мы могли бы также записать это просто как $(x-5)+2(y)+3(z-7)=0$, что для
много целей прекрасное представление; всегда можно умножить
чтобы получить $x+2y+3z=26$.
$\квадрат$
Мы могли бы также записать это просто как $(x-5)+2(y)+3(z-7)=0$, что для
много целей прекрасное представление; всегда можно умножить
чтобы получить $x+2y+3z=26$.
$\квадрат$Пример 12.5.2 Найдите вектор нормали к плоскости $2x-3y+z=15$.
Одним из примеров является $\langle 2, -3,1\rangle$. Любой вектор, параллельный или антипараллельно с этим также работает, например $-2\langle 2, -3,1\rangle=\langle -4,6,-2\rangle$ также нормальна к плоскости. $\квадрат$
Нам часто нужно будет найти уравнение для плоскости при заданных информация о самолете. Хотя иногда может быть немного более короткие пути к желаемому результату, это всегда возможно, и обычно целесообразно использовать данную информацию, чтобы найти нормаль к плоскость и точку на плоскости, а затем найти уравнение в виде выше.
Пример 12.5.3. Плоскости $x-z=1$ и $y+2z=3$ пересекаются по прямой. Найти третья плоскость, содержащая эту прямую и перпендикулярная плоскости $x+y-2z=1$.
Во-первых, заметим, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны.
 Таким образом, мы ищем вектор $\langle
a,b,c\rangle$, то есть
перпендикулярно $\langle 1,1,-2\rangle$. Кроме того, поскольку
желаемая плоскость должна содержать определенную линию, $\langle
a,b,c\rangle$ должны быть перпендикулярны любому вектору, параллельному этому
линия. Так как $\langle
a,b,c\rangle$ должны быть перпендикулярны двум векторам, мы можем найти это по
вычисление перекрестного произведения двух. Итак, нам нужен вектор, параллельный
к линии пересечения данных плоскостей. Для этого достаточно
знать две точки на прямой. Чтобы найти две точки на этой прямой,
необходимо найти две точки, находящиеся одновременно на двух плоскостях,
$x-z=1$ и $y+2z=3$. Любая точка на обеих плоскостях будет удовлетворять
$x-z=1$ и $y+2z=3$. Легко найти значения для $x$ и $z$
удовлетворяющие первому, такие как $x=1, z=0$ и $x=2, z=1$. затем
мы можем найти соответствующие значения для $y$, используя второе уравнение,
а именно $y=3$ и $y=1$, поэтому
$(1,3,0)$ и $(2,1,1)$ находятся на прямой
пересечения, потому что оба находятся в обеих плоскостях.
Таким образом, мы ищем вектор $\langle
a,b,c\rangle$, то есть
перпендикулярно $\langle 1,1,-2\rangle$. Кроме того, поскольку
желаемая плоскость должна содержать определенную линию, $\langle
a,b,c\rangle$ должны быть перпендикулярны любому вектору, параллельному этому
линия. Так как $\langle
a,b,c\rangle$ должны быть перпендикулярны двум векторам, мы можем найти это по
вычисление перекрестного произведения двух. Итак, нам нужен вектор, параллельный
к линии пересечения данных плоскостей. Для этого достаточно
знать две точки на прямой. Чтобы найти две точки на этой прямой,
необходимо найти две точки, находящиеся одновременно на двух плоскостях,
$x-z=1$ и $y+2z=3$. Любая точка на обеих плоскостях будет удовлетворять
$x-z=1$ и $y+2z=3$. Легко найти значения для $x$ и $z$
удовлетворяющие первому, такие как $x=1, z=0$ и $x=2, z=1$. затем
мы можем найти соответствующие значения для $y$, используя второе уравнение,
а именно $y=3$ и $y=1$, поэтому
$(1,3,0)$ и $(2,1,1)$ находятся на прямой
пересечения, потому что оба находятся в обеих плоскостях. В настоящее время
$\langle 2-1,1-3,1-0\rangle=\langle 1,-2,1\rangle$ параллелен
линия. Наконец, мы можем выбрать $\langle a,b,c\rangle=\langle
1,1,-2\rangle\times \langle 1,-2,1\rangle=\langle -3,-3,-3\rangle$.
Хотя этот вектор прекрасно подойдет, любой вектор, параллельный или
антипараллельное к нему также будет работать, поэтому, например, мы могли бы выбрать
$\langle 1,1,1\rangle$, который ему антипараллелен.
В настоящее время
$\langle 2-1,1-3,1-0\rangle=\langle 1,-2,1\rangle$ параллелен
линия. Наконец, мы можем выбрать $\langle a,b,c\rangle=\langle
1,1,-2\rangle\times \langle 1,-2,1\rangle=\langle -3,-3,-3\rangle$.
Хотя этот вектор прекрасно подойдет, любой вектор, параллельный или
антипараллельное к нему также будет работать, поэтому, например, мы могли бы выбрать
$\langle 1,1,1\rangle$, который ему антипараллелен.Теперь мы знаем, что $\langle 1,1,1\rangle$ нормальна к искомой плоскости. и $(2,1,1)$ — точка на плоскости. Поэтому уравнение плоскость равна $x+y+z=4$. В качестве быстрой проверки, поскольку $(1,3,0)$ также находится на линия, она должна быть в самолете; поскольку $1+3+0=4$, мы видим, что это действительно дело.
Обратите внимание, что если бы мы использовали $\langle -3,-3,-3\rangle$ в качестве нормали, мы открыли бы уравнение $-3x-3y-3z=-12$, то мы вполне могли бы заметили, что мы можем разделить обе части на $-3$, чтобы получить эквивалент $x+y+z=4$. $\квадрат$
Итак, теперь мы понимаем уравнения плоскостей; давайте обратимся к линии.
 К сожалению, это оказывается весьма неудобным
представить типичную линию одним уравнением; нам нужно подойти
линии по-другому.
К сожалению, это оказывается весьма неудобным
представить типичную линию одним уравнением; нам нужно подойти
линии по-другому.В отличие от плоскости, линия в трех измерениях имеет очевидную направление, а именно направление любого параллельного ему вектора. Фактически линия может быть определена и однозначно идентифицирована путем предоставления одной точки на прямой и вектор, параллельный прямой (в одном из двух возможных направления). То есть линия состоит именно из тех точек, которые мы можем достичь, начав с точки и пройдя некоторое расстояние в направление вектора. Давайте посмотрим, как мы можем перевести это на более математический язык.
Предположим, что прямая содержит точку $\ds (v_1,v_2,v_3)$ и параллельна к вектору $\langle a,b,c\rangle$; мы называем $\langle a,b,c\rangle$ a вектор направления для линии. Если мы поместим вектор $\ds \langle v_1,v_2,v_3\rangle$ с хвостом в начале координат и головой в $\ds (v_1,v_2,v_3)$, и если мы поместим вектор $\langle a,b,c\rangle$ хвостом в $\ds (v_1,v_2,v_3)$, то голова $\langle a,b,c\rangle$ находится в точке на прямой.
 Мы можем добраться до через любые точек на линии, делая то же самое, за исключением использования
$t\langle a,b,c\rangle$ вместо $\langle a,b,c\rangle$, где $t$
некоторое действительное число. Из-за того, как работает сложение векторов,
точка в начале вектора $t\langle a,b,c\rangle$ — это точка
в начале вектора $\ds\langle v_1,v_2,v_3\rangle+t\langle
a,b,c\rangle$, а именно $\ds (v_1+ta,v_2+tb,v_3+tc)$; видеть
рисунок 12.5.2.
Мы можем добраться до через любые точек на линии, делая то же самое, за исключением использования
$t\langle a,b,c\rangle$ вместо $\langle a,b,c\rangle$, где $t$
некоторое действительное число. Из-за того, как работает сложение векторов,
точка в начале вектора $t\langle a,b,c\rangle$ — это точка
в начале вектора $\ds\langle v_1,v_2,v_3\rangle+t\langle
a,b,c\rangle$, а именно $\ds (v_1+ta,v_2+tb,v_3+tc)$; видеть
рисунок 12.5.2.Рисунок 12.5.2. Векторная форма линии.
Другими словами, когда $t$ проходит через все возможные действительные значения, вектор $\ds \langle v_1,v_2,v_3\rangle+t\langle a,b,c\rangle$ указывает на каждая точка на линии, когда ее конец находится в начале координат. Другая общий способ записать это как набор параметрических уравнения : $$ x= v_1+ta\qquad y=v_2+tb \qquad z=v_3+tc.$$ Иногда полезно использовать эту форму линии даже в двух случаях. Габаритные размеры; векторная форма прямой на плоскости $x$-$y$ есть $\ds \langle v_1,v_2\rangle+t\langle a,b\rangle$, что совпадает с $\ds \langle v_1,v_2,0\rangle+t\langle a,b,0\rangle$.

Пример 12.5.4. Найдите векторное выражение для линии, проходящей через $(6,1,-3)$ и $(2,4,5)$. Чтобы получить вектор, параллельный прямой, мы вычитаем $\langle 6,1,-3\rangle-\langle2,4,5\rangle=\langle 4,-3,-8\rangle$. Линия тогда задается как $\langle 2,4,5\rangle+t\langle 4,-3,-8\rangle$; там конечно, много других возможностей, таких как $\langle 6,1,-3\rangle+t\langle 4,-3,-8\rangle$. $\квадрат$
Пример 12.5.5 Определить, совпадают ли прямые $\langle 1,1,1\rangle+t\langle 1,2,-1\rangle$ и $\langle 3,2,1\rangle+t\langle -1,-5,3\rangle$ параллельны, пересекаются или ни один.
В двух измерениях две линии либо пересекаются, либо параллельны; в В трех измерениях линии, которые не пересекаются, могут быть не параллельны. В этом случае, поскольку векторы направления линий не параллельны или антипараллельны, мы знаем, что прямые не параллельны. Если они пересекаются, то должно быть два значения $a$ и $b$, так что $\langle 1,1,1\rangle+a\langle 1,2,-1\rangle= \langle 3,2,1\rangle+b\langle -1,-5,3\rangle$, то есть $$\выравнивание{ 1+а&=3-б\кр 1+2а&=2-5б\кр 1-а&=1+3б\кр }$$ Это дает три уравнения с двумя неизвестными, поэтому может быть, а может и не быть.
 решение в общем. В этом случае легко обнаружить, что $a=3$
и $b=-1$ удовлетворяет всем трем уравнениям, поэтому прямые пересекаются в
точка $(4,7,-2)$.
$\квадрат$
решение в общем. В этом случае легко обнаружить, что $a=3$
и $b=-1$ удовлетворяет всем трем уравнениям, поэтому прямые пересекаются в
точка $(4,7,-2)$.
$\квадрат$Пример 12.5.6. Найти расстояние от точки $(1,2,3)$ до плоскости $2x-y+3z=5$. Расстояние от точки $P$ до плоскости является кратчайшим расстояние от $P$ до любой точки плоскости; это расстояние, измеряемое от $P$ перпендикулярно плоскости; видеть рисунок 12.5.3. Это расстояние является абсолютным значением скалярной проекции $\ds \overrightarrow{\распорка QP}$ на вектор нормали $\bf n$, где $Q$ — любая точка плоскости. Легко найти точку на плоскости, скажем, $(1,0,1)$. Таким образом, расстояние равно $$ {\ overrightarrow {\ распорка QP} \ cdot {\ bf n} \ over | {\ bf n} |} = {\ langle 0,2,2 \ rangle \ cdot \ langle 2, -1,3 \ rangle \ over | \ langle 2, — 1,3 \ rangle |} = {4\over\sqrt{14}}. $$ $\квадрат$
Рисунок 12.5.3. Расстояние от точки до плоскости.
Пример 12.5.7. Найти расстояние от точки $(-1,2,1)$ до прямой $\langle 1,1,1\rangle + t\langle 2,3,-1\rangle$.
 Мы снова хотим расстояния
измеряется перпендикулярно линии, как показано на
рисунок 12.5.4. Желаемое расстояние равно
$$
|\overrightarrow{\ распорка QP}|\sin\theta=
{|\overrightarrow{\strut QP}\times{\bf A}|\over|{\bf A}|},
$$
где $\bf A$ — любой вектор, параллельный прямой. Из уравнения
линии, мы можем использовать $Q=(1,1,1)$ и ${\bf A}=\langle 2,3,-1\rangle$, поэтому
расстояние
$$
{|\langle -2,1,0\rangle\times\langle2,3,-1\rangle|\over\sqrt{14}}=
{|\langle-1,-2,-8\rangle|\over\sqrt{14}}={\sqrt{69}\over\sqrt{14}}.
$$
$\квадрат$
Мы снова хотим расстояния
измеряется перпендикулярно линии, как показано на
рисунок 12.5.4. Желаемое расстояние равно
$$
|\overrightarrow{\ распорка QP}|\sin\theta=
{|\overrightarrow{\strut QP}\times{\bf A}|\over|{\bf A}|},
$$
где $\bf A$ — любой вектор, параллельный прямой. Из уравнения
линии, мы можем использовать $Q=(1,1,1)$ и ${\bf A}=\langle 2,3,-1\rangle$, поэтому
расстояние
$$
{|\langle -2,1,0\rangle\times\langle2,3,-1\rangle|\over\sqrt{14}}=
{|\langle-1,-2,-8\rangle|\over\sqrt{14}}={\sqrt{69}\over\sqrt{14}}.
$$
$\квадрат$Рисунок 12.5.4. Расстояние от точки до прямой.
Вы можете использовать Sage для вычисления расстояний до линий и плоскостей, так как это просто включает векторную арифметику, которую мы уже видели. Конечно, вы также можете использовать Sage для выполнения некоторых вычислений, связанных с нахождение уравнений плоскостей и прямых.
Пример 12.5.1 Найдите уравнение плоскости, содержащее $(6,2,1)$ и перпендикулярно $\langle 1,1,1\rangle$.
 (отвечать)
(отвечать)Пример 12.5.2 Найдите уравнение плоскости, содержащее $(-1,2,-3)$ и перпендикулярно $\langle 4,5,-1\rangle$. (отвечать)
Пример 12.5.3 Найдите уравнение плоскости, содержащее $(1,2,-3)$, $(0,1,-2)$ и $(1,2,-2)$. (отвечать)
Пример 12.5.4 Найдите уравнение плоскости, содержащее $(1,0,0)$, $(4,2,0)$ и $(3,2,1)$. (отвечать)
Пример 12.5.5 Найдите уравнение плоскости, содержащее $(1,0,0)$ и строка $\langle 1,0,2\rangle + t\langle 3,2,1\rangle$. (отвечать)
Пример 12.5.6 Найдите уравнение плоскости, содержащей прямую пересечение $x+y+z=1$ и $x-y+2z=2$ и перпендикулярно плоскость $2x+3y-z=4$. (отвечать)
Пример 12.5.7 Найдите уравнение плоскости, содержащей прямую пересечение $x+2y-z=3$ и $3x-y+4z=7$ и перпендикулярно плоскость $6x-y+3z=16$. (отвечать)
Пример 12.5.8 Найдите уравнение плоскости, содержащей прямую пересечение $x+3y-z=6$ и $2x+2y-3z=8$ и перпендикулярно плоскость $3x+y-z=11$.
 (отвечать)
(отвечать)Пример 12.5.9 Найдите уравнение прямой через $(1,0,3)$ и $(1,2,4)$. (отвечать)
Пример 12.5.10 Найдите уравнение прямой через $(1,0,3)$ и перпендикулярно плоскости $x+2y-z=1$. (отвечать)
Пример 12.5.11 Найдите уравнение прямой, проходящей через начало координат и перпендикулярно плоскости $x+y-z=2$. (отвечать)
Пример 12.5.12 Найдите $a$ и $c$ так, чтобы $(a,1,c)$ лежало на прямой, проходящей через $(0,2,3)$ и $(2,7,5)$. (отвечать)
Пример 12.5.13 Объясните, как найти решение в пример 12.5.5.
Пример 12.5.14 Определить, являются ли строки $\langle 1,3,-1\rangle+t\langle 1,1,0\rangle$ и $\langle 0,0,0\rangle+t\langle 1,4,5\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.15 Определить, являются ли строки $\langle 1,0,2\rangle+t\langle -1,-1,2\rangle$ и $\langle 4,4,2\rangle+t\langle 2,2,-4\rangle$ параллельны, пересекаются или ни то, ни другое.
 (отвечать)
(отвечать)Пример 12.5.16 Определить, являются ли строки $\langle 1,2,-1\rangle+t\langle 1,2,3\rangle$ и $\langle 1,0,1\rangle+t\langle 2/3,2,4/3\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.17 Определить, являются ли строки $\langle 1,1,2\rangle+t\langle 1,2,-3\rangle$ и $\langle 2,3,-1\rangle+t\langle 2,4,-6\rangle$ параллельны, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.18 Найдите единичный вектор нормали к каждой из координатных плоскостей.
Пример 12.5.19 Покажите, что $\langle 2,1,3 \rangle + t \langle 1,1,2 \rangle$ и $\langle 3, 2, 5 \rangle + s \langle 2, 2, 4 \rangle$ одинаковы линия.
Пример 12.5.20 Дайте краткое описание каждого из следующих процессов:
а. Даны две различные точки, найти прямую, которая проходит через них.
б. Даны три точки (не все на одной прямой), найдите плоскость что проходит через них. Зачем нужна оговорка, что не все точки лежат на одной прямой?
в.
 Даны прямая и точка, не лежащие на этой прямой, найти плоскость, на которой
содержит их обоих.
Даны прямая и точка, не лежащие на этой прямой, найти плоскость, на которой
содержит их обоих.д. Даны плоскость и точка, не лежащие на плоскости, найти прямую, перпендикулярен плоскости, проходящей через данную точку.
Пример 12.5.21 Найдите расстояние от $(2,2,2)$ до $x+y+z=-1$. (отвечать)
Пример 12.5.22 Найдите расстояние от $(2,-1,-1)$ до $2x-3y+z=2$. (отвечать)
Пример 12.5.23 Найдите расстояние от $(2,-1,1)$ до $\langle 2,2,0\rangle+t\langle 1,2,3\rangle$. (отвечать)
Пример 12.5.24 Найдите расстояние от $(1,0,1)$ до $\langle 3,2,1\rangle+t\langle 2,-1,-2\rangle$. (отвечать)
Пример 12.5.25 Найдите расстояние между линиями $\langle 5,3,1\rangle+t\langle 2,4,3\rangle$ и $\langle 6,1,0\rangle+t\langle 3,5,7\rangle$. (отвечать)
Пример 12.5.26 Найдите расстояние между линиями $\langle 2,1,3\rangle+t\langle -1,2,-3\rangle$ и $\langle 1,-3,4\rangle+t\langle 4,-4,1\rangle$.


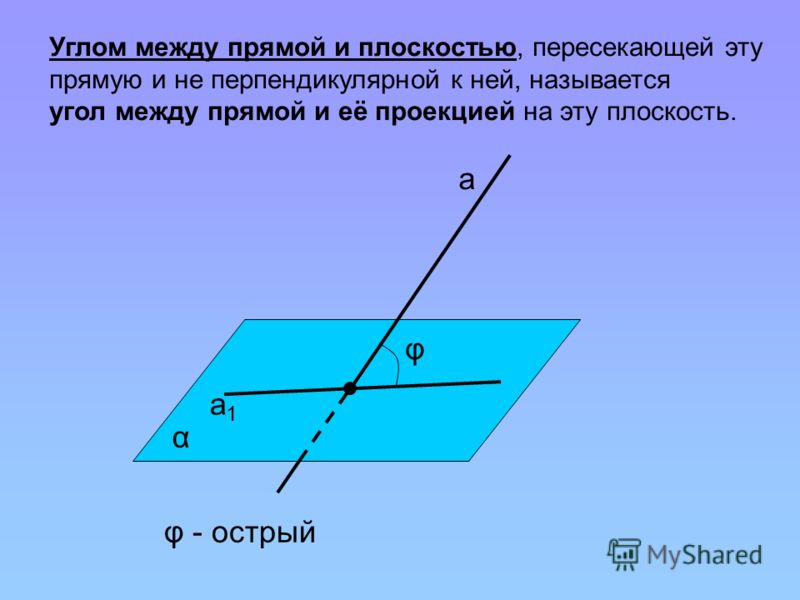 Построим рисунок на плоскости, выделим знакомые элементы. Изобразим плоскость α в виде замкнутой кривой линии. Такой рисунок плоскости, как и любой другой, вполне допустим, так как плоскость не имеет границ.
Построим рисунок на плоскости, выделим знакомые элементы. Изобразим плоскость α в виде замкнутой кривой линии. Такой рисунок плоскости, как и любой другой, вполне допустим, так как плоскость не имеет границ.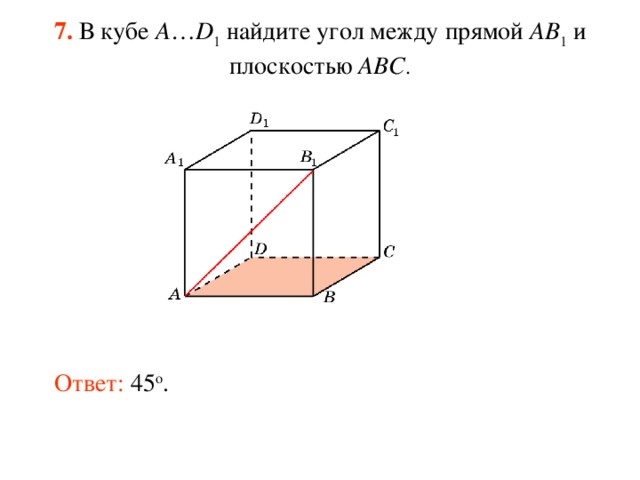
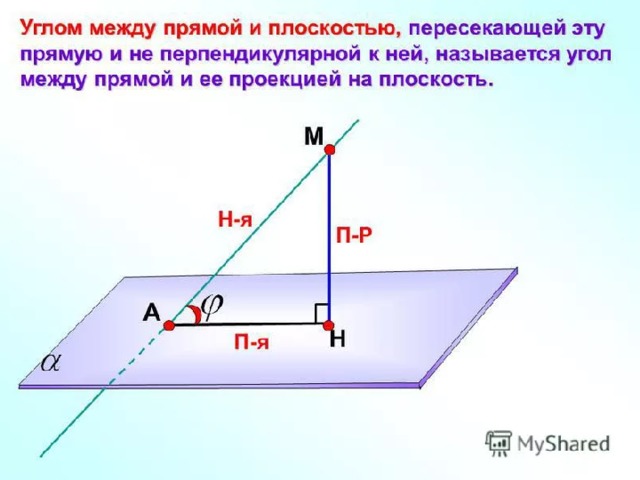


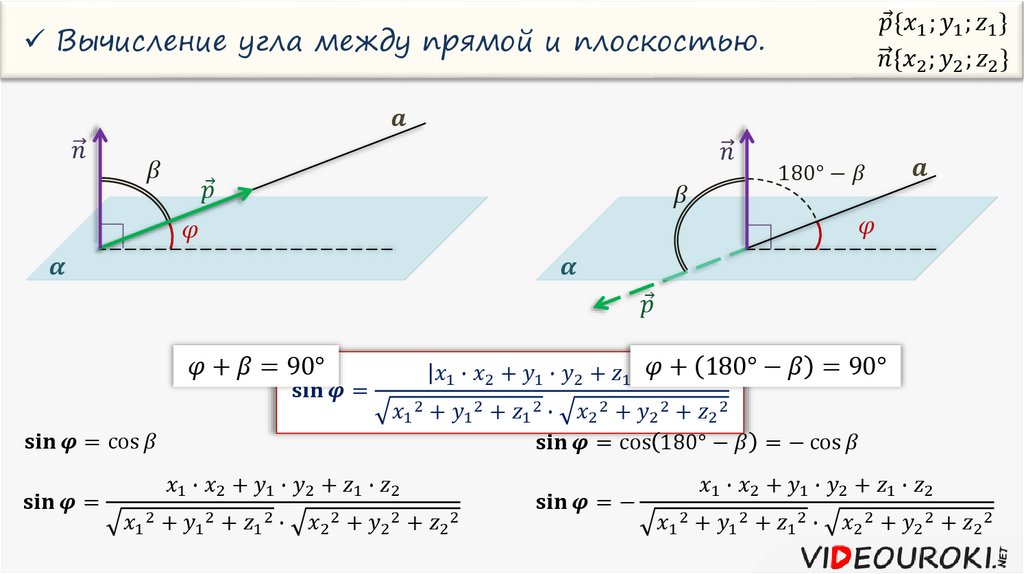 к. М1Н1, М1Н1а1, тогда Н=Н1.
к. М1Н1, М1Н1а1, тогда Н=Н1.
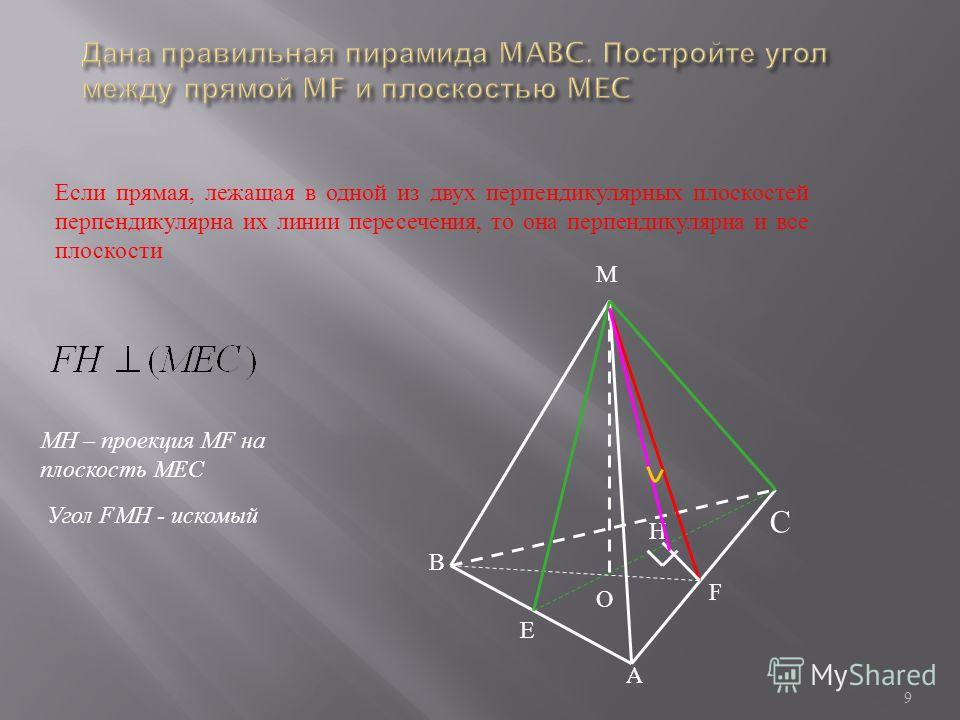
 Сторона АВ равна 1дм. Найдите величину угла между диагональю куба B1D и плоскостью ABC.
Сторона АВ равна 1дм. Найдите величину угла между диагональю куба B1D и плоскостью ABC. Найдите величину угла между диагональю куба B1D и плоскостью ABC.
Найдите величину угла между диагональю куба B1D и плоскостью ABC.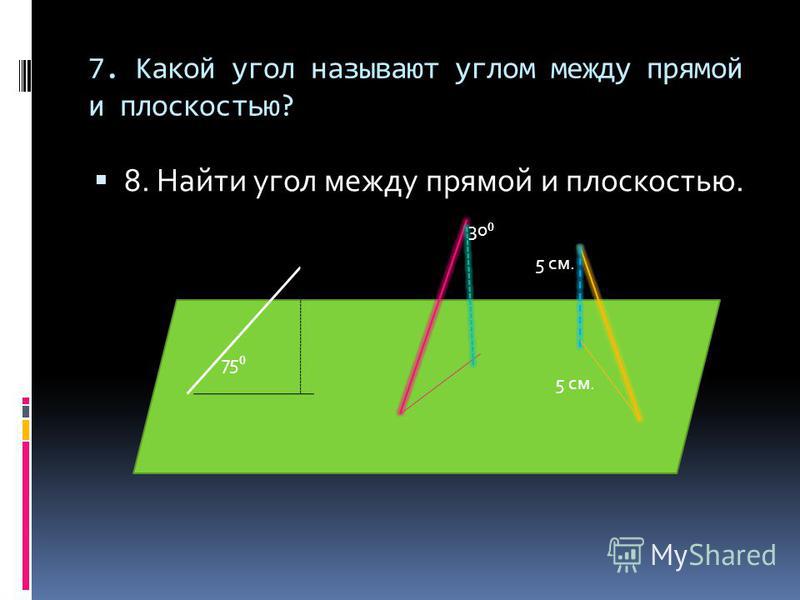
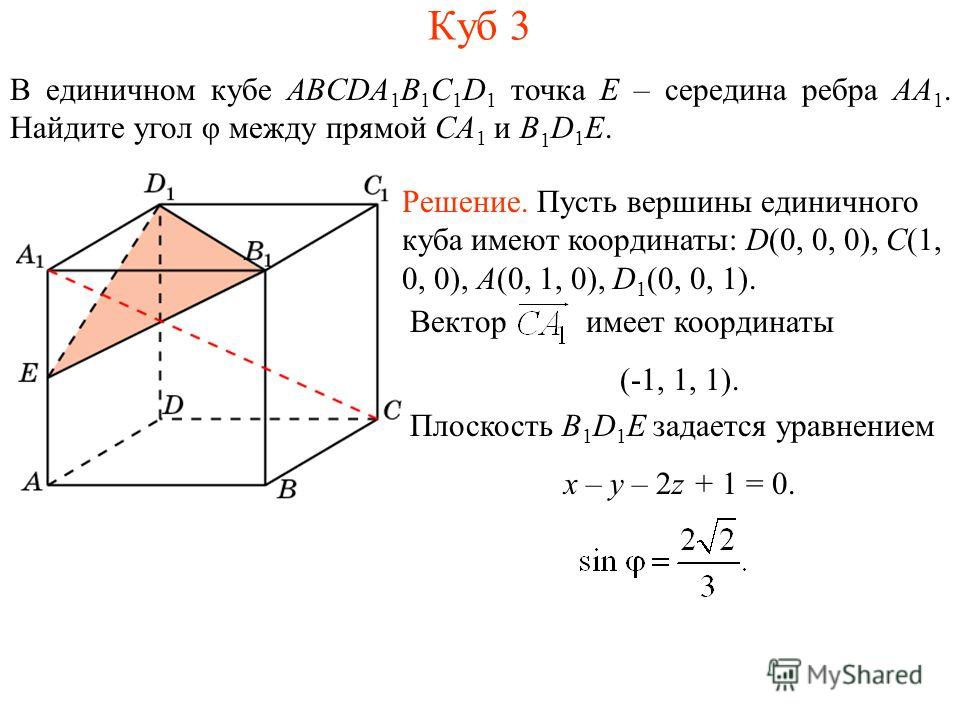

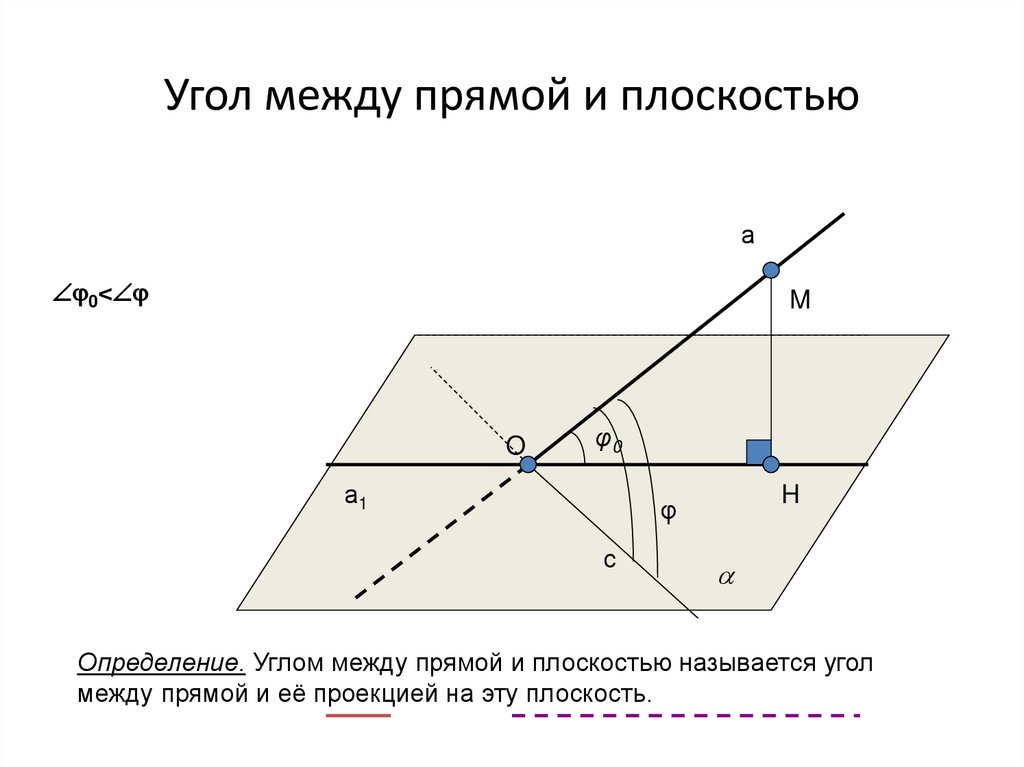 {-1} \frac{\sqrt{42}}{7}\end{выровнено}\) 9{\circ}\end{выровнено}\)
{-1} \frac{\sqrt{42}}{7}\end{выровнено}\) 9{\circ}\end{выровнено}\)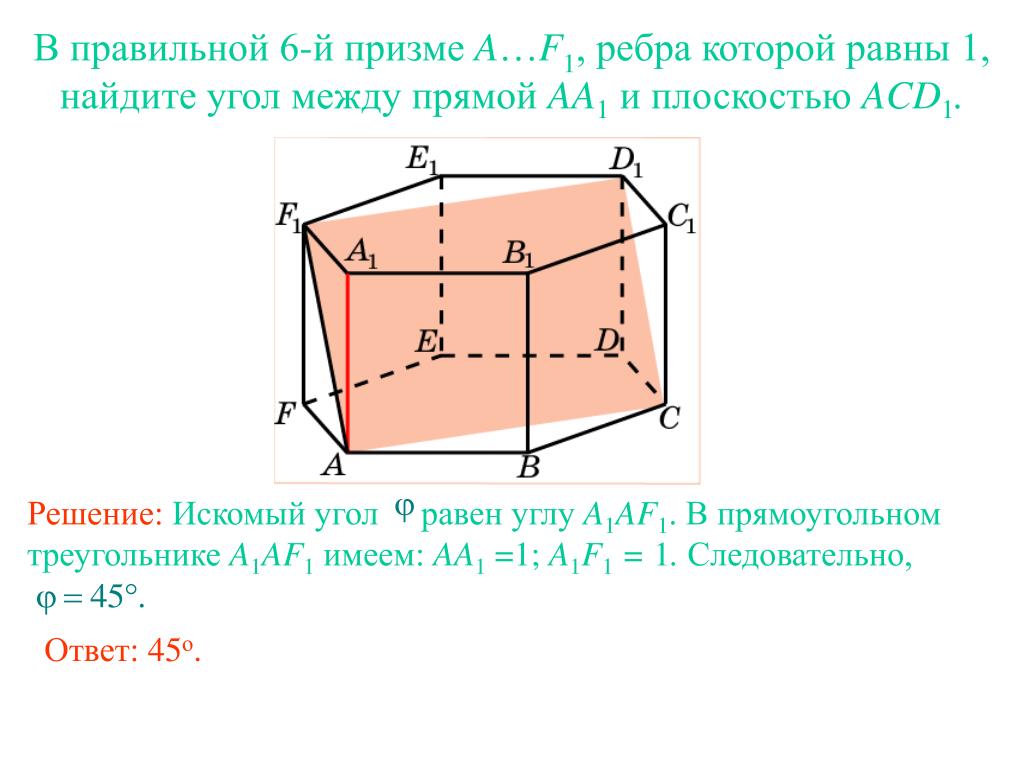
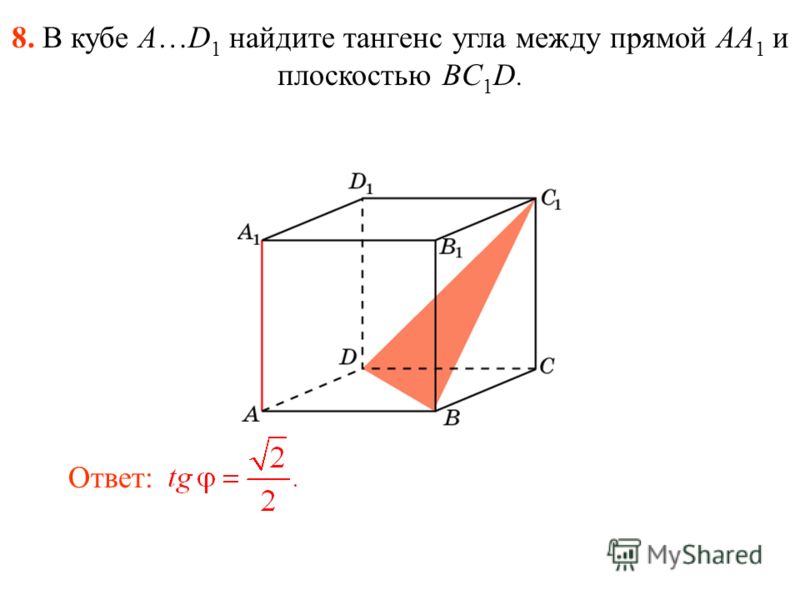 \circ \end{массив}$$$
\circ \end{массив}$$$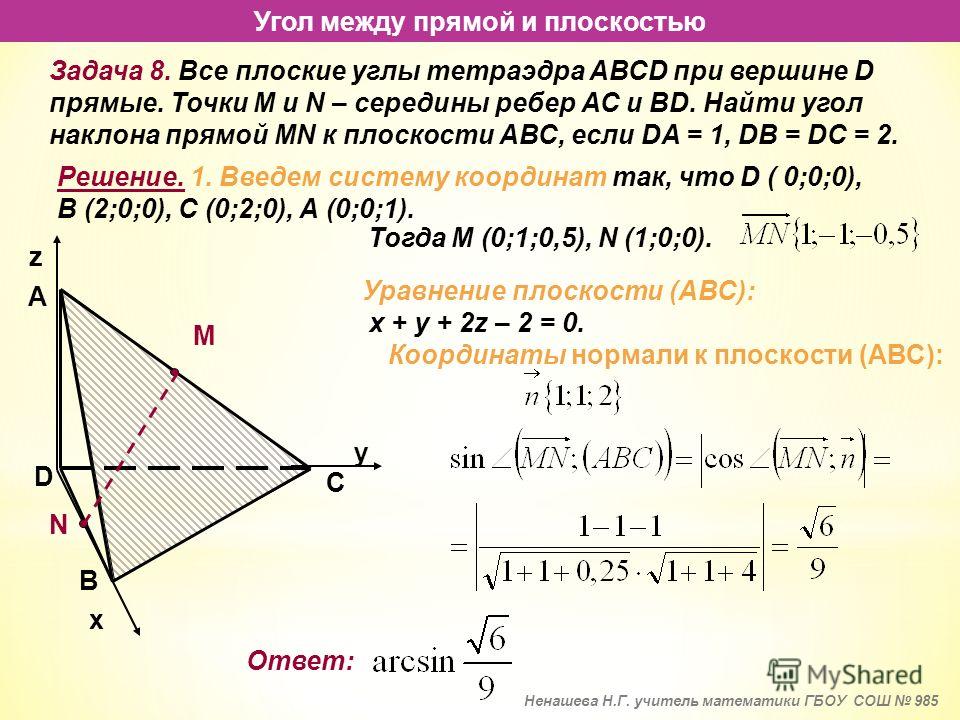 В результате любой вектор, перпендикулярный плоскости,
перпендикулярно $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$. На самом деле, это
Легко видеть, что плоскость состоит из ровно тех точек
$\ds (w_1,w_2,w_3)$, для которых $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$ равно
перпендикулярно нормали к плоскости, как показано на
рисунок 12.5.1. То есть предположим
мы знаем, что $\langle a,b,c\rangle$ нормальна к плоскости, содержащей
точка $\ds (v_1,v_2,v_3)$. Тогда $(x,y,z)$ лежит в плоскости тогда и только тогда
если $\langle a,b,c\rangle$ перпендикулярно $\ds \langle
x-v_1,y-v_2,z-v_3\rangle$. В свою очередь, мы знаем, что это правда
именно тогда, когда $\ds \langle a,b,c\rangle\cdot\langle
x-v_1,y-v_2,z-v_3\rangle=0$. Таким образом, $(x,y,z)$ лежит в плоскости, если и
только если
$$\выравнивание{
\langle a,b,c\rangle\cdot\langle x-v_1,y-v_2,z-v_3\rangle&=0\cr
a(x-v_1)+b(y-v_2)+c(z-v_3)&=0\cr
топор+by+cz-av_1-bv_2-cv_3&=0\cr
топор+by+cz&=av_1+bv_2+cv_3.\cr
}$$
Работая в обратном направлении, обратите внимание, что если $(x,y,z)$ — точка, удовлетворяющая
$ax+by+cz=d$ тогда
$$\выравнивание{
топор+by+cz&=d\cr
топор+by+cz-d&=0\cr
a(x-d/a)+b(y-0)+c(z-0)&=0\cr
\langle a,b,c\rangle\cdot\langle x-d/a,y,z\rangle&=0.
В результате любой вектор, перпендикулярный плоскости,
перпендикулярно $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$. На самом деле, это
Легко видеть, что плоскость состоит из ровно тех точек
$\ds (w_1,w_2,w_3)$, для которых $\ds \langle w_1-v_1,w_2-v_2,w_3-v_3\rangle$ равно
перпендикулярно нормали к плоскости, как показано на
рисунок 12.5.1. То есть предположим
мы знаем, что $\langle a,b,c\rangle$ нормальна к плоскости, содержащей
точка $\ds (v_1,v_2,v_3)$. Тогда $(x,y,z)$ лежит в плоскости тогда и только тогда
если $\langle a,b,c\rangle$ перпендикулярно $\ds \langle
x-v_1,y-v_2,z-v_3\rangle$. В свою очередь, мы знаем, что это правда
именно тогда, когда $\ds \langle a,b,c\rangle\cdot\langle
x-v_1,y-v_2,z-v_3\rangle=0$. Таким образом, $(x,y,z)$ лежит в плоскости, если и
только если
$$\выравнивание{
\langle a,b,c\rangle\cdot\langle x-v_1,y-v_2,z-v_3\rangle&=0\cr
a(x-v_1)+b(y-v_2)+c(z-v_3)&=0\cr
топор+by+cz-av_1-bv_2-cv_3&=0\cr
топор+by+cz&=av_1+bv_2+cv_3.\cr
}$$
Работая в обратном направлении, обратите внимание, что если $(x,y,z)$ — точка, удовлетворяющая
$ax+by+cz=d$ тогда
$$\выравнивание{
топор+by+cz&=d\cr
топор+by+cz-d&=0\cr
a(x-d/a)+b(y-0)+c(z-0)&=0\cr
\langle a,b,c\rangle\cdot\langle x-d/a,y,z\rangle&=0. \cr
}$$
А именно, $\langle a,b,c\rangle$ перпендикулярен вектору с
хвост в $(d/a,0,0)$ и голова в $(x,y,z)$. Это означает, что точки
$(x,y,z)$, удовлетворяющие уравнению $ax+by+cz=d$, образуют плоскость
перпендикулярно $\langle a,b,c\rangle$. (Это не
работать, если $a=0$, но в этом случае мы можем использовать $b$ или $c$ в роли
$а$. То есть либо $a(x-0)+b(y-d/b)+c(z-0)=0$, либо
$a(x-0)+b(y-0)+c(z-d/c)=0$.)
\cr
}$$
А именно, $\langle a,b,c\rangle$ перпендикулярен вектору с
хвост в $(d/a,0,0)$ и голова в $(x,y,z)$. Это означает, что точки
$(x,y,z)$, удовлетворяющие уравнению $ax+by+cz=d$, образуют плоскость
перпендикулярно $\langle a,b,c\rangle$. (Это не
работать, если $a=0$, но в этом случае мы можем использовать $b$ или $c$ в роли
$а$. То есть либо $a(x-0)+b(y-d/b)+c(z-0)=0$, либо
$a(x-0)+b(y-0)+c(z-d/c)=0$.) Мы могли бы также записать это просто как $(x-5)+2(y)+3(z-7)=0$, что для
много целей прекрасное представление; всегда можно умножить
чтобы получить $x+2y+3z=26$.
$\квадрат$
Мы могли бы также записать это просто как $(x-5)+2(y)+3(z-7)=0$, что для
много целей прекрасное представление; всегда можно умножить
чтобы получить $x+2y+3z=26$.
$\квадрат$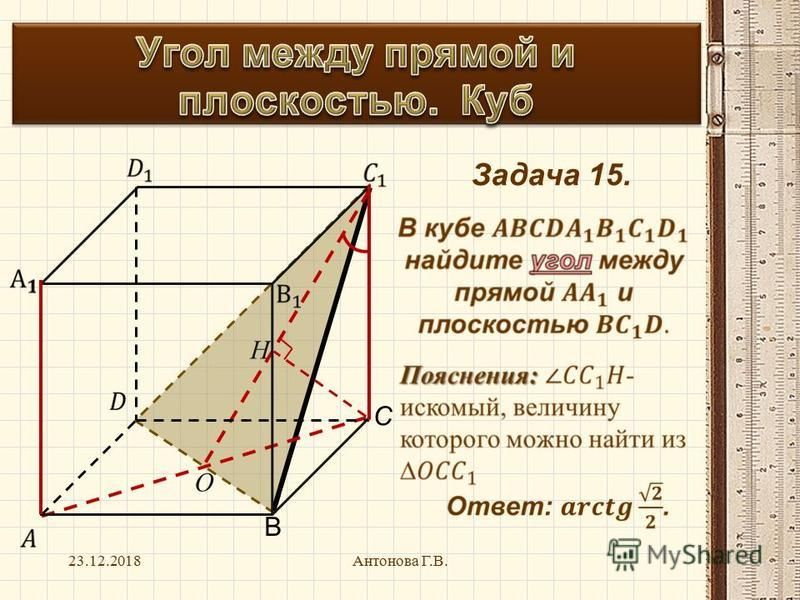 Таким образом, мы ищем вектор $\langle
a,b,c\rangle$, то есть
перпендикулярно $\langle 1,1,-2\rangle$. Кроме того, поскольку
желаемая плоскость должна содержать определенную линию, $\langle
a,b,c\rangle$ должны быть перпендикулярны любому вектору, параллельному этому
линия. Так как $\langle
a,b,c\rangle$ должны быть перпендикулярны двум векторам, мы можем найти это по
вычисление перекрестного произведения двух. Итак, нам нужен вектор, параллельный
к линии пересечения данных плоскостей. Для этого достаточно
знать две точки на прямой. Чтобы найти две точки на этой прямой,
необходимо найти две точки, находящиеся одновременно на двух плоскостях,
$x-z=1$ и $y+2z=3$. Любая точка на обеих плоскостях будет удовлетворять
$x-z=1$ и $y+2z=3$. Легко найти значения для $x$ и $z$
удовлетворяющие первому, такие как $x=1, z=0$ и $x=2, z=1$. затем
мы можем найти соответствующие значения для $y$, используя второе уравнение,
а именно $y=3$ и $y=1$, поэтому
$(1,3,0)$ и $(2,1,1)$ находятся на прямой
пересечения, потому что оба находятся в обеих плоскостях.
Таким образом, мы ищем вектор $\langle
a,b,c\rangle$, то есть
перпендикулярно $\langle 1,1,-2\rangle$. Кроме того, поскольку
желаемая плоскость должна содержать определенную линию, $\langle
a,b,c\rangle$ должны быть перпендикулярны любому вектору, параллельному этому
линия. Так как $\langle
a,b,c\rangle$ должны быть перпендикулярны двум векторам, мы можем найти это по
вычисление перекрестного произведения двух. Итак, нам нужен вектор, параллельный
к линии пересечения данных плоскостей. Для этого достаточно
знать две точки на прямой. Чтобы найти две точки на этой прямой,
необходимо найти две точки, находящиеся одновременно на двух плоскостях,
$x-z=1$ и $y+2z=3$. Любая точка на обеих плоскостях будет удовлетворять
$x-z=1$ и $y+2z=3$. Легко найти значения для $x$ и $z$
удовлетворяющие первому, такие как $x=1, z=0$ и $x=2, z=1$. затем
мы можем найти соответствующие значения для $y$, используя второе уравнение,
а именно $y=3$ и $y=1$, поэтому
$(1,3,0)$ и $(2,1,1)$ находятся на прямой
пересечения, потому что оба находятся в обеих плоскостях.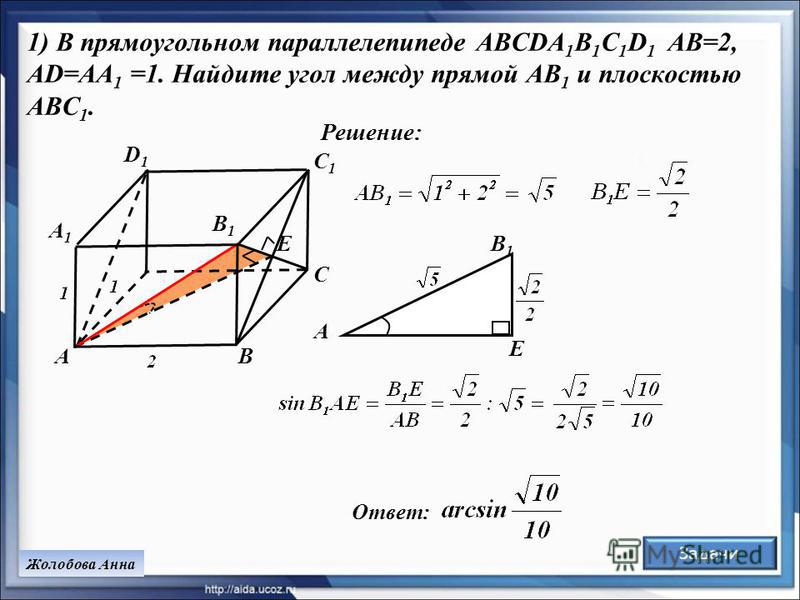 В настоящее время
$\langle 2-1,1-3,1-0\rangle=\langle 1,-2,1\rangle$ параллелен
линия. Наконец, мы можем выбрать $\langle a,b,c\rangle=\langle
1,1,-2\rangle\times \langle 1,-2,1\rangle=\langle -3,-3,-3\rangle$.
Хотя этот вектор прекрасно подойдет, любой вектор, параллельный или
антипараллельное к нему также будет работать, поэтому, например, мы могли бы выбрать
$\langle 1,1,1\rangle$, который ему антипараллелен.
В настоящее время
$\langle 2-1,1-3,1-0\rangle=\langle 1,-2,1\rangle$ параллелен
линия. Наконец, мы можем выбрать $\langle a,b,c\rangle=\langle
1,1,-2\rangle\times \langle 1,-2,1\rangle=\langle -3,-3,-3\rangle$.
Хотя этот вектор прекрасно подойдет, любой вектор, параллельный или
антипараллельное к нему также будет работать, поэтому, например, мы могли бы выбрать
$\langle 1,1,1\rangle$, который ему антипараллелен. К сожалению, это оказывается весьма неудобным
представить типичную линию одним уравнением; нам нужно подойти
линии по-другому.
К сожалению, это оказывается весьма неудобным
представить типичную линию одним уравнением; нам нужно подойти
линии по-другому. Мы можем добраться до через любые точек на линии, делая то же самое, за исключением использования
$t\langle a,b,c\rangle$ вместо $\langle a,b,c\rangle$, где $t$
некоторое действительное число. Из-за того, как работает сложение векторов,
точка в начале вектора $t\langle a,b,c\rangle$ — это точка
в начале вектора $\ds\langle v_1,v_2,v_3\rangle+t\langle
a,b,c\rangle$, а именно $\ds (v_1+ta,v_2+tb,v_3+tc)$; видеть
рисунок 12.5.2.
Мы можем добраться до через любые точек на линии, делая то же самое, за исключением использования
$t\langle a,b,c\rangle$ вместо $\langle a,b,c\rangle$, где $t$
некоторое действительное число. Из-за того, как работает сложение векторов,
точка в начале вектора $t\langle a,b,c\rangle$ — это точка
в начале вектора $\ds\langle v_1,v_2,v_3\rangle+t\langle
a,b,c\rangle$, а именно $\ds (v_1+ta,v_2+tb,v_3+tc)$; видеть
рисунок 12.5.2.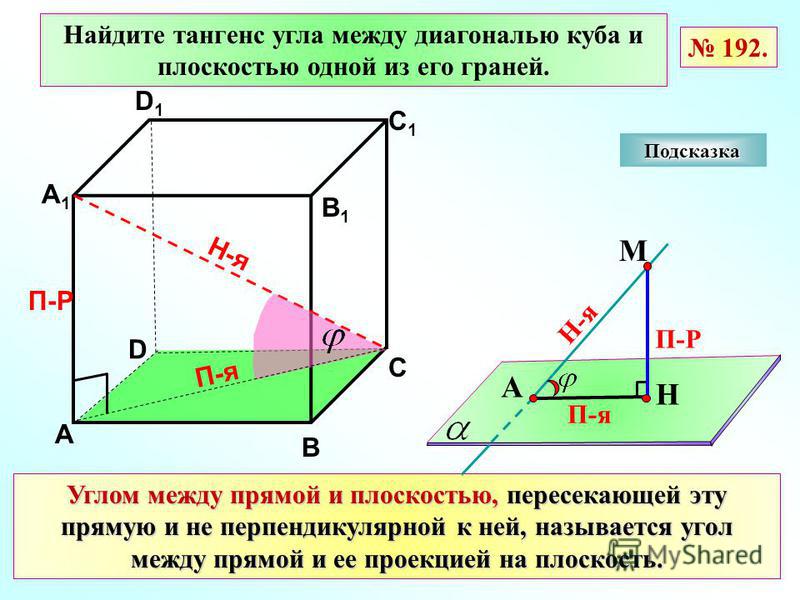
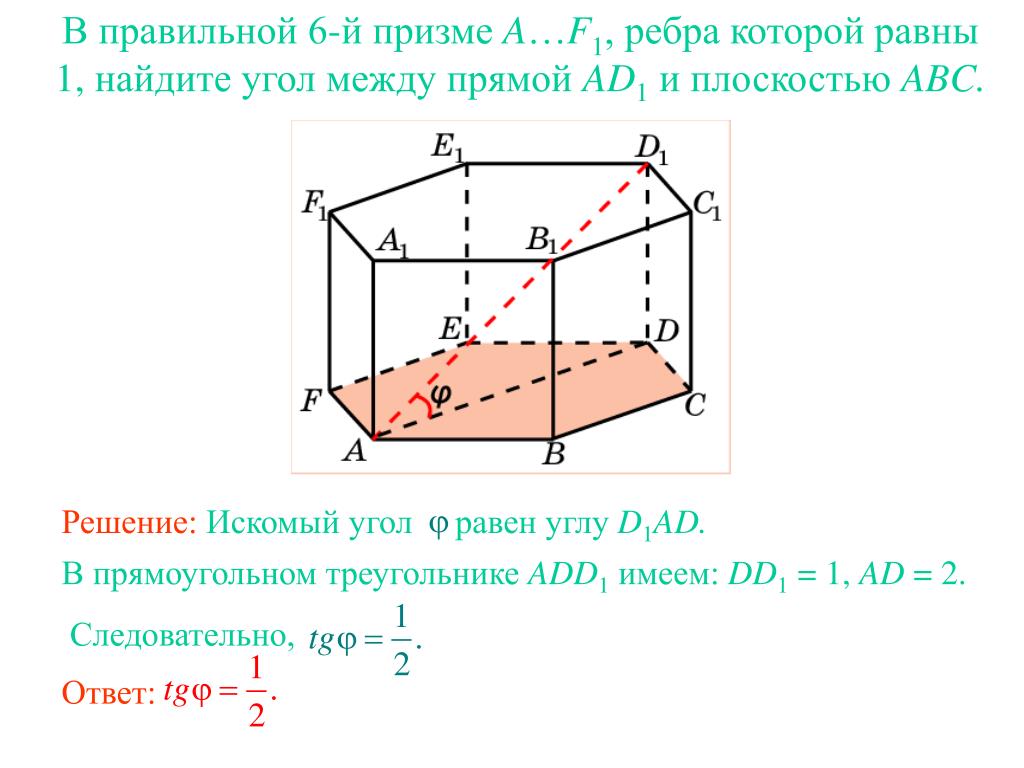 решение в общем. В этом случае легко обнаружить, что $a=3$
и $b=-1$ удовлетворяет всем трем уравнениям, поэтому прямые пересекаются в
точка $(4,7,-2)$.
$\квадрат$
решение в общем. В этом случае легко обнаружить, что $a=3$
и $b=-1$ удовлетворяет всем трем уравнениям, поэтому прямые пересекаются в
точка $(4,7,-2)$.
$\квадрат$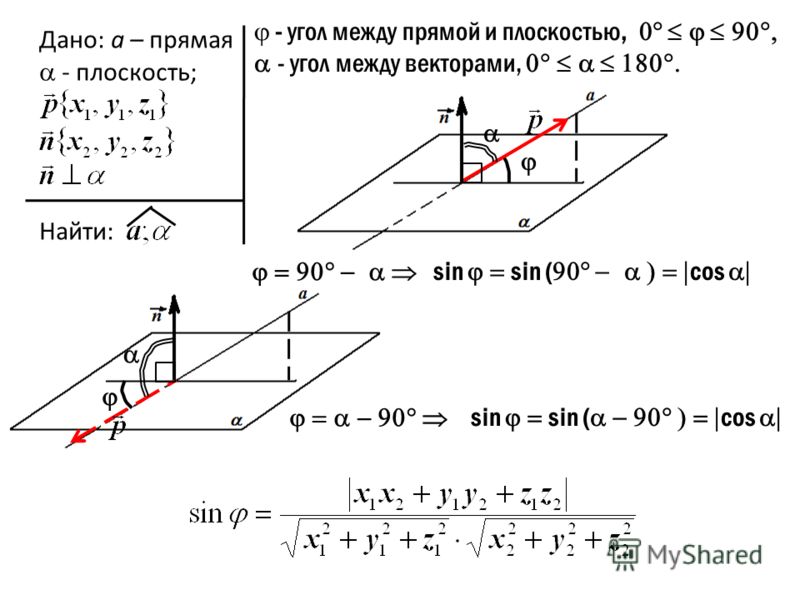 Мы снова хотим расстояния
измеряется перпендикулярно линии, как показано на
рисунок 12.5.4. Желаемое расстояние равно
$$
|\overrightarrow{\ распорка QP}|\sin\theta=
{|\overrightarrow{\strut QP}\times{\bf A}|\over|{\bf A}|},
$$
где $\bf A$ — любой вектор, параллельный прямой. Из уравнения
линии, мы можем использовать $Q=(1,1,1)$ и ${\bf A}=\langle 2,3,-1\rangle$, поэтому
расстояние
$$
{|\langle -2,1,0\rangle\times\langle2,3,-1\rangle|\over\sqrt{14}}=
{|\langle-1,-2,-8\rangle|\over\sqrt{14}}={\sqrt{69}\over\sqrt{14}}.
$$
$\квадрат$
Мы снова хотим расстояния
измеряется перпендикулярно линии, как показано на
рисунок 12.5.4. Желаемое расстояние равно
$$
|\overrightarrow{\ распорка QP}|\sin\theta=
{|\overrightarrow{\strut QP}\times{\bf A}|\over|{\bf A}|},
$$
где $\bf A$ — любой вектор, параллельный прямой. Из уравнения
линии, мы можем использовать $Q=(1,1,1)$ и ${\bf A}=\langle 2,3,-1\rangle$, поэтому
расстояние
$$
{|\langle -2,1,0\rangle\times\langle2,3,-1\rangle|\over\sqrt{14}}=
{|\langle-1,-2,-8\rangle|\over\sqrt{14}}={\sqrt{69}\over\sqrt{14}}.
$$
$\квадрат$ (отвечать)
(отвечать)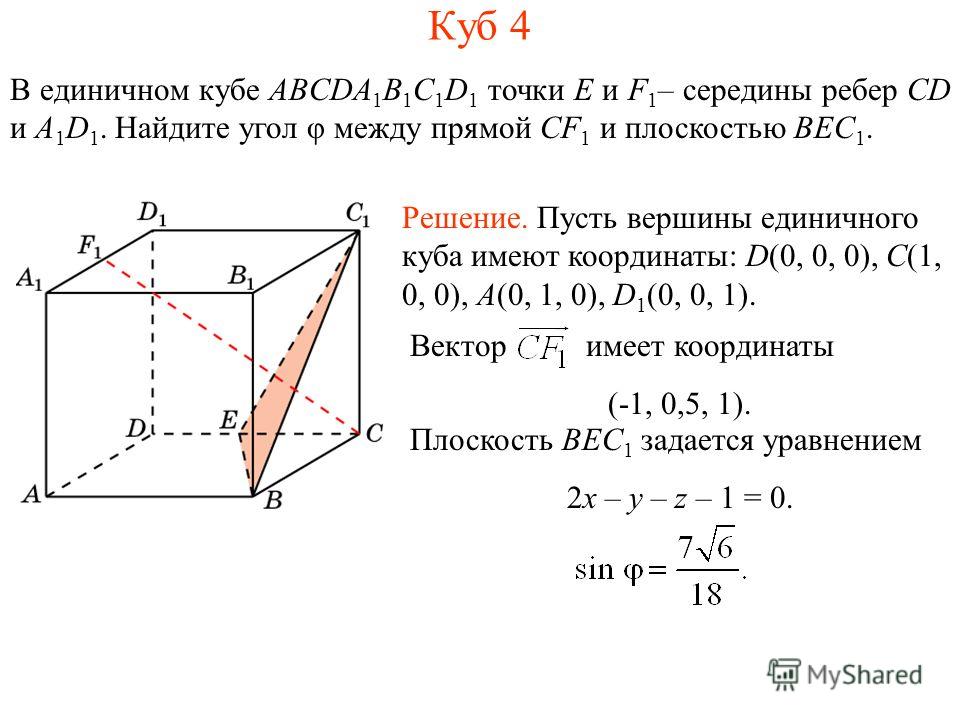 (отвечать)
(отвечать) (отвечать)
(отвечать)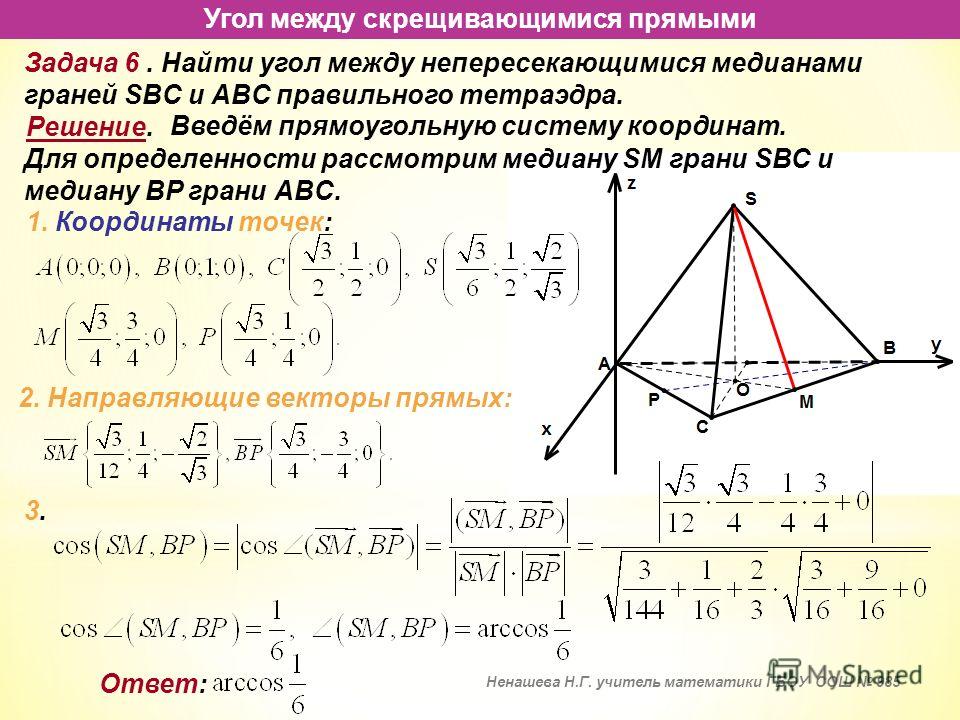 Даны прямая и точка, не лежащие на этой прямой, найти плоскость, на которой
содержит их обоих.
Даны прямая и точка, не лежащие на этой прямой, найти плоскость, на которой
содержит их обоих.