(x+1)-3)=6 2)(2lgx)/(lg(5x-4)… — Учеба и наука Лучший ответ по мнению автора
| |||||||||||||||||
04.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .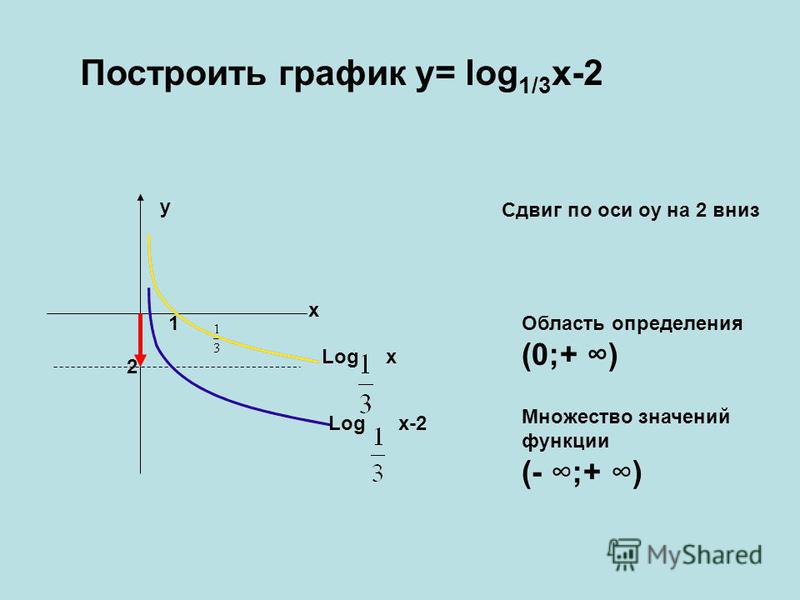
.. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
Решено
в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?
Решено
Вася проехал 3 ч на велосипеде со скоростью 12 км/ч. Отдохнув час, он отправился дальше с прежней скоростью. Спустя 4 ч после старта велосипедиста из того же места ему вдогонку выехал Миша на мотоцикл
Решено
В «Детском мире» продавали двухколесные и трехколесные велосипеды. Коля пересчитал все рули и колеса.Получилось 11 рулей и 29 колес.Сколько трехколесных велосипедов продавали в «Детском мире»?
На рисунке АВ и АС — касательные к окружности с центром О. Найдите длину отрезка АВ, если АС=24 см, а отрезок ВМ в 2 раза больше отрезка СМ.
Пользуйтесь нашим приложением
3-8
решить уравнение log3 (3x-6) = log3 (2x+1)
Хизер Х.
решить уравнение log3 (3x-6) = log3 (2x+1)
Подписаться І 4
Подробнее
Отчет
4 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшийНовыйСтарый
Джордж Т. ответил 01.11.13
Репетитор
Новое в Византе
Джордж Т. — «Все дело в математике!»
Смотрите таких репетиторов
Смотрите таких репетиторов
Хизер:
В этой задаче вас не должен смущать журнал 3 , поскольку мы знаем, что когда журнал 3 a = log 3 b, то очень просто a должно быть равно b. В этой задаче a = 3x-6 и b = 2x+1
SO: 3x-6 = 2x+1
3x-2x = 1+6
1x = 7
x = 7
x = 7
x = 7
Надеюсь, это поможет!
Джордж Т.
Голосовать за 2 Понизить
Подробнее
9Отчет 1810 г.
Вивиан Л. ответил 01.11.13
Репетитор
3 (1)
Microsoft Word/Excel/Outlook, составление эссе, математика; Я ЛЮБЛЮ УЧИТЬ
Смотрите таких репетиторов
Смотрите таких репетиторов
Привет, Хизер;
log 3 (3x-6) = log 3 (2x+1)
Прежде чем я отвечу на этот вопрос, я хотел кратко повторить логарифмы.
Скажем так…
log 3 (3x-6) = 5
Я случайно выбрал число 5.
Это разрешится как…
Видите, как основание 3 переместилось на другую сторону знака = и стало 3, тогда как 5 поднялось до экспоненциального статуса 5 ?
Мне нравится, как Меган описала компоненты как основу, экспоненту и «ответ».
Если она не против, я намерен использовать это в будущих ответах.
В приведенном вами уравнении основание 3 появляется в обеих частях уравнения. Отныне…
log 3 (3x-6) = log 3 (2x+1)
мы можем их отменить.
3x-6=2x+1
Прибавим по 6 к обеим сторонам по мере выделения x…
3x-6+6=2x+1+6
3x=2x+7
2x с обеих сторон…
-2x+3x=2x+7-2x
x=7
Проверим…
(3x-6) ??? (2x+1)
[3(7)-6] ??? [2(7)+1]
21-6 ??? 14+1
15=15
Все хорошо!
Голосовать за 1 Понизить
Подробнее
Отчет
Меган Х. ответил 01.11.13
Репетитор
5,0 (416)
Репетиторство по математике – все классы
Об этом репетиторе ›
Об этом репетиторе ›
Привет, Хизер!
log 3 9=2 —> пример
3 — основание, 2 — показатель степени, а 9 — то, что я называю ответом.
Вы можете переписать это выражение как 3 2 =9, чтобы вы могли это видеть. В выражении, которое у вас есть, оба ваших журнала имеют одинаковую базу 3, и, поскольку они установлены равными друг другу, говорят вам, что они должны иметь одинаковую степень. Следовательно, ответы должны быть равными, поэтому вы можете просто установить 3x-6=2x+1 и найти x.
В этой похожей задаче:
log2(2x-2)=log2(x+1)
2x-2 = x+1 —> установить ответы равными друг другу
x-2=1 —> решить for x
x=3
Удачи!
Голосовать за 1 Понизить
Подробнее
Отчет
Али Дж. ответил 01.11.13
Репетитор
Новое в Византе
Смотрите таких репетиторов
Смотрите таких репетиторов
ккнкм ккмл
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Решение логарифмических уравнений – объяснение и примеры
Как вы хорошо знаете, логарифм – это математическая операция, обратная возведению в степень. Логарифм числа обозначается аббревиатурой «9».1845, журнал ».
Прежде чем мы приступим к решению логарифмических уравнений, давайте ознакомимся со следующими правилами логарифмирования:
- Правило произведения: произведение логарифмов.
Первый закон представлен как;⟹ log b (x) + log b (y) = log b (xy)
- Правило частных:
Разность двух логарифмов x и y равна отношению логарифмов.
⟹ log b (x) – log b (y) = log (x/y)
- Степенное правило:
⟹ log b 1x 9184 log b (x)
- Изменение базового правила.
⟹ log b x = (log a x) / (log a b)
- Правило идентификации
Логарифм любого положительного числа по тому же основанию этого числа всегда равен 1.
b 1 =b ⟹ log b (b)=1.Пример:
- Логарифм числа 1 по любому ненулевому основанию всегда равен нулю.
b 0 =1 ⟹ log b 1 = 0.
Уравнение, в показателях которого стоят переменные, называется показательным уравнением.
Напротив, уравнение, включающее логарифм выражения, содержащего переменную, называется логарифмическим уравнением.Целью решения логарифмического уравнения является нахождение значения неизвестной переменной.
В этой статье мы узнаем, как решать общие два типа логарифмических уравнений, а именно:
- Уравнения, содержащие логарифмы на одной стороне уравнения.
- Уравнения с логарифмами по разные стороны от знака равенства.
Как решать уравнения с логарифмами на одной стороне?
Уравнения с логарифмами на одной стороне занимают журнал б М = п ⇒ М = б п .
Чтобы решить этот тип уравнений, выполните следующие шаги:
- Упростите логарифмические уравнения, применяя соответствующие законы логарифмирования.
- Перепишите логарифмическое уравнение в экспоненциальной форме.
- Теперь упростите показатель степени и найдите переменную.
- Проверьте свой ответ, подставив его обратно в логарифмическое уравнение. Следует отметить, что приемлемый ответ логарифмического уравнения дает только положительный аргумент.
Пример 1
Решение log 2 (5x + 7) = 5
Раствор
ПЕРЕДАЧА. СВЯЗАЯ СОВЕТА. 2 5 = 5x + 7
⇒ 32 = 5x + 7
⇒ 5x = 32 — 7
5x = 25
Разделение обеих сторон на 5 до получения
x = 5
181818
88 4184181212x = 5
11818
841812
x = 5
111818
x = 5
111818
.
Найдите x в log (5x -11) = 2
Решение
Поскольку основание этого уравнения не дано, мы предполагаем основание 10.
Теперь измените логарифм в экспоненциальной форме.
⇒ 10 2 = 5x – 11
⇒ 100 = 5x -11
111= 5x
111/5 = x
Следовательно, x = 11.
Пример 3
Лог решения 10 (2x + 1) = 3
Решение
Перепишите уравнение в экспоненциальной форме
log 10 (2x + 1) = 3N порядка 2x + 1 = 10 3
⇒ 2x + 1 = 1000
2x = 999
1111111112
2x = 999
111111111111111111111111111111.
, мы получаем;x = 499,5
Проверьте свой ответ, подставив его в исходное логарифмическое уравнение;
⇒ log 10 (2 x 499,5 + 1) = log 10 (1000) = 3 с 10 3 = 1000
8
812Вычислить ln (4x -1) = 3
Решение
Переписать уравнение в экспоненциальной форме как;
ln (4x -1) = 3 ⇒ 4x – 3 =e 3
But as you know, e = 2.718281828
4x – 3 = (2.718281828) 3 = 20.085537
x = 5.271384
Пример 52215
Сначала упростите логарифмы, применив правило отношения, как показано ниже.
log 2 (x +1) – log 2 (x – 4) = 3 ⇒ log 2 [(x + 1)/ (x – 4)] = 3
Теперь перепишем уравнение в экспоненциальной форме
⇒ 2 3 = [(x + 1)/ (x – 4)]
⇒ 8 = [(x + 1)/ (x – 4)]
Перемножить уравнение
⇒ [(x + 1) = 8(x – 4)]
⇒ x + 1 = 8x -32
7x = 33 …… (собирая подобные члены)
x = 33/7
Example 6
Solve for x if log 4 (x) + log 4 (x -12) = 3
Solution
Simplify the logarithm с помощью правила продукта следующим образом;
log 4 (x) + log 4 (x -12) = 3 ⇒ log 4 [(x) (x — 12)] = 3
⇒ log 4 (1x 2 – 12x) = 3
Преобразуйте уравнение в экспоненциальную форму.
⇒ 4 3 = x 2 – 12x
⇒ 64 = x 2 – 12x
x 2 -12x – 64 ⇒ (x + 4) (x – 16) = 0
x = -4 или 16
Подставив x = -4 в исходное уравнение, мы получим отрицательный ответ что воображаемое. Поэтому 16 — единственное приемлемое решение.
Как решать уравнения с логарифмами в обеих частях уравнения?
Уравнения с логарифмами по обе стороны от знака равенства принимают log M = log N, что совпадает с M = N.
Процедура решения уравнений с логарифмами по обе стороны от знака равенства.
- Если логарифмы имеют общее основание, упростите задачу и перепишите ее без логарифмов.
- Упростите, собрав одинаковые члены, и найдите переменную в уравнении.
- Проверьте свой ответ, подставив его обратно в исходное уравнение. Помните, что приемлемый ответ приведет к положительному аргументу.
Пример 7
Решение log 6 (2x — 4) + log 6 ( 4) = log 6 (40)
4141446.
логарифм 6 (2x – 4) + логарифм 6 (4) = логарифм 6 (40) ⇒ логарифм 6 [4(2x – 4)] = логарифм 6 (40)
Теперь отбросьте логарифмы
⇒ [4(2x – 4)] = (40)
⇒ 8x – 16 = 40
⇒ 8x = 40 + 16
8x = 56
x = 7
Пример 8
Решайте логарифмическое уравнение: log 7 (x — 2) + log (logarithmic . ) = log 7 14
Решение
Упростите уравнение, применив правило произведения.
Log 7 [(x – 2) (x + 3)] = log 7 14
Отбросить логарифмы.
⇒ [(x – 2) (x + 3)] = 14
Раздайте ФОЛЬГА, чтобы получить;
⇒ х 2 – х – 6 = 14
⇒ х 2 – х – 20 = 0
⇒ (х + 4) (х – 5) = 0
х = -4 или х = -4 5
, когда x = -5 и x = 5 подставляются в исходное уравнение, они дают отрицательный и положительный аргумент соответственно.
Следовательно, x = 5 является единственным приемлемым решением. Пример Решение Учитывая уравнение; log 3 (x 2 + 3x) = log 3 (2x + 6), отбросьте логарифмы, чтобы получить;
⇒ x 2 + 3x = 2x + 6
⇒ x 2 + 3x – 2x – 6 = 0
x 2 + x – 6 = 0……………… (Квадратное уравнение6) получить квадратное уравнение;(x – 2) (x + 3) = 0
x = 2 и x = -3Проверяя оба значения x, мы получаем, что x = 2 является правильным ответом.
Пример 10
Решение log 5 (30x — 10) — 2 = log 5 (x + 6)
Раствор
Log 5 (30x — 2
Log 5 (30x — 2
5 (30x — 2
5 (30x — 2
. 5 (x + 6)
Это уравнение можно переписать как;
⇒ log 5 (30x – 10) – log 5 (x + 6) = 2
Упростим логарифмы
log 5
Преобразуйте логарифм в экспоненциальной форме.
⇒ 5 2 = [(30x – 10)/ (x + 6)]
⇒ 25 = [(30x – 10)/ (x + 6)]
При перекрестном умножении получаем;
⇒ 30x — 10 = 25 (x + 6)
⇒ 30x — 10 = 25x + 150
⇒ 30x — 25x = 150 + 10
⇒ 5x = 160
x = 32
118. ChiliMath
Обычно существует два типа логарифмических уравнений. Внимательно изучите каждый случай, прежде чем приступить к просмотру приведенных ниже рабочих примеров.
- Первый тип выглядит так.
Если у вас есть один логарифм с каждой стороны уравнения с одинаковым основанием, вы можете установить аргументы равными друг другу, а затем решить. Аргументами здесь являются алгебраические выражения, представленные \color{blue}M и \color{red}N.
- Второй тип выглядит так.
Если у вас есть один логарифм на одной стороне уравнения, вы можете выразить его как показательное уравнение и решить его.
Давайте научимся решать логарифмические уравнения, рассмотрев несколько примеров.
Примеры решения логарифмических уравнений
Пример 1: Решите логарифмическое уравнение.
Поскольку мы хотим преобразовать левую часть в одно логарифмическое уравнение, мы должны использовать правило произведения в обратном порядке, чтобы сжать его. Вот правило, если вы забыли.
- Дано
- Применить правило продукта из правил журнала.
- Распределить: \left( {x + 2} \right)\left( 3 \right) = 3x + 6
- Отбросить журналы, установить аргументы (вещи в скобках) равными друг другу.
- Затем решите линейное уравнение. Я знаю, что ты справился с этой частью!
Просто большое предостережение. ВСЕГДА сверяйте решенные значения с исходным логарифмическим уравнением.
Запомните:
- Это МОЖНО для x быть равным 0 или отрицательным.
- Однако НЕ ДОПУСКАЕТСЯ иметь логарифм отрицательного числа или логарифм нуля, 0, при подстановке или вычислении в исходное логарифмическое уравнение.
ВНИМАНИЕ: Логарифм отрицательного числа и логарифм нуля не определены .
{\log _b}\left( {\rm{отрицательное\,\,число}}} \right) = {\rm{undefined}}
{\log _b}\left(0 \right) = {\rm{undefined}}
Давайте проверим наш ответ, чтобы убедиться, что x=7 является допустимым решением. Подставьте его обратно в исходное логарифмическое уравнение и проверьте, дает ли оно верное утверждение.
Да! Поскольку x = 7 проверок, у нас есть решение при \color{blue}x = 7.
Пример 2: Решите логарифмическое уравнение.
Начните с объединения логарифмических выражений слева в один логарифм, используя правило произведения. Мы хотим иметь одно логарифмическое выражение на каждой стороне уравнения. Однако будьте готовы решить квадратное уравнение, так как x будет иметь степень 2.
- Дано
- Применить правило произведения из правил журнала 92} — 2x
- Отбросьте логи, установите аргументы (в скобках) равными друг другу
- Решите квадратное уравнение, используя метод факторинга. Но вам нужно переместить все на одну сторону, заставив противоположную сторону равняться 0.
- Установите каждый коэффициент равным нулю, затем найдите x.
x — 5 = 0 означает, что x = 5
x + 2 = 0 означает, что x = — 2
Таким образом, возможные решения: x = 5 и x = — 2. Не забывайте всегда подставлять возможные решения обратно к исходному логарифмическому уравнению.
Давайте проверим наши возможные ответы x = 5 и x = — 2, если они будут правильными решениями.
После проверки наших значений x мы обнаружили, что x = 5 определенно является решением. Однако x =-2 генерирует отрицательные числа внутри круглых скобок (логарифм нуля и отрицательных чисел не определен), что заставляет нас исключить x =-2 как часть нашего решения.
Таким образом, окончательное решение равно \color{blue}x=5. Мы пренебрегаем x=-2, потому что это лишнее решение.
Пример 3: Решите логарифмическое уравнение.
Это интересная задача. Здесь мы имеем разность логарифмических выражений в обеих частях уравнения. Упростите или сократите журналы с обеих сторон, используя правило частного.
- Дано
- Разница в журналах говорит нам использовать правило частного. Преобразуйте операцию вычитания снаружи в операцию деления внутри круглых скобок. Проделайте это с обеими частями уравнений.
- Я думаю, что мы готовы установить каждый аргумент равным друг другу, так как мы можем уменьшить проблему, чтобы иметь одно логарифмическое выражение на каждой стороне уравнения.
- Отбросьте журналы и установите аргументы (содержание в скобках) равными друг другу. Обратите внимание, что это рациональное уравнение. Один из способов решить эту проблему — получить перекрестный продукт .
- Это выглядит так после получения перекрестного произведения.
- =Упростить обе стороны с помощью Распределяющего свойства. В этот момент мы понимаем, что это просто квадратное уравнение. Тогда ничего страшного. Переместите все в одну сторону, что заставит одну часть уравнения быть равной нулю.
- Это легко вычислить. Теперь установите каждый фактор равным нулю и найдите x.
- Итак, это наши возможные ответы.
Я оставлю вам проверить наши возможные ответы обратно в исходное уравнение журнала. Вы должны убедиться, что \color{blue}x=8 — единственное решение, а x =-3 — нет, поскольку оно создает сценарий, в котором мы пытаемся получить логарифм отрицательного числа. Нехорошо!
Пример 4: Решите логарифмическое уравнение.
Если вы видите «журнал» без явного или письменного основания, предполагается, что оно имеет основание 10. Фактически, логарифм с основанием 10 известен как десятичный логарифм .
Нам нужно сжать обе части уравнения в одно логарифмическое выражение. С левой стороны мы видим разницу в журналах, что означает, что мы применяем правило отношения, в то время как справа требуется правило продукта, потому что они представляют собой сумму журналов.
Есть только одна вещь, на которую вы должны обратить внимание с левой стороны. Вы видите этот коэффициент \Large{1 \over 2}\,?
Что ж, мы должны представить его в виде показателя степени, используя правило степени в обратном порядке.
- Дано
- Поднимите этот коэффициент \large{1 \over 2} как показатель степени (обратитесь к крайнему левому члену)
- Упростите показатель степени (по-прежнему ссылаясь на крайний левый член)
- Тогда , уплотните журналы по обе стороны уравнения. Используйте Частное правило слева и Правило произведения справа.
Первый закон представлен как;
Напротив, уравнение, включающее логарифм выражения, содержащего переменную, называется логарифмическим уравнением.
Следует отметить, что приемлемый ответ логарифмического уравнения дает только положительный аргумент.
, мы получаем;
Следовательно, x = 5 является единственным приемлемым решением. Пример Решение 
Но вам нужно переместить все на одну сторону, заставив противоположную сторону равняться 0.
В этот момент мы понимаем, что это просто квадратное уравнение. Тогда ничего страшного. Переместите все в одну сторону, что заставит одну часть уравнения быть равной нулю.
- Здесь я использовал разные цвета, чтобы показать, что, поскольку у нас одно и то же основание (если это не указано явно, предполагается, что оно равно 10), можно установить их равными друг другу.
- Отбрасывание логов и просто приравнивание аргументов внутри скобок.
- На этом этапе вы можете решить рациональное уравнение, выполнив перекрестное произведение. Переместите все члены в одну часть уравнения, а затем вынесите их за скобки.
Переместите все члены в одну часть уравнения, а затем вынесите их за скобки.- Приравняйте каждый множитель к нулю и найдите x.
Пришло время проверить ваши возможные ответы. Когда вы снова проверите x=0 в исходном логарифмическом уравнении, вы получите выражение, которое включает в себя получение логарифма нуля, который не определен, а это означает – нехорошо! Итак, мы должны проигнорировать или отбросить \color{red}x=0 в качестве решения.
Проверка \Large{x = {3 \over 4}} подтверждает, что \Large{\color{blue}{x = {3 \over 4}}} является единственным решением .
Пример 5: Решите логарифмическое уравнение.
Эта проблема связана с использованием символа \ln вместо \log для обозначения логарифма.
Думайте о \ln как о особом виде логарифма, использующем основание e, где e \ приблизительно 2,71828.
- Дано
- Используйте Правило произведения справа
- Сначала запишите переменную, а затем константу, чтобы подготовить метод FOIL.
- Упростите два двучлена, перемножив их вместе.
- В этот момент я просто выделил цветом выражение внутри скобок, чтобы показать, что мы готовы установить их равными друг другу.
- Ага! Здесь мы говорим, что содержимое левой скобки равно содержанию правой скобки.
- Решите квадратное уравнение, используя метод квадратного корня. Вы делаете это, изолируя переменную в квадрате с одной стороны и константу с другой. Затем мы применяем квадратный корень с обеих сторон.
Не забудьте символ \pm .
- Упрощая далее, мы должны получить эти возможные ответы.
Проверьте, являются ли потенциальные ответы, найденные выше, возможными ответами, подставив их обратно в исходные логарифмические уравнения.
Вы должны быть уверены, что ЕДИНСТВЕННОЕ правильное решение — это \large{\color{blue}x = {1 \over 2}}, что делает \large{\color{red}x = -{1 \over 2}} посторонний ответ.
Пример 6: Решите логарифмическое уравнение.
В этом уравнении есть только одно логарифмическое выражение. Мы рассматриваем это как второй случай, когда у нас есть
. Мы преобразуем уравнение из логарифмической формы в экспоненциальную форму, а затем решим его.
- Дано
- Я выделил цветом части логарифмического уравнения, чтобы показать, куда они идут при преобразовании в экспоненциальную форму.
- Синее выражение остается на своем текущем местоположении, но красное число становится показателем степени основания логарифма, равного 3. 94} = 81.
- Завершите вычисление, решив возникающее двухшаговое линейное уравнение.
Вы должны убедиться, что значение \color{blue}x=12 действительно является решением логарифмического уравнения.
Пример 7: Решите логарифмическое уравнение.
Соберите все логарифмические выражения в одной части уравнения (оставьте ее слева) и перенесите константу в правую часть. Используйте правило отношения, чтобы выразить разницу журналов в виде дробей в круглых скобках логарифма.
- Дано
- Переместите все логарифмические выражения влево от уравнения, а константу вправо.
- Используйте правило отношения, чтобы сжать выражения журнала в левой части.
- Приготовьтесь записать логарифмическое уравнение в экспоненциальной форме.
- Синее выражение остается на своем текущем месте, но красная константа оказывается показателем степени основания журнала. {\цвет{красный}1}=5.
- Это рациональное уравнение из-за наличия переменных в числителе и знаменателе.
Я бы решил это уравнение, используя правило перекрестного произведения. Но я должен сначала выразить правую часть уравнения с явным знаменателем 1. То есть 5 = {\large{{5 \over 1}}}
- Выполнить перекрестное умножение, а затем решить полученное линейное уравнение.
Когда вы сверяете x=1 с исходным уравнением, вы должны согласиться с тем, что \large{\color{blue}x=1} является решением логарифмического уравнения.
Пример 8: Решите логарифмическое уравнение.
Эта задача очень похожа на №7. Соберем все логарифмические выражения слева, сохранив константу справа. Поскольку у нас есть разница в журналах, мы будем использовать правило частного.
- Дано
- Переместите выражения журнала в левую часть, а константу оставьте в правой.
- Примените правило частного, так как они являются разницей журналов.
- Здесь я использовал разные цвета, чтобы показать, куда они идут после перезаписи в экспоненциальной форме.
- Обратите внимание, что выражение в скобках остается на своем текущем местоположении, а \color{red}5 становится показателем степени основания.
- Чтобы решить это рациональное уравнение, примените правило перекрестного произведения.
- Упростите правую часть по распределительному свойству. Похоже, мы имеем дело с квадратным уравнением.
- Переместите все в левую сторону и сделайте правую сторону просто нулевой.
Вынесите трехчлен на множители. Установите каждый фактор равным нулю, затем найдите x.
- Когда вы решаете для x, вы должны получить эти значения x как возможные решения.
Убедитесь, что вы проверили возможные ответы из исходного логарифмического уравнения.
Согласитесь, \color{blue}x=-32 — единственное решение. Это делает \color{red}x=4 посторонним решением, так что не обращайте на него внимания.
Пример 9: Решите логарифмическое уравнение
Надеюсь, теперь вы уловили основное представление о том, как решать задачи такого типа. Здесь мы видим три логарифмических выражения и константу. Давайте разделим логарифмические выражения и константу на противоположных сторонах уравнения.
- Давайте сохраним выражения журнала слева, а константу справа.
- Начните с сокращения выражений журнала с помощью правила продукта для обработки суммы журналов.
- Затем еще больше уплотните выражения журнала, используя правило отношения, чтобы справиться с разницей журналов.
- На этом этапе я использовал разные цвета, чтобы показать, что я готов выразить логарифмическое уравнение в его экспоненциальной форме.
- Сохраните выражение внутри символа группировки ( синий ) в том же месте, сделав константу \color{red}1 справа в качестве показателя степени основания 7.
- Решите это рациональное уравнение, используя векторное произведение. Выразите 7 как \large{7 \over 1}.
- Крест умножить.
- Переместите все члены в левую часть уравнения. Вынеси трехчлен. Затем установите каждый фактор равным нулю и найдите x.
- Это ваши возможные ответы. Всегда проверяйте свои значения.
Очевидно, что когда мы снова подставляем x=-8 в исходное уравнение, получается логарифм с отрицательным числом.
Поэтому вы исключаете \color{red}x=-8 как часть своего решения.
Таким образом, единственным решением является \color{blue}x=11.
Пример 10: Решите логарифмическое уравнение.
- Оставьте выражение журнала слева, а все константы переместите справа.
- Упрощение.
- Думаю, мы готовы преобразовать это логарифмическое уравнение в показательное уравнение.
- Выражение в круглых скобках остается на своем текущем местоположении, а константа 3 становится показателем степени логарифмической базы 3. 93}=27. Здесь мы имеем простое радикальное уравнение.
Просмотрите этот отдельный урок, если вам нужно освежить знания о том, как решать различные типы радикальных уравнений.
- Чтобы избавиться от радикального символа в левой части, возведите в квадрат обе части уравнения.
- После возведения обеих сторон в квадрат получается линейное уравнение. Просто решите это как обычно.
Просто решите это как обычно.Верните свой потенциальный ответ в исходное уравнение.
Сделав это, вы должны убедиться, что \color{blue}x=-104 действительно верное решение.
Вы также можете быть заинтересованы в:
Condensing Logarithms
Расширение логаритов
Logarithm объяснил
Logarithm. Решите логарифмические уравнения, включая некоторые сложные вопросы. Представлены подробные решения. Логарифмические уравнения в примерах 4, 5, 6 и 7 включают логарифмы с разными основаниями и поэтому являются сложными.
|
