Калькулятор размера выборки. Какой бывает выборка
Приступить к работе
Скольким участникам следует отправить опрос? Вопрос о размере выборки может поставить в тупик даже специалиста по статистике.
Хотите узнать, как рассчитать размер выборки? Воспользуйтесь нашим калькулятором. В этой статье мы расскажем о том, как получить необходимое количество ответов.
Что представляет из себя размер выборки?
Размер выборки — это количество начатых и завершенных анкет. Слово «выборка» здесь означает то, что оцениваем мы лишь часть из всей совокупности людей, принявших участие в опросе (т. е. целевой совокупности), мнение и поведение которых вас интересует. Выборка бывает разной, в зависимости от выбранных параметров. Например, можно использовать «случайную выборку», в которой респонденты выбираются случайным образом из всей целевой совокупности.
Теперь, когда мы знаем, что означает размер выборки, давайте подробнее изучим следующие темы:
- Возможности интерпретации результатов выборки.

- Формула, по которой рассчитывается размер выборки.
- Почему для опроса важно подобрать правильный размер выборки.
- Насколько важным может быть размер выборки в зависимости от типа опроса.
Каким бывает размер выборки
Для того, чтобы рассчитать необходимый размер выборки для своего опроса, важно иметь представление о следующих трех понятиях.
Объем совокупности — общее количество человек в той группе, которую Вы изучаете. Например, если бы случайной выборкой вашего опроса были жители США, то объем вашей совокупности составил бы 317 миллионов человек. А если бы вы опрашивали сотрудников своей компании, то объем совокупности составил бы общее количество людей в штате вашей организации.
Погрешность — это разница, выраженная в процентах, между результатами, которые вы получите, и фактическими результатами всего объема совокупности. Чем меньше погрешность, тем выше ваши шансы получить достоверный ответ, с учетом выбранной степени достоверности.
Степень достоверности выборки — это величина, выраженная в процентах, которая указывает на степень уверенности, с которой можно сказать, что совокупность выберет ответ в заданном пределе. Например, степень достоверности в 95 % означает, что вы можете быть на 95 % уверены в том, что получите ответы в диапазоне от x до y.
Как рассчитать размер выборки
Вас наверняка интересует ответ на вопрос «Как рассчитать размер выборки?». Например, можно воспользоваться следующей формулой:
N = объем совокупности • e = погрешность (выраженная в виде десятичной дроби) • z = z–показатель
Z–показатель — это значение, которое указывает, сколько отклонений происходит от среднего значения. Найти свой z–показатель вы можете в таблице ниже.
На что стоит обратить внимание при расчете размера выборки
- Если вам необходима незначительная погрешность, то следует увеличить выборку целевой совокупности.
- Чем более высокая степень достоверности выборки вас интересует, тем больше должна быть сама выборка.

Насколько важен статистически значимый размер выборки?
Как правило, чем больше выборка, тем более она статистически значима, т. е. случайность результатов практически минимальна.
Вы, возможно, задаетесь вопросом, насколько существенна статистически значимая выборка. Это, во многом, зависит от конкретной ситуации. Вы можете получить ценные ответы, даже если ваша выборка не является адекватным представлением общей совокупности. Отзывы клиентов — это всего лишь один пример опроса, результаты которого не зависят от того, является ли выборка статистически значимой. Прислушиваться к отзывам клиентов следует в любом случае — так вы получите уникальный взгляд на свою работу и возможности ее улучшения.
С другой стороны, специалистам, проводящим опрос общественного мнения, следует быть весьма осторожными с размером выборки — для них важно убедиться в том, что выборка сбалансирована и отражает всю совокупность. Далее представлены несколько примеров, позволяющих определить важность статистически значимой выборки.
Как размер выборки влияет на точность результатов
Опросы сотрудников
Работаете над опросом для оценки уровня удовлетворенности сотрудников? Опросы отдела кадров позволяют получить важную обратную связь о том, насколько комфортно сотрудники чувствуют себя на работе. Статистически значимая выборка — это возможность получить более всесторонние выводы. Но даже если ваша выборка не является статистически значимой, опрос следует разослать в любом случае. Опросы сотрудников помогают оценить недостатки и способствуют повышению качества рабочей атмосферы.
Опросы об уровне удовлетворенности клиентов
В случае с опросами для получения отзывов клиентов нет необходимости выверять выборку таким образом, чтобы она была статистически значимой. С одной стороны, очень важно получить точную и достоверную информацию о том, что о вас думают клиенты, но с другой стороны, в таких опросах нужно уделять внимание каждому отдельно взятому ответу, поскольку любой из них — как положительный, так и отрицательный — имеет вес и ценность.
Исследование рынка
При проведении опроса об исследовании рынка статистически значимая выборка может иметь решающее значение. Опросы об исследовании рынка помогают узнать более подробные сведения о целевой аудитории и рынке. То есть статистически значимая выборка в таком случае позволяет сделать выводы о целевом рынке в целом. Кроме того, такая выборка является гарантией получения наиболее достоверной информации.
Опросы об образовании
Если вы составляете опросы, касающиеся образования, мы рекомендуем использовать статистически значимую выборку, которая предельно точно отразит общую совокупность. Если вы планируете вносить изменения в своем учебном заведении, основываясь на отзывах учащихся об образовательном учреждении, преподавателях и т. д., статистически значимая выборка будет как раз кстати. Однако если ваша цель — просто получить обратную связь от учащихся, не используя ее для преобразования организации, то статистически значимая выборка будет для вас не столь важна.
Здравоохранение
При проведении опросов в сфере здравоохранения статистически значимая выборка поможет выявить более серьезные проблемы, беспокоящие ваших пациентов. Она также послужит важным звеном при формировании выводов медицинского исследования. Однако, если вы используете опросы в сфере здравоохранения исключительно с целью оценки степени удовлетворенности пациентов, а также проведения регулярного анкетирования, то статистически значимая выборка вряд ли окажет какое-то влияние. Вы и так получите ценную информацию о нуждах и клиентском опыте пациентов.
Опросы для развлечения
Возможно, вы на регулярной основе отправляете своим друзьям, коллегам и родственникам развлекательные опросы. Здесь важна ваша конечная цель. Вы хотите использовать результаты в качестве доказательства? Тогда вам потребуется статистически значимая выборка. Если же вы рассылаете опросы SurveyMonkey исключительно для развлечения, то размер выборки не так важен.
Вам нужно получить больше ответов?
Вы можете углубиться в изучение таких терминов, как вероятностная выборка и модель распределения вероятностей, или просто гадать, сколько человек вам нужно опросить. Но легче всего — воспользоваться нашим калькулятором размера выборки. Изучите такие понятия, как ошибка выборки, размер выборки, статистически значимый размер выборки, а также узнайте, как получать больше ответов. Совсем скоро у вас будут все необходимые инструменты для извлечения максимальных выводов из результатов ваших опросов.
Но легче всего — воспользоваться нашим калькулятором размера выборки. Изучите такие понятия, как ошибка выборки, размер выборки, статистически значимый размер выборки, а также узнайте, как получать больше ответов. Совсем скоро у вас будут все необходимые инструменты для извлечения максимальных выводов из результатов ваших опросов.
Калькулятор посчитал, что вам нужно набрать больше респондентов? Не проблема! SurveyMonkey вам поможет. Расскажите нам о своей целевой совокупности, а мы найдем респондентов для вашего опроса. Благодаря миллионам квалифицированных респондентов по всему миру панель SurveyMonkey Audience позволяет моментально получать ответы на опрос от респондента практически с любым набором параметров.
Получайте больше ответов
SurveyMonkey Audience располагает миллионами респондентов, готовых пройти Ваш опрос.
ВЫБРАТЬ АУДИТОРИЮ
всемирная статистика в реальном времени
Население мира
Sources:
- World Population Prospect: the 2019 Revision — United Nations, Department of Economic and Social Affairs, Population Division (June 2019)
- International Programs Center at the U.
 S. Census Bureau, Population Division
S. Census Bureau, Population Division
More info:
- World Population (Worldometer)
trends & more >
Этот год = с 1го января (00:00) до настоящего момента
Сегодня = с начала текущего дня до данного момента
Прирост населения = Рождено — Умерло
Правительство и Экономика
быстрые факты:
- Total global healthcare expenditure represent around 10% of world GDP
- Government portion of healthcare expenditure is around 60%
источники и информация:
- Global Health Expenditure Database — World Health Organization (WHO)
- World Health Statistics — World Health Organization (WHO)
- World Economic Outlook (WEO) — International Monetary Fund (IMF)
- World Development Indicators (WDI) — World Bank
быстрые факты:
- Public spending on education in the world is around 5% of global GDP
источники и информация:
- Human Development Report — United Nations
- Global Education Digest — Unesco Institute for Statistics (UIS)
- World Bank Public Expenditure Database — edstats — World Bank
больше информации >
источники и информация:
- SIPRI military expenditure data — SIPRI
больше информации >
источники и информация:
- Car Production Statistics — International Organization of Motor Vehicle Manufacturers (OICA)
- Global Auto Report [Pdf file] — ScotiaBank
- Light Vehicle Production Forecasts — IHS
больше информации >
быстрые факты:
- As recently as 1965, bicycle and car production volumes were essentially the same, at nearly 20 million each per year, but as of 2003 bike production had climbed to over 100 million per year compared with around 50 million cars produced that year.

источники и информация:
- Elaboration of Worldwatch Institute data
- Bicycle Retailer and Industry News — Statistics
больше информации >
источники и информация:
- Worldwide PC Shipments — Gartner
- Worldwide Quarterly PC Tracker — IDC
больше информации >
Общество и СМИ
источники и информация:
- Bowker Book Industry Statistics
- UNESCO Institute for Statistics (UIS) — (United Nations Educational, Scientific and Cultural Organization)
больше информации >
источники и информация:
- World Press Trends — World Association of Newspapers and News Publishers (WAN-IFRA)
больше информации >
источники и информация:
- Display Search — worldwide leader in display market research
источники и информация:
- Gartner
- IDC Telecom and Networks
источники и информация:
- Gartner
- DFC Intelligence
- NDP Group — Entertainment Market Research
источники и информация:
- World Development Indicators (WDI) — World Bank
- Measuring the Information Society — International Telecommunications Union (ITU)
- comScore
- GfK group
trends & more >
источники и информация:
- The Radicati Group
источники и информация:
- Technorati on State of the Blogosphere reports and elaboration of other data
- WordPress Stats — Automattic Inc.

больше информации >
источники и информация:
- Internet Live Stats (InternetLiveStats.com)
trends & more >
источники и информация:
- comScore
- Google Inc.
trends & more >
Окружающая среда
быстрые факты:
- The number shown above is net of reforestation
источники и информация:
- Global Forest Resources Assessment (2010) — FAO
источники и информация:
- Dimensions of need: Restoring the land — FAO
быстрые факты:
- CO2 Emissions shown are from Fuel Combustion
источники и информация:
- International Energy Agency (IEA) Statistics
- Carbon Dioxide Information Analysis Center (CDIAC) — United States Department of Energy
- U.
 S. Energy Information Administration (EIA)
S. Energy Information Administration (EIA)
источники и информация:
- United Nations Convention to Combat Desertification
источники и информация:
- Toxic Release Inventory (TRI) Program — U.S. Environmental Protection Agency (EPA)
- United Nations Environment Program
- U.S. Environmental Protection Agency
больше информации >
Продовольствие
источники и информация:
- The State of Food Insecurity in the World — FAO
больше информации >
источники и информация:
- Obesity and overweight — World Health Organization (WHO)
больше информации >
источники и информация:
- Obesity and overweight — World Health Organization (WHO)
больше информации >
источники и информация:
- Hunger Stats — United Nations World Food Programme
- World Health Report — World Health Organization (WHO)
- The State of the World’s Children — United Nations Children’s Fund (UNICEF)
источники и информация:
- Featured Page
больше информации >
источники и информация:
- Annual Medical Spending Attributable To Obesity: Payer-And Service-Specific Estimates
by:
RTI International
Agency for Healthcare Research and Quality — US Dept of Health and Human Services
Centers for Disease Control and Prevention (CDC) - America’s Health Rankings (report by the United Health Foundation, the American Public Health Association and Partnership for Prevention)
- The U.
 S. Weight Loss & Diet Control Market — MarketData Enterprises, Inc., May 1, 2011
S. Weight Loss & Diet Control Market — MarketData Enterprises, Inc., May 1, 2011 - America’s Health Rankings (report by the United Health Foundation, the American Public Health Association and Partnership for Prevention)
больше информации >
Водные ресурсы
источники и информация:
- Global Water Outlook to 2025 — International Food Policy Research Institute (IFPRI) and the International Water Management Institute (IWMI)
больше информации >
источники и информация:
- Water Sanitation and Health (WSH) — World Health Organization (WHO)
источники и информация:
- Water Sanitation and Health (WSH) — World Health Organization (WHO)
Энергетика
источники и информация:
- BP Statistical Review of World Energy — British Petroleum
- World Energy Consumption — Wikipedia
источники и информация:
- International Energy Agency (IEA) Statistics
источники и информация:
- Renewables Global Status Report — REN21
источники и информация:
- Energy: A beginner’s guide — Vaclav Smil
- Solar Energy — Wikipedia
быстрые факты:
- бочка = 159 л
источники и информация:
- World Proved Reserves of Oil and Natural Gas, Most Recent Estimates — Energy Information Administration (EIA) — Data from BP Statistical Review, Oil & Gas Journal, World Oil, BP Statistical Review, CEDIGAZ, and Oil & Gas Journal.

источники и информация:
- World Proved Reserves of Oil and Natural Gas, Most Recent Estimates — Energy Information Administration (EIA) — Data from BP Statistical Review, Oil & Gas Journal, World Oil, BP Statistical Review, CEDIGAZ, and Oil & Gas Journal.
Обратный отсчет до истощения нефтяных ресурсов:
…
предположение:
- При поддержании текущих темпов потребления
источники и информация:
- World Proved Reserves of Oil and Natural Gas, Most Recent Estimates — Energy Information Administration (EIA) — Data from BP Statistical Review, Oil & Gas Journal, World Oil, BP Statistical Review, CEDIGAZ, and Oil & Gas Journal.
быстрые факты:
- boe = баррель в нефтяном эквиваленте
- «газа» = природного газа
источники и информация:
- World Proved Reserves of Oil and Natural Gas, Most Recent Estimates — Energy Information Administration (EIA) — Data from BP Statistical Review, Oil & Gas Journal, World Oil, BP Statistical Review, CEDIGAZ, and Oil & Gas Journal.

…Дней до истощения запасов
природного газа
Здравоохранение
источники и информация:
- Global Burden of Disease (GBD) — World Health Organization (WHO)
источники и информация:
- Young child survival and development — UNICEF
- Child Mortality — Childinfo (UNICEF)
источники и информация:
- Sexual and reproductive health — World Health Organization (WHO)
- Shah, I.; Ahman, E. (December 2009). «Unsafe abortion: global and regional incidence, trends, consequences, and challenges» (Pdf). Journal of Obstetrics and Gynaecology Canada 31 (12): 1149–58. PMID 20085681
больше информации >
источники и информация:
- Why do so many women still die in pregnancy or childbirth? — World Health Organization (WHO)
- Maternal mortality for 181 countries, 1980—2008: a systematic analysis of progress towards Millennium Development Goal 5
источники и информация:
- HIV/AIDS Statistics — World Health Organization
- Global HIV and AIDS estimates — AVERT
больше информации >
источники и информация:
- UNAIDS
больше информации >
источники и информация:
- Cancer — World Health Organization (WHO)
больше информации >
источники и информация:
- Malaria — World Health Organization (WHO)
источники и информация:
- Cigarette Consumption — Tobacco Atlas [Pdf] — World Health Organization (WHO)
источники и информация:
- Tobacco Control, Global Health Observatory (GHO) — World Health Organization (WHO)
источники и информация:
- Global Information System on Alcohol and Health (GISAH) — World Health Organization (WHO)
больше информации >
источники и информация:
- Suicide prevention (SUPRE) — World Health Organization (WHO)
источники и информация:
- The illegal drugs global business — Frontline, PBS special report
больше информации >
источники и информация:
- Global launch of the Decade of Action for Road Safety 2011-2020 — World Health Organization (WHO)
делиться!
Калькулятор таможенных платежей 2022.
 Расчет таможенной пошлины
Расчет таможенной пошлины
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
19 сайтов, похожих на statskingdom.com
socscistatistics.com
Статистика социальной науки
Статистические ресурсы для социальных ученых, в том числе Z Test, Chi-Square & T Test Статистические калькуляторы.
graphpad.com
Главная — GraphPad
На данный момент нет описания для этого сайта…
alcula.com
Онлайн калькуляторы для математики и статистики
Онлайн расширенные калькуляторы для математики и статистики. Также имеется счеты и единицы измерительных инструментов преобразования измерения.
mathcracker.com
Бесплатная математическая помощь — уроки математики, учебники, решатели и статистики калькуляторов онлайн
Свободная математическая помощь ресурсам, пошаговые статистические калькуляторы, уроки, уроки, учебные пособия и выборки решений. Домашние инструменты для средней школы и колледжа.
Домашние инструменты для средней школы и колледжа.
datatab.net
Статистический калькулятор: T-Test, Chi-Square, регрессия, корреляция
WebApp для статистического анализа данных.
stats.blue
Онлайн статистический люкс
Stats.lue — это бесплатное, простое в использовании, онлайн статистический программный пакет.
hackmath.net
Математический портал для начальных и средних школьников
Математический портал. 7485 решают математические проблемы и тесты. Предупреждает отсчет. Математические калькуляторы для школы и практики.
danielsoper.com
Главная — Danielsoper.com.
Цифровой дом доктора Даниэля Сопер — Полимат, мыслитель и человек букв.
statisticssolutions.com
Статистические данные Решения: Диссертация и исследования Консалтинг для статистического анализа
Лидер в диссертации и исследовательском консультировании более 20 лет. Продвижение статистического анализа с онлайн-ресурсами, программным обеспечением и консультированием.
Продвижение статистического анализа с онлайн-ресурсами, программным обеспечением и консультированием.
easymedstat.com
EasymedStat — дайте крыльям к клиническим исследованиям
Лучшие исследовательские команды используют EasymedStat для сбора данных, проанализировать его и публиковать свои результаты исследований
statisticshowto.com
Статистические данные Как: начальная статистика для остальных из нас!
Сотни статистики Как статьи и шаг за шагом видео для элементарных статистики и вероятности, плюс AP и современные темы статистики.
lumigram.com
Lumigram светящиеся ткани
Светящаяся ткань и волоконно-оптическая ткань для декора, одежды, специальных мероприятий, архитектуры; Tssu Lumineux EN Волоконно-оптическая оптика заливает украшение
vassarstats.net
Vassarstats: статистический вычислений веб-сайт
Веб-сайт для статистических вычислений; вероятность; линейная корреляция и регрессия; хи-квадрат; T-процедуры; T-тесты; анализ дисперсии; Анова; Анализ ковариации; Акова; параметрический; непараметрический; биномиальный; нормальное распределение; Распределение Пуассона; Фишер Точный; Манн-Уитни; Уилкоксон; Крускаль-Уоллис; Ричард Лоури, Вассарский колледж
scistatcalc. blogspot.com
blogspot.com
Scistatcalc: Главная
Статистические тесты Калькуляторы, гипотеза, CDF, Quantile Online калькуляторы, Mann Whitney U Test, Wilcoxon подписанный рейтинговый тест, ANOVA, GAUSSIAN Distribation, функция ошибок, функция гамма, среднее, медиана, дисперсия, асимметрия, калькулятор барнарда, калькулятор Kruskal Wallis , Шапиро-Уилк испытательный калькулятор, биостатистика, распределение F, онлайн-плоттер, геометрический средний, гармоничный средний
statisticsbyjim.com
Статистика Джима — Статистика по Джиму
Я помогу вам интуитивно понимать статистику, подчеркивая концепции и используя простого английского, поэтому вы можете сосредоточиться на понимании ваших результатов.
inches-to-cm.com
Дюйма к CM конвертер
Дюймов к CM конвертер. Легко преобразовать дюймы в сантиметры, с формулой, графиком преобразования, автоматическое преобразование к общей длине, более
stattrek. com
com
Статистика
Бесплатные учебники охватывают статистику AP, вероятность, отбор проб, регресс, анова и алгебру матрицы. Написанные и видео уроки. Онлайн калькуляторы.
wessa.net
Wessa.net — бесплатная статистика и программное обеспечение для прогнозирования (калькуляторы) v.1.2.1
Wessa.net предлагает бесплатное программное обеспечение для прогнозирования образования (анализ временной серии) и программное обеспечение статистики.
statisticshelper.com
Статистика помощника — статистика помощник
Таблица с использованием стандартного отклонения. Калькулятор чего стандартное отклонение? Что подразумевает большое стандартное отклонение? Пример дохода — сравнение двух Citiessymbol для стандартного отклонения отключения для отсутствия изменений, используемых для стандартного отклонения, что является дисперсией? Применение стандартного отклонения и отклонения формулу Формула дисперсии и формула выборки образца $$ {\ sigma ^ 2} = \ frac {{\ sum} {x ^ 2} — \ frac {({\ sum} {x}) ^ 2} {n}} {n} $$$$ {S ^ 2} = . ..
..
A/B-тестирование – ошибки и примеры. Проблема подглядывания при анализе ab тестов. Влияние на расчет статистической значимости
При дизайне, запуске и анализе A/B тестов можно допустить много ошибок, но одна из них особенно коварна. Речь о «peeking problem» или «проблеме подглядывания», когда решение об изменениях в продукте принимается на основе промежуточных результатов теста.
Эту ошибку допускают и те, у кого много опыта в A/B тестировании и кто понимает, как оценить статистическую значимость наблюдаемых изменений.
В этом материале мы разберем, зачем измерять статистическую значимость и как проблема подглядывания мешает правильному анализу результатов эксперимента.
Если вы хотите глубже разобраться в том, как создаются, развиваются и масштабируются продукты, пройдите обучение в симуляторах GoPractice.
→ «Симулятор управления продуктом на основе данных» поможет научиться принимать решения с помощью данных и исследований при создании продукта (путь от 0 к 1).
→ «Симулятор управления ростом продукта» поможет найти пути управляемого роста и масштабирования продукта. Вы построите модель роста и составите стратегию развития продукта (путь от 1 к N).
→ «Симулятор SQL для продуктовой аналитики» поможет освоить SQL и применять его для решения продуктовых и маркетинговых задач.
Не знаете с чего начать? Пройдите бесплатный тест для оценки навыков управления продуктом. Вы определите свои сильные стороны и слепые зоны, получите план профессионального развития.
Еще больше ценных материалов и инсайтов — в телеграм-канале GoPractice.
Статистическая значимость простыми словами
Представим, что вы привлекли в игру 10 новых пользователей и случайно разделили их между старой и новой версией. Из 5 пользователей, которые попали в старую версию игры, на следующий день вернулись 2 (40%). Из 5 пользователей, которые попали в новую версию, на следующий день вернулись 3 (60%).
Можно ли на основе собранных данных сказать, что Retention 1 дня новой версии игры лучше, чем старой?
К сожалению, нельзя. Выборка очень маленькая, поэтому велика вероятность, что наблюдаемая разница — случайность, а не результат изменений.
Выборка очень маленькая, поэтому велика вероятность, что наблюдаемая разница — случайность, а не результат изменений.
Математическая статистика предоставляет инструменты, помогающие понять, можно ли различия в метрике между группами связать с изменениями продукта, а не со случайностью. Другими словами, является изменение статистически значимым или нет.
Способ проверки статистической значимости в рамках частотного подхода к теории вероятности, которому обычно учат в университетах, работает следующим образом:
- Собираются данные для версии A и B.
- Делается предположение, что тестовые группы между собой не отличаются.
- В рамках предположения идентичности групп считается, какова вероятность получить наблюдаемую в эксперименте или большую разницу между группами. Такое значение называют p-value.
- Если p-value меньше определенного порогового значения (обычно 5%), то изначальное предположение об идентичности тестовой и контрольной группы отвергается.
 В этом случае можно с высокой степенью уверенности утверждать, что наблюдаемая разница между группами значима (связана с их различиями, а не случайностью).
В этом случае можно с высокой степенью уверенности утверждать, что наблюдаемая разница между группами значима (связана с их различиями, а не случайностью). - Если p-value больше порогового значения, то тестируемые версии на основе собранных данных неразличимы. При этом в реальности между ними как может быть различие, которое мы просто не выявили, так его может и не быть. Мы не знаем.
Это очень поверхностное объяснение основной идеи того, как и зачем считать статистическую значимость. В реальности все сложнее: необходимо изучить структуру данных, очистить их, выбрать правильный критерий, интерпретировать результаты. Все эти шаги таят в себе много подводных камней.
Простой пример расчета статистической значимости
Давайте вернемся к игре из прошлого примера.
Команда учла недостатки дизайна первого A/B теста и на этот раз привлекла 2000 новых пользователей (по 1000 в каждую из версий). На 1 день в первой версии вернулись 330, а во второй 420.
Во второй версии больше пользователей вернулись на 1 день, но команда не могла быть уверена, что это произошло из-за влияния продуктовых изменений, а не в результате случайного колебания метрики.
Для разрешения вопроса надо было посчитать, является ли наблюдаемая разница в Retention 1 дня статистически значимой или нет.
В данном случае изучалась простая метрика (конверсия новых пользователей в определенное действие — возвращение на 1 день), поэтому можно было воспользоваться онлайн-калькулятором для расчета статистической значимости.
Калькулятор выдал p-value < 0.001, то есть вероятность увидеть наблюдаемое различие при идентичных тестовых группах очень мала. Значит, можно с высокой степенью уверенности связать рост Retention 1 дня с влиянием продуктовых изменений.
Автоматизация проверки результатов A/B теста c неожиданными последствиями
Команда, воодушевленная прогрессом с Retention, решила переключиться на улучшение монетизации игры. Сначала там решили сфокусироваться на увеличении конверсии в первую покупку. Спустя 2 недели новая версия игры ушла в A/B тест.
Разработчики проявили инициативу и написали скрипт, который каждые несколько часов считал конверсию в первую покупку для тестовой и контрольной версии и проверял, является ли разница значимой.
Спустя несколько дней система выдала сообщение о наличии значимой разницы. Эксперимент признали успешным и новую версию раскатили на всех пользователей.
Вы могли не заметить, но в процесс анализа эксперимента закралась коварная ошибка.
Peeking problem или проблема подглядывания
Применение стандартных критериев в рамках частотного подхода к статистике (Хи-квадрат, критерий Стюдента), которые используются для расчета p-value и статистической значимости, требуют выполнения различных условий. Например, многие критерии подразумевают нормальное распределение изучаемой величины.
Но есть еще одно важное условие, о существовании которого многие забывают: размер выборки для эксперимента должен быть определен заранее.
Вы должны заранее решить, сколько наблюдений хотите собрать. Потом посчитать результаты и принять решение. Если вдруг выявить значимую разницу на собранном количестве данных не получилось, то продолжать эксперимент с целью сбора дополнительных наблюдений нельзя. Можно только запустить тест заново.
Можно только запустить тест заново.
Описанная логика звучит странно в контексте A/B тестов в интернете, где можно смотреть на результаты в режиме реального времени, где добавление новых пользователей в эксперимент ничего не стоит.
Дело в том, что используемый для A/B тестов математический аппарат в рамках частотного подхода к статистике разрабатывался задолго до появления интернета. Тогда большинство прикладных задач подразумевало фиксированный и заранее определенный размер выборки для проверки гипотезы.
Интернет поменял парадигму A/B тестирования. Вместо выбора фиксированного размера выборки перед запуском эксперимента большинство предпочитают собирать данные, пока разница между тестом и контролем не станет значимой. Следствием такого изменения в процедуре проведения экспериментов стало то, что расчеты p-value старыми способами перестали работать. Реальное p-value при регулярной проверке результатов теста становится намного больше, чем то p-value, который вы получаете, используя обычные статистические критерии, которые при такой процедуре перестают работать.
Проблема подглядывания проявляется, когда вы проверяете промежуточные результаты с готовностью принять решение: раскатить одну из версий, если различие между тестом и контролем окажется значимым. Если вы зафиксировали размер выборки и просто наблюдаете за результатами в процессе набора наблюдений (и ничего не делаете на их основе), а потом принимаете решение, когда набралось нужное количество данных, то никаких проблем не возникает.
Правильная процедура A/B тестирования (в рамках частотного подхода):
Неправильная процедура A/B тестирования:
Почему подглядывания увеличивают p-value
Давайте вернемся к эксперименту про конверсию в первую покупку в игре. Предположим, мы знаем, что в реальности сделанные изменения не оказали никакого влияния.
Ниже изображена динамика разницы конверсий в покупку между тестовой и контрольной версиями продукта (синяя линия). Зеленая и красная линия отражают границы диапазона неразличимости при условии, что заранее было выбрано соответствующее количество наблюдений.
При правильном процессе A/B тестирования надо заранее определить количество пользователей, на основе которых будет оцениваться результат, собрать наблюдения, посчитать результаты и сделать вывод. Такая процедура гарантирует, что при многократном ее повторении в 95% случаев критерий не увидит разницы между одинаковыми версиями (при соответствующем уровне доверия).
Все меняется, если вы начинаете проверять результаты с определенной частотой и готовы действовать на основе наблюдаемых различий. В таком случае вместо вопроса о том, является ли разница значимой в определенный заранее выбранный момент в будущем, вы спрашиваете, выходит ли разница за диапазон неразличимости хотя бы раз в процессе сбора данных. Это два совершенно разных вопроса.
Даже если две группы идентичны, то разница конверсий может периодически выходить за границы зоны неразличимости по мере накопления наблюдений. Это совершенно нормально, так как границы сформированы так, чтобы при тестировании одинаковых версий лишь в 95% случаев разница оказывалась в их пределах.
Поэтому при регулярной проверке результатов в процессе проведения теста с готовностью принять решение при наличии значимой разницы вы начинаете кумулятивно накапливать возможные случайные моменты, когда разница выходит за пределы диапазона. Следствие — p-value растет с каждой новой проверкой.
Вот наглядный пример того, как именно подглядывания увеличивают на p-value.
Влияние подглядываний на p-value
Чем чаще вы смотрите на промежуточные результаты A/B теста с готовностью принять на их основе решение, тем выше становится вероятность, что критерий покажет значимую разницу, когда ее нет:
- 2 подглядывания с готовностью принять решение о завершении теста увеличивают p-value в 2 раза;
- 5 подглядываний в 3.2 раза;
- 10 000 подглядываний более чем в 12 раз.
Варианты решения проблемы подглядывания
Фиксировать размер выборки заранее и не проверять результаты, пока все данные не собраны
Очень правильный и очень непрактичный подход. Если эксперимент не даст никакого сигнала, то придется все начинать заново.
Если эксперимент не даст никакого сигнала, то придется все начинать заново.
Математические пути решения проблемы: Sequential experiment design, байесовский подход к A/B тестированию, снижение чувствительности критерия
Проблема подглядывания может быть решена математическим путем. Например, Optimizely и Google Experiments используют для ее решения микс байесовского подхода к A/B тестированию и Sequential experiment design. Рассуждения выше мы вели в рамках частотного подхода, подробнее о разнице байесовского и частотного подходов — по ссылкам в конце статьи.
Для сервисов вроде Optimizely — это необходимость, так как их ценность сводится к тому, что они определяют лучший вариант на основе регулярной проверки результатов A/B теста на лету. Подробнее можно почитать по следующим ссылкам: Optimizely, Google.
Продуктовый подход с мягким обязательством по времени теста и коррекцией на суть проблемы подглядывания
При работе над продуктом ваша цель — получить сигнал, необходимый для принятия решения.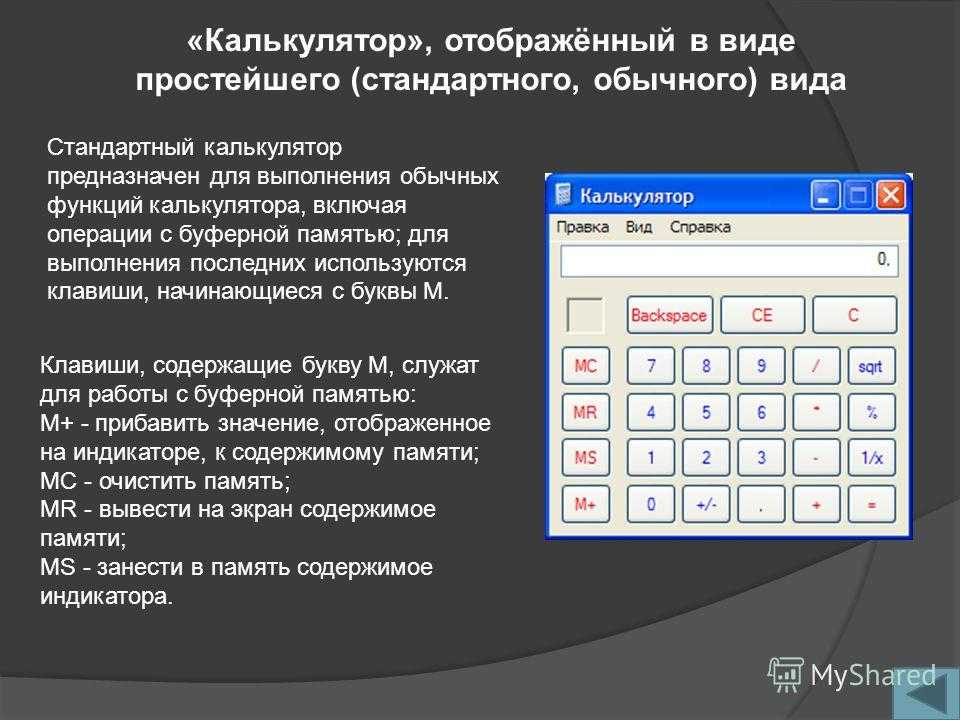 Описанная ниже логика неидеальна с математической точки зрения, но решает продуктовую задачу.
Описанная ниже логика неидеальна с математической точки зрения, но решает продуктовую задачу.
Суть подхода сводится к тому, чтобы предварительной оценить необходимую выборку для выявления эффекта в A/B тесте и учесть природу проблемы подглядывания в процессе промежуточных проверок. Это позволяет минимизировать негативные последствия при анализе результатов.
Перед стартом эксперимента стоить оценить, какая нужна выборка, чтобы с приемлемой вероятностью увидеть изменение, если это изменение в реальности есть.
Это полезное упражнение безотносительно проблемы подглядывания, так как для некоторых продуктовых фич требуется столь большая выборка, чтобы идентифицировать их эффект, что тестировать их на текущем этапе развития продукта нет смысла.
Держа в уме посчитанную ранее выборку, после запуска эксперимента можно (и даже нужно) следить за динамикой изменений, но не принимать решений, при первом выходе разницы в зону значимости.
Нужно продолжать наблюдать. Если разница зафиксируется, то, скорее всего, влияние есть. Если же станет вновь неразличимой, то сделать однозначного вывода об улучшении нельзя.
Если же станет вновь неразличимой, то сделать однозначного вывода об улучшении нельзя.
Давайте посмотрим на результаты двух экспериментов ниже. Оба эксперимента шли 20 дней, каждая точка на графике — относительная разница в метрике между тестом и контролем на конец соответствующего дня с доверительным интервалом. Если доверительный интервал не пересекает ноль (идентично выполнению условия p-value < x), то разница является значимой (при выборе соответствующей выборки заранее). В этом случае точка выделяется зеленым.
В первом эксперименте, начиная с 6 дня, разница между версиями стала значимой и доверительный интервал больше не пересекал 0. Такая устойчивая картина дает четкий сигнал о том, что с высокой степенью вероятности тестовая версия работает лучше контрольной. Сложностей с интерпретацией результатов нет.
Во втором эксперименте разница иногда выходила в зону значимости, но потом вновь становилась неразличимой. Если бы мы не знали о проблеме подглядывания, то мы закончили бы эксперимент на 4 день, решив, что тестовая версия выиграла. Но предложенный способ визуализации динамики A/B теста во времени показывает, что устойчивой измеримой разницы между группами нет.
Но предложенный способ визуализации динамики A/B теста во времени показывает, что устойчивой измеримой разницы между группами нет.
Возможны пограничные случаи, когда однозначно интерпретировать результаты сложно. Единого способа их разрешения нет, все зависит от рискованности и стоимости принимаемого решения.
- Есть обычные эксперименты, где вы тестируете разные реализации фичи или небольшие изменения, и готовы принимать решение с большей степенью риска.
- Есть дорогие решения, когда вы, например, пытаетесь проверить новый вектор развития продукта. В этом случае стоит уделить анализу и изучению данных больше времени. Иногда можно провести эксперимент еще раз.
Описанная логика может звучать как излишнее упрощение с точки зрения математики, но для продуктовой работы она вполне подходит. Когда в продуктовой работе начинают больше заниматься математикой, чем продуктом, то обычно дело в том, что эффект от изменений слишком мал или отсутствует, а эту проблему математикой не решить.
В заключение
Ключевая мысль этого материала такова:
Если вы проводите A/B тест и в определенный момент разница стала значимой, то не надо сразу заканчивать эксперимент, считая, что одна из групп выиграла. Продолжайте наблюдать. А лучше заранее выберите размер выборки, соберите наблюдения, а потом на их основе посчитайте результаты.
Дополнительное чтение
- Хорошая статья про peeking problem.
- Еще одна хорошая статья про проблему подглядвания, но с ошибочным утверждением, что использование байесовский подхода ее решает.
- Сравнение байесовского и частотного (frequentist) подходов простым языком.
- Математическим языком про разницу байесовского и частотного подходов.
- Наглядное объяснение, что байесовский подход к A/B тестам не решает проблему подглядывания от команды Stack Exchange.
- Еще одна статья про то, что байесовский подход чувствителен к подглядываниям, а также о том, как проблему решают разные сервисы A/B тестов на рынке.

- Обсуждение плюсов и минусов bayesian vs frequentist подходов к математической статистике на Reddit.
- Статья от Optimizely про их подход решению проблемы подглядывания.
- Много интересного про Sequential анализ для A/B тестов — тут, тут и тут.
- Статья про то, как растет p-value при мониторинге результатов с готовностью принять решение.
Если вы хотите глубже разобраться в том, как создаются, развиваются и масштабируются продукты, пройдите обучение в симуляторах GoPractice.
→ «Симулятор управления продуктом на основе данных» поможет научиться принимать решения с помощью данных и исследований при создании продукта (путь от 0 к 1).
→ «Симулятор управления ростом продукта» поможет найти пути управляемого роста и масштабирования продукта. Вы построите модель роста и составите стратегию развития продукта (путь от 1 к N).
→ «Симулятор SQL для продуктовой аналитики» поможет освоить SQL и применять его для решения продуктовых и маркетинговых задач.
Не знаете с чего начать? Пройдите бесплатный тест для оценки навыков управления продуктом. Вы определите свои сильные стороны и слепые зоны, получите план профессионального развития.
Еще больше ценных материалов и инсайтов — в телеграм-канале GoPractice.
Онлайн-калькулятор для Омахи — лучшие приложения для подсчета аутов, вероятностей
/
Обновлено: 02.09.2022
Каждая разновидность покера имеет свои особенности, учитывать которые не всегда просто при переключении с Техасского Холдема на Омаху или другие покерные игры. В первую очередь изменяется частота вероятности выпадения выигрышных комбинаций, шансы на получение прибыли исчисляются по-другому, поэтому игроку приходится тратить много времени на адаптацию и изучение вероятностей и шансов.
На помощь в таких ситуациях придет статистический софт и калькуляторы шансов. Не все покер румы одобряют использование дополнительного программного обеспечения, но те онлайн комнаты, в которых играет большое количество профессиональных и опытных покеристов, позволяют подключать статистические программы и калькуляторы.
Получи бесплатный курс по покеру. Каждому ученику чарты стартовых рук и крутой софт в подарок.
- Ты сформируешь крепкую покерную базу
- Научишься работать с софтом
- Узнаешь стратегии на каждый этап игры
На занятиях тренер составит тебе индивидуальный план развития.
Выбирай себе курс и оставляй заявку!
Что такое Омаха калькулятор
Покерные калькуляторы, в том числе и разработанные специально для поклонников Омахи, представляют собой программу, позволяющую пользователю более точно рассчитать свои шансы в конкретной раздаче, вследствие чего избежать проигрыша.
Омаха калькуляторы предназначены для использования на любом этапе раздачи. Внеся всю имеющуюся информацию относительно известных карт, игрок в течение нескольких секунд получает результат, исходя из которого, он может планировать свои дальнейшие действия: оставаться в игре или сбрасывать карты.
Среди главных достоинств Омаха калькулятора пользователи отмечают следующие:
— использование данной программы значительно увеличивает шансы игрока на победу и позволяет более разумно оперировать собственным банкроллом, поскольку позволяет своевременно и более точно определить шансы покериста;
— программа производит необходимые расчеты быстро и с большим процентом точности;
— в Интернете можно бесплатно скачать и установить калькулятор или использовать его без загрузки в онлайн-режиме.
Омаха калькуляторы одинаково полезны как для опытных покеристов, как и для начинающих игроков. Профессионалам они позволяют сэкономить время, а новичкам — научиться определять комбинации, приносящие выигрыш и правильно оценивать свои шансы в раздаче.
Разновидности Омаха калькуляторов
Омаха калькуляторы можно использовать в виде установленного на ПК софта или открывать выбранный инструмент онлайн. Пользователи могут выбрать различные по функционалу и сложности программы – от самых простых до полноценного статистического программного обеспечения.
Пользователи могут выбрать различные по функционалу и сложности программы – от самых простых до полноценного статистического программного обеспечения.
Простые Омаха калькуляторы. Одним из примеров простого калькулятора является инструмент, который можно найти на ресурсе CardPlayer.com. Несмотря на то, что он имеет только англоязычный вариант, разобраться с его функционалом не составит труда пользователю, у которого есть некоторые навыки игры в онлайн покер. Используя его, игрок получает актуальную информацию, обновляющуюся в процессе игры. Помимо подсчета шансов, данный инструмент предоставляет ссылки на таблицу шансов и аутов, статистику и примеры анализа раздач.
Полноценные программы. Многие игроки, остановившие свой выбор на Омахе, используют программу Omaha Indicator,которая является специализированным софтом как для обычного формата Омахи, так и для Хай-Лоу. Данное программное обеспечение поддерживает большое число онлайн комнат, поэтому проблем с его использованием не возникнет. Среди инструментов программы есть калькулятор и все необходимые функции, использовать которые будет несложно и полезно даже новичку.
Среди инструментов программы есть калькулятор и все необходимые функции, использовать которые будет несложно и полезно даже новичку.
Другие варианты Омаха калькуляторов. Альтернативными вариантами калькуляторов для Омахи могут послужить такие инструменты как OmahaChecker, предоставленный pokersmartstudio.com или omahacalculator.com. Каждый калькулятор имеет свои функциональные особенности, но результат использования не имеет принципиальных отличий. Все они предоставляют информацию о шансах, вероятностях и аутах игрока в интересующей раздаче.
Итог
Споры о том, следует ли использовать статистические программы и калькуляторы, не прекращается с самого момента их появления. Сторонники и противники выдвигают свои веские аргументы, но нельзя не согласиться с тем, что наличие подобных инструментов в арсенале игрока, поможет ему изучить и проанализировать информацию намного быстрее, чем это получится без сторонней помощи.
Приложение VesPoker в твоем телефоне!
4.7|11000 установок
Узнайте, как и где играть в покер онлайн. Обзоры покер-румов и статьи для начинающих. Акции и бонуы от ведущих брендов.
Калькуляторы быстрой статистики
Калькуляторы быстрой статистики- Дом
- Калькуляторы
- Описательная статистика
- Товар
- Учебники
- Викторины
- Какой тест статистики?
- Контакт
Здесь вы найдете набор интуитивно понятных и простых в использовании статистических калькуляторов. Включены различные тесты значимости, а также калькуляторы корреляции, размера эффекта и доверительного интервала.
Включены различные тесты значимости, а также калькуляторы корреляции, размера эффекта и доверительного интервала.
Если вы не уверены, какой калькулятор статистики вам нужен, ознакомьтесь с нашим Какой тест статистики? волшебник.
Тесты значимости
- Однофакторный дисперсионный анализ для независимых измерений
- Калькулятор однофакторного дисперсионного анализа для повторяющихся измерений
- Калькулятор биномиального теста
- Калькулятор хи-квадрата для таблицы непредвиденных обстоятельств 2 x 2
- Калькулятор хи-квадрата для непредвиденных обстоятельств 5 x 5 (или меньше) Таблица
- Калькулятор хи-квадрата для определения качества подгонки
- Калькулятор точного теста Fisher для таблицы непредвиденных обстоятельств 2 x 2
- Тест Фридмана для повторных измерений
- Критерий нормальности Колмогорова-Смирнова
- Калькулятор критерия Крускала-Уоллиса для независимых измерений
- Калькулятор критерия однородности дисперсии Левена
- Калькулятор U-критерия Манна-Уитни
- Калькулятор теста знаков
- Калькулятор стандартных ошибок
- Калькулятор Т-критерия для 2 независимых средних
- Калькулятор Т-критерия для 2 зависимых средних
- Калькулятор Т-критерия для одного образца
- Калькулятор знакового рангового теста Уилкоксона
- Калькулятор Z-счета для одного необработанного значения
- Калькулятор Z-Test для одного образца
- Калькулятор Z-теста для 2 пропорций населения
Прогноз
- Калькулятор линейной регрессии
- Калькулятор множественной регрессии
Тесты корреляции
- Калькулятор коэффициента корреляции Пирсона
- Калькулятор коэффициента Фи
- Калькулятор коэффициента точечно-бисериальной корреляции
- Калькулятор Ро Спирмена (корреляция)
P-значения
- P-значение из Z-показателя.

- P-значение по t-баллу.
- P-значение по показателю хи-квадрат.
- P-значение из F — показатель соотношения.
- P-значение по шкале Пирсона (r).
- Калькулятор критических значений
. - Калькулятор Tukey Q.
Теорема Байеса
- Быстрый калькулятор теоремы Байеса
Размер эффекта
- Калькулятор размера эффекта
Доверительные интервалы
- Калькулятор доверительного интервала для одной выборки (T-статистика)
- Калькулятор доверительного интервала для одной выборки (Z-статистика)
- Калькулятор доверительного интервала независимых выборок
Биостатистика
- Число, необходимое для лечения Калькулятор
- Калькулятор относительного риска и отношения шансов
Коммунальные услуги
- Калькулятор объема выборки
- Генератор случайных чисел
- Калькулятор процентилей роста ребенка
- Генератор нормального распределения
- Калькулятор рангов
- Калькулятор наивысшего общего коэффициента
- Форматеры и преобразователи чисел
- Средство форматирования чисел: перевод европейского формата в североамериканский формат
- Средство форматирования чисел: преобразование североамериканского формата в европейский формат
- Калькулятор темпа бега
Не знаете, какой статистический тест следует использовать? Проверьте наш мастер!
| Конфиденциальность | Правовая оговорка | Цитировать | Контакт | О | © 2022
Статистика онлайн — проверяет предположения, интерпретирует результаты
Статистические тесты, графики, вероятности и четкие результаты. Автоматически проверяет предположения, интерпретирует результаты и выводит графики, гистограммы и другие диаграммы.
Автоматически проверяет предположения, интерпретирует результаты и выводит графики, гистограммы и другие диаграммы.
Статистические онлайн-калькуляторы поддерживают не только статистику теста и p-значение, но и другие результаты, такие как размер эффекта, мощность теста и уровень нормальности.
Если одна из проверок не пройдена, средство рекомендует решение.
Какой статистический тест следует использовать? следующая ссылка поможет вам выбрать: выбрать статистический тест (опросник для принятия решения).
Test statistic calculators
Find the test statistic calculator
| Test | Assumptions | Required sample data | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Test name | Check | Statistic | Ind | σ | σ 1 =σ 2 | d | μ/p | x̄/p̂; | n | S | |||||
| 1 | One Sample Z-Test | Mean | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||
| 2 | Одновыборочный Т-критерий | Среднее | ✔ | ✔ | ✘ | 9 40246 | ✔ | ✔ | ||||||||
| 3 | Two Sample Z-Test | Mean | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||
| 4 | Two Sample T-Test (Pooled variance) | Mean | ✔ | ✔ | ✘ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||
| 5 | Two Sample T-Test (Welch’s) | Mean | ✔ | ✔ | ✘ | ✘ | ✔ | ✔ | ✔ | ✔ | ||||||
| 6 | Two Sample Mann-Whitney U Test | Rank | ✔ | ✔ | ✔ | |||||||||||
| 7 | Paired T-Test | Mean | ✔ | Paired | ✔ | |||||||||||
| 8 | Paired Wilcoxon Sign Rank Test | Rank | Paired | ✔ | ||||||||||||
| 9 | One Way ANOVA Test | Mean | ✔ | ✔ | ✔ | ✔ | ||||||||||
| 10 | Repeated Measures ANOVA Test | Mean | ✔ | Dependent groups | Sphericity | ✔ | ||||||||||
| 11 | Kruskal-Wallis Test | Mean | ✔ | ✔ | ||||||||||||
| 12 | Двухлет Anova Test | |||||||||||||||
| 12 | . 0524 0524 | Mean | ✔ | ✔ | ✔ | ✔ | ||||||||||
| 13 | One Way MANOVA Test | Mean | F | ✔ | ✔ | ✔ | ✔ | |||||||||
| 13 | One Sample Proportion Test | Proportion | Binomial | ✔ | ✔ | ✔ | ✔ | |||||||||
| 14 | Two Sample Proportion Test | Proportion | Binomial | ✔ | ✔ | ✔ | ||||||||||
| 15 | Chi-Squared Test For Variance | σ | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||
| 16 | F Test For Variances | σ | ✔ | ✔ | ✔ | ✔ | ||||||||||
| 17 | Levene’s Test For Variances | σ | ✘ | ✔ | ✔ | Fit | ✔ | ✔ | ||||||||
| 19 | Shapiro-Wilk Test | Fit | ✔ | ✔ | ✔ | |||||||||||
| 20 | Колмогоров Смирновский Тест | FIT | D = MAX6 1≤N (D I + , D I + , D I + | , D .✔ | ✔ | |||||||||||
| 21 | Kaplan Meier Survival Analysis | Survival | ✔ | ✔ | ||||||||||||
** ✔- да, ✘- нет, пусто — не имеет значения
Калькулятор регрессии
| # | Регрессия | Статистика |
|---|---|---|
| 1 | Простая линейная регрессия0246 | |
| 2 | Multiple Linear Regression | |
| 3 | *Bulk Linear Regression | |
| 4 | Binary Logistic Regression | χ2 = 2(LL 1 -LL 0 ) |
| 5 | Многономическая логистическая регрессия | χ2 = 2 (LL 1 -LL 0 ) |
*)
*).
Sample size calculators
| # | Calculator | Image |
|---|---|---|
| 1 | Sample size | |
| 2 | Test power | |
| 3 | Effect size | |
| 4 | Доверительные интервалы (среднее, стандартное отклонение, доля, корреляция) |
Калькуляторы распределения
| # | Distribution | Image |
|---|---|---|
| 1 | P-value | |
| 2 | Distributions | |
| 2 | Normal Distribution | |
| 2 | Binomial Distribution | |
| 3 | Т-распределение (студенческое) | |
| 4 | Распределение хи-квадрат | |
| 5 | F Distribution (Fisher-Snedecor) |
Statistical tables
| # | Table |
|---|---|
| 1 | Z table |
| 2 | T table |
Статистические калькуляторы
Каждый статистический калькулятор содержит пошаговые расчеты.
| # | Статистический калькулятор | Изображение | ||
|---|---|---|---|---|
| 1 | Средний средний режим (Q 1 , Q 3 , IRQ, диапазон) | |||
| 2 | Стандартный (VARIANT, SEM, SEM, SEM, SEM, MAD) | 2 | . 3Среднее (сумма, счет) | x̄ |
| 3 | Среднее значение (сумма, Count) | x̄ | ||
| 4 | 96 | |||
| 4 | 45 | |||
| 4 | 46 | |||
| . | ||||
| 5 | Среднее гармоническое | H | ||
| 6 | Вероятность (вероятность, формула, зависимые события, теорема Bayes, Salcement). Калькулятор корреляции (корреляция Пирсона, ранговая корреляция Спирмена)0246 | |||
| 10 | Цепочный калькулятор марковского марковского (вектор NTH-стадии, стационарный вектор) | |||
| 11 | . Расчет падений. калькулятор коэффициентов (дробные коэффициенты, десятичные коэффициенты, американские коэффициенты) | |||
| 13 | Калькулятор среднего абсолютного отклонения (калькулятор MAD) | |||
| 14 | Median absolute deviation calculator (MAD calculator) |
Chart makers
| # | Chart | Image | |
|---|---|---|---|
| 1 | Histogram maker | ||
| 2 | Box plot maker | ||
| 3 | Maker | ||
| 4 | Maker | . 0246 0246 | |
| 6 | Scatter chart maker | ||
| 7 | Area chart maker |
Guide
- Guide
- Bonferroni correction
- Central Limit Theorem
- Confidence interval
- Линейная регрессия
- Логистическая регрессия
- Выбросы
- P-значение
- Асимметрия и эксцесс
- Стандартное отклонение
- Test power
Statistical Tests
- Chi-squared test
- Levene’s test
- Mann-Whitney U Rank test
- One Way ANOVA test
- Proportion test
- Shapiro Wilk test
- T-test
- T -test vs Z-Test
- Tukey HSD test
- Wilcoxon Sign Rank test
Goal
Целью этого веб-сайта является сделать статистику доступной для всех, переводя сложный статистический жаргон на обычный повседневный язык.
Мы помогаем всем подсчитывать статистику.
Калькуляторы также предоставляют R-коды для вашего удобства.
Мы начали добавлять пошаговое руководство для образовательных целей, простое руководство по подсчету тестовой статистики.
Условия
Мы приложили много усилий, чтобы предоставить точные результаты, и мы автоматически тестируем каждую новую страницу. Старые страницы тестировались вручную, но мы постепенно также автоматизируем старые страницы.
Обычно мы сравниваем результаты с результатами R.
Информация и инструменты на этом веб-сайте предоставляются КАК ЕСТЬ, БЕЗ КАКИХ-ЛИБО ГАРАНТИЙ.
Подсчет статистики
Лучший онлайн-калькулятор для подсчета статистики.
| Variable | Value |
|---|---|
| $_SERVER[‘LSPHP_ENABLE_USER_INI’] | on |
| $_SERVER[‘PATH’] | /usr/local/bin:/usr /bin:/bin |
| $_SERVER[‘TEMP’] | /tmp |
| $_SERVER[‘TMP’] | /tmp |
| $_SERVER[‘TMPDIR’] | /tmp |
| $_SERVER[‘PWD’] | / |
| $_SERVER [‘HTTP_ACCEPT’] | text/html,application/xhtml+xml,application/xml;q=0. 9,*/*;q=0.8 9,*/*;q=0.8 |
| $_SERVER[‘HTTP_ACCEPT_CHARSET’] | windows-1251,utf -8;q=0.7,*;q=0.7 |
| $_SERVER[‘HTTP_ACCEPT_ENCODING’] | gzip |
| $_SERVER[‘HTTP_ACCEPT_LANGUAGE’] | en-US,en;q=0.5 |
| $_SERVER[‘CONTENT_TYPE’] | application/x-www-form-urlencoded;charset024-8 |
| $_SERVER[‘CONTENT_LENGTH’] | 0 |
| $_SERVER[‘HTTP_HOST’] | www.statskingdom.com |
| $_SERVER[‘HTTP_USER_AGENT’] | Mozilla/5.0 (X11; Linux x86_64;rv:33.0) Gecko/20100101 Firefox/33.0 |
| $_SERVER[‘HTTP_CACHE_CONTROL’] | no-cache |
| $_SERVER[‘HTTP_X_FORWARDED_FOR’] | 176.9.44.166 |
| $_SERVER[‘HTTP_CF_IPCOUNTRY’] | DE |
| $_SERVER[ ‘HTTP_CDN_LOOP’] | cloudflare |
| $_SERVER[‘HTTP_CF_RAY’] | 74e8143a7f32c25b-VIE |
| $_SERVER[‘HTTP_X_FORWARDED_PROTO’] | https |
| $_SERVER[‘HTTP_CF_VISITOR’] | {«scheme»:»https»} |
| $_SERVER[‘HTTP_CF_CONNECTING_IP’] | 176. 9.44.166 9.44.166 |
| $_SERVER[‘HTTP_X_HTTPS’] | 1 |
| $_SERVER[‘REDIRECT_UNIQUE_ID ‘] | YyvbnVod5jZj1hYTOzZbMAAAHgY |
| $_SERVER[‘REDIRECT_SCRIPT_URL’] | /210varchi1.html |
| $_SERVER[‘REDIRECT_SCRIPT_URI’] | https://www.statskingdom.com/210varchi1.html |
| $_SERVER[‘REDIRECT_GD-USERNAME’] | qtlgsguvxu0r |
| $_SERVER[‘REDIRECT_HTTPS’] | on |
| $_SERVER[‘REDIRECT_SSL_TLS_SNI’] | www.statskingdom.com |
| $_SERVER[‘REDIRECT_HTTP2’] | on |
| $_SERVER[‘REDIRECT_h3PUSH’] | off |
| $_SERVER[‘REDIRECT_h3_PUSH’] | off |
| $_SERVER[‘REDIRECT_h3_PUSHED’] | no value |
| $_SERVER[‘REDIRECT_h3_PUSHED_ON’] | no value |
| $_SERVER[‘REDIRECT_h3_STREAM_ID’] | 3 |
| $_SERVER[‘REDIRECT_h3_STREAM_TAG’] | 30-3 |
| $_SERVER[‘REDIRECT_REQUEST_METHOD’] | GET |
| $_SERVER[‘REDIRECT_STATUS’] | 404 |
| $_SERVER[‘UNIQUE_ID’] | YyvbnVod5jZj1hYTOzZbMAAAHgY |
| $_SERVER[‘SCRIPT_URL’] | /210varchi1. html html |
| $_SERVER[‘SCRIPT_URI’] | https://www.statskingdom.com/210varchi1.html |
| $_SERVER[ ‘GD-USERNAME’] | qtlgsguvxu0r |
| $_SERVER[‘HTTPS’] | on |
| $_SERVER[‘SSL_TLS_SNI’] | www.statskingdom.com |
| $_SERVER[‘HTTP2 ‘] | на |
| $_SERVER[‘h3PUSH’] | off |
| $_SERVER[‘h3_PUSH’] | off |
| $_SERVER[‘h3_PUSHED’] | no value |
| $_SERVER[‘h3_PUSHED_ON’] | no value |
| $_SERVER[‘h3_STREAM_ID’] | 3 |
| $_SERVER[‘h3_STREAM_TAG’] | 30-3 |
| $_SERVER[‘SERVER_SIGNATURE’] | no value |
| $_SERVER[‘SERVER_SOFTWARE’] | Apache |
| $_SERVER[‘SERVER_NAME’] | www. statskingdom.com statskingdom.com |
| $_SERVER[‘SERVER_ADDR’] | 166.62.72.160 |
| $ _SERVER[‘SERVER_PORT’] | 443 |
| $_SERVER[‘REMOTE_ADDR’] | 172.68.51.36 |
| $_SERVER[‘DOCUMENT_ROOT’] | /home/qtlgsguvxu0r/public_html |
| $_SERVER [‘REQUEST_SCHEME’] | https |
| $_SERVER[‘CONTEXT_PREFIX’] | no value |
| $_SERVER[‘CONTEXT_DOCUMENT_ROOT’] | /home/qtlgsguvxu0r/public_html |
| $_SERVER[‘SERVER_ADMIN’] | [email protected] |
| $_SERVER[‘SCRIPT_FILENAME’] | /home/qtlgsguvxu0r/public_html/404.php |
| $_SERVER[‘REMOTE_PORT’] | 21990 |
| $_SERVER[‘REDIRECT_URL’] | /210varchi1.html |
| $_SERVER[‘SERVER_PROTOCOL’] | HTTP/2.0 |
| $_SERVER[‘REQUEST_METHOD’] | GET |
| $_SERVER [‘QUERY_STRING’] | no value |
| $_SERVER[‘REQUEST_URI’] | /210varchi1. html html |
| $_SERVER[‘SCRIPT_NAME’] | /404.php |
| $ _SERVER[‘PHP_SELF’] | /404.php |
| $_SERVER[‘REQUEST_TIME_FLOAT’] | 1663818653.9335 |
| $_SERVER[‘REQUEST_TIME’] | 1663818653 |
| $_ENV[‘LSPHP_ENABLE_USER_INI’] | on |
| $_ENV[‘PATH’] | /usr/local/bin:/usr/bin:/bin |
| $_ENV[‘TEMP’] | /tmp |
| $’_ENV[‘TMP | /tmp |
| $_ENV[‘TMPDIR’] | /tmp |
| $_ENV[‘PWD’] | / |
Статистика онлайн — проверка предположений, интерпретация результатов
Статистические тесты, диаграммы, вероятности и четкие результаты. Автоматически проверяет предположения, интерпретирует результаты и выводит графики, гистограммы и другие диаграммы.
Статистические онлайн-калькуляторы поддерживают не только статистику теста и p-значение, но и другие результаты, такие как размер эффекта, мощность теста и уровень нормальности.
Если одна из проверок не пройдена, средство рекомендует решение.
Какой статистический тест следует использовать? следующая ссылка поможет вам выбрать: выбрать статистический тест (опросник для принятия решения).
Test statistic calculators
Find the test statistic calculator
| Test | Assumptions | Required sample data | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Test name | Check | Statistic | Ind | σ | σ 1 =σ 2 | d | μ/p | x̄/p̂; | n | S | |||||
| 1 | One Sample Z-Test | Mean | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||
| 2 | Одновыборочный Т-критерий | Среднее | ✔ | ✔ | ✘ | 9 40246 | ✔ | ✔ | ||||||||
| 3 | Two Sample Z-Test | Mean | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||||
| 4 | Two Sample T-Test (Pooled variance) | Mean | ✔ | ✔ | ✘ | ✔ | ✔ | ✔ | ✔ | ✔ | ||||||
| 5 | Two Sample T-Test (Welch’s) | Mean | ✔ | ✔ | ✘ | ✘ | ✔ | ✔ | ✔ | ✔ | ||||||
| 6 | Two Sample Mann-Whitney U Test | Rank | ✔ | ✔ | ✔ | |||||||||||
| 7 | Paired T-Test | Mean | ✔ | Paired | ✔ | |||||||||||
| 8 | Paired Wilcoxon Sign Rank Test | Rank | Paired | ✔ | ||||||||||||
| 9 | One Way ANOVA Test | Mean | ✔ | ✔ | ✔ | ✔ | ||||||||||
| 10 | Repeated Measures ANOVA Test | Mean | ✔ | Dependent groups | Sphericity | ✔ | ||||||||||
| 11 | Kruskal-Wallis Test | Mean | ✔ | ✔ | ||||||||||||
| 12 | Двухлет Anova Test | |||||||||||||||
| 12 | . 0524 0524 | Mean | ✔ | ✔ | ✔ | ✔ | ||||||||||
| 13 | One Way MANOVA Test | Mean | F | ✔ | ✔ | ✔ | ✔ | |||||||||
| 13 | One Sample Proportion Test | Proportion | Binomial | ✔ | ✔ | ✔ | ✔ | |||||||||
| 14 | Two Sample Proportion Test | Proportion | Binomial | ✔ | ✔ | ✔ | ||||||||||
| 15 | Chi-Squared Test For Variance | σ | ✔ | ✔ | ✔ | ✔ | ✔ | |||||||||
| 16 | F Test For Variances | σ | ✔ | ✔ | ✔ | ✔ | ||||||||||
| 17 | Levene’s Test For Variances | σ | ✘ | ✔ | ✔ | Fit | ✔ | ✔ | ||||||||
| 19 | Shapiro-Wilk Test | Fit | ✔ | ✔ | ✔ | |||||||||||
| 20 | Колмогоров Смирновский Тест | FIT | D = MAX6 1≤N (D I + , D I + , D I + | , D .✔ | ✔ | |||||||||||
| 21 | Kaplan Meier Survival Analysis | Survival | ✔ | ✔ | ||||||||||||
** ✔- да, ✘- нет, пусто — не имеет значения
Калькулятор регрессии
| # | Регрессия | Статистика |
|---|---|---|
| 1 | Простая линейная регрессия0246 | |
| 2 | Multiple Linear Regression | |
| 3 | *Bulk Linear Regression | |
| 4 | Binary Logistic Regression | χ2 = 2(LL 1 -LL 0 ) |
| 5 | Многономическая логистическая регрессия | χ2 = 2 (LL 1 -LL 0 ) |
*)
*).
Sample size calculators
| # | Calculator | Image |
|---|---|---|
| 1 | Sample size | |
| 2 | Test power | |
| 3 | Effect size | |
| 4 | Доверительные интервалы (среднее, стандартное отклонение, доля, корреляция) |
Калькуляторы распределения
| # | Distribution | Image |
|---|---|---|
| 1 | P-value | |
| 2 | Distributions | |
| 2 | Normal Distribution | |
| 2 | Binomial Distribution | |
| 3 | Т-распределение (студенческое) | |
| 4 | Распределение хи-квадрат | |
| 5 | F Distribution (Fisher-Snedecor) |
Statistical tables
| # | Table |
|---|---|
| 1 | Z table |
| 2 | T table |
Статистические калькуляторы
Каждый статистический калькулятор содержит пошаговые расчеты.
| # | Статистический калькулятор | Изображение | ||
|---|---|---|---|---|
| 1 | Средний средний режим (Q 1 , Q 3 , IRQ, диапазон) | |||
| 2 | Стандартный (VARIANT, SEM, SEM, SEM, SEM, MAD) | 2 | . 3Среднее (сумма, счет) | x̄ |
| 3 | Среднее значение (сумма, Count) | x̄ | ||
| 4 | 96 | |||
| 4 | 45 | |||
| 4 | 46 | |||
| . | ||||
| 5 | Среднее гармоническое | H | ||
| 6 | Вероятность (вероятность, формула, зависимые события, теорема Bayes, Salcement). Калькулятор корреляции (корреляция Пирсона, ранговая корреляция Спирмена)0246 | |||
| 10 | Цепочный калькулятор марковского марковского (вектор NTH-стадии, стационарный вектор) | |||
| 11 | . Расчет падений. калькулятор коэффициентов (дробные коэффициенты, десятичные коэффициенты, американские коэффициенты) | |||
| 13 | Калькулятор среднего абсолютного отклонения (калькулятор MAD) | |||
| 14 | Median absolute deviation calculator (MAD calculator) |
Chart makers
| # | Chart | Image | |
|---|---|---|---|
| 1 | Histogram maker | ||
| 2 | Box plot maker | ||
| 3 | Maker | ||
| 4 | Maker | . 0246 0246 | |
| 6 | Scatter chart maker | ||
| 7 | Area chart maker |
Guide
- Guide
- Bonferroni correction
- Central Limit Theorem
- Confidence interval
- Линейная регрессия
- Логистическая регрессия
- Выбросы
- P-значение
- Асимметрия и эксцесс
- Стандартное отклонение
- Test power
Statistical Tests
- Chi-squared test
- Levene’s test
- Mann-Whitney U Rank test
- One Way ANOVA test
- Proportion test
- Shapiro Wilk test
- T-test
- T -test vs Z-Test
- Tukey HSD test
- Wilcoxon Sign Rank test
Goal
Целью этого веб-сайта является сделать статистику доступной для всех, переводя сложный статистический жаргон на обычный повседневный язык.
Мы помогаем всем подсчитывать статистику.
Калькуляторы также предоставляют R-коды для вашего удобства.
Мы начали добавлять пошаговое руководство для образовательных целей, простое руководство по подсчету тестовой статистики.
Условия
Мы приложили много усилий, чтобы предоставить точные результаты, и мы автоматически тестируем каждую новую страницу. Старые страницы тестировались вручную, но мы постепенно также автоматизируем старые страницы.
Обычно мы сравниваем результаты с результатами R.
Информация и инструменты на этом веб-сайте предоставляются КАК ЕСТЬ, БЕЗ КАКИХ-ЛИБО ГАРАНТИЙ.
Подсчет статистики
Лучший онлайн-калькулятор для подсчета статистики.
Калькулятор статистических таблиц
Калькуляторы для записей в статистических таблицах
| | з до Р | |
| | хи-квадрат в P | |
| | т к Р | |
| | р к П | |
| | Ф до Ф | |
| | Преобразование Фишера r-to-z | |
| | . 05 и .01 критические значения 05 и .01 критические значения Статистика студенческого диапазона Q | |
| | Коэффициенты и журнал коэффициентов |
Калькулятор от Z до P
Для любого заданного значения z этот раздел рассчитает
| º | соответствующие односторонние вероятности z и +z; | |
| º | двусторонняя вероятность ±z; | |
| º | и долю нормального распределения между z и +z. |
Для продолжения введите значение z в обозначенную ячейку и нажмите «Рассчитать». Обратите внимание, что программирование для этого раздела способно выполнять осмысленные расчеты вероятностей только для случаев, когда |z|
Обратите внимание, что программирование для этого раздела способно выполнять осмысленные расчеты вероятностей только для случаев, когда |z|
5.
| Нажмите здесь, чтобы увидеть подробности выборочного распределения к которому любое конкретное значение z принадлежит. |
| Вероятности | Р |
Вернуться к началу
Калькулятор хи-квадрат в P
Для значений df от 1 до 20 включительно в этом разделе будет рассчитана доля соответствующего выборочного распределения, которая находится справа от определенного значения хи-квадрат. Чтобы продолжить, введите значения хи-квадрат и df в указанные ячейки и нажмите «Рассчитать».
Чтобы продолжить, введите значения хи-квадрат и df в указанные ячейки и нажмите «Рассчитать».
| Хи-квадрат | df | P | ||
| 4141 Нажмите здесь, чтобы увидеть подробности отбора проб распределения, к которому любое конкретное значение хи-квадрат принадлежит. В командной строке введите подходящее значение df. Вернуться к началу В этом разделе будут вычислены односторонние и двусторонние вероятности t для любого заданного значения df. Чтобы продолжить, введите значения t и df в указанные ячейки и нажмите «Рассчитать».
Нажмите здесь, чтобы увидеть подробности отбора проб Если истинная корреляция между X и Y в общей популяции составляет rho=0,, и если размер выборки N, на которой основано наблюдаемое значение r, равен или больше 6, то количество
распределяется примерно как t с df=N2.Применение этой формулы к любому конкретному наблюдаемому выборочному значению r соответственно проверит нулевую гипотезу о том, что наблюдаемое значение исходит из совокупности, в которой ро=0. Чтобы оценить значимость любого конкретного экземпляра r, введите значения N [ > 6] и r в указанные ниже ячейки, затем нажмите кнопку «Рассчитать».
Вернуться к началу Для любого конкретного значения r, коэффициента корреляции момента продукта Пирсона, в этом разделе будет выполнено преобразование Fisher r-to-zпо формуле
Если введено значение n (необязательно), стандартная ошибка z r также будет рассчитана как
| ||||
|---|---|---|---|---|



 S. Census Bureau, Population Division
S. Census Bureau, Population Division
 S. Energy Information Administration (EIA)
S. Energy Information Administration (EIA) S. Weight Loss & Diet Control Market — MarketData Enterprises, Inc., May 1, 2011
S. Weight Loss & Diet Control Market — MarketData Enterprises, Inc., May 1, 2011



 В этом случае можно с высокой степенью уверенности утверждать, что наблюдаемая разница между группами значима (связана с их различиями, а не случайностью).
В этом случае можно с высокой степенью уверенности утверждать, что наблюдаемая разница между группами значима (связана с их различиями, а не случайностью).
 0246
0246 0246
0246 В командной строке введите соответствующий
В командной строке введите соответствующий  Чтобы продолжить, введите значения F и df в указанные ячейки и нажмите «Рассчитать».
Чтобы продолжить, введите значения F и df в указанные ячейки и нажмите «Рассчитать». Чтобы продолжить, введите количество групп в анализе (k) и количество степеней свободы, а затем нажмите «Рассчитать». Обратите внимание, что значение k должно быть от 3 до 10 включительно.
Чтобы продолжить, введите количество групп в анализе (k) и количество степеней свободы, а затем нажмите «Рассчитать». Обратите внимание, что значение k должно быть от 3 до 10 включительно. При вводе p это может быть либо десятичная дробь, либо обыкновенная дробь.
При вводе p это может быть либо десятичная дробь, либо обыкновенная дробь. Задайте вопросы или просмотрите примеры задач.
Задайте вопросы или просмотрите примеры задач. Выберите самый простой вариант. Здесь
некоторые вещи, чтобы рассмотреть.
Выберите самый простой вариант. Здесь
некоторые вещи, чтобы рассмотреть. Это мера среднего расстояния
индивидуальные наблюдения от среднего значения группы.
Это мера среднего расстояния
индивидуальные наблюдения от среднего значения группы. Числа от 0 до 1 количественно
неопределенность, связанная с событием. Например, вероятность
подбрасывание монеты, в результате которого выпадет орел (а не решка), будет равно 0,50. Пятьдесят процентов
в то время при подбрасывании монеты выпадал орел; и пятьдесят процентов
время, это приведет к хвостам.
Числа от 0 до 1 количественно
неопределенность, связанная с событием. Например, вероятность
подбрасывание монеты, в результате которого выпадет орел (а не решка), будет равно 0,50. Пятьдесят процентов
в то время при подбрасывании монеты выпадал орел; и пятьдесят процентов
время, это приведет к хвостам. д.). Таким образом, мы спрашиваем о кумулятивной вероятности.
д.). Таким образом, мы спрашиваем о кумулятивной вероятности.
 Ан
альтернативной стратегией, не требующей вычисления t-статистики, была бы
использовать калькулятор в режиме «средний балл». Эта стратегия может быть немного
немного проще. Это показано в следующем примере.
Ан
альтернативной стратегией, не требующей вычисления t-статистики, была бы
использовать калькулятор в режиме «средний балл». Эта стратегия может быть немного
немного проще. Это показано в следующем примере. (В подобных ситуациях количество
степеней свободы равно количеству наблюдений минус 1. Следовательно,
число степеней свободы равно 14 — 1 или 13.)
(В подобных ситуациях количество
степеней свободы равно количеству наблюдений минус 1. Следовательно,
число степеней свободы равно 14 — 1 или 13.)