| 1 | Найти число возможных исходов | 7 выбор 3 | |
| 2 | Найти число возможных исходов | 8 выбор 3 | |
| 3 | Найти число возможных исходов | 5 выбор 2 | |
| 4 | Найти число возможных исходов | 4 выбор 2 | |
| 5 | Найти число возможных исходов | 8 выбор 4 | |
| 6 | Найти число возможных исходов | 10 выбор 3 | |
| 7 | Найти число возможных исходов | 7 выбор 4 | |
| 8 | Найти число возможных исходов | 6 выбор 3 | |
| 9 | Найти число возможных исходов | 9 выбор 3 | |
| 10 | Найти число возможных исходов | 3 выбор 2 | |
| 11 | Найти число возможных исходов | 6 выбор 4 | |
| 12 | Найти число возможных исходов | 5 выбор 4 | |
| 13 | Найти число возможных исходов | 7 перестановка 3 | |
| 14 | Найти число возможных исходов | 7 выбор 2 | |
| 15 | Найти число возможных исходов | 10 выбор 5 | |
| 16 | Найти число возможных исходов | 10 выбор 6 | |
| 17 | Найти число возможных исходов | 13 выбор 5 | |
| 18 | Найти число возможных исходов | 3 выбор 3 | |
| 19 | Найти число возможных исходов | 4 выбор 1 | |
| 20 | Найти число возможных исходов | 4 выбор 4 | |
| 21 | Найти число возможных исходов | ||
| 22 | Найти число возможных исходов | 6 перестановка 3 | |
| 23 | Найти число возможных исходов | 8 выбор 5 | |
| 24 | Найти число возможных исходов | 9 перестановка 4 | |
| 25 | Найти число возможных исходов | 13 выбор 3 | |
| 26 | Найти число возможных исходов | 12 выбор 2 | |
| 27 | Найти число возможных исходов | 12 выбор 4 | |
| 28 | Найти число возможных исходов | 12 выбор 3 | |
| 29 | Найти число возможных исходов | 9 выбор 5 | |
| 30 | Найти число возможных исходов | 9 выбор 2 | |
| 31 | Найти число возможных исходов | 7 выбор 5 | |
| 32 | Найти число возможных исходов | 6 перестановка 6 | |
| 33 | Найти число возможных исходов | 8 перестановка 5 | |
| 34 | Найти число возможных исходов | 8 перестановка 3 | |
| 35 | Найти число возможных исходов | 7 перестановка 5 | |
| 36 | Найти число возможных исходов | 52 выбор 5 | |
| 37 | Найти число возможных исходов | 5 перестановка 3 | |
| 38 | Найти число возможных исходов | 12 выбор 5 | |
| 39 | Найти число возможных исходов | 3 выбор 1 | |
| 40 | Найти число возможных исходов | 11 выбор 5 | |
| 41 | Найти число возможных исходов | 10 выбор 2 | |
| 42 | Найти число возможных исходов | 15 выбор 3 | |
| 43 | Найти число возможных исходов | 52 выбор 4 | |
| 44 | Найти число возможных исходов | 9 выбор 4 | |
| 45 | Найти число возможных исходов | 9 перестановка 3 | |
| 46 | Найти число возможных исходов | 7 перестановка 4 | |
| 47 | Найти число возможных исходов | 7 перестановка 2 | |
| 48 | Найти число возможных исходов | ||
| 49 | Найти число возможных исходов | 11 выбор 2 | |
| 50 | Найти число возможных исходов | 11 выбор 3 | |
| 51 | Найти число возможных исходов | 10 перестановка 5 | |
| 52 | Найти число возможных исходов | 5 выбор 5 | |
| 53 | Найти число возможных исходов | 6 выбор 1 | |
| 54 | Найти число возможных исходов | 8 перестановка 4 | |
| 55 | Найти число возможных исходов | 8 выбор 6 | |
| 56 | Найти число возможных исходов | 13 выбор 4 | |
| 57 | Вычислить | e | |
| 58 | Найти уравнение, перпендикулярное прямой | -7x-5y=7 | |
| 59 | Найти число возможных исходов | 13 выбор 2 | |
| 60 | Найти число возможных исходов | 10 перестановка 2 | |
| 61 | Найти число возможных исходов | 10 перестановка 3 | |
| 62 | Найти число возможных исходов | 10 выбор 7 | |
| 63 | Найти число возможных исходов | 20 выбор 4 | |
| 64 | Найти число возможных исходов | 6 перестановка 4 | |
| 65 | Найти число возможных исходов | 5 перестановка 4 | |
| 66 | Найти число возможных исходов | 6 выбор 5 | |
| 67 | Найти число возможных исходов | 52 выбор 3 | |
| 68 | Найти число возможных исходов | 4 выбор 0 | |
| 69 | Найти число возможных исходов | 9 перестановка 7 | |
| 70 | Найти число возможных исходов | 6 выбор 2 | |
| 71 | Найти число возможных исходов | 5 перестановка 5 | |
| 72 | Найти число возможных исходов | 5 перестановка 2 | |
| 73 | Найти число возможных исходов | 6 выбор 6 | |
| 74 | Найти число возможных исходов | 7 выбор 6 | |
| 75 | Найти число возможных исходов | 8 перестановка 6 | |
| 76 | Найти число возможных исходов | 7 перестановка 7 | |
| 77 | Найти число возможных исходов | 9 перестановка 5 | |
| 78 | Найти число возможных исходов | 2 перестановка 2 | |
| 79 | Найти число возможных исходов | 10 выбор 8 | |
| 80 | Найти число возможных исходов | 12 выбор 7 | |
| 81 | Найти число возможных исходов | 15 выбор 5 | |
| 82 | Найти обратный элемент | [[1,0,1],[2,-2,-1],[3,0,0]] | |
| 83 | Определить область значений | 1/4x-7 | |
| 84 | Найти число возможных исходов | 10 перестановка 7 | |
| 85 | Найти число возможных исходов | 12 выбор 6 | |
| 86 | Найти число возможных исходов | 2 выбор 1 | |
| 87 | Найти число возможных исходов | 30 выбор 3 | |
| 88 | Найти число возможных исходов | 9 выбор 6 | |
| 89 | Найти число возможных исходов | 8 перестановка 2 | |
| 90 | Найти число возможных исходов | 7 выбор 1 | |
| 91 | Найти число возможных исходов | 6 перестановка 2 | |
| 92 | Найти число возможных исходов | 4 перестановка 2 | |
| 93 | Найти число возможных исходов | 4 перестановка 3 | |
| 94 | Найти число возможных исходов | 3 перестановка 3 | |
| 95 | Найти число возможных исходов | 46 выбор 6 | |
| 96 | Найти число возможных исходов | 5 перестановка 1 | |
| 97 | Найти число возможных исходов | 52 выбор 7 | |
| 98 | Найти число возможных исходов | 52 перестановка 5 | |
| 99 | Найти число возможных исходов | 9 выбор 1 | |
| 100 | Найти число возможных исходов | 9 перестановка 6 |
ЕГЭ Профиль №8.
 Тригонометрические уравнения и неравенства — math200.ru Skip to content
Тригонометрические уравнения и неравенства — math200.ru Skip to contentЕГЭ Профиль №8. Тригонометрические уравнения и неравенстваadmin2022-09-19T20:44:02+03:00
Скачать файл в формате pdf.
ЕГЭ Профиль №8. Тригонометрические уравнения и неравенства
| Задача 1. Мяч бросили под углом \(\alpha \) к плоской горизонтальной поверхности земли. Время полета мяча (в секундах) определяется по формуле \(t = \frac{{2\,{v_0}\,\sin \alpha }}{g}\). При каком наименьшем значении угла \(\alpha \) (в градусах) время полета будет не меньше 3 секунд, если мяч бросают с начальной скоростью \({v_0} = 30\) м/с? Считайте, что ускорение свободного падения \(g = 10\) м/с2. Ответ ОТВЕТ: 30. Решение Задача сводится к решению неравенства: \(\frac{{2{v_0}\sin \,\alpha }}{g} \geqslant 3,\) где v0 = 30 м/с, g = 10 м/c2 и \(\alpha \in \left( {0;{{90}^\circ }} \right). Ответ: 0,01. |
| Задача 10. Скорость колеблющегося на пружине груза меняется по закону \(v\left( t \right) = 5\sin \pi \,t\) (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых. Ответ ОТВЕТ: 0,67. Решение Задача сводится к решению неравенства: \(5\sin \pi \,t > 2,5\) при \(t \in \left[ {0;\,1} \right].\) \(5\sin \pi t > 2,5\,\,\,\,\,\,\, \Leftrightarrow \,\,\,\,\,\,\,\sin \pi t > \frac{1}{2}\,\,\,\,\,\,\, \Leftrightarrow \,\,\,\,\,\,\,\frac{\pi }{6} + 2\pi k < \pi \,t < \frac{{5\pi }}{6} + 2\pi k\,\,\,\,\, \Leftrightarrow \) \( \Leftrightarrow \,\,\,\,\,\frac{1}{6} + 2k < t < \frac{5}{6} + 2k,\,\,\,\,k \in z.\) При k = 0 получим \(\frac{1}{6} < t < \frac{5}{6}.\) Так как по условию \(t \in \left[ {0;\,1} \right]\), то \(t \in \left( {\frac{1}{6};\frac{5}{6}} \right)\), что составляет \(\frac{5}{6} — \frac{1}{6} = \frac{4}{6} = \frac{2}{3}\) от первой секунды, то есть, округляя до сотых, получим 0,67. При k = 0 получим \(0 \leqslant t \leqslant \frac{4}{5}.\) Так как по условию \(t \in \left[ {0;\,1} \right]\), то \(t \in \left[ {0;\,\frac{4}{5}} \right]\), что составляет \(\frac{4}{5}\) от первой секунды, то есть 80%. Если k ≠ 0, то \(t \notin \left[ {0;\,1} \right]\). Ответ: 80. |
Реклама
Поддержать нас
4.3 Двойной угол, половинный угол и формулы приведения
Результаты обучения
- Используйте формулы двойного угла, чтобы найти точные значения.
- Используйте формулы двойного угла для проверки тождества.
- Используйте формулы сокращения для упрощения выражения.
- Используйте формулы половинного угла, чтобы найти точные значения.
Использование формул двойного угла для нахождения точных значений
В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций. Теперь еще раз взглянем на те же формулы. формулы двойного угла являются частным случаем формул суммы, где [латекс]\альфа =\бета [/латекс]. Вывод формулы двойного угла для синуса начинается с формулы суммы
Теперь еще раз взглянем на те же формулы. формулы двойного угла являются частным случаем формул суммы, где [латекс]\альфа =\бета [/латекс]. Вывод формулы двойного угла для синуса начинается с формулы суммы
[латекс]\sin \left(\alpha +\beta \right)=\sin \alpha \cos \beta +\cos \alpha \sin \beta [/latex]
Если мы допустим [латекс]\альфа =\бета =\тета [/латекс], то мы получим
[латекс]\начало{выравнивание}\sin \left(\theta +\theta \right )&=\sin\theta\cos\theta+\cos\theta\sin\theta\\\sin\left(2\theta\right)&=2\sin\theta\cos\theta\end{align}[ /латекс] 9{2}\theta }\end{align}[/latex]
Как сделать: Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение.
- Нарисуйте треугольник, чтобы отразить полученную информацию.
- Определите правильную формулу двойного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.

Пример 1. Использование формулы двойного угла для нахождения точного значения, включающего тангенс
Учитывая, что [латекс]\тан \тета =-\фрак{3}{4}[/латекс] и [латекс]\тета [/латекс] находится в квадранте II, найдите следующее:
- [латекс] \sin\left(2\theta\right)[/латекс]
- [латекс]\cos\влево(2\тета\вправо)[/латекс]
- [латекс]\загар \влево(2\тета\вправо)[/латекс]
Показать решение
Попробуйте
Дано [латекс]\sin \alpha =\frac{5}{8}[/latex], с [латекс]\тета [/латекс] в квадранте I, найдите [латекс]\cos \left (2\альфа\справа)[/латекс].
Показать решение
Попробуйте
Пример 2. Использование формулы двойного угла для косинуса без точных значений
Используйте формулу двойного угла для косинуса, чтобы записать [латекс]\cos \left(6x\right)[/latex] в терминах из [латекс]\cos\left(3x\right)[/латекс].
Показать решение
Использование формул двойного угла для проверки тождественности
Установление тождества с использованием формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для получения формул суммы и разности. Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной. 9{2}\тета [/латекс].
Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной. 9{2}\тета [/латекс].
Показать решение
Использование формул приведения для упрощения выражения
Формулы двойного угла можно использовать для получения формул приведения , которые являются формулами, которые мы можем использовать для уменьшения мощности данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны в курсах математики более высокого уровня, в частности исчисления. Также называемые формулами уменьшения степени, включены три тождества, которые легко выводятся из формул двойного угла. 9{2}\theta} \\ &=\frac{\frac{1-\cos\left(2\theta\right)}{2}}{\frac{1+\cos\left(2\theta\right) )}{2}}&& \text{Подставьте формулы приведения.} \\ &=\left(\frac{1-\cos \left(2\theta \right)}{2}\right)\left(\ frac{2}{1+\cos \left(2\theta\right)}\right) \\ &=\frac{1-\cos \left(2\theta \right)}{1+\cos \left (2\theta \right)} \end{align}[/latex]
A Общее примечание: формулы приведения
Формулы приведения резюмируются следующим образом:
[латекс]\begin{align} &{\ sin } ^ {2} \ theta = \ frac {1- \ cos \ left (2 \ theta \ right)} {2} \\ & {\ cos } ^ {2} \ theta = \ frac {1+ \ cos \left(2\theta\right)}{2} \\ &{\tan}^{2}\theta=\frac{1-\cos\left(2\theta\right)}{1+\cos\ влево(2\тета\вправо)} \end{выравнивание}[/latex] 9{4}x=\frac{15}{4}+5\cos\left(2x\right)+\frac{5}{4}\cos\left(4x\right)[/latex].
Показать решение
Попробуйте
Использование формул половинного угла для нахождения точных значений
Следующий набор тождеств — это набор из формул половинного угла , которые можно вывести из формул приведения и использовать, когда у нас есть угол это половина размера специального угла. Если мы заменим [латекс]\тета [/латекс] на [латекс]\фракция{\альфа}{2}[/латекс], формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для [латекс]\ sin \left(\frac{\alpha}{2}\right)[/latex]. Обратите внимание, что формулам половинного угла предшествует знак [латекс]\pm [/латекс]. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается [latex]\frac{\alpha }{2}[/latex]. 9{2}\left(\frac{\alpha}}{2}\right)&=\frac{1-\cos\left(2\cdot \frac{\alpha}{2}\right)}{1+\ cos \left(2\cdot \frac{\alpha }{2}\right)} \\ &=\frac{1-\cos \alpha }{1+\cos \alpha}\hfill \\ \tan \left (\ frac{\ alpha} {2} \ right) & = \ pm \ sqrt {\ frac {1- \ cos \ alpha } {1+ \ cos \ alpha}} \ end {align} [/latex]
Общее примечание: формулы половинного угла
Формулы половинного угла следующие:
[латекс]\begin{align}\sin \left(\frac{\alpha}{2}\right)&= \pm \sqrt{\frac{1-\cos\alpha}}{2}} \\\text{} \\ \cos\left(\frac{\alpha}{2}\right)&=\pm \sqrt {\ frac {1+ \ cos \ alpha} {2}} \\ \ text { } \\ \ tan \ left (\ frac {\ alpha {2} \ right) & = \ pm \ sqrt {\ frac { 1-\cos\alpha}{1+\cos\alpha}} \\ &=\frac{\sin\alpha}}{1+\cos\alpha} \\ &=\frac{1-\cos\alpha} {\ грех \ альфа} \ конец {выравнивание} [/латекс] 9{\circ}\right)[/latex] по формуле половинного угла.
Показать решение
Как: Даны тангенс угла и квадрант, в котором находится угол, найти точные значения тригонометрических функций половины угла.
- Нарисуйте треугольник для представления данной информации.
- Определите правильную формулу половинного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.
Пример 8. Нахождение точных значений с использованием тождеств половинного угла
Учитывая, что [латекс]\тангенс \альфа =\фрак{8}{15}[/латекс] и [латекс]\альфа [/латекс] лежат в квадранте III, найдите точное значение следующего:
- [латекс]\sin\left(\frac{\alpha }{2}\right)[/latex]
- [латекс]\cos\left(\frac{\alpha}{2}\right)[/latex]
- [латекс]\загар \влево(\фракция{\альфа}{2}\вправо)[/латекс]
Показать решение
Попробуйте
Учитывая, что [латекс]\sin \alpha =-\frac{4}{5}[/latex] и [латекс]\альфа [/латекс] лежат в квадранте IV, найдите точное значение [ латекс]\cos\left(\frac{\alpha }{2}\right)[/latex].
Показать решение
Попробуйте
Пример 9: Нахождение измерения половинного угла
Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа предназначена для соревнований высокого уровня с углом [латекс]\тета [/латекс], образованным рампой и землей. Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если [латекс]\тан \тета =\фрак{5}{3}[/латекс] для соревнований более высокого уровня, каково измерение угла для соревнований новичков? 9{2}\theta =\frac{1-\cos\left(2\theta\right)}{1+\cos \left(2\theta\right)} \end{align}[/latex]
Ключевые понятия
- Тождества двойных углов получаются из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса.

- Формулы редукции особенно полезны в математических вычислениях, поскольку они позволяют уменьшить мощность тригонометрического члена.
- Формулы половинного угла позволяют нам найти значение тригонометрических функций, содержащих половинные углы, независимо от того, известен исходный угол или нет.
Глоссарий
- формулы двойного угла
- тождества, полученные из формул суммы синуса, косинуса и тангенса, в которых углы равны
- формулы половинного угла
- тождества, полученные из формул приведения и используемые для определения значений половинных углов тригонометрических функций
- формулы сокращения
- тождества, полученные из формул двойного угла и используемые для уменьшения степени тригонометрической функции
Тригонометрические тождества половинного угла — Тригонометрические формулы и вывод половинного угла
Триггерные тождества половинного угла или функции, фактически участвующие в тех тригонометрических функциях, в которых есть половинные углы. Квадратный корень первых двух функций синуса и косинуса, отрицательный или положительный, полностью зависит от наличия угла в квадранте. Узнайте больше о Trig Identities на сайте trigidentities.info.
Квадратный корень первых двух функций синуса и косинуса, отрицательный или положительный, полностью зависит от наличия угла в квадранте. Узнайте больше о Trig Identities на сайте trigidentities.info.
Вот исчерпывающая таблица, которая ясно изображает полуугловые тождества всех основных тригонометрических тождеств. Узнайте больше о Обратные тождества триггеров .
Сегодня мы собираемся вывести следующие формулы полуугла треугольника.
Формула половинного угла – синусТеперь, если мы допустим
- θ = α/2
затем 2 θ = α and our formula becomes:
- cos α = 1 − 2 sin 2 ( 2 α )
Теперь найдем
- Sin (α/2)
- 2 sin 2 ( 2 α ) =1-cos α
- SIN ˆ 2 (2 α 3 ) = 1– Cos 3339 ) = 1– Cos 3333 ) = 1 – COS 3333 ) = 1 – COS 3333 ) = 1–10333333 ) = 1–10333333 ).

Решение дает нам следующий синус полуугла тождество:
Теперь поговорим о положительном или отрицательном знаке Sin (α/2).
- Если угол лежит в первом квадранте, то все положительные значения синусоидальной половинной идентичности угла будут положительными.
- И если он находится в квадранте 3 rd или 4 th , мы введем отрицательный знак с синусоидальной половинной идентичностью угла.
Просто используя аналогичный процесс, с теми же заменами, которые мы сделали выше. Теперь мы должны подставить эти значения в следующее тождество триггера.
- COS 2 θ = 2COS 2 θ 3393


 2}}}{2} = 0,04 \cdot 0,25 = 0,01\) Дж.
2}}}{2} = 0,04 \cdot 0,25 = 0,01\) Дж.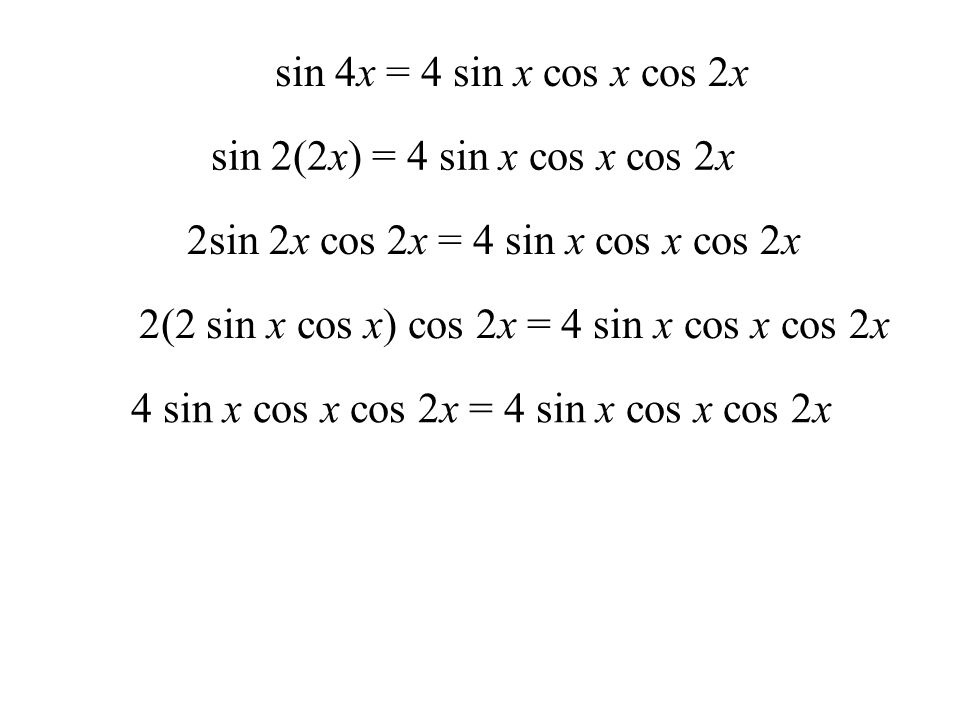 \circ } \cdot k\,\,\,\,\,\,\, \Leftrightarrow \,\,\,\,\,\,\frac{{12}}{5}k \leqslant t \leqslant \frac{4}{5} + \frac{{12}}{5}k,\,\,\,\,\,k \in z.\)
\circ } \cdot k\,\,\,\,\,\,\, \Leftrightarrow \,\,\,\,\,\,\frac{{12}}{5}k \leqslant t \leqslant \frac{4}{5} + \frac{{12}}{5}k,\,\,\,\,\,k \in z.\)