Формулы, применяемые как для синуса, так и косинуса половинного угла не зависит от заданного значения угла α. Для тангенса в независимости от угла α определяется следующим видом \[\tan \frac{\alpha}{2}\], где значение угла a≠π+2π•z, а значение z равняется любому целому числу. Значение выражения 1+cosα не должно быть равно нулю. Формула котангенса угла будет считаться верной, если любой угол α, где имеет место быть половинный угол α в тригонометрии, принимает следующий вид α ≠2π•z.
Самыми важными тригонометрическими формулами половинного угла являются тригонометрических функций с квадратами, которые могут быть выведены и через положительные, и отрицательное значение арифметического квадратного корня. Получаются следующие формулы половинного угла:
\[ \frac{\sin \sin \alpha}{2}=\pm \frac{\sqrt{1-\cos \alpha}}{\sqrt{2}}, \frac{\cos \cos \alpha}{2}=\pm \frac{\sqrt{1+\cos \alpha}}{\sqrt{2}}, \quad \tan \frac{\alpha}{2}=\frac{\sqrt{1-\cos \alpha}}{\sqrt{1+\cos \alpha}}, \cot \frac{\alpha}{2}=\frac{\sqrt{1+\cos \alpha}}{\sqrt{1-\cos \alpha}} \]
Знак «-» свидетельствуют о том, что тригонометрическая функция определяется четвертью угла \[\frac{\alpha}{2}\]
Доказательство тригонометрических функций половинного угла
Доказательство тригонометрических формул половинного угла строится на основании формулы косинуса двойного угла \[\cos \alpha=1-2 \times \frac{\alpha}{2}\] и \[\cos \alpha=2 \times \frac{\alpha}{2}-1\].
{\circ}=\frac{\sqrt{2+\sqrt{3}}}{2}\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Рассмотрим ещё одно задание.
Необходимо вычислить значение указанного выражения \[\frac{4 \cos \alpha}{2}+2 \cos \alpha+5\], где \[\cos \alpha=\frac{1}{8}\].
Решение:
Нужно использовать ту же самую формулу, которую применяли в первом примере \[\frac{\cos \alpha}{2}=\pm \frac{\sqrt{1+\cos \alpha}}{\sqrt{2}}\]. Подставим значение косинуса, упростим данное выражение:
\[ \frac{4 \sqrt{1+\cos \alpha}}{\sqrt{2}}+2 \cos \alpha+5=\frac{4 \sqrt{1+\frac{1}{8}}}{\sqrt{2}}+2 \times \frac{1}{8}+5=\frac{4 \sqrt{9}}{\sqrt{16}}+\frac{1}{4}+5=8 \frac{1}{4} \]
Ответ: \[\frac{4 \cos \alpha}{2}+2 \cos \alpha+5=8 \frac{1}{4}\].
Применяя формулы тригонометрического половинного угла, нужно учитывать, что угол может быть и нестандартного вида a2 и a, а его нужно будет привести к такому стандартному виду.
2\frac{23π}{12}-\sqrt{27}=\sqrt{108}\)\( \frac{1+\cos\frac{2\cdot 23π}{12}}{2}\)\(-\sqrt{27}=\sqrt{108}\)\(\frac{1+\cos\frac{23π}{6}}{2}\)\(-\sqrt{27}=\)…
\(\frac{23π}{6}=\frac{24π-π}{6}=\frac{24π}{6}-\frac{π}{6}=4π-\frac{π}{6}\).
Попали в самое большое из трех стандартных значений косинуса: \(\frac{1}{2}\), \(\frac{\sqrt{2}}{2}\), \(\frac{\sqrt{3}}{2}\). Значит \(\cos\frac{23π}{6}=\frac{\sqrt{3}}{2}\).
…\(=\sqrt{108}\)\(\frac{1+\frac{\sqrt{3}}{2}}{2}\)\(-\sqrt{27}=\sqrt{27\cdot 4}\)\(\frac{1+\frac{\sqrt{3}}{2}}{2}\)\(-\sqrt{27}=2\sqrt{27}\cdot\)\(\frac{1+\frac{\sqrt{3}}{2}}{2}\)\(-\sqrt{27}=\sqrt{27}(1+\frac{\sqrt{3}}{2})-\sqrt{27}=\)
\(=\sqrt{27}+\frac{\sqrt{27\cdot 3}}{2}-\sqrt{27}=\frac{\sqrt{81}}{2}=\frac{9}{2}=4,5\).
Это решение не самое простое из всех возможных (наиболее легкое приведено в статье «формулы двойного угла»), но до него легче всего догадаться, если знаешь формулу половинного угла.
2\frac{7π}{8}\).
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\cos\frac{7π}{4}}{2}\)\(=\)
Вычислим косинус с помощью формулы приведения. Для этого сначала преобразуем \(\frac{7π}{4}\):
\(\frac{7π}{4}=\frac{8π-π}{4}=\frac{8π}{4}-\frac{π}{4}=2π-\frac{π}{4}\)
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\cos(2π-\frac{π}{4})}{2}\)\(=\)
Теперь применим к косинусу формулу приведения:
-
\((2π-\frac{π}{4})\) – это четвертая четверть, косинус в ней положителен. Значит, знак перед косинусом останется прежним.
-
\(2π\) — находится на «горизонтали» — функция остается прежней.
\(\cos(2π-\frac{π}{4})=\cos\frac{π}{4}\).
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\cos\frac{π}{4}}{2}\)\(=\)
\(\cos\frac{π}{4}=\frac{\sqrt{2}}{2}\).
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\frac{\sqrt{2}}{2}}{2}\)\(=\)
Домножим числитель и знаменатель дроби на \(2\), чтоб избавиться от «трехэтажности».
\(=\sqrt{32}-\sqrt{128}\)\(\frac{2-\sqrt{2}}{4}\)\(=\)
Игнорировать корни больше невозможно. Вынесем из \(\sqrt{128}\) четверку, чтоб она сократилась со знаменателем:
\(\sqrt{128}=\sqrt{16\cdot 8}=4\sqrt{8}\)
\(=\sqrt{32}-4\sqrt{8}\)\(\frac{2-\sqrt{2}}{4}\)\(=\)
Сократим четверки.
\(=\sqrt{32}-\sqrt{8}(2-\sqrt{2})=\)
Раскроем скобки.
\(=\sqrt{32}-2\sqrt{8}+\sqrt{16}=\)
Занесем \(2\) под корень и вычислим \(\sqrt{16}\).
\(=\sqrt{32}-\sqrt{32}+4=4\).
Ответ: \(4\).
Смотрите также:
Формулы тригонометрии с примерами
Формулы половинного угла — Примеры | Тождества половинного угла
Мы изучаем формулы половинного угла (или тождества половинного угла) в тригонометрии. Формулы половинного угла можно получить, используя формулы двойного угла.
Как известно, формулы двойного угла можно вывести, используя формулы суммы и разности углов тригонометрии. Полууглы в формулах половинного угла обычно обозначаются как θ/2, x/2, A/2 и т. д., а половинный угол представляет собой дольный угол. Формулы половинного угла используются для нахождения точных значений тригонометрических соотношений таких углов, как 22,5° (что составляет половину стандартного угла 45°), 15° (что составляет половину стандартного угла 30°) и т. д.
Давайте рассмотрим формулы половинного угла вместе с их доказательствами и несколькими примерами решения здесь.
| 1. | Что такое формулы половинного угла? |
| 2. | Полуугольные тождества |
| 3. | Вывод формул половинного угла с использованием формул двойного угла |
| 4. | Полуугольная формула защиты от греха |
| 5. | Формула половинного угла для вычисления Cos |
6. | Формула полуугла получения загара |
| 7. | Формула половинного угла с использованием полупериметра |
| 8. | Часто задаваемые вопросы о Half Angle Formula |
Что такое формулы половинного угла?
В этом разделе мы увидим формулы половинного угла для sin, cos и tan. Мы знаем значения тригонометрических функций (sin, cos, tan, cot, sec, cosec) для таких углов, как 0°, 30°, 45°, 60° и 9°.0° из тригонометрической таблицы. Но чтобы узнать точные значения sin 22,5°, tan 15° и т. д., формулы половинного угла чрезвычайно полезны. Кроме того, они помогают доказать несколько тригонометрических тождеств. У нас есть формулы половинного угла, полученные из формул двойного угла, и они выражаются через половинные углы, такие как θ/2, x/2, A/2 и т. д. Вот список важных формул половинного угла:
Полуугольные тождества
Вот популярные тождества половины угла , которые мы используем при решении многих задач тригонометрии, следующие:
- Формула половинного угла sin: sin A/2 = ±√[(1 — cos A) / 2]
- Формула половинного угла для cos: cos A/2 = ±√[(1 + cos A) / 2]
- Формула половины угла tan: tan A/2 = ±√[1 — cos A] / [1 + cos A] (или) sin A / (1 + cos A) (или) (1 — cos A) / грех А
Вывод формул половинного угла с использованием формул двойного угла
Чтобы вывести приведенные выше формулы, сначала выведем следующие формулы половинного угла.
Формулы двойного угла основаны на двойных углах, таких как 2θ, 2A, 2x и т. д. Мы знаем, что формулы двойного угла для sin, cos и tan равны
- sin 2x = 2 sin x cos x .
- cos 2x = cos 2 x — sin 2 x (или)
= 1 — 2 sin 2 х (или)
= 2 cos 2 х — 1 - тангенс 2x = 2 тангенс х / (1 — тангенс 2 х)
Если мы заменим x на A/2 в обеих частях каждого уравнения формулы двойного угла, мы получим половинные тождества углов (поскольку 2x = 2(A/2) = A).
- sin A = 2 sin(A/2) cos(A/2)
- cos A = cos 2 (A/2) — sin 2 (A/2) (или)
= 1 — 2 sin 2
= 2 cos 2 (А/2) — 1 - tan A = 2 tan (A/2) / (1 — tan 2 (A/2))
Мы также можем вывести одну формулу половины угла, используя другую формулу половины угла. Например, только из формулы cos A мы можем вывести 3 важных тождества полууглов для sin, cos и tan, которые упомянуты в первом разделе.
Вот доказательство формулы половинного угла.
Полуугольная формула защиты от греха
Теперь докажем формулу половины угла для синуса. Используя одну из приведенных выше формул для cos A, мы имеем
cos A = 1 — 2 sin 2 (A/2)
Отсюда
2 sin 2 (A/2) = 1 — cos A
sin 2 (A/2) = (1 — cos A) / 2
sin (A/2) = ±√[(1 — cos A) / 2]
Формула половинного угла для вычисления Cos
Теперь докажем формулу половины угла для функции косинуса. Используя одну из приведенных выше формул cos A,
cos A = 2 cos 2 (A/2) — 1
Отсюда
2 cos 2 (A/2) = 1 + cos A
cos 2 (A/2) = (1 + cos A) / 2
cos (A/2) = ±√[(1 + cos A) / 2]
Полуугольная формула получения загара
Мы знаем, что tan (A/2) = [sin (A/2)] / [cos (A/2)]
Из формул половинного угла sin и cos,
tan (A/2) = [±√(1 — cos A)/2] / [±√(1 + cos A)/2]
= ±√[(1 — cos A) / (1 + cos A)]
Это является одной из формул загара (A/2).
Выведем две другие формулы, рационализировав здесь знаменатель.
тангенс (A/2) = ±√[(1 — cos A) / (1 + cos A)] × √[(1 — cos A) / (1 — cos A)]
= √[(1 — cos A) 2 / (1 — cos 2 A)]
= √[(1 — cos A) 2 / sin 2 A]
= (1 — cos с А) / sin A
Это вторая формула тангенса (A/2). Чтобы вывести другую формулу, давайте умножим и разделим приведенную выше формулу на (1 + cos A). Тогда мы получаем
тангенс (A/2) = [(1 — cos A) / sin A] × [(1 + cos A) / (1 + cos A)]
= (1 — cos 2 A) / [sin A (1 + cos A)]
= sin 2 A / [sin A (1 + cos A)]
= sin A / ( 1 + cos A)
Таким образом, tan (A/2) = ±√[(1 — cos A) / (1 + cos A)] = (1 — cos A) / sin A = sin A / (1 + cos А).
Формула половинного угла с использованием полупериметра
В этом разделе мы увидим формулы половинного угла с использованием полупериметра.
т. е. это формулы половины угла через стороны треугольника. Рассмотрим треугольник ABC, где AB = c, BC = a и CA = b.
Давайте выведем здесь одну из этих формул. Мы знаем, что полупериметр треугольника равен s = (a + b + c)/2. Отсюда имеем 2s = a + b + c. Из одной из приведенных выше формул
cos A = 2 cos²(A/2) — 1 (или)
2 cos²(A/2) = 1 + cos A
Теперь, используя закон косинусов,
2 cos 2 (A/2) = 1 + [ (b 2 + c 2 — a 2 ) / (2bc) ]
2 cos 2 (A/2) = [2 до н.э + b² + c² — a²] / [2bc]
2 cos 2 (A/2) = [ (b + c)² — a²] / [2bc] [с использованием формулы (a+b)²]
2 cos 2 (A/2) = [ (b + c + a) (b + c — a) ] / [2bc] [Используя формулу a² — b²]
2 cos 2 (A/2) = [ 2s (2s — 2a) ] / [ 2bc] [As 2s = a + b + c]
2 cos 2 (A/2) = [ 2s (s — a) ] / [bc]
cos 2 (A/2) = [ s(s — a) ] / [bc]
cos (A/2) = √[ s (s — a) ] / [bc]
Мы получили формулу полуугла для косинуса угла A/2 .
Точно так же мы можем получить другие тождества половинного угла косинуса, используя полупериметр. Другая формула синусов половинного угла может быть получена с использованием полупериметра.
sin 2 (A/2) = (1 − cos A)/2
= (1/2)[1−(b 2 +c 2 −a 2 )/2bc] (Используя закон косинусов)
= (1/2)(a 2 − (b−c) 2 )/2bc
= (1/2)(a + b − c)(a + c − b)/2bc
= (1/2){(a + b + c) − 2c}{(a + b + c) − 2b}/2bc
= (1/2)(2s − 2c )(2s − 2b)/2bc
= (s − b)(s − c)/bc
⇒ sin (A/2) = √[(s − b)(s − c)/bc]
Точно так же мы можем вывести другие формулы половинного угла синуса. Формулы половинного угла для функции тангенса можно вывести по формуле tan (A/2) = sin (A/2)/cos (A/2).
☛ Связанные темы:
- Формулы углов
- Тригонометрические функции
- Тригонометрические уравнения
Часто задаваемые вопросы о Half Angle Formula
Что такое формулы половинного угла в тригонометрии?
Формулы половинных углов дают значение половинных углов, таких как A/2, x/2 и т.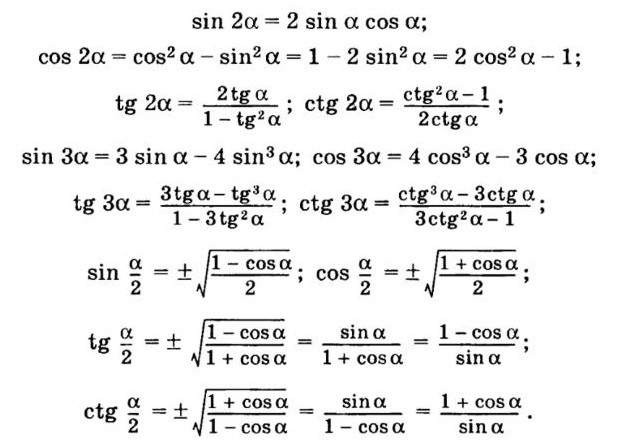
д. тригонометрических соотношений. Формулы половинного угла для sin, cos и tan:
- sin A/2 = ±√[(1 — cos A) / 2]
- cos A/2 = ±√[(1 + cos A) / 2]
- tan A/2 = ±√[1 — cos A] / [1 + cos A]
Что такое формула половинного угла для греха?
Формула половины угла для sin в тригонометрии: sin A/2 = ±√[(1 — cos A) / 2]. У нас есть другая формула половинного угла греха в терминах полупериметра. Если a, b и c — стороны треугольника, а A, B и C — соответствующие им противоположные углы, то sin A/2 = √[(s — b) (s — c)/bc].
Что такое формула половинного угла для косинуса?
Формула половинного угла для cos: cos A/2 = ±√[(1 + cos A)/2]. У нас есть еще одна формула половинного угла cos через полупериметр. Если a, b и c — стороны треугольника, а A, B и C — соответствующие им противоположные углы, то cos (A/2) = √[s (s — a)/bc].
Что такое формула половинного угла для касательной?
Формула половины угла тангенса: tan (A/2) = ±√[1 — cos A] / [1 + cos A] = (1 — cos A) / sin A = sin A / (1 + cos A ).
У нас есть еще одна формула половинного угла тангенса в терминах полупериметра. Если a, b и c — стороны треугольника, а A, B и C — соответствующие им противоположные углы, то sin A/2 = √[(s — b) (s — c)] / [s(s) — а)].
Зачем использовать формулы половинного угла?
Мы используем формулы половины угла для нахождения тригонометрических отношений половин стандартных углов, например, мы можем найти тригонометрические отношения углов, таких как 15°, 22,5° и т. д., используя тождества половинного угла. Их можно использовать для доказательства различных тригонометрических тождеств. Они также используются при решении интегралов.
Как вывести формулу половинного угла для Cos?
Используя формулу двойного угла для cos,
cos 2x = 2cos 2 x — 1
Заменив x на (A/2), мы получим
cos A = 2 cos 2 (A/2) — 1
Мы решим это для cos (A/2) .
2 cos 2 (A/2) = 1 + cos A
cos 2 (A/2) = (1 + cos A) / 2
cos A/2 = ±√(1 + cos A) / 2
Что такое tan 15°, используя тождества половинного угла?
Используя тождество половинного угла tan,
tan (A/2) = (1 — cos A) / sin A
Замена A = 30°,
тангенс (30°/2) = (1 — cos 30°) / sin 30°
= [1 — (√3/2)] / (1/2) (из таблицы триггеров)
= [ (2 — √3) / 2] / (1/2)
= 2 — √3
Следовательно, тангенс 15° = 2 — √3.
В чем разница между формулами двойного угла и половинного угла?
Формулы двойного угла в тригонометрии:
- sin 2x = 2 sin x cos x
- cos 2x = cos 2 x — sin 2 x (или)
= 1 — 2 sin 2 х (или)
= 2 cos 2 х — 1 - тан 2x = 2 тан х / (1 — тан 2 х)
Формулы половинного угла (которые получены из приведенных выше формул) в тригонометрии:
- sin A/2 = ±√[(1 — cos A) / 2]
- cos A/2 = ±√[(1 + cos A) / 2]
- tan A/2 = ±√[1 — cos A] / [1 + cos A]
Тригонометрические тождества половинного угла — Тригонометрические формулы и вывод половинного угла
Триггерные тождества или функции половинного угла, фактически участвующие в тех тригонометрических функциях, в которых есть половинные углы. Квадратный корень первых двух функций синуса и косинуса, отрицательный или положительный, полностью зависит от наличия угла в квадранте.
Узнать больше о Trig Identities на сайте trigidentities.info.
Вот исчерпывающая таблица, которая ясно изображает полуугловые тождества всех основных тригонометрических тождеств. Узнайте больше о тождествах обратного триггера .
Сегодня мы собираемся вывести следующие формулы полуугла треугольника.
Формула половинного угла – синус- cos 2 0472
Теперь, если мы допустим
- θ = α/2
, затем 2 θ = α и наша формула принимает вид:
- cos α = 1 − 2 sin 2 ( 2 α )
Теперь найдем
- Sin (α/2)
- 2 sin 2 ( 2 α ) =1−cos α
- sin ˆ 2 (2 α 904 71 ) = 1 – cos α
Решение дает нам следующее синус полуугла тождество:
Теперь поговорим о положительном или отрицательном знаке Sin (α/2).
- Если угол лежит в первом квадранте, то все положительные значения синуса половинного угла будут положительными.
- И если он находится в квадранте 3 rd или 4 th , мы введем отрицательный знак с синусоидальной половинной идентичностью угла.
Просто используя аналогичный процесс, с теми же заменами, которые мы сделали выше. Теперь мы должны подставить эти значения в следующее тождество триггера.
- cos 2 θ = 2cos 2 9 0004 θ – 1
После подстановки значений We
- Cos α = 2 cosˆ2(α/2)-1 —–(1)
Теперь вам нужно изменить уравнение.
Обратное уравнение:
- 2 cosˆ2(α/2)-1 = Cos α —–(2)
Добавьте оба уравнения (1) и (2)
- 2 cosˆ2(α/2) = 1+cos α
Разделить на 2 с обеих сторон
- cosˆ2(α/2) = 1+cos α/2
Взяв квадратный корень с обеих сторон, мы получили формулу половины угла косинуса .