правила применения формул сокращенного умножения Примеры на сумму и разность кубов
Формулы сокращенного умножения.
Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.
Применение формул сокращенного умножения при решении примеров.
Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .
Пусть а, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b) 2 = a 2 + 2ab + b 2
2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a — b) 2 = a 2 — 2ab + b 2
3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
a 2 — b 2 = (a -b) (a+b)
4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.
a 3 — b 3 = (a — b) (a 2 + ab + b 2)
Применение формул сокращенного умножения при решении примеров.
Пример 1.
Вычислить
а) Используя формулу квадрата суммы двух выражений, имеем
(40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681
б) Используя формулу квадрата разности двух выражений, получим
98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604
Пример 2.
Вычислить
Используя формулу разности квадратов двух выражений, получим
Пример 3.
Упростить выражение
(х — у) 2 + (х + у) 2
Воспользуемся формулами квадрата суммы и квадрата разности двух выражений
(х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2
Формулы сокращенного умножения в одной таблице:
(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)
Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.
Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.
Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).
Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.
Квадрат суммы
Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².
Квадрат разности
Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².
Разность квадратов
Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).
Куб суммы
Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.
Сумма кубов
Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).
В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).
Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.
Если значения сторон небольшие, то выполнить вычисления просто.
Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.
Куб разности
Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.
Разность кубов
Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы.
В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки .
В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения .
Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку .
Вспомним, как выглядит формула разности кубов.
a 3 − b 3 = (a − b)(a 2 + ab + b 2)
Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.
Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .
(a − b)(a 2 + ab + b 2) = a 3 − b 3
Рассмотрим пример. Необходимо разложить на множители разность кубов.
Обратим внимание, что «27а 3
» — это
«(3а) 3
», значит, для формулы разности кубов
вместо «a
» мы используем «3a
».
Используем формулу разности кубов. На месте «a 3 » у нас стоит «27a 3 », а на месте «b 3 », как и в формуле, стоит «b 3 ».
Применение разности кубов в обратную сторону
Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.
Обратите внимание, что произведение многочленов «(x − 1)(x 2 + x + 1) » напоминает правую часть формулы разности кубов «», только вместо «a » стоит «x », а на месте «b » стоит «1 ».
Используем для «(x − 1)(x 2 + x + 1) » формулу разности кубов в обратную сторону.
Рассмотрим пример сложнее. Требуется упростить произведение многочленов.
Если сравнить «(y 2 − 1)(y 4 + y 2 + 1)
» с правой частью
формулы разности кубов
Формулы сокращенного умножения — intmag24.ru
Формулы сокращенного умножения включают:
- Квадрат суммы и квадрат разности двух выражений,
- Куб суммы и куб разности выражений,
- Умножение разности двух выражений на их сумму,
- Умножение разности двух выражений на неполный квадрат их суммы,
- Умножение суммы двух выражений на неполный квадрат их разности.

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
| (a + b)2 = a2 + 2ab + b2 |
Пример: преобразовать (2x + 3y)2
Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)
(2x + 3y)2 = (2x + 3y)(2x + 3y)
Выполним умножение: (2x + 3y)2 = (2x + 3y)(2x + 3y) = 4x2 + 6xy + 6xy + 9y2 = 4x2 + 12xy + 9y2
Получим: (2x + 3y)2 = 4x2 + 12xy + 9y2
То есть, мы получили выражение, которое также получается из формулы.
Геометрический смысл:
Для вычисления площади квадрата нужно возвести его сторону во вторую степень.
Достроим отсутствующие стороны:
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты:
1) квадрат со стороной a — его площадь будет равна a2.
2) прямоугольники со сторонами a и b — они будут равны ab.
3) квадрат со стороной b — его площадь будет равна b2.
В результате получается следующая сумма площадей: a2 + ab + ab + b2
Квадрат разности двух выраженийКвадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
| (a — b)2 = a2 — 2ab + b2 |
Выражение (a − b)2 представляет собой произведение двух многочленов, каждый из которых равен (a − b):
(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2
Пример. Преобразовать выражение (7x − 5)2
Воспользуемся формулой квадрата разности двух выражений: (a − b)2 = a2 − 2ab + b2
Получим: (7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49x2 − 70x + 25
Если мы попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:
У нас должен получиться тот же результат:
(7x − 5)2 = (7x − 5)(7x − 5) = 49x2 − 35x − 35x + 25 = 49x2 − 70x + 25.
Геометрический смысл:
Если площадь квадрата со стороной a равна a2, то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)2
Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b
Получился новый квадрат, который меньше предыдущего. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:
Покажем эти прямоугольники:
— старая площадь a2 минус площадь ab минус площадь (a − b)b
a2 − ab − (a − b)b
— Раскроем скобки: a2 − ab − ab + b2
— Приведем подобные слагаемые: a2 − 2ab + b2
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
| (a + b)3 = a3 + 3a2b + 3ab2 + b3 |
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
| (a − b)3 = a3 − 3a2b + 3ab2 − b3 |
При решении задач желательно знать эти формулы наизусть. Если не запомнили — их можно выводить самостоятельно:
Формула куба суммы двух выражений
(a + b)3 = (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2)
(a + b)3 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3
Формула куба разности двух выражений
(a − b)3 = (a − b)(a2 − 2ab + b2)
(a − b)3 = a3 − 2a2b + ab2 − a2b + 2ab2 − b3 = a3 − 3a2b + 3ab2 − b3
Пример 1. Преобразуйте выражение (x + 1)3 в многочлен:
Преобразуйте выражение (x + 1)3 в многочлен:
(x + 1)3 = x3 + 3 × x2 × 1 + 3 × x × 12 + 13 = x3 + 3x2 + 3x + 1
Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:
(x + 1)3 = (x + 1)(x + 1)(x + 1) = (x + 1)(x2 + 2x + 1) = x3 + 2x2 + x + x2 + 2x + 1 = x3 + 3x2 + 3x + 1
Пример 2. Преобразовать выражение (n2 − 3)3 в многочлен:
(n2 − 3)3 = (n2)3 − 3 × (n2)2 × 3 + 3 × n2 × 32 − 33 = n6 − 9n4 + 27n2 − 27
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
| (a − b)(a + b) = a2 − b2 |
Выполним данное умножение: (a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2
Пример. Выполнить умножение (2x − 5)(2x + 5):
(2x − 5)(2x + 5) = (2x)2 − 52 = 4x2 − 25
При этом нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a2 − b2, поскольку от перестановки множителей произведение не меняется.
Умножение разности двух выражений на неполный квадрат их суммыПроизведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.
| (a − b)(a2 + ab + b2) = a3 − b3 |
- первый многочлен (a − b) является разностью двух выражений
- второй многочлен (a2 + ab + b2) является неполным квадратом суммы этих двух выражений. Неполный квадрат суммы это многочлен вида a2 + ab + b2. Он похож на обычный квадрат суммы a2 + 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Умножим разность (a − b) на неполный квадрат суммы a2 + ab + b2
(a − b)(a2 + ab + b2) = a(a2 + ab + b2) − b(a2 + ab + b2) = a3 + a2b + ab2 − a2b − ab2 − b3 = a3 − b3
То есть выражение (a − b)(a2 + ab + b2) = a3 − b3
Пример. Выполнить умножение (2x − 3y)(4x2 + 6xy + 9y2)
Выполнить умножение (2x − 3y)(4x2 + 6xy + 9y2)
Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y.
Второй многочлен 4x2 + 6xy + 9y2 это неполный квадрат суммы двух выражений 2x и 3y. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3. В нашем случае умножение (2x − 3y)(4x2 + 6xy + 9y2) можно заменить на разность кубов 2x и 3y.
(2x − 3y)(4x2 + 6xy + 9y2) = (2x)3 − (3y)3 = 8x3 − 27y3
Попробуем решить этот же пример, не пользуясь формулой (a − b)(a2 + ab + b2) = a3 − b3. У нас получится тот же результат, но решение станет длиннее:
У нас получится тот же результат, но решение станет длиннее:
(2x − 3y)(4x2 + 6xy + 9y2) = 2x(4x2 + 6xy + 9y2) − 3y(4x2 + 6xy + 9y2) =
8x3 + 12x2y + 18xy2 − 12x2y − 18xy2 − 27y3 = 8x3 − 27y3
Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.
| (a + b)(a2 — ab + b2) = a3 + b3 |
- первый многочлен (a + b) является суммой двух выражений,
- второй многочлен (a2 − ab + b2) является неполным квадратом разности этих двух выражений.
 Неполный квадрат разности это многочлен вида a2 − ab + b2. Он похож на обычный квадрат разности a2 − 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Неполный квадрат разности это многочлен вида a2 − ab + b2. Он похож на обычный квадрат разности a2 − 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Умножим сумму a + b на неполный квадрат разности a2 − ab + b2
(a + b)(a2 − ab + b2) = a(a2 − ab + b2) + b(a2 − ab + b2) = a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3
То есть выражение (a + b)(a2 − ab + b2) равно a3 + b3
Пример. Выполнить умножение (2x + 3y)(4x2 − 6xy + 9y2)
Выполнить умножение (2x + 3y)(4x2 − 6xy + 9y2)
Первый многочлен (2x + 3y) это сумма двух выражений 2x и 3y.
Второй многочлен 4x2 − 6xy + 9y2 это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3. В нашем случае умножение (2x + 3y)(4x2 − 6xy + 9y2) можно заменить на сумму кубов 2x и 3y
(2x + 3y)(4x2 − 6xy + 9y2) = (2x)3 + (3y)3 = 8x3 + 27y3
Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:
У нас получится тот же результат, но решение станет длиннее:
(2x + 3y)(4x2 − 6xy + 9y2) = 2x(4x2 − 6xy + 9y2) + 3y(4x2 − 6xy + 9y2) =
8x3 − 12x2y + 18xy2 + 12x2y − 18xy2 + 27y3 = 8x3 + 27y3
Формулы сокращенного умножения также применяются для разложения многочлена на множители для последующих операций с многочленами: сложения, вычитания, умножения или деления.
Метод ФОЛЬГИ | Как фольгировать и примеры
Написано
Малкольм МакКинси
Проверенный факт
Paul Mazzola
Метод FOIL
Метод FOIL FOIL используется для умножения. ФОЛЬГА — это аббревиатура. Буквы обозначают «первый», «снаружи», «внутри» и «последний», указывая на порядок умножения терминов. Вы умножаете первые термины, затем внешние термины, затем внутренние термины, затем последние термины, а затем комбинируете одинаковые термины для своего ответа.
ФОЛЬГА — это аббревиатура. Буквы обозначают «первый», «снаружи», «внутри» и «последний», указывая на порядок умножения терминов. Вы умножаете первые термины, затем внешние термины, затем внутренние термины, затем последние термины, а затем комбинируете одинаковые термины для своего ответа.
Как FOIL
Мнемоника FOIL точно говорит нам, какие члены умножать и в каком порядке:
F irst – умножить первые члены
O O
I nside – умножить внутренние/внутренние члены
L ast – умножить последние члены термин в любом биноме. Все члены первого двучлена правильно сочетаются с членами второго двучлена. Все подсчитывается. 9{2}+33n+185n2+33n+18
FOIL математический примерНаш окончательный ответ, произведение двух двучленов, содержит три члена, поэтому это трехчлен.
Умножение трех двучленов
Умножение трех двучленов является особым случаем для FOIL, поскольку метод FOIL может использоваться только для умножения двух двучленов одновременно.

Вы можете использовать FOIL для умножения трех или более двучленов, если вы разделите их на пары, а затем разложите ответ на оставшийся двучлен.
FOIL нельзя использовать для биномиального сложения, вычитания или деления.
Вот уравнение умножения с тремя биномами:
Для начала мы разделим первые два бинома на пары:
Затем перемножим их, используя метод FOIL, и получим:
Затем мы объединим одинаковые члены:
Теперь мы умножаем наш новый двучлен на оставшийся двучлен из исходного уравнения:
Затем разложение на множители и упрощение является последним шагом:
Умножение трех двучленовЕсли вы столкнулись с большим количеством умножения двух двучленов, решите два за раз, используя FOIL пока не останется только один многочлен.
Термин полином относится к выражению констант, переменных и показателей степени, которые складываются, вычитаются или умножаются, как в выделенном ответе выше. Каждый член сам по себе называется мономом.

кубических чисел | Определение, примеры, 1-100, шаблоны, применение
ВведениеПредположим, что в каждом из двух наборов кубиков есть восемь синих и семь желтых кубиков.
Попробуйте упорядочить эти кубики, создав кубики большего размера. На приведенном ниже рисунке показано, как восемь маленьких синих кубиков объединяются в один большой куб. Сколько бы мы ни расставляли семь желтых кубиков, мы не сможем создать куб большего размера.
Этот пример демонстрирует, что 8 — это число в кубе, а 7 — нет. Используя такое же количество меньших кубиков, число куба — это любое число, которое может быть сформировано в куб. Помимо 8, существует бесконечное количество кубических чисел. Есть 27, 64, 125, 216, 343, 512, 729, 1000 и так далее.
В этой статье мы подробнее изучим кубические числа, их характеристики и несколько примеров с решениями.
Что такое кубические числа?Определение
Кубическое число является результатом умножения числа само на себя, а затем повторного умножения его самого на себя.
 По сути, умножение трех одинаковых чисел дает кубическое число. Совершенный куб — это числовое значение, которое можно получить путем возведения в куб любого заданного числа.
По сути, умножение трех одинаковых чисел дает кубическое число. Совершенный куб — это числовое значение, которое можно получить путем возведения в куб любого заданного числа.Некоторые примеры: 1, 8, 27, 64, 125, 216, 343 и так далее.
1 в кубе равно 1 x 1 x 1 = 1
2 в кубе равно 2 x 2 x 2 = 8
3 в кубе равно 3 x 3 x 3 = 27
4 в кубе равно 4 x 4 x 4 = 64
5 в кубе равно 5 х 5 х 5 =125
6 в кубе равно 6 x 6 x 6 = 216
7 в кубе равно 7 x 7 x 7 = 343
8 в кубе равно 8 x 8 x 8 = 512
9 в кубе равно 9 x 9 x 9 = 729
10 в кубе равно 10 x 10 x 10=1000Приложение
Используя кубические блоки, число куба — это любое число, которое может быть сформировано в куб, используя меньшие кубы. Вот несколько примеров кубических чисел.
В красном кубе всего 8 меньших кубиков, а в желтом кубе всего 27 меньших кубиков. Обратите внимание, что у красного куба каждая сторона имеет 2 единицы измерения, а у желтого куба — 3 единицы с каждой стороны.
 Это также объясняет практическое применение кубических чисел, то есть получение объема трехмерных фигур.
Это также объясняет практическое применение кубических чисел, то есть получение объема трехмерных фигур.Следовательно, объем каждого куба можно вычислить, трижды умножив длины его сторон на самих себя. В геометрии объем куба равен произведению его длины, ширины и высоты.
В приведенном ниже решении обратите внимание на использование показателя степени « 3 » или степени числа 3. Поскольку 2 для объема красного куба умножается на себя в три раза так же, как число 3 для объема желтого куба. Говоря 2 3 , 2 в кубе, это то же самое, что 2×2×2. Говоря 3 3 , 3 в кубе равно 3×3×3.
Объем красного куба =2×2×2=2 3
Объем ( красный куб=8 кубических единицОбъем желтого куба =3×3×3=3 3
Объем желтого куба =27 куб. единицыВ метрических мерах кубические метры, кубические сантиметры и кубические дюймы, кубические футы являются несколькими примерами кубических единиц.Таким образом, если, например, красный куб имеет каждую сторону размером 2 сантиметра, а желтый куб сторона, которая измеряет 3 сантиметра, у нас есть,
Объем красного куба = 8 см 3 или 8 куб.
 сантиметров
сантиметровОбъем желтого куба = 27 см 3 или 27 куб. корни и предлагает практическое применение в реальной жизни.
Например, если вы хотите найти объем кубического контейнера, решением будет куб длины его стороны. Если, например, вам известен объем кубического сосуда и вы хотите найти площадь его поверхности, полезно получить длины сторон, извлекая кубический корень из объема. Поскольку вы уже знаете размер кубического контейнера, теперь вы можете быстро рассчитать необходимое количество краски.
Список кубиков от 1 до 100Кубики от 1 до 100 или кубики первых 100 чисел отображаются в таблицах ниже и могут использоваться для решения связанных задач со словами.
Cubes 1 to 25 1 3 =1 6 3 =216 11 3 =1331 16 3 =4096 21 3 =9261 2 3 =8 7 3 =343 12 3 =1728 17 3 =4913 22 3 =10648 3 3 =27 8 3 =512 13 3 =2197 18 3 =5832 23 3 =12167 4 3 =64 9 3 =729 14 3 =2744 19 3 =6859 24 3 =13824 5 3 =125 10 3 =1000 15 3 =3375 20 3 =8000 25 3 =15625 Cubes 26 to 50 26 3 =17576 31 3 =29791 36 3 =46656 41 3 =68921 46 3 =97336 27 3 =19683 32 3 =32768 37 3 =50653 42 3 =74088 47 3 =103823 28 3 =21952 33 3 =35937 38 3 =54872 43 3 =79507 48 3 =110592 29 3 =24389 34 3 =39304 39 3 =59319 44 3 =85184 49 3 =117649 30 3 =27000 35 3 =42875 40 3 =64000 45 3 = 50 3 =125000 Cubes 51 to 75 51 3 = 132651 56 3 =175616 61 3 =226981 66 3 =287496 71 3 =357911 52 3 =140608 57 3 =185193 62 3 =238328 67 3 =300763 72 3 =373248 53 3 =148877 58 3 =195112 63 3 =250047 68 3 =314432 73 3 =389017 54 3 =157464 59 3 =205379 64 3 =262144 69 3 =328509 74 3 =405224 55 3 =166375 60 3 =216000 65 3 =274625 70 3 =343000 75 3 =421875
Interesting Cube Number FactsCubes 76 to 100 76 3 =438976 81 3 =531441 86 3 =636056 91 3 =753571 96 3 =884736 77 3 =456533 82 3 =551368 87 3 =658503 92 3 =778688 97 3 =3 78 3 =474552 83 3 =571787 88 3 =681472 93 3 =804357 98 3 =941192 79 3 =493039 84 3 =592704 89 3 =704969 94 3 =830584 99 3 =970299 80 3 =512000 85 3 =614125 90 3 =729000 95 3 =857375 100 3 =1000000 A number that is even will produce an четное число в кубе.

Например, число 6 в кубе равно 216, число 12 в кубе равно 1728, а число 14 в кубе равно 2744. .
Число нечетное даст число четное , если его возвести в куб.
Например, куб числа 4 равен 64, куб числа 11 равен 1331, а куб числа 45 равен .
и соответственно) — все четные числа.
Куб положительного числа положителен.
Например, 8×8×8=512; и 8, и 512 — четные числа.
Другой пример, 12×12×12=1728; и 12, и 1728 — четные числа.
Куб отрицательного числа является отрицательным числом.
Например, (-3) х (-3) х (-3). Учитывая, что это включает в себя умножение отрицательных чисел, важно иметь в виду, что положительное число получается при умножении двух положительных чисел, тогда как произведение двух чисел с другим знаком отрицательно.
 Таким образом,
Таким образом,-3 3 = (-3) x (-3) x (-3) =9 × (-3) = -27
Другой пример — куб -14.
-14 3 =(-14) x (-14) x (-14)=196 × (-14) = -2744
нулей кратно 3.
Когда мы говорим, что сумма нулей кратна 3, мы имеем в виду 3, 6, 9, 12 и так далее.
Некоторые примеры: 8000, 64000 и 1000000.
20×20×20=8000 (с 3 нулями)
40×40×40=64000 (с 3 нулями)
100×100×100=1000000 (с 6 нулями) с последними цифрами 1, 4, 5, 6 или 9 результат также будет заканчиваться той же цифрой.
Примеры:
Куб чисел 11, 21, 31 и 41 равен 1331, 9261, 29791 и 68921 соответственно. 11, 21, 31 и 41 и их кубики тоже оканчиваются на 1.
Куб чисел 16, 26, 36 и 46 равен 4096, 17576, 46656 и 97336 соответственно. 16, 26, 36 и 46 и их кубы тоже оканчиваются на 6.
Образцы кубических чиселСумма последовательных нечетных чисел является совершенным кубом.
 Ряды нечетных чисел, которые при сложении образуют идеальный куб, находятся в порядке нечетных чисел числовой строки.
Ряды нечетных чисел, которые при сложении образуют идеальный куб, находятся в порядке нечетных чисел числовой строки. В отношении приведенного ниже первый столбец представляет собой последовательные нечетные числа, второй столбец представляет собой сумму последовательных нечетных чисел, а третий столбец представляет собой эквивалентные кубические числа.
1 1 1 3 3 + 5 8 2 3 7 + 9 + 11 27 3 3 13 + 15 + 17 + 19 64 4 3 21 + 23 + 27 + 29 125 9 + 23 + 27 + 2125 3 125 9086 3 321086 21. 210896 2 21. 21 + 23. + 37 +39 + 41 216 6 3 43 + 45 + 47 + 49 + 51 + 53 + 55 . равно числу, рассматриваемому для куба.
равно числу, рассматриваемому для куба. Например, для 4 в кубе добавление 4 нечетных чисел 13, 15, 17 и 29 дает нам 64. То же самое с 5 в кубе, добавление 5 последовательных чисел 21 + 23 + 25 + 27 + 29 даст нам 125
1 1 odd number 1 3 3 + 5 2 odd numbers 2 3 7 + 9 + 11 3 odd numbers 3 3 13 + 15 + 17 + 19 4 нечетные числа 4 3 21 + 27 + 27 + 21 + 27 + 27 + 21 + 27 + 27 + 21 + 27 + 27 + 21 + 27 + 21. 31 + 33 + 35 + 37 +39+ 41 6 odd numbers 6 3 43 + 45 + 47 + 49 + 51 + 53 + 55 7 odd numbers 7 3 Examples
Пример 1
Найдите кубическое число числа 43.

Решение:
Чтобы найти кубическое число числа 43, мы должны умножить 43 само на себя, а затем снова умножить его на себя, поэтому мы есть 43 3 .
43 3 = 43 x 43 x 43 = 43 3 = 79507
Чтобы проверить ответ, вы можете использовать приведенный выше список чисел куба. Таким образом, Куб 43 равен 79507.
Пример 2
Найдите номер куба 101.
Решение:
до. умножьте 101 на себя, а затем снова умножьте на себя, так что у нас есть 101 3 .
101 3 = 101 × 101 × 101 = 101 3 = 1030301
Таким образом, Куб 101 IS 1030301.
. Примере 3
. Пример 3
.
а. 125
б. 1331
г. 2750
д. 5832
эл. 8000
Решение: Только 2750 не является кубическим числом среди заданных чисел.

125 — кубическое число 5 или 5 3 = 125.
1331 — кубическое число 11 или 11 3 = 1331.
5832 — кубическое число 18 или 18 3 = 5832. или 20 3 = 8000.
Пример 4
Запишите каждое данное, используя степень числа 3 или символ в кубе, затем оцените.
а. 9×9×9
б. 11×11×11
в. (-4)×(-4)×(-4)
д. 12×12×12
эл. 20×20×20
ф. -25 -25 ×(-25)
Решение:
а. 9×9×9=9 3 =729
б. 11×11×11=11 3 =1331
в. (-4) х (-4) х (-4) = (-4) 3 =-64
d. 12×12×12=12 3 =1728
e. 20×20×20=20 3 =8000
ф. (-25) x (-25) x (-25) = -15625
Пример 5
Решение: 63 3 +21 3
Solution: Мы. 63 и 21 в качестве первого шага. Кубическое число 63 равно 63 3 , что равно 250047.
 Кубическое число 21 равно 21 3 , что равно 9261. 21 × 21) = 250047 + 9261 = 259308
Кубическое число 21 равно 21 3 , что равно 9261. 21 × 21) = 250047 + 9261 = 259308Таким образом, 63 3 +21 3 равен 259308.
Пример 6
Посмотреть для двух чисел Cube 9604. Решение:
В представленном ранее списке кубических чисел два кубических числа, которые дают нам сумму 9603 — 2744 и 6859.
2744 — это номер куба 14, в то время как 6859 — это номер куба 19.
9603 = 2744 +6859 = 14 3 +19 3
Пример 7 40004444444444444444444444444497
44444444497
4 40004444444497
4444444497
444444497
4 400044 400044444497
4497
9 . До 1000 какие числа в кубе?
Решение:
1 в кубе равно 1×1×1=1 3 =1
2 в кубе равно 2×2×2=2 3× = 3
в кубе ×3=3 3 =27
4 в кубе равно 4×4×4=4 3 =64
5 в кубе равно 5×5×5=5 3 =125
6 в кубе равно 6×6×6=6 3 =216
7 в кубе равно 7×7×7=7 3 = 343
8 в кубе равно 8×8×8=8 3 =512
9 в кубе равно 9×9×9=9 3 =729
10 в кубе равно 10×10×10=106 3 =1000
Таким образом, кубические числа до 1000 равны 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000.

Пример 8
У Виктории есть деревянные кубики, как показано ниже. Если длина стороны каждого куба равна 2 дюймам, найдите общий объем кубов.
Решение:
Сначала нам нужно найти объем каждого куба, то есть
Объем каждого куба = 2 дюйма × 2 дюйма × 2 дюйма
Объем каждого куба = 8 кубических дюймов или 8 в 3Чтобы получить общий объем кубов, нам просто нужно добавить объем каждого куба или умножить 8 в 3 на 8.
Итак, мы имеем, 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 = 64 или
8 в 3 × 8 = 64 в 3
Следовательно, общий объем кубов равен 64 кубических дюйма.
Мы также можем попробовать сложить из 8 маленьких кубиков куб большего размера. На приведенном ниже рисунке показано, что длина стороны большего куба составляет 4 дюйма.
Следовательно, чтобы получить объем куба со стороной 4 дюйма, мы имеем
Объем=4×4×4
Объем=16×4
Объем=64 дюйма 3Пример 9
Найдите кубические числа от 1 до 1000, которые также являются квадратными числами.

Решение:
В таблице ниже показаны числа кубов от 1 до 1000.
1 3 = 1 6 3 = 216 6 3 = 216 6 3 = 216 6 3 = 216 6 3 = 216 . 7 3 =343 3 3 =27 8 3 =512 4 3 =64 9 3 =729 5 3 =125 10 3 =1000 Теперь нам нужно выбрать среди этих кубических чисел и квадратные числа. Таким образом, мы имеем
1 2 = 18 2 = 6427 2 = 729
Следовательно, от 1 до 1000 кубическими числами, которые также являются квадратными числами, являются 1, 64 и 729.
 Резюме
Резюме Кубическое число получается в результате умножения числа само на себя, а затем повторного умножения его самого на себя. По сути, умножение трех одинаковых чисел дает кубическое число.
Сокращенный способ записи числа куба — использовать показатель степени « 3 » или степень числа 3.
Объем каждого куба можно рассчитать, умножив длины его сторон на самих себя три раза. В геометрии объем куба равен произведению его длины, ширины и высоты.
Четное число даст четное число при возведении в куб.
Нечетное число даст четное число при возведении в куб.
Куб положительного числа положителен.
Куб отрицательного числа является отрицательным числом.
Если число в кубе содержит нули в конце, общее количество нулей кратно 3.
Если вы возьмете в куб числа с последними цифрами 1, 4, 5, 6 или 9, результат также будет заканчиваться на та же цифра.
Сумма последовательных нечетных чисел является совершенным кубом.
 Ряды нечетных чисел, которые при сложении образуют идеальный куб, находятся в порядке нечетных чисел числовой строки.
Ряды нечетных чисел, которые при сложении образуют идеальный куб, находятся в порядке нечетных чисел числовой строки.Количество последовательных нечетных чисел, сумма которых образует совершенный куб, равно числу, рассматриваемому для куба.
Часто задаваемые вопросы (FAQ) Как возвести число в куб?Чтобы возвести число в куб, нужно умножить его само на себя, а затем еще раз на само себя.
Так, например, чтобы возвести в куб число 6, у нас есть 6×6×6 или 6 3 , что дает 216.
6 3 =6×6×6=36×6=216
Другим примером является 78 3 , поэтому мы должны умножить 78 на 78 и их произведение на 78. Таким образом,
78 3 =78×78×78=6084×78=474552
Какое применение кубических чисел?При определении объема кубов номера кубов особенно полезны. Поскольку куб представляет собой трехмерную фигуру со сторонами одинакового размера (длина, ширина и высота), легко вычислить объем, «возведя в куб» одну из его сторон.

Например, если у нас есть куб со стороной, равной 4 единицам, у нас будет объем 64 кубических единицы. Это делается путем возведения числа 4 в куб. Вот решение: 9.0003
4 3 =4×4×4=16×4=64 кубических единицы
Другой пример: если у нас есть конкретные метрические единицы, такие как куб со стороной 9 сантиметров. Если мы возьмем число 9 в куб, мы получим его объем. То есть
9 3 =9×9× 9=81×9=729 см 3
Чем квадратные числа отличаются от кубических?Число умножается само на себя один раз, чтобы получить квадратное число, а операция выполняется дважды, чтобы образовать кубическое число.
Например, возьмем число 6. 36 — это результат умножения 6 на само себя. Следовательно, 36 — это квадрат числа 5.
6 × 6=36 или
6 2 = 36
Обратите внимание на использование показателя степени « 2 » для получения квадрата числа.
Отсюда умножение 6 2 на 6 снова дает нам куб 6 или 6 3 .
 Следовательно,
Следовательно,6 3 =6×6×6=36×6=216
Как найти куб отрицательного числа?Куб отрицательного числа является отрицательным числом.
Например, (-3) х (-3) х (-3). Учитывая, что это связано с умножением отрицательных чисел, важно помнить, что произведение двух чисел с одним и тем же знаком положительно, а произведение двух чисел с разными знаками отрицательно. Таким образом,
(-3) 3 = (-3) x (-3) x (-3) = 9× (-3) = -27
Другим примером является куб -14.
-14 3 =(-14) x (-14) x (-14)=196 × (-14)=-2744
Какие первые 10 кубических чисел?Это первые десять чисел куба: 1, 8, 27, 64, 125, 216, 343-512, 729 и 1000.
Что такое кубическое число, записанное стенографией?
1 3 = 1 6 3 = 216 2 3 = 8 7 3 = 3434343434343434343434343434343434343434343434343434343434343434343434343434343434343434343434343434343434343434343434343434343434343434349er9343434934934 3 7 .0196 3 =27 8 3 =512 4 3 =64 9 3 =729 5 3 =125 10 3 =1000 Сокращенный способ записи числа куба состоит в использовании показателя степени « 3 » или степени числа 3.
В приведенных ниже примерах показаны кубы от 1 до 10 в сокращенной и расширенной формах написания.

1 в кубе равно 1×1×1=1 3 =1
2 в кубе равно 2×2×2=2 3 =8
3 в кубе равно 3×3×3=3 3 = 27
4 в кубе равно 4×4×4=4 3 =64
5 в кубе равно 5×5×5=5 3 =125
6 в кубе равно 6×6×6=6 3 =216
7 в кубе равно 7×7×7=7 3 =343
8 в кубе равно 8×8×8=8 3 =512
9 в кубе равно 9×9×9=9 3 =729
10 в кубе равно 10×10×10=10 3 =1000
Сколько четных кубических чисел от 1 до 1000?Существует 5 четных кубических чисел от 1 до 1000. Это числа 8, 64, 216, 512 и 1000.
Сколько нечетных кубических чисел от 1 до 1000?Существует 5 нечетных кубических чисел от 1 до 1000. Это числа 1, 27, 125, 343 и 729.
Как определить, является ли число совершенным кубом или нет?Можно определить, является ли число совершенным кубом или нет, с помощью метода простой факторизации.
 Скажем, например, давайте отождествим, если 512 и 729и 1728 — совершенные кубы с использованием простой факторизации.
Скажем, например, давайте отождествим, если 512 и 729и 1728 — совершенные кубы с использованием простой факторизации.Мы получим 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 как простые множители числа 512.
Мы можем составить 3 группы по 2 кубика, и у нас есть (2×2×2) ×(2×2×2)×(2×2×2) или 2 3 x 2 3 x 2 3 .
Таким образом, 512=( 2×2×2 ) 3 =8 3 .
Для 729 простая факторизация равна 3×3×3×3×3×3.
Из простых множителей можно составить 2 группы по 3 куба, следовательно,
( 3×3×3 )×( 3×3×3 ) или 3 3 x 3 3
Следовательно, 729= ( 3×3 ) 3 =9 3 .
Теперь, чтобы показать, является ли 1728 совершенным кубом, давайте также разложим его на простые множители.
Разложение числа 1728 на простые множители равно 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3.
Мы можем создать 3 группы, каждая из которых имеет множители 2×2×3, поэтому мы имеем
.


 Неполный квадрат разности это многочлен вида a2 − ab + b2. Он похож на обычный квадрат разности a2 − 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Неполный квадрат разности это многочлен вида a2 − ab + b2. Он похож на обычный квадрат разности a2 − 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.

 По сути, умножение трех одинаковых чисел дает кубическое число. Совершенный куб — это числовое значение, которое можно получить путем возведения в куб любого заданного числа.
По сути, умножение трех одинаковых чисел дает кубическое число. Совершенный куб — это числовое значение, которое можно получить путем возведения в куб любого заданного числа. Это также объясняет практическое применение кубических чисел, то есть получение объема трехмерных фигур.
Это также объясняет практическое применение кубических чисел, то есть получение объема трехмерных фигур. сантиметров
сантиметров
 Таким образом,
Таким образом, Ряды нечетных чисел, которые при сложении образуют идеальный куб, находятся в порядке нечетных чисел числовой строки.
Ряды нечетных чисел, которые при сложении образуют идеальный куб, находятся в порядке нечетных чисел числовой строки. 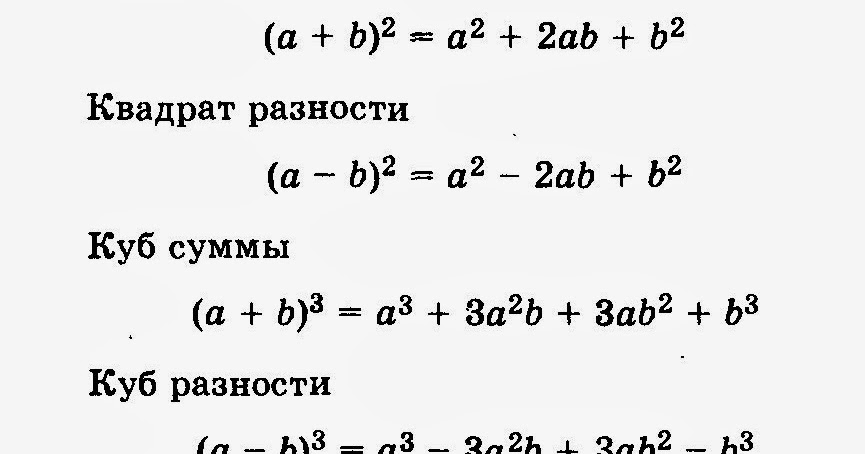 равно числу, рассматриваемому для куба.
равно числу, рассматриваемому для куба. 

 Кубическое число 21 равно 21 3 , что равно 9261. 21 × 21) = 250047 + 9261 = 259308
Кубическое число 21 равно 21 3 , что равно 9261. 21 × 21) = 250047 + 9261 = 259308

 Резюме
Резюме  Ряды нечетных чисел, которые при сложении образуют идеальный куб, находятся в порядке нечетных чисел числовой строки.
Ряды нечетных чисел, которые при сложении образуют идеальный куб, находятся в порядке нечетных чисел числовой строки.
 Следовательно,
Следовательно,

 Скажем, например, давайте отождествим, если 512 и 729и 1728 — совершенные кубы с использованием простой факторизации.
Скажем, например, давайте отождествим, если 512 и 729и 1728 — совершенные кубы с использованием простой факторизации.