Степени числа 2 для людей и для кошек « Папа Карп
Наверное, число 2 именно потому нам так часто и встречается в жизни, что в нем существует некая особая правда…
На мой взгляд, весьма целесообразно познакомить ребенка уже в начальной школе (или даже до школы) со всеми степенями числа 2 (от 4 до 1024).
Зачем это надо?
Математика – подразумевает умение мыслить четкими логическими шагами. Да, иногда в данном процессе очень помогают другие навыки: образы, интуиция, примеры из жизни, специальные приемы, неожиданные идеи… Но основа все равно именно в четкой последовательной логике.
На начальных этапах (да и в дальнейшем тоже) весьма удобно сохранять в памяти некоторые “лесенки” из чисел. Они укладываются в голове как своеобразные последовательности “ступенек”, то есть запоминаются сразу целиком, почти как стихи или песенки.
Так мы изучаем таблицу умножения. Для каждого десятка получается “лесенка” из последовательности примеров, ее довольно легко запомнить – и держать потом в голове всю жизнь, использовать в любых ситуациях.
Последовательность степеней числа 2 тоже является такой своеобразной “математической лесенкой” – которую удобно просто запомнить навсегда. И она будет очень помогать – и в начальных классах, и в средних, и в старших, и далее в вузе.
Смысл не только в том, что ученик запоминает некоторые числа. Смысл еще и в том, что знание степеней числа 2 – это надежная опора для математического мышления. Такое знание увеличивает скорость решения самых разных примеров и задач, а также делает обучение математике более энергичным и уверенным, более осознанным.
Фактически, степени числа 2 – это некие “опорные точки для ориентирования на огромном пространстве математических знаний”.
Когда ребенок вдруг узнает среди чисел какую-то степень числа 2, ему сразу делается легче и веселее, он сразу же ощущает себя более уверенно. Знакомый ориентир. Удобный и надежный сигнал.
Мне захотелось описать данную методическую идею в виде незатейливой сказки. Возможно, она пригодится вам для занятий с детьми.
Или просто наведет на собственные педагогические находки…
Жил-был человек. И у него была кошка. Они очень дружили и часто вместе играли и изучали всякие математические штуки.
Однажды кошка спросила:
– Что за странную последовательность чисел ты написал? Зачем?
Человек ей улыбнулся и ответил:
– Я начал с числа 2. А следующее число в 2 раза больше него, то есть 4. Следующее число еще в 2 раза больше, чем 4. То есть уже 8 получилось. А затем я написал 16, это как раз в 2 раза больше, чем 8. Понятно?
– Понятно, мяу, – молвила кошка задумчиво.
А человек продолжал объяснять:
– Дальше я действовал по тому же принципу. Каждое следующее число в 2 раза больше, чем предыдущее. Вот 32 в 2 раза больше, чем 16. А число 64 в 2 раза больше, чем 32. Ну и 128 – это в 2 раза больше, чем 64. А теперь ты и сама можешь сообразить, как я получил следующие числа.
Кошка почесала задней лапой у себя за ухом, поразмышляла немного и догадалась:
– Наверное, число 256 получилось потому, что оно в 2 раза больше, чем 128, да? А 512 в 2 раза больше, чем 256, так? Ну а 1024 в 2 раза больше, чем 512, правда? Мяу.
Я не считала эти большие числа, а просто догадалась, мяу.
– Ты моя умная кошка! – похвалил ее человек. И ласково погладил по голове. – Ты все правильно поняла и догадалась. Молодец! Но хорошо бы разобраться в данной теме поподробнее, чтобы ты уже все очень хорошо осознала и запомнила.
– Да, я бы с радостью разобралась получше, мяу, – согласно кивнула кошка.
Тогда человек стал писать для нее примеры на сложение. Сначала 2 + 2, затем 4 + 4, потом 8 + 8, далее 16 + 16, после этого 32 + 32, и наконец 64 +64.
А кошка не спеша решала эти примеры один за другим и говорила ответ.
Минутку отдохнув и посмотрев в окно на птичек, прилетевших на ветку березы, они продолжили решение примеров. Теперь уже пошли более трудные. Но кошка уверенно справилась и с ними со всеми. А человек лишь записывал за ней ответы.
Потом они, глядя на все решенные только что примеры, записали в столбик все те же числа, но уже не как сложение, а как умножение.
Конечно, сделать это было совсем не трудно.
Кошка с удовольствием диктовала, а человек аккуратно рисовал цифры.
Но вдруг прямо на карниз за окном прилетел голубь!
Какая уж тут математика!
Голубь стал прохаживаться по карнизу туда-сюда, поклевывать там что-то, чистить себе перышки… Он вел себя абсолютно без всякого страха! Он был уверен, что оконное стекло полностью его защищает. Он вообще не обращал внимания на кошку!
А она, наоборот, не сводила с него глаз. Она замерла и следила за голубем через стекло. Хотя и понимала, конечно, что поймать его не сумеет.
А человек, наблюдая за этой сценой, размышлял… И кошке своей любимой он сочувствовал, понимал ее желание поймать голубя и поиграть с ним… И голубю он тоже сочувствовал, понимал, что тому совсем не хочется, чтобы с ним играла кошка…
Наконец голубь улетел.
Тогда человек и кошка вернулись к математике.
Они решили еще несколько примеров, теперь уже на деление. После сложения и умножения решить их было очень легко.
Кошка быстро переключилась от мыслей о недоступном голубе на мысли о делении чисел пополам.
Здесь ведь даже и таблица умножения не особенно нужна. Мы действуем все с теми же самыми числами. И запоминаем, и понимаем их все лучше и лучше…
– Знаешь, для всего данного ряда чисел ученые придумали специальное слово. Все это степени числа 2. Первая степень – это само число 2. Вторая степень – это 2 умножить на 2. А третья степень – это 2 умножить на 2 и еще раз умножить на 2… – стал человек дальше рассказывать не спеша.
А кошка слушала и кивала. Хотя слово “степень” было новым для нее, она быстро уловила суть: это сколько раз мы берем число 2 в умножении его на само себя. Объяснять можно разными словами, конечно. Главное – понять идею.
Потом она спросила:
– Мур-р… А надо запоминать, каким именно степеням числа 2 соответствуют числа из нашего ряда? Ну, начало я уже запомнила. Число 4 – это вторая степень. А число 8 – это третья степень. Мяу.
– Нет, совсем не обязательно. Если сам собой запоминается постепенно номер степени для некоторых случаев, то и ладно.
А если не запоминается, то и ничего страшного. Я просто хотел тебе объяснить саму суть понятия “степень”. В математике ты с ним еще много раз потом встретишься, – ответил человек. И снова погладил кошку.
А она довольно замурчала и прикрыла глаза.
Так они посидели минут десять…
Потом человек пересел к компьютеру и собрался за ним поработать. И вдруг вспомнил:
– Кстати. Я забыл тебе сказать еще одну важную вещь. Степени числа 2 очень широко используются в программировании, во всем устройстве компьютеров. И особенно известно число 1024…
– Мяу. И что же в нем такого особенного? – с интересом перебила кошка.
– Гм… Как бы попроще тебе объяснить… Самое маленькое, что может запомнить компьютер в своей памяти – это бит… – начал человек.
Но кошка снова перебила его:
– Слово “бит” происходит от слова “бить”?
– Нет. Это английское слово. По-английски оно пишется “bit”, – улыбнулся человек и написал это на листке бумаги. – Переводится как “кусочек”, “немножко”, “небольшое количество”… Как раз подходит для обозначения самого маленького количества информации.
– Ясно, мур-р, – кивнула кошка.
– Для удобства эти самые маленькие биты обычно объединяют по 8 штук… – продолжал рассказывать человек.
– Да, я уже поняла, что 8 – это одна из степеней числа 2, мур-р, – муркнула кошка негромко.
Человек еще раз ее погладил и сказал:
– Умница ты моя хвостатая! А 8 бит вместе называют специальным словом – “байт”. Оно тоже английское. Но это тоже не очень много информации, конечно. Поэтому биты или байты объединяют в большущие килобиты и килобайты. Ты ведь знаешь, что означает приставка “кило-”?
– Знаю. Мяу. Килограмм – это тысяча грамм. Километр – это тысяча метров. Мяу. Наверное, килобит – это тысяча битов. А килобайт – тысяча байтов, – сообразила кошка.
– Примерно так, – кивнул человек. – Но не совсем. Поскольку в компьютерах очень широко используют число 2 и его степени, то килобитом называют 1024 бит. А килобайт – это 1024 байта. Как раз примерно 1000.
– Удобно придумали, мяу, – согласилась кошка.
Она побродила по комнате, подошла к дивану, забралась на него, выбрала удобное место, потопталась на нем, мурча себе тихонечко под нос, а затем улеглась, уютно свернувшись и закрыв глаза.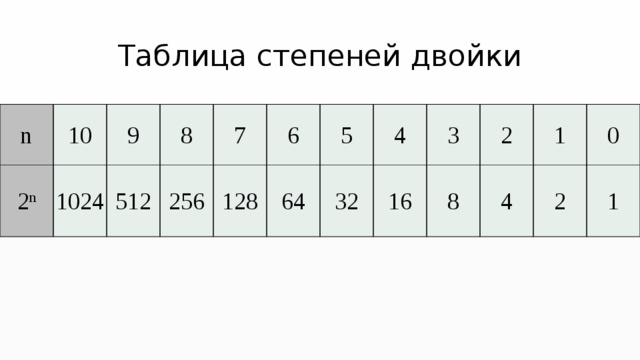
И уснула спокойно.
Ей снились степени числа 2 – в виде летающих в воздухе чисел. Она во сне смотрела на них и ощущала полное довольство. Потому что это были уже хорошо знакомые ей числа, понятные и привычные. Кошка улыбалась во сне и чувствовала волшебство простой математики…
Такая вот сказка.
Возможно, она пригодится не только кошкам, но и детям, и взрослым…
Конечно, изложенная здесь методическая последовательность вовсе не является такой уж однозначно обязательной. Я описал лишь общую схему. А вы можете подобрать свой вариант – уже с учетом конкретных особенностей тех детей, которых вы учите.
А может быть, вы вместе с детишками сочините еще сказки про разных кошек, которые изучают математику вместе с людьми?
Уделяя внимание знакомству со степенями числа 2 (до десятой), мы показываем ребенку устройство мира чисел. Да, это только небольшая часть огромного мира математики. Но в ней есть все, что нам помогает: и стройная логика, и естественная красота, и связь с жизнью, и простые алгоритмы…
Степени числа два — возведение числа 2 в степень
Главная ›
С частичным указанием числа знаков (цифр) в получающихся числах.
20 = 1
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
29 = 512
210 = 1024
211 = 2048
212 = 4096
213 = 8192
214 = 16384 (5 знаков)
215 = 32768
216 = 65536
217 = 131072
218 = 262144
219 = 524288
220 = 1048576
221 = 2097152
222 = 4194304
223 = 8388608
224 = 16777216
225 = 33554432
226 = 67108864
227 = 134217728
229 = 536870912
230 = 1073741824 (10 знаков)
231 = 2147483648
232 = 4294967296
233 = 8589934592
234 = 17179869184
235 = 34359738368
236 = 68719476736
237 = 137438953472
238 = 274877906944
239 = 549755813888
240 = 1099511627776
241 = 2199023255552
242 = 4398046511104
243 = 8796093022208
244 = 17592186044416
245 = 35184372088832
246 = 70368744177664
247 = 140737488355328 (15 знаков)
248 = 281474976710656
249 = 562949953421312
250 = 1125899906842624
251 = 2251799813685248
252 = 4503599627370496
253 = 9007199254740992
254 = 18014398509481984
2 55 = 36028797018963968
256 = 72057594037927936
257 = 144115188075855872
258 = 288230376151711744
259 = 576460752303423488
260 = 1152921504606846976
261 = 2305843009213693952
262 = 4611686018427387904
263 = 9223372036854775808
264 = 18446744073709551616 (20 знаков)
265 = 36893488147419103232
266 = 73786976294838206464
267 = 147573952589676412928
268 = 295147905179352825856
269 = 590295810358705651712
270 = 1180591620717411303424
271 = 2361183241434822606848
272 = 4722366482869645213696
273 = 9444732965739290427392
274 = 18889465931478580854784
275 = 37778931862957161709568
276 = 75557863725914323419136
277 = 151115727451828646838272
279 = 604462909807314587353088
280 = 1208925819614629174706176 (25 знаков)
281 = 2417851639229258349412352
282 = 4835703278458516698824704
283 = 9671406556917033397649408
284 = 19342813113834066795298816
285 = 38685626227668133590597632
286 = 77371252455336267181195264
287 = 154742504910672534362390528
288 = 309485009821345068724781056
289 = 618970019642690137449562112
290 = 1237940039285380274899124224
291 = 2475880078570760549798248448
292 = 4951760157141521099596496896
293 = 9903520314283042199192993792
294 = 19807040628566084398385987584
295 = 39614081257132168796771975168
296 = 79228162514264337593543950336
297 = 158456325028528675187087900672 (30 знаков)
298 = 316912650057057350374175801344
299 = 633825300114114700748351602688
2100 = 1267650600228229401496703205376
2101 = 2535301200456458802993406410752
2102 = 5070602400912917605986812821504
2103 = 10141204801825835211973625643008
2104 = 20282409603651670423947251286016
2105 = 40564819207303340847894502572032
2106 = 81129638414606681695789005144064
2107 = 162259276829213363391578010288128
2108 = 324518553658426726783156020576256
2109 = 649037107316853453566312041152512
2110 = 1298074214633706907132624082305024
2111 = 2596148429267413814265248164610048
2112 = 5192296858534827628530496329220096
2113 = 10384593717069655257060992658440192 (35 знаков)
2114 = 20769187434139310514121985316880384
2
2116 = 83076749736557242056487941267521536
2117 = 166153499473114484112975882535043072
2118 = 332306998946228968225951765070086144
2119 = 664613997892457936451903530140172288
2120 = 1329227995784915872903807060280344576
2121 = 2658455991569831745807614120560689152
2122 = 5316911983139663491615228241121378304
2123 = 10633823966279326983230456482242756608
2124 = 21267647932558653966460912964485513216
2125 = 42535295865117307932921825928971026432
2126 = 85070591730234615865843651857942052864
2127 = 170141183460469231731687303715884105728
2128 = 340282366920938463463374607431768211456
2129 = 680564733841876926926749214863536422912
2130 = 1361129467683753853853498429727072845824 (40 знаков)
2131 = 2722258935367507707706996859454145691648
2132 = 5444517870735015415413993718908291383296
2133 = 10889035741470030830827987437816582766592
2134 = 21778071482940061661655974875633165533184
2135 = 43556142965880123323311949751266331066368
2136 = 87112285931760246646623899502532662132736
2137 = 174224571863520493293247799005065324265472
2138 = 348449143727040986586495598010130648530944
2139 = 696898287454081973172991196020261297061888
2140 = 1393796574908163946345982392040522594123776
2021 (чуть ранее в 2021 на странице /page-1001-11.
html на «pg» сайте)
Генерация степеней двойки — онлайн-инструменты для работы с числами
Генерация чисел Numberwang
Создание списка номеров numberwang.
Создание магических чисел
Создание списка аккуратно выглядящих чисел.
Нарисовать магический квадрат
Создать матрицу чисел, в которой строки и столбцы имеют одинаковую сумму.
Переписать числа
Учитывая числа и грамматику, рекурсивно переписать их.
Создание числа с плавающей запятой
Создание числа из мантиссы, основания и экспоненты.
Визуализация числа с плавающей запятой
Показать, как число fp представляется в компьютере.
Преобразование числа в экспоненциальную запись
Преобразование числа в формат a×10 b .
Преобразование научной записи в число
Преобразование числа в научной записи в обычное число.
Создать унарную нумерацию
Создать список унарных чисел (1, 11, 111, 1111, …).
Создать символьную нумерацию
Создать список буквенных чисел (a, b, c, …, z, aa, ab, …).
Создать римскую нумерацию
Создать список римских цифр (i, ii, iii, iv, v…).
Создать нумерацию Брайля
Создать список цифр Брайля (⠂, ⠆, ⠒, ⠲, ⠢, …).
Создание случайных двоичных чисел
Создание списка случайных двоичных чисел.
Создание случайных восьмеричных чисел
Создание списка случайных восьмеричных чисел.
Генерация случайных десятичных чисел
Создать список случайных десятичных чисел.
Создание случайных шестнадцатеричных чисел
Создание списка случайных шестнадцатеричных чисел.
Вычислить текущую сумму
Вычислить кумулятивную сумму списка чисел.
Вычислить текущую разницу
Вычислить кумулятивную разницу списка чисел.
Вычисление текущего произведения
Вычисление кумулятивного произведения списка чисел.
Расчет числового коэффициента
Разделите два числа и найдите их частное.
Вычислить числовое частное
Разделить цифры заданного числа.
Вычислить факториал
Найти факториал числа.
Создание числовых анаграмм
Создание одной или нескольких числовых анаграмм.
Создание числовых биграмм
Создание списка цифровых биграмм из числа.
Создание числовых триграмм
Создание списка цифровых триграмм из числа.
Генерация числовых N-грамм
Создание списка цифровых nграмм из числа.
Создание полиномиальной последовательности
Создание списка чисел полиномиальной прогрессии.
Создание префиксов SI
Создание списка префиксов метрик.
Анализ числа
Сообщить, сколько цифр встречается сколько раз.
Преобразование числа в порядковое
Преобразование количественного числительного в порядковое.
Преобразование порядкового номера в число
Преобразование порядкового числа в кардинальное.
Преобразование числа в римское число
Преобразование арабских цифр в римские.
Преобразование римских чисел в обычные числа
Преобразование римских цифр в арабские.
Создание чисел Негафибоначчи
Вычисление серии расширенных чисел Фибоначчи.
Генерация простых чисел Фибоначчи
Поиск чисел, которые являются одновременно числами Фибоначчи и простыми числами.
Тест чисел Фибоначчи
Проверить, является ли число числом Фибоначчи.
Проверка простых чисел Фибоначчи
Проверяет, является ли число одновременно числом Фибоначчи и простым числом.
Построить слова Фибоначчи
Создать последовательность слов Фибоначчи.
Создать слова Трибоначчи
Создать последовательность слов Трибоначчи.
Создать слова Тетраначчи
Создать последовательность слов Тетраначчи.
Создать слова Пентаначчи
Создать последовательность слов Пентаначчи.
Генерировать числа Негалука
Вычислить серию расширенных чисел Лукаса.
Генерировать простые числа Лукаса
Вычислить серию расширенных чисел Лукаса.
Lucas Prime Test
Проверить, является ли число одновременно числом Лукаса и простым числом.
Генерация чисел Мозера де Брюйна
Вычисление последовательности чисел Мозера-Брейна.
Сгенерировать числа Колакоски
Вычислить последовательность чисел Ольденбургера-Колакоски.
Сгенерировать числа Стэнли
Вычислить последовательность чисел Стэнли.
Генерировать числа Гийсвейта
Вычислить последовательность самоописывающих чисел Гийсвейта.
Сгенерировать числа Рудина-Шапиро
Вычислить последовательность чисел Русина-Шапиро.
Генерация чисел Баума-Свита
Вычисление последовательности чисел Баума-Свита.
Генерация последовательности Туэ-Морса
Вычисление членов ряда чисел Туэ-Морса.
Создание идеальных чисел
Создание списка совершенных чисел.
Создание почти идеальных чисел
Создание списка почти идеальных чисел.
Создать последовательность избыточных чисел
Вычислить последовательность избыточных чисел.
Создать последовательность неполных чисел
Вычислить последовательность неполных чисел.
Вычислить числа Dragon Curve
Сгенерировать список порядковых номеров складывания бумаги.
Создать составные числа
Создать список чисел, которые не являются простыми.
Нарисовать число на ЖК-дисплее
Создать ЖК-дисплей, отображающий заданное число.
Нарисовать таблицу чисел
Создать таблицу чисел.
Проверить, является ли число совершенным
Проверить, является ли заданное число совершенным числом.
Проверить, является ли число обильным
Проверить, является ли данное число обильным числом.
Проверить, является ли число недостаточным
Проверить, является ли данное число недостаточным.
Вычислить модуль
Найти модуль числа.
Группировка цифр числа
Группировка цифр числа.
Разделить число на цифры
Создать список цифр из числа.
Printf Numbers
Применение функций sprintf или printf к числам.
Создайте номера Zalgo
Позвольте Zalgo уничтожить ваши номера.
Повторить цифру
Повторить число несколько раз.
Зеркальное отображение номера
Создание зеркальной копии номера.
Дополнение числа нулями
Добавление нулей к числу.
Пользовательское дополнение числа
Добавление пользовательских символов к числу.
Обратный порядок цифр
Обратный порядок цифр в числе.
Поворот числа
Циклический поворот цифр числа влево или вправо.
Увеличение числа
Добавить единицу к заданному числу.
Увеличить все цифры в числе
Добавить единицу к каждой цифре в числе.
Уменьшить число
Вычесть единицу из заданного числа.
Уменьшить все цифры в числе
Вычесть единицу из каждой цифры в числе.
Находить закономерности в числах
Находить закономерности в последовательностях чисел.
Подсчет числа вхождений
Узнайте, как часто появляются числовые значения.
Расчет процентов
Найти x% числа.
Распечатать Google
Распечатать номер Google/Google, который равен 10 100 .
Создание больших чисел
Создание списка больших чисел.
Создание малых чисел
Создание списка малых чисел.
Создание натуральных чисел
Создание списка натуральных чисел.
Создание рациональных чисел
Создание списка рациональных чисел.
Генерация постоянной последовательности
Создайте серию чисел, в которой все термины одинаковы.
Создание действительных чисел
Создание последовательности действительных чисел.
Создание комплексных чисел
Создание списка комплексных чисел.
Создание двоичных чисел
Создание последовательности двоичных чисел.
Создание пар чисел
Создание последовательности пар чисел.
Создание троек чисел
Создание последовательности троек чисел.
Создание кортежей чисел
Создание последовательности n-кортежей чисел.
Создать короткий номер
Создать номер с небольшим количеством цифр.
Создать длинный номер
Создать номер с большим количеством цифр.
Переплетение чисел
Переплетение двух или более чисел поразрядно.
Найти десятичное представление числа
Переписать число в десятичной форме.
Преобразование дроби в десятичную
Преобразование дроби в десятичное число.
Преобразование десятичного числа в дробь
Преобразование десятичного числа в дробь.
Преобразование двоичного числа в восьмеричное
Преобразование числа с основанием два в число с основанием восемь.
Преобразование двоичного числа в десятичное число
Преобразование числа с основанием два в число с основанием десять.
Преобразование двоичного числа в шестнадцатеричное
Преобразование числа с основанием два в число с основанием шестнадцать.
Преобразование восьмеричного числа в двоичное число
Преобразовать число с основанием восемь в число с основанием два.
Преобразование восьмеричного числа в десятичное
Преобразование числа с основанием восемь в число с основанием десять.
Преобразование восьмеричного числа в шестнадцатеричное
Преобразование числа с основанием восемь в число с основанием шестнадцать.
Преобразование десятичного числа в двоичное
Преобразование числа с основанием десять в число с основанием два.
Преобразование десятичного числа в восьмеричное
Преобразование десятичного числа в восьмеричное.
Преобразование десятичного числа в шестнадцатеричное
Преобразование числа с основанием десять в число с основанием шестнадцать.
Преобразование шестнадцатеричного числа в двоичное число
Преобразование числа с основанием шестнадцать в число с основанием два.
Преобразование шестнадцатеричного числа в восьмеричное
Преобразование числа с основанием шестнадцать в число с основанием восемь.
Преобразование шестнадцатеричного числа в десятичное число
Преобразование числа с основанием шестнадцать в число с основанием десять.
Преобразование любого числа в любое число с основанием
Преобразование любого числа в любой системе счисления в любую другую систему счисления.
Изменение мантиссы числа
Изменение значения числа.
Изменить показатель степени числа
Изменить степень числа.
Замена цифр буквами
Замена цифр в числе буквами алфавита.
Создание спирали чисел
Создание спирали из цифр числа.
Создать числовой круг
Сформировать круг из цифр числа.
Создать числовое дерево
Сформировать дерево из заданных чисел.
Создание дерева цифр числа
Создание дерева из цифр числа.
Удалить десятичную точку
Удалить десятичный разделитель из десятичного числа.
Добавить ошибки в числа
Изменить числа, чтобы они были почти одинаковыми, но содержали ошибки.
Создание поддельных номеров
Замена цифр в номере на двойники Unicode.
Число возмущений
Немного изменить указанные числа.
Возмущенные цифры числа
Немного измените цифры данных чисел.
Найти энтропию числа
Вычислить сложность (энтропию) числа.
Проверка числа Numberwang
Проверка, является ли данный номер числом numberwang.
Программа Python для отображения степени двойки
питон Джава С С++ HTML CSS JavaScript PHP SQL Контрольный опрос
Эта статья посвящена некоторым программам на Python, которые находят и печатают степень двойки до любого конкретного значения. термин, определяемый пользователем во время выполнения. Вот список использованных подходов:
- Простая программа для отображения степеней двойки до N терминов. Значение N должно быть введено пользователем .
- Отображение степеней двойки с использованием обычной функции
- Использование анонимной (лямбда) функции
Отображение степеней двойки до N терминов
Чтобы отобразить степени двойки до заданных терминов в Python, вы должны попросить пользователя ввести общее количество терминов, затем отображать степень двойки от 0 до N-1 , как показано в программе, приведенной ниже:
print("Введите общее количество терминов:")
тот = целое (ввод ())
для i в диапазоне (tot):
print("2 в степени ", i, " is ", 2 ** i) Вот начальный вывод, полученный этой программой Python:
Теперь введите ввод, скажем, 8 и нажмите клавишу ENTER найти и вывести все степени числа 2 до 8 термины, начинающиеся с 0, как показано на снимке ниже:
Примечание — Оператор ** (возведение в степень) в Python используется для поиска возведенного в степень значения.
Например а**б оценивается как a b . Итак, 2 ** 3 возвращает 2*2*2 , то есть 8
Если пользователь вводит ввод как 8 , то 8 сохраняется в to . Итак, из приведенной выше программы следующий код (после замены значения переменной на ):
для i в диапазоне (8):
создается для выполнения следующего оператора (присутствует внутри его тела):
print("2 в степени", i, " is ", 2 ** i) восемь раз со значением i от 0 до 7 (8-1).
Отображение степеней двойки с использованием нормальной функции
Эта программа выполняет ту же работу, что и предыдущая программа, но использует функцию с именем MyFun()
по умолчанию MyFun(x):
вернуть 2 ** х
print("Введите номер термина: ", end="")
тот = целое (ввод ())
Распечатать()
для i в диапазоне (tot):
print("2 возведено в степень ", i," is ", MyFun(i)) Вот его пример запуска с пользовательским вводом 11 как общее количество терминов:
end= в приведенной выше программе , используется для пропуска автоматической вставки новой строки.