Формула сокращенного умножения кубы: Применение формул сокращённого умножения. Алгебра, 7 класс: уроки, тесты, задания.

afront, я не ставил под сомнение что конкретно у вашей версии определённого компилятора функция pow каким-то образом определяется без явного указания заголовочного файла.
Но это не значит, что так делать правильно. Так как стандарт не гарантирует, что данный код будет работать и вы закладываетесь на определённую версию определённого компилятора.

Добавлено через 29 секунд
Функция system, кстати, определена в cstdlib, который у вас тоже не подключен

, без которой код не компилируется

Добавлено через 29 секунд
но я не увидел ее и код компилируется, странно это все

Получить натуральные числа куб суммы цифр которых равен заданному числу
Получить все меньшие n натуральные числа, квадрат суммы цифр которых равен m. #include .

Определить, равен ли квадрат заданного трехзначного числа кубу суммы цифр этого числа VS2010
тупая задача на новый лад — С++: Определить, равен ли квадрат заданного трехзначного числа кубу.

Найти среди двузначных чисел такие, что квадрат числа равен кубу суммы цифр этого числа
Найти среди двузначных чисел такие, что квадрат числа равен кубу суммы цифр этого числа. Помогите.

Квадрат заданного трехзначного числа равен кубу суммы цифр этого числа
квадрат заданного трехзначного числа равен кубу суммы цифр этого числа

Проверить, квадрат заданного трехзначного числа равен кубу суммы цифр этого числа
ОЧЕНЬ СРОЧНО НУЖНА ПОМОЩЬ ПО ПРОГРАММИРОВАНИЮ, НА СТИПУХУ НАДО ВЫХОДИТЬ. Задание 1 Написать.

Даны числа m и n. Получить все натуральные числа,меньшие n, квадрат суммы цифр которых равен m
Доброго времени суток) прошу вашей помощи. Даны числа m и n. Получить все натуральные.

Источник

Куб суммы: формула и примеры

В данной публикации мы рассмотрим одну из формул сокращенного умножения, позволяющую разложить куб суммы на множители, а также, подробно разберем пример решения задачи.

Формула куба суммы

Куб суммы слагаемых a и b равняется кубу a плюс утроенное произведение квадрата a на b плюс утроенное произведение квадрата b на a плюс куб b .

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Формула равносильна и в обратном порядке:

a 3 + 3a 2 b + 3ab 2 + b 3 = (a + b) 3

Доказательство формулы

Куб числа/выражения – это его возведение в третью степень. Давайте представим наше выражение в виде куба:
(a + b) 3 = (a + b)(a + b)(a + b) .

Перемножаем скобки с учетом арифметических правил:
(a + b)(a + b)(a + b) = (a + b)(a + b) 2 = (a + b)(a 2 + 2ab + b 2 ) = a 3 + 2a 2 b + ab 2 + a 2 b + 2ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Примечание: при раскрытии скобок использовалась формула квадрата суммы:
(a + b) 2 = a 2 + 2ab + b 2 .

Пример

Чему равен куб суммы (5x + 7y) 3 ?

Решение
Используем формулу сокращенного умножения:
(5x + 7y) 3 = (5x) 3 + 3 ⋅ (5x) 2 ⋅ 7y + 3 ⋅ 5x ⋅ (7y) 2 + (7y) 3 = 125x 3 + 525x 2 y + 735xy 2 + 343y 3

Проверка
Выполним перемножение трех одинаковых скобок:
(5x + 7y) 3 = (5x + 7y)(5x + 7y)(5x + 7y) = (5x + 7y)(5x + 7y) 2 = (5x + 7y)(25x 2 + 70xy + 49y 2 ) = 125x 3 + 350x 2 y + 245xy 2 + 175x 2 y + 490xy 2 + 343y 3 = 125x 3 + 525x 2 y + 735xy 2 + 343y 3

Источник

Формулы сокращённого умножения

При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения. Всего таких формул семь. Их все необходимо знать наизусть.

Следует также помнить, что вместо « a » и « b » в формулах могут стоять как числа, так и любые другие алгебраические многочлены.

Разность квадратов

Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.

• 15 2 − 2 2 = (15 − 2)(15 + 2) = 13 · 17 = 221
• 9a 2 − 4b 2 с 2 = (3a − 2bc)(3a + 2bc)

Квадрат суммы

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик. Поясним на примере:

• Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.
  112 = 100 + 1
• Запишем сумму чисел в скобки и поставим над скобками квадрат.
  112 2 = (100 + 12) 2
• Воспользуемся формулой квадрата суммы:
  112 2 = (100 + 12) 2 = 100 2 + 2 · 100 · 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544

Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.

• (8a + с) 2 = 64a 2 + 16ac + c 2

Предостережение!

Квадрат разности

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.

Также стоит запомнить весьма полезное преобразование:

Формула выше доказывается простым раскрытием скобок:

(a − b) 2 = a 2 −2ab + b 2 = b 2 − 2ab + a 2 = (b − a) 2

Куб суммы

Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Как запомнить куб суммы

Запомнить эту «страшную» на вид формулу довольно просто.

• Выучите, что в начале идёт « a 3 ».
• Два многочлена посередине имеют коэффициенты 3 .
• Вспомним, что любое число в нулевой степени есть 1 . (a 0 = 1, b 0 = 1) . Легко заметить, что в формуле идёт понижение степени « a » и увеличение степени « b ». В этом можно убедиться:
  (a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3

Предостережение!

Куб разности

Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.

(a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Запоминается эта формула как и предыдущая, но только с учётом чередования знаков « + » и « − ». Перед первым членом « a 3 » стоит « + » (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять « − », затем опять « + » и т.д.

(a − b) 3 = + a 3 − 3a 2 b + 3ab 2 − b 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Сумма кубов

Не путать с кубом суммы!

Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.

a 3 + b 3 = (a + b)(a 2 − ab + b 2 )

Сумма кубов — это произведение двух скобок.

• Первая скобка — сумма двух чисел.
• Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:
  (a 2 − ab + b 2 )
  Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.

Разность кубов

Не путать с кубом разности!

Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.

a 3 − b 3 = (a − b)(a 2 + ab + b 2 )

Будьте внимательны при записи знаков.

Применение формул сокращенного умножения

Следует помнить, что все формулы, приведённые выше, используется также и справа налево.

Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберёте многочлен обратно.

• a 2 + 2a + 1 = (a + 1) 2
• (aс − 4b)(ac + 4b) = a 2 c 2 − 16b 2

Таблицу со всеми формулами сокращённого умножения вы можете скачать в разделе «Шпаргалки».

Источник

Геометрический смысл формул сокращенного умножения.

На данном уроке мы познакомимся с формулами квадрата суммы и квадрата разности и выведем их. Формулу квадрата суммы докажем геометрически. Кроме того, решим много различных примеров с применением этих формул.

Рассмотрим формулу квадрата суммы:

Итак, мы вывели формулу квадрата суммы:

Словесно эта формула выражается так: квадрат суммы равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

Данную формулу легко представить геометрически.

Рассмотрим квадрат со стороной :

Площадь квадрата.

С другой стороны, этот же квадрат можно представить иначе, разбив сторону на а и b (рис. 1).

Рис. 1. Квадрат

Тогда площадь квадрата можно представить в виде суммы площадей:

Поскольку квадраты были одинаковы, то их площади равны, значит:

Итак, мы доказали геометрически формулу квадрата суммы.

Рассмотрим примеры:

Комментарий: пример решен с применением формулы квадрата суммы.

Выведем формулу квадрата разности:

Итак, мы вывели формулу квадрата разности:

Словесно эта формула выражается так: квадрат разности равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа.

Рассмотрим примеры:

Формулы квадрата суммы и квадрата разности могут работать как слева направо, так и справа налево. При использовании слева направо это будут формулы сокращенного умножения, они применяются при вычислении и преобразовании примеров. А при использовании справа налево — формулы разложения на множители.

Рассмотрим примеры, в которых нужно разложить заданный многочлен на множители, применяя формулы квадрата суммы и квадрата разности. Для этого нужно очень внимательно посмотреть на многочлен и определить, как именно его правильно разложить.

Комментарий: для того, чтобы разложить многочлен на множители, нужно определить, что представлено в данном выражении. Итак, мы видим квадрат и квадрат единицы. Теперь нужно найти удвоенное произведение — это . Итак, все необходимые элементы есть, нужно только определить, это квадрат суммы или разности. Перед удвоенным произведением стоит знак плюс, значит, перед нами квадрат суммы.

Содержание урока

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y ) 2 .

Выражение (2x + 3y ) 2 это перемножение двух многочленов, каждый из которых равен (2x + 3y )

(2x + 3y ) 2 = (2x + 3y )(2x + 3y )

Получили умножение многочлена на многочлен. Выполним его:

(2x + 3y ) 2 = (2x + 3y )(2x + 3y ) = 4x 2 + 6xy + 6xy + 9y 2 = 4x 2 + 12xy + 9y 2

То есть выражение (2x + 3y ) 2 равно 4x 2 + 12xy + 9y 2

(2x + 3y ) 2 = 4x 2 + 12xy + 9y 2

Решим аналогичный пример, который попроще:

(a + b ) 2

Выражение (a + b ) 2 это перемножение двух многочленов, каждый из которых равен (a + b )

(a + b ) 2 = (a + b )(a + b )

Выполним это умножение:

(a + b ) 2 = (a + b )(a + b ) = a 2 + ab + ab + b 2 = a 2 + 2ab + b 2

То есть выражение (a + b ) 2 равно a 2 + 2ab + b 2

(a + b ) 2 = a 2 + 2ab + b 2

Оказывается, что случай (a + b ) 2 можно распространить для любых a и b . Первый пример, который мы решили, а именно (2x + 3y ) 2 можно решить с помощью тождества (a + b ) 2 = a 2 + 2ab + b 2 . Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y ) 2 . В данном случае переменной a соответствует член 2x , а переменной b соответствует член 3y

a = 2x

b = 3y

И далее можно воспользоваться тождеством (a + b ) 2 = a 2 + 2ab + b 2 , но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:

(2x + 3y ) 2 = (2x ) 2 + 2 × 2x × 3y + (3y ) 2 = 4x 2 + 12xy + 9y 2

Как и в прошлый раз получили многочлен 4x 2 + 12xy + 9y 2 . Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:

(2x + 3y ) 2 = 4x 2 + 12xy + 9y 2

Тождество (a + b ) 2 = a 2 + 2ab + b 2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Рассмотрим выражение (2 + 3) 2 . Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3) 2 = 5 2 = 25

Второй способ:

(2 + 3) 2 = 2 2 + 2 × 2 × 3 + 3 2 = 4 + 12 + 9 = 25

Пример 2 . Преобразовать выражение (5a + 3) 2 в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

(a + b ) 2 = a 2 + 2ab + b 2

(5a + 3) 2 = (5a ) 2 + 2 × 5a × 3 + 3 2 = 25a 2 + 30a + 9

Значит, (5a + 3) 2 = 25a 2 + 30a + 9.

Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:

(5a + 3) 2 = (5a + 3)(5a + 3) = 25a 2 + 15a + 15a + 9 = 25a 2 + 30a + 9

Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.

Например, площадь квадрата со стороной a будет равна a 2 . Если увеличить сторону квадрата на b , то площадь будет равна (a + b ) 2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b . У квадрата все стороны равны. Если его сторону увеличить на b , то остальные стороны тоже увеличатся на b

Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:

Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.

Сначала можно вычислить квадрат со стороной a — его площадь будет равна a 2 . Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab . Затем можно вычислить квадрат со стороной b

В результате получается следующая сумма площадей:

a 2 + ab + ab + b 2

Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab , которое буквально будет означать «повторить два раза площадь прямоугольника ab» . Алгебраически это получается путём приведения подобных слагаемых ab и ab . В результате получается выражение a 2 + 2ab + b 2 , которое является правой частью формулы квадрата суммы двух выражений:

(a + b ) 2 = a 2 + 2ab + b 2

Квадрат разности двух выражений

Формула квадрата разности двух выражений выглядит следующим образом:

(a − b ) 2 = a 2 − 2ab + b 2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b ) 2 представляет собой произведение двух многочленов, каждый из которых равен (a − b )

(a − b ) 2 = (a − b )(a − b )

Если выполнить это умножение, то получится многочлен a 2 − 2ab + b 2

(a − b ) 2 = (a − b )(a − b ) = a 2 − ab − ab + b 2 = a 2 − 2ab + b 2

Пример 1 . Преобразовать выражение (7x − 5) 2 в многочлен.

Воспользуемся формулой квадрата разности двух выражений:

(a − b ) 2 = a 2 − 2ab + b 2

(7x − 5) 2 = (7x ) 2 − 2 × 7x × 5 + 5 2 = 49x 2 − 70x + 25

Значит, (7x − 5) 2 = 49x 2 + 70x + 25.

Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:

(7x − 5) 2 = (7x − 5) (7x − 5) = 49x 2 − 35x − 35x + 25 = 49x 2 − 70x + 25.

Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a 2 , то площадь квадрата, сторона которого уменьшена на b , будет равна (a − b ) 2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b . У квадрата все стороны равны. Если одну сторону уменьшить на b , то остальные стороны тоже уменьшатся на b

Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b , поскольку старая сторона a уменьшилась на b . Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a 2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:

Тогда можно написать следующее выражение: старая площадь a 2 минус площадь ab минус площадь (a − b )b

a 2 − ab − (a − b )b

Раскроем скобки в выражении (a − b )b

a 2 − ab − ab + b 2

Приведем подобные слагаемые:

a 2 − 2ab + b 2

В результате получается выражение a 2 − 2ab + b 2 , которое является правой частью формулы квадрата разности двух выражений:

(a − b ) 2 = a 2 − 2ab + b 2

Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения . Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.

Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.

Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.

Например, если дано выражение (5x − 2y ) 2 , и мы хотим воспользоваться формулой (a − b ) 2 = a 2 − 2ab + b 2 , то вместо b нужно подставлять 2y , а не −2y . Это особенность работы с формулами, которую не следует забывать.

(5x − 2y ) 2
a = 5x
b = 2y
(5x − 2y ) 2 = (5x ) 2 − 2 × 5x × 2y + (2y ) 2 = 25x 2 − 20xy + 4y 2

Если подставлять −2y , то это будет означать, что разность в скобках исходного выражения была заменена на сумму:

(5x − 2y ) 2 = (5x + (−2y )) 2

и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:

(5x + (−2y ) 2
a = 5x
b = −2y
(5x + (−2y )) 2 = (5x ) 2 + 2 × 5x × (−2y ) + (−2y ) 2 = 25x 2 − 20xy + 4y 2

Исключением могут быть выражения вида (x − (−y )) 2 . В данном случае, применяя формулу (a − b ) 2 = a 2 − 2ab + b 2 вместо b следует подставить (−y )

(x − (−y )) 2 = x 2 − 2 × x × (−y ) + (−y ) 2 = x 2 + 2xy + y 2

Но возводя в квадрат выражения вида x − (−y ) , удобнее будет заменять вычитание на сложение x + y . Тогда первоначальное выражение примет вид (x + y ) 2 и можно будет воспользоваться формулой квадрата суммы, а не разности:

(x + y ) 2 = x 2 + 2xy + y 2

Куб суммы и куб разности

Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:

(a + b ) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

(a − b ) 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Формулу куба суммы двух выражений можно прочитать так:

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

А формулу куба разности двух выражений можно прочитать так:

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.

Выведем формулу куба суммы самостоятельно:

(a + b ) 3

Выражение (a + b ) 3 представляет собой произведение из трёх многочленов, каждый из которых равен (a + b )

(a + b ) 3 = (a + b )(a + b )(a + b )

Но выражение (a + b ) 3 также может быть записано как (a + b )(a + b ) 2

(a + b ) 3 = (a + b )(a + b ) 2

При этом сомножитель (a + b ) 2 является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a 2 + 2ab + b 2 .

Тогда (a + b ) 3 можно записать как (a + b )(a 2 + 2ab + b 2) .

(a + b ) 3 = (a + b )(a 2 + 2ab + b 2)

А это есть умножение многочлена на многочлен. Выполним его:

(a + b ) 3 = (a + b )(a 2 + 2ab + b 2) = a 3 + 2a 2 b + ab 2 + a 2 b + 2ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Аналогично можно вывести формулу куба разности двух выражений:

(a − b ) 3 = (a − b )(a 2 − 2ab + b 2) = a 3 − 2a 2 b + ab 2 − a 2 b + 2ab 2 − b 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Пример 1 . Преобразуйте выражение (x + 1) 3 в многочлен.

(a + b ) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

(x + 1) 3 = x 3 + 3 × x 2 × 1 + 3 × x × 1 2 + 1 3 = x 3 + 3x 2 + 3x + 1

Попробуем решить данный пример, не используя формулу куба суммы двух выражений

(x + 1) 3 = (x + 1)(x + 1)(x + 1) = (x + 1)(x 2 + 2x + 1) = x 3 + 2x 2 + x + x 2 + 2x + 1 = x 3 + 3x 2 + 3x + 1

Пример 2 . Преобразовать выражение (6a 2 + 3b 3) 3 в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(a + b ) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

(6a 2 + 3b 3) 3 = (6a 2) 3 + 3 × (6a 2) 2 × 3b 3 + 3 × 6a 2 × (3b 3) 2 + (3b 3) 3 = 216a 6 + 3 × 36a 4 × 3b 3 + 3 × 6a 2 × 9b 6 + 27b 9

Пример 3 .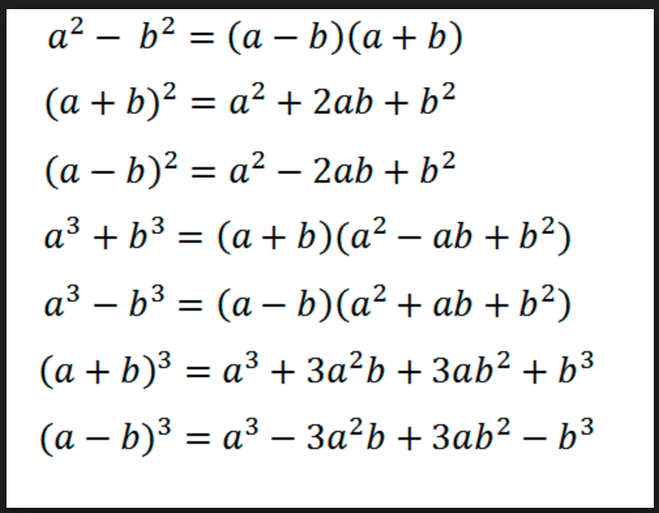 Преобразовать выражение (n 2 − 3) 3 в многочлен.

(a − b ) = a 3 − 3a 2 b + 3ab 2 − b 3

(n 2 − 3) 3 = (n 2) 3 − 3 × (n 2) 2 × 3 + 3 × n 2 × 3 2 − 3 3 = n 6 − 9n 4 + 27n 2 − 27

Пример 4 . Преобразовать выражение (2x 2 − x 3) 3 в многочлен.

Воспользуемся формулой куба разности двух выражений:

(a − b ) = a 3 − 3a 2 b + 3ab 2 − b 3

(2x 2 − x 3) 3 = (2x 2) 3 − 3 × (2x 2) 2 × x 3 + 3 × 2x 2 × (x 3) 2 − (x 3) 3 =
8x 6 − 3 × 4x 4 × x 3 + 3 × 2x 2 × x 6 − x 9 =
8x 6 − 12x 7 + 6x 8 − x 9

Умножение разности двух выражений на их сумму

Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:

(a − b )(a + b )

В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:

(a − b )(a + b ) = a 2 + ab − ab − b 2 = a 2 − b 2

То есть выражение (a − b )(a + b ) равно a 2 − b 2

(a − b )(a + b ) = a 2 − b 2

Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Случай (a − b )(a + b ) можно распространить для любых a и b . Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.

Пример 1 . Выполнить умножение (2x − 5)(2x + 5)

В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b )(a + b ) = a 2 − b 2 имеем:

(2x − 5)(2x + 5) = (2x ) 2 − 5 2

Вычислим правую часть, получим 4x 2 − 25

(2x − 5)(2x + 5) = (2x ) 2 − 5 2 = 4x 2 − 25

Попробуем решить данный пример, не пользуясь формулой (a − b )(a + b ) = a 2 − b 2 . У нас получится тот же результат 4x 2 − 25

(2x − 5)(2x + 5) = 4x 2 − 10x + 10x − 25 = 4x 2 − 25

Пример 2 . Выполнить умножение (4x − 5y )(4x + 5y )

(a − b )(a + b ) = a 2 − b 2

(4x − 5y )(4x + 5y ) = (4x ) 2 − (5y ) 2 = 16x 2 − 25y 2

Пример 3 . Выполнить умножение (2a + 3b )(2a − 3b )

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b )(a + b ) = a 2 − b 2

(2a + 3b )(2a − 3b ) = (2a ) 2 − (3b ) 2 = 4a 2 − 9b 2

В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b )(a + b ) = a 2 − b 2 разность располагается раньше.

Нет никакой разницы как располагаются сомножители (a − b ) в (a + b ) в формуле. Они могут быть быть записаны как (a − b )(a + b ) , так и (a + b )(a − b ) . Результат по прежнему будет равен a 2 − b 2 , поскольку от перестановки сомножителей произведение не меняется.

Так и в данном примере сомножители (2a + 3b ) и (2a − 3b ) можно записать как (2a + 3b )(2a − 3b ) , так и (2a − 3b )(2a + 3b ) . Результат всё так же будет равен 4a 2 − 9b 2 .

Пример 3 . Выполнить умножение (7 + 3x )(3x − 7)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b )(a + b ) = a 2 − b 2

(7 + 3x )(3x − 7) = (3x ) 2 − 7 2 = 9x 2 − 49

Пример 4 . Выполнить умножение (x 2 − y 3)(x 2 + y 3)

(a − b )(a + b ) = a 2 − b 2

(x 2 − y 3)(x 2 + y 3) = (x 2) 2 − (y 3) 2 = x 4 − y 6

Пример 5 . Выполнить умножение (−5x − 3y )(5x − 3y )

В выражении (−5x − 3y ) вынесем за скобки −1 , тогда исходное выражение примет следующий вид:

(−5x − 3y )(5x − 3y ) = −1(5x + 3y )(5x − 3y )

Произведение (5x + 3y )(5x − 3y ) заменим на разность квадратов:

(−5x − 3y )(5x − 3y ) = −1(5x + 3y )(5x − 3y ) = −1((5x ) 2 − (3y ) 2)

Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x ) 2 . А это приведет к ошибке и изменению значения исходного выражения.

(−5x − 3y )(5x − 3y ) = −1(5x + 3y )(5x − 3y ) = −1((5x ) 2 − (3y ) 2) = −1(25x 2 − 9x 2)

Теперь умножим −1 на выражение в скобках и получим окончательный результат:

(−5x − 3y )(5x − 3y ) = −1(5x + 3y )(5x − 3y ) = −1((5x ) 2 − (3y ) 2) =
−1(25x 2 − 9y 2) = −25x 2 + 9y 2

Умножение разности двух выражений на неполный квадрат их суммы

Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:

(a − b )(a 2 + ab + b 2)

Первый многочлен (a − b ) является разностью двух выражений, а второй многочлен (a 2 + ab + b 2) является неполным квадратом суммы этих двух выражений.

Неполный квадрат суммы это многочлен вида a 2 + ab + b 2 . Он похож на обычный квадрат суммы a 2 + 2ab + b 2

Например, выражение 4x 2 + 6xy + 9y 2 является неполным квадратом суммы выражений 2x и 3y .

Действительно, первый член выражения 4x 2 + 6xy + 9y 2 , а именно 4x 2 является квадратом выражения 2x , поскольку (2x ) 2 = 4x 2 . Третий член выражения 4x 2 + 6xy + 9y 2 , а именно 9y 2 является квадратом выражения 3y , поскольку (3y ) 2 = 9y 2 . Член находящийся в середине 6xy , является произведением выражений 2x и 3y.

Итак, умножим разность (a − b ) на неполный квадрат суммы a 2 + ab + b 2

(a − b )(a 2 + ab + b 2) = a (a 2 + ab + b 2) − b (a 2 + ab + b 2) =
a 3 + a 2 b + ab 2 − a 2 b − ab 2 − b 3 = a 3 − b 3

То есть выражение (a − b )(a 2 + ab + b 2) равно a 3 − b 3

(a − b )(a 2 + ab + b 2) = a 3 − b 3

Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы. Эту формулу можно прочитать так:

Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.

Пример 1 . Выполнить умножение (2x − 3y )(4x 2 + 6xy + 9y 2)

Первый многочлен (2x − 3y ) это разность двух выражений 2x и 3y . Второй многочлен 4x 2 + 6xy + 9y 2 это неполный квадрат суммы двух выражений 2x и 3y . Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b )(a 2 + ab + b 2) = a 3 − b 3 . В нашем случае умножение (2x − 3y )(4x 2 + 6xy + 9y 2) можно заменить на разность кубов 2x и 3y

(2x − 3y )(4x 2 + 6xy + 9y 2) = (2x ) 3 − (3y ) 3 = 8x 3 − 27y 3

(a − b )(a 2 + ab + b 2) = a 3 − b 3 . У нас получится тот же результат, но решение станет длиннее:

(2x − 3y )(4x 2 + 6xy + 9y 2) = 2x (4x 2 + 6xy + 9y 2) − 3y (4x 2 + 6xy + 9y 2) =
8x 3 + 12x 2 y + 18xy 2 − 12x 2 y − 18xy 2 − 27y 3 = 8x 3 − 27y 3

Пример 2 . Выполнить умножение (3 − x )(9 + 3x + x 2)

Первый многочлен (3 − x ) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b )(a 2 + ab + b 2) = a 3 − b 3

(3 − x )(9 + 3x + x 2) = 3 3 − x 3 = 27 − x 3

Умножение суммы двух выражений на неполный квадрат их разности

Встречаются задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Выглядит это произведение следующим образом:

(a + b )(a 2 − ab + b 2)

Первый многочлен (a + b (a 2 − ab + b 2) является неполным квадратом разности этих двух выражений.

Неполный квадрат разности это многочлен вида a 2 − ab + b 2 . Он похож на обычный квадрат разности a 2 − 2ab + b 2 за исключением того, что в нём произведение первого и второго выражений не удваивается.

Например, выражение 4x 2 − 6xy + 9y 2 является неполным квадратом разности выражений 2x и 3y .

(2x ) 2 − 2x × 3y + (3y ) 2 = 4x 2 − 6xy + 9y 2

Вернёмся к изначальному примеру. Умножим сумму a + b на неполный квадрат разности a 2 − ab + b 2

(a + b )(a 2 − ab + b 2) = a (a 2 − ab + b 2) + b (a 2 − ab + b 2) =
a 3 − a 2 b + ab 2 + a 2 b − ab 2 + b 3 = a 3 + b 3

То есть выражение (a + b )(a 2 − ab + b 2) равно a 3 + b 3

(a + b )(a 2 − ab + b 2) = a 3 + b 3

Это тождество называют формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:

Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.

Пример 1 . Выполнить умножение (2x + 3y )(4x 2 − 6xy + 9y 2)

Первый многочлен (2x + 3y ) это сумма двух выражений 2x и 3y , а второй многочлен 4x 2 − 6xy + 9y 2 это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b )(a 2 − ab + b 2) = a 3 + b 3 . В нашем случае умножение (2x + 3y )(4x 2 − 6xy + 9y 2) можно заменить на сумму кубов 2x и 3y

(2x + 3y )(4x 2 − 6xy + 9y 2) = (2x ) 3 + (3y ) 3 = 8x 3 + 27y 3

Попробуем решить этот же пример, не пользуясь формулой (a + b )(a 2 − ab + b 2) = a 3 + b 3 . У нас получится тот же результат, но решение станет длиннее:

(2x + 3y )(4x 2 − 6xy + 9y 2) = 2x (4x 2 − 6xy + 9y 2) + 3y (4x 2 − 6xy + 9y 2) =
8x 3 − 12x 2 y + 18xy 2 + 12x 2 y − 18xy 2 + 27y 3 = 8x 3 + 27y 3

Пример 2 . Выполнить умножение (2x + y )(4x 2 − 2xy + y 2)

Первый многочлен (2x + y ) является суммой двух выражений, а второй многочлен (4x 2 − 2xy + y 2) является неполным квадратом разности этих выражений. Это позволяет воспользоваться формулой (a + b )(a 2 − ab + b 2) = a 3 + b 3

(2x + y )(4x 2 − 2xy + y 2) = (2x ) 3 + y 3 = 8x 3 + y 3

Попробуем решить этот же пример, не пользуясь формулой (a + b )(a 2 − ab + b 2) = a 3 + b 3 . У нас получится тот же результат, но решение станет длиннее:

(2x + y )(4x 2 − 2xy + y 2) = 2x (4x 2 − 2xy + y 2) + y (4x 2 − 2xy + y 2) =
8x 3 − 4x 2 y + 2xy 2 + 4x 2 y − 2xy 2 + y 3 = 8x 3 + y 3

Задания для самостоятельного решения

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.

В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.

Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.

Формулы сокращенного умножения

1. формула квадрата суммы: a + b 2 = a 2 + 2 a b + b 2
2. формула квадрата разности: a — b 2 = a 2 — 2 a b + b 2
3. формула куба суммы: a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3
4. формула куба разности: a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3
5. формула разности квадратов: a 2 — b 2 = a — b a + b
6. формула суммы кубов: a 3 + b 3 = a + b a 2 — a b + b 2
7. формула разности кубов: a 3 — b 3 = a — b a 2 + a b + b 2

Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.

Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.

Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.

При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.

Во-первых, рассмотрим формулу бинома Ньютона.

a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . + C n n — 1 · a · b n — 1 + C n n · b n

Здесь C n k — биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике паскаля. Биномиальные коэффициенты вычисляются по формуле:

C n k = n ! k ! · (n — k) ! = n (n — 1) (n — 2) . . (n — (k — 1)) k !

Как видим, ФСУ для квадрата и куба разности и суммы — это частный случай формулы бинома Ньютона при n=2 и n=3соответственно.

Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.

a 1 + a 2 + . . + a n 2 = a 1 2 + a 2 2 + . . + a n 2 + 2 a 1 a 2 + 2 a 1 a 3 + . . + 2 a 1 a n + 2 a 2 a 3 + 2 a 2 a 4 + . . + 2 a 2 a n + 2 a n — 1 a n

Еще одна формула, которая может пригодится — формула формула разности n-ых степеней двух слагаемых.

a n — b n = a — b a n — 1 + a n — 2 b + a n — 3 b 2 + . . + a 2 b n — 2 + b n — 1

Эту формулу обычно разделяют на две формулы — соответственно для четных и нечетных степеней.

Для четных показателей 2m:

a 2 m — b 2 m = a 2 — b 2 a 2 m — 2 + a 2 m — 4 b 2 + a 2 m — 6 b 4 + . . + b 2 m — 2

Для нечетных показателей 2m+1:

a 2 m + 1 — b 2 m + 1 = a 2 — b 2 a 2 m + a 2 m — 1 b + a 2 m — 2 b 2 + . . + b 2 m

Формулы разности квадратов и разности кубов, как вы догадались, являются частными случаями этой формулы при n = 2 и n = 3 соответственно. Для разности кубов b также заменяется на — b .

Как читать формулы сокращенного умножения?

Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.

a + b 2 = a 2 + 2 a b + b 2 .

Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.

Все остальные формулы читаются аналогично. Для квадрата разности a — b 2 = a 2 — 2 a b + b 2 запишем:

квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.

Прочитаем формулу a + b 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 . Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.

Переходим к чтению формулы для разности кубов a — b 3 = a 3 — 3 a 2 b + 3 a b 2 — b 3 . Куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.

Пятая формула a 2 — b 2 = a — b a + b (разность квадратов) читается так: разность квадратов двух выражений равна произведению разности и суммы двух выражений.

Выражения типа a 2 + a b + b 2 и a 2 — a b + b 2 для удобства называют соответственно неполным квадратом суммы и неполным квадратом разности.

С учетом этого, формулы суммы и разности кубов прочитаются так:

Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

Доказательство ФСУ

Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.

Для примера рассмотрим формулу квадрата разности.

a — b 2 = a 2 — 2 a b + b 2 .

Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.

a — b 2 = a — b a — b .

Раскроем скобки:

a — b a — b = a 2 — a b — b a + b 2 = a 2 — 2 a b + b 2 .

Формула доказана. Остальные ФСУ доказываются аналогично.

Примеры применения ФСУ

Цель использования формул сокращенного умножения — быстрое и краткое умножение и возведение выражений в степень. Однако, это не вся сфера применения ФСУ. Они широко используются при сокращении выражений, сокращении дробей, разложении многочленов на множители. Приведем примеры.

Пример 1. ФСУ

Упростим выражение 9 y — (1 + 3 y) 2 .

Применим формулу суммы квадратов и получим:

9 y — (1 + 3 y) 2 = 9 y — (1 + 6 y + 9 y 2) = 9 y — 1 — 6 y — 9 y 2 = 3 y — 1 — 9 y 2

Пример 2. ФСУ

Сократим дробь 8 x 3 — z 6 4 x 2 — z 4 .

Замечаем, что выражение в числителе — разность кубов, а в знаменателе — разность квадратов.

8 x 3 — z 6 4 x 2 — z 4 = 2 x — z (4 x 2 + 2 x z + z 4) 2 x — z 2 x + z .

Сокращаем и получаем:

8 x 3 — z 6 4 x 2 — z 4 = (4 x 2 + 2 x z + z 4) 2 x + z

Также ФСУ помогают вычислять значения выражений. Главное — уметь заметить, где применить формулу. Покажем это на примере.

Возведем в квадрат число 79 . Вместо громоздких вычислений, запишем:

79 = 80 — 1 ; 79 2 = 80 — 1 2 = 6400 — 160 + 1 = 6241 .

Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.

Еще один важный момент — выделение квадрата двучлена. Выражение 4 x 2 + 4 x — 3 можно преобразовать в вид 2 x 2 + 2 · 2 · x · 1 + 1 2 — 4 = 2 x + 1 2 — 4 . Такие преобразования широко используются в интегрировании.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Формулы сокращённого умножения позволяют производить тождественные преобразования выражений — многочленов. С их помощью многочлены можно разложить на множители, а применяя формулы в обратном порядке — представлять произведения двучленов, квадраты и кубы в виде многочленов. Рассмотрим все общепринятые формулы сокращённого умножения, их вывод, распространённые задачи на тождественные преобразования выражений с помощью этих формул, а также домашние задания (ответы к ним открываются по ссылкам).

Квадрат суммы

Формулой квадрата суммы называется равенство

(квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа).

Вместо a и b в эту формулу могут быть подставлены любые числа.

Формула квадрата суммы часто применяется для упрощения вычислений. Например,

С помощью формулы квадрата суммы многочлен можно разложить на множители, а именно, представить в виде произведения двух одинаковых множителей .

Пример 1.

.

Пример 2. Записать в виде многочлена выражение

Решение. По формуле квадрата суммы получаем

Квадрат разности

Формулой квадрата разности называется равенство

(квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа).

Формула квадрата разности часто применяется для упрощения вычислений. Например,

С помощью формулы квадрата разности многочлен можно разложить на множители, а именно, представить в виде произведения двух одинаковых множителей .

Формула следует из правила умножения многчлена на многочлен:

Пример 5. Записать в виде многочлена выражение

Решение. По формуле квадрата разности получаем

.

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Выделение полного квадрата

Часто в многочлене второй степени содержится квадрат суммы или разности, но содержится в скрытом виде. Чтобы получить полный квадрат в явном виде, нужно преобразовать многочлен. Для этого, как правило, одно из слагаемых многочлена представляется в виде удвоенного произведения, а затем к многочлену прибавляется и из него вычитается одно и то же число.

Пример 7.

Решение. Этот многочлен можно преобразовать следующим образом:

Здесь мы представили 5x в виде удвоенного произведения 5/2 на x , прибавили к многочлену и вычли из него одно и то же число , далее применили формулу квадрата суммы для двучлена .

Итак, мы доказали равенство

,

равен полному квадрату плюс число .

Пример 8. Рассмотрим многочлен второй степени

Решение. Проведём над ним следующие преобразования:

Здесь мы представили 8x в виде удвоенного произведения x на 4 , прибавили к многочлену и вычли из него одно и то же число 4² , применили формулу квадрата разности для двучлена x − 4 .

Итак, мы доказали равенство

,

показывающее, что многочлен второй степени

равен полному квадрату плюс число −16 .

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Куб суммы

Формулой куба суммы называется равенство

(куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго и плюс куб второго числа).

Формула куба суммы выводится так:

Пример 10. Записать в виде многочлена выражение

Решение. По формуле куба суммы получаем

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Куб разности

Формулой куба разности называется равенство

(куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго минус куб второго числа).

С помощью формулы куба суммы многочлен можно разложить на множители, а именно, представить в виде произведения трёх одинаковых множителей .

Формула куба разности выводится так:

Пример 12. Записать в виде многочлена выражение

Решение. По формуле куба разности получаем

Применить формулу сокращённого умножения самостоятельно, а затем посмотреть решение

Разность квадратов

Формулой разности квадратов называется равенство

(разность квадратов двух чисел равна произведению суммы эти чисел на их разность).

С помощью формулы куба суммы любой многочлен вида можно разложить на множители.

Доказательство формулы получено с применением правила умножения многочленов:

Пример 14. Записать в виде многочлена произведение

.

Решение. По формуле разности квадратов получаем

Пример 15. Разложить на множители

Решение. Это выражение в явной форме ни под одно тождество не подходит. Но число 16 можно представить в виде степени с основанием 4: 16=4² . Тогда исходное выражение примет иной вид:

,

а это уже формула разности квадратов, и, применив эту формулу, получим

При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения . Всего таких формул семь. Их все необходимо знать наизусть.

Следует также помнить, что вместо «a » и «b » в формулах могут стоять как числа, так и любые другие алгебраические многочлены.

Разность квадратов

Запомните!

Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.

a 2 − b 2 = (a − b)(a + b)

• 15 2 − 2 2 = (15 − 2)(15 + 2) = 13 · 17 = 221
• 9a 2 − 4b 2 с 2 = (3a − 2bc)(3a + 2bc)

Квадрат суммы

Запомните!

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

(a + b) 2 = a 2 + 2ab + b 2

Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел , не используя калькулятор или умножение в столбик. Поясним на примере:

Найти 112 2 .

• Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.
  112 = 100 + 1
• Запишем сумму чисел в скобки и поставим над скобками квадрат.
  112 2 = (100 + 12) 2
• Воспользуемся формулой квадрата суммы:
  112 2 = (100 + 12) 2 = 100 2 + 2 · 100 · 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544

Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.

• (8a + с) 2 = 64a 2 + 16ac + c 2

Предостережение!

(a + b) 2 не равно (a 2 + b 2)

Квадрат разности

Запомните!

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.

(a − b) 2 = a 2 − 2ab + b 2

Также стоит запомнить весьма полезное преобразование:

(a − b) 2 = (b − a) 2

Формула выше доказывается простым раскрытием скобок:

(a − b) 2 = a 2 −2ab + b 2 = b 2 − 2ab + a 2 = (b − a) 2

Куб суммы

Запомните!

Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Как запомнить куб суммы

Запомнить эту «страшную» на вид формулу довольно просто.

• Выучите, что в начале идёт «a 3 ».
• Два многочлена посередине имеют коэффициенты 3 .
• Вспомним, что любое число в нулевой степени есть 1 . (a 0 = 1, b 0 = 1) . Легко заметить, что в формуле идёт понижение степени «a » и увеличение степени «b ». В этом можно убедиться:
  (a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3

Предостережение!

(a + b) 3 не равно a 3 + b 3

Куб разности

Запомните!

Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.

(a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+ » и «− ». Перед первым членом «a 3 » стоит «+ » (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «− », затем опять «+ » и т.д.

(a − b) 3 = + a 3 − 3a 2 b + 3ab 2 − b 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Сумма кубов

Не путать с кубом суммы!

Запомните!

Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.

a 3 + b 3 = (a + b)(a 2 − ab + b 2)

Сумма кубов — это произведение двух скобок.

• Первая скобка — сумма двух чисел.
• Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:
  (a 2 − ab + b 2)
  Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.

Разность кубов

Не путать с кубом разности!

Запомните!

Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.

a 3 − b 3 = (a − b)(a 2 + ab + b 2)

Будьте внимательны при записи знаков.

Применение формул сокращенного умножения

Следует помнить, что все формулы, приведённые выше, используется также и справа налево.

Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберёте многочлен обратно.

• a 2 + 2a + 1 = (a + 1) 2
• (aс − 4b)(ac + 4b) = a 2 c 2 − 16b 2

Таблицу со всеми формулами сокращённого умножения вы можете скачать в разделе «

Семь формул сокращённого (краткого) умножения: упрощение выражений, примеры задач с решением

Одной из первых тем, изучаемых в курсе алгебры, являются формулы сокращённого умножения. В 7 классе они применяются в самых простых ситуациях, где требуется распознать в выражении одну из формул и выполнить разложение многочлена на множители или, наоборот, быстро возвести сумму или разность в квадрат или куб. В дальнейшем ФСУ используют для быстрого решения неравенств и уравнений и даже для вычисления некоторых числовых выражений без калькулятора.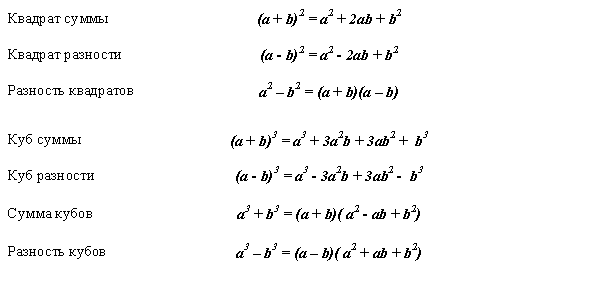

Содержание

Как выглядит список формул

Существует 7 основных формул, позволяющих быстро осуществить перемножение многочленов в скобках.

Иногда в этот список также включается разложение для четвёртой степени, которое следует из представленных тождеств и имеет вид:

a⁴ b⁴ = (a — b)(a + b)(a² + b²).

Все равенства имеют пару (сумма — разность), кроме разности квадратов. Для суммы квадратов формула не приводится.

Остальные равенства легко запоминаются:

1. Разница между квадратом суммы и разности заключается в знаке перед удвоенным произведением величин.
2. В случае с суммой и разностью кубов в (a ± b) знак совпадает со знаком (a3±b3). Второй сомножитель — так называемый неполный квадрат, поскольку он напоминает квадратный трёхчлен, возникающий после раскрытия скобок в квадрате суммы или разности. Здесь в ситуации с суммой появляется знак минуса перед ab, в противном случае знак заменяется на +.
3. В кубе суммы все знаки положительные, в случае с разностью появляются минусы перед 3a²b и b³.

Следует помнить, что ФСУ работают в любом случае и для любых величин a и b: это могут быть как произвольные числа, так и целые выражения.

В ситуации, если вдруг не получается вспомнить, какой знак стоит в формуле перед тем или иным слагаемым, можно раскрыть скобки и получить тот же результат, что и после использования формулы. Например, если проблема возникла при применении ФСУ куба разности, нужно записать исходное выражение и поочерёдно выполнить умножение:

(a — b)³ = (a — b)(a — b)(a — b) = (a² ab — ab + b²)(a — b) = a³ a²b — a²b + ab² a²b + ab² + ab² b³ = a³ 3a²b + 3ab² b³.

В результате после приведения всех подобных членов был получен такой же многочлен, как и в таблице. Такие же манипуляции можно проводить и со всеми остальными ФСУ.

Применение ФСУ для решения уравнений

К примеру, нужно решить уравнение, содержащее многочлен 3 степени:

x³ + 3x² + 3x + 1 = 0.

В школьной программе не рассматриваются универсальные приёмы для решения кубических уравнений, и подобные задания чаще всего решаются более простыми методами (например, разложением на множители). Если заметить, что левая часть тождества напоминает куб суммы, то уравнение можно записать в более простом виде:

(x + 1)³ = 0.

Корень такого уравнения вычисляется устно: x = -1.

Аналогичным способом решаются неравенства. Для примера можно решить неравенство x³ 6x² + 9x &gt, 0.

В первую очередь необходимо разложить выражение на множители. Вначале нужно вынести за скобку x. После этого следует обратить внимание, что выражение в скобках можно преобразовать в квадрат разности.

Затем необходимо найти точки, в которых выражение принимает нулевые значения, и отметить их на числовой прямой. В конкретном случае это будут 0 и 3. Затем методом интервалов определить, в каких промежутках x будет соответствовать условию неравенства.

ФСУ могут оказаться полезными при выполнении некоторых расчётов без помощи калькулятора:

703² 203² = (703 + 203)(703 — 203) = 906 ∙ 500 = 453000.

Кроме того, раскладывая выражения на множители, можно легко выполнять сокращение дробей и упрощение различных алгебраических выражений.

Примеры задач для 7−8 класса

В заключение разберём и решим два задания на применение формул сокращённого умножения по алгебре. Если вы новичек, то лучше всего начать играть без настоящих ставок. Однако если уже вы решились, то найти интернет казино вулкан с выводом на реальные деньги можно с помощью рейтингов или же обратившись за советом к более опытным гемблерам. В принципе можно попробовать метод проб и ошибок, но это будет сложнее и дольше.

Задача 1. Упростить выражение:

(m + 3)² + (3m + 1)(3m — 1) — 2m (5m + 3).

Решение. В условии задания требуется упростить выражение, т. е. раскрыть скобки, выполнить действия умножения и возведения в степень, а также привести все подобные слагаемые. Условно разделим выражение на три части (по числу слагаемых) и поочерёдно раскроем скобки, применяя ФСУ там, где это возможно.

• (m + 3)² = m² + 6m + 9 (квадрат суммы),
• (3m + 1)(3m — 1) = 9m² 1 (разность квадратов),
• В последнем слагаемом необходимо выполнить перемножение: 2m (5m + 3) = 10m² + 6m.

Подставим полученные результаты в исходное выражение:

(m² + 6m + 9) + (9m² 1) — (10m² + 6m).

С учётом знаков раскроем скобки и приведём подобные слагаемые:

m² + 6m + 9 + 9m² 1 — 10m² 6m = 8.

Задача 2. Решить уравнение, содержащее неизвестное k в 5 степени:

k⁵ + 4k⁴ + 4k³ 4k² 4k = k³.

Решение. В этом случае необходимо воспользоваться ФСУ и методом группировки. Нужно перенести последнее и предпоследнее слагаемое в правую часть тождества.

k⁵ + 4k⁴ + 4k³ = k³ + 4k² + 4k.

Из правой и из левой части выносится общий множитель (k² + 4k +4):

k³(k² + 4k + 4) = k (k² + 4k + 4).

Всё переносится в левую часть уравнения, чтобы в правой остался 0:

k³(k² + 4k + 4) — k (k² + 4k + 4) = 0.

Снова необходимо вынести общий множитель:

(k³ k)(k² + 4k + 4) = 0.

Из первого полученного сомножителя можно вынести k. По формуле краткого умножения второй множитель будет тождественно равен (k + 2)²:

k (k² 1)(k + 2)² = 0.

Использование формулы разности квадратов:

k (k — 1)(k + 1)(k + 2)² = 0.

Поскольку произведение равно 0, если хотя бы один из его множителей нулевой, найти все корни уравнения не составит труда:

1. k = 0,
2. k — 1 = 0, k = 1,
3. k + 1 = 0, k = -1,
4. (k + 2)² = 0, k = -2.

На основании наглядных примеров можно понять, как запомнить формулы, их отличия, а также решить несколько практических задач с применением ФСУ. Задачи простые, и при их выполнении не должно возникнуть никаких сложностей.

Формула сокращенного умножения

математика

21 февраля 2021 г. Питагор

Наиболее важные формулы сокращенного умножения.

Формулы сокращенного умножения позволяют выполнять расчеты намного быстрее.
Наиболее часто используемые формулы сокращенного умножения:

(

(

(

. − б ² = ( a + b )( a − b )

(

a + b ) ³ = a ³ + 3 a ² b + 3 from ² + b ³

(

a − b ) ³ = a ³ − 3 a ² б + 3 из ² — B ³

A ³ + B ³ = ( A + B ) ( A + B ) ( A + B) ( A + B) ( A + B) ( A + ) ( A + ) ( A + ) ( A + ). B ² )

A ³ — B ³ = ( A — B ) ( A 2

6 + + + + + + + + + + + + + + + + + + + + + + + + + + + + ) ( A — B ) ( — B ). )

 

Формулы сокращенного умножения полезны для умножения или расширения алгебраических выражений. Они облегчают эффективный подсчет. Этих узоров очень много. Мы перечислим несколько ниже, которые используются чаще всего.

Квадрат суммы чисел

• ( A + B ) ² = A ² + 2 из + B ²
  : 31 ² = (30 + 1) ² = 31 ² = (30 + 1) ² = 30202020 2 = (30 + 1) ² . ² +2×30+1 = 900+60+1 = 961

• не встречается равенство: ( a + b ) ² = a ² + b ²
  например 25 = (3+2) ² ≠ 3 ² + 2 ² = 13

• justification of the formula by the bill:
  ( a + b ) ² = ( a + b ) × ( a + b ) ^{= aa + от + ba + bb = a 2 + 2 от + b 2}

Квадрат разности чисел

• ( A — B ) ² = A ² -2 из + B ²
  : 29 ² = (30-1 ² = 30021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 3021 = 300021 = 300021 = 3021 = 3021. ² -2×30+1 = 900-60+1 = 841

• не происходит Равенство: ( A- B ) ² = A ² — B ²
  E.G 1 = (3-2-2) ² 1110 2
  E.G. 1 = (3-2) ² 10 2
  E.G. – 2 ² = 5

• Обоснование формулы:
  ( A — B ) ² = ( A — B ) × ( A — B ) ^{= AA B ) = AA B ) = AA — ) = AA B ) = AA B ) = AA B ) = AA B ) = AA B ) ba + bb = a 2 – 2 от + b 2}

   

Квадрат суммы трех чисел

• ( A + B + C ) ² = A ² + B ² + C ² + 2 из + 2 AC ² + 2 из + 2 AC ² + 2 из + 2 AC ² + 2 .
  например: 111 ² = (100+10+1) ² = 100 ² + 10 ² +1 +2×100×10 + 2×100 + 2×10 = 10000 1 + 2000 + 200 + 20 = 12321

• не встречается равенство: ( a+b + c ) ² = A ² + B ² + C ²
  Например, 36 = (3 + 2 + 1) ² гать 3 ² + 2 21 2 2 2 2 2 2 2 2 2 2 2 2 2 2 гать 3 ² 1 + 2 2 2 2 ² ↓ 3 ² 11 + 2 2 2 2 ² . + 1 ² = 14

• Обоснование формулы:
  ( A + B + C ) ² = ( A + B + C ) × ( A + B +

  7 +
  7 + + + + + + + + + + + + + + + + + + + + +
  17) ) = а. о. + from + ac + ba + bb + bc + that + cb + cc = a ² + b ² + c ² + 2 from + 2 ак + 2 бк

Произведение суммы и разности чисел = разность квадратов чисел

• ( a + b ) × ( a – b ) = a ² – b ²
  например: 101×99 = (100+1)×(100-1) = 100 ² – 1 = 9999

• Обоснование формулы:
  ( A + B ) × ( A — B ) ^{= AA — из + BA — . = 2 = BB 2. – б 2}

Куб суммы чисел

• ( a + b ) ³ = a ³ + 3 a ² b + 3 from ² + b ³
  e. g: 101 ³ = (100+1) ³ = ^{100 3 + 3×100 2 + 3×100 + 1 =
  = 1000000 + 30000 + 300 + 1 = 1030301 1 1}

• не встречается равенство: ( a + b ) ³ = a ³ + b ³
  например 125 = (3+2) ³ ≠ 3 ³ + 2 ³ = 35

• Обоснование формулы по законопроекту:
  ( A + B ) ³ = ( A + B ) × ( A + B ) × ( A + B ) × ( A + B ) × ( A + B ) × ( A + B ) × ( A + B ). ) ^{= ( аа + из + ба + bb ) × ( а + б ) = ааа + aab + aba + fig + baa + chapter + bba + bbb =
  = a 3 + 3 a 2 b + 3 из 2 + б 3}

Куб разности чисел

• ( a – b ) ³ = a ³ – 3 A ² B + 3 из ² — B ³
  Например: 99 ³ = (100-1) ³ = 100 ^{3 -3 -3} -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3 . 100 ² + 3×100 – 1 =
  = 1000000 – 30000 + 300 – 1 = 970299

Сумма кубиков номеров

A ³ + B ³ = ( A + B ) × ( A ^{2 — ).0017 + B 2 )}

Обоснование формулы:

( A + B ) × ( A ² — из + B ^{202020 2} — из + B ^{20202020 2} — из + B ^{2020202020 2} — из + B 202020202020 2 — из + B ² — . ² – aab + from ² + ba ² – chapter + bb ² = a ³ – a ² b + из ² + a ² b – from ² + b ³ =
= a ³ + b ³

The difference of the Кубики чисел

A ³ — B ³ = ( A — B ) × ( A ² + от + 2 + ) от + 1717171717171717171717171717 2 + ).

обоснование формулы:

( a – b )×( a ² + from + b ² ) = aa ² + aab + from ² – BA ² — ГЛАВА — BB ² = A ³ + A ² B + от ² — B + от ² — B + от ² — B + . – из ² – b ³ =
= a ³ – b ³

Difference of fourth powers of numbers

a ⁴ – b ⁴ = ( A — B ) × ( A ³ + A ² B + из ² + B ^{30202020202020202111). 2} + B 3

). 3

11) =

111111) =

113) =

113) =

113) = =

11). б )×( а ³ — A ² B + от ² — B ³ )

SUM N -THERSERSE . !!)

a ⁿ + b ⁿ = ( a + b ) ( a ^{n -1} – a ^{n -2} б + а ^{п -3} B ² -… + B ^{N -1} )

Разница N -THESE Powers of Числа (для N ETHLAR N -THESE Powers of Tils (для N ETH N -THESE (для N n n n n n n n -these (для n n .

a ⁿ – b ⁿ = ( a + b ) ( a ^{n -1} – a ^{n -2} b + а ^{п -3} b ² – … + b ^{n -1} )

 

Difference n -these powers of numbers (for everyone n natural)

a ⁿ — B ^N = ( A — B ) ( A ^{N -1} + A ^{N -2} A ^{N -2} A + + + + + + + + + + + + + + + . ^-3 б ² + … + a ² b ^{n -3} + from ^{n -2} + b ^{n -1} )

сокращенный шаблон умножения

Формула расширения куба. Формулы сокращенного умножения

Содержание урока

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Так, например, бывает (2 х + 3 у ) 2 .

Выражение (2 x + 3 y ) 2 есть произведение двух многочленов, каждый из которых равен (2 x + 3 y )

(2 x + 3 y ) 2 = (2 x + 3 y )(2 x + 3 y )

Мы получили произведение многочлена на многочлен. Выполним его:

(2 x + 3 y ) 2 = (2 x + 3 y )(2 x + 3 y ) = 4 x 2 + 6 xy + 6 ху + 9 у 2 = 4 х 2 + 12 ху + 9 у 2

То есть выражение (2 х + 3 у ) 2 равно 4 х 2 + 12 х у + 9 у 2

(2 x + 3 y ) 2 = 4 x 2 + 12 xy + 9 y 2

Решим аналогичный пример, но попроще:

( а+б ) 2

Выражение ( a+b ) 2 есть произведение двух многочленов, каждый из которых равен ( a+b )

( а+б ) 2 = ( а+б )( а+б )

Давайте сделаем это умножение:

( A + B ) 2 = ( A + B ) ( A + B ) = A 2 + AB + AB + B 2 2 AB + AB + B 2 2 2 + . = а 2 + 2 аб + б 2

То есть выражение ( a+b ) 2 равно a 2 + 2 ab + b 2

( а+б ) 2 = а 2 + 2 аб + б 2

Получается, что кейс ( a+b ) 2 можно расширить на любые a и b . Первый пример, который мы решили, а именно (2 x + 3 y ) 2 можно решить, используя тождество ( a+b ) 2 = a 2 + 2 аб + б 2 . Для этого нужно вместо переменных подставить и b соответствующие члены из выражения (2 x + 3 y ) 2 . В этом случае переменная a соответствует члену 2 x , а переменная b соответствует члену 3 y .

a = 2 х

б = 3 у

И тогда мы можем использовать тождество ( а+б ) 2 = а 2 + 2 аб + б 2 , но вместо переменных а и Ь нужно подставить выражения 2 х и 3 у соответственно:

(2 х + 3 у ) 2 = (6 1 907 ) 2 = 1 х 907 + 2 × 2 x × 3 y + (3 y ) 2 = 4 x 2 + 12 xy + 9 y 2

Как и в прошлый раз, мы получили многочлен 4 x 2 + 12 ху + 9 у 2 . Решение обычно записывают короче, производя в уме все элементарные преобразования:

(2 х + 3 у ) 2 = 4 х 2 + 12 ху + 9 у 2

Идентичность ( a+b ) 2 = a 2 + 2 ab + b 2 называется формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения и второго плюс квадрат второго выражения.

Рассмотрим выражение (2 + 3) 2 . Его можно вычислить двумя способами: выполнить сложение в скобках и возвести результат в квадрат или воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3) 2 = 5 2 = 25

Второй способ:

(2 + 3) 2 = 2 2 + 2 × 2 × 3 + 3 2 = 4 + 12 + 9 = 25

Пример 2 . Преобразуйте выражение (5 a + 3) 2 в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

( а+б ) 2 = а 2 + 2 аб + б 2

(5 а + 3) 2 = (5 а ) 2 + 2 × 5 а × 3 + 3 2 = 25 а 2 + 30 а + 9

Значит, (5 а + 3) 2 = 25 а 2 + 30 а + 9.

Попробуем решить этот пример без использования формулы суммы квадратов. Мы должны получить тот же результат:

(5 а + 3) 2 = (5 а + 3)(5 а + 3) = 25 а 2 + 15 а + 15 и + 9 = 25 и 2 + 30 и + 9

Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести его сторону во вторую степень.

Например, площадь квадрата со стороной а будет равна а 2. Если увеличить сторону квадрата на , то площадь будет равна ( а+б ) 2

Рассмотрим следующий рисунок:

Представьте, что сторона квадрата, изображенного на этом рисунке, увеличена на b . У квадрата все стороны равны. Если его сторону увеличить на b , то и другие стороны увеличатся на b

В результате получается новый квадрат, который больше предыдущего. Чтобы хорошо было видно, дополним недостающие стороны:

Чтобы вычислить площадь этого квадрата, можно отдельно вычислить входящие в него квадраты и прямоугольники, затем сложить результаты.

Сначала можно вычислить квадрат со стороной a — его площадь будет равна a 2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны a . Тогда можно вычислить квадрат со стороной b

Результатом является следующая сумма площадей:

a 2 + ab+ab + b 2

Сумма площадей одинаковых прямоугольников может быть заменена умножением 2 ab , что буквально означает «повторить два раза площадь прямоугольника ab» . Алгебраически это получается путем сокращения подобных слагаемых ab и ab . Результатом является выражение a 2 + 2 ab + b 2 , что является правой частью формулы квадрата суммы двух выражений:

( a+b ) 2 = а 2 + 2 аб + б 2

Квадрат разности двух выражений

Формула квадрата разности двух выражений выглядит следующим образом:

( a-b ) 2 = a 2 − 2 аб + б 2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения и второго плюс квадрат второго выражения.

Формула квадрата разности двух выражений выводится так же, как формула квадрата суммы двух выражений. Выражение ( a-b ) 2 есть произведение двух многочленов, каждый из которых равен ( a-b )

( а-б ) 2 = ( а-б )( а-б )

Если вы выполните это умножение, вы получите многочлен a 2 — 2 аб + б 2

( A-B ) 2 = ( A-B ) ( A-B ) = A 2- AB — AB + B 2 = A 2 o 2 аб + б 2

Пример 1 . Преобразуйте выражение (7 x − 5) 2 в многочлен.

Воспользуемся формулой квадрата разности двух выражений:

( a-b ) 2 = a 2 − 2 аб + б 2

(7 х — 5) 2 = (7 х ) 2 — 2 х 7 х х 5 + 5 2 = 49 х 2 — 70 х + 25

Средства, (7 х — 5) 2 = 49 х 2 + 70 х + 25.

Попробуем решить этот пример без использования формулы квадрата разности. Мы должны получить тот же результат:

(7 x − 5) 2 = (7 х — 5) (7 х — 5) = 49 х 2 — 35 х − 35 х + 25 = 49 х 2 — 70 х + 25.

Формула квадрата разности двух выражений также имеет геометрический смысл. Если площадь квадрата со стороной a равно a 2 , то площадь квадрата, сторона которого уменьшена на b , будет равна ( a-b ) 2

Рассмотрим следующий рисунок:

Представьте, что сторона квадрата, показанная на этом рисунке, уменьшена на b . У квадрата все стороны равны. Если одну сторону уменьшить на b , то и другие стороны уменьшится на b

В результате получается новый квадрат, который меньше предыдущего. На рисунке он выделен желтым цветом. Его сторона равна a − b так как старая сторона a уменьшилась на b . Для вычисления площади этого квадрата можно использовать исходную площадь квадрата а 2 вычесть площади прямоугольников, которые были получены в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:

Тогда мы можем написать следующее выражение: старая площадь a 2 минус площадь ab минус площадь ( a-b ) б

а 2 − аб − ( а-б ) б

Раскройте скобки в выражении ( a-b ) b

а 2 − аб — аб + б 2

Вот аналогичные термины:

a 2 − 2 ab + b 2

Результатом является выражение a 2 − 2 ab + b 2 , что является правой частью формулы квадрата разности двух выражений:

( a-b ) 2 = a 2 − 2 аб + б 2

Формулы квадрата суммы и квадрата разности обычно называются формулами сокращенного умножения . Эти формулы позволяют значительно упростить и ускорить процесс умножения многочленов.

Ранее мы говорили, что рассматривая член полинома отдельно, его нужно рассматривать вместе со знаком, который стоит перед ним.

Но при применении формул сокращенного умножения знак исходного многочлена не следует рассматривать как знак самого этого слагаемого.

Например, учитывая выражение (5 x — 2 y ) 2 , и мы хотим использовать формулу ( a-b ) 2 = a 2 — 2 аб + б 2 , то вместо b нужно подставить 2 y , а не −2 y . Это особенность работы с формулами, о которой нельзя забывать.

(5 х − 2 у ) 2
а = 5 х
б = 2 у
(5 х — 2 у ) 2 = (5 х ) 2 — 2 х 5 х х 2 у + (2 у ) 7 6 6 х 9001 ху + 4 у 2

Если мы подставим −2 y , то это будет означать, что разность в скобках исходного выражения заменена суммой:

(5 x — 2 y ) 2 = (5 x + (-2 y )) 2

и в этом случае надо применять не формулу квадрата разности, а формулу квадрата суммы:

(5 х + (−2 y ) 2
а = 5 х
б = -2 у
(5 x + (−2 y )) 2 = (5 x ) 2 + 2 × 5 x × (−2 y ) + (−2 у ) 2 = 25 х 2 − 20 ху + 4 у 2

Исключением могут быть выражения вида ( x − (− y )) 2 . В этом случае, используя формулу ( a-b ) 2 = a 2 — 2 аб + б 2 вместо следует заменить b (− y )

( х — (- у )) 2 = х 2 — 2 × х × (- у ) + (- у ) 2 = х 2 + 2 ху + у 2

Но при возведении в квадрат выражений вида x − (− y ) удобнее заменить вычитание сложением x+y . Тогда исходное выражение примет вид ( х + у ) 2 и можно будет использовать формулу квадрата суммы, а не разности:

( х + у ) 2 = х 2 + 2 ху + у 2

Куб суммы и куб разности

Формулы для куба суммы двух выражений и куба разности двух выражений следующие: 3 + 3 а 2 б + 3 аб 2 + б 3

( a-b ) 3 = a 3 − 3 a 2 b + 3 ab 2 − б 3

Формула куба суммы двух выражений может быть прочитана так:

Куб суммы двух выражений равен кубу первого выражения плюс утроенный квадрат первого выражения, умноженный на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

А формулу куба разности двух выражений можно прочитать так:

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

При решении задач желательно знать эти формулы наизусть. Если вы не помните, не волнуйтесь! Вы можете вывести их самостоятельно. Мы уже знаем как.

Выведем формулу куба суммы самостоятельно:

( а+б ) 3

Выражение ( a+b ) 3 является произведением трех многочленов, каждый из которых равен ( a + b )

( a+b ) 3 = ( a + b )( a + b )( a + b )

Но выражение ( a+b ) 3 можно также записать как ( a + b )( a + b ) 2

( а+б ) 3 = ( а + б )( а + б ) 2

В этом случае множитель ( a + b ) 2 является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a 2 + 2 ab + b 2 .

Тогда ( a+b ) 3 можно записать как ( a + b )( a 2 + 2 ab + b 2) .

( а+б ) 3 = ( а + б )( а 2 + 2 аб + б 2)

А это умножение многочлена на многочлен. Давайте выполнить это:

( A + B ) 3 = ( A + B ) ( A 2 + 2 AB + B 2) = A 3 + 2 A 2) = A 3 + 2 A A 2) = A 3 + 2 A A 2) = A 3 + 2 A . 2 б + аб 2 + а 2 б + 2 аб 2 + б 3 = а 3 + 3 а 2 б + 3 аб 2 + б 3

Аналогично можно вывести формулу куба разности двух выражений:

( a-b ) 3 = ( a- b )( a 2 − 2 ab + b 2) = а 3 − 2 а 2 б + аб 2 − а 2 б + 2 аб 2 − б 3 = а 3 − 3 а 2 б + 3 аб 2 − б 3

Пример 1 . Преобразуйте выражение ( x + 1) 3 в многочлен.

( а + б ) 3 = а 3 + 3 а 2 б + 3 аб 2 + б 3

( x + 1) 3 = x 3+3× x 2×1 + 3× x × 1 2 + 1 3 = x 3 + 3 x 210317 х + 1

Попробуем решить этот пример без использования формулы куба суммы двух выражений

( х + 1) 3 = ( х + 1)( х + 1)( х + 1) = ( х + 1)( х 2 + 2 х + 1) = х 3 + 7 3 + 2 х 2 + х + х 2 + 2 х + 1 = х 3 + 3 х 2 + 3 х + 1

Пример 2 . Преобразование выражения (6 a 2 + 3 b 3) 3 в полином.

Используем формулу куба для суммы двух выражений:

( a + b ) 3 = a 3 + 3 a 2 b + 3 b 2 + b 3

(6 a 2 + 3 b 3) 3 = (6 a 2) 3 + 3 × (6 a 2) 2×3 b 3+3×6 a 2 × (3 б 3) 2 + (3 б 3) 3 = 216 а 6+3×36 а 4×3 б 3+3×6 а 0169 0169 6 + 27 б 9

Пример 3 . Преобразуйте выражение ( n 2 − 3) 3 в многочлен.

( a-b ) = a 3 − 3 a 2 b + 3 ab 2 − b 3

( n 2 − 3) 3 = ( n 2) 3 − 3 × ( n 2) 2 × 3 + 3 × n 2 × 3 2 − 3 3 = n 6 − 9 n 4 + 27 n 2 − 27

Пример 4 . Преобразовать выражение (2 х 2 − х 3) 3 в полином.

Воспользуемся формулой куба разности двух выражений:

( a-b ) = a 3 − 3 a 2 b + 3 ab 107 2 − 90

(2 x 2 − x 3) 3 = (2 x 2) 3 − 3 × (2 x 2) 2 × x 3 × 3 × 2 2 () х 3) 2 — ( х 3) 3 =
8 x 6 − 3 × 4 x 4× x 3+3×2 x 2× x 6 − x 9 =
8 x 6 − 12 x 7 + 6 x 8 − x 9

Умножение разности двух выражений на их сумму

Существуют задачи, в которых требуется умножить разность двух выражений на их сумму. Например:

( a-b )( a+b )

В этом выражении разница двух выражений a и b , умноженные на сумму тех же двух выражений. Давайте сделаем это умножение:

( A-B ) ( A + B ) = A 2 + AB — AB — B 2 = A 2- B 9007 2 2 2 = A 2- B 2 2 = A 2- B 2 2 = A 2- B 2 = A 2- B 2 = A 2-— B 2 = A 2-— B 2 = A 2-— B .

Это выражение ( a-b )( a+b ) равно a 2 − b 2

( a-b )( a+b ) = a 2 − b 2

Мы видим, что при умножении разности двух выражений на их сумму мы получаем разность квадратов этих выражений.

Произведение разности двух выражений на их сумму равно разности квадратов этих выражений.

Событие ( a-b )( a+b ) можно расширить до любых a и b . Проще говоря, если при решении задачи необходимо умножить разность двух выражений на их сумму, то это умножение можно заменить разностью квадратов этих выражений.

Пример 1 . Выполнить умножение (2 x − 5) (2 x + 5)

В этом примере разница выражений равна 2 x и 5, умноженным на сумму этих же выражений. Тогда по формуле ( a-b )( a+b ) = a 2 − b 2 имеем:

(2 х — 5)(2 х + 5) = (2 х ) 2 — 5 2

Вычисляем правую часть, получаем 4 х 2 − 25

(2 х — 5)(2 х + 5) = (2 х ) 2 — 5 2 = 4 х 2 — 25

Попробуем решить этот пример без использования формулы ( a-b )( a+b ) = a 2 − b 2 . Мы получим тот же результат 4 x 2 − 25

(2 х — 5)(2 х + 5) = 4 х 2 — 10 х + 10 х — 25 = 4 х 2 — 25

Пример 2 . Выполнить умножение (4 x − 5 y ) (4 x + 5 y )

( a-b )( a+b ) = a 2 − b 2

(4 x — 5 y ) (4 x + 5 y ) = (4 x ) 2 — (5 y ) 2 = 16 x 2 — 25 y 2

Пример 3 . Выполнить умножение (2 a + 3 b )(2 a − 3 б )

Воспользуемся формулой умножения разности двух выражений на их сумму:

( a-b )( a+b ) = a 2 − b 2

(2 а + 3 б )(2 а — 3 б ) = (2 а ) 2 — (3 б ) 9 б 2 а — 2

В этом примере сумма слагаемых 2 a и 3 b расположена раньше разности этих слагаемых. А в формуле ( a-b )( a+b ) = a 2 − b 2 разница расположена раньше.

Не имеет значения, как расположены коэффициенты ( a-b ) в ( a+b ) в формуле. Их можно записать как ( a-b )( a+b ) и ( а+б )( а-б ) . Результат все равно будет a 2 − b 2 , так как произведение не меняется от перестановки множителей.

Итак, в этом примере множители (2 a + 3 b ) и 2 a- 3 b ) можно записать как (2 a + 3 b )(2 a- 3 b ) , и (2 a- 3 b )(2 a + 3 b ) . Результат все равно будет 4. a 2 − 9 b 2 .

Пример 3 . Выполнить умножение (7 + 3 x )(3 x — 7)

Воспользуемся формулой умножения разности двух выражений на их сумму:

( a-b )( a+b ) = a 2 − b 2

(7 + 3 х )(3 х — 7) = (3 х ) 2 — 7 2 = 9 х 2 — 49

Пример 4 . Выполнить умножение ( x 2 − y 3)( x 2 + y 3)

( a-b )( a+b ) = a 2 − b 2

( х 2 − у 3)( х 2 + y 3) = ( x 2) 2 − ( y 3) 2 = x 4 − y 6

Пример 5 . Выполнить умножение (−5 x — 3 y ) (5 x — 3 y )

В выражении (−5 x − 3 y ) вычитаем −1, тогда исходное выражение примет следующий вид: х — 3 у ) = -1 (5 х + 3 у )(5 х — 3 у )

Работа (5 x + 3 y )(5 x − 3 y ) заменить на разность квадратов:

(−5 x − 3 y )(5 x − 3 y ) = −1 (5 x + 3 y ) 1 (6 x ) 1 (6 x ) — 3 y ) = -1((5 x ) 2 — (3 y ) 2)

Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5 x ) 2 . А это приведет к ошибке и изменению значения исходного выражения.

(−5 x — 3 y ) (5 x — 3 y ) = −1 (5 x + 3 y ) (5 x — 3 y )) (5 ​​ x — 3 y )) (5 ​​ x — 3 y ) (5 x — 3 y ) (5 x — 3 )) = -1 ((5 x ) 2 — (3 y ) 2) = -1 (25 x 2 — 9 x 2)

Теперь умножьте -1 на выражение в скобках и получите окончательный результат:

(-5 x — 3 y )(5 x — 3 y ) = -1(5 x + 3 y )(5 x — 3 y ) = -1((5 x ) 9 0 2 — (6 3 017 ) 9 0 2 — (6 3 017 ) 9 0 2 ) 2) =
-1(25 х 2 — 9 у 2) = -25 х 2 + 9 у 2

Умножение разности двух выражений на неполный квадрат их суммы

Существуют задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Эта часть выглядит так:

( a-b )( a 2 + ab + b 2)

Первый многочлен ( a-b ) есть разность двух выражений, а второй многочлен ( a 2 + ab + b 2) есть неполный квадрат суммы этих двух выражений.

Неполный квадрат суммы представляет собой многочлен вида a 2 + ab + b 2 . Это похоже на обычный квадрат суммы а 2 + 2 аб + б 2

Например, выражение 4 x 2 + 6 xy + 9 y 2 представляет собой неполный квадрат суммы выражений 2 x и 3 y .

Действительно, первый член выражения 4 x 2 + 6 xy + 9 y 2 , а именно 4 х 2 является квадратом выражения 2 х , так как (2 х ) 2 = 4 х 2. Третий член выражения 4 х 2 + 6 ху + 9 у 2 , а именно 9 y 2 является квадратом 3 y , потому что (3 y ) 2 = 9 y 2. средний член 6 xy , является произведением выражений 2 x 1300170 и 6 x 0 у.

Итак, умножим разницу ( a-b ) на неполный квадрат суммы a 2 + ab + b 2

( аб )( а 2 + аб + b 2) = a ( a 2 + ab + b 2) − b ( a 2 + ab + b 2) =
a 3 + a 2 b + ab 2 − a 2 b − ab 2 − b 3 = a 3 − b 3

Это выражение ( a-b )( a 2 + ab + b 2) равно a 3 − б 3

( a-b )( a 2 + ab + b 2) = a 3 − b 3

Это тождество называется формулой умножения разности двух выражений на неполный квадрат их суммы. Эту формулу можно прочитать так:

Произведение разности двух выражений на неполный квадрат их суммы равно разности кубов этих выражений.

Пример 1 . Выполнить умножение (2 x − 3 y )(4 x 2 + 6 xy + 9 y 2)

Первый полином (2 x − 3 y ) представляет собой разность двух выражений 2 x и 3 y . Второй многочлен 4 x 2 + 6 xy + 9 y 2 является неполным квадратом суммы двух выражений 2 x и 3 y . Это позволяет использовать формулу, не производя длительных вычислений ( a-b )( a 2 + ab + b 2) = a 3 − b 3 . В нашем случае умножение (2 x − 3 y )(4 x 2 + 6 xy + 9 y 2) можно заменить разностью кубов 2 х и 3 у

(2 x — 3 Y ) (4 x 2 + 6 XY + 9 Y 2) = (2 x ) 3 — (3 Y ) 3 = 8 х 3 − 27 г 3

( a-b )( a 2 + ab + b 2) = a 3 − b 3 . Мы получаем тот же результат, но решение становится длиннее:

(2 x − 3 y )(4 x 2 + 6 xy + 9 y 2) = 2 x 4 x 2 + 6 xy + 9 y 2) − 3 y (4 x 2 + 6 xy + 9 y 2) =
8 x 3 + 12 x 2 y + 18 xy 2 — 12 x 2 y — 18 x 2 — 27 Y 3 = 8 x 3 — 27 Y 3 = 8 x 3 3 — 27 Y 3 = 8 x 3 — 27 Y 3 = 8 x 3 — 27 Y 3

Пример 2 . Выполнить умножение (3 − x ) (9 + 3 x + x 2)

Первый полином (3 − x ) представляет собой разность двух выражений, а второй полином представляет собой неполный квадрат суммы этих двух выражений. Это позволяет использовать формулу ( a-b )( a 2 + ab + b 2) = a 3 − b 3

(3 — х )(9 + 3 х + х 2) = 3 3 — х 3 = 27 — х 3

Умножение суммы двух выражений на неполный квадрат их разности

Существуют задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Эта часть выглядит так:

( a+b )( a 2 − ab + b 2)

Первый многочлен ( a+b ( a 2 − ab + b 2) есть неполный квадрат разности этих двух выражений.

Неполный квадрат разности представляет собой многочлен вида a 2 − ab + b 2 . Это похоже на обычную квадратную разность a 2 − 2 ab + b 2 за исключением того, что в нем произведение первого и второго выражений не удваивается.

Например, выражение 4 x 2 − 6 xy + 9 y 2 есть неполный квадрат разности выражений 2 x и 3 y .

(2 x ) 2 − 2 x × 3 y + (3 y ) 2 = 4 x 2 − 6 xy + 1 9 900

Вернемся к исходному примеру. Умножаем сумму на a+b на неполный квадрат разности a 2 − ab + b 2

( A + B ) ( A 2 — AB + B 2) = A ( A 2 — AB + B 2) + B ( AB + B 2) + B ( AB + B 2) + B ( AB + B 2) + B ( AB + B 2) + B ( AB + B 2) + B ( AB + B 2). − аб + б 2) =
a 3 − a 2 b + ab 2 + a 2 b − ab 2 + b 3 0016 а 3 + б 3

Это выражение ( a+b )( a 2 − ab + b 2) равно a 3 + b 3

( a+b )( a 2 − ab + b 2) = a 3 + b 3

Это тождество называется формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:

Произведение суммы двух выражений на неполный квадрат их разности равно сумме кубов этих выражений.

Пример 1 . Выполнить умножение (2 x + 3 y ) (4 x 2 − 6 xy + 9 y 2)

Первый многочлен (2 x + 3 y ) является суммой двух выражений 2 x и 3 y , а второй многочлен 4 x 2 − 6 ху + 9 у 2 есть неполный квадрат разности этих выражений. Это позволяет использовать формулу без длительных вычислений ( a+b )( a 2 − ab + b 2) = a 3 + b 3 . В нашем случае умножение (2 x + 3 y )(4 x 2 − 6 xy + 9 y 2) можно заменить суммой кубов 2 x и 3 г

(2 x + 3 Y ) (4 x 2 — 6 XY + 9 Y 2) = (2 x ) 3 + (3 Y ) 3 = 8 х 3 + 27 у 3

Попробуем решить тот же пример без использования формулы ( a+b )( a 2 − ab + b 2) = a 3 + b 3 . Получаем тот же результат, но решение становится длиннее:

(2 х + 3 y )(4 x 2 − 6 xy + 9 y 2) = 2 x (4 x 2 − 6 xy + 9 y 2) + 3 y (4 x 2 − 6 xy + 9 y 2) =
8 x 3 — 12 x 2 y + 18 xy 2 + 12 x 2 y — 18 xy 2 + 27 Y 3 = 8 xy 2 + 27 Y 3 = 8 x 2 + 27 Y 3 = 8 xy 2 + 27 Y г 3

Пример 2 . Выполнить умножение (2 x + y )(4 x 2 − 2 xy + y 2)

Первый многочлен (2 x + y ) представляет собой сумму двух выражений, а второй многочлен (4 x 2 − 2 xy + y 2) есть неполный квадрат разности этих выражений. Это позволяет нам использовать формулу ( a+b )( a 2 − ab + b 2) = a 3 + b 3

(2 x + Y ) (4 x 2 — 2 XY + Y 2) = (2 X ) 3 + Y 3 = 8 x 3 + Y 3

Попробуем решить тот же пример без использования формулы ( a+b )( a 2 − ab + b 2) = a 3 + b 3 . Получаем тот же результат, но решение становится длиннее:

(2 x + y )(4 x 2 − 2 XY + Y 2) = 2 x (4 x 2 — 2 xy + y 2) + y (4 x 2 — 2 xy + x x 2 — 2 x + + + + + + + + + + + + + + + + + + + + + + x 2 — 2 x + + x 2). 2) =
8 x 3 − 4 x 2 y + 2 xy 2 + 4 x 2 y − 2 xy 2 + y 3 = 8 x 3 + y 3

Задания для самостоятельного решения

Понравился урок?
Присоединяйтесь к нашей новой группе Вконтакте и начните получать уведомления о новых уроках

В этом уроке мы познакомимся с формулами квадрата суммы и квадрата разности и выведем их. Докажем формулу квадрата суммы геометрически. Кроме того, по этим формулам мы будем решать множество различных примеров.

Рассмотрим формулу квадрата суммы:

Итак, мы вывели формулу квадрата суммы:

Условно эта формула выражается так: квадрат суммы равен квадрат первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

Эту формулу легко представить геометрически.

Рассмотрим квадрат со стороной:

Площадь квадрата.

С другой стороны, один и тот же квадрат можно представить иначе, разделив сторону на a и b (рис. 1).

Рис. 1. Квадрат

Тогда площадь квадрата можно представить как сумму площадей:

Так как квадраты были одинаковыми, то их площади равны, значит:

Итак, мы доказали геометрически формулу на квадрат суммы.

Рассмотрим примеры:

Комментарий: пример решается по формуле суммы квадратов.

Выводим формулу квадрата разности:

Итак, мы вывели формулу квадрата разности:

Условно эта формула выражается так: квадрат разности равен квадрат первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа.

Рассмотрим примеры:

Формулы квадрата суммы и квадрата разности могут работать как слева направо, так и справа налево. При использовании слева направо это будут формулы сокращенного умножения, они используются при вычислении и преобразовании примеров. А при использовании справа налево — формулы факторизации.

Рассмотрим примеры, в которых нужно разложить заданный многочлен на множители, применяя формулы квадрата суммы и квадрата разности. Для этого нужно очень внимательно посмотреть на полином и точно определить, как его правильно разложить.

Комментарий: чтобы разложить полином на множители, нужно определить, что представлено в этом выражении. Итак, мы видим квадрат и квадрат единства. Теперь нам нужно найти двойное произведение — это . Итак, все необходимые элементы есть, осталось только определить, квадрат ли это суммы или разности. Перед удвоенным произведением стоит знак плюс, что означает, что перед нами квадрат суммы.

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрат суммы и квадрат разности двух выражений; разность квадратов двух выражений; куб суммы и куб разности двух выражений; суммы и разности кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, разложения многочленов на множители и приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .

Пусть a, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения и второго плюс квадрат второго выражения.

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений на их сумму.

а 2 — b 2 = (а — b) (а + b)

4. сумма куба двух выражений равна кубу первого выражения плюс утроенный квадрат первого выражения умноженное на второе плюс умноженное на три произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрат первого выражения и второго плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражений на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов двух выражений равна произведению разности первого и второго выражения неполным квадратом суммы этих выражений.

а 3 — b 3 = (а — b) (а 2 + ab + b 2)

Применение формул сокращенного умножения при решении примеров.

Пример 1

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40+1) 2 = 40 2 + 2 40 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получаем

98 2 = ( 100 — 2) 2 = 100 2 — 2 100 2 + 2 2 = 10000 — 400 + 4 = 9604

Пример 2

Вычислить

по формулам квадратов разностей, двух выражений разностей получаем

Пример 3

Упростить выражение

(x — y) 2 + (x + y) 2

Используем формулы квадрата суммы и квадрата разности двух выражений

(x — y) 2 + (x + y) 2 = x 2 — 2xy + y 2 + x 2 + 2xy + y 2 = 2x 2 + 2y 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
а 3 — б 3 = (а — б) (а 2 + аб + б 2)

Также будут задания для самостоятельного решения, ответы на которые вы можете посмотреть.

Формулы сокращенного умножения позволяют производить идентичные преобразования выражений — многочленов. С их помощью можно разложить многочлены на множители, а с помощью формул в обратном порядке произведения двучленов, квадратов и кубов представить в виде многочленов. Рассмотрим все общепринятые формулы сокращенного умножения, их вывод, типовые задания на тождественные преобразования выражений по этим формулам, а также домашние задания (ответы на них открываются по ссылкам).

квадрат суммы

Формула квадрата суммы равна равенству

(квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа).

Вместо a и b в эту формулу можно подставить любое число.

Формула суммы квадратов часто используется для упрощения вычислений. Например,

Используя формулу квадрата суммы, многочлен можно разложить на множители, а именно представить в виде произведения двух одинаковых множителей.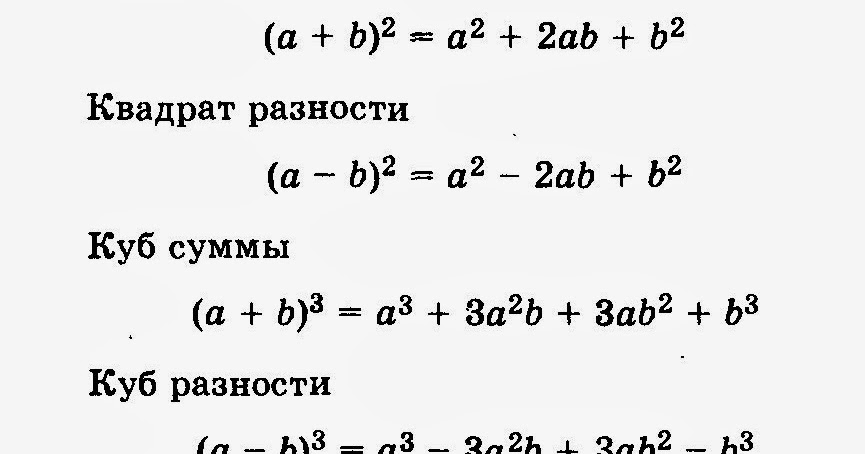

Пример 1

.

Пример 2 Запишите в виде полиномиального выражения

Решение. По формуле квадрата суммы получаем

Квадрат разности

Формула квадрата разности есть равенство

(квадрат разности двух чисел равен квадрат первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа).

Формула квадрата разницы часто используется для упрощения вычислений. Например,

Используя формулу квадрата разности, многочлен можно разложить на множители, а именно представить в виде произведения двух одинаковых множителей.

Формула следует из правила умножения многочлена на многочлен:

Пример 5 Запишите в виде полиномиального выражения

Решение. По формуле квадрата разности получаем

.

Примените сами формулу сокращенного умножения, а затем посмотрите решение

Выбор полного квадрата

Часто многочлен второй степени содержит квадрат суммы или разности, но содержится в скрытом виде. Чтобы получить полный квадрат явно, вам нужно преобразовать многочлен. Для этого, как правило, один из членов многочлена представляют в виде двойного произведения, а затем к многочлену прибавляют и вычитают одно и то же число.

Пример 7

Решение. Этот многочлен можно преобразовать следующим образом:

Здесь мы представили 5 х в виде двойного произведения 5/2 на х , прибавили к многочлену и вычли из него такое же число, затем применили формула квадрата суммы для двучлена.

Итак, мы доказали равенство

,

равно полному квадрату плюс число.

Пример 8 Рассмотрим многочлен второй степени

Решение. Произведем над ним следующие преобразования:

Здесь мы представили 8 х в виде двойного произведения х на 4, прибавив к многочлену и вычтя из него то же число 4², применили формулу квадрата разности для бином х — 4 .

Итак, мы доказали равенство

,

, показывающее, что многочлен второй степени

равен полному квадрату плюс число −16.

Примените сами формулу сокращенного умножения, а потом посмотрите решение

куб суммы

Формула куба суммы равна равенству

(куб суммы двух чисел равен кубу первого числа плюс умноженный на три квадрат первого числа умноженный на второе, плюс умноженный на три произведение первого числа на квадрат второго плюс куб второго числа).

Формула куба суммы получается следующим образом:

Пример 10 Запишите в виде полиномиального выражения

Решение. По формуле куба суммы получаем

Примените сами формулу сокращенного умножения, а затем посмотрите решение

куб разности

Формула куба разности есть равенство

(куб разности двух чисел равен кубу первого числа минус три умножить на квадрат первого числа и второго плюс утроить произведение первого числа на квадрат второго минус куб второго числа).

Используя формулу куба суммы, многочлен можно разложить на множители, а именно представить в виде произведения трех одинаковых множителей.

Формула куба разности получается следующим образом:

Пример 12. Запишите в виде полиномиального выражения

Решение. Используя формулу куба разности, получаем

Примените сами формулу сокращенного умножения, а затем посмотрите решение

Разность квадратов

Формула разности квадратов есть равенство квадратов двух чисел равен произведению суммы этих чисел на их разность).

С помощью формулы куба суммы можно разложить на множители любой многочлен вида.

Доказательство формулы получено с помощью правила умножения многочленов:

Пример 14 Запишите произведение в виде многочлена

.

Решение. По формуле разности квадратов получаем

Пример 15 Факторизация

Решение. Это выражение в явном виде не соответствует никакому тождеству. Но число 16 можно представить как степень с основанием 4: 16=4². Тогда исходное выражение примет другой вид:

,

а это формула разности квадратов и применяя эту формулу получаем

Что такое куб суммы двух чисел.

Формулы сокращенного умножения

При вычислении алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения . Всего таких формул семь. Их всех нужно знать наизусть.

Также следует помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.

Разность квадратов

Разность квадратов двух чисел равна произведению разности этих чисел на их сумму.

а 2 — б 2 = (а — б) (а + б)

сумма квадратная

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

(а + б) 2 = а 2 + 2аб + б 2

Обратите внимание, что с помощью этой сокращенной формулы умножения легко найти квадраты больших чисел без использования калькулятора или длинного умножения. Поясним на примере:

Найти 112 2 .

Разложим 112 на сумму чисел, квадраты которых мы хорошо помним. 2
112 = 100 + 1

Запишем сумму чисел в скобках и поставим над скобками квадрат.
112 2 = (100 + 12) 2

Давайте воспользуемся формулой суммы квадратов:
112 2 = (100 + 12) 2 = 100 2 + 2 x 100 x 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544

Помните, что формула суммы квадратов также действительна. для любых алгебраических многочленов.

(8a + c) 2 = 64a 2 + 16ac + c 2

Внимание!!!

(a + b) 2 не равно a 2 + b 2

Квадрат разности

Квадрат разницы между двумя числами равен квадрату первого числа минус удвоенное произведение первого и второго плюс квадрат второго числа.

(а — б) 2 = а 2 — 2аб + б 2

Также стоит запомнить очень полезное преобразование:

(a — b) 2 = (b — a) 2
Приведенная выше формула доказывается простым раскрытием скобок:

(a — b) 2 = a 2 — 2ab + b 2 = b 2 — 2ab + a 2 = (b — a) 2

сумма куб

Куб суммы двух чисел равен кубу первого числа плюс умноженный на три квадрат первого числа умноженный на второе плюс умноженное на три произведение первого умноженное на квадрат второго плюс куб секунда.

(а + б) 3 = а 3 + 3а 2 б + 3аб 2 + б 3

Запомнить эту «ужасную» формулу довольно просто.

Узнайте, что 3 идет первым.

Два полинома в середине имеют коэффициенты 3.

AПомните, что любое число в нулевой степени равно 1 (a 0 = 1, b 0 = 1). Легко видеть, что в формуле есть уменьшение степени а и увеличение степени b. Вы можете проверить это:
(a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3

Внимание!!!

(a + b) 3 не равно a 3 + b 3

куб разностей

Куб разности двух чисел равен кубу первого числа минус умноженный на три квадрат первого числа и второго плюс умноженный на три произведения первого числа на квадрат второго минус куб второй.

(а — б) 3 = а 3 — 3а 2 б + 3аб 2 — б 3

Эта формула запоминается как и предыдущая, но только с учетом чередования знаков «+» и «-». Первому члену числа 3 предшествует «+» (по правилам математики мы его не пишем). Это означает, что перед следующим элементом будет стоять «-», затем снова «+» и т. д.

(а — б) 3 = + 3 — 3а 2б + 3аб 2 — b 3 = a 3 — 3a 2 b + 3ab 2 — b 3

Сумма кубов ( Не путать с суммирующим кубом!)

Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.

а 3 + Ь 3 = (а + Ь)(а 2 — аб + Ь 2)

Сумма кубов равна произведению двух скобок.

Первая скобка представляет собой сумму двух чисел.

Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называется выражение:

A 2 — ab + b 2
Этот квадрат является неполным, так как в середине вместо двойного произведения стоит обыкновенное произведение чисел.

Куб Разностей (Не путать с Кубом Разностей!!!)

Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.

а 3 — б 3 = (а — б) (а 2 + аб + б 2)

Будьте внимательны при написании символов. Следует помнить, что все приведенные выше формулы также используются справа налево.

Трудно запомнить формулы сокращенного умножения? Помочь делу легко. Нужно только помнить, как изображается такая простая вещь, как треугольник Паскаля. Тогда вы будете помнить эти формулы всегда и везде, вернее, не запоминать, а восстанавливать.

Что такое треугольник Паскаля? Этот треугольник состоит из коэффициентов, входящих в разложение любой степени двучлена вида в многочлен.

Разобьем, например:

В этой записи легко запомнить, что в начале стоит куб первого числа, а в конце — куб второго числа. А вот то, что посередине, трудно вспомнить. И даже то, что в каждом следующем члене степень одного множителя все время уменьшается, а второго возрастает — это легко заметить и запомнить, труднее запомнить коэффициенты и знаки (плюс или минус?).

Итак, сначала шансы. Вам не нужно запоминать их! На полях тетради быстро рисуем треугольник Паскаля, и вот они — коэффициенты, уже перед нами. Начинаем рисовать с трех единиц, одну сверху, две снизу, справа и слева — ага, уже треугольник получается:

Первая строка, с одной единицей, нулевая. Затем идет первая, вторая, третья и так далее. Чтобы получить вторую строку, нужно снова прибавить единицы по краям, а в центре записать число, полученное при сложении двух чисел над ним:

Пишем третью строку: снова по краям единицы, и снова, чтобы получить следующую цифру в новой строке, добавляем цифры над ней в предыдущей:

Как у вас угадали, получаем в каждой строке коэффициенты от разложения двучлена в многочлен:

Ну а еще проще запомнить знаки: первый такой же, как и в развернутом двучлене (раскладываем сумма — значит плюс, разность — значит минус), а дальше знаки чередуются!

Вот такая полезная штука — треугольник Паскаля. Наслаждаться!

Формулы или правила сокращенного умножения используются в арифметике, а точнее в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами формулы выведены из существующих в алгебре правил умножения нескольких многочленов.

Использование этих формул обеспечивает достаточно быстрое решение различных математических задач, а также помогает упростить выражения. Правила алгебраических преобразований позволяют производить некоторые манипуляции с выражениями, следуя которым можно получить выражение в левой части равенства, которое в правой части, или преобразовать правую часть равенства (чтобы получить выражение в слева после знака равенства).

Формулы сокращенного умножения удобно знать по памяти, так как они часто используются при решении задач и уравнений. Основные формулы, включенные в этот список, и их названия приведены ниже.

квадрат суммы

Чтобы вычислить квадрат суммы, нужно найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения это правило записывается так: (a + c)² = a² + 2ac + c².

Квадрат разности

Для вычисления квадрата разности нужно вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с обратным знаком ) и квадрат второго числа. В виде выражения это правило выглядит так: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел в квадрате равна произведению суммы этих чисел на их разность. В виде выражения это правило выглядит так: а² — с² = (а + с) (а — с).

куб суммы

Чтобы вычислить куб суммы двух слагаемых, нужно вычислить сумму, состоящую из куба первого слагаемого, утроить произведение квадрата первого слагаемого и второго, утроить произведение первого члена на квадрат второго и куб второго члена. В виде выражения это правило выглядит так: (a + c)³ = a³ + 3a²c + 3ac² + c³.

Сумма кубов

Согласно формуле равна произведению суммы этих слагаемых на их неполный квадрат разности. В виде выражения это правило выглядит так: а³ + с³ = (а + с) (а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образуется при сложении двух кубиков. Известны только величины их сторон.

Если значения сторон малы, то легко произвести расчеты.

Если длины сторон выражены громоздкими числами, то в этом случае проще применить формулу «Сумма кубов», что значительно упростит расчеты.

куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена утроить отрицательное произведение квадрата первого члена на второй утроить произведение первого члена на квадрат второго и отрицательный куб второго члена. В виде математического выражения куб разности выглядит так: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов только одним знаком. Таким образом, разность кубов представляет собой формулу, равную произведению разности этих чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит так: а 3 — с 3 = (а — с) (а 2 + ас + с 2).

Пример. Необходимо рассчитать объем фигуры, который останется после вычитания желтой объемной фигуры, которая также является кубом, из объема синего куба. Известен только размер стороны малого и большого куба.

Если значения сторон небольшие, то расчеты достаточно просты. А если длины сторон выражены значащими числами, то стоит воспользоваться формулой под названием «Разность кубов» (или «Разностный куб»), которая значительно упростит расчеты.

Формулы сокращенных выражений очень часто используются на практике, поэтому желательно выучить их все наизусть. До сего момента верой и правдой будем служить, которые рекомендуем распечатать и постоянно держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и кубировать сумму или разность два выражения. Пятый предназначен для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называется выражение вида a 2 −a b + b 2 ) и разности двух выражений a и b на неполный квадрат их суммы (a 2 + a b+b 2 ) соответственно.

Отдельно стоит отметить, что каждое равенство в таблице является тождеством. Это объясняет, почему формулы сокращенного умножения также называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение полинома на множители, часто используется БСС в виде с перестановкой левой и правой частей:

Последние три тождества в таблице имеют собственные названия. Формула a 2 −b 2 =(a−b)(a+b) называется формула разности квадратов , a 3 +b 3 =(a+b) (a 2 −a b+b 2) — формула суммы кубов , a a 3 −b 3 =(a−b) (a 2 +a b+b 2) — формула разности кубов . Обратите внимание, мы не назвали соответствующие формулы с переставленными частями из предыдущей таблицы БСС.

Дополнительные формулы

Не помешает добавить еще несколько тождеств в таблицу формул сокращенного умножения.

Области применения формул сокращенного умножения (ФСУ) и примеры

Основное назначение формул сокращенного умножения (ФСУ) объясняется их названием, т.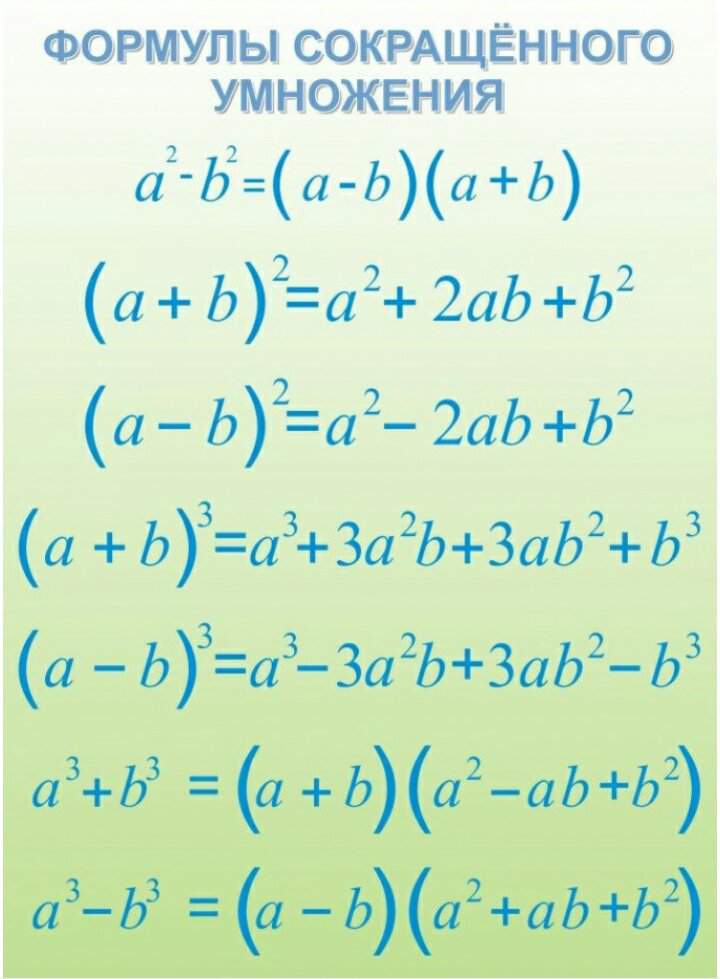 е. заключается в кратком умножении выражений. Однако область применения FSO намного шире и не ограничивается коротким умножением. Перечислим основные направления.

Несомненно, центральное применение формулы сокращенного умножения было найдено в выполнении тождественных преобразований выражений. Чаще всего эти формулы используются в процессе упрощений выражений .

Пример.

Упростите выражение 9·y−(1+3·y) 2 .

Решение.

В этом выражении возведение в квадрат можно выполнить сокращенно, имеем 9 y−(1+3 y) 2 =9 y−(1 2 +2 1 3 y+(3 y) 2). Остается только раскрыть скобки и дать такие же члены: 9 y−(1 2 +2 1 3 y+(3 y) 2)= 9 y−1−6 y−9 y 2 =3 y−1−9 y 2 .

Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.

Сбор и использование личной информации

Личная информация относится к данным, которые могут быть использованы для идентификации конкретного лица или связи с ним.

Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.

Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую ​​информацию.

Какую личную информацию мы собираем:

• Когда вы подаете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т. д.

Как мы используем вашу личную информацию:

• Личная информация, которую мы собираем, позволяет нам связываться с вами и информировать вас об уникальных предложениях, рекламных акциях и других событиях и предстоящих событиях.
• Время от времени мы можем использовать вашу личную информацию для отправки вам важных уведомлений и сообщений.
• Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудитов, анализ данных и различные исследования, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.
• Если вы участвуете в розыгрыше призов, конкурсе или аналогичном поощрении, мы можем использовать предоставленную вами информацию для управления такими программами.

Раскрытие третьим лицам

Мы не раскрываем полученную от вас информацию третьим лицам.

Исключения:

• В случае необходимости — в соответствии с законом, судебным приказом, в порядке судопроизводства и/или на основании публичных запросов или запросов государственных органов на территории РФ — раскрыть свои Персональные данные. Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес.
• В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующему правопреемнику третьей стороны.

Защита личной информации

Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и неправомерного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Обеспечение конфиденциальности на уровне компании

Чтобы обеспечить безопасность вашей личной информации, мы сообщаем нашим сотрудникам о правилах конфиденциальности и безопасности и строго следим за соблюдением правил конфиденциальности.

В предыдущем уроке мы занимались факторизацией. Мы освоили два метода: вынос общего множителя за скобки и группировку. В этом уроке, следующий мощный метод: формул сокращенного умножения . В краткой заметке — БСС.

Формулы сокращенного умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) необходимы во всех разделах математики. Они используются при упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Словом, есть все основания иметь с ними дело. Понять, откуда они берутся, зачем нужны, как их запомнить и как применять.

Понятно?)

Откуда берутся формулы сокращенного умножения?

Равенства 6 и 7 записываются не совсем обычно.

No related posts.