Формула сокращенного умножения в 4 степени: Формулы сокращённого умножения

Формулы сокращенного умножения.

Формулы сокращенного умножения.

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности. Поделиться:

Вы сейчас находитесь в каталоге:    Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности.

Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности. «>

Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности.

Разность квадратов	a2-b2 = (a-b)(a+b)
Квадрат суммы	(a+b)2 = a2+2ab+b2
Квадрат разности	(a-b)2 = a2-2ab+b2
Куб суммы	(a+b)3 = a3+3a2b+3ab2+b3
Куб разности	(a-b)3 = a3-3a 2b+3ab2-b3
Сумма кубов	a3+b3 = (a+b)(a2-ab+b2)
Разность кубов	a3-b3 = (a-b)(a2+ab+b2)
Разность четвертых степеней	a4-b4 = (a2-b2)(a2+b2)=(a-b)(a+b)(a2+b2)

Справочно, только для тех кто хочет больше представлять тему: Бином Ньютона. Целая положительная степень n суммы. (a + b)ⁿ=

Повторяем и систематизируем школьный курс алгебры и начал анализа

Повторяем и систематизируем школьный курс алгебры и начал анализа

Крамор В. С. Повторяем и систематизируем школьный курс алгебры и начал анализа.—М.: Просвещение, 1990.— 416 с. В книге в конспективной форме изложен теоретический материал по алгебре и началам анализа. К каждому пункту теоретического материала приведены упражнения с решениями и упражнения трех уровней сложности для самостоятельного решения. Она может быть использована при подготовке к экзаменам в высшие учебные заведения. Оглавление ПРЕДИСЛОВИЕ ГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3. ВЫЧИТАНИЕ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. ПРЕДЕЛ ФУНКЦИИ § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1. 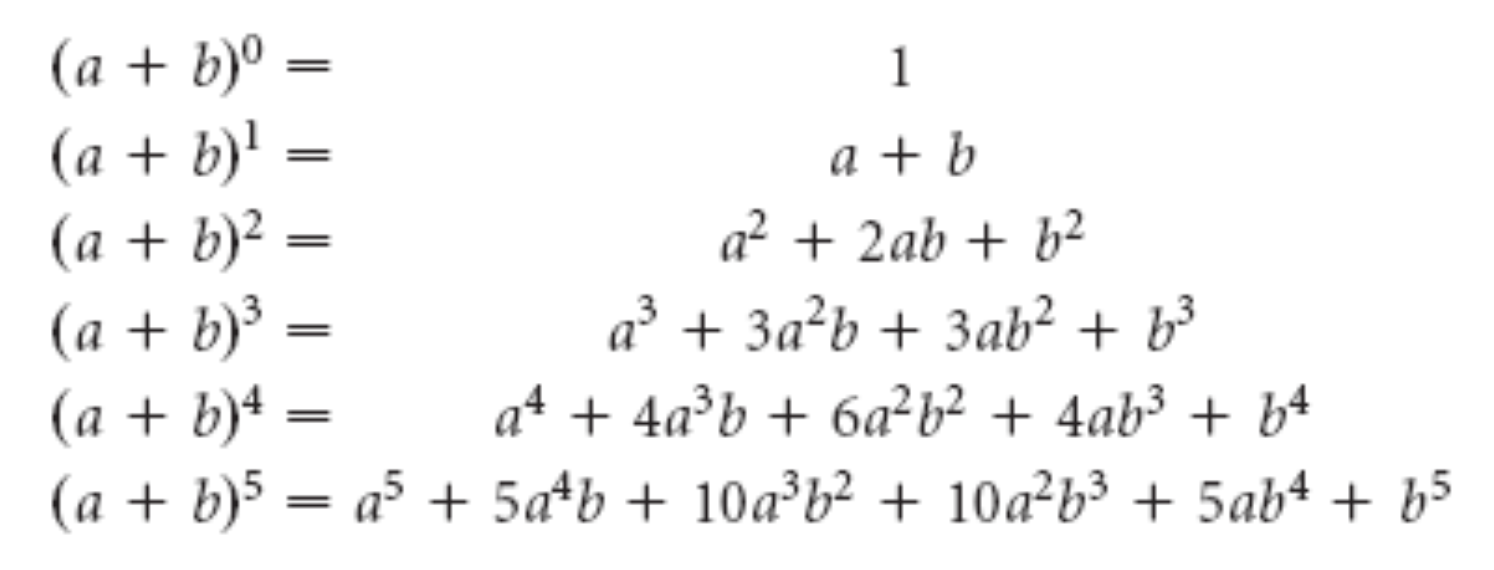ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление

Что такое BODMAS, BIDMAS и PEMDAS?

Если вам нужна PDF-версия этой страницы, просто нажмите Bodmas PDF

BODMAS объясняет «Порядок операций» в математике, а BIDMAS и PEMDAS делают то же самое, но используют немного разные слова. Если вышеизложенное звучит для вас как абракадабра, посмотрите наше короткое видео ниже, где Али объясняет, как все это работает.

Что такое аббревиатура?

Акроним — это слово, состоящее из начальных букв слов в фразе. Аббревиатуры могут произноситься как отдельные слова.

Подумайте о НАСА и часто задаваемых вопросах. Оба они произносятся так, как если бы они были самостоятельным словом. Тем не менее, НАСА означает N National A Aeronautics и S темп A администрация и FAQ означает F часто A sked Q uest ионы.

Аналогичным образом буквы в BODMAS, BIDMAS и PEMDAS обозначают слова.

BODMAS, BIDMAS и PEMDAS — это аббревиатуры для запоминания порядка операций в математике.

Что означают буквы в словах BODMAS, BIDMAS и PEMDAS?

В случае с математическими аббревиатурами BODMAS, BIDMAS и PEMDAS все они означают одно и то же и служат одной и той же цели. Вот что означают буквы:

• Кронштейны
• Заказов
• Подразделение
• Умножение
• Дополнение
• Вычитание

• Скобки
• Индексы
• Подразделение
• Умножение
• Дополнение
• Вычитание

• Скобки
• Экспоненты
• Умножение
• Подразделение
• Дополнение
• Вычитание

Третья серия выше наиболее часто используется в США, в то время как британские школы почти всегда принимают серию 1 или серию 2 выше. Когда ваш ребенок впервые столкнется с одним из них, вам следует запомнить, какой именно, потому что в разных школах используются разные. Придерживаясь того же, который используется в вашей школе, вы, по крайней мере, избежите одного уровня сложности.

Что такое ордера, индексы и экспоненты?

Порядки, индексы и экспоненты — это маленькие надстрочные числа, которые представляют степени в математике.

Скобки, Деление, Умножение, Сложение и Вычитание — все это слова, с которыми мы знакомы, но что насчет второго элемента акронимов — Порядков, Индексов или Экспонент? Это «числа половинного размера», которые часто встречаются в математических выражениях. В следующем примере 2 является индексом (единственное число множественного числа индексы ):

3 ² = 3 х 3

Что такое математические операции?

Математическая операция может рассматриваться как один из символов, который заставляет что-то происходить в математике.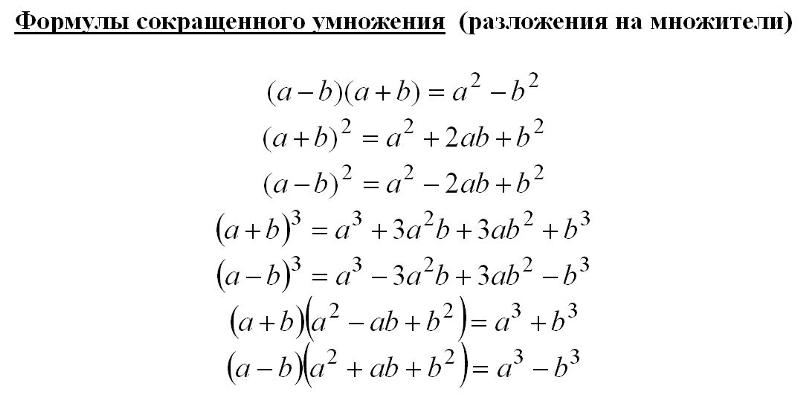 Знак умножения (х) означает, что нужно умножить два числа, а знак сложения (+) означает, что нужно сложить два числа. Это операций .

Каков правильный порядок операций в математике?

Правильный порядок действий в математике: B ракетки, O ряды, D провидение, M умножение, A сложение и S вычитание.

Если вы используете BIDMAS, замените O заказов на I индексов.

Весь смысл BIDMAS и BODMAS в том, чтобы помочь вам запомнить, какие операции выполнять в каком порядке. К сожалению, математика подсказывает, что это не порядок слева направо, как можно было бы ожидать: давайте рассмотрим типичный пример и посмотрим, получите ли вы правильный ответ:

2 + 3 х 4

Вы пришли к выводу, что ответ равен 20? Если да, то вы произвели вычисления слева направо и сказали, что 2 плюс 3 равно 5 , а затем умножить на 4, чтобы получить 20 . К сожалению, с математической точки зрения это неверно!

Если вы посмотрите на правила BIDMAS/BODMAS, вы увидите, что умножение предшествует сложению (две операции, с которыми мы имеем дело), ​​и поэтому вы должны были иметь дело с умножением ДО вы имели дело с Дополнением. Таким образом, правильная логика такова: 3 умножить на 4, получится 12 , а затем прибавить к 2, чтобы получить 14 . 14 это правильный ответ.

Я уже сбился со счета, сколько раз мне звонил родитель, который говорил: «Ты просто ошибаешься. Смотри, я сделал это на своем калькуляторе и набрал 2 + 3 x 4, и это всегда, но всегда дает мне ответ 20».

Среди многих тысяч вопросов на сайте Education Quizzes именно этот выпуск Порядка операций чаще всего вызывает вопросы у наших учителей — и когда кажется, что у родителей есть калькуляторы на их стороне, неудивительно, почему!

Порядки, индексы и экспоненты — это маленькие надстрочные числа, которые представляют степени в математике.

Используются ли на экзамене 11-Plus BODMAS или BIDMAS?

Вообще говоря, нет. В это может потребоваться некоторое доверие, но на экзамене 11-Plus неправильный ответ часто помечается как правильный, а правильный ответ занижается! Это связано с тем, что некоторые авторитетные лица считают, что дети в возрасте до 11 лет не должны знать порядок операций, определенный BIDMAS / BODMAS, и поэтому они ожидают, что учащиеся ошибочно будут выполнять вычисления слева направо.

Во избежание возможности того, что кандидат 11-Plus может быть занижен за правильный ответ (!) обязательно уточните в своей школе, следует ли применять правила порядка операций в математических вопросах.

Каковы правила BODMAS или BIDMAS?

Чтобы увидеть, как правила BIDMAS (или BODMAS) применяются в более сложных сценариях, нам нужно проанализировать математическое выражение, содержащее все различные элементы. Если вы готовы, то давайте начнем!

2 x 20 ÷ 2 + (3+4) x 3 ² – 6 + 15

Этап 1

Разберитесь со скобами, чтобы получить:

2 х 20 ÷ 2 + 7 х 3 ² – 6 + 15

Этап 2

Сделка с индексами (если вы думаете о BIDMAS) или ордерах (если вы думаете о BODMAS), чтобы получить:

2 х 20 ÷ 2 + 7 х 9 – 6 + 15

Этап 3

Деление и умножение имеют одинаковый ранг, поэтому действуйте вместе слева направо, чтобы получить:

20 + 63 – 6 + 15

Этап 4

Сложение и вычитание имеют одинаковый ранг, поэтому действуйте вместе слева направо, чтобы получить:

92

СОВЕТ. Работайте поэтапно и не пытайтесь срезать путь.

Я надеюсь, что эта статья помогла вам понять, что такое BODMAS, BIDMAS и PEMDAS. Для более подробного ознакомления с порядком операций, а также с некоторыми интересными примерами, вы можете прочитать статью Wiki по адресу: Порядок операций, но не ожидайте, что отделаетесь без головной боли!

Итак, это объяснение BODMAS, BIDMAS и PEMDAS — есть ли что-нибудь еще, что вы хотели бы знать? Просмотрите наш Банк знаний, если у вас есть вопросы об образовании. У нас есть множество статей, наполненных информацией, советами и советами для родителей. Это ценное оружие в арсенале любого родителя!

Нечего бояться. Это проще, чем вы думали!

Правило BODMAS — Полная форма BODMAS

Правило BODMAS — это аббревиатура, используемая для запоминания порядка операций, которым необходимо следовать при решении математических выражений. BODMAS означает B — скобки, O — порядок степеней или корней (в некоторых случаях «из»), D — деление, M — умножение, A — сложение и S — вычитание. Это означает, что выражения с несколькими операторами необходимо упрощать слева направо только в этом порядке. Сначала мы решаем скобки, затем степени или корни, затем деление или умножение (в зависимости от того, что окажется первым из левой части выражения) и, наконец, вычитание или сложение, в зависимости от того, что окажется в левой части выражения.

В этом уроке мы узнаем о правиле БОДМАС, которое помогает решать арифметические выражения, содержащие несколько операций, таких как сложение (+), вычитание (-), умножение (×), деление (÷) и скобки ( ). .

1.	Что такое БОДМАС?
2.	Полная форма БОДМАС
3.	БОДМАС или ПЕМДАС
4.	Часто задаваемые вопросы о правиле BODMAS

Что такое БОДМАС?

BODMAS, который называется порядком операций, представляет собой последовательность для выполнения операций в арифметическом выражении. Математика основана на логике и некоторых стандартных правилах, упрощающих наши расчеты. Итак, BODMAS — это одно из стандартных правил упрощения выражений с несколькими операторами.

В арифметике выражение или уравнение состоит из двух компонентов:

• Номера
• Операторы

Числа

Числа — это математические значения, используемые для подсчета и представления величин, а также для выполнения вычислений. В математике числа могут быть классифицированы как натуральные числа, целые числа, целые числа, рациональные числа, иррациональные числа, действительные числа, комплексные числа и мнимые числа.

Операторы или операции

Оператор — это символ, который объединяет два числа и дает выражение или уравнение. В математике наиболее распространенными операторами являются сложение (+), вычитание (-), умножение (×), деление (÷). Для математических выражений или уравнений, в которых задействован только один оператор, найти ответ довольно просто. В случае нескольких операторов найти решение становится немного сложнее! Давайте разберемся в этом на примере. Дженни и Рон по отдельности решили математическое выражение 6 × 3 + 2. Ниже приведены два разных метода, с помощью которых Дженни и Рон решили выражение:

Метод Дженни: 6 × 3 + 2 = 6 × 5 = 30, Метод Рона: 6 × 3 + 2 = 18 + 2 = 20.

Как мы видим, Дженни и Рон получили разные ответы. В математике мы знаем, что может быть только один правильный ответ на это выражение. Как определить, кто прав? В таких случаях мы используем BODMAS , чтобы найти правильный ответ. Давайте посмотрим на приведенный ниже пример, чтобы получить представление о том, как работает BODMAS:

Примеры Bodmas

Давайте разберемся с этим, используя примеры BODMAS.

Пример 1: Упростите выражение, используя BODMAS.

10 + (5 × 3 + 2)

Решение: Пошагово решим 10 + (5 × 3 + 2).

• Шаг 1: Сначала нам нужно решить скобки. Итак, это будет 10 + (15 + 2)
.
• Шаг 2: В результате получится 10 + 17 = 27

Пример 2: Упростите выражение, используя BODMAS.

15 + (30 ÷ 2)

Решение:

Пошагово решим 15 + (30 ÷ 2).

• Шаг 1: Сначала нам нужно решить скобки. Итак, 15 + (30 ÷ 2) = 15 + 15
• Шаг 2: В результате получится 15 + 15 = 30

Полная форма БОДМАС

Правило BODMAS используется для оценки математических выражений и выполнения сложных вычислений более простым и стандартным способом.

BODMAS Значение

В соответствии с правилом BODMAS, чтобы решить любое арифметическое выражение, мы сначала решаем термины, записанные в скобках, а затем упрощаем экспоненциальные члены, или решаем операцию «из», что означает умножение, и перемещаем впереди операции деления и умножения, а затем, в конце, работа над сложением и вычитанием. Следование порядку операций в правиле BODMAS всегда приводит к правильному ответу. Упрощение терминов внутри скобок можно сделать напрямую. Это означает, что мы можем выполнять операции внутри скобки в порядке деления, умножения, сложения и вычитания. Если в выражении несколько скобок, все одинаковые типы скобок могут быть решены одновременно. Например, (14 + 19) ÷ (13 — 2) = 33 ÷ 11 = 3.

Обратите внимание на приведенную ниже таблицу, чтобы понять термины и операции, обозначаемые аббревиатурой BODMAS, в правильном порядке.

Б	[{()}]	Кронштейны
О	х²	Орден Сил или Корней (в некоторых случаях «из»)
Д	÷	Подразделение
М	×	Умножение
А	+	Дополнение
С	—	Вычитание

• Следует отметить, что когда у нас есть все 3 типа скобок, мы начинаем решение с самых внутренних скобок/круглых скобок (), за которыми следуют фигурные скобки {}, а затем квадратные скобки [ ].
• Еще один момент, который следует помнить, это то, что для буквы «О» мы используем «Порядок степеней или корней», однако в некоторых случаях, когда дается «из», мы решаем «из», что означает умножение.

БОДМАС или ПЕМДАС

BODMAS и PEMDAS — это две аббревиатуры, которые используются для запоминания порядка операций. Правило BODMAS почти аналогично правилу PEMDAS. Существует разница в аббревиатуре, потому что некоторые термины известны под разными названиями в разных странах. При использовании правила BODMAS или правила PEMDAS мы должны помнить, что когда мы подходим к шагу деления и умножения, мы решаем операцию, которая идет первой с левой стороны выражения. То же правило относится к сложению и вычитанию, то есть решаем то действие, которое стоит первым в левой части.

Когда использовать БОДМАС?

BODMAS используется, когда в математическом выражении имеется более одной операции. Существует ряд определенных правил, которые необходимо соблюдать при использовании метода БОДМАС. Это дает правильную структуру для получения уникального ответа для каждого математического выражения.

Условия для выполнения:

• Если есть какие-либо скобки, откройте скобки, затем добавьте или вычтите члены. а + (Ь + с) = а + Ь + с, а + (Ь — с) = а + Ь — с
• Если есть отрицательный знак, просто откройте скобку и умножьте отрицательный знак на каждое слагаемое внутри скобки. а — (б + в) ⇒ а — б — в
• Если за скобками находится какой-либо термин, умножьте этот внешний термин на каждый термин внутри скобки. а(б + в) ⇒ аб + ас

Простые способы запомнить правило BODMAS

Ниже приведены простые правила для запоминания правила BODMAS:

• Сначала упростите скобки.
• Решите все экспоненциальные члены.
• Выполнить деление или умножение (слева направо)
• Выполнить сложение или вычитание (слева направо)

Распространенные ошибки при использовании правила BODMAS

При применении правила BODMAS для упрощения выражений можно допустить некоторые распространенные ошибки, и эти ошибки приведены ниже: неправильный ответ. Таким образом, если в выражении несколько скобок, все одинаковые типы скобок могут быть решены одновременно.

В некоторых случаях возникает ошибка из-за отсутствия правильного понимания сложения и вычитания целых чисел. Например, 1-3+4 = -2+4 = 2. Но иногда делаются следующие ошибки, которые приводят к неправильному ответу, например, 1-3+4 = 1-7 = -6.

Ошибка, связанная с предположением, что деление имеет более высокий приоритет, чем умножение, а сложение имеет более высокий приоритет, чем вычитание. Соблюдение правила слева направо при выборе этих операций помогает получить правильный ответ.

Умножение и деление являются операциями одного уровня и должны выполняться в последовательности слева направо (в зависимости от того, что идет первым в выражении) и то же самое со сложением и вычитанием, которые являются операциями одного уровня, которые должны выполняться после умножения и деления. Если кто-то сначала решает деление перед умножением (которое находится слева от операции деления), поскольку D стоит перед M в BODMAS, он может в конечном итоге получить неправильный ответ.

☛ Похожие темы

• Дополнение
• Вычитание
• Умножение
• Подразделение
• Порядок операций
• Порядок действий Рабочие листы 5-й класс
• Рабочие листы PEMDAS 5-й класс

Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

 

Примеры правил BODMAS

1. Пример 1: Упростите выражение, используя правило BODMAS: [18 — 2(5 + 1)] ÷ 3 + 7

   Решение:

   Данное выражение равно [18 — 2(5 + 1) ] ÷ 3 + 7

   • Шаг 1: Начнем с решения самой внутренней скобки. Начиная с 5 + 1 = 6. Таким образом, [18 — 2(6)] ÷ 3 + 7
   • Шаг 2: Далее работаем с порядком, тем самым умножая 2(6) или 2×6=12. Таким образом, [18 — 12] ÷ 3 + 7
   • Шаг 3: Осталась одна скобка, [18 — 12] = 6. Итак, 6 ÷ 3 + 7
   • Шаг 4: После В и О следует D, следовательно, 6 ÷ 3 = 2. Итак, 2 + 7
   • Шаг 5: И, наконец, сложение, 2 + 7 = 9

   ∴ Выражение упрощается, и ответ равен 9.

2. Пример 2: Вычислите порядок операций по правилу BODMAS: (1 + 20 — 16 ÷ 4²) ÷ {(5 — 3)² + 12 ÷ 2}

   Решение:

   • Шаг 1: Во-первых, нам нужно упростить самую внутреннюю скобку, (1 + 20 — 16 ÷ 4²) ÷ {2² + 12 ÷ 2}
   • Шаг 2: Теперь мы должны вычислить показатели степени, (1 + 20 — 16 ÷ 16) ÷ {4 + 12 ÷ 2}
   • Шаг 3: Теперь нам нужно разделить 16 на 16 и 12 на 2 в скобках, и мы получим (1 + 20 — 1) ÷ {4 + 6}
   • Шаг 4: Прибавьте 1 к 20 и 4 к 6, (21 — 1) ÷ 10
   • Шаг 5: Вычтем из 21 1, чтобы решить скобку, получим, 20 ÷ 10
   • Шаг 6: Делим 20 на 10, чтобы получить окончательный ответ, получаем 2.

   ∴ ​(1 + 20 — 16 ÷ 4²) ÷ {(5 — 3)² + 12 ÷ 2} = 2

3. Пример 3: Упростите выражение, используя правило BODMAS: ​(9 × 3 ÷ 9 + 1) × 3

   Решение:

   • Шаг 1: чтобы исправить какие-либо операции приходите первым, мы последуем за этим). Здесь сначала нам нужно умножить 9на 3 в данном выражении, (9 × 3 ÷ 9 + 1) × 3, и мы получаем, (27 ÷ 9 + 1) × 3
   • Шаг 2: Теперь нам нужно разделить 27 на 9 внутри скобки, и мы получим (3 + 1) × 3
   • Шаг 3: Удаляем скобки после добавления 3 и 1, получаем, 4×3
   • Шаг 4: Умножьте 4 на 3, чтобы получить окончательный ответ, равный 12.

   ∴ ​(9 × 3 ÷ 9 + 1) × 3 = 12

4. Пример 4: Решите данное выражение, применяя правило BODMAS: [50-{3×(9+7)}]

   Решение:

   Чтобы решить это выражение, [50-{3×(9+) 7)}], мы будем использовать следующие шаги:

   • Шаг 1: Решите самую внутреннюю скобку, прибавив 9 к 7, то есть 16. Таким образом, упрощенное выражение будет [50-{3×16}]
   • Шаг 2: Умножьте 3 на 16, чтобы получить [50-48]
   • Шаг 3: Вычтите 48 из 50, чтобы получить окончательный ответ, т. е. 2.

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы BODMAS

 

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о правиле BODMAS

Что такое правило Бодмаса в математике?

Правило BODMAS относится к правилу, которому следуют для решения математических выражений. BODMAS — это порядок операций для математических выражений, включающий более одной операции. Аббревиатура BODMAS означает B — скобки, O — порядок степеней, D — деление, M — умножение, A — сложение и S — вычитание.

Как работает правило BODMAS?

В любом арифметическом выражении, если используется несколько операций, нам нужно решать члены в порядке правила BODMAS. Сначала решаем часть, написанную в скобках. После решения скобок выполняем операции умножения и деления, в зависимости от того, что стоит первым в выражении слева направо. Затем мы получаем упрощенное выражение только с операциями сложения и вычитания. Решаем сложение и вычитание слева направо и получаем окончательный ответ. Вот как работает БОДМАС.

Применяется ли BODMAS при отсутствии скобок?

Да, даже если нет скобок, все равно используется правило BODMAS. Нам нужно решить другие операции в том же порядке. Следующим шагом после скобок (B) является порядок степеней или корней, за которым следует деление, умножение, сложение и затем вычитание.

Что такое О в правиле Бодмаса?

O в Bodmas означает порядок, что означает упрощение показателей степени или корней в выражении, если таковые имеются, перед арифметическими операциями. В некоторых странах буква «О» используется для обозначения «из», что опять-таки означает умножение.

Как применить правило Бодмаса?

Правило BODMAS можно применять в случае выражений, содержащих более одного оператора. В этом случае мы упрощаем скобки сначала от самой внутренней скобки до самой внешней [{()}], затем мы вычисляем значения показателей или корней, затем упрощаем умножение и деление, а затем, наконец, выполняем операции сложения и вычитания. при движении слева направо.

Почему в реальной жизни важен порядок действий?

Порядок операций — это сокращенное правило, позволяющее соблюдать правильный порядок при решении различных частей математического выражения. Универсальным правилом является выполнение всех математических операций для получения правильного ответа.

Когда правило Бодмаса неприменимо?

Правило BODMAS неприменимо к уравнениям. Он применим к математическим выражениям, имеющим более одного оператора.

Кто изобрел правило Бодмаса? Когда он был представлен?

Правило БОДМА было введено математиком Ахиллесом Реселфельтом в 1800-х годах.