Формула стерджесса в excel: Построение гистограмм в Excel_2014

Содержание

Построение гистограмм в Excel_2014

Построение гистограмм в Microsoft Excel

Перед построением гистограммы выполняется группировка данных по близким признакам. При группировании по количественному признаку все множество значений признака делится на

интервалы.

Для определения оптимального количества интервалов может быть использована формула Стерджесса:

n = 1 + (3,322× lgN)

где N — количество наблюдений. В этом случае величина интервала:

h = (Vmax — Vmin)/n

Поскольку количество групп не может быть дробным числом, то полученную по этой формуле величину округляют до целого большего числа.

Нижнюю границу первого интервала принимают равной минимальному значению xmin. Верхняя граница первого интервала соответствует значению (xmin + h). Для последующих групп

границы определяются аналогично, то есть последовательно прибавляется величина интервала h.

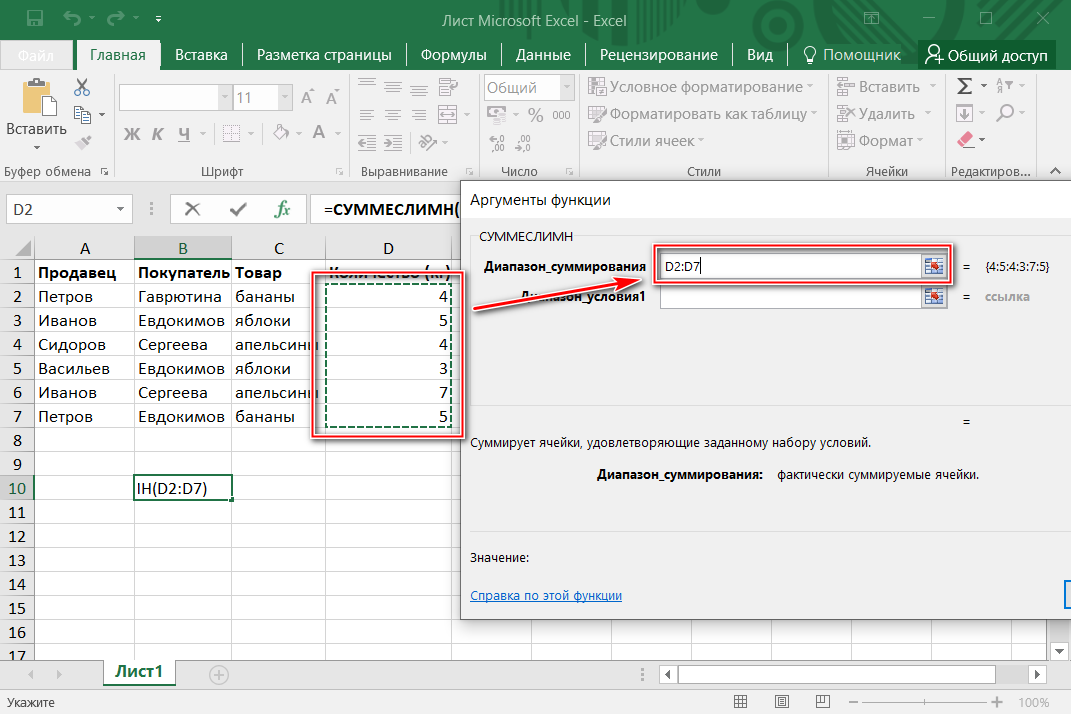
В Excel для построения гистограмм используются статистическая функция ЧАСТОТА в сочетании с мастером построения обычных диаграмм и процедура Гистограмма из пакета анализа.

Функция ЧАСТОТА (массив_данных, двоичный_массив) вычисляет частоты появления случайной величины в интервалах значений и выводит их как массив цифр, где

•Массив_данных —массив исходных данных, для которых вычисляются частоты;

•Массив_интервалов — это массив интервалов, по которым группируются значения выборки.

Перед вызовом функции ЧАСТОТА необходимо выделить столбец c числом ячеек, равным числу интервалов n, в который будут выведены результаты выполнения функции.

Вызвать Мастер функций (кнопка fx):

и функцию ЧАСТОТА.

В поле Массив_данных ввести диапазон данных наблюдений А3:А102 (с листа ‘Расчетные данные’). В поле Массив_интервалов ввести диапазон интервалов с того же листа ([‘Расчетные данные’!F16:F23] – в данном примере).

При завершении ввода данных нажать комбинацию клавиш Ctrl+Shift+Enter.

В предварительно выделенном столбце (C5:C12 – в данном примере) должен появиться массив

абсолютных частот.

Столбец Накопленные частоты получается последовательным суммированием относительных частот (в процентном формате) в направлении от первого интервала к последнему.

В завершении с помощью Мастера диаграмм строится диаграмма абсолютных и накопленных частот с выбором типа диаграммы соотвественно гистограмма и график.

Для автоматизированного построения гистограммы средствами Excel необходимо обратиться к меню «Сервис  Анализ данных». (Excel 2003) или на вкладке Данные выбрать Анализ данных

(Excel 2007…2010):

В появившемся списке выбрать инструмент Гистограмма и щелкнуть на кнопке ОК. Появится окно гистограммы, где задаются следующие параметры:

Входной интервал:– адреса ячеек, содержащие выборочные данные.

Интервал карманов: (необязательный параметр) – адреса ячеек, содержащие границы интервалов. Это поле предлагается оставить пустым, предоставив Excel самому вычислить границы интервалов (карманов – в терминах Excel).

Метки – флажок, включаемый, если первая строка во входных данных содержит заголовки. Если заголовки отсутствуют, то флажок следует выключить.

Выходной интервал: / Новый рабочий лист: / Новая рабочая книга.

Включенный переключатель Выходной интервал требует ввода адреса верхней ячейки, начиная с которой будут размещаться вычисленные относительные частоты j .

Вположении переключателя Новый рабочий лист: открывается новый лист, в котором начиная с ячейки А1 размещаются частности j .

Вположении переключателя Новая рабочая книга открывается новая книга, на первом листе которой начиная с ячейки А1 размещаются частности j .

Парето (отсортированная гистограмма) – устанавливается, чтобы представить j в порядке их убывания. Если параметр выключен, то j приводятся в порядке следования интервалов.

Интегральный процент – устанавливается в активное состояние для расчета выраженных в процентах накопленных относительных частот (аналог значений столбца Накопленные частоты).

Вывод графика – устанавливается в активное состояние для автоматического создания встроенной диаграммы на листе, содержащем частоты.

Замечание.

Как правило, гистограммы изображаются в виде смежных прямоугольных областей.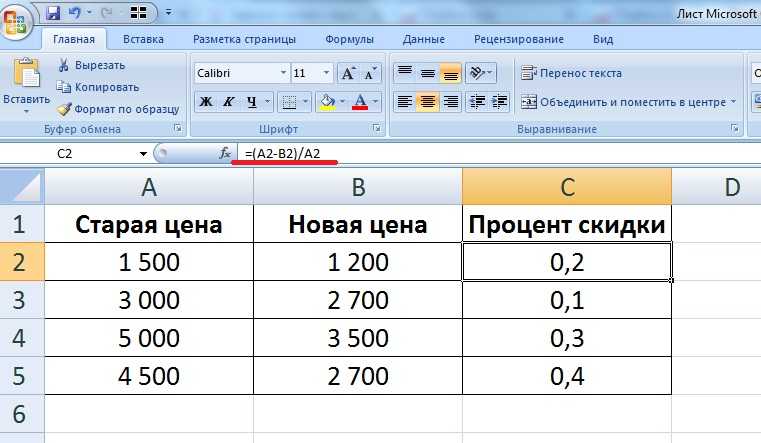 Поэтому столбики гистограммы следует расширить до соприкосновения друг с другом. Для этого необходимо щелкнуть мышью на диаграмме, далее на панель инструментов Диаграмма, раскрыть список инструментов и выбрать элемент Ряд ‘Частота’, после чего щелкнуть на кнопке Формат ряда. В появившемся одноименном диалоговом окне необходимо активизировать закладку Параметры и в поле Ширина зазора установить значение 0 ((Excel 2003):

В Excel 2007…2010 встать на любой столбик гистограммы и правой кнопкой мыши выбрать

Формат ряда данных:

Для построения теоретической кривой нормального распределения по эмпирическим данным необходимо найти теоретические частоты.

В Excel для вычисления значений нормального распределения используются функция НОРМРАСП, которая вычисляет значения вероятности нормальной функции распределения для указанного среднего и стандартного отклонения.

Функция имеет параметры:

НОРМРАСП (х; среднее; стандартное_откл; интегральная), где:

х — значения выборки, для которых строится распределение; среднее — среднее арифметическое выборки; стандартное_откл — стандартное отклонение распределения;

интегральный — логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности распределения.

Для получения абсолютных значений плотностей распределения (теоретических частот) достаточно найденные значения вероятности умножить на величину интервала h и количество наблюдений N = 100 по каждой строке.

Для завершения выполнения задания необходимо внести полученные значения теоретических частот на рисунок с гистограммой, добавив ряд в закладке Исходные данные и выбрав тип диаграммы

– график ((Excel 2003):

В Excel 2007…2010 находясь в обласи гистограммы по правой кнопке мыши выбрать Выбрать данные (или по одноименной кнопке на вкладке Конструктор):

и в появившемся окне провести манипуляции с вводом нового ряда «Теоретические частоты»:

Группировка данных в статистике. Формула Стерджесса

Провести группировку жителей поселка по доходу с равными интервалами и оптимальным числом групп и представить полученные данные в виде статистического ряда распределения и гистограммы. На основе гистограммы построить полигон, кумуляту и огиву распределения жителей поселка по доходу.

№	Дох.	№	Дох.
1	3820	13	6660
2	9470	14	5490
3	3490	15	5980
4	7790	16	6250
5	4210	17	8390
6	3870	18	3630
7	4490	19	6090
8	9620	20	10450
9	6200	21	6800
10	6350	22	6470
11	7430	23	9160
12	7670	24	5110

Определяем число групп по формуле Стерджесса:

n = 1 + 3,322lgN = 1 + 3,322lg24 = 5,6

принимаем n = 5

Определяем шаг интервала:

Xmax, Xmin- максимальное и минимальное значение
n – число групп

Произведем группировку с равными интервалами

Интервалы	Диапазон	частота, f	Накопленная частота, f
1	3490 — 4882	6	6
2	4882 – 6274	6	12
3	6274 – 7666	5	17
4	7666 – 9058	3	20
5	9058 — 10450	4	24

Гистограмма.

Полигон. Кумулята. Огива

Если Вас интересуют задачи по статистике заходите сюда.

Материалы сайта

Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.

Таблицы частот | Реальная статистика с использованием Excel

Основные понятия

Часто данные представляются в виде таблицы частот. Например, данные в диапазоне A4:A11 на рисунке 1 могут быть выражены таблицей частот в диапазоне C4:D7.

Рисунок 1 – Таблица частот

Таблица на рисунке 1 показывает, что элемент данных 2 встречается 4 раза, элемент 4 встречается 2 раза, а элементы 3 и 5 встречаются 1 раз.

Когда данные представлены в виде таблицы частот, расчет среднего значения и стандартного отклонения не может быть выполнен непосредственно с помощью обычных функций Excel СРЗНАЧ и СТАНДОТКЛОН. Пример данных { x ₁ , …, x _m } с соответствующими подсчетами частоты f ₁ , …, f _m соответственно и размером выборки n 1 f + = ₂ + … + f _m , исходя из определения выборочного среднего (см.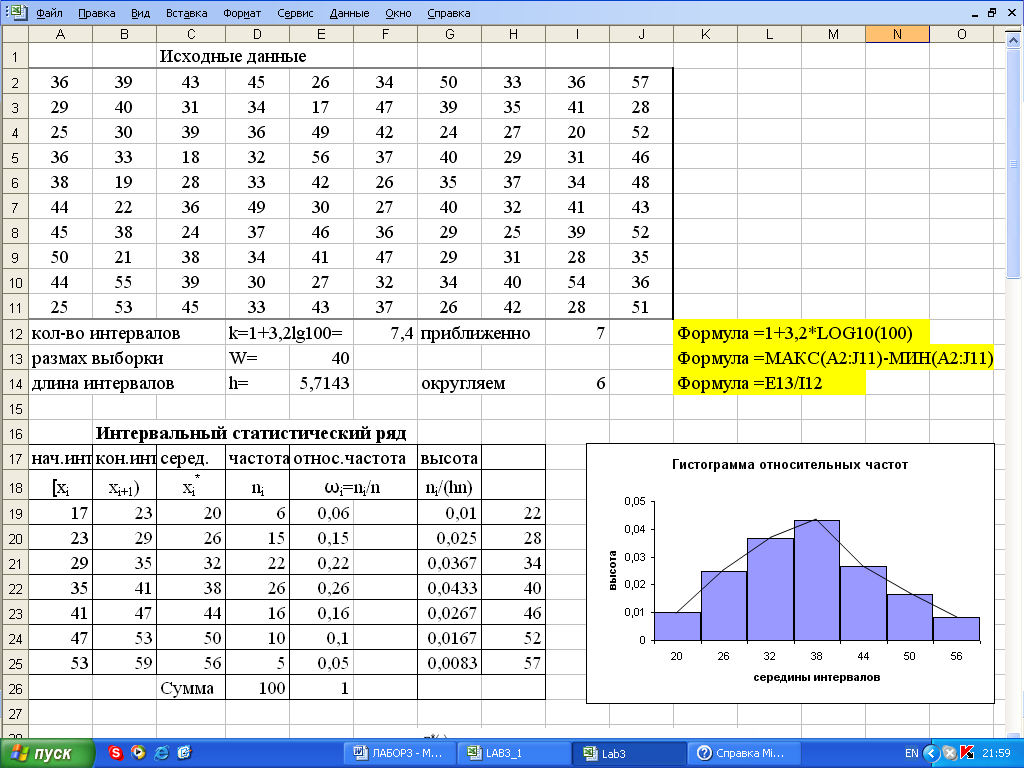 Показатели центральной тенденции), мы видим, что

Описательная статистика в Excel
=СУММПРОИЗВ(R1, R2) / СУММ(R2) 92)/(SUM(R2)-1)
Используя эти формулы, мы можем вычислить среднее значение и дисперсию выборочных данных, представленных в виде таблицы частот. Продемонстрируем это на следующем примере.
См. Описательная статистика для таблиц частот для получения информации о расчете дополнительной описательной статистики для данных, представленных таблицей частот.
Простой пример
Пример 1 : Рассчитайте среднее значение и дисперсию выборочных данных из таблицы частот на рисунке 1.
Рисунок 2. Расчет среднего значения и дисперсии из таблицы частот
На рисунке 2 показаны необходимые расчеты. Здесь ячейка F11 содержит формулу =D11/E11, которая вычисляет среднее значение. Ячейка G14 содержит формулу =(D14-E14*F14)/(E14-1), которая вычисляет дисперсию. Результаты будут такими же, как и при вычислении среднего значения и дисперсии по формулам СРЗНАЧ(A4:A11) и ДИСП.С(A4:A11) со ссылкой на ячейки на рис. 1.
Также обратите внимание, что таблица частот связаны с частотной функцией, как определено в Определении 1 дискретных распределений. Например. поскольку в наборе данных на рисунке 2 8 элементов, мы видим, что функция частоты для случайной величины x показано на рисунке 3, где каждое значение частоты делится на 8:
Рисунок 3 – Частотная функция, соответствующая таблице частот диапазон значений данных, то есть с интервалами для значений x . В этом случае средней точке каждого интервала присваивается значение x _i .
Пример 2 : Рассчитать среднее значение и дисперсию для данных в таблице частот на рисунке 4.
Рисунок 4 – Расчеты для таблицы частот с интервалами
Первый интервал на рисунке 4 0 < x ≤ 4, второй 4 < x ≤ 10 и т. д. На рисунке 2 показано, как вычислить среднее значение и дисперсию, за исключением того, что теперь в качестве значения используется средняя точка каждого интервала. В результате среднее значение равно 9,714 (ячейка S11), а дисперсия — 79,24 (ячейка T14).
Наблюдение : Иногда первый и/или последний интервал неограничен: например. предположим, что последний интервал на рис. 4 заменен на «более 20». В этом случае невозможно установить среднюю точку. В результате все, что вы можете сделать, это сделать наилучшую оценку подходящего репрезентативного значения для этого интервала.
Функция рабочего листа Excel
Функция Excel : Когда у вас много данных, удобно поместить данные в ячейки, обычно одинакового размера, а затем создать график количества элементов данных в каждой мусорное ведро Для этого в Excel предусмотрена функция массива FREQUENCY (R1, R2), где R1 = входной массив, а R2 = массив бинов.
Чтобы использовать функцию массива ЧАСТОТА, введите данные в рабочий лист, а затем введите массив бинов. Массив интервалов определяет интервалы, из которых состоят интервалы. Например, если массив бинов = 10, 20, 30, то есть 4 бина, а именно данные со значениями x ≤ 10, данные со значениями x , где 10 < x ≤ 20, данные со значениями x , где 20 < x ≤ 30, и, наконец, данные со значениями x > 30. Функция ЧАСТОТА просто возвращает массив, состоящий из количества элементов данных в каждом из бинов.
Пример использования функции ЧАСТОТА D8 не является частью массива бинов). 9Рисунок 5. Пример функции ЧАСТОТА (A4:B11,D4:D7)
Поскольку это формула массива, необходимо нажать Ctrl-Shft-Enter . Теперь Excel вставляет значения частоты в выделенный диапазон E4:E8. Здесь E4 содержит количество элементов данных во входном диапазоне со значением в первом бине (т. е. количество элементов данных, значение которых ≤ 20). Точно так же E5 содержит количество элементов данных во входном диапазоне со значением во втором бине (т. е. элементы данных, значение которых > 20 и ≤ 40). Последняя выходная ячейка (E8) содержит количество элементов данных во входном диапазоне, значение которых больше, чем значение последнего бина (т.е.> 80 для этого примера).
Функция реальной статистики
Как описано в разделе «Распределения дискретных вероятностей», пакет ресурсов «Реальная статистика» предоставляет функцию FREQTABLE . Эту функцию также можно использовать для создания таблицы частот с равноудаленными интервалами.
Функция реальной статистики : Реальный пакет ресурсов статистики предоставляет следующую функцию массива для создания таблицы частот0022 ) = функция массива, которая создает таблицу частот для данных в R1, предполагая, что бины одинакового размера имеют размер bsize , где bmax – максимальное значение размера бина
Чтобы использовать функцию, вы должны выделить массив с 3 столбцами и не менее k строк, где k = ( bmax – MIN(R1)) / bsize + 1. Вы можете выделить больше строк, чем вам нужно; любые дополнительные строки будут иметь значение #N/A.
Аргумент bmax является необязательным. Если этот параметр не указан, по умолчанию используется значение 9.0017 bmax = МАКС(R1). Если bmax не опущен, вы должны убедиться, что bmax ≥ MAX(R1): в противном случае некоторые данные будут потеряны.
Аргумент bsize также необязателен. Если опущено, то вместо создания таблицы частот, как описано здесь, используется таблица с ячейкой для каждого значения в R1. Аргумент bmax игнорируется. В результате получается таблица, аналогичная таблице, описанной в примере 3 дискретных распределений.
Пример использования функции FREQTABLE
Пример 4 : Создайте таблицу частот для 22 элементов данных в диапазоне A4:B14 на рисунке 5 на основе бинов размером 15.
Требуемую таблицу частот можно создать, используя формулу массива A4:B14,15)
, как показано в диапазоне M4:O11 на рисунке 6.
Рисунок 6 – Функция FREQTABLE с размером ячейки 15
Заголовки не выводятся функцией, а добавляются вручную. Обратите внимание, что выделены две дополнительные строки; любые дополнительные строки будут иметь значение #N/A.
Инструменты анализа данных
Вы также можете использовать инструмент анализа данных Real Statistics Histogram with Normal Curve Overlay для создания таблицы частот. См. Гистограммы для примера того, как использовать этот инструмент анализа данных.
Также см. Описательная статистика для таблиц частот для описания инструмента анализа данных Real Statistics, который выводит описательную статистику для данных, представленных таблицей частот.
Преобразование данных
См. Преобразование таблицы частот для описания того, как преобразовать данные в таблице частот в формат необработанных данных и наоборот.
Ссылка
Служба поддержки Майкрософт (2012) Функция ЧАСТОТА
text=Функция%20FREQUENCY%20%20вычисляет%20как,%20вводится%20как%20массив%20формулы%20.
Расчет частотного распределения в Excel
Частотное распределение
Частотное распределение представляет собой сводку того, как часто встречается каждое значение путем группировки значений вместе.
Например, у вас есть данные по разделам класса с количеством учащихся в каждом разделе.
Excel: частотное распределение
Существует несколько способов расчета частотного распределения (таблица) в Excel.
С СЧЁТ Функция
С ЧАСТОТА Функция
Расчет частотного распределения в Excel
1. Введите приведенные выше данные в ячейки B3:C15. В первой строке таблицы есть заголовки.

Те же данные, введенные на лист в Excel, выглядят следующим образом:
2. Выберите нужные интервалы класса
3. Создайте таблицу со столбцами — Интервалы класса, Нижний предел, Верхний предел и Частота.
Как рассчитать нижний и верхний пределы с помощью формулы Excel —
Предположим, столбец интервала класса начинается с ячейки E5 (исключая заголовок).
Нижний предел —
Введите следующую формулу в ячейку F5 и вставьте ее до последней строки таблицы.
=СРЕДН(E5,1,НАЙТИ(«-«,E5,1)-1)
Верхний предел —

Введите следующую формулу в ячейку G5 и вставьте ее до последней строки таблицы.
=MID(E5,FIND(«-«,E5,1)+1,2)

Частотное распределение с функцией СЧЁТЕСЛИМН —
Чтобы вычислить последний столбец приведенной выше таблицы, введите следующую формулу в ячейку H5 и вставьте его до последней строки таблицы
=COUNTIFS($C$4:$C$15,»>=»&F5,$C$4:$C$15,»<="&G5)
Частотное распределение с функцией FREQUENCY
Создайте таблицу со столбцами — Класс Интервалы, верхний предел и количество секций
Верхний предел можно рассчитать по приведенной ниже формуле в ячейке F5 —
— СРЕДН(E5,НАЙТИ(«-«,E5,1)+1,2)
Вставьте формулу вниз до ячейки F9. Убедитесь, что вы вводите двойной минус (—) перед функцией MID.
На следующем этапе выберите диапазон G5:G9 и введите ЧАСТОТА Функция
=FREQUENCY(C4:C15, F5:F9)

F5:F9 относится к ячейкам верхнего предела.
Нажмите CTRL SHIFT ENTER , чтобы отправить приведенную выше формулу FREQUENCY , поскольку это формула массива. Если он введен правильно, вы увидите формулу, заключенную в фигурные скобки { }
Гистограмма
Мы можем построить гистограмму, используя таблицу частот.
Шаги:
1. Выделите значения в интервалах классов столбце (столбец E) и частоте столбце ( столбец H) таблицы распределения частот. (удерживая нажатой клавишу Ctrl при выделении двух диапазонов)
2. Щелкните вкладку Вставка и выберите 2-D Clustered Column .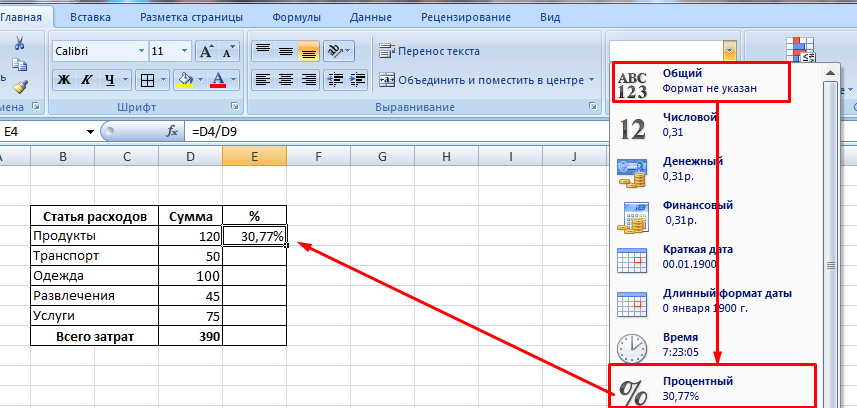
3. Удалить Series1 — Выберите Series1 и нажмите Delete

Добавление названия оси

1. Нажмите на график.
2. Перейдите на вкладку Layout под Chart Tools .
3. Нажмите Названия осей в группе Метки .
4. Выберите Заголовок основной горизонтальной оси , а затем выберите Заголовок под осью .
5. Выберите Заголовок основной вертикальной оси , а затем выберите Заголовок под осью .
Изменение масштаба оси
1. Выберите диаграмму.
2. Перейдите на вкладку Макет в разделе Инструменты для работы с диаграммами .
3. На Layout на вкладке ленты нажмите на кнопку Axes .
4. Выберите Основная вертикальная ось >> Выберите Дополнительные параметры вертикальной оси .
5.

No related posts.