Формула тригонометрии таблица: Таблица формул приведения тригонометрических функций

Содержание

Таблица формул приведения тригонометрических функций

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Формулы приведения в тригонометрии

Ниже представлена таблица с основными формулами приведения тригонометрических функций: синусов (sin), косинусов (cos), тангенсов (tg) и котангенсов (ctg).


Угол	-α	π/2-α	π/2+α	π-α	π+α	3π/2-α	3π/2+α	2π-α	2π+α
Функция	α°	90°-α	90°+α	180°-α	180°+α	270°-α	270°+α	360°-α	360°+α
sin α	-sin α	cos α	cos α	sin α	-sin α	-cos α	-cos α	-sin α	sin α
cos α	cos α	sin α	-sin α	-cos α	-cos α	-sin α	sin α	cos α	cos α
tg α	-tg α	ctg α	-ctg α	-tg α	tg α	ctg α	-ctg α	-tg α	tg α
ctg α	-ctg α	tg α	-tg α	-ctg α	ctg α	tg α	-tg α	-ctg α	ctg α

microexcel. ru

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Электронный справочник по математике для школьников тригонометрия формулы приведения таблица формул приведения

Справочник по математике

Тригонометрия

Содержание

Таблица формул приведения

Рассмотрим рисунок 1.

Рис.1

На этом рисунке

Следовательно, справедливы формулы:

(1)

откуда вытекают формулы:

(2)

Если же в формулах (1) и (2) сделать замену: α → – α, то, воспользовавшись свойствами четности тригонометрических функций, мы получим формулы:

(3)

Формулы (1), (2), (3) называют формулами приведения.

Таблица формул приведения

В целом формулы приведения удобно представить в виде следующей таблицы.

ТАБЛИЦА — ФОРМУЛЫ ПРИВЕДЕНИЯ

Аргумент	Формула приведения
Аргумент	синус	косинус	тангенс	котангенс
– α	– sin α	cos α
	cos α	sin α
	cos α	– sin α
π – α	sin α	– cos α
π + α	– sin α	– cos α
	– cos α	– sin α
	– cos α	sin α
2π – α	– sin α	cos α
2π + α	sin α	cos α

sin (– α) = – sin α;

cos (– α) = cos α;

sin (π – α) = sin α;

cos (π – α) = – cos α;

sin (π + α) = – sin α

cos (π + α) = – cos α

sin (2π – α) = – sin α

cos (2π – α) = cos α

sin (2π + α) = sin α

cos (2π + α) = cos α

Наверх

Демонстрационные варианты ЕГЭ и ОГЭ

С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.

Наши учебные пособия для школьников

При подготовке к ЕГЭ и к ОГЭ по математике Вам могут также пригодиться наши учебные пособия.

Решение рациональных неравенств
Задачи на проценты
Решение показательных неравенств
Квадратный трехчлен
Метод координат на плоскости
Решение иррациональных неравенств
Фигуры на координатной плоскости
Решение алгебраических уравнений
Уравнения и неравенства с модулями
Решение показательных уравнений
Арифметическая и геометрическая прогрессии
Решение логарифмических уравнений
Решение логарифмических неравенств
Системы уравнений
Решение тригонометрических уравнений
Тригонометрия в ЕГЭ по математике
Степень с рациональным показателем

Тригонометрия Формулы для функций, отношений и тождеств PDF

Тригонометрия — раздел математики, изучающий углы, длины и высоты треугольников и отношения между различными частями кругов и других геометрических фигур. Математические формулы — тригонометрические отношения и тождества очень полезны, и изучение приведенных ниже формул помогает лучше решать проблемы. Тригонометрические формулы необходимы для решения вопросов по тригонометрическим соотношениям и тождествам на конкурсных экзаменах.

Тригонометрические тождества — это равенства, включающие тригонометрические функции и истинные для каждого значения встречающихся переменных, где определены обе стороны равенства. Геометрически это тождества, включающие определенные функции одного или нескольких углов.

Тригонометрическое отношение соотношение между величиной углов и длиной стороны прямоугольного треугольника. Эти формулы связывают длины и площади определенных кругов или треугольников. На следующей странице вы найдете личности. Тождества не относятся к конкретным геометрическим фигурам, но справедливы для всех углов.

Формулы для дуг и секторов окружностей

Вы можете легко найти длину дуги и площадь сектора для угла θ в окружности радиусом r .

Длина дуги. Длина дуги равна радиусу r, умноженному на угол θ, где угол измеряется в радианах. Чтобы перевести градусы в радианы, умножьте количество градусов на π/180.

Дуга = rθ .

Тригонометрические формулы – прямой угол

Наиболее важными формулами для

тригонометрии являются формулы для прямоугольного треугольника. Если θ является одним из острых углов в треугольнике, то синус тета – это отношение противолежащего катета к гипотенузе, косинус – отношение прилежащего катета к гипотенузе, а тангенс – это отношение

Теорема Пифагора , известная геометрическая теорема о том, что сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы (сторона, противоположная прямому углу ) — или, в привычных алгебраических обозначениях, (P) ² + (B) ² = (H) ²

Применяя теорему Пифагора для данной прямоугольной теоремы, мы имеем: Гипотенуза) ²

^⇒ (P) ² + (B) ² = (H) ²

Тригонометичные свойства приведены ниже

Magical Hexagon для тригонометрии

Magical Hexagon для тригонометрии

Magical Hexagon для тригонометрии

.
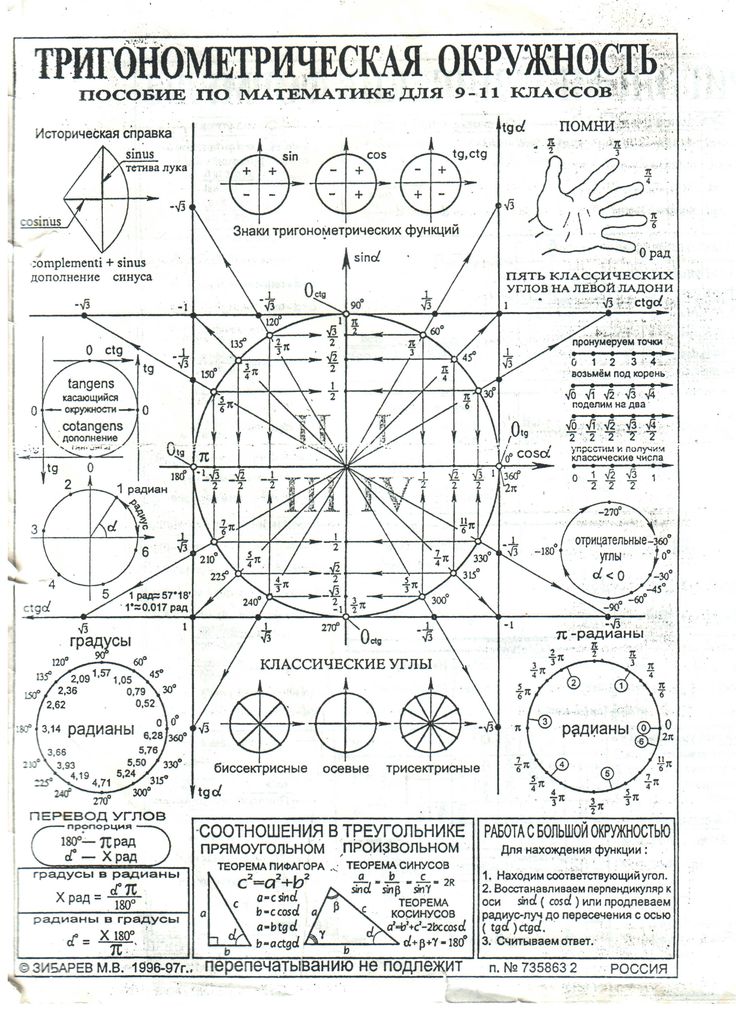
По часовой стрелке:
tan(x) = sin(x) / cos(x)
sin(x) = cos(x) / кроватка(x)
cos(x) = кроватка(x) / csc(x)
раскладушка(х) = csc(х) / сек(х)
csc(x) = сек(x) / tan(x)
сек(х) = тангенс(х) / грех(х)
Против часов:
cos(x) = sin(x) / tan(x)
sin(x) = tan(x) / sec(x)
тангенс(х) = сек(х) / csc(х)
сек(х) = csc(х) / раскладушка(х)
csc(x) = детская кроватка(x) / cos(x)
раскладушка(х) = cos(х) / sin(х)
Отношения взаимности
Тригонометрические формулы PDF
Формулы квадратного закона
Наряду со знанием того, что два острых угла дополняют друг друга, говорят, любой прямоугольный треугольник:
Если известны две из трех сторон, то можно найти третью сторону и оба острых угла.
Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.

Знаки тригонометрических отношений
Многие формулы тригонометрии основаны на знаках тригонометрических отношений, основанных на квадрантах, в которых они лежат. Поэтому для нас становится чрезвычайно важным понять, как тригонометрические отношения получают положительные или отрицательный знак
. Знак основан на квадранте, в котором лежит угол.
Предположим, что угол θ1 лежит в 1-м квадранте, а угол θ в первом и втором квадранте вместе взятые.
Итак, давайте посмотрим, как меняются знаки относительно квадранта, в котором они лежат.
В Q1 все тригонометрические отношения положительны. (Углы между 0 ⁰ – 90 ⁰ )
В Q2 все тригонометрические отношения sinθ и cosecθ положительны. (Углы между 90 ⁰ – 180 ⁰ )

В Q3 все тригонометрические отношения cosθ и secθ положительны. (Углы между 180 ⁰ – 270 ⁰ )
В Q4 все тригонометрические отношения tanθ и cotθ положительны. (Углы между 270 ⁰ – 360 ⁰ )
θ — угол между осью X и линией в направлении против часовой стрелки. Если мы будем двигаться по часовой стрелке, угол будет принят равным – θ. Мы знаем, что в квадранте 4 только cosθ и secθ будут положительными, остальные будут отрицательными, поэтому-
Sin (– θ) = – Sin θ
Cos (– θ) = Cos θ
Тан (– θ) = – Тан θ
Сек (– θ) = + Сек θ
Детская кроватка (– θ) = – Детская кроватка θ
Мы должны понимать, что тригонометрические соотношения изменятся для углов-
90 ^O ± θ и 270 ^O ± θ , и они останутся одинаковыми для 180 ^O ± θ и 3604888. ± θ. Давайте посмотрим, что произойдет, если мы добавим или вычтем θ из 90 ^o ± θ и 270 ^o ± θ
сек (90 ^o + θ ) = Cos θ
Детская кроватка (90 ^o – θ ) = Cos θ
Тан (90 ^o + θ ) = – Кот θ
Tan (90 ^o – θ ) = Cot θ
сек (90 ^o + θ ) = Cosec θ
сек (90 ^o + θ ) = Cosec θ
Sin (270 ^o – θ ) = – Cos θ
Sin (270 ^o – θ ) = – Cos θ

Это потому, что любой угол, равный 2700+θ, попадает в квадрант 4, а в этом квадранте только тригонометрические отношения cos
и sec положительны. Таким образом, вышесказанное будет отрицательным. 2700-θ попадет в квадрант 3, и в этом квадранте тригонометрические отношения tan и cot положительны, поэтому он снова будет отрицательным. Для 180 ^o ± θ и для 360 ^o ± θ знаки останутся прежними.
Sin (360 ^или + θ ) = Sin θ
Sin (360 ^o – θ ) = – Sin θ
Для 3600+θ угол совершит один полный оборот и затем окажется в квадранте 1, где все тригонометрические отношения положительны. Итак, нужно помнить 2 важные вещи:
Знак тригонометрических отношений меняется в зависимости от значения θ.
sin становится cos, а cos становится sin для 900 + θ и для 2700 + θ и остается таким же для 1800 + θ
и для 3600 + θ.
Тригонометрические формулы | Тригонометрические тождества
После рассмотрения тригонометрических соотношений давайте перейдем к тригонометрическим тождествам, которые являются основой большинства тригонометрических формул. Приведенные выше тождества верны для любого значения θ.
Идентификаторы продуктов:
Тригонометрические формулы | Сумма и разность углов
Тригонометрические формулы | Формулы двойного угла
Формулы тригонометрии | Формулы тройного угла
Формулы тригонометрии | Преобразование произведения в сумму и разность
Тригонометрические формулы | Значения тригонометрических отношений
Сводка тригонометрических тождеств
Периодичность и периодические тождества
Тождества половинного угла
Сложные соотношения
Inverse trigonometric functions
Complimentary angle
Negative arguments
Reciprocal arguments
Values of Trigonometric Functions
Trigonometry Table: Trigonometry Formula, Examples, Tips
Basic Формулы тригонометрии и таблица тригонометрии Мы обычно рассматриваем только прямоугольные треугольники для формул тригонометрии, но ее также можно использовать для обычных треугольников.
В прямоугольном треугольнике у нас есть три стороны, а именно – Прилежащая сторона, Гипотенуза и Противоположная сторона. Эти три стороны показаны в прямоугольном треугольнике, приведенном ниже.
AB = сторона, прилежащая к углу A
BC = сторона, противолежащая углу A
CA = гипотенуза к углу A
Сторона, противоположная углу, перпендикулярна,
Сторона, на которую опирается гипотенуза и противолежащая ей сторона, является основанием.
Прежде чем перейти к тригонометрической таблице, давайте познакомимся с основными формулами тригонометрии.
Эти формулы помогают найти связь между тригонометрическими отношениями и отношением соответствующих сторон прямоугольного треугольника.
Существует шесть тригонометрических соотношений или тригонометрических функций: –
синус (sin)
косинус (cos)
секанс (сек)
косеканс (косеканс)
тангенс (тангенс)
котангенс (котангенс)
Все тригонометрические функции относятся к сторонам прямоугольного треугольника, и мы можем найти их формулы, используя следующие соотношения.
sin θ = противолежащая сторона/гипотенуза
cos θ = Смежная сторона/гипотенуза
tan θ = Противоположная сторона/Смежная сторона
с θ = Гипотенуза/Смежная сторона
косек θ = гипотенуза/противоположная сторона
кроватка θ = соседняя/противоположная сторона

Чтобы запомнить эти формулы, есть небольшой прием.
« У некоторых людей вьющиеся каштановые волосы навсегда стали черными »
Эта фраза состоит из трех частей. Каждый алфавит первого слова представляет собой тригонометрическое тождество, а первый алфавит следующих двух слов описывает его формулу.
Подобно алфавиту «S» в «Some» указывает на функцию «sin». Теперь первый алфавит следующих двух слов описывает формулу греха. Алфавит «P» в «People» представляет «Перпендикуляр», а алфавит «H» в «Have» представляет «Гипотенузу».
Таким образом, мы можем запомнить, sin (некоторые) = Перпендикуляр (люди) / Гипотенуза (есть)
Точно так же
cos(кудрявый) = основание (коричневый) / гипотенуза (волосы)
tan(повернутый)= перпендикулярно( постоянно) / основа (черная)

Что такое тригонометрическая таблица?
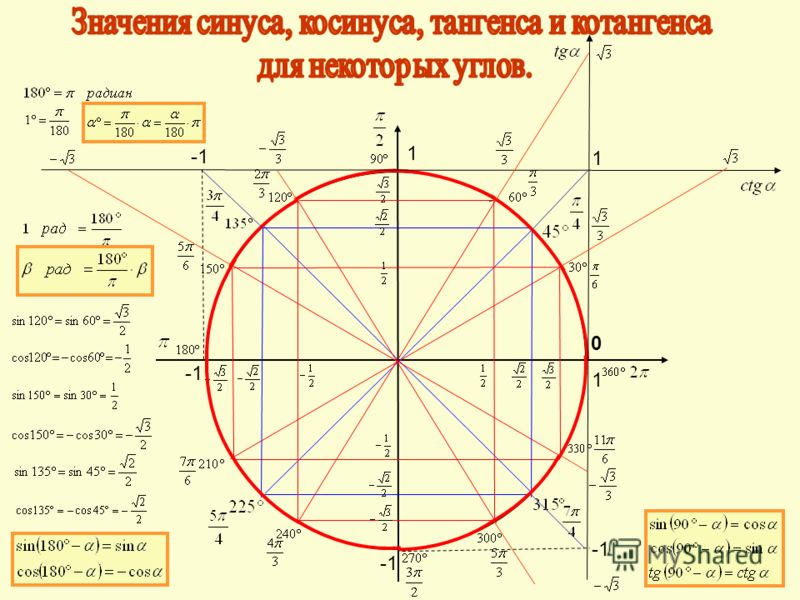
Таблица тригонометрии представляет собой табличное представление значений тригонометрических функций различных стандартных углов, включая 0°, 30°, 45°, 60°, 90°, 180°, 270° и 360°. Значения тригонометрических функций этих углов необходимы для решения задач тригонометрии.

Советы по запоминанию тригонометрической таблицы
Тригонометрическая таблица может показаться сложной для запоминания, но ее можно легко запомнить с помощью хитрости. Прежде чем раскрыть этот трюк, ниже приведены некоторые формулы, которые очень важно усвоить.
tan x = (sin x/cos x)
косек х = (1/sin х)
сек х = (1/cos х)
детская кроватка х = (1/загар х)
sin x = cos (90° – x)
cos x = sin (90° – х)
tan x = кроватка (90° – x)
кроватка x = коричневый (90° – x)
сек х = косек (90° – х)
косек х = сек (90° – х)
Теперь воспользуемся трюком, чтобы составить и запомнить тригонометрическую таблицу.
Создайте таблицу и укажите в верхней строке такие углы, как 0°, 30°, 45°, 60°, 90°, и запишите тригонометрическое отношение в первом столбце, например, sin (например).
Теперь определим значения sin. Напишите числа 0, 1, 2, 3, 4 под углами 0°, 30°, 45°, 60°, 90° соответственно.
Теперь разделите числа на 4 и найдите квадратный корень. Мы получим √(0/4), √(¼), √(2/4), √(¾) и √(4/4).
Упрощая это, мы получим значения синуса для этих 5 углов.
Теперь для оставшихся трех углов используйте следующие формулы:
sin (180° — x) = sin x
sin (180° + x) = -sin x
sin (360° — x) = -sin x
Это означает,
sin 180° = sin (180° − 0°) = sin 0° = 0
sin 270° = sin (180° + 90°) = -sin 90° = -1
Sin 360° = sin (360° − 0°) = -sin 0° = 0
Теперь определим значения cos по формуле cos x = sin (90° – x).
No related posts.