Уравнение сферы
Пусть сфера имеет радиус , а ее центр находится в точке . Точка лежит на сфере тогда и только тогда, когда модуль вектораравен, то есть. А последнее равенство выполнено тогда и только тогда, когда
(1)
Уравнение (1) и является искомым уравнением сферы.
Пусть плоскость проходит через точку перпендикулярно вектору .
Точка лежит на плоскости тогда и только тогда, когда векторы иперпендикулярны. Векторыиперпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю, то есть. Тогда уравнение плоскости записываем в виде
(2)
Рассмотрим пример. Найти уравнение плоскости, проходящей через середину отрезка АВ перпендикулярно этому отрезку если координаты точек соответственно равны А(1;6;9), В(5;4;7).
Будем
рассуждать следующим образом. Чтобы
найти уравнение плоскости мы должны
знать точку, через которую эта плоскость
проходит, и вектор перпендикулярный
этой плоскости. Вектором, перпендикулярным
данной плоскости, будет вектор
,
поскольку, по условию задачи, плоскость
перпендикулярна отрезку АВ.
Выясним вопрос, проходит ли эта плоскость через точку М(7;3;0).
Имеем , значит, эта плоскость не проходит через указанную точку.
Решим еще одну задачу. Найти уравнение плоскости, проходящей через точку , параллельно векторам.
Чтобы найти уравнение плоскости, мы должны знать точку и вектор, перпендикулярный этой плоскости. Точка у нас имеется, а вот вектора не хватает. Но мы имеем в качестве компенсации два параллельных вектора. Теперь давайте вспомним свойства векторного произведения векторов. А оно гласит, что векторное произведение двух векторов направлено перпендикулярно плоскости, в которой эти векторы расположены. Следовательно, в качестве перпендикулярного вектора может быть взято векторное произведение векторов. Имеем
.
Уравнение плоскости примет вид
Еще
один пример. Найти уравнение плоскости, проходящей
через точки
.
Как видим в наличии целых три точки и ни одного вектора. Но если вспомнить, что вектор, соединяющий две точки параллелен плоскости, в которой эти точки лежат, то задача сводится к предыдущей. Следовательно, плоскости параллельны вектор и вектор.
Тогда
.
Уравнение примет вид
Заметим, что нетрудно получить общую формулу уравнения плоскости, проходящей через три точки . Она получается из следующих соображений. Точка лежит в данной плоскости тогда и только тогда, когда векторы,
являются компланарными, а значит, их смешанное произведение равно нулю. Тогда получаем
или окончательно
. (3)
Общее уравнение плоскости
Определение. Общим уравнением поверхности первого порядка на плоскости называется уравнение вида , где.
Теорема. Всякая плоскость может быть задана в
виде уравнения поверхности первого
порядка, и всякое уравнение поверхности
первого порядка является уравнением
некоторой плоскости.
Первая часть этой теоремы доказывается просто. На всякой плоскости можно указать некоторую точку перпендикулярный ей вектор . Тогда, согласно (2), уравнение такойплоскости имеет вид . Обозначим. Тогда уравнение примет вид .
Теперь перейдем ко второй части теоремы. Пусть имеется уравнение , где. Будем считать для определенности.
Перепишем уравнение в виде;;.
Рассмотрим точку , где. Тогда полученное уравнение имеет вид , и является уравнениемплоскости, проходящей через точку перпендикулярно вектору .
Попутно мы доказали, что если имеется уравнение плоскости вида , то вектор перпендикулярен даннойплоскости.
Итак, уравнение вида называется общим уравнением плоскости в пространстве.
Далее выведем формулу вычисления расстояния от произвольной точки до плоскости, заданной общим уравнением.
Пусть
имеется плоскость
и точка.
Требуется определить расстояние от
указанной точки доплоскости.
Рассмотрим произвольную точку наплоскости. Имеем . Расстояниеот точкидоплоскости равно модулю проекции вектора на вектор , перпендикулярный данной плоскости.
Имеем
,
преобразуя, получаем:
.
Пусть даны две плоскости, заданные общими уравнениями
, . Тогда векторы перпендикулярны первой и второй прямой соответственно. Уголмежду прямыми равен углу между векторами. Тогда
.
Условие перпендикулярности плоскостей имеет вид:
.
Плоскости параллельны или совпадают тогда и только тогда, когда векторы колинеарны.
При этом условие совпадения плоскостей имеет вид: ,
а условие отсутствия пересечения записывается в виде: .
Последние два условия докажите самостоятельно.
Исследуем характер поведения плоскости по ее общему уравнению.
Пусть
дано общее уравнение плоскости
.
Если
,
топлоскость
проходит через начало координат.
Рассмотрим случай, когда ни один из коэффициентов не равен нулю . Уравнение перепишем в виде , ,
,
где. Выясним смысл параметров . Найдем точки пересечения плоскости с осями координат. Приимеем, а приимеем, при имеем.То есть- это отрезки, которые отсекает плоскость на координатных осях. Поэтому уравнение называется уравнением плоскости в отрезках.
В случае имеем,,,
где. То есть плоскость будет параллельна оси .
В случае имеем,,,
где. То есть плоскость будет параллельна оси .
В случае имеем,,,
где. То есть плоскость будет параллельна оси .
В случае имеем,,
где. То есть плоскость будет перпендикулярна оси .
В случае имеем,,
где. То есть плоскость будет перпендикулярна оси .
В случае имеем,,
где. То есть плоскость будет перпендикулярна оси .
Сфера. Уравнение сферы. Площадь сферы и шара
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Сфера . 11 класс.
2. ДЗ учить формулы ц+ к+ с+ ш № 582,584 циркуль доклады-2
Зачерпни воду,и луна окажется в твоей руке…
Китайская мудрость
ДЗ
учить формулы ц+ к+ с+ ш
№ 582,584
циркуль
доклады-2
Определение сферы!
Сферой называется поверхность, состоящая из всех
точек пространства, расположенных на данном
расстоянии (R) от данной точки (центра — точки О).
dО
R
т. О – центр сферы
R – радиус сферы – отрезок,
соединяющий любую точку
сферы с центром.
d – диаметр сферы – отрезок,
соединяющий любые 2 точки
сферы и проходящий через центр.

Уравнение
сферы !
R = (x–x0)2+(y–y0)2+(z–z0)2
CM
M(x;y;z)
I
I
z
I
I
I
C(x0;y0;z0)
I
I
I
y
x
R2
2+(y–y )2+(z–z )2
(x–x
)
=
0
0
0
Задача 1
Зная координаты центра С(0;-3;9) и радиус сферы
R=1,5, запишите уравнение сферы!
Решение:
Так как уравнение сферы с радиусом R и
центром в точке С(х0;у0;z0) имеет вид
(х-х0)2 + (у-у0)2 + (z-z0)2=R2, а координаты
центра данной сферы С(0;-7;1,3) и радиус
R=1,5, то уравнение данной сферы
x2 + (y+7)2 + (z-1,3)2=2,25
Ответ: x2 + (y+7)2 + (z-9)2=2,25
Уравнение сферы
Центр
r
C(1;-2;-5)
r=2
C(-5;3;0)
C(-1;0;0)
r=5
r= 8
C(0;-2;-8)
C(0;0;0)
r= 2
r=3
C(3; 2;0)
C(-7; 5;-1)
r = 0,3
r = 2,5
5
r= 2
C(0;-4;9)
Уравнение сферы
Центр
r
Найди ошибки:
(x–1)2+(y+2)2+(z+5)2 = 4
C(1;-2;-5)
r=2
(x+5)2+(y–3)2 + z2 = 25
(x +
— 1 )2 + y 2 + z 2 = 8
C(-1;0;0)
r=5
r= 8
x2 +(y+2)2 +(z+8)2 = 2
C(0;-2;-8)
C(0;0;0)
r= 2
r=3
x 2 + y 2 + z 2= 9
(x–3 )2+(y–2)2 + z 2 = 0,09
0,9
C(3; 2;0)
(x+7)2+(y–5)2 +(z+1)2 = 2,5 C(-7; 5;-1)
1
2
2
2
C(0;-4;9)
x +(y+4) + (z+4) = 6 4
r = 0,3
r = 2,5
5
r= 2
Площадь сферы и шара
Сферу нельзя развернуть на плоскость.

Площадь сферы радиуса R:
Sсф=4πR2
Sшара=4 Sкруга
т.е.: площадь поверхности шара
равна учетверенной площади
большего круга
Задача 2
Найти площадь поверхности сферы,
радиус которой равен 6 см.
Дано:
сфера
R = 6 см
Найти:
Sсф = !
Решение:
1. Sсф = 4πR2
2. Sсф = 4π 62 = 144π ( см2)
Ответ: 144π см2
Задача 3
Найти площадь поверхности шара, площадь
центрального сечения которого равна 6.
Найти площадь поверхности шара, площадь
центрального сечения которого равна 0,8.
Найти площадь поверхности шара, площадь
центрального сечения которого равна 30,5.
№ 4 Вершины треугольника АВС лежат на сфере радиуса 13
см. Найдите расстояние от центра сферы до плоскости
треугольника, если АВ=6см, ВС=8см, АС=10см.
102=82+62 ABC прямоуголь ный
А
С
O1
А
В
O
O1
В
С
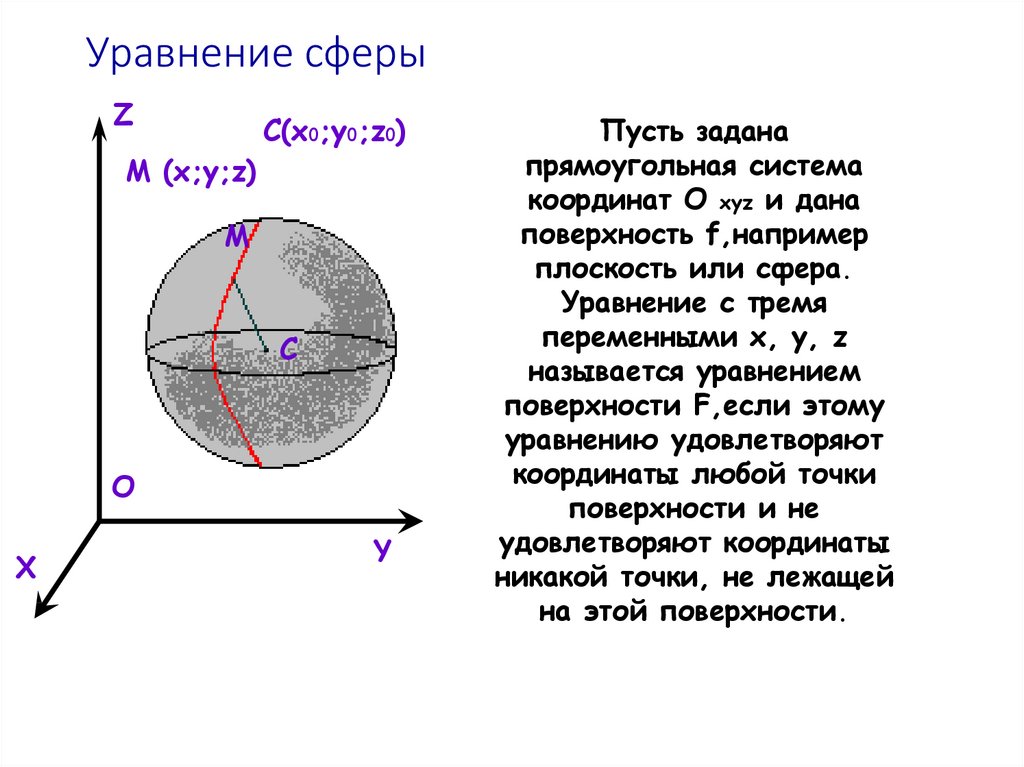
№ 5 Все стороны ромба, диагонали которого равны 15см и
20см, касаются сферы радиуса 10см. Найдите расстояние от
плоскости сферы до плоскости ромба.
D
F
M
K
C
O1
A
N
P
B
D
O
K
M
C
A
P
N
B
Итоги урока:
Сегодня мы вспомнили:
определение и уравнение сферы;
некоторые сведения из планиметрии;
Познакомились с :
сечениями сферы и шара;
площадью поверхности сферы и шара;
Применяли на практике знания и
оценивали свои действия.
Спасибо за работу!
Спасибо за работу!
English Русский Правила
Объяснение урока: Уравнение сферы
В этом объяснении мы узнаем, как найти уравнение сферы, зная ее центр, и как найти центр и радиус, зная уравнение сферы.
Начнем с определения сферы.
Определение: Сфера
Сфера — это геометрическое место всех точек (𝑥,𝑦,𝑧), находящихся на расстоянии 𝑟 от фиксированной точки (𝑎,𝑏,𝑐).
В этом определении 𝑟 — это радиус сферы, а фиксированная точка (𝑎, 𝑏, 𝑐) — это центр сферы. Теперь мы хотим использовать это определение, чтобы получить уравнение сферы в стандартной форме.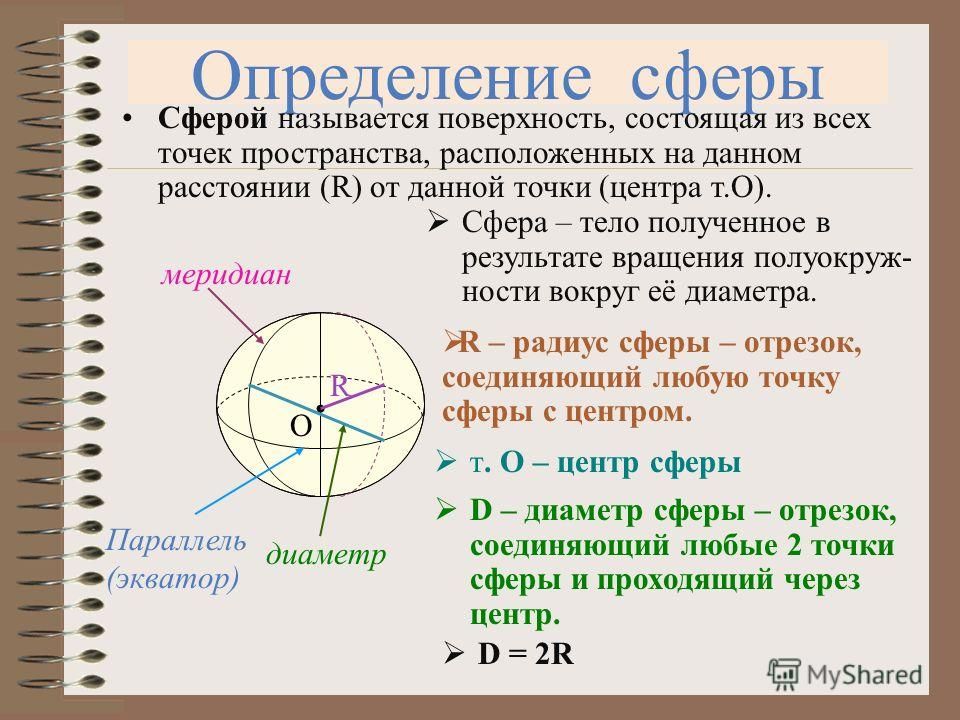
Во-первых, напомним, что мы можем вычислить расстояние между двумя точками (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) по формуле 𝑑=(𝑥−𝑥)+(𝑦− 𝑦)+(𝑧−𝑧).
В нашем определении сферы у нас есть набор точек (𝑥,𝑦,𝑧), которые находятся на фиксированном расстоянии 𝑟 от центра сфера (𝑎,𝑏,𝑐). Следовательно, подставляя в формулу расстояния, мы получаем, что 𝑟=(𝑥−𝑎)+(𝑦−𝑏)+(𝑧−𝑐),, которое является уравнением для сферы. Однако это не стандартная форма уравнения сферы. Если возвести в квадрат обе части уравнения, мы получим 𝑟=(𝑥−𝑎)+(𝑦−𝑏)+(𝑧−𝑐),, что является стандартной формой уравнения сферы с радиусом 𝑟 ( отметив, что 𝑟>0) и центр (𝑎,𝑏,𝑐).
Определение: уравнение сферы в стандартной форме
Декартово уравнение сферы с радиусом 𝑟 и центром (𝑎,𝑏,𝑐) в стандартной форме имеет вид (𝑥−𝑎)+(𝑦−𝑏)+ (𝑧−𝑐)=𝑟.
Это означает, что если мы знаем координаты центра сферы вместе с длиной ее радиуса или если мы можем вычислить эти две части информации, то мы можем найти уравнение сферы.
Имея это в виду, давайте посмотрим на нашу первую пару примеров.
Пример 1. Нахождение уравнения сферы с учетом ее центра и радиуса
Приведите уравнение сферы с центром (11,8,−5) и радиусом 3 в стандартной форме.
Ответ
Мы знаем, что стандартная форма уравнения сферы имеет вид (𝑥−𝑎)+(𝑦−𝑏)+(𝑧−𝑐)=𝑟,, где — центр, а 𝑟 — длина радиуса. Здесь нам даны координаты центра сферы, и, следовательно, мы можем сделать вывод, что 𝑎=11, 𝑏=8 и 𝑐=−5. Нам также говорят, что 𝑟=3. Подставляя эти значения, мы находим, что (𝑥−11)+(𝑦−8)+(𝑧+5)=3.
Наконец, вычисление правой части дает (𝑥−11)+(𝑦 −8)+(𝑧+5)=9.
Пример 2. Нахождение центра и радиуса сферы по ее уравнению
Учитывая, что уравнение сферы (𝑥+5)+(𝑦−12)+(𝑧−2)−289=0, определить его центр и радиус.
Ответ
Мы знаем, что стандартная форма уравнения сферы имеет вид (𝑥−𝑎)+(𝑦−𝑏)+(𝑧−𝑐)=𝑟,, где — центр, а 𝑟 — длина радиуса. Нам нужно преобразовать данное уравнение в эту форму. Во-первых, мы добавляем 289 к обеим частям уравнения, чтобы получить (𝑥+5)+(𝑦−12)+(𝑧−2)=289.
Во-первых, мы добавляем 289 к обеим частям уравнения, чтобы получить (𝑥+5)+(𝑦−12)+(𝑧−2)=289.
Затем мы перепишем выражение в первом наборе скобок, чтобы оно соответствовало уравнению стандартной формы, чтобы получить (𝑥−(−5))+(𝑦−12)+(𝑧−2)=289.
Наконец, заметив, что квадратный корень из 289 = 17, мы можем переписать наше уравнение еще раз, чтобы получить (𝑥−(−5))+(𝑦−12)+(𝑧−2)=17.
Отсюда мы можем определить, что центр сферы имеет координаты (−5,12,2) и что радиус равен 17.
Давайте теперь рассмотрим пример, где мы применяем то, что мы узнали о уравнение сферы для решения геометрической задачи.
Пример 3: Нахождение конечной точки диаметра сферы по другой конечной точке и уравнению сферы )+(𝑧−1)=38, в чем смысл 𝐵?
Ответ
Мы можем решить эту проблему двумя способами. Мы можем либо решить задачу геометрически, используя векторы, либо решить ее алгебраически, рассматривая относительные положения известных нам точек.
Сначала напомним стандартную форму уравнения сферы: (𝑥−𝑎)+(𝑦−𝑏)+(𝑧−𝑐)=𝑟,, где (𝑎,𝑏,𝑐) — центр а 𝑟 — длина радиуса. Используя это, мы можем видеть, что центр нашей сферы имеет координаты (-2,-1,1), и мы можем сделать быстрый набросок сферы, чтобы помочь нам визуализировать проблему.
Заметим, что точки 𝐴, 𝐶 и 𝐵 лежат на одной прямой, и поскольку 𝐴𝐵 — это диаметр сферы, мы знаем, что 𝐶 — это середина 𝐴𝐵.
Метод 1
Сначала рассмотрим, как решить задачу алгебраически. Поскольку 𝐴 и 𝐵 — конечные точки диаметра сферы, а 𝐶 — центр, мы знаем, что 𝐶 является серединой 𝐴𝐵. Для линии в трехмерном пространстве середина 𝐶, отрезка с концами 𝐴(𝑥,𝑦,𝑧) и 𝐵(𝑥,𝑦,𝑧) можно вычислить по формуле 𝐶=𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2.
Затем мы можем вывести, что 0+𝑥2,4+𝑦2,4+𝑧2=(−2,−1,1).
Это дает нам три уравнения: 𝑥2=−2,4+𝑦2 =−1,4+𝑧2=1.
Решая их, мы получаем 𝑥=−4, 𝑦=−6 и 𝑧=−2. Следовательно, координаты 𝐵 равны (−4,−6,−2).
Метод 2
Для интереса, если мы хотим решить задачу геометрически, используя векторы, мы можем сделать вывод, что 𝐴𝐶=𝐶𝐵; поэтому, учитывая, что точка 𝑂 является относительным центром системы, мы имеем, что 𝑂𝐵=𝑂𝐶+𝐴𝐶.
У нас есть 𝑂𝐶=(−2,−1,1) и 𝐴𝐶=𝑂𝐶−𝑂𝐴. Следовательно, 𝐴𝐶=(−2,−1,1)−(0,4,4), что упрощается до (−2,−5,−3).
Теперь мы можем вычислить 𝑂𝐵 следующим образом: 𝑂𝐵=(−2,−1,1)+(−2,−5,−3), что упрощается до (−4,−6,−2).
Следовательно, координаты 𝐵 равны (−4,−6,−2).
Прежде чем мы рассмотрим наш последний пример, давайте вспомним, как составить квадрат для квадратного выражения.
Как дополнить квадрат квадратного выражения
Рассмотрим выражение 𝑎𝑥+𝑏𝑥+𝑐.
Чтобы завершить квадрат, мы начинаем с факторизации 𝑎: 𝑎𝑥+𝑏𝑎𝑥+𝑐𝑎.
Теперь рассмотрим выражение 𝑎𝑥+𝑏2𝑎. Если мы расширим квадрат бинома, мы обнаружим, что 𝑎𝑥+𝑏2𝑎=𝑎𝑥+𝑏𝑎𝑥+𝑏(2𝑎),, которое, как мы отмечаем, совпадает с выражением выше, за исключением постоянного члена .
Следовательно, мы можем переписать исходное выражение следующим образом: 𝑎𝑥+𝑏2𝑎−𝑏(2𝑎)+𝑐𝑎. 𝑐.
Это форма нашего исходного выражения после завершения квадрата.
Мы можем использовать описанный выше метод, чтобы преобразовать общую форму уравнения сферы в стандартную форму. Если мы рассмотрим сферу, общее уравнение которой имеет вид 𝑥+𝑦+𝑧−2𝑎𝑥−2𝑏𝑦−2𝑐𝑧+𝑑=0,, то мы можем преобразовать это в стандартную форму, заполнив квадраты для квадратичных уравнений в каждой из трех переменных. Если мы начнем с перестановки уравнения, чтобы сгруппировать все члены, содержащие одни и те же переменные, мы получим0003
Теперь мы можем заполнить квадрат для каждой из трех квадратичных величин, чтобы получить (𝑥−𝑎)−𝑎+(𝑦−𝑏)−𝑏+(𝑧−𝑐)−𝑐+𝑑=0.
Наконец, если мы сгруппируем постоянные члены, мы увидим, что 𝑟=𝑎+𝑏+𝑐−𝑑, и центр сферы имеет координаты (𝑎,𝑏,𝑐).
Чтобы закончить, давайте рассмотрим пример, где нам нужно определить центр и радиус сферы, уравнение которой дано в общем виде.
Пример 4. Определение центра и радиуса сферы по ее уравнению в общей форме
Задайте центр и радиус сферы 𝑥+𝑦+𝑧−8𝑥+8𝑦+10𝑧+8=0.
Ответ
Здесь нам дана общая форма уравнения сферы, но нам нужно будет сравнить это уравнение со стандартной формой уравнения сферы, чтобы определить ее центр и радиус. Напомним, что стандартная форма уравнения сферы имеет вид (𝑥−𝑎)+(𝑦−𝑏)+(𝑧−𝑐)=𝑟,, где (𝑎,𝑏,𝑐) — центр, а 𝑟 — длина радиуса.
Сначала сгруппируем термы, содержащие одни и те же переменные: 𝑥−8𝑥+𝑦+8𝑦+𝑧+10𝑧+8=0.
Теперь нам нужно заполнить квадрат для квадратичных чисел в каждой из трех переменных, что даст нам (𝑥−4)−16+(𝑦+4)−16+(𝑧+5)−25+8=0.
Сбор постоянных членов дает (𝑥−4)+(𝑦+4)+(𝑧+5)−49=0,, а добавление 49 к каждой стороне дает нам (𝑥−4)+( 𝑦+4)+(𝑧+5)=49.
Наконец, если мы сравним это со стандартной формой уравнения сферы, мы увидим, что центр сферы равен (4,−4 ,−5), а радиус сферы равен √49=7.
Ключевые точки
- Сфера — это трехмерная фигура, каждая точка которой находится на расстоянии 𝑟 (радиус сферы) от центра.

- Сфера с центром в точке (𝑎,𝑏,𝑐) и радиусом 𝑟 имеет уравнение (в стандартной форме) (𝑥−𝑎)+(𝑦−𝑏)+(𝑧−𝑐)=𝑟. Если нам дано уравнение сферы не в стандартной форме, мы можем преобразовать его к этой форме алгебраическими методами и определить центр и радиус, сравнив полученное уравнение с общей формой.
- Чтобы определить центр и радиус сферы, уравнение которой дано в общей форме, мы можем преобразовать уравнение в стандартную форму, заполнив квадрат для каждой квадратичной функции в каждой из трех переменных.
Уравнение сферы
шара. Подобно кругу в двумерном пространстве, сферу можно математически определить как набор всех точек, находящихся на одинаковом расстоянии от данной точки. Эта заданная точка называется центром сферы. Расстояние между центром и любой точкой на поверхности сферы называется радиусом, обозначаемым буквой r.
Предположим, что на противоположных сторонах сферы есть две точки A и B. Если мы проведем линию, соединяющую эти две точки, проходящую через центр, то максимальное расстояние, измеренное ею, будет называться диаметром сферы, обозначаемой d.
Если мы проведем линию, соединяющую эти две точки, проходящую через центр, то максимальное расстояние, измеренное ею, будет называться диаметром сферы, обозначаемой d.
На приведенном ниже рисунке r — это радиус, а d — диаметр.
Диаметр делит сферу на две равные половины, известные как полусферы. Это очень похоже на разрезание мяча пополам. Общее уравнение сферы: x2 + y2 + z2 = r2 , и в этой статье мы узнаем о выводе уравнения сферы вместе с ее объемом и площадью поверхности.
Вывод уравнения сферы
Для окружности, центр которой лежит в начале координат (0,0), уравнение имеет вид:
x2 + y2 = r2
На приведенном выше рисунке точка, координаты которой представлены (x,y), лежит на окружности окружности. Фигура, отмеченная синим цветом, на самом деле представляет собой прямоугольный треугольник, основание и перпендикуляр которого обозначены x и y соответственно, а радиус r является гипотенузой.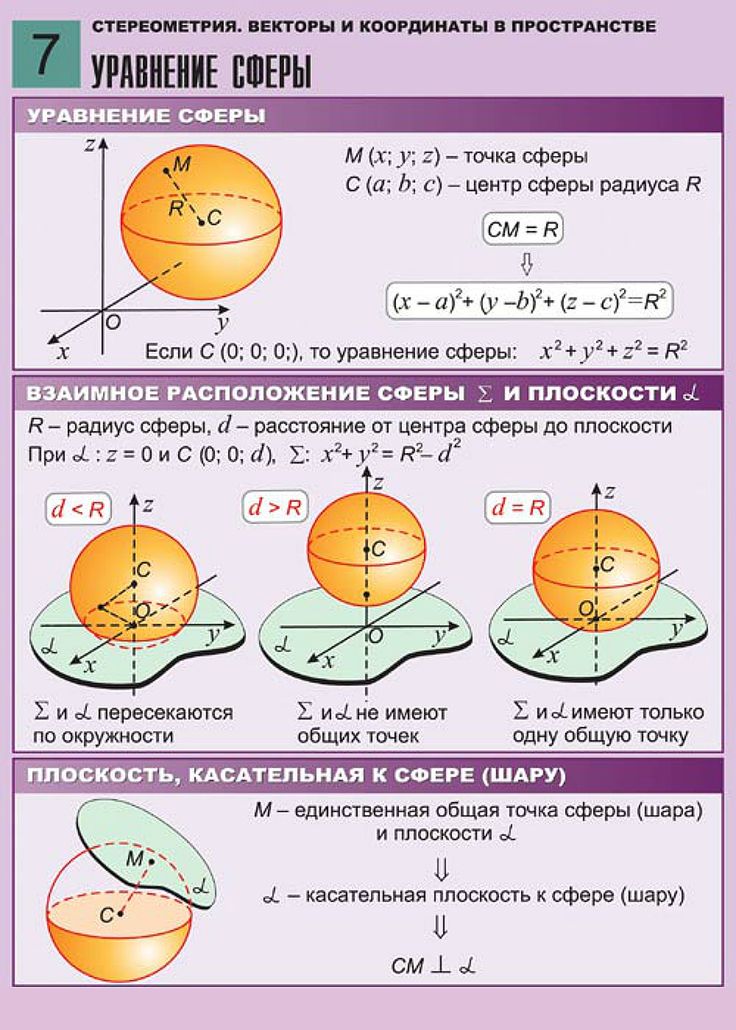
Применяя здесь теорему Пифагора, получаем
x2 + y2 = r2
k), то уравнение окружности принимает вид:
(x-h)2 + (y-k)2 = r2
Чтобы получить уравнение сферы, нужно дважды применить теорему Пифагора.
На приведенном выше рисунке P — это точка, координаты которой представлены (x, y, z).
MON – это прямоугольный треугольник, катетами которого являются x и y, а t – гипотенуза.
x2 + y2 = t2 ——- Ур. 1
PON также является прямоугольным треугольником, катетами которого являются t и z, а r — гипотенуза.
t2 + z2 = r2 ——- Ур. 2
Теперь, если мы подставим значение t2 во второе уравнение из первого уравнения, мы получим,
x2 + y2 + z2 = r2
Это называется уравнением сферы, также известным как общее уравнение сферы или уравнение сферы через окружность.
Здесь расстояние между точками O и P является радиусом, поэтому r в приведенном выше уравнении также можно записать как OP.
Тогда уравнение станет таким:
x2 + y2 + z2 = OP2
Это общее уравнение сферы останется в силе, только если мы возьмем начало координат в качестве центра сферы. Если в качестве центра сферы взять любую случайную точку (a,b,c) в трехмерном пространстве, уравнение сферы запишется так:
(x-a)2 + (y-b)2 + (z-c )2 = r2
Объем сферы:
Объем любой фигуры определяется как количество занимаемого ею трехмерного пространства.
Формула для расчета объема сферы:
V= 4/3πr3
, где r — радиус сферы.
Площадь поверхности сферы:
Площадь поверхности твердого объекта — это мера общей площади, которую занимает поверхность объекта.
Формула для расчета площади поверхности сферы:
A= 4πr2
, где r — радиус сферы.
Решенные примеры
Пример 1
Каким будет уравнение сферы, проходящей через окружность в стандартной форме, центр и радиус которой равны (-1,-2,3) и 4 см соответственно?
Решение:
Дано: Center- (-1,-2,3)
Это значения a,b,c соответственно.
Радиус = 4 см
Как мы узнали выше, общее уравнение сферы в стандартной форме имеет вид
(x-a)2 + (y-b)2 + (z-c)2 = r2
Теперь, подставляя значения x,y,z и r на -1,-2 и 3 и 4 соответственно, получаем
(x-(-1))2 + (y-(-2))2 + (z-3)2 = 42
(x+1)2 + (y+2)2 + (z-3)2 = 16
Пример 2
Диаметр сферы имеет концы в точках (4, 1,2) и (10,3,4). {2}}\] (10−4)2 +(3−1)2+(4−2)2 9{2}}\]
{2}}\] (10−4)2 +(3−1)2+(4−2)2 9{2}}\]
=\[\sqrt{44}\] 44
Таким образом, радиус = 1/2 \[\sqrt{44}\] 44
=\[\sqrt{11}\] 11
Следовательно, координаты центра будут ((10+4)/2, (3+1)/2, (4+2)/2) т.е. (7,2,3)
Следовательно, уравнение принимает вид (x-7)2 + (y-2)2 + (z-3)2 = 11
Знаете ли вы?
Кратчайшее возможное расстояние между любыми двумя точками на сфере называется геодезической.
Большой круг, также известный как ортодромия, является важным понятием, связанным со сферой. Это окружность на поверхности сферы, которая лежит в плоскости, проходящей через центр сферы. Малая дуга большого круга между двумя точками является кратчайшим поверхностным путем между ними.
Забавный факт:
Эта концепция используется для определения кратчайшего маршрута, по которому может двигаться самолет или корабль.
Архимед обнаружил, что площадь поверхности сферы равна площади боковой поверхности цилиндра с радиусом основания, равным радиусу сферы, и высотой, равной диаметру сферы, вычислив площадь поверхности сферы формула.
Важные элементы сферы
Радиус: расстояние между центром сферы и любой точкой на ее поверхности, измеренное в линейных отрезках. Если «О» — это центр сферы, а А — любая точка на ее поверхности, то ОА — это радиус сферы.
Диаметр: Диаметр сферы определяется как длина отрезка, проходящего через центр сферы от одной точки поверхности до противоположной точки. Диаметр сферы равен половине длины радиуса сферы.
Окружность: Окружность сферы — это расстояние или длина вокруг границы или внешней поверхности сферы.

Объем: Сфера занимает пространство так же, как и любой другой трехмерный объект. Объем сферы – это количество места, которое она занимает. Для его выражения используются кубические единицы.
Площадь поверхности: Площадь поверхности сферы — это площадь, занимаемая ее поверхностью. Он основан на квадратных единицах измерения.
Свойства сферы
Сфера представляет собой трехмерный объект, все точки внешней поверхности которого равноудалены от центра. Следующие сферические особенности упрощают распознавание сферы:
Сфера симметрична во всех направлениях.
Сфера имеет только изогнутую поверхность.
Все точки поверхности сферы находятся на одинаковом расстоянии от центра.




