Формула включений исключений: Формула включений-исключений — Википедия

Формула включений-исключений — это… Что такое Формула включений-исключений?

Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом.

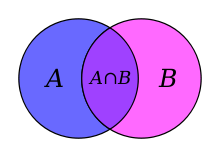Случай двух множеств

Например, в случае двух множеств формула включений-исключений имеет вид:

В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.

Таким же образом и в случае множеств процесс нахождения количества элементов объединения состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.

Впервые формулу включений-исключений опубликовал португальский математик Даниэль да Сильва (

англ.) в 1854 году ^[1]. Но еще в 1713 году Николай Бернулли (англ.) использовал этот метод для решения задачи Монмора (англ.), известной как задача о встречах (фр. «Le problème des rencontres»)^[2], частным случаем которой является задача о беспорядках. Также формулу включений-исключений связывают с именами французского математика Абрахама де Муавра^{[источник не указан 1272 дня]} и английского математика Джозефа Сильвестра ^[3]. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре^[1].

Формулировка

Формулу включений-исключений можно сформулировать в разных формах.

В терминах множеств

Пусть — конечные множества. Формула включений-исключений утверждает:

При получаем формулу для двух множеств, приведенную выше.

В терминах свойств

Принцип включений-исключений часто приводят в следующей альтернативной формулировке

[4]. Пусть дано конечное множество , состоящее из элементов, и пусть имеется набор свойств . Каждый элемент множества может обладать или не обладать любым из этих свойств. Обозначим через количество элементов, обладающих свойствами (и, может быть, некоторыми другими). Также через обозначим количество элементов, не обладающих ни одним из свойств . Тогда имеет место формула:

Формулировка принципа включений-исключений в терминах множеств эквивалентна формулировке в терминах свойств. Действительно, если множества являются подмножествами некоторого множества , то в силу правил де Моргана (черта над множеством — дополнение в множестве ), и формулу включений-исключений можно переписать так:

Если теперь вместо «элемент принадлежит множеству » говорить «элемент обладает свойством », то мы получим формулировку принципа включений-исключений в терминах свойств, и наоборот.

Обозначим через количество элементов, обладающих

в точности свойствами из набора .Тогда формулу включений-исключений можно переписать в следующей замкнутой форме (англ.)

Доказательство

Существует несколько доказательств формулы включений-исключений.

По индукции

Формулу включений-исключений можно доказать по индукции ^{[1] [5]}.

При формула включений-исключений тривиальна:

Пусть формула верна для , докажем ее для .

Пусть каждый элемент множества может обладать или не обладать любым из свойств . Применим формулу включений-исключений для свойств :

Теперь применим формулу для свойств к множеству объектов, для которых выполнено свойство :

Наконец, применим формулу для одного свойства к совокупности , объектов, которые не обладают свойствами :

Комбинируя выписанные три формулы, получим формулу включений-исключений для свойств . Что и требовалось доказать.

Комбинаторное доказательство

Рассмотрим произвольный элемент и подсчитаем, сколько раз он учитывается в правой части формулы включений-исключений^[4].

Если элемент не обладает ни одним из свойств , то в правой части формулы он учитывается ровно 1 раз (в члене ).

Пусть элемент обладает в точности свойствами, скажем . Он дает по 1 в тех слагаемых суммы , для которых есть подмножество , и 0 для остальных. Число таких подмножеств по определению есть число сочетаний . Следовательно, вклад элемента в правую часть равен

При числа сочетаний равны нулю. Оставшаяся сумма в силу биномиальной теоремы равна

Таким образом, правая часть формулы включений-исключений учитывает каждый элемент, не имеющий указанных свойств точно по одному разу, а каждый элемент, обладающий хотя бы одним из свойств — нуль раз. Следовательно, она равна количеству элементов, не обладающих ни одним из свойств , то есть . Что и требовалось доказать.

Используя индикаторные функции

Пусть — произвольные

(не обязательно конечные) множества, являющиеся подмножествами некоторого множества , и пусть — индикаторные функции (или, эквивалентно, свойств ).

Индикаторные функции их дополнений равны

а индикаторная функция пересечения дополнений:

Раскрывая скобки в правой части и еще раз используя тот факт, что индикаторная функция пересечения множеств равна произведению их индикаторных функций, получим

Это соотношение — одна из форм принципа включений-исключений. Оно выражает собой логическое тождество^[1] и верно для произвольных множеств . В случае конечных множеств (и, соответственно, в предположении конечности множества ), просуммировав это соотношение по всем и воспользоваться тем, что для произвольного подмножества его мощность равна

получим формулировку принципа включений-исключений в терминах мощностей множеств (или в терминах свойств).

Применение

Задача о беспорядках

Основная статья:

Задача о беспорядках

Классический пример использования формулы включений-исключений — задача о беспорядках ^[4]. Требуется найти число перестановок множества таких что для всех . Такие перестановки называются беспорядками.

Пусть — множество всех перестановок и пусть свойство перестановки выражается равенством . Тогда число беспорядков есть . Легко видеть, что — число перестановок, оставляющих на месте элементы , и таким образом сумма содержит одинаковых слагаемых. Формула включений-исключений дает выражение для числа беспорядков:

Это соотношение можно преобразовать к виду

Нетрудно видеть, что выражение в скобках является частичной суммой ряда . Таким образом, с хорошей точностью число беспорядков составляет долю от общего числа перестановок:

Вычисление функции Эйлера

Другой пример применения формулы включений-исключений — нахождение явного выражения для функции Эйлера ^[6].

Для целого положительного функция Эйлера дает количество чисел ряда , взаимно простых с . Найдем явное выражение для функции Эйлера.

Пусть каноническое разложение числа на простые множители имеет вид

Число взаимно просто с тогда и только тогда, когда ни один из простых делителей не делит . Если теперь свойство означает, что делит , то количество чисел взаимно простых с есть .

Количество чисел, обладающих свойствами равно , поскольку .

По формуле включений-исключений находим

Эта формула преобразуется к виду:

Вариации и обобщения

Принцип включения-исключения для вероятностей

Пусть — вероятностное пространство. Тогда для произвольных событий справедлива формула ^{[1] [5] [7]}

Эта формула выражает принцип включений-исключений для вероятностей. Ее можно получить из принципа включений-исключений в форме индикаторных функций:

Пусть — события вероятностного пространства , то есть . Возьмем математическое ожидание от обеих частей этого соотношения, и, воспользовавших линейностью математического ожидания и равенством для произвольного события , получим формулу включения-исключения для вероятностей.

Принцип включений-исключений в пространствах с мерой

Пусть — пространство с мерой. Тогда для произвольных измеримых множеств конечной меры имеет место формула включений-исключений:

Очевидно, принцип включений-исключений для вероятностей и для мощностей конечных множеств являются частными случаями этой формулы. В первом случае мерой является, естественно, вероятностная мера в соответствующем вероятностном пространстве: . Во втором случае в качестве меры берется мощность множества: .

Вывести принцип включений-исключений для пространств с мерой можно также, как для указанных частных случаев, из тождества для индикаторных функций:

Пусть — измеримые множества пространства , то есть . Проинтегрируем обе части этого равенства по мере , воспользуемся линейностью интеграла и соотношением , и получим формулу включений-исключений для меры.

Тождество максимумов и минимумов

Формула включений-исключений может рассматриваться как частный случай тождества максимумов и минимумов:

Это соотношение справедливо для произвольных чисел . В частном случае, когда мы получаем одну из форм принципа включений-исключений. В самом деле, если положить , где — произвольный элемент из , то получим соотношение для индикаторных функций множеств:

Обращение Мёбиуса

Пусть — конечное множество, и пусть — произвольная функция, определенная на совокупности подмножеств и принимающая действительные значения. Определим функцию следующим соотношением:

Тогда имеет место следующая формула обращения^{[8] [9]}:

Это утверждение является частным случаем общей формулы обращения Мёбиуса для алгебры инцидентности (англ.) совокупности всех подмножеств множества , частично упорядоченных по отношению включения .

Покажем, как из этой формулы следует принцип включения-исключения для конечных множеств. Пусть дано семейство подмножеств конечного множества , обозначим — множество индексов. Для каждого набора индексов определим как число элементов, входящих

только в те множества , для которых . Математически это можно записать так:

Тогда функция , определенная формулой

дает количество элементов, каждый из которых входит во все множества , , и, быть может, еще в другие. То есть

Заметим далее, что — количество элементов, не обладающих ни одним из свойств:

С учетом сделанных замечаний запишем формулу обращения Мёбиуса:

Это есть в точности формула включений-исключений для конечных множеств, только в ней не сгруппированы слагаемые, относящиеся к одинаковым значениям .

См. также

Примечания

1. ↑ ^{1 2 3 4 5} Риордан Дж. Введение в комбинаторный анализ = An Introduction to Combinatorial Analysis. — М.: Изд-во иностранной литературы, 1963. — С. 63-66. — 289 с.
2. ↑ Weisstein, Eric W. Derangement (англ.) на сайте Wolfram MathWorld.
3. ↑ Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 264. — 309 с.
4. ↑ ^{1 2 3} Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 18-20. — 424 с.
5. ↑ ^{1 2} Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 69-73. — 309 с.
6. ↑ Рыбников К. А. Введение в комбинаторный анализ. — 2-е изд. — М.: Изд-во МГУ, 1985. — С. 266. — 309 с.
7. ↑ Боровков, А. А. Теория вероятностей. — 2-е изд. — М.: «Наука», 1986. — С. 24. — 431 с.
8. ↑ Холл М. Комбинаторика = Combinatorial Theory. — М.: «Мир», 1970. — С. 30-31. — 424 с.
9. ↑ Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 103-107. — 440 с.

Ссылки

Формула включений-исключений Википедия

Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре^[1].

Случай двух множеств

Например, в случае двух множеств A , B {\displaystyle A,B} формула включений-исключений имеет вид:

| A ∪ B | = | A | + | B | − | A ∩ B | . {\displaystyle |A\cup B|=|A|+|B|-|A\cap B|.}

В сумме | A | + | B | {\displaystyle |A|+|B|} элементы пересечения A ∩ B {\displaystyle A\cap B} учтены дважды, и чтобы компенсировать это мы вычитаем | A ∩ B | {\displaystyle |A\cap B|} из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.

Таким же образом и в случае n > 2 {\displaystyle n>2} множеств процесс нахождения количества элементов объединения A 1 ∪ A 2 ∪ … ∪ A n {\displaystyle A_{1}\cup A_{2}\cup \ldots \cup A_{n}} состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.

Формула включений и исключений — 7 Июля 2016 — Примеры решений задач

Пусть задано конечное множество А. Число его элементов обозначим n(А). Найдем сколько элементов содержится в множестве А ∪ В. Основная формула нахождения числа элементов суммы двух множеств

n(А ∪ В) = n(А) + n(В) – n(А ∩ В)        (1)

Действительно, n(А ∪ В) — это сумма числа элементов множеств А и В, но при подсчете элементы, принадлежащие А ∩ В учитывались дважды. С помощью формулы (1) можно получить формулы для определения числа элементов суммы любого числа множеств. Например,

n(А ∪ В ∪ С) = n(А ∪ (В ∪ С)) = n(А) + n(В ∪ С) – n(А ∩ (В ∪ С)) =

= n(А) + n(В) + n(С) – n(В ∩ С) – n((А ∩ В) ∪ (А ∩ С)) =

= n(А) + n(В) + n(С) – n(В ∩ С) – (n(А ∩ В) + n(А ∩ С) – n((А ∩ В) ∩ (А ∩ С))) =

=n(А) + n(В) + n(С) – n(В ∩ С) – n(А ∩ В) – n(А ∩ C) + n(А ∩ В ∩ С).

n(А ∪ В ∪ С) = n(А) + n(В) + n(С) – n(А ∩ В) – n(В ∩ С) – n(А ∩ C) + n(А ∩ В ∩ С)    (2)

Формулы (1) и (2) называют формулами включений и исключений.

Примеры с подробным решением.

Задача 1. Из 100 школьников английский знают 42, немецкий — 30, французский — 28, английский и немецкий — 5, английский и французский — 10, немецкий и французский — 8, английский, немецкий и французский — 3 школьника. Сколько школьников не знают ни одного языка?

Решение. I способ.

Обозначим через А — множество школьников, знающих английский язык; N — множество школьников, знающих немецкий язык; F — множество школьников, знающих французский язык.

Тогда n(A) = 42, n(N) = 30, n(F) = 28, n(A ∩ N) = 5,

n(A ∩ F) = 10, n(N ∩ F) = 8, n(A ∩ N ∩ F) = 3.

Найдем с помощью формулы включений и исключений количество школьников, знающих хотя бы один из перечисленных иностранных языков.

n(A ∪ N ∪ F) = n(A) + n(N) + n(F) =

= n(A ∩ N) – n(A ∩ F) – n(N ∩ F) + n(A ∩ N ∩ F) =

= 42 + 30 + 28 – 5 – 10 – 8 + 3 = 80.

Следовательно, не знают ни одного иностранного языка:

100 – 80 = 20 школьников.

II способ.

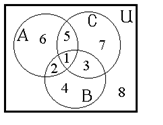
Эту же задачу можно решить с помощью диаграммы Эйлера–Венна (рис. 1).

Так как 3 языка знают 3 школьника, то английский и немецкий знают 5 – 3 = 2, английский и французский — 10 – 3 = 7,

немецкий и французский — 8 – 3 = 5 школьников.

Только английский знают 42 –(2 + 3 + 7) = 30,

только немецкий — 30 – (2 + 3 + 5) = 20,

только французский — 28 – (3 + 5 + 7) = 13 школьников.

Ни одного языка не знают 100 – (2 + 3 + 5 + 7 + 13 + 20 + 30) = 20 школьников.

Задача 2. Сколько двузначных чисел не делятся ни на 2, ни на 3, ни на 5, ни на 11?

Решение. Обозначим: А — множество двузначных чисел, делящихся на 2;

В — множество двузначных чисел, делящихся на 3;

С — множество двузначных чисел, делящихся на 5;

D — множество двузначных чисел, делящихся на 11.

n(A ∪ B ∪ C ∪ D) — количество двузначных чисел, делящихся хотя бы на одно из чисел 2; 3; 5; 11.

n(A ∪ B ∪ C ∪ D) = n(A) + n(B) + n(C) + n(D) –

– n(A ∩ B) – n(A ∩ C) – n(A ∩ D) – n(B ∩ C) –

– n(B ∩ D) – n(C ∩ D) + n(A ∩ B ∩ C) + n(A ∩ B ∩ D) +

+ n(A ∩ C ∩ D) + n(B ∩ C ∩ D) – n(A ∩ B ∩ C ∩ D).

n(A) = 45, n(B) = 30, n(C) = 18, n(D) = 9,

n(A ∩ B) = 15, n(A ∩ C) = 9, n(A ∩ D) = 4, n(B ∩ C) = 6,

n(B ∩ D) = 3, n(C ∩ D) = 1, n(A ∩ B ∩ C) = 3,

n(A ∩ B ∩ D) = 1, n(A ∩ C ∩ D) = n(B ∩ C ∩ D) = n(A ∩ B ∩ C ∩ D) = 0.

Итак, n(A ∪ B ∪ C ∪ D) = 45 + 30 +18 + 9 – 15 – 9 – 4 – 6 – 3 – 1 + 3 + 1  = 68.

Так как всего 90 двузначных чисел, то чисел, не делящихся ни на одно из заданных чисел:

90 – 68 = 22.

Задача 3. Известно, что из n учеников спортом увлекаются a учеников, программированием b, математикой c, спортом и программированием d, спортом и математикой e, программированием и математикой f , спортом, математикой и программированием g учеников. Сколько учеников увлекается только программированием? Сколько учеников увлекается только математикой? Сколько учеников ничем не увлекается?

Вариант	n	a	b	c	d	e	f	g
14	70	32	21	23	8	12	4	3

 

Решение. Пусть A —множество учеников, которые увлекаются спортом,

B — программированием, С — математикой.

Тогда |A| = 32, |B| = 21, |C| = 23, |A ∩ B| = 8, |A ∩ C| = 12, |B ∩ C| =4 |A ∩ B ∩ C| = 3

|(A ∩ B) ∪ ( B ∩ C) | = |A ∩ B| + |B ∩ C| − |A ∩ B ∩ C| = 8 + 4 – 3 = 9

Тогда, только программированием занимается 21 – 9 = 12 учеников.

|(A ∩ C) ∪ ( B ∩ C) | = |A ∩ C| + |B ∩ C| − |A ∩ B ∩ C| = 12 + 4 – 3 = 13

Тогда, только математикой занимается 23 – 13 = 10 учеников.

По формуле включений и исключений для трёх множеств находим число учеников увлекающихся спортом, программированием или математикой:

|A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| − |A ∩ C| − |B ∩ C| + |A ∩ B∩ C| = =32+21+23-8-12-4+3 = 55

Значит, ничем не увлекается 70 − 55 = 15 человек. Ответ: 15.

 

Упражнения

1. В спортивном классе обучаются 24 человека. Каждый учащийся занимается хотя бы одним видом спорта (баскетболом или волейболом), из них баскетболом и волейболом занимаются 12 человек. Сколько человек занимается только волейболом, если их в 3 раза больше, чем тех, кто занимается только баскетболом?

2. В одном украинском городе все жители говорят на русском или украинском языке. По-украински говорят 80 % всех жителей, а по-русски — 75 %. Сколько процентов всех жителей говорят на обоих языках?

3. Группа ребят отправилась в поход. Семеро из них взяли с собой бутерброды, шестеро — фрукты, пятеро — печенье. Четве- ро ребят взяли с собой бутерброды и фрукты, трое — бутерброды  и печенье, двое — фрукты и печенье, а один — и бутерброды, и фрукты, и печенье. Сколько ребят пошли в поход?

4. Староста класса, в котором 40 человек, подводил итоги по успеваемости группы за I полугодие. Получилась следующая картина: из 40 учащихся не имеют троек по русскому языку 25 человек, по математике — 28 человек, по русскому языку и мате- матике — 16 человек, по физике — 31 человек, по физике и ма- тематике — 22 человека, по физике и русскому языку 16 человек. Кроме того, 12 человек учатся без троек по всем трем предметам. Классный руководитель, просмотрев результаты, сказал: «В тво- их расчетах есть ошибка». Составьте диаграмму Эйлера–Венна и объясните, почему это так.

5. В лаборатории института работают несколько человек. Каждый из них знает хотя бы один иностранный язык. 7 человек знают английский, 7 — немецкий, 8 — французский, 5 знают английский и немецкий, 4 — немецкий и французский, 3 — французский и английский, 2 человека знают все три языка. Сколько человек работает в лаборатории? Сколько из них знает только французский язык? Сколько человек знает ровно 1 язык?

6. Сколько целых чисел от 0 до 999 не делятся ни на 5, ни на 7, ни на 11?

Ответы: 1. 9. 2. 55 %. 3. 10. 4. Если на диаграмме Эйлера– Венна отметить данные в непересекающихся множествах класса, то общее число учащихся класса получится равным 42, а не 40, как сказано в условии. 5. 12; 3; 4. 6. 376.

Формула включения-исключения Википедия

Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре^[1].

Случай двух множеств

Например, в случае двух множеств A , B {\displaystyle A,B} формула включений-исключений имеет вид:

| A ∪ B | = | A | + | B | − | A ∩ B | . {\displaystyle |A\cup B|=|A|+|B|-|A\cap B|.}

В сумме | A | + | B | {\displaystyle |A|+|B|} элементы пересечения A ∩ B {\displaystyle A\cap B} учтены дважды, и чтобы компенсировать это мы вычитаем | A ∩ B | {\displaystyle |A\cap B|} из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.

Таким же образом и в случае n > 2 {\displaystyle n>2} множеств процесс нахождения количества элементов объединения A 1 ∪ A 2 ∪ … ∪ A n {\displaystyle A_{1}\cup A_{2}\cup \ldots \cup A_{n}} состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.

Принцип включения-исключения Википедия

Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре^[1].

Случай двух множеств

Например, в случае двух множеств A , B {\displaystyle A,B} формула включений-исключений имеет вид:

| A ∪ B | = | A | + | B | − | A ∩ B | . {\displaystyle |A\cup B|=|A|+|B|-|A\cap B|.}

В сумме | A | + | B | {\displaystyle |A|+|B|} элементы пересечения A ∩ B {\displaystyle A\cap B} учтены дважды, и чтобы компенсировать это мы вычитаем | A ∩ B | {\displaystyle |A\cap B|} из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.

Таким же образом и в случае n > 2 {\displaystyle n>2} множеств процесс нахождения количества элементов объединения A 1 ∪ A 2 ∪ … ∪ A n {\displaystyle A_{1}\cup A_{2}\cup \ldots \cup A_{n}} состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.

Формула включений-исключений — Вики

Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре^[1].

Случай двух множеств

Например, в случае двух множеств A , B {\displaystyle A,B} формула включений-исключений имеет вид:

| A ∪ B | = | A | + | B | − | A ∩ B | . {\displaystyle |A\cup B|=|A|+|B|-|A\cap B|.}

В сумме | A | + | B | {\displaystyle |A|+|B|} элементы пересечения A ∩ B {\displaystyle A\cap B} учтены дважды, и чтобы компенсировать это мы вычитаем | A ∩ B | {\displaystyle |A\cap B|} из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.

Таким же образом и в случае n > 2 {\displaystyle n>2} множеств процесс нахождения количества элементов объединения A 1 ∪ A 2 ∪ … ∪ A n {\displaystyle A_{1}\cup A_{2}\cup \ldots \cup A_{n}} состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.

Формулу включений-исключений можно сформулировать в разных формах.

В терминах множеств

Пусть A 1 , A 2 , … , A n {\displaystyle A_{1},A_{2},\ldots ,A_{n}} — конечные множества. Формула включений-исключений утверждает:

Формула включений и исключений — Студопедия

Часто комбинаторная конфигурация является объединением других, число комбинаций в которых вычислить проще. В таком случае требуется уметь вычислять число комбинаций в объединении.

Пусть А₁ и А₂ – 2 конечных множества. Тогда если А₁ÇА₂=Æ, то 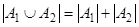. Пусть теперь А₁ÇА₂¹Æ, тогда в 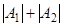каждый элемент из А₁ÇА₂ будет учтен дважды. Поэтому 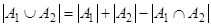. Последнюю формулу можно обобщить на случай произвольного числа множеств:

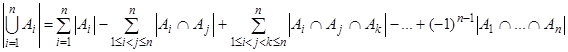. (2)

Равенство (2) называется формулой включений и исключений. В частности, для трех множеств эта формула имеет вид:

.

Доказывается формула (1) методом математической индукции.

Пример 6.

Сколько существует натуральных чисел, меньших 1000, которые не делятся ни на 3, ни на 5, ни на 7?

Всего чисел, меньших тысячи, 999. Из них 999:3=333 делятся на 3,

999:5=199 (ост. 4) делятся на 5,

999:7=142 (ост. 5) делятся на 7,

999:(3х5)=66 (ост. 9) делятся на 3 и на 5,

999:(3х7)=47 (ост. 12) делятся на 3 и на 7,

999:(5х7)=28 (ост. 10) делятся на 5 и на 7,

999:(3х5х7)=9 (ост. 45) делятся на 3, на 5 и на 7.

В итоге искомых чисел 999-(333+199+142-66-47-28+9)=457.

Следствие.Пусть А – конечное множество, А₁, …, А_n – его подмножества. Тогда

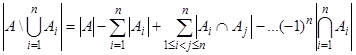. (3)

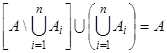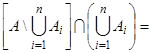Доказательство. Поскольку , а Æ, то 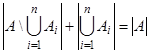. Следовательно, 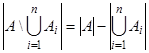. Применив для правой части последнего равенства формулу включений и исключений, получим искомый результат.

Пример 7.

Дано множество А={0, 1, …, 10} и 3 его подмножества:
А₁={a | a – четное}, А₂={a | a>6}, А₃={a | 2<a<8}. Сколько элементов множества А не принадлежат ни одному из этих подмножеств?

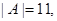
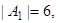
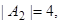
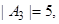
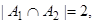
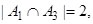
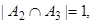
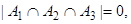тогда по формуле (3)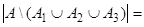 . Очевидно, что таким элементом является 1.

Формула включения-исключения — Математическая энциклопедия

Принцип включения-исключения, метод включения-исключения

Принцип включения-исключения используется во многих разделах чистой и прикладной математики. В теории вероятностей это означает следующую теорему: пусть $ A _ {1}, \ ldots, A _ {n} $ — события в вероятностном пространстве и

(a1)

\ begin {уравнение *} k = 1, \ dots, n.{n — 1} S _ {n}. \ Конец {} уравнение

Эту теорему легко доказать индукцией по $ n $. Еще одно доказательство может быть дано с использованием индикаторных переменных следующим образом. В связи с событием $ A $ определяется $ I _ {A} = 1 $, если происходит $ A $, и $ I _ {A} = 0 $ в противном случае. Тогда уравнение

(a3) ​​

трюмов. Принимая ожидания с обеих сторон, следующая теорема.

Если кто-то хочет найти вероятность $ A _ {1} \ cap \ ldots \ cap A _ {n} $, то сначала нужно заметить, что $ \ mathsf {P} (A _ {1} \ cap \ ldots \ cap A _ {n}) = 1 — \ mathsf {P} (\ overline {A} _ {1} \ cup \ ldots \ cup \ overline {A} _ {n}) $, а затем использует (a2) для события $ \ overline {A} _ {1}, \ dots, \ overline {A} _ {n} $.

Эту теорему часто приписывают А. Пуанкаре [a8]. Однако она уже была известна А. Де Муавру [a2], и даже более общая формула для вероятности того, что произойдет не менее $ r $ событий, была найдена с помощью уравнения r ‘,’ .. / p / p072950.htm ‘, ‘Положительное изменение функции’, ‘.. / p / p073970.htm’, ‘Спрямляемая кривая’, ‘.. / r / r080130.htm’, ‘Изменение функции’, ‘.. / v / v096110. htm ‘) «> C. Jordan [a4]. См. также [a5] для дальнейших ссылок. Все эти формулы относятся к булевым функциям случайных событий.

Примером применения формулы (a2) является решение классической проблемы совпадений, предложенное П. Р. Монмортом [a7]: в коробке находится $ n $ карточек с пометкой $ 1, \ dots, n $, и все карточки вытянуты, одну за другой, без замены, где каждая последовательность имеет одинаковую вероятность; говорят, что на розыгрыше $ i $ происходит совпадение или событие $ A_i $, если вытянутая карта помечена как $ i $; проблема состоит в том, чтобы найти вероятность того, что произойдет хотя бы одно совпадение (см. также задачу сопоставления Монморта).Легко видеть, что для любого $ 1 \ leq i _ {1} <\ ldots

\ begin {уравнение *} \ mathsf {P} (A _ {i_ {1}} \ bigcap \ ldots \ bigcap A _ {i_ {k}}) = \ frac {(n — k)! } {п! }, \ end {уравнение *}

отсюда

\ begin {уравнение *} S _ {k} = \ left (\ begin {array} {c} {n} \\ {k} \ end {array} \ right) \ frac {(n — k)! } {п! } \ end {уравнение *}

и

\ begin {уравнение *} \ mathsf {P} (A _ {1} \ bigcap \ ldots \ bigcap A _ {n}) = \ sum _ {k = 1} ^ {n} (- 1) ^ { к — 1} \ frac {1} {к! }.\ Конец {уравнение *}

Числа $ S _ {k} $ имеют другую вероятностную интерпретацию: $ S _ {k} = \ mathsf {E} \ left [\ left (\ begin {array} {l} {X} \\ {k} \ end {array} \ right) \ right] $, где $ X = I _ {A _ {1}} + \ ldots + I _ {A _ {n}} $, т.е. $ X $ — количество происходящие события. Говорят, что $ S _ {k} $ — это $ k $ -й биномиальный момент $ X $. Для доказательства приведенного выше уравнения см., Например, [a11].

Существует множество практических приложений, в которых необходимо вычислить вероятность объединения или другой булевой функции событий.Известны те, кто занимается теорией надежности. Например, в сети связи, где каналы работают случайным образом или выходят из строя, может потребоваться найти надежность с двумя терминалами или надежность со всеми терминалами. В первом случае нужно найти вероятность того, что все ссылки хотя бы в одном пути, соединяющем два конечных узла, работают, а во втором случае — вероятность того, что все ссылки хотя бы в одном связующем дереве работают. В обоих случаях количество случайных событий слишком велико для применения исключения-включения.Фактически, можно вычислить только несколько задействованных биномиальных моментов. В таких случаях ищут границы. Самыми простыми для вероятности объединения являются границы Бонферрони:

\ begin {уравнение *} \ mathsf {P} (A _ {1} \ bigcup \ ldots \ bigcup A _ {n}) \ geq S _ {1} — S _ {2} + \ ldots + S _ {m — 1} — S _ {m} \ end {уравнение *}

, если $ m $ четное, и

, если $ m $ нечетное, где $ m

Общий эффективный метод ограничения $ \ mathsf {P} (A _ {1} \ cup \ ldots \ cup A _ {n}) $ и других булевых функций событий был разработан А. Прекопой (см. [a10] и ссылки в нем). В случае ограничения вероятности объединения можно заметить, что $ S _ {k} = \ mathsf {E} \ left [\ left (\ begin {array} {l} {X} \\ {k} \ end { массив} \ right) \ right] = \ sum _ {i = 1} ^ {n} \ left (\ begin {array} {l} {i} \\ {k} \ end {array} \ right) p _ {i} $, где $ p _ {i} $ — вероятность того, что произойдет ровно $ i $ событий.Затем, если кто-то знает $ S _ {1}, \ ldots, S _ {m} $, где $ m

(a4)

Если и $ P _ {\ text {max}} $ — оптимальные значения, соответствующие задачам min и max, соответственно, то это точные границы вероятности объединения, т. Е.

\ begin {уравнение *} P _ {\ operatorname {min}} \ leq \ mathsf {P} (A _ {1} \ bigcup \ dots \ bigcup A _ {n}) \ leq P _ {\ text { max}} \ end {уравнение *}

, и на основе знания $ S _ {1}, \ ldots, S _ {m} $ нельзя дать более точных оценок.{T} $ — оптимальные решения двойников минимальной и максимальной задач соответственно. Было показано, что компоненты $ \ mathbf {x} $ и $ \ mathbf {y} $ имеют чередующиеся знаки, начиная с $ + $, и $ | x _ {1} | \ geq \ ldots \ geq | x _ {m} | $, $ | y _ {1} | \ geq \ ldots \ geq | у _ {м} | $. Оптимальные значения можно выразить формулами, если $ m \ leq 4 $ (см. Ссылки в [a10]).

Формула (a2) верна для любой конечно-аддитивной функции множества $ \ mu $, определенной на алгебре $ \ mathcal {S} $ некоторых подмножеств $ \ Omega $ (если $ A \ in \ mathcal S $, то $ \ overline {A} \ in \ mathcal {S} $, и если $ A, B \ in \ mathcal S $, то $ A \ cup B \ in \ mathcal {S} $).В частности, можно взять $ \ Omega $ произвольное конечное множество, $ \ mathcal {S} $ — все подмножества $ \ Omega $ и $ \ mu (A) = | A | $, мощность множества $ A $. Последний случай имеет множество приложений в комбинаторике, особенно в задачах перечисления. Хороший образец комбинаторных задач, в которых используется включение-исключение, представлен в [a6].

Включение-исключение также играет важную роль в теории чисел. Здесь один около

г.

включение / исключение

В 2017 году профессор математического образования Рошель Гутьеррес написала, что «математика действует как белизна». Слухи об этом быстро распространились, что вызвало резкую реакцию ненависти и оскорбительных комментариев в социальных сетях Гутьерреса [1]. Этот саундбайт часто цитируют без контекста, так что вот некоторый контекст:

«Кто получает признание за изучение и развитие математики и кто рассматривается как часть математического сообщества, как правило, считается белым.В школьных программах по математике с акцентом на такие термины, как теорема Пифагора и пи, закрепляется представление о том, что математика была в значительной степени развита греками и другими европейцами. Возможно, что еще более важно, математика имеет незаслуженную привилегию в обществе, как и Белизна ». [2]

В этом смысле, по крайней мере, в США, можно с уверенностью утверждать, что математика действует как белизна. В этом блоге я хотел бы задать вопрос: может ли математика поступить иначе? Может ли математика быть антирасистской?

В прошлом семестре я разработал курс под названием Неравенство: числа и справедливость , предназначенный для неосновных.Мои ученики варьировались от старшеклассников до учеников местной средней школы, со специальностями от правительства до китайского и компьютерных наук. Это было второе воплощение курса, который я преподавал много лет назад, в котором мы прорабатывали идеи из книги Гутштейна и Петерсона «Переосмысление математики: преподавание социальной справедливости с помощью чисел », написанной на уровне средней школы [3]. В Inequalities, я надеялся развить эти идеи в курс на уровне колледжа.

В течение семестра мы изучали, как понятия справедливости и равенства рассматриваются с точки зрения математики и экономики. Какими способами были определены эти идеи и как их можно измерить? Мы рассмотрели самые разные темы: от злоупотребления статистикой до мошенничества и расового капитализма и изменения климата. В конце концов, студенты смогли оценить сложность справедливости, глубокое неравенство, порождаемое капитализмом, и подвергли сомнению идею о том, что математика является политически нейтральной.

Может ли математика, особенно выше уровня K-12, быть антирасистской? Обязательно ли противопоставляются педагогика критической математики (применение критической теории к математическому образованию) и «высшая» математика (математика в вузах и выше)? Социальная справедливость — популярное выражение в наши дни даже в математических кругах, но что оно означает? В недавнем выпуске «Математика для социальной справедливости: ресурсы для колледжа » редакторы Гзем Караали и Лили Хаджави описывают эту работу как часть «национального движения за включение материалов по социальной справедливости в преподавание математики» [4].Хотя книга представляет собой важное усилие по привлечению дискуссий о расе, поле, классе и власти в класс математики в колледже, мне все же хочется большего.

Попытки включить социальную справедливость в учебные программы по математике, возможно, говорят о политических предпочтениях учителя больше, чем что-либо еще. В то же время мы должны опасаться инициатив разнообразия в математике, которые просто воспроизводят другой класс ученых, увековечивающих структуры господства и угнетения, вместо работы, чтобы разрушить белизну, которой работает математика, и по-настоящему подготовить студентов к мир растущего неравенства и климатической катастрофы.В конце концов, было бы лучше, если бы атомную бомбу разработали небелые люди? Или технологии для наблюдения, заключения и депортации уязвимых сообществ?

Эти мелкомасштабные реформы системы оставляют нетронутыми более крупные проблемы капитализма, империализма и белого превосходства. Как писала Пайпер Х. в более раннем посте,

«У большинства из нас нет хороших примеров для подражания, как феминистский факультет математики мог бы выглядеть. У меня есть этот разговор, который я делаю, и после этого я часто беспокоюсь, что белые мужчины спрашивают меня, что они могут сделать для борьбы с сексизмом.Но на самом деле они не думают о прекращении сексизма. Они думают о прогрессе. Они хотят знать, какие преимущества цис-мужчины, обладающие властью, могут предложить женщинам, чтобы мы не чувствовали себя так плохо, так много жаловались и вносили свой вклад в такое унылое число. Это естественно, даже разумно, но все же сексистски.

В самом деле, как феминистка — интерсекциональная, антирасистская и сознательно феминистская — выглядела на математическом факультете?

Должна ли математика быть антирасистской?

Прежде чем мы рассмотрим этот вопрос дальше, мы должны спросить, должна ли математика выполнять работу социальной справедливости.Такие вопросы уже давно задают в физических науках. Смотрите обновление ниже.

Для того, чтобы быть уверенными, математика педагоги думали долго и упорно о том, каком образе математики образование пересекается с вопросами расы, пола, класса и мощности, по крайней мере, с Фрейром педагогики угнетенные [6]. Преподавание математики глубоко укоренилось в политике, и поскольку некоторые предпочитают рассматривать абстрактную математику как происходящую в вакууме, социальный аспект математического образования имеет большое значение.

Но как насчет большинства профессоров математики в колледжах, которые обучаются не математике, а математике? Они активно участвуют в разработке специальностей STEM (наука, технология, инженерия и математика) и в обслуживании структур власти в классах и на факультетах математики колледжей. Этих математиков принимают на работу не только из-за их педагогических способностей, даже во многих гуманитарных школах.

Между исследовательской математикой и математическим образованием существуют практические и культурные различия (допустим этот двоичный код в целях обсуждения).Можно сказать, что математическое образование заботится о формировании математически грамотных учеников, о взаимодействии между угнетением, властью и привилегиями в контексте математического образования, особенно в школах до 12 лет; тогда как в математике нас беспокоит математика как математика, часто как оторванная от социальной реальности (за исключением случаев, когда это применяется к физическим наукам и инженерным наукам). Действительно, в моей области, теории чисел, общепринято хвастаться, что решение знаменитых проблем, таких как Великая теорема Ферма, не имеет непосредственного практического применения.Следовательно, просто попытаться иметь абстрактную и социально вовлеченную математику одновременно — значит иметь своего рода математическое двойное сознание, а попытка соединить эти два понятия — весьма нетривиальная задача.

Тем не менее, ясно одно: если математика является политической (а также расовой и гендерной), то мы должны быть на стороне справедливости, как бы это ни выглядело. Другими словами, если математика может быть антирасистской, то так и должно быть.

На пути к критическому исследованию математики

Исследования в области математического образования показали, что преподавание математики — это в высшей степени политический акт.А как насчет содержания математики? Другими словами, какая «чистая» математика может быть полезна антирасистской математике? Это вообще правильный вопрос? Могут ли абстракции университетской математики и не только, идеи, скажем, теории категорий, дифференциальной геометрии или абстрактной алгебры, открыть новые пути критического подхода к социальному?

В Inequalities мы обсуждали приложения теории социального выбора, метрической геометрии и случайных блужданий к джерримандерингу.Некоторые из них следуют за работой Группы метрической геометрии и Джерримандеринга Муна Дучина (MGGG) в Тафтсе и Массачусетском технологическом институте, которая выполняет захватывающую работу, особенно с учетом предстоящей переписи населения 2020 года. Мы обсудили скандальную статью Эндрю Хакера «Нужна ли алгебра?», В которой предлагается заменить стандартную учебную программу по математике «гражданской статистикой», которая «знакомит студентов с числами, которые описывают и определяют нашу личную и общественную жизнь».

Мы также потратили время на справедливое деление — подполе поведенческой экономики, которую первоначально изучали математики, такие как Хьюго Штайнхаус [7], которая продолжает вызывать интерес у математиков [8].Более сложные задачи справедливого деления приводят к проблемам сопоставления в теории графов, например к алгоритму Гейла-Шепли в задаче стабильного брака. Последний был применен к проблеме выбора школы для сопоставления учащихся школам, как описано в модуле [9]. Это пример класса задач, которые строят упрощенные модели социальной реальности, как это делают в физических науках, для ее изучения.

Другой пример — множитель Петри, который описывает степенной закон в модели сексизма.Модель предполагает, что мужчины и женщины в равной степени сексистские, аналогично тому, как модель сегрегации Шеллинга предполагает, что люди в равной степени (не) расисты и просто предпочитают быть с себе подобными [10]. Кто-то может возразить, что этот подход раскрывает математические законы, которые заставляют происходить определенные явления, не обсуждая, как внешние факторы могут вмешиваться в реальность. Возможно ли, чтобы модели социальных явлений объясняли сложность расы, пола, класса и нации?

Я не претендую на ответы на вопросы, которые задаю.Эта небольшая выборка предлагает несколько возможностей для математики как, скажем, интерсекционального, антирасистского и сознательно феминистского предприятия. В любом случае, если мы можем согласиться с тем, что математика может действовать как белизна, то у нас есть моральный долг спросить, как могла бы быть математика в противном случае. Еще много работы. Что мы могли бы придумать, если бы осмелились вообразить, с силой нашего объединенного математического творчества?

Обновление: (1/2/2020) В предыдущей версии цитировалась работа Чанды Прескод-Вайнштейн, которая еще не была опубликована.Я удалил ссылку и извиняюсь за ошибку. Вот правильная ссылка. См. Здесь, здесь, здесь и здесь образец работы, которая в настоящее время опубликована. Я с готовностью признаю стирание и античерный расизм, сознательно и бессознательно увековеченный небезгранными людьми, такими как я, в том числе в естественных науках и математике, извлекая выгоду из работы и труда чернокожих. Я хочу, чтобы меня вызвали из-за этого. Я также обратил внимание на то, что есть и другие люди, такие как Даниэль Н.Ли, Стефани Пейдж, Рэйчел Бёркс и Джедида Ислер тоже, которые проделывают аналогичную работу в других областях науки.

Артикул:

[1] Гутьеррес, Р. «Почему математика (образование) опоздала с отрицательной реакцией: необходимость революции». Журнал городского математического образования 10.2 (2017): 8-24.

[2] Гутьеррес Р. (2017b). Политический conocimiento для обучения математике: зачем учителям и как развивать. В С. Кастберге, А.М. Тимински, А. Лишка и В. Санчес (редакторы), Создание поддержки научных практик в области математических методов (стр. 11–38). Шарлотта, Северная Каролина: информационный век.

[3] Gutstein, E., & Peterson, B. (Eds.). (2005). Переосмысление математики: Обучение социальной справедливости числами . Переосмысление школ.

[4] Караали Г., & Хаджави Л. С. (2019). Приглашение к математике для социальной справедливости. Математика для социальной справедливости: ресурсы для колледжа , 60 , 1.

[6] Фрейре, П. (2018). Педагогика угнетенных . Издательство Bloomsbury USA.

[7] Steinhaus, H. Проблема справедливого разделения, Econometrica 16 (1948), 101–104.

[8] Брамс, С.Дж., М. Килгур, и Кристиан Кламлер. «Справедливое разделение неделимых предметов двумя людьми: эффективный алгоритм без зависти». Уведомления AMS 61, no. 2 (2014): 130-141.

[9] Гласс Дж. И Караали Г. (2019). Соответствие детей школам: проблема выбора школы. Математика для социальной справедливости: ресурсы для колледжа , 60 , 155.

[10] Schelling, T. C. (1971). Динамические модели сегрегации. Журнал математической социологии , 1 (2), 143-186.

,

No related posts.