Функция ДИСП
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Оценивает дисперсию по выборке.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция ДИСП.В.
Синтаксис
ДИСП(число1;[число2];…)
Аргументы функции ДИСП описаны ниже.
-
Число2… Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности.
Число1 Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
Замечания
-
В функции ДИСП предполагается, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, для вычисления дисперсии следует использовать функцию ДИСПР.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.

-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСПА.

-
Функция ДИСП вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
|
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание |
Результат |
|
=ДИСП(A2:A11) |
Дисперсия предела прочности для всех протестированных инструментов. |
754,2667 |
Выборочная средняя и выборочная дисперсия
Пусть для изучения генеральной совокупности относительно количественного признака Х произведена выборка объёма n.
Выборочной средней называется среднее арифметическое значение выборки.
Если все значения х1, х2, …, хn выборки различны, то
| (7.1) |
Если же значения признака х1, х2, …, хk имеют соответственно частоты n1,n2,…,nk, причем n1+n2+…+nk=n, то
| (7.2) |
Иногда бывает целесообразным выборочные значения случайной величины разбить на отдельные группы. Для каждой группы можно найти её среднюю.
Для каждой группы можно найти её среднюю.
Групповой средней называется среднее арифметическое значений выборки, принадлежащих группе.
По групповым средним можно найти среднее для всей выборки.
Общей средней называется среднее арифметическое значение групповых средних.
Пример 7.1.Найти общую среднюю на основе выборки.
| Группа | |||||
| Значение варианты | |||||
| Частота | |||||
| объем |
Решение: Находим групповые средние:
Общая средняя
Если варианты хi– большие числа, то для облегчения вычисления выборочной средней используют следующий приём. Пусть
Пусть
Так как
, то формула (7.1) преобразуется к виду:
| (7.3) |
Константу С (так называемый ложный нуль) берут такой, чтобы во-первых, разности хi -C были небольшими и, во-вторых, число С было по возможности целым.
Пример 7.2.Имеется выборка:
| х1=71,88 | х2=71,93 | х3=72,05 | х4=72,07 | х5=71,90 |
| х6=72,02 | х7=71,93 | х8=71,77 | х9=71,77 | х10=71,96 |
Найти выборочную среднюю.
Решение: Берем С=72 и вычисляем разности
| α1=-0,12 | α2=-0,07 | α3=0,05 | α4=0,07 | α5=-0,10 |
| α6=0,02 | α7=-0,07 | α8=-0,23 | α9=0,11 | α10=-0,04 |
Их сумма: α1+α2+…+α10=-0,38; их среднее арифметическое: ; выборочная средняя: .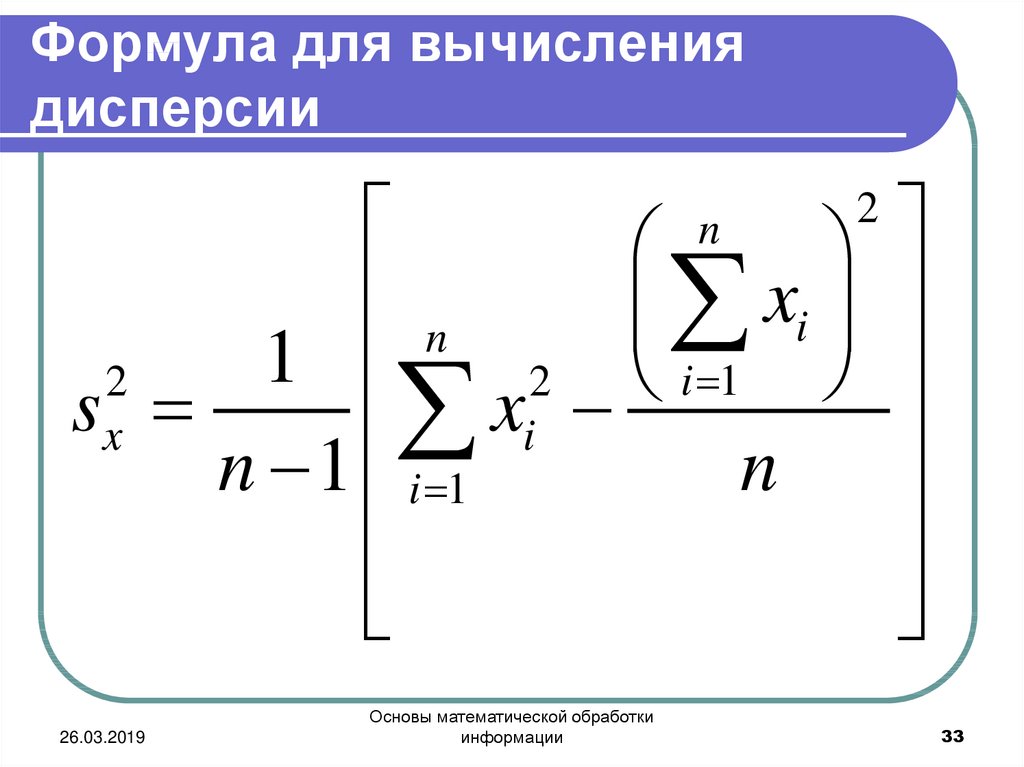
Для того, чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки относительно выборочного среднего вводят понятие выборочной дисперсии.
Выборочной дисперсией Dв называется среднее арифметическое квадратов отклонений наблюдаемых значений признака
Если все значения х1, х2, …, хn признака выборки объёма n различны, то
| (7.4) |
Если же значения признака х1, х2, …, хk имеют соответственно частоты n1,n2,…,nk, причем n1+n2+…+nk=n, то
| (7.5) |
Пример 7.3.Выборочная совокупность задана таблицей распределения:
Найти выборочную дисперсию.
Решение: Согласно формулам (7.2) и (7.5) имеем:
.
Выборочным средним квадратическим отклонением называется квадратный корень из выборочной дисперсии:
Можно доказать, что
| (7.6) |
Так как М(Dв)¹Dr, то выборочная дисперсия Dв является смещенной оценкой генеральной дисперсии Dr. Чтобы получить несмещенную оценку генеральной дисперсии Dr, вводят понятие так называемой исправленной (эмпирической) дисперсии S2, которая определяется формулой:
| (7.7) |
Исправленная дисперсия (7.7) является несмещенной оценкой генеральной дисперсии
Если варианты хi – большие числа, то для облегчения вычисления выборочной дисперсии Dвформулу (7. 4) преобразуют к следующему виду:
4) преобразуют к следующему виду:
| (7.8) |
где С – ложный нуль.
Пример 7.4.Через каждый час измерялось напряжение тока в электросети. Результаты измерений в вольтах представлены в таблице 7.1:
Таблица 7.1
| i | ||||||||||||
| xi | ||||||||||||
| i | ||||||||||||
| xi |
Найти оценки для математического ожидания и дисперсии результатов измерений.
Решение: Оценки для математического ожидания и дисперсии найдем по формулам (7.3) и (7.8), положив С=220. Все необходимые вычисления приведены в таблице 7.2:
Таблица 7.2
| i | xi-C | (xi-C)2 | i | xi-C | (xi-C)2 | i | xi-C | (xi-C)2 |
| -5 | ||||||||
| -1 | -2 | -1 | ||||||
| -2 | ||||||||
| -3 | -2 | |||||||
| -4 | -1 | |||||||
| Σ |
Следовательно,
Дата добавления: 2020-10-25; просмотров: 448; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Дисперсия выборочной средней — Энциклопедия по экономике
Поскольку, как правило, генеральная средняя ц неизвестна, этой формулой нельзя воспользоваться. Кроме того, в социально-экономических исследованиях из одной и той же совокупности выборки не проводятся многократно. Используют следующее соотношение квадрат средней ошибки (дисперсия выборочных средних) прямо пропорционален дисперсии признака х в генеральной совокупности а и обратно пропорционален объему выборки п [c.166]
Кроме того, в социально-экономических исследованиях из одной и той же совокупности выборки не проводятся многократно. Используют следующее соотношение квадрат средней ошибки (дисперсия выборочных средних) прямо пропорционален дисперсии признака х в генеральной совокупности а и обратно пропорционален объему выборки п [c.166] Дисперсия выборочной средней у [c.65]
Дисперсия выборочной средней для повторной выборки равна дисперсии изучаемого признака в генеральной совокупности, разделенной на объем выборки, т. е. [c.33]
Если из генеральной совокупности объема N производится бесповторная выборка объемом п, то дисперсия выборочной средней равна [c.33]
Когда дисперсия о2 генеральной совокупности неизвестна, тогда для больших значений п с большой вероятностью малой ошибки можно дисперсию выборочной средней вычислять приближенно по формуле [c.33]
Таким образом, для нахождения генеральных числовых характеристик необходим анализ всей генеральной совокупности. В силу того, что в реальности практически всегда имеют дело с выборками, приходится находить оценки указанных выше генеральных характеристик — выборочные числовые характеристики выборочное среднее, выборочную дисперсию, выборочное среднее квадратическое отклонение.
[c.52]
В силу того, что в реальности практически всегда имеют дело с выборками, приходится находить оценки указанных выше генеральных характеристик — выборочные числовые характеристики выборочное среднее, выборочную дисперсию, выборочное среднее квадратическое отклонение.
[c.52]
Ошибка выборки или, иначе говоря, ошибка репрезентативности — это разница между значением показателя, полученного по выборке, и генеральным параметром. Так, ошибка репрезентативности выборочной средней равна ег = х — ц, выборочной относительной величины гг=р-п, дисперсии едЛ = s1 — а2, коэффициента корреляции ЕГ = г — р. [c.165]
Если представить, что было проведено бесконечное число выборок равного объема из одной и той же генеральной совокупности, то показатели отдельных выборок образовали бы ряд возможных значений выборочных средних величин х,, х-,, х3,. … относительных величин / ,, р2, ръ. … дисперсий s, s 2, s . .., и т. д. Каждая выборка имеет свою ошибку репрезентативности. Следовательно, можно построить ряды распределения выборок по величине ошибки репрезентативности для каждого показателя для средней, относительной величины и т. д. В таких распределениях улавливается тенденция к концентрации ошибок около центрального значения. Число выборок с той или иной величиной ошибки репрезентативности может быть симметрично или асимметрично относительно этого центрального значения. При бесконечно большом числе выборок получится кривая частот, которая представляет кривую выборочного распределения. Свойства таких распределений используются для получения статистических заключений, установления вероятности той или иной величины ошибки репрезентативности. [c.165]
д. В таких распределениях улавливается тенденция к концентрации ошибок около центрального значения. Число выборок с той или иной величиной ошибки репрезентативности может быть симметрично или асимметрично относительно этого центрального значения. При бесконечно большом числе выборок получится кривая частот, которая представляет кривую выборочного распределения. Свойства таких распределений используются для получения статистических заключений, установления вероятности той или иной величины ошибки репрезентативности. [c.165]
Если п велико, то сомножитель п/(п — 1) 1 и можно принять выборочную дисперсию в качестве оценки величины генеральной дисперсии. Подставив выражение (7.10) в формулу средней ошибки выборочной средней, получим [c.169]
Табл. 7.2 содержит формулы средней ошибки выборки для выборочной средней и выборочной относительной величины для разных видов выборки. В приведенных формулах требуют пояснения выражения дисперсий выборочной относительной величины. [c.
 173]
173]Найдем дисперсию групповой средней у, представляющей выборочную оценку M Y). С этой целью уравнение регрессии (3.12) представим в виде [c.64]
В целях повышения однородности изучаемой совокупности и большей точности расчета совокупность стратифицируют, разбивают на ряд групп по какому-то признаку. В маркетинговом исследовании наиболее распространено деление по социальным группам (в частности, по уровню дохода). Формула численности выборки отличается от предыдущей только тем, что выборочная дисперсия заменяется средней из внутригрупповых дисперсий ( 2 ). Однако в этом случае целесообразно вести отбор по каждой группе пропорционально дифференциации признака (п.). Тогда формула численности выборки (по каждой группе) значительно упрощается [c.52]
Сущность метода состоит в том, что из всей совокупности (генеральной — N) отбирается малое число единиц п (выборочная совокупность не больше 20). Для каждой выборки вычисляются выборочная средняя (х) или доля (W) и выборочная дисперсия (о2) [c. 170]
170]
Когда распределение х в генеральной совокупности нормально, тогда выборочная средняя х подчинена также нормальному распределению со средней а и с дисперсией а =— [c.33]
Определение неизвестной генеральной средней по выборочной средней. Предположим, что сделана выборка из генеральной совокупности с нормальным распределением, среднее значение которой и дисперсия неизвестны. Необходимо по выборочному значению х и среднему квадратическому отклонению 5, вычисленному по этой же выборке объемом п, оценить генеральную среднюю а, задавшись некоторым уровнем гарантии Р и точностью е. [c.37]
Пусть случайная величина X имеет математическое ожидание JU и генеральную дисперсию математического ожидания и дисперсии по выборке (xl,X2,…,XN) будут выборочная средняя и выборочная дисперсия [c.65]
В момент проведения контроля с помощью выборки объема п выборочные среднее х и дисперсия S2 будут отличаться от математического ожидания MX vi дисперсии DX. Отклонения оценок от указанных параметров могут существенно отразиться на результатах контроля. Возникает вопрос оценки уровня входного качества контролируемой продукции с учетом этих отклонений,
[c.139]
Возникает вопрос оценки уровня входного качества контролируемой продукции с учетом этих отклонений,
[c.139]
В данной главе речь идет о выборочной средней, выборочной дисперсии, выборочных коэффициентах связи, корреляции, регрессии. Мы будем обозначать выборочные величины теми же буквами, что и соответствующие им оценки генеральной совокупности, со значком над буквой. См. [11, 18, 27, 35]. [c.161]
Сначала рассмотрим относительно незначительные параметры с и 5. 5 -параметр положения. По существу, распределение может иметь средние значения, отличные от 0 (стандартного нормального среднего), что зависит от 5. В большинстве случаев исследуемое распределение нормализовано, и 5 = 0 то есть среднее распределения полагается равным 0. Параметр с — масштабный параметр. Он наиболее важен при сравнении реальных распределений. Опять же, в пределах понятия нормализации параметр с походит на выборочное отклонение он является мерой дисперсии. При нормализации выборочное среднее обычно вычитается (чтобы дать среднее равное 0) и делится на стандартное отклонение, так чтобы единицы были в терминах выборочного стандартного отклонения. Нормализация выполняется, чтобы сравнить эмпирическое распределение со стандартным нормальным распределением со средним равным 0 и стандартным отклонением равным 1. с используется, чтобы задать единицы, которыми распределение расширяется и сжимается около 5. Значение с по умолчанию равно 1. Единственная цель этих двух параметров — задать масштаб распределения относительно среднего и дисперсии. Они не являются действительно характерными для какого-либо из распределений, и поэтому они менее важны. Когда с = 1, а 5 = 0, распределение, как говорят, принимает приведенный вид.
[c.193]
Нормализация выполняется, чтобы сравнить эмпирическое распределение со стандартным нормальным распределением со средним равным 0 и стандартным отклонением равным 1. с используется, чтобы задать единицы, которыми распределение расширяется и сжимается около 5. Значение с по умолчанию равно 1. Единственная цель этих двух параметров — задать масштаб распределения относительно среднего и дисперсии. Они не являются действительно характерными для какого-либо из распределений, и поэтому они менее важны. Когда с = 1, а 5 = 0, распределение, как говорят, принимает приведенный вид.
[c.193]
Разница заключается в том, что устойчивое распределение имеет среднее 0 и с = 1. Обычно мы нормализуем временной ряд, вычитая выборочное среднее и осуществляя деление на стандартное отклонение. Стандартизированная форма устойчивого распределения, по существу, является такой же. 8 — среднее распределения. Тем не менее, вместо деления на стандартное отклонение, мы делим на параметр масштабирования с. Вспомните из Главы 14, что дисперсия нормального распределения равна 2 с2. Следовательно, стандартизированное устойчивое распределение, где а = 2,0, не будет таким же, как стандартное нормальное распределение, поскольку коэффициент масштабирования будет другим. Устойчивое распределение изменяет масштаб на половину дисперсии нормального распределения. Мы начинаем со стандартизированной переменной, потому что ее логарифмическая характеристическая функция может быть упрощен. следующим образом [c.276]
Следовательно, стандартизированное устойчивое распределение, где а = 2,0, не будет таким же, как стандартное нормальное распределение, поскольку коэффициент масштабирования будет другим. Устойчивое распределение изменяет масштаб на половину дисперсии нормального распределения. Мы начинаем со стандартизированной переменной, потому что ее логарифмическая характеристическая функция может быть упрощен. следующим образом [c.276]
Центральная предельная теорема может быть использована для доказательства утверждения о том, что выборочная средняя нормально распределена при условии, что объем выборки больше 30. В случае с малыми выборками необходимо допустить, что мы производим выборку из нормально распределенной совокупности для того, чтобы выборочная средняя была нормально распределена. Кроме того, только при выборках малого объема наша оценка генеральной дисперсии не будет надежной. В этом случае /-распределение позволит сделать поправку на эту дополнительную степень изменчивости.
[c. 232]
232]
Что вы понимаете по терминами «выборочное распределение выборочной средней» и «выборочное распределение выборочной дисперсии». Рассчитайте стандартную ошибку средней по отношению к доходу по финансовому индексу со средним значением в 10% и средним квадратическим отклонением 16% на основе 60 наблюдений. [c.252]
Советская часть в ИСО проводит работы по преобразованию отечественных стандартов в международные, например, ГОСТ 20427—75 Статистическое регулирование технологических процессов методом кумулятивных сумм выборочного среднего и ГОСТ 20737—75 Статистическое регулирование технологических процессов методом групп качества в 1976 г. на 1-м заседании ИСО/ТК 69 П1 4 были одобрены и приняты за основу для разработки международных стандартов. На этом же заседании ИСО/ТК 69 ПК 4 была одобрена программа работ по стандартизации методов статистического регулирования технологических процессов, предложенная советскими специалистами. Программа предусматривает разработку международных стандартов, включающих методы с использованием контрольных карт средних арифметических значений, дисперсий или среднеквадратических отклонений, раз-махов при нормальном распределении контролируемого параметра, а также комбинированных контрольных карт. Предусмотрена также разработка стандартов на методы регулирования по альтернативному признаку, основанных на контрольных картах доли дефектности, числа дефектов, числа дефектных единиц продукции.
[c.51]
Предусмотрена также разработка стандартов на методы регулирования по альтернативному признаку, основанных на контрольных картах доли дефектности, числа дефектов, числа дефектных единиц продукции.
[c.51]
Тейлор [159] изучил вопросы экономического обоснования контрольных карт кумулятивных сумм выборочного среднего для нормального распределения с известной дисперсией показателя качества. Он исходил из того, что контрольные карты кумулятивных сумм предназначаются для обнаружения разладки процесса формирования заданного показателя качества в предположении, что разладка наступает внезапно с известным смещением параметра. Ожидаемое время разладки предполагалось известным. Процесс прекращается для устранения неисправности. Если сигнал о разладке не является ошибочным, то требуется дополнительное время для обнаружения причины неполадки и ее устранения. Приближенно функция затрат основывалась на следующих допущениях [c.137]
При статистическом регулировании в качестве средних значений обычно используют выборочное среднее арифметическое х или выборочную медиану , а в качестве меры рассеяния — выборочное среднее квадратическое отклонение 5 или выборочную дисперсию S2 или размах R. [c.18]
[c.18]
Выборочными статистиками, значения которых накапливаются при статистическом регулировании методом кумулятивных сумм, могут быть выборочное среднее арифметическое значение, выборочная дисперсия или размах, а также число дефектов или число дефектных единиц продукции, и т. д. [c.23]
Дисперсия среднего выборки (выборочного среднего) на основании априорной информации может быть получена исходя из определения дисперсии [c.115]
Дисперсия среднего выборки представляет собой сумму дисперсии распределения математического ожидания про»-цесса и дисперсии среднего выборки при заданном частном значении математического ожидания процесса. Иными словами, мы можем представлять себе выборочное среднее состоящим из двух независимых аддитивных компонент. Оно равно сумме математического ожидания процесса и [c.115]
Если приведенные два сообщения эквивалентны, то тро и v должны быть независимы от получаемого сообщения. Если с=с(0)=с (1), то такая независимость действительно имеет место. Это сводит нашу проблему к проблеме, рассмотренной выше, когда было показано, что выборочное среднее является достаточным, за исключением того, что v (0) не обязательно будет равно v (1). Следовательно, в первом приближении можно сказать, что если мы имеем одинаково хорошую относительную информацию (измеряемую по с(0) и с(1)) о / и / ,, то наши два сообщения эквивалентны. Если же соотношение с— с(0)—с(1) не выполняется, то эти два сообщения в общем случае уже не эквивалентны следовательно, в этом случае Р уже нельзя считать достаточным сообщением. Интуитивно ясно, что сообщение о / о и R содержит больше информации . Если это толковать в том смысле, что апостериорная дисперсия для этого сообщения будет меньше, чем для сообщения Р, то без труда можно показать, что этот интуитивный вывод действительно подтверждается. [c.143]
Это сводит нашу проблему к проблеме, рассмотренной выше, когда было показано, что выборочное среднее является достаточным, за исключением того, что v (0) не обязательно будет равно v (1). Следовательно, в первом приближении можно сказать, что если мы имеем одинаково хорошую относительную информацию (измеряемую по с(0) и с(1)) о / и / ,, то наши два сообщения эквивалентны. Если же соотношение с— с(0)—с(1) не выполняется, то эти два сообщения в общем случае уже не эквивалентны следовательно, в этом случае Р уже нельзя считать достаточным сообщением. Интуитивно ясно, что сообщение о / о и R содержит больше информации . Если это толковать в том смысле, что апостериорная дисперсия для этого сообщения будет меньше, чем для сообщения Р, то без труда можно показать, что этот интуитивный вывод действительно подтверждается. [c.143]
ОР (т—/ns)—апостериорная плотность распределения т при заданном выборочном среднем т тро—апостериорное среднее значение т vpo — апостериорная дисперсия т [c. 296]
296]
X —наблюденное значение величины х (1= 1,2,…,/г) ms—выборочное среднее (среднее по выборке) LK(ms /п)—функция правдоподобия выборочного среднего ms V (ms)—дисперсия выборочного среднего E(ms)—ожидаемое значение выборочного среднего PR (т)—априорная плотность распределения от гПрГ—априорное среднее значение т Vpr—априорная дисперсия т [c.296]
Типический отбор используется в случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. При обследованиях населения такими группами могут быть, например, районы, социальные, возрастные или образовательные группы при обследовании предприятий — отрасль и подотрасль, форма собственности и т.п. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки, которая в этом случае определяется только внут-ригрупповой вариацией. [c.137]
[c.137]
Феллер (Feller, 1951) пришел к схожему результату, но он работал строго с откорректированным диапазоном R. Херст постулировал уравнение (5.1) для нормированного размаха, но оно фактически не было доказано в формальном смысле. Феллер работал с откорректированным диапазоном (то есть накопленные отклонения с удаленным выборочным средним) и пришел к ожидаемому значению R и его дисперсии. Нормированный размах, R/S, считался трудноразрешимым из-за поведения выборочного стандартного отклонения, особенно для небольших значений N. Существовало мнение, что результат был достаточно близок, так как откорректированный диапазон мог быть решен и должен был асимптотически (то есть в бесконечности) быть эквивалентным нормированному размаху. [c.74]
Для большинства индивидуумов, которые обучены стандартной гауссовой статистике, идея бесконечных среднего или дисперсии кажется абсурдной или даже извращенной. Мы всегда можем вычислить дисперсию или среднее выборки. Как оно может быть бесконечным Еще раз повторим, что мы применяем частный случай, гауссову статистику, ко всем случаям. В семействе устойчивых распределений нормальное распределение — частный случай, который существует, когда а = 2,0. В этом случае математическое ожидание и дисперсия действительно существуют. Бесконечная дисперсия означает, что не существует «дисперсии совокупности», к которой стремится распределение в пределе. Когда мы берем выборочную дисперсию, мы делаем это, согласно гауссову предположению, как оценку неизвестной дисперсии совокупности. Шарп (Sharpe, 1963) говорил, что беты (в смысле современной теории портфеля (МРТ)) должны рассчитываться на основании ежемесячных данных за пять лет. Шарп выбрал пять лет, потому что этот период дает статистически значимую выборочную дисперсию, необходимую для оценки дисперсии совокупности. Пятилетний период статистически значим, только если лежащее в основе распределение является гауссовым. Если оно не является гауссовым и а выборочная дисперсия ничего не говорит о дисперсии совокупности, потому что дисперсии совокупности нет. Выборочные дисперсии, как ожидалось бы, будут неустойчивыми и не будут стремиться ни к какому значению, даже при увеличении объема выборки.
В семействе устойчивых распределений нормальное распределение — частный случай, который существует, когда а = 2,0. В этом случае математическое ожидание и дисперсия действительно существуют. Бесконечная дисперсия означает, что не существует «дисперсии совокупности», к которой стремится распределение в пределе. Когда мы берем выборочную дисперсию, мы делаем это, согласно гауссову предположению, как оценку неизвестной дисперсии совокупности. Шарп (Sharpe, 1963) говорил, что беты (в смысле современной теории портфеля (МРТ)) должны рассчитываться на основании ежемесячных данных за пять лет. Шарп выбрал пять лет, потому что этот период дает статистически значимую выборочную дисперсию, необходимую для оценки дисперсии совокупности. Пятилетний период статистически значим, только если лежащее в основе распределение является гауссовым. Если оно не является гауссовым и а выборочная дисперсия ничего не говорит о дисперсии совокупности, потому что дисперсии совокупности нет. Выборочные дисперсии, как ожидалось бы, будут неустойчивыми и не будут стремиться ни к какому значению, даже при увеличении объема выборки. Если а [c.194]
Если а [c.194]
В этой специальной асимптотике, которую мы в дальнейшем будем называть асимптотикой Колмогорова — Деева, нарушаются многие привычные свойства статистических процедур. Например, если X имеет многомерное нормальное распределение с нулевым вектором средних и независимыми координатами с дисперсией а2 и Хг- (/ — 1,. .., п) — независимая выборка объема п, то квадрат длины вектора выборочного среднего [c.155]
§ 9. Выборочная дисперсия
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения , вводят сводную характеристику — выборочную дисперсию.
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .
Если все значения x1, х2, …, xn признака выборки объема п различны, то
.
Если же значения признака x1, х2, …, xk имеют соответственно частоты п1, n2,…, nk, причем n1 + n2+…+nk = n, то
,
т.е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
Пример. Выборочная совокупность задана таблицей распределения
xi 1 2 3 4
ni 20 15 10 5
Найти выборочную дисперсию.
Решение. Найдем выборочную среднюю (см. § 4):
.
Найдем выборочную дисперсию:
.
Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой-средним квадратическим отклонением.
Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:
.
§ 10. Формула для вычисления дисперсии
Вычисление дисперсии, безразлично-выборочной или генеральной, можно упростить, используя следующую теорему.
Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней:
.
Доказательство. Справедливость теоремы вытекает из преобразований:
.
Итак,
,
где ,.
Пример. Найти дисперсию по данному распределению
xi 1 2 3 4
ni 20 15 10 5
Решение. Найдем
общую среднюю:
Найдем
общую среднюю:
.
Найдем среднюю квадратов значений признака:
.
Искомая дисперсия
=5-22=1.
§11. Групповая, внутригрупповая, межгрупповая и общая дисперсии
Допустим, что все значения количественного признака X совокупности, безразлично-генеральной или выборочной, разбиты на k групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти групповую среднюю (см. § 6) и дисперсию значений признака, принадлежащих группе, относительно групповой средней.
Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней
,
где ni —
частота значения xi;
j —
номер группы; — групповая средняя
группы j;
—
объем группыj.
Пример 1. Найти групповые дисперсии совокупности, состоящей из следующих двух групп:
первая группа | вторая группа | ||||||||
xi | ni | xi | ni | ||||||
2 | 1 | 3 | 2 | ||||||
4 | 7 | 8 | 3 | ||||||
5 | 2 | ||||||||
Решение. Найдем
групповые средние:
Найдем
групповые средние:
;
.
Найдем искомые групповые дисперсии:
;
.
Зная дисперсию каждой группы, можно найти их среднюю арифметическую.
Внутригрупповой дисперсией называют среднюю арифметическую дисперсий, взвешенную по объемам групп:
,
где Nj — объем группы j; п =— объем всей совокупности.
Пример 2. Найти внутригрупповую дисперсию по данным примера 1.
Решение. Искомая внутригрупповая дисперсия равна
Зная групповые средние и общую среднюю, можно найти дисперсию групповых средних относительно общей средней.
Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:
,
где
—
групповая средняя группыj; Nj — объем группы j; — общая средняя; n =-
объем всей совокупности.
Пример 3. Найти межгрупповую дисперсию по данным примера 1.
Решение. Найдем общую среднюю:
.
Используя вычисленные выше величины = 4,= 6, найдем искомую межгрупповую дисперсию:
.
Теперь целесообразно ввести специальный термин для дисперсии всей совокупности.
Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней:
,
где ni — частота значения xi ; — общая средняя; n — объем всей совокупности.
Пример 4. Найти общую дисперсию по данным примера 1.
Решение. Найдем искомую общую дисперсию, учитывая, что общая средняя равна 14/3:
Замечание. Найденная общая дисперсия равна сумме
внутригрупповой и межгрупповой дисперсий:
Найденная общая дисперсия равна сумме
внутригрупповой и межгрупповой дисперсий:
Dобщ= 148/45;
Dвнгр + Dмежгр= 12/5 + 8/9= 148/45.
В следующем параграфе будет доказано, что такая закономерность справедлива для любой совокупности.
Дисперсия и стандартное отклонение в EXCEL. Примеры и описание
Вычислим в MS EXCEL дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим дисперсию , затем стандартное отклонение .
Дисперсия выборки
Дисперсия выборки ( выборочная дисперсия, sample variance ) характеризует разброс значений в массиве относительно среднего .
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления дисперсии выборки используется функция ДИСП() , англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог ДИСП.В() , англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция ДИСП.Г(), англ. название VARP, т.е. Population VARiance, которая вычисляет дисперсию для генеральной совокупности . Все отличие сводится к знаменателю: вместо n-1 как у ДИСП.В() , у ДИСП.Г() в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция ДИСПР() .
Дисперсию выборки можно также вычислить непосредственно по нижеуказанным формулам (см. 2)/ (СЧЁТ(Выборка)-1
) –
формула массива
2)/ (СЧЁТ(Выборка)-1
) –
формула массива
Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению . Обычно, чем больше величина дисперсии , тем больше разброс значений в массиве.
Дисперсия выборки является точечной оценкой дисперсии распределения случайной величины, из которой была сделана выборка . О построении доверительных интервалов при оценке дисперсии можно прочитать в статье Доверительный интервал для оценки дисперсии в MS EXCEL .
Дисперсия случайной величины
Чтобы вычислить дисперсию случайной величины, необходимо знать ее функцию распределения .
Для дисперсии случайной величины Х часто используют обозначение Var(Х). Дисперсия равна математическому ожиданию квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X)) 2 ]
Если случайная величина имеет дискретное распределение , то дисперсия вычисляется по формуле:
где x i – значение, которое может принимать случайная величина, а μ – среднее значение (
математическое ожидание случайной величины
), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет непрерывное распределение , то дисперсия вычисляется по формуле:
где р(x) – плотность вероятности .
Для распределений, представленных в MS EXCEL , дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q.
Примечание : Дисперсия, является вторым центральным моментом , обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно математического ожидания .
Примечание : О распределениях в MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .
Некоторые свойства дисперсии :
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(aХ)=a 2 Var(X)
Var(Х)=E[(X-E(X)) 2 ]=E[X 2 -2*X*E(X)+(E(X)) 2 ]=E(X 2 )-E(2*X*E(X))+(E(X)) 2 =E(X 2 )-2*E(X)*E(X)+(E(X)) 2 =E(X 2 )-(E(X)) 2
Это свойство дисперсии используется в
статье про линейную регрессию
.
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их ковариация равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе стандартной ошибки среднего .
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1) 2 Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения доверительного интервала для разницы 2х средних .
Примечание : квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки — это мера того, насколько широко разбросаны значения в выборке относительно их
среднего
.
По определению, стандартное отклонение равно квадратному корню из дисперсии :
Стандартное отклонение не учитывает величину значений в выборке , а только степень рассеивания значений вокруг их среднего . Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется Коэффициент вариации (Coefficient of Variation, CV) — отношение Стандартного отклонения к среднему арифметическому , выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления Стандартного отклонения выборки используется функция
=СТАНДОТКЛОН()
, англ. 2)/(СЧЁТ(Выборка)-1))
2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция КВАДРОТКЛ() вычисляет с умму квадратов отклонений значений от их среднего . Эта функция вернет тот же результат, что и формула =ДИСП.Г( Выборка )*СЧЁТ( Выборка ) , где Выборка — ссылка на диапазон, содержащий массив значений выборки ( именованный диапазон ). Вычисления в функции КВАДРОТКЛ() производятся по формуле:
Функция СРОТКЛ() является также мерой разброса множества данных. Функция СРОТКЛ() вычисляет среднее абсолютных значений отклонений значений от среднего . Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка) , где Выборка — ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции СРОТКЛ () производятся по формуле:
Иногда исследователь ставит перед собой более конкретную проблему: как, основываясь на выборке, оценить интересующие его числовые характеристики неизвестного распределения, не прибегая к приближению этого распределения как такового, то есть без построения выборочных функций распределения, гистограмм и т.п. В данном параграфе мы обсудим простые (но, как увидим в дальнейшем, весьма хорошие)
выборочные аппроксимации для математического ожидания и дисперсии. Замечательно
то, что они применимы в очень общей ситуации. Мы будем предполагать, что независимая
выборка
взята из неизвестного распределения,
у которого существует математическое ожидание и дисперсия (обозначим эти неизвестные
значения через и соответственно). Определение 6.2 Величины, вычисляемые по выборке,
и
называются выборочным средним и выборочной дисперсией. Следует особо подчеркнуть, что определенные выше величины зависят только от выборки. Следующее предложение объясняет, почему естественно считать выборочным аналогом математического ожидания, а — выборочным аналогом дисперсии. Предложение 6.1 Математические ожидания и совпадают с оцениваемыми неизвестными величинами:
Дисперсия стремится к нулю при росте объема выборки. Доказательство. Используя линейность математического ожидания, получим Так как выборка независимая, то . Следовательно, при . Покажем теперь, что . Первое замечание состоит в том, что не зависит от сдвига всех элементов выборки на одну и ту же константу, то есть, значения выражения (30) для выборок и одинаковы. Поэтому без ограничения общности мы будем считать, что . При этом предположении Теперь, проводя очевидные преобразования и применяя свойства математического ожидания, легко получаем необходимое утверждение
Это утверждение свидетельствует о том, что и являются
«качественными приближениями» для неизвестных величин и . Замечание 6.4 Для оценивания дисперсии по выборке может быть использована также функция Формально ее можно получить, заменив в определении дисперсии оператор математического ожидания средним арифметическим. Ясно, что величина в отличие от является смещенной: . Хотя для больших выборок эта смещенность не очень существенна. Предложение 6.2 При росте объема выборки Доказательство. Как и при доказательстве Предложения 6.1 без ограничения общности будем считать, что . При этом предположении . Из (32) вытекает, что
Применяя закон больших чисел в форме Хинчина к последовательности , имеем В силу предположения по закону больших чисел при .  Следовательно (см. Упражнение 2.10),
. Отсюда вытекает, что
. Следовательно (см. Упражнение 2.10),
. Отсюда вытекает, что
.Замечание 6.5 Здесь мы воспроизводим замечание о вычислениях, приведенное в [12, с. 116]. Из соотношения (33) вытекает следующее представление для :
Математически формулы (30) и (34) дают одно и то же значение. Но, если нам необходимо вручную вычислить выборочную дисперсию, то следует это делать только по формуле (30), так как вычисления по формуле (34) потребовали бы учета намного большего числа значащих цифр, чем в случае применения формулы (30). Имеется большое число практически важных приемов, призванных облегчить вычислительную
работу с конкретными числовыми выборками. Для знакомства с ними рекомендуем
читателю обратиться к книге [11]. В настоящее время существует много прикладных компьютерных программ, которые можно и нужно использовать для обработки числовых данных. С некоторыми наиболее популярными специализированными статистическими пакетами (Stadia, StatGraphics) можно познакомиться по книге [13], к которой также приводится их сравнение. Для статистической обработки небольших массивов данных вполне подойдет любой хороший универсальный математический пакет (Mathematica, Maple, Matlab). Пример 6.5 Вычислим выборочное среднее и выборочную дисперсию для числовых данных Примера 6.4 на странице . Подставив данные в формулы (29) и (30), найдем для выборки и для выборки Полезной величиной является также корень из выборочной дисперсии как оценка среднеквадратичного уклонения:
| ||||||||||||||||||||||||||||||
| А.Д. Манита, 2001-2011 | ||||||||||||||||||||||||||||||
Выборочная дисперсия – определение, значение, формула, примеры
Выборочная дисперсия используется для расчета изменчивости в данной выборке. Выборка — это набор наблюдений, взятых из генеральной совокупности и способных полностью ее представить. Выборочная дисперсия измеряется относительно среднего значения набора данных. Он также известен как расчетная дисперсия.
Поскольку данные могут быть двух типов, сгруппированные и разгруппированные, следовательно, для расчета выборочной дисперсии доступны две формулы. Кроме того, квадратный корень выборочной дисперсии дает стандартное отклонение выборки. В этой статье мы подробно остановимся на выборочной дисперсии, ее формулах и различных примерах.
В этой статье мы подробно остановимся на выборочной дисперсии, ее формулах и различных примерах.
| 1. | Что такое выборочная дисперсия? |
| 2. | Образец формулы отклонения |
| 3. | Как рассчитать выборочную дисперсию? |
| 4. | Выборочная дисперсия по сравнению с дисперсией генеральной совокупности |
| 5. | Часто задаваемые вопросы о пробной дисперсии |
Что такое выборочная дисперсия?
Выборочная дисперсия используется для измерения разброса точек данных в заданном наборе данных относительно среднего значения. Все наблюдения группы известны как совокупность. Когда количество наблюдений начинает увеличиваться, становится трудно вычислить дисперсию населения. В такой ситуации выбирается определенное количество наблюдений, которые можно использовать для описания всей группы. Этот конкретный набор наблюдений образует выборку, и рассчитанная таким образом дисперсия является выборочной дисперсией.
Этот конкретный набор наблюдений образует выборку, и рассчитанная таким образом дисперсия является выборочной дисперсией.
Выборочная дисперсия Определение
Выборочная дисперсия может быть определена как математическое ожидание квадрата разности точек данных от среднего значения набора данных. Это абсолютная мера дисперсии, которая используется для проверки отклонения точек данных по отношению к среднему значению данных.
Пример выборочной дисперсии
Предположим, что набор данных задан как 3, 21, 98, 17 и 9. Определяется среднее значение (29.6) набора данных. Среднее значение вычитается из каждой точки данных и производится суммирование квадрата полученных значений. Это дает 6043.2. Чтобы получить выборочную дисперсию, это число делится на единицу меньше, чем общее количество наблюдений. Таким образом, выборочная дисперсия составляет 1510,8. 9{n}x_{i}}{n}\)
Выборочная дисперсия в среднем равна дисперсии генеральной совокупности.
Давайте разберем формулу выборочной дисперсии на примере.
Пример: В классе 45 учеников. Из этого класса случайным образом были выбраны 5 учеников, и их рост (в см) был записан следующим образом:
131 | 148 | 9{2}}{5-1}\)
Связанные статьи:
- Стандартное отклонение
- Сводная статистика
- Калькулятор дисперсии
Важные примечания по выборочной дисперсии
- Дисперсия, вычисленная с использованием выборочных данных, называется выборочной дисперсией.
- Выборочная дисперсия может быть определена как среднее квадратов отличий от среднего. 9{2}}{Н — 1}\)
Как найти выборочную дисперсию?
Шаги для нахождения выборочной дисперсии следующие:
- Найдите среднее значение данных.
- Вычтите среднее из каждой точки данных.
- Проведите суммирование квадратов значений, полученных на предыдущем шаге.
- Разделите это значение на n — 1.
 {2}}{n}\)
{2}}{n}\)Что означает малая и большая дисперсия в формуле выборочной дисперсии?
Небольшая дисперсия, полученная с использованием формулы выборочной дисперсии, указывает на то, что точки данных близки к среднему значению и друг к другу. Большая дисперсия указывает на то, что значения данных разбросаны от среднего значения и друг от друга.
Выборочная дисперсия: простое определение, как найти ее за несколько простых шагов
Содержание :- Что такое выборочная дисперсия?
- Определение
- Для чего используется выборочное отклонение?
- Образец формулы отклонения
- Почему в формуле выборочной дисперсии используются квадраты?
- Расчет выборочной дисперсии
- Пример отклонения в Excel
Выборочная дисперсия , s 2 , используется для расчета разнообразия выборки. Выборка — это выбранное количество элементов, взятых из генеральной совокупности.
 Например, если вы измеряете вес американцев, вам будет невозможно (ни с точки зрения времени, ни с денежной точки зрения) измерить вес каждого человека в популяции. Решение состоит в том, чтобы взять выборку населения, скажем, 1000 человек, и использовать этот размер выборки для оценки фактических весов всего населения. Дисперсия поможет вам понять, насколько распределены ваши веса.
Например, если вы измеряете вес американцев, вам будет невозможно (ни с точки зрения времени, ни с денежной точки зрения) измерить вес каждого человека в популяции. Решение состоит в том, чтобы взять выборку населения, скажем, 1000 человек, и использовать этот размер выборки для оценки фактических весов всего населения. Дисперсия поможет вам понять, насколько распределены ваши веса.Посмотрите видео с примером того, как найти дисперсию выборки:
Как найти дисперсию выборки
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Типы телосложения разнообразны — они бывают всех форм и размеров. Дисперсия математически определяется как среднее квадратов отличий от среднего . Но что это на самом деле означает на английском языке? Чтобы понять, что вы рассчитываете с дисперсией, разбейте ее на шаги:
- Шаг 1: Рассчитайте среднее значение (средний вес).
- Шаг 2: Вычтите среднее значение и возведите результат в квадрат.

- Шаг 3: Определите среднее значение этих разностей.
- Используйте калькулятор выборочной дисперсии и стандартного отклонения
- Или см.: как рассчитать выборочную дисперсию (вручную).
Хотя дисперсия полезна в математическом смысле, на самом деле она не дает никакой информации, которую можно использовать. Например, если вы возьмете выборочную совокупность весов, вы можете получить дисперсию 9801. Это может заставить вас почесать голову о том, почему вы вычисляете это в первую очередь! Ответ заключается в том, что вы можете использовать дисперсию, чтобы определить стандартное отклонение — гораздо лучшую меру того, насколько разбросаны ваши веса. Чтобы получить стандартное отклонение, возьмите квадратный корень выборочной дисперсии:
√9801 = 99.
Стандартное отклонение в сочетании со средним значением скажет вам, какой вес у большинства людей. Например, если ваш средний вес составляет 150 фунтов, а стандартное отклонение равно 9. 9 фунтов, большинство людей весят от 51 фунта (в среднем 99) до 249 фунтов (в среднем +99).
9 фунтов, большинство людей весят от 51 фунта (в среднем 99) до 249 фунтов (в среднем +99).Если вы находите выборочную дисперсию вручную, «обычная» формула, которую вам дают в учебниках:
Однако, если вы работаете с формулой вручную, это может быть немного громоздко, особенно нотация суммирования (&Sigma). Альтернативной версией является вычислительная формула, с которой может быть немного проще работать:
Причина, по которой значения представляют собой квадраты (вместо, скажем, кубов), связана с теоремой Пифагора и ортогональностью (другим способом сказать « независимый»). Для двух независимых случайных величин X и Y имеем:
Var (X + Y) = Var(X) + Var(Y)
что аналогично следующему:
Если длины двух сторон треугольника a и b ортогональны, то длина гипотенузы равна √ (a 2 + b 2 ) (Кьос-Ханссен, 2019).Вычисление выборочной дисперсии
Формула дисперсии может быть сложной в использовании, особенно если вы плохо знаете порядок операций.
 Безусловно, самый простой способ найти дисперсию — использовать онлайн-калькулятор стандартного отклонения. Вы также можете использовать его для проверки своей работы. Должны работать формулы вручную? Читать дальше!
Безусловно, самый простой способ найти дисперсию — использовать онлайн-калькулятор стандартного отклонения. Вы также можете использовать его для проверки своей работы. Должны работать формулы вручную? Читать дальше!Как найти выборочную дисперсию вручную
Нажмите для примеров:
- Пример 1: Дисперсия (расчетная формула).
- Пример 2: Стандартное отклонение.
- Пример 3 (расчетная формула, обе).
- Пример 4 (обычная формула, обе).
- Пример 5 (расчетная формула, обе).
- Как найти примерную дисперсию в Excel
Вопрос : Найдите дисперсию для следующего набора данных, представляющих деревья в Калифорнии (высота в футах): 3, 21, 98, 203, 17, 9
Шаг 1: Сложите числа в заданном наборе данных.3 + 21 + 98 + 203 + 17 + 9 = 351
Шаг 2: Возведите ответ в квадрат:
351 × 351 = 123 201
… и разделите на количество элементов.
 В нашем примере у нас есть 6 элементов, поэтому:
В нашем примере у нас есть 6 элементов, поэтому:123 201 / 6 = 20 533,5
Отложите это число на мгновение.
Шаг 3: Возьмите исходный набор чисел из шага 1 и на этот раз возведите их в квадрат по отдельности:
3 × 3 + 21 × 21 + 98 × 98 + 203 × 203 + 17 × 17 + 9 × 9
Сложите эти числа (квадраты) вместе:
9 + 441 + 9604 + 41209 + 289 + 81 = 51 633
Шаг 4: Вычтите сумму из Шаг 2 из суммы на шаге 3.
51 633 – 20 533,5 = 31 099,5
Отложите это число на мгновение.
Шаг 5: Вычтите 1 из количества элементов в вашем наборе данных*. Для нашего примера:
6 – 1 = 5
Шаг 6: Разделите число из шага 4 на число из шага 5. Это даст вам дисперсия :
31 099,5 / 5 = 6 219,9
Как найти выборочную дисперсию: Пример стандартного отклонения 2
Шаг 6. Извлеките квадратный корень из вашего стандарта. отклонение :
√6 219,9 = 78,86634
Вот и все!
*Важное примечание: Формула стандартного отклонения немного отличается от для совокупностей и выборок (часть совокупности).
 Если у вас есть население, вы будете делить на «n» (количество элементов в вашем наборе данных). Однако, если у вас есть выборка (а это относится к большинству вопросов по статистике, которые вы получите на уроке!) вам нужно будет разделить на n-1. О том, почему используется n-1, см.: Поправка Бесселя.
Если у вас есть население, вы будете делить на «n» (количество элементов в вашем наборе данных). Однако, если у вас есть выборка (а это относится к большинству вопросов по статистике, которые вы получите на уроке!) вам нужно будет разделить на n-1. О том, почему используется n-1, см.: Поправка Бесселя.Нравится объяснение? Ознакомьтесь со Справочником по статистике практического мошенничества, в котором есть еще сотни пошаговых решений, таких как это!
Наверх
Ваша зарплата за последние несколько недель: 600, 470, 430, 300 и 170 долларов. Что такое стандартное отклонение?
Шаг 1: Сложите все числа:
170 + 300 + 430 + 470 + 600 = 1970Шаг 2: Возведите сумму в квадрат, а затем разделите на количество элементов в наборе данных
1970 x 1970 = 3880900
3880900 / 5 = 776180Шаг 3: Возьмите исходный набор чисел из шага 1 и на этот раз возведите их в квадрат. Затем сложите их все вместе:
(170 x 170) + (300 x 300) + (430 x 430) + (470 x 470) + (600 x 600) = 884700Шаг 4: Вычтите сумму на шаге 2 из сумма на шаге 3:
884700 – 776180 = 108520Шаг 5: Я вычел 1 из количества элементов в моем наборе данных:
5 – 1 = 4Шаг 6: Разделите число в шаге 4 на число в шаге 5:
108520 / 4 = 27130
Это моя дисперсия!Шаг 7: Возьмите квадратный корень из числа из шага 6 (Дисперсия),
√(27130) = 164,71186963
Это мое стандартное отклонение!
Вернуться к началуВ этом примере используется та же формула, только немного другой способ ее работы.

Вы обследуете домохозяйства в вашем районе, чтобы определить среднюю арендную плату, которую они платят. Найдите стандартное отклонение по следующим данным:
1550 долларов, 1700 долларов, 9 долларов.00, 850 долларов, 1000 долларов, 950 долларов.Шаг 1. Найдите среднее значение:
(1550 долл. США + 1700 долл. США + 900 долл. США + 850 долл. США + 1000 долл. США + 950 долл. США)/6 = 1158,33 долл. СШАШаг 2: Вычтите среднее значение из каждого значения. This gives you the differences:
$1550 – $1158.33 = $391.67
$1700 – $1158.33 = $541.67
$900 – $1158.33 = -$258.33
$850 – $1158.33 = -$308.33
$1000 – $1158.33 = $158.33
$950 – $1158.33 = $208.33Step 3: Square различия, которые вы нашли на шаге 3:
$391,67 2 = 153405,3889
$541.67 2 = 293406.3889
-$258.33 2 = 66734.3889
-$308.33 2 = 95067.3889
$158.33 2 = 25068.3889
$208. 33 2 = 43401.3889
33 2 = 43401.3889Step 4: Add up all of the squares you found в Шаге 3 и разделите на 5 (что равно 6 – 1):
(153405,3889 + 293406,3889 + 66734,3889 + 95067,3889 + 25068,3889 + 43401,3889) / 5 = 135416,666682 (дисперсия):
√135416,66668 = 367,99
Стандартное отклонение равно 367,99.Вернуться к началу
Как найти выборочную дисперсию: шаги
Пример вопроса: Найти выборочную дисперсию/стандартное отклонение для следующего набора данных: 1245, 1257, 1788, 888, 154 , 2011, 2145, 2545, 2656.
Шаг 1: Сложите все числа в наборе данных :
1245 + 1255 + 1547 + 1654 + 1787 + 1878 + 1989 + 2011 + 25145 + 6 20712Шаг 2: Возведите в квадрат число, которое вы нашли на шаге 1:
20712 x 20712 = 428986944
… а затем разделите на количество элементов в вашем наборе данных.
428986944 / 11 = 38998813,009
Отложите это число на мгновение.
Шаг 3: Возведите в квадрат все числа в вашем наборе данных, а затем сложите их вместе .
(1245 x 1245) + (1255 x 1255) + (1547 x 1547) + (1654 x 1654) + (1787 x 1787) + (1878 x 1878) + (1989 x 1989) + (2011 x 2011) + ( 2145 х 2145) + (2545 х 2545) + (2656 х 2656) = 41106856Шаг 4: Вычтите число, которое вы рассчитывали на шаге 2 по номеру, который вы рассчитывали на шаге 3 :
41106856 — 38998813.009 = 2108042.90904 Шаг 5: Подпрограмм 1 С. 11 – 1 = 10.
Шаг 6: Разделите число, рассчитанное на шаге 4, на число, рассчитанное на шаге 5.
Шаг 7: Извлеките квадратный корень из шага 6, чтобы найти стандартное отклонение:
√ 210804,290903 = 459,13. Вот и все!
В начало
Содержание:
- Как найти примерную дисперсию в Excel 2013 и более поздних версиях.
- Как найти примерную дисперсию в Excel 2007-2010.

Пример отклонения в Excel 2013 и более поздних версиях
Посмотрите видео с инструкциями:
Пример отклонения в Excel
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Sample Variance Excel 2013: Обзор
Variance — это инструмент, который показывает, насколько сильно различается набор данных. Его основное использование в статистике — это способ найти стандартное отклонение, которое является более полезной мерой разброса и на самом деле используется гораздо шире, чем выборочная дисперсия. Уравнения для нахождения выборочной дисперсии довольно уродливы. Технологии — лучший способ найти его, не допуская математических ошибок.
Excel предлагает два варианта. Если вы еще этого не сделали, обязательно загрузите пакет инструментов анализа данных (Как загрузить пакет инструментов анализа данных). Это мощный инструмент, который вы будете использовать снова и снова в статистике. Если у вас нет пакета инструментов (или вы не хотите его устанавливать), второй вариант — использовать функцию VAR.
Если у вас нет пакета инструментов (или вы не хотите его устанавливать), второй вариант — использовать функцию VAR.Пример отклонения Excel 2013: пакет инструментов для анализа данных
Шаг 1. Щелкните вкладку «Данные», а затем щелкните «Анализ данных».
Шаг 2: Нажмите «Описательная статистика», а затем нажмите «ОК».
Шаг 3. Щелкните поле «Диапазон ввода» и введите местоположение для ваших данных. Например, если вы ввели данные в ячейки от A1 до A10, введите в это поле «A1:A10»
. Шаг 4. Установите переключатель «Строки» или «Столбцы» в зависимости от того, как расположены ваши данные.
Шаг 5. Щелкните поле «Ярлыки в первой строке», если ваши данные содержат заголовки столбцов.
Шаг 6: Установите флажок «Описательная статистика».
Шаг 7: Выберите место для вывода. Например, щелкните переключатель «Новый рабочий лист».
Шаг 8: Нажмите «ОК».
Пример отклонения Excel 2013: функция VAR
Шаг 1. Введите данные в один столбец.

Шаг 2. Щелкните пустую ячейку.
Шаг 3: Введите «=VAR(A1:A100)», где A1:A100 — расположение вашего набора данных (т. е. в ячейках от A1 до A100). Нажмите клавишу «Ввод», чтобы получить дисперсию образца.
В начало
Выборочная дисперсия в Excel 2010
Выборочная дисперсия в Excel 2007–2010 вычисляется с использованием функции «Переменная». Посмотрите это минутное видео о том, как его рассчитать, или прочитайте приведенные ниже шаги.
Как рассчитать выборочную дисперсию в Excel
Посмотрите это видео на YouTube.
Пример вопроса: Найдите выборочную дисперсию в Excel 2007-2010 для следующих выборочных данных: 123, 129, 233, 302, 442, 542, 545, 600, 694, 777
Шаг 1: Введите данные в один столбец на листе Excel. В этом примере я ввел «123, 129, 233, 302, 442, 542, 545, 600, 694, 777» в столбец А. Не оставляйте пустых ячеек между вашими данными.
Шаг 2: Щелкните любую пустую ячейку .

Шаг 3: Нажмите кнопку «Вставить функцию» на панели инструментов. Откроется диалоговое окно «Вставить функцию».
Шаг 4: Введите «Var» в текстовое поле «Поиск функции» , а затем нажмите «Перейти». VAR должна быть выделена в списке функций.
Шаг 5: Нажмите «ОК».
Шаг 6: Введите местоположение данных выборки в текстовое поле Number1 . Этот образец данных был введен в ячейки от A1 до A10, поэтому я ввел «A1: A10» в текстовое поле. Не забудьте разделить первую и последнюю ячейки двоеточием (A1 : A10).
Шаг 7: Нажмите «ОК». Excel вернет выборочную дисперсию в ячейке, которую вы выбрали на шаге 2. Для этого вопроса дисперсия 123, 129, 233, 302, 442, 542, 545, 600, 694, 777 равно 53800,46.
Совет: Вы также можете получить доступ к функции VAR на вкладке «Формулы» в Excel. Перейдите на вкладку «Формулы», а затем нажмите кнопку «Вставить функцию» в крайнем левом углу панели инструментов.
 Продолжайте с шага 4 выше, чтобы вычислить дисперсию.
Продолжайте с шага 4 выше, чтобы вычислить дисперсию.
Совет: У вас нет для ввода данных образца в рабочий лист. Технически, вы можете открыть диалоговое окно функции VAR, а затем ввести свои данные в поля Number1, Number2 и т. д. Однако преимущество ввода данных непосредственно в рабочий лист заключается в том, что вы можете выполнять больше функций над своими данными (например, стандартное отклонение), если вам это нужно.Посетите наш канал YouTube, чтобы получить дополнительную помощь и советы по Excel!
Ссылки
Kenney, J. F. and Keeping, E. S. Математика статистики, Pt. 2, 2-е изд. Принстон, Нью-Джерси: Ван Ностранд, 1951.
Кьос-Ханссен, Б. (2019). Статистика для студентов исчисления. Получено 28 апреля 2021 г. с: https://dspace.lib.hawaii.edu/bitstream/10790/4572/s4cs.pdf
Папулис, А. Вероятность, случайные величины и случайные процессы, 2-е изд. Нью-Йорк: McGraw-Hill, стр. 144–145, 1984.
Робертс М.Дж. и Риккардо Р. Руководство для студентов по дисперсионному анализу. London: Routledge, 1999.
Руководство для студентов по дисперсионному анализу. London: Routledge, 1999.УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Выборочная дисперсия: простое определение, как найти ее простыми шагами» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/descriptive-statistics/sample-variance/————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Как рассчитать дисперсию в Excel – формула дисперсии выборки и генеральной совокупности
В этом уроке мы рассмотрим, как проводить анализ дисперсии в Excel и какие формулы использовать для нахождения дисперсии выборки и генеральной совокупности.

Дисперсия — один из самых полезных инструментов в теории вероятностей и статистике. В науке он описывает, насколько далеко каждое число в наборе данных от среднего. На практике это часто показывает, насколько сильно что-то меняется. Например, температура вблизи экватора имеет меньшую дисперсию, чем в других климатических зонах. В этой статье мы проанализируем различные методы расчета дисперсии в Excel.
- Что такое дисперсия?
- Как найти дисперсию в Excel
- Функции отклонения Excel
- VAR.S против VARA и VAR.P против VARPA
- Как рассчитать выборочную дисперсию в Excel
- Функция VAR
- Функция VAR.S
- Функция ВАРА
- Примеры формулы расчета дисперсии
- Как найти дисперсию населения в Excel
- Функция VARP
- Функция VAR.P
- Функция ВАРПА
- Примеры формулы дисперсии населения
- Формула отклонения в Excel — примечания по использованию
- Дисперсия по сравнению со стандартным отклонением в Excel
Что такое дисперсия?
Дисперсия — это мера изменчивости набора данных, показывающая, насколько далеко разбросаны разные значения.
 Математически он определяется как среднее квадратов отличий от среднего.
Математически он определяется как среднее квадратов отличий от среднего.Чтобы лучше понять, что вы на самом деле рассчитываете с помощью дисперсии, рассмотрите этот простой пример.
Предположим, в вашем местном зоопарке есть 5 тигров в возрасте 14, 10, 8, 6 и 2 лет.
Чтобы найти дисперсию, выполните следующие простые действия:
- Вычислите среднее (простое среднее) пяти чисел:
- Из каждого числа вычтите среднее значение, чтобы найти различия. Для наглядности нанесем на график разницу:
- Возведение в квадрат каждой разницы.
- Определите среднее значение квадратов разностей.
Итак, дисперсия равна 16. Но что на самом деле означает это число?
По правде говоря, дисперсия просто дает вам очень общее представление о дисперсии набора данных. Значение 0 означает отсутствие изменчивости, т. е. все числа в наборе данных одинаковы. Чем больше число, тем больше разбросаны данные.
Этот пример относится к дисперсии популяции (т.
 е. 5 тигров — это вся интересующая вас группа). Если ваши данные являются выборкой из большей совокупности, вам необходимо рассчитать выборочную дисперсию, используя немного другую формулу.
е. 5 тигров — это вся интересующая вас группа). Если ваши данные являются выборкой из большей совокупности, вам необходимо рассчитать выборочную дисперсию, используя немного другую формулу.Как рассчитать дисперсию в Excel
В Excel имеется 6 встроенных функций для расчета дисперсии: VAR, VAR.S, VARP, VAR.P, VARA и VARPA.
Ваш выбор формулы дисперсии определяется следующими факторами:
- Используемая версия Excel.
- Вычисляете ли вы выборочную или генеральную дисперсию.
- Хотите ли вы оценивать или игнорировать текстовые и логические значения.
Функции вариации Excel
В таблице ниже представлен обзор функций вариации, доступных в Excel, которые помогут вам выбрать формулу, наиболее подходящую для ваших нужд.
Имя Версия Excel Тип данных Текст и логика ВАР 2000 — 2019 Образец Игнорируется ВАР.  С
С2010 — 2019 Образец Игнорируется ВАРА 2000 — 2019 Образец Оценка ВАРП 2000 — 2019 Население Игнорируется ВАР.П 2010 — 2019 Население Игнорируется ВАРПА 2000 — 2019 Население Оценка VAR.S против VARA и VAR.P против VARPA
VARA и VARPA отличаются от других функций дисперсии только тем, как они обрабатывают логические и текстовые значения в ссылках. В следующей таблице приведены сводные данные о том, как оцениваются текстовые представления чисел и логических значений.
Тип аргумента ВАР, ВАР.С, ВАРП, ВАР.П ВАРА И ВАРПА Логические значения в массивах и ссылках Игнорируется Оценено
(ИСТИНА=1, ЛОЖЬ=0)Текстовые представления чисел в массивах и ссылках Игнорируется Оценивается как ноль Логические значения и текстовые представления чисел, вводимые непосредственно в аргументы Оценено
(ИСТИНА=1, ЛОЖЬ=0)Пустые ячейки Игнорируется Как рассчитать дисперсию выборки в Excel
Выборка представляет собой набор данных, извлеченных из всей совокупности.
 А дисперсия, рассчитанная по выборке, называется выборочной дисперсией .
А дисперсия, рассчитанная по выборке, называется выборочной дисперсией .Например, если вы хотите узнать, как меняется рост людей, вам будет технически невозможно измерить каждого человека на земле. Решение состоит в том, чтобы взять выборку населения, скажем, 1000 человек, и оценить рост всего населения на основе этой выборки.
Выборочная дисперсия рассчитывается по следующей формуле:
Где:
- x̄ — среднее (простое среднее) значений выборки.
- n — размер выборки, т. е. количество значений в выборке.
В Excel имеется 3 функции для нахождения выборочной дисперсии: VAR, VAR.S и VARA.
Функция VAR в Excel
Это самая старая функция Excel для оценки дисперсии на основе выборки. Функция VAR доступна во всех версиях Excel с 2000 по 2019..
VAR(число1, [число2], …)
Примечание. В Excel 2010 функция VAR была заменена функцией VAR.S, которая обеспечивает повышенную точность. Хотя VAR по-прежнему доступен для обратной совместимости, рекомендуется использовать VAR.
 S в текущих версиях Excel.
S в текущих версиях Excel.Функция VAR.S в Excel
Это современный аналог функции Excel VAR. Используйте функцию VAR.S, чтобы найти выборочную дисперсию в Excel 2010 и более поздних версиях.
ВАР.С(число1, [число2], …)
Функция VARA в Excel
Функция Excel VARA возвращает примерную дисперсию на основе набора чисел, текста и логических значений, как показано в этой таблице.
VARA(value1, [value2], …)
Формула выборочной дисперсии в Excel
При работе с числовым набором данных вы можете использовать любую из вышеперечисленных функций для расчета выборочной дисперсии в Excel.
В качестве примера найдем дисперсию выборки, состоящей из 6 элементов (B2:B7). Для этого вы можете использовать одну из следующих формул:
=ДСП(B2:B7)=ДСП.С(B2:B7)=ДСП(B2:B7)Как показано на снимке экрана, все формулы возвращают одинаковый результат. (округлено до 2 знаков после запятой):
Чтобы проверить результат, давайте вычислим переменную вручную:
- Найдите среднее значение с помощью функции СРЗНАЧ:
=СРЗНАЧ(B2:B7)Среднее значение идет в любую пустую ячейку, скажем, B8.

- Вычесть среднее из каждого числа в выборке: 92
- Сложите квадраты разностей и разделите результат на количество элементов в выборке минус 1:
=СУММ(D2:D7)/(6-1)
Как видите, результат нашего ручного вычисления var точно такой же, как и число, возвращаемое встроенными функциями Excel:
Функция VARA вернет другой результат. Причина в том, что VAR и VAR.S игнорируют любые значения, отличные от чисел, в ссылках, в то время как VARA оценивает текстовые значения как нули, TRUE как 1 и FALSE как 0. Поэтому, пожалуйста, тщательно выбирайте функцию дисперсии для своих расчетов в зависимости от того, хотите обработать или игнорировать текст и логические операции.
Как рассчитать дисперсию совокупности в Excel
Население – это все члены данной группы, т.е. все наблюдения в области исследования. Дисперсия населения описывает, как распределены точки данных во всей совокупности.

Дисперсия населения может быть найдена по следующей формуле:
Где:
- x̄ — среднее значение населения.
- n — размер совокупности, т. е. общее количество значений в совокупности.
В Excel имеется 3 функции для расчета дисперсии генеральной совокупности: VARP, VAR.P и VARPA.
Функция VARP в Excel
Функция Excel VARP возвращает дисперсию генеральной совокупности на основе всего набора чисел. Он доступен во всех версиях Excel с 2000 по 2019.
VARP(число1, [число2], …)
Примечание. В Excel 2010 VARP был заменен на VAR.P, но по-прежнему сохранен для обратной совместимости. В текущих версиях Excel рекомендуется использовать ДИСП.П, поскольку нет гарантии, что функция ДИСП будет доступна в будущих версиях Excel.
Функция VAR.P в Excel
Это улучшенная версия функции VARP, доступная в Excel 2010 и более поздних версиях.
ДИСП.П(число1, [число2], …)
Функция ДСПСП в Excel
Функция ДСПСП вычисляет дисперсию генеральной совокупности на основе всего набора чисел, текста и логических значений.
 Он доступен во всех версиях Excel с 2000 по 2019.
Он доступен во всех версиях Excel с 2000 по 2019.VARA(value1, [value2], …)
Формула дисперсии населения в Excel
баллы были выбраны из большей группы студентов. Если вы соберете данные обо всех учащихся в группе, эти данные будут представлять все население, и вы рассчитаете дисперсию населения, используя вышеуказанные функции.
Допустим, у нас есть экзаменационные баллы группы из 10 студентов (B2:B11). Баллы составляют всю совокупность, поэтому мы вычислим дисперсию по следующим формулам:
=ДСП(В2:В11)=ДСП.П(В2:В11)=ДСП(В2:В11)И все формулы вернут одинаковый результат:
Чтобы убедиться, что Excel правильно рассчитал дисперсию, вы можете проверить ее с помощью формулы ручного расчета переменной, показанной на снимке экрана ниже:
Если кто-то из студентов не сдал экзамен и вместо количества баллов указано N/A, функция VARPA вернет другой результат.
 Причина в том, что VARPA оценивает текстовые значения как нули, в то время как VARP и VAR.P игнорируют текстовые и логические значения в ссылках. Подробную информацию см. в разделе VAR.P и VARPA.
Причина в том, что VARPA оценивает текстовые значения как нули, в то время как VARP и VAR.P игнорируют текстовые и логические значения в ссылках. Подробную информацию см. в разделе VAR.P и VARPA. Формула дисперсии в Excel – примечания по использованию
Чтобы правильно выполнить анализ дисперсии в Excel, следуйте этим простым правилам:
- Аргументы следует указывать в виде значений, массивов или ссылок на ячейки.
- В Excel 2007 и более поздних версиях можно указать до 255 аргументов, соответствующих выборке или генеральной совокупности; в Excel 2003 и старше — до 30 аргументов.
- Чтобы оценить только чисел в ссылках, игнорируя пустые ячейки, текст и логические значения, используйте функцию VAR или VAR.S для расчета выборочной дисперсии и VARP или VAR.P для нахождения дисперсии генеральной совокупности.
- Для оценки логических значений и текстовых значений в ссылках используйте функцию VARA или VARPA.

- Введите не менее двух числовых значений в формулу выборочной дисперсии и не менее одно числовое значение в формулу дисперсии генеральной совокупности в Excel, иначе #ДЕЛ/0! возникает ошибка.
- Аргументы, содержащие текст, который нельзя интерпретировать как числа, приводят к ошибке #ЗНАЧ! ошибки.
Дисперсия по сравнению со стандартным отклонением в Excel
Дисперсия, несомненно, полезная концепция в науке, но она дает очень мало практической информации. Например, мы нашли возраст популяции тигров в местном зоопарке и вычислили дисперсию, которая равна 16. Вопрос в том, как мы можем использовать это число?
Вы можете использовать дисперсию для расчета стандартного отклонения, которое является гораздо лучшим показателем количества вариаций в наборе данных.
Стандартное отклонение вычисляется как квадратный корень из дисперсии. Итак, мы извлекаем квадратный корень из 16 и получаем стандартное отклонение 4.

В сочетании со средним значением стандартное отклонение может сказать вам, сколько лет большинству тигров. Например, если среднее значение равно 8, а стандартное отклонение равно 4, возраст большинства тигров в зоопарке составляет от 4 (8 — 4) до 12 лет (8 + 4).
Microsoft Excel имеет специальные функции для расчета стандартного отклонения выборки и генеральной совокупности. Подробное объяснение всех функций можно найти в этом руководстве: Как рассчитать стандартное отклонение в Excel.
Вот как сделать дисперсию в Excel. Чтобы поближе познакомиться с формулами, обсуждаемыми в этом руководстве, вы можете загрузить наш образец рабочей книги в конце этого поста. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Практическая рабочая тетрадь
Вычисление дисперсии в Excel — примеры (файл .xlsx)
Вас также может заинтересовать
Счет, математика и статистика — Набор академических навыков
Дисперсия и стандартное отклонение
ContentsToggle Главное меню 1 Дисперсия1.
 1 Определение 1.2 Дисперсия генеральной совокупности 1.3 Дисперсия выборки 1.4 Дисперсия случайной величины 1.5 Дисперсия дискретной случайной величины 1.6 Дисперсия непрерывной случайной величины 2 Стандартное отклонение 2.1 Определение 2.2 Стандартное отклонение генеральной совокупности 2.3 Стандартное отклонение выборки 3 Обработка Example3.1 Пример видео 4 Рабочая тетрадь 5 Внешние ресурсы 92 \text{.}\]
1 Определение 1.2 Дисперсия генеральной совокупности 1.3 Дисперсия выборки 1.4 Дисперсия случайной величины 1.5 Дисперсия дискретной случайной величины 1.6 Дисперсия непрерывной случайной величины 2 Стандартное отклонение 2.1 Определение 2.2 Стандартное отклонение генеральной совокупности 2.3 Стандартное отклонение выборки 3 Обработка Example3.1 Пример видео 4 Рабочая тетрадь 5 Внешние ресурсы 92 \text{.}\]Убедитесь, что вы знаете, когда делать это различие. Чтобы использовать дисперсию совокупности, вам нужны все доступные данные, тогда как для использования дисперсии выборки вам нужна только ее часть. Например, если мы возьмем наугад десять слов с этой страницы, чтобы вычислить дисперсию их длины, потребуется выборочная дисперсия. Чтобы найти дисперсию населения, потребуется длина каждого слова на странице.
Дисперсия случайной величины
Для дискретной случайной величины $X$ дисперсию можно вычислить следующим образом: 92\text{.} \end{align*}
Эти результаты получены путем объединения определения дисперсии с формулами для ожидаемого значения для обоих случаев.

Примечание: В дискретном случае среднее $\mu = \displaystyle \sum\limits_{x\in S} \mathrm{P}[X=x] \cdot x$, тогда как в непрерывном случае $\displaystyle \mu = \int\limits_{x\in S} f(x)\cdot x \mathrm{d} x$.
Стандартное отклонение
Определение
Стандартное отклонение , часто обозначаемое как $\sigma$, представляет собой положительный квадратный корень из дисперсии. Наборы данных с небольшим стандартным отклонением тесно сгруппированы вокруг среднего значения, тогда как большее стандартное отклонение указывает на то, что данные более разбросаны. 92}\], где $n$ — количество наблюдений, полученных в выборке, $x_1, x_2, \ldots, x_n$ — полученные наблюдения, а $\bar{x}$ — среднее значение выборки. Чтобы понять, почему используется $\frac{1}{n-1}$, а не $\frac{1}{n}$, см. Степени свободы.
Рабочий пример
Рабочий пример
Продолжительность в секундах тринадцати песен в альбоме: 252\text{.}\] Вычислите стандартное отклонение.

Решение 92}\] получаем \[\sigma = 130,4627\text{.}\]
Пример видео
Доктор Ли Фосетт вычисляет стандартное отклонение набора данных.
Рабочая тетрадь
Эта рабочая тетрадь, созданная HELM, является хорошим пособием по повторению, содержащим ключевые моменты для исправления и множество рабочих примеров.
- Описательная статистика, включая работу над стандартным отклонением и дисперсией.
Внешние ресурсы
- Дисперсия и стандартное отклонение в Массачусетском технологическом институте
Формула дисперсии населения | Пошаговый расчет
Формула дисперсии населения представляет собой меру средних расстояний между данными о населении и рассчитывается путем нахождения среднего значения формулы населения, а дисперсия рассчитывается как сумма квадрата переменных минус среднее, которое делится на количество наблюдений в популяции.

Дисперсия населения — это мера разброса данных о населении. Следовательно, дисперсия населения может быть определена как среднее расстояний от каждой точки данных в конкретной совокупности до среднего квадрата, и она указывает, как точки данных распределены в совокупности. Дисперсия населения — важная мера дисперсии, используемая в статистике. В статистике статистика — это наука, стоящая за выявлением, сбором, организацией и обобщением, анализом, интерпретацией и, наконец, представлением таких данных, как качественных, так и количественных, что помогает принимать более эффективные и эффективные решения с уместностью. читать далее. Статистики рассчитывают дисперсию, чтобы определить, как отдельные числа в наборе данных связаны друг с другом.
При расчете дисперсии населения дисперсия рассчитывается относительно среднего значения населения. Следовательно, мы должны найти среднее значение населения. Выяснить среднее значение населения. Среднее значение населения — это среднее или среднее значение всех значений в данной совокупности, которое рассчитывается как сумма всех значений в совокупности, обозначаемая суммой X, деленной на количество значения в популяции, которые обозначаются N.
 читать далее, чтобы рассчитать дисперсию популяции. Одним из самых популярных уведомлений о дисперсии населения является σ 2 . Это произносится как сигма в квадрате.
читать далее, чтобы рассчитать дисперсию популяции. Одним из самых популярных уведомлений о дисперсии населения является σ 2 . Это произносится как сигма в квадрате.Population variance can be calculated by using the following formula:
σ 2 = ∑ n i=1 (x i – μ) 2 / N
You are free Чтобы использовать это изображение на своем веб-сайте, в шаблонах и т. д., предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Формула дисперсии населения (wallstreetmojo.com), где
- σ 2 является дисперсией популяции,
- x 1, x 2 , x 3, … x n — это наблюдения
- .. x n .
- µ — среднее значение набора данных
Содержание
- Формула для расчета дисперсии совокупности
- Пошаговый расчет дисперсии совокупности
- Примеры
- Пример #1 0068
- Пример № 3
- Пример № 4
- Актуальность и использование
- Рекомендуемые статьи
Пошаговый расчет дисперсии населения с помощью пяти шагов можно рассчитать для населения по дисперсии с помощью пяти шагов
:
- Шаг 1: Вычислите среднее значение (µ) заданных данных.
 Чтобы рассчитать среднее значениеРассчитать Среднее значение означает среднее математическое значение, рассчитанное для двух или более значений. В основном есть два способа: среднее арифметическое, когда все числа складываются и делятся на их веса, и среднее геометрическое, когда мы умножаем числа вместе, берем корень N и вычитаем из него единицу. Подробнее, складываем все наблюдения и затем разделите это на количество наблюдений (N).
Чтобы рассчитать среднее значениеРассчитать Среднее значение означает среднее математическое значение, рассчитанное для двух или более значений. В основном есть два способа: среднее арифметическое, когда все числа складываются и делятся на их веса, и среднее геометрическое, когда мы умножаем числа вместе, берем корень N и вычитаем из него единицу. Подробнее, складываем все наблюдения и затем разделите это на количество наблюдений (N).
- Сделать стол. Обратите внимание, что составление таблицы не является обязательным, но представление ее в табличном формате облегчит расчеты. В первом столбце запишите каждое наблюдение (x 1, x 2 , x 3, …..x n ).
- Во втором столбце запишите отклонение каждого наблюдения от среднего (x i – µ).
- В третьем столбце запишите квадрат каждого наблюдения от среднего (x i – µ) 2 .
 Другими словами, возведите в квадрат каждое из чисел, полученных в столбце 2.
Другими словами, возведите в квадрат каждое из чисел, полученных в столбце 2.
- В дальнейшем нам нужно сложить числа, полученные в третьем столбце. Найдите сумму квадратов отклонений и разделите полученную сумму на количество наблюдений (N). Это поможет нам получить дисперсию населения.
Примеры
Вы можете скачать этот шаблон Excel формулы дисперсии населения здесь – Шаблон Excel 9 формулы дисперсии населения0003
Пример #1
Рассчитайте дисперсию совокупности по следующим 5 наблюдениям: 50, 55, 45, 60, 40.
Решение:
Используйте следующие данные для расчета дисперсии совокупности.
Всего 5 наблюдений. Следовательно, N=5.
µ=(50+55+45+60+40)/5 =250/5 =50
Таким образом, расчет дисперсии совокупности σ 2 можно выполнить следующим образом:
σ 2 = 250 /5
Дисперсия популяции σ 2 будет составлять
Дисперсия популяции (σ 2 ) = 50
Дисперсия населения 50.

Пример № 2
xyz Ltd. всего из 6 сотрудников. Генеральный директор считает, что не должно быть большой дисперсии в зарплатах этих сотрудников. Для этого он хочет, чтобы вы рассчитали дисперсию этих зарплат. Заработная плата этих сотрудников указана ниже. Рассчитайте дисперсию населения по заработной плате генерального директора.
Решение:
Используйте следующие данные для расчета дисперсии генеральной совокупности.
Всего 6 наблюдений. Следовательно, N=6.
=(30+27+20+40+32+31)/6 =180/6 = 30$
Таким образом, расчет дисперсии генеральной совокупности σ 2 можно выполнить следующим образом:
σ 2 = 214/6
Дисперсия населения σ 2 будет —
Дисперсия населения (σ 2 ) = 35,67
Дисперсия заработной платы населения составляет 35,67.
Пример №3
Sweet Juice Ltd производит соки различных вкусов.
 Департамент управления закупает 7 больших контейнеров для хранения этого сока на заводе. Отдел контроля качества принял решение, что контейнеры будут отклонены, если дисперсия контейнеров превышает 10. Даны веса 7 контейнеров в кг: 105, 100, 102, 95, 100, 98 и 107. Пожалуйста, сообщите Отдел контроля качества о том, следует ли отбраковывать контейнеры.
Департамент управления закупает 7 больших контейнеров для хранения этого сока на заводе. Отдел контроля качества принял решение, что контейнеры будут отклонены, если дисперсия контейнеров превышает 10. Даны веса 7 контейнеров в кг: 105, 100, 102, 95, 100, 98 и 107. Пожалуйста, сообщите Отдел контроля качества о том, следует ли отбраковывать контейнеры. Решение:
Используйте следующие данные для расчета дисперсии генеральной совокупности.
Всего 7 наблюдений. Следовательно, N = 7
= (105 + 100 + 102 + 95 + 100 + 98 + 107)/7 = 707/7 = 101
Таким образом, расчет дисперсии населения σ 2 можно выполнить следующим образом:
σ 2 = 100/7
Дисперсия населения σ 2 будет-
Дисперсия населения (σ 2 )= 14,29
Поскольку отклонение (14.29) превышает предел 10, установленный отделом контроля качества, контейнеры должны быть забракованы.

Пример №4
Руководство больницы Sagar Healthcare зафиксировало, что в первую неделю марта 2019 года родилось 8 детей. Врач хотел оценить состояние здоровья детей, а также разницу в росте. . Рост этих малышек следующий: 48 см, 47 см, 50 см, 53 см, 50 см, 52 см, 51 см, 60 см. Вычислите дисперсию роста этих 8 младенцев.
Решение:
Используйте следующие данные для расчета дисперсии генеральной совокупности.
Итак, расчет дисперсии совокупности σ 2 можно выполнить следующим образом:
В Excel имеется встроенная формула дисперсии совокупности, которую можно использовать для расчета дисперсии совокупности группы чисел. Выберите пустую ячейку и введите эту формулу =VAR.P(B2:B9). Здесь B2: B9 — это диапазон ячеек, из которых вы хотите рассчитать дисперсию совокупности.
Дисперсия населения σ 2 будет-
Дисперсия населения (σ 2 ) = 13,98
Релевантность и использование дисперсии
7 9000 Рассмотрим два множества населения с одним и тем же средним значением и числом наблюдений. Набор данных 1 состоит из 5 чисел — 55, 50, 45, 50 и 50. Набор данных 2 состоит из 10, 50, 85, 90 и 15. Оба набора данных имеют одинаковое среднее значение, равное 50. Но, в наборе данных 1 значения близки друг к другу, в то время как в наборе данных 2 значения разбросаны. Дисперсия дает научную меру этой близости/дисперсии. Набор данных 1 имеет дисперсию всего 10, тогда как набор данных 2 имеет огромную дисперсию 1130. Таким образом, большая дисперсия указывает на то, что числа далеки от среднего и друг от друга. Небольшая дисперсия указывает на то, что числа близки друг к другу.
Набор данных 1 состоит из 5 чисел — 55, 50, 45, 50 и 50. Набор данных 2 состоит из 10, 50, 85, 90 и 15. Оба набора данных имеют одинаковое среднее значение, равное 50. Но, в наборе данных 1 значения близки друг к другу, в то время как в наборе данных 2 значения разбросаны. Дисперсия дает научную меру этой близости/дисперсии. Набор данных 1 имеет дисперсию всего 10, тогда как набор данных 2 имеет огромную дисперсию 1130. Таким образом, большая дисперсия указывает на то, что числа далеки от среднего и друг от друга. Небольшая дисперсия указывает на то, что числа близки друг к другу.Дисперсия используется в области управления портфелем при распределении активовРаспределение активовРаспределение активов — это процесс инвестирования ваших денег в различные классы активов, такие как долговые обязательства, акции, взаимные фонды и недвижимость, в зависимости от ваших ожиданий доходности и допустимого риска. . Это облегчает достижение ваших долгосрочных финансовых целей.Подробнее. Инвесторы рассчитывают дисперсию доходности активов для определения оптимальных портфелей.
 Оптимальные портфели Оптимизация портфеля относится к стратегическому процессу внесения улучшений или положительных изменений в портфель инвестора, содержащий различные активы. Коэффициент Шарпа помогает анализировать доходность оптимального портфеля. Подробнее, оптимизируя два основных параметра — доходность и волатильность. Волатильность, измеряемая дисперсией, является мерой риска конкретной финансовой ценной бумаги.
Оптимальные портфели Оптимизация портфеля относится к стратегическому процессу внесения улучшений или положительных изменений в портфель инвестора, содержащий различные активы. Коэффициент Шарпа помогает анализировать доходность оптимального портфеля. Подробнее, оптимизируя два основных параметра — доходность и волатильность. Волатильность, измеряемая дисперсией, является мерой риска конкретной финансовой ценной бумаги.Рекомендуемые статьи
Это руководство по формуле дисперсии населения. Здесь мы обсуждаем, как рассчитать дисперсию населения, используя ее формулу, а также практические примеры и загружаемый шаблон Excel. Вы можете узнать больше о моделировании в Excel из следующих статей —
- Формула ковариацииФормула ковариацииКовариация — это статистическая мера, используемая для нахождения взаимосвязи между двумя активами, которая рассчитывается как стандартное отклонение доходности двух активов, умноженное на его корреляцию. . Если он дает положительное число, то говорят, что активы имеют положительную ковариацию, т.
 е. когда доходность одного актива увеличивается, доходность второго актива также увеличивается, и наоборот для отрицательной ковариации. подробнее
е. когда доходность одного актива увеличивается, доходность второго актива также увеличивается, и наоборот для отрицательной ковариации. подробнее - Формула дисперсии портфеляФормула дисперсии портфеляДисперсия портфеля — это статистическая величина современной теории инвестиций, которая измеряет отклонение средней доходности портфеля от его среднего значения. Короче говоря, он определяет общий риск портфеля. Дисперсия портфеля = w12 * ơ12+w22 * ơ22+2 * ρ1,2 * w1 * w2 * ơ1 * ơ2Подробнее
- Корреляция против ковариации Корреляция против ковариацииКовариация и корреляция — это два термина, которые прямо противоположны друг другу; оба используются для статистики и регрессионного анализа. Ковариация отражает то, как две переменные отличаются друг от друга, тогда как корреляция отображает взаимосвязь между двумя переменными.Подробнее
- Отклонение от стандартного отклонения Отклонение от стандартного отклонения Отклонение — это числовое значение, определяющее изменчивость каждого наблюдения по среднему арифметическому, а стандартное отклонение — это мера, позволяющая определить, насколько разбросаны наблюдения по среднему арифметическому.
 читать далее
читать далее
Как рассчитать дисперсию в Excel [Пошаговое руководство]
Вычисление дисперсии позволяет определить разброс чисел в наборе данных по отношению к среднему. Это отличный инструмент для аналитиков данных, которые могут использовать Excel для расчета дисперсии с помощью таких функций, как VAR.S и VAR.P. В этом пошаговом руководстве мы объясним, как использовать функции дисперсии.
В математических терминах дисперсия — это вычисление того, насколько набор значений отличается от среднего значения (среднего). Если дисперсия равна нулю, разнообразия нет — все числа, скорее всего, будут одинаковыми. По мере роста этого числа растет и дисперсия.
Это может быть использовано аналитиками во всех сферах: от определения разного возраста в группе до определения распределения доходности по различным инвестиционным портфелям. Excel позволяет вычислять такую дисперсию, используя функции, предназначенные для целых наборов данных (дисперсия совокупности) или небольшого подмножества большей группы данных (дисперсия выборки).

Это важное отличие, так как Excel вычисляет дисперсию по-разному в зависимости от размера набора данных. Если вы работаете с выборкой меньшего размера, вам потребуется использовать функции VAR, VAR.S или VARA для расчета дисперсии. Для дисперсии населения вам нужно будет использовать вместо этого VARP, VAR.P, или VARPA .
Несмотря на то, что между этими функциями есть сходство, перед их использованием необходимо учитывать некоторые важные моменты. В этой статье мы объясним:
- Что такое функции дисперсии в Excel и для чего они используются?
- Как работают функции отклонения в Microsoft Excel?
- На что обратить внимание перед использованием функций дисперсии в Excel
- Как рассчитать дисперсию в Excel: пошаговое руководство
Как работают функции дисперсии в Excel? Чтобы помочь вам, давайте пробежимся по основам.
1. Что такое функции дисперсии в Excel и для чего они используются?
Дисперсия работает путем определения разброса значений по отношению к среднему.
 Если у вас есть набор результатов экзаменов для группы студентов, вы можете получить совершенно разные значения на двух отдельных экзаменах, но с одним и тем же средним значением. Определив дисперсию, вы можете определить, насколько хорошо группа выступила в целом.
Если у вас есть набор результатов экзаменов для группы студентов, вы можете получить совершенно разные значения на двух отдельных экзаменах, но с одним и тем же средним значением. Определив дисперсию, вы можете определить, насколько хорошо группа выступила в целом.Вы можете рассчитать этот спред (дисперсию) с помощью функций дисперсии Excel. Как мы уже упоминали, существует две основные формы дисперсии, которые вы можете рассчитать в Excel: дисперсия генеральной совокупности и выборочная дисперсия . В этом контексте совокупность представляет собой весь набор данных, а не выборку (или меньшую ее подмножество).
Чтобы вычислить эти значения, вы можете использовать одну из шести функций отклонения в Excel. Для выборочной дисперсии вы можете использовать VAR, VAR.S или VARA функций. VAR — это исходная функция, а VAR.S — более новая замена, предлагающая некоторые улучшения скорости по сравнению с оригиналом.

VAR и VAR.S поддерживают только числовые значения, но если вы хотите использовать текстовые строки или логические тесты для набора образцов, вам нужно вместо этого использовать VARA .
Для дисперсии совокупности вам необходимо использовать функции VARP, VAR.P или VARPA . Как и в случае функций выборочной дисперсии, VARP является оригинальным, а VAR.P является более новой (и рекомендуемой) заменой, при этом обе функции работают только с числовыми значениями. Для работы с текстовыми строками или логическими выражениями используйте вместо этого VARPA .
Если вы думаете, что это очень похоже на стандартное отклонение, то это потому, что оно (почти) так и есть. Стандартное отклонение вычисляет, в среднем, насколько ваши значения далеки от среднего. Вариация — это просто квадрат значения стандартного отклонения, который дает вам представление о том, насколько далеко все ваши числа разбросаны от среднего.

2. Как работают функции дисперсии в Excel?
Как мы уже упоминали, существует шесть функций дисперсии, которые вы можете использовать в Excel, разделенных на две категории для работы либо с популяцией, либо с выборкой.
Это:
- VAR, VAR.S или VARA для дисперсии выборки, и
- VARP, VAR.P или VARPA для VARIANCE .
Из этих шести две функции ( VAR и VARP ) считаются устаревшими, будучи замененными на VAR.S и VAR.P . В настоящее время они взаимозаменяемы, но в будущем могут быть удалены из Excel.
Четыре из этих функций ( VAR, VARP, VAR.S и VAR.P ) фокусируются на числовых данных . Это означает, что если вы начинающий аналитик данных, пытающийся определить дисперсию набора чисел, используя либо выборку набора данных, либо весь набор данных, вам следует использовать эти функции.

Однако, если ваши данные смешаны, вам нужно будет использовать вместо них VARA или VARPA . Эти функции поддерживают текст, числа и логические значения ( ИСТИНА, ЛОЖЬ , 1 или 0 ).
Под поддержкой мы подразумеваем, что текстовые строки и логические результаты преобразуются в числовой эквивалент, где текстовая строка считается как 0 (или FALSE ). Логические значения считаются как их числовой эквивалент ( 0 для ЛОЖЬ или 1 для ИСТИНА ). Это может повлиять на ваши общие результаты, поэтому тщательно выбирайте функции.
Если вы хотите создать формулу с использованием любой из этих функций дисперсии, вам потребуется использовать заданную структуру. Структура остается неизменной для каждой из шести функций:
- =ПЕРЕМНАЯ(значение1, значение2, …)
- =ПЕР.
 С(значение1,
С(значение1, 40388
,…) - = VARP (Value1, Значение 2 ,…)
- = var.p (значение1,
- = VAR.P (Value1, 787878787, = VAR.P (Value1, 7878787, = VAR.P. = VARA (значение1, Value2, …)
- = VARPA (значение1, Value2, ** . использование этих функций является ссылкой на данные, которые вы используете ( значение1 ). На это можно ссылаться как на диапазон ячеек или как значения напрямую (где значение1 — ваше первое значение, значение2 — ваше второе значение и т. д.).
Для работы функции отклонения требуется только одно значение ( значение1 ). Для диапазонов ячеек это рассматривается как одно значение ( value1 ) для целей создания формулы.

3. На что следует обратить внимание перед использованием функций дисперсии в Excel
Перед тем, как вы решите вычислить дисперсию в Excel с помощью этих функций, необходимо принять во внимание множество соображений. В частности, вам необходимо учитывать:
- Хотя VAR и VAR.S технически взаимозаменяемы, VAR.S является заменой функции Excel для выборочных наборов данных и должна использоваться в первую очередь. Аналогично, VAR.P следует использовать поверх VARP для наборов данных населения в качестве более новой функции.
- VAR, VAR.S, VARP и VARP поддерживают только числовых значения . Другие значения (текстовые строки, логические значения и т. д.) игнорируются и не учитываются при подсчете результата.
- Если вы хотите подсчитывать текстовые или логические значения при расчете дисперсии, вам нужно использовать VARA (для образцов) или VARPA (для популяционных наборов).

- Вы можете использовать ссылки на диапазоны ячеек (например, =VAR.S(A1:D10) ) в формулах дисперсии или ссылаться на каждое значение отдельно (например, =VAR.S(1,2,3,4) ) ).
- Если вы ссылаетесь на каждое значение отдельно, вы можете использовать до 254 различных значений . Это ограничение Excel, и его нельзя увеличить. Если вам нужно больше, сначала заполните электронную таблицу, а затем вместо этого используйте ссылку на диапазон ячеек, содержащий эти ячейки.
- Требуется только один аргумент ( значение1 ), который может содержать одно значение или ссылку на диапазон ячеек. Однако вычисление дисперсии по одному значению излишне, поэтому вам потребуется использовать больше аргументов, если вы вводите их напрямую в формулу.
- Если вы добавляете текстовую строку в качестве значения в формулу отклонения, вам нужно будет указать ее в другой ячейке, чтобы формула работала, как прямое добавление текстовой строки в качестве значения 9Аргумент 0065 приведет к появлению ошибки # VALUE .

4. Как рассчитать дисперсию в Excel: пошаговое руководство для расчета дисперсии. Если вы пытаетесь рассчитать дисперсию в Excel, используя набор данных совокупности (то есть весь набор данных, а не меньшую выборку), вы можете сделать это, используя
VARP, VAR.P или вместо VARPA .В данном руководстве ссылки на VAR и VAR.S взаимозаменяемы. Мы использовали VAR.S , которая является более новой и рекомендуемой функцией, но более старую VAR можно использовать (на данный момент) в старых книгах. Однако, если вы можете, используйте VAR.S .
Аналогично, ссылки на VARP и VAR.P также взаимозаменяемы, но вы должны использовать VAR.P в первую очередь. VARA и VARPA остаются доступными для всех пользователей Excel, независимо от используемой версии.

Шаг 1. Выберите пустую ячейку
Чтобы вставить функцию отклонения в новую формулу, начните с открытия рабочей книги Excel, содержащей ваши данные, и выбора пустой ячейки. Кроме того, вы можете открыть новую книгу, убедившись, что лист, содержащий ваши данные, остается открытым и свернутым.
Выделив ячейку, нажмите строка формул в нижней части ленточной панели, пока не появится мигающий курсор.
Когда появится мигающий курсор, вы готовы начать вставлять новую формулу.
Шаг 2. Вставьте набор данных напрямую или с помощью ссылок на ячейки
Как мы объясняли ранее, все функции отклонения в Excel используют одну и ту же структуру для создания новых формул. Чтобы вставить новую функцию дисперсии с использованием выборочного набора данных (меньшая выборка из большего набора совокупности), начните с ввода =VAR.S( или =VAR.S( или =VARA( ) в строке формул вверху.

Если вы работаете с набором данных совокупности (весь набор данных), введите =VAR.P( или =VARPA( вместо этого.
Когда ваша формула открыта, вам нужно будет вставить свои данные дальше. Большинство пользователей, вероятно, предпочтут ссылаться на данные в другом месте вашей текущей книги (или в свернутой книге), используя диапазон ячеек.
Например, =VAR.S(C2:C10) или =VAR.P(C2:C20) завершает формулу, используя числовые данные в диапазоне ячеек между ячейками C2 и C10 (для выборки) или C2 и C20 (для совокупности установлен). Обязательно замените эти ссылки своими собственными.
Если вы работаете с данными, содержащими числа, текст и/или логические значения, лучше всего подойдет =ДИСПЕР(C2:C10) или =ДСП(C2:C20) . Вместо того, чтобы игнорировать текст или логические значения (как это сделали бы VAR, VAR.
 S, VARP или VAR.P), значения в формуле VARA или VARPA будут учитываться при подсчете общего результата.
S, VARP или VAR.P), значения в формуле VARA или VARPA будут учитываться при подсчете общего результата.Вы также можете ссылаться на каждую ячейку отдельно. Например, =VARA(C2:C10) и =VARA(C2,C3,C4,C5,C6,C7,C8,C9,C10) вернут тот же результат.
Если вы добавляете числовые значения непосредственно в формулу, вам нужно добавлять значения одно за другим. Каждое значение должно быть разделено запятыми. Например, =VAR.S(1,2,3,4,5,6) или =VAR.P(1,2,3,4,5,6,7,8,9,10) даст вам разницу между числами 1 и 6 (или 1 и 10 для набора населения) напрямую.
То же самое можно сделать с VARA или VARPA . Например, =VARA(1,2,TRUE,3) будет работать, а значение TRUE считается его числовым эквивалентом ( 1 ). Аналогично, =VARPA(1,2,TRUE,3,4,10,8) подсчитывает эти значения таким же образом, при этом TRUE считается как 1 .

VARA и VARPA поддерживают текст, но для их использования вам потребуется использовать ссылку на ячейку или диапазон ячеек. Например, = VARA(1,2,TRUE,D5,3,4,10,8) или =VARA(D2:D9) будет работать, где D5 содержит текст, который считается значением FALSE ( 0 ). Однако если вы попытаетесь добавить текстовую строку напрямую, Excel вернет ошибку #ЗНАЧ .
Если вы добавили ссылку на диапазон ячеек, обязательно после этого закройте формулу закрывающей скобкой, затем нажмите , введите , чтобы просмотреть результаты (или щелкните другую пустую ячейку). Для значений, добавляемых напрямую, поместите закрывающую скобку после того, как окончательное значение будет вставлено в формулу.
Заключительные мысли
Рассчитав дисперсию, вы можете многое узнать о данных, с которыми работаете. Это делает жизнь типичного аналитика данных еще проще, позволяя вам подтверждать теории и гипотезы с помощью одной формулы Excel.

- Что такое выборочная дисперсия?




 4 Выборочное среднее и выборочная дисперсия
4 Выборочное среднее и выборочная дисперсия

 Свойство (31) называется несмещенностью.
Тот факт, что дисперсия исчезает с увеличением объема выборки
дает основание для вывода о том, что, чем больше данных измерений мы возьмем
для статистической обработки, тем точнее будут наши выводы.
Свойство (31) называется несмещенностью.
Тот факт, что дисперсия исчезает с увеличением объема выборки
дает основание для вывода о том, что, чем больше данных измерений мы возьмем
для статистической обработки, тем точнее будут наши выводы.
 5 Оценивание неизвестных параметров …
5 Оценивание неизвестных параметров …  Сложите все значения данных и разделите на размер выборки n. Таким образом, (5 + 6 + 1) / 3 = 4
Сложите все значения данных и разделите на размер выборки n. Таким образом, (5 + 6 + 1) / 3 = 4  Однако значение выборочной дисперсии выше, чем дисперсии генеральной совокупности. В приведенной ниже таблице показана разница между выборочной дисперсией и дисперсией генеральной совокупности. 9{2}}{н}\)
Однако значение выборочной дисперсии выше, чем дисперсии генеральной совокупности. В приведенной ниже таблице показана разница между выборочной дисперсией и дисперсией генеральной совокупности. 9{2}}{н}\) {2}}{n}\)
{2}}{n}\) Например, если вы измеряете вес американцев, вам будет невозможно (ни с точки зрения времени, ни с денежной точки зрения) измерить вес каждого человека в популяции. Решение состоит в том, чтобы взять выборку населения, скажем, 1000 человек, и использовать этот размер выборки для оценки фактических весов всего населения. Дисперсия поможет вам понять, насколько распределены ваши веса.
Например, если вы измеряете вес американцев, вам будет невозможно (ни с точки зрения времени, ни с денежной точки зрения) измерить вес каждого человека в популяции. Решение состоит в том, чтобы взять выборку населения, скажем, 1000 человек, и использовать этот размер выборки для оценки фактических весов всего населения. Дисперсия поможет вам понять, насколько распределены ваши веса.
 9 фунтов, большинство людей весят от 51 фунта (в среднем 99) до 249 фунтов (в среднем +99).
9 фунтов, большинство людей весят от 51 фунта (в среднем 99) до 249 фунтов (в среднем +99). Безусловно, самый простой способ найти дисперсию — использовать онлайн-калькулятор стандартного отклонения. Вы также можете использовать его для проверки своей работы. Должны работать формулы вручную? Читать дальше!
Безусловно, самый простой способ найти дисперсию — использовать онлайн-калькулятор стандартного отклонения. Вы также можете использовать его для проверки своей работы. Должны работать формулы вручную? Читать дальше! В нашем примере у нас есть 6 элементов, поэтому:
В нашем примере у нас есть 6 элементов, поэтому: Если у вас есть население, вы будете делить на «n» (количество элементов в вашем наборе данных). Однако, если у вас есть выборка (а это относится к большинству вопросов по статистике, которые вы получите на уроке!) вам нужно будет разделить на n-1. О том, почему используется n-1, см.: Поправка Бесселя.
Если у вас есть население, вы будете делить на «n» (количество элементов в вашем наборе данных). Однако, если у вас есть выборка (а это относится к большинству вопросов по статистике, которые вы получите на уроке!) вам нужно будет разделить на n-1. О том, почему используется n-1, см.: Поправка Бесселя.
 33 2 = 43401.3889
33 2 = 43401.3889

 Если у вас нет пакета инструментов (или вы не хотите его устанавливать), второй вариант — использовать функцию VAR.
Если у вас нет пакета инструментов (или вы не хотите его устанавливать), второй вариант — использовать функцию VAR.

 Продолжайте с шага 4 выше, чтобы вычислить дисперсию.
Продолжайте с шага 4 выше, чтобы вычислить дисперсию.  Руководство для студентов по дисперсионному анализу. London: Routledge, 1999.
Руководство для студентов по дисперсионному анализу. London: Routledge, 1999.
 Математически он определяется как среднее квадратов отличий от среднего.
Математически он определяется как среднее квадратов отличий от среднего. е. 5 тигров — это вся интересующая вас группа). Если ваши данные являются выборкой из большей совокупности, вам необходимо рассчитать выборочную дисперсию, используя немного другую формулу.
е. 5 тигров — это вся интересующая вас группа). Если ваши данные являются выборкой из большей совокупности, вам необходимо рассчитать выборочную дисперсию, используя немного другую формулу. С
С А дисперсия, рассчитанная по выборке, называется выборочной дисперсией .
А дисперсия, рассчитанная по выборке, называется выборочной дисперсией . S в текущих версиях Excel.
S в текущих версиях Excel.

 Он доступен во всех версиях Excel с 2000 по 2019.
Он доступен во всех версиях Excel с 2000 по 2019. Причина в том, что VARPA оценивает текстовые значения как нули, в то время как VARP и VAR.P игнорируют текстовые и логические значения в ссылках. Подробную информацию см. в разделе VAR.P и VARPA.
Причина в том, что VARPA оценивает текстовые значения как нули, в то время как VARP и VAR.P игнорируют текстовые и логические значения в ссылках. Подробную информацию см. в разделе VAR.P и VARPA. 

 1 Определение 1.2 Дисперсия генеральной совокупности 1.3 Дисперсия выборки 1.4 Дисперсия случайной величины 1.5 Дисперсия дискретной случайной величины 1.6 Дисперсия непрерывной случайной величины 2 Стандартное отклонение 2.1 Определение 2.2 Стандартное отклонение генеральной совокупности 2.3 Стандартное отклонение выборки 3 Обработка Example3.1 Пример видео 4 Рабочая тетрадь 5 Внешние ресурсы 92 \text{.}\]
1 Определение 1.2 Дисперсия генеральной совокупности 1.3 Дисперсия выборки 1.4 Дисперсия случайной величины 1.5 Дисперсия дискретной случайной величины 1.6 Дисперсия непрерывной случайной величины 2 Стандартное отклонение 2.1 Определение 2.2 Стандартное отклонение генеральной совокупности 2.3 Стандартное отклонение выборки 3 Обработка Example3.1 Пример видео 4 Рабочая тетрадь 5 Внешние ресурсы 92 \text{.}\]


 читать далее, чтобы рассчитать дисперсию популяции. Одним из самых популярных уведомлений о дисперсии населения является σ 2 . Это произносится как сигма в квадрате.
читать далее, чтобы рассчитать дисперсию популяции. Одним из самых популярных уведомлений о дисперсии населения является σ 2 . Это произносится как сигма в квадрате. Чтобы рассчитать среднее значениеРассчитать Среднее значение означает среднее математическое значение, рассчитанное для двух или более значений. В основном есть два способа: среднее арифметическое, когда все числа складываются и делятся на их веса, и среднее геометрическое, когда мы умножаем числа вместе, берем корень N и вычитаем из него единицу. Подробнее, складываем все наблюдения и затем разделите это на количество наблюдений (N).
Чтобы рассчитать среднее значениеРассчитать Среднее значение означает среднее математическое значение, рассчитанное для двух или более значений. В основном есть два способа: среднее арифметическое, когда все числа складываются и делятся на их веса, и среднее геометрическое, когда мы умножаем числа вместе, берем корень N и вычитаем из него единицу. Подробнее, складываем все наблюдения и затем разделите это на количество наблюдений (N).  Другими словами, возведите в квадрат каждое из чисел, полученных в столбце 2.
Другими словами, возведите в квадрат каждое из чисел, полученных в столбце 2. 
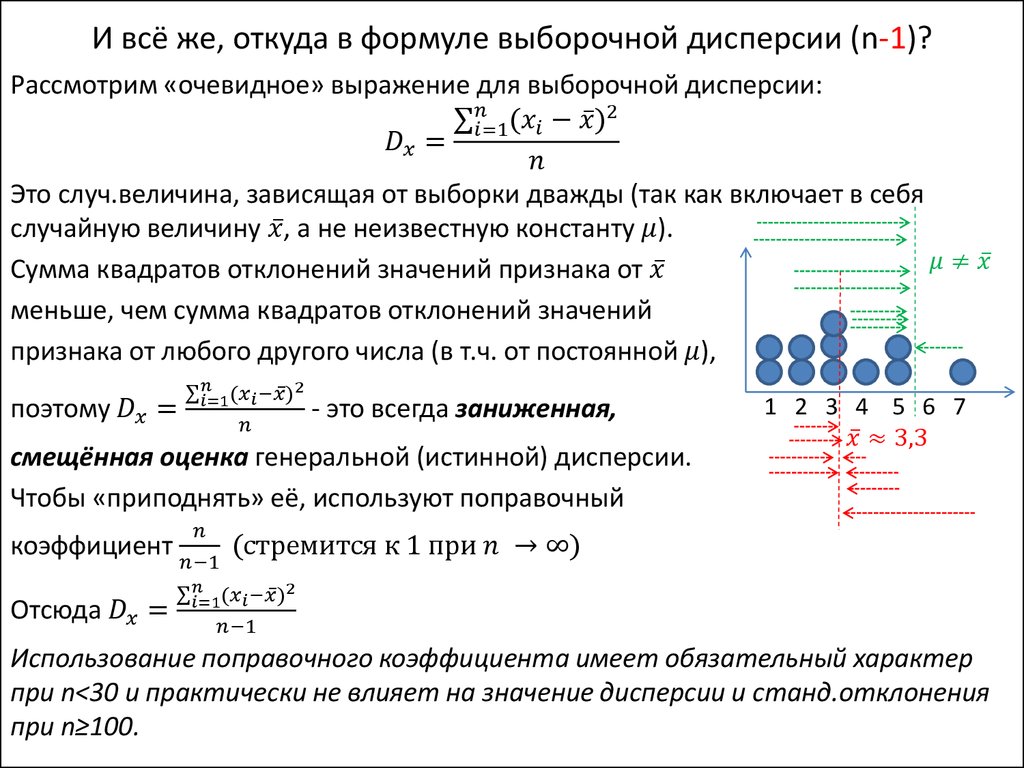 Департамент управления закупает 7 больших контейнеров для хранения этого сока на заводе. Отдел контроля качества принял решение, что контейнеры будут отклонены, если дисперсия контейнеров превышает 10. Даны веса 7 контейнеров в кг: 105, 100, 102, 95, 100, 98 и 107. Пожалуйста, сообщите Отдел контроля качества о том, следует ли отбраковывать контейнеры.
Департамент управления закупает 7 больших контейнеров для хранения этого сока на заводе. Отдел контроля качества принял решение, что контейнеры будут отклонены, если дисперсия контейнеров превышает 10. Даны веса 7 контейнеров в кг: 105, 100, 102, 95, 100, 98 и 107. Пожалуйста, сообщите Отдел контроля качества о том, следует ли отбраковывать контейнеры. 
 Набор данных 1 состоит из 5 чисел — 55, 50, 45, 50 и 50. Набор данных 2 состоит из 10, 50, 85, 90 и 15. Оба набора данных имеют одинаковое среднее значение, равное 50. Но, в наборе данных 1 значения близки друг к другу, в то время как в наборе данных 2 значения разбросаны. Дисперсия дает научную меру этой близости/дисперсии. Набор данных 1 имеет дисперсию всего 10, тогда как набор данных 2 имеет огромную дисперсию 1130. Таким образом, большая дисперсия указывает на то, что числа далеки от среднего и друг от друга. Небольшая дисперсия указывает на то, что числа близки друг к другу.
Набор данных 1 состоит из 5 чисел — 55, 50, 45, 50 и 50. Набор данных 2 состоит из 10, 50, 85, 90 и 15. Оба набора данных имеют одинаковое среднее значение, равное 50. Но, в наборе данных 1 значения близки друг к другу, в то время как в наборе данных 2 значения разбросаны. Дисперсия дает научную меру этой близости/дисперсии. Набор данных 1 имеет дисперсию всего 10, тогда как набор данных 2 имеет огромную дисперсию 1130. Таким образом, большая дисперсия указывает на то, что числа далеки от среднего и друг от друга. Небольшая дисперсия указывает на то, что числа близки друг к другу. Оптимальные портфели Оптимизация портфеля относится к стратегическому процессу внесения улучшений или положительных изменений в портфель инвестора, содержащий различные активы. Коэффициент Шарпа помогает анализировать доходность оптимального портфеля. Подробнее, оптимизируя два основных параметра — доходность и волатильность. Волатильность, измеряемая дисперсией, является мерой риска конкретной финансовой ценной бумаги.
Оптимальные портфели Оптимизация портфеля относится к стратегическому процессу внесения улучшений или положительных изменений в портфель инвестора, содержащий различные активы. Коэффициент Шарпа помогает анализировать доходность оптимального портфеля. Подробнее, оптимизируя два основных параметра — доходность и волатильность. Волатильность, измеряемая дисперсией, является мерой риска конкретной финансовой ценной бумаги. е. когда доходность одного актива увеличивается, доходность второго актива также увеличивается, и наоборот для отрицательной ковариации. подробнее
е. когда доходность одного актива увеличивается, доходность второго актива также увеличивается, и наоборот для отрицательной ковариации. подробнее читать далее
читать далее
 Если у вас есть набор результатов экзаменов для группы студентов, вы можете получить совершенно разные значения на двух отдельных экзаменах, но с одним и тем же средним значением. Определив дисперсию, вы можете определить, насколько хорошо группа выступила в целом.
Если у вас есть набор результатов экзаменов для группы студентов, вы можете получить совершенно разные значения на двух отдельных экзаменах, но с одним и тем же средним значением. Определив дисперсию, вы можете определить, насколько хорошо группа выступила в целом.

