Соотношение косинуса и синуса. Что такое синус? Простейшие тригонометрические тождества
Понятия синуса, косинуса, тангенса и котангенса являются основными категориями тригонометрии — раздела математики, и неразрывно связаны с определением угла. Владение этой математической наукой требует запоминания и понимания формул и теорем, а также развитого пространственного мышления. Именно поэтому у школьников и студентов тригонометрические вычисления нередко вызывают трудности. Чтобы побороть их, следует подробнее познакомиться с тригонометрическими функциями и формулами.
Понятия в тригонометрии
Чтобы разобраться в базовых понятиях тригонометрии, следует сначала определиться с тем, что такое прямоугольный треугольник и угол в окружности, и почему именно с ними связаны все основные тригонометрические вычисления. Треугольник, в котором один из углов имеет величину 90 градусов, является прямоугольным. Исторически эта фигура часто использовалась людьми в архитектуре, навигации, искусстве, астрономии. Соответственно, изучая и анализируя свойства этой фигуры, люди пришли к вычислению соответствующих соотношений её параметров.
Соответственно, изучая и анализируя свойства этой фигуры, люди пришли к вычислению соответствующих соотношений её параметров.
Основные категории, связанные с прямоугольными треугольниками — гипотенуза и катеты. Гипотенуза — сторона треугольника, лежащая против прямого угла. Катеты, соответственно, это остальные две стороны. Сумма углов любых треугольников всегда равна 180 градусам.
Сферическая тригонометрия — раздел тригонометрии, который не изучается в школе, однако в прикладных науках типа астрономии и геодезии, учёные пользуются именно им. Особенность треугольника в сферической тригонометрии в том, что он всегда имеет сумму углов более 180 градусов.
Углы треугольника
В прямоугольном треугольнике синусом угла является отношение катета, противолежащего искомому углу, к гипотенузе треугольника. Соответственно, косинус — это отношение прилежащего катета и гипотенузы. Оба эти значения всегда имеют величину меньше единицы, так как гипотенуза всегда длиннее катета.
Тангенс угла — величина, равная отношению противолежащего катета к прилежащему катету искомого угла, или же синуса к косинусу. Котангенс, в свою очередь, это отношение прилежащего катета искомого угла к противолежащему кактету. Котангенс угла можно также получить, разделив единицу на значение тангенса.
Единичная окружность
Единичная окружность в геометрии — окружность, радиус которой равен единице. Такая окружность строится в декартовой системе координат, при этом центр окружности совпадает с точкой начала координат, а начальное положение вектора радиуса определено по положительному направлению оси Х (оси абсцисс). Каждая точка окружности имеет две координаты: ХХ и YY, то есть координаты абсцисс и ординат. Выбрав на окружности любую точку в плоскости ХХ, и опустив с неё перпендикуляр на ось абсцисс, получаем прямоугольный треугольник, образованный радиусом до выбранной точки (обозначим её буквой С), перпендикуляром, проведённым до оси Х (точка пересечения обозначается буквой G), а отрезком оси абсцисс между началом координат (точка обозначена буквой А) и точкой пересечения G. Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG. Аналогично, sin α=CG.
Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG. Аналогично, sin α=CG.
Кроме того, зная эти данные, можно определить координату точки С на окружности, так как cos α=AG, а sin α=CG, значит, точка С имеет заданные координаты (cos α;sin α). Зная, что тангенс равен отношению синуса к косинусу, можно определить, что tg α = y/х, а ctg α = х/y. Рассматривая углы в отрицательной системе координат, можно рассчитать, что значения синуса и косинуса некоторых углов могут быть отрицательными.
Вычисления и основные формулы
Значения тригонометрических функций
Рассмотрев сущность тригонометрических функций через единичную окружность, можно вывести значения этих функций для некоторых углов. k * arcsin α + πk.
k * arcsin α + πk.
Тождества со значением cos х = а, где k — любое целое число:
- cos х = 0, х = π/2 + πk.
- cos х = 1, х = 2πk.
- cos х = -1, х = π + 2πk.
- cos х = а, |a| > 1, нет решений.
- cos х = а, |a| ≦ 1, х = ±arccos α + 2πk.
Тождества со значением tg х = а, где k — любое целое число:
- tg х = 0, х = π/2 + πk.
- tg х = а, х = arctg α + πk.
Тождества со значением ctg х = а, где k — любое целое число:
- ctg х = 0, х = π/2 + πk.
- ctg х = а, х = arcctg α + πk.
Формулы приведения
Эта категория постоянных формул обозначает методы, с помощью которых можно перейти от тригонометрических функций вида к функциям аргумента, то есть привести синус, косинус, тангенс и котангенс угла любого значения к соответствующим показателям угла интервала от 0 до 90 градусов для большего удобства вычислений.
Формулы приведения функций для синуса угла выглядят таким образом:
- sin(900 — α) = α;
- sin(900 + α) = cos α;
- sin(1800 — α) = sin α;
- sin(1800 + α) = -sin α;
- sin(2700 — α) = -cos α;
- sin(2700 + α) = -cos α;
- sin(3600 — α) = -sin α;
- sin(3600 + α) = sin α.

Для косинуса угла:
- cos(900 — α) = sin α;
- cos(900 + α) = -sin α;
- cos(1800 — α) = -cos α;
- cos(1800 + α) = -cos α;
- cos(2700 — α) = -sin α;
- cos(2700 + α) = sin α;
- cos(3600 — α) = cos α;
- cos(3600 + α) = cos α.
Использование вышеуказанных формул возможно при соблюдении двух правил. Во-первых, если угол можно представить как значение (π/2 ± a) или (3π/2 ± a), значение функции меняется:
- с sin на cos;
- с cos на sin;
- с tg на ctg;
- с ctg на tg.
Значение функции остаётся неизменным, если угол может быть представлен как (π ± a) или (2π ± a).
Во-вторых, знак приведенной функции не изменяется: если он изначально был положительным, таким и остаётся. Аналогично с отрицательными функциями.
Формулы сложения
Эти формулы выражают величины синуса, косинуса, тангенса и котангенса суммы и разности двух углов поворота через их тригонометрические функции.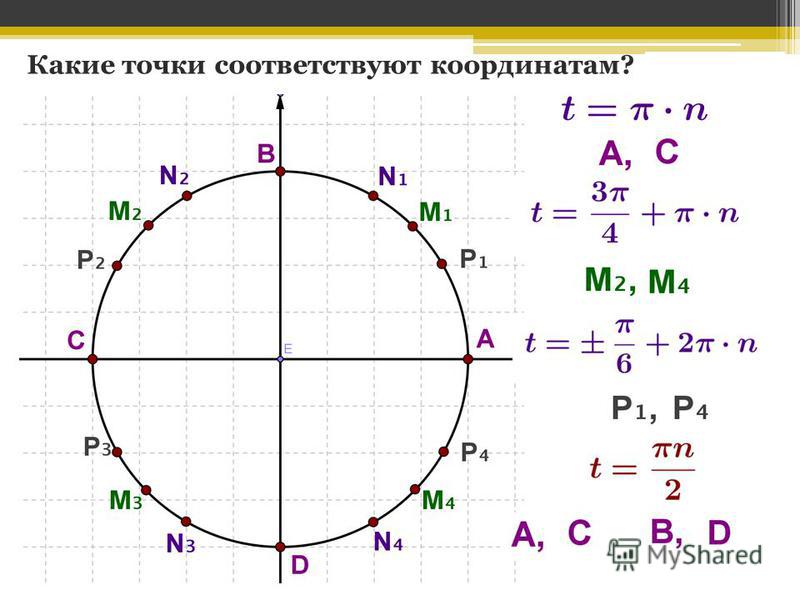 2 x/2) / (2tgx/2), при этом х = π + 2πn.
2 x/2) / (2tgx/2), при этом х = π + 2πn.
Частные случаи
Частные случаи простейших тригонометрических уравнений приведены ниже (k — любое целое число).
Частные для синуса:
| Значение sin x | Значение x |
|---|---|
| 0 | πk |
| 1 | π/2 + 2πk |
| -π/2 + 2πk | |
| 1/2 | π/6 + 2πk или 5π/6 + 2πk |
| -1/2 | -π/6 + 2πk или -5π/6 + 2πk |
| √2/2 | π/4 + 2πk или 3π/4 + 2πk |
| -√2/2 | -π/4 + 2πk или -3π/4 + 2πk |
| √3/2 | π/3 + 2πk или 2π/3 + 2πk |
| -√3/2 | -π/3 + 2πk или -2π/3 + 2πk |
Частные для косинуса:
| Значение cos x | Значение х |
|---|---|
| 0 | π/2 + 2πk |
| 1 | 2πk |
| -1 | 2 + 2πk |
| 1/2 | ±π/3 + 2πk |
| -1/2 | ±2π/3 + 2πk |
| √2/2 | ±π/4 + 2πk |
| -√2/2 | ±3π/4 + 2πk |
| √3/2 | ±π/6 + 2πk |
| -√3/2 | ±5π/6 + 2πk |
Частные для тангенса:
| Значение tg x | Значение х |
|---|---|
| 0 | πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3/3 | π/6 + πk |
| -√3/3 | -π/6 + πk |
| √3 | π/3 + πk |
| -√3 | -π/3 + πk |
Частные для котангенса:
| Значение ctg x | Значение x |
|---|---|
| 0 | π/2 + πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3 | π/6 + πk |
| -√3 | -π/3 + πk |
| √3/3 | π/3 + πk |
| -√3/3 | -π/3 + πk |
Теоремы
Теорема синусов
Существует два варианта теоремы — простой и расширенный.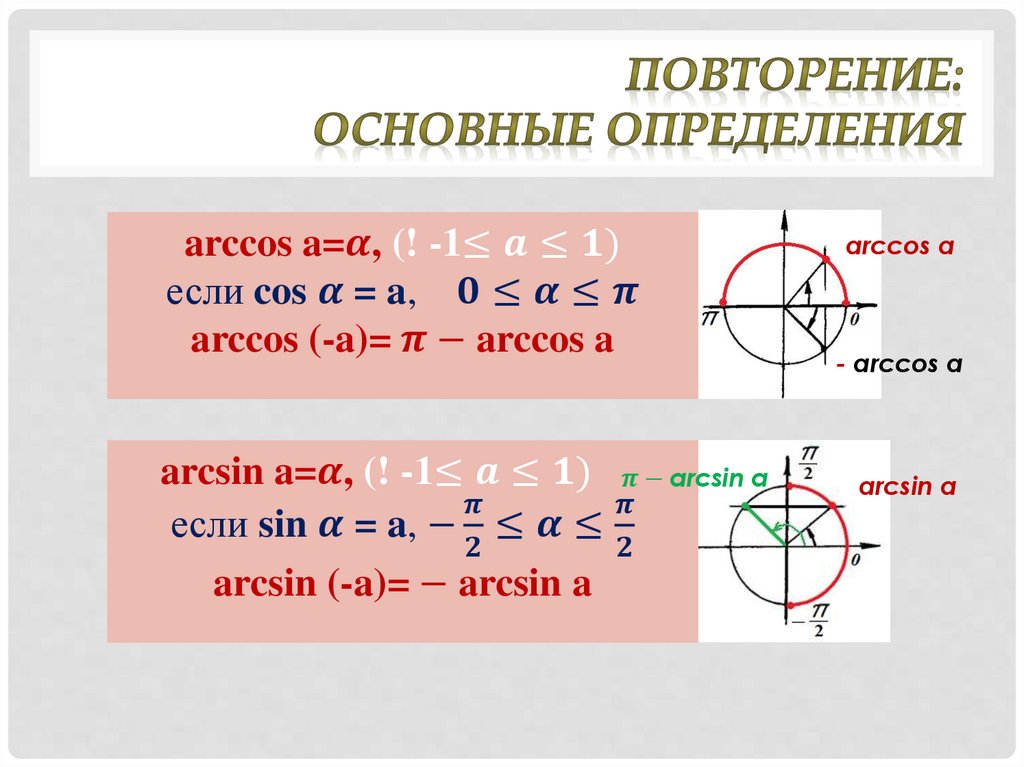 2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
Теорема тангенсов
Формула выражает связь между тангенсами двух углов, и длиной сторон, им противолежащих. Стороны обозначены как a, b, c, а соответствующие противолежащие углы — α, β, γ. Формула теоремы тангенсов: (a — b) / (a+b) = tg((α — β)/2) / tg((α + β)/2).
Теорема котангенсов
Связывает радиус вписанной в треугольник окружности с длиной его сторон. Если a, b, c — стороны треугольника, и А, В, С, соответственно, противолежащие им углы, r — радиус вписанной окружности, и p — полупериметр треугольника, справедливы такие тождества:
- ctg A/2 = (p-a)/r;
- ctg B/2 = (p-b)/r;
- ctg C/2 = (p-c)/r.
Прикладное применение
Тригонометрия — не только теоретическая наука, связанная с математическими формулами. Её свойствами, теоремами и правилами пользуются на практике разные отрасли человеческой деятельности — астрономия, воздушная и морская навигация, теория музыки, геодезия, химия, акустика, оптика, электроника, архитектура, экономика, машиностроение, измерительные работы, компьютерная графика, картография, океанография, и многие другие.
Синус, косинус, тангенс и котангенс — основные понятия тригонометрии, с помощью которых математически можно выразить соотношения между углами и длинами сторон в треугольнике, и найти искомые величины через тождества, теоремы и правила.
Изначально синус и косинус возникли из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Именно так и были введены понятия синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут применяться не только в прямоугольных треугольниках. Чтобы найти значение тупого или острого угла, стороны любого треугольника, достаточно применить теорему косинусов и синусов.
Теорема косинусов довольно проста: «Квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними».
Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная — математический инструмент, показывающий, как быстро меняется функция относительно изменения ее аргумента. Производные используются , геометрии, и , ряде технических дисциплин.
При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса — синус, но со знаком «минус».
Применение в математике
Особенно часто синусы и косинусы используются при решении прямоугольных треугольников и задач, связанных с ними.
Удобство синусов и косинусов нашло свое отражение и в технике. Углы и стороны было просто оценивать по теоремам косинусов и синусов, разбивая сложные фигуры и объекты на «простые» треугольники.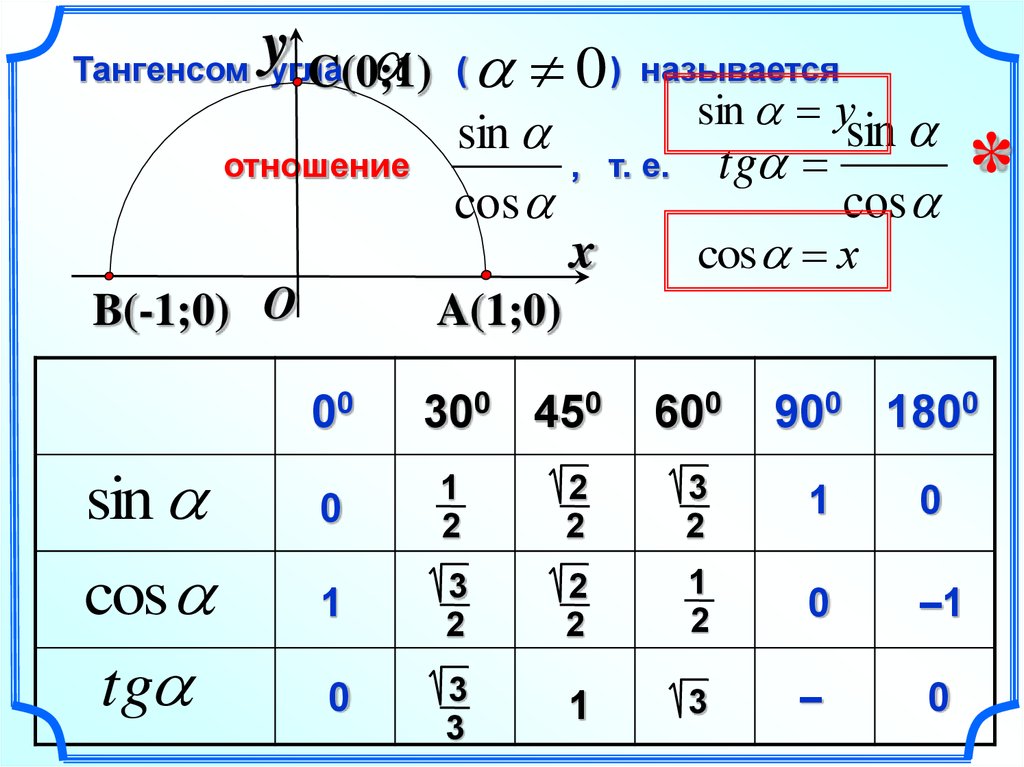 Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов разных углов. В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
π = 3.141592653589793238462… (приблизительное значение числа Пи).
Синус острого угла α прямоугольного треугольника – это отношение противолежащего
катета к гипотенузе.
Обозначается так: sin α.
Косинус острого угла α прямоугольного треугольника – это отношение прилежащего
катета к гипотенузе.
Обозначается так: cos α.
Тангенс острого угла α – это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg α.
Котангенс острого угла α – это отношение прилежащего катета к противолежащему.
Обозначается так: ctg α.
Синус, косинус, тангенс и котангенс угла зависят только от величины угла.
Правила:
Основные тригонометрические тождества в прямоугольном треугольнике:
(α – острый угол, противолежащий катету b и прилежащий к катету a . Сторона с – гипотенуза. β – второй острый угол).
b | sin 2 α + cos 2 α = 1 | |
a | 1 | |
b | 1 | |
a | 1 1 | |
sin α |
При возрастании острого угла sin α и tg α возрастают, а cos α убывает.
Для любого острого угла α:
sin (90° – α) = cos α
cos (90° – α) = sin α
Пример-пояснение :
Пусть в прямоугольном треугольнике АВС
АВ = 6,
ВС = 3,
угол А = 30º.
Выясним синус угла А и косинус угла В.
Решение .
1) Сначала находим величину угла В. Тут все просто: так как в прямоугольном треугольнике сумма острых углов равна 90º, то угол В = 60º:
В = 90º – 30º = 60º.
2) Вычислим sin A. Мы знаем, что синус равен отношению противолежащего катета к гипотенузе. Для угла А противолежащим катетом является сторона ВС. Итак:
BC 3 1
sin A = — = — = —
AB 6 2
3) Теперь вычислим cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла В прилежащим катетом является все та же сторона ВС. Это значит, что нам снова надо разделить ВС на АВ – то есть совершить те же действия, что и при вычислении синуса угла А:
BC 3 1
cos B = — = — = —
AB 6 2
В итоге получается:
sin A = cos B = 1/2.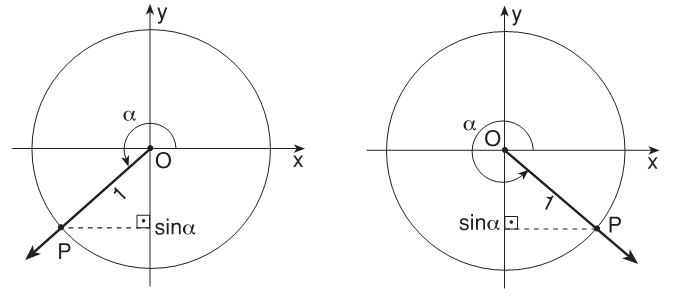
sin 30º = cos 60º = 1/2.
Из этого следует, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла – и наоборот. Именно это и означают наши две формулы:
sin (90° – α) = cos α
cos (90° – α) = sin α
Убедимся в этом еще раз:
1) Пусть α = 60º. Подставив значение α в формулу синуса, получим:
sin (90º – 60º) = cos 60º.
sin 30º = cos 60º.
2) Пусть α = 30º. Подставив значение α в формулу косинуса, получим:
cos (90° – 30º) = sin 30º.
cos 60° = sin 30º.
(Подробнее о тригонометрии — см.раздел Алгебра)
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.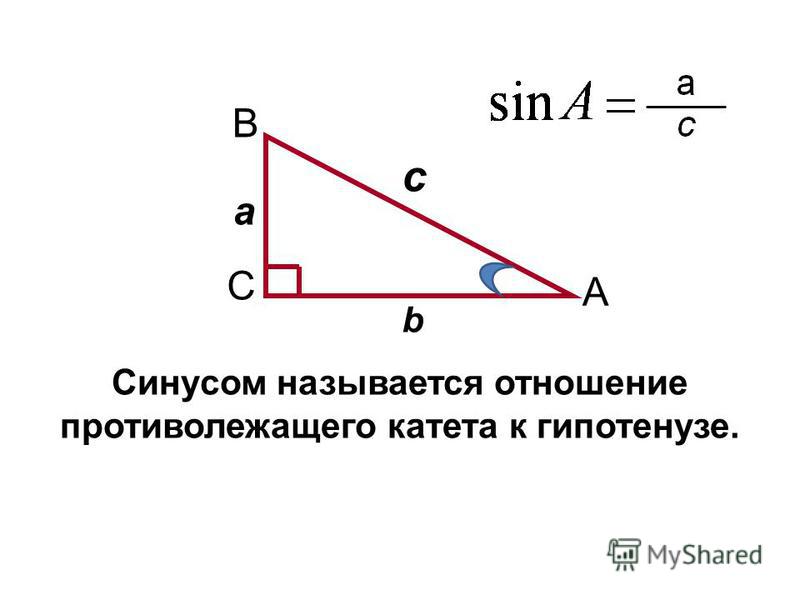
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.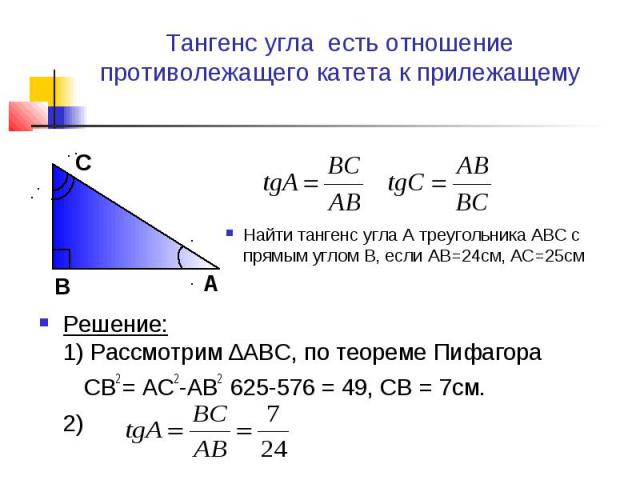
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.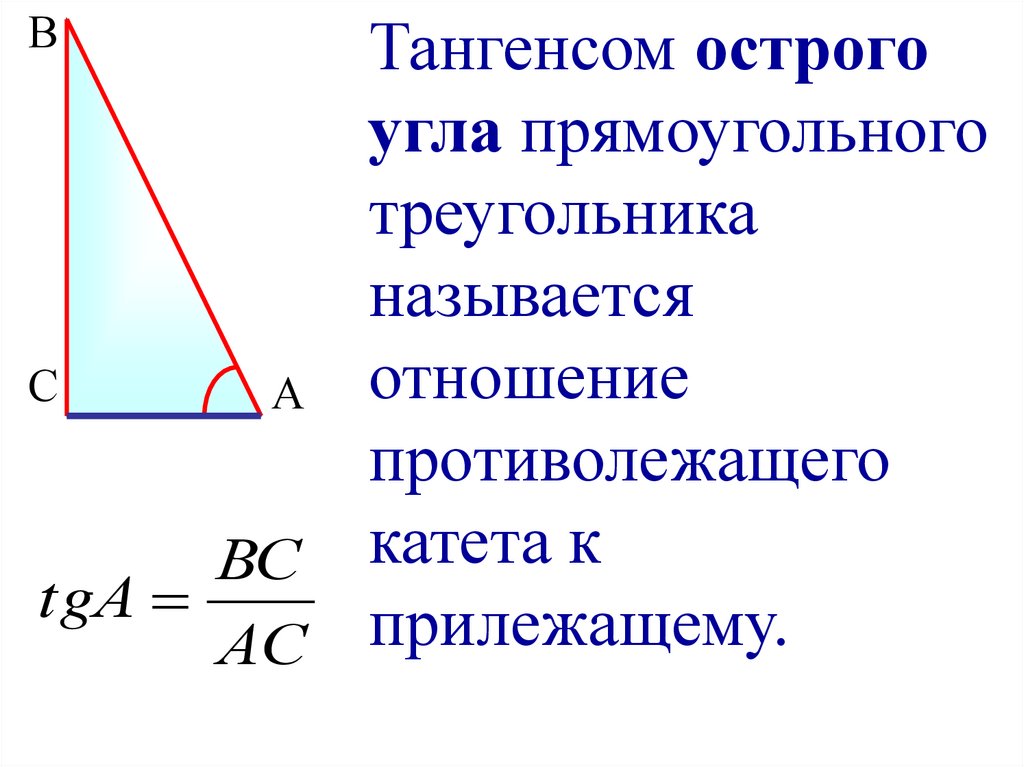
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число.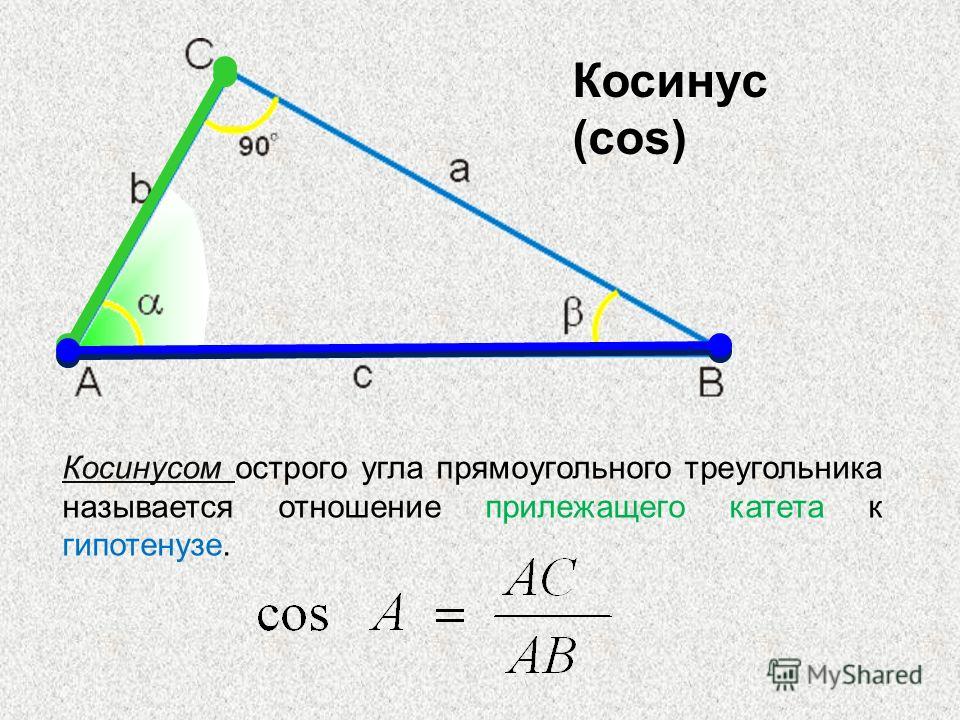 Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/». См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Синус пи, косинус пи, тангенс пи и других углов в радианахПриведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
| ||||||||
| \sin\alpha | 0 | \frac12 | \frac{\sqrt 2}{2} | \frac{\sqrt 3}{2} | 1 | 0 | −1 | 0 |
| \cos\alpha | 1 | \frac{\sqrt 3}{2} | \frac{\sqrt 2}{2} | \frac12 | 0 | −1 | 0 | 1 |
| tg \alpha | 0 | \frac{\sqrt 3}{3} | 1 | \sqrt3 | — | 0 | — | 0 |
| ctg \alpha | — | \sqrt3 | 1 | \frac{\sqrt 3}{3} | 0 | — | 0 | — |
Учителя считают, что каждый школьник должен уметь проводить расчёты, знать тригонометрические формулы, но далеко не каждый преподаватель объясняет, что такое синус и косинус. Каков их смысл, где они используются? Почему мы говорим про треугольники, а в учебнике нарисована окружность? Попробуем связать все факты воедино.
Школьный предмет
Изучение тригонометрии начинается обычно в 7-8 классе средней школы. В это время учащимся объясняют, что такое синус и косинус, предлагают решать геометрические задачи с применением этих функций. Позже появляются более сложные формулы и выражения, которые требуется алгебраическим способом преобразовывать (формулы двойного и половинного угла, степенные функции), проводится работа с тригонометрической окружностью.
В это время учащимся объясняют, что такое синус и косинус, предлагают решать геометрические задачи с применением этих функций. Позже появляются более сложные формулы и выражения, которые требуется алгебраическим способом преобразовывать (формулы двойного и половинного угла, степенные функции), проводится работа с тригонометрической окружностью.
Однако учителя далеко не всегда могут доходчиво объяснить смысл используемых понятий и применимость формул. Поэтому ученик зачастую не видит смысла в данном предмете, а заученная информация быстро забывается. Однако стоит один раз объяснить старшекласснику, например, связь между функцией и колебательным движением, и логическая связь запомнится на многие годы, а шутки на тему бесполезности предмета уйдут в прошлое.
Использование
Заглянем ради любопытства в различные разделы физики. Хотите определить дальность полёта снаряда? Или высчитываете силу трения между объектом и некой поверхностью? Раскачиваете маятник, следите за лучами, проходящими сквозь стекло, высчитываете индукцию? Практически в любой формуле фигурируют тригонометрические понятия. Так что такое синус и косинус?
Так что такое синус и косинус?
Определения
Синус угла представляет собой отношение противолежащего катета к гипотенузе, косинус — прилежащего катета всё к той же гипотенузе. Здесь нет совершенно ничего сложного. Возможно, учеников обычно смущают значения, которые они видят в тригонометрической таблице, ведь там фигурируют квадратные корни. Да, получать из них десятичные дроби не очень удобно, но кто сказал, что все числа в математике должны быть ровными?
На самом деле в задачниках по тригонометрии можно найти забавную подсказку: большинство ответов здесь ровные и в худшем случае содержат корень из двух или из трёх. Вывод прост: если у вас в ответе получилась «многоэтажная» дробь, перепроверьте решение на предмет ошибок в расчётах или в рассуждениях. И вы их, скорее всего, найдете.
Что нужно запомнить
Как и в любой науке, в тригонометрии есть такие данные, которые необходимо выучить.
Во-первых, следует запомнить числовые значения для синусов, косинусов прямоугольного треугольника 0 и 90, а также 30, 45 и 60 градусов. Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде.
Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде.
Нужно помнить, что значение обеих функций не может превышать единицу. Если где-либо в расчетах вы получите значение, выходящее за пределы диапазона 0-1, остановитесь и решите задачу заново.
Сумма квадратов синуса и косинуса равна единице. Если вы уже нашли одно из значений, воспользуйтесь этой формулой для нахождения оставшегося.
Теоремы
В базовой тригонометрии существует две основные теоремы: синусов и косинусов.
Первая гласит, что отношение каждой стороны треугольника к синусу противолежащего угла одинаково. Вторая — что квадрат любой стороны можно получить, если сложить квадраты двух оставшихся сторон и вычесть удвоенное их произведение, умноженное на косинус лежащего между ними угла.
Таким образом, если в теорему косинусов подставить значение угла в 90 градусов, мы получим… теорему Пифагора. Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать — две рассмотренные теоремы существенно упростят решение задачи.
Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать — две рассмотренные теоремы существенно упростят решение задачи.
Цели и задачи
Изучение тригонометрии значительно упростится, когда вы осознаете один простой факт: все выполняемые вами действия направлены на достижения всего одной цели. Любые параметры треугольника могут быть найдены, если вы знаете о нём самый минимум информации — это может быть величина одного угла и длины двух сторон или, например, три стороны.
Для определения синуса, косинуса, тангенса любого угла этих данных достаточно, с их же помощью можно легко высчитать площадь фигуры. Практически всегда в качестве ответа требуется привести одно из упомянутых значений, а найти их можно по одним и тем же формулам.
Нестыковки при изучении тригонометрии
Одним из непонятных вопросов, которых школьники предпочитают избегать, является обнаружение связи между различными понятиями в тригонометрии. Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.
Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.
Более того, углы измеряются то в градусах, то в радианах, а число Пи, записывающееся просто как 3,14 (без единиц измерения), почему-то фигурирует в формулах, соответствуя 180 градусам. Как всё это связано между собой?
Единицы измерения
Почему число Пи равняется именно 3,14? Помните ли вы, что это за значение? Это количество радиусов, умещающихся в дуге на половине окружности. Если диаметр круга — 2 сантиметра, длина окружности составит 3,14*2, или 6,28.
Второй момент: возможно, вы замечали сходство слов «радиан» и «радиус». Дело в том, что один радиан численно равен величине угла, отложенного из центра окружности на дугу длиной в один радиус.
Теперь совместим полученные знания и поймем, почему сверху на оси координат в тригонометрии пишется «Пи пополам», а слева — «Пи». Это угловая величина, измеренная в радианах, ведь полукруг — это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.
Это угловая величина, измеренная в радианах, ведь полукруг — это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.
Заглянем в будущее
Тригонометрия, изучаемая в школе, имеет дело с прямолинейной системой координат, где, как бы это странно ни звучало, прямая — это прямая.
Но есть и более сложные способы работы с пространством: сумма углов треугольника здесь будет больше 180 градусов, а прямая в нашем представлении будет выглядеть как самая настоящая дуга.
Перейдем от слов к делу! Возьмите яблоко. Сделайте ножом три надреза, чтобы при взгляде сверху получался треугольник. Выньте получившийся кусок яблока и посмотрите на «рёбра», где заканчивается кожура. Они вовсе не прямые. Фрукт в ваших руках условно можно назвать круглым, а теперь представьте, какими сложными должны быть формулы, с помощью которых можно найти площадь вырезанного куска. А ведь некоторые специалисты решают такие задачи ежедневно.
А ведь некоторые специалисты решают такие задачи ежедневно.
Тригонометрические функции в жизни
Обращали ли вы внимание, что самый короткий маршрут самолёта из точки А в точку Б на поверхности нашей планеты имеет ярко выраженную форму дуги? Причина проста: Земля имеет форму шара, а значит, с помощью треугольников многого не вычислишь — здесь приходится использовать более сложные формулы.
Не обойтись без синуса/косинуса острого угла в любых вопросах, связанных с космосом. Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.
В целом поле для деятельности человека, владеющего тригонометрией, очень широко и, по-видимому, со временем будет только расширяться.
Заключение
Сегодня мы узнали или, во всяком случае, повторили, что такое синус и косинус. Это понятия, которых не нужно бояться — стоит захотеть, и вы поймете их смысл. Помните, что тригонометрия — это не цель, а лишь инструмент, который можно использовать для удовлетворения реальных человеческих потребностей: строить дома, обеспечивать безопасность движения, даже осваивать просторы вселенной.
Действительно, сама по себе наука может казаться скучной, но как только вы найдете в ней способ достижения собственных целей, самореализации, процесс обучения станет интересным, а ваша личная мотивация возрастёт.
В качестве домашнего задания попробуйте найти способы применить тригонометрические функции в той сфере деятельности, которая интересна лично вам. Пофантазируйте, включите воображение, и тогда наверняка окажется, что новые знания пригодятся вам в будущем. Да и кроме того, математика полезна для общего развития мышления.
Что больше синус или косинус.
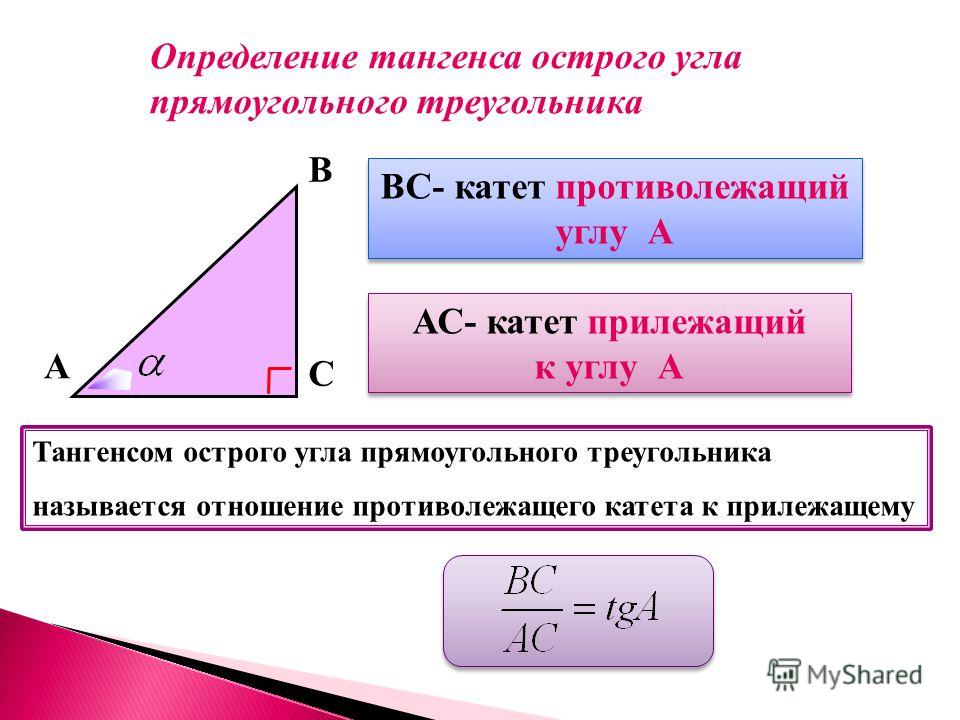 Основные тригонометрические тождества, их формулировки и вывод
Основные тригонометрические тождества, их формулировки и выводДля начала рассмотрим круг с радиусом 1 и с центром в (0;0). Для любого αЄR можно провести радиус 0A так, что радианная мера угла между 0A и осью 0x равна α. Направление против часовой стрелки считается положительным. Пусть конец радиуса А имеет координаты (a,b).
Определение синуса
Определение: Число b, равное ординате единичного радиуса, построенного описанным способом, обозначается sinα и называется синусом угла α.
Пример: sin 3π cos3π/2 = 0 0 = 0
Определение косинуса
Определение: Число a, равное абсциссе конца единичного радиуса, построенного описанным способом, обозначается cosα и называется косинусом угла α.
Пример: cos0 cos3π + cos3,5π = 1 (-1) + 0 = 2
Эти примеры используют определение синуса и косинуса угла через координаты конца единичного радиуса и единичной окружности. Для более наглядного представления необходимо нарисовать единичную окружность и отложить на ней соответствующие точки, а затем посчитать их абсциссы для вычисления косинуса и ординаты для вычисления синуса.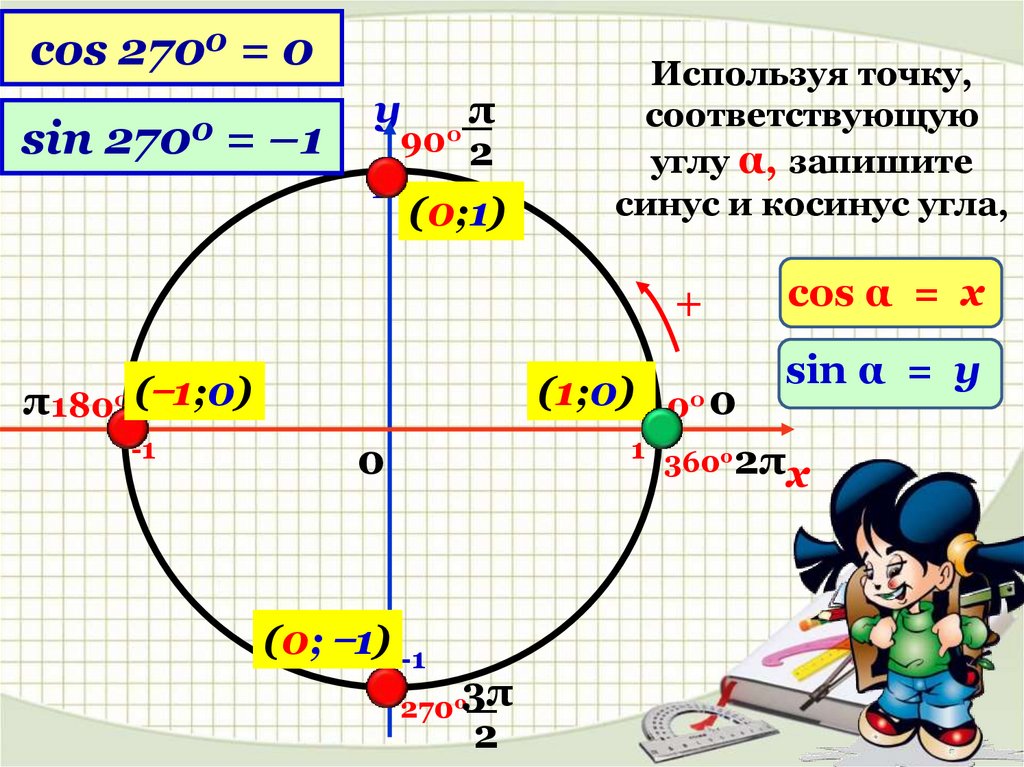
Определение тангенса
Определение: Функция tgx=sinx/cosx при x≠π/2+πk, kЄZ, называется котангенсом угла x. Область определения функции tgx это все действительные числа, кроме x=π/2+πn, nЄZ.
Пример: tg0 tgπ = 0 0 = 0
Этот пример аналогичен предыдущему. Для вычисления тангенса угла нужно поделить ординату точки на её абсциссу.
Определение котангенса
Определение: Функция ctgx=cosx/sinx при x≠πk, kЄZ называется котангенсом угла x. Область определения функции ctgx = -все действительные числа кроме точек x=πk, kЄZ.
Рассмотрим пример на обычном прямоугольном треугольнике
Чтобы было понятнее, что же такое косинус, синус, тангенс и котангенс. Рассмотрим пример на обычном прямоугольном треугольнике с углом y и сторонами a,b,c . Гипотенуза с, катеты соответственно a и b. Угол между гипотенузой c и катетом b y.
Определение: Синус угла y — это отношение противолежащего катета к гипотенузе: siny = а/с
Определение: Косинус угла y это отношение прилежащего катета к гипотенузе: сosy= в/с
Определение: Тангенс угла у — это отношение противолежащего катета к прилежащему: tgy = а/в
Определение: Котангенс угла y -это отношение прилежащего катета к противолежащему: ctgy= в/а
Cинус, косинус, тангенс и котангенс называют ещё тригонометрическими функциями. У каждого угла есть свой синус и косинус. И практически у каждого есть свой тангенс и котангенс.
У каждого угла есть свой синус и косинус. И практически у каждого есть свой тангенс и котангенс.
Считается, что если нам дан угол, то его синус, косинус, тангенс и котангенс нам известны! И наоборот. Дан синус, или любая другая тригонометрическая функция соответственно, мы знаем угол. Созданы даже специальные таблицы, где расписаны тригонометрические функции для каждого угла.
Учителя считают, что каждый школьник должен уметь проводить расчёты, знать тригонометрические формулы, но далеко не каждый преподаватель объясняет, что такое синус и косинус. Каков их смысл, где они используются? Почему мы говорим про треугольники, а в учебнике нарисована окружность? Попробуем связать все факты воедино.
Школьный предмет
Изучение тригонометрии начинается обычно в 7-8 классе средней школы. В это время учащимся объясняют, что такое синус и косинус, предлагают решать геометрические задачи с применением этих функций. Позже появляются более сложные формулы и выражения, которые требуется алгебраическим способом преобразовывать (формулы двойного и половинного угла, степенные функции), проводится работа с тригонометрической окружностью.
Однако учителя далеко не всегда могут доходчиво объяснить смысл используемых понятий и применимость формул. Поэтому ученик зачастую не видит смысла в данном предмете, а заученная информация быстро забывается. Однако стоит один раз объяснить старшекласснику, например, связь между функцией и колебательным движением, и логическая связь запомнится на многие годы, а шутки на тему бесполезности предмета уйдут в прошлое.
Использование
Заглянем ради любопытства в различные разделы физики. Хотите определить дальность полёта снаряда? Или высчитываете силу трения между объектом и некой поверхностью? Раскачиваете маятник, следите за лучами, проходящими сквозь стекло, высчитываете индукцию? Практически в любой формуле фигурируют тригонометрические понятия. Так что такое синус и косинус?
Определения
Синус угла представляет собой отношение противолежащего катета к гипотенузе, косинус — прилежащего катета всё к той же гипотенузе. Здесь нет совершенно ничего сложного. Возможно, учеников обычно смущают значения, которые они видят в тригонометрической таблице, ведь там фигурируют квадратные корни. Да, получать из них десятичные дроби не очень удобно, но кто сказал, что все числа в математике должны быть ровными?
Да, получать из них десятичные дроби не очень удобно, но кто сказал, что все числа в математике должны быть ровными?
На самом деле в задачниках по тригонометрии можно найти забавную подсказку: большинство ответов здесь ровные и в худшем случае содержат корень из двух или из трёх. Вывод прост: если у вас в ответе получилась «многоэтажная» дробь, перепроверьте решение на предмет ошибок в расчётах или в рассуждениях. И вы их, скорее всего, найдете.
Что нужно запомнить
Как и в любой науке, в тригонометрии есть такие данные, которые необходимо выучить.
Во-первых, следует запомнить числовые значения для синусов, косинусов прямоугольного треугольника 0 и 90, а также 30, 45 и 60 градусов. Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде.
Нужно помнить, что значение обеих функций не может превышать единицу. Если где-либо в расчетах вы получите значение, выходящее за пределы диапазона 0-1, остановитесь и решите задачу заново.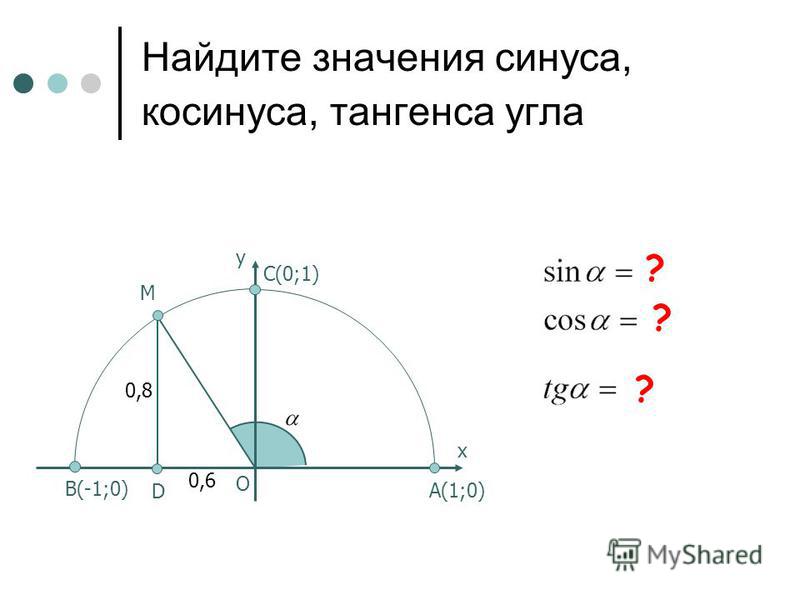
Сумма квадратов синуса и косинуса равна единице. Если вы уже нашли одно из значений, воспользуйтесь этой формулой для нахождения оставшегося.
Теоремы
В базовой тригонометрии существует две основные теоремы: синусов и косинусов.
Первая гласит, что отношение каждой стороны треугольника к синусу противолежащего угла одинаково. Вторая — что квадрат любой стороны можно получить, если сложить квадраты двух оставшихся сторон и вычесть удвоенное их произведение, умноженное на косинус лежащего между ними угла.
Таким образом, если в теорему косинусов подставить значение угла в 90 градусов, мы получим… теорему Пифагора. Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать — две рассмотренные теоремы существенно упростят решение задачи.
Цели и задачи
Изучение тригонометрии значительно упростится, когда вы осознаете один простой факт: все выполняемые вами действия направлены на достижения всего одной цели. Любые параметры треугольника могут быть найдены, если вы знаете о нём самый минимум информации — это может быть величина одного угла и длины двух сторон или, например, три стороны.
Любые параметры треугольника могут быть найдены, если вы знаете о нём самый минимум информации — это может быть величина одного угла и длины двух сторон или, например, три стороны.
Для определения синуса, косинуса, тангенса любого угла этих данных достаточно, с их же помощью можно легко высчитать площадь фигуры. Практически всегда в качестве ответа требуется привести одно из упомянутых значений, а найти их можно по одним и тем же формулам.
Нестыковки при изучении тригонометрии
Одним из непонятных вопросов, которых школьники предпочитают избегать, является обнаружение связи между различными понятиями в тригонометрии. Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.
Более того, углы измеряются то в градусах, то в радианах, а число Пи, записывающееся просто как 3,14 (без единиц измерения), почему-то фигурирует в формулах, соответствуя 180 градусам. Как всё это связано между собой?
Как всё это связано между собой?
Единицы измерения
Почему число Пи равняется именно 3,14? Помните ли вы, что это за значение? Это количество радиусов, умещающихся в дуге на половине окружности. Если диаметр круга — 2 сантиметра, длина окружности составит 3,14*2, или 6,28.
Второй момент: возможно, вы замечали сходство слов «радиан» и «радиус». Дело в том, что один радиан численно равен величине угла, отложенного из центра окружности на дугу длиной в один радиус.
Теперь совместим полученные знания и поймем, почему сверху на оси координат в тригонометрии пишется «Пи пополам», а слева — «Пи». Это угловая величина, измеренная в радианах, ведь полукруг — это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.
Заглянем в будущее
Тригонометрия, изучаемая в школе, имеет дело с прямолинейной системой координат, где, как бы это странно ни звучало, прямая — это прямая.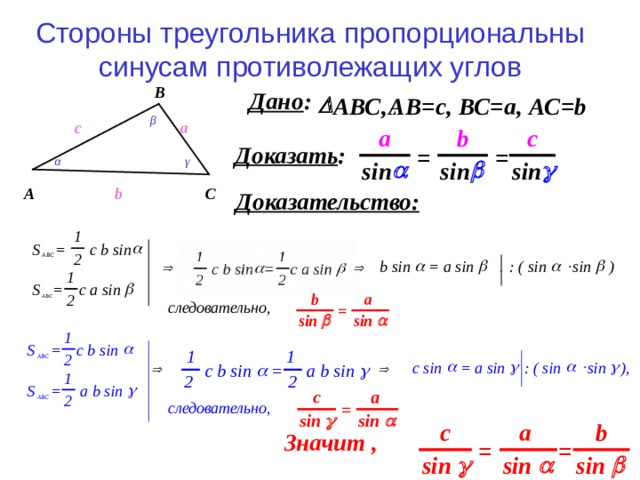
Но есть и более сложные способы работы с пространством: сумма углов треугольника здесь будет больше 180 градусов, а прямая в нашем представлении будет выглядеть как самая настоящая дуга.
Перейдем от слов к делу! Возьмите яблоко. Сделайте ножом три надреза, чтобы при взгляде сверху получался треугольник. Выньте получившийся кусок яблока и посмотрите на «рёбра», где заканчивается кожура. Они вовсе не прямые. Фрукт в ваших руках условно можно назвать круглым, а теперь представьте, какими сложными должны быть формулы, с помощью которых можно найти площадь вырезанного куска. А ведь некоторые специалисты решают такие задачи ежедневно.
Тригонометрические функции в жизни
Обращали ли вы внимание, что самый короткий маршрут самолёта из точки А в точку Б на поверхности нашей планеты имеет ярко выраженную форму дуги? Причина проста: Земля имеет форму шара, а значит, с помощью треугольников многого не вычислишь — здесь приходится использовать более сложные формулы.
Не обойтись без синуса/косинуса острого угла в любых вопросах, связанных с космосом. Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.
Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.
В целом поле для деятельности человека, владеющего тригонометрией, очень широко и, по-видимому, со временем будет только расширяться.
Заключение
Сегодня мы узнали или, во всяком случае, повторили, что такое синус и косинус. Это понятия, которых не нужно бояться — стоит захотеть, и вы поймете их смысл. Помните, что тригонометрия — это не цель, а лишь инструмент, который можно использовать для удовлетворения реальных человеческих потребностей: строить дома, обеспечивать безопасность движения, даже осваивать просторы вселенной.
Действительно, сама по себе наука может казаться скучной, но как только вы найдете в ней способ достижения собственных целей, самореализации, процесс обучения станет интересным, а ваша личная мотивация возрастёт.
В качестве домашнего задания попробуйте найти способы применить тригонометрические функции в той сфере деятельности, которая интересна лично вам. Пофантазируйте, включите воображение, и тогда наверняка окажется, что новые знания пригодятся вам в будущем. Да и кроме того, математика полезна для общего развития мышления.
В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.
Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье. Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Навигация по странице.
Связь между синусом и косинусом одного угла
Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида . Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.
Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.
Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений . Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Тангенс и котангенс через синус и косинус
Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .
Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .
Благодаря такой очевидности тождеств и часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
В заключение этого пункта следует отметить, что тождества и имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z — любое .
Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида .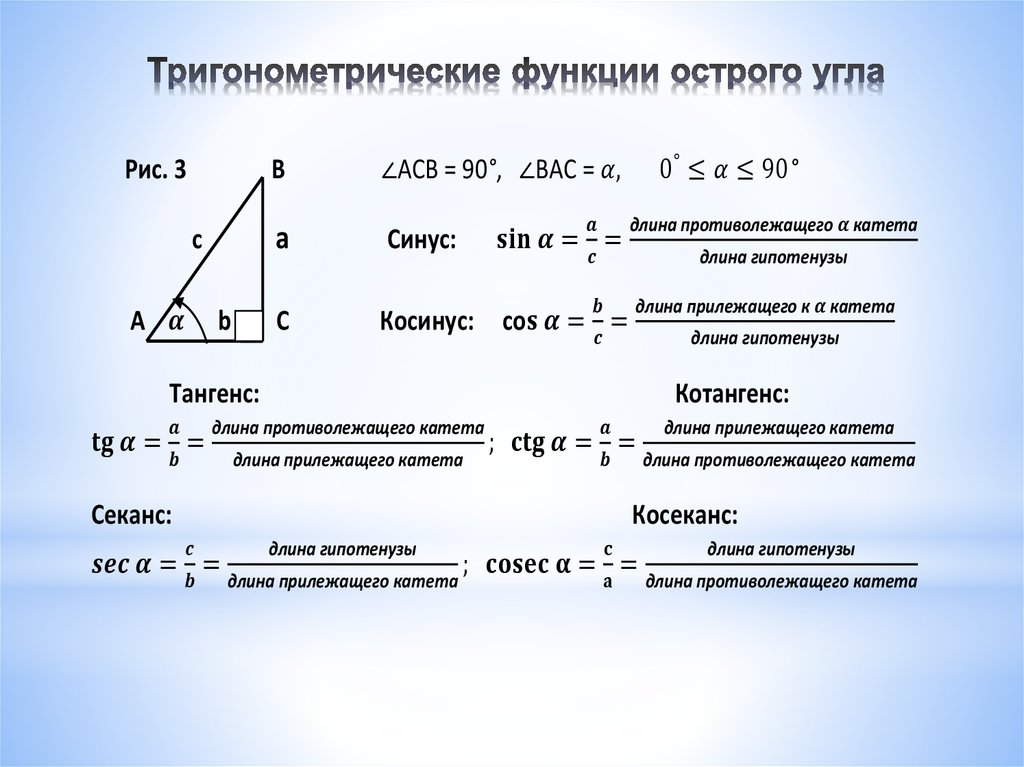 Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Yandex.RTB R-A-339285-1
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.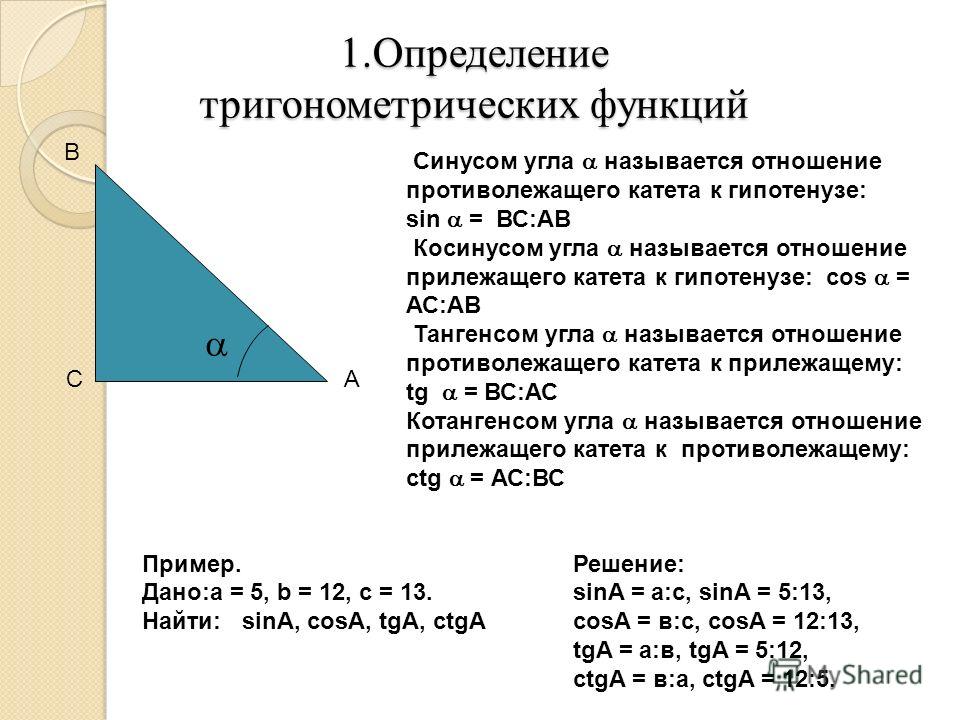
Определения тригонометрических функций
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cos α) — отношение прилежащего катета к гипотенузе.
Тангенс угла (t g α) — отношение противолежащего катета к прилежащему.
Котангенс угла (c t g α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1 , 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 (x , y).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 (x , y). sin α = y
Косинус (cos) угла поворота
Косинус угла поворота α — это абсцисса точки A 1 (x , y). cos α = х
Тангенс (tg) угла поворота
Тангенс угла поворота α — это отношение ординаты точки A 1 (x , y) к ее абсциссе. t g α = y x
Котангенс (ctg) угла поворота
Котангенс угла поворота α — это отношение абсциссы точки A 1 (x , y) к ее ординате.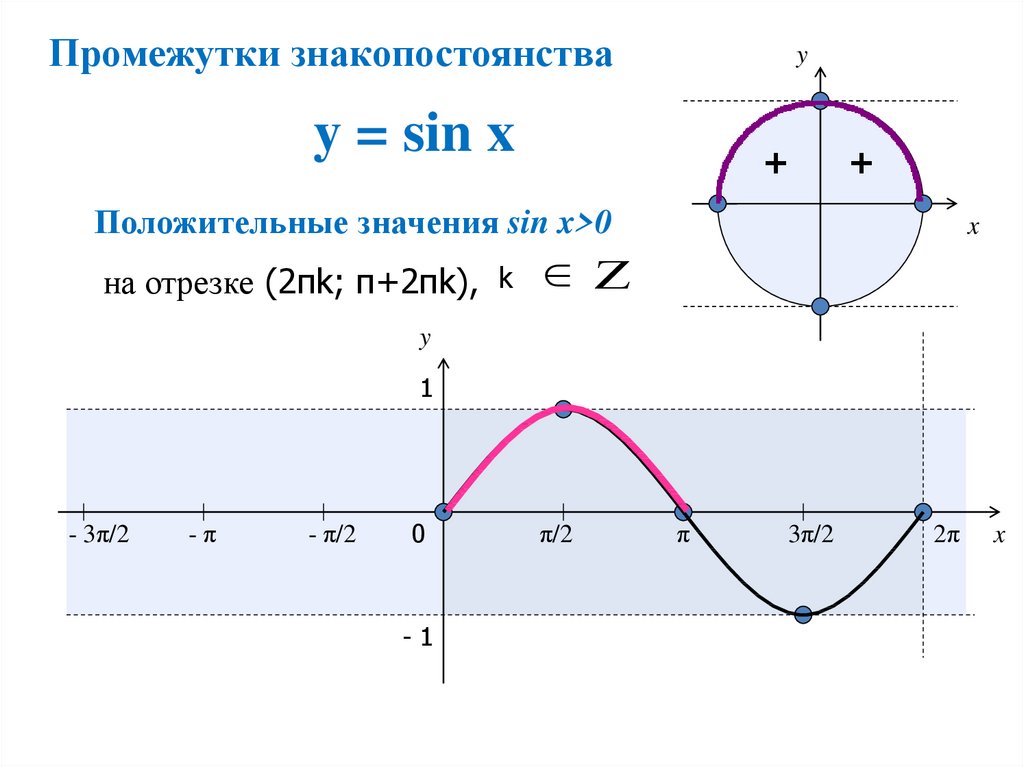 c t g α = x y
c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0 , 1) и (0 , — 1). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.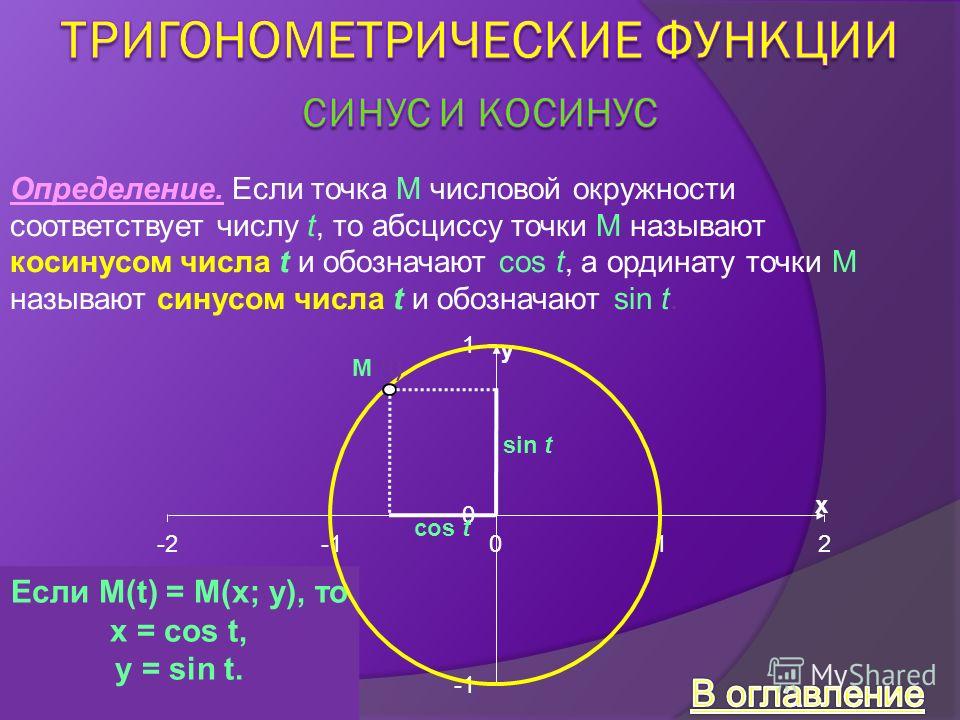
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1 , 0).
Положительному числу t
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс (tg) числа t
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла.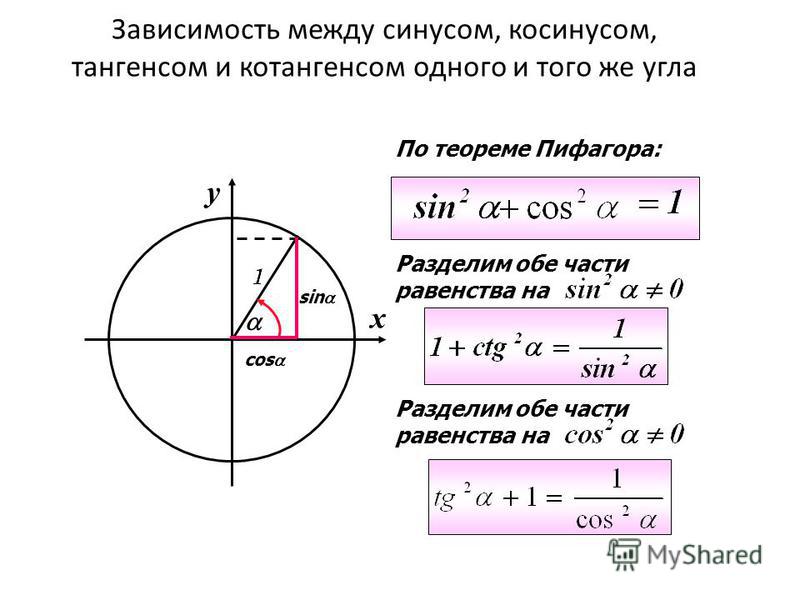 Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t . Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A (1 , 0) на угол величиной до 90 градусов и проведем из полученной точки A 1 (x , y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) . Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.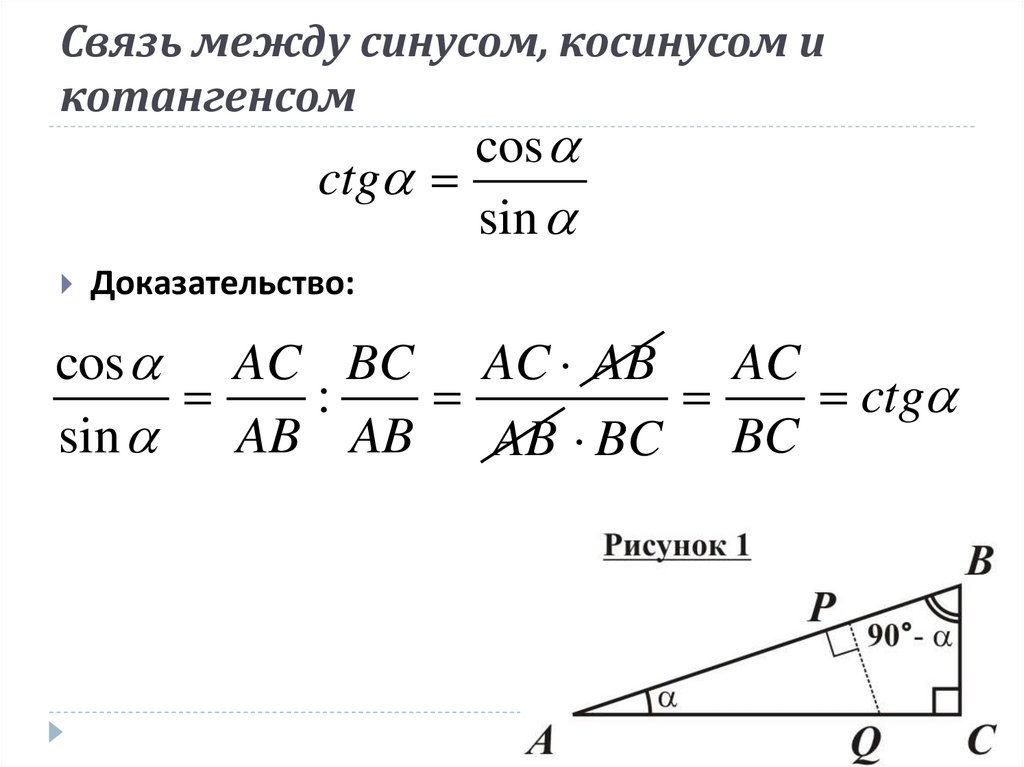
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Где были рассмотрены задачи на решение прямоугольного треугольника, я пообещал изложить приём запоминания определений синуса и косинуса. Используя его, вы всегда быстро вспомните – какой катет относится к гипотенузе (прилежащий или противолежащий). Решил в «долгий ящик не откладывать», необходимый материал ниже, прошу ознакомиться 😉
Дело в том, что я не раз наблюдал, как учащиеся 10-11 классов с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный бал.
Информация, которую я представлю непосредственно к математике не имеет никакого отношения. Она связана с образным мышлением, и с приёмами словесно-логической связи. Именно так, я сам, раз и на всегда запомнил
данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.
Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.
Напомню определения синуса и косинуса в прямоугольном треугольнике:
Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Итак, какие ассоциации у вас вызывает слово косинус?
Наверное, у каждого свои 😉 Запоминайте связку:
Таким образом, у вас сразу в памяти возникнет выражение –
«… отношение ПРИЛЕЖАЩЕГО катета к гипотенузе ».
Проблема с определением косинуса решена.
Если нужно вспомнить определение синуса в прямоугольном треугольнике, то вспомнив определение косинуса, вы без труда установите, что синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.
Как быть с тангенсом и котангенсом? Путаница та же. Учащиеся знают, что это отношение катетов, но проблема вспомнить какой к которому относится – то ли противолежащий к прилежащему, то ли наоборот.
Определения:
Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему:
Как запомнить? Есть два способа. Один так же использует словесно-логическую связь, другой – математический.
СПОСОБ МАТЕМАТИЧЕСКИЙ
Есть такое определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
*Запомнив формулу, вы всегда сможете определить, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему.
Аналогично. Котангенсом острого угла называется отношение косинуса угла к его синусу:
Итак! Запомнив указанные формулы вы всегда сможете определить, что:
— тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему
— котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему.
СПОСОБ СЛОВЕСНО-ЛОГИЧЕСКИЙ
О тангенсе. Запомните связку:
То есть если потребуется вспомнить определение тангенса, при помощи данной логической связи, вы без труда вспомните, что это
«… отношение противолежащего катета к прилежащему»
Если речь зайдёт о котангенсе, то вспомнив определение тангенса вы без труда озвучите определение котангенса –
«… отношение прилежащего катета к противолежащему»
Есть интересный приём по запоминанию тангенса и котангенса на сайте » Математический тандем » , посмотрите.
СПОСОБ УНИВЕРСАЛЬНЫЙ
Можно просто зазубрить. Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.
Надеюсь, материал был вам полезен.
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
определения в тригонометрии, примеры, формулы
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.
Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.
В этой статье мы покажем, как даются определения синуса, косинуса, тангенса и котангенса угла и числа в тригонометрии . Здесь же мы поговорим об обозначениях, приведем примеры записей, дадим графические иллюстрации. В заключение проведем параллель между определениями синуса, косинуса, тангенса и котангенса в тригонометрии и геометрии.
Навигация по странице.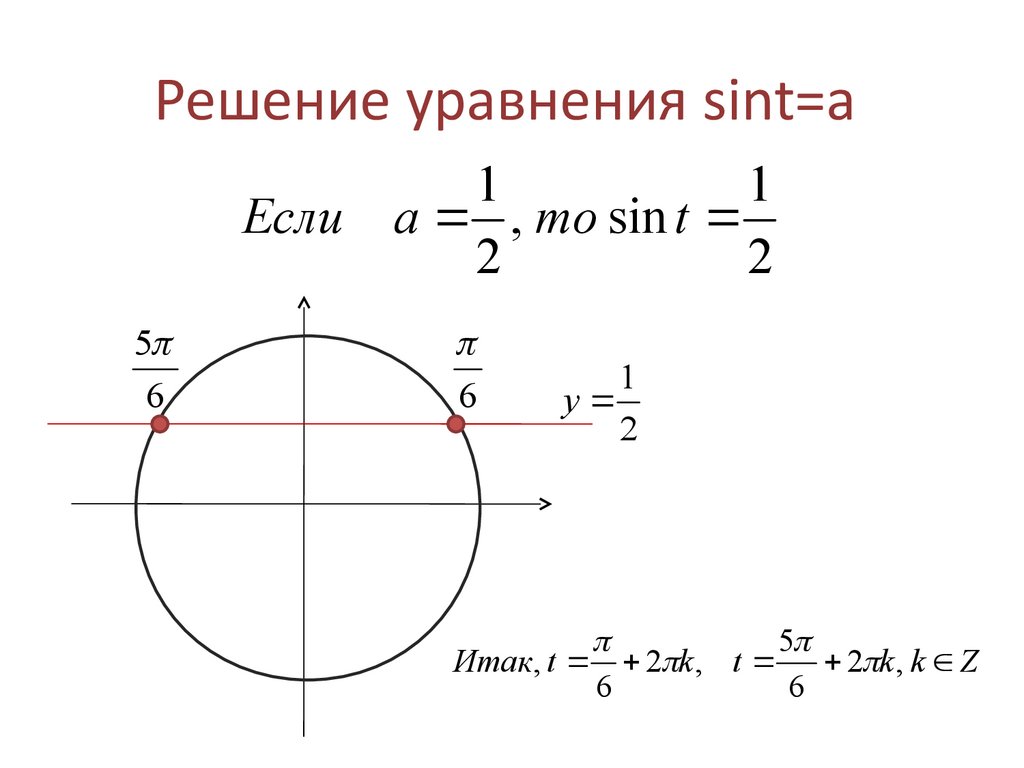
Определение синуса, косинуса, тангенса и котангенса
Проследим за тем, как формируются представление о синусе, косинусе, тангенсе и котангенсе в школьном курсе математики. На уроках геометрии дается определение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. А позже изучается тригонометрия, где говорится о синусе, косинусе, тангенсе и котангенсе угла поворота и числа. Приведем все эти определения, приведем примеры и дадим необходимые комментарии.
Острого угла в прямоугольном треугольнике
Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки.
Определение.
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.
Определение.
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
Определение.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Определение.
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.
Там же вводятся обозначения синуса, косинуса, тангенса и котангенса – sin , cos , tg и ctg соответственно.
Например, если АВС – прямоугольный треугольник с прямым углом С , то синус острого угла A равен отношению противолежащего катета BC к гипотенузе AB , то есть, sin∠A=BC/AB .
Эти определения позволяют вычислять значения синуса, косинуса, тангенса и котангенса острого угла по известным длинам сторон прямоугольного треугольника, а также по известным значениям синуса, косинуса, тангенса, котангенса и длине одной из сторон находить длины других сторон. Например, если бы мы знали, что в прямоугольном треугольнике катет AC
равен 3
, а гипотенуза AB
равна 7
, то мы могли бы вычислить значение косинуса острого угла A
по определению: cos∠A=AC/AB=3/7
.
Угла поворота
В тригонометрии на угол начинают смотреть более широко — вводят понятие угла поворота . Величина угла поворота, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов, угол поворота в градусах (и в радианах) может выражаться каким угодно действительным числом от −∞ до +∞ .
В этом свете дают определения синуса, косинуса, тангенса и котангенса уже не острого угла, а угла произвольной величины — угла поворота. Они даются через координаты x и y точки A 1 , в которую переходит так называемая начальная точка A(1, 0) после ее поворота на угол α вокруг точки O – начала прямоугольной декартовой системы координат и центра единичной окружности .
Определение.
Синус угла поворота α — это ордината точки A 1 , то есть, sinα=y .
Определение.
Косинусом угла поворота α называют абсциссу точки A 1 , то есть, cosα=x .
Определение.
Тангенс угла поворота α
— это отношение ординаты точки A 1
к ее абсциссе, то есть, tgα=y/x
.
Определение.
Котангенсом угла поворота α называют отношение абсциссы точки A 1 к ее ординате, то есть, ctgα=x/y .
Синус и косинус определены для любого угла α , так как мы всегда можем определить абсциссу и ординату точки, которая получается в результате поворота начальной точки на угол α . А тангенс и котангенс определены не для любого угла. Тангенс не определен для таких углов α , при которых начальная точка переходит в точку с нулевой абсциссой (0, 1) или (0, −1) , а это имеет место при углах 90°+180°·k , k∈Z (π/2+π·k рад). Действительно, при таких углах поворота выражение tgα=y/x не имеет смысла, так как в нем присутствует деление на нуль. Что же касается котангенса, то он не определен для таких углов α , при которых начальная точка переходит к в точку с нулевой ординатой (1, 0) или (−1, 0) , а это имеет место для углов 180°·k , k∈Z (π·k рад).
Итак, синус и косинус определены для любых углов поворота, тангенс определен для всех углов, кроме 90°+180°·k
, k∈Z
(π/2+π·k
рад), а котангенс – для всех углов, кроме 180°·k
, k∈Z
(π·k
рад).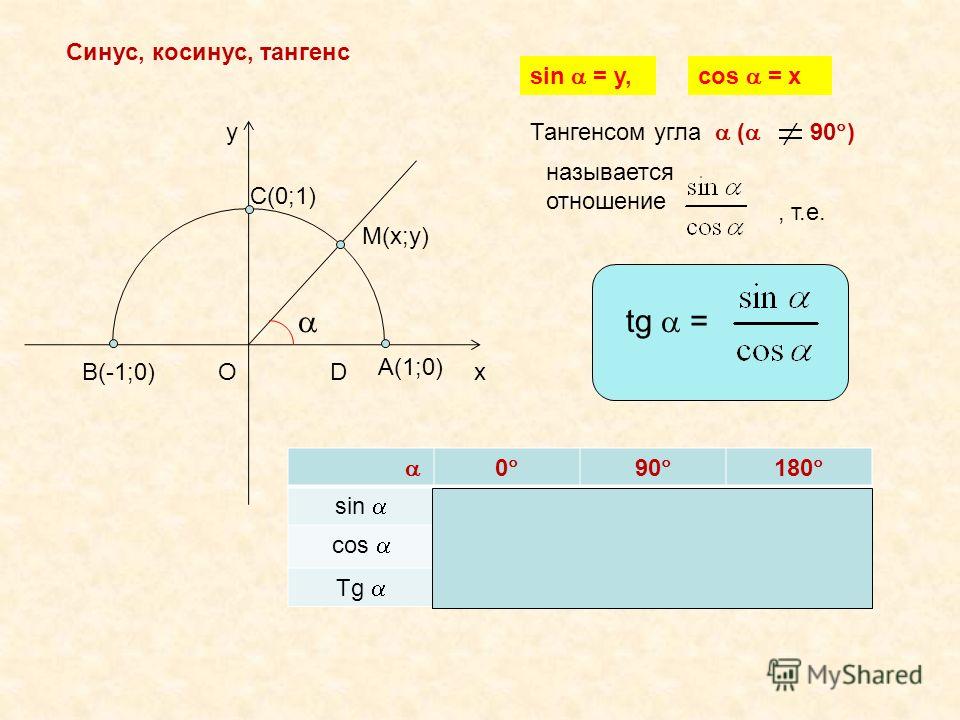
В определениях фигурируют уже известные нам обозначения sin , cos , tg и ctg , они используются и для обозначения синуса, косинуса, тангенса и котангенса угла поворота (иногда можно встретить обозначения tan и cot , отвечающие тангенсу и котангенсу). Так синус угла поворота 30 градусов можно записать как sin30° , записям tg(−24°17′) и ctgα отвечают тангенс угла поворота −24 градуса 17 минут и котангенс угла поворота α . Напомним, что при записи радианной меры угла обозначение «рад» часто опускают. Например, косинус угла поворота в три пи рад обычно обозначают cos3·π .
В заключение этого пункта стоит заметить, что в разговоре про синус, косинус, тангенс и котангенс угла поворота часто опускают словосочетание «угол поворота» или слово «поворота». То есть, вместо фразы «синус угла поворота альфа» обычно используют фразу «синус угла альфа» или еще короче – «синус альфа». Это же касается и косинуса, и тангенса, и котангенса.
Также скажем, что определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике согласуются с только что данными определениями синуса, косинуса, тангенса и котангенса угла поворота величиной от 0
до 90
градусов.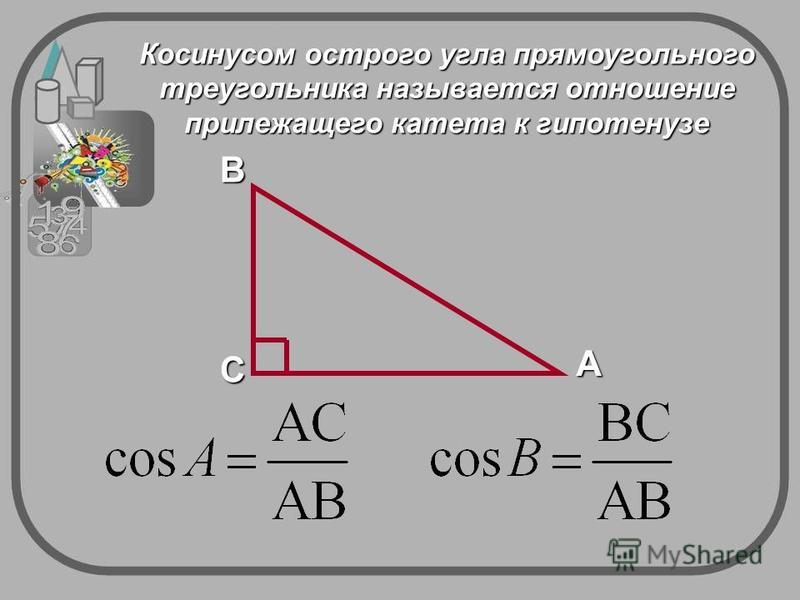 Это мы обоснуем .
Это мы обоснуем .
Числа
Определение.
Синусом, косинусом, тангенсом и котангенсом числа t называют число, равное синусу, косинусу, тангенсу и котангенсу угла поворота в t радианов соответственно.
Например, косинус числа 8·π по определению есть число, равное косинусу угла в 8·π рад. А косинус угла в 8·π рад равен единице, поэтому, косинус числа 8·π равен 1 .
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Он состоит в том, что каждому действительному числу t ставится в соответствие точка единичной окружности с центром в начале прямоугольной системы координат, и синус, косинус, тангенс и котангенс определяются через координаты этой точки. Остановимся на этом подробнее.
Покажем, как устанавливается соответствие между действительными числами и точками окружности:
- числу 0 ставится в соответствие начальная точка A(1, 0) ;
- положительному числу t ставится в соответствие точка единичной окружности, в которую мы попадем, если будем двигаться по окружности из начальной точки в направлении против часовой стрелки и пройдем путь длиной t ;
- отрицательному числу t
ставится в соответствие точка единичной окружности, в которую мы попадем, если будем двигаться по окружности из начальной точки в направлении по часовой стрелке и пройдем путь длиной |t|
.

Теперь переходим к определениями синуса, косинуса, тангенса и котангенса числа t . Допустим, что числу t соответствует точка окружности A 1 (x, y) (например, числу &pi/2; отвечает точка A 1 (0, 1) ).
Определение.
Синусом числа t называют ординату точки единичной окружности, соответствующей числу t , то есть, sint=y .
Определение.
Косинусом числа t называют абсциссу точки единичной окружности, отвечающей числу t , то есть, cost=x .
Определение.
Тангенсом числа t называют отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t , то есть, tgt=y/x . В другой равносильной формулировке тангенс числа t – это отношение синуса этого числа к косинусу, то есть, tgt=sint/cost .
Определение.
Котангенсом числа t
называют отношение абсциссы к ординате точки единичной окружности, соответствующей числу t
, то есть, ctgt=x/y
. Другая формулировка такова: тангенс числа t
– это отношение косинуса числа t
к синусу числа t
: ctgt=cost/sint
.
Здесь отметим, что только что данные определения согласуются с определением, данным в начале этого пункта. Действительно, точка единичной окружности, соответствующая числу t , совпадает с точкой, полученной в результате поворота начальной точки на угол в t радианов.
Еще стоит прояснить такой момент. Допустим, перед нами запись sin3 . Как понять, о синусе числа 3 или о синусе угла поворота в 3 радиана идет речь? Обычно это ясно из контекста, в противном случае это скорее всего не имеет принципиального значения.
Тригонометрические функции углового и числового аргумента
Согласно данным в предыдущем пункте определениям, каждому углу поворота α
соответствуют вполне определенное значение sinα
, как и значение cosα
. Кроме того, всем углам поворота, отличным от 90°+180°·k
, k∈Z
(π/2+π·k
рад) отвечают значения tgα
, а отличным от 180°·k
, k∈Z
(π·k
рад) – значения ctgα
. Поэтому sinα
, cosα
, tgα
и ctgα
— это функции угла α
. Другими словами – это функции углового аргумента.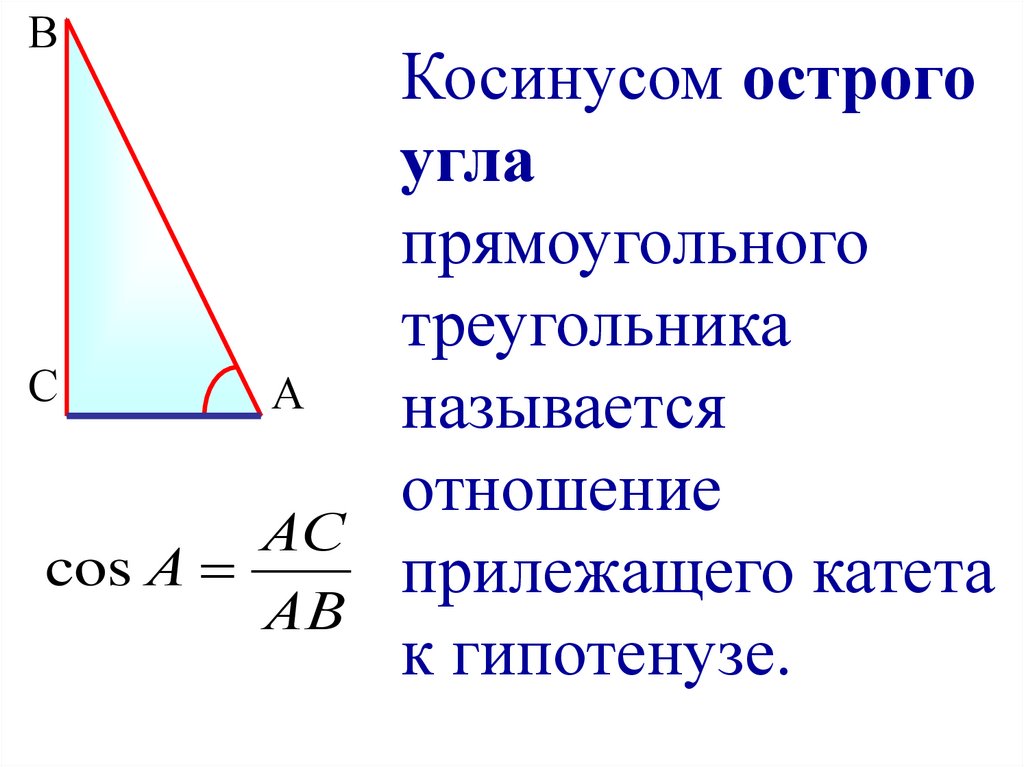
Аналогично можно говорить и про функции синус, косинус, тангенс и котангенс числового аргумента. Действительно, каждому действительному числу t отвечает вполне определенное значение sint , как и cost . Кроме того, всем числам, отличным от π/2+π·k , k∈Z соответствуют значения tgt , а числам π·k , k∈Z — значения ctgt .
Функции синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями .
Из контекста обычно понятно, с тригонометрическими функциями углового аргумента или числового аргумента мы имеем дело. В противном случае мы можем считать независимую переменную как мерой угла (угловым аргументом), так и числовым аргументом.
Однако, в школе в основном изучаются числовые функции, то есть, функции, аргументы которых, как и соответствующие им значения функции, являются числами. Поэтому, если речь идет именно о функциях, то целесообразно считать тригонометрические функции функциями числовых аргументов.
Связь определений из геометрии и тригонометрии
Если рассматривать угол поворота α
величиной от 0
до 90
градусов, то данные в контексте тригонометрии определения синуса, косинуса, тангенса и котангенса угла поворота полностью согласуются с определениями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике, которые даются в курсе геометрии. Обоснуем это.
Обоснуем это.
Изобразим в прямоугольной декартовой системе координат Oxy единичную окружность. Отметим начальную точку A(1, 0) . Повернем ее на угол α величиной от 0 до 90 градусов, получим точку A 1 (x, y) . Опустим из точки А 1 на ось Ox перпендикуляр A 1 H .
Легко видеть, что в прямоугольном треугольнике угол A 1 OH
равен углу поворота α
, длина прилежащего к этому углу катета OH
равна абсциссе точки A 1
, то есть, |OH|=x
, длина противолежащего к углу катета A 1 H
равна ординате точки A 1
, то есть, |A 1 H|=y
, а длина гипотенузы OA 1
равна единице, так как она является радиусом единичной окружности. Тогда по определению из геометрии синус острого угла α
в прямоугольном треугольнике A 1 OH
равен отношению противолежащего катета к гипотенузе, то есть, sinα=|A 1 H|/|OA 1 |=y/1=y
. А по определению из тригонометрии синус угла поворота α
равен ординате точки A 1
, то есть, sinα=y
. Отсюда видно, что определение синуса острого угла в прямоугольном треугольнике эквивалентно определению синуса угла поворота α
при α
от 0
до 90
градусов.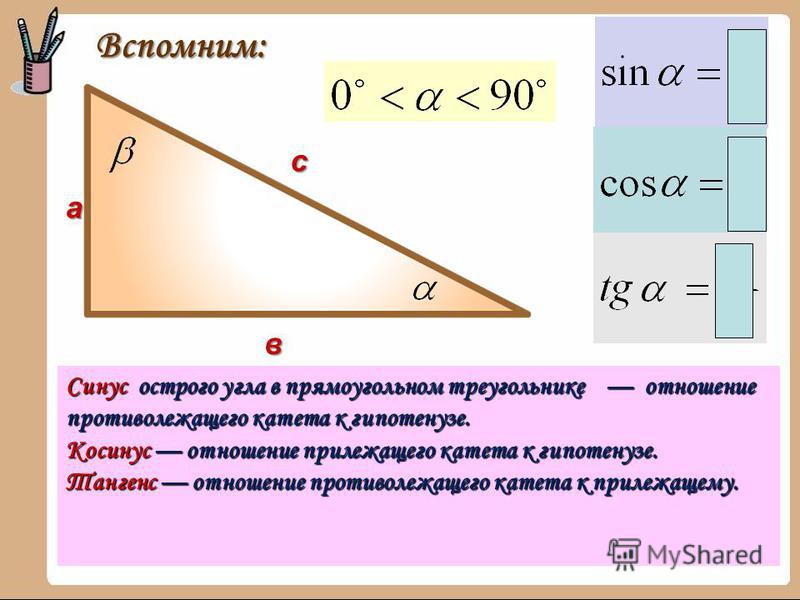
Аналогично можно показать, что и определения косинуса, тангенса и котангенса острого угла α согласуются с определениями косинуса, тангенса и котангенса угла поворота α .
Список литературы.
- Геометрия. 7-9 классы : учеб. для общеобразоват. учреждений / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. — 20-е изд. М.: Просвещение, 2010. — 384 с.: ил. — ISBN 978-5-09-023915-8.
- Погорелов А. В. Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений/ А. В. Погорелов. — 2-е изд — М.: Просвещение, 2001. — 224 с.: ил. — ISBN 5-09-010803-X.
- Алгебра и элементарные функции : Учебное пособие для учащихся 9 класса средней школы / Е. С. Кочетков, Е. С. Кочеткова; Под редакцией доктора физико-математических наук О. Н. Головина.- 4-е изд. М.: Просвещение, 1969.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.
 : ил.- ISBN 5-09-002727-7
: ил.- ISBN 5-09-002727-7 - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Мордкович А. Г. Алгебра и начала анализа. 10 класс. В 2 ч. Ч. 1: учебник для общеобразовательных учреждений (профильный уровень)/ А. Г. Мордкович, П. В. Семенов. — 4-е изд., доп. — М.: Мнемозина, 2007. — 424 с.: ил. ISBN 978-5-346-00792-0.
- Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни /[Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. — 3-е изд. — И.: Просвещение, 2010.- 368 с.: ил.- ISBN 978-5-09-022771-1.
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В.
 А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.
Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье. Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Навигация по странице.
Связь между синусом и косинусом одного угла
Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида . Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
Подробнее об этом поговорим в следующих пунктах.
То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.
Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.
Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений . Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Тангенс и котангенс через синус и косинус
Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .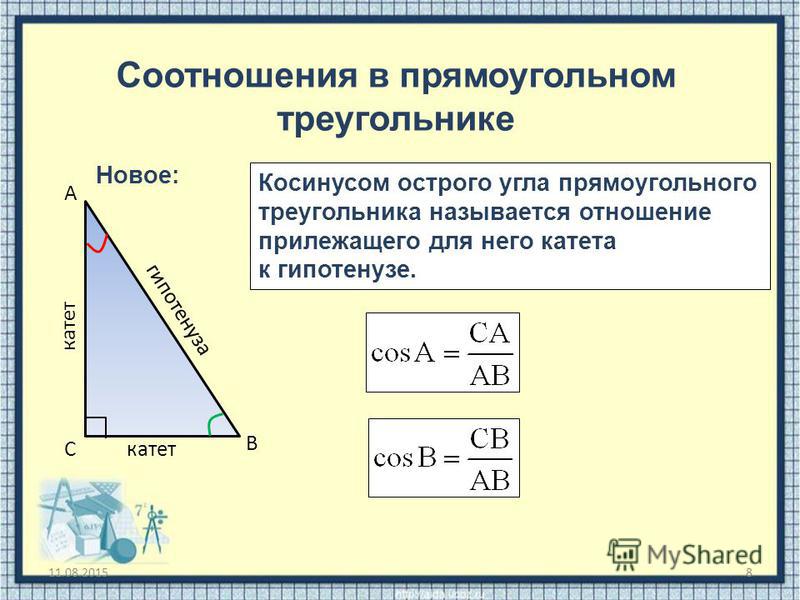
Благодаря такой очевидности тождеств и часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
В заключение этого пункта следует отметить, что тождества и имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z — любое .
Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .
Можно было доказательство провести и немного иначе. Так как и , то .
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
Отношение противолежащего катета к гипотенузе называют синусом острого угла прямоугольного треугольника.
\sin \alpha = \frac{a}{c}
Косинус острого угла прямоугольного треугольника
Отношение близлежащего катета к гипотенузе называют косинусом острого угла прямоугольного треугольника.
\cos \alpha = \frac{b}{c}
Тангенс острого угла прямоугольного треугольника
Отношение противолежащего катета к близлежащему катету называют тангенсом острого угла прямоугольного треугольника.
tg \alpha = \frac{a}{b}
Котангенс острого угла прямоугольного треугольника
Отношение близлежащего катета к противолежащему катету называют котангенсом острого угла прямоугольного треугольника.
ctg \alpha = \frac{b}{a}
Синус произвольного угла
Ордината точки на единичной окружности , которой соответствует угол \alpha
называют синусом произвольного угла поворота \alpha
.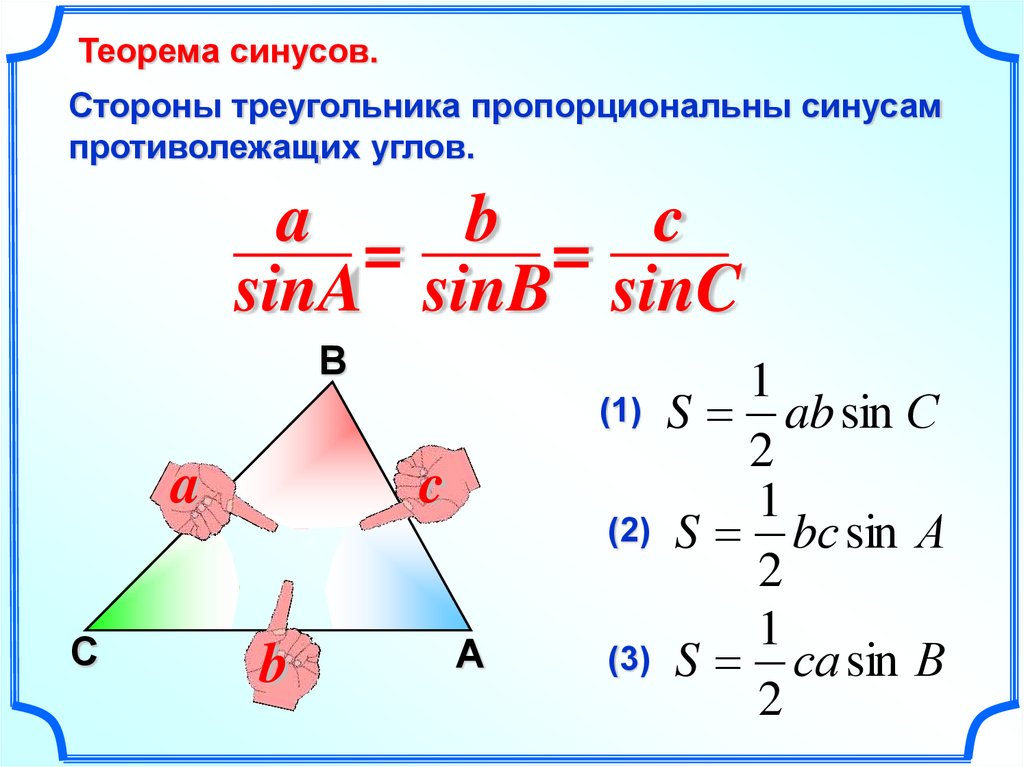
\sin \alpha=y
Косинус произвольного угла
Абсцисса точки на единичной окружности, которой соответствует угол \alpha называют косинусом произвольного угла поворота \alpha .
\cos \alpha=x
Тангенс произвольного угла
Отношение синуса произвольного угла поворота \alpha к его косинусу называют тангенсом произвольного угла поворота \alpha .
tg \alpha = y_{A}
tg \alpha = \frac{\sin \alpha}{\cos \alpha}
Котангенс произвольного угла
Отношение косинуса произвольного угла поворота \alpha к его синусу называют котангенсом произвольного угла поворота \alpha .
ctg \alpha =x_{A}
ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
Пример нахождения произвольного угла
Если \alpha — некоторый угол AOM , где M — точка единичной окружности, то
\sin \alpha=y_{M} , \cos \alpha=x_{M} , tg \alpha=\frac{y_{M}}{x_{M}} , ctg \alpha=\frac{x_{M}}{y_{M}} .
Например, если \angle AOM = -\frac{\pi}{4} , то: ордината точки M равна -\frac{\sqrt{2}}{2} , абсцисса равна \frac{\sqrt{2}}{2} и потому
\sin \left (-\frac{\pi}{4} \right)=-\frac{\sqrt{2}}{2} ;
\cos \left (\frac{\pi}{4} \right)=\frac{\sqrt{2}}{2} ;
tg ;
ctg
\left (-\frac{\pi}{4} \right)=-1
. {\circ}\left(2\pi\right)
{\circ}\left(2\pi\right)
Инструкция
Первый вариант — классический, с использованием бумаги, транспортира и карандаша (или ручки).По определению синус угла равен противолежащего катета к гипотенузе прямоугольного треугольника. То есть, чтобы вычислить значение, вам надо при помощи транспортира построить прямоугольный треугольник, один из углов которого равен тому, синус которого вас интересует.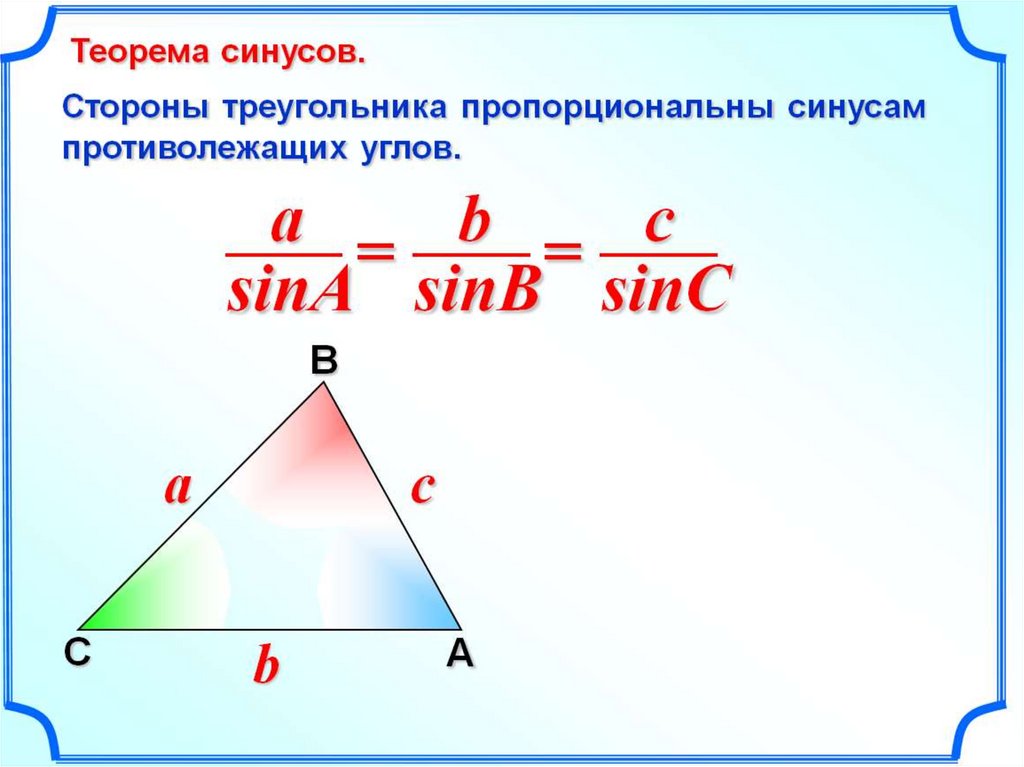 Затем измерить длину гипотенузы и противолежащего катета и разделить второе на первое с нужной точности.
Затем измерить длину гипотенузы и противолежащего катета и разделить второе на первое с нужной точности.
Второй вариант — школьный. Со школы все помнят «таблицы Брадиса», содержащие тысячи значений тригонометрических от разных углов. Можно поискать как бумажное издание, так и его электронный аналог в формате pdf — они есть в сети. Найдя таблицы, найти значение синуса нужного угла не составит труда.
Третий вариант — оптимальный. Если есть доступ к , то можно воспользоваться стандартным калькулятором ОС Windows. Его следует переключить в расширенный режим. Для этого в разделе «Вид» меню выберите пункт «Инженерный». Вид калькулятора изменится — в нем появятся, в частности, кнопки для вычисления тригонометрических функций.Теперь введите значение угла , синус которого вам требуется вычислить. Можно сделать это как с клавиатуры, так и щелкая курсором мыши нужные клавиши калькулятора. А можно просто и вставить нужное вам значение (CTRL + C и CTRL + V). После этого выберите единицы измерения, в которых должен быть рассчитан — для тригонометрических функций это могут быть радианы, градусы или рады. Делается это выбором одного из трех значений переключателя, расположенного ниже поля ввода вычисляемого значения. Теперь, нажав кнопку с надписью «sin», получите ответ на свой вопрос.
Делается это выбором одного из трех значений переключателя, расположенного ниже поля ввода вычисляемого значения. Теперь, нажав кнопку с надписью «sin», получите ответ на свой вопрос.
Четвертый вариант — самый современный. В эру интернета в сети существуют , предлагающие чуть ли не каждую возникающую проблему. Он-лайн калькуляторы тригонометрических функций с удобным интерфейсом, более продвинутыми функциональными возможностями найти совсем не . Лучшие из них предлагают вычислить не только значения отдельной функции, но и достаточно сложных выражений из нескольких функций.
Функции синус и косинус относятся к области математики, которую называют тригонометрией, поэтому и сами функции называют тригонометрическими. Согласно самому старому из определений они выражают величину острого угла в прямоугольном треугольнике через отношения длин его сторон. Вычисление значений синус а при современном уровне развития электронной техники — довольно простая задача.
Вам понадобится
- Калькулятор Windows.

Инструкция
Используйте для вычисления синус а угла — вычисление тригонометрических функций предусмотрено в большинстве из них. Учитывая наличие калькулятора во многих мобильных телефонах, некоторых наручных и других мобильных гаджетах, не говоря уже о компьютерах, это, пожалуй, доступный способ вычисления синус а. Если вы решите воспользоваться программным калькулятором компьютера, то ссылку на его запуск ищите в главном меню ОС. Если это Windows, нажмите кнопку Win, выберите в меню пункт «Все программы», перейдите в подраздел «Стандартные» и кликните по строчке «Калькулятор». Чтобы открыть в запустившемся приложении доступ к командам вычисления тригонометрических функций нажмите сочетание клавиш Alt + 2.
Если в исходных величина угла, синус которого требуется вычислить, дана в , убедитесь, что рядом с надписью « » в интерфейсе калькулятора
Соотношение косинуса. Что такое синус и косинус
С центром в точке A .
α — угол, выраженный в радианах.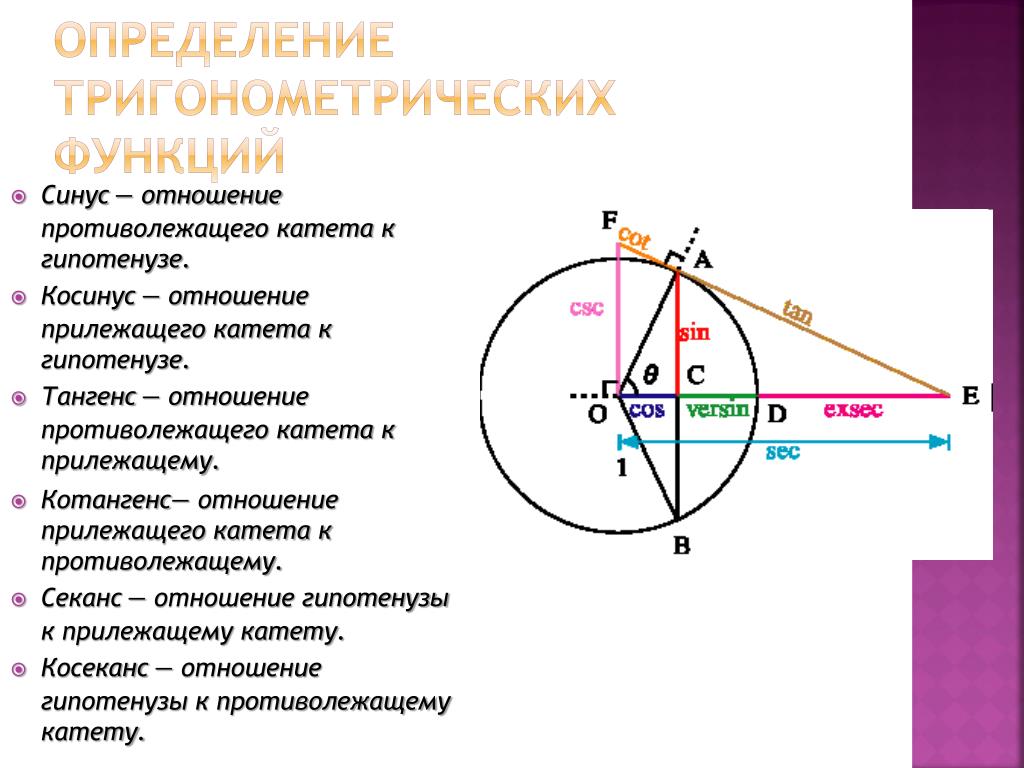
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x
(см. доказательство непрерывности). Их основные свойства представлены в таблице (n
— целое).
Их основные свойства представлены в таблице (n
— целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.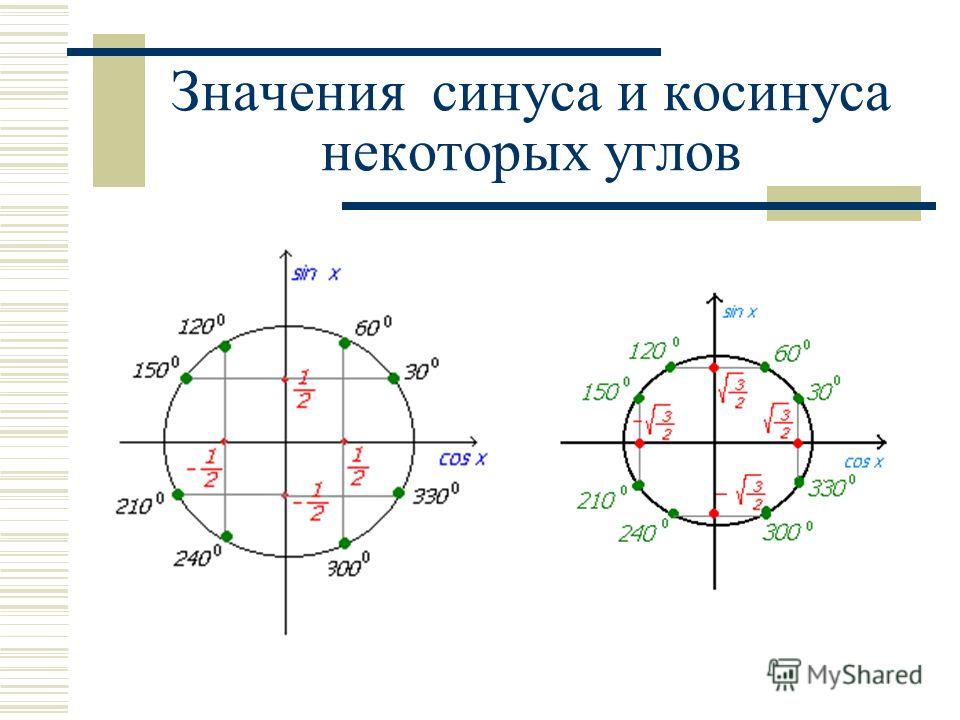
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
В этой статье мы покажем, как даются определения синуса, косинуса, тангенса и котангенса угла и числа в тригонометрии . Здесь же мы поговорим об обозначениях, приведем примеры записей, дадим графические иллюстрации. В заключение проведем параллель между определениями синуса, косинуса, тангенса и котангенса в тригонометрии и геометрии.
В заключение проведем параллель между определениями синуса, косинуса, тангенса и котангенса в тригонометрии и геометрии.
Навигация по странице.
Определение синуса, косинуса, тангенса и котангенса
Проследим за тем, как формируются представление о синусе, косинусе, тангенсе и котангенсе в школьном курсе математики. На уроках геометрии дается определение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. А позже изучается тригонометрия, где говорится о синусе, косинусе, тангенсе и котангенсе угла поворота и числа. Приведем все эти определения, приведем примеры и дадим необходимые комментарии.
Острого угла в прямоугольном треугольнике
Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки.
Определение.
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.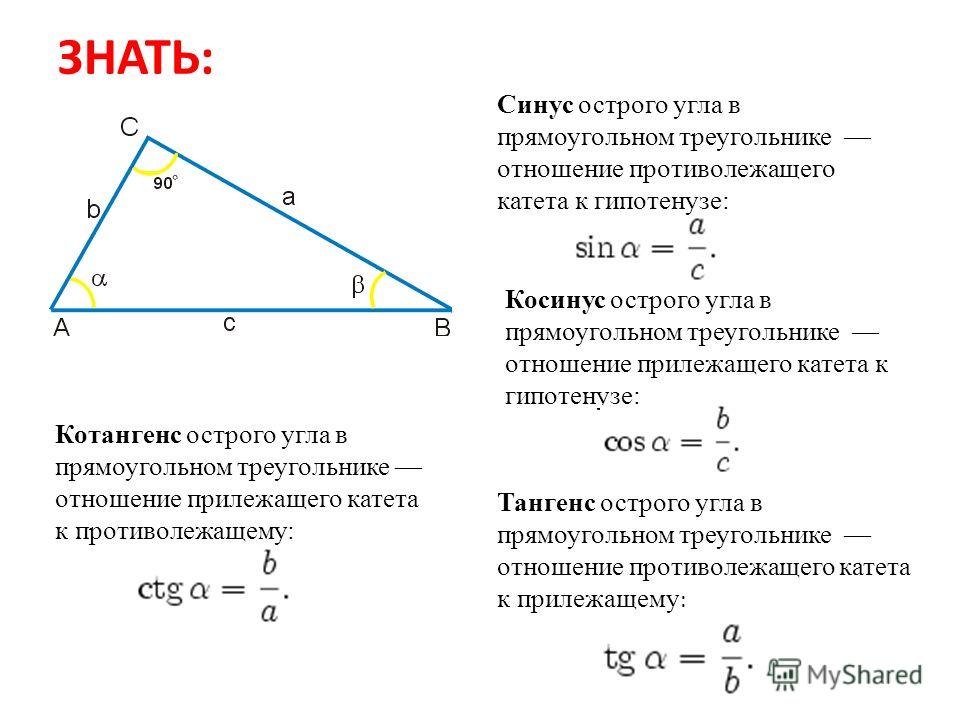
Определение.
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
Определение.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Определение.
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.
Там же вводятся обозначения синуса, косинуса, тангенса и котангенса – sin , cos , tg и ctg соответственно.
Например, если АВС – прямоугольный треугольник с прямым углом С , то синус острого угла A равен отношению противолежащего катета BC к гипотенузе AB , то есть, sin∠A=BC/AB .
Эти определения позволяют вычислять значения синуса, косинуса, тангенса и котангенса острого угла по известным длинам сторон прямоугольного треугольника, а также по известным значениям синуса, косинуса, тангенса, котангенса и длине одной из сторон находить длины других сторон. Например, если бы мы знали, что в прямоугольном треугольнике катет AC
равен 3
, а гипотенуза AB
равна 7
, то мы могли бы вычислить значение косинуса острого угла A
по определению: cos∠A=AC/AB=3/7
.
Например, если бы мы знали, что в прямоугольном треугольнике катет AC
равен 3
, а гипотенуза AB
равна 7
, то мы могли бы вычислить значение косинуса острого угла A
по определению: cos∠A=AC/AB=3/7
.
Угла поворота
В тригонометрии на угол начинают смотреть более широко — вводят понятие угла поворота . Величина угла поворота, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов, угол поворота в градусах (и в радианах) может выражаться каким угодно действительным числом от −∞ до +∞ .
В этом свете дают определения синуса, косинуса, тангенса и котангенса уже не острого угла, а угла произвольной величины — угла поворота. Они даются через координаты x и y точки A 1 , в которую переходит так называемая начальная точка A(1, 0) после ее поворота на угол α вокруг точки O – начала прямоугольной декартовой системы координат и центра единичной окружности .
Определение.
Синус угла поворота α
— это ордината точки A 1
, то есть, sinα=y
.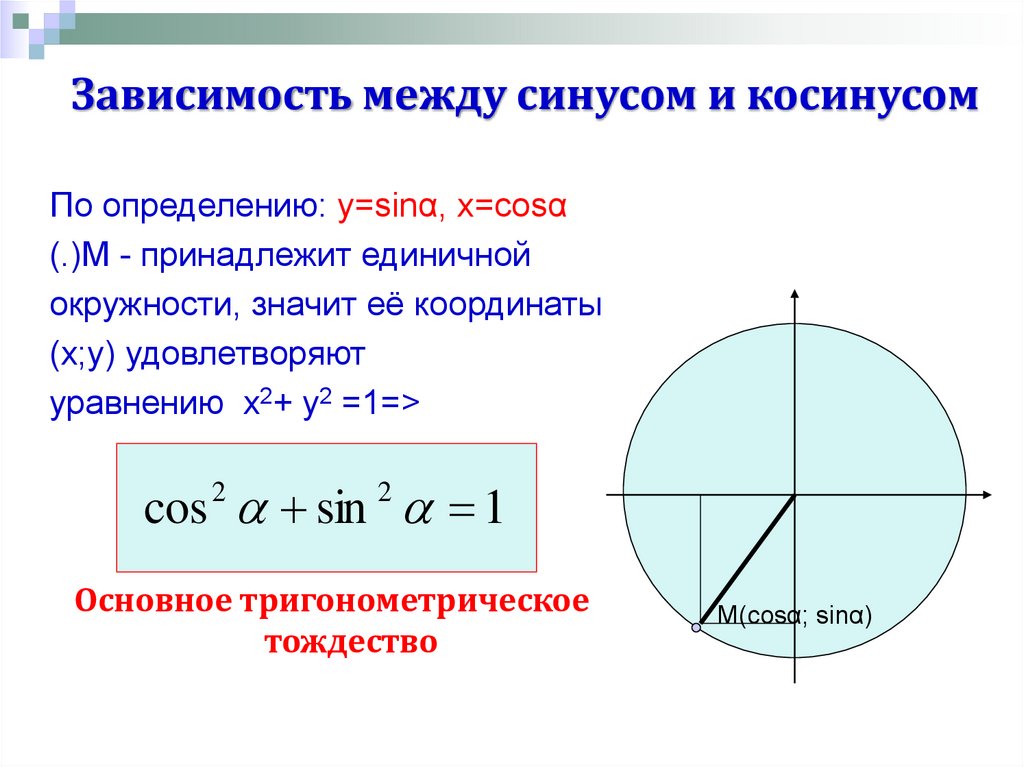
Определение.
Косинусом угла поворота α называют абсциссу точки A 1 , то есть, cosα=x .
Определение.
Тангенс угла поворота α — это отношение ординаты точки A 1 к ее абсциссе, то есть, tgα=y/x .
Определение.
Котангенсом угла поворота α называют отношение абсциссы точки A 1 к ее ординате, то есть, ctgα=x/y .
Синус и косинус определены для любого угла α
, так как мы всегда можем определить абсциссу и ординату точки, которая получается в результате поворота начальной точки на угол α
. А тангенс и котангенс определены не для любого угла. Тангенс не определен для таких углов α
, при которых начальная точка переходит в точку с нулевой абсциссой (0, 1)
или (0, −1)
, а это имеет место при углах 90°+180°·k
, k∈Z
(π/2+π·k
рад). Действительно, при таких углах поворота выражение tgα=y/x
не имеет смысла, так как в нем присутствует деление на нуль. Что же касается котангенса, то он не определен для таких углов α
, при которых начальная точка переходит к в точку с нулевой ординатой (1, 0)
или (−1, 0)
, а это имеет место для углов 180°·k
, k∈Z
(π·k
рад).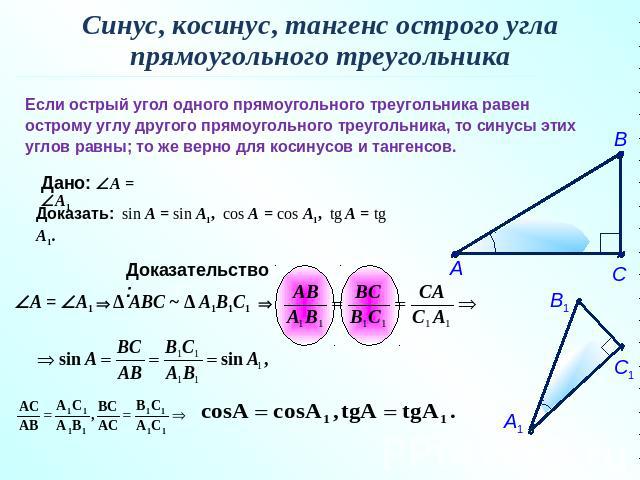
Итак, синус и косинус определены для любых углов поворота, тангенс определен для всех углов, кроме 90°+180°·k , k∈Z (π/2+π·k рад), а котангенс – для всех углов, кроме 180°·k , k∈Z (π·k рад).
В определениях фигурируют уже известные нам обозначения sin , cos , tg и ctg , они используются и для обозначения синуса, косинуса, тангенса и котангенса угла поворота (иногда можно встретить обозначения tan и cot , отвечающие тангенсу и котангенсу). Так синус угла поворота 30 градусов можно записать как sin30° , записям tg(−24°17′) и ctgα отвечают тангенс угла поворота −24 градуса 17 минут и котангенс угла поворота α . Напомним, что при записи радианной меры угла обозначение «рад» часто опускают. Например, косинус угла поворота в три пи рад обычно обозначают cos3·π .
В заключение этого пункта стоит заметить, что в разговоре про синус, косинус, тангенс и котангенс угла поворота часто опускают словосочетание «угол поворота» или слово «поворота». То есть, вместо фразы «синус угла поворота альфа» обычно используют фразу «синус угла альфа» или еще короче – «синус альфа».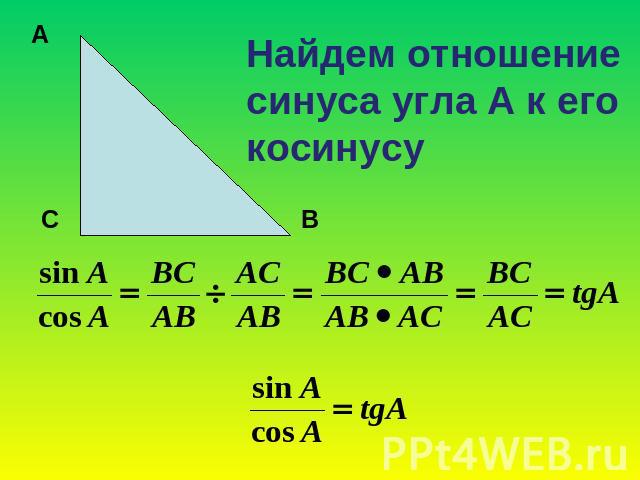 Это же касается и косинуса, и тангенса, и котангенса.
Это же касается и косинуса, и тангенса, и котангенса.
Также скажем, что определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике согласуются с только что данными определениями синуса, косинуса, тангенса и котангенса угла поворота величиной от 0 до 90 градусов. Это мы обоснуем .
Числа
Определение.
Синусом, косинусом, тангенсом и котангенсом числа t называют число, равное синусу, косинусу, тангенсу и котангенсу угла поворота в t радианов соответственно.
Например, косинус числа 8·π по определению есть число, равное косинусу угла в 8·π рад. А косинус угла в 8·π рад равен единице, поэтому, косинус числа 8·π равен 1 .
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Он состоит в том, что каждому действительному числу t
ставится в соответствие точка единичной окружности с центром в начале прямоугольной системы координат, и синус, косинус, тангенс и котангенс определяются через координаты этой точки.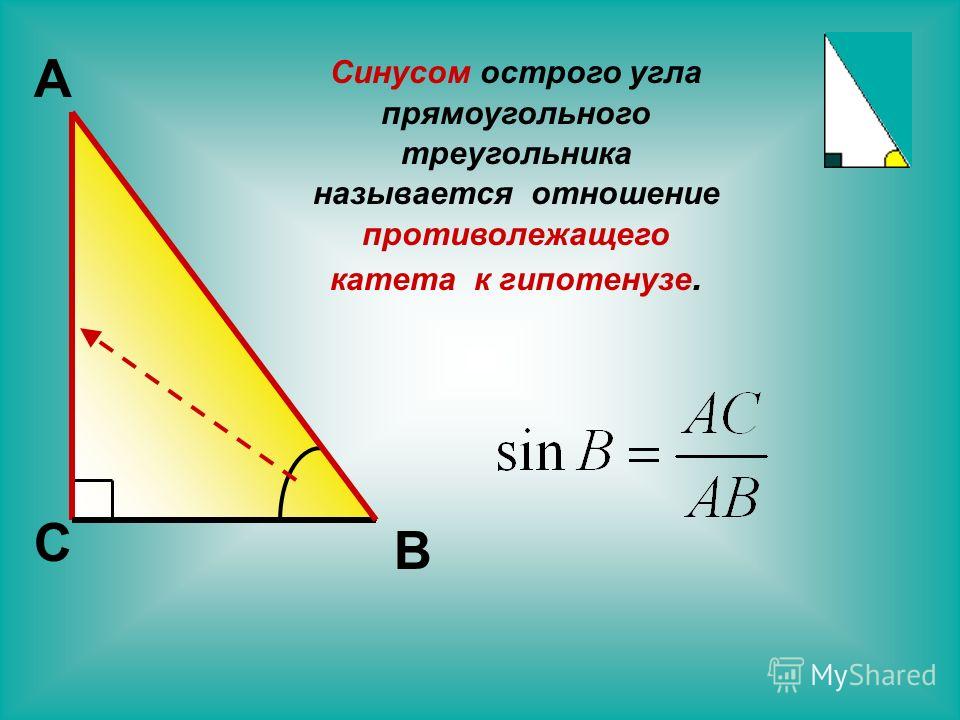 Остановимся на этом подробнее.
Остановимся на этом подробнее.
Покажем, как устанавливается соответствие между действительными числами и точками окружности:
- числу 0 ставится в соответствие начальная точка A(1, 0) ;
- положительному числу t ставится в соответствие точка единичной окружности, в которую мы попадем, если будем двигаться по окружности из начальной точки в направлении против часовой стрелки и пройдем путь длиной t ;
- отрицательному числу t ставится в соответствие точка единичной окружности, в которую мы попадем, если будем двигаться по окружности из начальной точки в направлении по часовой стрелке и пройдем путь длиной |t| .
Теперь переходим к определениями синуса, косинуса, тангенса и котангенса числа t . Допустим, что числу t соответствует точка окружности A 1 (x, y) (например, числу &pi/2; отвечает точка A 1 (0, 1) ).
Определение.
Синусом числа t
называют ординату точки единичной окружности, соответствующей числу t
, то есть, sint=y
.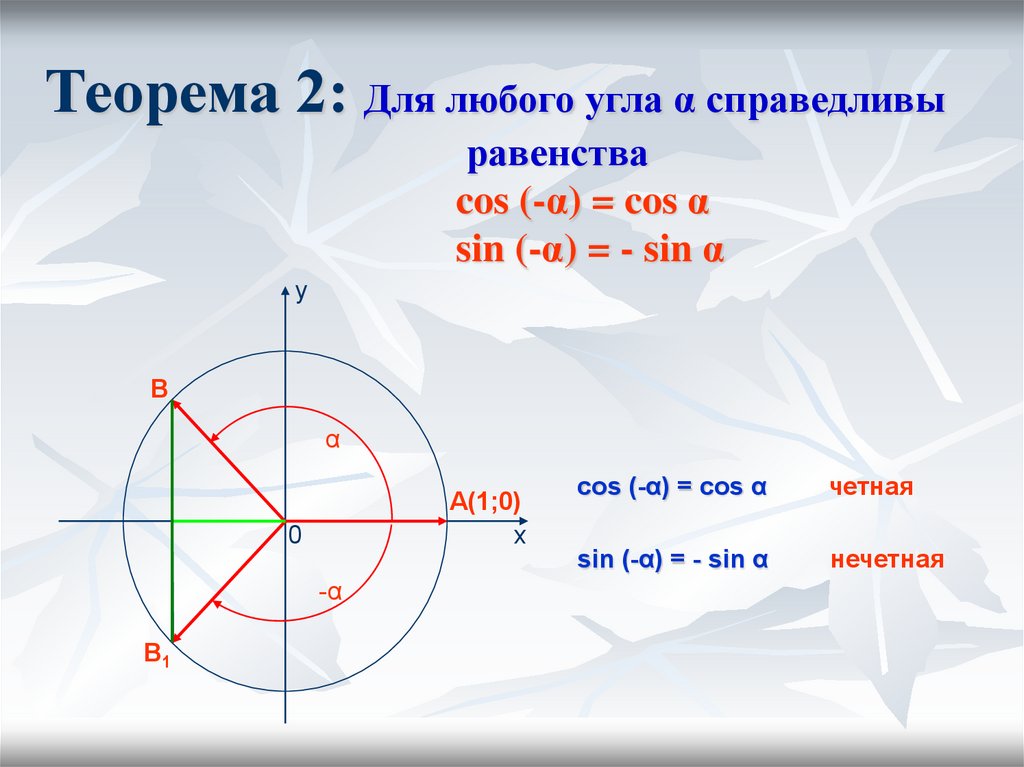
Определение.
Косинусом числа t называют абсциссу точки единичной окружности, отвечающей числу t , то есть, cost=x .
Определение.
Тангенсом числа t называют отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t , то есть, tgt=y/x . В другой равносильной формулировке тангенс числа t – это отношение синуса этого числа к косинусу, то есть, tgt=sint/cost .
Определение.
Котангенсом числа t называют отношение абсциссы к ординате точки единичной окружности, соответствующей числу t , то есть, ctgt=x/y . Другая формулировка такова: тангенс числа t – это отношение косинуса числа t к синусу числа t : ctgt=cost/sint .
Здесь отметим, что только что данные определения согласуются с определением, данным в начале этого пункта. Действительно, точка единичной окружности, соответствующая числу t , совпадает с точкой, полученной в результате поворота начальной точки на угол в t радианов.
Еще стоит прояснить такой момент. Допустим, перед нами запись sin3
. Как понять, о синусе числа 3
или о синусе угла поворота в 3
радиана идет речь? Обычно это ясно из контекста, в противном случае это скорее всего не имеет принципиального значения.
Допустим, перед нами запись sin3
. Как понять, о синусе числа 3
или о синусе угла поворота в 3
радиана идет речь? Обычно это ясно из контекста, в противном случае это скорее всего не имеет принципиального значения.
Тригонометрические функции углового и числового аргумента
Согласно данным в предыдущем пункте определениям, каждому углу поворота α соответствуют вполне определенное значение sinα , как и значение cosα . Кроме того, всем углам поворота, отличным от 90°+180°·k , k∈Z (π/2+π·k рад) отвечают значения tgα , а отличным от 180°·k , k∈Z (π·k рад) – значения ctgα . Поэтому sinα , cosα , tgα и ctgα — это функции угла α . Другими словами – это функции углового аргумента.
Аналогично можно говорить и про функции синус, косинус, тангенс и котангенс числового аргумента. Действительно, каждому действительному числу t
отвечает вполне определенное значение sint
, как и cost
. Кроме того, всем числам, отличным от π/2+π·k
, k∈Z
соответствуют значения tgt
, а числам π·k
, k∈Z
— значения ctgt
.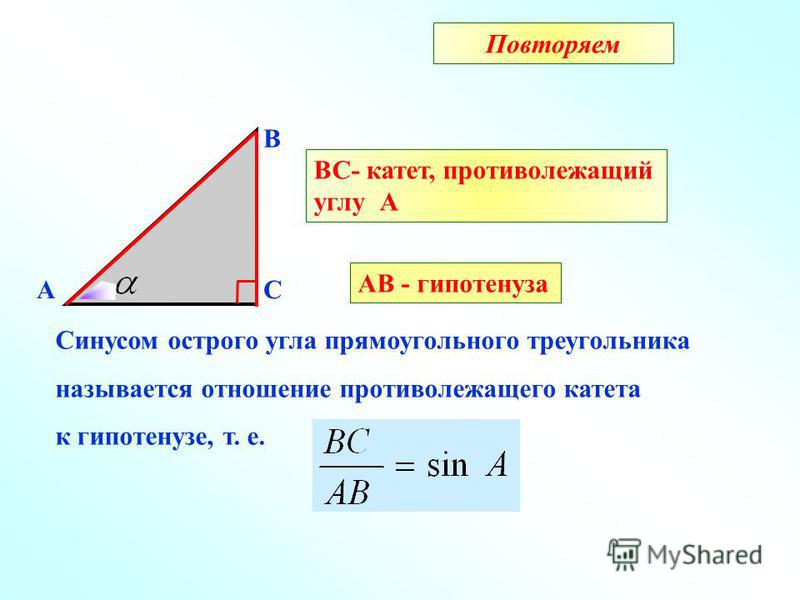
Функции синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями .
Из контекста обычно понятно, с тригонометрическими функциями углового аргумента или числового аргумента мы имеем дело. В противном случае мы можем считать независимую переменную как мерой угла (угловым аргументом), так и числовым аргументом.
Однако, в школе в основном изучаются числовые функции, то есть, функции, аргументы которых, как и соответствующие им значения функции, являются числами. Поэтому, если речь идет именно о функциях, то целесообразно считать тригонометрические функции функциями числовых аргументов.
Связь определений из геометрии и тригонометрии
Если рассматривать угол поворота α
величиной от 0
до 90
градусов, то данные в контексте тригонометрии определения синуса, косинуса, тангенса и котангенса угла поворота полностью согласуются с определениями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике, которые даются в курсе геометрии. Обоснуем это.
Обоснуем это.
Изобразим в прямоугольной декартовой системе координат Oxy единичную окружность. Отметим начальную точку A(1, 0) . Повернем ее на угол α величиной от 0 до 90 градусов, получим точку A 1 (x, y) . Опустим из точки А 1 на ось Ox перпендикуляр A 1 H .
Легко видеть, что в прямоугольном треугольнике угол A 1 OH
равен углу поворота α
, длина прилежащего к этому углу катета OH
равна абсциссе точки A 1
, то есть, |OH|=x
, длина противолежащего к углу катета A 1 H
равна ординате точки A 1
, то есть, |A 1 H|=y
, а длина гипотенузы OA 1
равна единице, так как она является радиусом единичной окружности. Тогда по определению из геометрии синус острого угла α
в прямоугольном треугольнике A 1 OH
равен отношению противолежащего катета к гипотенузе, то есть, sinα=|A 1 H|/|OA 1 |=y/1=y
. А по определению из тригонометрии синус угла поворота α
равен ординате точки A 1
, то есть, sinα=y
. Отсюда видно, что определение синуса острого угла в прямоугольном треугольнике эквивалентно определению синуса угла поворота α
при α
от 0
до 90
градусов.
Аналогично можно показать, что и определения косинуса, тангенса и котангенса острого угла α согласуются с определениями косинуса, тангенса и котангенса угла поворота α .
Список литературы.
- Геометрия. 7-9 классы : учеб. для общеобразоват. учреждений / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. — 20-е изд. М.: Просвещение, 2010. — 384 с.: ил. — ISBN 978-5-09-023915-8.
- Погорелов А. В. Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений/ А. В. Погорелов. — 2-е изд — М.: Просвещение, 2001. — 224 с.: ил. — ISBN 5-09-010803-X.
- Алгебра и элементарные функции : Учебное пособие для учащихся 9 класса средней школы / Е. С. Кочетков, Е. С. Кочеткова; Под редакцией доктора физико-математических наук О. Н. Головина.- 4-е изд. М.: Просвещение, 1969.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.
 : ил.- ISBN 5-09-002727-7
: ил.- ISBN 5-09-002727-7 - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Мордкович А. Г. Алгебра и начала анализа. 10 класс. В 2 ч. Ч. 1: учебник для общеобразовательных учреждений (профильный уровень)/ А. Г. Мордкович, П. В. Семенов. — 4-е изд., доп. — М.: Мнемозина, 2007. — 424 с.: ил. ISBN 978-5-346-00792-0.
- Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни /[Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. — 3-е изд. — И.: Просвещение, 2010.- 368 с.: ил.- ISBN 978-5-09-022771-1.
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В.
 А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов . Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М.
 И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4. - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой.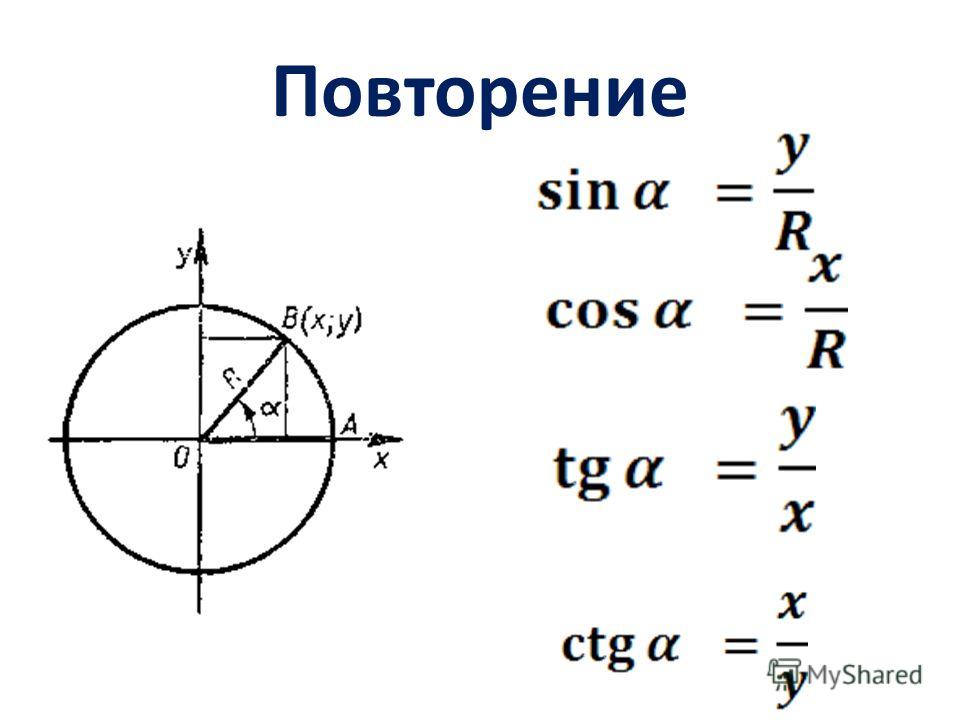 Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус.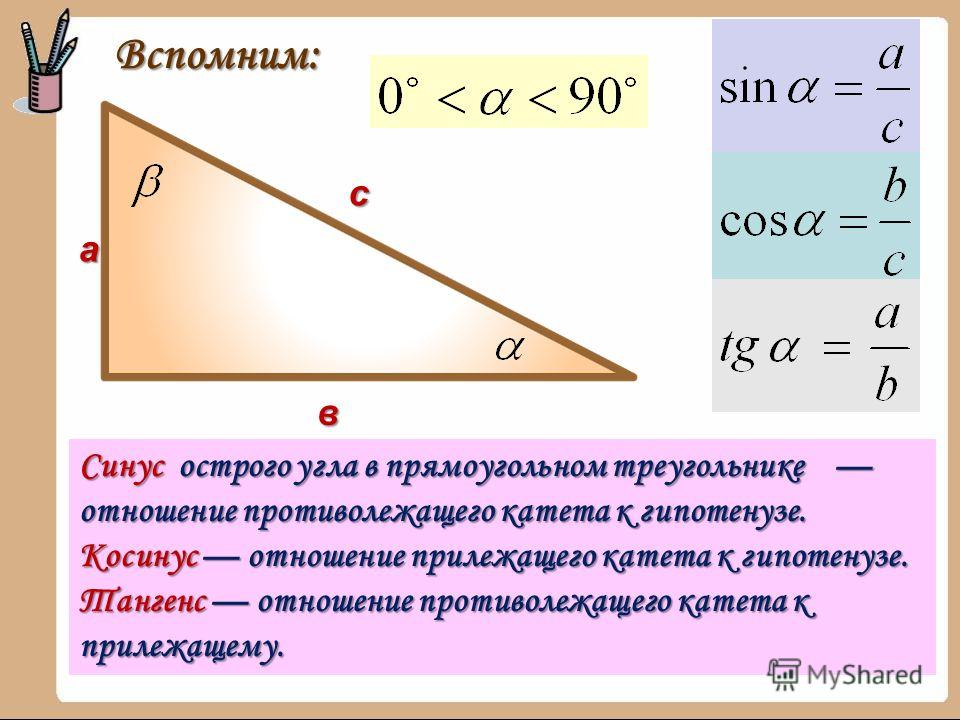 Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Изначально синус и косинус возникли из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Именно так и были введены понятия синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут применяться не только в прямоугольных треугольниках. Чтобы найти значение тупого или острого угла, стороны любого треугольника, достаточно применить теорему косинусов и синусов.
Теорема косинусов довольно проста: «Квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними».
Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная — математический инструмент, показывающий, как быстро меняется функция относительно изменения ее аргумента. Производные используются , геометрии, и , ряде технических дисциплин.
При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса — синус, но со знаком «минус».
Применение в математике
Особенно часто синусы и косинусы используются при решении прямоугольных треугольников и задач, связанных с ними.
Удобство синусов и косинусов нашло свое отражение и в технике. Углы и стороны было просто оценивать по теоремам косинусов и синусов, разбивая сложные фигуры и объекты на «простые» треугольники. Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов разных углов. В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
π = 3.141592653589793238462… (приблизительное значение числа Пи).
Таблица косинусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Угол х (в градусах) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Угол х (в радианах) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π |
| cos x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Зависимость между синусом, косинусом и тангенсом одного и того же угла
Урок 25.
 Алгебра 10 класс ФГОС
Алгебра 10 класс ФГОСВ этом видеоуроке мы узнаем, какое равенство называют основным тригонометрическим тождеством. Выясним зависимость между синусом и косинусом. Найдём зависимость между тангенсом и котангенсом, между тангенсом и косинусом.
Конспект урока «Зависимость между синусом, косинусом и тангенсом одного и того же угла»
Вспомним, что синусом угла называется ордината точки , полученной поворотом точки вокруг начала координат на угол .
Косинусом угла называется абсцисса точки , полученной поворотом точки вокруг начала координат на угол .
Тангенсом угла называется отношение синуса угла к его косинусу.
Котангенсом угла называется отношение косинуса угла к его синусу.
Итак, выясним зависимость между синусом и косинусом.
Пусть на координатной плоскости изображена
единичная окружность с центром в начале координат. Точка совершает поворот против часовой стрелки на угол
и
оказывается в точке .
Точка совершает поворот против часовой стрелки на угол
и
оказывается в точке .
По определению синуса и косинуса можно сказать, что абсцисса точки равна косинусу угла поворота, то есть , а ордината точки равна синусу угла поворота, то есть . Тогда можем записать, что точка .
Теперь вспомним, что уравнение единичной окружности имеет вид: . Так как точка принадлежит нашей единичной окружности, то её координаты удовлетворяют этому уравнению. А значит, можем записать: .
А как называется это равенство? Это равенство называют основным тригонометрическим тождеством. Оно выполняется при любых значениях . Основное тригонометрическое тождество часто используется при преобразовании тригонометрических выражений.
Давайте из этого тождества выразим . Итак, перенесём в правую часть равенства: . Извлекаем квадратный корень из обеих частей
равенства: , , если – угол I или II четверти. И , если – угол III или IV четверти.
В общем, можем записать так: .
Теперь выразим . Перенесём в правую часть равенства: . Извлекаем квадратный корень из обеих частей равенства: , . , если – угол I или IV четверти. , если – угол II или III четверти.
В общем, можем записать так: .
Вот таким образом мы получили равенства, которые связывают значения синуса и косинуса одного и того же угла.
Давайте вычислим , если и . Воспользуемся формулой . Так как а, то есть угол альфа – это угол III четверти, то . Поэтому в формуле перед корнем нужно поставить знак «»: . Тогда подставим значение в формулу: . Выполним вычисления: .
Теперь давайте вычислим , если и . Воспользуемся формулой . Так как , то есть угол альфа – это угол IV четверти, то .
Поэтому в формуле перед корнем нужно поставить знак «»? Верно. Запишем формулу: . Подставим значение в формулу: . Выполним вычисления: .
Ну а теперь выясним зависимость между тангенсом и котангенсом. По
определению , а . Перемножим почленно эти равенства:
. И получим: Выразим из этого равенства и получим, что . И выразим и получим, что . Важно отметить, что так как на нуль делить
нельзя, то и , то есть , .
Перемножим почленно эти равенства:
. И получим: Выразим из этого равенства и получим, что . И выразим и получим, что . Важно отметить, что так как на нуль делить
нельзя, то и , то есть , .
Вычислим , если . Подставляем в формулу значение котангенса: . Вычисляем и получаем .
Вычислим , если и . По формуле найдём . Так как , то есть угол – это угол II четверти, то . Поэтому в формуле перед корнем нужно поставить знак «»: . Подставим значение . Выполним вычисления: .
Теперь найдём значение . Подставим значения и . Выполним вычисления: .
И нам осталось найти зависимость между тангенсом и косинусом. Для этого мы с вами разделим обе части основного тригонометрического тождества на : . При этом не должен равняться нулю, то есть , . Преобразуем левую часть равенства: . Первое слагаемое в левой части можем записать как , второе – как : .
Эта формула и показывает зависимость между тангенсом и косинусом? Да.
Из этой формулы мы можем выразить тангенс через косинус и косинус через
тангенс.
Давайте вычислим , если и . Выразим из формулы : . Подставим значение : . Выполним вычисления: . , то есть это угол II четверти. Тангенс во второй четверти принимает отрицательные значения. Поэтому .
И вычислим , если и . Из формулы выразим : . Подставим значение : . Выполним вычисления: . У нас . Косинус в III четверти принимает отрицательные значения. Поэтому .
А сейчас выполним несколько заданий.
Задание первое. Найдите , и , если и .
Решение.
Задание второе. Найдите , и , если и .
Решение.
Предыдущий урок 24 Знаки синуса, косинуса и тангенса угла
Следующий урок 26 Тригонометрические тождества
Получите полный комплект видеоуроков, тестов и презентаций Алгебра 10 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
коэффициентов синуса, косинуса и тангенса.
 – Бизнес/Техническая математика
– Бизнес/Техническая математика5. Тригонометрия
Ожидается, что к концу этого раздела вы сможете
- Находить недостающую сторону прямоугольного треугольника, используя отношения синуса, косинуса или тангенса
- Найдите недостающий угол прямоугольного треугольника, используя отношения синуса, косинуса или тангенса
- Решение приложений с помощью тригонометрии прямого угла
Теперь, когда мы знаем основы алгебры и геометрии, связанные с прямоугольным треугольником, мы можем приступить к изучению тригонометрии. Многие реальные жизненные задачи можно представить и решить с помощью прямоугольной тригонометрии.
Мы знаем, что любой прямоугольный треугольник имеет три стороны и прямой угол. Сторона, противолежащая прямому углу, называется гипотенузой. Два других угла прямоугольного треугольника — острые углы (с мерой меньше 90 градусов). Один из этих углов мы называем опорным углом, и мы используем θ (тета) для его представления.
Гипотенуза всегда является наибольшей стороной прямоугольного треугольника. Две другие стороны называются противоположной стороной и смежной стороной. Названия этих сторон зависят от того, какой из двух острых углов используется в качестве опорного угла.
Рисунок 1.В прямоугольном треугольнике каждая сторона помечена строчной буквой, соответствующей прописной букве противоположной вершины.
Назовите стороны треугольника и найдите гипотенузу, противоположную и прилежащую.
Решение
Мы пометили стороны строчными буквами, чтобы они совпадали с прописными буквами противоположной вершины.
с — гипотенуза
а — против
b — примыкает
Назовите стороны треугольника и найдите гипотенузу, противолежащую и прилежащую.
Показать ответy — гипотенуза
z противоположно
х рядом
Тригонометрические отношения — это отношения сторон прямоугольного треугольника. Для любого прямоугольного треугольника мы можем определить три основных тригонометрических соотношения: синус, косинус и тангенс.
Давайте обратимся к рисунку 1 и определим три основных тригонометрических отношения как:
- синус θ =
- косинус θ =
- тангенс θ =
Где θ — мера опорного угла, измеренная в градусах.
Очень часто мы используем сокращения для синуса, косинуса и тангенса.
- sin θ =
- , потому что θ =
- тангенс θ =
Некоторые люди помнят определение тригонометрических соотношений как SOH CAH TOA.
Давайте воспользуемся примером из примера 1, чтобы найти три соотношения.
Для данного треугольника найти отношение синуса, косинуса и тангенса.
Решение
sin θ =
cos θ =
tan θ =
Для данного треугольника найти отношение синуса косинуса и тангенса.
Показать ответsin θ =
, потому что θ =
тангенс θ =
В примере 2 опорные углы могут быть или . Используя определение тригонометрических отношений, мы можем написать sinE = , cosE = и tanE = .
При расчетах мы обычно округляем отношения до четырех знаков после запятой, а в конце наш окончательный ответ — до одного знака после запятой, если не указано иное.
Для данного треугольника найти отношения синуса, косинуса и тангенса. При необходимости округлить до четырех знаков после запятой.
Решение
У нас есть два возможных опорных угла: R и S.
Используя определения, тригонометрические соотношения для угла R составляют:
- sin R= 0,8
- потому что R= = 0,6
- тангенс R= = 1,3333…
Используя определения, тригонометрические соотношения для угла S:
- sin S = = 0,6
- cos S = = 0,8
- тангенс S = = 0,75
Для данного треугольника найти отношения синуса, косинуса и тангенса. При необходимости округлить до четырех знаков после запятой.
Показать ответ- sin F = = 0,8
- cos F = =0,6
- тангенс F = = 1,3333…
- sin D = = 0,6
- cos D = = 0,8
- тангенс D = = 0,75
Теперь воспользуемся научным калькулятором, чтобы найти тригонометрические соотношения. Сможете ли вы найти кнопки sin, cos и tan на своем калькуляторе? Чтобы найти тригонометрические соотношения, убедитесь, что ваш калькулятор находится в режиме градусов.
Сможете ли вы найти кнопки sin, cos и tan на своем калькуляторе? Чтобы найти тригонометрические соотношения, убедитесь, что ваш калькулятор находится в режиме градусов.
С помощью калькулятора найдите тригонометрические соотношения. При необходимости округлить до 4 знаков после запятой.
a) sin 30°
b) cos 45°
c) tan 60°
Решение
Убедитесь, что ваш калькулятор находится в режиме Градусов.
а) С помощью калькулятора найдите, что sin 30° = 0,5
б) С помощью калькулятора найдите, что cos 45° = 0,7071 Округлив до 4 знаков после запятой.
c) С помощью калькулятора найдите тангенс 60° = 1,7321. Округлите до 4 знаков после запятой.
Найдите тригонометрические соотношения. При необходимости округлить до 4 знаков после запятой.
a) sin 60°
b) cos 30°
c) tan 45°
Показать ответa) sin 60° = 0,8660
б) cos 30° = 0,8660
в) тангенс 45° = 1
В этом разделе вы будете использовать тригонометрические отношения для решения задач прямоугольного треугольника. Мы адаптируем нашу стратегию решения задач для приложений тригонометрии. Кроме того, поскольку в этих задачах будет фигурировать прямоугольный треугольник, будет полезно нарисовать его (если рисунок не предоставлен) и пометить его заданной информацией. Мы включим это в первый шаг стратегии решения задач для тригонометрических приложений. .
Мы адаптируем нашу стратегию решения задач для приложений тригонометрии. Кроме того, поскольку в этих задачах будет фигурировать прямоугольный треугольник, будет полезно нарисовать его (если рисунок не предоставлен) и пометить его заданной информацией. Мы включим это в первый шаг стратегии решения задач для тригонометрических приложений. .
- Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
- Определите , что мы ищем.
- Пометьте то, что мы ищем, выбрав переменную для ее представления.
- Найдите требуемое тригонометрическое отношение.
- Решите отношение, используя хорошие методы алгебры.
- Проверьте ответ, подставив его обратно в соотношение на шаге 4 и убедившись, что он имеет смысл в контексте задачи.

- Ответьте на вопрос полным предложением.
В следующих нескольких примерах, зная меру одного острого угла и длину одной стороны прямоугольного треугольника, мы решим прямоугольный треугольник относительно недостающих сторон.
Найти недостающие стороны. Округлите окончательный ответ до двух знаков после запятой
Решение
| 1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. | Дается чертеж. Угол Y — это наш опорный угол, y — противоположная сторона, z — смежная сторона, а x = 14 — гипотенуза. | |
| 2. Определите , что мы ищем. | а) противоположная сторона | б) смежная сторона |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | у=? | г=? |
4. Найдите искомое тригонометрическое отношение. Найдите искомое тригонометрическое отношение. | sin 35° = | cos 35° = |
| 5. Решите отношение , используя хорошие методы алгебры. | 14 sin 35° = у 8.03 = у | 14 cos 35° = z 11,47 = z |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | 0,57 8,03 14 0,57 = 0,57 | 0,82 11,47 14 0,82 = 0,82 |
| 7. Ответьте на вопрос полным предложением. | Противоположная сторона 8.03 | Прилежащая сторона 11,47 |
Найти недостающие стороны. Округлите окончательный ответ до одного знака после запятой.
Показать ответа = 20,2
б = 16,4
Найдите гипотенузу. Округлите окончательный ответ до одного знака после запятой.
Решение
1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. Нарисуйте прямоугольный треугольник и обозначьте указанные части. | Дается чертеж. Угол S – это исходный угол, s – противоположная сторона, r = 4 – прилежащая сторона, а p – гипотенуза 90 224. |
| 2. Определите , что мы ищем. | гипотенуза |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | р=? |
| 4. Найдите искомое тригонометрическое отношение. | cos 32° = |
| 5. Решите отношение , используя хорошие методы алгебры. | 0,8480 = р = 4,7170 Округление долей до 4 знаков после запятой |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | 0,8480 0,8480 = 0,8480 |
| 7. Ответьте на вопрос полным предложением. | Гипотенуза равна 4,7 Округлите мой окончательный ответ до одного знака после запятой. |
Найдите гипотенузу. Округлите окончательный ответ до одного знака после запятой.
Показать ответp = 22,7
Иногда у нас есть прямоугольный треугольник с данными только сторонами. Как найти недостающие углы? Чтобы найти недостающие углы, мы используем обратные тригонометрические соотношения. Обратные кнопки sin -1 , cos -1 и tan -1 находятся на вашем научном калькуляторе.
Найдите углы. Округлите окончательный ответ до одного знака после запятой.
а) sin A = 0,5
b) cos B = 0,9735
c) tan C = 2,89358
Solution
Воспользуйтесь калькулятором и нажмите 2-ю клавишу FUNCTINAN или SOS, а затем нажмите Ключ
A) A = SIN -1 0,5
= 30 °
B) B = COS -1 0,9735
= 13,2 ° округлен до одного десятичного места
C) C = TAN -1 -1 2,89358
= 70,9° Округлено до одного десятичного знака
Найдите углы. Округлите окончательный ответ до одного знака после запятой.
Округлите окончательный ответ до одного знака после запятой.
a) sin X = 1
b) cos Y = 0,375
c) tan Z = 1,676767
Показать ответa) = 90°
б) = 68°
в) = 59,2°
В приведенном ниже примере у нас есть прямоугольный треугольник с двумя заданными сторонами. У нас отсутствуют острые углы. Давайте посмотрим, каковы шаги, чтобы найти недостающие углы.
Найдите пропавший . Округлите окончательный ответ до одного знака после запятой.
Решение
| 1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. | Дается чертеж. Угол T — это наш исходный угол, t = 7 — противоположная сторона, s — смежная сторона, r = 11 — гипотенуза 90 224. |
| 2. Определите , что мы ищем. | угол T |
3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | =? |
| 4. Найдите искомое тригонометрическое отношение. | грех Т = |
| 5. Решите отношение , используя хорошие методы алгебры. | sin Т = 0,6364 T = sin -1 0,6364 = 39,5239° |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | sin 39,5239° 0,6364 0,6364 = 0,6364 |
| 7. Ответьте на вопрос полным предложением. | Недостающий угол T равен 39,5°. |
Найдите недостающий угол X. Округлите окончательный ответ до одного знака после запятой.
Показать ответ20.1°
Найдите недостающий угол A. Округлите окончательный ответ до одного десятичного знака.
Решение
1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. Нарисуйте прямоугольный треугольник и обозначьте указанные части. | Дается чертеж. Угол A — это наш исходный угол, a = 9 — противолежащая сторона, c = 5 — прилежащая сторона, а b — гипотенуза 90 224. |
| 2. Определите , что мы ищем. | угол А |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | =? |
| 4. Найдите искомое тригонометрическое отношение. | загар А = |
| 5. Решите отношение , используя хорошие методы алгебры. | тангенс А = 1,8 А = рыжевато-коричневый -1 1,8 = 60,9° |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | тангенс 60,9° 1,8 1,8 = 1,8 |
| 7. Ответьте на вопрос полным предложением. | Недостающий угол A равен 60,9°. |
Найдите недостающий угол C. Округлите окончательный ответ до одного знака после запятой.
Показать ответ29.1°
Из предыдущего раздела мы знаем, что любой треугольник имеет три стороны и три внутренних угла. В прямоугольном треугольнике, когда известны все шесть частей треугольника, мы говорим, что прямоугольный треугольник решен.
Решите прямоугольный треугольник. Округлите окончательный ответ до одного знака после запятой.
Решение
Поскольку сумма углов в любом треугольнике равна 180°, величину угла B можно легко вычислить.
= 180° − 90° − 42°
= 48°
| 1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части. | Дается чертеж. Угол A — это исходный угол, a = 8 — противолежащая сторона, b — прилежащая сторона, а c — гипотенуза. | |
2. Определите , что мы ищем. Определите , что мы ищем. | а) соседняя сторона | б) гипотенуза |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | б = ? | с = ? |
| 4. Найдите искомое тригонометрическое отношение. | тангенс 42° = | sin 42° = |
| 5. Решите отношение , используя хорошие методы алгебры. | 0,9004 = 0,9004 б = 8 б = 8,8849 | 0,6691 = 0,6691 с = 8 с = 11,9563 |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | тангенс 42° 0,9 = 0,9 | sin 42° 0,6691 = 0,6691 |
| 7. Ответьте на вопрос полным предложением. | Смежная сторона равна 8,9. Округляется до одного десятичного знака. | Гипотенуза равна 12 |
Мы решили прямоугольный треугольник
= 42°
= 48°
= 90°
a = 8
b = 8,9
c = 12
Решите прямоугольный треугольник. Округлите окончательный ответ до одного знака после запятой.
Округлите окончательный ответ до одного знака после запятой.
= 21°
= 69°
= 90°
Показать ответa = 6
б = 15,6
с = 16,7
Решите прямоугольный треугольник. Округлить до двух знаков после запятой.
Решение
| 1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. | Дается чертеж. Пусть угол D — наш опорный угол, d = 4 — противолежащая сторона, f — прилежащая сторона, а e = 9 — гипотенуза 90 224. | |
| 2. Определите , что мы ищем. | а) уголок D | б) смежный |
| 3. Пометьте то, что мы ищем, выбрав переменную для ее представления. | =? | е = ? |
| 4. Найдите искомое тригонометрическое отношение. | sin D = | 4 2 + f 2 = 9 2 |
5. Решите отношение , используя хорошие методы алгебры. Решите отношение , используя хорошие методы алгебры. | sin D = 0,4444 D = sin -1 0,4444 = 26,3850° | 16 + ф 2 = 81 ф 2 = 81 – 16 ф 2 = 65 f = квадратный корень из 65 f = 8,06 |
| 6. Проверка ответ в задаче и убедившись, что это имеет смысл. | sin 26,3850° 0,4444 = 0,4444 | 4 2 + 8,06 2 9 2 81 = 81 |
| 7. Ответьте на вопрос полным предложением. | Недостающий угол D равен 26,39°. | Смежная сторона равна 8,06 Округлено до двух знаков после запятой |
Недостающий угол F = 180° – 90° – 26,39° = 63,64 °
Мы решили правый треугольник
= 26,39 °
= 90 °
= 63,61 °
D = 4
E =
F = 8,06
Solve Triangle. Округлить до одного десятичного знака.
Округлить до одного десятичного знака.
= 29,3°
= 90°
= 60,7°
Показать ответd = 29,4
е = 18,4
f = 60,6
В предыдущих примерах мы смогли найти недостающие стороны и недостающие углы прямоугольного треугольника. Теперь давайте воспользуемся тригонометрическими отношениями для решения задач из реальной жизни.
Многие применения тригонометрических соотношений связаны с пониманием угла подъема или угла наклона.
Угол возвышения – это угол между горизонтальной линией (землей) и линией визирования наблюдателя.
Угол наклона — это угол между горизонтальной линией (параллельной земле) и линией обзора наблюдателя.
Джеймс стоит в 31 метре от базы Harbour Center в Ванкувере. Он смотрит на вершину здания под углом 78°. Какова высота Harbour Centre?
Решение
1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. | Угол X — это исходный угол, x — противоположная сторона, y = 31 м — прилежащая сторона, а z — гипотенуза. |
| 2. Определите , что мы ищем. | Противоположная сторона |
| 3. Этикетка то, что мы ищем, выбрав переменную для ее представления. | х=? |
| 4. Найдите искомое тригонометрическое отношение. | тангенс 78° = |
| 5. Решите отношение , используя хорошие методы алгебры. | 4,7046 = х = 145,8426 |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | 4,7046 4,7046 = 4,7046 |
| 7. Ответьте на вопрос полным предложением. | Harbour Center составляет 145,8426 метра или округляется до 146 метров. |
Марта стоит в 23 метрах от основания самого высокого многоквартирного дома в Принс-Джордже и смотрит на крышу здания под углом 62°. Насколько высокое здание?
Насколько высокое здание?
43,3 метра
Томас стоит на вершине здания высотой 45 метров и смотрит на свою подругу, стоящую на земле в 22 метрах от основания здания. Что такое угол депрессии?
Решение
| 1. Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части. | Угол Y – это исходный угол, y = 45 м – противолежащая сторона, z = 22 м – прилежащая сторона, а x – гипотенуза |
| 2. Определите , что мы ищем. | угол Y |
| 3. Этикетка то, что мы ищем, выбрав переменную для ее представления. | =? |
| 4. Найдите искомое тригонометрическое отношение. | загар Y = |
5. Решите отношение , используя хорошие методы алгебры. | тангенс Y = 2,0455 Y = желто-коричневый – №2.0455 = 63,9470° |
| 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл. | загар 63,9470° 2,0455 2,0455 = 2,0455 |
| 7. Ответьте на вопрос полным предложением. | Угол наклона составляет 63,9470° или 64° с округлением до одного десятичного знака. |
Хемант стоит на вершине скалы на высоте 250 футов над землей и смотрит на своего друга, стоящего на земле в 40 футах от основания скалы. Что такое угол депрессии?
Показать ответ80,9°
- Три основных тригонометрических отношения: (Где θ — мера опорного угла, измеренная в градусах.)
- синус θ =
- косинус θ =
- тангенс θ =
- Стратегия решения проблем для приложений тригонометрии
- Прочтите задачу и убедитесь, что все слова и идеи понятны.
 Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Нарисуйте прямоугольный треугольник и обозначьте указанные части. - Определите , что мы ищем.
- Пометьте то, что мы ищем, выбрав переменную для ее представления.
- Найдите требуемое тригонометрическое отношение.
- Решите отношение, используя хорошие методы алгебры.
- Проверьте ответ, подставив его обратно в соотношение, найденное на шаге 5, и убедившись, что оно имеет смысл в контексте задачи.
- Ответьте на вопрос полным предложением.
- Прочтите задачу и убедитесь, что все слова и идеи понятны.
Обозначьте стороны треугольника.
| 1 | 2. |
- Если исходный угол в вопросе 1 равен B, найдите смежный угол ?
- Если исходный угол в вопросе 2 равен Z, найти противоположный угол?
Обозначьте стороны треугольника и найдите гипотенузу, противолежащую и прилежащую.
| 5. | 6. |
Используйте свой калькулятор, чтобы найти данные отношения. При необходимости округлить до четырех знаков после запятой:
.Для заданных треугольников найдите синус, косинус и тангенс θ.
| 11. | 12. |
| 13. | 14. |
Для данных треугольников найдите недостающую сторону. Округлите его до одного десятичного знака.
| 15. Найдите гипотенузу. | 16. Найдите b, если a = 6. |
| 17. Найдите противоположное. | 18. Найдите соседнее. |
Найдите недостающие стороны данных треугольников. Округлите его до одного десятичного знака.
19. | 20. |
Решите треугольники. Округлить до одного десятичного знака.
| 21. | 22. |
| 23. | 24. |
- Ким стоит в 75 метрах от низа дерева и смотрит на верхушку дерева под углом 48°. Насколько высокое дерево?
- Дерево отбрасывает тень длиной 6 метров, когда угол подъема к солнцу составляет 52°. Насколько высокое дерево?
- Лестница высотой 15 футов прислонена к дому и образует с землей угол 45°. На каком расстоянии основание лестницы от дома?
- Роксана запускает воздушного змея и выпустила веревку длиной 100 футов. Угол возвышения с землей 38°. Как высоко ее воздушный змей над землей?
- Марта запускает воздушного змея и выпустила 28 метров веревки. Если воздушный змей находится на высоте 10 метров над землей, каков угол возвышения?
- Самолет взлетает с земли под углом 25°.
 Если самолет пролетел 200 км, на какой высоте он находится над землей?
Если самолет пролетел 200 км, на какой высоте он находится над землей?
| 1. | 3. с | 5. g противоположно , f смежно, e гипотенуза |
| 7. 0,7314 | 9. 0,2126 | 11. sin θ = , cos θ = , tan θ = |
- sin θ = , cos θ = , tan θ =
- б = 19,8
- с = 12
- у = 19,3, г = 8,2
- = 61° = 29° = 90°b = 38,5c = 21,3d = 44
- = 36,9° = 90° = 53,1°t = 15r = 25s = 20
- 83,3 м
- 10,6 футов
- 20,9°
Эта глава была адаптирована из книги «Решение приложений: отношения синуса, косинуса и тангенса» в книге «Введение в алгебру» Изабелы Мазур, которая находится под лицензией CC BY 4.0. Дополнительную информацию см. в Заявлении об адаптации.
Отношение косинуса к синусу.
 Что такое синус? Простейшие тригонометрические тождества
Что такое синус? Простейшие тригонометрические тождестваПонятия синуса, косинуса, тангенса и котангенса являются основными категориями тригонометрии — раздела математики и неразрывно связаны с определением угла. Владение этой математической наукой требует запоминания и понимания формул и теорем, а также развитого пространственного мышления. Именно поэтому тригонометрические расчеты часто вызывают затруднения у школьников и студентов. Чтобы их преодолеть, следует лучше познакомиться с тригонометрическими функциями и формулами.
Понятия тригонометрии
Чтобы понять основные понятия тригонометрии, необходимо сначала решить, что такое прямоугольный треугольник и угол в окружности, и почему все основные тригонометрические вычисления связаны с ними. Треугольник, в котором один из углов равен 90 градусов, является прямоугольным. Исторически эта фигура часто использовалась людьми в архитектуре, мореплавании, искусстве, астрономии. Соответственно, изучая и анализируя свойства этой фигуры, люди пришли к расчету соответствующих соотношений ее параметров.
Основными категориями, связанными с прямоугольными треугольниками, являются гипотенуза и катет. Гипотенуза – это сторона треугольника, лежащая против прямого угла. Ноги, соответственно, две другие стороны. Сумма углов любого треугольника всегда равна 180 градусам.
Сферическая тригонометрия – это раздел тригонометрии, который не изучается в школе, но в таких прикладных науках, как астрономия и геодезия, ученые его используют. Особенностью треугольника в сферической тригонометрии является то, что он всегда имеет сумму углов больше 180 градусов.
Углы треугольника
В прямоугольном треугольнике синус угла представляет собой отношение катета, противоположного искомому углу, к гипотенузе треугольника. Соответственно, косинус — это отношение прилежащего катета к гипотенузе. Обе эти величины всегда имеют значение меньше единицы, так как гипотенуза всегда длиннее катета.
Тангенс угла представляет собой величину, равную отношению противолежащего катета к прилежащему катету желаемого угла или синуса к косинусу. Котангенс, в свою очередь, есть отношение прилежащего катета искомого угла к противолежащему кактету. Котангенс угла также можно получить, разделив единицу на величину тангенса.
Котангенс, в свою очередь, есть отношение прилежащего катета искомого угла к противолежащему кактету. Котангенс угла также можно получить, разделив единицу на величину тангенса.
единичный круг
Единичный круг в геометрии — это круг, радиус которого равен единице. Такая окружность строится в декартовой системе координат, при этом центр окружности совпадает с началом координат, а начальное положение радиус-вектора определяется положительным направлением оси X (ось абсцисс). Каждая точка окружности имеет две координаты: XX и YY, то есть координаты абсцисс и ординат. Выделив любую точку на окружности в плоскости ХХ и опустив перпендикуляр из нее на ось абсцисс, получим прямоугольный треугольник, образованный радиусом к выбранной точке (обозначим ее буквой С), перпендикуляром, проведенным к ось X (точка пересечения обозначена буквой G) и отрезок оси абсцисс между началом координат (точка обозначена буквой A) и точкой пересечения G. Полученный треугольник ACG является прямоугольным треугольником, вписанным в окружность, где AG — гипотенуза, а AC и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG определим как α (альфа). Итак, cos α = AG/AC. Учитывая, что AC — это радиус единичной окружности, а он равен единице, получается, что cos α=AG. Точно так же sin α=CG.
Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG определим как α (альфа). Итак, cos α = AG/AC. Учитывая, что AC — это радиус единичной окружности, а он равен единице, получается, что cos α=AG. Точно так же sin α=CG.
Кроме того, зная эти данные, можно определить координату точки C на окружности, так как cos α=AG, а sin α=CG, а значит, точка C имеет заданные координаты (cos α; sin α ). Зная, что тангенс равен отношению синуса к косинусу, можно определить, что tg α = y/x, а ctg α = x/y. Рассматривая углы в отрицательной системе координат, можно вычислить, что значения синуса и косинуса некоторых углов могут быть отрицательными.
Расчеты и основные формулы
Значения тригонометрических функций
Рассмотрев сущность тригонометрических функций через единичную окружность, мы можем вывести значения этих функций для некоторых углов. Значения указаны в таблице ниже.
Простейшие тригонометрические тождества
Уравнения, в которых под знаком тригонометрической функции стоит неизвестное значение, называются тригонометрическими. Тождества со значением sin x = α, k — любое целое число: 9k * arcsin α + πk.
Тождества со значением sin x = α, k — любое целое число: 9k * arcsin α + πk.
Тождества со значением cos x = a, где k — любое целое число:
- cos x = 0, x = π/2 + πk.
- потому что х = 1, х = 2πk.
- cos х = -1, х = π + 2πk.
- потому что х = а, |а| > 1, решений нет.
- потому что х = а, |а| ⩽ 1, х = ±arccos α + 2πk.
Тождества со значением tg x = a, где k — любое целое число:
- tg x = 0, x = π/2 + πk.
- tg x = a, x = arctg α + πk.
Тождества со значением ctg x = a, где k — любое целое число:
- ctg x = 0, x = π/2 + πk.
- ctg x = a, x = arcctg α + πk.
Формулы приведения
Эта категория постоянных формул обозначает методы, с помощью которых можно перейти от тригонометрических функций вида к функциям аргумента, то есть преобразовать синус, косинус, тангенс и котангенс угла любого значения в соответствующие показатели угла интервала от 0 до 90 градусов для большего удобства расчетов.
Формулы приведения функций для синуса угла выглядят так:
- sin(900 — α) = α;
- sin(900 + α) = cos α;
- sin(1800 — α) = sin α;
- sin(1800 + α) = -sin α;
- sin(2700 — α) = -cos α;
- sin(2700 + α) = -cos α;
- sin(3600 — α) = -sin α;
- грех(3600 + α) = грех α.
Для косинуса угла:
- cos(900 — α) = sin α;
- cos(900 + α) = -sin α;
- cos(1800 — α) = -cos α;
- cos(1800 + α) = -cos α;
- cos(2700 — α) = -sin α;
- cos(2700 + α) = sin α;
- cos(3600 — α) = cos α;
- потому что (3600 + α) = потому что α.
Использование вышеуказанных формул возможно при соблюдении двух правил. Во-первых, если угол можно представить в виде величины (π/2 ± a) или (3π/2 ± a), значение функции изменится:
- от греха к cos;
- от cos до sin;
- из ТГ в ККТ;
- из КТГ в ТКГ.
Значение функции остается неизменным, если угол можно представить в виде (π ± a) или (2π ± a).
Во-вторых, знак приведенной функции не меняется: если она изначально была положительной, то такой и остается. То же самое верно и для отрицательных функций.
Формулы сложения
Эти формулы выражают значения синуса, косинуса, тангенса и котангенса суммы и разности двух углов поворота через их тригонометрические функции. Углы обычно обозначают как α и β.
Формулы выглядят так:
- sin(α ± β) = sin α * cos β ± cos α * sin.
- cos(α ± β) = cos α * cos β ∓ sin α * sin.
- тангенс (α ± β) = (тангенс α ± тангенс β) / (1 ∓ тангенс α * тангенс β).
- ctg(α ± β) = (-1 ± ctg α * ctg β) / (ctg α ± ctg β).
Эти формулы справедливы для любых углов α и β.
Формулы двойного и тройного угла
Тригонометрические формулы двойного и тройного угла — это формулы, связывающие функции углов 2α и 3α соответственно с тригонометрическими функциями угла α. Получено из формул сложения: 92 а).
Переход от суммы к произведению
Учитывая, что 2sinx*cosy = sin(x+y) + sin(x-y), упрощая эту формулу, получаем тождество sinα + sinβ = 2sin(α + β)/2 * cos( α − β)/2. Точно так же sinα — sinβ = 2sin(α — β)/2 * cos(α + β)/2; cosα + cosβ = 2cos(α + β)/2 * cos(α − β)/2; cosα — cosβ = 2sin(α + β)/2 * sin(α − β)/2; tgα + tgβ = sin(α + β)/cosα * cosβ; tgα — tgβ = sin(α — β)/cosα * cosβ; cosα + sinα = √2sin(π/4 ∓ α) = √2cos(π/4 ± α).
Точно так же sinα — sinβ = 2sin(α — β)/2 * cos(α + β)/2; cosα + cosβ = 2cos(α + β)/2 * cos(α − β)/2; cosα — cosβ = 2sin(α + β)/2 * sin(α − β)/2; tgα + tgβ = sin(α + β)/cosα * cosβ; tgα — tgβ = sin(α — β)/cosα * cosβ; cosα + sinα = √2sin(π/4 ∓ α) = √2cos(π/4 ± α).
Переход от произведения к сумме 92 х/2)/(2tgx/2), при этом х = π + 2πn.
Частные случаи
Ниже приведены частные случаи простейших тригонометрических уравнений (k — любое целое число).
Частный для синуса:
| sin x значение | х значение |
|---|---|
| 0 | шт. |
| 1 | π/2 + 2πk |
| -1 | -π/2 + 2πk |
| 1/2 | π/6 + 2πk или 5π/6 + 2πk |
| -1/2 | -π/6 + 2πk или -5π/6 + 2πk |
| √2/2 | π/4 + 2πk или 3π/4 + 2πk |
| -√2/2 | -π/4 + 2πk или -3π/4 + 2πk |
| √3/2 | π/3 + 2πk или 2π/3 + 2πk |
| -√3/2 | -π/3 + 2πk или -2π/3 + 2πk |
Коэффициенты косинуса:
| значение cos x | х значение |
|---|---|
| 0 | π/2 + 2πk |
| 1 | 2πк |
| -1 | 2 + 2πk |
| 1/2 | ±π/3 + 2πk |
| -1/2 | ±2π/3 + 2πk |
| √2/2 | ±π/4 + 2πk |
| -√2/2 | ±3π/4 + 2πk |
| √3/2 | ±π/6 + 2πk |
| -√3/2 | ±5π/6 + 2πk |
Частная для касательной:
| tg x значение | х значение |
|---|---|
| 0 | шт. |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3/3 | π/6 + πk |
| -√3/3 | -π/6 + πk |
| √3 | π/3 + πk |
| -√3 | -π/3 + πk |
Коэффициенты котангенса:
| ctg x значение | х значение |
|---|---|
| 0 | π/2 + πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3 | π/6 + πk |
| -√3 | -π/3 + πk |
| √3/3 | π/3 + πk |
| -√3/3 | -π/3 + πk |
Теоремы
Теорема синусов
Есть две версии теоремы — простая и расширенная. Простая теорема синусов: a/sin α = b/sin β = c/sin γ. При этом a, b, c — стороны треугольника, а α, β, γ — противоположные углы соответственно.
Расширенная теорема синусов для произвольного треугольника: a/sin α = b/sin β = c/sin γ = 2R. В этом тождестве R обозначает радиус окружности, в которую вписан данный треугольник.
— 2*b*c*cos α. В формуле a, b, c — стороны треугольника, а α — угол, противолежащий стороне a.
Теорема о касательной
Формула выражает отношение между касательными двух углов и длинами противоположных им сторон. Стороны обозначены буквами a, b, c, а соответствующие противоположные углы — α, β, γ. Формула теоремы о касательной: (a — b) / (a+b) = tg((α — β)/2) / tg((α + β)/2).
Теорема о котангенсе
Сопоставляет радиус окружности, вписанной в треугольник, с длинами его сторон. Если a, b, c — стороны треугольника, а A, B, C — их противоположные углы соответственно, r — радиус вписанной окружности, а p — полупериметр треугольника, то выполняются следующие тождества удерживать:
- ctg A/2 = (p-a)/r;
- ctg B/2 = (p-b)/r;
- ctg C/2 = (p-c)/r.

Приложения
Тригонометрия — это не только теоретическая наука, связанная с математическими формулами. Его свойства, теоремы и правила используются на практике различными отраслями человеческой деятельности — астрономией, воздушным и морским плаванием, теорией музыки, геодезией, химией, акустикой, оптикой, электроникой, архитектурой, экономикой, машиностроением, измерительными работами, компьютерной графикой, картография, океанография и многие другие.
Синус, косинус, тангенс и котангенс — основные понятия тригонометрии, с помощью которых можно математически выразить взаимосвязь между углами и длинами сторон в треугольнике, а также найти нужные величины с помощью тождеств, теорем и правил.
Изначально синус и косинус возникли из-за необходимости вычисления величин в прямоугольных треугольниках. Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не изменить, то соотношение сторон, как бы ни изменились эти стороны по длине, всегда остается одним и тем же.
Так были введены понятия синуса и косинуса. Синус острого угла прямоугольного треугольника — это отношение противолежащего катета к гипотенузе, а косинус — отношение прилежащего катета к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы можно использовать не только в прямоугольных треугольниках. Чтобы найти значение тупого или острого угла, стороны любого треугольника, достаточно применить теорему косинусов и синусов.
Теорема косинусов довольно проста: «Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними».
Существует две интерпретации теоремы синусов: малая и расширенная. По малому: «В треугольнике углы пропорциональны противолежащим сторонам». Эта теорема часто расширяется за счет свойства окружности, описанной вокруг треугольника: «В треугольнике углы пропорциональны противоположным сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная — это математический инструмент, показывающий, насколько быстро функция изменяется в зависимости от изменения ее аргумента. Производные используются в геометрии и в ряде технических дисциплин.
При решении задач необходимо знать табличные значения производных тригонометрических функций: синуса и косинуса. Производная синуса — это косинус, а производная косинуса — это синус, но со знаком минус.
Применение в математике
Особенно часто синусы и косинусы используются при решении прямоугольных треугольников и связанных с ними задач.
Удобство синусов и косинусов находит свое отражение и в технологии. Углы и стороны было легко вычислить, используя теоремы косинуса и синуса, разбивая сложные формы и объекты на «простые» треугольники. Инженеры и, часто занимаясь расчетами соотношений сторон и градусных мер, тратили много времени и сил на вычисление косинусов и синусов нетабличных углов.
Тут на помощь пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов разных углов. В советское время некоторые учителя заставляли своих подопечных заучивать страницы таблиц Брадиса.
В советское время некоторые учителя заставляли своих подопечных заучивать страницы таблиц Брадиса.
Радиан — угловая величина дуги, по длине равная радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360 окружности или 1/90 прямого угла.
π = 3,1415589793238462… (приблизительное значение числа пи).
Синус острый угол α прямоугольного треугольника равен отношению противоположного катетера к гипотенузе.
Обозначается следующим образом: sin α.
Косинус острого угла α прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Обозначается следующим образом: cos α.
Тангенс острого угла α является отношением противолежащего катета к прилежащему катету.
Обозначается следующим образом: tg α.
Котангенс острого угла α есть отношение прилежащего катета к противолежащему.
Обозначается следующим образом: ctg α.
Синус, косинус, тангенс и котангенс угла зависят только от величины угла.
Правила:
Основные тригонометрические тождества в прямоугольном треугольнике:
( α — острый угол напротив полки б и рядом с ножкой и . Сторона с — гипотенуза. β — второй острый угол).
b | sin 2 α + cos 2 α = 1 | |
а | 1 | |
б | 1 | |
а | 1 1 | |
sinα |
С увеличением острого угла sinα и tg α увеличиваются, а cos α уменьшаются.
Для любого острого угла α:
sin (90° — α) = cos α
cos (90° — α) = sin α
Пояснительный пример:
Пусть в прямоугольном треугольнике ABC
AB = 6,
BC = 3,
угол A = 30º.
Найдите синус угла A и косинус угла B.
Решение .
1) Сначала находим значение угла В. Здесь все просто: так как в прямоугольном треугольнике сумма острых углов равна 90º, то угол В = 60º:
В = 90º — 30º = 60º .
2) Вычислите sin A. Мы знаем, что синус равен отношению противолежащего катета к гипотенузе. Для угла А противоположным катетом является сторона ВС. Итак:
BC 3 1
sin A = — = — = —
AB 6 2
3) Теперь вычисляем cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла B соседним катетом является та же сторона BC. Это значит, что нам снова нужно разделить ВС на АВ — то есть произвести те же действия, что и при вычислении синуса угла А:
ВС 3 1
cos B = — = — = —
АВ 6 2
результат:
sin A = cos B = 1/2.
sin 30° = cos 60° = 1/2.
Отсюда следует, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла — и наоборот. Именно это и означают две наши формулы:
sin (90° — α) = cos α
cos (90° — α) = sin α
Проверим еще раз:
1) Пусть α = 60º. Подставив значение α в формулу синуса, получим:
sin(90º — 60º) = cos 60º.
sin 30º = cos 60º.
2) Пусть α = 30º. Подставляя значение α в формулу косинуса, получаем:
cos (90° — 30°) = sin 30°.
cos 60° = sin 30°.
(Подробнее о тригонометрии см. в разделе Алгебра)
Одним из разделов математики, с которым школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: чтобы свободно овладеть этой областью знаний, необходимо пространственное мышление, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь использовать число пи в расчетах. Кроме того, нужно уметь применять тригонометрию при доказательстве теорем, а для этого требуется либо развитая математическая память, либо умение выводить сложные логические цепочки.
Истоки тригонометрии
Знакомство с этой наукой следует начать с определения синуса, косинуса и тангенса угла, но сначала нужно разобраться, что вообще делает тригонометрия.
Исторически прямоугольные треугольники были основным объектом изучения в этом разделе математической науки. Наличие угла 90 градусов дает возможность проводить различные операции, позволяющие определить значения всех параметров рассматриваемой фигуры с помощью двух сторон и одного угла или двух углов и одной стороны. В прошлом люди заметили эту закономерность и стали активно использовать ее в строительстве зданий, мореплавании, астрономии и даже искусстве.
Первый этап
Изначально о соотношении углов и сторон говорили исключительно на примере прямоугольных треугольников. Затем были открыты специальные формулы, позволившие расширить границы использования в повседневной жизни этого раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учащимися в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в средней школе.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют разные правила, а сумма углов в треугольнике всегда более 180 градусов. Этот раздел в школе не изучается, но знать о его существовании необходимо, хотя бы потому, что поверхность земли, да и поверхность любой другой планеты, выпукла, а значит, любая поверхностная разметка будет «дугообразной» в трехмерное пространство.
Возьмите глобус и нить. Прикрепите нить к любым двум точкам на земном шаре так, чтобы она была натянута. Обратите внимание — она приобрела форму дуги. Именно с такими формами имеет дело сферическая геометрия, используемая в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного познакомившись со способами использования тригонометрии, вернемся к основам тригонометрии, чтобы еще лучше понять, что такое синус, косинус, тангенс, какие расчеты можно производить с их помощью и какими формулами пользоваться.
Первый шаг — понять понятия, связанные с прямоугольным треугольником. Во-первых, гипотенуза — это сторона, противоположная углу 90 градусов. Она самая длинная. Мы помним, что по теореме Пифагора его числовое значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы будет равна 5 сантиметрам. Кстати, древние египтяне знали об этом около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, образующие прямой угол, называются сторонами. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равна 180 градусам.
Определение
Наконец, имея твердое представление о геометрической основе, мы можем перейти к определению синуса, косинуса и тангенса угла.
Синус угла — это отношение противолежащего катета (т. е. стороны, противоположной искомому углу) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Помните, что ни синус, ни косинус не могут быть больше единицы! Почему? Потому что гипотенуза по умолчанию самая длинная. Какой бы длины ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если в ответе на задачу вы получили синус или косинус со значением больше 1, ищите ошибку в вычислениях или рассуждениях. Этот ответ явно неверен.
Наконец, тангенс угла — это отношение противолежащего катета к прилежащему. Такой же результат даст деление синуса на косинус. Смотрите: в соответствии с формулой делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же соотношение, что и при определении тангенса.
Котангенс, соответственно, является отношением стороны, примыкающей к углу, к противолежащей стороне. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения того, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии без формул не обойтись — как без них найти синус, косинус, тангенс, котангенс? А это именно то, что требуется при решении задач.
Первая формула, которую нужно знать, приступая к изучению тригонометрии, гласит, что сумма квадратов синуса и косинуса угла равна единице. Эта формула является прямым следствием теоремы Пифагора, но она экономит время, если вы хотите узнать значение угла, а не стороны.
Многие ученики не могут запомнить вторую формулу, которая также очень популярна при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же утверждение, что и в первой формуле, только обе части тождества были поделены на квадрат косинуса. Оказывается, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько основных формул, вы сможете в любой момент самостоятельно вывести на листе бумаги требуемые более сложные формулы.
Формулы двойного угла и сложение аргументов
Еще две формулы, которые необходимо выучить, связаны со значениями синуса и косинуса для суммы и разности углов. Они показаны на рисунке ниже. Обратите внимание, что в первом случае синус и косинус умножаются оба раза, а во втором складывается попарное произведение синуса и косинуса.
Существуют также формулы, связанные с аргументами двойного угла. Они полностью производны от предыдущих — для практики попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла могут быть преобразованы для уменьшения степени синуса, косинуса, тангенса альфа.
Теоремы
Две основные теоремы базовой тригонометрии — это теорема синусов и теорема косинусов. С помощью этих теорем легко понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла получаем одинаковое число. Причем это число будет равно двум радиусам описанной окружности, то есть окружности, содержащей все точки данного треугольника.
Причем это число будет равно двум радиусам описанной окружности, то есть окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя ее на любые треугольники. Получается, что из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус прилежащего к ним угла — полученное значение будет равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко ошибиться по рассеянности или ошибиться в простейших вычислениях. Чтобы избежать таких ошибок, давайте познакомимся с самыми популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные, пока не будет получен окончательный результат — можно оставить ответ в виде обыкновенной дроби, если в условии не указано иное. Такое преобразование нельзя назвать ошибкой, но следует помнить, что на каждом этапе выполнения задания могут появляться новые корни, которые, по задумке автора, следует редуцировать. В этом случае вы потратите время на ненужные математические операции. Особенно это касается таких значений, как корень из трех или двух, потому что они встречаются в задачах на каждом шагу. То же самое относится и к округлению «некрасивых» чисел.
В этом случае вы потратите время на ненужные математические операции. Особенно это касается таких значений, как корень из трех или двух, потому что они встречаются в задачах на каждом шагу. То же самое относится и к округлению «некрасивых» чисел.
Далее, обратите внимание, что теорема косинусов применима к любому треугольнику, но не теорема Пифагора! Если вы по ошибке забудете дважды вычесть произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем неосторожная ошибка.
В-третьих, не путайте значения углов 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, в результате чего вы неизбежно получите ошибочный результат.
Приложение
Многие студенты не торопятся начинать изучение тригонометрии, так как не понимают ее прикладного значения. Что такое синус, косинус, тангенс для инженера или астронома? Это концепции, благодаря которым можно рассчитать расстояние до далеких звезд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них невозможно построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения объекта. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется везде, от музыки до медицины.
Что такое синус, косинус, тангенс для инженера или астронома? Это концепции, благодаря которым можно рассчитать расстояние до далеких звезд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них невозможно построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения объекта. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется везде, от музыки до медицины.
Наконец
Итак, вы получили синус, косинус, тангенс. Вы можете использовать их в расчетах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что неизвестные параметры необходимо вычислить по известным параметрам треугольника. Всего параметров шесть: длины трех сторон и величины трех углов. Вся разница в задачах заключается в том, что даны разные входные данные.
Как найти синус, косинус, тангенс по известным длинам катетов или гипотенузы, вы теперь знаете. Поскольку эти термины означают не что иное, как отношение, а отношение — это дробь, то основная цель тригонометрической задачи — найти корни обыкновенного уравнения или системы уравнений. И здесь вам поможет обычная школьная математика.
Поскольку эти термины означают не что иное, как отношение, а отношение — это дробь, то основная цель тригонометрической задачи — найти корни обыкновенного уравнения или системы уравнений. И здесь вам поможет обычная школьная математика.
1.2: Тригонометрические отношения — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 37208
- Ричард В. Беверидж
- Общественный колледж Клэтсопа
Существует шесть общих тригонометрических отношений, которые связывают стороны прямоугольного треугольника с углами внутри треугольника. Три стандартных соотношения — это синус, косинус и тангенс. Часто их называют сокращенно sin, cos и tan. Остальные три (косеканс, секанс и котангенс) являются величинами, обратными синусу, косинусу и тангенсу, и часто обозначаются аббревиатурами csc, sec и cot.
Часто их называют сокращенно sin, cos и tan. Остальные три (косеканс, секанс и котангенс) являются величинами, обратными синусу, косинусу и тангенсу, и часто обозначаются аббревиатурами csc, sec и cot.
Для угла, расположенного в прямоугольном треугольнике, функция синуса определяется как отношение стороны, противоположной углу, к гипотенузе, косинус определяется как отношение стороны, прилегающей к углу, к гипотенузе, а тангенс определяется как отношение стороны, противолежащей углу, к стороне, примыкающей к углу.
\[
\begin{align}
\sin \theta &=\frac{o p p}{h y p} \\
\cos \theta &=\frac{a d j}{h y p} \\
\tan \theta &=\frac{o p p }{а д й}
\ конец {выровнено}
\]
Распространенным мнемоническим приемом, помогающим запомнить эти отношения, является
-SOHCAHTOA, который идентифицирует грех как Opp над Hyp Cos как Adj над Hyp и Tan как Opp над Adj.
Острый угол, помещенный в другое положение прямоугольного треугольника, имел бы разные противолежащие и прилежащие стороны, хотя гипотенуза осталась бы той же.
Примеры: тригонометрические соотношения
Найдите \(\sin\theta, \cos\theta\) и \(\tan\theta\) для заданного угла \(\theta\) 9{2} \\
\sqrt{34}=c
\end{массив}
\]
Теперь, когда мы знаем гипотенузу \((\sqrt{34}),\), мы можем определить sin, cos и tan для угла \(\theta\)
\[
\begin{align}
\sin \theta &=\frac{3}{\sqrt{34}} \\
\cos \theta &=\frac{5}{\sqrt{34}} \\
\tan \theta &=\frac{3}{5}
\end{выровнено}
\]
Найдите \(\sin\theta, \cos\theta\) и \(\tan\theta\) для заданного угла \(\theta\)
Опять же, чтобы найти sin, cos и тангенс угла \(\theta,\), мы должны найти недостающую сторону треугольника, используя теорему Пифагора. поскольку в этом случае мы знаем гипотенузу и один из катетов, значение гипотенузы должно быть заменено на \(с\), а длина данного катета может быть заменена либо 9{2}=65 \\
b=\sqrt{65}
\end{массив}
\]
Теперь, когда мы знаем длину другого катета треугольника \((\sqrt{65}),\), мы можем определить sin, cos и tan для угла \(\theta\)
\[
\begin{align}
\sin \theta &=\frac{\sqrt{65}}{9} \\
\cos \theta &=\frac{4}{9} \\
\tan \theta &= \frac{\sqrt{65}}{4}
\end{выровнено}
\]
В дополнение к приведенным выше примерам, если нам задано значение одного из тригонометрических соотношений, мы можем найти значение двух других. {\prime}\) s сокращаются, поэтому мы просто опустим их для начала и назовем стороны 1 и 3 9{2} \\
{\prime}\) s сокращаются, поэтому мы просто опустим их для начала и назовем стороны 1 и 3 9{2} \\
\sqrt{54}=3 \sqrt{6}=c
\end{массив}
\]
Итак:
\[
\ sin \ theta = \ frac {\ sqrt {5}} {\ sqrt {54}} = \ sqrt {\ frac {5} {54}}
\]
\[
\cos \theta=\frac{7}{\sqrt{54}}=\frac{7}{3 \sqrt{6}}
\]
Упражнения 1.2
Найдите \(\sin \theta, \cos \theta\) и \(\tan \theta\) для данных треугольников.
Используйте полученную информацию, чтобы найти два других тригонометрических отношения.
11. \(\quad \tan \theta=\frac{1}{2}\)
12. \(\quad \sin \theta=\frac{3}{4}\)
13. \(\quad \cos \theta=\frac{3}{\sqrt{20}}\)
14. \(\quad \tan \theta=2\)
15. \(\sin \theta =\frac{5}{\sqrt{40}}\)
16. \(\sin \theta=\frac{7}{10}\)
17. \(\cos \theta=\frac{9} {40}\)
18. \(\quad \tan \theta=\sqrt{3}\)
19. \(\cos \theta=\frac{1}{2}\)
20. \(\ cos \theta=\frac{3}{7}\)
21. \(\sin \theta=\frac{\sqrt{5}}{7}\)
22. \(\quad \tan \theta= 1,5\)
\(\quad \tan \theta= 1,5\)
Эта страница под названием 1.2: The Trigonometric Ratios распространяется в соответствии с лицензией CC BY-NC-SA и была создана, изменена и/или курирована Ричардом В. Бевериджем.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Ричард В. Беверидж
- Лицензия
- CC BY-NC-SA
- Показать страницу TOC
- нет
- Теги

Соотношение тригонометрических функций | Brilliant Math & Science Wiki
Хеманг Агарвал, Александр Кац, Махиндра Джейн, а также
способствовал
Содержимое
- Формальные определения
- Примеры проблем
- Смотрите также
Рассмотрим следующий прямоугольный треугольник:
Стороны относительно угла θ \thetaθ равны
a= adjacentb= oppositec= гипотенуза.\begin{выровнено}
a &= \text{соседний}\\
б &= \текст{напротив}\\
c &= \text{гипотенуза}. \end{align}abc= adjacent= opposite= hypotenuse.
\end{align}abc= adjacent= opposite= hypotenuse.
Тогда основные тригонометрические функции определяются как
sinθ=(противоположное)(гипотенуза)=bccosθ=(прилежащее)(гипотенуза)=actan θ=(напротив)(смежно)=ba.\begin{выровнено} \sin \theta &= \frac{(\text{напротив})}{(\text{гипотенуза})} = \frac{b}{c} \\ \cos \theta &= \frac{(\text{adjacent})}{(\text{гипотенуза})} = \frac{a}{c}\\ \tan \theta &= \frac{(\text{напротив})}{(\text{adjacent})} = \frac{b}{a}. \end{выравнивание}sinθcosθtanθ=(гипотенуза)(противоположное)=cb=(гипотенуза)(примыкающее)=ca=(прилегающее)(противоположное)=ab.
У нас также есть следующие обратные функции
cscθ=1sinθsecθ=1cosθcotθ=1tanθ.\begin{align} \csc \theta &= \frac{1}{\sin \theta} \\ \sec \theta &= \frac{1}{\cos \theta} \\ \cot \theta &= \frac{1}{\tan \theta}. \end{align}cscθsecθcotθ=sinθ1=cosθ1=tanθ1.
Например, cotθ \cot \thetacotθ можно выразить как
cotθ=1tanθ=1ba=ab=(adjacent )(противоположный). \cot \theta = \frac{1}{\tan \theta} = \frac{1}{\frac{b}{a}} = \frac{a}{b} = \frac{(\text{adjacent })}{(\текст{напротив})}. cotθ=tanθ1=ab1=ba=(напротив)(прилегает). 92\\
\Стрелка вправо (\text{прилегающий}) &= 4.
\end{выровнено} (гипотенуза)252⇒(прилегающий)=(противоположный)2+(прилегающий)2=32+(прилегающий)2=4.
\cot \theta = \frac{1}{\tan \theta} = \frac{1}{\frac{b}{a}} = \frac{a}{b} = \frac{(\text{adjacent })}{(\текст{напротив})}. cotθ=tanθ1=ab1=ba=(напротив)(прилегает). 92\\
\Стрелка вправо (\text{прилегающий}) &= 4.
\end{выровнено} (гипотенуза)252⇒(прилегающий)=(противоположный)2+(прилегающий)2=32+(прилегающий)2=4.
Следовательно, cosθ=(прилегающий)(гипотенуза)=45. □ \cos \theta = \dfrac{(\text{adjacent})}{(\text{гипотенуза})} = \frac{4}{5}. \ _ \square cosθ=(гипотенуза)(прилегающая)=54. □
Если sinθ=12 \sin \theta= \frac{1}{2} sinθ=21 и cosθ=13 \cos \theta = \frac{1}{\sqrt{3}} cosθ=3 1 в прямоугольном треугольнике, то что такое tanθ? \тан \тета ?tanθ?
Так как tanθ=sinθcosθ, \tan\theta =\frac{\sin \theta}{\cos \theta} ,tanθ=cosθsinθ,
тангенсθ=sinθcosθ= 12 13=32. □ \ tan \ theta = \ frac {\ sin \ theta} {\ cos \ theta} = \ frac {\ \, \ frac {1} {2} \ {\ frac {1} {\ sqrt {3}} } = \ гидроразрыва {\ sqrt {3}} {2}.
\ _ \square tanθ=cosθsinθ=31 21 =23. □
Если cotθ=13 \cot \theta=\frac{1}{3} cotθ=31 в прямоугольном треугольнике, что такое tanθ? \тан \тета ?tanθ?
Так как tanθ \tan \theta tanθ и cotθ \cot \thetacotθ обратны друг другу, 92 \theta}{\sin\theta\cdot\cos\theta} \\ 2 &= \frac{1}{\sin\theta\cdot\cos\theta} \\ \стрелка вправо \sin \theta \cdot \cos \theta &= \frac{1}{2}. \ _ \площадь \end{выравнивание} tanθ+cotθ2⇒sinθ⋅cosθ=sinθ⋅cosθsin2θ+cos2θ=sinθ⋅cosθ1=21. □
- Тригонометрия
- Основные тригонометрические функции
Процитировать как: Отношение тригонометрических функций. Brilliant.org . Извлекаются из https://brilliant.org/wiki/отношение тригонометрических функций/
Что делать с углами? Тригонометрия в науках о Земле
Введение в тригонометрию
Насколько крут этот склон и не провалится ли он? Насколько высока эта гора? Такого рода вопросы возникают повсюду в науках о Земле — от тектоники плит до карт и океанских волн, и они требуют, чтобы вы нашли либо угол, либо расстояние. Для этого мы часто используем тригонометрию, что намного проще, когда речь идет о прямоугольном треугольнике.
Для этого мы часто используем тригонометрию, что намного проще, когда речь идет о прямоугольном треугольнике.
Прямоугольный треугольник (подобный тому, что на рисунке справа) имеет один угол, равный 90°. Два других угла всегда меньше 90° и в сумме дают 90°. Обратите внимание, что треугольник справа имеет 3 угла a, b и c и 3 стороны, A, B и H, и 3 угла a, b и c. Сторона, «противоположная» углу (в данном случае), помечается заглавной буквой, соответствующей метке на углу. Сторона, противоположная прямому углу Н, всегда является наибольшей стороной и называется гипотенузой.
Некоторые правила/рекомендации по тригонометрии прямоугольных треугольников
Мы можем использовать отношения (или частное) длин сторон прямоугольного треугольника, чтобы вычислить углы в прямоугольном треугольнике. Три тригонометрических отношения, которые мы используем в науках о Земле, называются синусом, косинусом и тангенсом, хотя их часто обозначают сокращенно sin, cos и tan соответственно.
Поскольку тригонометрические функции встречаются снова и снова, полезно придумать способ запомнить их определения. Большинству студентов (и, честно говоря, ваших преподавателей!) полезна мнемоника SOH-CAH-TOA (сказал «так-ка-то-а-а»).
Мнемоническое устройство использует первые буквы в следующих уравнениях:
- (это SOH , где S=sin, O=противоположный и H=гипотенуза)
(это CAH , где c=cos, a=соседний и H=гипотенуза)
(это TOA , где t = загар, a = соседний и O = противоположный)
Для получения дополнительной информации о том, что подразумевается под «примыкающими» и «противоположными», см. приведенные ниже задачи. право). Например, как определить размер угла a :
- , ,
Потому что это уравнений , их можно переставить так, чтобы вы также могли вычислить длину стороны (если вы знаете угол a в приведенном выше примере)!
Вычисление расстояний и углов с помощью тригонометрии
Для выполнения тригонометрических вычислений у вас должен быть калькулятор с кнопками для tan, cos и sin. Прежде чем начать, убедитесь, что ваш калькулятор находится в режиме градусов, а не в радианах. Если вам нужна помощь, перейдите к разделу «Как это сделать» в разделе «Калькулятор».
Прежде чем начать, убедитесь, что ваш калькулятор находится в режиме градусов, а не в радианах. Если вам нужна помощь, перейдите к разделу «Как это сделать» в разделе «Калькулятор».
Показать разницу между радианом и градусом
Hide
В науках о земле углы почти всегда измеряются в градусах, где окружность равна 360 градусам. Математики часто измеряют в единицах, называемых радианами. Полный круг равен 2π радианам, так как длина окружности с радиусом 1 равна 2π. Чтобы преобразовать измерение угла в радианах в градусы, умножьте на 57,3. Чтобы перевести градусы в радианы, разделите на 57,3.
Как рассчитать расстояние?Часто при вычислении расстояния до удаленного объекта вы знаете угол и одну длину, но вам нужно знать второй катет треугольника.
Измерение уклона берега
Показать кредиты
Скрыть
Рисунок 130 с веб-сайта EPA
Чтобы вычислить отсутствующую сторону, вы подставите значения в одну из приведенных выше триггерных формул и найдете отсутствующее значение. Например, если вы знаете сторону, прилегающую к углу, и вам нужно знать гипотенузу, вы можете использовать формулу для косинуса и найти нужную вам длину.
Например, если вы знаете сторону, прилегающую к углу, и вам нужно знать гипотенузу, вы можете использовать формулу для косинуса и найти нужную вам длину.
Показать конкретный пример
Скрыть
Часто в науках о Земле мы хотим знать расстояние до холма или другого объекта. Мы можем сделать это с помощью триангуляции. Итак, если вы измерите угол холма, который составляет 135 градусов с севера, а затем пройдете 200 метров перпендикулярно этому и измерите угол, равный 120 градусам с севера, как далеко от второго положения находится холм?
- Вам, вероятно, потребуется сделать набросок этой задачи, чтобы решить ее, и выяснить, какое из уравнений — синус, косинус или тангенс вам понадобится.
Покажи мне, как это сделать
Hide
Поскольку вы шли перпендикулярно первому пеленгу, вы знаете, что образовали прямоугольный треугольник и можете использовать тригонометрию, чтобы найти расстояние до холма из моего второго положения.
 Два пеленга смещены на 15 градусов (135-120), таким образом, вершина треугольника составляет 15 градусов.
Два пеленга смещены на 15 градусов (135-120), таким образом, вершина треугольника составляет 15 градусов.
- Выберите правильную формулу, зная угол и сторону, которые вы знаете, и какую сторону вы хотите.
Покажи мне, как это сделать
Скрыть
В этом вопросе вы не знаете и не заботитесь о стороне, прилегающей к вершине, поэтому это означает, что вы захотите использовать уравнение для синуса:
- Перестройте уравнение так, чтобы то, что вы знаете, оказалось в одной части, а то, чего вы не знаете, — в другой, а затем подставьте известные значения.
Покажи мне, как это сделать
Скрыть
Поскольку у вас есть угол и противоположная сторона, вам нужно переставить уравнение так, чтобы гипотенуза была одна: ( нужна помощь с этим? попробуйте переставить уравнения на странице )
подставив известные значения, получим:
- С помощью калькулятора определите значение тригонометрической функции (т.
 е. синуса, косинуса или тангенса) и найдите неизвестное значение.
е. синуса, косинуса или тангенса) и найдите неизвестное значение.Покажи мне, как это сделать
Скрыть
Ваш калькулятор скажет вам, что sin(15) равен 0,2588, поэтому
поэтому гипотенуза, то есть расстояние до холма, равна 772 метра
Как рассчитать угол?
Показать подпись
Скрыть
Измерение угла падения из коллекции Клиффа Форда
Часто геологам необходимо знать уклон дороги вверх по холму или угол наклона горных пород; чтобы вычислить эти углы, вам нужно знать длины двух сторон треугольника. Отсюда вы можете определить синус, косинус или тангенс нужного вам угла.
Если вы вычислили синус, косинус или тангенс угла и вам нужно знать его величину (в градусах), вам придется использовать обратные функции на вашем калькуляторе. (Если вы не знаете, как использовать их на своем калькуляторе, перейдите к разделу «Как пользоваться калькулятором?».) Например, если вы хотите найти размер угла с синусом 0,6, вам нужно найти арксинус 0,6 (записано sin -1 (0,6)). Попробуйте сделать это на своем калькуляторе. Должно получиться 36,87 , так что угол в данном случае чуть меньше 37 градусов.
(Если вы не знаете, как использовать их на своем калькуляторе, перейдите к разделу «Как пользоваться калькулятором?».) Например, если вы хотите найти размер угла с синусом 0,6, вам нужно найти арксинус 0,6 (записано sin -1 (0,6)). Попробуйте сделать это на своем калькуляторе. Должно получиться 36,87 , так что угол в данном случае чуть меньше 37 градусов.
Sin -1 называется «обратным синусоидальным», потому что он выполняет функцию, противоположную синусоидальной. Точно так же арккосинус (cos -1 ) даст значение угла, если вы знаете его косинус, а тангенс -1 даст вам угол, если вы знаете тангенс. Таким образом, вы можете найти размер любого неизвестного угла прямоугольного треугольника, если вы просто знаете 2 стороны этого треугольника.
Показать конкретный пример
Скрыть
Вы отвечаете за строительство дороги на вершину холма. Из топографических карт вы знаете, что холм имеет высоту 150 футов, а горизонтальное расстояние на карте составляет 1300 футов. Насколько крутой будет дорога?
Из топографических карт вы знаете, что холм имеет высоту 150 футов, а горизонтальное расстояние на карте составляет 1300 футов. Насколько крутой будет дорога?
- Выясните, что известно, и какой угол вы хотите, а затем выберите правильное уравнение — для синуса, косинуса или тангенса.
Покажи мне, как это сделать
Скрыть
Холм образует прямоугольный треугольник с основанием 1200 и вертикальной стороной 150. Поскольку рассматриваемый угол является нижним углом, противолежащим вертикальной стороне, две известные стороны — это противолежащая и прилежащая стороны. Таким образом, воспользуемся формулой тангенса:
- Подставьте известные стороны в полученное уравнение.
Покажи мне, как это сделать
Скрыть
Подставляя в наши известные значения противолежащие и примыкающие стороны, и делим
так,
- Используйте обратную функцию, чтобы решить это уравнение для нужного вам угла.

Покажи мне, как это сделать
Скрыть
возьмем арктангенс обеих сторон:
Так как tan -1 (a) делает прямо противоположное tan(a), tan -1 (tan(a)) просто a , так что это становится
- а = рыжевато-коричневый -1 (0,125)
который вы можете ввести в свой калькулятор, чтобы получить результат, 7,125 градусов , наклон холма.
Готовы ли вы попробовать некоторые примеры задач? Перейдите на страницу примера задачи триггера
Показать кредиты
Скрыть
Научный калькулятор TI
Как мне сделать это на моем калькуляторе?
Часто незнание того, как пользоваться калькулятором, является самой сложной задачей при проблемах с триггерами. Чтобы выяснить, в каком режиме находится ваш калькулятор, в градусах или в радианах, попробуйте найти sin(30). Если ваш калькулятор выдает результат 0,5, значит он в режиме градусов, а если вы получаете -,988031, он в радианном режиме и его нужно переключить!
Чтобы выяснить, в каком режиме находится ваш калькулятор, в градусах или в радианах, попробуйте найти sin(30). Если ваш калькулятор выдает результат 0,5, значит он в режиме градусов, а если вы получаете -,988031, он в радианном режиме и его нужно переключить!
Чтобы использовать инверсные кнопки, обычно вам нужно нажать кнопку с надписью 2 nd на вашем калькуляторе, а затем кнопку sin , cos или tan . Это дает sin -1 на экране калькулятора.
Многие производители калькуляторов предлагают интерактивные руководства, если вам нужна дополнительная помощь, включая TI, Sharp и HP.
Почему это работает?
Три подобных треугольника. Угол с одинаков в каждом случае, как и тангенс угла с.
Показать титры
Скрыть
Из руководства НАСА по ракетам для начинающих
Хотя вы можете просто «включи и пыхни» и используй уравнения тригонометрии, не понимая их, некоторые люди считают полезным понять, почему они работают. Секрет в том, что называется подобными треугольниками. Подобные треугольники — это треугольники с тремя одинаковыми углами, но разной длиной сторон, как, например, на диаграмме справа.
Секрет в том, что называется подобными треугольниками. Подобные треугольники — это треугольники с тремя одинаковыми углами, но разной длиной сторон, как, например, на диаграмме справа.
Подобные треугольники являются просто «раздутыми» или «сжатыми» (правильнее сказать, масштабированными) версиями друг друга, поэтому соотношение длин сторон остается прежним. Другими словами, кратчайшая сторона, деленная на гипотенузу, всегда будет давать один и тот же результат, если треугольники подобны. Вы, наверное, уже поняли, что это соотношение является косинусом или синусом. Так как подобные треугольники всегда имеют одинаковые углы, то отношение одинаково для любого заданного угла. Таким образом, каждое отношение (будь то sin, cos или tan) имеет определенный угол, который соответствует ему, и каждый угол имеет определенное соотношение сторон.
Где используется тригонометрия в науках о Земле?
Вы обнаружите, что тригонометрия используется в следующих областях, которые обычно преподаются на вводных курсах по геонаукам, а также во многих других областях:
Следующие шаги
Я готов к практике! (Эти проблемы имеют рабочие ответы.
 )
)Мне все еще нужна помощь!
(см. ссылки ниже для получения дополнительной помощи по тригонометрии).Ресурсы по тригонометрии
Краткий курс Дейва по тригонометрии 9В 0028 есть раздел об измерении углов, тригонометрии в прямоугольных треугольниках и тригонометрических функциях, а также многие другие тригонометрические темы, которые должны быть полезны.
Страница Mathworld Trigonometry содержит огромное количество ресурсов, которые выходят далеко за рамки материала, обычно изучаемого во вводном курсе.
S.O.S. В Mathematics есть тригонометрический указатель (подробнее) с таблицей тригонометрических тождеств, уроками по функциям и формулам, а также разделом с упражнениями и решениями.
Тригонометрический указатель Math Help (дополнительная информация) обеспечивает хорошее освежение основных тождеств, функций и углов триггера. Также включает диаграммы для тригонометрии единичного круга и треугольника.
Эта страница была написана и составлена доктором Эриком М. Бэром, программа геологии, Общественный колледж Хайлайн, 4555555555 Обзор триггеров Math.com Триггерные функции: обзор По простейшему определению, тригонометрический (буквально «измерение треугольника»)
функция, является одной из многих функций, которые связывают один непрямой угол
из прямоугольный треугольник к отношению длин любых двух сторон
треугольника (или наоборот). Таким образом, любая тригонометрическая функция (f) всегда удовлетворяет либо
из следующих уравнений: f(q) = a / b ИЛИ f(a/b) = q, где q — мера некоторого угла в
треугольника, а a и b — длины двух конкретных сторон. Это означает, что Это соотношение между углом и отношением сторон в прямоугольном треугольнике
— одна из важнейших идей тригонометрии. Кроме того, тригонометрический
функции работают для любого прямоугольного треугольника . Следовательно — для прямоугольного треугольника
— если мы возьмем измерение одного из непрямых углов треугольника,
мы можем математически вывести отношение длин любых двух
стороны треугольника триггерными функциями. И если мы измерим любое соотношение сторон,
мы можем математически вывести меру одной из неправильных сторон треугольника.
углы обратными триггерными функциями. Что еще более важно, если мы знаем измерение
одного из углов треугольника, и затем мы используем тригонометрическую функцию
определить отношение длин двух сторон треугольника, и мы случайно знаем длины одной из этих сторон в
отношение, мы можем тогда алгебраически определить длину другого
из этих двух сторон. Поскольку в прямоугольном треугольнике три стороны и два непрямых угла,
тригонометрическим функциям потребуется способ указать, какие стороны
относятся к какому углу. (Знать, что отношение
длин двух сторон равна 2, если мы не знаем, какая из сторон
три стороны, о которых мы говорим. Точно так же, если мы определим, что
из углов равен 40°, было бы неплохо узнать, какой угол этот
утверждение верно. Согласно определенному соглашению, мы обозначаем стороны как напротив , рядом с и гипотенузой относительно к нашему углу
интерес к. полный
объяснение Как упоминалось ранее, первый тип тригонометрической функции,
которая связывает угол с отношением сторон, всегда удовлетворяет следующему
уравнение: f(q) = a / b. Поскольку для любого угла q существует три способа
выбор числителя (а) и три способа выбора знаменателя
(b), мы можем создать следующие девять тригонометрических функций: Три диагональные функции, показанные красным цветом, всегда равны единице. Они есть
вырождены и, следовательно, бесполезны для нас. Поэтому мы удаляем
эти вырожденные функции и присваивают метки оставшимся шести, обычно
пишется в следующем порядке: Кроме того, функции обычно обозначаются аббревиатурой: синус (sin), косинус
(cos), тангенс (tan), косеканс (csc), секанс (sec) и котангенс (cot). Не расстраивайтесь. Безусловно, две самые важные триггерные функции
запомнить синус и косинус. Все остальные триггерные функции
из этих двух функций можно получить первый вид. Например,
функции справа являются просто мультипликативными обратными
соответствующую функцию слева (что делает их гораздо менее полезными).
Кроме того, sin(x) / COs(x) = (opp/hyp) / (adj/hyp) = opp / adj
= загар (х). Следовательно, функция тангенса совпадает с частным
функций синуса и косинуса (функция тангенса по-прежнему довольно
удобно). Рассмотрим эти функции подробнее. синус(90° — q) = косинус(q) секанс(90° — q) = косеканс(q) тангенс(90° — q) = котангенс(q) тем самым оправдывая соглашение об именах. Триггерные функции оцениваются по-разному в зависимости от единиц измерения. Так же, как мы можем определить тригонометрические функции вида f(q) = а/б которые принимают непрямой угол в качестве параметра и возвращают отношение
длины двух сторон треугольника, мы можем сделать обратное: определить триггерные функции
формы f(a / b) = q которые принимают отношение длин двух сторон в качестве параметра и возвращают
измерение одного из непрямых углов. Как и прежде, функции обычно обозначаются аббревиатурой: арксинус (arcsin),
арккосинус (arccos), арктангенс (arctan) арккосеканс (arccsc), арксеканс
(угловые секунды) и арккотангенс (арккот). © 2000-2005 Math.
, и доктором Дженнифер М. Веннер, факультет геологии, Университет Висконсина, Ошкош
Ресурсы ·
·
·
·
·
·
4 9022 Поиск
Обзор ( Математика | Алгебра
| Функция |Обзор) 
 (Они называются обратными триггерными функциями , поскольку они выполняют
инверсия или наоборот предыдущих триггерных функций.)
(Они называются обратными триггерными функциями , поскольку они выполняют
инверсия или наоборот предыдущих триггерных функций.) (т. е. если мы определим, что a/b = 2, и мы знаем
a = 6, то мы заключаем, что b = 3.)
(т. е. если мы определим, что a/b = 2, и мы знаем
a = 6, то мы заключаем, что b = 3.)
f(q) = опп/опп f(q) = опп/прил f(q) = опп/гип f(q) = прил/опп f(q) = прил/прил f(q) = прил/гип f(q) = hyp/opp f(q) = hyp/adj f(q) = гип/гип синус(q)
= опп/хайп косеканс(q) = hyp/opp косинус(q)
= прил/гип секанс(q) = hyp/adj тангенс(q) = opp/adj котангенс(q) = прил/опп 
синус(q)
= опп/хайп CSC(q) = 1/sin(q) COs(q) = adj/hyp сек(кв) = 1/COs(кв) tan(q) = sin(q)/COs(q) раскладушка(q) = 1/tan(q)  Вы заметите, что там
функции синуса, секанса и тангенса, и существуют соответствующие
«ко»-функции. Они получили свои странные имена от различных похожих идей.
в геометрии. Вы можете предположить, что кофункции должно быть перемаркированы как мультипликативные инверсии соответствующего синуса,
функции секанса и тангенса. Однако у этого безумия есть метод.
Кофункция данной триггерной функции (f) по определению есть
берется функция, полученная после дополнения ее параметра.
Так как дополнение любого угла q равно 90°
— q, тот факт, что следующие соотношения
можно показать, что выполняется:
Вы заметите, что там
функции синуса, секанса и тангенса, и существуют соответствующие
«ко»-функции. Они получили свои странные имена от различных похожих идей.
в геометрии. Вы можете предположить, что кофункции должно быть перемаркированы как мультипликативные инверсии соответствующего синуса,
функции секанса и тангенса. Однако у этого безумия есть метод.
Кофункция данной триггерной функции (f) по определению есть
берется функция, полученная после дополнения ее параметра.
Так как дополнение любого угла q равно 90°
— q, тот факт, что следующие соотношения
можно показать, что выполняется: q, например градусов, радиан или градусов.
Например, sin(90°) = 1, а sin(90)=0,89399…. объяснение
q, например градусов, радиан или градусов.
Например, sin(90°) = 1, а sin(90)=0,89399…. объяснение арксинус (opp/hyp) = q арккосеканс(hyp/opp) = q арккосинус (прил/гип) = q арксеканс(гип/прил) = q арктангенс (opp/adj) = q арккотангенс (прил/опп) = q  Согласно стандартным обозначениям
для обратных функций (f -1 ), вы также часто будете видеть эти
пишется как sin -1 , cos-1 , tan -1 csc-1 ,
сек -1 и детская кроватка -1 . Остерегайтесь : Есть еще один
общее обозначение, которое записывает квадрат триггерных функций, например
(sin(x)) 2 как sin 2 (x). Это может сбивать с толку, поскольку
вы тогда могли бы потом подумать что грех -1 (х)
= (грех (х)) -1 , что равно , а не . Отрицательный
верхний индекс здесь — это специальное обозначение, обозначающее обратные функции
(не мультипликативные инверсии).
Согласно стандартным обозначениям
для обратных функций (f -1 ), вы также часто будете видеть эти
пишется как sin -1 , cos-1 , tan -1 csc-1 ,
сек -1 и детская кроватка -1 . Остерегайтесь : Есть еще один
общее обозначение, которое записывает квадрат триггерных функций, например
(sin(x)) 2 как sin 2 (x). Это может сбивать с толку, поскольку
вы тогда могли бы потом подумать что грех -1 (х)
= (грех (х)) -1 , что равно , а не . Отрицательный
верхний индекс здесь — это специальное обозначение, обозначающее обратные функции
(не мультипликативные инверсии).
Связаться с нами | Реклама и спонсорство | Товарищество | Ссылка на нас 


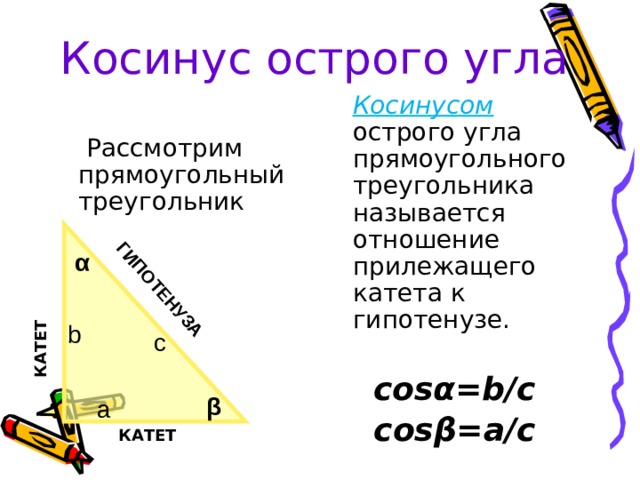
 Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.

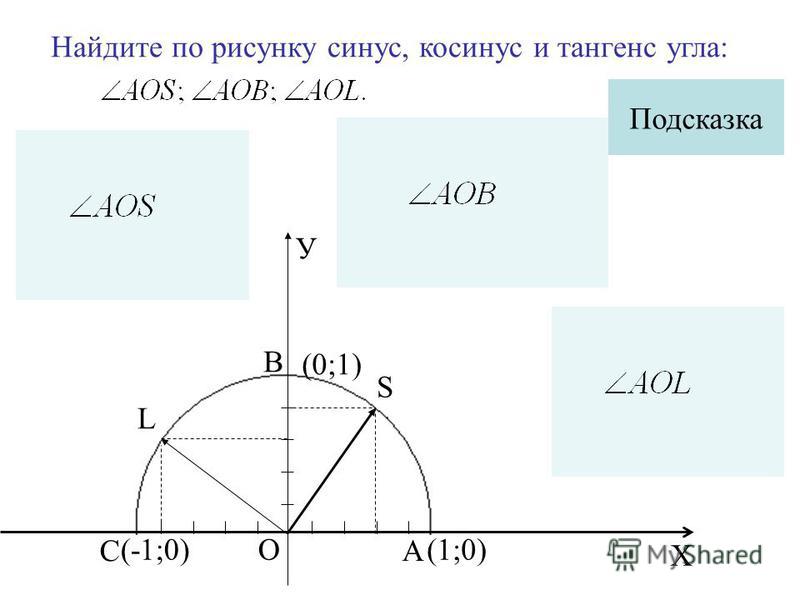
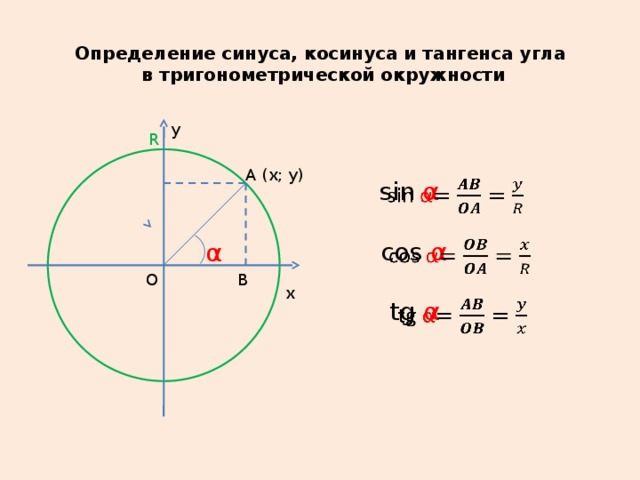 Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.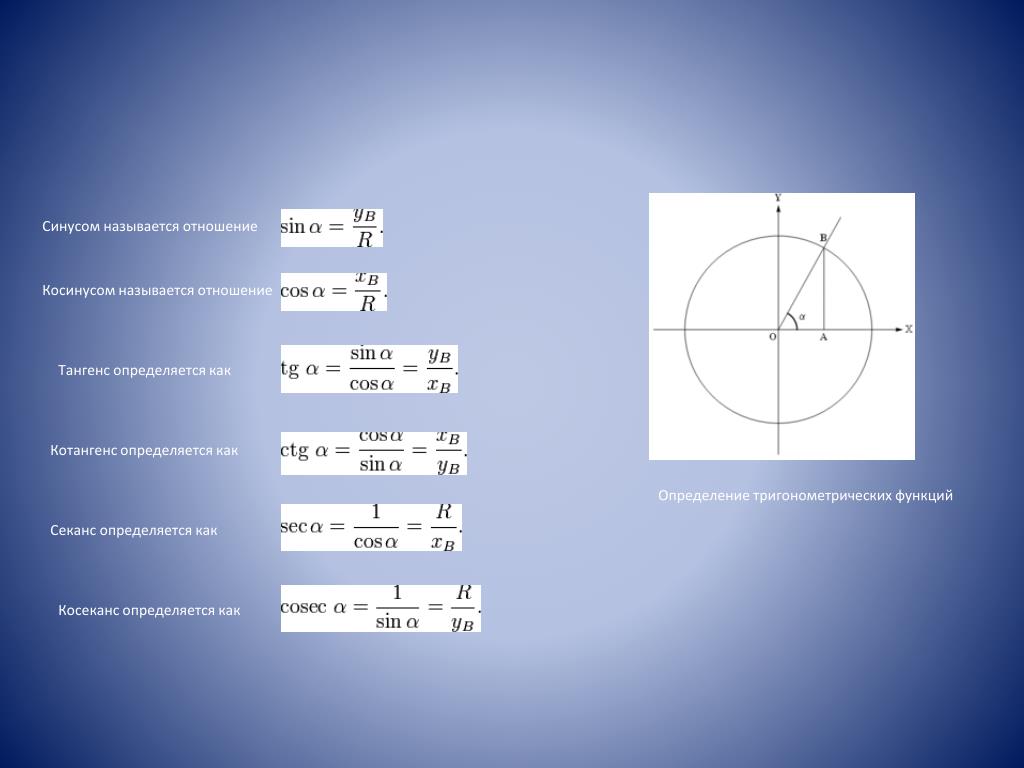
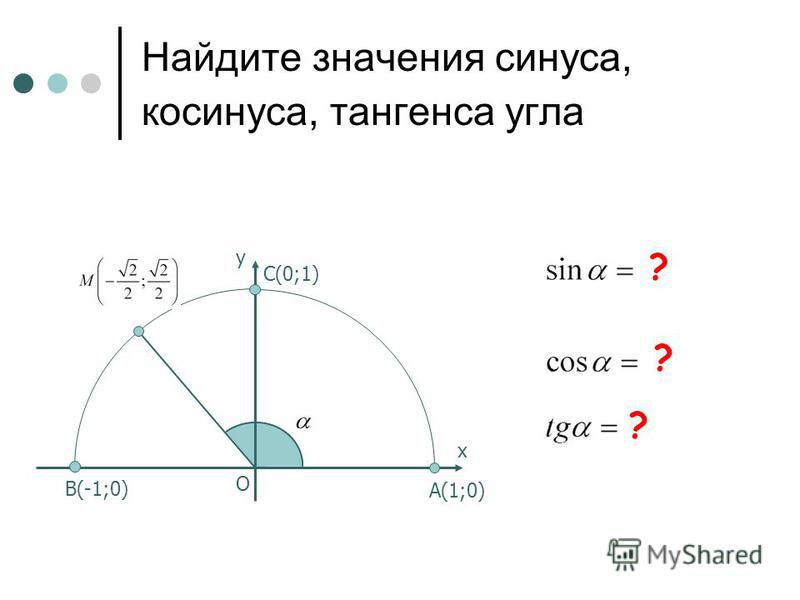 Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.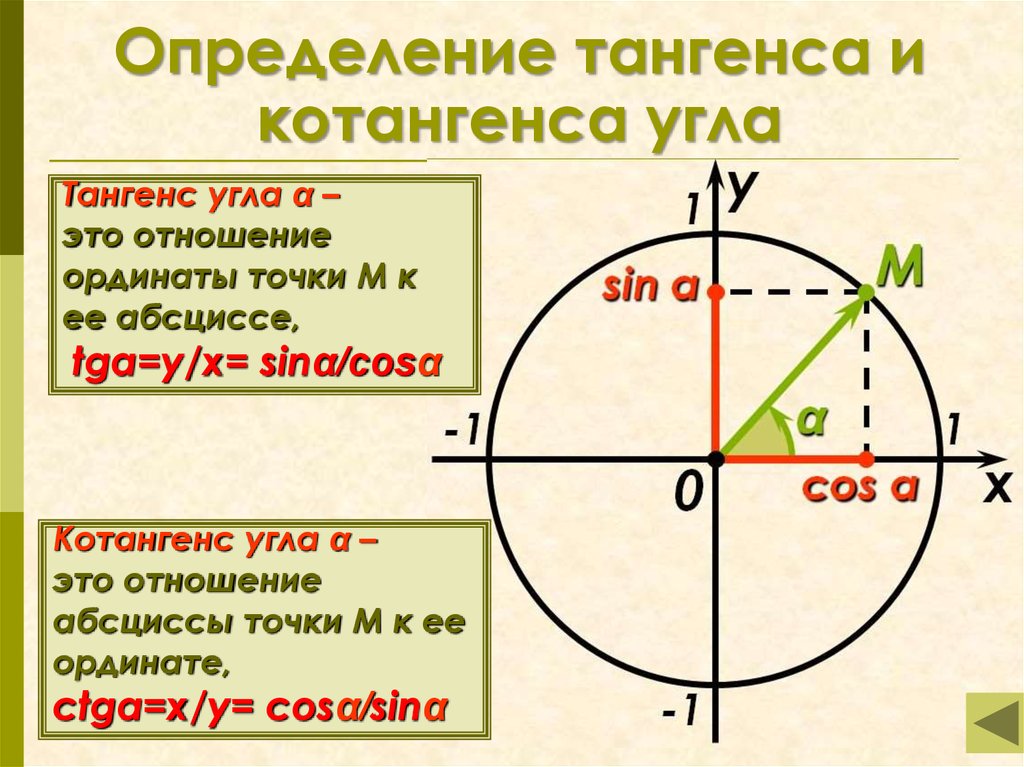 Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
 Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов. Таким образом, пи радиан равны 180 градусам.
Таким образом, пи радиан равны 180 градусам.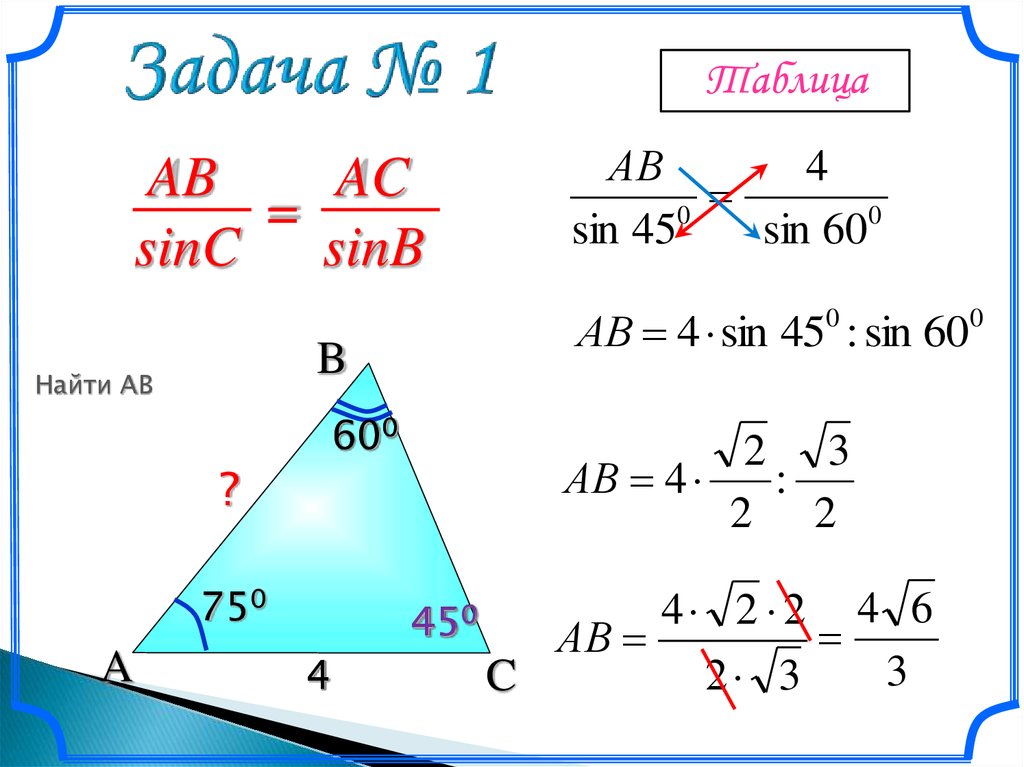 Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.

 {\circ}\left(2\pi\right)
{\circ}\left(2\pi\right)
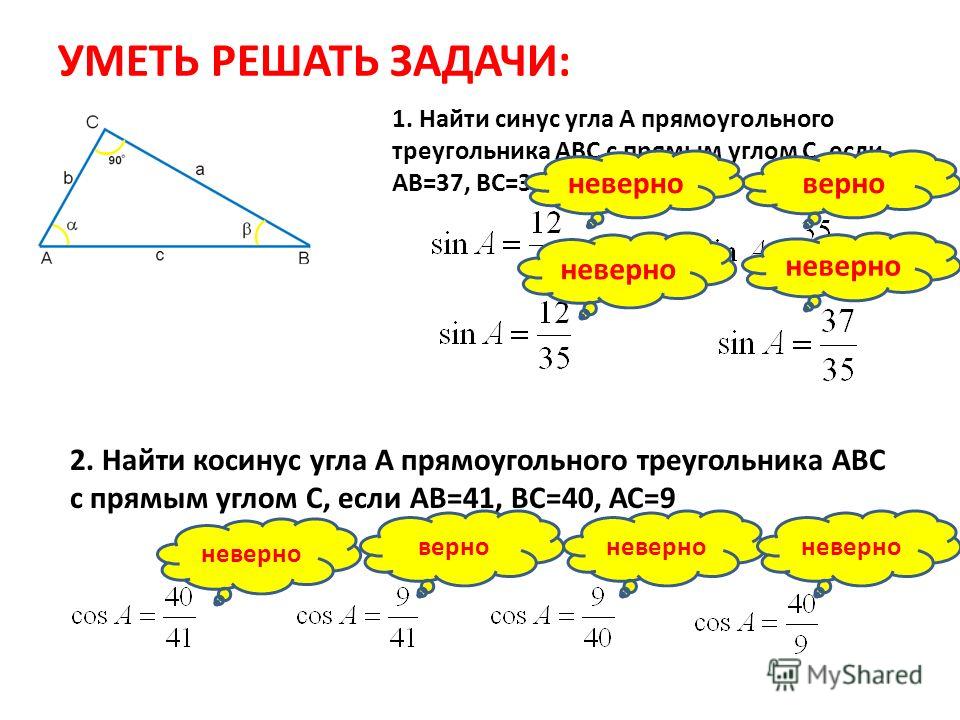 : ил.- ISBN 5-09-002727-7
: ил.- ISBN 5-09-002727-7 А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
 : ил.- ISBN 5-09-002727-7
: ил.- ISBN 5-09-002727-7 А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.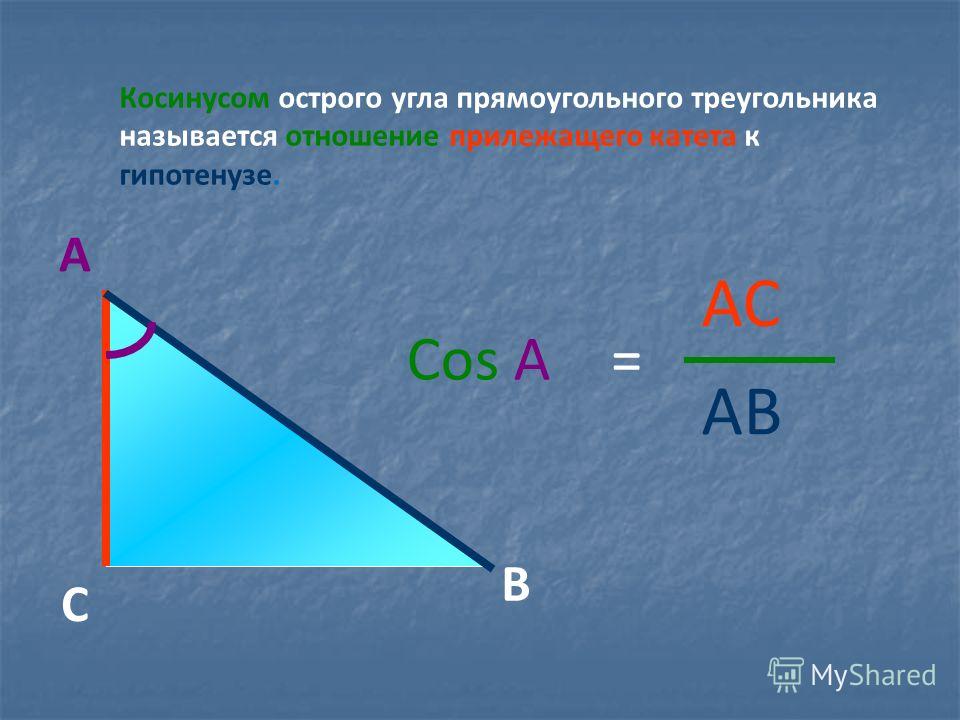 И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.