Расчет объема куба
Куб это геометрическое тело, ограниченное шестью квадратами, которое ещё можно назвать правильный шестигранник, а так же правильный многогранник. Слово «куб» образовано от греческого слова «kybos».
Определение объема куба
Расчет объема куба можно произвести с помощью следующей формулы:
V = a3
a – сторона куба
V – объем куба
Куб представляет собой правильный многогранник, каждая из граней которого является квадратом. Это геометрическое тело является частным случаем других (а именно – параллелепипеда и призмы) и в повседневной жизни встречается достаточно часто. Инженерам и архитекторам при разработке проектов различных машин и зданий нередко приходится производить расчет объема куба, причем ввиду относительной его простоты решение этой задачи обычно не представляет большой сложности.
На практике с кубами и параллелепипедами чаще всего приходится встречаться в архитектуре. Их форму имеют многие современные здания и сооружения, причем она считается одной из наиболее практичных: такие сооружения проще и быстрее как проектировать, так и возводить. При этом формула объема куба используется преимущественно для точного определения размеров внутренних пространств, что особенно важно для таких зданий, как склады, цеха промышленных предприятий, объекты социально-культурного назначения.
Их форму имеют многие современные здания и сооружения, причем она считается одной из наиболее практичных: такие сооружения проще и быстрее как проектировать, так и возводить. При этом формула объема куба используется преимущественно для точного определения размеров внутренних пространств, что особенно важно для таких зданий, как склады, цеха промышленных предприятий, объекты социально-культурного назначения.
Форму куба нередко имеют различные предметы корпусной мебели, и при их разработке конструкторам требуется определять, в том числе, и такую величину, как объем, для того, чтобы достичь наиболее рациональной компоновки этих элементов. Вычислить объем куба часто бывает необходимо и тем инженерам, которые занимаются созданием проектов контейнеров, железнодорожных вагонов, а также стеллажных систем, использующихся в складском хозяйстве.
Одним из наиболее ярких примеров кубов является знаменитый «магический куб» – оригинальная головоломка, созданная талантливым венгерским преподавателем архитектуры и скульптором Эрне Рубиком и впоследствии названная в его честь. Каждая из граней этого кубика состоит из нескольких квадратов, окрашенных в один цвет. С помощью поворотов их можно комбинировать в различных вариантах, а задача игрока состоит в том, чтобы «разобранную» конструкцию (то есть такую, грани которой содержат квадратики разных цветов) привести в изначальное состояние. Согласно статистике, «Кубик Рубика» за все время своего существования (с
Каждая из граней этого кубика состоит из нескольких квадратов, окрашенных в один цвет. С помощью поворотов их можно комбинировать в различных вариантах, а задача игрока состоит в том, чтобы «разобранную» конструкцию (то есть такую, грани которой содержат квадратики разных цветов) привести в изначальное состояние. Согласно статистике, «Кубик Рубика» за все время своего существования (с 1974 года) был продан в количестве около 350 000 000 экземпляров, и на сегодняшний день является одной из признанных в мире головоломок. Изначально каждая из его граней состояла из девяти квадратов, но впоследствии появились и более сложные варианты (например, содержащие по двадцать пять элементов). В различных странах проводятся соревнования по сборке этой головоломки на время, а также чемпионаты Европы и мира, организатором которого является организация «World Cube Association» («Всемирная ассоциация кубика»).
Форму куба имеют не только рукотворные, но и некоторые природные сущности, например, кристаллические решетки такого минерала, как флюорит, а также обычной поваренной соли. Наконец, следует заметить, что с этими геометрическими телами все мы знакомы еще с детства, поскольку одними из самых любимых игрушек для многих из нас были именно кубики.
Наконец, следует заметить, что с этими геометрическими телами все мы знакомы еще с детства, поскольку одними из самых любимых игрушек для многих из нас были именно кубики.
Узнаем как найти объем куба разными способами
Если представить себе обычные детские кубики, то легко можно понять, как найти объем куба. Приняв объём одного кубика за кубическую меру объёма, например, за кубический дециметр, начинаем строить из них большой куб. Сложив первый квадратный «этаж», например, размерами 4Х4, следует выложить ещё 4 «этажа», чтобы все рёбра нашего куба были равны. Равенство всех сторон куба – это основное правило, которое доказывает, что перед нами именно куб.
Найти размер одной квадратной грани легко, стоит лишь перемножить ширину и длину основания, то есть возвести ребро в квадрат. Так как у нас получается несколько рядов – «этажей», вернее, их получается по счёту равное количество ребру куба, то полученный квадрат ещё раз умножаем на высоту куба, то есть, на его ребро. Получается, таким образом, что ребро мы возводим в третью степень, по-другому — в куб.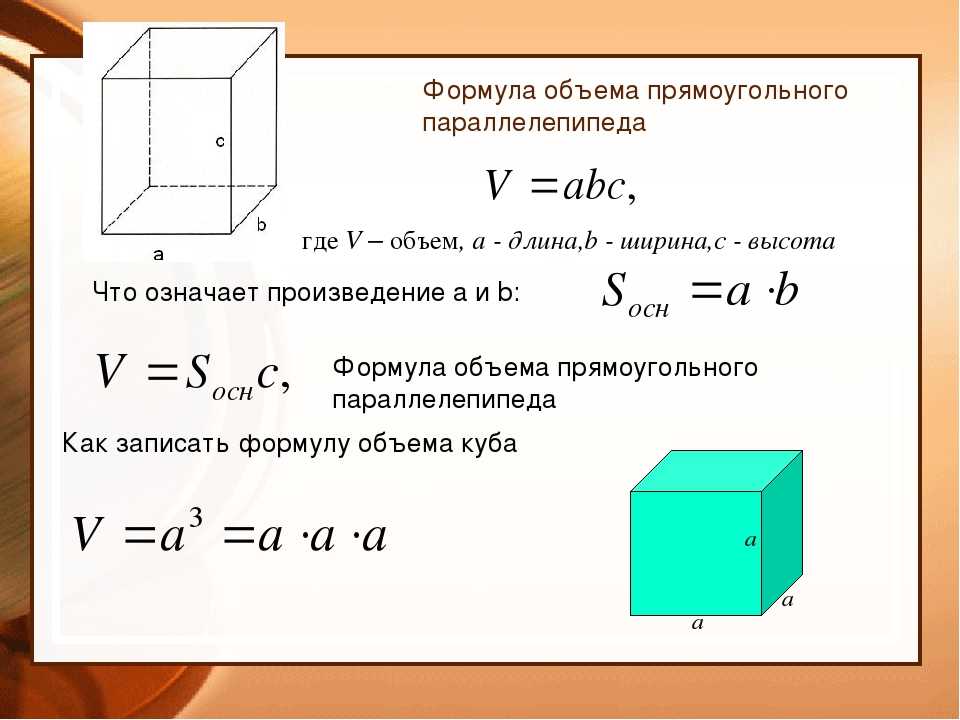 Вот так просто, оказывается, найти объём куба!
Вот так просто, оказывается, найти объём куба!
Именно отсюда и берёт своё название возведение в третью степень – «в куб». То есть, для «возведения в куб» нужно три раза умножить число на само себя – само выражение уже имеет в своей основе решение задачи нахождения кубического объёма.
Но если величина кубического ребра, то есть одной стороны куба, неизвестна, но дана диагональ одной из его граней, как найти объем куба?Можно ли это сделать? Оказывается, и это вполне вычислимо.
По диагонали стороны следует вычислить сторону одной грани и ввести её величину в куб, то есть в третью степень. Для того чтобы было понятнее, начертим одну из кубических граней – это будет квадрат, например, PMNK, где MN – диагональ, которая нам известна. Используя теорему Пифагора, возведём известное значение диагонали в квадрат или во вторую степень. В прямоугольном треугольнике PMN сторона MN является гипотенузой, и её квадрат равняется сумме катетов, возведённых в квадрат.
Но мы знаем, что катеты – это стороны квадратной грани куба. Значит, полученный результат следует разделить на два и найти квадратный корень. Этот результат и будет равняться величине стороны – ребра куба. Теперь уже вопрос, как вычислить объем куба, решается самым простым способом. Всего-то навсего возводим сторону куба в третью степень – и результат налицо.
Значит, полученный результат следует разделить на два и найти квадратный корень. Этот результат и будет равняться величине стороны – ребра куба. Теперь уже вопрос, как вычислить объем куба, решается самым простым способом. Всего-то навсего возводим сторону куба в третью степень – и результат налицо.
Часто бывает так, что в условии задачи есть такая величина, как площадь одной из граней куба. В таком случае сначала нужно найти сторону квадрата – грани куба. Для этого достаточно найти квадратный корень заданной площади. Затем вычисленную величину грани умножают на известную площадь.
Иногда просто необходимо знать, как найти объем куба,но нет ни одного размера, ни ребра, ни площади стороны куба. Однако если эта задача имеет в условии такие данные, как плотность и масса, то вычислить отчет можно, перемножив данные величины: плотность и массу. Искомый объём будет получен в произведении.
А если у человека вообще нет ни одного измерения, как поступить в этом случае? В практике часто пользуются таким несложным приёмом, как погружение тела в жидкость. Так как найти объем куба без сантиметровой ленты или линейки?
Так как найти объем куба без сантиметровой ленты или линейки?
Нужно отмерить определённое количество жидкости в ёмкости, например, в кастрюле, налив её до краёв. Затем следует поставить ёмкость в другую посуду. Погрузив куб в жидкость, нужно постараться собрать всю перелившуюся через край жидкость. Затем, измерив её мензуркой или банками (это зависит от величины объёма куба), можно делать вывод об объёме куба – он будет равен количеству жидкости, которую куб вытеснил своим погружением.
К сожалению, довольно сложно или даже невозможно измерить этим способом объёмы кубов значительных размеров. Зато так можно узнать объём не только куба, но предметов любой формы.
Существуют ещё и другие возможности нахождения объёма кубов. Например, при известной длине диагонали куба (не грани!). Известно, что формула диагонали куба выражается произведением его ребра на квадратный корень из 3. Следовательно, делим диагональ на квадратный корень из 3 и получаем длину ребра. Дальше всё очень просто: возводим результат в куб и получаем искомый ответ.
Вычисление объема и вместимости кубов и прямоугольных параллелепипедов | Хацуди
В математике мы часто думаем о фигурах в терминах трехмерных объектов, а не двухмерных объектов. На самом деле все вокруг нас трехмерно.
Итак, давайте удостоверимся, что мы умеем вычислять размеры трехмерных объектов. В начальной школе геометрии мы изучаем формулы для вычисления размеров трехмерных фигур. Также размер трехмерной фигуры называется объемом. Используя формулу, вы сможете рассчитать объем.
Итак, давайте сначала вычислим объем куба и параллелепипеда. Тогда мы сможем понять вместимость сосуда. В этом разделе мы объясним, как рассчитать объем и вместимость кубов и прямоугольных параллелепипедов.
Содержание
- 1 Что такое кубы и прямоугольные параллелепипеды?
- 1.1 Как рассчитать объем куба и параллелепипеда
- 2 Расчет вместимости сосуда: объем воды, заполненный трехмерным объектом
- 2.1 Случаи, когда объем и вместимость различаются
- 3 Почему мы можем рассчитать объем и емкость?
- 3.
 1 Расчет длин сторон по объему
1 Расчет длин сторон по объему
- 3.
- 4 Узнайте, как рассчитать объем и вместимость
Что такое кубы и прямоугольные параллелепипеды?
Во-первых, давайте разберемся, что такое куб и прямоугольный параллелепипед. Куб — это объект, окруженный шестью квадратами. Кроме того, прямоугольный параллелепипед — это объект, окруженный шестью прямоугольниками.
Ниже приведены куб и прямоугольный параллелепипед.
Вы должны уметь вычислять размер таких цифр.
Как рассчитать объем куба и прямоугольного параллелепипеда
Поймите, что объем — это размер трехмерного объекта. Вы будете вычислять размер объекта, который имеет высоту, а также длину и ширину.
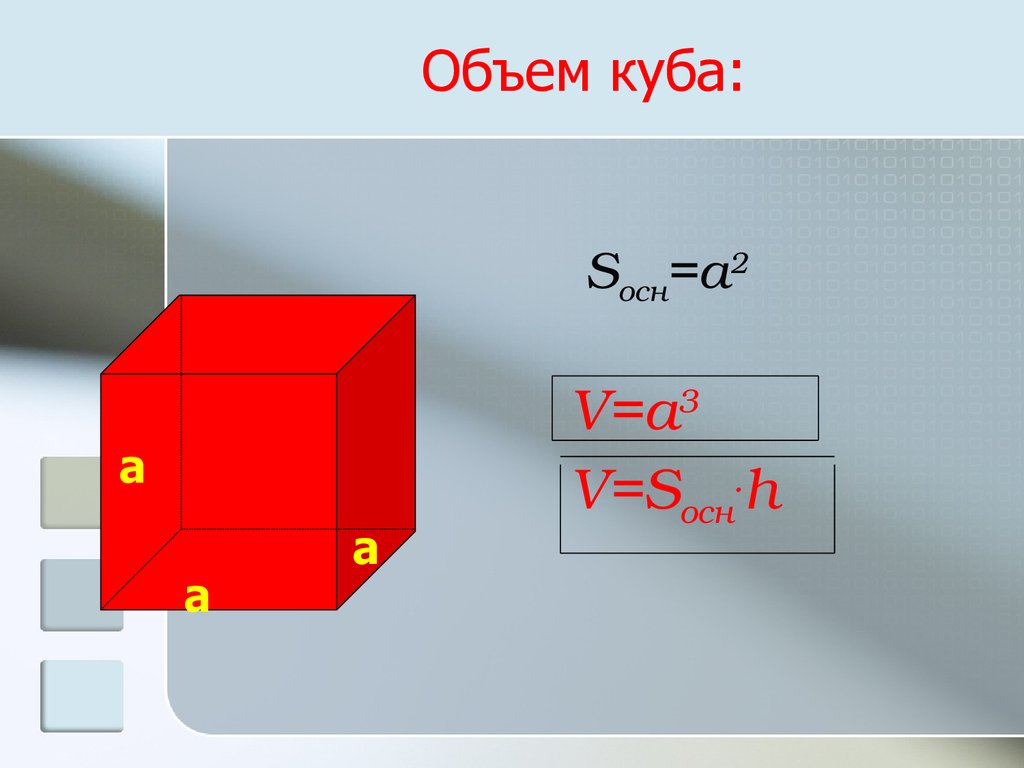
При расчете объема куба или параллелепипеда используйте следующую формулу.
- Объем трехмерного объекта = длина × ширина × высота
Например, каков объем следующего куба и параллелепипеда?
В случае куба все стороны имеют одинаковую длину.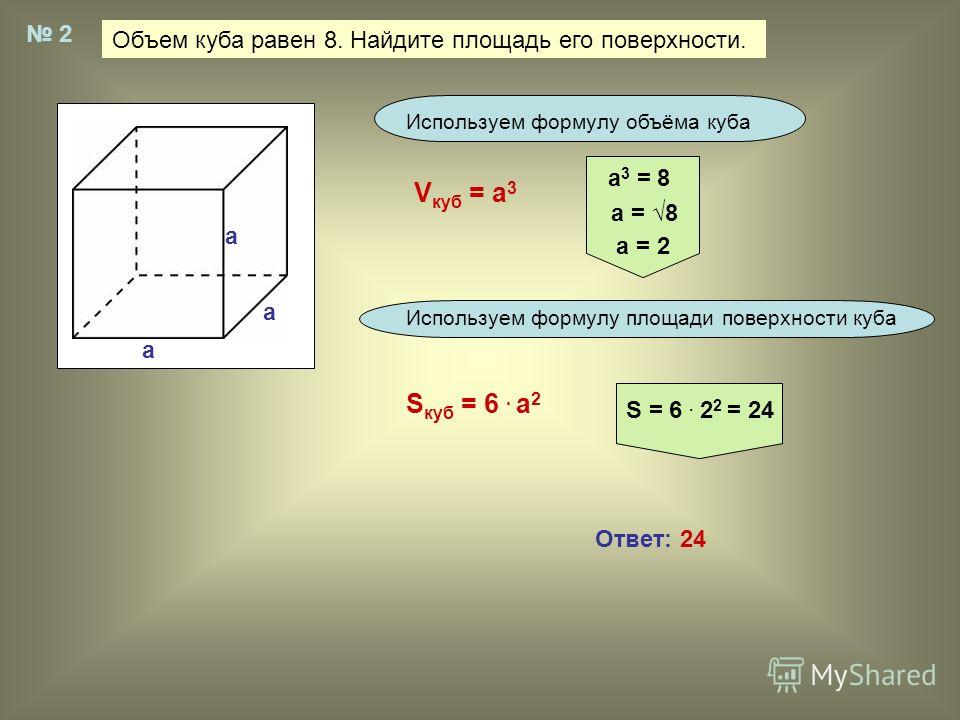 Итак, давайте умножим одно и то же число три раза. Так как длина стороны 3 см, объем куба следующий.
Итак, давайте умножим одно и то же число три раза. Так как длина стороны 3 см, объем куба следующий.
- $3×3×3=27$
Таким образом, ответ равен 27 см 3 . В площади длина стороны умножается в два раза, поэтому единица равна см 2 . С другой стороны, при вычислении объема длина стороны умножается на три раза, поэтому единицей измерения является см 3 .
Далее вычислим объем прямоугольного параллелепипеда, у которого длины сторон прямоугольника различны. Итак, давайте умножим длину, ширину и высоту соответственно. Результат следующий.
- $4×3×2=24$
Таким образом, мы видим, что объем прямоугольного параллелепипеда равен 24 см 3 .
Расчет вместимости сосуда: объем воды, заполненный трехмерным объектом
После понимания объема давайте узнаем о вместимости сосуда. Когда жидкость (например, воду) наливают в сосуд, емкость показывает, сколько жидкости можно налить в этот сосуд.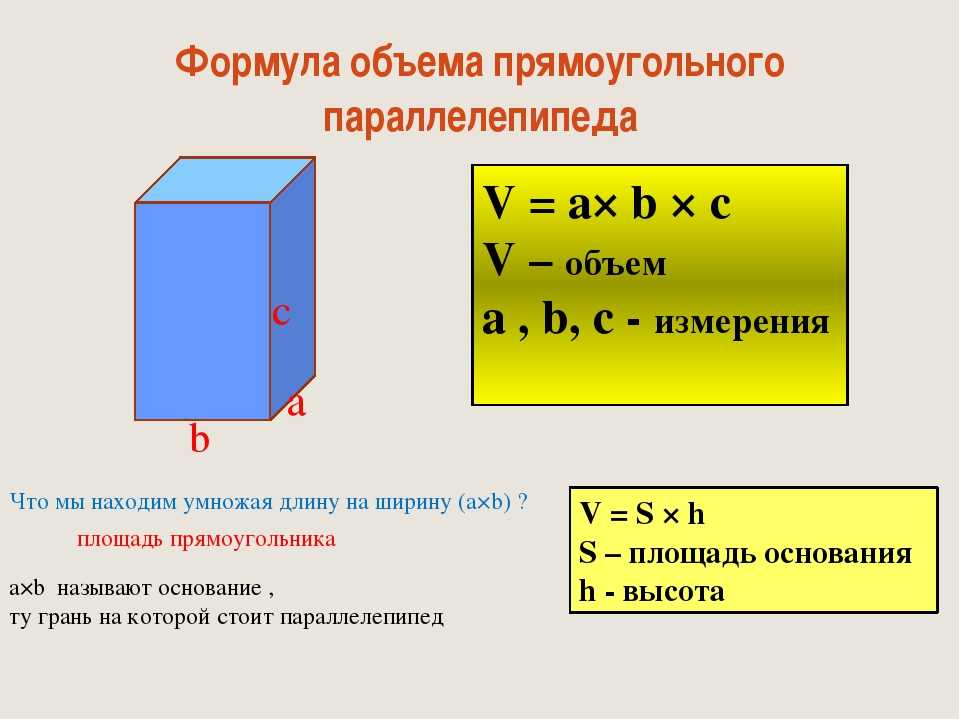 Объем и вместимость сосуда — это одни и те же понятия, и формула используется одна и та же.
Объем и вместимость сосуда — это одни и те же понятия, и формула используется одна и та же.
При вычислении объема мы умножали длину, ширину и высоту соответственно. При расчете вместимости сосуда умножьте длину, ширину и высоту сосуда соответственно.
В этом случае вместимость судна следующая.
- 15×8×10=1200$
Таким образом, мы можем рассчитать, что этот сосуд может быть наполнен до 1200 см 3 воды. 1 л равен 1000 см 3 , поэтому мы также можем видеть, что этот сосуд может вместить 1,2 л воды.
Случаи, когда объем и вместимость различаются
Как упоминалось ранее, формула для расчета объема и вместимости судна одинакова. Однако в реальности объем и емкость могут отличаться. Это связано с толщиной контейнера.
Например, каковы объем и вместимость следующего контейнера?
Объем равен размеру всего контейнера. Итак, давайте умножим на внешнюю длину контейнера. Так как длина 8 см, ширина 6 см и высота 5 см, объем следующий.
- $8×6×5=240$
С другой стороны, как рассчитать вместимость судна? В емкости важно знать, сколько воды можно залить. Только внутренняя часть контейнера может удерживать воду. Итак, давайте умножим внутреннюю длину контейнера. Так как длина 6 см, ширина 4 см и высота 4 см, объем следующий.
- $6×4×4=96$
Таким образом, мы можем рассчитать объем и вместимость сосуда. Поймите, что если емкость имеет толщину, то объем и вместимость будут другими.
Почему мы можем рассчитать объем и емкость?
Почему можно рассчитать объем и вместимость сосуда путем умножения длины, ширины и высоты? Давайте выясним, почему.
Прежде всего, каков объем куба со стороной 1 см?
Поскольку все стороны имеют длину 1 см, объем этого куба равен 1 см 3 . Тогда каков объем этого куба, если он устроен следующим образом?
Всего кубиков 12. Следовательно, мы знаем, что это 12 см 3 . Однако подсчет количества кубиков по одному затруднителен. Итак, посчитаем объем.
Итак, посчитаем объем.
В отличие от куба, все стороны которого имеют длину 1 см, кубоид на рисунке выше имеет высоту 1 см, но его вертикальная и горизонтальная длины различны. Итак, давайте умножим длину на ширину так же, как вычисляем площадь.
- $3×4×1=12$
Высота 1 см. Однако умножение на единицу не меняет ответ. Следовательно, в этом прямоугольном параллелепипеде вычисление площади такое же, как вычисление объема.
Далее рассмотрим прямоугольный параллелепипед высотой 3 см вместо 1 см. Результат следующий.
В этом прямоугольном параллелепипеде есть три параллелепипеда размером $3×4×1$, поставленные друг на друга. Поскольку блоки имеют высоту 3 см, мы вычисляем высоту в 3 см вместо 1 см следующим образом.
- $3×4×3=36$
Когда вы думаете об этом таким образом, вы можете понять, почему умножение на длину, ширину и высоту позволит вам вычислить объем.
Расчет длин сторон по объему
Если объем известен, в некоторых случаях можно вычислить длины сторон.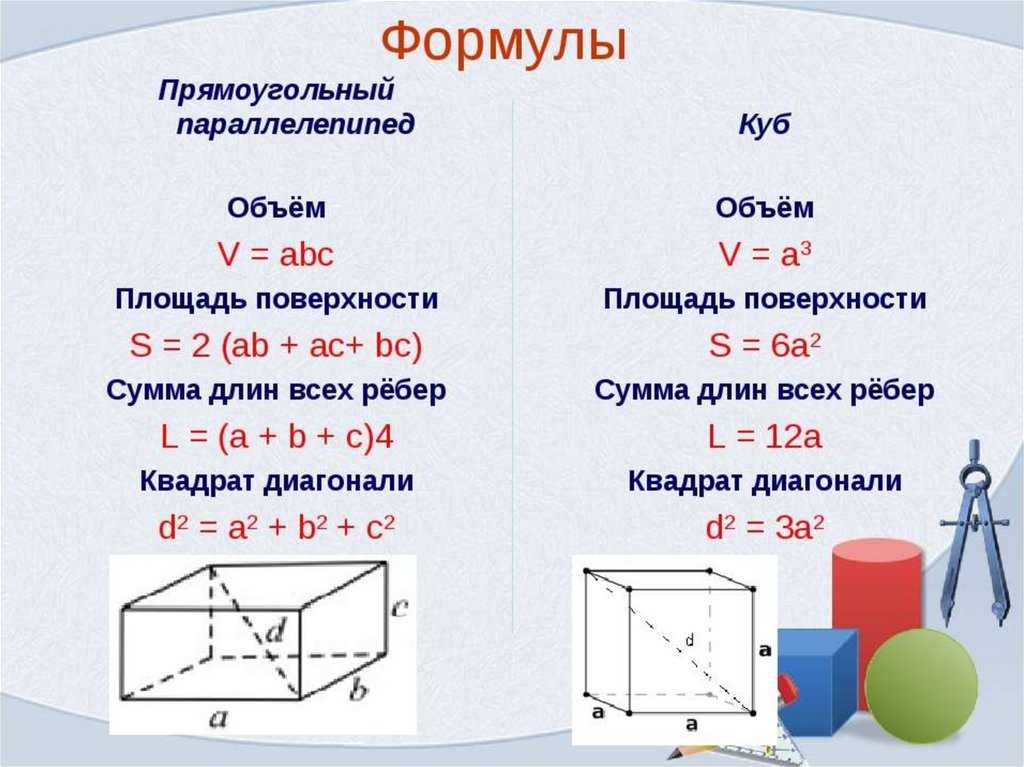 Например, если объем следующего прямоугольного параллелепипеда равен 16 см3, какова длина $a$?
Например, если объем следующего прямоугольного параллелепипеда равен 16 см3, какова длина $a$?
Мы уже знаем объем. Кроме того, мы знаем длину и высоту. Итак, если мы установим ширину как $□$, мы можем составить следующее уравнение.
- $16=4×2×□$
Теперь давайте посчитаем стоимость $□$. Измените его на следующее уравнение.
- $□=16÷4÷2$
Вычислив это выражение, мы видим, что ширина равна 2 см. В математике вы можете вычислить длину стороны по ее объему.
Узнайте, как рассчитать объем и емкость
Объекты вокруг нас не плоские, а трехмерные. Следовательно, мы должны уметь вычислять размеры трехмерных фигур. В частности, много кубических и прямоугольных объектов. Если вы осмотрите свой дом, вы обнаружите, что в нем много кубических и прямоугольных предметов.
Размер куба равен объему. При расчете объема мы можем использовать формулу.
Другим понятием, аналогичным объему, является вместимость судна. Когда жидкость наливается в контейнер и контейнер полон, вместимость определяется тем, сколько жидкости может вместить контейнер. Если вы можете рассчитать объем, вы можете рассчитать вместимость сосуда.
Когда жидкость наливается в контейнер и контейнер полон, вместимость определяется тем, сколько жидкости может вместить контейнер. Если вы можете рассчитать объем, вы можете рассчитать вместимость сосуда.
Когда вы узнаете о кубах и прямоугольных параллелепипедах, вы сможете вычислить объем. Кроме того, поймите, почему объем можно рассчитать, умножив длину, ширину и высоту. Изучив эти вещи, вы сможете рассчитать объем и мощность.
Объем кубического или прямоугольного резервуара – Математика для профессий: Том 2
Том
Нажмите кнопку воспроизведения в следующем аудиоплеере, чтобы прослушать этот раздел
Если бы вас попросили описать объем предмета, как бы это выглядело? Как бы вы описали единицы, в которых будут производиться ваши расчеты?
В этой главе рассматривается расчет объема и единицы измерения, используемые при расчете объема.
В предыдущей главе мы имели дело с периметром, который является линейным измерением. Как мы выяснили, периметр является одномерным и по существу приобретает характеристики линии. Хорошим примером периметра может быть прогулка по футбольному полю. Вы бы прошлись по периметру поля.
Как мы выяснили, периметр является одномерным и по существу приобретает характеристики линии. Хорошим примером периметра может быть прогулка по футбольному полю. Вы бы прошлись по периметру поля.
Затем мы взглянули на площадь, которая представляет собой двумерное измерение. Хорошим примером этого является столешница. Если бы вы взяли кисть и перекрасили верхнюю часть стола, вы бы закрасили область столешницы.
Имея дело с объемом, мы добавляем еще одно измерение, и в результате объем становится трехмерным измерением. Хорошим примером трехмерного объекта может быть планета Земля.
Вот еще одно визуальное представление каждого из трех. Каждая линия представляет собой плоскость.
Теперь вернемся к юнитам. Когда мы имеем дело с линейными измерениями, мы имеем дело с единицами измерения такими, какие они есть. Под этим я подразумеваю, что мы получим ответ в метрах, футах, дюймах, сантиметрах и так далее.
Когда мы имеем дело с площадью, мы продолжаем иметь дело с такими единицами, как метры, но они возведены в квадрат, чтобы показать, что они имеют два измерения.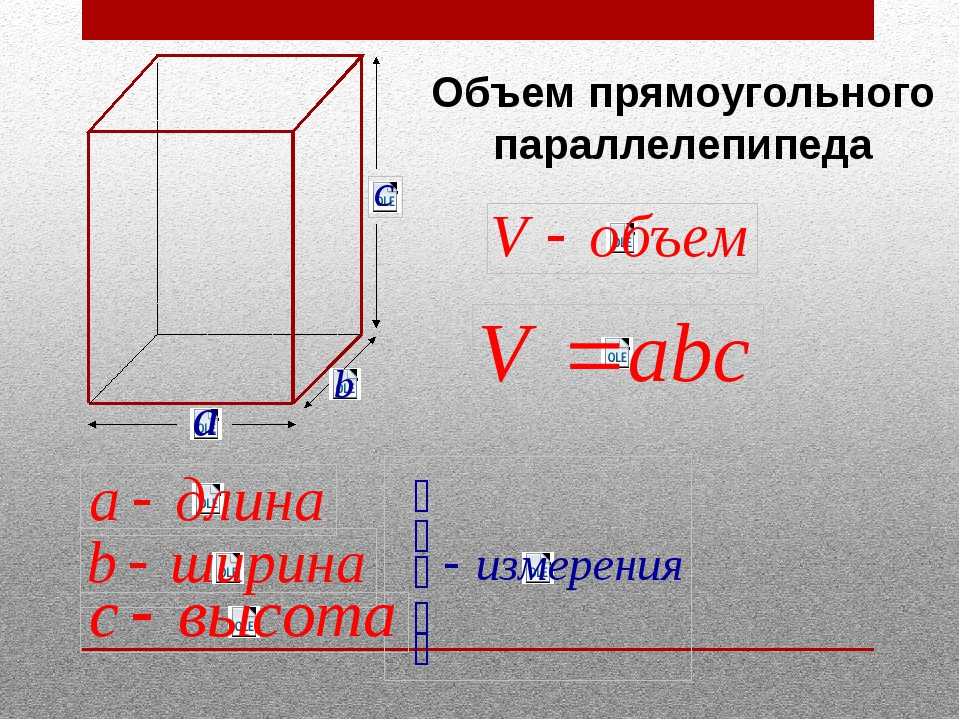 Например, площадь квартиры может составлять 1200 квадратных футов или 1200 футов². Квадратность ножек указывает на два измерения, такие как ширина И длина.
Например, площадь квартиры может составлять 1200 квадратных футов или 1200 футов². Квадратность ножек указывает на два измерения, такие как ширина И длина.
А теперь добавим еще одно измерение. У нас может быть не только длина и ширина, но и глубина. Это заставляет нас задаться вопросом: «Какими были бы единицы в этой ситуации?» 9{3}[/латекс]
«3» в данном случае представляет три измерения и отвечает за термин «кубический», когда мы произносим его. Теперь мы готовы идти дальше и узнать формулу объема конкретных предметов.
Когда произносится слово «куб», мы можем думать о квадрате, но только с дополнительным измерением. Каждое измерение квадрата идентично, и куб следует той же логике.
Если вы добавите третье измерение, вы получите все возможные измерения одинаковыми. Взгляните на один из самых известных кубов в мире:
Чтобы найти объем куба, нам нужно перемножить три стороны. Более конкретно, мы рассмотрим умножение длины, ширины и высоты.
[латекс]\Большой \текст{объем куба} = \текст{сторона} \times \текст{сторона} \times \text{сторона}[/латекс]
Найти площадь куба довольно просто. Все, что вам нужно знать, это длину одной стороны, и у вас есть вся необходимая информация.
Найдите объем куба, если одна сторона равна 7 дм.
Шаг 1: Запишите формулу.
[латекс]\Большой \текст{объем куба} = \текст{сторона} \times \текст{сторона} \times \text{сторона}[/латекс]
Шаг 2: Найдите объем.
Поскольку все стороны куба одинаковы, это означает, что каждая сторона равна 7 дюймам.
Таким образом, при подстановке переменных в уравнение все они равны.
[латекс]\Large \begin{array}{c} \text{объем куба} = \text{сторона} \times \text{сторона} \times \text{сторона} \\ \text{объем} = 7 \text{in} \times 7 \text{in} \times 7 \text{in} \\ \text{volume} = 343 {\text{in}}^{3} \end{array}[/ латекс]
Расчет объема прямоугольного резервуара очень похож на расчет объема куба, за исключением того факта, что все размеры прямоугольного резервуара будут другими. С этого момента мы будем называть его просто танком.
С этого момента мы будем называть его просто танком.
Мы также получаем, что имена переменных в баке разные. Когда мы имели дело с прямоугольником, мы ссылались на переменные длины и ширины.
Теперь мы просто добавляем еще одну переменную, которую назовем «высота».
Опять же, мы работаем с тремя измерениями, и формула будет похожа на формулу куба, только переменная «сторона» будет заменена тремя разными переменными танка.
Формула:
[латекс]\Большой \текст{объем резервуара} = \текст{длина} \times \text{ширина} \times \text{высота}[/latex]
Рассчитайте объем резервуара, имеющего длину 17 дюймов, ширину 12 дюймов и высоту 13 дюймов.
{3} \end{array}[/latex]
Теперь давайте изменим это и представим ответ в кубических футах.
Первое, что нам нужно сделать, это подсчитать, сколько кубических дюймов содержится в кубическом футе, и лучший способ сделать это визуально.
Мы все согласны с тем, что 1 фут равен 12 дюймам.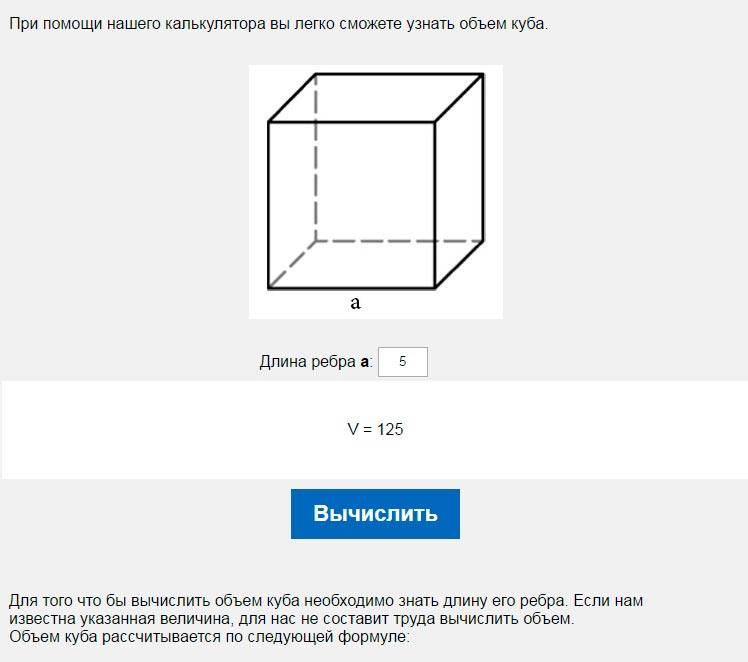 {3} \end{массив}[/латекс] 9{3}= 1,53 \end{array}[/latex]
{3} \end{массив}[/латекс] 9{3}= 1,53 \end{array}[/latex]
Давайте рассмотрим еще один пример и еще раз изменим вопрос.
Найдите ширину резервуара, имеющего длину 22 дюйма, высоту 14 дюймов и общий объем 3080 кубических дюймов.
Шаг 1: Запишите формулу.
[латекс]\Большой \текст{объем} = \текст{длина} \times \text{ширина} \times \text{высота}[/latex]
Шаг 2: Измените формулу для определения ширины . 9{3}}{22 \text{ дюймов} \times 14 \text{ дюймов}} \\ \text{ширина} = 10 \text{ дюймов} \end{массив}[/latex]
Попробуйте сами ответить на пару практических вопросов. Не забудьте проверить видео ответы, чтобы увидеть, как вы это сделали.
Лайл работает в газовой компании под названием «Ночное и дневное отопление». Он проектирует систему отопления для здания, спроектированного эксцентричным архитектором. Здание имеет форму куба, одна из сторон которого составляет 30 футов.
Перед проектированием системы Лайл должен принять во внимание объем здания.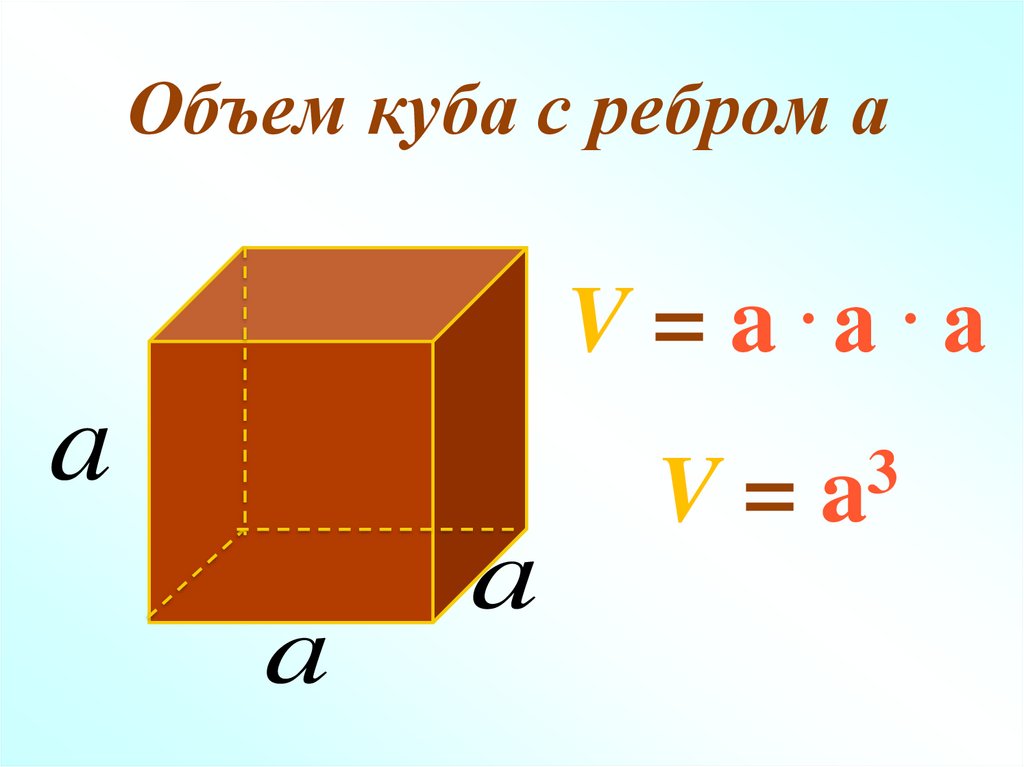

 1 Расчет длин сторон по объему
1 Расчет длин сторон по объему