По какой формуле вычисляется периметр прямоугольника. Периметр и площадь прямоугольника. Изучение новой темы
Прямоугольник обладает многими отличительными особенностями, исходя из которых, выработаны правила вычисления его различных числовых характеристик. Итак, прямоугольник:
Плоская геометрическая фигура;
Четырехугольник;
Фигура, у которой противоположные стороны равны и параллельны, все углы прямые.
Периметр – это общая длина всех сторон фигуры.
Вычисление периметра прямоугольника — довольно простая задача.
Все, что вам нужно знать, это ширину и длину прямоугольника. Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.
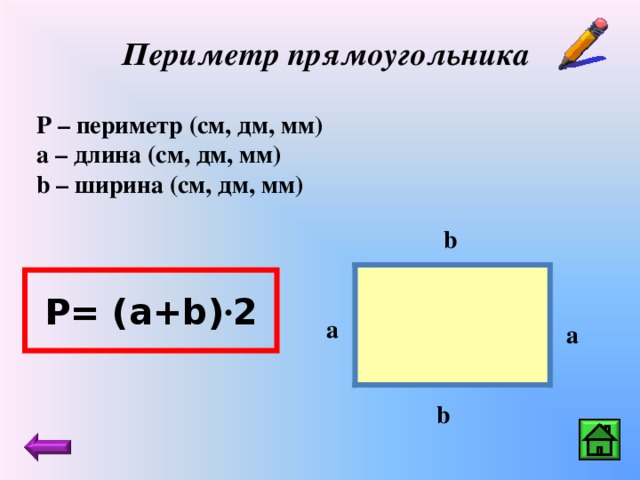
Периметр прямоугольника равен удвоенной сумме 2-х его сторон длины и ширины.
P = (a + b) 2, где a — длина прямоугольника, b — ширина прямоугольника.
Так же периметр прямоугольника можно найти при помощи суммы всех сторон.
P= a+a+b+b, где а– длина прямоугольника, b – ширина прямоугольника.
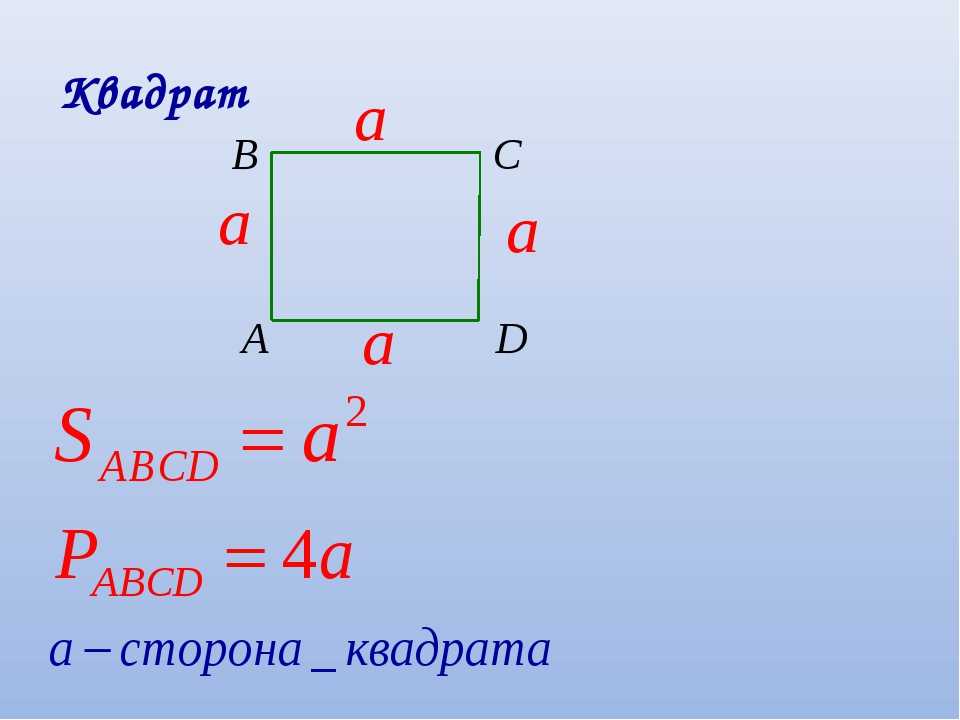
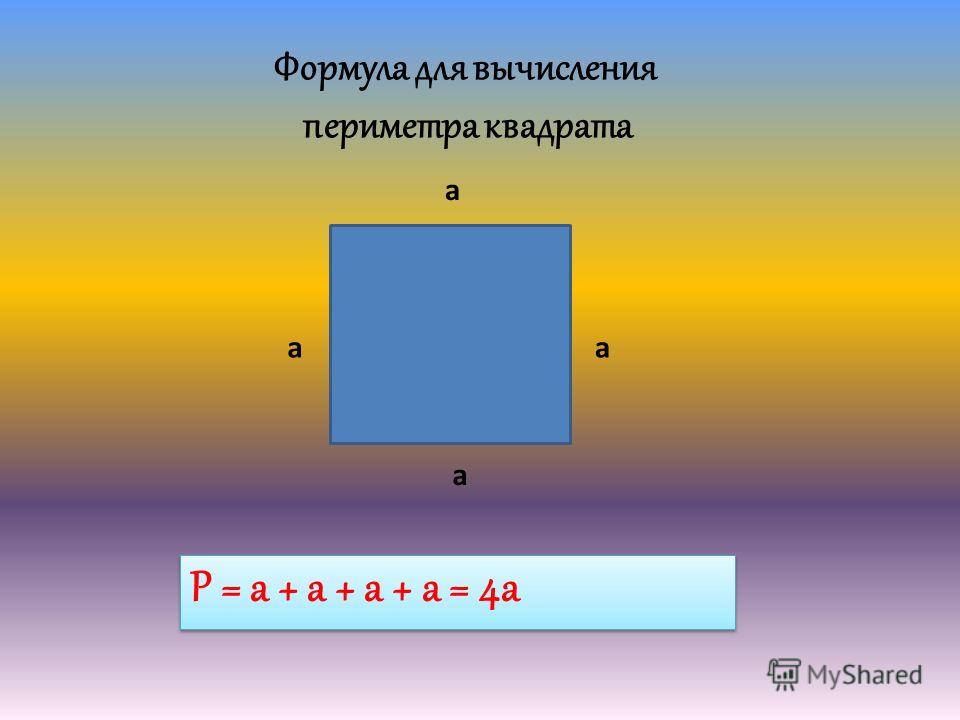
Периметр квадрата — это длина стороны квадрата, умноженная на 4.
P = a 4, где a — длина стороны квадрата.
Дополнение: Нахождение найти площади и периметра прямоугольников
В программе обучения за 3 класс предусмотрено изучение многоугольников и их особенностей. Для того чтобы понять, как найти периметр прямоугольника и площадь, разберемся, что подразумевается под этими понятиями.
Основные понятия
Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:
- Прямой угол. Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
- Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной. Как известно, противоположные стороны этой фигуры равны.
- Квадрат. Является четырехугольником, все стороны которого равны.
При знакомстве с многоугольниками их вершины могут называться АВСД.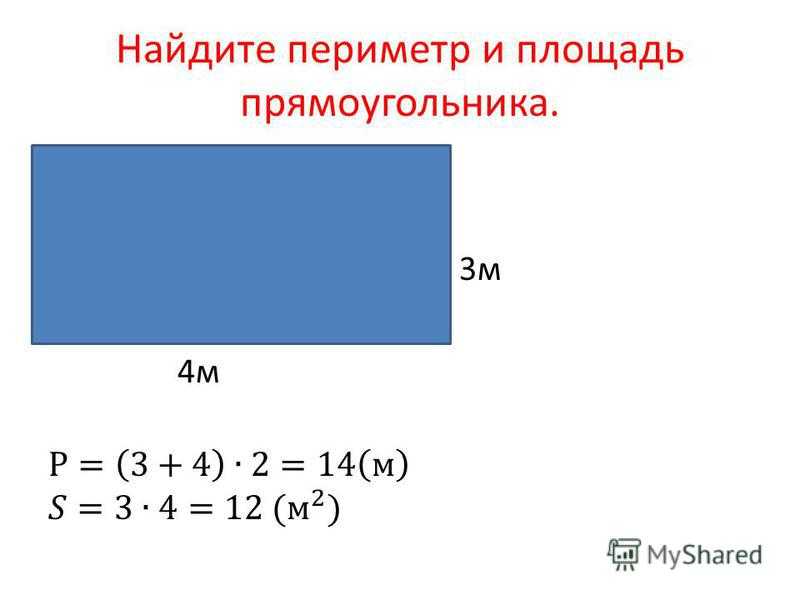 В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.
В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.
Вычисление периметра
Периметр многоугольника — это сумма длин всех его сторон. Эта величина обозначается латинской буквой P. Уровень знаний для предложенных примеров — 3 класс.
Задача №1: «Начертите прямоугольник 3 см шириной и 4 см длиной с вершинами ABCD. Найдите периметр прямоугольника ABCD».
Формула будет выглядеть так: P=AB+BC+CD+AD либо P=AB×2+BC×2.
Ответ: P=3+4+3+4=14 (см) либо P=3×2 + 4×2=14 (см).
Задача №2: «Как найти периметр прямоугольного треугольника ABC, если значения сторон равны 5, 4 и 3 см?».
Ответ: P=5+4+3=12 (см).
Задача №3: «Найдите периметр прямоугольника, одна сторона которого равна 7 см, а другая на 2 см длиннее».
Ответ: P=7+9+7+9=32 (см).
Задача №4: «Соревнования по плаванию проходили в бассейне, периметр которого составляет 120 м. Сколько метров проплыл участник соревнований, если ширина бассейна 10 м?».
В данной задаче стоит вопрос, как найти длину бассейна. Для решения найдите длины сторон прямоугольника. Ширина известна. Сумма длин двух неизвестных сторон должна составить 100 м. 120-10×2=100. Чтобы узнать расстояние, которое преодолел пловец, нужно разделить полученный результат на 2. 100:2=50.
Ответ: 50 (м).
Вычисление площади
Более сложной величиной является площадь фигуры. Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.
Площадь квадрата со стороной 1 см равна 1 см². Квадратный дециметр обозначен как дм², а квадратный метр — м².
Области применения единиц измерения могут быть такими:
- В см² измеряют маленькие предметы, например фотографии, обложки учебников, листы бумаги.
- В дм² можно измерить географическую карту, оконное стекло, картину.
- Для измерения пола, квартиры, земельного участка используют м².
Если начертить прямоугольник 3 см длиной и 1 см шириной и разбить на квадраты со стороной 1 см, то в нем поместится 3 квадрата, а значит, его площадь составит 3 см². Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.
Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.
Другой способ посчитать количество квадратов, вмещающихся в фигуру, — это использование палетки. Начертим на кальке квадрат площадью 1 дм², что составляет 100 см². Поместим кальку на фигуру и посчитаем число квадратных сантиметров в одном ряду. После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.
Способы сравнения площадей:
- На глаз. Иногда достаточно просто взглянуть на предметы, поскольку в некоторых случаях и невооруженным глазом видно, что одна фигура занимает больше места, как, например, учебник, лежащий на столе рядом с пеналом.
- Наложение. Если фигуры совпадают при наложении, их площади равны. Если же одна из них полностью помещается внутри второй, то ее площадь меньше. Места, занимаемые тетрадным листом и страницей из учебника, можно сравнить, наложив их друг на друга.

- По количеству мерок. Фигуры при наложении могут и не совпадать, однако иметь одинаковую площадь. Сравнить в этом случае можно, подсчитав количество квадратов, на которые разбита фигура.
- Числа. Сравниваются численные значения, измеренные одной и той же меркой, например, в м².
Пример №1: «Швея сшила детское одеяло из квадратных разноцветных лоскутков. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Чтобы решить задачу, нужно ответить на вопрос, как найти длину прямоугольника. Далее найдем периметр прямоугольника, составленного из квадратов. Из задачи ясно, что ширина одеяла — 5 дм, вычисляем длину, разделив 50 на 5, и получаем 10 дм. Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.
Ответ: 30 (м).
Пример №2: «На раскопках обнаружен участок, где могут находиться древние сокровища. Сколько территории придется исследовать ученым, если известен периметр 18 м и ширина прямоугольника 3 м?».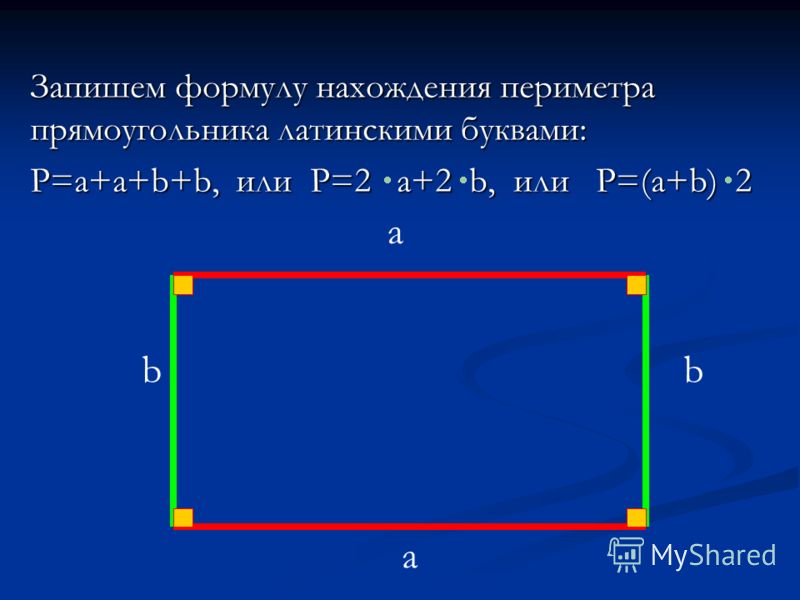
Определим длину участка, проделав 2 действия. 18-3×2=12. 12:2=6. Искомая территория будет также равна 18 м² (6×3=18).
Ответ: 18 (м²).
Таким образом, зная формулы, вычислить площадь и периметр не составит труда, а приведенные выше примеры помогут попрактиковаться в решении математических задач.
Периметр — один из математических, а точнее — геометрических терминов, применяется в основном для вычисления сторон фигуры.
Из нашей статьи вы узнаете, что такое периметр и как он измеряется на примере основных геометрических фигур.
Определение периметра
Периметром называют общую длину всех сторон или окружности той или иной фигуры. Обозначается периметр большой буквой «Р», а измерять его можно в различных единицах длины, таких как миллиметры (мм), сантиметры (см), метры (м) и т. д. Для различных фигур существуют различные формулы для нахождения периметра. Ниже мы приведем несколько примеров, как узнать периметр у прямоугольника и некоторых других фигур.
Измеряем периметр
Если вам необходимо узнать периметр у сложной фигуры (к таким фигурам можно отнести фигуры с неровными линиями), то для этого вам понадобится веревка или нитка. При помощи этих вещей необходимо описать точный контур фигуры, а чтобы не запутаться, вы можете на веревке сделать отметки карандашом. Или же можно просто ее обрезать, а после приложить все части к линейке. Таким образом, вы узнаете, чему равен периметр практически у любой сложной фигуры.
Существует еще одно приспособление для вычисления периметра у сложных фигур: его называют курвиметр (роликовый дальномер). С его помощью вам нужно установить ролик в любую точку фигуры и описать роликом контур фигуры. Полученное число и будет равно периметру. О нахождении периметра у других геометрических фигур вы сможете узнать из нашей статьи . Ну а мы расскажем ещё о нескольких способах изменения периметра для разных фигур.
Круг, квадрат, равносторонний треугольник
Давайте также рассмотрим, как узнать периметр круга. Это довольно-таки просто: достаточно лишь определить длину окружности, а сделать это можно, умножив радиус «r» на число π≈3,14 и затем на 2 (P=L=2∙π∙r).
Это довольно-таки просто: достаточно лишь определить длину окружности, а сделать это можно, умножив радиус «r» на число π≈3,14 и затем на 2 (P=L=2∙π∙r).
Класс: 2
Цель: ознакомить с приёмом нахождения периметра прямоугольника.
Задачи: формировать умение решать задачи, связанные с нахождением периметра фигур, вырабатывать умения чертить геометрические фигуры, закрепить умение вычислять, применяя с переместительное свойство сложения, развивать навык устного счёта, логическое мышление, воспитывать познавательную активность и умение работать в коллективе.
Оборудование: ИКТ (мультимедийный проектор, презентация к уроку), картинки с геометрическими фигурами для физминутки, модель магического квадрата, у учеников – модели геометрических фигур, маркерные доски, линейки, учебники, тетради.
ХОД УРОКА
1. Организационный момент
Проверка готовности к уроку. Приветствие.
Начинается урок,
И внимательно считать.
Он пойдёт ребятам впрок.
Постарайтесь всё понять –
2. Устный счёт
а) Использование магических фигур. (Приложение 1 )
– Заполним клетки магического квадрата, назовите его особенности (сумма чисел по горизонталям, вертикалям и диагоналям равны) и определите волшебное число. (39)
По цепочке дети заполняют квадрат на доске и в тетрадях .
б) Знакомство со свойствами магических треугольников. (Приложение 2 )
– Суммы чисел в углах, образующие треугольник равны. Найдём волшебные числа у треугольника. Определи пропущенное число. Отметь его на маркерной доске.
3. Подготовка к изучению нового материала
– Перед Вами геометрические фигуры. Назовите
их одним словом. (Четырёхугольники).
– Разделите их на 2 группы. (Приложение
3 )
– Что такое прямоугольники. (Прямоугольники –
четырехугольники, у которых все углы прямые.)
– Что можно узнать, зная длины сторон
четырёхугольников? Периметр – сумма длин сторон
фигур.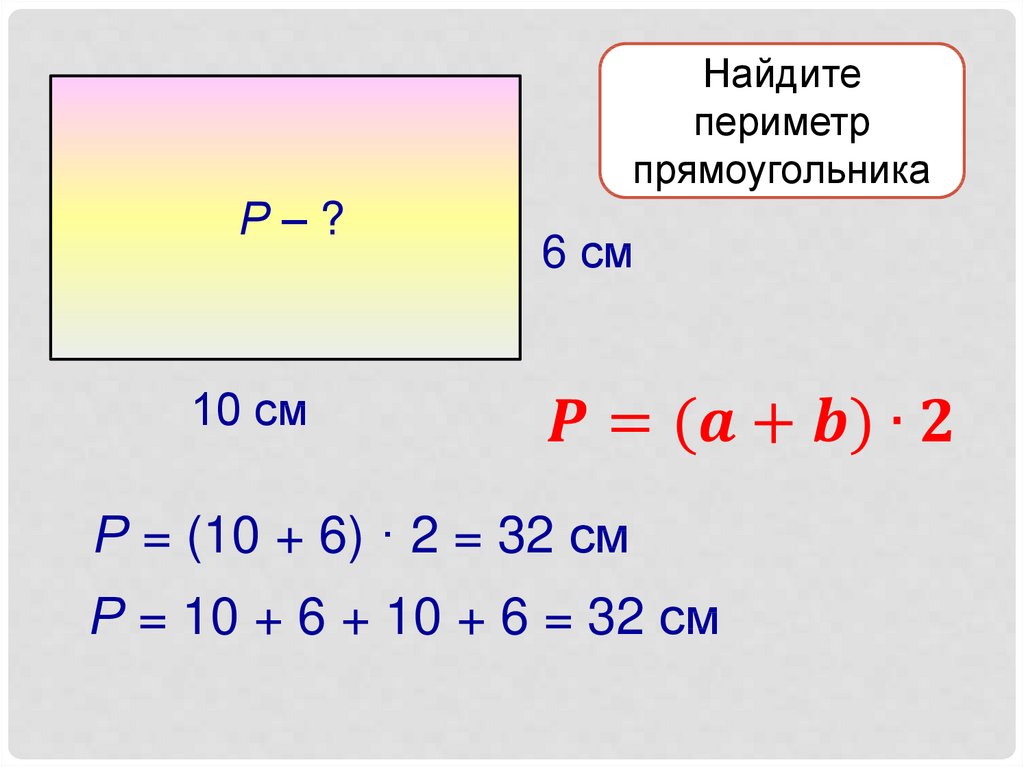
– Найдите периметр белой фигуры, жёлтой.
– Почему у прямоугольников известны не все стороны?
– Какие свойства у противолежащих сторон прямоугольников? (У прямоугольника противоположные стороны равны).
– Если противоположные стороны равны, надо ли измерять все стороны? (Нет.)
– Правильно, достаточно измерить длину и ширину.
– Как вычислить удобным способом? (Учащиеся работают устно с комментированием.)
4. Изучение новой темы
– Прочитайте тему нашего урока: «Периметр
прямоугольника». (Приложение 4 )
– Помогите найти периметр данной фигуры, если её
длина равна – а , а ширина – в .
Желающие находят Р у доски. Учащиеся в тетрадях записывают решение.
– Как записать это по-другому?
Р = а + а + в + в ,
Р = а х 2 + в х 2,
Р = (а + в ) х 2.
– Мы получили формулу нахождения периметра
прямоугольника. (Приложение 5 )
(Приложение 5 )
5. Закрепление
Стр. 44 № 2.
Дети читают и записывают условие, вопрос, чертят фигуру, находят Р разными способами, записывают ответ.
6. Физминутка. Сигнальные карточки
Сколько клеточек зелёных,
Столько выполним наклонов.
Столько раз руками хлопнем.
Столько раз ногами топнем.
Сколько здесь у нас кружков,
Столько сделаем прыжков.
Мы присядем столько раз,
Столь подтянемся сейчас.
7. Практическая работа
– У Вас на партах лежат в конвертах
геометрические фигуры. Как мы их назовём?
– Что вы знаете о противолежащих сторонах прямоугольников?
– Измерьте стороны фигур по вариантам, найдите периметр разными способами.
– Проверяем у соседа.
Взаимопроверка тетрадей .
– Прочитайте: Как нашли периметр? Что можно
сказать о периметрах данных фигур? (Они равны) .
– Начертите прямоугольник с таким же Р, но
другими сторонами.
Р 1 = (2 + 6) х 2 = 16 Р 1 = 2 х 2 + 6 х 2 = 16
Р 1 = 2 + 2 + 6 + 6 = 16
Р 2 = 3 + 3 + 5 + 5 = 16 Р 2 = (3 + 5) х 2 = 16
Р 3 = 4 + 4 + 4 + 4 = 16 Р 4 = 1 + 1 + 7 + 7 = 16
8. Графический диктант
Слева 6 клеток. Поставили точку. Начинаем движение. 2 – вправо, 4 – вправо вниз, 10 – влево, 4 – вправо вверх. Какая фигура? Преврати её в прямоугольник. Дострой. Найди Р разными способами.
Р = (5 + 2) х 2 = 14.
Р = 5 + 5 + 2 + 2 = 14.
Р = 5 х 2 + 2 х 2 = 14.
9. Пальчиковая гимнастика
Умножали, умножали.
Очень, очень мы устали.
Наши пальчики сплетём и соединим ладошки.
А потом, как только можем, крепко накрепко сожмём.
На дверях висит замок.
Кто его открыть не смог?
Мы замочком постучали,
Мы замочек повертели,
Мы замочек покрутили и открыли.
(Слова сопровождаются движениями)
10. Составление и решение задачи по условию (Приложение 8 )
Длина прямоугольника – 12 дм
Ширина – на 3 дм м.
Р – ?
В первом действии найдём ширину: 12 – 3 = 9 (дм) –
ширина
Зная длину и ширину, узнаем Р одним из способов.
Р = (12 + 9) х 2 = 42 дм
11. Самостоятельная работа
12. Итог урока
– Чему учились. Как находили Р прямоугольника?
13.Оценивание
Оцениваются ответы учащихся у доски и выборочно в процессе самостоятельной работы.
14.Домашнее задание
С. 44 № 5 (с пояснениями).
Периметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.

- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Существует 2 способа его нахождения:
- 1 способ. Складываем все стороны. P = a + а + b + b
- 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .

- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
Геометрия, если не ошибаюсь, в мое время изучалась с пятого класса и периметр был и есть одним из ключевых понятий. Итак, периметр — это сумма длин всех сторон (обозначается латинской литерой P) . Вообще, трактуют данный термин по разному, например,
Итак, периметр — это сумма длин всех сторон (обозначается латинской литерой P) . Вообще, трактуют данный термин по разному, например,
- общая длина границы фигуры,
- длина всех ее сторон,
- сумма длин ее граней,
- длина ограничивающей фигуру линии,
- сумма всех длин сторон многоугольника
Для различных фигур существуют свои формулы определения периметра. Чтобы понять сам смысл, предлагаю самостоятельно вывести несколько несложных формул:
- для квадрата,
- для прямоугольника,
- для параллелограмма,
- для куба,
- для параллелепипеда
Периметр квадрата
Для примера возьмем самое простое — периметр квадрата.
Все стороны квадрата равны. Пусть одна сторона носит название «a» (также, как и остальные три), тогда
P = a + a + a + a
или более компактная запись
Периметр прямоугольника
Усложним задачу и возьмем прямоугольник. В данном случае уже нельзя сказать, что все стороны равны, поэтому пусть длины сторон прямоугольника будут равны a и b.
Тогда формула будет иметь следующий вид:
P = a + b + a + b
Периметр параллелограмма
Аналогичная ситуация будет и с параллелограммом (см. периметр прямоугольника)
Периметр куба
Что же делать, если мы имеем дело с объемной фигурой? Например, возьмем куб. Куб имеет 12 сторон и все они равны. Соответственно, периметр куба можно вычислить следующим образом:
Периметр параллелепипеда
Ну, и для закрепления материала вычислим периметр параллелепипеда. Тут необходимо немного поразмышлять. Давайте делать это вместе. Как мы знаем, прямоугольный параллелепипед представляет собой фигуру, сторонами которой являются прямоугольники. У каждого параллелепипеда есть два основания. Возьмем одно из оснований и посмотрим на его стороны — они имеют длину a и b. Соответственно, периметр основания есть P = 2a + 2b. Тогда периметр двух оснований есть
(2a + 2b) * 2 = 4a + 4b
Но ведь у нас есть еще и сторона «c». Значит формула для вычисления периметра параллелепипеда будет иметь следующий вид:
P = 4a + 4b + 4c
Как видно из примеров выше, всё, что необходимо сделать для определения периметра фигуры — найти длину каждой из сторон, а затем их сложить.
В заключение хочется отметить, что не всякая фигура имеет периметр. К примеру, у шара периметра нет.
Как найти площадь и периметр формулы. Калькулятор вычисления периметра и площади геометрических фигур
Определение.
Прямоугольник — это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника , а короткую — шириной прямоугольника .
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d 2 = 2a 2 + 2b 2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
| AO = BO = CO = DO = | d | ||
| 2 |
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d 2 — b 2
b = √d 2 — a 2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
| b = d cos | β |
| 2 |
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a 2 + b 2
2. Формула диагонали прямоугольника через площадь и любую сторону:
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = D о
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S: sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
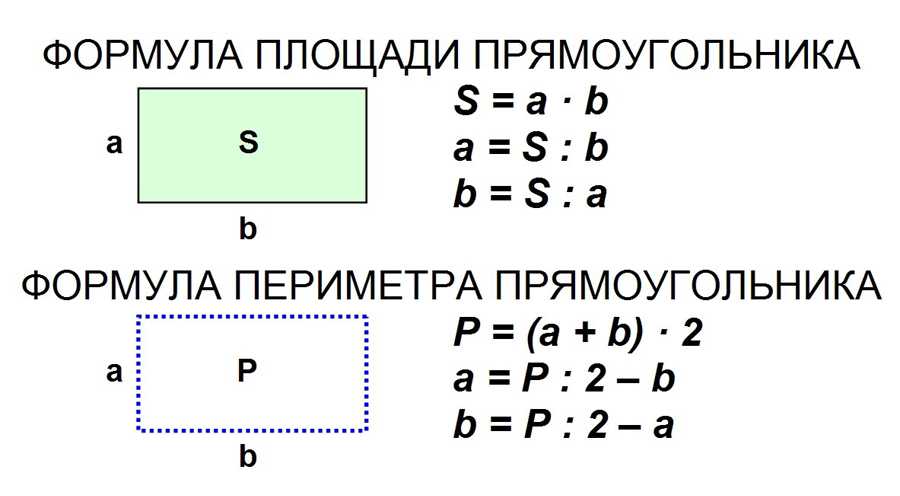
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b )
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a 2 | = | 2S + 2b 2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d 2 — a 2 ) = 2(b + √d 2 — b 2 )
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R 2 — a 2 ) = 2(b + √4R 2 — b 2 )
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √D o 2 — a 2 ) = 2(b + √D o 2 — b 2 )
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.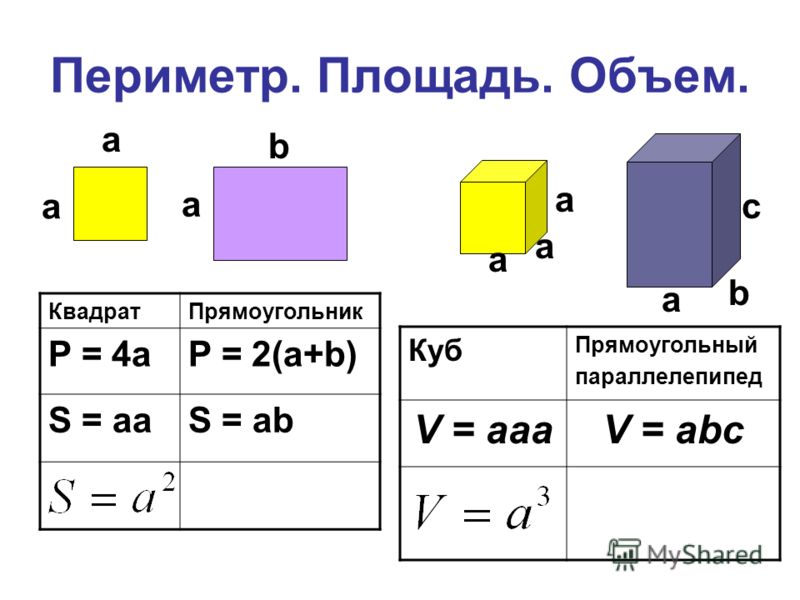
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a √4R 2 — a 2 = b √4R 2 — b 2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a √D o 2 — a 2 = b √D o 2 — b 2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
Пери́метр (др. -греч. περίμετρον — окружность, др. -греч. περιμετρέο — измеряю вокруг) — общая длина границы фигуры (чаще всего на плоскости). Имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.
Имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.
Пло́щадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры , неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.
Периметр фигуры обладает только одним параметром — протяжённостью, или длиной, выраженной в единицах длины: метр, ярд, аршин, локоть. Или производных от них: километр, сантиметр, дециметр.
Площадь фигуры обладает двумя параметрами — например, длиной и шириной, или радиусом и коэффициентом Пи, в зависимости от формы. Величина площади выражается в единицах в квадрате: квадратных метрах, гектарах, квадратных милях
Периметр и его определение
Периметром принято называть протяжённость границы плоской фигуры, состоящей из прямых отрезков, где начало каждого последующего примыкает к окончанию предыдущего.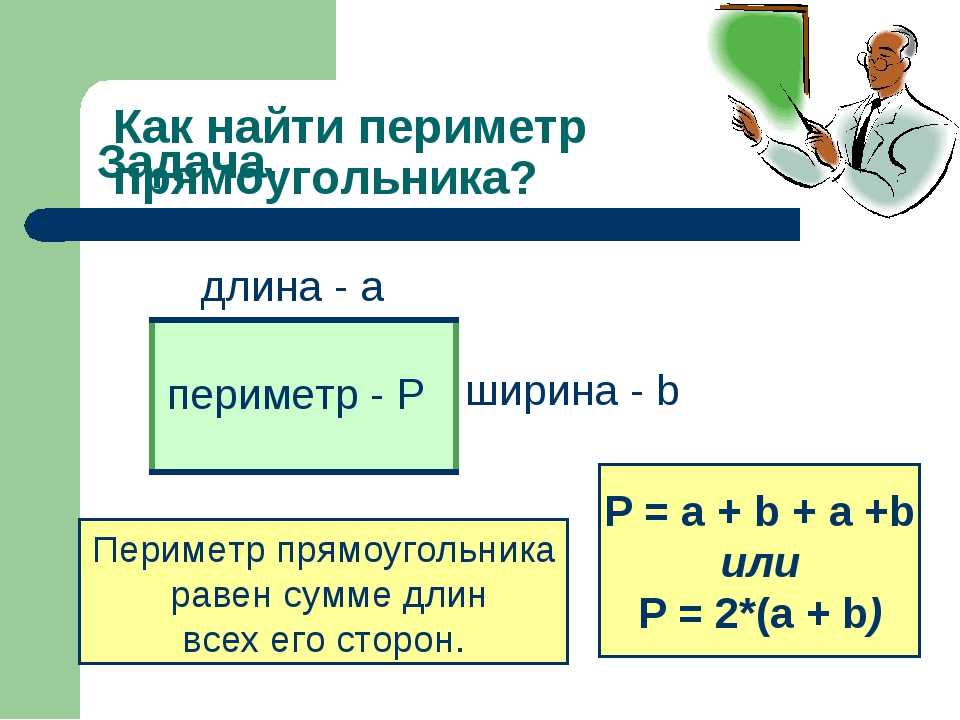
Строго говоря, окружность тоже обладает периметром, но для криволинейных границ принято говорить о длине окружности, или длине дуги
Для определения длины периметра, необходимо измерить, или вычислить, длину каждой стороны фигуры, а затем суммировать полученные числа.
Площадь фигуры и её определение
Площадь простейших геометрических фигур определяется по формулам.
Площадь прямоугольника равна произведению длин сторон.
Площадь круга равна произведению квадрата радиуса на число Пи=3,1415
Свои формулы есть для треугольника, сектора, трапеции, параллелограмма.
Площадь сложных криволинейных фигур вычисляется интегралом. Взятие интеграла формулы, описывающей границу фигуры, даст в результате площадь. В этом и есть геометрический смысл интеграла — он вычисляет площадь, ограниченную графиком функции на заданном участке.
Сложная фигура, lkz которой нет общей формулы, для определения площади мысленно разбивается на простейшие фигуры. Площади простых фигур вычисляются и затем суммируются.
Периметр и площадь геометрической фигуры связаны и один параметр всегда может быть вычислен из другого с минимальными дополнительными данными.
Периметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.
- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Существует 2 способа его нахождения:
- 1 способ. Складываем все стороны. P = a + а + b + b
- 2 способ.
 Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.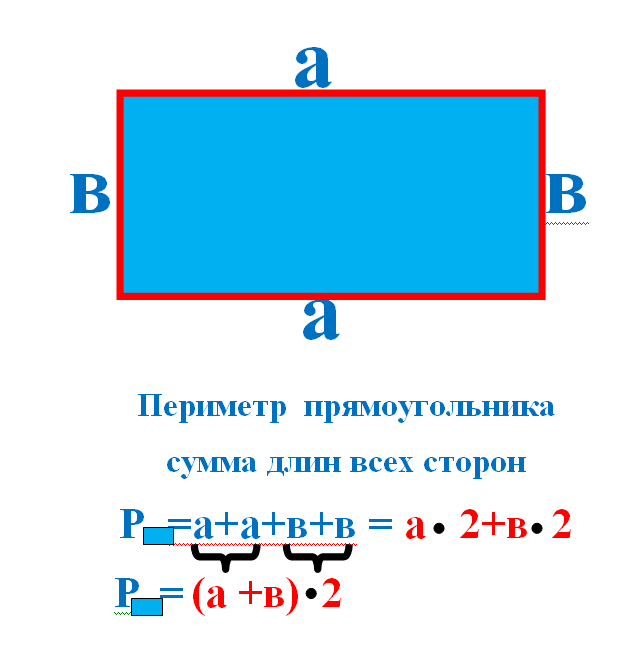
- : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
При решении, необходимо принять во внимание, что решить задачу о нахождении площади прямоугольника только из длины его сторон нельзя .
В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. (1 + 9) * 2 = 20 точно также как и (2 + 8) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов размеров сторон прямоугольника, периметр которого будет равен заданному значению.
Площадь прямоугольников с заданным периметром 20 см, но с различными сторонами будет различна. Для приведенного примера — 9, 16 и 21 квадратных сантиметров соответственно.
S 1 = 1 * 9 = 9 см 2
S 2 = 2 * 8 = 16 см 2
S 3 = 3 * 7 = 21 см 2
Как видим, вариантов площади фигуры при заданном периметре — бесконечное количество.
Замечание для любознательных . В случае с прямоугольником, у которого задан периметр, максимальную площадь будет иметь квадрат.
Таким образом, для того, чтобы вычислить площадь прямоугольника из его периметра, нужно обязательно знать либо соотношение его сторон, либо длину одной из них. Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.
В этом уроке:
- Задача 4. Изменение длины сторон при сохранении площади прямоугольника
Задача 1. Найти стороны прямоугольника из площади
Периметр прямоугольника равен 32 сантиметрам, а сумма площадей квадратов, построенных на каждой из его сторон — 260 квадратных сантиметров. Найдите стороны прямоугольника.
Найдите стороны прямоугольника.
Решение.
2(x+y)=32
Согласно условию задачи, сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
2x 2 +2y 2 =260
x+y=16
x=16-y
2(16-y) 2 +2y 2 =260
2(256-32y+y 2)+2y 2 =260
512-64y+4y 2 -260=0
4y 2 -64y+252=0
D=4096-16×252=64
x 1 =9
x 2 =7
Теперь примем во внимание, что исходя из того, что x+y=16 (см. выше) при x=9, то y=7 и наоборот, если x=7, то y=9
Ответ : Стороны прямоугольника равны 7 и 9 сантиметров
Задача 2. Найти стороны прямоугольника из периметра
Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x 2 +y 2 =89
Решаем полученную систему уравнений.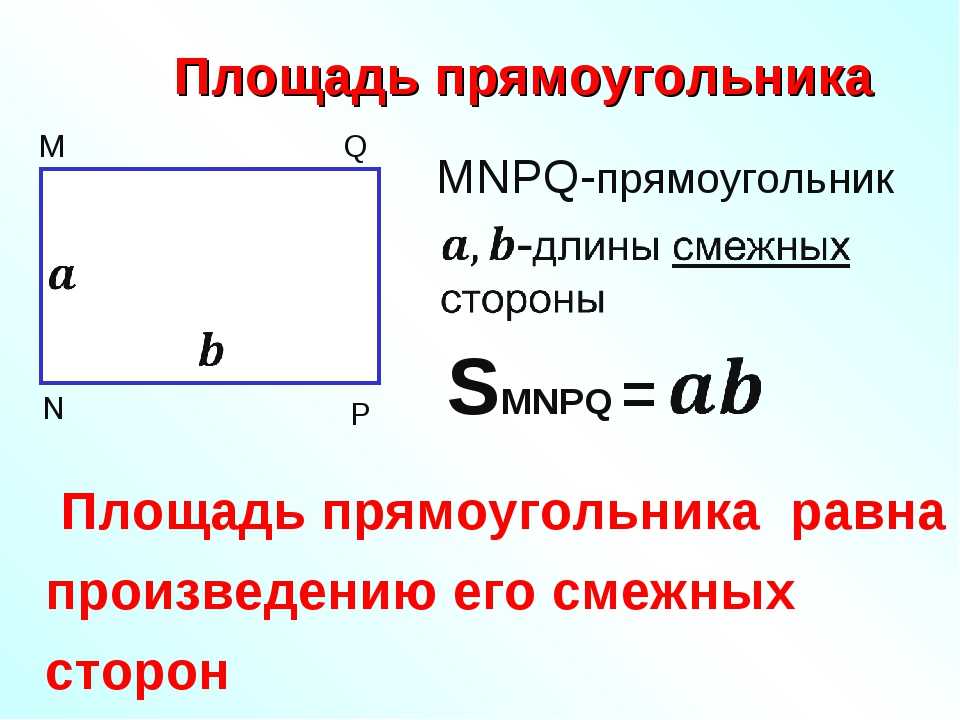 Из первого уравнения выводим, что
Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
(13-y) 2 +y 2 =89
169-26y+y 2 +y 2 -89=0
2y 2 -26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x 1 =5
x 2 =8
Теперь примем во внимание, что исходя из того, что x+y=13 (см. выше) при x=5, то y=8 и наоборот, если x=8, то y=5
Ответ: 5 и 8 см
Задача 3. Найти площадь прямоугольника из пропорции его сторон
Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.
Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x.
Откуда длина одной стороны будет равна 2x, другой — 3х.
Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см 2
Длина прямоугольника увеличена на 25%.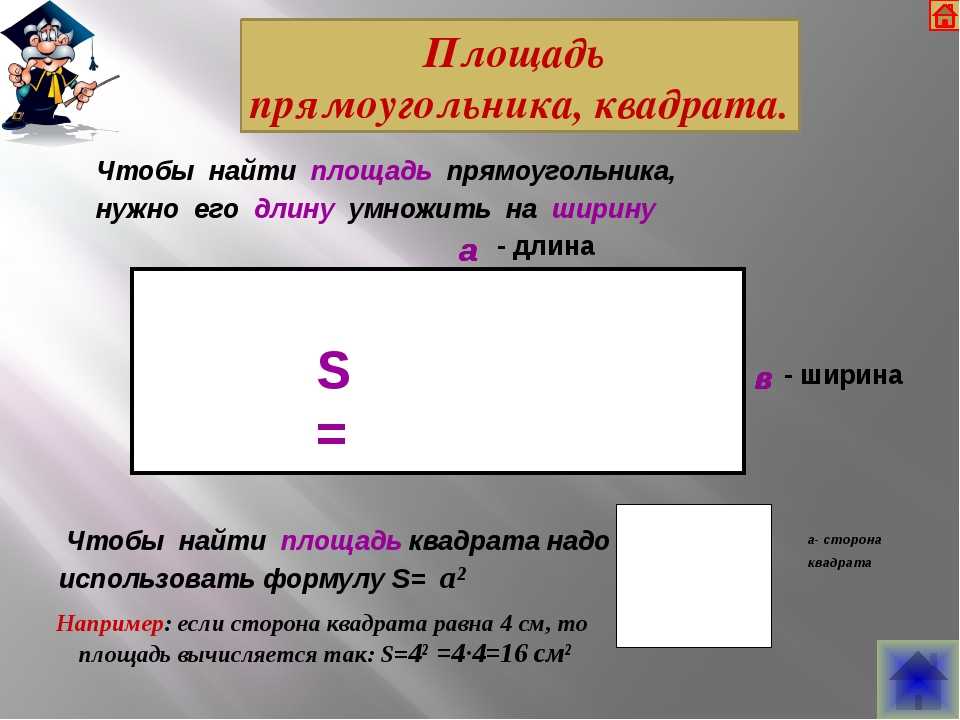 На сколько процентов надо уменьшить ширину, чтобы его площадь не изменилась?
На сколько процентов надо уменьшить ширину, чтобы его площадь не изменилась?
Решение .
Площадь прямоугольника равна
S = ab
В нашем случае один из множителей увеличился на 25%, что означает a 2 = 1,25a . Таким образом, новая площадь прямоугольника должна быть равна
S 2 = 1,25ab
Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S 2 = S / 1.25
S 2 = 1,25ab / 1.25
Поскольку новый размер а изменять нельзя, то
S 2 = (1,25a) b / 1.25
1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на (1 — 0,8) * 100% = 20%
Ответ : ширину нужно уменьшить на 20%.
Прежде, чем решать задачи на нахождение периметра и площади геометрических фигур, напомню, что….
I уровень
1.Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь.
2.Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
3.У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Узнайте площадь и периметр прямоугольника.
4.Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.
5.Длина прямоугольника 8 дм, ширина 5 дм. Найди его площадь.
6.Вычисли площадь прямоугольника, длины сторон которого равны 6 мм и 8 мм.
7.Ширина прямоугольника 7 дм, а длина 12 дм. Вычисли площадь.
8.Длина прямоугольника 9 дм, ширина 7 см. Найди его площадь.
9.Длина стороны квадрата 6 см. Узнай площадь.
10.Вычисли периметр квадрата со стороной 4 см.
11.Ширина прямоугольника равна 9 дм, а длина на 6 дм больше. Найдите его площадь.
12.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
13.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 3 раза больше. Найди его периметр и площадь.
14.Начерти прямоугольник, длина одной стороны которого 6 см, а длина другой в 2 раза больше. Найди его периметр и площадь.
15.Начерти прямоугольник, ширина которого равна 2 см, а длина на 3 см больше.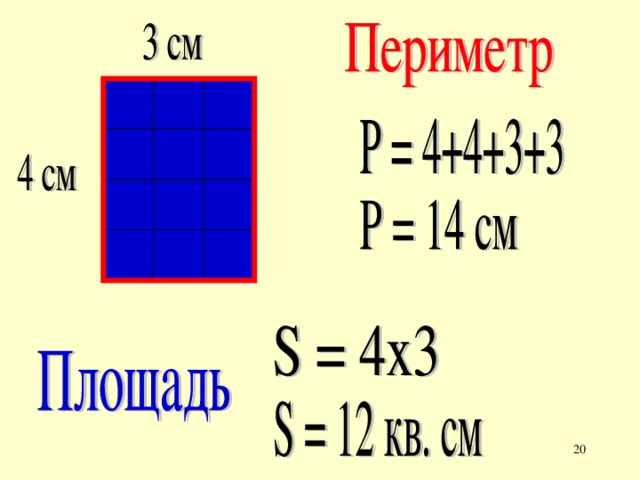 Вычисли его периметр.
Вычисли его периметр.
16.Сторона квадрата равна 3 см. Чему равен периметр?
17.Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?
18.Начерти квадрат со стороной 6 см. Найдите его периметр. Периметр квадрата равен 28 см. Чему равна его сторона?
19.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
20.Ширина прямоугольника 4 дм, а длина в 5 раз больше ширины. Найди площадь прямоугольника.
21.Площадь прямоугольника 36 см², его длина 9 см. Чему равна ширина прямоугольника?
II уровень
1.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 4 раза больше. Найди его периметр и площадь.
2.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
3.Дано: прямоугольник, а = 8 дм, в — на 2 см меньше. Найди Р и S.
4.Длина прямоугольника 12 см, а его ширина на 2 см меньше. Найдите площадь и периметр прямоугольника.
5.Сумма двух сторон квадрата 12 дм. Найдите периметр и площадь квадрата.
6.Найдите длину прямоугольника по его ширине – 8 дм и периметру–30 дм.
7.Периметр квадрата равен 32 см. Чему равна его сторона?
8.Периметр треугольника 21 см. Надите длину третьей стороны этого треугольника, если длины двух сторон 7 см и 8 см.
9.Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.
10.Площадь прямоугольника равна 270 кв.см, его длина 9 дм. Найдите периметр этого прямоугольника.
11.Периметр прямоугольника равен 54 м . Найдите площадь этого прямоугольника, если одна его сторона равна 18 м.
12. Найдите площадь квадрата, периметр которого равен 360 мм.
13. Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?
14. Начерти квадрат, периметр которого равен периметру прямоугольника со сторонами 2 см и 6 см.
15. Дачный участок прямоугольной формы имеет длину 20 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?
Какой длины забор надо поставить вокруг участка?
16. Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?
17. У какой фигуры площадь больше и на сколько: у квадрата со стороной 4см или у прямоугольника со сторонами 2 см и 6 см?
18. Периметр прямоугольника равен 54 м. Найди площадь этого прямоугольника, если одна его сторона равна 18 м.
19. Периметр квадратной песочницы 12 м. Найдите площадь этой песочницы.
20. Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.
Составила К ислова Людмила Борисовна
Три формулы нахождения периметра прямоугольника. Периметр квадрата и прямоугольника
Достаточно узнать длину всех ее сторон и найти их сумму. Периметром называется совокупная длина границ плоской фигуры. Иными словами, это сумма длин ее сторон. Единица измерения периметра должна соответствовать единице измерения его сторон. Формула периметра многоугольника имеет вид Р = a + b + c…+ n, где Р — периметр, а вот а, b, с и n — длина каждой из сторон.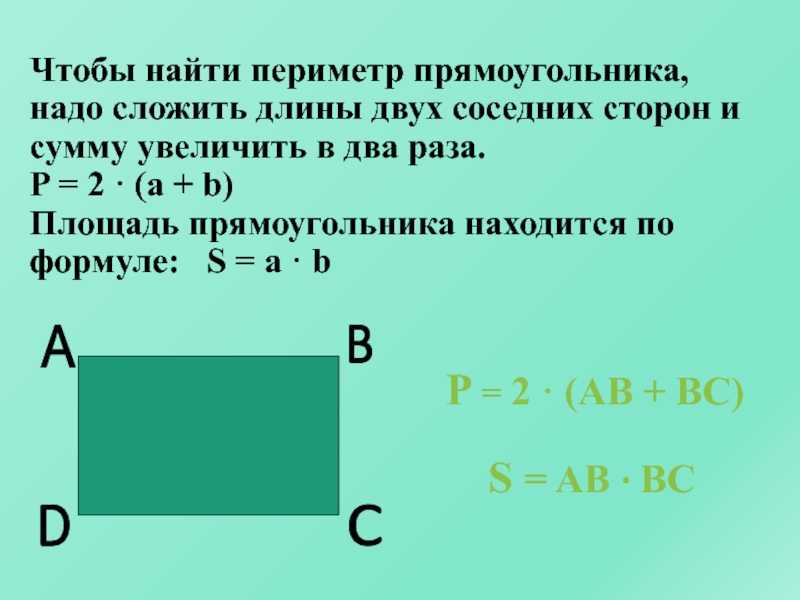 Иначе вычисляется (или периметр круга): используется формула р = 2 * π * r, где r — радиус, а π — постоянное число, приблизительно равное 3,14. Рассмотрим несколько простых примеров, наглядно демонстрирующих, как найти периметр. В качестве образца возьмем такие фигуры как квадрат, параллелограмм и окружность.
Иначе вычисляется (или периметр круга): используется формула р = 2 * π * r, где r — радиус, а π — постоянное число, приблизительно равное 3,14. Рассмотрим несколько простых примеров, наглядно демонстрирующих, как найти периметр. В качестве образца возьмем такие фигуры как квадрат, параллелограмм и окружность.
Как найти периметр квадрата
Квадратом называется правильный четырехугольник, у которого равны все стороны и углы. Так как все стороны квадрата равны, сумму длин его сторон можно вычислить по формуле Р = 4 * a, где а — длина одной из сторон. Таким образом, со стороной 16,5 см равен Р = 4 * 16,5 = 66 см. Так же можно вычислить периметр равностороннего ромба.
Как найти периметр прямоугольника
Прямоугольник — это четырехугольник, все углы которого равны 90 градусам. Известно, что в такой фигуре, как прямоугольник, длины сторон равны попарно. Если ширина и высота прямоугольника имеют одинаковую длину, то он называется квадратом. Обычно длиной прямоугольника называют наибольшую из сторон, а шириной — наименьшую. Таким образом, чтобы получить периметр прямоугольника, необходимо удвоить сумму его ширины и высоты: P = 2 * (а + b), где а — высота, а b — ширина. Имея в наличии прямоугольник, одна сторона которого является длиной и равна 15 см, а другая шириной с установленным значением в 5 см, мы получим периметр, равный Р = 2 * (15 + 5) = 40 см.
Таким образом, чтобы получить периметр прямоугольника, необходимо удвоить сумму его ширины и высоты: P = 2 * (а + b), где а — высота, а b — ширина. Имея в наличии прямоугольник, одна сторона которого является длиной и равна 15 см, а другая шириной с установленным значением в 5 см, мы получим периметр, равный Р = 2 * (15 + 5) = 40 см.
Как найти периметр треугольника
Треугольник образован тремя отрезками, которые соединяются в точках (вершинах треугольника), не лежащих на одной и той же прямой. Треугольник называется равносторонним, если равны все три его стороны, и равнобедренным, если равных сторон две. Чтобы узнать периметр необходимо длину его стороны умножить на 3: Р = 3 * a, где а — одна из его сторон. Если стороны треугольника не равны между собой, необходимо провести операцию сложения: Р = а + b + с. Периметр равнобедренного треугольника со сторонами 33, 33 и 44 соответственно будет равен: P = 33 + 33 + 44 = 110 см.
Как найти периметр параллелограмма
Параллелограмм — это четырехугольник с попарно параллельными противоположными сторонами.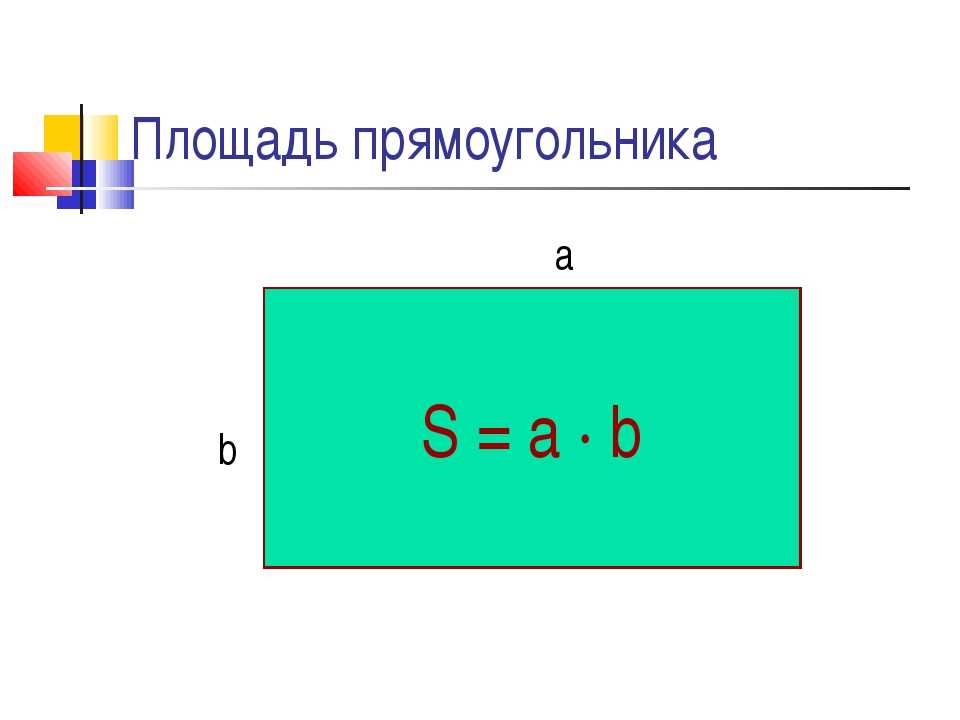 Квадрат, ромб и прямоугольник являются частными случаями фигуры. Противоположные стороны любого параллелограмма равны, поэтому для вычисления его периметра воспользуемся формулой P = 2 (а + b). В параллелограмме со сторонами 16 см и 17 см сумма сторон, или периметр, равна Р = 2 * (16 + 17) = 66 см.
Квадрат, ромб и прямоугольник являются частными случаями фигуры. Противоположные стороны любого параллелограмма равны, поэтому для вычисления его периметра воспользуемся формулой P = 2 (а + b). В параллелограмме со сторонами 16 см и 17 см сумма сторон, или периметр, равна Р = 2 * (16 + 17) = 66 см.
Как найти длину окружности
Окружность является замкнутой прямой, все точки которой расположены на равном удалении от центра. Длина окружности и ее диаметр всегда имеют одинаковое отношение. Это отношение выражено константой, записывается при помощи буквы π и равняется примерно 3,14159. Узнать периметр круга можно по произведению радиуса на 2 и на π. Получается, что длина окружности с радиусом в 15 см будет равна Р = 2 * 3,14159 * 15 = 94,2477
Периметр — один из математических, а точнее — геометрических терминов, применяется в основном для вычисления сторон фигуры.
Из нашей статьи вы узнаете, что такое периметр и как он измеряется на примере основных геометрических фигур.
Определение периметра
Периметром называют общую длину всех сторон или окружности той или иной фигуры. Обозначается периметр большой буквой «Р», а измерять его можно в различных единицах длины, таких как миллиметры (мм), сантиметры (см), метры (м) и т. д. Для различных фигур существуют различные формулы для нахождения периметра. Ниже мы приведем несколько примеров, как узнать периметр у прямоугольника и некоторых других фигур.
Измеряем периметр
Если вам необходимо узнать периметр у сложной фигуры (к таким фигурам можно отнести фигуры с неровными линиями), то для этого вам понадобится веревка или нитка. При помощи этих вещей необходимо описать точный контур фигуры, а чтобы не запутаться, вы можете на веревке сделать отметки карандашом. Или же можно просто ее обрезать, а после приложить все части к линейке. Таким образом, вы узнаете, чему равен периметр практически у любой сложной фигуры.
Существует еще одно приспособление для вычисления периметра у сложных фигур: его называют курвиметр (роликовый дальномер). С его помощью вам нужно установить ролик в любую точку фигуры и описать роликом контур фигуры. Полученное число и будет равно периметру. О нахождении периметра у других геометрических фигур вы сможете узнать из нашей статьи . Ну а мы расскажем ещё о нескольких способах изменения периметра для разных фигур.
С его помощью вам нужно установить ролик в любую точку фигуры и описать роликом контур фигуры. Полученное число и будет равно периметру. О нахождении периметра у других геометрических фигур вы сможете узнать из нашей статьи . Ну а мы расскажем ещё о нескольких способах изменения периметра для разных фигур.
Круг, квадрат, равносторонний треугольник
Давайте также рассмотрим, как узнать периметр круга. Это довольно-таки просто: достаточно лишь определить длину окружности, а сделать это можно, умножив радиус «r» на число π≈3,14 и затем на 2 (P=L=2∙π∙r).
Ниже в статье вы узнаете что такое и как найти периметр прямоугольника если известны его стороны. А также как найти стороны прямоугольника, если известен его периметр. И ещё одна интересная строительная прикладная задача.
Немного теории:
Периметр — это длина геометрической фигуры по её внешней границе.
Периметр прямоугольника — это сумма длин его сторон.
Формулы для вычисления периметра прямоугольника: P = 2*(a+b) или P = a + a + b + b.
Резюмируем! Для того чтобы вычислить периметр прямоугольника необходимо сложить все его стороны.
Типовые математические и практические задачи:
Задача №1:
Исходные данные: Определить периметр прямоугольника с длинами сторон 5 см и 10 см.
Решение:
Согласно формуле периметр прямоугольника равен = 2 * (5 + 10) = 30 см.
Ответ: 30 см.
Задача №2:
Исходные данные: Определить стороны прямоугольника выраженные целыми числами, если периметр прямоугольника равен 10.
Решение:
По формуле определяем сумму длин сторон (a + b) = P / 2 = 10 / 2 = 5
Целыми значениями сторон могут быть только значения 1 + 4 = 5 и 2 + 3 = 5
Ответ: Длины сторон могут быть только 2 и 3 или 1 и 4.
Задача №3 (практическая):
Исходные данные: Определить число плинтусов в достаточном количестве для ремонта пола в комнате длиной 5 метров и шириной 3 метра, если длина одного плинтуса равна 3 метра.
Решение:
Периметр комнаты = 2 * (5 + 3) = 16 метров
Количество плинтусов = 16 / 3 = 5,33 штук
Обычно в строительных магазинах плинтусы продаются не погонными метрами, а поштучно.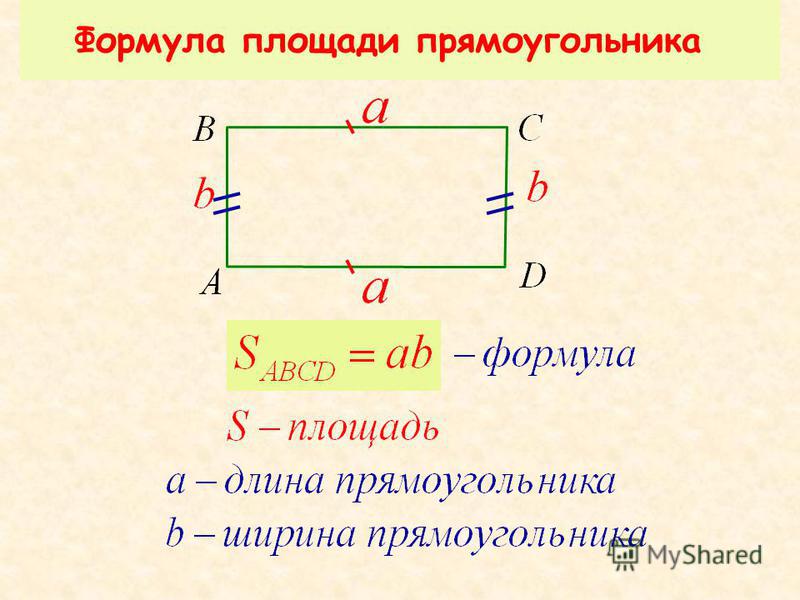 Поэтому принимаем следующее целое число. Это шесть.
Поэтому принимаем следующее целое число. Это шесть.
Ответ: Количество плинтусов 6 штук.
В заключение:
Решение задачи вычисления периметра является достаточно простой математической задачей, но имеющей очень важное практическое значение например в строительстве или генеральном планировании территории.
На этой странице представлен самый простой онлайн калькулятор для расчета периметра прямоугольника. С помощью этой программы вы в один клик сможете найти периметр прямоугольника, если известны его длина и ширина.
Класс: 2
Цель: ознакомить с приёмом нахождения периметра прямоугольника.
Задачи: формировать умение решать задачи, связанные с нахождением периметра фигур, вырабатывать умения чертить геометрические фигуры, закрепить умение вычислять, применяя с переместительное свойство сложения, развивать навык устного счёта, логическое мышление, воспитывать познавательную активность и умение работать в коллективе.
Оборудование: ИКТ (мультимедийный
проектор, презентация к уроку), картинки с
геометрическими фигурами для физминутки, модель
магического квадрата, у учеников – модели
геометрических фигур, маркерные доски, линейки,
учебники, тетради.
ХОД УРОКА
1. Организационный момент
Проверка готовности к уроку. Приветствие.
Начинается урок,
Он пойдёт ребятам впрок.
Постарайтесь всё понять –
И внимательно считать.
2. Устный счёт
а) Использование магических фигур. (Приложение 1 )
– Заполним клетки магического квадрата, назовите его особенности (сумма чисел по горизонталям, вертикалям и диагоналям равны) и определите волшебное число. (39)
По цепочке дети заполняют квадрат на доске и в тетрадях .
б) Знакомство со свойствами магических треугольников. (Приложение 2 )
– Суммы чисел в углах, образующие треугольник равны. Найдём волшебные числа у треугольника. Определи пропущенное число. Отметь его на маркерной доске.
3. Подготовка к изучению нового материала
– Перед Вами геометрические фигуры. Назовите
их одним словом. (Четырёхугольники).
– Разделите их на 2 группы. (Приложение
3 )
(Приложение
3 )
– Что такое прямоугольники. (Прямоугольники –
четырехугольники, у которых все углы прямые.)
– Что можно узнать, зная длины сторон
четырёхугольников? Периметр – сумма длин сторон
фигур.
– Найдите периметр белой фигуры, жёлтой.
– Почему у прямоугольников известны не все
стороны?
– Какие свойства у противолежащих сторон
прямоугольников? (У прямоугольника
противоположные стороны равны).
– Если противоположные стороны равны, надо ли
измерять все стороны? (Нет.)
– Правильно, достаточно измерить длину и ширину.
– Как вычислить удобным способом? (Учащиеся
работают устно с комментированием.)
4. Изучение новой темы
– Прочитайте тему нашего урока: «Периметр
прямоугольника». (Приложение 4 )
– Помогите найти периметр данной фигуры, если её
длина равна – а , а ширина – в .
Желающие находят Р у доски. Учащиеся в тетрадях записывают решение.
– Как записать это по-другому?
Р = а + а + в + в ,
Р = а х 2 + в х 2,
Р = (а + в ) х 2.
– Мы получили формулу нахождения периметра прямоугольника. (Приложение 5 )
5. Закрепление
Стр. 44 № 2.
Дети читают и записывают условие, вопрос, чертят фигуру, находят Р разными способами, записывают ответ.
6. Физминутка. Сигнальные карточки
Сколько клеточек зелёных,
Столько выполним наклонов.
Столько раз руками хлопнем.
Столько раз ногами топнем.
Сколько здесь у нас кружков,
Столько сделаем прыжков.
Мы присядем столько раз,
Столь подтянемся сейчас.
7. Практическая работа
– У Вас на партах лежат в конвертах
геометрические фигуры. Как мы их назовём?
– Что такое прямоугольники?
– Что вы знаете о противолежащих сторонах
прямоугольников?
– Измерьте стороны фигур по вариантам,
найдите периметр разными способами.
– Проверяем у соседа.
Взаимопроверка тетрадей .
– Прочитайте: Как нашли периметр? Что можно
сказать о периметрах данных фигур? (Они равны) .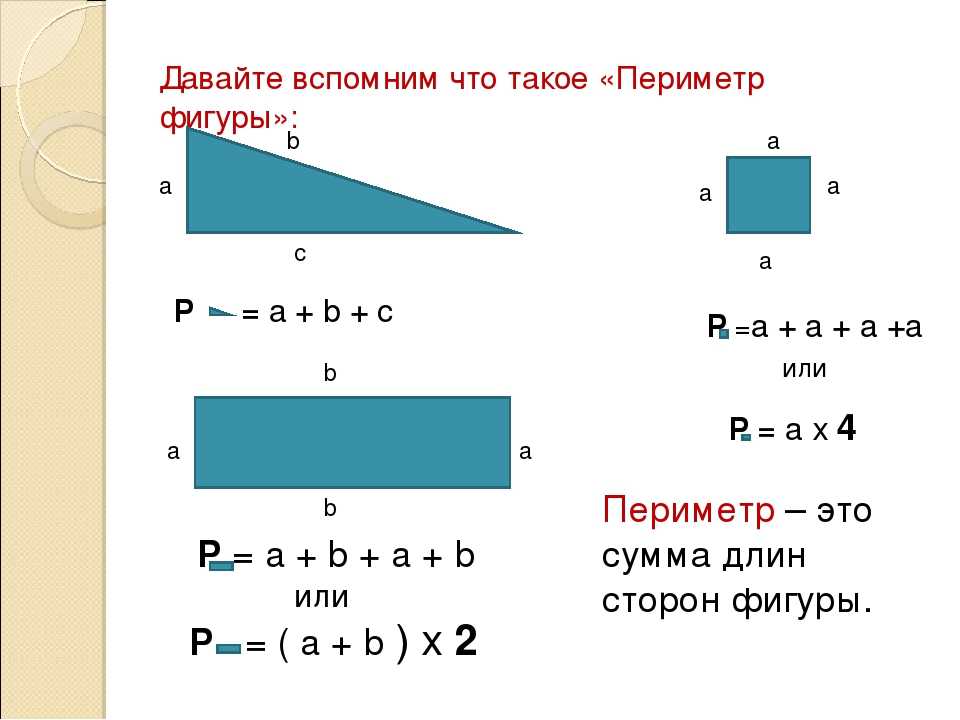
– Начертите прямоугольник с таким же Р, но
другими сторонами.
Р 1 = (2 + 6) х 2 = 16 Р 1 = 2 х 2 + 6 х 2 = 16
Р 1 = 2 + 2 + 6 + 6 = 16
Р 2 = 3 + 3 + 5 + 5 = 16 Р 2 = (3 + 5) х 2 = 16
Р 3 = 4 + 4 + 4 + 4 = 16 Р 4 = 1 + 1 + 7 + 7 = 16
8. Графический диктант
Слева 6 клеток. Поставили точку. Начинаем движение. 2 – вправо, 4 – вправо вниз, 10 – влево, 4 – вправо вверх. Какая фигура? Преврати её в прямоугольник. Дострой. Найди Р разными способами.
Р = (5 + 2) х 2 = 14.
Р = 5 + 5 + 2 + 2 = 14.
Р = 5 х 2 + 2 х 2 = 14.
9. Пальчиковая гимнастика
Умножали, умножали.
Очень, очень мы устали.
Наши пальчики сплетём и соединим ладошки.
А потом, как только можем, крепко накрепко сожмём.
На дверях висит замок.
Кто его открыть не смог?
Мы замочком постучали,
Мы замочек повертели,
Мы замочек покрутили и открыли.
(Слова сопровождаются движениями)
10. Составление и решение задачи по условию (Приложение 8 )
Составление и решение задачи по условию (Приложение 8 )
Длина прямоугольника – 12 дм
Ширина – на 3 дм м.
Р – ?
В первом действии найдём ширину: 12 – 3 = 9 (дм) –
ширина
Зная длину и ширину, узнаем Р одним из способов.
Р = (12 + 9) х 2 = 42 дм
11. Самостоятельная работа
12. Итог урока
– Чему учились. Как находили Р прямоугольника?
13.Оценивание
Оцениваются ответы учащихся у доски и выборочно в процессе самостоятельной работы.
14.Домашнее задание
С. 44 № 5 (с пояснениями).
На этом занятии мы познакомимся с новым понятием — периметр прямоугольника. Мы сформулируем определение этого понятия, выведем формулу для его вычисления. Также повторим сочетательный закон сложения и распределительный закон умножения.
На данном уроке мы познакомимся с периметром прямоугольника и его вычислением.
Рассмотрим следующую геометрическую фигуру (рис. 1):
Рис.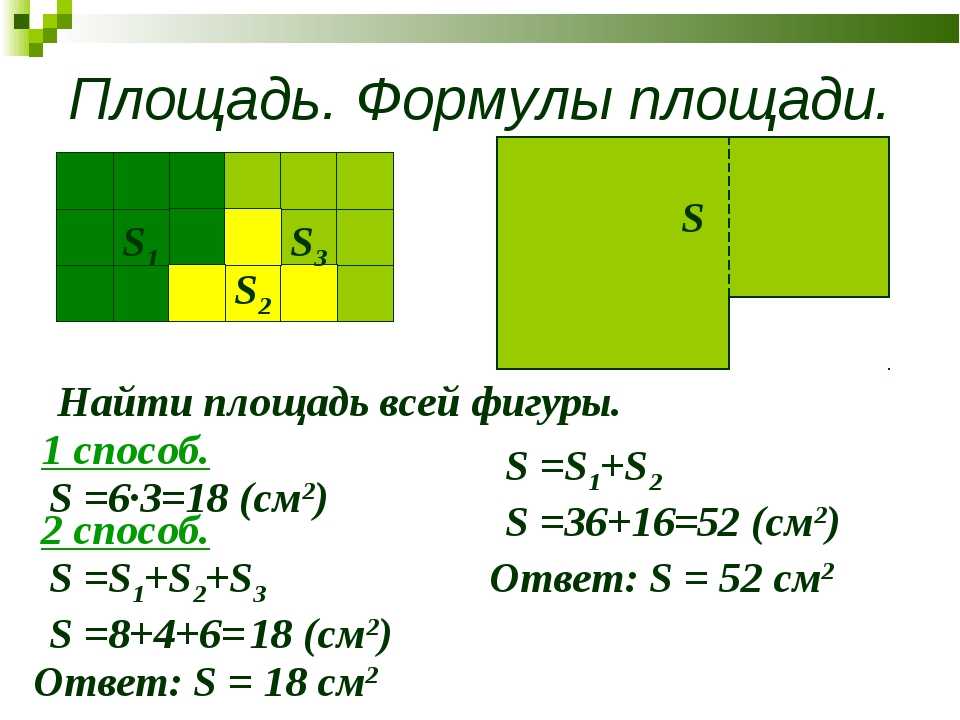 1. Прямоугольник
1. Прямоугольник
Данная фигура — прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник — это четырехугольник, у которого четыре прямых угла и стороны попарно равны.
Что в нашей жизни может иметь прямоугольную форму? Например, книга, крышка стола или земельный участок.
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка — 5 метров, длина — 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
Ответ: 30 метров.
Периметр прямоугольника — сумма длин всех его сторон. Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 7 см и 3 см: (7+3)·2=20 (см).
Периметр любой фигуры измеряется в линейных единицах.
На данном уроке мы познакомились с периметром прямоугольника и формулой его вычисления.
Произведение числа и суммы чисел равно сумме произведений данного числа и каждого из слагаемых.
Если периметр — это сумма длин всех сторон фигуры, то полупериметр — сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. — М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. — М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. — М.: Просвещение, 2012.
- Festival.1september.ru ().
- Nsportal.ru ().
- Math-prosto.ru ().
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина — 7 метров.
- Найти полупериметр прямоугольника, если его длина — 8 см, а ширина — 4 см.
- Найти периметр прямоугольника, если его полупериметр — 21 дм.
Периметр прямоугольника Формула
Мы сталкиваемся со многими фигурами, расстояние вокруг которых должно быть рассчитано, и это называется периметром фигур. Мы видим много форм вокруг, таких как квадрат, прямоугольник, круг, многоугольник и т.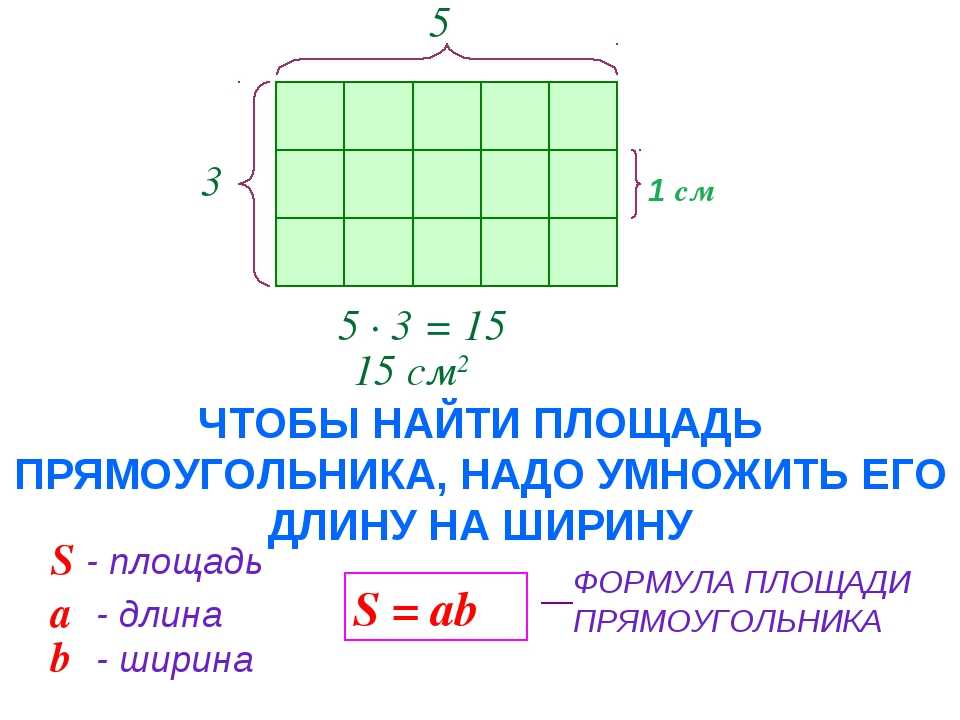 д. Каждая форма имеет свои уникальные свойства и размеры. Следовательно, каждая форма имеет различный периметр, основанный на их измерениях. Периметр – это длина границы, ограниченной любой геометрической фигурой. Периметр формы зависит от длины формы. Например, металлическая проволока длиной 10 см может образовывать как круг, так и квадрат.
д. Каждая форма имеет свои уникальные свойства и размеры. Следовательно, каждая форма имеет различный периметр, основанный на их измерениях. Периметр – это длина границы, ограниченной любой геометрической фигурой. Периметр формы зависит от длины формы. Например, металлическая проволока длиной 10 см может образовывать как круг, так и квадрат.
Предположим, вам нужно обнести свой дом забором. Длина забора равна периметру дома. Периметры двух фигур могут быть равны, только если их длина равна.
В этой статье мы изучим, что такое прямоугольник и пример формулы периметра прямоугольника.
Формула периметра прямоугольника = 2 x (длина + ширина) |
Прямоугольник – это четырехугольник, имеющий четыре стороны. Противоположные стороны прямоугольника параллельны и имеют одинаковую длину. Поскольку у прямоугольника четыре стороны, у него четыре угла.
Все углы прямоугольника равны. Это равноугольный прямоугольник с четырьмя прямыми углами, равными 90 градусам. Еще одно свойство прямоугольника состоит в том, что у него две диагонали одинаковой длины. Диагонали — это линии, проведенные внутри прямоугольника и соединяющие противоположные углы или вершины, поэтому диагонали прямоугольника равны.
Когда мы обходим замкнутую фигуру или тело, вдоль его границы, в кои-то веки мы преодолеваем расстояние. Мерой расстояния является периметр фигуры или тела. Чтобы понять и измерить периметр прямоугольного поля, мы путешествуем по границе четырех сторон поля, начиная с точки и заканчивая той же точкой. При этом мы замечаем, что измеряем длину и ширину дважды.
Примерами прямоугольников являются цементные блоки, рамы для картин, плакаты, листы бумаги, лицевые стороны игровых кубиков, которые соединяются друг с другом, стороны коробок для обуви и коробок с хлопьями, а также множество других предметов повседневного обихода.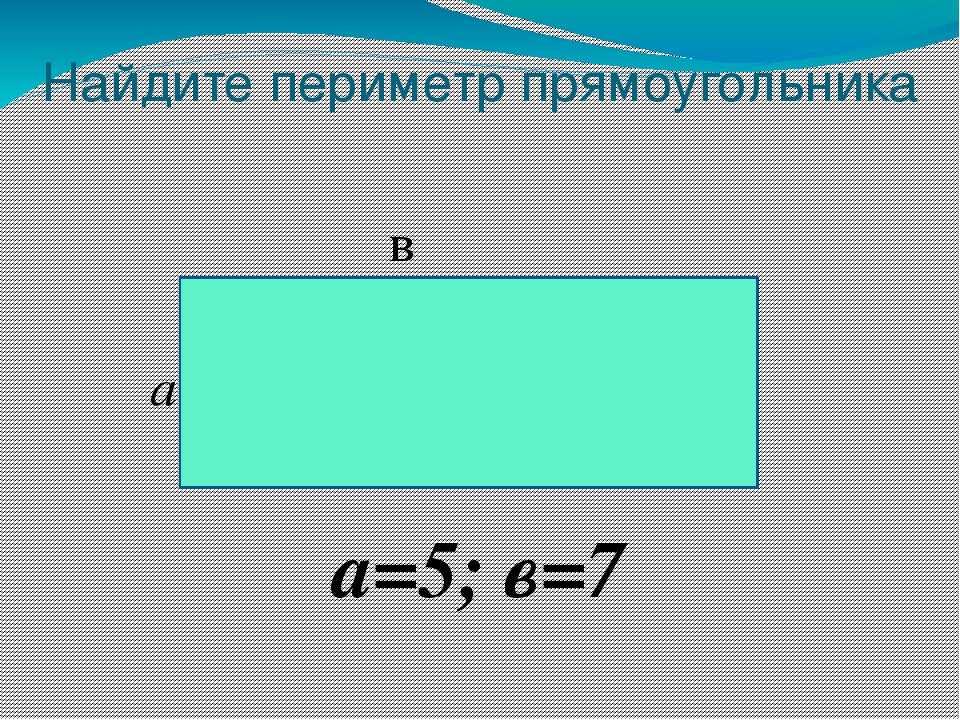
Свойства прямоугольника
Это плоская форма.
Имеет 4 стороны (ребра).
Имеет 4 угла (вершины).
Имеет 4 прямых угла.
Периметр прямоугольника
Четырехсторонний многоугольник, имеющий два измерения, то есть длину и ширину, называется прямоугольником. Общее расстояние, пройденное границами или сторонами в случае прямоугольника, известно как периметр прямоугольника. Чтобы вычислить периметр прямоугольника, мы должны сложить все четыре стороны прямоугольника. В прямоугольнике общее количество сторон равно 4, поэтому его периметр определяется как сумма его четырех сторон. Единица измерения прямоугольника представлена в метрах, сантиметрах, миллиметрах, дюймах, футах, квадратных футах и так далее.
Периметр прямоугольника. Формула
Периметр прямоугольника — это мера суммы всех его сторон, которые в случае прямоугольника составляют четыре стороны. Периметр любого многоугольника определяется как общее расстояние, покрываемое его сторонами. Поскольку противоположные стороны прямоугольника имеют равные длины и ширины, периметр прямоугольника равен удвоенной длине прямоугольника плюс удвоенная ширина прямоугольника.
(Изображение скоро будет загружено)
Формула периметра прямоугольника = сумма всех четырех сторон
= длина + ширина + длина + ширина
= 2 длина + 2 ширина
Формула периметра прямоугольника = 2 × (длина + ширина)
Формула периметра прямоугольника = 2 × (длина + ширина) = 2( l + b ) |
Предположим, что длина и ширина прямоугольника ABCD равны a и b соответственно.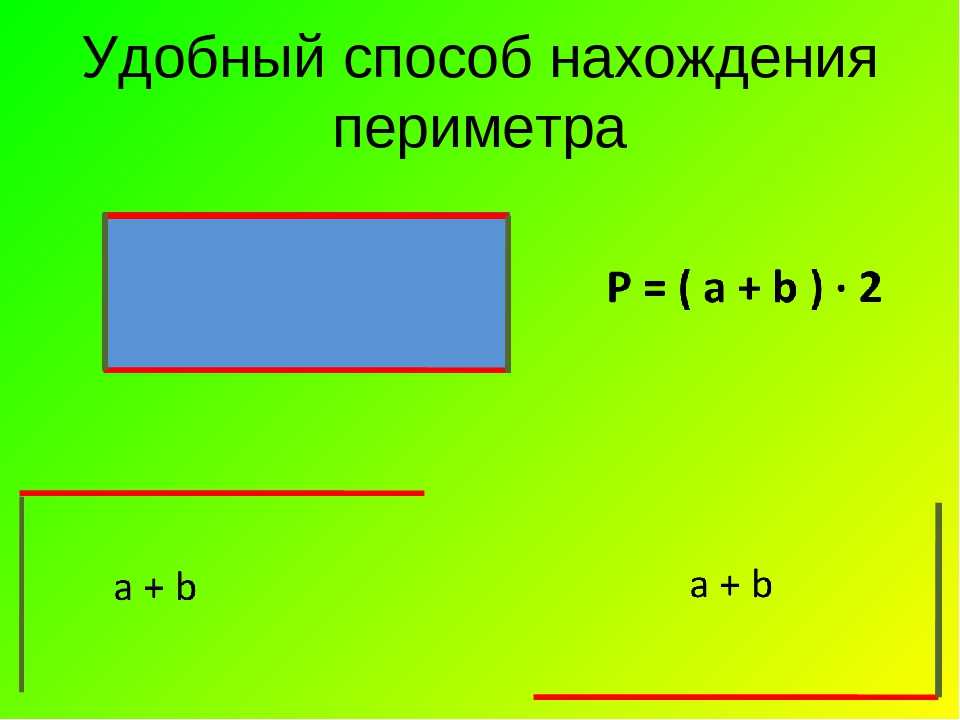
Мы знаем, что
Периметр прямоугольника P= 2(a+b) единиц
где длина прямоугольника представлена как
ширина прямоугольника представлена как b стороны, противоположные друг другу, равны периметру прямоугольника ABCD длины a и ширины b будет:
P= сумма всех его сторон
P= a+b+a+b
P= (a +б)
Следовательно Доказано. 9{2} \right )}\]
Диаграмма формул периметра для различных форм
Вот список формул для периметра различных форм.
Formula of Perimeter of Different Shapes:
Name of Geometric Shapes | Figure | Perimeter Formula | Variables | ||
Rectangle | (image will be uploaded soon) | Perimeter of rectangle = 2(l +w) | l = length w = width | ||
Square | (изображение скоро будет загружено) | Периметр квадрата = 4a | a = стороны квадрата | ||
Треугольник | 40003 | Периметр треугольника = сумма всех сторон | B = базовая H = высота | ||
Трейпезоид | (Image будет загружено в ближайшее время) 9003 | (Image будет загружено) Сумма всех сторон. | a = основание 1 b = основание 2 h = высота по вертикали | ||
Параллелограмм | (изображение скоро будет загружено)0003 | Периметр параллелограммы = 2 (a+b) | A = сторона B = основание H = вертикальная высота | ||
Rhombus | |||||
Rhombus | |||||
. ) | Периметр ромба = 4A | A = Сторона ромба H = высота | |||
Circle | (Image будет загружено в ближайшее время) | (Изображение будет загружено в ближайшее время) | (Изображение будет загружено) | (изображение будет загружено)0014 Периметр круга/окружности = 2πr | R = радиус круга π = 22/7 или 3,1416 |
Полув. | r = радиус круга | ||||
Сектор | (изображение будет загружено в ближайшее время) | PERIMER (СЕКТОР СКОРОСТЬ) = 2 (RADER) = 2 (RADER) = 2 (SEC SECER) = 2 (SEC SECRES) = 2 (СЕКТО длина | r = радиус окружности |
Периметр прямоугольника — Приложения длину заплывов можно определить по периметру прямоугольника, если бассейн построен прямоугольной формы.
Длину бетонного ограждения перед строительством дома можно определить с помощью периметра.
Длину садовых заборов можно определить по формуле периметра.
Формула периметра прямоугольника может использоваться во многих проектах в области искусства и ремесел, требующих рисования границ прямоугольных фигур.
Периметр прямоугольника — решенный пример
Пример 1:
Найдите периметр прямоугольника, длина и ширина которого равны 11 см и 13 см соответственно.
Решение:
Если длина = 11 см, а ширина = 13 см см
P = 56 см
Следовательно, периметр прямоугольника равен 56 см.
Пример 2:
Длина прямоугольного поля 15м, ширина 6м. Найдите периметр прямоугольного поля, а также найдите его площадь.
Решение:
Учитывая, что Длина = 15 м
Ширина = 6 м
У нас есть формула площади A = длина x ширина
= 15 x 6
= 90 м²
формула для расчета периметра прямоугольника P = 2 (длина + ширина )
= 2 х (15 + 6)
= 2 х 21
= 42 м.
Пример 3:
Если длина и ширина прямоугольника равны 12 см и 15 см соответственно. Определить периметр.
Определить периметр.
Решение:
Дано
Длина= 12 см
Ширина= 15 см
Мы знаем, что для прямоугольника
Периметр= 2(длина + ширина)
Периметр= 2(12+15)
Периметр= 254 x 27 см
Забавные факты
Многие исторические здания имеют прямоугольную форму, напр. Парфенон в Афинах.
Заключение
Вот как мы вычисляем периметр прямоугольника и применяем его в различных аспектах. Поймите, как вычисляется периметр других замкнутых фигур и выводятся формулы.
Периметр прямоугольника – определение, формула, примеры, приложения
Периметр прямоугольника – это расстояние, пройденное вдоль его границы. Это общее расстояние, пройденное при полном обходе прямоугольника. Он равен удвоенной сумме длины и ширины прямоугольника. Периметр — это сумма всех сторон любой фигуры. Предположим, мы берем любой четырехугольник со сторонами a, b, c и d, тогда его периметр определяется как сумма всех сторон, так как периметр равен сумме a, b, c и d. В случае круга периметр называется Окружность.
Предположим, мы берем любой четырехугольник со сторонами a, b, c и d, тогда его периметр определяется как сумма всех сторон, так как периметр равен сумме a, b, c и d. В случае круга периметр называется Окружность.
Прямоугольник представляет собой двумерный плоский четырехугольник, у которого противоположные стороны равны и все четыре угла равны. Самая длинная сторона прямоугольника может быть обозначена как длина (l), а самая короткая сторона – как ширина (b). В прямоугольнике все углы равны 90°. Периметр прямоугольника рассчитывается как P = 2 × (l + b).
Что такое периметр прямоугольника?
Периметр можно определить как сумму длин всех четырех сторон прямоугольника. В прямоугольнике все четыре стороны не имеют одинаковой длины, как у квадратов, стороны, противоположные друг другу, имеют одинаковую длину, и обе диагонали прямоугольника имеют одинаковую длину. Таким образом, периметр прямоугольника представляет собой линейную сумму всех сторон прямоугольника и измеряется в м или см. Мы можем преобразовать см в м, так как стандартной единицей измерения является 9.0463 метра (м).
Мы можем преобразовать см в м, так как стандартной единицей измерения является 9.0463 метра (м).
Периметр прямоугольника Формула
Периметр прямоугольника – это сумма всех четырех сторон. Периметр прямоугольника является фундаментальной формулой и обычно представляется как ‘P’ . Формула для нахождения периметра прямоугольника обсуждается ниже:
Предположим, что мы берем прямоугольник длины l и ширины b, тогда его периметр равен
Периметр(P) = 2 × (l + b)
Где,
l длина прямоугольника
b ширина прямоугольника по две равные стороны, давайте рассмотрим длину одной стороны как «l», а длину другой стороны как «b». Итак, будут l, l и b, b.
В соответствии с определением периметра сумма всех сторон равна l + l + b + b = 2l + 2b
Итак, возьмем 2 обычных, Периметр = 2(l + b)
Следовательно,
Периметр прямоугольника равен 2(l + b)
Как найти периметр прямоугольника?
Периметр прямоугольника можно рассчитать за несколько простых шагов.
Эти шаги перечислены ниже:
Шаг 1: Для вычисления периметра прямоугольника отмечаются Длина (l) и Ширина (b) данной фигуры
Шаг 2: Значения длины (l) и Ширина (b) заменены в формуле. P = 2 × (l+b)
Шаг 3: Решите формулу, и полученное значение будет окончательным периметром данной фигуры.
Применение периметра прямоугольника в реальном миреПериметр прямоугольника может иметь множество применений в реальной жизни. Некоторые из них перечислены ниже:
- Длину прямоугольного поля или сада для его ограждения можно определить по формуле периметра.
- Периметр прямоугольника полезен при создании рамок для различных объектов.
- Строительство зданий и других сооружений требует определения их границ, которые можно легко рассчитать с помощью формулы периметра.
- Периметр прямоугольника используется в столярном деле для определения размеров прямоугольных объектов, таких как двери, столы, кровати и т.
д.
Решаемые примеры на периметре прямоугольника
Пример 1. Нахождение периметра прямоугольника , длина которого 8 см, а ширина 12 см.
Решение:
Дано, l = 8 и b = 12 см
Итак, подставим оба значения в формулу периметра,
P = 2(l + b) = 2(12 + 8) = 40 см
Следовательно, периметр прямоугольника, длина которого 8 см, а ширина 12 см, равен 40 см.
Пример 2: Найдите периметр прямоугольника, стороны которого равны 2 см и 4 см.
Раствор :
Дано,
l = 2 и другая сторона b = 4 см.
Итак, подставьте оба значения в формулу периметра,
P = 2(l + b) = 2(2 + 4) = 12 см
Следовательно, периметр прямоугольника, сторона которого равна 2 см, а другая сторона равна 4 см это 12 см.
Пример 3: Найдите периметр прямоугольной доски, стороны которой равны 10 см и 20 см.

Решение :
Дано,
l = 10 и другая сторона b = 20 см карромной доски.
Итак, подставьте оба значения в формулу периметра,
P = 2(l + b) = 2(10 + 20) = 60 см.
Следовательно, периметр прямоугольной доски, сторона которой равна 10 см, а другая сторона 20 см, равен 60 см.
Пример 4: Найдите периметр кроватки со сторонами 100 см и 200 см.
Решение :
Дано,
l = 100 и другая сторона b = 200 см кроватки.
Итак, подставьте оба значения в формулу периметра,
P = 2(l + b) = 2(100 + 200) = 600 см.
Следовательно, периметр кроватки со сторонами 100 см и 200 см равен 600 см.
Пример 5: Найдите периметр компостной ямы, у которой самая длинная сторона 100 см, а самая короткая сторона 34 см.
Решение :
Дано,
Самая длинная сторона = 100 см, поэтому длина (l) будет самой длинной стороной.
So l = 100 см.
Самая короткая сторона = 34 см, поэтому ширина (b) будет самой короткой стороной.
So b = 34 см
Итак, подставьте оба значения в формулу периметра,
P = 2(l + b) = 2(100 + 34) = 268 см
Следовательно, периметр компостной ямы, самая длинная сторона которой равна 100 см, а самая короткая сторона 34 см равна 268 см
Часто задаваемые вопросы о периметре прямоугольника
Вопрос 1: Что понимают под площадью и периметром прямоугольника?
Ответ:
Площадь прямоугольника определяется как пространство, которое покрыто прямоугольником в двумерном пространстве. Площадь прямоугольника также можно определить как количество квадратных единиц, необходимых для полного заполнения прямоугольника.
Площадь = l × b
Периметр прямоугольника можно определить как общее расстояние, пройденное вокруг границ прямоугольника.
Проще говоря, периметр прямоугольника — это его общая граница.
Периметр = 2 × (l + b)
Вопрос 2: Как найти периметр прямоугольника?
Ответ:
Периметр прямоугольника можно найти, сложив все его стороны. Сумма всех четырех сторон прямоугольника называется его периметром.
Вопрос 3: Какова формула периметра прямоугольника?
Ответ:
Формула для периметра прямоугольника:
P = 2(l + b)
, где l длина прямоугольника, а b ширина прямоугольника.
Вопрос 4: Как найти длину прямоугольника, если известны его ширина и периметр?
Ответ:
Мы знаем, что периметр прямоугольника P = 2 (длина + ширина) единиц
Таким образом,
P/2 = длина + ширина
тогда длина прямоугольника = {(P/2) – ширина} единиц.Вопрос 5. В какой единице измеряется периметр прямоугольника?
Ответ:
Периметр прямоугольника измеряется в тех же единицах, что и длина и ширина прямоугольника, например, см, м, фут, дюйм и т. д.
Вопрос 6: Как найдите периметр прямоугольника, если дана его диагональ?
Ответ:
Связанные статьиПусть «l» — длина, а «d» — диагональ прямоугольника, тогда периметр прямоугольника равен:
P = 2l + 2√( d 2 – l 2 ) шт.
Математические заметки CBSE класса 8. Понимание четырехугольников
Математические решения NCERT для класса 8. Понимание четырехугольников
RD Sharma, решение класса 8, глава 91 и глава.0003
Периметр прямоугольника с формулами и диаграммой
Периметр любой двумерной геометрической фигуры — это расстояние, пройденное вокруг ее края.
В этой статье мы узнаем, как найти периметр прямоугольника с помощью формул и примеров.
Что такое периметр прямоугольника
Периметр прямоугольника — это общее расстояние, пройденное вокруг края прямоугольника.
Поскольку прямоугольник является четырехсторонней фигурой, его периметр также определяется как сумма четырех сторон.
Периметр — общая мера длины или расстояния. Выражение периметра в линейных единицах. Таким образом, единицей измерения периметра прямоугольника являются ярды, футы, дюймы, метры или любая другая линейная единица.
Формула
Формула для нахождения периметра прямоугольника приведена ниже:
Периметр прямоугольникаВывод
Так как периметр четырехугольника (геометрическая фигура с 4 сторонами) является суммой всех сторон, поэтому , периметр (P) равен,
P = сумма всех четырех сторон = w + w + l + l = 2(w + l), где w = ширина, а l = длина.
Таким образом, мы получаем стандартную формулу периметра прямоугольника (P) = 2(w + l)
Как найти периметр прямоугольника
Основные шаги для вычисления периметра прямоугольника, зная его длину (l ) и ширина (w) следующие:
- Запишите формулу Периметра прямоугольника 2(w + l).
- Подставьте значения длины (l) и ширины (w) в формулу.
- Запишите ответ в линейных единицах.
Давайте решим несколько примеров, чтобы лучше понять концепцию.
Решенные примеры
Найдите периметр прямоугольного сада длиной 10 м и шириной 6 м.
Решение:
Как известно,
P = 2(w + l), здесь w = 6 м, l = 10 м
= 2 х (10 + 6)
= 32 м.Сколько кружев понадобится Джону, чтобы украсить простыню длиной 150 дюймов и 95 дюймов в ширину?
Решение:
Длина шнурка равна периметру (P) простыни.
Как мы знаем,
P = 2(w + l), здесь w = 95 дюймов, l = 150 дюймов
= 2 x (95 + 150)
= 490 дюймов
Итак, Джону нужен шнурок 490 дюймов для украшения простыни.Нахождение периметра прямоугольника, когда известны ДИАГОНАЛЬ и любая ОДНА СТОРОНА
Найдите периметр прямоугольника с диагональю 9 футов и длиной 8 футов.

Решение:
Здесь мы будем использовать формулу = диагональ, l = длина
Как мы знаем,
P = 2l + 2√(d 2 – l 2 ), где d = 9 футов, а l = 8 футов
= 2 x 8 + 2 x √ (9 2 – 8 2 )
≈ 24,25 футаНайдите периметр прямоугольника шириной 16 дюймов и диагональю 32 дюйма.
Решение:
Здесь мы используем формулу = диагональ, w = ширина
Как мы знаем,
P = 2w + 2√(d 2 – w 2 ), где w = 16 дюймов, d = 32 дюйма
= 2 x 16 + 2√(32 2 – 16 2 )
≈ 87.42 inchesFinding the perimeter of a rectangle when AREA and any ONE SIDE are known
Find the perimeter of a rectangular swimming pool whose area составляет 700 кв.
футов и имеет ширину 100 футов.
Решение:
Здесь мы будем использовать формулу P = 2w + 2A/w , чтобы найти периметр (P) как A = w × l и P = 2(w + l), где w = ширина , l = длина, A = площадь.
Как известно,
P = 2w + 2A/w, здесь w = 100 футов, а A = 700 кв. футов.
= 2 × 100 + 2 × (700/100)
= 214 футов. Найдите периметр прямоугольника, площадь которого 3750 кв.см, а длина 75см.Решение:
Здесь мы будем использовать формулу P = 2l + 2A/l , чтобы найти периметр (P) как A = w × l и P = 2(w + l),
Где w = ширина, l = длина, A = площадь.
Как известно,
P = 2l + 2A/l, здесь l = 75 см, а A = 3750 кв. см
= 2 × 75 + 2 × (3750/75)
= 250 cmFinding the measure of any one side when PERIMETER and any ONE SIDE are known
Find the длина парка, если длина парка в два раза больше его ширины, а периметр равен 390 ярдам.



 Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
 Периметр полукруга = πr + 2r
Периметр полукруга = πr + 2r Эти шаги перечислены ниже:
Эти шаги перечислены ниже: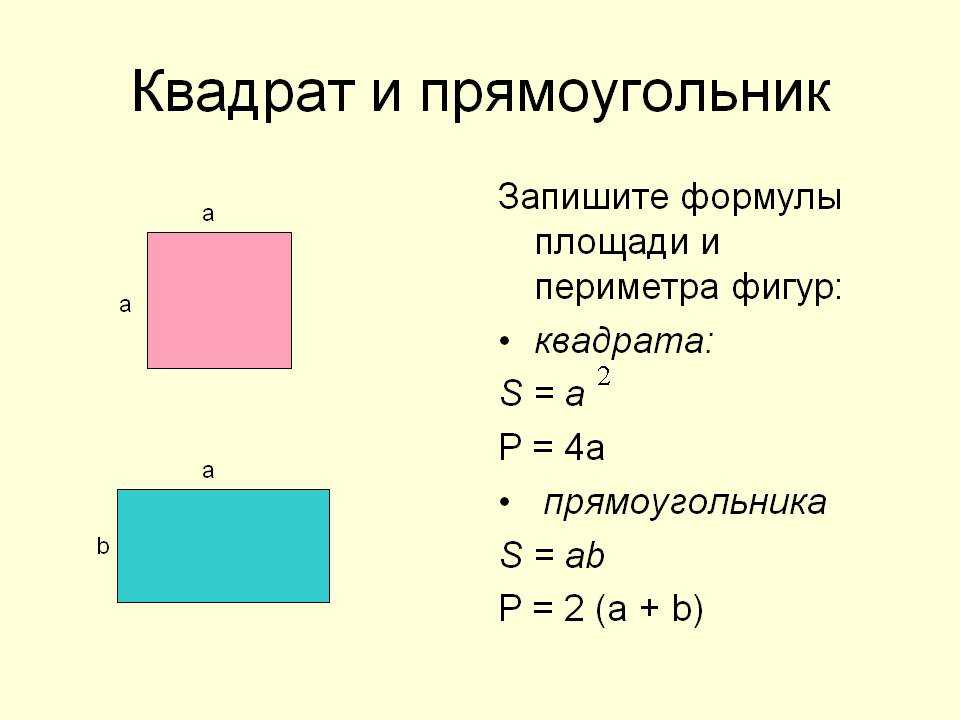 д.
д.
 Проще говоря, периметр прямоугольника — это его общая граница.
Проще говоря, периметр прямоугольника — это его общая граница.
 В этой статье мы узнаем, как найти периметр прямоугольника с помощью формул и примеров.
В этой статье мы узнаем, как найти периметр прямоугольника с помощью формул и примеров.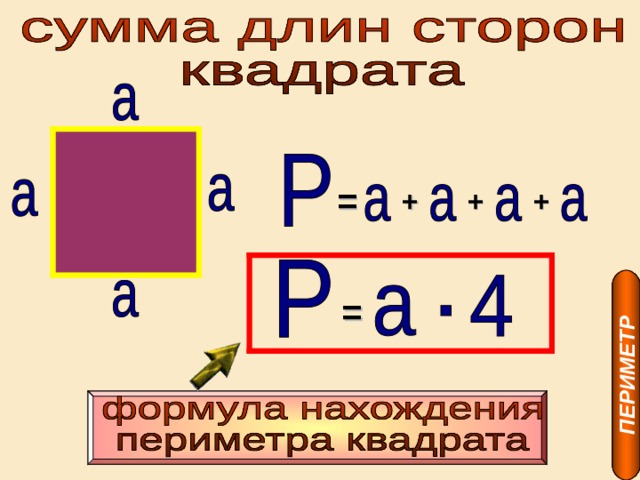

 футов и имеет ширину 100 футов.
футов и имеет ширину 100 футов. 