Высшая математика 1 курс — интернет энциклопедия для студентов
- Линейная алгебра Матрицы
- Метод Крамера
- Метод Гаусса
- Векторная алгебра Векторы и операции над ними
Несмотря на то, что зачастую этот предмет в вузах преподается разное количество времени (от 1 семестра для гуманитарных специальностей, и до 3 – для технических), список тем мало отличается. Чаще всего в дисциплине рассматриваются следующие разделы высшей математики: линейная и векторная алгебра, аналитическая геометрия, и линии второго порядка.
Линейная алгебра Матрицы
Изучаются матрицы размерностью n на m следующих видов: квадратные, диагональные, равные, единичные, трапецевидные, и треугольные.
Среди действий, которые возможно над ними выполнять рассматривают следующие:
- Сложение и вычитание матриц, сходных по размерности.
- Умножение их на число, вектор, и на другую матрицу.
Определитель
Изучают понятие определителя, его основные свойства, среди которых следующие:
- Для квадратных матриц А и В действует правило, что определитель произведения чисел А на В равняется определителю произведения В на А.

- Определитель и его транспонируемая версия равны между собой.
- Если определитель содержит ряд из 0, или какие-либо 2 его ряда параллельны, то он равен нулю.
- Если матрица диагональная, то ее определитель есть числа, расположенные по диагонали, умноженные между собой. То же самое правило действует и для треугольных матриц.
- Если у чисел имеется общий множитель, то его можно вынести из определителя.
Изучаются основные правила теоремы Лапласа, связанной с разложением определителя.
Обратная матрица
Изучается понятие невырожденной матрицы. В связи с ним существует следующая схема, по которой вычисляется обратная матрица с положительным определителем:
- Элементы матрицы последовательно заменяются на соответствующие им алгебраические дополнения. В результате этого действия возникает союзная матрица.
- Происходит транспонирование.

- Элементы полученной матрицы нужно разделить на определитель матрицы.
Ранг матрицы
Понятие представляется как самое большое число линейно-зависимых строк матрицы и самый большой порядок, не равняющийся нулю, из миноров первоначальной матрицы.
Ранг матрицы имеет следующие два свойства:
- Он не подвержен изменению после транспонирования, после убирания нулевого ряда, и после совершения преобразований.
- Найти ранг можно по общему числу элементов на главной диагонали, отличающихся от нуля.
Метод Крамера
Используется для нахождения корней уравнений, в которых произведение А и Х равняется В. При этом важно, чтобы определитель А был отличным от нуля.
Если это условие совпадает, то можно воспользоваться следующим алгоритмом:
Находим ak, равное определителю Ак деленному на определитель А. Ак получают из А, подставив в него столбец свободного члена из В.
Метод Гаусса
Для его понятия изучают расширенную матрицу. А также несколько видов систем уравнений: совместные, определенные, равносильные, однородные.
А также несколько видов систем уравнений: совместные, определенные, равносильные, однородные.
Алгоритм для их решений таков:
- Первым делом находят ранги основной и расширенной.
- Если они отличаются друг от друга, то система является несовместной и на этом решение прекращают.
- Иначе сначала высчитывают базисный минор порядка, затем общее решение системы, и в итоге получают частные решения при подставлении произвольных значений в уравнения.
Векторная алгебра Векторы и операции над ними
Рассматривается основное определение вектора, его свойства, такие как длина и направления. Кроме этого изучают следующие различные векторы: противоположные, нулевые, коллинеарные и компланарные.
Существуют следующие действия над векторами:
- Суммирование;
- Скалярное, векторное и смешанное умножение на другой вектор, а также на другое число.
Аналитическая геометрия
Рассматривает определения плоскостей и трехмерного пространства.
Прямая на плоскости
Изучают несколько ее основных уравнений: нормальное уравнение, с угловым коэффициентом, через точку и направление, через 2 точки, в отрезках.
Плоскость и прямая в пространстве
Рассматривают уравнения, по которым плоскость задается в пространстве. Такие как: уравнения через точку перпендикулярно к вектору, через 3 точки, нормальное, и в отрезках.
При изучении прямой важно знать каноническое и по 2 точкам, общее, векторное, с направляющими коэффициентами.
Во всех трех случаях рассматривают формулы, по которым можно найти различные углы.
Взаимное расположение плоскостей и прямых
При рассмотрении данного вопроса изучают формулы углов, параллельность, перпендикулярность, принадлежность прямой к плоскости.
Линии второго порядка
В этом разделе рассматриваются определения и свойства нескольких фигур: эллипса, гиперболы и параболы.
В связи с эллипсом изучают его каноническое уравнение, а также определения эксцентриситета и директрис.
При рассмотрении гиперболы, изучают тоже самое, что и у эллипса. Но к этому добавляются понятия фокальных радиусов, а также уравнения асимптот.
При изучении параболы рассматривают, что представляет собой полуфокальный диаметр.
Чаще всего дисциплина высшей математики для первокурсников, заканчивается на изучении вышестоящей темы, но программа предмета может несущественно изменяться в зависимости от вуза.
Высшая математика 1 курс 1 семестр
4
дисциплина «ВЫСШАЯ МАТЕМАТИКА»
1 курс, I семестр
СОДЕРЖАНИЕ УЧЕБНОГО МАТЕРИАЛА
Тема 1. Матрицы
Понятие
матрицы. Операции над матрицами.
Определители второго и третьего порядков
и их свойства. Понятие определителя n-го
порядка. Ранг матрицы. Обратная матрица.
Собственные числа и собственные векторы
матрицы. Понятие о квадратичных формах
и их преобразовании к каноническому
виду.
Понятие о квадратичных формах
и их преобразовании к каноническому
виду.
Тема 2. Системы линейных уравнений и неравенств
Системы линейных уравнений. Правило Крамера. Метод Гаусса. Матричный метод решения систем линейных уравнений. Теорема Кронекера-Капелли. Системы линейных неравенств. Графический метод решения системы линейных неравенств с двумя переменными. Смешанные системы линейных уравнений и неравенств. Применение элементов линейной алгебры в экономике.
Тема 3. Векторная алгебра
Понятие вектора на плоскости и в трехмерном пространстве. Основные операции над векторами. Скалярное произведение векторов. Векторы в n-мерном пространстве. Линейная зависимость векторов. Базис системы векторов. Разложение вектора по базису. Размерность и базис пространства. Понятие о векторных пространствах. Евклидово пространство.
Тема 4. Аналитическая геометрия на плоскости
Предмет
аналитической геометрии. Метод координат.
Декартова и полярная системы координат.
Основные виды уравнения прямой. Угол
между прямыми. Условия параллельности
и перпендикулярности двух прямых.
Расстояние от точки до прямой. Кривые
второго порядка: окружность, эллипс,
парабола, гипербола. Параметрическое
и полярное представления линий.
Метод координат.
Декартова и полярная системы координат.
Основные виды уравнения прямой. Угол
между прямыми. Условия параллельности
и перпендикулярности двух прямых.
Расстояние от точки до прямой. Кривые
второго порядка: окружность, эллипс,
парабола, гипербола. Параметрическое
и полярное представления линий.
Тема 5. Элементы аналитической геометрии в пространстве
Простейшие задачи аналитической геометрии в пространстве. Основные виды уравнений плоскости и прямой в пространстве. Угол между плоскостями. Угол между двумя прямыми. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Понятие о поверхностях второго порядка и их классификации.
Тема 6. Комплексные числа.
Комплексная плоскость. Формы представления комплексных чисел. Действия над комплексными числами. Формулы Эйлера.
Тема 7. Числовая последовательность и ее предел
Действительные
числа. Числовые множества. Числовые
последовательности. Бесконечно малые
и бесконечно большие последовательности.
Предел последовательности. Свойства
сходящихся последовательностей.
Монотонные последовательности.
Экономическая интерпретация числа
Числовые
последовательности. Бесконечно малые
и бесконечно большие последовательности.
Предел последовательности. Свойства
сходящихся последовательностей.
Монотонные последовательности.
Экономическая интерпретация числа
Тема 8. Предел функции одной переменной
Функции и отображения, их области определения и значений, способы задания и
график функции. Основные элементарные функции. Сложная функция. Предел
функции в точке. Основные теоремы о пределах функций. Замечательные преде-
лы. Односторонние пределы. Бесконечные пределы и пределы на бесконечности.
Тема 9. Непрерывные функции одной переменной
Непрерывность функции в точке. Односторонняя непрерывность. Классификация точек разрыва. Непрерывность сложной функции и обратной функции. Непрерывность элементарных функций. Непрерывность функции на множестве. Функции, непрерывные на отрезке, и их свойства.
Тема 10. Производная и дифференциал функции одной переменной
Производная
функции.
Тема 11. Основные теоремы о дифференцируемых функциях
Стационарные точки. Теоремы Ферма и Ролля. Теорема Лагранжа и формула конечных приращений. Теорема Коши. Правило Лопиталя.
Тема 12. Приложения дифференциального исчисления
Условие
постоянства функций. Условия монотонности
функций. Экстремум функции. Необходимое
условие экстремума дифференцируемой
функции. Наибольшее и наименьшее значение
функции. Достаточные условия экстремума.
Условия выпуклости и вогнутости.
Л И Т Е Р А Т У Р А
Учебники
1. Высшая математика: Общий курс: учеб. для вузов / А.В. Кузнецов [и др.]; под ред. А.И. Яблонского. − Мн.: Выш. шк., 1993. − 349 с.
2. Карасев, А.И. Курс высшей математики для экономических вузов. Ч. 1. Основы высшей математики: учеб. пособие для студ. экон. спец. вузов /
А.И. Карасев, З.М. Аксютина, Т.И. Савельева. − М.: Высш. шк., 1982. − 272 с.
3. Кудрявцев, В.А. Краткий курс высшей математики: учеб. пособие для естеств. спец. ун-тов / В.А. Кудрявцев, Б.П. Демидович. − М.: Наука, 1989. −
656 с.
4. Марков,
Л.Н. Высшая математика. Ч. 1. Элементы линейной
и векторной алгебры. Основы аналитической
геометрии: учеб. пособие для вузов / Л.Н.
Марков, Г.П. Размыслович. − Мн.: Амалфея,
1999. − 208 с.
Основы аналитической
геометрии: учеб. пособие для вузов / Л.Н.
Марков, Г.П. Размыслович. − Мн.: Амалфея,
1999. − 208 с.
5. Минюк, С.А. Высшая математика: учеб. пособие для вузов / С.А. Минюк, Е.А. Ровба. − Гродно: ГрГУ, 2000. − 394 с.
6. Шипачев, В.С. Высшая математика: учеб. для немат. спец. вузов /
В.С. Шипачев; под ред. А.Н. Тихонова. − М.: Высш. шк., 1990. − 479 с.
7. Высшая математика для экономистов: учеб. для вузов / Н.Ш. Кремер [и др.]; под ред. Н.Ш. Кремера. − М.: ЮНИТИ, 2002. − 471 с.
9. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1: учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. − М.: Оникс, 2002. − 304 с.
10. Данко,
П.Е. Высшая математика в упражнениях и
задачах. В 2 ч. Ч.2: учеб. пособие для вузов
/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевников.
− М.: ООО «Изд. дом «Оникс 21 век», 2003. −
416 с.
В 2 ч. Ч.2: учеб. пособие для вузов
/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевников.
− М.: ООО «Изд. дом «Оникс 21 век», 2003. −
416 с.
11. Красс, М.С. Математика для экономических специальностей: учеб. для вузов / М.С. Красс. − М.: Дело, 2002. − 704с.
12. Шипачев, В. С. Высшая математика: учеб. для вузов / В.С. Шипачев. − М.: Высш. шк., 1998. − 479 с.
13. Общий курс высшей математик для экономистов: учебник / под ред.
В.И. Ермакова. − М.: ИНФРА-М, 2001.
14. Натансон, И.П. Краткий курс высшей математики / И.П. Натансон. − СПб, Издательство «Лань», 2001.
15. Малыхин, В. И. Математика в экономике / В.И. Малыхин. − М.: ИНФРА-М, 2002. − 352 с.
16. Красс, М.С. Математика для экономистов / М.С. Красс, Б.П. Чупрынов. − М.: ООО «Питер пресс», 2008. − 464 с.
17. Высшая математика / А.В. Кузнецов [и др.]. − Мн.: Высшая школа, 1993.
18. Математический словарь высшей школы / В. Т. Воднев [и
др.]. − Мн.: Высшая школа, 1984.
Т. Воднев [и
др.]. − Мн.: Высшая школа, 1984.
19. Кастрица, О.А. Высшая математика: учебное пособие / О.А. Кастрица. − Мн.: Новое знание, 2005.
20. Плющ, О.Б. Высшая математика. Часть 1. Элементарная математика, аналитическая геометрия, высшая алгебра / О.Б. Плющ. − Мн.: Академия управления при Президенте Республики Беларусь, 2004. − 168 с.
Задачники
21. Гусак, А.А. Задачи и упражнения по высшей математике. В 2 ч. Ч. 1: учеб. пособие для вузов / А.А. Гусак. − Мн.: Выш. шк., 1988. − 246 с.
22. Гусак, А.А. Задачи и упражнения по высшей математике. В 2 кн. Кн. 2: учеб. пособие для вузов / А А. Гусак. − Мн.: Выш. шк., 1988. − 228с.
23. Минорский, В.П. Сборник задач по высшей математике: учеб. пособие для втузов / В.П. Минорский. − М.: Наука, 1987. − 349 с.
24. Сборник задач и упражнений по высшей математике:
Общий курс: учеб. пособие / А.В. Кузнецов
[и др.]. − Мн.: Выш. шк., 1994. − 284 с.
пособие / А.В. Кузнецов
[и др.]. − Мн.: Выш. шк., 1994. − 284 с.
25. Сборник индивидуальных заданий по высшей математике. В 3 ч. Ч. 1: учеб. пособие для вузов / А.П. Рябушко [и др.]; под ред. А.П. Рябушко. − Мн.: Выш. шк., 1990. − 269 с.
26. Сборник индивидуальных заданий по высшей математике. В 3 ч. Ч. 2: учеб. пособие для вузов / А.П. Рябушко [и др.]; под ред. А.П. Рябушко. − Мн.: Выш. шк., 1991. − 351 с.
27. Гусак, А.А. Справочник по высшей математике: учеб. для вузов /
А.А. Гусак, Г.М. Гусак, Е.А. Бричкова. − Мн.: ТетраСистемс, 2000. − 640 с.
28. Практикум по высшей математике для экономистов: учеб. пособие для вузов / под ред. Н.Ш. Кремера. − М.: ЮНИТИ-ДАНА, 2004. − 423 с.
Наглядные и методические пособия
29. Черняк, А.А. Сборник
задач по высшей математике с
демонстрационными примерами:
Учебно-методическое пособие. / А.А.
Черняк, Ю.А. Доманова. − Мн.: МИТСО, 2002. −
98 с.
/ А.А.
Черняк, Ю.А. Доманова. − Мн.: МИТСО, 2002. −
98 с.
30. Буснюк, Н.Н. Основы высшей математики и информатики: метод. Пособие для студ. юрид. спец. / Н.Н. Буснюк, Н.О. Берестнева. − Мн.: МИТСО, 2007. − 72 с.
31. Методика решения задач по высшей математике: метод. пособие /
Н.А. Докукова, Е.Н. Кафтайкина. − Мн.: МИТСО, 2008. − 63 c.
Высшая математика
Высшая математикаВЫСШАЯ МАТЕМАТИКА 2023
Основные разделы высшей математики, изучаемые на первом и втором курсе.
ШКОЛА
ВУЗ
ОБ АВТОРЕ
КАК ПРОХОДИТ ОБУЧЕНИЕ
ОТЗЫВЫ
НА ГЛАВНУЮ
Автор всех программ – кандидат физико-математических наук, выпускник мехмата МГУ им. М.В. Ломоносова – Павликов Андрей Николаевич
Узнать подробнее
Записаться на курс
ФОРМАТ ЗЯНЯТИЙ
•3 группы не более 10 человек в каждой
•Первая группа — Задача 13
•Вторая группа — Задача 15
•Третья группа — Задача 17
•Каждое занятие по 2 часа
•Ежедневно май-июнь 2020г
ДЛЯ КОГО?
Для студентов первого и второго курсов вузов с дисциплиной «высшая математика». Для тех, кого не устраивает текущий уровень знаний, кто хочет повысить его и спокойно сдать сессию
Для тех, кого не устраивает текущий уровень знаний, кто хочет повысить его и спокойно сдать сессию
ПОЧЕМУ?
На просторах русскоязычного интернета практически отсутствуют полноценные обучающие программы по высшей математике. Чтобы исправить данную ситуацию, я начал разрабатывать целую серию курсов по высшей математике
Все курсы носят практический характер. Цель – научить решать задачи.
ПОЧЕМУ Я СОЗДАЛ ДАННЫЕ КУРСЫ
Высшая математика состоит из большого количества разделов, и пробелы в любом из них несут проблемы в остальных. Поэтому времени «на раскачку» нет, надо сразу включаться в работу и закрывать возникающие вопросы.
В первую очередь высшая математика — это умение решать задачи. По своему опыту могу сказать, что любому студенту, владеющему базовыми школьными знаниями математики на должном уровне, по силам освоить и высшую.
Именно поэтому я решил создать курсы, имеющие практическую направленность и позволяющие студентам научиться решать задачи по высшей математике за разумное время.
Записаться на курс
ПРОГРАММЫ
КУРСОВ
- Урок 1. Последовательность
- Урок 2. Предел последовательности
- Урок 3. Функции и их свойства
- Урок 4. Предел функции
- Урок 5. Первый замечательный предел
- Урок 6. Второй замечательный предел
- Урок 7. Непрерывность и точки разрыва функции
- Контрольная работа
- Урок 1. Производная. Определение. Правила вычисления производных. Таблица производных элементарных функций
- Урок 2. Производная сложной функции
- Урок 3. Производная функции, заданной параметрически
- Урок 4. Производная неявной функции
- Урок 5. Производные высших порядков
- Урок 6. Дифференциал
- Урок 7. Касательная и нормаль
- Урок 8. Правило Лопиталя
- Урок 9. Формула Тейлора
- Контрольная работа
- Урок 1. Общая схема исследования функции. Возрастание/убывание. Экстремумы. Выпуклость/вогнутость/точки перегиба.
 Асимптоты
Асимптоты - Урок 2. Степенные функции и многочлены
- Урок 3. Дробно-рациональные функции
- Урок 4. Иррациональные функции
- Урок 5. Тригонометрические функции
- Урок 6. Показательные функции
- Урок 7. Логарифмические функци
- Контрольная работа
- Урок 1. Табличное интегрирование
- Урок 2. Интегрирование заменой переменной
- Урок 3. Интегрирование по частям
- Урок 4. Интегралы содержащие квадратный трехчлен
- Урок 5. Интегрирование рациональных функций
- Урок 6. Интегрирование иррациональных функций
- Урок 7. Интегрирование тригонометрических функций
- Урок 8. Смешанные примеры на интегрирование
- Контрольная работа
- Ряды, определения, сумма ряда. Необходимый признак сходимости
- Ряды с положительными членами (признаки сравнения, Даламбера, Коши, интегральный)
- Ряды со знакопеременными членами
- Приближенные вычисления сумм рядов
- Функциональные ряды, область сходимости
- Степенные ряды
- Ряды Тейлора
- Ряды Фурье
- Урок 1.
 Определители
Определители - Урок 2. Операции над матрицами
- Урок 3. Ранг матрицы
- Урок 4. Обратная матрица. Матричные уравнения
- Урок 5. Системы линейных уравнений. Формулы Крамера
- Урок 6. Системы линейных уравнений. Метод обратной матрицы
- Урок 7. Системы линейных уравнений. Метод Гаусса
- Урок 8. Системы однородных линейных уравнений. Фундаментальные решения
- Контрольная работа
- Урок 1. Прямоугольная система координат
- Урок 2. Полярная система координат
- Урок 3. Прямая линия на плоскости
- Урок 4. Расстояние от точки до прямой; угол и расстояние между прямыми
- Урок 5. Окружность
- Урок 6. Эллипс
- Урок 7. Гипербола
- Урок 8. Парабола
- Урок 9. Общее уравнение кривой второго порядка
- Урок 1. Комплексные числа. Определения. Геометрические изображения комплексных чисел. Формы записи комплексных чисел
- Урок 2. Действия над комплексными числами.
 Теория
Теория - Урок 3. Действия над комплексными числами. Практика
- Урок 4. Уравнения в комплексных числах
- Контрольная работа
- Элементы комбинаторики
- Случайные события
- Классическое определение вероятности
- Условные вероятности
- Формула полной вероятности. Формула Байеса
- Схема Бернулли
- Предельные теоремы схемы Бернулли
- Дискретные случайные величины. Законы распределения
- Непрерывные случайные величины. Законы распределения
- Числовые характеристики случайных величин
- Важные распределения случайные величины (биномиальное, Пуассона, геометрическое; равномерное, показательное, нормальное)
- Совместные функции распределения случайных величин
- Функции случайных величин
- Предельные теоремы теории вероятностей (неравенство Чебышева, ЗБЧ, ЦПТ)
- Определение. Уравнения с разделяющимися переменными
- Однородные уравнения
- Линейные уравнения первого порядка
- Уравнения в полных дифференциалах
- Уравнения, не разрешенные относительно производной
- Уравнения, допускающие понижение порядка
- Однородные линейные уравнения высших порядков
- Неоднородные линейные уравнения высших порядков
- Системы дифференциальных уравнений
КАК ПРОХОДЯТ УРОКИ?
МИНИМУМ ТЕОРИИ И МАКСИМУМ ПРАКТИКИ
Каждый курс по высшей математике имеет практическую направленность. Минимум необходимой теории и максимум полезных приемов и методов решения задач
Минимум необходимой теории и максимум полезных приемов и методов решения задач
КАК ПРОХОДИТ ОБУЧЕНИЕ
4 МЕСЯЦА
Вы можете учиться, выполнять домашние задания, задавать свои вопросы автору курса Павликову Андрею в любое удобное для вас время в течение всего срока действия абонемента (доступ к любому курсу по высшей математике выдаётся на 4 месяца со дня приобретения). Доступ к каждому новому уроку открывается после выполнения и проверки ДЗ.
Каждый урок состоит из двух частей: половину задач мы разбираем вместе, вторую половину вы прорабатываете самостоятельно, чтобы закрепить полученные знания. Эти задачи по уровню аналогичны разобранным
Записаться на курс
ЧЕМУ УЧАТ ДАННЫЕ КУРСЫ
Учат математике, дают практические знания
Каждый курс учит математике, а не «натаскивает» на решение определённых задач. Вы получаете фундаментальное знание по каждой теме, что позволит справиться с любой практической задачей. В курсе мы подробно обсуждаем методы решения задач, учимся понимать, какие наши действия ведут к успеху.
Дают веру в свои силы
Каждую тему начинаем с решения самых простых задач. Студент, владеющий математикой на уровне школьной программы, прорабатывая материал курса, идёт по пути «от простого к сложному», приобретает главное – веру в свои силы и способности.
Выберите курс:
Математический анализ I
(доступ на 4 месяца)
- Последовательность
- Предел последовательности
- Функции и их свойства
- Предел функции
- Первый замечательный предел
- Второй замечательный предел
- Непрерывность и точки разрыва функции
7900 руб
| Купить |
Математический анализ II
(доступ на 4 месяца)
- Производная
- Производная сложной функции
- Производная функции, заданной параметрически
- Производная неявной функции
- Производные высших порядков
- Дифференциал
- Касательная и нормаль
- Правило Лопиталя
7900 руб
| Купить |
Математический анализ III
(доступ на 4 месяца)
- Общая схема исследования функции
- Степенные функции и многочлены
- Дробно-рациональные функции
- Иррациональные функции
- Тригонометрические функции
- Показательные функции
- Логарифмические функции
7900 руб
| Купить |
Математический анализ IV
(доступ на 4 месяца)
- Таблица интегралов
- Метод замены переменной
- Интегрирование по частям
- Рациональные функции
- Иррациональные функции
- Тригонометрические функции
- Сложный интеграл
7900 руб
| Купить |
Математический анализ V
(доступ на 4 месяца)
- Ряды, определения, сумма ряда.
 Необходимый признак сходимости
Необходимый признак сходимости - Ряды с положительными членами
- Ряды со знакопеременными членами
- Приближенные вычисления сумм рядов
- Функциональные ряды
- Степенные ряды
- Ряды Тейлора
- Ряды Фурье
7900 руб
| Купить |
Линейная алгебра
(доступ на 4 месяца)
- Определители
- Матрицы
- Матричные уравнения
- Системы линейных уравнений
- Метод Гаусса
- Метод Крамера
7900 руб
| Купить |
Аналитическая геометрия I
(доступ на 4 месяца)
- Прямоугольная система координат
- Полярная система координат
- Прямая линия на плоскости
- Окружность
- Эллипс
- Гипербола
- Парабола
- Уравнение кривой второго порядка
7900 руб
| Купить |
Комплексные числа
(доступ на 4 месяца)
- Алгебраическая форма
- Тригонометрическая форма
- Показательная форма
- Действия с комплексными числами
- Уравнения в комплексных числах
3400 руб
| Купить |
Дифференциальные уравнения
(доступ на 4 месяца)
- Уравнения с разделяющимися переменными
- Однородные уравнения
- Линейные уравнения первого порядка
- Уравнения в полных дифференциалах
- Уравнения, не разрешенные относительно производной
- Уравнения, допускающие понижение порядка
- Однородные линейные уравнения высших порядков
- Неоднородные линейные уравнения высших порядков
- Системы ДУ
7900 руб
| Купить |
большой список — Какие темы/задачи вы могли бы показать способному первокурснику-математику?
Спросил
Изменено 11 лет, 7 месяцев назад
Просмотрено 3к раз
$\begingroup$
Я преподаю односеместровый курс (с января по июнь) для студентов первого курса, получающих различные степени. Поскольку есть студенты, изучающие актуарные науки, физику, другие науки, другие науки в области управления или бизнеса и т. д., курс должен быть общим. Под этим я подразумеваю, что мы преподаем исчисление почти исключительно. Конечно, есть такие темы, как биномиальная теорема и общие замечания по доказательству теорем, но студенты, интересующиеся математикой, не находят этот материал особенно интересным. Более того, я могу к ним относиться, так как первые два года университетской математики показались мне несколько скучными. Это включало исчисление, линейную алгебру, сходящиеся/расходящиеся последовательности, множественные интегралы и т. д. Настоящий анализ (кроме последовательностей), комплексный анализ, абстрактная алгебра, топология и даже элементарная теория чисел появляются только на третьем курсе.
Поскольку есть студенты, изучающие актуарные науки, физику, другие науки, другие науки в области управления или бизнеса и т. д., курс должен быть общим. Под этим я подразумеваю, что мы преподаем исчисление почти исключительно. Конечно, есть такие темы, как биномиальная теорема и общие замечания по доказательству теорем, но студенты, интересующиеся математикой, не находят этот материал особенно интересным. Более того, я могу к ним относиться, так как первые два года университетской математики показались мне несколько скучными. Это включало исчисление, линейную алгебру, сходящиеся/расходящиеся последовательности, множественные интегралы и т. д. Настоящий анализ (кроме последовательностей), комплексный анализ, абстрактная алгебра, топология и даже элементарная теория чисел появляются только на третьем курсе.
Печально то, что многие студенты изучают математику только до второго года обучения и не видят ничего из «крутой»/»интересной» математики, даже если они интересуются математикой. Поэтому я задался вопросом: можно ли как-то познакомить их с «интересной» математикой? («Они» — в частности, первокурсники, но этот вопрос актуален и для второкурсников, у которых может быть более высокая степень зрелости.)
Поэтому я задался вопросом: можно ли как-то познакомить их с «интересной» математикой? («Они» — в частности, первокурсники, но этот вопрос актуален и для второкурсников, у которых может быть более высокая степень зрелости.)
Некоторые вещи, о которых я (и другие лекторы этого курса) подумали:
Добавление сложных вопросов в учебники (например, IMC или Патнэм, хотя они сложнее, чем хотелось бы)
Написание коротких вводных «статей» о полях или группах или, возможно, характеристике Эйлера (в качестве введения в топологию) и т. д. Конечно , это очень идеалистично, так как на это часто нет ни времени, ни сил.
Направление их к библиотечным книгам, где объясняются некоторые из этих вещей. Тоже довольно идеалистично, но сколько на самом деле пойдет в библиотеку.
Вероятно, лучшее решение — объединить все три. У вас есть вопрос со странным ответом или решением, которое можно объяснить интересной математикой. Кратко объясните, как это делается, и дайте ссылку, куда студент может обратиться, если он достаточно заинтересован, чтобы продолжить изучение.
Есть ли другие способы достижения этой цели? Знаете ли вы какие-либо вопросы, к которым можно применить эту (комбинированную) процедуру?
- математика-образование
- большой список
$\endgroup$
2
$\begingroup$
Некоторое время назад я проводил занятие для продвинутых первокурсников своего университета с целью показать им интересные аспекты университетской математики. По сути, он превратился в детский курс по многообразию — с целью понимания концепции когомологий де Рама. Дело в том, что, используя немного больше механизмов, чем теория, которую они уже знали из исчисления (например, div, curl, производные), можно было доказать некоторые довольно интересные результаты, такие как теорема Брауэра о неподвижной точке.
Мне казалось, что эта «цель» в курсе весьма эффективна: у студентов всегда было какое-то представление о том, куда движется курс, и, самое главное, они знали, почему вводятся новые понятия. Есть много мотивирующих примеров и вопросов, например: «Как можно определить форму пространства»? Это упростило мотивацию таких понятий, как касательные пространства, дифференциалы и т. д.
Есть много мотивирующих примеров и вопросов, например: «Как можно определить форму пространства»? Это упростило мотивацию таких понятий, как касательные пространства, дифференциалы и т. д.
Несмотря на то, что вашим ученикам, вероятно, будет полезно изучить стандартный материал по математическому анализу (вы говорите, что они не специализируются на математике), я думаю, вы сможете включить в свой курс несколько интересных примеров, подобных приведенным выше. Например, говоря о рядах Тейлора, вы могли бы привести прекрасное доказательство иррациональности $e$ или $\pi$.
Это, безусловно, сделало бы ваше обучение более увлекательным и, возможно, не заняло бы слишком много вашего времени. 92$,
стереографическая проекция, коники,
постулат Бертрана, расхождение
$\sum_{простые числа}\frac1p$, производящие функции,дифференцируемые
коллекторы, вектор
пространства, касательные пространства, дифференциальные формы, теорема Стокса, когомологии де Рама, фиксированные
точечная теорема, основная теорема
алгебра, фундаментальная группа.
Есть много хороших книг, которые вы могли бы просмотреть, чтобы найти интересные примеры, например, я нашел следующие книги полезными.
Гравюры из книги М. Айгнера, Г. Циглера
От исчисления к когомологиям Иб Мадсен, Йорген Торнехаве
Основная теорема алгебры Б. Файна, Г. Розенбергера.
$\endgroup$
$\begingroup$
Если цель состоит в том, чтобы показать им «интересную» математику, есть много доступных источников, в зависимости от того, что, по вашему мнению, относится к категории «интересных», а также уместных.
Для начала, книги Мартина Гарднера (и, если у вас есть хороший индекс цитирования, некоторые книги, в которых цитируются книги Гарднера) должны занять вас на некоторое время. Используя только его книги, вы можете написать краткое описание 10 задач, каждая с тремя или четырьмя параграфами установки, результата и применения, и обратиться к одной из книг Гарднера для расширения темы. Вместо Гарднера вы могли бы использовать других авторов.
Вместо Гарднера вы могли бы использовать других авторов.
Если цель состоит в том, чтобы стимулировать их интерес к математике, показывая им задачи, я скромно предлагаю следующее: просмотреть открытые списки задач, а также указатели таких книг, как книга Гарднера, выбрать около 100 задач из каждой и начать составлять 10 списков. из 20 задач, половина которых решена/понятна, половина — нет, и все они доступны. Только на MathOverflow вы видите как минимум одну такую задачу каждые два-три дня. Затем на следующие десять семестров у вас есть список из двадцати задач из разных областей, чтобы захватить воображение студентов. Бонусные баллы для вас, если вы можете заставить их исследовать и цитировать литературу о том, какая работа была проделана по проблемам. Держите под рукой записи ваших источников, чтобы сравнить их с найденными вашими учениками.
Если вы спрашиваете меня о конкретных проблемах, в вашем вопросе должно быть указано, что это так, и в этом случае я могу рассказать вам о некоторых доступных проблемах, над которыми я работал, которые можно было бы решить, приложив к ним еще немного локтя и мозговой смазки.
Герхард «Спросите меня о проектировании системы» Пасеман, 12.03.2011
$\endgroup$
1
$\begingroup$
Я буду писать с точки зрения студента бакалавриата. Я думаю, что одна из причин, по которой математика в бакалавриате не интересна, — это технический жаргон, с которым студенты сталкиваются в процессе обучения. Обычно нужно было понять, почему приходится придумывать такой конкретный метод, концепцию или теорию, чтобы понять предмет. Полезность любой математики, которую они изучили, обычно проявляется только в примерах расчетов или задач.
Но есть нечто гораздо большее. Для действительно способного первокурсника-математика, я бы предположил, что обычного учебного материала недостаточно, а учебник+лекция+офисные часы не решают его или ее проблемы. Тем не менее имеющиеся в его распоряжении технические средства не позволяют ему или ей проводить настоящие исследования. Помню, когда я учился в старшей школе, я спросил аспиранта-математика, существуют ли две разные голоморфные структуры на четырехмерном многообразии. В то время я знал кое-какой комплексный анализ и кое-какие дифференциальные многообразия, но их недостаточно, чтобы дать ответ на этот вопрос. Даже сейчас я не знаю да или нет ответьте в понятной мне форме. Действительно сообразительный первокурсник-математик, скорее всего, будет задавать странные вопросы, которые он или она не может решить, и это настолько его или ее зацепило, что он или она решили бросить математику. Столь же вероятно, что он или она сочтет задачи Патнэма слишком техническими, решение задач слишком трудоемким, и в конце концов изучение математики превратится в освоение машины. Я до сих пор помню те дни, когда я застрял со своими проблемами в чтении Хэтчера, в то время я серьезно рассматривал возможность перехода к истории. И я едва ли могучий студент-математик.
Помню, когда я учился в старшей школе, я спросил аспиранта-математика, существуют ли две разные голоморфные структуры на четырехмерном многообразии. В то время я знал кое-какой комплексный анализ и кое-какие дифференциальные многообразия, но их недостаточно, чтобы дать ответ на этот вопрос. Даже сейчас я не знаю да или нет ответьте в понятной мне форме. Действительно сообразительный первокурсник-математик, скорее всего, будет задавать странные вопросы, которые он или она не может решить, и это настолько его или ее зацепило, что он или она решили бросить математику. Столь же вероятно, что он или она сочтет задачи Патнэма слишком техническими, решение задач слишком трудоемким, и в конце концов изучение математики превратится в освоение машины. Я до сих пор помню те дни, когда я застрял со своими проблемами в чтении Хэтчера, в то время я серьезно рассматривал возможность перехода к истории. И я едва ли могучий студент-математик.
Решение такой проблемы должно заключаться в том, чтобы направить его или ее к чтению какой-нибудь магистерской работы. Если он или она сможет понять, как работающий математик решил задачу, развил математическую концепцию или расширил теорию, это было бы очень полезно, поскольку помогает ученику достичь более высокого уровня математической зрелости, недостижимого в обычной учебной программе. Абель однажды ответил: «Я читаю мастеров, а не их учеников». Ясно, что многие прошлые математические работы были отброшены или забыты, однако профессор всегда может выбрать что-то относительно более читабельное. Если это невозможно, профессор должен, по крайней мере, разработать индивидуальный класс с хорошей дополнительной литературой.
Если он или она сможет понять, как работающий математик решил задачу, развил математическую концепцию или расширил теорию, это было бы очень полезно, поскольку помогает ученику достичь более высокого уровня математической зрелости, недостижимого в обычной учебной программе. Абель однажды ответил: «Я читаю мастеров, а не их учеников». Ясно, что многие прошлые математические работы были отброшены или забыты, однако профессор всегда может выбрать что-то относительно более читабельное. Если это невозможно, профессор должен, по крайней мере, разработать индивидуальный класс с хорошей дополнительной литературой.
Чего я никак не могу понять, так это почему профессор использует бесполезный учебник для бакалавриата в своем классе вместо того, чтобы читать хорошие математические статьи или даже конспекты лекций. Я надеюсь, что профессор сможет указать, где материала недостаточно, где результаты были обновлены, а где были разработаны лучшие стратегии. Хороший список типовых задач в сочетании с хорошим чтением по математике может изменить людей. К сожалению, у меня не было возможности провести такой класс в США. В результате мне пришлось поехать в Москву, где я заново открыл для себя математику. Но я надеюсь, что будущих студентов ждет лучшая судьба.
К сожалению, у меня не было возможности провести такой класс в США. В результате мне пришлось поехать в Москву, где я заново открыл для себя математику. Но я надеюсь, что будущих студентов ждет лучшая судьба.
$\endgroup$
$\begingroup$
Мы читаем ежегодный курс математики из 8 лекций по топологии поверхностей, характеристике Эйлера и петлям на поверхностях. Это скорее дискуссионная сессия, чем лекция. Хотя он в первую очередь предназначен для определенной группы студентов-женщин, участвующих в какой-либо программе, я считаю, что темы могут быть представлены любой группе студентов, которые достаточно заинтересованы! Вот ссылка, кому интересно:
http://www.math.sunysb.edu/~basu/courses/WSE187-spring11/WSE187.html
Мы предполагаем, что у них нет базовых знаний (в области исчисления или линейной алгебры). Это очень практично, и они пытаются разработать концепцию того, что такое поверхность и какие числовые инварианты помогают различать их.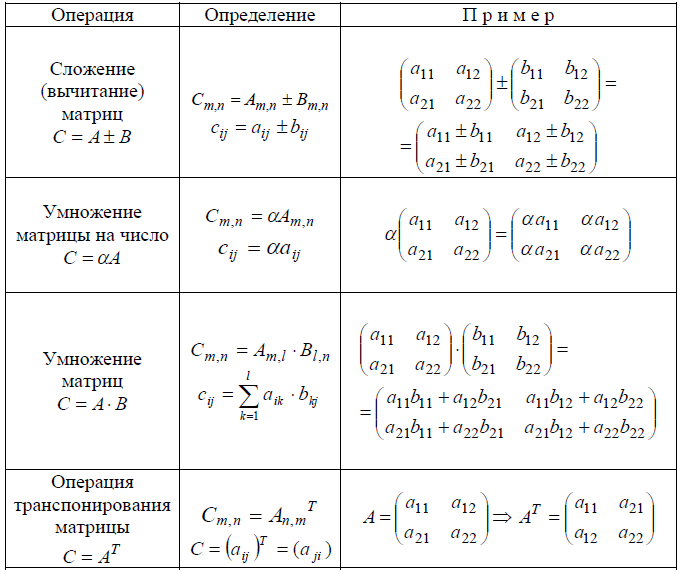 Помимо прочего, мы рекомендуем им использовать пластилин для моделирования заполненных поверхностей и помогать им визуализировать деформации. Мы также развлекаемся, разрезая ленты Мебиуса по различным кривым и нарезая рогалики на звенья! По моему опыту (а я учил его только дважды), некоторые из этих практических занятий всегда вызывают восторг даже у тех, кто не проявляет особого интереса. В конце концов, им весело узнавать, что в футбольном мяче так много пятиугольников и шестиугольников, в основном благодаря Эйлеру! В конце они должны сделать презентацию, выясняя и объясняя (из основных принципов), как некоторая задача (назначенная им) может быть решена с помощью топологии — решение может быть в виде картинок, пластилина или любого другого материала, если это необходимо. быть. Кому интересно, посмотрите презентации прошлого года:
Помимо прочего, мы рекомендуем им использовать пластилин для моделирования заполненных поверхностей и помогать им визуализировать деформации. Мы также развлекаемся, разрезая ленты Мебиуса по различным кривым и нарезая рогалики на звенья! По моему опыту (а я учил его только дважды), некоторые из этих практических занятий всегда вызывают восторг даже у тех, кто не проявляет особого интереса. В конце концов, им весело узнавать, что в футбольном мяче так много пятиугольников и шестиугольников, в основном благодаря Эйлеру! В конце они должны сделать презентацию, выясняя и объясняя (из основных принципов), как некоторая задача (назначенная им) может быть решена с помощью топологии — решение может быть в виде картинок, пластилина или любого другого материала, если это необходимо. быть. Кому интересно, посмотрите презентации прошлого года:
http://www.math.sunysb.edu/~basu/courses/WSE187-spring10/Lectures_WSE187.html
Наконец, хотя мы и не прошли курс, упомянутый выше, включая кое-что, ведущее к четырем Теорема о цвете тоже должна доставить массу удовольствия как учителям, так и ученикам!
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Начальная математика в колледже | Колледж искусств и наук
Начальное размещение на соответствующем уровне математики имеет важное значение для успеха учащихся в естественных науках, технике, экономике, бизнесе и многих других областях. Для большинства студентов, которые изучают математику на первом курсе, выбор между курсами в последовательности исчисления первого года обучения МАТЕМАТИКА 1300, МАТЕМАТИКА 1400, МАТЕМАТИКА 1410 или МАТЕМАТИКА 1700 или МАТЕМАТИКА 2100.
Диагностический экзамен по математике
Учащиеся, которые намереваются пройти курс математического анализа в Пенсильвании, должны пройти Диагностику по математике, доступную через систему Canvas, и поработать со своим научным руководителем, чтобы определить, какой курс математики подходит, учитывая их предыдущее знакомство с математикой и результаты экзамена.
Ведомственные экзамены на кредит
Все учащиеся имеют право сдавать внутренние экзамены факультета математики для получения кредита, которые предлагаются в начале осеннего семестра. Более подробная информация доступна на веб-сайте отдела математики.
Более подробная информация доступна на веб-сайте отдела математики.
Расширенное размещение
Учащийся может получить зачет по МАТЕМАТИКЕ 1400 (1 у.е.), набрав:
- 5 баллов на экзамене Advanced Placement (A.P.) Calculus BC
- 7 баллов по международному бакалавриату (математика [высший уровень] плюс дополнительная математика).
Зачет по экзамену A.P. Calculus AB не засчитывается независимо от количества баллов.
Математический факультет не засчитывает иностранных экзаменов, таких как немецкий Abitur, французский бакалавриат и английский A-Levels.
Курсы по математическому анализу
МАТЕМАТИКА 1300 готовит учащихся с небольшими математическими способностями или вообще без них к старшей школе или нуждающихся в укреплении основ своих математических навыков. Учащиеся, чья программа средней школы не дала им необходимых знаний по алгебре и тригонометрии, должны проконсультироваться со своим контактным консультантом в колледже, прежде чем продолжить курс математического анализа.
МАТЕМАТИКА 1400 — следующий курс в последовательности вычислений. Учащиеся с кредитом MATH 1400 могут выбрать продолжение последовательности исчисления для своих основных или интеллектуальных интересов. Для некоторых специальностей (таких как биохимия, химия, математика, физика) специально требуются МАТЕМАТИКА 1400 и МАТЕМАТИКА 1410; в противном случае учащиеся, которым требуется второй семестр математического анализа, могут пройти либо 1410, либо 1510. Не всем учащимся нужно пройти второй семестр математического анализа; если вы сомневаетесь, проконсультируйтесь с пред-специалистом или консультантом отдела.
МАТЕМАТИКА 1410 и более продвинутые курсы математики подойдут учащимся с кредитом MATH 1400 и прохождением диагностического экзамена. Учащиеся, интересующиеся математикой или естественными науками, могут также рассмотреть более сложную версию экзаменов «Исчисление» с отличием, МАТЕМАТИКА 1610 и МАТЕМАТИКА 2600 (аналоги МАТЕМАТИКА 1410 и МАТЕМАТИКА 2400). Эти курсы будут охватывать материал более глубоко и включать обсуждение теории, а также расчеты.
Эти курсы будут охватывать материал более глубоко и включать обсуждение теории, а также расчеты.
Для получения дополнительной информации и рекомендаций по выбору правильного курса математики и других курсов STEM в зависимости от места обучения, образования в старшей школе и текущих интересов см. нашу инфографику Entering the STEM Fields в Penn, а также PDF-файл Calculus@Penn.
Примечание. Учащиеся, которые запрашивают математический курс, могут не получить именно ту лекцию или раздел декламации, который им нужен. Чтобы попасть на курс, может потребоваться некоторое упорство. Департамент никогда не отказывает студенту, потому что курс заполнен. Учащийся всегда может куда-то вписаться, хотя и не обязательно в секцию или в то время, которое предпочитает учащийся. Учащимся, которым нужна помощь в поступлении на курс, следует связаться с отделом математики.
Ключевые особенности курсов по математическому анализу
- Согласованные секции.
 Все разделы курса имеют одинаковый темп, структуру и лекции, независимо от того, кто является инструктором. Это дает студентам более однородный опыт, менее зависимый от получения конкретной профессии.
Все разделы курса имеют одинаковый темп, структуру и лекции, независимо от того, кто является инструктором. Это дает студентам более однородный опыт, менее зависимый от получения конкретной профессии. - Асинхронные видеолекции. Все лекции проходят в виде коротких видеороликов. Это должно помочь вам управлять своим временем, позволяя смотреть лекции в любое время.
- Активное обучение. В обычное время лекции будет активное решение проблем или другие действия, в зависимости от инструктора. Это должно дать вам возможность больше взаимодействовать со своими сверстниками и вашим инструктором.
- Промежуточных экзаменов нет. Промежуточные экзамены заменяются викторинами из расчета три раза в месяц. Выпускной экзамен все равно будет, но он будет иметь меньшее значение, чем в прошлом. Это снижает тревогу в середине недели.
- Учебник не требуется. Мы разработали собственные «тексты» на основе видео и создали дополнительные материалы, которые могут служить в качестве ресурсов.
 Это спасет вас от неприятных расходов.
Это спасет вас от неприятных расходов. - Перенесенные чтения. Поскольку вы тратите время на просмотр лекций в Интернете, класс не будет собираться так часто. В частности, во время лекций будут проводиться декламации с вашим ТА. Это означает, что больше никаких декламаций в 8 утра.
Преимущества и подготовка к курсам по математическому анализу
- Меньше стресса; больше справедливости. С большим количеством викторин с низкими ставками и периодическими пересдачами вся ваша оценка не зависит от одного экзамена с высокими ставками.
- Лучшее управление временем. Без декламации в 8 утра и просмотра лекций, когда вы хотите, у вас будет больше гибкости в том, как проходит ваша неделя. Еженедельная структура курса будет мотивировать вас оставаться в курсе материала.
- Меньшая разница между секциями. Поскольку все просматривают один и тот же набор лекций, вам не нужно так сильно беспокоиться о том, в какой раздел вы попадете.
 Если ваш друг находится в другой секции, вы все равно можете заниматься вместе.
Если ваш друг находится в другой секции, вы все равно можете заниматься вместе. - Меньше расходов. Нет дорогого обязательного учебника.
- Современная учебная программа. Поскольку мы не привязаны к определенному тексту (как правило, созданному для массового обращения), мы можем адаптировать наши инструкции к тому, что лучше всего подходит для студентов Пенна. Мы прилагаем все усилия, чтобы модернизировать учебную программу, чтобы показать вам примеры и приложения, имеющие отношение к вам и вашим областям обучения.
Как мне подготовиться? Если вы какое-то время не занимались математикой (т. е. не проходили курс предварительного исчисления или исчисления в старшем классе средней школы), было бы неплохо просмотреть материал из последнего курса, который вы прошли — почистить на эти производные формулы и тригонометрические тождества! Но самое главное — быть готовым взяться за дело на одном из этих суровых и динамичных курсов. Для вас будет важно не отставать от течения и посвящать некоторое время изучению математических понятий и/или отработке методов почти каждый день.
Для вас будет важно не отставать от течения и посвящать некоторое время изучению математических понятий и/или отработке методов почти каждый день.
Я новый студент. Какой курс мне выбрать? Диагностический тест по математике, который вы проходите этим летом онлайн, даст разумные рекомендации относительно того, какой курс (из 1300, 1400 и 1410) вам следует пройти этой осенью. Но, как правило, если вы изучали математический анализ AB в старшей школе, вам следует начать с математики 1400, если вы сдавали математический анализ BC и получили 5 на экзамене (если вы его сдавали) и очень уверены в своих силах, тогда берите 114. Работайте с вашим консультантом. чтобы выбрать подходящий курс, а если есть серьезные сомнения, свяжитесь с математическим факультетом.
Как это будет работать с моей инвалидностью? Во многом новый формат должен предоставить учащимся с ограниченными возможностями более широкие возможности для изучения лекций в своем собственном темпе и повторения разделов при необходимости. Как обычно, инструкторы на курсах будут следовать рекомендациям Управления по делам студентов с ограниченными возможностями относительно соответствующих условий для еженедельных викторин и выпускного экзамена.
Как обычно, инструкторы на курсах будут следовать рекомендациям Управления по делам студентов с ограниченными возможностями относительно соответствующих условий для еженедельных викторин и выпускного экзамена.
Математика Размещение | Математика | Колледж науки и техники
Информация о вступительных экзаменах и экзаменах по математике
Все первокурсники должны сдать вступительный экзамен по алгебре факультета математики, даже если у них есть баллы SAT, ACT или AP. Новые студенты, которые приезжают в Сиэтлский университет с курсовой работой на уровне колледжа, которая может учитываться при выполнении требований SU по математике, свяжитесь со своим академическим консультантом, чтобы обсудить, следует ли вам сдавать вступительный экзамен по алгебре. Если вы планируете получить степень в области бизнеса, сестринского дела или в области, связанной с STEM, и приносите кредиты Running Start в SU, вам необходимо сдать экзамен по алгебре.
Есть два вступительных экзамена по математике: тест по алгебре из 30 вопросов и тест по тригонометрии из 9 вопросов. Тригонометрический тест должны пройти только учащиеся, желающие пройти наши занятия с сопутствующими триггерными предметами, МАТЕМАТИКА 1230, исчисление для наук о жизни или МАТЕМАТИКА 1334, исчисление I. Вступительные тесты представляют собой онлайн-тесты, которые можно пройти в удобное для вас время. Но учтите, что первокурсники должны сдать тест по алгебре до 1 июля. Тест по алгебре можно сдать только один раз, триггерный тест можно сдать дважды. Оба экзамена имеют ограничение по времени (тест по алгебре — 60 минут, тригонометрический тест — 30 минут), но без прокторинга. Ограниченное дополнительное время может быть добавлено с одобрения Службы поддержки людей с ограниченными возможностями.
Большинство первокурсников будут автоматически зарегистрированы для сдачи этих тестов. Но если вы обнаружите, что это не так, отправьте свой адрес электронной почты SU нашему ассистенту кафедры математики по адресу teegardj@seattleu. edu.
edu.
Вы можете узнать больше о вступительных экзаменах по математике в нашем документе с часто задаваемыми вопросами: Страница часто задаваемых вопросов находится здесь!
Баллы, необходимые для поступления на следующие математические курсы:| Курс | ACT Оценка | Оценка SAT | Минимум S.U. Оценка размещения |
|---|---|---|---|
| МАТЕМАТИКА 1000 | 18-22 | 490-550 | Оценка по алгебре 4 |
| МАТЕМАТИКА 1010 | 23-27 | 560-650 | Оценка по алгебре 15 |
| МАТЕМАТИКА 1021 | 23-27 | 560-650 | Оценка по алгебре 15 |
| МАТЕМАТИКА 1022 | 27-36 | 640-800 | Оценка по алгебре 23 |
| МАТЕМАТИКА 1130 | 27-36 | 640-800 | Оценка по алгебре 23 |
| МАТЕМАТИКА 1210 | 27-36 | 640-800 | Оценка по алгебре 23 |
| МАТЕМАТИКА 1230 | 27-36 и тригонометрическая оценка 4* | 640-800 и оценка триггерного теста 4* | 23 балла по алгебре и либо MATH 1022, взятые одновременно, либо Trig. оценка 4 оценка 4 |
| МАТЕМАТИКА 1331 | 27-36 | 640-800 | Оценка по алгебре 23 |
| МАТЕМАТИКА 1334 | 28-36 и триггер. оценка теста 6* | 660-800 и триггер. оценка теста 6* | 25 баллов по алгебре и либо MATH 1022, сдаваемые одновременно, либо Trig. оценка 6 |
*Сопутствующим условием для MATH 1230 и 1334 является MATH 1022 или указанный балл на вступительном экзамене Trig
AP/Advanced Placement
Учащийся, сдавший экзамен AP по математическому анализу (AB или BC) и набравший 3 балла или выше, получит 5 кредитов за один или несколько курсов по математическому анализу. Рекомендации приведены ниже. Для получения дополнительной информации обратитесь в офис регистратора или в отдел математики.
Advanced Placement AB Calculus Exam:
| Оценка | Кредит предоставлен: |
|---|---|
| 3 | MATH 1130/Исчисление для бизнеса или MATH 1230/Исчисление для наук о жизни |
| 4 | МАТЕМАТИКА 1334/Исчисление I |
| 5 | МАТЕМАТИКА 1334/Исчисление I и МАТЕМАТИКА 1335/Исчисление II |
Advanced Placement BC Calculus Exam:
| Оценка | Кредит предоставлен: |
|---|---|
| 3 | МАТЕМАТИКА 1334/Исчисление I |
| 4 | МАТЕМАТИКА 1334/Исчисление I, МАТЕМАТИКА 1335/Исчисление II |
| 5 | МАТЕМАТИКА 1334/Исчисление I, МАТЕМАТИКА 1335/Исчисление II и, возможно, МАТЕМАТИКА 1336/Исчисление III* |
* Зачет по МАТЕМАТИКЕ 1336 может быть предоставлен после консультации с заведующим кафедрой математики.
В исключительных случаях учащийся может выбрать сдачу экзамена на факультете для освобождения от требований или зачета одного или нескольких курсов. Если будет предоставлен отказ, Департамент математики подаст ходатайство об исключении из политики. Чтобы получить зачет, студент должен следовать Политике экзамена Seattle University Credit by Exam. За этот процесс взимается плата в размере 475 долларов США. Предлагаются следующие ведомственные экзамены:
- Поступающие студенты, сдавшие экзамен по математическому анализу для повышения квалификации по МАТЕМАТИКЕ 1334 с оценкой B или выше, а затем завершившие MATH 1335 с оценкой C или выше, получат право на освобождение от предварительного зачисления или зачет по МАТЕМАТИКЕ 1334.
- Поступающие студенты, которые сдали экзамен отделения по математическому анализу для повышения квалификации по МАТЕМАТИКЕ 1334 и МАТЕМАТИКА 1335 с оценкой B или выше, а затем завершили МАТЕМАТИКА 1336 с оценкой C или выше, получат право на освобождение от предварительного зачисления или зачет по МАТЕМАТИКЕ 1334 и 1335.

A-Levels и IB/Международный бакалавриат
Учащийся, имеющий квалификацию A-Level или международный бакалавриат по математическому анализу, может получить кредит за один или несколько курсов по математическому анализу. Пожалуйста, ознакомьтесь с приведенными ниже ссылками на политику для получения подробной информации или свяжитесь с отделом математики для получения дополнительной информации.
Политика зачисления на экзамен A-Level
Политика международного бакалавриата
Информация о специальном зачислении
Для начала найдите ниже путь, который лучше всего описывает ваши интересы и специальность.
- Биология и науки о жизни
- Бизнес (кроме специальностей, связанных с экономикой в аспирантуре)
- Гуманитарные и социальные науки
- Сестринское дело
- Специальности STEM (включая специальности экономики для аспирантов)
ПРИМЕЧАНИЕ: Эта важная информация не предназначена для замены рекомендаций консультанта. Он отражает понимание Отдела математики по состоянию на январь 2017 года, но, пожалуйста, проконсультируйтесь с консультантом в вашей основной области относительно самых последних требований.
Он отражает понимание Отдела математики по состоянию на январь 2017 года, но, пожалуйста, проконсультируйтесь с консультантом в вашей основной области относительно самых последних требований.
Биология и науки о жизни
Студенты первого курса без кредита AP по математическому анализу или предыдущих кредитов по математике в колледже будут зачислены на один или несколько из следующих курсов математики:
- МАТЕМАТИКА 1000 Функции и алгебраические методы
- МАТЕМАТИКА 1021 Предварительное исчисление: алгебра
- МАТЕМАТИКА 1022 Предварительное исчисление: тригонометрия
- MATH 1230 Расчет для наук о жизни (только осень и весна)
Бизнес
(кроме экономических специальностей, поступающих в аспирантуру)
Учащиеся первого года обучения, не имеющие зачетных единиц AP по математическому анализу или предыдущих зачетных единиц по математике в колледже, будут зачислены на один или несколько из следующих математических курсов. Примечание: Специалисты, специализирующиеся в области экономики, заинтересованные в том, чтобы иметь сильный количественный опыт, должны подготовиться к прохождению полной последовательности исчисления.
Примечание: Специалисты, специализирующиеся в области экономики, заинтересованные в том, чтобы иметь сильный количественный опыт, должны подготовиться к прохождению полной последовательности исчисления.
- МАТЕМАТИКА 1000 Функции и алгебраические методы
- МАТЕМАТИКА 1010 Колледж Алгебра для бизнеса
- МАТЕМАТИКА 1130 Расчет для бизнеса
Гуманитарные и социальные науки
Если ваша специальность находится в Колледже искусств и наук, вам, скорее всего, потребуется сдать только UCOR 1200, если только вы не решите изучать высшую математику. UCOR 1200 не требует дополнительных условий, кроме поступления на бакалавриат Сиэтлского университета. UCOR 1200 не дает вам право посещать дополнительные занятия по математике. UCOR 1200 регулярно предлагается со следующими тематическими вариациями:
- Моделирование эпидемий (Cole, Oliveras)
- Математическое рассуждение (Бахо, Стюарт)
- Мультикультурная математика (Хамфрис)
- Количественная грамотность и социальная справедливость (Бахо, Генрих, Робертсон)
Специальности по сестринскому делу
Студенты первого курса, интересующиеся сестринским делом, должны пройти курс MATH 1010 или выше. Перед поступлением в SU студенты-переводчики, заинтересованные в сестринском деле, должны выполнить требования по математике. Пожалуйста, свяжитесь с колледжем медсестер для получения более подробной информации. Следующие курсы могут представлять интерес:
Перед поступлением в SU студенты-переводчики, заинтересованные в сестринском деле, должны выполнить требования по математике. Пожалуйста, свяжитесь с колледжем медсестер для получения более подробной информации. Следующие курсы могут представлять интерес:
- МАТЕМАТИКА 1010 Колледж Алгебра для бизнеса
- МАТЕМАТИКА 1021 Предварительное исчисление: алгебра
Специальности STEM
(включая специальности экономики, связанные с аспирантурой)
Учащиеся первого года обучения, не имеющие кредитов по математическому анализу Advanced Placement или предыдущих кредитов по математике в колледже, будут поступать на один или несколько из следующих математических курсов:
- MATH 1000 Functions & Алгебраические методы
- МАТЕМАТИКА 1021 Предварительное исчисление: алгебра
- МАТЕМАТИКА 1022 Предварительное исчисление: тригонометрия
- МАТЕМАТИКА 1334 Исчисление I
Блок-схема курса
Следующая загружаемая таблица представляет собой руководство по правильной последовательности математических занятий в Сиэтлском университете.



 Асимптоты
Асимптоты Определители
Определители Теория
Теория Необходимый признак сходимости
Необходимый признак сходимости Все разделы курса имеют одинаковый темп, структуру и лекции, независимо от того, кто является инструктором. Это дает студентам более однородный опыт, менее зависимый от получения конкретной профессии.
Все разделы курса имеют одинаковый темп, структуру и лекции, независимо от того, кто является инструктором. Это дает студентам более однородный опыт, менее зависимый от получения конкретной профессии.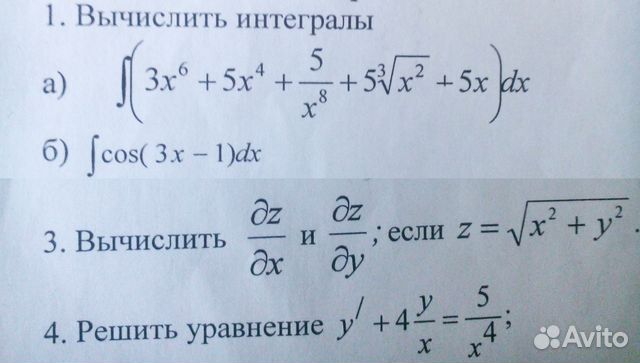 Это спасет вас от неприятных расходов.
Это спасет вас от неприятных расходов. Если ваш друг находится в другой секции, вы все равно можете заниматься вместе.
Если ваш друг находится в другой секции, вы все равно можете заниматься вместе.