Формулы сокращенного умножения — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Формулы сокращенного умножения
1) Квадрат суммы.
2) Квадрат разности.
3) Разность квадратов.
4) Куб суммы.
5) Куб разности.
6) Сумма кубов.
7) Разность кубов.
8) Треугольник Паскаля.
9) Бином Ньютона.
(a b) a 2ab b
2
2
Квадрат суммы двух чисел равен:
квадрату первого числа,
плюс удвоенное произведение
первого числа на второе,

(
=
+
+2
2
) =
+
2
Например:
1). m n
m 2mn n
2). 1 p
1 2 p p
3). 2m 5n
4m 20mn 25n
2
2
2
2
4). 3 x 4 y
2
2 2
3 2
2
3
5 2
2
2
9 x 24 xy 16 y
6) 3ab 2c
7). p q
5). a b
2
2
2
a 2a b b
4
2
2
2
2
4
9a b 12ab c 4c
2
4
2 3
p 2p q q
6
3
5
10
6
(a b) a 2ab b
2
2
2
Квадрат разности двух чисел равен:
квадрату первого числа,
минус удвоенное произведение
первого числа на второе,
плюс квадрат второго числа.
Формула шутка
(
=
— ) =
-2
+
2
Например:
1). m n
m 2mn n
2). 1 p
1 2 p p
3). 2m 5n
4m 20mn 25n
2
2
2
2
4). 3 x 4 y
2
2 2
3 2
2
3
5 2
2
2
9 x 24 xy 16 y
6) 3ab 2c
7). p q
5). a b
2
2
2
a 2a b b
4
2
2
2
2
4
9a b 12ab c 4c
2
4
2 3
p 2p q q
6
3
5
10
6
a b a b a b
2
2
Разность квадратов двух чисел равна:
произведению
разности этих чисел на их сумму.

Формула шутка
2
=(
—
2
=
.
— )( + )
Например:
y x y x
2
2). 9 3m 3 3m 3 3m
1). y x
2
2
3). 16 p
4
4). 25 a
6
5). m n
4
2
6). 1 x
4
7). p 49
8
4 p 4 p
5 a 5 a
m n m n
1 x 1 x
p 7 p 7
2
2
3
2
3
2
2
4
2
4
( a b)
3
a 3a b 3ab b
3
2
2
Куб суммы двух чисел равен
кубу первого числа плюс утроенное
произведение квадрата первого
числа на второе, плюс утроенное
числа на квадрат второго числа, плюс
куб второго числа.
3
Например:
1). x y
3
x 3 x y 3 xy y
3
2
2
3
2). a 2 a 3 6a 2 12a 8
3
3). 2a 3b 8a 3 3 4a 2 3b 3 2a 9b 2 27b 3
3
4). m 4 m 3 3 m 2 4 3 m 16 64
3
5). x 3 z x 3 x 3 z 3 x 9 z 27 z
3
3
2
2
6). 2b 3 8b 3 4b 3 3 2b 9 27
3
3
2
7). n 1 n 3n 3n 1
2
3
6
4
2
3
( a b)
3
a 3a b 3ab b
3
2
2
3
Куб разности двух чисел равен
кубу первого числа минус утроенное
произведение квадрата первого
числа на второе плюс утроенное
произведение первого
числа на квадрат второго числа минус куб
второго числа.
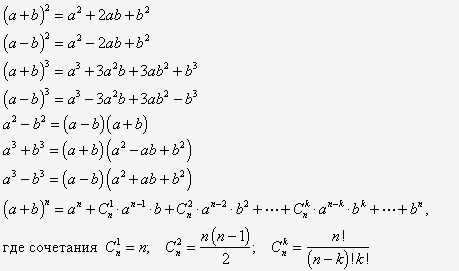
Например:
1). x y
3
x 3 x y 3 xy y
3
2
2
3
2). a 2 a 3 6a 2 12a 8
3
3). 2a 3b 8a 3 3 4a 2 3b 3 2a 9b 2 27b 3
3
4). m 4 m 3 3 m 2 4 3 m 16 64
3
5). x 3 z x 3 3 x 2 3 z 3 x 9 z 2 27 z 3
3
6). 2b 3 8b 3 3 4b 2 3 3 2b 9 27
3
3
7). n 1 n 3n 3n 1
2
6
4
2
a b
3
3
a b a ab b
2
2
Сумма кубов равна
произведению суммы этих чисел
на неполный квадрат их разности.
Например:
1).m n
3
3
2).x 8
3
m n m mn n
2
x 2 x 2 x 4
2
2
1 m 1 m m
4).x 8 y x 2 y x 2 x y 4 y
5).8m n 2m n 4m 2m n n
6).27 a 3 a 9 3a a
7).64 p q 4 p q 16 p 4 p q q
3).1 m
6
6
2
3
6
2
2
9
4
4
2
3
2
4
3
9
2
2
3
6
3
4
8
2
12
3
4
6
a b
3
3
a b a ab b
2
2
Разность кубов равна
произведению разности этих чисел
на неполный квадрат их суммы.

Например:
1).m n
3
3
2).x 8
3
m n m mn n
2
x 2 x 2 x 4
2
2
1 m 1 m m
4).x 8 y x 2 y x 2 x y 4 y
5).8m n 2m n 4m 2m n n
3 a 9 3a a
6).27 a
7).64 p q 4 p q 16 p 4 p q q
3).1 m
6
6
2
3
6
2
2
9
4
4
2
3
2
4
3
9
2
2
3
6
3
4
8
2
12
3
4
6
Треугольник Паскаля.
Степень
двучлена
Коэффициенты
a b
1
a b
0
a b
2
1
1 1
1 2 1
a b
1 3 3 1
a b
1 4 6 4 1
3
4
a b
5
1 5 10 10 5 1
6
1 6 15 20 15 6 1
a b
Бином Ньютона.
a b
n
1 n 1
n
2 n 2 2
n
n 1
n
a C a b C a b … C ab
n
n 1
b
n!
n n 1 … n k 1
C
n k !k!
k!
k
n
n
English Русский Правила
Таблица квадратов натуральных чисел. Формулы сокращенного умножения
Как научиться считать быстро и без калькулятора? Ведь и на ЕГЭ, и на ОГЭ по математике пользоваться калькулятором вы не можете.
Первое, что вам поможет, — это знание таблицы квадратов натуральных чисел. Учите наизусть, как таблицу умножения!
Все мы изучали в средней школе формулы сокращенного умножения. Правда, тогда мы не вполне понимали, зачем нам это надо. Все эти квадраты суммы и разности квадратов… А нужны они для того, чтобы быстро считать. И когда на ЕГЭ по математике на решение варианта у вас всего 3 часа 55 минут, а успеть надо очень много, — эти формулы просто незаменимы.
Как применять эти формулы на практике?
Например,
;
.
И более сложная ситуация. Она может вам встретиться в задании 7 Профильного ЕГЭ по математике, если вдруг придется считать площадь криволинейной под графиком функции как разность первообразных.
Правда, есть и более простое решение этой задачи. И в нем тоже используется одна из формул сокращенного умножения.
А вот и еще один полезный лайфхак:
Числа, оканчивающиеся на 5, в квадрат возводятся мгновенно.
Чтобы найти квадрат числа ( – не обязательно цифра, любое натуральное число), умножаем на и к результату приписываем 25.)
Например,
.
Разберем еще несколько примеров на формулы сокращенного умножения.
1. Вычислите:
Решение:
Применим формулу разности кубов для выражения в числителе.
Ответ: 123.
2. Вычислите
Решение:
Конечно, мы не будем отдельно вычислять значения выражений в числителе и знаменателе дроби.
Применим формулы сокращенного умножения. В числителе – квадрат разности. В знаменателе – разность квадратов.
Ответ: 1,25.
Такие задания могут встретиться в первой части ЕГЭ по математике. А вычисления этого типа – в «экономической» задаче из второй части.
3. Найдите значение выражения если a = 47, b = 999.
Решение:
Числитель дроби является полным квадратом;
Знаменатель дроби преобразуем к виду:
Получим:
Если a = 47, b = 999, получаем:
4. Найдите значение выражения:
Найдите значение выражения:
Решение:
Сделаем замену переменной: тогда
Запишем выражение в виде:
Квадратный трехчлен имеет корни и поэтому
Ответ: 2.
Рассмотрим задачи по теме: разложение на множители. Здесь мы тоже применяем формулы сокращенного умножения: разность квадратов, квадрат суммы и квадрат разности, разность кубов, сумма кубов… Все это может пригодиться, например, при решении задач с параметрами, а также уравнений и неравенств на ЕГЭ по математике.
Разложите на множители:
5.
Решение:
Применим формулу разности квадратов.
6.
Каждое из слагаемых содержит m в целой степени. Вынесем за скобки Также за скобки можно вынести 12. Получим:
Здесь мы применили формулу квадрата суммы.
7.
Решение:
Представим выражение в виде:
Выражение в скобках – это квадрат суммы. Получим:
Это разность квадратов. Применяем формулу:
разложили на множители.
8.
Такое выражение может встретиться в задаче с параметрами. Разложим его на множители:
9.
Решение:
Первые три слагаемые образуют полный квадрат:
Следовательно,
10.
Решение. Последние три слагаемые после вынесения знака минус образуют полный квадрат:
Тогда
Воспользуемся формулой разности квадратов и получим:
Тогда
Ответ:
Формулы сокращенного умножения помогут также при решении уравнений.
11. Решите уравнение:
Решение: По формуле разности кубов,
Тогда
Подставив в наше уравнение, получим:
Ответ: 2
3-8Обозначение суммирования
|

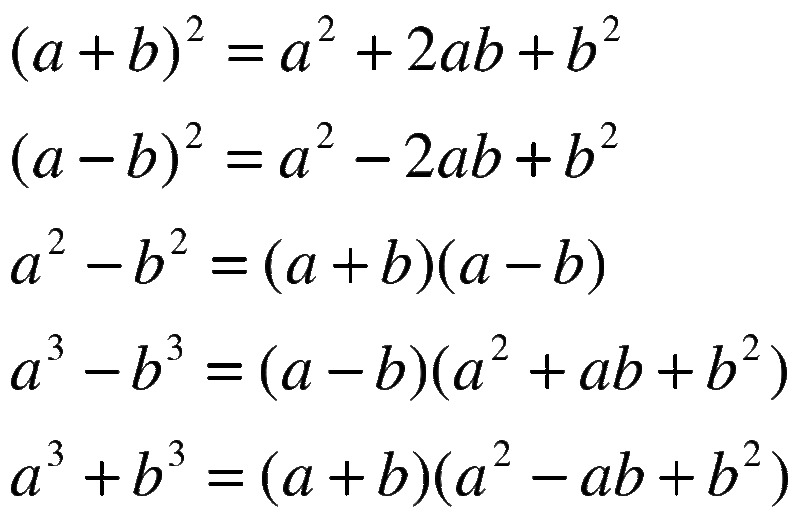 Лейн
Лейн д. Следующее
формула означает суммирование весов четырех виноградин:
д. Следующее
формула означает суммирование весов четырех виноградин:
