Формула x0 физика: В физике есть формула под названием закон равнопеременного движения , x=x0+v0t+-at^2/2, для чего она используется…

Формулы по физике

Механика

1. Давление Р=F/S

2. Плотность ρ=m/V

3. Давление на глубине жидкости P=ρ∙g∙h

4. Сила тяжести Fт=mg

5. Архимедова сила Fa=ρ_ж∙g∙Vт

6. Уравнение движения при равноускоренном движении

X=X₀+υ₀∙t+(a∙t²)/2 S= (υ²—υ₀²)/2а S= (υ+υ₀) ∙t /2

7. Уравнение скорости при равноускоренном движении υ=υ₀+a∙t

8. Ускорение a=(υ—υ ₀)/t

9. Скорость при движении по окружности υ=2πR/Т

10. Центростремительное ускорение a=

    υ²/R

11. Связь периода с частотой ν=1/T=ω/2π

12. II закон Ньютона F=ma

13. Закон Гука Fy=-kx

14. Закон Всемирного тяготения F=G∙M∙m/R²

15. Вес тела, движущегося с ускорением а↑ Р=m(g+a)

16. Вес тела, движущегося с ускорением а↓ Р=m(g-a)

17. Сила трения Fтр=µN

18. Импульс тела p=mυ

19. Импульс силы Ft=∆p

20. Момент силы M=F∙ℓ

21. Потенциальная энергия тела, поднятого над землей Eп=mgh

22. Потенциальная энергия упруго деформированного тела Eп=kx²/2

23. Кинетическая энергия тела Ek=mυ²/2

24. Работа A=F∙S∙cosα

25. Мощность N=A/t=F∙

    υ

26. Коэффициент полезного действия η=Aп/Аз

27. Период колебаний математического маятника T=2π√ℓ/g

28. Период колебаний пружинного маятника T=2 π √m/k

29. Уравнение гармонических колебаний Х=Хmax∙cos ωt

30. Связь длины волны, ее скорости и периода λ= υТ

Молекулярная физика и термодинамика

31. Количество вещества ν=N/ Na

32. Молярная масса М=m/ν

33. Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT

34. Основное уравнение МКТ P=nkT=1/3nm₀υ²

35. Закон Гей – Люссака (изобарный процесс) V/T =const

36. Закон Шарля (изохорный процесс) P/T =const

37. Относительная влажность φ=P/P₀∙100%

38. Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT

39. Работа газа A=P∙ΔV

40. Закон Бойля – Мариотта (изотермический процесс) PV=const

41. Количество теплоты при нагревании Q=Cm(T₂-T₁)

42. Количество теплоты при плавлении Q=λm

43. Количество теплоты при парообразовании Q=Lm

44. Количество теплоты при сгорании топлива Q=qm

45. Уравнение состояния идеального газа PV=m/M∙RT

46. Первый закон термодинамики ΔU=A+Q

47. КПД тепловых двигателей η= (Q₁ — Q₂)/ Q₁

48. КПД идеал. двигателей (цикл Карно) η= (Т₁ — Т₂)/ Т₁

Электростатика и электродинамика

49. Закон Кулона F=k∙q₁∙q₂/R²

50. Напряженность электрического поля E=F/q

51. Напряженность эл. поля точечного заряда E=k∙q/R²

52. Поверхностная плотность зарядов σ = q/S

53. Напряженность эл. поля бесконечной плоскости E=2πkσ

54. Диэлектрическая проницаемость ε=E₀/E

55. Потенциальная энергия взаимод. зарядов W= k∙q₁q₂/R

56. Потенциал φ=W/q

57. Потенциал точечного заряда φ=k∙q/R

58. Напряжение U=A/q

59. Для однородного электрического поля U=E∙d

60. Электроемкость C=q/U

61. Электроемкость плоского конденсатора C=S∙ε∙ε₀

    /d

62. Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2

63. Сила тока I=q/t

64. Сопротивление проводника R=ρ∙ℓ/S

65. Закон Ома для участка цепи I=U/R

66. Законы послед. соединения I₁=I₂=I, U₁+U₂=U, R₁+R₂=R

67. Законы паралл. соед. U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R

68. Мощность электрического тока P=I∙U

69. Закон Джоуля-Ленца Q=I²Rt

70. Закон Ома для полной цепи I=ε/(R+r)

71. Ток короткого замыкания (R=0) I=ε/r

72. Вектор магнитной индукции B=Fmax/ℓ∙I

73. Сила Ампера Fa=IBℓsin α

74. Сила Лоренца Fл=Bqυsin α

75. Магнитный поток Ф=BSсos α Ф=LI

76. Закон электромагнитной индукции Ei=ΔФ/Δt

77. ЭДС индукции в движ проводнике Ei=Вℓυsinα

78. ЭДС самоиндукции Esi=-L∙ΔI/Δt

79. Энергия магнитного поля катушки Wм=LI²/2

80. Период колебаний кол. контура T=2π ∙√LC

81. Индуктивное сопротивление X_L=ωL=2πLν

82. Емкостное сопротивление Xc=1/ωC

83. Действующее значение силы тока Iд=Imax/√2,

84. Действующее значение напряжения Uд=Umax/√2

85. Полное сопротивление Z=√(Xc-X_L)²+R²

Оптика

86. Закон преломления света n₂₁=n₂/n₁= υ ₁/ υ ₂

87. Показатель преломления n₂₁=sin α/sin γ

88. Формула тонкой линзы 1/F=1/d + 1/f

89. Оптическая сила линзы D=1/F

90. max интерференции: Δd=kλ,

91. min интерференции: Δd=(2k+1)λ/2

92. Диф. решетка d∙sin φ=k λ

Квантовая физика

93. Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U_зе

94. Красная граница фотоэффекта ν_к = Aвых/h

95. Импульс фотона P=mc=h/ λ=Е/с

Физика атомного ядра

96. Закон радиоактивного распада N=N₀∙2^—t/T

97. Энергия связи атомных ядер

E_CB=(Zm_p+Nm_n-Mя)∙c²

СТО

98. t=t₁/√1-υ²/c²

99. ℓ=ℓ₀∙√1-υ²/c²

100. υ₂=(υ₁+υ)/1+ υ₁∙υ/c²

101. Е = mс²

Формула равноускоренного движения в физике

Содержание:

• Определение и формула равноускоренного движения
• Основные кинематические величины при равноускоренном движении
• Примеры решения задач

Определение и формула равноускоренного движения

Определение

Движение, при котором за любые равные промежутки времени скорость меняется на одну величину, называют равнопеременным.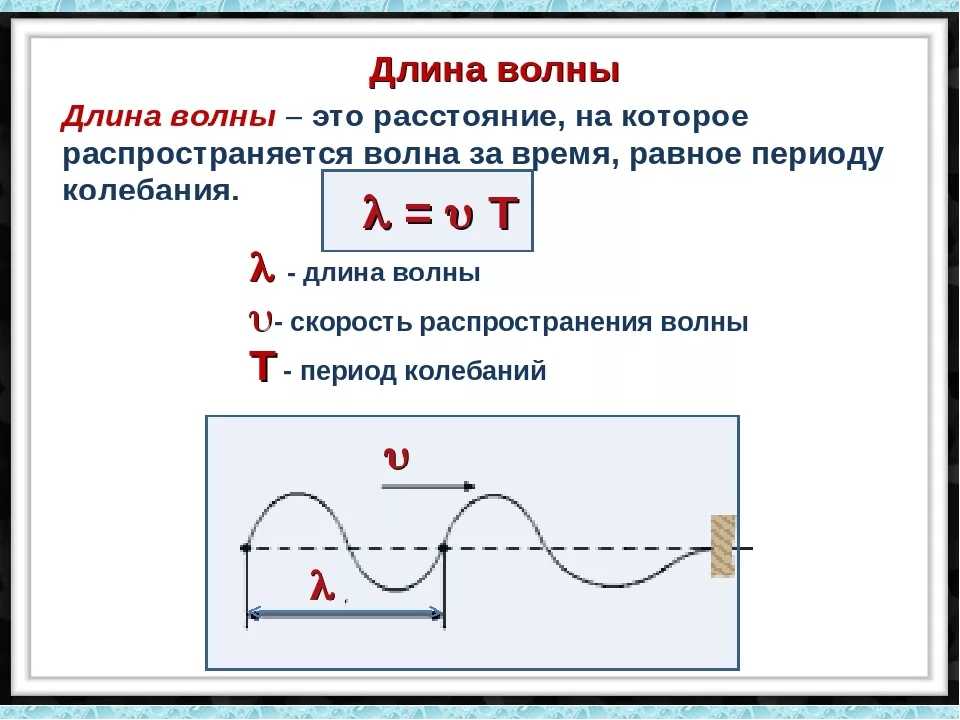 {2}}{l}$

Читать дальше: Формула силы Лоренца.

Уравнение скорости (формула): как найти скорость

Уравнение скорости — одна из фундаментальных формул в физике. Хотя многие понятия в физике имеют научные определения, отличные от их использования в разговорной речи, ваше интуитивное восприятие скорости, вероятно, довольно похоже на ее определение в физике. Уравнение скорости:

v _avg = xf-x0/tf-t0

Скорость — это просто скорость изменения положения объекта относительно выбранной точки отсчета, поэтому изменение положения, деленное на время. «Xf» — конечное положение объекта, а «X0» — начальное положение. Точно так же «Tf» — это конечный период времени, а «T0» — начальный период времени.

«Мне нравится физика. Я думаю, что это лучшая наука из всех трех, потому что в целом она более полезна. Вы узнаете о скорости, скорости и времени, и это все умные вещи». — Том Фелтон

Большое изменение положения за достаточно короткий промежуток времени означает, что объект имеет высокую скорость, в то время как небольшое изменение положения в течение большего периода времени означает, что объект имеет более низкую скорость.

Уравнение скорости

Фото: My Own

Единицы измерения скорости делятся на время. Подумайте, как скорость автомобиля часто выражается в километрах в час или милях в час. Средняя скорость объекта может быть определена как изменение положения объекта, деленное на время, затраченное на перемещение.

В обозначениях формулы скорости V(avg) — это средняя скорость объекта, а Δx — величина изменения положения объекта, называемая смещением. X0 — начальное положение объекта в момент времени t0, а Xf — конечное положение объекта в момент времени tf. Обратите внимание, что когда начальное время задано равным нулю, уравнение для средней скорости дается следующим образом:

Vavg = Δx/t

В этом уравнении скорость задается в виде вектора. Векторы — это геометрические объекты, имеющие как направление, так и величину, и поэтому их можно использовать для отслеживания движения чего-либо в пространстве. По отношению к скорости объекта скорость считается вектором, потому что перемещение считается вектором (обладающим как направлением, так и величиной). Скорость обычно указывается в метрах в секунду, так как метры — это международная система единиц. Однако вы часто будете видеть скорость, указанную в других единицах, таких как мили в час, километры в час и даже сантиметры в секунду.

Примеры

Давайте заполним формулу для скорости практическим примером:

Если кто-то идет по тротуару, начиная с дальнего конца тротуара, со скоростью -4 метра каждые пять секунд (отрицательно, потому что они движутся влево от своего начального положения), скорость смещения может быть выражена следующим образом: не предоставляют нам информацию о том, как человек действовал между их конечной точкой и их отправной точкой. Имея только среднюю скорость, мы не можем сказать, споткнулся ли человек и, следовательно, ему потребовалось больше времени, чтобы преодолеть расстояние, чем обычно. Вы можете разбить расстояние поездки на более мелкие участки и рассчитать эти отдельные скорости, чтобы получить больше информации о поездке. Например, общую скорость поездки, или Δxtot, можно представить в виде четырех различных сегментов — Δxa, Δxb, Δxc, Δxd.

«Все, что я делаю, так или иначе связано со скоростью». — Hansulrich Obrist

Чем меньшие фрагменты вы разбиваете на расчет скорости, тем больше информации вы можете получить о событиях во время полного движения объекта, или тем более подробной становится доступная информация. Для кусков интервалов измеренная скорость называется «мгновенной скоростью». Мгновенная скорость — это, по сути, скорость объекта в конкретный момент времени или средняя скорость в конкретный момент. Спидометр автомобиля показывает величину автомобиля, скорость изменения (а не направление изменения). Чтобы сделать эту разницу более явной: когда полицейский останавливает машину, он будет использовать мгновенную скорость машины, чтобы выписать штраф, но когда вы пытаетесь рассчитать, сколько времени вам потребуется, чтобы пересечь два разных города, вы хотите использовать среднюю скорость.

Давайте рассмотрим еще один пример:

Если автомобиль движется по маршруту 1000 метров и достигает конечной точки, двигаясь с максимальной скоростью за 1 минуту и ​​20 секунд (80 секунд), какова будет скорость транспортного средства? Скорость транспортного средства можно рассчитать следующим образом:

Vavg = (Xf – Xi)/t = Δx/t
или…
Vavg = 1000 м – 0,00 м/80,0 с (где конечная точка пути – 1000 м).
Vср = 1000 м/80.с
Vср = 12,5 м/с

Следовательно, скорость автомобиля равна 12,5 м/с.

Разница между скоростью и скоростью

Фото: LoggaWiggler через Pixabay, CC0

Большинство людей используют термин «скорость» так, как будто он эквивалентен термину «скорость», поэтому в разговорной речи эти термины взаимозаменяемы. Тем не менее, вы должны знать, что в области физики скорость и скорость — это две разные вещи со своими собственными значениями. Одно из основных различий между скоростью и скоростью состоит в том, что скорость имеет направление, а скорость — нет. Скорость — это всего лишь скалярная величина, переменная, имеющая только одно значение в каждый момент времени.

Подобно тому, как существует разница между средней скоростью и мгновенной скоростью, существует также разница между средней скоростью и мгновенной скоростью. Мгновенную скорость можно рассматривать как эквивалент величины мгновенной скорости. Таким образом, в то время как скорость может быть отрицательной относительно начальной точки объекта, как в приведенном выше примере -4,0 м/5 с, мгновенная скорость будет положительной 4,0 м/5 с.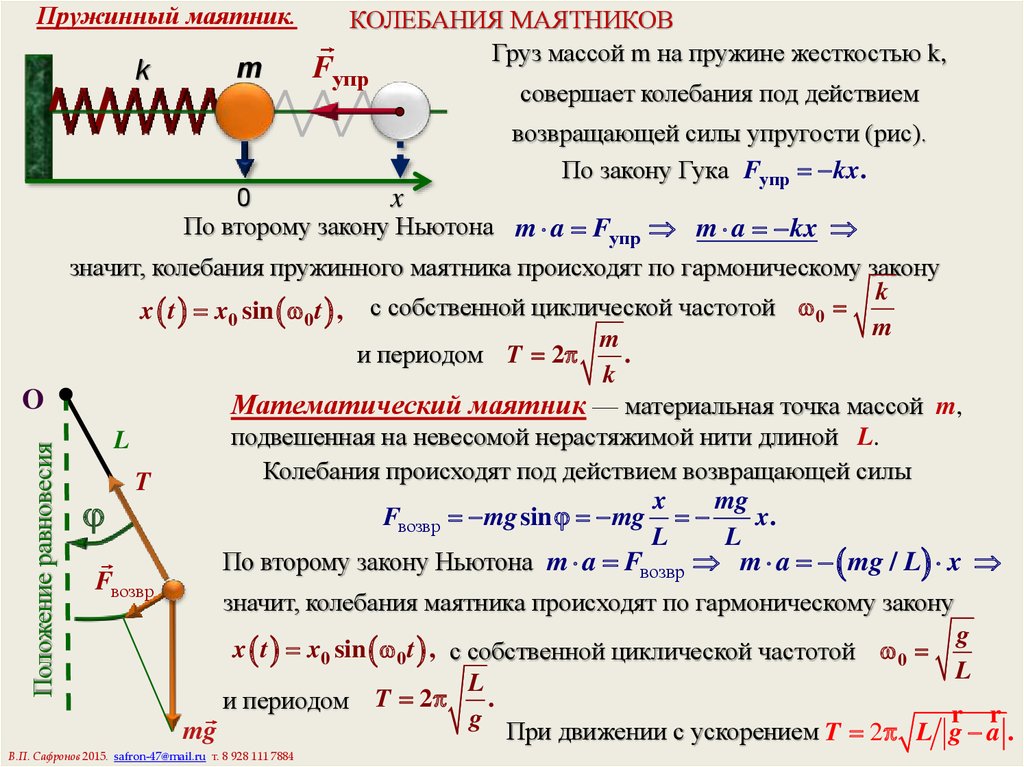

«Энергия зависит от квадрата скорости, так что если вам нужна пятикратная скорость, это 25-кратная энергия». — Базз Олдрин

Вот еще одна иллюстрация:

В данный момент во время поездки на автомобиле ваша мгновенная скорость составляет 55 км/ч строго на запад. Мгновенная скорость для этой мгновенной скорости была бы 55 км/ч, точно такая же величина или скорость изменения, но не было бы направления. Если это определение мгновенной скорости, то каково определение средней скорости?

Средняя скорость равна общему расстоянию, пройденному объектом, деленному на время, необходимое для прохождения этого расстояния. Это означает, что хотя величина мгновенной скорости и скорость всегда будут одинаковыми, могут быть существенные различия в величине средней скорости и величине средней скорости.

Суммируем:

Основное определение средней скорости: Vavg = Δx/Δt = Xf – X0/tf – t0

Это изменение положения, деленное на время движения.

Вы должны знать, что уравнение скорости/времени — это только одно важное уравнение, использующее скорость, но существуют и другие. Уравнение положение-время (s = s0 + v̅t [a]) предназначено для выяснения того, где объект, вероятно, остановится, учитывая его скорость и начальное положение за заданное время.

3.6: Движение с постоянным ускорением (часть 2)

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5280

• OpenStax
• OpenStax

Составление уравнений

В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного больше алгебраических манипуляций. Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для удобства обращения к необходимым уравнениям. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных и нужно два уравнения из набора для решения неизвестных. Нам нужно столько уравнений, сколько неизвестных, чтобы решить данную ситуацию. 9{2} + 2a(x — x_{0})\]

Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях. Переставляя \(v = v_0 + at\), мы имеем

\[a = \frac{v — v_{0}}{t} \ldotp\]

Отсюда мы видим, что за конечное время, если разница между начальной и конечной скоростями мала, ускорение мало, приближаясь к нулю в пределе равенства начальной и конечной скоростей. Наоборот, в пределе t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным. 9{2}}{2(x — x_{0})} \ldotp\]

Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе перемещение стремится к нулю. Ускорение стремится к нулю в пределе, когда разность начальной и конечной скоростей стремится к нулю при конечном перемещении.

Пример 3.10: Как далеко едет машина?

На сухом бетоне автомобиль может замедляться со скоростью 7,00 м/с ² , тогда как на мокром бетоне он может замедляться только со скоростью 5,00 м/с ² . Найдите расстояние, необходимое для остановки автомобиля, движущегося со скоростью 30,0 м/с (около 110 км/ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите перемещение от точки, в которой водитель видит красный сигнал светофора, учитывая время его реакции 0,500 с, чтобы нажать на педаль тормоза.

Стратегия

Сначала нам нужно нарисовать рисунок \(\PageIndex{1}\). Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.

Рисунок \(\PageIndex{1}\): Пример эскиза для визуализации замедления и тормозного пути автомобиля. {2})} \ldotp$$ Таким образом, $$x = 64,3\; м\; на\; сухой\; бетон \ldotp$$

Эту часть можно решить точно так же, как (а). Единственная разница в том, что ускорение равно −5,00 м/с ² . Результат: $$x_{мокрый} = 90,0\; м\; на\; влажный\; бетон \ldotp$$

Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и мокрого бетона. Итак, чтобы ответить на этот вопрос, нам нужно рассчитать, какое расстояние автомобиль проедет за время реакции, а затем добавить это ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя. Для этого мы, опять же, идентифицируем известные и то, что мы хотим решить. Мы знаем, что \(\bar{v}\) = 30,0 м/с, t _{реакция} = 0,500 с, а _{реакция} = 0. Примем х _{0-реакцию} равной нулю. Ищем х _{реакцию} . Во-вторых, как и прежде, мы определяем наилучшее уравнение для использования. В этом случае x = x ₀ + \(\bar{v}\)t работает хорошо, потому что единственным неизвестным значением является x, для которого мы и хотим найти. В-третьих, подставляем известные значения для решения уравнения: $$x = 0 + (30,0\; м/с)(0,500\; с) = 15,0\; м \ldotp$$Это означает, что автомобиль проезжает 15,0 м, пока водитель реагирует, что делает общее перемещение в двух случаях с сухим и влажным бетоном на 15,0 м больше, чем если бы он реагировал мгновенно. Наконец, мы прибавляем смещение за время реакции к смещению при торможении (рис. \(\PageIndex{2}\)), $$x_{торможение} + x_{реакция} = x_{общий},$$ и находим (а) быть 64,3 м + 15,0 м = 79.3 м в сухом состоянии и (b) 90,0 м + 15,0 м = 105 м во влажном состоянии.

Рисунок \(\PageIndex{2}\): Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны тормозные пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, движущегося изначально со скоростью 30,0 м/с. Также показано общее расстояние, пройденное от точки, когда водитель впервые видит красный свет, при условии времени реакции 0,500 с.

Значение

Перемещения, обнаруженные в этом примере, кажутся подходящими для остановки быстро движущегося автомобиля. На мокром асфальте машина останавливается дольше, чем на сухом. Интересно, что к перемещениям существенно добавляет время реакции, но важнее общий подход к решению задач. Мы идентифицируем известные и определяемые величины, затем находим соответствующее уравнение. Если имеется более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных для решения. Часто существует более одного способа решения проблемы. Различные части этого примера на самом деле могут быть решены другими методами, но представленные здесь решения являются самыми короткими.

Пример 3.11: Расчет времени

Предположим, что автомобиль въезжает в полосу движения на съезде длиной 200 м. Если его начальная скорость равна 10,0 м/с, а ускорение составляет 2,00 м/с ² , за какое время автомобиль проедет 200 м вверх по пандусу? (Эта информация может быть полезна инженеру по транспорту. )

Стратегия

Сначала мы рисуем набросок Рисунок \(\PageIndex{3}\). Нас просят решить за время t. Как и прежде, мы отождествляем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t.)

Рисунок \(\PageIndex{3}\): Эскиз автомобиля, ускоряющегося на съезде с автомагистрали.

Решение

Опять же, мы идентифицируем известные и то, что мы хотим решить. Мы знаем, что x ₀ = 0, v ₀ = 10 м/с, a = 2,00 м/с ² и x = 200 м.

Нам нужно найти t. Уравнение x = x ₀ + v ₀ t + \(\frac{1}{2}\)at ² работает лучше всего, потому что единственной неизвестной в уравнении является переменная t, для которой нам нужно решать. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение. 9{2} — 4ac}}{2a},\]

, что дает два решения: t = 10,0 и t = -20,0. Отрицательное значение времени неразумно, так как это означало бы, что событие произошло за 20 с до начала движения. Мы можем отказаться от этого решения. Таким образом,

\[ t = 10,0\; s \ldotp\]

Значение

Всякий раз, когда уравнение содержит неизвестное в квадрате, есть два решения. В некоторых задачах оба решения имеют смысл; в других разумно только одно решение. Ответ 10,0 с кажется разумным для типичного съезда с автострады.

Упражнение 3.5

Пилотируемая ракета разгоняется со скоростью 20 м/с ² во время запуска. За какое время ракета достигнет скорости 400 м/с?

Пример 3.12: Разгон космического корабля

Космический корабль покинул орбиту Земли и направляется к Луне. Он разгоняется со скоростью 20 м/с ² за 2 мин и преодолевает расстояние 1000 км. Каковы начальная и конечная скорости космического корабля?

Стратегия

9{2})(120,0\; с) = 9533,3\; м/с \ldotp\]

Значение

В смещении, времени, скорости и ускорении есть шесть переменных, описывающих движение в одном измерении. Начальными условиями данной задачи может быть множество комбинаций этих переменных. Из-за этого разнообразия решения могут быть не такими простыми, как простые подстановки в одно из уравнений. Этот пример показывает, что для решения кинематики может потребоваться решение двух одновременных кинематических уравнений.

Познакомившись с основами кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также заметили общий подход к решению задач, который дает как правильные ответы, так и понимание физических взаимосвязей. Следующий уровень сложности наших задач кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .

Задачи преследования двух тел

До этого момента мы рассматривали примеры движения одного тела. Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В 9В задаче преследования двух тел 0150 движения объектов связаны, то есть искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти задачи, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на рисунке \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\): Сценарий преследования двух тел, в котором автомобиль 2 движется с постоянной скоростью, а автомобиль 1 отстает с постоянным ускорением. Автомобиль 1 догоняет автомобиль 2 позже.

Время и расстояние, необходимые для того, чтобы автомобиль 1 догнал автомобиль 2, зависят от начального расстояния между автомобилем 1 и автомобилем 2, а также от скоростей обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.

Рассмотрим следующий пример.

Пример 3.13: Гепард ловит газель

Гепард ждет, прячась за кустом. Гепард замечает газель, пробегающую мимо со скоростью 10 м/с. В момент, когда газель проходит мимо гепарда, гепард ускоряется из состояния покоя со скоростью 4 м/с ² поймать газель. а) Сколько времени потребуется гепарду, чтобы поймать газель? б) Каково водоизмещение газели и гепарда?

Стратегия

Для решения этой задачи используем систему уравнений для постоянного ускорения. Поскольку движутся два объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но что связывает уравнения, так это общий параметр, который имеет одинаковое значение для каждого животного. Если мы внимательно посмотрим на проблему, станет ясно, что общим параметром для каждого животного является их позиция x в более поздний момент времени t. Поскольку они оба начинаются с x ₀ = 0, их перемещения одинаковы в более поздний момент времени t, когда гепард догонит газель. Если мы выберем уравнение движения, которое определяет смещение для каждого животного, мы можем тогда установить уравнения равными друг другу и найти неизвестное, то есть время. {2} — 50\; m \ldotp$$Водоизмещение газели: $$x = \bar{v} t = 10(5) = 50\; m \ldotp$$Мы видим, что оба смещения равны, как и ожидалось.

Значение

Важно проанализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания движения каждого отдельного объекта. Также важно иметь хорошее визуальное представление о задаче преследования двух тел, чтобы увидеть общий параметр, связывающий движение обоих объектов.

Упражнение 3.6

Велосипед движется с постоянной скоростью 10 м/с. Человек стартует с состояния покоя и начинает бежать, чтобы догнать велосипед через 30 с, когда велосипед находится в том же положении, что и человек. Каково ускорение человека?

---

Эта страница под названием 3.6: Движение с постоянным ускорением (часть 2) распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts.