Формулы арифметической и геометрической прогрессии: Арифметическая и геометрическая прогрессии — урок. Основной государственный экзамен (9 класс), Математика.

Содержание

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Поиск по сайту:

Справочник по математике

Алгебра

Последовательности чисел

Определение арифметико-геометрической прогрессии

Вывод формулы для общего члена арифметико-геометрической прогрессии

Определение арифметико-геометрической прогрессии

Рассмотрим более сложный, чем арифметическая или геометрическая прогрессии, тип последовательности чисел. Эта последовательность носит название арифметико-геометрической прогрессии, поскольку обладает рядом свойств, присущих, как арифметической, так и геометрической прогрессиям.

Определение. Арифметико-геометрической прогрессией называют числовую последовательность

x₁, x₂, … x_n , …

заданную рекуррентной формулой

x_n = q x_{n – 1} + d , n > 1

(1)

с начальным условием

x₁ = c₁,

(2)

где буквами

q , d , c₁,

обозначены заданные числа, удовлетворяющие условиям

(3)

Замечание. Условия (3) входят в определение, поскольку при q = 1 арифметико–геометрическая прогрессия превращается в арифметическую прогрессию, а при d = 0 арифметико–геометрическая прогрессия превращается в геометрическую прогрессию.

Вывод формулы общего члена арифметико-геометрической прогрессии

Перейдем от последовательности

x₁, x₂, … x_n , …

к последовательности

y₁, y₂, … y_n , …

по формулам

x_n = y_n + t ,

(4)

где t – некоторое число, которое мы определим чуть позже.

Поскольку

x_{n – 1} = y_{n – 1} + t ,

то формула (1) преобразуется следующим образом:

Следовательно,

y_n = q y_{n – 1} +
+ ( q – 1) t + d , n > 1 .

(5)

Если теперь положить

(6)

то формула (5) принимает вид

y_n = q y_{n – 1} , n > 1 ,

(7)

откуда вытекает, что последовательность

y₁, y₂, … y_n , …

является геометрической прогрессией со знаменателем q.

Для того, чтобы найти первый член этой геометрической прогрессии, воспользуемся равенствами (2) и (4):

Итак,

(8)

Поскольку

y_n = y₁q ^{n – 1},

то из формул (7) и (8) получаем формулу для общего члена геометрической прогрессии (7):

(9)

Из формулы (9) с помощью равенств (4) и (6) получаем формулу общего члена арифметико-геометрической прогрессии:

Итак, формула общего члена арифметико-геометрической прогрессии имеет вид:

Вывод формулы общего члена закончен.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Формулы прогрессий — онлайн справочник для студентов

Формулы арифметических прогрессий

ОПРЕДЕЛЕНИЕ

Арифметическая прогрессия представляет собой последовательность чисел \(\ \left\{a_{1}, a_{2}, \dots, a_{n}, \dots\right\} \) , каждая из которых (начиная со второй) равна сумме некоторого предыдущего постоянного числа d для этой последовательности:

\(\ a_{n}=a_{n-1}+d \)

Число d называется разностью арифметической прогрессии. Любой член арифметической прогрессии (если известен его первый член и разность) вычисляется следующим образом:

\(\ a_{n}=a_{1}+d(n-1) \)

Сумма первых n членов арифметической прогрессии может быть рассчитана с использованием формул:

\(\ S_{n}=\frac{a_{1}+a_{n}}{2} \cdot n \)

или если известны первый термин и разница в прогрессии,

\(\ S_{n}=\frac{2 a_{1}+d(n-1)}{2} \cdot n \)

Формулы для геометрических прогрессий

ОПРЕДЕЛЕНИЕ

Геометрическая прогрессия представляет собой последовательность чисел \(\ \left\{b_{1}, b_{2}, \dots, b_{n}, \dots\right\}, b_{1} \neq 0 \) , каждая из которых (начиная со второй) равна произведению предыдущего на некоторое фиксированное число q, называемое знаменателем геометрической прогрессии:

\(\ b_{n}=b_{n-1} \cdot q \)

Зная первый член и знаменатель геометрической прогрессии, любой его член можно вычислить по формуле:

\(\ b_{n}=b_{1} \cdot q^{n-1} \)

Если последовательность чисел \(\ \left\{b_{1}, b_{2}, \dots, b_{n}, \dots\right\} \) является геометрической прогрессией, то для любого из ее членов равенство

\(\ S_{n}=\frac{b_{1}\left(q^{n}-1\right)}{q-1} \)

Сумма первых n членов геометрической прогрессии может быть вычислена по формуле:

\(\ S_{n}=\frac{b_{1}\left(q^{n}-1\right)}{q-1} \)

Если знаменатель прогрессии \(\ |\mathrm{q}|\(\ S_{n}=\frac{b_{1}}{1-q} \)

Примеры решения проблем

ПРИМЕР 1

Задача

Между числами 2 и 11 записывать пять чисел, чтобы они вместе с заданными числами составляли арифметическую прогрессию. {n-1} \Rightarrow n=6 \)

Ответ \(\ \mathrm{n}=6 \)

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Формула суммы геометрической прогрессии Формула суммы арифметической прогрессии Формулы геометрической прогрессии Формулы арифметической прогрессии

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю Политику конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

2.

2: Арифметические и геометрические последовательности

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 14755

Оскар Левин
Университет Северного Колорадо

Расследуй!

Для узоров из точек ниже нарисуйте следующий узор в последовательности. Затем дайте рекурсивное определение и замкнутую формулу для количества точек в \(n\)-м шаблоне.

Перейдем теперь к вопросу о нахождении замкнутых формул для отдельных типов последовательностей.

Арифметические последовательности

Если члены последовательности отличаются на константу, мы говорим, что последовательность равна арифметика . Если начальный член (\(a_0\)) последовательности равен \(a\), а общая разность

равна \(d\text{,}\), то мы имеем,

Рекурсивное определение: \(a_n = a_{n-1} + d\) с \(a_0 = a\text{.}\)

Замкнутая формула: \(a_n = a + dn\text{.}\)

Откуда мы это знаем? Для рекурсивного определения нам нужно указать \(a_0\text{.}\) Затем нам нужно выразить \(a_n\) в терминах \(a_{n-1}\text{.}\) Если мы вызовем первый член \(a\text{,}\), затем \(a_0 = a\text{.}\) Для рекуррентного отношения по определению арифметической последовательности разница между последовательными терминами является некоторой константой, скажем, \ (d\text{.}\) Итак, \(a_n — a_{n-1} = d\text{,}\) или, другими словами,

\begin{уравнение*} a_0 = a \qquad a_n=a_{n-1}+d. \end{уравнение*}

Чтобы найти замкнутую формулу, сначала выпишите последовательность в общем виде:

\begin{align*} a_0 & = a\\ a_1 & = a_0 + d = a+d\\ a_2 & = a_1 + d = a+d+d = a+2d\\ a_3 & = a_2 + d = a+2d+d = a+3d\\ & \vdots \end{align*}

Мы видим, что для нахождения \(n\)-го члена нам нужно начать с \(a\), а затем добавить \(d\) несколько раз.

Фактически, добавьте его \(n\) раз. Таким образом, \(a_n = a+dn\text{.}\)

Пример \(\PageIndex{1}\)

Найдите рекурсивные определения и замкнутые формулы для приведенных ниже последовательностей. Предположим, что первым перечисленным термином является \(a_0\text{.}\)

\(2, 5, 8, 11, 14, \ldots\text{.}\)
\(50, 43, 36, 29, \ldots\text{.}\)

Раствор

Сначала мы должны проверить, что эти последовательности действительно являются арифметическими, взяв разности последовательных членов. Это покажет общую разницу \(d\text{.}\)

\(5-2 = 3\text{,}\) \(8-5 = 3\text{,}\) и т. д. Чтобы перейти от каждого члена к следующему, мы добавляем три, так что \(d = 3\text{.}\) Таким образом, рекурсивное определение имеет вид \(a_n = a_{n-1} + 3\) с \(a_0 = 2\text{.}\) Замкнутая формула \(a_n = 2 + 3n\текст{.}\)

Здесь общая разница: \(-7\text{,}\), так как мы прибавляем \(-7\) к 50, чтобы получить 43, и так далее. Таким образом, у нас есть рекурсивное определение \(a_n = a_{n-1} — 7\) с \(a_0 = 50\text{.}\) Замкнутая формула \(a_n = 50 — 7n\text{.} \)

Как насчет таких последовательностей, как \(2, 6, 18, 54, \ldots\text{?}\) Это не арифметика, поскольку разница между членами не является постоянной. Однако отношение между последовательными терминами является постоянным. Мы называем такие последовательности геометрическими .

Рекурсивное определение геометрической последовательности с начальным членом \(a\) и знаменателем \(r\) выглядит следующим образом: \(a_n = a_{n}\cdot r; a_0 = a\text{.}\) Чтобы получить следующий член мы умножаем предыдущий член на \(r\text{.}\) Мы можем найти замкнутую формулу, как мы это делали для арифметической прогрессии. Напишите 9{п}\текст{.}\)

Пример \(\PageIndex{3}\)

Найдите рекурсивную и замкнутую формулу для приведенных ниже последовательностей. Опять же, первым перечисленным термином является \(a_0\text{. }\)

\(3, 6, 12, 24, 48, \ldots\)
\(27, 9, 3, 1, 1/3, \ldots\)

Раствор: Опять же, мы должны сначала проверить, действительно ли эти последовательности являются геометрическими, на этот раз путем деления каждого члена на его предыдущий член. Предполагая, что это отношение постоянно, мы нашли \(r\text{.}\) 9{п}\текст{.}\)

В приведенных выше примерах и формулах мы предполагали, что начальный термин был \(a_0\text{.}\). Если ваша последовательность начинается с \(a_1\text{,}\), вы можете легко найти термин, который было бы \(a_0\) и использовать это в формуле. Например, если мы хотим получить формулу для последовательности \(2, 5, 8,\ldots\) и настаиваем на том, что \(2= a_1\text{,}\), то мы можем найти \(a_0 = -1\) (поскольку последовательность арифметическая с общей разностью 3, имеем \(a_0 + 3 = a_1\)). Тогда замкнутая формула будет \(a_n = -1 + 3n\text{. }\)

Расследуй!

В вашем соседнем продуктовом магазине есть кондитерская, полная Skittles.

Предположим, что автомат для конфет в настоящее время содержит ровно 650 кеглей, и каждый раз, когда кто-то вставляет четвертак, из автомата выходит ровно 7 кеглей.
1. Сколько кеглей останется в автомате после того, как будут вставлены 20 четвертаков?
2. Когда-нибудь в автомате останется ровно ноль кеглей? Объяснять.
Что, если автомат выдает 7 кеглей первому покупателю, положившему четвертак, 10 — второму, 13 — третьему, 16 — четвертому и т. д. машина?
Что, если автомат выдает 4 кегли первому покупателю, 7 — второму, 12 — третьему, 19 — четвертому и т. д. Сколько кеглей выдал автомат после того, как 20 четвертаков были помещены в автомат?

Посмотрите на последовательность \((T_n)_{n\ge 1}\), которая начинается с \(1, 3, 6, 10, 15,\ldots\text{.}\) Они называются треугольными числами поскольку они представляют собой количество точек в равностороннем треугольнике (представьте, как вы расположите 10 кеглей для боулинга: ряд из 4 плюс ряд из 3 плюс ряд из 2 и ряд из 1).

Является ли эта последовательность арифметической? Нет, поскольку \(3-1 = 2\) и \(6-3 = 3 \ne 2\text{,}\) общего различия нет. Является ли последовательность геометрической? Нет. \(3/1 = 3\), но \(6/3 = 2\text{,}\), поэтому общего соотношения нет. Что делать?

Обратите внимание, что различия между терминами образуют арифметическую последовательность: \(2, 3, 4, 5, 6,\ldots\text{.}\) Это говорит о том, что \(n\)-й член последовательности \(1 ,3,6,10,15,\ldots\) — это сумма первых \(n\) членов последовательности \(1,2,3,4,5,\ldots\text{.}\ ) Мы говорим, что первая последовательность — это последовательность частичных сумм второй последовательности (частичных сумм, потому что мы не берем сумму всех бесконечно многих членов). Если бы мы знали, как складывать члены арифметической последовательности, мы могли бы использовать это, чтобы найти замкнутую формулу для последовательности, разности которой являются членами этой арифметической последовательности.

Это должно стать яснее, если мы напишем треугольные числа так:

Подумайте, как найти сумму первых 100 положительных целых чисел (то есть \(T_{100}\)). Вместо того, чтобы складывать их по порядку, мы перегруппируем и добавим \(1+100 = 101\text{.}\) Следующая пара для объединения: \(2+99 = 101\text{.}\) Затем \(3+ 98 = 101\text{.}\) Продолжайте. Это дает 50 пар, каждая из которых в сумме дает \(101\text{,}\), поэтому \(T_{100} = 101\cdot 50 = 5050\text{.}\) ¹ Это озарение обычно приписывают Карлу Фридриху Гауссу, одному из величайших математиков всех времен, который открыл его еще ребенком, когда его неприятный учитель начальных классов решил, что он займет класс, заставив их вычислить длинную сумму.

В общем случае, используя такую же перегруппировку, мы находим, что \(T_n = \frac{n(n+1)}{2}\text{. }\) Между прочим, это в точности то же самое, что и \({n +1 \выберите 2}\text{,}\), что имеет смысл, если вы думаете о треугольных числах как о подсчете количества рукопожатий на вечеринке с \(n+1\) людьми: первый человек пожимает \ (n\) рук, следующий пожимает еще \(n-1\) рук и так далее.

Суть всего этого в том, что некоторые последовательности, хотя и не являются арифметическими или геометрическими, могут быть интерпретированы как последовательности частичных сумм арифметических и геометрических последовательностей. К счастью, есть методы, которые мы можем использовать для быстрого вычисления этих сумм.

Суммирование арифметических последовательностей: перевернуть и сложить

Вот метод, который позволяет нам быстро найти сумму арифметической последовательности.

Пример \(\PageIndex{4}\)

Найдите сумму: \(2 + 5 + 8 + 11 + 14 + \cdots + 470\text{.}\)

Решение

Идея состоит в том, чтобы подражать тому, как мы нашли формулу для треугольных чисел. Если мы сложим первый и последний члены, мы получим 472. Второй член и предпоследний член также в сумме дают 472. Чтобы отслеживать все, мы могли бы выразить это следующим образом. Вызовите сумму \(S\text{.}\) Затем

\(S =\)	\(2\)	\(+\)	\(5\)	\(+\)	\(8\)	\(+ \cdots +\)	\(467\)	\(+\)	470
\(+ \quad S =\)	\(470\)	\(+\)	\(467\)	\(+\)	\(464\)	\(+ \cdots +\)	\(5\)	\(+\)	2
\(2S =\)	\(472\)	\(+\)	\(472\)	\(+\)	\(472\)	\(+ \cdots +\)	\(472\)	\(+\)	\(472\)

Чтобы найти \(2S\), мы прибавляем 472 к самому себе несколько раз. Какой номер? Нам нужно решить, сколько слагаемых ( слагаемых ) в сумме. Поскольку термины образуют арифметическую последовательность, \(n\)-й член в сумме (считая \(2\) как 0-й член) может быть выражен как \(2 + 3n\text{.}\) Если \( 2 + 3n = 470\), тогда \(n = 156\text{.}\) Таким образом, \(n\) находится в диапазоне от 0 до 156, что дает в сумме 157 членов. Это число 472 в сумме для \(2S\text{.}\) Таким образом,

\begin{уравнение*} 2S = 157\cdot 472 = 74104 \end{уравнение*}

Теперь легко найти \(S\text{:}\)

\begin{уравнение*} S = 74104/2 = 37052 \end{уравнение*}

Это будет работать для любой суммы арифметических последовательностей. Вызовите сумму \(S\text{.}\) в обратном порядке и добавьте. Это дает одно число, добавленное к самому себе много раз. Найдите количество раз. Умножить. Разделить на 2. Готово.

Пример \(\PageIndex{5}\)

Найдите замкнутую формулу для \(6 + 10 + 14 + \cdots + (4n — 2)\text{. }\)

Решение

Опять у нас есть сумма арифметической прогрессии. Нам нужно знать, сколько членов в последовательности. Ясно, что каждый член последовательности имеет вид \(4k — 2\) (о чем свидетельствует последний член). Но для каких значений \(k\)? Чтобы получить 6, \(k = 2\text{.}\) Чтобы получить \(4n-2\), возьмите \(k = n\text{.}\) Итак, чтобы найти количество терминов, нам нужно знать сколько целых чисел находится в диапазоне \(2,3,\ldots, n\text{.}\) Ответ: \(n-1\text{.}\) (есть \(n\) чисел от 1 в \(n\text{,}\), так что на единицу меньше, если мы начнем с 2.)

Теперь переверните и добавьте:

\(S =\)	\(6\)	\(+\)	\(10\)	\(+ \cdots +\)	\(4н-6\)	\(+\)	\(4н-2\)
\(+ \quad S =\)	\(4н-2\)	\(+\)	\(4н-6\)	\(+ \cdots +\)	\(10\)	\(+\)	6
\(2S =\)	\(4n+4\)	\(+\)	\(4n+4\)	\(+ \cdots +\)	\(4n+4\)	\(+\)	\(4n+4\)

Так как членов \(n-2\), мы получаем

\begin{equation*} 2S = (n-2)(4n+4)\qquad \mbox{ поэтому } \qquad S = \frac{(n-2)(4n+4)}{2} \end{ уравнение*}

Помимо нахождения сумм, мы можем использовать эту технику для нахождения замкнутых формул для последовательностей, которые мы распознаем как последовательности частичных сумм.

Пример \(\PageIndex{6}\)

Используйте частичные суммы, чтобы найти замкнутую формулу для \((a_n)_{n\ge 0}\), которая начинается с \(2, 3, 7, 14, 24 , 37,\ldots \ldots\)

Решение

Во-первых, если вы посмотрите на различия между терминами, вы получите последовательность различий: \(1,4,7,10,13, \ldots\text{,}\), которая является арифметической последовательностью. Написано по-другому:

\begin{align*} a_0 & = 2\\ a_1 & = 2+1\\ a_2 & = 2+1+4\\ a_3 & = 2+1+4+7 \end{align*}

и так далее. Мы можем записать общий член \((a_n)\) в терминах арифметической последовательности следующим образом:

\begin{equation*} a_n = 2 + 1 + 4 + 7 + 10 + \cdots + (1+3(n-1)) \end{equation*}

(мы используем \(1+3(n-1)\) вместо \(1+3n\), чтобы правильно выровнять индексы; для \(a_3\) мы добавляем 7, что равно \( 1+3(3-1)\)).

Мы можем перевернуть и сложить, но начальная цифра 2 не соответствует нашему шаблону. Это просто означает, что нам нужно убрать 2 из обратной части:

\(a_n =\)	\(2\)	\(+\)	\(1\)	\(+\)	\(4\)	\(+ \cdots +\)	\(1+3(n-1)\)
\(+ ~ a_n =\)	\(2\)	\(+\)	\(1+3(n-1)\)	\(+\)	\(1+3(n-2)\)	\(+ \cdots +\)	\(1\)
\(2a_n =\)	\(4\)	\(+\)	\(2+3(n-1)\)	\(+\)	\(2+3(n-1)\)	\(+ \cdots +\)	\(2+3(n-1)\)

Не считая первого члена (4), есть \(n\) слагаемых \(2+3(n-1) = 3n-1\), поэтому правая часть становится \(2+(3n-1 )n\текст{. }\)

Наконец, найдя \(a_n\), мы получим

\begin{уравнение*} a_n = \d \frac{4+(3n-1)n}{2}. \end{уравнение*}

На всякий случай проверяем \(a_0 = \frac{4}{2} = 2\text{,}\) \(a_1 = \frac{4+2}{2} = 3\text{,} \) и т. д. Имеем правильную замкнутую формулу.

Суммирование геометрических последовательностей: умножение, сдвиг и вычитание

Чтобы найти сумму геометрической последовательности, мы не можем просто обратить вспять и сложить. Вы понимаете, почему? Причина, по которой один и тот же термин добавлялся сам к себе много раз, заключается в том, что существовала постоянная разница. Таким образом, когда мы добавили эту разницу в одном направлении, мы вычли разницу в другом направлении, оставив постоянную сумму. Для геометрических сумм у нас есть другая техника.

Пример \(\PageIndex{7}\)

Что такое \(3 + 6 + 12 + 24 + \cdots + 12288\text{?}\)

Решение: Умножьте каждый член на 2, обыкновенный коэффициент. Вы получаете \(2S = 6 + 12 + 24 + \cdots + 24576\). Теперь вычтите: \(2S — S = -3 + 24576 = 24573\text{.}\) Так как \(2S — S = S\text{,}\) у нас есть ответ.

Чтобы лучше понять, что произошло в приведенном выше примере, попробуйте записать его так:

Хотя это может показаться новой техникой, вы, вероятно, использовали ее раньше.

Пример \(\PageIndex{9}\)

Выразите \(0,464646\ldots\) в виде дроби.

Раствор: Пусть \(N = 0,46464646\ldots\text{. }\) Рассмотрим \(0,01N\text{.}\) Получим:

\(С=\)	\(3\, +\)	\(6 + 12 + 24 + \cdots + 12288\)
\(-~2S=\)		\(6 + 12 + 24 + \cdots + 12288\)	\(+ 24576\)
\(-S = \)	\(3\, +\)	\(0 + 0 + 0 + \cdots + 0 \)

	\(Н =\)	\(0,4646464\ldotts\)
\(-\)	\(0,01Н =\)	\(0,00464646\ldots\)
	\(0,99Н =\)	\(0,46\)

Итак, \(N = \frac{46}{99}\text{.}\) Что мы сделали? Мы рассматривали повторяющуюся десятичную дробь \(0,464646\ldots\) как сумму геометрической последовательности \(0,46, 0,0046, 0,000046, \ldots\). Обычное отношение равно \(0,01\text{.}\). Единственная реальная разница что мы сейчас вычисляем 9n k = n!\text{.}\)

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Оскар Левин
Лицензия
СС BY-SA
Показать страницу TOC
нет
Теги

Арифметические и геометрические последовательности | bartleby

Использование арифметических и геометрических последовательностей в реальном мире

Рассмотрим два примера ниже:

(A) Боб — фанатик фитнеса, который бегает по 50 минут в день, чтобы поддерживать свое здоровье, но после несчастного случая он подвергается операция на колене. На этапе восстановления его тренер говорит ему, что он может вернуться к своей беговой программе, но в более медленном темпе. Тренер предлагает начать с 10-минутного бега. После этого он предлагает увеличить время выполнения на 5 минут в день. Предполагая эту модель, сколько дней пройдет, прежде чем Боб вернется к бегу по 50 минут в день?

(B) У Джорджа есть сбережения в размере 2000 долларов. Он решает инвестировать их в банк. Он планирует оставить деньги в банке сроком на три года, за которые банк обязуется выплатить ему сложные проценты в размере 6%. Сколько денег будет у Джорджа через три года при заданных критериях?

Это примеры из жизни. Для того, чтобы ответить на них, нам нужно расшифровать закономерность по данным, указанным в вопросе.

Раствор для примера A:

Добавление 5 минут каждую неделю к начальному значению 10 минут приведет к набору чисел, который выглядит следующим образом:

10, 15, 20, 25…

Если мы продолжим эту последовательность чисел, пока не достигнем 50 , получим 9 слагаемых. Следовательно, ответ для примера А равен 9 дням.

Решение для примера B:

Для года 1: 6% годовых на 2000 долларов =

6100×2000 долларов = 120 долларов

Сумма на конец 1 года равна

2000 долларов + 120 долларов = 21320 долларов

1
Для 2-го года: 6% годовых на 2120 долл. США =
6100×2120 долл. США = 127,2 долл. США
Таким образом, сумма на конец 2-го года составляет проценты на 2247,5 долл. США =
6100 × 2247,2 долл. США = 134,8
Следовательно, сумма на конец 3-го года равна
2247,2 долл. США + 134,8 долл.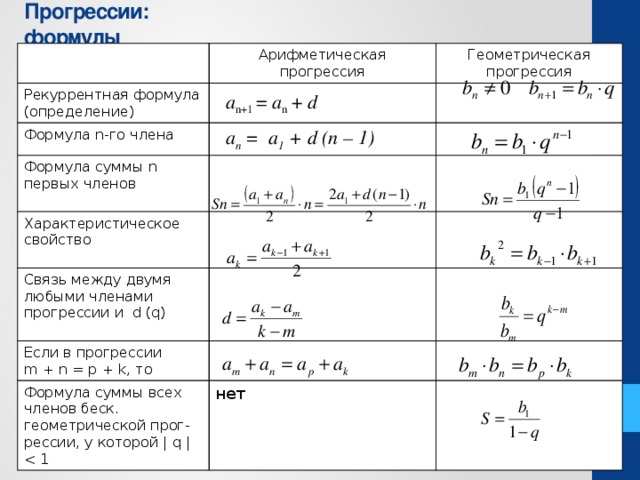 США = 2382
нужно было вычислить всего несколько членов. Но что, если в примере А увеличение количества минут в день было ограничено двумя минутами? Что, если в примере Б количество лет начисления сложных процентов равно 12 годам? В таких случаях было бы много времени, чтобы вычислить каждый термин, пока мы не получим желаемое значение. Более простым способом решения таких примеров было бы расшифровать последовательность чисел и разработать для них формулу.
Если мы идентифицируем последовательность чисел в Примере А, мы увидим, что существует постоянная разница в 5 между любыми двумя последовательными числами.
10,15, 20, 25=10, 10+5, (10+5+5), (10+5+5+5)

Когда разница между любыми двумя последовательными терминами всегда одинакова в A рифметика P прогрессия ( АР). Это означает, что следующее число в заданной последовательности вычисляется путем прибавления фиксированного числа к предыдущему числу в последовательности.

Чтобы выразить это в математической формуле, если мы назовем « первый член последовательности » a и фиксированный член, который нужно добавить d ( обычно называют общей разностью), тогда последовательность чисел может быть записана как:
a, a+d, a+2d, a+3d …
Чтобы написать формулу для n терминов, обратите внимание, что будет ( n – 1) количество различий между последовательными терминами.
Чтобы найти количество членов до заданного значения n , то есть найти n -й член арифметической прогрессии (АП), обозначаемый как Tn , последовательность может быть обобщена как:
Tn=a+( n-1)d
По этой формуле можно вычислить
- Определенный член арифметической прогрессии Tn
- Количество членов в данной арифметической последовательности n
- Первое число арифметической последовательности a
- Общая разность арифметической последовательности d
Однако концепция и формула, упомянутые выше, не подходят для примера B. Числа для примера B равны
2000, 2120, 2247,2, 2382
Разница между любыми двумя последовательными данными числами не является константой, но обратите внимание, что отношение второго числа к первому числу является константой.
23822247,2=2247,22120=21202000=1,06

Пример B представляет собой случай Геометрическая прогрессия (ГП). В GP , отношение любых двух последовательных терминов всегда одинаково. Следовательно, следующее число в последовательности вычисляется путем умножения фиксированного числа на предыдущее число в последовательности.
Чтобы выразить это в математической формуле, назовите первый член последовательности a , а фиксированный член, который нужно умножить, r (обычно называемое «общим отношением »). Тогда последовательность чисел может быть записана как
a, ar, ar2, ar3 …
Чтобы найти количество термов до заданного значения n , то есть найти n ^th термин GP, обозначенный Tn , мы можем обобщить последовательность как
Tn=ar(n-1)

Эту формулу можно использовать для вычисления
Арифметических и геометрических рядов
Когда складывается последовательность чисел, результат известен как ряд. Когда мы добавляем конечное число членов в арифметическую последовательность, мы получаем конечную арифметическую последовательность, например, сумму первых 50 целых чисел.
Рассмотрим последовательность терминов в AP , заданную как
a, a+d, a+2d, a+3d, …,a+(n−1)d

Чтобы получить арифметический ряд , нам нужно добавить их. Результатом будет
a+a+d+a+2d+a+3d+ … +a+(n−1)d

Потребуется много времени, чтобы получить окончательный ответ, используя термин- досрочное добавление. Следовательно, обобщенная формула для нахождения суммы первых n членов арифметической прогрессии, обозначенная как S _n задается как
Sn=n2{2a+(n-1)d}
Если известен первый член a и последний член l данной арифметической последовательности, то формула записывается как
Sn=n2{a+l}
Если существует бесконечное число членов, мы называем это бесконечным рядом. Сумма первых n слагаемых S _n называется «частичной суммой». Поскольку n стремится к бесконечности, S _n стремится к ∞.
Сумма до бесконечности для арифметического ряда не определена.
В случае геометрической прогрессии , сумма слагаемых будет
a+ar+ar2+ar3+…
Обобщенная формула для нахождения суммы первых n7 9009 членов геометрической прогрессии обозначаются как S _n обозначаются как
Sn=a(1-rn)1-r
Если требуется сумма до бесконечности геометрического ряда, мы перепишем уравнение как
S∞=a1-r где -1
https://www.bartleby.com/questions-and- ответы/арифметические-или-геометрические-а-если-а-аз-аз-..-это-арифметическая-последовательность-это-последовательность-а-2-аз-2-аза-2…- /4545b4b5-e006-4d70-aef4-41633cb124c5
https://www.
No related posts.