Арифметическая прогрессия, формула суммы элементов, разности, произведения, примеры с решением, чем отличается от геометрической
Часто, при решении задач, связанных с наблюдениями и присвоением значения определенному событию за определенный промежуток времени, получается ряд чисел, который именуется арифметической прогрессией.
Одна из главных отличительных особенностей такая математическая модель имеет закономерность, по которой можно вычислить любой неизвестный член, что упрощает прогнозирование при вычислении физических ситуаций.
Примерами повседневного использования могут являться наблюдение за температурой воздуха, прогнозирование расходов с занесением результатов в таблицу и др.
Содержание
Онлайн-калькулятор арифметической прогрессии
Определение и примеры арифметической прогрессии
Это последовательность из чисел, где каждое последующее число ряда (начиная со второго) увеличивается или уменьшается на определенную сумму, являющуюся константой.
Кроме этого для описания используется ряд сопутствующих терминов и определений. Членом (аn) называется единичное число из последовательности.
Разностью (d) называется фиксированное число, на которое увеличивается или уменьшается последующее число прогрессии.
Кроме этого, существуют виды таких рядов:
- возрастающая – числа ряда увеличиваются по своему значению,
- убывающая – каждое последующее число ряда уменьшается.
В качестве примера представим последовательность чисел «3, 9, 15, 21, 27». Данный случай – этот ряд чисел попадает под характеристику арифметической прогрессии. Этот вывод делается в том случае, когда разница между членами ряда фиксирована и равняется 6.
Виды арифметической (алгебраической) прогрессии
Разновидности строятся на основании характеристики разности (d), а именно на основании отличия последней от нуля.
Таким образом, можно встретить определенные вариации:
- разность d<,0 – прогрессия будет считаться убывающей, а каждый последующий член будет меньше предыдущего,
- разность d>,0 – это предполагает, что каждый член в ряду будет больше предыдущего, а прогрессию будут называть возрастающей,
- при d=0 ряд тоже будет иметь свойства прогрессии, которую именуют стационарной, и все члены будут одинаковыми (не будут изменяться).
Если прогрессия не изменяется с каждым шагом на одну и ту же разность, то эта прогрессия непостоянная и арифметической не является.
Важно знать: арифметическая от геометрической отличается тем, что в последней производится увеличение каждого последующего на один и тот же множитель.
Формулы арифметической прогрессии
Одно из важнейших свойств заключается в возможности вычисления любого числа конкретного места ряда.
Чтобы решать это, необходима формула, показывающая, как находится член арифметической прогрессии. В общем виде она будет выглядеть, как значение предыдущего числа в ряду (an-1), к которому прибавляют разность (d):
Также может возникнуть задача, когда надо просуммировать все числа ряда арифметической прогрессии (сумма членов). Если их малое количество, то можно посчитать это вручную, но если количество чисел перевалит за сотню, то проще будет воспользоваться специальной формулой для обработки.
Итак, нам понадобится значение первого числа в ряду (a1) и последнего (an), а также информация об общем количестве чисел в ряду.
Рекуррентная формула, показывающая, как искать сумму, будет выглядеть в таком случае следующим образом:
Обратите внимание: под значением n подразумевается именно количество членов ряда, для которых производится нахождение суммы.
Произведение членов арифметической прогрессии можно находить по похожей формуле:
где, Pn – произведение, b1 и bn – соответственно первое и последнее числа, а n – количество членов.
Отдельно следует коснуться такого понятия, как характеристическое свойство прогрессии. Оно сводится к выполнению определенного условия для каждого элемента:
Примеры задач с решением
Рассмотрим как решать задачи на заданную тему.
Пример 1
Требуется вычислить 574 член в ряду арифметической прогрессии, первые три члена которой «8, 15, 22…».
Вариант рассуждений по примеру 1. Для нахождения любого конкретного элемента ряда нам необходима информация о значении первого члена (a1) и о разности (d).
Чтобы вычислить разность, вычитаем из второго члена ряда первый (15 – и получаем d = 7. Теперь мы можем считать по формуле:
Подставляя полученные значения, получим выражение вида a574 = 8 + (574-1) * 7.
После вычисления получаем ответ: a574 = 4019.
Пример 2
Требуется вычислить 544 член ряда, являющийся арифметической прогрессией, при условии, что 154-ый член равен 17, а разность (d) равна 8.
Вариант рассуждений по примеру 2. Пользоваться в данной ситуации мы будем формулой из предыдущего примера:
Подставляя известные значения, получаем выражение – а544 = 17 + (544 1) * 8.
Вычисляя, получаем ответ а544 = 4361.
Пример 3
Для подготовки к экзамену по биологии студенту Смирнову необходимо выучить 730 вопросов (включая загадки). Известно, что он весьма обеспокоен и по мере приближения даты экзамена учит ежедневно на 27 вопросов больше, чем в предыдущий день. Друг Смирнова выяснил, что тот в первый день выучил всего 17 вопросов.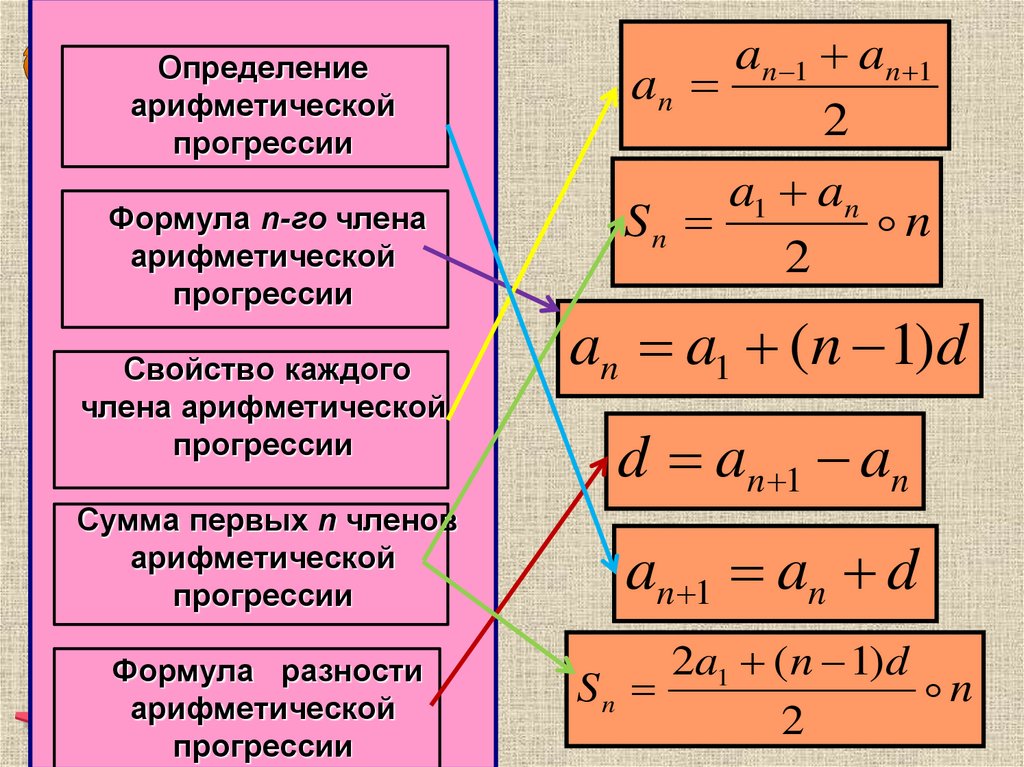
Требуется выяснить, сколько времени у студента ушло на подготовку.
Вариант рассуждений по примеру 3. Очевидно, что случай с подготовкой студента к экзамену решается через формулы арифметической прогрессией (поскольку присутствует фиксированная разность d = 17). Производим подстановку известных данных:
После подстановки получаем выражение: 730 = 17 + (n 1) * 27.
После вычислений определяем ответ – 27 дней.
Арифметическая прогрессия является наиболее простой из всех числовых зависимостей. Использование описанных формул позволит намного ускорить вычисления в задачах, где это требуется.
Кроме этого, для упрощения можно использовать онлайн калькулятор. В школе данную тему изучают в программе за 9 класс, а основные задания касаются нахождения членов и сумм.
Девушки бывают разные, но найти среди них идеальную непросто.
Зато вы легко найдете свой идеал в сексе на пару часов или горячую ночку, если полюбопытствуете в нашем каталоге проститутки Самара Барышни легки на подъем, легки в общении, характером обладают тоже легким, а еще легче – их поведение!
Формула суммы n-первых членов арифметической прогрессии презентация, доклад
Открытый урок в 9 «А» классе
по теме:
Формула суммы n-первых членов арифметической прогрессии
Цели урока:
отрабатывать навыки применения формулы n-го члена арифметической прогрессии, формулы суммы n-членов арифметической прогрессии;
воспитывать аккуратность и дисциплинированность;
развивать умение выделять главное, сравнивать, обобщать изучаемые факты, логически излагать свои мысли.
Фронтальная беседа
1. Приведите примеры последовательности.
2. Сформулируйте определение арифметической прогрессии.
3. По какой формуле вычисляется n-й член арифметической прогрессии?
4. По какой формуле находится сумма первых n-членов арифметической прогрессии?
Из истории математики
С формулой суммы n-первых членов арифметической прогрессии был связан эпизод из жизни немецкого математика Карла Фридриха Гаусса (1777-1855). Когда ему было 9 лет, учитель, занятый проверкой учеников других классов, задал на уроке следующую задачу: «Сосчитать сумму натуральных чисел от 1 до 100 включительно», надеясь, что это займёт много времени. Каково же было удивление учителя, когда один из учеников (это был Гаусс) через минуту воскликнул : «Я уже решил…»
Большинство учеников после долгих вычислений получили неверный результат. В тетради Гаусса было написано одно число и притом верное. Маленький Гаусс сразу сообразил, что 1+100=101, 2+99=101 и т.д. И таких чисел будет 50.
Осталось умножить 101 на 50, что он сделал в уме. Изумленный учитель понял, что это самый способный ученик в его практике. В дальнейшем Гаусс сделал много замечательных открытий. Его даже называли «царём математики».
Задача 1: Найдите сумму первых шестнадцати членов арифметической прогрессии, в которой a1 = 6, d= 4
Решение:
Найдём сумму по формуле:S=(a1 + аn) :2 ·n
По формуле аn=a1+ d(n-1) найдём сначала а16.
а16 = 6 + 4 (16 – 1) = 6 + 4·15=66, тогда
S16= (6 +66) : 2 ·16 = 72·8 =576
Ответ:576
Решение задач:
Задача 2: Тело в первую секунду прошло 16 метров, а в каждую следующую проходило на 3 метра больше, чем в предыдущую. Какой путь прошло это тело за 7 секунд?
Решение:
Найдём сумму по формуле:S=(a1 + аn) :2 ·n
По формуле аn=a1+ d(n-1) найдём сначала а7.
а7 = 16 + 3 (7 – 1) = 16+18=34, тогда
S7= (16 +34) : 2 ·7 = 50:2 ·7 =175
Ответ:175
Задача 3: Вертикальные стержни фермы имеют такую длину: наименьший 5 дм, а каждый следующий на 2 дм длиннее.
Найдите длину семи стержней.
Решение:
Составим последовательность (аn) : 5; 7; …
а1= 5 d= 2 S7=?
а7= 5 + 2 (7 – 1) = 17
S7=(5 +17) : 2·7= 77
Ответ:77
Задача 4: Какое из следующих чисел не является членом арифметической прогрессии 12; 14;16;…
А) 60 Б) 62 В) 63 Г) 66
Ответ В
Задача 5: Шары расположены в форме треугольника так, что в первом ряду один шар, во втором – два, в третьем – три и т.д. Во сколько рядов размещены шары, если их число равно 120?
Ответ : 15
Самостоятельная работа:
Вариант 1
№1Выберите последовательность, которая
является арифметической прогрессией
В) 12;17;22;27 … Г) 29; -28;27; -26;…
№2Выберите последовательность, которая НЕ
является арифметической прогрессией
А) 1;2;3;4… Б) -10; -9; -7;-4;0;5;….
В) -3; -8; -13; -18;…Г) 1,2; 2,7; 4,2…
№3 Найдите разность арифметической
прогрессии 15;30;45;…
А) 15 Б) -15 В) 2 Г) ½
№4 Найдите сумму первых восьми членов
арифметической прогрессии, если известно, что
её первый член равен -4, а разность равна 2
А) 12 Б) 10 В) 24 Г) 32
№5 Найдите пятый член арифметической
прогрессии, если ее первый член равен 7, а
разность равна -2
А) -3 Б) -1 В) 0,4375 Г) 112
Вариант 2
№1Выберите последовательность, которая
является арифметической прогрессией
А) 7;14;-7;-14;14;21… Б) -8;-5;-2;…
В) -40;-39;-38;38;39;40;-37;-36; ….
№2Выберите последовательность, которая НЕ
является арифметической прогрессией
А) 10;20;30;40… Б) 6;4;8/3;16/9;….
В)7,5;5,5;3,5;1,5;… Г) 3;6;9;12;…
№3 Найдите разность арифметической
прогрессии 4;8;12;16….
А) 2 Б) 1/2 В) -4 Г) 4
№4 Найдите сумму первых десяти членов
арифметической прогрессии, если известно, что
её первый член равен -7, а разность равна 3
А) 65 Б) 23 В) 80 Г) 20
№5 Найдите девятый член арифметической
прогрессии, если ее первый член равен 3, а
разность равна 0,5
А) 7,5 Б) 7 В) 768 Г) 0,01171875
В заключении вспомним строки А.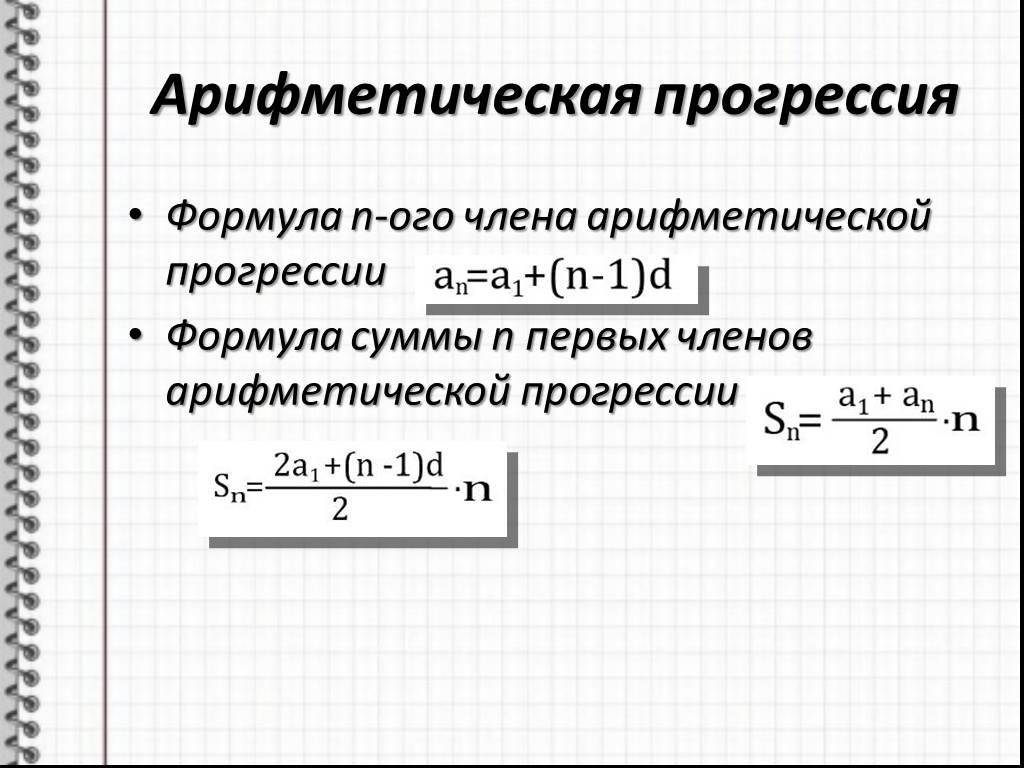
С.Пушкина из романа «Евгений Онегин», сказанные о его герое:
«…не мог он ямба от хорея, как мы ни бились, отличить». Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха. Ямб — стихотворный метр с ударениями на чётных слогах стиха, то есть ударными слогами являются 2-й, 4-й,6-й,8-й и так далее слоги. Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и с разностью, равной двум: 2;4;6;8;… Хорей – стихотворный размер с ударением на нечётных слогах стиха. Номера ударных слогов также образуют арифметическую прогрессию, но её первый член равен единице, а разность по-прежнему равна двум:1;3;5;7;….
Итог урока:
1. Пятый член арифметической прогрессии равен 8,4, а её десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии.
2. Сколько положительных членов в арифметической прогрессии
96,4; 91,8;….?
3. Между числами 6 и 17 вставьте четыре числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию
Домашнее задание:
Урок проведён 24 февраля 2009 года
Презентацию подготовила учитель
математики: Лавринова Ольга Николаевна
МОУ Совхозная сош
Сумма формулы арифметической прогрессии для n-го и суммы n членов
Сумма формулы арифметической прогрессии \(S_n=a_1+(a_1 + d) + (a_1 + 2d) + … + [a_1 + (n–1)d] \).
Арифметическая прогрессия (АП) — это последовательность, в которой каждый член получается прибавлением постоянного числа к предыдущему члену. Пример арифметической прогрессии: дни в месяце следуют определенной последовательности, количество учеников в классе следует арифметической прогрессии и так далее.
Первый член равен \(a_1\), второй член равен \(a_1 + d\), третий член равен \(a_1 + 2d\) и т. д. Это приводит к нахождению суммы арифметического ряда , \(S_n\), начиная с первого члена и последовательно добавляя общую разность.
Формула суммы арифметической прогрессии: \(S_n=a_1+(a_1 + d) + (a_1 + 2d) + … + [a_1 + (n–1)d]\)
Мы могли бы также начать с n-й член и последовательно вычитаем общую разность, так что
\(S_n = a_n + (a_n – d) + (a_n– 2d) + … + [a_n – (n–1)d]\)
Если сложить оба уравнения, получим,
\(S_n=a_1+ (a_1 + d) + (a_1 + 2d) + … + [a_1 + (n–1)d]\)
\(S_n = a_n + (a_n – d) + (a_n– 2d) + … + [a_n – (n–1)d]\)
где,
- S = сумма n членов AP
- n = общее количество членов
- a = первый член
- d = общая разность
n членов формулы арифметической прогрессии
\(2S_n = (a_1 + a_n) + (a_1 + a_n) + (a_1 + a_n) + … + [a_1 + a_n]\)
\(2S_n = n (a_1 + a_n)\)
\ (S_n = {n(a_1 + a_n )\over2}\)
\(S_n = {n\over2}(a_1 + a_n )\)
Подставив \(a_n = a_1 + (n – 1)d\ ) в последнюю формулу имеем
\(S_n = {n\over2}[a_1 + a_1 + (n – 1)d]\)
Сумма n членов формулы арифметической прогрессии: \(S_n = {n\over2}[2 a_1 + (n – 1)d]\)
где,
- \(S_n\) = сумма n членов AP
- n = общее количество членов
- a = первый член
- d = общая разность
Эти две формулы позволяют нам быстро найти сумму арифметического ряда.
Мы можем найти n-й член в арифметической прогрессии, используя следующую формулу.
N-й член формулы арифметической прогрессии: \(a_n=a_1+(n – 1)d\)
где,
- a – первый член
- d — общая разность
- n — количество членов
- \(a_n\) — n-й член
первые 35 членов арифметической прогрессии, третий член которой равен 7, а седьмой член в два раза больше третьего члена.
Решение: Предположим, что «а» — первый член, а «d» — общая разность данной арифметической прогрессии.
Согласно задаче,
3-й член арифметической прогрессии равен 7
т.е. 3-й член = 7
a + (3 – 1)d = 7
a + 2d = 7 ……………… . (i)
, а седьмой член в два раза больше третьего члена.
т. е. 7-й член = 3 × 3-й член + 2
a + (7 – 1)d = 3 × [a + (3 – 1)d] + 2
a + 6d = 3 × [a + 2d ] + 2
Подставляем значение a + 2d = 7 получаем,
a + 6d = 3 × 7 + 2
а + 6d = 21 + 2
а + 6d = 23 ……………….
(ii)
Теперь вычтите уравнение (i) из (ii), мы получим,
4d = 16
d = 4
Подставим значение d = 4 в уравнение (i), мы получим,
a + 2 × 4 = 7
a + 8 = 7
a = 7 – 8
a = -1
Следовательно, первый член арифметической прогрессии равен -1, а общая разность арифметической прогрессии равна 4.
Теперь сумма первых 35 членов арифметической прогрессии \(S_{35} = {35\over2}[2 × (-1) + (35 – 1) × 4]\),
\(\begin{массив}
={35\over2}[-2 + 34 × 4] ={35\over2}[-2 + 136] ={35\over2}[134] \end{массив} \)
= 35 × 67
= 2345.
вы также можете прочитать о Матрицах.
Пример 2: Если 5-й и 12-й члены арифметической прогрессии равны 30 и 65 соответственно, найдите сумму 26 ее членов.
A. Предположим, что «а» — первый член, а «d» — общая разность данной арифметической прогрессии.
По задаче
Пятый член арифметической прогрессии равен 30
т.
е. (i)
и 12-й член арифметической прогрессии равен 65
т. е. 12-й член = 65
a + (12 – 1)d = 65
a + 11d = 65 ……………….. ( ii)
Теперь, вычтем уравнение (i) из (ii), мы получим,
7d = 35
d = 357357
d = 5
Подставим значение d = 5 в уравнение (i) мы получить,
а + 4 × 5 = 30
а + 20 = 30
а = 30 – 20
а = 10
Следовательно, первый член арифметической прогрессии равен 10, а общая разность арифметической прогрессии равна 5.
Теперь сумма первых 26 членов арифметической прогрессии \(S_{26} = {26\over}[2 × 10 + (26 – 1) × 5]\),
= 13[20 + 25 × 5]
= 13[20 + 125]
= 13[145]
= 1885
Надеюсь, что эта статья о формуле суммы арифметической прогрессии была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о формуле суммы арифметической прогрессии В.
1 Что такое арифметическая прогрессия?
Ans.1 Арифметическая прогрессия (AP) представляет собой последовательность, в которой каждый член получается путем добавления постоянного числа к предыдущему члену.
Q.2 Что такое формула суммы арифметической прогрессии?
Ans.2 Формула суммы арифметической прогрессии: \(S_n=a_1+(a_1 + d) + (a_1 + 2d) + … + [a_1 + (n–1)d]\)
Q.3 Что такое сумма n членов формулы арифметической прогрессии?
Ответ 3 Сумма n членов формулы арифметической прогрессии: \(S_n = {n\over2}[2 a_1 + (n – 1)d]\)
Термин в формуле арифметической прогрессии?Ans.4 N-й член в формуле арифметической прогрессии: \(a_n=a_1+(n – 1)d\)
Q.5 Приведите несколько примеров арифметической прогрессии.
Ответ 5 Некоторые примеры арифметической прогрессии: дни в месяце следуют определенной последовательности, число учащихся в классе следует арифметической прогрессии.
| Центр масс: твердого тела, тонкого стержня и центра тяжести с условиями равновесия | |
| Столкновения, второй закон Ньютона для системы частиц0273 | Состояние вещества и характеристики твердого тела, жидкости, газа, плазмы |
| Открытие электрона, протона и нейтрона | |
| Составные функции: символ, домен, диапазон, свойства и примеры |
Подсказка: В этом вопросе нам нужно написать формулу суммы слагаемых в арифметической прогрессии. Для этого мы сначала предположим общую арифметическую прогрессию, имеющую «а» в качестве первого члена и «d» в качестве общей разности. Затем мы попытаемся найти сумму n слагаемых, используя предполагаемую арифметическую прогрессию. 9{th}} $ термин AP задается как, $ {{a}_{n}}=a+\left( n-1 \right)d $, поэтому наш AP становится \[a,a+d,a+ 2d,\ldots \ldots ,a+\left( n-2 \right)d,a+\left( n-1 \right)d\].
Предположим, что последний член AP обозначается через l, т. е. \[a+\left( n-1 \right)d=l\], так что предпоследний член становится l-d и так далее. Наш ряд выглядит так:
\[a,a+d,a+2d,\ldots \ldots ,\left( l-d \right),l\].
Обозначим его сумму через $ {{S}_{n}} $ так,
\[{{S}_{n}}=a+a+d+a+2d+\ldots \ldots +l-d +l\cdots \cdots \cdots \left( 1 \right)\].
Точно так же, если мы перевернем ряд, сумма останется той же, поэтому
\[{{S}_{n}}=l+l-d+l-2d+\ldots \ldots +a+d+a \cdots \cdots \cdots \left( 2 \right)\].
Сложим уравнение (1) и (2) и получим
\[{{S}_{n}}+{{S}_{n}}=\left( a+l \right)+\left ( a+d+l-d \right)+\left( a+2d+l-2d \right)+\ldots \ldots +\left( l+a \right)\].
Упрощая, получаем,
$ 2{{S}_{n}}=\underset{\text{n раз}}{\mathop{\left( a+l \right)+\left( a+l \right )+\left( a+l \right)+\ldots \ldots +\left( a+l \right)}}\, $ .
Таким образом, добавляя одни и те же термины n раз, мы получаем
$ 2{{S}_{n}}=n\left( a+l \right) $ .
