Как считать в уме
Метки
Загадки Математика Примеры Смекалка СообразительностьКак научиться считать в уме? И зачем это делать, ведь под рукой почти всегда есть калькулятор? Дело в том, что устный счет развивает мышление. Кроме того, когда ты считаешь без подручных средств, чувствуется совсем другой уровень контроля реальности.
© Pexels
Ты заранее знаешь, сколько сдачи тебе дадут в магазине и стоит ли набиваться всемером в лифт, если его грузоподъемность 400 кг. Использование же калькулятора, напротив, приучает нас слепо доверять технике, принципа работы которой мы даже не понимаем. Это притупляет внимание и отучает нас самостоятельно думать.
Как считать в уме
Ранее мы уже делились математическими секретами и хитростями, которые помогают умножать и делить в уме. А сегодня предлагаем твоему вниманию несколько проверочных примеров. Хорошо помнишь школьную программу? Тогда попробуй справиться с нашими заданиями за 15 секунд!
- Посчитай без калькулятора
Сложи 1000 и 40.
Прибавь еще 1000. Теперь 30. И снова 1000. Затем прибавь 20. И снова 1000. Еще 10. Решая эту задачку, постарайся все вычисления делать быстро и в уме. Ничего не пиши и не используй калькулятор. Уверены, что результат тебя удивит. - Сколько получится?
В школе мы щелкали такие примеры, как орешки. Но со временем много позабылось. Например, хоть кто-нибудь помнит, как делить на дробь? - Сложный пример и 15 секунд времени
Сплошные дроби, да еще и возведенные в степень… Кажется, что пример слишком сложный. Но, как говорил учитель математики, любое выражение можно упростить. - Будь внимателен
Ого, отрицательная степень! Сдаюсь. Кажется, я болел, когда мы это проходили.
Прибавь еще 1000. Теперь 30. И снова 1000. Затем прибавь 20. И снова 1000. Еще 10. Решая эту задачку, постарайся все вычисления делать быстро и в уме. Ничего не пиши и не используй калькулятор. Уверены, что результат тебя удивит.Ответы
- Казалось бы, всё просто. Однако комментарии убеждают в обратном. У большинства пользователей Сети почему-то получается 5000. А есть и такие, кто насчитал 5100, 4910 и даже 2060. При этом к последнему варианту ответа тяготеют юристы: мол, если перед числом нет слова «прибавь», значит считать его не обязательно.
© Pexels
На самом деле, правильным ответом будет 4100. 1000 + 40 = 1040; 1040 + 1000 = 2040; 2040 + 30 = 2070; 2070 + 1000 = 3070; 3070 + 1000 = 4090; 4090 + 10 = 4100. Но после 4090, когда люди прибавляют 10, у многих получается 5000. Видимо, в одних случаях мы психологически пытаемся подогнать ответ к более круглому числу. В других — вместо 90 запоминаем 900. Одним словом, это задача на внимательность, которой нам так часто не хватает.
- Поделить число на дробь — это всё равно что умножить ее на эту же дробь, предварительно поменяв числитель и знаменатель местами. А любое число, умноженное на 0, всё равно 0. Тогда наш пример получает более понятный вид: 15 х 10 : 3 – 144 = 50 – 144 = –94.
- С дробями мы уже немного разобрались. Умножение на дробь, в числителе которой единица, заменяем делением на знаменатель той же дроби. Поделить на одну вторую то же самое, что умножить на два. В результате получаем: 32 : 16 + 61 х 2 =
- Похоже, что придется стряхнуть пыль с позабытого порядка математических действий. Мы все учили его в начальной школе: скобки, степень, умножение, деление, сложение, вычитание. Применяем правило и первым делом возводим в отрицательную степень одну пятую.
Для этого всего лишь нужно поменять местами числитель и знаменатель и возвести получившееся число в квадрат. Получается 25. Далее выполним деление, потом умножение и складываем. 25 : 25 + 12 : 2 х 3 = 1 + 6 х 3 = 1 + 18 = 19. Правильный ответ: 19.
Мы все учили его в начальной школе: скобки, степень, умножение, деление, сложение, вычитание. Применяем правило и первым делом возводим в отрицательную степень одну пятую.Мы частенько возмущаемся, что в школе учат совсем не тому, что пригодится в реальной жизни. Да, наша система образования слишком устарела и продолжает устаревать каждый день. Но разносторонне образованный человек никогда не потеряется в какой-то затруднительной ситуации и обязательно сможет найти из нее выход.
Поделиться
Калькулятор экспоненциальной записи чисел
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Калькулятор экспоненциальной записи чисел переведет число, либо выражение в научную запись и также может перевести число из экспоненциальной записи в обыкновенную и десятичную дробь.
Чтобы перевести выражение в экспоненциальную запись, воспользуйтесь правилами ввода чисел и выражений, чтобы перевести число из экспоненциальной записи, введите числа, типа 2.3e+5, 5.8e-123 и т.д.
Представление разрядности результата
Без разделенияПробелЗапятаяАпострофТочка
Пожалуйста, опишите возникшую ошибку.
Подтвердите, что вы не робот
Что такое экспоненциальная запись чисел
Очень большие и очень маленькие числа более удобно представить в виде экспоненциальной записи. Экспоненциальной записью называется представление действительных чисел в виде мантиссы и порядка. На компьютере такая запись может быть представлена как MEp, где
M – мантисса
Е – буква, означающая 10n
p – показатель степени (может быть как положительный, так и отрицательный)
Примеры
14e+6 = 14 ∙ 106 = 14 ∙ 1000000 = 14000000
16e-4 = 16 ∙ 10-4 = 16 ∙ 0.
0001 = 0.0016
3.96e+3 = 3.96 ∙ 103 = 3.96 ∙ 1000 = 3960
17.356e-4 = 17.356 ∙ 10-4 = 17.356 ∙ 0.0001 = 0.0017356
0.23e+5 = 0.23 ∙ 105 = 0.23 ∙ 100000 = 23000
Pow(32, 7) = 327 = 3.43597384e+010
Sqrt(1934402) = √1934402 = 1.39082781E+3
Root(3/5, 43.6) = 43.6√(3/5) = 9.88352183E-1
(1/2)-Sqrt(3.5)*206 = -3.84890711E+2
Sin(167, deg) = Sin(167°) = 2.24951054E-1
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
| Формулы
Автор: Ханна Памула, доктор философии
Рецензию сделали Богна Шик и Джек Боуотер
Последнее обновление: 01 февраля 2023 г.
Содержание:- Что такое котерминальный угол?
- Как найти котерминальные углы? Формула котерминальных углов
- Как найти котерминальный угол между 0 и 360° (или 0 и 2π)?
- Положительный и отрицательный котерминальные углы
- Что такое котерминальный угол. ..
- Часто задаваемые вопросы
..Добро пожаловать в наш калькулятор котерминальных углов — инструмент, который решит многие ваши проблемы с котерминальными углами:
- Вы хотите найти котерминальный угол заданного угла , желательно в пределах [0,360°) [0, 360\градус)[0,360°) диапазон? Отличные новости: вы можете здесь.
- Вы ищете положительных и отрицательных котерминальных углов ? Также здесь.
- Вы хотите проверить, являются ли два угла котерминальными ? Проверять! ✔️
- Вы ищете калькулятор котерминальных углов для радианов ? Хорошо для вас, наш инструмент работает как для π радиан, так и для градусов.
- Или, может быть, вы ищете определение котерминальных углов с некоторыми примерами ? Тогда вы не будете разочарованы этим калькулятором.
- Гарантирует ли инструмент получение проходного балла за контрольную по математике? ❌ Ну, наш инструмент универсален, но это на ваше усмотрение 🙂
Воспользуйтесь нашим калькулятором, чтобы решить проблемы с котерминальными углами, или прокрутите вниз, чтобы узнать больше.
Начнем с определения котерминальных углов.
Что такое котерминальный угол?
Котерминальные углы — это углы, которые разделяют конечную сторону угла, занимающего стандартное положение . Стандартное положение означает, что одна сторона угла закреплена вдоль положительной оси x, а вершина расположена в начале координат.
Другими словами, два угла являются котерминальными, когда сами углы различны, но их стороны и вершины совпадают . Также можно запомнить определение котерминального угла как углов, отличающихся целым числом полных окружностей .
Посмотрите на картинку ниже, и все должно быть понятно!
Итак, как мы сказали: все котерминальные углы начинаются с одной и той же стороны (исходной стороны) и имеют общую конечную сторону.
Иногда может сбивать с толку различие между определениями опорного угла и котерминального угла . Помните, что это не одно и то же — опорный угол — это угол между конечной стороной угла и осью x, и он всегда находится в диапазоне [0,90°][0, 90\градус][0 ,90°] (или [0,π/2][0, \pi/2][0,π/2]): чтобы узнать больше по теме, посетите наш калькулятор эталонного угла!
Как найти котерминальные углы? Формула котерминальных углов
Чтобы найти котерминальные углы к заданному углу, вам нужно прибавить или вычесть число, кратное 360° (или 2π, если вы работаете в радианах).
Итак, чтобы проверить, являются ли углы α и β котерминальными, проверьте, согласуются ли они с формулой котерминальных углов:
а) Для углов, измеренных в градусах:
β=α±(360°×k)\beta=\alpha\pm(360\градус\k)β=α±(360°×k)
Где kkk — целое положительное число.
b) Для углов, измеренных в радианах:
β=α±(2π×k)\beta = \alpha \pm(2\pi\times k)β=α±(2π×k)
здесь k является положительным целым числом
Полезной особенностью является то, что при вычислении тригонометрических функций любые два котерминальных угла имеют точно такие же тригонометрические значения. Итак, если β\betaβ и α\alphaα котерминальны, то их синусы, косинусы и тангенсы равны.
При вычислении синуса, например, мы говорим
sin(α)=sin(α±(360°×k))\sin(\alpha) = \sin(\alpha\pm(360\степень) \times k))sin(α)=sin(α±(360°×k))
Как найти котерминальный угол между 0 и 360° (или 0 и 2π)?
Чтобы определить котерминальный угол между 0°0\градусом 0° и 360°360\градусом 360°, все, что вам нужно сделать, это вычислить по модулю, другими словами, разделить заданный угол на 360°360\градус360° и проверить, что осталось.
Мы покажем вам, как это работает, на двух примерах, охватывающих как положительные, так и отрицательные углы. Мы хотим найти котерминальный угол с мерой θ\thetaθ такой, что 0°≤θ<360°0\градус \leq \theta < 360\степень0°≤θ<360°, для заданного угла, равного:
420°\жирныйсимвол{420\градус}420°
420°mod 360°=60°420\градус\текст{mod}\ 360\градус = 60\градус420°mod 360°=60°
Как это сделать вручную?
- Сначала разделим одно число на другое, округлив в меньшую сторону (вычисляем функцию пола): ⌊420°/360°⌋=1\влево\lfloor420\градус/360\градус\вправо\rfloor = 1⌊420° /360°⌋=1.
- Затем умножьте делитель на полученное число (называемое частным): 360°×1=360°360\градус\умножить на 1 = 360\градус360°×1=360°.
- Вычтите это число из исходного числа: 420°−360°=60°420\градус — 360\градус = 60\градус420°−360°=60°.
Подстановка этих углов в формулу котерминальных углов дает 420°=60°+360°×1420\градус = 60\градус + 360\градус\умножить на 1420°=60°+360°×1.
−858°-858\градус−858°
−858°mod 360°=222°-858\градус \text{mod}\ 360\градус = 222\градус-858°mod 360°=222 °
Повторяя шаги, описанные выше:
- Рассчитать пол: ⌊−858°/360°⌋=−3\влево\lпол-858\градус / 360\градус\вправо\rпол = -3⌊−858° /360°⌋=−3.
- Найдите общее количество полных окружностей: 360°×−3=−1080°360\градус \times -3 = -1080\степень360°×−3=−1080°.
- Вычислить остаток: -858°+1080°=222°-858\градус + 1080\градус = 222\градус-858°+1080°=222°.
Таким образом, формула котерминальных углов, β=α±360°×k\beta = \alpha \pm 360\степень \times kβ=α±360°×k, для нашего примера с отрицательным углом будет выглядеть следующим образом:
− 858°=222°−360°×3-858\градус = 222\градус — 360\градус\умножить на 3−858°=222°−360°×3
То же самое работает для [0,2π)[0 ,2\pi)[0,2π), все, что вам нужно изменить, это делитель — вместо 360°360\степень360° используйте 2π2\pi2π.
Теперь проверьте результаты с помощью нашего калькулятора котерминального угла — он отображает котерминальный угол между 0°0\градусом 0° и 360°360\градусом 360° (или 000 и 2π2\pi2π), а также несколько образцовых положительных и отрицательные котерминальные углы.
Положительные и отрицательные котерминальные углы
Если вы хотите найти несколько положительных и отрицательных котерминальных углов , вам нужно вычесть или добавить несколько полных окружностей. Но сколько?
Один из методов заключается в нахождении котерминального угла в диапазоне 0°0\градус 0° и 360°360\градус 360° (или диапазоне $$[0,2\pi)), как это было сделано в предыдущем абзаце (если ваш угол уже находится в этом диапазоне, вам не нужно делать этот шаг). Затем просто добавьте или вычтите диапазон) , как мы делали в предыдущем абзаце (если ваш угол уже находится в этом диапазоне, вам не нужно делать этот шаг). Затем просто добавьте или вычтите диапазон), как это было сделано в предыдущем абзаце (если ваш угол уже находится в этом диапазоне, вам не нужно делать этот шаг). \pi,6\pi…), чтобы получить положительный или отрицательный котерминальный угол к вашему заданному углу. Например, если…), чтобы получить положительный или отрицательный котерминальный угол к вашему заданному углу.
Например, если …), чтобы получить положительный или отрицательный котерминальный угол к вашему заданному углу. Например, если\ альфа = 1400\градус, тогда котерминальный угол в, затем котерминальный угол в ,тогда котерминальный угол в [0,360\градус)диапазон составляет 320\градус$$ — что уже является одним из примеров положительного котерминального угла.
остальные положительные котерминальные углы равны 680°680\градус680°, 1040°1040\градус1040°…
другие отрицательные котерминальные углы: -40°-40\градус-40°, -400°-400\градус-400°, -760°-760\градус-760°…
Кроме того, вы можете просто сложить и вычесть количество оборотов , если все, что вам нужно, это любой положительный и отрицательный котерминальный угол . Для нашего ранее выбранного угла α=1400°\alpha = 1400\градусα=1400° прибавим и вычтем 101010 оборотов (или 100100100, почему бы и нет):
положительный котерминальный угол: β=α+360°\time10=1400°+3600°=5000°\beta = \alpha + 360\градус \time 10 = 1400\градус + 3600\градус = 5000\градусβ=α+360 °\время10=1400°+3600°=5000°.
отрицательный котерминальный угол: β=α−360°×10=1400°−3600°=−2200°\бета = \альфа — 360\градус\умножить на 10 = 1400\градус — 3600\градус = -2200\градусβ=α −360°×10=1400°−3600°=−2200°.
Число оборотов должно быть достаточно большим, чтобы изменить знак при сложении/вычитании. Например, одного оборота для нашего примерного α недостаточно, чтобы иметь как положительный, так и отрицательный котерминальный угол — мы получим два положительных, 1040°1040\градус1040° и 1760°1760\градус1760°.
Что такое котерминальный угол…
Если вам интересно, что такое котерминальный угол некоторого угла, не стесняйтесь использовать наш инструмент — он здесь, чтобы помочь вам!
Но если вы по какой-то причине предпочитаете список примерных котерминальных углов (но мы действительно не понимаем почему …), то вам сюда:
Котерминальный угол 0°0\градус 0°: 360°360\градус 360°, 720°720\градус 720°, -360°-360\градус-360°, -720°-720\градус-720°.
Котерминальный угол 1°1\градус 1°: 361°361\градус 361°, 721°721\градус 721° -359°-359\градус-359°, -719°-719\градус-719°.
Котерминальный угол 5°5\градус 5°: 365°365\градус 365°, 725°725\градус 725°, -355°-355\градус-355°, -715°-715\градус-715°.
Котерминальный угол 10°10\градус 10°: 370°370\градус 370°, 730°730\градус 730°, -350°-350\градус-350°, -710°-710\градус-710°.
Котерминальный угол 15°15\градус 15°: 375°375\градус 375°, 735°735\градус 735°, -345°-345\градус-345°, -705°-705\градус-705°.
Котерминальный угол 20°20\градус 20°: 380°380\градус 380°, 740°740\градус 740°, -340°-340\градус-340°, -700°-700\градус-700°.
Котерминальный угол 25°25\градус 25°: 385°385\градус 385°, 745°745\градус 745°, -335°-335\градус-335°, -695°-695\градус-695°.
Котерминальный угол 30°30\градус 30° (π/6\pi / 6π/6): 390°390\градус 390°, 750°750\градус 750°, -330°-330\градус-330°, -690° -690\градус-690°.
Котерминальный угол 45°45\градус 45° (π/4\pi / 4π/4): 495°495\градус495°, 765°765\градус765°, -315°-315\градус-315°, -675°-675\градус-675°.
Котерминальный угол 60°60\градус 60° (π/3\pi / 3π/3): 420°420\градус420°, 780°780\градус780°, −300°-300\градус−300°, −660° -660\градус-660°
Котерминальный угол 75°75\градус75°: 435°435\градус435°, 795°795\градус795°,-285°-285\градус-285°, -645°-645\градус-645°
Котерминальный угол 90°90\градус90° (π/2\pi / 2π/2): 450°450\градус450°, 810°810\градус810°, -270°-270\градус-270°, -630° -630\градус-630°.
Котерминальный угол 105°105\градус 105°: 465°465\градус 465°, 825°825\градус 825°,-255°-255\градус-255°, -615°-615\градус-615°.
Котерминальный угол 120°120\градус 120° (2π/32\pi/32π/3): 480°480\градус480°, 840°840\градус840°, -240°-240\градус-240°, -600° -600\градус-600°.
Котерминальный угол 135°135\градус 135° (3π/43\pi / 43π/4): 495°495\градус 495°, 855°855\градус 855°, -225°-225\градус-225°, -585° -585\градус-585°.
Котерминальный угол 150°150\градус 150° (5π/65\pi/65π/6): 510°510\градус510°, 870°870\градус870°, -210°-210\градус-210°, -570° -570\градус-570°.
Котерминальный угол 165°165\градус 165°: 525°525\градус 525°, 885°885\градус 885°, -195°-195\градус-195°, -555°-555\градус-555°.
Котерминальный угол 180°180\градус 180° (π\piπ): 540°540\градус540°, 900°900\градус900°, -180°-180\градус-180°, -540°-540\градус-540 °*
Котерминальный угол 195°195\градус 195°: 555°555\градус 555°, 915°915\градус 915°, -165°-165\градус-165°, -525°-525\градус-525°.
Котерминальный угол ∗∗210°**210\градус*∗∗210° (7π/67\pi / 67π/6): 570°570\градус570°, 930°930\градус930°, −150°-150\градус −150°, −510°-510\градус−510°.
Котерминальный угол 225°225\градус 225° (5π/45\pi / 45π/4): 585°585\градус 585°, 945°945\градус 945°, -135°-135\градус-135°, -495° -495\градус-495°.
Котерминальный угол ∗∗240°**240\градусов*∗240° (4π/34\pi / 34π/3: 600°600\градус600°, 960°960\градус960°, 120°120\градус120°, − 480°-480\градус-480°
Котерминальный угол 255°255\градус 255°: 615°615\градус 615°, 975°975\градус 975°, -105°-105\градус-105°, -465°-465\градус-465°.
Котерминальный угол 270°270\градус 270° (3π/23\pi / 23π/2): 630°630\градус630°, 990°990\градус990°, -90°-90\градус-90°, -450° -450\градус-450°.
Котерминальный угол 285°285\градус 285°: 645°645\градус 645°, 1005°1005\градус 1005°, -75°-75\градус-75°, -435°-435\градус-435°.
Котерминальный угол 300°300\градус300° (5π/35\pi / 35π/3): 660°660\градус660°, 1020°1020\градус1020°, −60°-60\градус−60°, −420° -420\градус-420°.
Котерминальный угол 315°315\градус 315° (7π/47\pi / 47π/4): 675°675\градус 675°, 1035°1035\градус 1035°, -45°-45\градус-45°, -405° -405\градус-405°.
Котерминальный угол 330°330\градус330° (11π/611\pi / 611π/6): 690°690\градус690°, 1050°1050\градус1050°, −30°-30\градус−30°, −390° -390\градус-390°.
Котерминальный угол 345°345\градус345°: 705°705\градус705°, 1065°1065\градус1065°, -15°-15\градус-15°, -375°-375\градус-375°.
Котерминальный угол 360°360\градус 360° (2π2\pi2π): 0°0\градус0°, 720°720\градус720°, -360°-360\градус-360°, -720°-720\градус-720 °.
Если вы не нашли свой запрос в этом списке, введите угол в наш калькулятор котерминального угла — вы получите ответ в мгновение ока!
Часто задаваемые вопросы
Каков котерминальный угол 1000° между 0° и 360°?
Ответ: 280° . Чтобы получить этот результат, вспомните формулу для котерминальных углов в 1000°:
1000° + 360°×k . Ясно, что для получения котерминального угла между 0° и 360° нам нужно использовать отрицательные значения к . При k=-1 получаем 640°, что слишком много. Итак, давайте попробуем k=-2: мы получим 280°, что находится между 0° и 360°, так что у нас есть ответ.
Как найти все котерминальные углы?
У данного угла бесконечно много котерминальных углов, поэтому вы не можете перечислить их все. Вы можете записать их с помощью формулы. Если ваш угол θ выражен в градусах, то котерминальные углы имеют вид θ + 360°×k , где k — целое число (возможно, отрицательное число!).
Если θ в радианах, тогда формула выглядит как θ + 2π×k .
Каковы котерминальные углы 45°?
Котерминальные углы 45° имеют форму 45° + 360°×k , где k — целое число. Подставляя различные значения k , мы получаем разные котерминальные углы 45° . Перечислим некоторые из них:
45°, 405°, 765°, -315°, -675° .
Как проверить, являются ли два угла котерминальными?
Два угла, α и β , являются котерминальными, если их разность кратна 360° . То есть, если β - α = 360°×k для некоторого целого числа k . Например, углы -170° и 550° являются котерминальными, потому что 550° - (-170°) = 720° = 360° × 2. Если ваши углы выражены в радианах, а не в градусах, то вы ищете кратных 2π , то есть формула β - α = 2π×k для некоторого целого числа k .
Hanna Pamuła, PhD
Я хочу…
Угол в
Посмотреть 6 похожих калькуляторов углов 🕑 Калькулятор котерминального угла — TrigCalc.com
градус
/
радиан
минимум
угловая совмещенная с
(
)°
минимум
угловая совмещенная с
(
)
Решение:
°
или
°
Требуется только два значения
Учебное пособие по котерминальному углу
Котерминальные углы — это углы, имеющие общие начальную и конечную стороны.
Чтобы найти угол, котерминальный другому, вы можете сделать это, просто добавив или вычтя любое число, кратное 360 градусам или 2 пи радианам.
Если вам нужно найти наименьший положительный угол, сотерминальный с 785 градусами, вы можете использовать следующий процесс расчета, показанный ниже.
Максимальное количество раз, когда 360 градусов можно вычесть из 785 градусов и остаться положительным, находится путем деления заданного угла на 785 градусов и деления его на 360, но с округлением до целого числа в меньшую сторону. Это число равно 2. Как только это число найдено, оно умножается на 360 и вычитается из 785 градусов. Если бы сказали найти наименьший отрицательный котерминал угла с 526 градусами, был бы использован аналогичный процесс вычисления с той лишь разницей, что нужно сложить делимое данного угла и 360 градусов. Как только это число найдено, его нужно снова вычесть из заданного угла 526 градусов.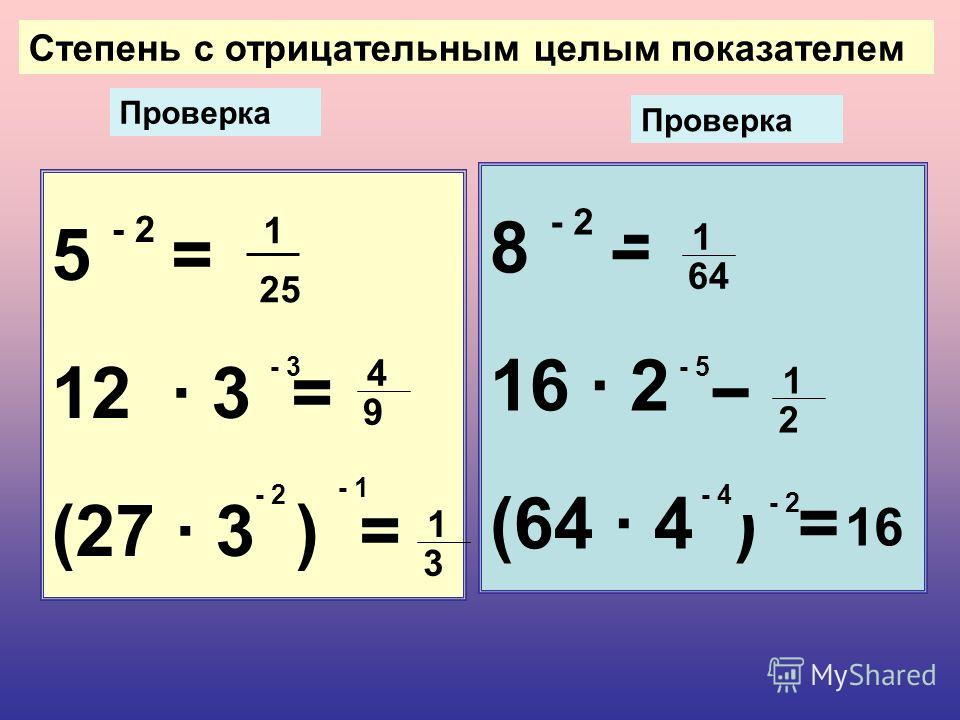
Это дает вам наименьший отрицательный котерминальный угол.
Таким же образом можно найти углы, котерминальные значениям в радианах. Если бы вам сказали найти котерминал наименьшего положительного угла с 32 пи радиан, вы бы использовали следующий процесс расчета:
Поскольку при вычислении наименьшего положительного значения делимое данного радиана и 2pi должно быть округлено до целого числа в меньшую сторону. Это целое число нужно умножить на 2 пи и вычесть из заданного значения. Это приводит к решению, пи. Но ты
Чтобы найти наименьший отрицательный угол, котерминальный другому углу, скажем, 78 пи, будет работать процесс вычисления, показанный ниже. В этом случае необходим наименьший отрицательный угол, что означает, что делимое 78 пи и 2 пи должно быть округлено до ближайшего целого числа. Затем это число нужно вычесть из 78 пи, чтобы найти решение.