Формулы двойного угла в тригонометрии, синус косинус двойного угла, вывод формул двойного угла
Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2α, используя тригонометрические функции угла α. Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид nα записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin nαимеет то же значение, что и sin (nα). При обозначении sinn α имеем аналогичную запись(sin α)n. Использование записи применимо для всех тригонометрических функций со степенями n.
Ниже приведены формулы двойного угла:
sin 2α=2·sin α·cos αcos 2α=cos2 α-sin2 α, cos 2α=1-2·sin2 α, cos 2α=2·cos2 α-1tg 2α=2·tg α1-tg2 αctg 2α-ctg2 α-12·ctg α
Отметим, что данные формулы sin и cos применимы с любым значением угла α. Формула тангенса двойного угла справедлива при любом значении α, где tg 2α имеет смысл, то есть α≠π4+π2·z, z является любым целым числом. Котангенс двойного угла существует при любом α, где ctg 2α определен на α≠π2·z.
Формула тангенса двойного угла справедлива при любом значении α, где tg 2α имеет смысл, то есть α≠π4+π2·z, z является любым целым числом. Котангенс двойного угла существует при любом α, где ctg 2α определен на α≠π2·z.
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin (α+β)=sin α ·cos β+cos α·sin βи косинуса суммы cos (α+β)=cos α ·cos β-sin α·sin β. Предположим, что β=α, тогда получим, что
sin (α+α)=sin α ·cos α+cos α·sin α=2·sin α·cos α и cos (α+α)=cos α ·cos α-sin α·sin α=cos2α-sin2α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2α= 2·sin α·cos α и cos 2α=cos2α-sin2α.
Остальные формулы cos 2α=1-2·sin2 α и cos 2α=2·cos2 α-1 приводят к виду cos 2α=cos 2α=cos2 α-sin2 α, при замене 1 на сумму квадратов по основному тождествуsin2 α+cos2 α=1. Получаем, что sin2 α+cos2 α=1.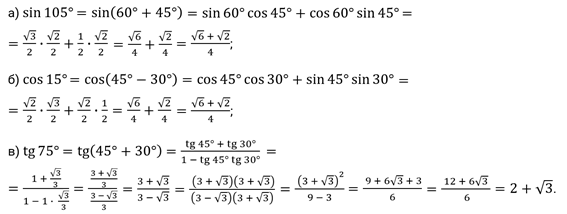 Так 1-2·sin2 α=sin2 α+cos2 α-2·sin2 α=cos2 α-sin2 α и 2·cos2 α-1=2·cos2 α-(sin2 α+ cos2 α)=cos2 α-sin2 α.
Так 1-2·sin2 α=sin2 α+cos2 α-2·sin2 α=cos2 α-sin2 α и 2·cos2 α-1=2·cos2 α-(sin2 α+ cos2 α)=cos2 α-sin2 α.
Для доказательства формул двойного угла тангенса и котангенса применим равенства tg 2α=sin 2αcos 2α и ctg 2α=cos 2αsin 2α. После преобразования получим, что tg 2α=sin 2αcos 2α=2·sin α·cos αcos2 α-sin2 α и ctg 2α=cos 2αsin 2α=cos2 α-sin2 α2·sin α·cos α. Разделим выражение на cos2 α, где cos2 α≠0 с любым значением α, когда tg α определен. Другое выражение поделим на sin2 α, где sin2 α≠0 с любыми значениями α, когда ctg 2α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
tg 2α=sin 2αcos 2α=2·sin α·cos αcos2 α-sin2 α=2·sin α·cos αcos2 αcos2 α-sin2 αcos2 α=2·sin2 αcos2 α1-sin2 αcos2 α=2·tg α1-tg2 αctg 2α=cos 2αsin 2α=cos2 α-sin2 α2·sin α·cos=cos2 α-sin2 αsin2 α2·sin α·cos αsin2 α=cos2 αsin2 α-12·cos αsin α=ctg2 α-12·ctg α
Примеры использования формул двойного угла
Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2α для α=30°, применим значения тригонометрических функций для этих углов. Если α=30°, тогда 2α=60°. Проверим значения sin 60°=2·sin 30°·cos 30°, cos 60°=cos2 30°-sin2 30°.
Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2α для α=30°, применим значения тригонометрических функций для этих углов. Если α=30°, тогда 2α=60°. Проверим значения sin 60°=2·sin 30°·cos 30°, cos 60°=cos2 30°-sin2 30°.
Подставив значения, получим tg 60°= 2·tg 30°1-tg2 30° и ctg 60°=ctg230°-12·ctg 30°..
Известно, что sin 30°=12, cos 30°=32, tg 30°=33, ctg 30°=3 и
sin 60°=32, cos 60°=12, tg 60°=3, ctg 60°=33, тогда отсюда видим, что
2·sin 30°·cos 30°=2·12·32=32, cos230°-sin230°=(32)2-(12)2=12,2·tg 30°1-tg230°=2·321-(33)=3
и ctg230°-12·ctg 30°=(3)2-12·3=33
Проведя вычисления, можно сделать вывод, что справедливость для α=30° подтверждена.
Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2α. В примере допускается применение формулы двойного угла 3π5. Тогда его необходимо преобразовать, в результате чего получим α=3π5:2=3π10.
Представить sin 2α3 через тригонометрические функции, при α6.
Решение
Заметим, что из условия имеем 2α3=4·α6. Тогда использовав 2 раза формулу двойного угла, выразим sin2α3 через тригонометрические функции угла α6. Применяя формулу двойного угла, получим sin 2α3=2·sin α3·cos α3. После чего к функциям sin α3 и cos α3применим формулы двойного угла: sin 2α2=2·sin α3·cosα3=2·(2·sinα5·cosα6)·(cos2α6-sinα6)==4·sinα6·cos3α6-4·sin3α6·cosα6
Ответ: sin2α3=4·sinα6·cos3α6-4·sin3α6·cosα6.
Формулы тройного, четверного и т.д. угла
Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.
sin 3α=sin(2α+α)=sin 2α·cos α+cos 2α·sin α=2·sin α·cosα·cos α+ (cos2 α-sin2α)·sin α==3·sin α·cos2α-sin3 α
При замене cos2α на 1-sin2α из формулы sin 3α=3·sin α·cos2α-sin3α, она будет иметь вид sin 3α=3·sin α-4·sin3 α.
Так же приводится формула косинуса тройного угла:
cos 3α=cos (2α+α)=cos 2α·cos α-sin 2α·sin α==(cos2 α-sin2 α)·cos α-2·sin α·cos α·sin α=cos3α-3·sin2α·cos α
При замене sin2 α на 1-cos2 α получим формулу вида cos 3α=-3·cos α+4·cos3 α.
При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:
tg 3α=sin 3αcos 3α=3·sin α·cos2 α-sin3 αcos3α-3·sin2α·cos α=3·sin α·cos2α-sin3αcos3αcos3α-3·sin2α·cos αcos3α==3·sin αcos α-sin3αcos3α1-3·sin2 αcos2 α=3·tg α-tg3α1-3·tg2α;ctg 3α=cos 3αsin 3α=cos3 α-3·sin2α·cosα3·sin α·cos2α-sin3α=cos3α-3·sin2α·cosαsin3α3·sin α·cos2α-sin3αsin3α==cos3αsin3α-3·cos αsin α3·cos2αsin2α-1=ctg3α-3·ctgα3·ctg2α-1
Чтобы выводить формулы четвертой степени, имеет смысл представить 4α как 2·2α, тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5α в виде 3α+2α, что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.
Их применение достаточно редкое в тригонометрии.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Вот теперь видно, что перед нами формула косинуса двойного угла.
\(=\sqrt{3}\cos(2\cdot\frac{5π}{12})=\)
Сокращаем \(2\) и \(12\).
\(=\sqrt{3}\cos(\frac{5π}{6})=\)
Разложим \(\frac{5π}{6}\): \(\frac{5π}{6}=\frac{6π-π}{6}=\frac{6π}{6}-\frac{π}{6}=π-\frac{π}{6}\)
\(=\sqrt{3}\cos(π-\frac{π}{6})=\)
Теперь применим к косинусу формулу приведения:
-
\((π-\frac{π}{6})\) – это вторая четверть, косинус в ней отрицателен.
Значит, знак будет минус;
-
\(π\) — находится на «горизонтали» — функция не меняется на кофункцию.
\(\cos(π-\frac{π}{6})=-\cos \frac{π}{6}\)
\(=-\sqrt{3}\cos\frac{π}{6}=-\sqrt{3}\cdot\frac{\sqrt{3}}{2}=\)
\(=-\frac{3}{2}=-1,5.\)
Ответ: \(-1,5\).
Смотрите также:
Формулы тригонометрии с примерами
Формулы двойного и тройного угла тригонометрических функций
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Кратные углы тригонометрических функций: двойные и тройные
В таблицах ниже представлены формулы двойного и тройного угла тригонометрических функций: синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Содержание
- Формулы двойного угла
- Формулы тройного угла
Формулы двойного угла
| Действие | Формула |
| Синус двойного угла | sin 2α = 2 sin α cos α |
| Косинус двойного угла | cos 2α = cos2α — sin2α |
| Тангенс двойного угла | tg 2α = 2 tg α / (1 — tg2α) |
| Котангенс двойного угла | ctg 2α = (ctg2α — 1) / 2 ctg α |
microexcel. ru
ru
Формулы тройного угла
| Действие | Формула |
| Синус тройного угла | sin 3α = 3 sin α — 4 sin3α |
| Косинус тройного угла | cos 3α = 4 cos3α — 3 cos α |
| Тангенс тройного угла | tg 3α = (3 tg α — tg3α) / (1 — 3 tg2α) |
| Котангенс тройного угла | ctg 3α = (ctg3α — 3 ctg α) / (3 ctg2α — 1) |
microexcel.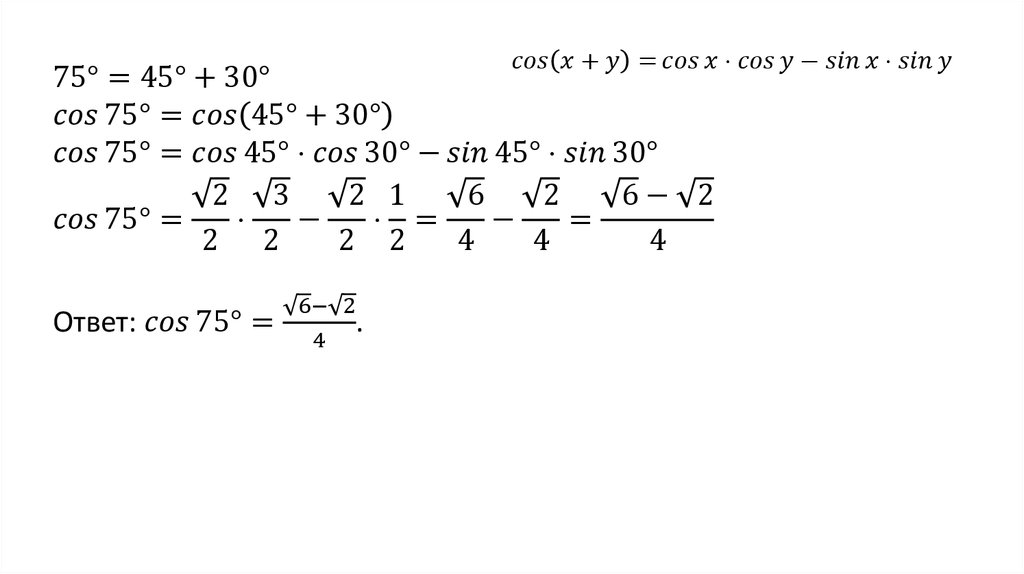 ru
ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Формулы двойного аргумента
- org/Person»>
Нечаева Светлана Валерьевна,
Разделы: Математика, Общепедагогические технологии
Цель: вывести и научиться применять формулы двойного угла.
Задачи:
Образовательные:
- повторить основные тригонометрические функции;
- вывести формулы двойного угла;
- показать применение формул синуса и косинуса двойного угла для преобразования тригонометрических выражений различного уровня сложности.
Развивающие:
- развивать регулятивные способности: совершенствовать умение работать по плану, планировать свое действие в соответствии с поставленной задачей, вносить необходимые коррективы, осуществлять оценку и самооценку результатов работы;
- формирование тестовой культуры учащихся, развитие учебно- познавательной компетенции;
- развивать навыки самостоятельной работы;
- способствовать развитию культуры математической речи, абстрактного и логического мышления, долговременной оперативной памяти и устойчивого внимания.

Воспитательные:
- воспитывать культуру поведения при индивидуальной и фронтальной работе;
- способствовать повышению самооценки учащихся на основе критерия успешности учебной деятельности.
Ход урока
ОРГАНИЗАЦИОННЫЙ МОМЕНТ (3 мин)Я хотела бы начать наш урок с воспоминания немецкого математика.
Давида Гильберта спросили об одном из его бывших учеников. «А, такой-то? — вспомнил Гильберт. — Он стал поэтом. Для математики у него было слишком мало воображения».
Сегодня мы поупражняем наше с вами воображение, по средством алгебры и ее разделов.
Предлагаю вам принять участие в квесте под названием «Тригонометрия». Вам знакомо слово «квест»? Что оно означает? (выполнение заданий для достижения цели).
Внимательно посмотрите на карту, где мы находимся?
Перед вами маршрутный лист. Определите первый этап и его содержание.
МАРШРУТНЫЙ ЛИСТ
| ЭТАП | РЕЗУЛЬТАТ |
Проверка знаний простейших тригонометрических формул |
|
Математический диктант |
|
| Страна Исследователей (вывод формул) |
|
Страна Творчества |
|
Страна демонстраций |
|
А) проверка вычислительных навыков – работа на «четвертушках» (2 мин) оценка в маршрутный лист.
Б) математический диктант (5 мин) с последующей проверкой.
Упростить выражения:
Ответы: 1) 1; 2) 1; 3) 1.
Проверка. Оценка в маршрутный лист.
ИЗУЧЕНИЕ НОВОЙ ТЕМЫ (7 мин)Следующий этап «Страна Исследователей» По маршрутному листу определите содержание работы.
Цель: получение формул синуса, косинуса и тангенса двойного угла, развитие логического мышления, внимания, умения говорить и слушать.
Вывод формул у доски с помощью учителя.
Заметим, что формула косинуса двойного угла имеет два разных продолжения, так как в ней можно выразить cos2x через sin2x, а можно выразить sin2x через cos2x :
Предложить вывести следующую формулу одному из учеников.
Аналогичную формулу можно получить и для ctg2x, но запоминать ее не обязательно, так как без нее всегда можно обойтись:
(5 слайд)
«Страна Творчества» (10 мин) Цель: показать применение формул синуса и косинуса двойного угла для преобразования тригонометрических выражений; развитие логического мышления, внимания, умения говорить и слушать.
Работа учащихся у доски.
№ 635 (1;4) Не используя таблицы, вычислить:
№ 636 (2;3) Не используя таблицы, вычислить:
№ 642 (1) Упростите выражение:
ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА (10 мин)«Страна Демонстраций»
Цель: формирование тестовой культуры учащихся, развитие учебно-познавательной компетенции. Проверка первичного усвоения знаний, самокоррекция.
Работа проходит индивидуально по тестовым заданиям.
1 уровень «3 балла» Заполните пропуски в равенствах так, чтоб они стали верными равенствами:
2 уровень «4 балла» Вычислите:
3 уровень «5 баллов» Упростите:
Обмениваемся в парах работами и выполняем проверку по готовому решению – карточке «Проверь себя». Выставляем друг другу баллы.
Выставляем друг другу баллы.
«Страна Знания» (3 мин)
Продолжи предложение:
- Мне было сложно… легко…
- Я узнал(а), как…
- Я понял(а), что…
- Меня удивило…
- Мне не понравилось… понравилось…
- Мне это нужно, потому что…
п.32 стр. 197-200.
№ 635 (2;3) Не используя таблицы, вычислить:
Формулы двойного угла — значения функций, свойства и примеры решений
На уроках математики школьники 8−11 классов изучают интегралы, знакомятся с таблицей значений аргумента (переменная). Через формулу двойного угла (ФДУ) выражаются косинус, синус, тангенс, котангенс с произведением 2α. В основе находится тригонометрическая функция угла альфа. Чтобы её отобразить на графике, используются координаты и окружность.
Чтобы её отобразить на графике, используются координаты и окружность.
Содержание
- Способы преобразования
- Доказательства равенств
- Решение задач
- Тождества при других значениях
- Область применения
Способы преобразования
Чтобы понять, как выражаются тригонометрические функции двойных углов, необходимо воспользоваться их записью в виде nα, где n принадлежит натуральному числу. Значение основного выражения отображается математически без скобок. Используя это свойство, можно составить следующее уравнение: sin nα = sin (nα).
Для приведения произведения sin nα х sin nα, используется аналогичное свойство. Выражение можно упростить до 2 (n sin α). Основой тождества является n sin α. В математике используются и другие равенства:

В геометрии и алгебре чаще применяются следующие известные формулы: синус2α = cos2α — sin2α, cos2α = 1 − 2·sin2α. Можно разложить производные sin и cos, если угол имеет любой градус. Решение тангенса потребуется, если в основе задачи находится tg2α, при этом значение угла отлично от суммы π4 и π2. Частный случай, когда в задании есть целое число z, а α ≠ π4 + π2·z. Если рассматривать для котангенса ФДУ при любом альфа, ctg2α не определён на промежутке π2. Для косинуса двойного угла характерна тройная запись.
Доказательства равенств
Чтобы подтвердить уравнения на сложение, вычитание и умножение, понадобится подойти к доказательству комплексным способом. Используя формулы синуса с плюсом для углов (α+β) и косинуса для β и α, получится синусα·косинусβ+косинусα·синусβ. Пример для вычитания: соsα ·cosβ-синусα·синусβ.
При вычислении разницы следует придерживаться аналогичного принципа. Результат будет следующим: косинус (α+α) равен двойному значению косинуса минус двойное значение синуса. Формула двойного угла косинуса и синуса доказана. При решении задач из дидактических материалов используются и другие уравнения при положительном и отрицательном значении альфа, при нуле либо половинном π.
Результат будет следующим: косинус (α+α) равен двойному значению косинуса минус двойное значение синуса. Формула двойного угла косинуса и синуса доказана. При решении задач из дидактических материалов используются и другие уравнения при положительном и отрицательном значении альфа, при нуле либо половинном π.
Для их доказательства необходимо находить корень из числа z, возводить целое значение в квадрат либо иную степень. Чтобы определиться с ходом решения, необходимо следить за графиком функции:
- возрастанием;
- понижением.
Сложные действия вычисляются с помощью калькулятора. Если задача состоит из нескольких частей, для нахождения результата потребуется преобразовать первичное уравнение в более простое. Используются следующие равенства:
- косинус2α=1−2⋅синус2α;
- косинус 2α=2·косинус2α — 1.
Их можно привести к косинус2α — синус2α. Если заменить единицу суммой квадратов, тогда sin2α + cos2α = 1.
Получается, что синус2α + косинус2α = 1. Подставив данные, выходит: 1 − 2·sin2α.
Чтобы доказать ФДУ котангенса, применяется равенство ctg2α = cos2αsin2α. Преобразовав данные, получится для tg2α равенство 2·sinα·cosαcos2α — sin2α. Разделив выражение на cos2α, отличное от нуля, получится, что tgα определен. Другое выражение поделится на sin2α. Значение sin2α ≠ 0 будет иметь смысл при любом α, если ctg2α имеет смысл.
Решение задач
Для убеждения в справедливости 2α для α=30° применяется значение тригонометрических функций для углов. Если α=30°, тогда 2α будет соответствовать 60°. Необходимо проверить значение sin 60° = 2·sin 30°·cos 30°, cos 60° = cos2 30° — sin2 30°. Если подставить данные, получится подробная функция: tg 60°= 2·tg 30°1 — tg2 30° и ctg 60° = ctg230° — 12·ctg 30°.
Так как sin 30° = 12, cos 30° = 32, tg 30° = 33, ctg 30° = 3 и sin 60° = 32, cos 60° = 12, tg 60° = 3, ctg 60° = 33, тогда выводится следующее: 2·sin 30°·cos 30° = 2·12·32 = 32, cos230° — sin230° = (32)2-(12)2 = 12,2·tg 30°1-tg230° = 2·321 — (33) = 3 и ctg230° — 12·ctg 30° = (3)2 − 12·3 = 33.
Задача 1: дан угол, отличный от 2α, например 3π5. Нужно найти его значение. Решение: угол 3π5 необходимо преобразовать. Получается α = 3π5:2 = 3π10. Из результата следует, что ФДУ для косинуса принимает следующий вид: cos3π5 = cos23π10 — sin23π10.
Задача 2: необходимо представить sin2α3 через функции, когда α = 6. Решение: заменить 2α3 = 4·α6. Если подставить данные, получится sin2α3. Выражая через функцию, принимая формулу двойного угла, записывается выражением: sin2α3 = 2·sinα3·cosα3. Используя cosα3, применяя sin2α2, получится результат sin2α3 = 4·sinα6·cos3α6 − 4·sin3α6·cosα6.
Тождества при других значениях
На практике студенты высших учебных заведений математических факультетов встречаются с задачами, для решения которых применяются формулы тройного, четверного и другого угла. В их основе находятся тригонометрические функции.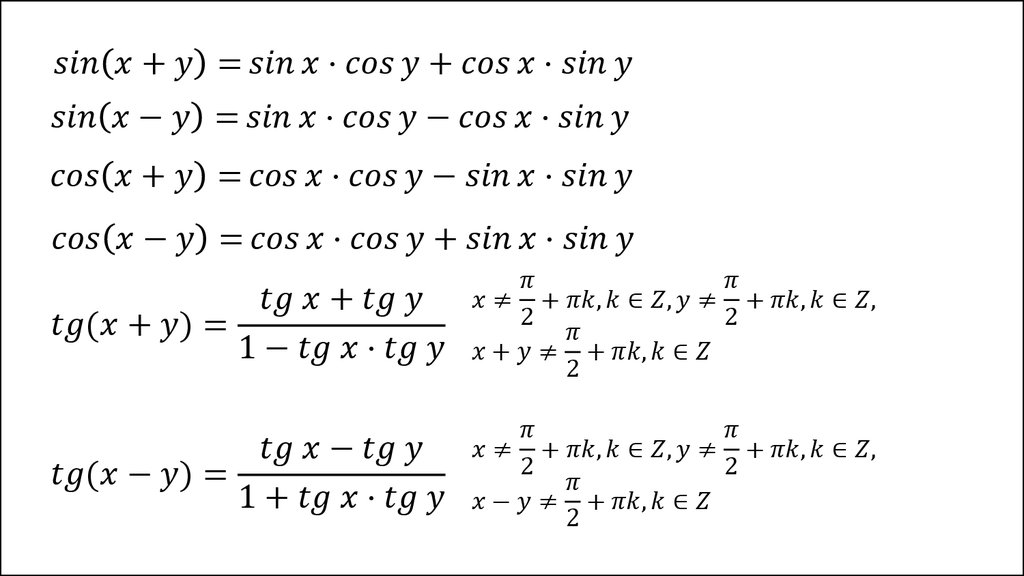 Чтобы их вывести, используются формулы сложения двойного угла: sin3α = sin (2α+α) = 3·sinα·cos2α — sin3α.
Чтобы их вывести, используются формулы сложения двойного угла: sin3α = sin (2α+α) = 3·sinα·cos2α — sin3α.
При замене cos2α на 1-sin2α формула примет новый вид: sin3α = 3·sinα-4·sin3α. По аналогичной схеме приводится формула косинуса тройного угла: косинус3α = косинус (2α+α) = косинус3α — 3·синус2α·косинусα.
При замене sin2α на 1-cos2α, получится формула вида cos3α = -3·cosα+4·cos3α. С помощью полученных равенств преобразовывается формула тройного угла для тангенса и котангенса: tg3α = sin3αcos3α = ctg3α — 3·ctgα3·ctg2α — 1.
По такой же методике выводятся формулы четвёртой степени. Значение 4α нужно представить в виде 2·2α. Равенство выводится с помощью ФДУ дважды. Для получения равенства пятой степени представляется значение угла 5α в виде 3α+2α.
Такая сумма позволяет использовать формулы двойного и тройного углов с целью преобразования в конечный результат. По аналогичной схеме преобразовываются разные степени тригонометрических функций, но их применяют в тригонометрии редко.
Область применения
Чтобы определить значение тригонометрической функции (ТФ), рассматривается окружность с радиусом в единицу и диаметрами, взаимно перпендикулярными. Для вычислений потребуется отложить от точки, принадлежащей окружности, дуги любых длин. Они будут положительными, если их отложить против часовой стрелки.
Отрицательное значение принимают те, которые размещены по часовой стрелке. Если конец дуги имеет длину f, тогда проекция радиуса на любом диаметре примет значение косинуса дуги. Под аргументом понимается число, которое рассматривается геометрически как f либо радианная мера угла. Если аргумент ТФ взят за угол, тогда его значение выражается и в градусах.
Доказано, что значение острых углов больше нуля, но меньше p/2. Для таких величин ТФ рассматривается как отношение катетов к гипотенузе. Эти элементы принадлежат прямоугольному треугольнику. Название связано с наличием угла в 90 градусов. Для решения задач с тригонометрическими функциями используется и теорема Пифагора, в основе которой находится свойство прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов.
Название связано с наличием угла в 90 градусов. Для решения задач с тригонометрическими функциями используется и теорема Пифагора, в основе которой находится свойство прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов.
Дуга делит окружность на несколько частей. Углы, размещенные в первой четверти, больше нуля, во второй косинус меньше, но синус больше, в третьей ТФ меньше 0, а в четвёртой получаются значения, противоположные второй. Для построения окружности потребуется циркуль, а для измерения углов транспортир.
Для получения точного чертежа рекомендуется наносить данные на миллиметровую бумагу либо тетрадь в клетку.
Предыдущая
МатематикаОсновные понятия, аксиомы и теоремы стереометрии
Следующая
МатематикаДеление на двузначное число — способы и примеры решений
Тригонометрические формулы двойного угла.
 Синус (sin x) и косинус (cos x) – свойства, графики, формулы
Синус (sin x) и косинус (cos x) – свойства, графики, формулыФормулы двойного угласлужат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Yandex.RTB R-A-339285-1
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin (n α) . При обозначении sin n α имеем аналогичную запись (sin α) n . Использование записи применимо для всех тригонометрических функций со степенями n .
Ниже приведены формулы двойного угла:
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α
Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .
Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin (α + β) = sin α · cos β + cos α · sin β и косинуса суммы cos (α + β) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что
sin (α + α) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos (α + α) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .
Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — (sin 2 α + cos 2 α) = cos 2 α — sin 2 α .
Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — (sin 2 α + cos 2 α) = cos 2 α — sin 2 α .
Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
Самые часто задаваемые вопросы
Возможно ли, изготовить печать на документе по предоставленному образцу?
Ответ
Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Какие виды оплаты вы принимаете?
Ответ
Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами?
Ответ
В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Что делать при обнаружении в документе опечаток и ошибок?
Ответ
Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Что нужно сделать, чтобы заказать диплом в вашей компании?
Ответ
Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.
Последние отзывы
Валентина:
Вы спасли нашего сына от увольнения! Дело в том что недоучившись в институте, сын пошел в армию. А вернувшись, восстанавливаться не захотел. Работал без диплома. Но недавно начали увольнять всех, кто не имеет «корочки. Поэтому решили обратиться к вам и не пожалели! Теперь спокойно работает и ничего не боится! Спасибо!
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т. д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений.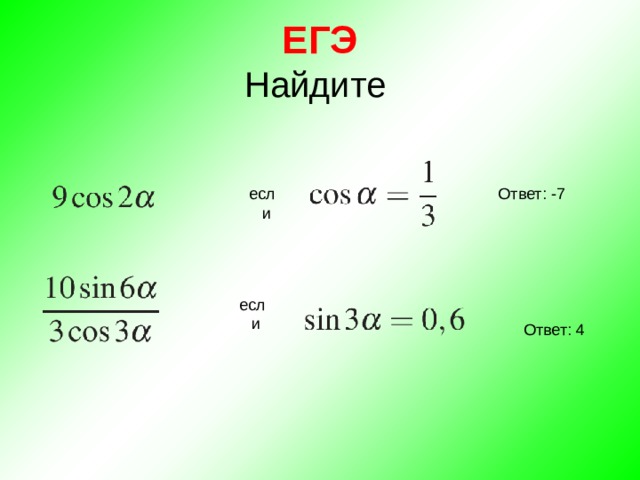 Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Самые часто задаваемые вопросы
Возможно ли, изготовить печать на документе по предоставленному образцу? Ответ Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Какие виды оплаты вы принимаете?
Ответ
Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами?
Ответ
В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Что делать при обнаружении в документе опечаток и ошибок?
Ответ
Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Что нужно сделать, чтобы заказать диплом в вашей компании?
Ответ
Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.
Последние отзывы
Валентина:
Вы спасли нашего сына от увольнения! Дело в том что недоучившись в институте, сын пошел в армию. А вернувшись, восстанавливаться не захотел. Работал без диплома. Но недавно начали увольнять всех, кто не имеет «корочки. Поэтому решили обратиться к вам и не пожалели! Теперь спокойно работает и ничего не боится! Спасибо!
Формулы двойного угла — Что такое формулы двойного угла? Примеры
Формулы двойных углов используются для выражения тригонометрических отношений двойных углов (2θ) через тригонометрические отношения одинарного угла (θ). Формулы двойного угла являются частными случаями (и, следовательно, выводятся из) формул суммы тригонометрии, а некоторые альтернативные формулы выводятся с использованием тождеств Пифагора. Напомним формулы сумм тригонометрии.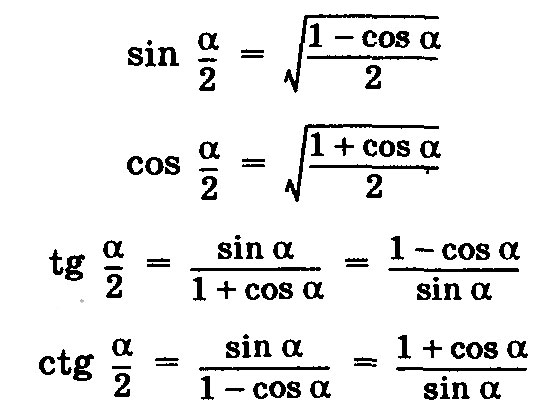
- sin (A + B) = sin A cos B + cos A sin B
- cos (A + B) = cos A cos B — sin A sin B
- tan (A + B) = (tan A + tan B) / (1 — tan A tan B)
Что такое формулы двойного угла?
Мы получим формулы двойного угла для sin, cos и tan, подставив A = B в каждую из вышеприведенных формул суммы. Кроме того, мы выведем некоторые альтернативные формулы, полученные с использованием тождеств Пифагора. Вот формулы двойного угла, за которыми следует вывод каждой формулы.
Формулы двойного угла
Формулы двойного угла для sin, cos и tan:
- sin 2A = 2 sin A cos A (или) (2 tan A) / (1 + tan 2 A)
- cos 2A = cos 2 A — sin 2 A (или) 2cos 2 A — 1 (или) 1 — 2sin 2 A (или) (1 — tan 2 A) / (1 + загар 2 А)
- тангенс 2A = (2 тангенс A) / (1 — тангенс 2 A)
Вывод формул двойного угла
Давайте выведем формулу(ы) двойного угла для каждого из sin, cos и tan одну за другой.
Формула двойного угла Sin
Формула суммы функции синуса:
sin (A + B) = sin A cos B + cos A sin B (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
Выведем альтернативную формулу для sin 2A через тангенс, используя тождество Пифагора, сек. 92A} \end{align}\)
Таким образом, формула двойного угла функции синуса:
Формулы двойного угла для косинуса
Формула суммы функции косинуса:
cos (A + B) = cos A cos B — sin A sin B
Когда A = B, приведенная выше формула принимает вид
cos ( A + A) = cos A cos A — sin A sin A
cos 2A = cos 2 A — sin 2 A
Используем эту формулу в качестве базовой для вывода двух других формул для cos 2A с помощью Пифагорейское тождество sin 92A} \end{align} \)
Таким образом, формулы двойного угла функции косинуса: или) 1 — 2sin 2 A (или) (1 — tan 2 A) / (1 + tan 2 A)
Формулы двойного угла Tan
Формула суммы функции тангенса:
tan (A + B) = (tan A + tan B) / (1 — tan A tan B)
Когда A = B, приведенная выше формула принимает вид
tan (A + A) = (tan A + tan A ) / (1 — тангенс A тангенс A) = (2 тангенс A) / (1 — тангенс 2 A)
Таким образом, формула функции тангенса двойного угла:
tan 2A = (2 tan A) / (1 — tan 2 A)
Есть вопросы по основным математическим понятиям ?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Закажите бесплатный пробный урок
Давайте рассмотрим применение формул двойного угла в разделе ниже.
Примеры использования формул двойного угла 92x \end{align} \)
Ответ: Данное тождество доказано.
Пример 3: Используйте формулы двойного угла, чтобы вывести формулу для sin 3x.
Решение:
sin (3x) = sin (2x + x)
= sin 2x cos x + cos 2x sin x (используя sin (A + B) = sin A cos B + cos A sin B)
= (2 sin x cos x) cos x + (1 — 2 sin 2 x) sin x (используя формулы двойного угла)
= 2 sin x cos 2 x + sin x — 2 sin 3 x
= 2 sin x (1 — sin 2 x) + sin x — 2 sin 3 x
= 2 sin x — 2 sin 3 x + sin x — 2 sin 3 x
= 3 sin x — 4 sin 3 x
Ответ: sin 3x = 3 sin x — 4 sin 3 x.
Часто задаваемые вопросы о формулах двойного угла
Что такое формулы двойного угла?
Формулы двойного угла — это формулы в тригонометрии, которые имеют дело с двойными углами тригонометрических функций. Некоторые важные формулы двойного угла:
- sin 2A = 2 sin A cos A
- cos 2A = cos 2 A — sin 2 A
- тангенс 2A = (2 тангенс A) / (1 — тангенс 2 A)
Как получить формулы двойного угла?
Подставим A = B в формулы суммы функций sin, cos и tan, чтобы получить формулы двойного угла. Для более подробного и ясного объяснения, пожалуйста, обратитесь к разделу «Вывод формул двойного угла» на этой странице.
Каковы применения формул двойного угла?
Формулы двойного угла используются для нахождения значений двойных углов тригонометрических функций, используя значения их одиночных углов. Например, значение cos 30 o можно использовать для нахождения значения cos 60 o .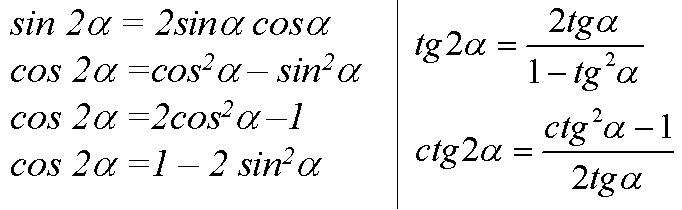 Кроме того, формулы двойного угла можно использовать для вывода формул тройного угла.
Кроме того, формулы двойного угла можно использовать для вывода формул тройного угла.
Как использовать формулы двойного угла в интегрировании?
При интегрировании используем формулы двойного интегрирования. Чтобы понять это, рассмотрим пример ниже.
∫ sin x cos x dx = (1/2) ∫ (2 sin x cos x) dx
= (1/2) ∫ sin 2x dx
= (1/2) (- cos 2x / 2) + C (путем замены 2x = u)
= -1/4 cos 2x + C
будет:
- Используйте формулы двойного угла, чтобы найти точные значения.
- Используйте формулы двойного угла для проверки тождества.
- Используйте формулы сокращения для упрощения выражения.
- Используйте формулы половинного угла, чтобы найти точные значения.
Рисунок 1 Велосипедные рампы для опытных райдеров имеют более крутой наклон, чем для новичков.
Велосипедные рампы, изготовленные для соревнований (см. рис. 1), должны различаться по высоте в зависимости от уровня квалификации участников.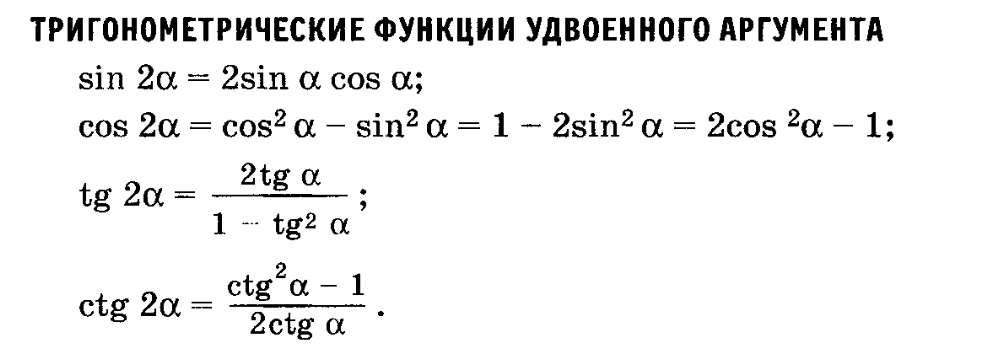 Для продвинутых участников угол, образованный рампой и землей, должен быть θθ таким, чтобы tanθ=53.tanθ=53. Угол делится пополам для новичков. Какая крутизна пандуса для новичков? В этом разделе мы исследуем три дополнительные категории тождеств, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
Для продвинутых участников угол, образованный рампой и землей, должен быть θθ таким, чтобы tanθ=53.tanθ=53. Угол делится пополам для новичков. Какая крутизна пандуса для новичков? В этом разделе мы исследуем три дополнительные категории тождеств, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
Использование формул двойного угла для нахождения точных значений
В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций. Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул сумм, где α=β.α=β. Вывод формулы двойного угла для синуса начинается с формулы суммы
.sin(α+β)=sinαcosβ+cosαsinβsin(α+β)=sinαcosβ+cosαsinβ
Если мы допустим α=β=θ,α=β=θ, то мы имеем
sin(θ+θ)=sinθcosθ+cosθsinθ sin(2θ)=2sinθcosθsin(θ+θ)=sinθcosθ+cosθsinθ sin(2θ)=2sinθcosθ
Получение двойного угла для косинуса дает нам три варианта. Во-первых, исходя из формулы суммы cos(α+β)=cosαcosβ−sinαsinβ,cos(α+β)=cosαcosβ−sinαsinβ и допуская α=β=θ,α=β=θ, мы имеем
Во-первых, исходя из формулы суммы cos(α+β)=cosαcosβ−sinαsinβ,cos(α+β)=cosαcosβ−sinαsinβ и допуская α=β=θ,α=β=θ, мы имеем
cos(θ+θ)=cosθcosθ−sinθsinθ cos(2θ)=cos2θ−sin2θcos(θ+θ)=cosθcosθ−sinθsinθ cos(2θ)=cos2θ−sin2θ
Используя свойства Пифагора, мы можем расширить эту формулу двойного угла для косинуса и получить еще две интерпретации. Первый:
cos(2θ)=cos2θ−sin2θ = (1–sin2θ)−sin2θ = 1−2sin2θcos(2θ)=cos2θ−sin2θ
Вторая интерпретация:
.
Аналогичным образом, чтобы вывести формулу тангенса двойного угла, заменив α=β=θα=β=θ в формуле суммы, получим
tan(α+β)=tanα+tanβ1−tanαtanβtan(θ+θ)=tanθ+tanθ1−tanθtanθtan(2θ)=2tanθ1−tan2θtan(α+β)=tanα+tanβ1−tanαtanβtan(θ+θ)=tanθ+ tanθ1−tanθtanθtan(2θ)=2tanθ1−tan2θ
Формулы двойного угла
Формулы с двойным углом суммированы следующим образом:
sin (2θ) = 2sinθcosθsin (2θ) = 2sinθcosθ
cos (2θ) = cos2θ-sin2θ = 1-2sin2θ = 2cos2θ-1cos (2θ) = cos2θ = 2sin2θ = 2cos2θ-1cos (2θ) = cos2θin2d2θ = 2cos2θ-1cos (2θ) = cos2θin2d2θ = 2cos2θ-1cos (2θ) = cos2d 2sin2θ = 2cos2θ-1cos (2θ) = =1−2sin2θ =2cos2θ−1
tan(2θ)=2tanθ1−tan2θtan(2θ)=2tanθ1−tan2θ
Как
Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение.
- Нарисуйте треугольник, чтобы отразить предоставленную информацию.
- Определите правильную формулу двойного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.
Пример 1
Использование формулы двойного угла для нахождения точного значения, включающего тангенс
Учитывая, что tanθ=-34tanθ=-34 и θθ находится в квадранте II, найдите следующее:
- ⓐ sin(2θ)sin(2θ)
- ⓑ потому что (2θ) потому что (2θ)
- ⓒ загар(2θ)загар(2θ)
Решение
Если мы нарисуем треугольник, чтобы отразить предоставленную информацию, мы сможем найти значения, необходимые для решения проблем на изображении. Нам заданы tanθ=−34,tanθ=−34, так что θθ находится в квадранте II. Тангенс угла равен стороне, противоположной соседней стороне, и, поскольку θθ находится во втором квадранте, смежная сторона находится на оси x и является отрицательной. Используйте теорему Пифагора, чтобы найти длину гипотенузы:
Используйте теорему Пифагора, чтобы найти длину гипотенузы:
(−4)2+(3)2=c216+9=c225=c2c=5(−4)2+(3)2=c216+9=c225=c2c=5
Теперь мы можем нарисовать треугольник аналогичен показанному на рис. 2.
Рис. 2
- ⓐНачнем с написания формулы двойного угла для синуса.
sin(2θ)=2sinθcosθsin(2θ)=2sinθcosθ
Мы видим, что нам нужно найти sinθsinθ и cosθ.cosθ. На основании рисунка 2 мы видим, что гипотенуза равна 5, поэтому sinθ=35,sinθ=35 и cosθ=−45.cosθ=−45. Подставьте эти значения в уравнение и упростите.
Итак,
sin(2θ)=2(35)(−45) =−2425sin(2θ)=2(35)(−45) =−2425
- ⓑ Напишите формулу двойного угла для косинуса.
cos(2θ)=cos2θ−sin2θcos(2θ)=cos2θ−sin2θ
Снова подставьте значения синуса и косинуса в уравнение и упростите.
cos(2θ)=(−45)2−(35)2 =1625−925 =725cos(2θ)=(−45)2−(35)2 =1625−925 =725
0006 - ⓒ Запишите формулу тангенса двойного угла.

tan(2θ)=2tanθ1−tan2θtan(2θ)=2tanθ1−tan2θ
В этой формуле нам нужен тангенс, который мы получили как tanθ=−34.tanθ=−34. Подставьте это значение в уравнение и упростите.
tan(2θ)=2(−34)1−(−34)2 =−321−916 = −32(167) =−247tan(2θ)=2(−34)1−(−34)2 =− 321−916 =−32(167) =−247
Попытайся #1
Для данного sinα=58,sinα=58 и θθ в квадранте I найдите cos(2α).cos(2α).
Пример 2
Использование формулы двойного угла для косинуса без точных значений
Используйте формулу двойного угла для косинуса, чтобы записать cos(6x)cos(6x) через cos(3x).cos(3x).
Решение
. ) =2cos2(3x)−1
Анализ
Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений. В нем подчеркивается, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.
В нем подчеркивается, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.
Использование формул двойного угла для проверки подлинности
Установление тождеств с помощью формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для вывода формул суммы и разности. Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной.
Пример 3
Использование формул двойного угла для установления тождества
Установите следующее тождество с помощью формул двойного угла:
1+sin(2θ)=(sinθ+cosθ)21+sin(2θ)=(sinθ+cosθ) 2
Решение
Мы будем работать с правой частью знака равенства и перепишем выражение, пока оно не совпадет с левой частью.
(sinθ+cosθ) 2 = sin2θ+2sinθcosθ+cos2θ = (sin2θ+cos2θ)+2sinθcosθ = 1+2sinθcosθ = 1+sin (2θ) (sinθ+cosθ) 2 = sin2θ+2sinθθ+cos2θ = (sinθ+cos2) 2 = sin2θ+2sinθ+cos2θ = (sinθ+cos2). )+2sinθcosθ =1+2sinθcosθ =1+sin(2θ)
)+2sinθcosθ =1+2sinθcosθ =1+sin(2θ)
Анализ
Этот процесс не сложен, если вспомнить формулу совершенного квадрата из алгебры:
(a±b)2=a2±2ab+b2(a±b)2=a2±2ab+b2
где a=sinθa=sinθ и b=cosθ.b=cosθ. Частью успеха в математике является способность распознавать закономерности. Хотя термины или символы могут меняться, алгебра остается неизменной.
Попытайся #2
Установить тождество: cos4θ−sin4θ=cos(2θ).cos4θ−sin4θ=cos(2θ).
Пример 4
Проверка идентичности двойного угла для касательной
Проверка идентичности:
tan(2θ)=2cotθ−tanθtan(2θ)=2cotθ−tanθ
Решение
В этом случае мы будем работать с левой частью уравнения и упрощать или переписывать, пока оно не сравняется с правой частью уравнения.
tan(2θ)=2tanθ1−tan2θФормула двойного угла = 2tanθ(1tanθ)(1−tan2θ)(1tanθ) Умножить на член, который дает желаемый числитель. =21tanθ−tan2θtanθ =2cotθ−tanθИспользовать взаимное тождество для 1tanθ.tan(2θ)=2tanθ1−tan2θФормула двойного угла =2tanθ(1tanθ)(1−tan2θ)(1tanθ) Множитель на член, который приводит к дескриптору. =21tanθ−tan2θtanθ =2cotθ−tanθИспользуйте взаимное тождество для 1tanθ.
Анализ
Вот случай, когда более сложная часть исходного уравнения появилась справа, но мы решили работать с левой частью. Однако, если бы мы выбрали для перезаписи левую часть, мы бы работали в обратном направлении, чтобы получить эквивалентность. Например, предположим, что мы хотим показать
2tanθ1−tan2θ=2cotθ−tanθ2tanθ1−tan2θ=2cotθ−tanθ
Давайте поработаем с правой стороны.
2cotθ -tanθ = 21tanθ -tanθ (tanθtanθ) = 2tanθ1tanθ (tanθ) −tanθ (tanθ) = 2tanθ1 -tan2doncotθ -tanθ = 21tanθ -tanθ (tanθtanθ = 2tanθθ (tanθ −tanθ (tanθtanθ) = 2tanθdud tan2) = 2tanθ (tanθ) =0003
При использовании тождеств для упрощения тригонометрического выражения или решения тригонометрического уравнения обычно существует несколько путей к желаемому результату. Не существует установленного правила относительно того, какой стороной следует манипулировать. Тем не менее, мы должны начать с руководящих принципов, изложенных ранее.
Не существует установленного правила относительно того, какой стороной следует манипулировать. Тем не менее, мы должны начать с руководящих принципов, изложенных ранее.
Попытайся #3
Проверка идентичности: cos(2θ)cosθ=cos3θ−cosθsin2θ.cos(2θ)cosθ=cos3θ−cosθsin2θ.
Использование формул сокращения для упрощения выражения
Формулы двойного угла можно использовать для вывода формул приведения, которые представляют собой формулы, которые мы можем использовать для уменьшения мощности данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны в курсах математики более высокого уровня, в частности исчисления. Также называемые формулами уменьшения степени, включены три тождества, которые легко выводятся из формул двойного угла.
Мы можем использовать две из трех формул двойного угла для косинуса, чтобы вывести формулы приведения для синуса и косинуса. Начнем с cos(2θ)=1−2sin2θ.cos(2θ)=1−2sin2θ. Найдите sin2θ:sin2θ:
Начнем с cos(2θ)=1−2sin2θ.cos(2θ)=1−2sin2θ. Найдите sin2θ:sin2θ:
cos(2θ)=1−2sin2θ2sin2θ=1−cos(2θ) sin2θ=1−cos(2θ)2cos(2θ)=1−2sin2θ2sin2θ=1−cos(2θ) sin2θ=1−cos(2θ)2
Далее используем формулу cos(2θ)=2cos2θ−1.cos(2θ)=2cos2θ−1. Найдите cos2θ:cos2θ:
cos(2θ)=2cos2θ−11+cos(2θ)=2cos2θ1+cos(2θ)2=cos2θ cos(2θ)=2cos2θ−11+cos(2θ)=2cos2θ1+cos(2θ)2=cos2θ
Последняя формула приведения получается путем записи тангенса через синус и косинус:
tan2θ=sin2θcos2θ =1−cos(2θ)21+cos(2θ)2Подставьте формулы редукции. =(1−cos(2θ)2)(21+cos(2θ)) =1−cos(2θ)1+cos(2θ)tan2θ=sin2θcos2θ =1−cos(2θ)21+cos(2θ)2 Подставляем сокращение формулы. =(1−cos(2θ)2)(21+cos(2θ)) =1−cos(2θ)1+cos(2θ)
Формулы приведения
Формулы приведения обобщаются следующим образом:
sin2θ=1−cos(2θ)2sin2θ=1−cos(2θ)2
cos2θ=1+cos(2θ)2cos2θ=1+cos(2θ)2
tan2θ=1−cos(2θ)1+ cos(2θ)tan2θ=1−cos(2θ)1+cos(2θ)
Пример 5
Написание эквивалентного выражения, не содержащего степени больше 1
Напишите эквивалентное выражение для cos4xcos4x, не содержащее степени синуса или косинуса больше 1.
Решение
Применим формулу приведения косинуса дважды.
cos4x=(cos2x)2 =(1+cos(2x)2)2Подставьте формулу приведения вместо cos2x. =14(1+2cos(2x)+cos2(2x)) =14+12cos(2x)+14(1+cos2(2x)2) Замените cos2x формулой приведения. =14+12cos(2x)+18+18cos(4x) =38+12cos(2x)+18cos(4x)cos4x=(cos2x)2 = (1+cos(2x)2)2Подставьте формулу приведения вместо cos2x. =14(1+2cos(2x)+cos2(2x)) =14+12cos(2x)+14(1+cos2(2x)2) Замените cos2x формулой приведения. =14+12cos(2x)+18+18cos(4x) =38+12cos(2x)+18cos(4x)
Анализ
Решение находится путем двойного использования формулы приведения, как уже отмечалось, и формулы полного квадрата из алгебры.
Пример 6
Использование формул уменьшения степени для доказательства тождества
Использование формул уменьшения степени для доказательства
sin3(2x)=[12sin(2x)][1−cos(4x)]sin3(2x)=[12sin (2x)][1-cos(4x)]
Решение
Будем работать над упрощением левой части уравнения:
sin3(2x)=[sin(2x)][sin2(2x)] =sin(2x)[1−cos(4x)2]Замените формулой уменьшения мощности. =sin(2x)(12)[1−cos(4x)] =12[sin(2x)][1−cos(4x)]sin3(2x)=[sin(2x)][sin2(2x)] = sin(2x)[1−cos(4x)2]Подставьте формулу уменьшения мощности. =sin(2x)(12)[1−cos(4x)] =12[sin(2x)][1−cos(4x)]
=sin(2x)(12)[1−cos(4x)] =12[sin(2x)][1−cos(4x)]sin3(2x)=[sin(2x)][sin2(2x)] = sin(2x)[1−cos(4x)2]Подставьте формулу уменьшения мощности. =sin(2x)(12)[1−cos(4x)] =12[sin(2x)][1−cos(4x)]
Анализ
Обратите внимание, что в этом примере мы заменили
1-cos(4x)21-cos(4x)2
вместо sin2(2x).sin2(2x). Формула гласит
sin2θ=1−cos(2θ)2sin2θ=1−cos(2θ)2
Допустим θ=2x,θ=2x, поэтому 2θ=4x.2θ=4x.
Попытайся #4
Используйте формулы уменьшения мощности, чтобы доказать, что 10cos4x=154+5cos(2x)+54cos(4x).10cos4x=154+5cos(2x)+54cos(4x).
Использование формул половинного угла для нахождения точных значений
Следующий набор тождеств — это набор формул половинного угла, которые могут быть получены из формул приведения и могут использоваться, когда у нас есть угол, который в два раза меньше специального угла. Если мы заменим θθ на α2,α2, формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для sin(α2).sin(α2). Обратите внимание, что перед формулами половинного угла стоит знак ±±. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается α2α2.
Если мы заменим θθ на α2,α2, формула половинного угла для синуса будет найдена путем упрощения уравнения и решения для sin(α2).sin(α2). Обратите внимание, что перед формулами половинного угла стоит знак ±±. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором заканчивается α2α2.
Формула половинного угла для синуса получается следующим образом:
sin2θ=1-cos(2θ)2sin2(α2)=1-cos(2⋅α2)2=1-cosα2sin(α2)=±1-cosα2 sin2θ=1-cos(2θ)2sin2(α2)=1- cos(2⋅α2)2=1−cosα2sin(α2)=±1−cosα2
Чтобы получить формулу половинного угла для косинуса, мы имеем
cos2θ=1+cos(2θ)2cos2(α2)=1+cos(2⋅α2)2 =1+cosα2 cos(α2)=±1+cosα2 cos2θ=1+cos(2θ)2cos2(α2)=1 +cos(2⋅α2)2 =1+cosα2 cos(α2)=±1+cosα2
Для тождества касательной имеем
tan2θ=1−cos(2θ)1+cos(2θ)tan2(α2)=1−cos(2⋅α2)1+cos(2⋅α2) =1–cosα1+cosα tan(α2)=±1− cosα1+cosα tan2θ=1−cos(2θ)1+cos(2θ)tan2(α2)=1−cos(2⋅α2)1+cos(2⋅α2) =1−cosα1+cosα tan(α2)=± 1-cosα1+cosα
Формулы половинного угла
Формулы половинного угла следующие:
tan(α2)=±1−cosα1+cosα=sinα1+cosα=1−cosαsinαtan(α2)=±1−cosα1+cosα=sinα1+cosα=1−cosαsinα
Пример 7
Использование формулы половинного угла для нахождения точного значения функции синуса
Найдите sin(15∘)sin(15∘) с помощью формулы половинного угла.
Решение
Поскольку 15∘=30∘2, 15∘=30∘2, используем формулу половинного угла для синуса: 2−32sin30∘2=1−cos30∘2 =1−322 =2−322 =2−34 =2−32
Анализ
Обратите внимание, что мы использовали только положительный корень, потому что sin(15o)sin(15o) положителен.
Как
Даны тангенс угла и квадрант, в котором находится угол, найти точные значения тригонометрических функций половины угла.
- Нарисуйте треугольник для представления данной информации.
- Определите правильную формулу половинного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.
Пример 8
Нахождение точных значений с помощью тождеств половинных углов
Учитывая, что tanα=815tanα=815 и αα лежит в квадранте III, найдите точное значение следующего:
- ⓐ sin(α2)sin(α2)
- ⓑ потому что (α2) потому что (α2)
- ⓒ загар(α2)загар(α2)
Решение
Используя данную информацию, мы можем нарисовать треугольник, показанный на рисунке 3. Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sinα=−817sinα=−817 и cosα=−1517.cosα=− 1517.
Используя теорему Пифагора, мы находим, что гипотенуза равна 17. Следовательно, мы можем вычислить sinα=−817sinα=−817 и cosα=−1517.cosα=− 1517.
Рисунок 3
- ⓐ Прежде чем мы начнем, мы должны помнить, что если αα находится в квадранте III, то 180°<α<270°, 180°<α<270°, поэтому 180°2<α2<270°2,180°2 <α2<270°2. Это означает, что крайняя сторона α2α2 находится в квадранте II, так как 90°<α2<135°,90°<α2<135°.
Чтобы найти sinα2,sinα2, начнем с записи формулы половинного угла для синуса. Затем подставляем значение найденного нами косинуса из треугольника на рисунке 3 и упрощаем.
SINα2 = ± 1 -COSα2 = ± 1 — ( — 1517) 2 = ± 32172 = ± 3217 ОТДЫХ. ±3217⋅12 =±1617 =±417 =41717
Мы выбираем положительное значение sinα2sinα2, потому что угол заканчивается в квадранте II, а синус положителен в квадранте II.
- ⓑ Чтобы найти cosα2,cosα2, мы напишем формулу половинного угла для косинуса, подставим значение косинуса, которое мы нашли из треугольника на рисунке 3, и упростим.

COSα2 = ± 1+COSα2 = ± 1+( — 1517) 2 = ± 2172 = ± 217 ОТДЫХА12 = ± 117 = −1717COSα2 = ± 1+COSα2 = ± 1+( — 1517) 2 = ± 2172 = ± 217 ⋅12 =±117 =−1717
Мы выбираем отрицательное значение cosα2cosα2, потому что угол находится в квадранте II, потому что косинус отрицателен в квадранте II.
- ⓒ Чтобы найти tanα2,tanα2, запишем формулу половинного угла для тангенса. Снова подставляем значение найденного нами косинуса из треугольника на рисунке 3 и упрощаем. 1+(−1517) =±3217217 =±322 =−16 =−4
Мы выбираем отрицательное значение tanα2tanα2, потому что α2α2 лежит в квадранте II, а тангенс отрицателен в квадранте II.
Попытайся #5
Учитывая, что sinα=-45sinα=-45 и αα лежит в квадранте IV, найдите точное значение cos(α2).cos(α2).
Пример 9
Нахождение измерения половинного угла
Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа сконструирована для соревнований высокого уровня с углом θθ, образованным рампой и землей. Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если tanθ=53tanθ=53 для соревнований более высокого уровня, каково измерение угла для соревнований новичков?
Велосипедная рампа сконструирована для соревнований высокого уровня с углом θθ, образованным рампой и землей. Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если tanθ=53tanθ=53 для соревнований более высокого уровня, каково измерение угла для соревнований новичков?
Решение
Поскольку угол для соревнований новичков измеряет половину крутизны угла для соревнований высокого уровня, а tanθ=53tanθ=53 для соревнований высокого уровня, мы можем найти cosθcosθ из прямоугольного треугольника и теоремы Пифагора, чтобы мы могли использовать полуугловые тождества. См. рис. 4.
32+52=34 c=3432+52=34 c=34
Рисунок 4
Мы видим, что cosθ=334=33434.cosθ=334=33434. Мы можем использовать формулу половинного угла для тангенса: tanθ2=1−cosθ1+cosθ.tanθ2=1−cosθ1+cosθ. Поскольку tanθtanθ находится в первом квадранте, то же самое относится и к tanθ2.tanθ2. Таким образом,
tanθ2 = 1–334341+33434 = 34–3343434+33434 = 34–33434+334 ≈0,57tanθ2 = 1–334341+33434 = 34–3343434+33434 = 34-33434+334. 334. арктангенс для нахождения угла: tan−1(0,57)≈29,7∘.tan−1(0,57)≈29,7∘. Таким образом, угол рампы для соревнований новичков составляет ≈29,7∘.≈29,7∘.
334. арктангенс для нахождения угла: tan−1(0,57)≈29,7∘.tan−1(0,57)≈29,7∘. Таким образом, угол рампы для соревнований новичков составляет ≈29,7∘.≈29,7∘.
7.3 Секционные упражнения
Устный
1.
Объясните, как определить редукционные тождества из тождества двойного угла cos(2x)=cos2x-sin2x.cos(2x)=cos2x-sin2x.
2.
Объясните, как определить формулу двойного угла для tan(2x)tan(2x), используя формулы двойного угла для cos(2x)cos(2x) и sin(2x).sin(2x).
3.
Формулу половинного угла для tan(x2)=1−cosx1+cosxtan(x2)=1−cosx1+cosx можно определить, разделив формулу для sin(x2)sin(x2) на cos(x2).cos (х2). Объясните, как определить две формулы для tan(x2)tan(x2) которые не содержат квадратных корней.
4.
Для формулы половинного угла, приведенной в предыдущем упражнении для tan(x2),tan(x2), объясните, почему деление на 0 не имеет значения. (Подсказка: проверьте значения cosxcosx, необходимые для того, чтобы знаменатель был равен 0.)
Алгебраический
Для следующих упражнений найдите точные значения a) sin(2x),sin(2x), b) cos(2x),cos(2x) и c) tan(2x)tan(2x) без решение для х.х.
5.
Если sinx=18,sinx=18 и xx находится в квадранте I.
6.
Если cosx=23,cosx=23 и xx находится в квадранте I.
7.
Если cosx=-12,cosx=-12 и xx находится в квадранте III.
8.
Если tanx=-8,tanx=-8 и xx находится в квадранте IV.
В следующих упражнениях найдите значения шести тригонометрических функций, если выполнены указанные условия.
9.
cos(2θ)=35cos(2θ)=35 и 90∘≤θ≤180∘90∘≤θ≤180∘
10.
cos(2θ)=12cos(2θ)=12 и 180∘≤θ≤270∘180∘≤θ≤270∘
Для следующих упражнений упростите до одного тригонометрического выражения.
11.
2sin(π4)2cos(π4)2sin(π4)2cos(π4)
12.
4sin(π8)cos(π8)4sin(π8)cos(π8)
Для следующих упражнений найдите точное значение, используя формулы половинного угла.
13.
грех (π8) грех (π8)
14.
cos(−11π12)cos(−11π12)
15.
грех(11π12)грех(11π12)
16.
потому что (7π8) потому что (7π8)
17.
тан (5π12) тангенс (5π12)
18.
тангенс (−3π12) тангенс (−3π12)
19.
тангенс (−3π8) тангенс (−3π8)
В следующих упражнениях найдите точные значения a) sin(x2),sin(x2), b) cos(x2),cos(x2) и c) tan(x2)tan(x2), не решая для x ,Икс, когда 0∘≤x≤360∘0∘≤x≤360∘
20.
Если tanx=-43,tanx=-43 и xx находится в квадранте IV.
21.
Если sinx=-1213,sinx=-1213 и xx находится в квадранте III.
22.
Если cscx=7,cscx=7 и xx находится в квадранте II.
23.
Если secx=-4, secx=-4 и xx находится в квадранте II.
В следующих упражнениях используйте рисунок 5, чтобы найти требуемые половинные и двойные углы.
Рисунок 5
24.
Найдите sin(2θ),cos(2θ),sin(2θ),cos(2θ) и tan(2θ).tan(2θ).
25.
Найдите sin(2α),cos(2α),sin(2α),cos(2α) и tan(2α).tan(2α).
26.
Найти sin(θ2),cos(θ2),sin(θ2),cos(θ2) и tan(θ2).tan(θ2).
27.
Найдите sin(α2),cos(α2),sin(α2),cos(α2) и tan(α2).tan(α2).
В следующих упражнениях упростите каждое выражение. Не оценивайте.
28.
cos2(28∘)−sin2(28∘)cos2(28∘)−sin2(28∘)
29.
2cos2(37∘)−12cos2(37∘)−1
30.
1−2sin2(17∘)1−2sin2(17∘)
31.
cos2(9x)−sin2(9x)cos2(9x)−sin2(9x)
32.
4sin(8x)cos(8x)4sin(8x)cos(8x)
33.
6sin(5x)cos(5x)6sin(5x)cos(5x)
Для следующих упражнений подтвердите данное тождество.
34.
(sint-cost)2=1-sin(2t)(sint-cost)2=1-sin(2t)
35.
sin(2x)=-2sin(-x)cos(-x)sin(2x)=-2sin(-x)cos(-x)
36.
cotx-tanx=2cot(2x)cotx-tanx=2cot(2x)
37.
1+cos(2θ)sin(2θ)tan2θ=tanθ1+cos(2θ)sin(2θ)tan2θ=tanθ
Для следующих упражнений перепишите выражение с показателем степени не выше 1.
38.
cos2(5x)cos2(5x)
39.
cos2(6x)cos2(6x)
40.
sin4(8x)sin4(8x)
41.
sin4(3x)sin4(3x)
42.
cos2xsin4xcos2xsin4x
43.
cos4xsin2xcos4xsin2x
44.
tan2xsin2xtan2xsin2x
Технология
Для следующих упражнений уменьшите уравнения до степени единицы, а затем проверьте ответ графически.
45.
tan4xtan4x
46.
sin2(2x)sin2(2x)
47.
sin2xcos2xsin2xcos2x
48.
tan2xsinxtan2xsinx
49.
tan4xcos2xtan4xcos2x
50.
cos2xsin(2x)cos2xsin(2x)
51.
cos2(2x)sinxcos2(2x)sinx
52.
tan2(x2)sinxtan2(x2)sinx
Для следующих упражнений алгебраически найдите эквивалентную функцию только в терминах sinxsinx и/или cosx,cosx, а затем проверьте ответ, построив оба уравнения в виде графика.
53.
грех (4x) грех (4x)
54.
cos(4x)cos(4x)
Расширения
Для следующих упражнений докажите тождества.
55.
sin(2x)=2tanx1+tan2xsin(2x)=2tanx1+tan2x
56.
cos(2α)=1−tan2α1+tan2αcos(2α)=1−tan2α1+tan2α
57.
tan(2x)=2sinxcosx2cos2x−1tan(2x)=2sinxcosx2cos2x−1
58.
(sin2x−1)2=cos(2x)+sin4x(sin2x−1)2=cos(2x)+sin4x
59.
sin(3x)=3sinxcos2x−sin3xsin(3x)=3sinxcos2x−sin3x
60.
cos(3x)=cos3x−3sin2xcosxcos(3x)=cos3x−3sin2xcosx
61.
1+cos(2t)sin(2t)−cost=2cost2sint−11+cos(2t)sin(2t)−cost=2cost2sint−1
62.
sin(16x)=16sinxcosxcos(2x)cos(4x)cos(8x)sin(16x)=16sinxcosxcos(2x)cos(4x)cos(8x)
63.
cos(16x)=(cos2(4x)−sin2(4x)−sin(8x))(cos2(4x)−sin2(4x)+sin(8x))cos(16x)=(cos2(4x)− sin2(4x)−sin(8x))(cos2(4x)−sin2(4x)+sin(8x))
Доказательство формул двойного угла и половинного угла. Тригонометрия с самого начала.
Доказательство формул двойного и половинного угла
Формулы двойного угла
Доказательство
Формулы двойного угла доказываются из формул сумм, полагая β = . У нас есть
| грех 2 = грех ( + ) | = | sin cos + cos sin |
| = | 2 sin cos . | |
| cos 2 = cos ( + ) | = | , потому что, потому что — грех грех |
| cos 2 | = | cos 2 − sin 2 . . . . . . . (1) |
Это первая из трех версий cos 2. Чтобы получить вторую версию, в строке (1) используйте это пифагорейское тождество:
.sin 2 = 1 − cos 2 .
Строка (1) становится
| соз 2 | = | потому что 2 — (1 — потому что 2 ) |
| = | cos 2 − 1 + cos 2 . | |
| cos 2 | = | 2 cos 2 − 1. . . . . . . . . . (2) |
Чтобы получить третью версию, в строке (1) используйте это пифагорейское тождество:
cos 2 = 1 − sin 2 .
У нас есть
| Кос 2 | = | 1 − sin 2 − sin 2 ;. |
| cos 2 | = | 1 − 2 грех 2 . . . . . . . . . . (3) |
Это три формы cos 2.
Формулы полууглов
. . . . . . . (2′)
. . . . . . . (3′)
Назовем ли мы переменную θ или не имеет значения. Что важно, так это форма.
Доказательство
Теперь это половина 2. Следовательно, в строке (2) мы поместим 2 = θ , так что
| становится | θ 2 | : |
| cos θ | = | 2 2 | θ 2 | − 1. |
| При алгебраическом решении для cos | θ 2 | , у нас будет полуугол |
для косинуса.
Итак, переставив 1 и поменяв местами стороны, мы имеем
| 2 cos 2 | θ 2 | = | 1 + cos θ |
| потому что 2 | θ 2 | = | ½(1 + cos θ ) |
| потому что | θ 2 | = | . |
Это формула половинного угла для косинуса. Знак ± будет зависеть от квадранта полуугла. Опять же, назовем ли мы аргумент θ или не имеет значения.
Обратите внимание, что эта формула помечена (2′) — «2-простое число»; это напомнит нам, что мы получили его из формулы (2).
| Формула греха | θ 2 | получается из подстановки 2 = θ в строке (3). На |
, строка (3) становится
| 2 грех 2 | θ 2 | = | 1 — cos θ , | |
| так что | ||||
| грех | θ 2 | = | . | |
Это формула полуугла для синуса.
Тригонометрические тождества
Содержание | Дом
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Тождества двойного угла – формулы, доказательства и примеры
Что такое тождества двойного угла?
Тождества с двойным углом — это тригонометрические тождества, которые используются, когда у нас есть тригонометрическая функция, входная величина которой равна удвоенному заданному углу. Например, мы можем использовать эти тождества для решения $latex\sin(2\theta)$.
Например, мы можем использовать эти тождества для решения $latex\sin(2\theta)$.
Таким образом, если у нас есть значение θ и нам нужно найти $latex \sin (2 \theta)$, мы можем использовать это тождество, чтобы упростить задачу.
Ниже приводится формула, которая выражает тождество двойного угла для синуса:
| формула, выражающая тождество двойного угла для косинуса. Это тождество может иметь две дополнительные вариации, которые получаются при использовании тождества Пифагора: 92}(x)}$ |
Доказательство тождеств двойных углов
Тождества двойных углов получаются с использованием тождеств суммы углов.
В случае суммы углов в синусе имеем:
$$\sin(\alpha + \beta)=\sin(\alpha)\cos(\beta)+\cos(\alpha) \sin(\beta)$$
Если бы α и β были одним и тем же углом, мы бы имели:
$$\sin(\alpha + \alpha)=\sin(\alpha)\cos( \alpha)+\cos(\alpha)\sin(\alpha)$$
$latex \sin(2\alpha)=2\sin(\alpha)\cos(\alpha)$
Это тождество двойного угла для синуса. Используя тот же процесс, мы находим идентичность двойного угла для косинуса. Поэтому начнем с тождества суммы углов косинуса:
Используя тот же процесс, мы находим идентичность двойного угла для косинуса. Поэтому начнем с тождества суммы углов косинуса:
$$\cos(\alpha + \beta)=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta) $$
Теперь используем тот же угол и имеем:
$$\cos(\alpha + \alpha)=\cos(\alpha)\cos(\alpha)-\sin(\alpha)\sin (\альфа)$$
92}(\alpha)}$$Начните прямо сейчас: изучите наши дополнительные ресурсы по математике
Тождества с двойным углом – примеры с ответами
Тождества с двойным углом для синуса, косинуса и тангенса используются для решения следующих примеров . Попробуйте решить примеры самостоятельно, прежде чем смотреть ответ.
ПРИМЕР 1Если у нас есть $latex \sin(A) = \frac{5}{13}$ и $latex \cos(A)= – \frac{12}{13}$, что значение $латекс \sin(2A)$?
Решение
Нам известны синус A и косинус A, поэтому мы можем напрямую применить формулу двойного угла для синуса. Таким образом, мы имеем:
$latex \sin(2A)=2\sin(A)\cos(A)$
$latex \sin(2A)=2(\frac{5}{13})(- \frac{12}{13})$
$latex \sin(2A)=-\frac{120}{169})$
ПРИМЕР 2Если $latex \sin(A) = \frac{5}{13}$ и $latex \cos(A) = – \frac{12}{13}$, каково значение $latex \cos(2A)$?
Решение 92}$
$latex \cos(2A)=\frac{144-25}{169}$
$latex \cos(2A)=\frac{119}{169}$
ПРИМЕР 3Каково значение $latex \cos(2A)$, если мы имеем $latex \sin(A) = \frac{2}{9}$?
Решение
В этом упражнении у нас есть только значение синуса A, но мы можем найти значение косинуса двойного угла A, используя третий вариант формулы двойного угла для косинуса. 2}(2А)$ 92}(A)+1$
2}(2А)$ 92}(A)+1$
Тождества с двойным углом – практические задачи
Используйте следующие задачи, чтобы попрактиковаться в использовании тождеств с двойным углом, показанных выше. Если вам нужна помощь в этом, вы можете посмотреть решенные примеры.
Если у нас есть $latex \sin(x)=\frac{4}{5}$ и $latex \cos(x)=-\frac{3}{5}$, каково значение $latex \ грех(2x)$?
Выберите ответ
$латекс \sin(2x)=-\frac{14}{15}$
$латекс \sin(2x)=\frac{14}{15}$
$латекс \sin(2x)=-\frac{17}{25}$
$latex \sin(2x)=-\frac{24}{25}$
Если у нас есть $latex \sin(x)=\frac{4}{5}$, каково значение $latex \ потому что (2x) $?
Выберите ответ
$латекс \cos(2x)=-\frac{14}{25}$
$латекс \cos(2x)=-\frac{7}{25}$
$латекс \cos(2x)=\frac{13}{25}$
$latex \cos(2x)=\frac{12}{21}$
Если у нас есть $latex \tan(x)=-\frac{4}{3}$, каково значение $latex \ загар(2x)$?
Выберите ответ
$латекс \tan(2x)=\frac{12}{9}$
$латекс \tan(2x)=-\frac{14}{9}$
$латекс \tan(2x)=\frac{24}{7}$
$latex \tan(2x)=\frac{17}{9}$
См.
 также
такжеХотите узнать больше о тригонометрических тождествах? Взгляните на эти страницы:
- Полуугольные тождества – формулы, доказательство и примеры
- Сумма и разностные тождества – формулы и примеры
- Сотерминальные углы – формулы и примеры
- Тригонометрические тождества. Упражнения
Формулы двойного угла, половинного угла и приведения
Цели обучения
точные значения.
Рис. 1. Велосипедные рампы для опытных райдеров имеют более крутой наклон, чем для новичков.
Велосипедные рампы, изготовленные для соревнований (см. (рис.)) должны различаться по высоте в зависимости от уровня квалификации участников. Для продвинутых участников угол, образованный рампой и землей, должен быть [латекс]\,\тета \,[/латекс]такой, чтобы [латекс]\,\mathrm{tan}\,\тета =\фрак{5} {3}. \,[/latex]Для новичков угол делится пополам. Какая крутизна пандуса для новичков? В этом разделе мы исследуем три дополнительные категории тождеств, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
\,[/latex]Для новичков угол делится пополам. Какая крутизна пандуса для новичков? В этом разделе мы исследуем три дополнительные категории тождеств, которые мы можем использовать, чтобы ответить на такие вопросы, как этот.
Использование формул двойного угла для нахождения точных значений
В предыдущем разделе мы использовали формулы сложения и вычитания для тригонометрических функций. Теперь еще раз взглянем на те же формулы. Формулы двойного угла являются частным случаем формул суммы, где [латекс]\,\альфа =\бета .\,[/латекс] Вывод формулы двойного угла для синуса начинается с формулы суммы,
[латекс ]\mathrm{sin}\left(\alpha +\beta \right)=\mathrm{sin}\,\alpha \,\mathrm{cos}\,\beta +\mathrm{cos}\,\alpha \, \mathrm{грех}\,\бета [/латекс]
Если мы позволим [латекс]\,\альфа =\бета =\тета ,[/латекс], то мы получим
[латекс]\начало{массив}{ccc}\hfill \mathrm{sin}\left(\ theta +\theta \right)& =& \mathrm{sin}\,\theta \,\mathrm{cos}\,\theta +\mathrm{cos}\,\theta \,\mathrm{sin}\,\ theta \hfill \\ \hfill \mathrm{sin}\left(2\theta \right)& =& 2\mathrm{sin}\,\theta \,\mathrm{cos}\,\theta \hfill \end{ array}[/latex]
Получение двойного угла для косинуса дает нам три варианта. {2}\theta}\hfill\end{массив}[/latex] 9{2}\theta }\hfill \end{array}[/latex]
{2}\theta}\hfill\end{массив}[/latex] 9{2}\theta }\hfill \end{array}[/latex]
Как сделать
Зная тангенс угла и квадрант, в котором он расположен, используйте формулы двойного угла, чтобы найти точное значение .
- Нарисуйте треугольник, чтобы отразить полученную информацию.
- Определите правильную формулу двойного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.
Использование формулы двойного угла для нахождения точного значения, включающего тангенс
Учитывая, что [латекс]\,\mathrm{tan}\,\theta =-\frac{3}{4}\,[/latex]и [латекс]\,\theta \,[/latex] находится в квадрант II, найдите следующее:
- [латекс]\mathrm{sin}\left(2\theta \right)[/latex]
- [латекс]\mathrm{cos}\влево(2\тета\вправо)[/латекс]
- [латекс]\mathrm{тан}\влево(2\тета\вправо)[/латекс]
Показать решение
Попробуйте
Данный[латекс]\,\mathrm{sin}\,\alpha =\frac{5}{8},[/latex]с[латекс]\,\theta \,[/latex]in квадрант I, найти[латекс]\,\mathrm{cos}\влево(2\альфа\вправо). [/латекс]
[/латекс]
Показать решение
Использование формулы двойного угла для косинуса без точных значений
Используйте формулу двойного угла для косинуса для записи [латекс]\,\mathrm{cos}\left(6x\right)\,[/latex]в терминах of[latex]\,\mathrm{cos}\left(3x\right).[/latex]
Показать решение
Анализ
Этот пример показывает, что мы можем использовать формулу двойного угла, не имея точных значений. В нем подчеркивается, что шаблон — это то, что нам нужно помнить, и что тождества верны для всех значений в области определения тригонометрической функции.
Использование формул двойного угла для проверки тождества
Установление тождества с использованием формул двойного угла выполняется с использованием тех же шагов, которые мы использовали для получения формул суммы и разности. Выберите более сложную часть уравнения и перепишите ее, пока она не совпадет с другой стороной.
Использование формул двойного угла для проверки тождества
Проверьте следующее тождество с помощью формул двойного угла:
[латекс]1+\mathrm{sin}\left(2\theta \right)={\left( \mathrm{sin}\,\theta +\mathrm{cos}\,\theta \right)}^{2}[/latex] 9{4}\theta =\mathrm{cos}\left(2\theta \right). [/latex]
[/latex]
Показать решение
Проверка идентичности двойного угла для касательной
Проверка идентичности:
[латекс]\mathrm{tan}\left(2\theta \right)=\frac{2}{\mathrm{cot}\,\ theta -\mathrm{tan}\,\theta }[/latex]
Показать решение
Анализ
Вот случай, когда более сложная часть исходного уравнения появилась справа, но мы решили работать с левой частью. Однако, если бы мы выбрали для перезаписи левую часть, мы бы работали в обратном направлении, чтобы получить эквивалентность. Например, предположим, что мы хотим показать 9{2}\theta }=\frac{2}{\mathrm{cot}\,\theta -\mathrm{tan}\,\theta }[/latex]
Давайте работать с правой стороной.
[латекс]\begin{array}{ccc}\hfill \frac{2}{\mathrm{cot}\,\theta -\mathrm{tan}\,\theta }& =& \frac{2}{ \ frac {1} {\ mathrm {tan} \, \ theta} — \ mathrm {tan} \, \ theta} \ left (\ frac {\ mathrm {tan} \, \ theta} {\ mathrm {tan} \ ,\theta }\right)\hfill \\ & =& \frac{2\,\mathrm{tan}\,\theta }{\frac{1}{\overline{)\mathrm{tan}\,\theta }}\left(\overline{)\mathrm{tan}\,\theta }\right)-\mathrm{tan}\,\theta \left(\mathrm{tan}\,\theta \right)}\hfill \\ & =& \frac{2\,\mathrm{tan}\,\theta}{1-{\mathrm{tan}}^{2}\theta}\hfill\end{array}[/latex] 9{2}\theta . [/latex]
[/latex]
Показать решение
Использование формул приведения для упрощения выражения
Формулы двойного угла можно использовать для получения формул приведения, которые можно использовать для уменьшения мощности данного выражения, включающего четные степени синуса или косинуса. Они позволяют нам переписать четные степени синуса или косинуса в терминах первой степени косинуса. Эти формулы особенно важны в курсах математики более высокого уровня, в частности исчисления. Также называемые формулами уменьшения степени, включены три тождества, которые легко выводятся из формул двойного угла. 9{2}\theta}\hfill & \\ & =& \frac{\frac{1-\mathrm{cos}\left(2\theta\right)}{2}}{\frac{1+\mathrm{ cos}\left(2\theta \right)}{2}}\hfill & \phantom{\rule{2em}{0ex}}\text{Подставить формулы редукции}\text{.}\hfill \\ & = & \left(\frac{1-\mathrm{cos}\left(2\theta \right)}{2}\right)\left(\frac{2}{1+\mathrm{cos}\left(2 \theta \right)}\right)\hfill & \\ & =& \frac{1-\mathrm{cos}\left(2\theta \right)}{1+\mathrm{cos}\left(2\ theta \right)}\hfill & \end{массив}[/latex] 9{4}x=\frac{15}{4}+5\,\mathrm{cos}\left(2x\right)+\frac{5}{4}\,\mathrm{cos}\left(4x\ справа). [/latex]
[/latex]
Показать решение
Использование формул половинного угла для нахождения точных значений
Следующий набор тождеств — это набор формул половинного угла, которые можно вывести из формул приведения, и которые мы можем использовать, когда имеем угол, равный половине размера особый угол. Если мы заменим [латекс]\,\тета\,[/латекс] на [латекс]\,\фракция {\ альфа} {2},[/латекс], формула половинного угла для синуса будет найдена путем упрощения уравнения и решение для [латекс]\,\mathrm{sin}\left(\frac{\alpha }{2}\right).\,[/latex] Обратите внимание, что формулам половинного угла предшествует [латекс]\, Знак ±\,[/латекс]. Это не означает, что допустимы как положительные, так и отрицательные выражения. Скорее, это зависит от квадранта, в котором [латекс]\,\фракция {\альфа} {2}\,[/латекс]оканчивается. 9{2}\left(\frac{\alpha}{2}\right)& =& \frac{1-\mathrm{cos}\left(2\cdot \frac{\alpha}{2}\right)} {1+\mathrm{cos}\left(2\cdot\frac{\alpha}{2}\right)}\hfill \\ & =& \frac{1-\mathrm{cos}\,\alpha}{ 1+\mathrm{cos}\,\alpha}\hfill \\ \hfill \mathrm{tan}\left(\frac{\alpha}{2}\right)& =& ±\sqrt{\frac{1- \mathrm{cos}\,\alpha }{1+\mathrm{cos}\,\alpha }}\hfill \end{array}[/latex]
Формулы половинного угла
Формулы половинного угла выглядят следующим образом: следует:
[латекс]\mathrm{sin}\left(\frac{\alpha }{2}\right)=±\sqrt{\frac{1-\mathrm{cos}\,\alpha}{2} }[/латекс]
[латекс] \ mathrm {cos} \ left (\ frac {\ alpha {2} \ right) = ± \ sqrt {\ frac {1+ \ mathrm {cos} \, \ alpha {2}} [ / латекс]
[латекс] \ begin {array} {l} \ mathrm {tan} \ left (\ frac {\ alpha {2} \ right) = ± \ sqrt {\ frac {1- \ mathrm {cos }\,\alpha }{1+\mathrm{cos}\,\alpha }}\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,=\frac{\mathrm{sin}\,\alpha }{1+\mathrm{cos}\,\alpha}\hfill \ \ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac {1-\mathrm{cos}\,\alpha }{\mathrm{sin}\,\alpha }\hfill \end{массив}[/latex]
Использование формулы половинного угла для нахождения точного значения синуса .

Показать решение
Анализ
Обратите внимание, что мы использовали только положительный корень, потому что [латекс]\,\mathrm{sin}\left(15°\right)\,[/latex] положительный.
How To
Зная тангенс угла и квадрант, в котором находится угол, найдите точные значения тригонометрических функций половины угла.
- Нарисуйте треугольник для представления данной информации.
- Определите правильную формулу половинного угла.
- Подставьте значения в формулу на основе треугольника.
- Упростить.
Нахождение точных значений с использованием тождеств половинного угла ,[/latex] лежит в квадранте III, найдите точное значение следующего:
- [латекс]\mathrm{sin}\left(\frac{\alpha }{2}\right)[/latex]
- [латекс]\mathrm{cos}\left(\frac{\alpha}{2}\right)[/latex]
- [латекс]\mathrm{tan}\left(\frac{\alpha }{2}\right)[/latex]
Показать решение
Попробуйте
Учитывая, что [латекс]\,\mathrm{sin}\,\alpha =-\frac{4}{5}\,[/latex]и [латекс]\,\alpha \,[/ латекс] лежит в квадранте IV, найдите точное значение [латекс]\,\mathrm{cos}\,\left(\frac{\alpha }{2}\right). [/latex]
[/latex]
Показать решение
Нахождение измерения половинного угла
Теперь вернемся к задаче, поставленной в начале раздела. Велосипедная рампа построена для соревнований высокого уровня с углом[латекс]\,\тета\,[/латекс], образованным рампой и землей. Еще одна рампа должна быть построена вполовину меньшей крутизны для соревнований новичков. Если[latex]\,\mathrm{tan}\,\theta =\frac{5}{3}\,[/latex]для соревнований более высокого уровня, каково измерение угла для соревнований новичков?
Показать решение
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с формулами двойного угла, половинного угла и сокращения.
- Двухугольные тождества
- Полуугольные тождества
Ключевые уравнения
| Формулы двойного угла | [латекс]\begin{массив}{ccc}\hfill\mathrm{sin}\left(2\theta\right)& =& 2\mathrm{sin}\,\theta \,\mathrm{cos}\, \ тета \ hfill \\ \ hfill \ mathrm {cos} \ left (2 \ theta \ right) & = & {\ mathrm {cos}} ^ {2} \ theta — {\ mathrm {sin}} ^ {2} \ тета \ hfill \\ & = & 1-2 {\ mathrm {sin}} ^ {2} \ тета \ hfill \\ & = & 2 {\ mathrm {cos}} ^ {2} \ тета -1 \ hfill \\ \ hfill \ mathrm {tan} \ left (2 \ theta \ right) & = & \ frac {2 \ mathrm {tan} \, \ theta }{1 — {\ mathrm {tan}} ^ {2} \ тета }\hfill \end{массив}[/latex] 9{2}\theta & =& \frac{1-\mathrm{cos}\left(2\theta\right)}{1+\mathrm{cos}\left(2\theta \right)}\hfill \end {массив}[/латекс] |
| Формулы полууглов | [латекс]\begin{array}{ccc}\hfill\mathrm{sin}\,\frac{\alpha}{2}& =& ±\sqrt{\frac{1-\mathrm{cos}\,\ альфа {2}} \ hfill \\ \ hfill \ mathrm {cos} \, \ frac {\ alpha {2} & = & ± \ sqrt {\ frac {1+ \ mathrm {cos} \, \ alpha} {2}}\hfill \\ \hfill \mathrm{tan}\,\frac{\alpha }{2}& =& ±\sqrt{\frac{1-\mathrm{cos}\,\alpha}{1 +\mathrm{cos}\,\alpha}}\hfill \\ & =& \frac{\mathrm{sin}\,\alpha}}{1+\mathrm{cos}\,\alpha}\hfill \\ & =& \frac{1-\mathrm{cos}\,\alpha }{\mathrm{sin}\,\alpha }\hfill \end{array}[/latex] |
Ключевые понятия
- Тождества двойных углов выводятся из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса.
 См. (Рисунок), (Рисунок), (Рисунок) и (Рисунок).
См. (Рисунок), (Рисунок), (Рисунок) и (Рисунок). - Формулы редукции особенно полезны в математических вычислениях, поскольку они позволяют уменьшить мощность тригонометрического члена. См. (Рисунок) и (Рисунок).
- Формулы половинного угла позволяют нам найти значение тригонометрических функций, содержащих половинные углы, независимо от того, известен исходный угол или нет. См. (Рисунок), (Рисунок) и (Рисунок). 9{2}x.[/latex]
Показать решение
Объясните, как определить формулу двойного угла для [латекс]\,\mathrm{tan}\left(2x\right)\,[/latex], используя формулы двойного угла для [латекс]\,\mathrm{ cos}\left(2x\right)\,[/latex]and[latex]\,\mathrm{sin}\left(2x\right).[/latex]
Мы можем определить формулу половинного угла для[ латекс] \, \ mathrm {tan} \ left (\ frac {x} {2} \ right) = \ frac {\ sqrt {1- \ mathrm {cos} \, x}} {\ sqrt {1+ \ mathrm {cos}\,x}}\,[/latex], разделив формулу для[latex]\,\mathrm{sin}\left(\frac{x}{2}\right)\,[/latex]на [латекс]\,\mathrm{cos}\left(\frac{x}{2}\right).
 \,[/latex]Объясните, как определить две формулы для [латекс]\,\mathrm{tan}\left (\frac{x}{2}\right)\,[/latex], которые не содержат квадратных корней.
\,[/latex]Объясните, как определить две формулы для [латекс]\,\mathrm{tan}\left (\frac{x}{2}\right)\,[/latex], которые не содержат квадратных корней.Показать решение
Для формулы половинного угла, приведенной в предыдущем упражнении для [латекс]\,\mathrm{tan}\left(\frac{x}{2}\right),[/latex]объясните, почему деление на 0 не является беспокойство. (Совет: проверьте значения [latex]\,\mathrm{cos}\,x\,[/latex], необходимые для того, чтобы знаменатель был равен 0.)
Алгебраический
Для следующих упражнений найдите точные значения a)[латекс]\,\mathrm{sin}\left(2x\right),[/latex] b)[латекс]\,\mathrm{cos}\left(2x\right),[/latex] и c )[латекс]\,\mathrm{tan}\left(2x\right)\,[/latex] без решения [латекс]\,х.[/латекс]
Если [латекс]\,\mathrm{sin}\,x=\frac{1}{8},[/latex]и [латекс]\,x\,[/latex] находится в квадранте I.
Показать решение
Если [латекс]\,\mathrm{cos}\,x=\frac{2}{3},[/latex]и [латекс]\,x\,[/latex] находится в квадранте I.

Если [латекс]\,\mathrm{cos}\,x=-\frac{1}{2},[/latex]и [латекс]\,x\,[/latex] находится в квадранте III.
Показать решение
Если [латекс]\,\mathrm{tan}\,x=-8,[/latex]и [латекс]\,x\,[/latex] находится в квадранте IV.
В следующих упражнениях найдите значения шести тригонометрических функций, если выполнены указанные условия.
[латекс]\mathrm{cos}\left(2\theta \right)=\frac{3}{5}\,[/latex]and[latex]\,90°\le \theta \le 180° [/latex]
Показать решение
[латекс]\mathrm{cos}\left(2\theta \right)=\frac{1}{\sqrt{2}}\,[/latex]and[latex]\,180°\le \theta \le 270°[/latex]
Для следующих упражнений упростите до одного тригонометрического выражения.
[латекс] 2 \, \ mathrm {sin} \ left (\ frac {\ pi} {4} \ right) \, 2 \, \ mathrm {cos} \ left (\ frac {\ pi} {4} \right)[/latex]
Показать решение
[латекс] 4 \, \ mathrm {sin} \ left (\ frac {\ pi} {8} \ right) \, \ mathrm {cos} \ left (\ frac {\ pi} {8} \ right) [ /latex]
В следующих упражнениях найдите точное значение, используя формулы половинного угла.

[латекс]\,\mathrm{sin}\left(\frac{\pi }{8}\right)\,[/latex]
Показать решение
[латекс]\mathrm{cos}\left(-\frac{11\pi }{12}\right)[/latex]
[латекс]\mathrm{sin}\left(\frac{11\pi }{12}\right)[/latex]
Показать решение
[латекс]\mathrm{cos}\left(\frac{7\pi }{8}\right)[/latex]
[латекс]\mathrm{tan}\left(\frac{5\pi }{12}\right)[/latex]
Показать решение
[латекс]\mathrm{tan}\left(-\frac{3\pi }{12}\right)[/latex]
[латекс]\mathrm{tan}\left(-\frac{3\ pi }{8}\right)[/latex]
Показать решение
Для следующих упражнений найдите точные значения a)[латекс]\,\mathrm{sin}\left(\frac{x}{2}\right),[/latex] b)[латекс]\, \mathrm{cos}\left(\frac{x}{2}\right),[/latex] и c)[latex]\,\mathrm{tan}\left(\frac{x}{2}\right )[/latex]без решения для[латекс]\,х,\,[/латекс]когда[латекс]\,0°\le x\le 360°.
 [/латекс]
[/латекс]Если [латекс]\,\mathrm{tan}\,x=-\frac{4}{3},[/latex]и [латекс]\,x\,[/latex] находится в квадранте IV.
Если [латекс]\,\mathrm{sin}\,x=-\frac{12}{13},[/latex]и [латекс]\,x\,[/latex] находится в квадранте III.
Показать решение
Если [латекс]\,\mathrm{csc}\,x=7,[/latex]и [латекс]\,x\,[/latex] находится в квадранте II.
Если [латекс]\,\mathrm{sec}\,x=-4,[/latex]и [латекс]\,x\,[/latex] находится в квадранте II.
Показать решение
В следующих упражнениях используйте (Рисунок), чтобы найти требуемые половинные и двойные углы.
Рисунок 5.
Найти[латекс]\,\mathrm{sin}\left(2\theta\right),\mathrm{cos}\left(2\theta\right),[/latex]и [латекс]\,\mathrm{tan}\left(2\theta\right).[/latex]
Найти[латекс]\,\mathrm{sin}\left(2\alpha \right),\mathrm{ cos}\left(2\alpha \right),[/latex]and[latex]\,\mathrm{tan}\left(2\alpha \right).[/latex]
Показать решение
Найти[латекс]\,\mathrm{sin}\left(\frac{\theta}{2}\right),\mathrm{cos}\left(\frac{\theta}{2}\right), [/латекс] и [латекс]\,\mathrm{tan}\left(\frac{\theta}{2}\right).
 [/latex] 9{2}\left(\frac{x}{2}\right)\,\mathrm{sin}\,x[/latex]
[/latex] 9{2}\left(\frac{x}{2}\right)\,\mathrm{sin}\,x[/latex]Для следующих упражнений алгебраически найдите эквивалентную функцию только в терминах[latex ]\,\mathrm{sin}\,x\,[/latex]и/или[latex]\,\mathrm{cos}\,x,[/latex], а затем проверьте ответ, построив график обеих функций.
[латекс]\mathrm{sin}\left(4x\right)[/latex]
Показать решение
[латекс]\mathrm{cos}\left(4x\right)[/латекс]
Расширения
Для следующих упражнений докажите тождества. 9{2}\left(4x\right)+\mathrm{sin}\left(8x\right)\right)[/latex]
Показать решение
Глоссарий
- формулы двойного угла
- тождеств, полученных из формул суммы синуса, косинуса и тангенса, в которых углы равны
- формулы половинного угла
- тождества, полученные из формул приведения и используемые для определения значений половинных углов тригонометрических функций
- формулы приведения
- тождеств, полученных из формул двойного угла и используемых для уменьшения степени тригонометрической функции
Узнать о формуле двойного угла для функции косинуса
Определение функции двойного угла
Формулы двойного угла, используемые для выражения тригонометрических тождеств угла 2θ2\theta2θ через функции угла θ\thetaθ.
 Формула двойного угла для функции sin равна 2sinθcosθ2\sin\theta\cos\theta2sinθcosθи математически она называется как
sin(2θ)=2sinθcosθ\sin\left( {2\theta} \right) = 2\sin\theta\cos\theta sin(2θ)=2sinθcosθ.
Формула двойного угла для функции sin равна 2sinθcosθ2\sin\theta\cos\theta2sinθcosθи математически она называется как
sin(2θ)=2sinθcosθ\sin\left( {2\theta} \right) = 2\sin\theta\cos\theta sin(2θ)=2sinθcosθ.Обзор формулы двойного угла для функции косинуса
Каждый человек, должно быть, видел шоу или трюк, в котором велосипедисты или мотоциклисты заставляют свое транспортное средство прыгать с рампы. Крутизна пандуса видна даже с большого расстояния. Рампы специально разработаны специально для трюков с идеальными расчетами.
Теперь вам может быть интересно, какие расчеты требуются для выполнения этих трюков на рампе.
Предположим, что угол или крутизна, длина или любые другие характеристики пандуса не рассчитаны или не рассчитаны точно. Тогда, в этом случае, может произойти опасная авария, или даже более того, может иметь место наихудшее состояние.
 Итак, для уменьшения подобных ситуаций необходимо знание тригонометрических тождеств и искомого угла. Всего существует шесть тождеств тригонометрического синуса, косинуса, тангенса, косеканса, секанса и котангенса. Мы применяем основные формулы сложения и вычитания для тригонометрических функций, чтобы определить новые отношения. Все эти тождества или почти все они будут использоваться для доказательства других тригонометрических тождеств и для решения тригонометрических уравнений. Здесь мы сосредоточимся на тождествах двойных углов, названных так потому, что они включают тригонометрические функции двойных углов, такие как sin2θ \sin 2\theta sin2θ. Формула двойного угла для функции синуса является частным случаем формулы сложения, которая выглядит следующим образом:
sin(2θ)=2sinθcosθ\sin\left( {2\theta} \right) = 2\sin\theta \cos\theta sin(2θ)=2sinθcosθ
Итак, для уменьшения подобных ситуаций необходимо знание тригонометрических тождеств и искомого угла. Всего существует шесть тождеств тригонометрического синуса, косинуса, тангенса, косеканса, секанса и котангенса. Мы применяем основные формулы сложения и вычитания для тригонометрических функций, чтобы определить новые отношения. Все эти тождества или почти все они будут использоваться для доказательства других тригонометрических тождеств и для решения тригонометрических уравнений. Здесь мы сосредоточимся на тождествах двойных углов, названных так потому, что они включают тригонометрические функции двойных углов, такие как sin2θ \sin 2\theta sin2θ. Формула двойного угла для функции синуса является частным случаем формулы сложения, которая выглядит следующим образом:
sin(2θ)=2sinθcosθ\sin\left( {2\theta} \right) = 2\sin\theta \cos\theta sin(2θ)=2sinθcosθ Вышеупомянутое уравнение известно как формула двойного угла для функции синуса, поэтому здесь выполняется удвоение угла, и можно сказать, что формула синуса двойного угла имеет тождество, за которым следует синус, а затем косинус.
 Большим преимуществом использования формулы двойного угла является то, что можно преобразовать любую тригонометрическую функцию в любое другое тригонометрическое тождество.
Большим преимуществом использования формулы двойного угла является то, что можно преобразовать любую тригонометрическую функцию в любое другое тригонометрическое тождество.Есть вопрос по этой теме?
Что вы узнаете:
- Определение функции двойного угла
- Обзор формулы двойного угла для функции косинуса
- Формула двойного угла для функции синуса
- Применение формулы двойного угла для функции синуса
Формула двойного угла для функции синуса
У нас может быть синус члены в данном тригонометрическом выражении, которые мы должны выразить через косинус так, чтобы все функции совпадали. Итак, мы используем формулу двойного угла для функции синуса, чтобы упростить решение уравнения.

Давайте посмотрим на это и докажем тождества двойных углов, используя тождества суммы.
Чтобы вывести формулу, нужно знать, что такое формула суммы синуса. Начните с того, что вспомните формулы сложения, представленные в виде
sin(A+B)=sinAcosB+cosAsinB\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin Bsin(A +B)=sinAcosB+cosAsinB
Если сделана замена, пусть A=θ и B=θ A = \theta\ и \ B= \thetaA=θ и B=θ
Подставьте эти значения в sin формула сложения будет иметь следующий вид:
грех(θ+θ)=sinθcosθ+cosθsinθ\sin\left({\theta + \theta} \right) = \sin\theta\cos\theta+\cos\theta \sin \theta sin(θ+θ)=sinθcosθ+cosθsinθ
Итак, известно свойство умножения, которое заключается в следующем:
а⋅b=b⋅аа \cdot b = b \cdot аа⋅b=b⋅а
Используя это свойство, можно переупорядочить две вышеупомянутые тригонометрические функции и записать их следующим образом:
Давайте разберемся, как можно использовать эту формулу с помощью числового примера.

Предположим, что известно, что sinA=35\sin A = \frac{3}{5}sinA=53 во втором квадранте, и необходимо найти точное значение sin2A\sin 2Asin2A Во-первых, напишите формулу для двойного угла греха, которая выглядит следующим образом:
sin(2θ)=2sinθcosθ\sin\left( {2\theta} \right) = 2\sin\theta\cos\theta sin(2θ)=2sinθcosθ
Теперь нарисуйте опорный треугольник, в котором угол имеет значение sinof35\sin of \frac{3}{5}sinof53, что означает обратное относительно гипотенузы.
Узнайте значение стоимости с помощью треугольника, который задается как cosA=35\cos A = \frac{3}{5}cosA=53. Также известно, что sinA=35 \ sin A = \frac{3}{5}sinA=53. Подставляем все эти значения в приведенную выше формулу, получается следующее:
Применение формулы двойного угла для функции синуса
Формулы двойного угла используются для решения сложных математических задач и для вывода формул приведения тригонометрического выражения или для решения тригонометрического уравнения.




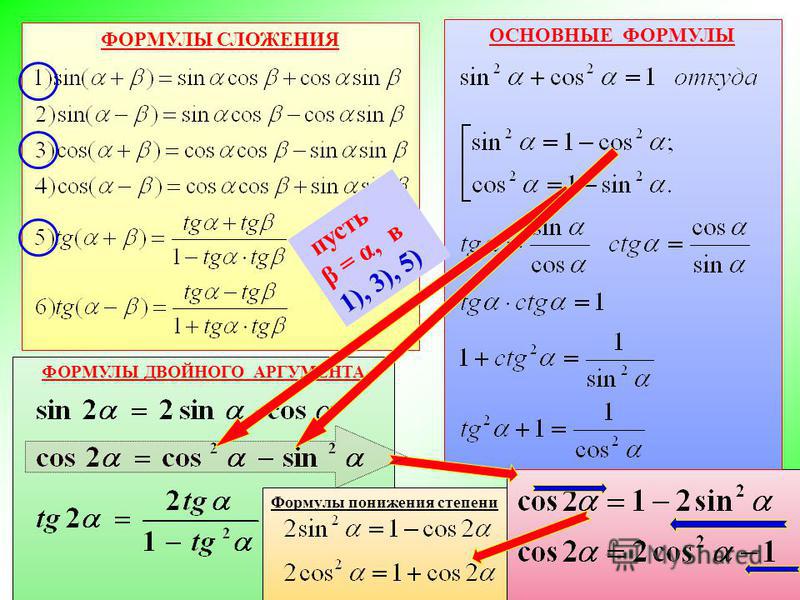 Получается, что синус2α + косинус2α = 1. Подставив данные, выходит: 1 − 2·sin2α.
Получается, что синус2α + косинус2α = 1. Подставив данные, выходит: 1 − 2·sin2α.
