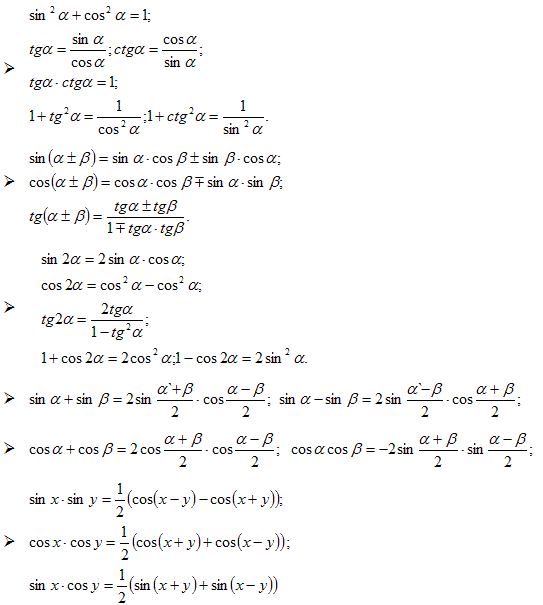вывод формул, примеры. Формулы суммы и разности синусов и косинусов
Данный электронный ресурс является отличным материалом для проведения интерактивного обучения в современных школах. Он составлен грамотно, обладает четкой структурой и соответствует школьному плану. Благодаря подробным объяснениям, тема, которая представлена в видеоуроке станет понятна как можно большему количеству учеников в классе. Учителя должны помнить, что не все ученики имеют одинаковую степень восприятия, быстроты понимания, базу. Справиться с трудностями и догнать своих сверстников, исправить успеваемость, помогут подобные материалы. С помощью них в домашней спокойной обстановке, самостоятельно либо вместе с репетитором, ученик может разобраться в той или иной теме, изучить теорию и просмотреть примеры практического применения той или иной формулы и т.д.
Данный видеоурок посвящен теме «Синус и косинус разности аргументов». Подразумевается, что ученики уже изучили основы тригонометрии, ознакомлены с основными функциями и их свойствами, формулами привидения и таблицами тригонометрических значений.
Также, до того, как перейти к изучению данной темы, необходимо иметь понятие о синусе и косинусе суммы аргументов, знать две основные формулы и уметь ими пользоваться.
Вначале видеоурока диктор напоминает школьникам эти две формулы. Далее демонстрируется первая формула — синус разности аргументов. Помимо того, как выводится сама формула, показывается каким образом она получается от другой. Таким образом, школьнику не придется зазубривать новую формулу без понимания, что является частой ошибкой. Это очень важно для учеников в этом классе. Нужно всегда помнить, что перед знаком минуса всего можно добавить знак +, а минуса на знак плюс в итоге превратится в минус. С помощью такого нехитрого шага, можно воспользоваться формулой синуса суммы и получить формулу синуса разности аргументов.
Аналогичным образом выводится формула косинуса разности из формулы косинуса суммы аргументов.
Диктор пошагово все объясняет, а в результате выводится общая формула косинуса суммы и разности аргументов и синуса, аналогично.
Первый пример из практической части данного видеоурока предлагает найти косинус Пи/12. Предлагается представить данное значение в виде некоторой разности, при котором уменьшаемое и вычитаемое будут являться табличными значениями. Далее применятся формула косинуса разности аргументов. Заменив выражение, можно подставить полученные значения и получить ответ. Диктор зачитывает ответ, который выводится в конце примера.
Второй пример представляет собой уравнение. И в правой, и в левой сторонах мы видим косинусы разностей аргументов. Диктор напоминает формулы приведений, которые используются для замены и упрощения этих выражения. Эти формулы записываются с правой стороны, чтобы школьники могли понять, откуда появляются те или иные изменения.
Еще один пример, третий, представляет собой некоторую дробь, где и в числителе и в знаменателе имеем тригонометрические выражения, а именно, разности произведений.
Здесь также при решении используются формулы приведений. Таким образом, школьники могут убедиться, что пропустив одну тему в тригонометрии, понять остальные будет все сложнее.
И, наконец, четвертый пример. Это также уравнение, при решении которых необходимо использовать новые изученные и старые формулы.
Примеры, которые приводятся в видеоуроке, можно рассмотреть более подробно и попробовать решить самостоятельно. Их можно задать в качестве домашнего задания школьникам.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тема занятия «Синус и косинус разности аргументов».
На предыдущем курсе мы познакомились с двумя тригонометрическими формулами синус и косинус суммы аргументов.
sin(x + y) = sin x cos y + cos x sin y,
cos (x + y) = cos x cos y — sin x sin y.
синус суммы двух углов равен сумме между произведением синуса первого угла и косинусом второго угла и произведением косинуса первого угла и синуса второго угла;
косинус суммы двух углов равен разности между произведением косинусов этих углов и произведением суммы этих углов.
При помощи этих формул выведем формулы Синус и косинус разности аргументов.
Синус разности аргументов sin(x- y)
Две формулы (синус суммы и синус разности) можно записать в виде:
sin(x y) = sin x cos y cos x sin y.
Аналогично выведем формулу косинуса разности:
Косинус разности аргументов перепишем в виде суммы и применим уже известную формулу косинуса суммы: cos (x + y) = cosxcosy — sinxsiny.
только для аргументов х и -y. Подставив данные аргументы в формулу, получим cosxcos(- y) — sinxsin(- y).
sin(- y)= — siny). и получим окончательное выражение cosxcosy + sinxsiny.
cos (x — y) = cos (x +(- y)) =cos xcos(- y) — sin x sin(- y)= cosx cos y + sin xsin y.
Значит, cos (x — y) = cosxcos y + sin xsin y.
косинус разности двух углов равен сумме между произведением косинусов этих углов и произведением синусов этих углов.
Объединяя две формулы (косинус суммы и косинус разности) в одну, запишем
cos (x y) = cosxcos y sin xsin y.
Запомним, что формулы на практике можно применять как слева направо, так и наоборот.
Рассмотрим примеры.
ПРИМЕР 1. Вычислить cos (косинус пи, деленное на двенадцать).
Решение. Запишем пи, деленное на двенадцать, как разность пи на три и пи, деленное на четыре: = — .
Подставим значения в формулу косинуса разности: cos (x — y) = cosxcosy + sinxsiny, таким образом cos = cos (-) = cos cos + sin sin
Нам известно, что cos = , cos = sin= , sin = . Показать таблицу значений.
Заменим значение синуса и косинуса числовыми значениями и получим ∙ + ∙ при умножении дробь на дробь числители и знаменатели перемножаем, получаем
cos = cos (-) = cos cos + sin sin = ∙ + ∙ = = =.
Ответ: cos =.
ПРИМЕР 2. Решить уравнение cos(2π — 5х) = cos(- 5х) (косинус два пи минус пять икс равно косинусу от пи на два минус пять икс).
Решение. К левой и правой частям уравнения применим формулы приведения cos(2π — cos (косинус два пи минус альфа равен косинусу альфа) и cos(- = sin (косинус пи на два минус альфа равно синусу альфа), получим cos 5х = sin 5х, приведем его к виду однородного уравнения первой степени и получим cos 5х — sin 5х = 0. Это однородное уравнение первой степени. Разделим почленно обе части уравнения на cos 5х. Имеем:
cos 5х: cos 5х — sin 5х: cos 5х = 0, т.
Так как мы уже знаем, что уравнение tgt = а имеет решение t = arctgа + πn, а так как у нас t=5х, а =1, то получим
5x = arctg 1 + πn,
а значение arctg 1, тогда tg 1= Показать таблицу
подставим значение в уравнение и решим его:
Ответ: х = + .
ПРИМЕР 3. Найти значение дроби. (в числителе разность произведения косинусов семидесяти пяти градусов и шестидесяти пяти градусов и произведения синусов семидесяти пяти градусов и шестидесяти пяти градусов, а в знаменателе разность произведения синуса восьмидесяти пяти градусов и косинуса тридцати пяти градусов и произведения косинуса восьмидесяти пяти градусов и синуса тридцати пяти градусов).
Решение. В числителе данной дроби разность можно «свернуть» в косинус суммы аргументов 75° и 65°, а в знаменателе — разность «свернем» в синус разности аргументов 85° и 35°. Получим
Ответ: — 1.
ПРИМЕР 4. Решить уравнение: cos(-х) + sin(-х) = 1(косинус разности пи на четыре и икс плюс синус разности пи на четыре и икс равно одному).
Решение. Применим формулы косинус разности и синус разности.
Показать общую формулу косинуса разности
Тогда cos (-х) = cos cos х + sinsinх
Показать общую формулу синуса разности
а sin (-х)= sin cosх — cos sinх
Подставим данные выражения в уравнение cos(-х) + sin(-х) = 1 и получим:
cos cos х + sinsin х + sin cos х — cos sin х = 1,
Так как cos= и sin= Показать таблицу значение синуса и косинуса
Получим ∙ cos х + ∙ sinх + ∙ cos х — ∙ sinх = 1,
второе и четвертое слагаемые противоположны, поэтому взаимно уничтожаются, остается:
∙ cos + ∙ cos = 1,
Решим данное уравнение и получим, что
2∙ ∙ cos x= 1,
Так ка мы уже знаем, что уравнение cos = а имеет решение t = arcos a + 2π k , а так как у нас t=x, а =, то получим
х = arccos + 2πn,
а так как значение arccos, тогда cos =
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 .
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Yandex.RTB R-A-339285-1
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению.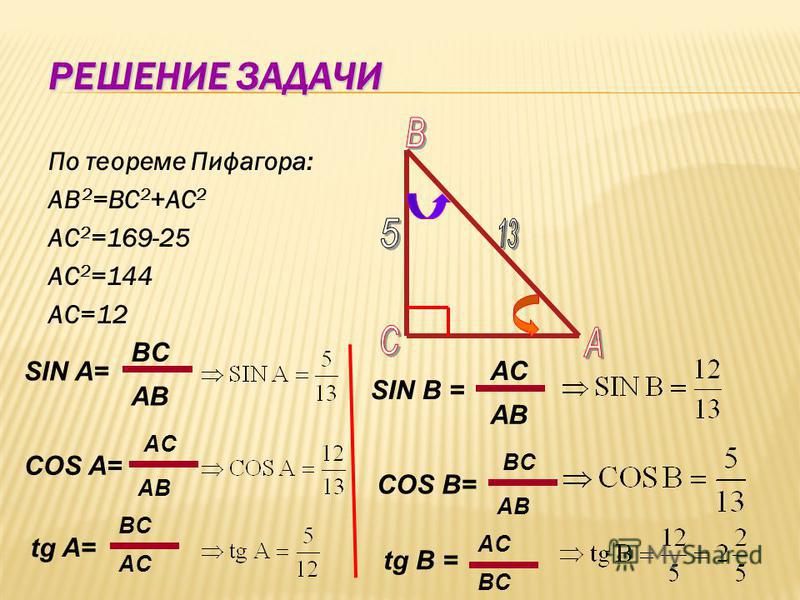
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
вывод формул, примеры Формула синуса суммы двух аргументов
Данный электронный ресурс является отличным материалом для проведения интерактивного обучения в современных школах. Он составлен грамотно, обладает четкой структурой и соответствует школьному плану. Благодаря подробным объяснениям, тема, которая представлена в видеоуроке станет понятна как можно большему количеству учеников в классе. Учителя должны помнить, что не все ученики имеют одинаковую степень восприятия, быстроты понимания, базу. Справиться с трудностями и догнать своих сверстников, исправить успеваемость, помогут подобные материалы. С помощью них в домашней спокойной обстановке, самостоятельно либо вместе с репетитором, ученик может разобраться в той или иной теме, изучить теорию и просмотреть примеры практического применения той или иной формулы и т.
д.
Данный видеоурок посвящен теме «Синус и косинус разности аргументов». Подразумевается, что ученики уже изучили основы тригонометрии, ознакомлены с основными функциями и их свойствами, формулами привидения и таблицами тригонометрических значений.
Также, до того, как перейти к изучению данной темы, необходимо иметь понятие о синусе и косинусе суммы аргументов, знать две основные формулы и уметь ими пользоваться.
Вначале видеоурока диктор напоминает школьникам эти две формулы. Далее демонстрируется первая формула — синус разности аргументов. Помимо того, как выводится сама формула, показывается каким образом она получается от другой. Таким образом, школьнику не придется зазубривать новую формулу без понимания, что является частой ошибкой. Это очень важно для учеников в этом классе. Нужно всегда помнить, что перед знаком минуса всего можно добавить знак +, а минуса на знак плюс в итоге превратится в минус. С помощью такого нехитрого шага, можно воспользоваться формулой синуса суммы и получить формулу синуса разности аргументов.
Аналогичным образом выводится формула косинуса разности из формулы косинуса суммы аргументов.
Диктор пошагово все объясняет, а в результате выводится общая формула косинуса суммы и разности аргументов и синуса, аналогично.
Первый пример из практической части данного видеоурока предлагает найти косинус Пи/12. Предлагается представить данное значение в виде некоторой разности, при котором уменьшаемое и вычитаемое будут являться табличными значениями. Далее применятся формула косинуса разности аргументов. Заменив выражение, можно подставить полученные значения и получить ответ. Диктор зачитывает ответ, который выводится в конце примера.
Второй пример представляет собой уравнение. И в правой, и в левой сторонах мы видим косинусы разностей аргументов. Диктор напоминает формулы приведений, которые используются для замены и упрощения этих выражения. Эти формулы записываются с правой стороны, чтобы школьники могли понять, откуда появляются те или иные изменения.
Еще один пример, третий, представляет собой некоторую дробь, где и в числителе и в знаменателе имеем тригонометрические выражения, а именно, разности произведений.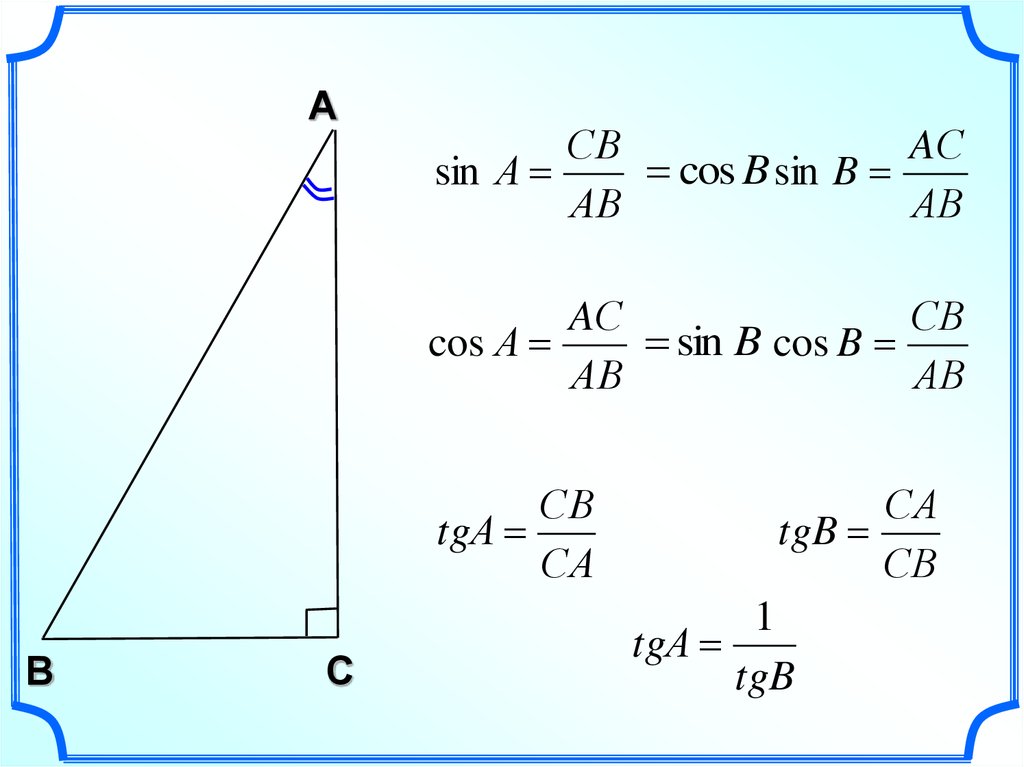
Здесь также при решении используются формулы приведений. Таким образом, школьники могут убедиться, что пропустив одну тему в тригонометрии, понять остальные будет все сложнее.
И, наконец, четвертый пример. Это также уравнение, при решении которых необходимо использовать новые изученные и старые формулы.
Примеры, которые приводятся в видеоуроке, можно рассмотреть более подробно и попробовать решить самостоятельно. Их можно задать в качестве домашнего задания школьникам.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тема занятия «Синус и косинус разности аргументов».
На предыдущем курсе мы познакомились с двумя тригонометрическими формулами синус и косинус суммы аргументов.
sin(x + y) = sin x cos y + cos x sin y,
cos (x + y) = cos x cos y — sin x sin y.
синус суммы двух углов равен сумме между произведением синуса первого угла и косинусом второго угла и произведением косинуса первого угла и синуса второго угла;
косинус суммы двух углов равен разности между произведением косинусов этих углов и произведением суммы этих углов.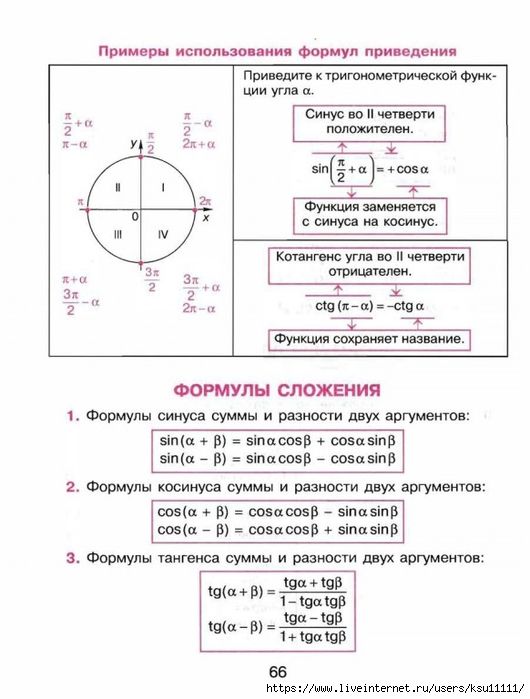
При помощи этих формул выведем формулы Синус и косинус разности аргументов.
Синус разности аргументов sin(x- y)
Две формулы (синус суммы и синус разности) можно записать в виде:
sin(x y) = sin x cos y cos x sin y.
Аналогично выведем формулу косинуса разности:
Косинус разности аргументов перепишем в виде суммы и применим уже известную формулу косинуса суммы: cos (x + y) = cosxcosy — sinxsiny.
только для аргументов х и -y. Подставив данные аргументы в формулу, получим cosxcos(- y) — sinxsin(- y).
sin(- y)= — siny). и получим окончательное выражение cosxcosy + sinxsiny.
cos (x — y) = cos (x +(- y)) =cos xcos(- y) — sin x sin(- y)= cosx cos y + sin xsin y.
Значит, cos (x — y) = cosxcos y + sin xsin y.
косинус разности двух углов равен сумме между произведением косинусов этих углов и произведением синусов этих углов.
Объединяя две формулы (косинус суммы и косинус разности) в одну, запишем
cos (x y) = cosxcos y sin xsin y.
Запомним, что формулы на практике можно применять как слева направо, так и наоборот.
Рассмотрим примеры.
ПРИМЕР 1. Вычислить cos (косинус пи, деленное на двенадцать).
Решение. Запишем пи, деленное на двенадцать, как разность пи на три и пи, деленное на четыре: = — .
Подставим значения в формулу косинуса разности: cos (x — y) = cosxcosy + sinxsiny, таким образом cos = cos (-) = cos cos + sin sin
Нам известно, что cos = , cos = sin= , sin = . Показать таблицу значений.
Заменим значение синуса и косинуса числовыми значениями и получим ∙ + ∙ при умножении дробь на дробь числители и знаменатели перемножаем, получаем
cos = cos (-) = cos cos + sin sin = ∙ + ∙ = = =.
Ответ: cos =.
ПРИМЕР 2. Решить уравнение cos(2π — 5х) = cos(- 5х) (косинус два пи минус пять икс равно косинусу от пи на два минус пять икс).
Решение. К левой и правой частям уравнения применим формулы приведения cos(2π — cos (косинус два пи минус альфа равен косинусу альфа) и cos(- = sin (косинус пи на два минус альфа равно синусу альфа), получим cos 5х = sin 5х, приведем его к виду однородного уравнения первой степени и получим cos 5х — sin 5х = 0.
Это однородное уравнение первой степени. Разделим почленно обе части уравнения на cos 5х. Имеем:
cos 5х: cos 5х — sin 5х: cos 5х = 0, т.к. cos 5х: cos 5х =1, а sin 5х: cos 5х= tg 5x, то получим:
Так как мы уже знаем, что уравнение tgt = а имеет решение t = arctgа + πn, а так как у нас t=5х, а =1, то получим
5x = arctg 1 + πn,
а значение arctg 1, тогда tg 1= Показать таблицу
подставим значение в уравнение и решим его:
Ответ: х = + .
ПРИМЕР 3. Найти значение дроби. (в числителе разность произведения косинусов семидесяти пяти градусов и шестидесяти пяти градусов и произведения синусов семидесяти пяти градусов и шестидесяти пяти градусов, а в знаменателе разность произведения синуса восьмидесяти пяти градусов и косинуса тридцати пяти градусов и произведения косинуса восьмидесяти пяти градусов и синуса тридцати пяти градусов).
Решение. В числителе данной дроби разность можно «свернуть» в косинус суммы аргументов 75° и 65°, а в знаменателе — разность «свернем» в синус разности аргументов 85° и 35°.
Получим
Ответ: — 1.
ПРИМЕР 4. Решить уравнение: cos(-х) + sin(-х) = 1(косинус разности пи на четыре и икс плюс синус разности пи на четыре и икс равно одному).
Решение. Применим формулы косинус разности и синус разности.
Показать общую формулу косинуса разности
Тогда cos (-х) = cos cos х + sinsinх
Показать общую формулу синуса разности
а sin (-х)= sin cosх — cos sinх
Подставим данные выражения в уравнение cos(-х) + sin(-х) = 1 и получим:
cos cos х + sinsin х + sin cos х — cos sin х = 1,
Так как cos= и sin= Показать таблицу значение синуса и косинуса
Получим ∙ cos х + ∙ sinх + ∙ cos х — ∙ sinх = 1,
второе и четвертое слагаемые противоположны, поэтому взаимно уничтожаются, остается:
∙ cos + ∙ cos = 1,
Решим данное уравнение и получим, что
2∙ ∙ cos x= 1,
Так ка мы уже знаем, что уравнение cos = а имеет решение t = arcos a + 2π k , а так как у нас t=x, а =, то получим
х = arccos + 2πn,
а так как значение arccos, тогда cos =
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 .
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Yandex.RTB R-A-339285-1
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.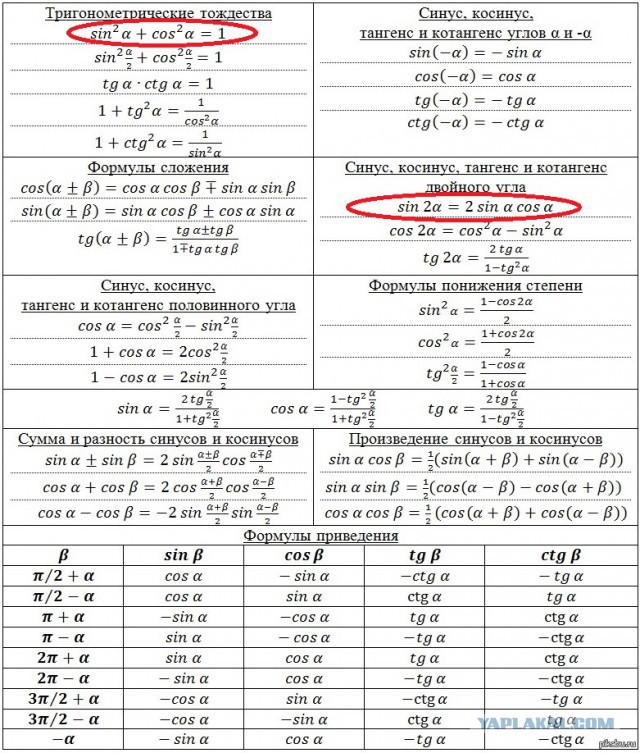
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению.