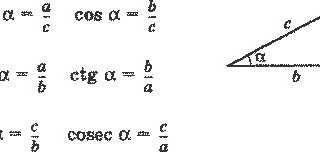Электронный справочник по математике для школьников тригонометрические функции острого угла синус косинус тангенс котангенс определения значения формулы
Катеты BC и AC прямоугольного треугольника ABC (рис. 1) называют противолежащим катетом угла α и прилежащим катетом угла α соответственно.
Рис.1
Катеты AC и BC прямоугольного треугольника ABC (рис. 2) называют противолежащим катетом угла β и прилежащим катетом угла β соответственно.
Рис.2
Синусом угла называют дробь:
Косинусом угла называют дробь:
Тангенсом угла называют дробь:
Котангенсом угла называют дробь:
Синус, косинус, тангенс и котангенс, и их комбинации называют тригонометрическими функциями.
Для синуса, косинуса, тангенса и котангенса угла α используют обозначения
sin α , cos α , tg α , ctg α
Рис.3
В соответствии с рисунком 3 справедливы формулы:
Следовательно,
Кроме того, справедливы формулы:
sin α = cos β, cos α = sin β, tg α = ctg β, ctg α = tg β,
которые можно переписать в виде:
sin α = cos (90° – α), cos α = sin (90° – α),
tg α = ctg (90° – α), ctg α = tg (90° – α).
ПРИМЕР. Найти тригонометрические функции углов 30°, 45°, 60°.
РЕШЕНИЕ. Рассмотрим равносторонний треугольник ABC, сторона которого равна 2 (рис. 4), и проведем высоту BD.
Рассмотрим равносторонний треугольник ABC, сторона которого равна 2 (рис. 4), и проведем высоту BD.
Рис.4
Тогда
Поэтому
Кроме того
Теперь рассмотрим прямоугольный равнобедренный треугольник ABC, катеты которого равны 1 (рис. 5).
Тогда
Поэтому
Определение тригонометрических функций произвольного угла приводится в разделе справочника «Тригонометрические функции произвольного угла».
| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник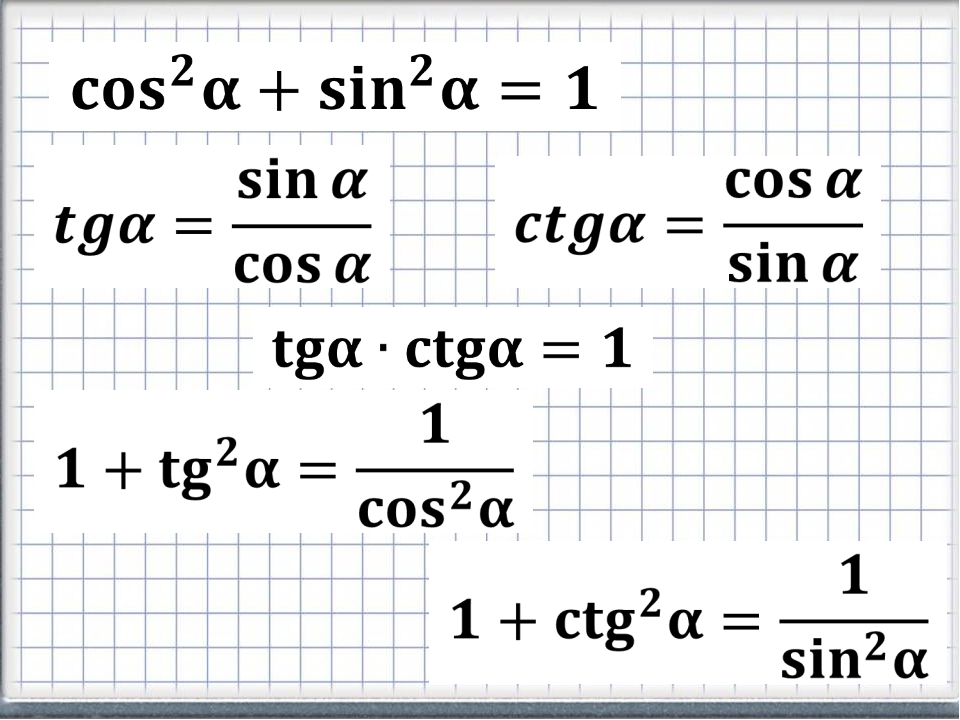 sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Основные тригонометрические формулы. Формулы приведения тригонометрических функций. Тригонометрические тождества. sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Основные тригонометрические формулы. Формулы приведения тригонометрических функций. Тригонометрические тождества.
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя.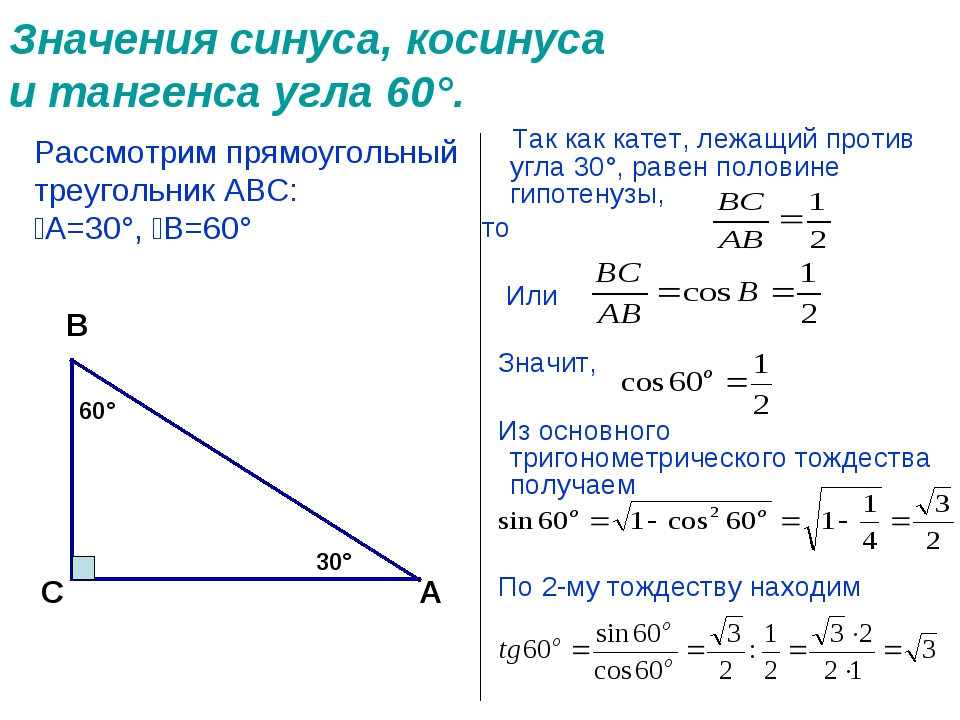 Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. |
Тригонометрические формулы
Тригонометрические формулы и их вывод. Мы знаем, что их много и что их нужно учить, что эту информацию очень сложно запомнить и её периодически требуется повторять. Так, верно! Ниже представлен вывод этих формул, думаю, пригодится. Если запомнить принципы вывода, то когда будет необходимо — вы всегда «вспомните» нужную формулу. В любом случае информация будет полезна — кому-то проще выучить, кому-то вывести.
Сначала сами формулы, это ещё не все, будет продолжение.
Основное тригонометрическое тождество, его запомнить нетрудно – формула «красивая»:
Откуда взялась? Посмотрите, здесь всё подробно описано.
Из неё следуют:
*Простые алгебраические преобразования.
Так же из неё получаем две другие необходимые формулы путём деления на квадрат синуса и квадрат косинуса:
Формулы тангенса и котангенса. Их проще выучить:
Их проще выучить:
Что дальше? Разберём некоторые группы формул! Рассмотрим эскиз:
Теорема! Косинус разности двух углов равен произведению косинусов этих углов сложенному с произведением синусов:
Доказательство:
Рассмотрим единичную окружность с углами α и β, которые образованы векторами
И положительным направлением оси ох. Угол между векторами равен:
Выразим скалярное произведение векторов по формуле:
Следовательно
Так как векторы имеют длину равную единице, а именно:
Теперь вычислим это же скалярное произведение по формуле:
Так как
Мы получили, что
Следовательно
Что и требовалось доказать!
Косинус суммы >>
Сумму α + β представляем как разность α–(–β) и подставляем a формулу для косинуса разности:
Так функция косинуса чётная а функция синуса нечётная
Значит
Синус суммы >>
Воспользуемся одной из формул приведения:
Теперь по формуле косинуса разности (1):
Получили
Синус разности >>
*Функция косинуса чётная, функция синуса нечётная
Следовательно
Получили группу формул:
Тангенс суммы >>
Используя формулу тангенса делим формулу (3) на (2):
Далее разделим числитель и знаменатель на cosα∙cosβ, получим:
Получили
Тангенс разности >>
Используя формулу тангенса делим формулу (4) на (1):
Также разделим числитель и знаменатель на cosα∙cosβ, получим:
Получили
Котангенс суммы >>
Используя формулу котангенса делим формулу (2) на (3):
Далее разделим числитель и знаменатель на sinα∙sinβ, получим:
Получили
Котангенс разности >>
Используя формулу котангенса делим формулу (1) на (4):
Далее разделим числитель и знаменатель на sinα∙sinβ, получим:
Получили
Пожалуйста, ещё группа:
Синус двойного угла >>
Используем формулу (3) — синуса суммы:
Косинус двойного угла >>
Используем формулу (2) — косинуса суммы:
Если из основного тригонометрического тождества выразим:
И подставим в (10), то получим:
Если выразим:
И подставим в (10), то получим:
Тангенс двойного угла >>
Используем формулу (5):
Котангенс двойного угла >>
Используем формулу (7):
Можем выделить группу формул:
Преобразование произведения тригонометрических функций в сумму и разность.
Возьмём формулы синуса суммы и синуса разности:
Сложим их почленно, то есть правую и левую части:
Возьмём формулы косинуса суммы и косинуса разности:
Сложим их почленно, то есть правую и левую части:
Теперь из cos (α–β) вычтем cos (α+β):
Получим:
Вот и ещё одна группа формул готова:
К этой статье будет дополнение-продолжение, разобрали ещё не всё, не пропустите! Успеха вам!
Скачать материал в формате PDF
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Формулы приведения. Как быстро получить любую формулу приведения
Формулы приведения разработаны для углов, представленных в одном из следующих видов: \(\frac{\pi}{2}+a\), \(\frac{\pi}{2}-a\), \(π+a\), \(π-a\), \(\frac{3\pi}{2}+a\), \(\frac{3\pi}{2}-a\), \(2π+a\) и \(2π-a\). Аналогично их можно использовать для углов представленных в градусах: \(90^°+a\), \(90^°-a\), \(180^°+a\), \(180^°-a\), \(270^°+a\), \(270^°-a\), \(180^°+a\), \(180^°-a\).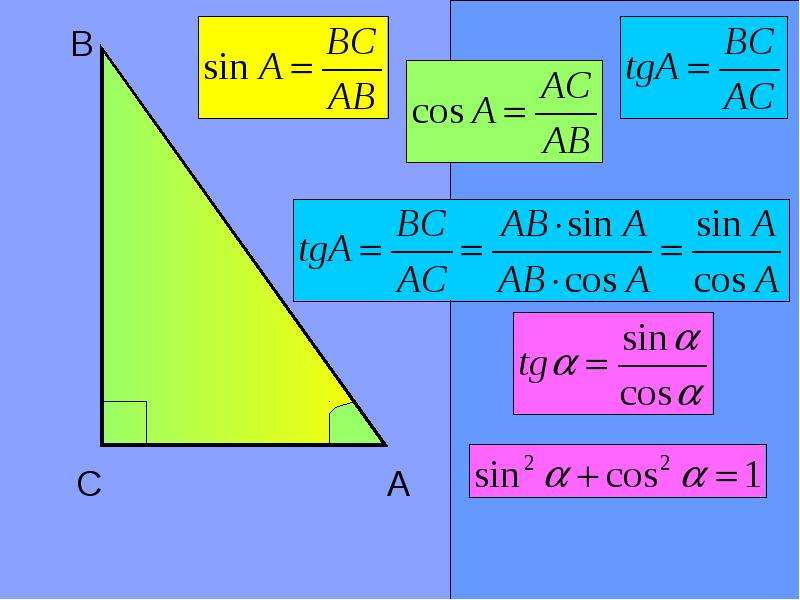 К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
Как быстро получить любую формулу приведения
Для начала обратите внимание, что все формулы имеют похожий вид:
Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.
Функция: Кофункция:
\(sin\) \(a\) \(→\) \(cos\) \(a\)
\(cos\) \(a\) \(→\) \(sin\) \(a\)
\(tg\) \(a\) \(→\) \(ctg\) \(a\)
\(ctg\) \(a\) \(→\) \(tg\) \(a\)
Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс
или котангенс, он либо останется синусом, либо превратиться в косинус. °}}=\)
°}}=\)
В числителе и знаменателе получились одинаковые косинусы. Сокращаем их.
\(= 18\)
Записываем ответ
Ответ: \(18\)
Пример. Найдите значение выражения \(\frac{3 \sin{(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}\)
Решение:|
\(\frac{3 \sin{(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Рассмотрим первое слагаемое числителя: \(\sin(π-a)\). Воспользуемся формулами приведения, выведя ее самостоятельно:
Таким образом, \(\sin(π-a)=\sina\) |
|
|
\(=\frac{3 \sin{a}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Второе слагаемое числителя: \(\cos{(\frac{π}{2} + a)}\):
Таким образом, \(\cos{(\frac{π}{2} + a)}=-\sina\) |
|
|
\(=\frac{3 \sin{a}-(-\sin{a}) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Теперь знаменатель: \(\cos(\frac{3π}{2} — a)\). |
|
|
\(=\frac{3 \sin{a}-(-\sin{a}) }{-\sin {a}}=\) |
Раскрываем скобки и приводим подобные слагаемые. |
|
|
\(=\frac{3 \sin{a}+\sin{a}}{-\sin {a}}=\frac{4\sin{a}}{-\sin{a}}\) |
Сократив на \(\sin{a}\), получаем ответ. |
|
|
\(=\frac{4 }{-1}=\)\(-4\) |
Ответ: \(-4\)
Пример. Вычислить чему равен \(ctg(-a-\frac{7π}{2})\), если \(tg\) \(a=2\)
Решение:
|
\(ctg(-a-\frac{7π}{2}) =\) |
Здесь сразу формулу приведения применять нельзя, так как аргумент нестандартный. |
|
|
\(= ctg(-\frac{7π}{2}-a) =\) |
Уже лучше, но все еще есть проблемы – «точка привязки» с минусом, а такого аргумента у нас нет. Избавимся от минуса, вынеся его за скобку внутри аргумента. |
|
|
\(= ctg(-(\frac{7π}{2}+a)) =\) |
Теперь вспомним о том, что котангенс – функция нечетная, то есть |
|
| \(= — ctg(\frac{7π}{2}+a) =\) |
Несмотря на то, что точка привязки \(\frac{7π}{2}\) мы все равно можем использовать формулы приведения, потому что \(\frac{7π}{2}\) лежит на пересечении одной из осей и числовой окружности (смотри пояснение ниже). |
|
|
\(= — (- tg\) \(a) = tg\) \(a = 2\) |
Готов ответ. |
Ответ: \(2\)
Еще раз проговорим этот важный момент: с точки зрения формулы приведения \(\frac{7π}{2}\) — это тоже самое, что и \(\frac{3π}{2}\). Почему? Потому что \(\frac{7π}{2}=\frac{3π+4π}{2}=\frac{3π}{2}+\frac{4π}{2}=\frac{3π}{2}+2π\). Иными словами, они отличаются ровно на один оборот \(2π\). А на значения тригонометрических функций количество оборотов никак не влияет:
\(cos\) \(t=cos (t+2π)=cos (t+4π)=cos (t+6π)= …=cos (t-2π)=cos (t-4π)=cos (t-6π)…\)
\(sin\) \(t=sin (t+2π)=sin (t+4π)=sin (t+6π)= . ..=sin (t-2π)=sin (t-4π)=sin (t-6π)…\)
..=sin (t-2π)=sin (t-4π)=sin (t-6π)…\)
Аналогично с тангенсом и котангенсом (только у них «оборот» равен \(π\)).
\(tg\) \(t=tg(t+π)=tg(t+2π)=tg(t+3π)= …=tg(t-π)=tg(t-2π)=tg(t-3π)…\)
\(ctg\) \(t=ctg(t+π)=ctg(t+2π)=ctg(t+3π)= …=ctg(t-π)=ctg(t-2π)=ctg(t-3π)…\)
Таким образом, \(-ctg(\frac{7π}{2}+a)=- ctg(\frac{3π}{2}+2π+a)=- ctg(\frac{3π}{2}+a)\).
То есть, для определения знака и необходимости смены функции важно лишь местоположение «точки привязки», а не её значение, поэтому так расписывать не обязательно (но можно если вы хотите впечатлить своими знаниями учительницу).
Ответы на часто задаваемые вопросы
Вопрос: Есть ли формулы приведения с аргументами \((\frac{π}{3}-a)\),\((\frac{π}{4}+a)\),\((\frac{7π}{6}+a)\) или тому подобное?
Ответ: К сожалению, нет. В таких ситуациях выгодно использовать формулы разности и суммы аргументов. Например, \(cos(\frac{π}{3}-a)=cos\frac{π}{3} cosa+sin\frac{π}{3} sina=\frac{1}{2}cosa+\frac{\sqrt{3}}{2} sina\).
Например, \(cos(\frac{π}{3}-a)=cos\frac{π}{3} cosa+sin\frac{π}{3} sina=\frac{1}{2}cosa+\frac{\sqrt{3}}{2} sina\).
Смотрите также Как доказать тригонометрическое тождество?
Скачать статьюФормулы тригонометрии
Взаимосвязь основных тригонометрических функций, каких как косинус и синус, тангенс и котангенс — называется
Мы разберем самые основные из тригонометрических формул. С помощью которых можно решить большинство тригонометрических заданий. Для большего удобства объединим их по значению, по таблицам.
Начнем с тригонометрических тождеств.
Основы в тригонометрических тождествах определяют взаимосвязь косинуса и синуса, тангенса и котангенса в одном угле.
 И выходят из их определения и единичной окружности. Дают возможность выделить через любую функцию другую.
И выходят из их определения и единичной окружности. Дают возможность выделить через любую функцию другую.Далее рассмотрим тригонометрические формулы приведения.
Они вытекают из свойств синусов, косинусов, котангенсов и тангенсов. Тем самым выражают такие свойства функции как: периодичность, симметричность и сдвиг к рассматриваемому углу. так же дают возможность работать с углами в радиусе до 90 градусов и произвольные углы.
Формулы на сложение.
Из данных формул видно что функции на сумму или разность от 2 углов выводятся из их же тригонометрических функций. Так же являются основой для формул двойных, тройных и других углов.
Формула для двойных, тройных и других углов.
Из них видно что тригонометрическая функция двойного, тройного или какого то ни было угла выводится из т.ф. одинарных углов.
Так же как и одинарные, двойные, тройные и т.д. существуют и половинные углы
Из формул половинного угла видно, что он выходит из косинуса угла целого.
Так же существуют методы понижения степени выглядят они как:
С помощью их использования возможно понизить функцию до первой степени. Взаимодействуя с натуральными степенями функций переводить до синусов и косинусов только кратных углов, в первую степень.
Сумма и разность в тригонометрической функции.
Помогают упростить тригонометрическое выражение, и разложить на множители синусы и косинусы.
Произведение синуса, косинуса, и одно на другое.
Метод универсальной тригонометрической подстановки.
Такая подстановка удобна тем, что функции получаются без корней.
Заметка: Актуальные предложения, участие в тендерах на строительство бесплатное! Перейдите по ссылке строительно монтажные тендеры (http://www.b2bsearch.ru/tenders/stroy) узнайте подробнее.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Внеклассный урок — Синус, косинус, тангенс, котангенс
Синус, косинус, тангенс, котангенсПрежде чем перейти к этому разделу, напомним определения синуса и косинуса, изложенные в учебнике геометрии 7-9 классов.
— Синус острого угла t прямоугольного треугольника равен отношению противолежащего катета к гипотенузе (рис.1):
sin t = b/c.
— Косинус острого угла t прямоугольного треугольника равен отношению прилежащего катета к гипотенузе (рис.1):
cos t = a/c.
Эти определения относятся к прямоугольному треугольнику и являются частными случаями тех определений, которые представлены в данном разделе.
Поместим тот же прямоугольный треугольник в числовую окружность (рис.2).
Мы видим, что катет b равен определенной величине y на оси Y (оси ординат), катет а равен определенной величине x на оси X (оси абсцисс). А гипотенуза с равна радиусу окружности (R).
Таким образом, наши формулы обретают иной вид.
Так как b = y, a = x, c = R, то:
y x
sin t = —— , cos t = ——.
R R
Кстати, тогда иной вид обретают, естественно, и формулы тангенса и котангенса.
Так как tg t = b/a, ctg t = a/b, то, верны и другие уравнения:
tg t = y/x,
ctg = x/y.
Но вернемся к синусу и косинусу. Мы имеем дело с числовой окружностью, в которой радиус равен 1. Значит, получается:
y
sin t = —— = y,
1
x
cos t = —— = x.
1
Так мы приходим к третьему, более простому виду тригонометрических формул.
Эти формулы применимы не только к острому, но и к любому другому углу (тупому или развернутому).
Определения и формулы cos t, sin t, tg t, ctg t.
Косинусом числа t числовой окружности называют абсциссу этого числа: cos t = x Синус числа t – это его ордината: sin t = y Тангенс числа t – это отношение синуса к косинусу: sin t π Котангенс числа t – это отношение косинуса к синусу: cos t |
Из формул тангенса и котангенса следует еще одна формула:
sin t cos t πk |
Уравнения числовой окружности.
Из предыдущего раздела мы знаем одно уравнение числовой окружности: x2 + y2 = 1 Но поскольку x = cos t, а y = sin t, то получается новое уравнение: cos2 t + sin2 t = 1 |
Знаки синуса, косинуса, тангенса и котангенса в четвертях окружности:
| 1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть |
cos t | + | – | – | + |
sin t | + | + | – | – |
tg t, ctg t | + | – | + | – |
Косинус и синус основных точек числовой окружности:
Как запомнить значения косинусов и синусов основных точек числовой окружности.
Прежде всего надо знать, что в каждой паре чисел значения косинуса стоят первыми, значения синуса – вторыми.
1) Обратите внимание: при всем множестве точек числовой окружности мы имеем дело лишь с пятью числами (в модуле):
1 √2 √3
0; —; ——; ——; 1.
2 2 2
Сделайте для себя это «открытие» — и вы снимете психологический страх перед обилием чисел: их на самом деле всего-то пять.
2) Начнем с целых чисел 0 и 1. Они находятся только на осях координат.
Не надо учить наизусть, где, к примеру, косинус в модуле имеет единицу, а где 0.
На концах оси косинусов (оси х), разумеется, косинусы равны модулю 1, а синусы равны 0.
На концах оси синусов (оси у) синусы равны модулю 1, а косинусы равны 0.
Теперь о знаках. Ноль знака не имеет. Что касается 1 – тут просто надо вспомнить самую простую вещь: из курса 7 класса вы знаете, что на оси х справа от центра координатной плоскости – положительные числа, слева – отрицательные; на оси у вверх от центра идут положительные числа, вниз – отрицательные. И тогда вы не ошибетесь со знаком 1.
И тогда вы не ошибетесь со знаком 1.
3) Теперь перейдем к дробным значениям.
— Во всех знаменателях дробей – одно и то же число 2. Уже не ошибемся, что писать в знаменателе.
— В серединах четвертей косинус и синус имеют абсолютно одинаковое значение по модулю: √2/2. В каком случае они со знаком плюс или минус – см.таблицу выше. Но вряд ли вам нужна такая таблица: вы знаете это из того же курса 7 класса.
— Все ближайшие к оси х точки имеют абсолютно одинаковые по модулю значения косинуса и синуса: (√3/2; 1/2).
— Значения всех ближайших к оси у точек тоже абсолютно идентичны по модулю – причем в них те же числа, только они «поменялись» местами: (1/2; √3/2).
Теперь о знаках – тут свое интересное чередование (хотя со знаками, полагаем, вы должны легко разобраться и так).
Если в первой четверти значения и косинуса, и синуса со знаком плюс, то в диаметрально противоположной (третьей) они со знаком минус.
Если во второй четверти со знаком минус только косинусы, то в диаметрально противоположной (четвертой) – только синусы.
Осталось только напомнить, что в каждом сочетании значений косинуса и синуса первое число – это значение косинуса, второе число – значение синуса.
— Обратите внимание еще на одну закономерность: синус и косинус всех диаметрально противоположных точек окружности абсолютно равны по модулю. Возьмем, к примеру, противоположные точки π/3 и 4π/3:
cos π/3 = 1/2, sin π/3 = √3/2
cos 4π/3 = -1/2, sin 4π/3 = -√3/2
Различаются значения косинусов и синусов двух противоположных точек только по знаку. Но и здесь есть своя закономерность: синусы и косинусы диаметрально противоположных точек всегда имеют противоположные знаки.
Важно знать:
Значения косинусов и синусов точек числовой окружности последовательно возрастают или убывают в строго определенном порядке: от самого малого значения до самого большого и наоборот (см. раздел «Возрастание и убывание тригонометрических функций» — впрочем, в этом легко убедиться, лишь просто посмотрев на числовую окружность выше).
В порядке убывания получается такое чередование значений:
√3 √2 1 1 √2 √3
1; ——; ——; —; 0; – —; – ——; – ——; –1
2 2 2 2 2 2
Возрастают они строго в обратном порядке.
Поняв эту простую закономерность, вы научитесь довольно легко определять значения синуса и косинуса.
Тангенс и котангенс основных точек числовой окружности.
Зная косинус и синус точек числовой окружности, легко можно вычислить их тангенс и котангенс. Делим синус на косинус — получаем тангенс. Делим косинус на синус — получаем котангенс. Результаты этого деления — на рисунке.
ПРИМЕЧАНИЕ: В некоторых таблицах значения тангенса и котангенса, равные модулю √3/3, указаны как 1/√3. Ошибки тут нет, так как это равнозначные числа. Если числитель и знаменатель числа 1/√3 умножить на √3, то получим √3/3.
Как запомнить значение тангенсов и котангенсов основных точек числовой окружности.
Здесь такие же закономерности, что и с синусами и косинусами. И чисел тут всего четыре (в модуле): 0, √3/3, 1, √3.
На концах осей координат – прочерки и нули. Прочерки означают, что в данных точках тангенс или котангенс не имеют смысла.
Как запомнить, где прочерки, а где нули? Поможет правило.
Тангенс – это отношение синуса к косинусу. На концах оси синусов (ось у) тангенс не существует.
Котангенс – это отношение косинуса к синусу. На концах оси косинусов (ось х) котангенс не существует.
В остальных точках идет чередование всего лишь трех чисел: 1, √3 и √3/3 со знаками плюс или минус. Как с ними разобраться? Запомните (а лучше представьте) три обстоятельства:
1) тангенсы и котангенсы всех середин четвертей имеют в модуле 1.
2) тангенсы и котангенсы ближайших к оси х точек имеют в модуле √3/3; √3.
3) тангенсы и котангенсы ближайших к оси у точек имеют в модуле √3; √3/3.
Не ошибитесь со знаками – и вы большой знаток.
Нелишне будет запомнить, как возрастают и убывают тангенс и котангенс на числовой окружности (см.числовую окружность выше или раздел «Возрастание и убывание тригонометрических функций»). Тогда еще лучше будет понятен и порядок чередования значений тангенса и котангенса.
Тригонометрические свойства чисел числовой окружности.
Представим, что определенная точка М имеет значение t.
Свойство 1:
| | | |
Пояснение. Пусть t = –60º и t = –210º.
Пусть t = –60º и t = –210º.
cos –60º равен 1/2. Но cos 60º тоже равен 1/2. То есть косинусы –60º и 60º равны как по модулю, так и по знаку: cos –60º = cos 60º.
cos –210º равен –√3/2. Но cos 210º тоже равен –√3/2. То есть: cos –210º = cos 210º.
Таким образом, мы доказали, что cos (–t) = cos t.
sin –60º равен –√3/2. А sin 60º равен √3/2. То есть sin –60º и sin 60º равны по модулю, но противоположны по знаку.
sin –210º равен 1/2. А sin 210º равен –1/2. То есть sin –210º и sin 210º равны по модулю, но противоположны по знаку.
Таким образом, мы доказали, что sin (–t) = –sin t.
Посмотрите, что происходит с тангенсами и котангенсами этих углов – и вы сами легко докажете себе верность двух других тождеств, приведенных в таблице.
Вывод: косинус – четная функция, синус, тангенс и котангенс – нечетные функции.
Свойство 2: Так как t = t + 2πk, то:
| |
Пояснение: t и t + 2πk – это одна и та же точка на числовой окружности.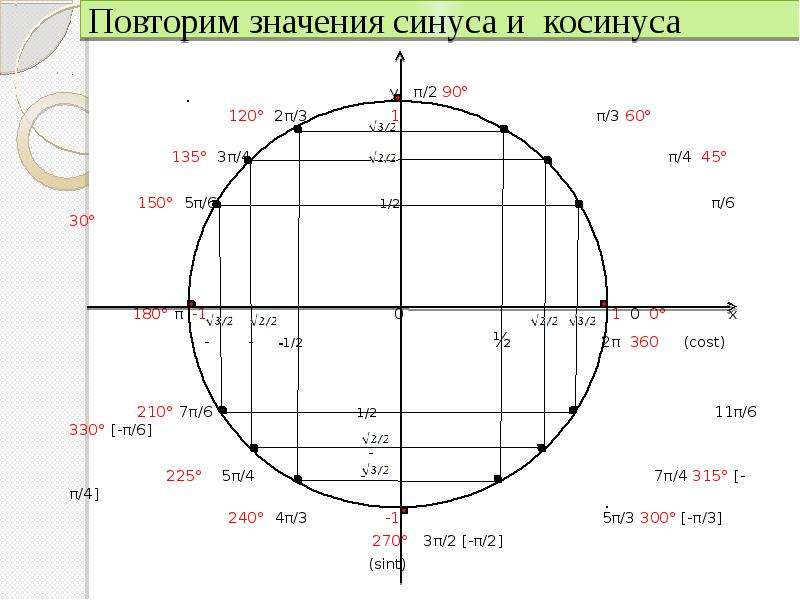 Просто в случае с 2πk мы совершаем определенное количество полных оборотов по окружности, прежде чем приходим к точке t. Значит, и равенства, изложенные в этой таблице, очевидны.
Просто в случае с 2πk мы совершаем определенное количество полных оборотов по окружности, прежде чем приходим к точке t. Значит, и равенства, изложенные в этой таблице, очевидны.
Свойство 3: Если две точки окружности находятся друг против друга относительно центра О, то их синусы и косинусы равны по модулю, но противоположны по знаку, а их тангенсы и котангенсы одинаковы как по модулю, так и по знаку.
| | | |
Пояснение: Пусть точка М находится в первой четверти. Она имеет положительное значение синуса и косинуса. Проведем от этой точки диаметр – то есть отрезок, проходящий через центр оси координат и заканчивающийся в точке окружности напротив. Обозначим эту точку буквой N. Как видите, дуга MN равна половине окружности. Вы уже знаете, что половина окружности – это величина, равная π. Значит, точка N находится на расстоянии π от точки М. Говоря иначе, если к точке М прибавить расстояние π, то мы получим точку N, находящуюся напротив. Она находится в третьей четверти. Проверьте, и увидите: косинус и синус точки N – со знаком «минус» (x и y имеют отрицательные значения).
Проведем от этой точки диаметр – то есть отрезок, проходящий через центр оси координат и заканчивающийся в точке окружности напротив. Обозначим эту точку буквой N. Как видите, дуга MN равна половине окружности. Вы уже знаете, что половина окружности – это величина, равная π. Значит, точка N находится на расстоянии π от точки М. Говоря иначе, если к точке М прибавить расстояние π, то мы получим точку N, находящуюся напротив. Она находится в третьей четверти. Проверьте, и увидите: косинус и синус точки N – со знаком «минус» (x и y имеют отрицательные значения).
Тангенс и котангенс точки М имеют положительное значение. А тангенс и котангенс точки N? Ответ простой: ведь тангенс и котангенс – это отношение синуса и косинуса. В нашем примере синус и косинус точки N – со знаком «минус». Значит:
–sin t
tg (t + π) = ———— = tg t
–cos t
–cos t
ctg (t + π) = ———— = ctg t
–sin t
Мы доказали, что тангенс и котангенс диаметрально противоположных точек окружности имеют не только одинаковое значение, но и одинаковый знак.
Свойство 4: Если две точки окружности находятся в соседних четвертях, а расстояние между точками равно одной четверти окружности, то синус одной точки равен косинусу другой с тем же знаком, а косинус одной точки равен синусу второй с противоположным знаком.
π | π |
| 01) | Основные тригонометрические тождества | |
01.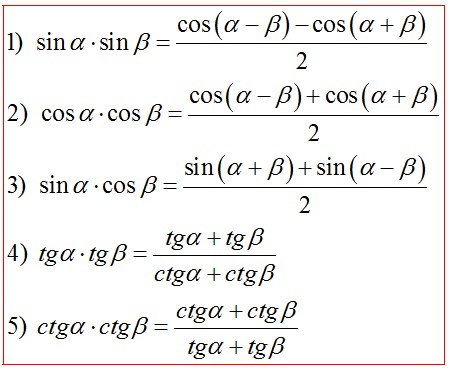 1) 1) | Основное тригонометрическое тождество | формула основного тригонометрического тождества |
| 01.2) | Основное тождество через тангенс и косинус | формула основного тождества через тангенс и косинус |
| 01.3) | Основное тождество через котангенс и синус | формула основного тождества через котангенс и синус |
| 01.4) | Соотношение между тангенсом и котангенсом | формула соотношения между тангенсом и котангенсом |
| 02) | Формулы двойного аргумента (угла) | |
| 02.1) | Синус двойного угла | формула синуса двойного угла |
| 02.2) | формула синуса двойного угла | |
| 02.3) | Косинус двойного угла | формула синуса двойного угла |
02. 4) 4) | формула синуса двойного угла | |
| 02.5) | Тангенс двойного угла | формула синуса двойного угла |
| 02.6) | Котангенс двойного угла | формула синуса двойного угла |
| 03) | Формулы тройного аргумента (угла) | |
| 03.1) | Синус тройного угла | формула синуса тройного угла |
| 03.2) | Косинус тройного угла | формула косинуса тройного угла |
| 03.3) | Тангенс тройного угла | формула тангенса тройного угла |
| 03.4) | Котангенс тройного угла | формула котангенса тройного угла |
| 04) | Формулы половинного аргумента (угла) | |
| 04.1) | Синус половинного угла | формула синуса половинного угла |
04.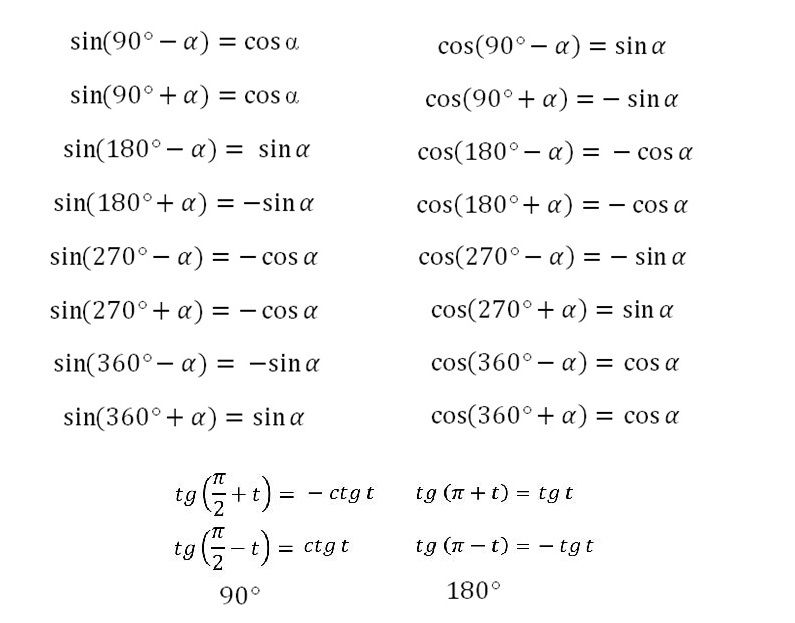 2) 2) | Косинус половинного угла | формула косинуса половинного угла |
| 04.3) | Тангенс половинного угла | формула тангенса половинного угла |
| 04.4) | Котангенс половинного угла | формула котангенса половинного угла |
| 04.5) | Тангенс половинного угла | формула тангенса половинного угла |
| 04.6) | Котангенс половинного угла | формула котангенса половинного угла |
| 05) | Формулы квадратов тригонометрических функций | |
| 05.1) | Квадрат синуса | формула квадрата синуса |
| 05.2) | Квадрат косинуса | формула квадрата косинуса |
| 05.3) | Квадрат тангенса | формула квадрата тангенса |
05. 4) 4) | Квадрат котангенса | формула квадрата котангенса |
| 05.5) | Квадрат синуса половинного угла | формула квадрата синуса половинного угла |
| 05.6) | Квадрат косинуса половинного угла | формула квадрата косинуса половинного угла |
| 05.7) | Квадрат тангенса половинного угла | формула квадрата тангенса половинного угла |
| 05.8) | Формулы кубов тригонометрических функций | формула квадрата котангенса половинного угла |
| 06) | Формулы кубов тригонометрических функций | |
| 06.1) | Куб синуса | формула куба синуса |
| 06.2) | Куб косинуса | формула куба косинуса |
| 06.3) | Куб тангенса | формула куба тангенса |
06. 4) 4) | Куб котангенса | формула куба котангенса |
| 07) | Формулы тригонометрических функций в четвертой степени | |
| 07.1) | Четвертая степень синуса | формула четвертой степени синуса |
| 07.2) | Четвертая степень косинуса | формула четвертой степени косинуса |
| 08) | Формулы сложения и вычитания аргументов | |
| 08.1) | Сложение аргументов синуса | формула сложения аргументов синуса |
| 08.2) | Сложение аргументов косинуса | формула сложения аргументов косинуса |
| 08.3) | Сложение аргументов тангенса | формула сложения аргументов тангенса |
| 08.4) | Сложение аргументов котангенса | формула сложения аргументов котангенса |
08.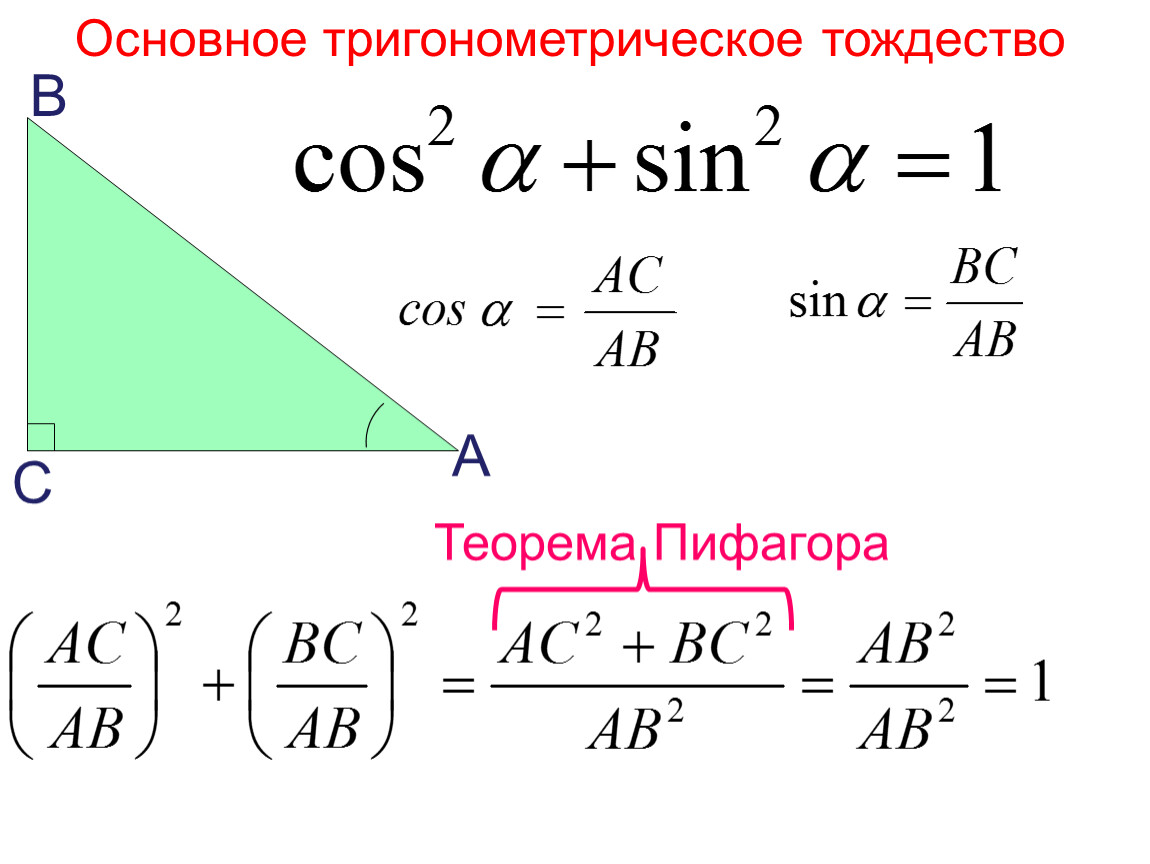 5) 5) | Вычитание аргументов синуса | формула вычитания аргументов синуса |
| 08.6) | Вычитание аргументов косинуса | формула вычитания аргументов косинуса |
| 08.7) | Вычитание аргументов тангенса | формула вычитания аргументов тангенса |
| 08.8) | Вычитание аргументов котангенса | формула вычитания аргументов котангенса |
| 09) | Формулы суммы тригонометрических функций | |
| 09.1) | Сумма синусов | формула суммы синусов |
| 09.2) | Сумма косинусов | формула суммы косинусов |
| 09.3) | Сумма тангенсов | формула суммы тангенсов |
| 09.4) | Сумма котангенсов | формула суммы котангенсов |
09. 5) 5) | Сумма синуса и косинуса | формула суммы синуса и косинуса |
| 10) | Формулы разности тригонометрических функций | |
| 10.1) | Разность синусов | формула разности суммы синусов |
| 10.2) | Разность косинусов | формула разности суммы косинусов |
| 10.3) | Разность тангенсов | формула разности суммы тангенсов |
| 10.4) | Разность котангенсов | формула разности котангенсов |
| 10.5) | Разность синуса и косинуса | формула разности синуса и косинуса |
| 11) | Формулы произведения тригонометрических функций | |
| 11.1) | Произведение синусов | формула произведения синусов |
| 11.2) | Произведение косинусов | формула произведения косинусов |
11. 3) 3) | Произведение синуса и косинуса | формула произведения синуса и косинуса |
| 11.4) | Произведение тангенсов | формула произведения тангенсов |
| 11.5) | Произведение котангенсов | формула произведения котангенсов |
| 11.6) | Произведение тангенса и котангенса | формула произведения тангенса и котангенса |
| 12) | Формулы понижения степени | |
| 12.1) | Понижение степени синуса | формула понижения степени синуса |
| 12.2) | Понижение степени косинуса | формула понижение степени косинуса |
| 13) | Формулы суммы и разности разных тригонометрических функций | |
| 13.1) | Сумма синуса и косинуса | формула суммы синуса и косинуса |
13.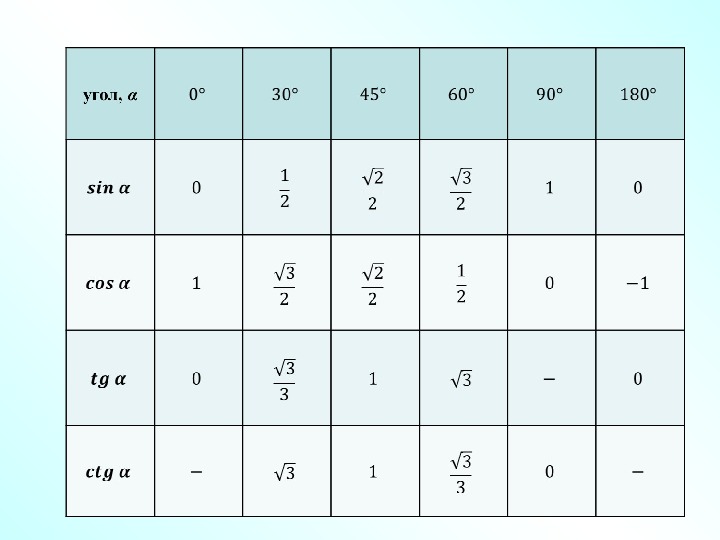 2) 2) | Разность синуса и косинуса | формула разности синуса и косинуса |
| 13.3) | Сумма синуса и косинуса с коэффициентами | формула суммы синуса и косинуса с коэффициентами |
| 13.4) | Разность синуса и косинуса с коэффициентами | формула разности синуса и косинуса с коэффициентами |
| 14) | Формулы общего вида | |
| 14.1) | Формула понижения nй четной степени синуса | формула формулы формулы понижения n четной степени синуса |
| 14.2) | Формула понижения nй четной степени косинуса | формула формулы понижения nй четной степени косинуса |
| 14.3) | Формула понижения nй нечетной степени синуса | формула формулы понижения nй нечетной степени синуса |
14. 4) 4) | Формула понижения nй нечетной степени косинуса | формула формулы понижения nй нечетной степени косинуса |
Доказательство формул сложения и вычитания для синуса, косинуса и тангенса — стенограмма видео и урока
Proof
Помните, как мы говорили о том, как эти идентичности были доказаны или получены математически, чтобы вы могли использовать их с уверенностью? Итак, вот обзор простого способа доказать эти тождества суммы углов и разностей. Я не ожидаю, что вы полностью поймете эти доказательства, поскольку эти выводы переносят вас в сферу высшей математики, такой как комплексные экспоненты и мнимые числа.ix = cos x + i sin x . Не волнуйтесь, если сейчас это не имеет смысла. Как только вы углубитесь в высшую математику, такую как исчисление и выше, вы поймете, как все это связано с тем, что вы изучаете сейчас. Хорошо, вот доказательство:
Внимательно изучите это доказательство, и мы увидим, что да, оно использует высшие математические навыки, но оно также использует наши базовые навыки алгебры для умножения вещей.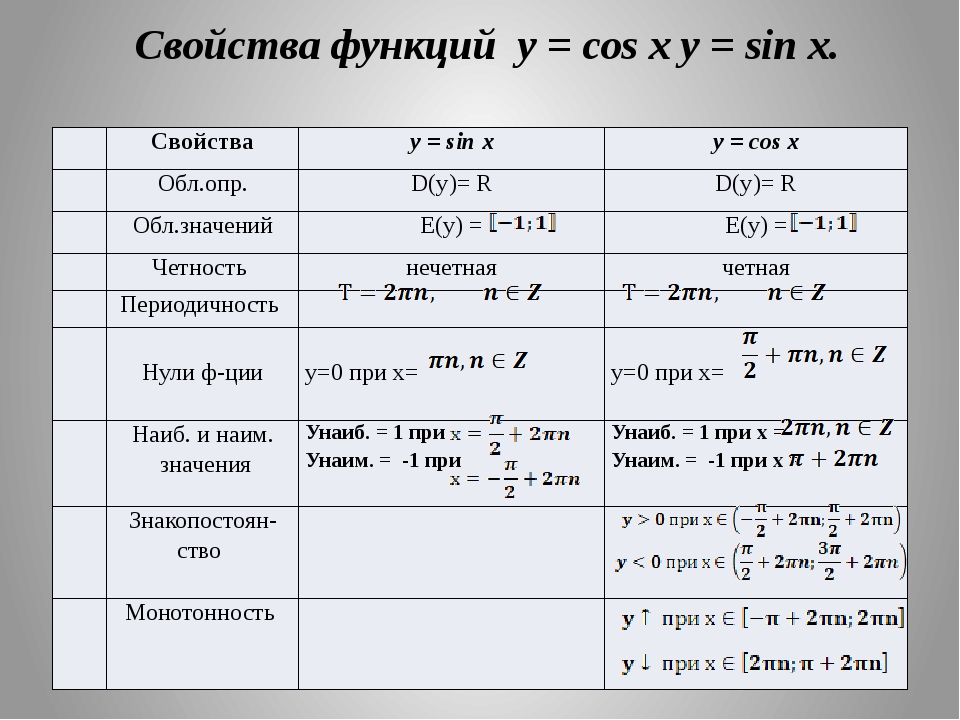 Вы можете спросить, как это влияет на нашу идентичность? Что ж, взгляните на последнюю строку и посмотрите, как у нас есть два набора круглых скобок.Теперь посмотрите на самую первую строку, левая часть уравнения дает нам сумму косинусов и сумму синусов. Если мы установим сумму косинусов равной первому набору круглых скобок в последней строке, мы увидим, что получаем нашу идентичность суммы косинусов. Если мы установим синусоидальную сумму, равную второму набору круглых скобок в четвертой строке, мы увидим, что мы получим тождество синусоидальной суммы.
Вы можете спросить, как это влияет на нашу идентичность? Что ж, взгляните на последнюю строку и посмотрите, как у нас есть два набора круглых скобок.Теперь посмотрите на самую первую строку, левая часть уравнения дает нам сумму косинусов и сумму синусов. Если мы установим сумму косинусов равной первому набору круглых скобок в последней строке, мы увидим, что получаем нашу идентичность суммы косинусов. Если мы установим синусоидальную сумму, равную второму набору круглых скобок в четвертой строке, мы увидим, что мы получим тождество синусоидальной суммы.
Чтобы получить наши различия, мы просто заменяем угол бета на угол минус бета.Чтобы получить наши касательные тождества, мы используем определение тангенса в терминах синуса и косинуса. Мы знаем, что тангенс равен синусу / косинусу, поэтому мы просто записываем тождество суммы касательных как тождество суммы синусов над тождеством суммы косинусов. Затем мы упрощаем, чтобы добраться до нашей касательной идентичности.
Довольно красиво, не правда ли?
Использует
Теперь вы знаете, что эти идентификаторы действительны; что ты можешь с ними делать? Эти идентификаторы очень полезны для решения триггерных проблем.Конечно, с помощью калькуляторов вы можете решить любую проблему, решив ее. Но понимаете, в свое время у людей не было удобных графических калькуляторов, которые могли бы выполнять все виды сложных вычислений. Им приходилось решать все вручную. Итак, эти личности помогли им в этом.
Там, где они не могли оценить триггерную функцию суммы пары углов, они могли оценить эти углы по отдельности и наоборот. Там, где они не могли оценить триггерные функции для отдельных углов, они могли оценить триггерные функции для суммы углов.То же самое относится и к некоторым тестам и экзаменам, которые вы будете сдавать. Возможно, вы не сможете использовать калькулятор, поэтому вам придется полагаться на эти идентификаторы, чтобы решить триггерные проблемы. Хотите посмотреть, как это работает?
Хотите посмотреть, как это работает?
Пример
Давайте посмотрим на пример.
Глядя на эту проблему, мы видим, что это правая часть тождества разности косинусов. Мы также видим, что сами по себе углы непросто оценить без калькулятора.Так что же нам делать? Мы используем тождество разности косинусов, чтобы помочь нам. Используя это тождество, мы обнаруживаем, что вся наша фраза равна косинусу 5 пи на 12 минус пи на 12 . Это упрощается до косинуса 4 пи на 12 . Это еще больше упрощается до косинуса числа пи над 3 . Это мы можем оценить с помощью нашего единичного круга, нашего специального круга с радиусом 1, который включает в себя углы, которые имеют четкие ответы для косинуса и синуса. Мы видим, что косинус числа пи над 3 равен 1/2.И готово!
Это было круто, правда? Мы перешли от проблемы, которая казалась очень сложной, к проблеме, которую очень легко решить. И помните, если вы видите пи в своем углу, значит, вы имеете дело с радианами.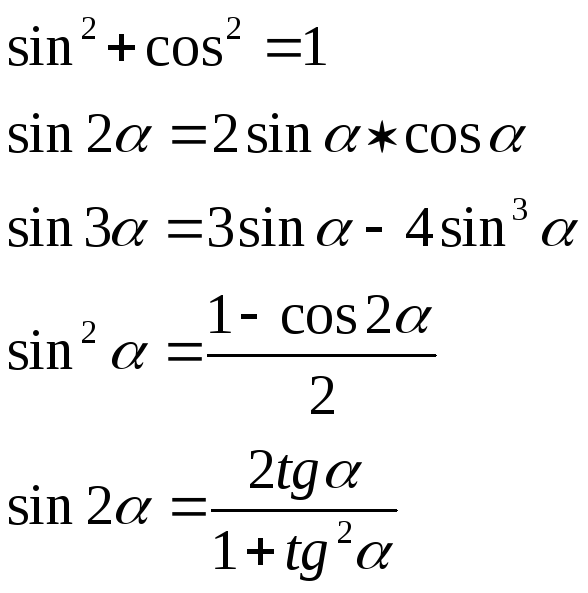 Если вы используете калькулятор, убедитесь, что ваш калькулятор настроен на вычисление в радианах, а не в градусах.
Если вы используете калькулятор, убедитесь, что ваш калькулятор настроен на вычисление в радианах, а не в градусах.
Резюме урока
Давайте рассмотрим то, что мы узнали.
Мы узнали, что тождества суммы углов и разности определяют, как превратить триггерную функцию двух углов, сложенных или вычтенных друг из друга, в триггерную функцию единичных углов.Всего их у нас шесть.
Доказательство этих тождеств включает использование комплексных экспонент, а также использование формулы Эйлера.
С помощью этих идентификаторов мы можем брать проблемы, которые мы не можем легко оценить, и превращать их в то, что мы можем. У нас может быть проблема с отдельными углами, которую мы не можем оценить сами по себе, но мы можем оценить ее, если сложим или вычтем углы.И наоборот — у нас может возникнуть проблема, когда мы не сможем оценить два добавленных или вычтенных угла, но можем оценить сами углы. \ circ $.(Для греков это были «два прямых угла», но я перевожу на более современную терминологию.)
\ circ $.(Для греков это были «два прямых угла», но я перевожу на более современную терминологию.)
Итак, предположим, что у вас есть два правильных треугольников. Тогда у этих двух треугольников уже есть углы одинакового размера, а именно прямой угол. Теперь предположим, что у них есть другой угол с общей мерой.\ circ $, третьи углы каждого также должны быть одинакового размера. Таким образом, прямоугольные треугольники должны иметь один и тот же угол, чтобы быть похожими.
Таким образом, соотношения сторон двух вышеуказанных треугольников должны быть одинаковыми: $$ \ frac aA = \ frac bB = \ frac cC $$
Немного алгебры дает нам $$ \ frac ac = \ frac AC, \ \ \ frac bc = \ frac BC, \ \ \ frac ba = \ frac BA $$
Обозначьте стороны по отношению к углу $ \ theta $:
Мы видим, что:
для любого прямоугольного треугольника с одним из углов, равным $ \ theta $, независимо от размера, отношения $ \ frac {\ text {смежный}} {\ text {hypotenuse}}, \ frac {\ text {напротив }} {\ text {hypotenuse}}, \ frac {\ text {противоположный}} {\ text {смежный}} $ такие же, как и для всех других таких прямоугольных треугольников.
Таким образом, $ \ theta $ полностью определяет эти три соотношения. По этой причине мы даем им специальные имена косинус , синус и тангенс .
$$ \ begin {align} \ cos \ theta & = \ frac {\ text {смежный}} {\ text {hypotenuse}} \\ \ sin \ theta & = \ frac {\ text {напротив}} {\ text {hypotenuse}} \\ \ tan \ theta & = \ frac {\ text {противоположный}} {\ text {смежный}} \ end {align} $$
(Название «касательная» происходит от того факта, что противоположная сторона касается окружности.Название «синус» произошло от названия «полуаккорда», но оно было сокращено арабскими математиками, а через некоторое время после того, как источник этого сокращения был забыт, было снова расширено до слова, означающего «пещера». Это слово было переведено обратно на латинское «синус», а значит, на «синус». «Косинус» происходит от дополнения к синусу.)
Итак, в чем смысл? Потому что иногда (на самом деле, очень часто) вы не можете напрямую измерить расстояние, которое хотите узнать.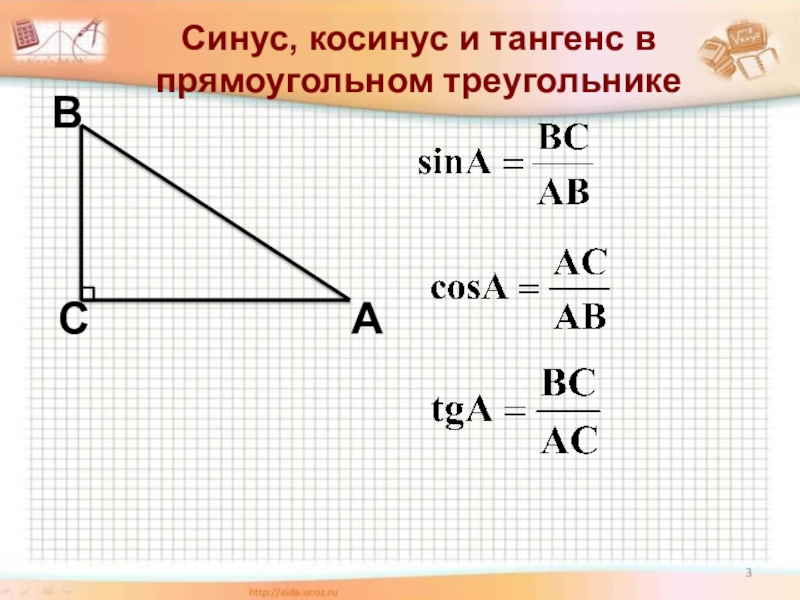 Видите это дерево снаружи? Хотите знать, какой он высокий? Если это большое дерево, то напрямую измерить его высоту очень сложно.
Видите это дерево снаружи? Хотите знать, какой он высокий? Если это большое дерево, то напрямую измерить его высоту очень сложно.
(Изображение заимствовано с http://www.monumentaltrees.com/en/content/measuringheight)
Но если вы можете найти точку прямо под ее самой высокой высотой, то измерьте расстояние по горизонтали до некоторой точки достаточно далеко, чтобы увидеть вершину. С этого момента измерьте угол, под которым ваша линия взгляда будет находиться в горизонтальном положении. Это образует прямоугольный треугольник с высотой дерева на противоположной стороне, расстояние, которое вы измерили по земле, как прилегающую сторону, и угол, который вы измерили как $ \ theta $.Итак, найдите тангенс угла и умножьте:
$$ \ text {противоположный} = \ text {смежный} \ times \ tan \ theta $$
, и теперь вы знаете высоту, не измеряя ее напрямую. Конечно, это простой пример. В реальных примерах математика немного сложнее, но варианты этого метода позволяют вам измерять всевозможные расстояния, на которых вы не можете попасть «прямо под его наивысшую точку». На этом основана вся геодезическая наука.
На этом основана вся геодезическая наука.
Итак, знание значений синуса, косинуса и тангенса для разных углов — очень и очень полезная вещь.\ circ $, и перечислил эти значения в таблицах. Чтобы найти значение угла, которого нет в таблице, вы нашли ближайшие углы вверху и внизу и линейно интерполировали между ними. Некоторых из нас старшего возраста этому учили, потому что, хотя калькуляторы тогда существовали, они не были универсальными, и нас все еще учили старым методам (я просто скучал по необходимости учиться пользоваться логарифмической линейкой).
4. Формулы полуугловых
М. Борна
Мы разработаем формулы для синуса, косинуса и тангенса половинного угла.
Формула полуугла — синус
Начнем с формулы косинуса двойного угла, с которой мы познакомились в предыдущем разделе.
cos 2 θ = 1− 2sin2 θ
Сводка формул
На этой странице мы выводим следующие формулы:
`sin (альфа / 2) = + — sqrt ((1-cos alpha) / 2`
`cos (альфа / 2) = + — sqrt ((1 + cos alpha) / 2`
`tan (alpha / 2) = (1-cos alpha) / (sin alpha`
Теперь, если мы допустим
`тета = альфа / 2`
, затем 2 θ = α , и наша формула принимает следующий вид:
`cos α = 1-2 \ sin ^ 2 (α / 2)`
Теперь решаем
`грех (альфа / 2)`
(То есть мы получаем sin (alpha / 2) слева от уравнения, а все остальное справа):
`2 \ sin ^ 2 (α / 2) = 1 — cos α`
`sin ^ 2 (α / 2) = (1 — cos α) / 2`
Решение дает нам следующий синус для тождества полуугла :
`sin (альфа / 2) = + — sqrt ((1-cos alpha) / 2`
Знак (положительный или отрицательный) sin (alpha / 2) зависит от квадранта. 2 (альфа / 2) = (1 + cos alpha) / 2`
2 (альфа / 2) = (1 + cos alpha) / 2`
Решая относительно cos (α / 2), получаем:
`cos (альфа / 2) = + — sqrt ((1 + cos alpha) / 2`
Как и раньше, нужный нам знак зависит от квадранта.
Если α / 2 находится в первом или четвертом квадранте , формула использует положительный случай:
`cos (альфа / 2) = sqrt ((1 + cos alpha) / 2`
Если α / 2 находится во втором или третьем квадранте , в формуле используется отрицательный регистр:
`cos (альфа / 2) = — sqrt ((1 + cos alpha) / 2`
Формула полуугла — касательная
Тангенс половины угла определяется по формуле:
`tan (alpha / 2) = (1-cos alpha) / (sin alpha)`
Проба
Сначала напомним `tan x = (sin x) / (cos x)`.2а)) `
Затем находим квадратный корень:
`= (1-cos a) / (sin a)`
Конечно, нам нужно будет делать поправку на положительные и отрицательные знаки, в зависимости от рассматриваемого квадранта. @`, используя соотношение половинного угла синуса, приведенное выше.(текст (o))) / 2) `
@`, используя соотношение половинного угла синуса, приведенное выше.(текст (o))) / 2) `
`= + — sqrt (((1 + 0.866)) / 2)`
`= 0,9659`
Первый квадрант, значит положительный.
2. Найдите значение sin (alpha / 2), если cos alpha = 12/13, где 0 ° < α <90 °.
Ответ
`sin (альфа / 2) = + — sqrt ((1-cos alpha) / 2)`
`= sqrt ((1-12 / 13) / 2)`
`= sqrt ((1/13) / 2)`
`= sqrt (1/26)`
`= 0,1961`
Мы выбираем позитив, потому что находимся в первом квадранте.2сек \ theta`
`= (1 + cos theta) sec \ theta`
`= (1 + cos theta) 1 / (cos theta)`
`= сек \ тета + 1`
`=» RHS «`
{\ Displaystyle {\ begin {выровнено} \ tan \ left ({\ frac {\ eta \ pm \ theta} {2}} \ right) & = {\ frac {\ sin \ eta \ pm \ sin \ theta} {\ cos \ eta + \ cos \ theta}} = — {\ frac {\ cos \ eta — \ cos \ theta} {\ sin \ eta \ mp \ sin \ theta}}, \\ [10pt] \ tan \ left (\ pm {\ frac {\ theta} {2}} \ right) & = {\ frac {\ pm \ sin \ theta} {1+ \ cos \ theta}} = {\ frac {\ pm \ tan \ theta} {\ sec \ theta +1}} = {\ frac {\ pm 1} {\ csc \ theta + \ cot \ theta}}, && (\ eta = 0) \\ [10pt] \ tan \ left ( \ pm {\ frac {\ theta} {2}} \ right) & = {\ frac {1- \ cos \ theta} {\ pm \ sin \ theta}} = {\ frac {\ sec \ theta -1} {\ pm \ tan \ theta}} = \ pm (\ csc \ theta — \ cot \ theta), && (\ eta = 0) \\ [10pt] \ tan \ left ({\ frac {1} {2} } (\ theta \ pm {\ frac {\ pi} {2}}) \ right) & = {\ frac {1 \ pm \ sin \ theta} {\ cos \ theta}} = \ sec \ theta \ pm \ tan \ theta = {\ frac {\ csc \ theta \ pm 1} {\ cot \ theta}}, && (\ eta = {\ frac {\ pi} {2}}) \\ [10pt] \ tan \ left ({\ frac {1} {2}} (\ theta \ pm {\ frac {\ pi} {2}}) \ right) & = {\ frac {\ cos \ theta} {1 \ mp \ sin \ theta }} = {\ frac {1} {\ sec \ theta \ mp \ tan \ theta}} = {\ frac {\ cot \ theta} {\ csc \ theta \ mp 1}}, && (\ et a = {\ frac {\ pi} {2}}) \\ [10pt] {\ frac {1- \ tan (\ theta / 2)} {1+ \ tan (\ theta / 2)}} & = \ pm {\ sqrt {\ frac {1- \ sin \ theta} {1+ \ sin \ theta}}} \\ [10pt] \ tan {\ frac {\ theta} {2}} & = \ pm {\ sqrt {\ frac {1- \ cos \ theta} {1+ \ cos \ theta}}} \ end {align}}}
{\ displaystyle {\ begin {align} \ tan \ left ({\ frac {\ eta \ pm \ theta} {2}} \ right) & = {\ frac {\ sin \ eta \ pm \ sin \ theta} {\ cos \ eta + \ cos \ theta}} = — {\ frac {\ cos \ eta — \ cos \ theta} {\ sin \ eta \ mp \ sin \ theta}}, \\ [10pt] \ tan \ left (\ pm {\ frac {\ theta} {2}} \ right) & = {\ гидроразрыв {\ pm \ sin \ theta} {1+ \ cos \ theta}} = {\ frac {\ pm \ tan \ theta} {\ sec \ theta +1}} = {\ frac {\ pm 1} {\ csc \ theta + \ cot \ theta}}, && (\ eta = 0) \\ [10pt] \ tan \ left (\ pm {\ frac {\ theta} {2}} \ right) & = {\ frac { 1- \ cos \ theta} {\ pm \ sin \ theta}} = {\ frac {\ sec \ theta -1} {\ pm \ tan \ theta}} = \ pm (\ csc \ theta — \ cot \ theta ), && (\ eta = 0) \\ [10pt] \ tan \ left ({\ frac {1} {2}} (\ theta \ pm {\ frac {\ pi} {2}}) \ right) & = {\ frac {1 \ pm \ sin \ theta} {\ cos \ theta}} = \ sec \ theta \ pm \ tan \ theta = {\ frac {\ csc \ theta \ pm 1} {\ cot \ theta} } , && (\ eta = {\ frac {\ pi} {2}}) \\ [10pt] \ tan \ left ({\ frac {1} {2}} (\ theta \ pm {\ frac {\ pi} {2}}) \ right) & = {\ frac {\ cos \ theta} {1 \ mp \ sin \ theta}} = {\ frac {1} {\ sec \ theta \ mp \ tan \ theta}} = {\ frac {\ cot \ theta} {\ csc \ theta \ mp 1}}, && (\ eta = {\ frac {\ pi} {2}}) \\ [10pt] {\ frac {1- \ tan (\ theta / 2)} {1+ \ tan (\ theta / 2)}} & = \ pm {\ sqrt {\ frac {1- \ sin \ theta} {1+ \ sin \ theta}}} \\ [10pt] \ tan {\ frac {\ theta} {2}} & = \ pm {\ sqrt {\ frac {1- \ cos \ theta} {1+ \ cos \ theta}}} \ end {выровнено}} }Как использовать двойные угловые идентификаторы
Использование двойных угловых идентификаторов в тригонометрии
Тождества в математике показывают нам уравнения, которые всегда верны.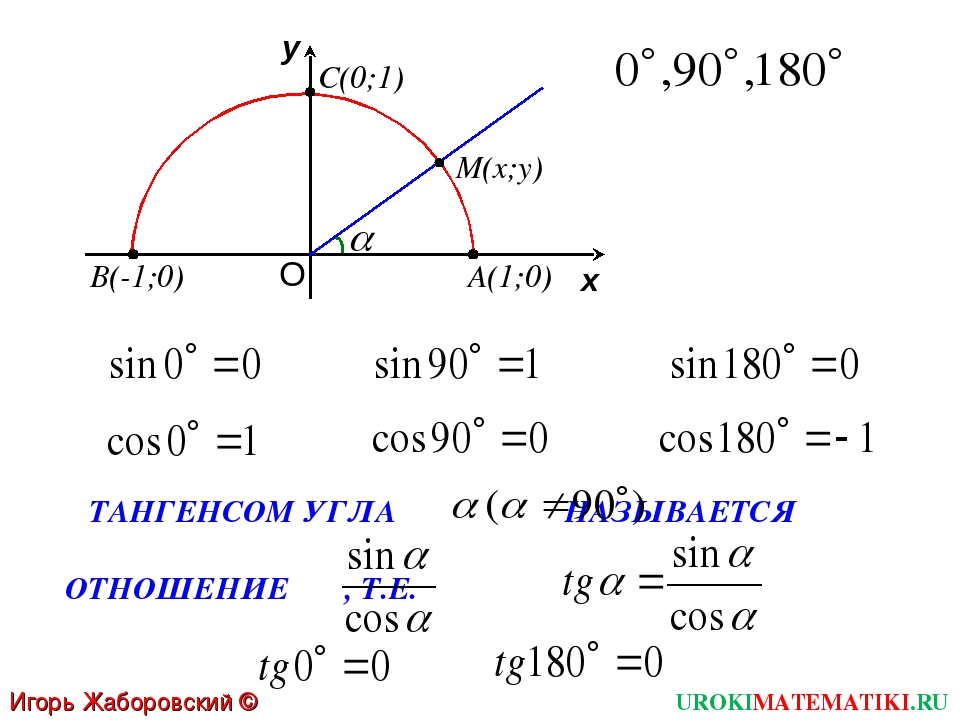 Существует много тригонометрических тождеств (загрузите здесь таблицу тригонометрических тождеств), но сегодня мы сосредоточимся на тождествах с двойным углом, названных из-за того, что они включают тригонометрические функции двойных углов, такие как sinθ \ thetaθ, cos2θ \ thetaθ, и tan2θ \ thetaθ. Без этих формул сложно упростить сложные тригонометрические функции.
Существует много тригонометрических тождеств (загрузите здесь таблицу тригонометрических тождеств), но сегодня мы сосредоточимся на тождествах с двойным углом, названных из-за того, что они включают тригонометрические функции двойных углов, такие как sinθ \ thetaθ, cos2θ \ thetaθ, и tan2θ \ thetaθ. Без этих формул сложно упростить сложные тригонометрические функции.
Как использовать тождества с двойным углом Во-первых, что такое тождество с двойным углом? Давайте посмотрим на таблицу идентичности тригонометрии здесь:
3 основных тригонометрических тождества В некотором смысле, двойные углы синуса и тангенса очень просты, потому что для них есть только одна формула.Косинус 2θ \ thetaθ на самом деле является сложным, потому что, когда вы видите вопрос, вы не знаете, использовать ли первое, второе или третье выражение. Но не беспокойтесь слишком сильно, потому что, поскольку у вас есть три версии косинуса на выбор, вы действительно сможете сделать свой выбор в зависимости от того, какую информацию вам предоставляет проблема и какую из них проще всего применить.
А пока давайте взглянем на некоторые примеры тождеств с двойным углом. Используя приведенную выше шпаргалку по тригонометрическим идентификаторам, мы можем пройти через это руководство по тригонометрическим идентификаторам:
ВопросЕсли вы посмотрите на диаграмму тригонометрических тождеств, вы не найдете числа, за которым следует синус, а затем косинус — ни в частных тождествах, ни во взаимных тождествах, ни в тождествах Пифагора, ни в суммах и различиях тождеств.
двойная угловая идентичность Однако вы можете найти этот образец в двойных углах для синуса. Идентичность двойного угла синуса имеет номер, за которым следует синус, а затем косинус. Теперь мы знаем, что хотим использовать эту формулу для ответа на этот конкретный вопрос. Мы должны изменить формулу, которая нам дана, на то, что мы хотим.Для обеих формул у нас есть синус, косинус, что хорошо. Но число впереди наших проблем — 14, тогда как в тождестве с двойным углом число впереди — 2. Каким должен быть наш следующий шаг? Умножьте все выражение на 7.Это даст нам 7 (sin2θ \ thetaθ). Умножив это на правую часть уравнения, мы получим:
двойной угол идентичности шаг 2 Теперь мы на шаг ближе к решению проблемы. Следующее, что нам нужно сделать, это заменить тэту на 6х.Позволять ? = 6x, что дает нам:
двойной угол идентичности шаг 2 Разве это не именно то, что был задан в первоначальном вопросе? Оказывается, что Вопрос фактически равно 7sin (2 * 6x). Вы только что завершили проверку идентификаторов триггеров с помощью идентификаторов с двойным углом.Это один из примеров доказательств множества тригонометрических тождеств, которые можно решить с помощью тригонометрических тождеств с двойным углом.Калькулятор сумм и разностей
Добро пожаловать в калькулятор сумм и разностей Omni , где мы изучим формулы суммы и разности для всех шести тригонометрических функций, например, формулы сложения синуса или cos . Они могут оказаться чрезвычайно полезными, когда аргумент функции априори не дает простого результата.В таких случаях мы можем выразить угол (а вместе с ним и функцию) как выражение с более подходящими элементами . В зависимости от выбора мы используем формулу суммы или разности, чтобы получить , что-то более простое для обработки .
Будем надеяться, что вычитание и сложение чисел для нас не проблема, поэтому формулы разности углов и суммы углов также не должны быть проблемой . Мы готовы встретиться с ними здесь и сейчас!
Тригонометрические функции
Хотя тригонометрия — это обширная тема с множеством обобщений, мы должны начать с того места, где все начиналось: в Древней Греции .
Хорошо, хорошо, это был , немного преувеличение , но мы не зашли слишком далеко. Ведь именно древних греков мы помним по сей день как тех, кто начал детально изучать математику с формулами и доказательствами . В частности, их внимание привлекла геометрия и изучение треугольников. Примером того, куда их привело это увлечение, является знаменитая теорема Пифагора. И вот здесь начинается наша сегодняшняя история.
Теорема соединяет стороны прямоугольного треугольника простой формулой.Другими словами, он говорит нам, что мир геометрии ни в коем случае не хаотичен: есть правила, которым мы должны следовать . В конце концов, мы легко видим, что если мы возьмем произвольный прямоугольный треугольник и увеличим один из его острых углов, то нам нужно будет соответственно удлинить одну из катетов. Тригонометрия основывается на этом наблюдении.
Тригонометрические функции описывают отношения между сторонами прямоугольного треугольника. Ниже вы можете найти картинку с формулами, определяющими все шесть из них .(Обратите внимание, как мы упоминаем их все в нашем калькуляторе тождеств сумм и разностей.)
Обратите внимание, что в формулах не упоминается размер треугольника . Фактически, в этом и заключается ключевое свойство функций: даже если мы масштабируем фигуру в два раза больше ее размера, значения функции останутся такими же , пока мы сохраняем неизменными углы.
Однако мы начали этот раздел с того, что сказали, что тригонометрия — это обширная тема с множеством обобщений, и здесь, , мы видим существенное препятствие .Действительно, определяя функции в прямоугольном треугольнике, нам требуется аргумент, т. Е. Угол между 0 и 90 градусов (или между 0 и π / 2 в радианы).
Но не бойтесь! Есть способ исправить это и разрешить все возможные углы, даже отрицательные. Единственное, что нам нужно сделать, это перевести все рассуждения в двумерное евклидово пространство , то есть на плоскость.
Пусть A = (x, y) — точка на плоскости. Определите α как угол, идущий против часовой стрелки от положительной половины горизонтальной оси к отрезку линии, конечные точки которого равны (0,0) и A . (Обратите внимание, как мы сказали, что α идет на от одной линии к другой, а не то, что это просто угол между ними. Вот почему мы часто называем α направленным углом .)
Очевидно, что угол α больше 90 градусов.Мы даже можем принять значения больше, чем полный угол 360 градусов — мы просто считаем 360 градусов полным кругом вокруг (0,0) , и с этого момента мы просто начинаем второй. И даже лучше — теперь мы можем понимать отрицательных значений и ! Поскольку мы определили угол α как направленный, мы можем сказать, что отрицательные углы просто меняют направление , то есть идут по часовой стрелке, а не против часовой стрелки.
Для такого произвольного α и точки A = (x, y) , мы расширяем определения всех шести тригонометрических функций , повторяя формулы из рисунка выше, но с некоторыми изменениями: мы подставляем b для x , a для y и c для √ (x² + y²) , т. е. расстояние от (0,0) до A .
В общем, вычисление тригонометрических функций — непростая задача .Обычно для этого мы используем внешние инструменты, поэтому позвольте нам воспользоваться этой возможностью, чтобы направить вас к ресурсам Omni , которые, несомненно, сделают задачу легкой задачей:
Однако, если вы столкнулись с проблемой, связанной с тригонометрическими функциями, и кажется, что поблизости нет Wi-Fi (о, жуткий сценарий , хорошо!), Тогда могут пригодиться некоторые дополнительные формулы . Примером таких тождеств являются тождества половинного угла, формулы уменьшения мощности и, конечно, триггерные тождества суммы и разности .
Формула сложения синуса, формула сложения cos
Формулы суммы и разности позволяют вычислить значение тригонометрической функции, описывая ее в терминах аналогичных функций, но с разными аргументами. По сути, мы берем угол, который мы получили изначально, и разлагаем его на сумму или разность двух других углов . Затем мы можем найти начальное значение, используя вместо него новые и применяя, соответственно, формулу суммы или разности.
Как мы видели в предыдущем разделе, существует шесть тригонометрических функций . Для каждого из них у нас есть одна формула сложения углов и одна формула вычитания углов. В общей сложности это составляет , двенадцать различных (но похожих) сумм и разностных тождеств . Помня об этом, давайте начнем с двух наиболее часто используемых: — формулы сложения синуса и — формулы сложения cos :
. sin (α + β) = sin (α) cos (β) + cos (α) sin (β) , cos (α + β) = cos (α) cos (β) - sin (α) sin (β) . Мы видим, что обе приведенные выше формулы суммы углов разлагают функцию α + β (с которым априори может быть сложно работать с углом) в выражение с α и β отдельно . Также обратите внимание, что формулы сложения cos и синуса используют обе функции. В самом деле, обычно триггерные тождества суммы и разности требуют наличия пары совместных функций в разложении.
В частности, , когда два угла совпадают , т.е.е., когда α = β , формулы сложения cos и синуса дают:
sin (α + α) = sin (α) cos (α) + cos (α) sin (α) , cos (α + α) = cos (α) cos (α) - sin (α) sin (α) .Если упростить обозначения, мы получим то, что часто называют формулами двойного угла:
sin (2α) = 2sin (α) cos (α) , cos (2α) = cos² (α) - sin² (α) , где в формуле косинуса показатель степени относится к значению функции, т. Е. cos² (α) = (cos (α)) ² .
Прежде чем мы закончим этот раздел, давайте применим изящный трюк , чтобы превратить приведенные выше формулы суммы углов в формулы разности углов.В конце концов, мы знаем, что вычитание числа — это то же самое, что прибавление этого числа с перевернутым знаком . Другими словами, мы можем использовать формулы сложения углов в своих интересах и написать:
sin (α - β) = sin (α + (-β)) = sin (α) cos (-β) + cos (α) sin (-β) ,
cos (α - β) = cos (α + (-β)) = cos (α) cos (-β) - sin (α) sin (-β) .
Далее мы можем использовать свойства синуса и косинуса. В частности, напомним, что sin — нечетная функция , а cos — четная .Это означает, что у нас есть sin (-β) = -sin (β) и cos (-β) = cos (β) . Следовательно, приведенные выше формулы дают нам тождества разности sin и cos :
sin (α - β) = sin (α) cos (β) - cos (α) sin (β) , cos (α - β) = cos (α) cos (β) + sin (α) sin (β) .Когда мы смотрим на формулы суммы или разности, мы видим, что меняется только знак в одном из слагаемых . Фактически, трюк, который мы придумали выше, можно применить ко всем формулам сложения углов, чтобы получить их аналоги: тождества вычитания угла .
Ну, раздел называется «Формула сложения синуса , формула сложения cos », но нам также удалось подкрасться в двух формулах разности . Это означает, что за нами стоит треть триггерных тождеств суммы и разницы. Мы более чем готовы перейти к следующему разделу и узнать о других , не так ли?
Прочие триггерные тождества суммы и разницы
Хотя формулы сложения cos и синуса являются наиболее распространенными, другие четыре тригонометрические функции также заслуживают любви .Ниже вы можете найти триггерные тождества суммы и разницы для всех из них. Для полноты картины упомянем также и из предыдущего раздела.
Обратите внимание, что после двух первых функций, становится немного сложнее . Тождества касательной и котангенса суммы и разности триггеров уже требуют некоторых дробей. И если мы посмотрим на формулу суммы или разности для секанса и косеканса, мы увидим , даже худшие выражения с множеством функций, умноженных вместе.
Однако основная идея остается актуальной: справа, α и β появляются отдельно . Также обратите внимание, что для какой бы то ни было функции формула сложения углов отличается от разницы только изменением знаков . Это свойство является прямым следствием того же трюка, который мы использовали в предыдущем разделе, и четности соответствующих функций.
Уф, , кажется, достаточно теории на сегодня , тебе не кажется? Как насчет того, чтобы мы нашли хорошее применение и решили числовой пример для разнообразия?
Пример: использование калькулятора сумм и разностей тождеств
Скажем, , что вы учитель между двумя школьными годами и что вам нужно спланировать, как подготовить класс к временам пандемии.Другими словами, вы должны выяснить, как расположить столы так, чтобы соответствовать новым стандартам , связанным с социальным дистанцированием.
Вы решили придерживаться (примерно) трапециевидной формы с большим количеством учеников в первом ряду и меньшим — в заднем. Однако с вы, кажется, забыли свою измерительную ленту , поэтому придется поступать нестандартно.
Используя обувь и длину шага, вы можете определить приблизительные расстояния между партами.Вы решаете, что угол, по которому вы их выравниваете, должен быть 75 градусов (вы забыли измерительную ленту, но не транспортир!). Кроме того, чтобы все было точным, где-то по пути вы столкнетесь с проблемой , которая найдет косинус угла .
Если есть проблема, есть также решение , и калькулятор сумм и разностей Omni кажется правильным инструментом для работы!
Первая переменная в калькуляторе позволяет нам выбрать функцию, с которой мы имеем дело .Нам нужен косинус, поэтому давайте начнем с выбора косинуса из списка в разделе «, функция ». Затем нам нужны α и β – — два угла, используемые в тождествах сумм и разностей триггеров в соответствии с формулой, показанной над полями переменных.
Наш угол составляет 75 градусов, но у нас нет ограничений на то, как его разложить . Например, мы можем заметить, что 75 = 30 + 45 (ниже мы указываем причину, по которой мы выбрали эти числа).Мы используем это разложение для , применяем формулу сложения углов , поэтому мы вводим в калькулятор сумм и разностей тождеств:
α = 30`, `β = 45 .В тот момент, когда мы введем второе значение , инструмент выдаст ответ . Обратите внимание на то, как калькулятор дает нам пошаговое приложение формулы и автоматически выдает идентичность разницы.
Тем не менее, для пугающих ситуаций, когда поблизости нет Wi-Fi, давайте посмотрим, как найти решение вручную .
Прежде всего, давайте вспомним, что мы хотели бы разложить угол как 75 = 30 + 45 . Чтобы объяснить наш выбор, вспомним, что 30 и 45 градусов появляются в двух очень особых прямоугольных треугольниках. Если быть точным, треугольник 90-60-30 на самом деле является половиной равностороннего треугольника, а 90-45-45 — половиной квадрата.
Это, в частности, сообщает нам точное соотношение между длинами сторон треугольников . И поскольку мы определили тригонометрические функции в первом разделе как отношения между сторонами прямоугольных треугольников, мы можем объединить всю эту информацию и написать:
sin (30 °) = 1 / 2`, `cos (30 °) = √3 / 2 , sin (45 °) = √2 / 2`, `cos (45 °) = √2 / 2 .(Обратите внимание, как точные значения с квадратными корнями также отображаются в калькуляторе тождеств сумм и разностей.)
Наконец, мы вспоминаем формулу сложения cos и применяем ее к нашему случаю:
cos (75 °) = cos (30 ° + 45 °) =
= cos (30 °) cos (45 °) - sin (30 °) sin (45 °) =
= √3 / 2 * √2 / 2 - 1/2 * √2 / 2 =
= √6 / 4 - √2 / 4 ≈
≈ 0,259 .
Вуаля! У нас есть косинус; теперь все должно идти гладко.Будем надеяться, что дети будут постоянно носить маски , чтобы ваши усилия не пропали даром .
далее_тригонометрия
Проект «Улучшение математического образования в школах» (TIMES)
вернуться к индексу
Предполагаемые знания
- Ознакомление с содержанием модуля «Вводная тригонометрия».
- Знакомство с базовой координатной геометрией.
- Учреждение с простой алгеброй, формулами и уравнениями.
- Знакомство с сердами.
Мотивация
В модуле «Вводная тригонометрия» мы показали, что, зная углы и одну сторону прямоугольного треугольника, мы можем найти другие стороны, используя тригонометрические отношения синуса, косинуса и тангенса. Точно так же знание любых двух сторон прямоугольного треугольника позволяет нам найти все углы.
Не все треугольники содержат прямой угол. Мы можем связать стороны и углы в произвольном треугольнике, используя две основные формулы, известные как правило синуса и правило косинуса.
Вооружившись ими, мы можем решить более широкий круг задач в двух измерениях, а также распространить эти идеи на трехмерные задачи. Это важный инструмент для геодезистов и инженеров-строителей.
Вскоре становится очевидным, что в некоторых случаях нам нужно уметь определять тригонометрическое соотношение тупого угла. Это позволяет нам решать более широкий круг задач и приложений. Это также предоставит модель для расширения определения тригонометрических соотношений на любой угол.Эта идея будет рассмотрена в модуле Тригонометрические функции.
Содержимое
В модуле «Вводная тригонометрия — годы 9–10» мы определили три стандартных тригонометрических отношения: синус, косинус и тангенс угла θ, называемого опорным углом,
в прямоугольном треугольнике.
Они определяются по:
sin θ =, cos θ =, tan θ =, где 0 ° <θ <90 °.
Студенты должны тщательно изучить эти соотношения.Одна простая мнемоника, которая может им помочь, — это SOH CAH TOA, состоящая из первой буквы каждого отношения и первой буквы сторон, составляющих это соотношение.
В прямоугольном треугольнике два других угла дополняют друг друга. Как показано на схеме ниже, сторона, противоположная одному из этих углов, примыкает к другому.
Таким образом, можно увидеть, что,
sin θ = cos (90 ° — θ) и cos θ = sin (90 ° — θ), если 0 ° <θ <90 °
Косинус (косинус) назван так, потому что косинус угла является синусом его дополнения.
Эти отношения можно использовать для определения сторон и углов прямоугольных треугольников.
ПРИМЕР
Найдите с точностью до двух десятичных знаков значение местоимения в каждом треугольнике.
Решение
| а | грех 15 ° | = | |
| = | |||
| х | = 8 × sin 15 ° | ||
| ≈ 2.07 | (с точностью до двух десятичных знаков) | ||
| б | cos 28 ° | = | |
| = | |||
| a | = 12.2 × cos 28 ° | ||
| ≈ 10,77 | (с точностью до двух десятичных знаков) | ||
ПРИМЕР
Вычислить значение θ с точностью до одного десятичного знака.
Решение
Обратите внимание, что для 0 Точные значения Тригонометрические отношения для углов 30 °, 45 ° и 60 ° могут быть выражены с помощью сурдов и очень часто встречаются во вводной тригонометрии, в высшей математике и в исчислении.Таким образом, учащимся важно познакомиться с ними. Один из способов быстро их найти — это нарисовать следующие треугольники, а затем просто записать соотношения. Прямоугольный треугольник, содержащий угол 45 °, будет равнобедренным, поэтому мы выбираем две более короткие стороны равными 1 единице в длину и используем теорему Пифагора, чтобы найти гипотенузу. Для углов 30 ° и 60 ° мы начинаем с равностороннего треугольника со стороной 2 единицы длины и опускаем перпендикуляр, как показано.Простая геометрия и теорема Пифагора дают остальную информацию, как показано на диаграмме. Таблица значений теперь может быть заполнена по этим диаграммам. Индексное обозначение В тригонометрии возникает несколько отклонений от обычных индексных обозначений. Студенты могут сначала запутать их. Мы запишем, например, (tan θ) 2 как tan2 θ, (sin θ) 3 как sin3 θ и так далее. Это не следует путать с обратной записью, рассмотренной выше.Мы не пишем, например, Трехмерные задачи Мы можем использовать наши знания тригонометрии для решения задач в трех измерениях. УПРАЖНЕНИЕ 2 Найдите CEG в кубе, показанном ниже. Правило синуса Во многих приложениях мы сталкиваемся с неправильными треугольниками.Мы можем расширить наши знания тригонометрии, чтобы иметь дело с этими треугольниками. Это делается с помощью двух основных формул, первая из которых называется правилом синуса. Предположим, что мы имеем дело с остроугольным треугольником ABC. Как показано на схеме, мы опускаем перпендикуляр CP длиной h из C в AB. Тогда в APC sin A =, поэтому h = b sin A. Аналогично, в CPB sin B =, поэтому h = a sin B. Приравнивая эти два выражения для h, мы получаем b sin A = a sin B, который мы можем записать как =. Тот же результат справедлив для стороны и угла, поэтому мы можем написать Это известно как правило синуса. На словах он говорит: любая сторона треугольника над синусом противоположного угла равна любой другой стороне треугольника над синусом его противоположного угла. Мы скоро увидим, как распространить этот результат на треугольники с тупыми углами. ПРИМЕР В ABC, AB = 9 см. ABC = 76 ° и ACB = 58 °. Найти с точностью до двух десятичных знаков: а AC b BC Решение Подшипники Истинные подшипники были рассмотрены в модуле «Вводная тригонометрия». УПРАЖНЕНИЕ 3 Из точки P, к западу от здания OA, угол подъема вершины A здания OA составляет 28 °. От точки Q на 10 м западнее P угол места составляет 20 °. Нарисуйте диаграмму, а затем используйте правило синуса, чтобы найти расстояние AP и, следовательно, точную высоту здания. Наконец, оцените рост OA с точностью до сантиметра. Нахождение углов Правило синуса можно использовать для определения углов и сторон треугольника.Однако одна из известных сторон должна быть напротив одного из известных углов. ПРИМЕР Предполагая, что все углы острые. Найдите угол θ в треугольнике FGH с точностью до градуса. Решение Как видно из приведенного выше примера, при поиске углов проще записать правило синуса как = перед заменой данной информации. Работа с тупыми углами И правило синуса, и правило косинуса используются для определения углов и сторон треугольников. Что происходит, если один из углов тупой? Чтобы справиться с этим, нам нужно расширить определение основных тригонометрических соотношений от острых до тупых углов. Мы используем координатную геометрию, чтобы мотивировать расширенные определения следующим образом. Мы рисуем единичную окружность с центром в декартовой плоскости и отмечаем точку на окружности в первом квадранте. На показанной диаграмме, поскольку = cos θ, мы можем Следовательно, координаты P равны (cos θ, sin θ). Теперь мы можем перевернуть эту идею и сказать, что Это определение может применяться ко всем углам, как положительным, так и отрицательным, но в этом модуле мы ограничим угол от 0 ° до 180 °. Согласованность определений В модуле Введение в тригонометрию мы определили sin θ = и cos θ =, где 0 ° <θ <90 °. В предыдущем разделе мы определили cos θ = OQ и sin θ = PQ. Мы должны показать, что эти два определения согласуются. На схеме ниже показаны прямоугольный треугольник OAB и треугольник OPQ, оба из которых содержат угол θ.Треугольник OPQ имеет вершину P на единичной окружности. Эти треугольники похожи, поэтому отношение = = PQ, которое является координатой y точки P. Аналогично = = 1, которое является координатой x точки P. Итак, мы показали, что эти два определения совпадают. Углы во втором квадранте В качестве примера возьмем θ равным 30 °, поэтому у него есть координаты (cos 30 °, sin 30 °). Теперь переместите точку P по окружности к P ′ так, чтобы OP ′ образовал угол 150 ° с положительной осью x.Обратите внимание, что 30 ° и 150 ° — дополнительные углы. Координаты P ′: (cos 150 °, sin 150 °). Но мы видим, что треугольники OPQ и OP′Q ′ совпадают, поэтому y-координаты Кроме того, координаты x точек P и P ‘имеют одинаковую величину, но противоположный знак, Из этого типичного примера мы видим, что если θ — любой тупой угол, то его дополнение, sin θ = sin (180 ° — θ), где 90 ° <θ <180 °. Аналогично, если θ — любой тупой угол, то косинус угла θ равен cos θ = −cos (180 ° — θ), где 90 ° <θ <180 °. На словах это говорит: Правило синуса действует также для треугольников с тупым углом. УПРАЖНЕНИЕ 4 Восстановите правило синуса = для треугольника с тупым углом A. Углы 0 °, 90 °, 180 ° Мы можем использовать расширенное определение тригонометрических функций, чтобы найти синус и косинус углов 0 °, 90 °, 180 °. УПРАЖНЕНИЕ 5 Нарисуйте диаграмму, показывающую точки на единичном круге под каждым из указанных выше углов. Используйте координаты для завершения записей в таблице ниже. Тангенс тупого угла Для θ в диапазоне 0 ° <θ <90 ° или 90 ° <θ <180 ° мы определяем тангенс угла θ как tan θ =, для cos θ ≠ 0. В случае, когда cos θ = 0, тангенциальное отношение не определено. Это произойдет, когда θ = 90 °. Если θ находится в диапазоне 0 ° <θ <90 °, это определение согласуется с обычным определением тангенса θ = Следовательно, если θ — тупой угол, то загар θ = (из определения) = (так как θ тупой) = −tan (180 ° — θ) (из определения). Следовательно, тангенс тупого угла является отрицательной величиной тангенса его дополнения. Обратите внимание, что tan 0 ° = 0 и tan 180 ° = 0, поскольку синус этих углов равен 0, и что tan 90 ° не определен, поскольку cos 90 ° = 0. УПРАЖНЕНИЕ 6 Найдите точные значения тангенса угла наклона 150 ° и тангенса угла 120 °. Неоднозначный случай В нашей работе над конгруэнтностью было подчеркнуто, что при применении теста на конгруэнтность SAS рассматриваемый угол должен быть углом между двумя сторонами.Таким образом, на следующей диаграмме показаны два несовпадающих треугольника ABC и ABC ‘с двумя парами совпадающих сторон, имеющих общий (невключенный) угол. Предположим, нам говорят, что треугольник PQR имеет PQ = 9, PQR = 45 ° и PR = 7. Тогда угол, противоположный PQ, не определен однозначно. Есть два несовпадающих треугольника, которые удовлетворяют заданным данным. Применяя правило синуса к треугольнику, получаем = и поэтому sin θ = ≈ 0.9091. Таким образом, θ ≈ 65 °, если предположить, что θ острый. Но дополнительный угол θ ′ = 115 °. Угол PR′Q также удовлетворяет приведенным данным. Эту ситуацию иногда называют неоднозначным случаем. Поскольку сумма углов треугольника равна 180 °, в некоторых случаях только один из двух вычисленных углов является геометрически правильным. УПРАЖНЕНИЕ 7 Найдите значение θ на следующей диаграмме, Правило косинуса Мы знаем из теста на соответствие SAS, что треугольник полностью определен, если нам даны две стороны и включенный угол. Однако, если мы знаем две стороны и включенный угол в треугольнике, правило синуса не поможет нам определить оставшуюся сторону. Вторая важная формула для обычных треугольников — это правило косинусов. Предположим, что ABC — треугольник, а углы A и C острые.Отбросьте перпендикуляр от B к AC и отметьте длины, как показано на схеме. В BDA теорема Пифагора дает с2 = h3 + (b — x) 2. Также в CBD другое применение теоремы Пифагора дает h3 = a2 — x2. Подставляя это выражение для в первое уравнение и раскладывая, Наконец, из CBD, мы имеем x = a cos C и, следовательно, c2 = a2 + b2 — 2abcos C Эта последняя формула известна как правило косинуса. Путем переназначения сторон и угла мы также можем записать a2 = b2 + c2 — 2bc cos A и b2 = a2 + c2 — 2ac cos B. Обратите внимание, что если C = 90 °, то, поскольку cos C = 0, мы получаем теорему Пифагора, и поэтому мы можем рассматривать правило косинусов как теорему Пифагора с поправочным членом. Правило косинуса также верно, когда C тупой, но учтите, что в этом случае последний член в формуле даст положительное число, потому что косинус тупого угла отрицателен.В этом случае следует проявлять осторожность. ПРИМЕР Найдите значение x с точностью до одного десятичного знака. раствор Применяя правило косинуса: х 2 = 72 + 82 — 2 × 7 × 8 cos 110 ° = 151.30 … т. х = 12,3 (с точностью до одного десятичного знака) УПРАЖНЕНИЕ 8 Докажите, что правило косинуса выполняется и в случае, когда C тупой. Нахождение углов Из теста на соответствие SSS мы знаем, что если известны три стороны треугольника, то эти три угла определяются однозначно. Опять же, правило синуса не помогает в их поиске, поскольку требует знания (по крайней мере) одного угла, но вместо этого мы можем использовать правило косинуса. Мы можем подставить три длины сторон a, b и c в формулу c2 = a2 + b2 — 2ab cos C, где C — угол, противоположный стороне c, а затем перестроить, чтобы найти cos C и, следовательно, C. В качестве альтернативы мы можем изменить формулу, чтобы получить cos C = , а затем замените. Студенты могут изменить правило косинуса или выучить другую формулу. Использование этой формы правила косинуса часто снижает арифметические ошибки. Напомним, что в любом треугольнике ABC, если a> b, то A> B. ПРИМЕР Треугольник имеет длину стороны 6 см, 8 см и 11 см.Найдите наименьший угол в треугольнике. Решение Наименьший угол в треугольнике противоположен самой маленькой стороне. Применяя правило косинуса: Удлинение — самая длинная сторона и наибольший угол треугольника В модуле «Конгруэнтность» мы доказали важную взаимосвязь между относительными размерами углов треугольника и относительными длинами его сторон: угол треугольника, противоположный длинной стороне, больше, чем угол, противоположный более короткой стороне. Для разносторонних треугольников это можно переформулировать с точки зрения неравенства всех трех сторон следующим образом: Если ABC — треугольник, в котором a> b> c, то A> B> C. Этот результат можно интересно доказать, используя либо правило синуса, либо правило косинуса. Самая длинная сторона и правило синуса В следующем упражнении используется тот факт, что sin θ увеличивается от 0 до 1, когда θ увеличивается от УПРАЖНЕНИЕ 9 Пусть ABC — треугольник, в котором a> b> c. Самая длинная сторона и правило косинуса В этом упражнении используется тот факт, что cos θ уменьшается от 1 до -1, когда θ увеличивается от 0 ° до 180 °. УПРАЖНЕНИЕ 10 Пусть ABC — треугольник, в котором a> b> c. УПРАЖНЕНИЕ 11 Площадь треугольника В модуле «Вводная тригонометрия» мы видели, что если мы возьмем любой треугольник с двумя заданными сторонами и с заданным (острым) углом θ, то площадь треугольника будет равна Площадь = ab sin θ. УПРАЖНЕНИЕ 12 Выведите эту формулу для случая, когда θ тупой. УПРАЖНЕНИЕ 13 Треугольник имеет две стороны длиной 5 и 4 см, содержащие угол θ. Его площадь 5 см2. Найдите два возможных (точных) значения θ и нарисуйте два треугольника, которые удовлетворяют заданной информации УПРАЖНЕНИЕ 14 Запишите два выражения для площади треугольника и выведите из них правило синуса. Ссылки вперед Правила синуса и косинуса могут использоваться для решения ряда практических задач в области геодезии и навигации. Трехмерные задачи ПРИМЕР Точка M находится прямо через реку от основания B дерева AB. Из точки, расположенной на 7 метров выше по течению от M, угол подъема вершины A дерева составляет 17 °. От точки Q, расположенной в 5 метрах ниже по течению от M, угол подъема вершины дерева составляет 19 °.Предполагая, что PMQ — прямая линия и что дерево находится на берегу реки, Решение В подобных задачах необходимо тщательно составить диаграмму. Пусть BP = a, BQ = b и AB = h, и затем, применив теорему Пифагора к треугольникам Из треугольников ABP и ABQ имеем h = a sin 17 °, h = b sin 19 °. Приравнивая их, подставляя значения a и b и возводя в квадрат, получаем (49 + w2) sin2 17 ° = (25 + w2) sin2 19 ° Теперь мы можем сделать w2 объектом и получить w2 =, так что Примечание. Не оценивайте до последнего шага, чтобы сохранить полную точность калькулятора. Инженеры-строители, анализирующие силы и напряжения в зданиях и других конструкциях, часто используют векторы для представления направления и величины этих сил.Вектор — это стрелка, у которой есть направление и величина. Правила синуса и косинуса используются в векторных диаграммах для нахождения равнодействующих сил и напряжений. Это важное приложение. Тригонометрические идентичности Помимо практического использования, правила синуса и косинуса могут использоваться для получения теоретических результатов, известных как тригонометрические тождества, которые имеют важные последствия и приложения в более поздних работах. Среди них результаты с двойным углом, которые мы опишем ниже. Используя формулу площади A = ab sin C, для треугольника с двумя сторонами a и b, содержащего угол C, мы можем сделать следующее: Зафиксируйте острые углы a и β, пусть угол C = a + β. Из точки C проведите CD длины y и постройте треугольник ABC, как показано на схеме, где BA перпендикулярно CD. Из диаграммы имеем Районы сравнения, ab sin (α + β) = ay sin α + через sin β. Подставляя значение y из (2) в первое слагаемое, а значение из (1) во второе, мы получаем после некоторого упрощения sin (α + β) = sin α cos β + cos α sin β. В приведенном выше обсуждении мы предположили, что α, β — острые углы. Это тождество справедливо для всех Обратите внимание, что sin (α + β) ≠ sin α + sin β. Например, sin (60 ° + 30 °) = sin 90 ° = 1, тогда как УПРАЖНЕНИЕ 15 Используйте приведенную выше формулу, чтобы показать, что точное значение sin 75 ° равно. Полагая α = β = θ в приведенной выше формуле, мы получаем формулу двойного угла sin 2θ = 2sin θ cos θ. Существует аналогичная формула двойного угла для косинуса, cos 2θ = cos2 θ — sin2 θ. Обе формулы чрезвычайно полезны, когда исчисление применяется к тригонометрическим функциям. Углы любой величины и тригонометрические функции В этом модуле мы увидели, как использовать единичную окружность для придания значения синусу и косинусу тупого угла. Это определение можно расширить, включив в него углы более 180 °, а также отрицательные углы. Таким образом, например, если θ находится между 180 ° и 270 °, тогда sin θ = −sin (θ — 180 °) и Как только мы можем найти значения sin θ и cos θ для значений θ, мы можем построить графики функций y = sin θ, y = cos θ. Эти идеи будут развиты в модуле «Тригонометрические функции». Графики функций синуса и косинуса используются для моделирования волнового движения и электрических сигналов. Они являются неотъемлемой частью современной обработки сигналов и телекоммуникаций. Это прекрасный пример того, как простая идея, связанная с геометрией и соотношением, была абстрагирована и превращена в замечательно мощный инструмент, который изменил мир. История В модуле «Вводная тригонометрия» мы упоминали, что у греков была версия тригонометрии, включающая аккорды. Это показано на схеме ниже. На схеме хорда угла — это длина хорды, которая образует угол α в центре окружности радиуса R. Птолемей (85–185 гг. Н. Э.), Который жил и работал в Александрии, написал чрезвычайно влиятельную книгу под названием «Математический синтаксис».Он был переведен на арабский язык и получил арабское название «Альмагест». Птолемей рассматривал хорды, проходящие под углом α на окружности. Используя современные обозначения, если мы возьмем диаметр AB длиной 1 единицу, как показано, и хорду AC, образующую угол α на окружности, то длины AC и BC равны соответственно sin α и cos α. Поскольку углы на окружности, образуемой одной и той же дугой, равны, если α — это угол, образуемый любой хордой в этой окружности, то длина этой хорды всегда равна sin α. Птолемей также показал, что если ABCD — вписанный четырехугольник, то AB.CD + BC.DA = AC.BD. То есть сумма произведений противоположных сторон вписанного четырехугольника равна произведению диагоналей. Этот результат известен как теорема Птолемея. Применяя теорему Птолемея на диаграмме ниже, где круг имеет диаметр 1, мы получаем результат sin (α + β) = sin α cos β + cos α sin β, который мы получили выше. Используя эту и другие формулы, Птолемей смог построить подробную таблицу хорд углов. Поскольку аккорды тесно связаны с соотношением синусов, у него, по сути, была таблица синусов. Правило синусов в круге Дан треугольник ABC, мы можем нарисовать его описанную окружность с диаметром BD, как показано. Пусть 2R — диаметр описанной окружности. Тогда для острого α синус угла BDC равен sin BDC = sin α =. Перестановка дает = 2R. Таким образом, в правиле синусов все величины и равны диаметру описанной окружности треугольника ABC. Региомонтан (1436–1476), написавший первую современную европейскую книгу по тригонометрии, включил в свою работу правило синуса и его вывод. Правильная пентаграмма и правильный пятиугольник Правильная пентаграмма и правильный пятиугольник всегда были источником восхищения и часто используются в астрологии.Он основан на треугольнике, свойства которого исследуются в следующем упражнении. УПРАЖНЕНИЕ 16 Начнем с равнобедренного треугольника с углами 72 °, 72 °, 36 °, как показано. Этот треугольник Возьмем точку D на AB так, что BDC = 72 °.Наконец, положим BC = 2x. a Покажите, что информация, указанная на схеме, верна. b Докажите, что треугольники ABC и CDB подобны. c Выведите, что =, и решите это уравнение, чтобы получить x = — 1. d Опустив перпендикуляр от A к BC, покажите, что cos 72 ° =. e Используйте тождество cos2 θ + sin2 θ = 1, чтобы показать, что sin 72 ° =. Ответы к упражнениям Упражнение 1 а -1 б 50 (+ 1) Упражнение 2 тан-1 ≈ 35.26 ° с точностью до двух десятичных знаков. Упражнение 3 AP = 24,57… м и OA = 11,54 м с точностью до см. Упражнение 4 Пусть CAM = θ Следовательно, CAB = 180 ° — θ h = b sin θ (треугольник CAM) и h = a sin B (треугольник CAB) отсюда и результат. Упражнение 5 sin 0 ° = 0, sin 90 ° = 1, sin 180 ° = 0 cos 0 ° = 1, cos 90 ° = 0, cos 180 ° = -1 Упражнение 6 -, — Упражнение 7 sin − 1 ≈ 22,62 ° (с точностью до двух десятичных знаков). Две стороны и прямой угол образуют уникальный треугольник (правое совпадение). Упражнение 8 В треугольнике BCM h3 = a2 — (c + MA) 2 В треугольнике CMA, h3 = b2 — MA2 Следовательно, a2 — (c + MA) 2 = b2 — MA2 a2 = b2 + c2 + 2c × MA Но MA = b cos (180 ° — A) = — b cos A Следовательно, a2 = b2 + c2 — 2bc cos A Упражнение 9 a sin A> sin B> sin C (если a> b и a sin B = b sin A, то sin A> sin B b Согласно замечанию в начале этого абзаца, A> B> C. c Углы P и Q складываются с θ, потому что сумма углов треугольника равна 180 °. d Из части c тупой угол равен A, который, следовательно, является наибольшим из трех углов. Упражнение 10 c Из a> b> c> 0 следует, что ab> c2 и a3> b3.Следовательно, cos B> cos A. d Аналогичный аргумент доказывает, что cos C> cos B, поэтому cos C> cos B> cos A. Согласно замечанию в начале этого абзаца, A> B> C. Упражнение 11 a Пусть ABC находится под прямым углом в C. Тогда AB2 = AC2 + BC2. Следовательно, AB2 больше, чем AC2 и BC2, поэтому AB длиннее, чем AC и BC. b В прямоугольном треугольнике два других угла острые, потому что сумма углов треугольника равна 180 °.Следовательно, прямой угол — это самый большой угол. Упражнение 12 Мы используем ту же диаграмму, что и для доказательства тупого угла правила синуса и косинуса. Указанный результат получается симметрией аргумента. Упражнение 13 θ = 30 ° или 150 ° Упражнение 14 Для данного треугольника ABC cb sin A = ca sin B.Следовательно, bsin A = asin B и =. Упражнение 15 Упражнение 16 b Треугольник ABC похож на треугольник CDB (AA) c = d cos B = e sin2 B = 1 — = Проект «Улучшение математического образования в школах» (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
sin-2 θ для (sin θ) -2, так как это могло бы спутать обычное значение индексов с обратными.
Теперь мы можем использовать правило синуса для решения простых задач геодезии, включающих неправильные треугольники.
видеть, что координата x точки P равна cos θ. Аналогично,
, координата y точки P равна sin θ.
, если θ — это угол между OP и положительной осью x, то:
точки P на единичной окружности и
P на единичной окружности.
P и P ′ совпадают. Таким образом, грех 150 ° = грех 30 °.
, поэтому cos 150 ° = −cos 30 °.
180 ° — θ является острым, а синус θ равен θ 0 ° 90 ° 180 ° sin θ cos θ
объясняя, почему ответ уникален. c2 = a2 — x2 + (b — x) 2 = a2 — x2 + b2 — 2bx + x2 = a2 + b2 — 2bx. 62 = 82 + 112 — 2 × 8 × 11 × cos θ cos θ = = и т. Д. θ ≈ 32.2 (с точностью до одного десятичного знака)
0 ° до 90 °.
=.
.
, мы хотим найти ширину реки w метров.
BMP и BMQ, получим a =, b =.
w ≈ 8,66 м с точностью до 2 десятичных знаков. = cos α => y = a cos α (1) и = cos β => y = b cos β (2).
α и β, но чтобы показать это, требуется другой подход.
sin 60 ° + sin 30 ° = ≠ 1.
для синуса, а именно
cos θ = −cos (θ — 180 °).
естественным образом встречается как внутри правильного пятиугольника, так и внутри правильной пентаграммы.
Для простоты вычислений мы берем две равные стороны равными 4 единицам в длину. Следовательно, a sin B = b sinθ = b sin (180 ° — A) = b sin A так =
Следовательно, P и Q меньше θ, поэтому sin P и sin Q меньше sin θ = sin P.
Следовательно, sin B> sin C, где B и C являются острыми, поэтому A> B> C. б Условия группировки, cos B — cos A = = = Площадь = c × h = cb sin θ = cb sin A

 Углы в угловых градусах и минутах.
Углы в угловых градусах и минутах. Значит, знак будет плюс;
Значит, знак будет плюс; Его мы разобрали выше, он равен минус синусу. \(\cos(\frac{3π}{2} — a)=-\sin{a}\)
Его мы разобрали выше, он равен минус синусу. \(\cos(\frac{3π}{2} — a)=-\sin{a}\) Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки.
Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки. \((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) .
\((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) .