Формулы круга: Формулы, как найти площадь круга

Содержание

Площадь круга: как ее найти по формулам

Содержание

Поиск площади круга – стандартная задача. Обычно, она задается школьникам в шестом классе, помогает мягко перейти к изучению более сложных примеров из тригонометрии.

В этом материале мы расскажем о том, как найти площадь круга с помощью формулы, обратим внимание на основные определения, отличия которых важно понимать учащемуся. Уже через непродолжительное время тренировок, вы сможете полностью освоить все методы решения задач и получать высокие оценки на уроке.

Важные определения

Прежде чем отвечать на вопрос о том, как найти площадь круга по радиусу или диаметру по формуле, нужно установить основные определения. Мы будем пользоваться следующими терминами:

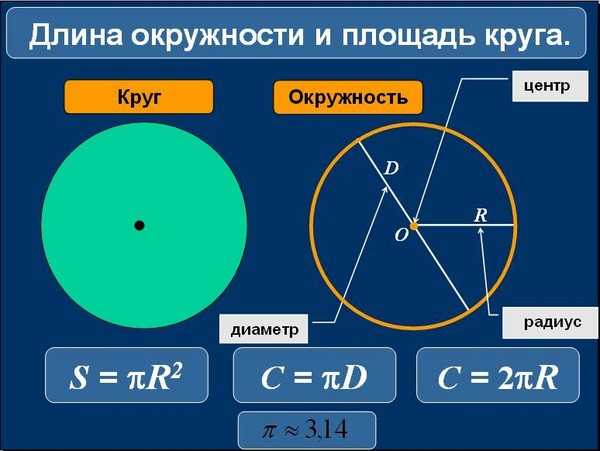
Круг. Так называют замкнутую плоскую кривую, в которой каждая точка имеет равное удаление от центральной.
Окружность. Это сразу множество точек, которые располагаются на плоскости. При этом расстояние удаления от центра не будет превышать диаметр.
Радиус. Расстояние от центра круга до любой его противоположной боковой точки.
Диаметр. Полное расстояние от двух точек, расположенных на равном удалении друг от друга.

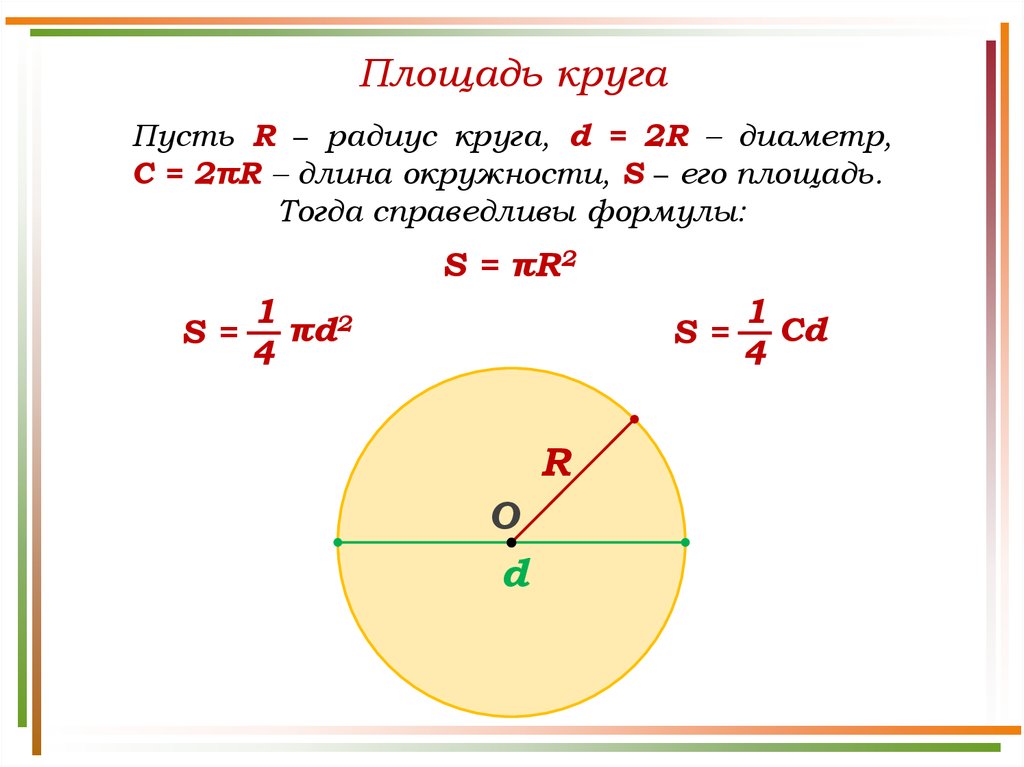
Как найти площадь круга по диаметру: формула

Формула поиска площади для диаметра будет выглядеть так:

S = d2 : 4 × π.

Здесь:

S – площадь.
d – диаметр.
π – константное число, которое в математических расчетах принимается как 3,14.

Как найти площадь круга по радиусу: формула

Ищем итоговое значение также по формуле. Это S = π × r2. За число π берем константу 3,14. R – это радиус круга.

Как найти площадь через длину окружности: формула

В математике иногда встречаются задачи, в которых известна длина окружности. В таком случае для решения нужно будет использовать стандартную формулу S = L2 : (4 × π).

Здесь L – это и есть площадь окружности.

Как ускорить процесс обучения: советы специалистов

Есть несколько простых рекомендаций, которые помогают значительно ускорить учебный процесс, помогают быстрее освоиться с тем, как искать площадь круга по разным известным параметрам.

К ним относятся такие, как:

Убедитесь в том, что ребенок хорошо понимает основные определения. Педагогическая практика показывает, что дети часто путают радиус и диаметр, что приводит к появлению ошибок и выставлению низких оценок учителями.
В геометрии очень важна наглядность. Все задачи стоит решать исключительно вместе с рисунками круга на бумаге. Это также поможет ребенку значительно быстрее освоиться с использованием циркуля, линейки. Такие навыки сильно помогут в учебе в будущем.
Не показывайте ученику своего непонимания предмета. Он всегда должен видеть в вас человека, который обладает уверенными знаниями по такому вопросу. Не стоит демотивировать его, рассказывать о бесполезности расчетов.
Хорошее понимание предмета достигается исключительно через многократное решение задач. Их вы сможете без труда составить своими силами. Все что нужно – ставить условие поиска площади с разными исходными параметрами – длиной окружности, диаметром, радиусом и другими.

Усложните задачи через введение разных параметров обозначения площади. Есть множество вариантов прописывания площади – это квадратные сантиметры, миллиметры, метры, дециметры и километры. Хорошей математической тренировкой станет перевод разных значений друг в друга. Также можно попробовать посчитать в гектарах. Все это помогает в таких предметах, как геометрия, тригонометрия и математика.

Почему важно тренироваться в решении задач с площадью круга

Мы рассмотрели, как найти площадь круга по формуле. Осталось только ответить на вопрос о том, почему понимание этого вопроса представляет такое большое значение для школьника. Вот лишь несколько важных причин:

Лучшее понимание геометрических терминов. Их проще всего освоить на практике. Это пригодится при решении значительно более сложных задач в старших классах.

Освоение единиц определения площади, решение примеров по переводу величин друг в друга. Это поможет в геометрии и математике. Можно воспользоваться умственным счетом или абакусом, что дополнительно повысит успешность всего учебного процесса.
Создание базиса для решения комплексных геометрических задач. Они часто направлены на то, чтобы ученик работал с разными фигурами. При этом если пропустить понимание определения площади, радиуса и диаметра круга, длины окружности, в будущем могут возникнуть проблемы, отставание от программы.

Так как в школе дети часто не понимают таких сложных предметов как геометрия до конца, рекомендуем уделить повышенное внимание домашним занятиям. Это нужно делать регулярно и системно, но без сильного давления на школьника, потенциально способного отбить интерес к учебе.

Понравилась статья? Расскажите друзьям:

Спасибо, что оставили заявку

Мы скоро свяжемся с вами!

Подпишитесь на группу ВКонтакте

SmartyKids

§ Круг. Площадь круга

Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара

Прежде чем определится, как рассчитать площадь круга, необходимо хорошо усвоить и понять в чём разница между окружностью и кругом. Что называется окружностью, а что подразумевают под словом круг.

Важно!

Замкнутая кривая (линия), чьи точки лежат на одинаковом расстоянии от одной точки её центра, называется

окружностью.

Окружность разбивает плоскость на две области: внутреннюю и внешнюю.

Важно!

Та часть плоскости, которая лежит внутри окружности (вместе с самой окружностью) называется кругом.

Другими словами, для простоты понимания, следует запомнить:

окружность — это замкнутая линия ( граница круга).
круг — это внутренняя область окружности.
У окружности нельзя посчитать площадь! А у круга найти площадь, зная формулу, достаточно легко.

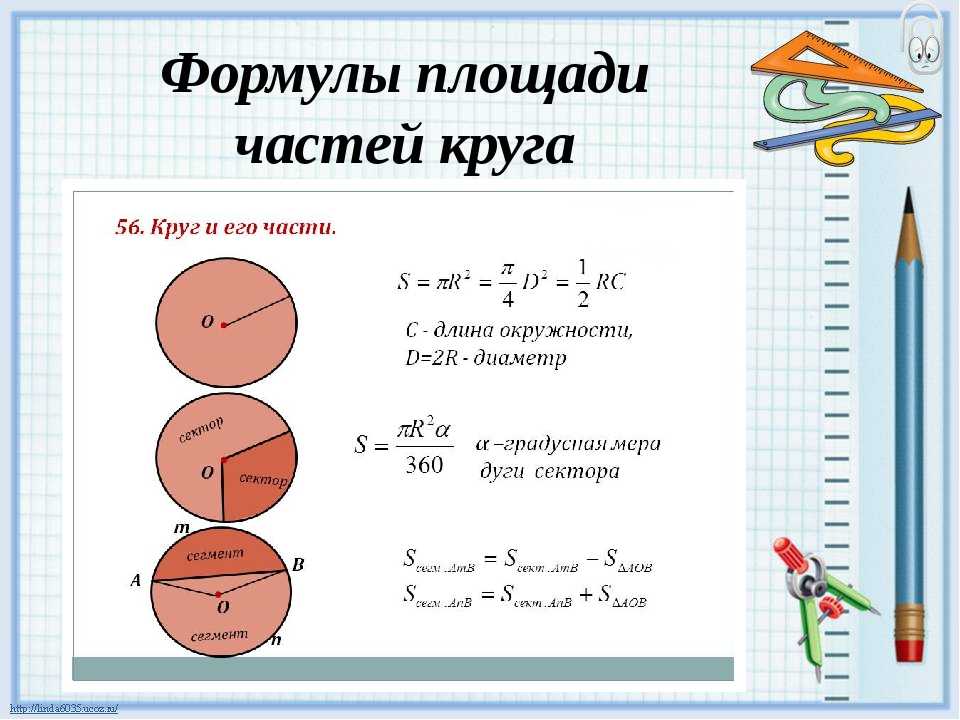
Как найти площадь круга

Запомните!

Для расчета площади круга используется формула:

S = πR², где R — радиус круга,
S = π ()² = π = π , где D — диаметр круга, т.к. R =

Как решать задачи на площадь круга

Теперь, зная, по какой формуле считается площадь круга, решим задачи на площадь круга.

Зубарева 6 класс. Номер 675(г)

Условие задачи:

Найдите площадь круга, радиус которого равен 1,2 см.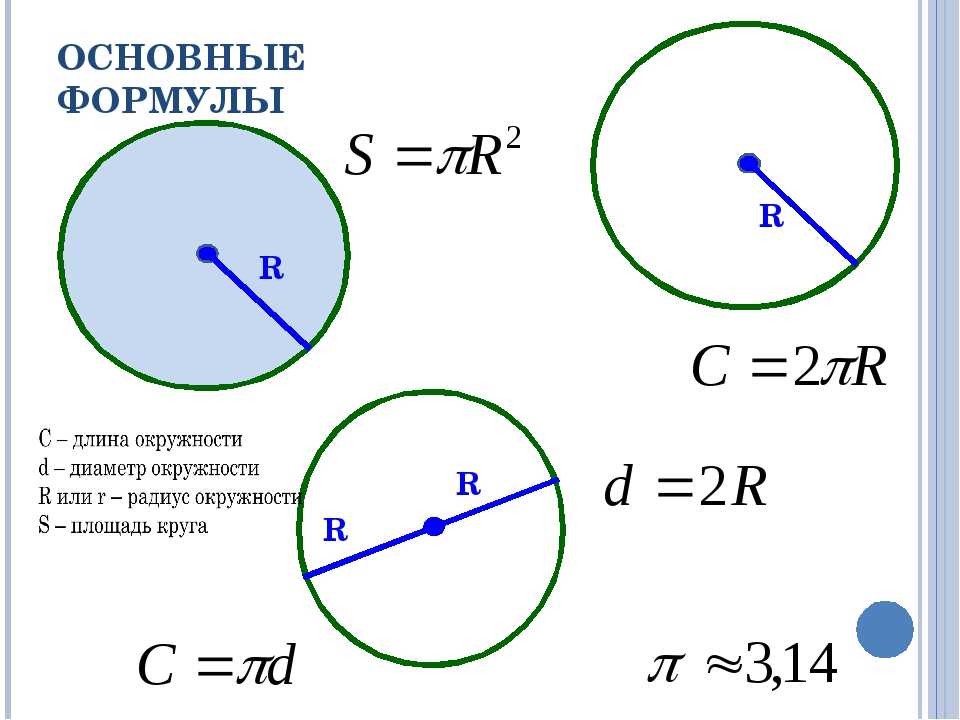

Воспользуемся формулой площади круга:
S = πR² = 3,14 · 1,2² = 3,14 · 1,44 = 4,5216 см²

Обратите внимание, что площадь измеряется в квадратных единицах. Всегда проверяйте свои ответы, правильно ли вы указали единицы измерения.

Зубарева 6 класс. Номер 677(б)

Условие задачи:

Определите радиус круга, площадь которого равна 1,1304 см

Выразим из формулы радиус:
S = πR²
R = √ S / π = √ 1,1304 / 3,14 = √ 0,36 = 0,6 см

Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:


Отправить

Формула, примеры и многое другое —

Если вы хотите получить высший балл по математическим разделам SAT или ACT, вам нужно кое-что знать о кругах.

Хотя вопросы по кругам не составляют большую часть вопросов SAT или ACT по математике, вы должны ожидать, что в тесте вы увидите их небольшое количество. Когда вы стремитесь к 99-му процентилю, каждый вопрос имеет значение. Таким образом, вы должны быть знакомы с тем, как вычислять площадь, длину окружности, радиус, диаметр, градусы, дуги и точки окружности.

В этом руководстве вы найдете всю необходимую информацию о кружках, чтобы вы могли ответить на все вопросы, связанные с кружками, с которыми вы столкнетесь в день экзамена.

Что такое круг?

Хотя это может показаться очевидным, очень важно, чтобы вы точно знали, что такое круг, прежде чем сдавать SAT или ACT.

Под окружностью понимаются определенные точки на плоскости, равноудаленные от одной точки, называемой центром окружности.

Этот набор точек образует замкнутую круглую двухмерную форму, которую мы называем кругом.

Ключевые термины

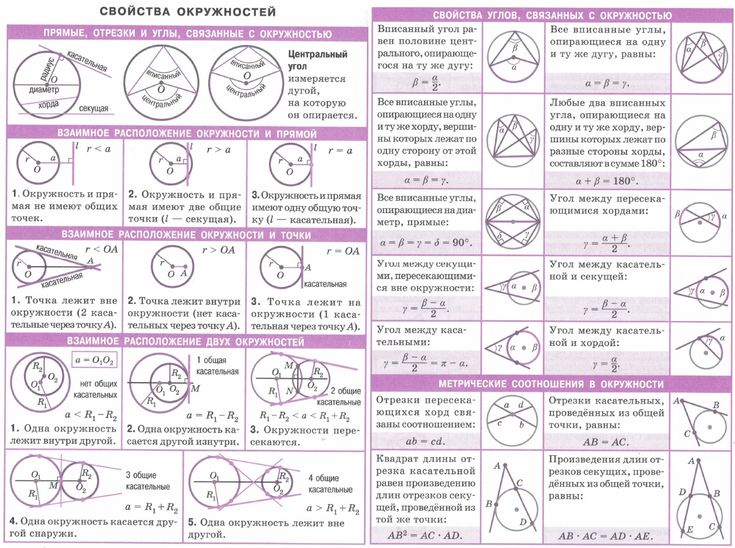
Есть несколько терминов, которые вам необходимо знать об окружностях, прежде чем вы начнете измерять их или использовать любые другие формулы окружности:

Окружность (c): расстояние вокруг окружности
Дуга: изогнутая часть окружности, лежащей между двумя заданными точками
Диаметр (d): длина отрезка, обозначающего наибольшее расстояние между двумя точками на окружности
Радиус (r): длина отрезка, соединяющего центр окружности с заданной точкой на окружности (половина диаметра)
Пи (π): число Пи, приблизительно эквивалентное 3,1415926, представляет собой отношение длины окружности к ее диаметру. на разделах SAT и ACT по математике.
Измерение окружности
Круги можно измерять в двух разных единицах измерения: радианах и градусах.
Радиан — это единица измерения угла. Когда дуга окружности имеет ту же длину, что и радиус той же окружности, угол этой дуги эквивалентен одному радиану.
Хотя вам нужно будет узнать о радианах для геометрии и других математических занятий, вы не будете часто использовать это измерение на SAT или ACT.
На стандартизированных тестах вы в основном будете полагаться на степени.
Окружность 360 градусов. Чтобы измерить часть круга, вам нужно будет увидеть, как эта часть вписывается в отведенные 360 градусов.
Например, если вы пытаетесь измерить угол дуги для одной половины круга, вы должны взять 360 градусов и разделить его пополам, чтобы получить 180 градусов. Точно так же, если бы вы пытались измерить угол дуги для четверти окружности, вы бы взяли 360 градусов и разделили их на 4, чтобы получить 9. 0 градусов.
Помните, что полный круг всегда равен 360 градусам, и вы сможете легко измерить дуги.
Ключевые формулы
Теперь, когда вы знаете ключевые термины, а также различные способы измерения окружности, вы сможете понять важные формулы окружности, которые вам необходимо знать для SAT и ACT.
Хотя эти ключевые формулы будут предоставлены вам, я рекомендую вам запомнить их, чтобы вам не пришлось тратить свое ограниченное время на пролистывание справочного раздела во время теста.
Область
Если вас попросили найти площадь круга, используйте эту формулу:
- A = πr ²
ARC
При измерении окружности дуги вы будете нужно взять градус дуги и разделить его на 360 (общее количество градусов в окружности). Затем вам нужно умножить это число на число Пи и диаметр круга. Вы можете использовать приведенную ниже формулу:
- c дуга = πd (градус дуги/360)
Вам также нужно знать, что количество радиан дуги в окружности равно 2π
Окружность
Чтобы найти длину окружности, вы можете использовать любую из этих двух формул:
- c=2πr
- c=πd
круг, помните, что это представляет собой максимально длинный отрезок линии между двумя заданными точками на окружности.
Вы можете рассчитать диаметр по следующей формуле:
- d=2r
Уравнение окружности
Уравнение окружности рассчитывается по этой формуле:
- (x-h) ² + (y-k) ² = r ²
В этой формуле (h,k) — это координаты центра окружности.
Примеры вопросов
Вот пример вопроса, с которым вы можете столкнуться на SAT (взято из пробного теста Совета колледжей):
Найдите минутку и попробуйте решить этот вопрос самостоятельно.
Готово?
Если вы выбрали вариант «А», вы правы!
Поскольку в этом вопросе указаны координаты центра круга (0,4), уравнение для круга будет (x-0) ² + (y-4) ² = r ²
Используя эту формулу и формулу расстояния с учетом конечной точки (4/3, 5), вы получите r ² = 25/9 .
Это сделало бы вариант «А» единственно возможным вариантом ответа.
Вот еще один пример вопроса:
Найдите время, чтобы ответить на этот вопрос, и посмотрите на ответ ниже, когда будете готовы.
Вы должны были выбрать вариант «А» для этого вопроса.
Вот почему (согласно совету колледжей): Круг имеет дугу 360 градусов. В показанном круге O — центр круга, а угол AOC — центральный угол круга. Из рисунка видно, что два диаметра, образующие угол AOC, перпендикулярны, поэтому угол AOC равен 9.0 градусов. Этот центральный угол пересекает меньшую дугу AC, что означает, что меньшая дуга AC имеет 90 градусов дуги. Поскольку длина окружности всего круга равна 36, длина малой дуги AC равна 90/360 x 36=9.
Если вы пропустили один (или оба) из этих вопросов, вам не о чем беспокоиться. С правильными ресурсами вы можете улучшить свои знания об кругах и других математических концепциях, которые появятся на SAT и ACT.
Вы можете узнать больше о кругах и различных формах, с которыми вы столкнетесь в математических разделах SAT и ACT, когда будете проходить подготовительные курсы через Prep Expert. На наших подготовительных курсах вы можете узнать советы и рекомендации по запоминанию формул, а также стратегии решения других математических вопросов, которые вы встретите в день экзамена.
Узнайте больше о Prep Expert или запишитесь на один из наших курсов подготовки к SAT или ACT сегодня, когда вы посетите наш веб-сайт.
3. Круг | Площадь круга
Формулы окружности:
Площадь окружности
Диаметр окружности
Длина окружности
Прежде чем мы перейдем к различным формулам для круга. Давайте быстро определим, что такое круг на самом деле и почему это важно. Открытый справочник по математике определяет круг как;

«Линия, образующая замкнутый контур, каждая точка которого находится на фиксированном расстоянии от центральной точки.»
Однако, если вы будете искать вокруг, вы найдете различные исследования и определения, которые затруднят понимание того, как точно определить круг. Мы разбираем различные определения в нашей статье Что такое круг? Мы можем упростить приведенное выше определение круга до;
Окружность представляет собой набор точек, равных по радиусу (радиусу) от фиксированной точки (центральной точки) на плоскости.
Теперь, когда у нас есть заданное определение круга, давайте быстро определим переменные, участвующие в формулах круга.
Площадь круга (переменная: A ) — площадь внутри круга.
Окружность (переменная:
C ) — периметр окружности.
Пи (переменная: π ) — это расстояние от центра круга до любой точки на окружности.
Радиус (переменная: r ) — это расстояние от центра окружности до любой точки на окружности.
Диаметр (переменная: d ) — это расстояние, проходящее через центр окружности, от любой точки окружности до другой противоположной точки окружности, или, другими словами, равно удвоенному радиусу окружности. .
С этим фундаментальным пониманием мы теперь можем решать различные формулы круга.
а. Формулы круга
Площадь круга
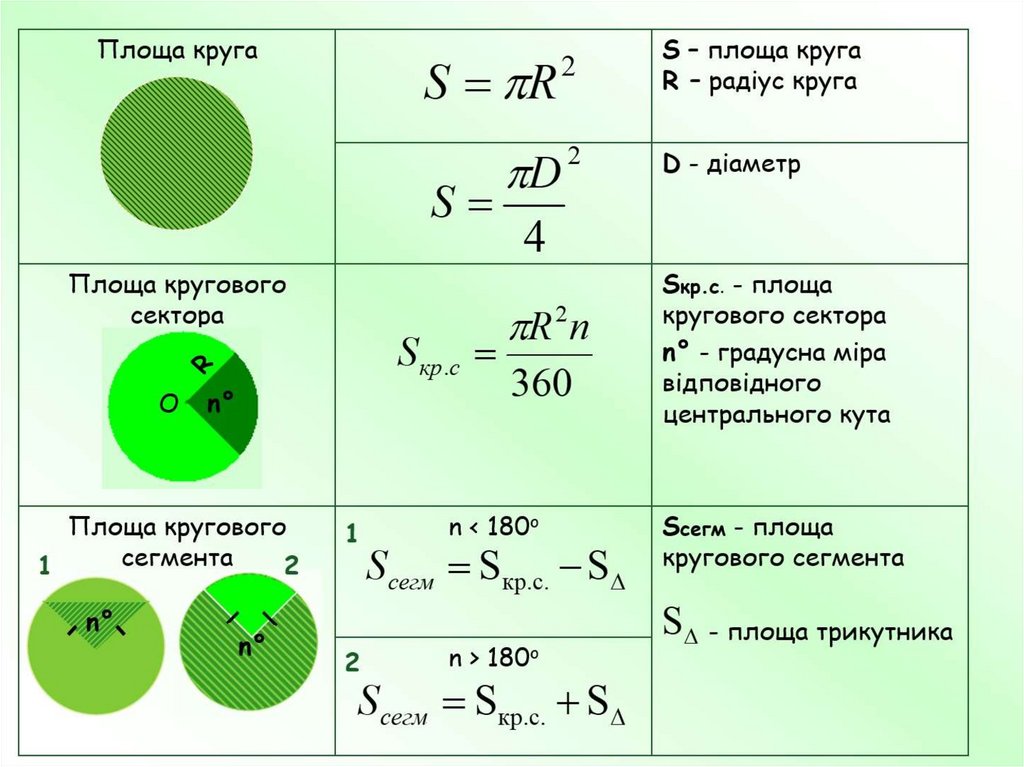
Формула площади круга может быть выражена следующим образом:
А = π r ²
Определение площади круга — полезный инструмент для измерения пространства внутри окружности круга.
Разобьем уравнение и определим переменные. Площадь круга представлена как A . С другой стороны уравнения имеем π (Пи) умножить на r ² (радиус) в квадрате.
Обычная мнемоника для запоминания этой формулы, которую вы выучили в школе: «Пирог в квадрате» . Повторите это несколько раз, чтобы убедиться, что вы можете быстро вспомнить его, чтобы вычислить площадь круга в следующем тесте!
Пример того, как найти радиус ( r ) в области формулы круга, можно найти в нашем уроке Основы алгебры — 5. Формулы и буквенные уравнения.
Диаметр круга
Формула диаметра круга может быть выражена следующим образом:
Д = 2 р
Как упоминалось выше, диаметр круга просто в два раза больше длины радиуса круга. Это самое длинное расстояние между двумя точками на окружности.
Окружность круга
Формула длины окружности может быть выражена следующим образом:
С = 2 π r
Длину окружности можно найти, умножив π на радиус r . Окружность так же важна, как и площадь уравнения окружности в реальной жизни. Представьте, что вы стоите на краю круглого катка, вы можете прокатиться от края к центру катка, чтобы найти радиус, и, продолжая движение к противоположному краю, вы можете найти диаметр. Теперь, зная, что число Пи равно π = 3,14 теперь вы можете решить все формулы круга и найти площадь, диаметр и окружность катка.
Теперь мы можем перейти к более сложным формулам окружности.
Центр в начале координат
xy(0, 0)(r, 0)rОткрыть изображение на новой странице
Окружность, центр (0, 0), радиус r .
Окружность с центром (0, 0) и радиусом r имеет уравнение:
х ² + у ² = р ²
Это означает, что любая точка ( x , y ) на окружности даст квадрат радиуса при подстановке в уравнение окружности.
Центр не в начале координат
xy(h, k)rОткрыть изображение на новой странице
Окружность, центр ( h , k ), радиус r .
Окружность с центром ( h , k ) и радиусом r имеет уравнение:
( х − h ) ² + ( y − k ) ² = r ²
Эти формулы являются прямым следствием формулы Пифагора для длины гипотенузы прямоугольного треугольника.
Нужна миллиметровка?
Значок миллиметровки
Скачать миллиметровку
Пример 1
Эскиз окружности x ² + y ² = 4.
Сначала найдите центр и радиус.
Ответить
Уравнение имеет вид x ² + y ² = r ² , поэтому у нас есть круг с центром (0, 0) и радиусом `r=sqrt4 =2`.
12-1-212-1-2xyОткрыть изображение на новой странице
Окружность, центр (0, 0), радиус 2.
Пример 2
Нарисуйте окружность ( x − 2) ² + ( y − 3) ² = 16
Сначала найдите центр и радиус.
Ответ
Уравнение имеет вид ( x − h ) ² + ( y − k ) ² = r 9006 2 2 , поэтому у нас есть круг с центром в (2 , 3) и радиус `r=sqrt(16)=4`.
123456-1-2-312345678-1xy(2, 3)r = 4Открыть изображение на новой странице
Окружность, центр (2, 3), радиус 4.
Пример 3
Нарисуйте окружность ( x + 4) ² + ( y − 5) ² = 36
Ответ
Уравнение имеет вид ( x − h ) ² + ( y − k ) ² = r 9006 2 2 .
У нас есть круг с центром в точке (−4, 5) и радиусом `r=sqrt(36)=6`.
-5-10510xy(−4, 5)r = 6Открыть изображение на новой странице
Окружность, центр (−4, 5), радиус 6.
Будьте осторожны с положительными и отрицательными и -значения в этой работе!
б. Общая форма круга
Уравнение, которое можно записать в следующем виде (с константами D , E , F ), представляет собой круг :
x ² + y ² + Dx + Ey + F = 0
Это называется общей формой круга .
Пример 4
Найти центр и радиус окружности
х ² + у ² + 8 х + 6 у = 0
Нарисуйте круг.
Ответить
Пожалуйста, пересмотрите Завершение Квадрат сначала…
Наша цель состоит в том, чтобы получить уравнение в виде: ( x − h ) ² + ( y − k ) ^{2 9006 3 = г ²}
Завершаем квадрат на х 92`
Теперь это в нужном нам формате, и мы можем определить центр и радиус круга.
Таким образом, центр круга равен (−4, −3), а радиус равен 5 единицы измерения.
2-2-4-6-8-1024-2-4-6-8xy(−4, −3)r = 5Открыть изображение на новой странице
Окружность, центр (−4, −3), радиус 5.
Обратите внимание, что окружность проходит через (0, 0). Это логично, так как:
Круг имеет радиус 5
Рассматривая прямоугольный треугольник, образованный точками (−4, −3), (0, −3) и (0, 0), мы можем применить теорему Пифагора и получить: (−4) 92`
Нет необходимости расширять это, так как это наиболее полезная форма уравнения.
2. Определите центр и радиус, а затем нарисуйте окружность:
3 x ² + 3 y ² − 12 x + 4 = 0
Ответить
Мы завершаем квадрат , как мы это делали в предыдущем примере выше.
Сначала собираем детали х вместе и 2=8/3`
Таким образом, у окружности есть центр `(2,0)` и радиус `sqrt(8/3)~~1,63`.
123412-1-2xyОткрыть изображение на новой странице
Окружность, центр (2, 0), радиус 1,63.
3. Найдите точки пересечения окружности
x ² + y ² − x − 3 y = 0
со строкой
у = х — 1,
Ответить
92-3x+2=0`
`(х-1)(х-2)=0`
Итак, мы видим, что решения для x равны `x = 1` или `x = 2`. Это дает соответствующие y-значения ‘y = 0’ и ‘y = 1’.
No related posts.