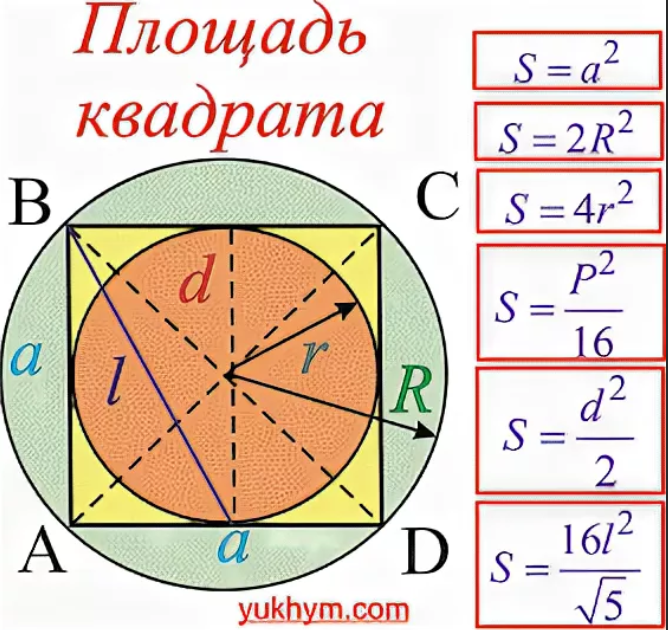
Вычисляем площадь квадрата: по стороне, диагонале, периметру
Площадь квадрата – базовое понятие, благодаря которому можно без проблем рассчитать расход материалов для ремонта, высчитать верные габариты мебели при замерах помещения, понять, сколько нужно удобрения и семян для высадки важных культур на огромном поле.
Приведенными формулами площади квадрата пользуются и строители, и мебельные производители, и представители сельского хозяйства.
Что такое квадрат?
Квадрат – правильный прямоугольник с равными сторонами. Каждый угол фигуры равен 90⁰. Квадрат относится к простым геометрическим фигурам, расположенным на плоскости. Найти площадь квадрата можно несколькими способами вычислений: по диагонали, по стороне, по периметру.
Формулы площади, примеры расчетов
Площадь простой фигуры – положительная величина, обладающая перечисленными ниже свойствами:
- Равные геометрические фигуры обладают равными площадями.
- В случае, если простая фигура разделена на несколько частей, ее общая площадь будет всегда равна сумме площадей всех элементов.

- Площадь квадрата всегда равна единице, если его сторона соответствует единице измерения.
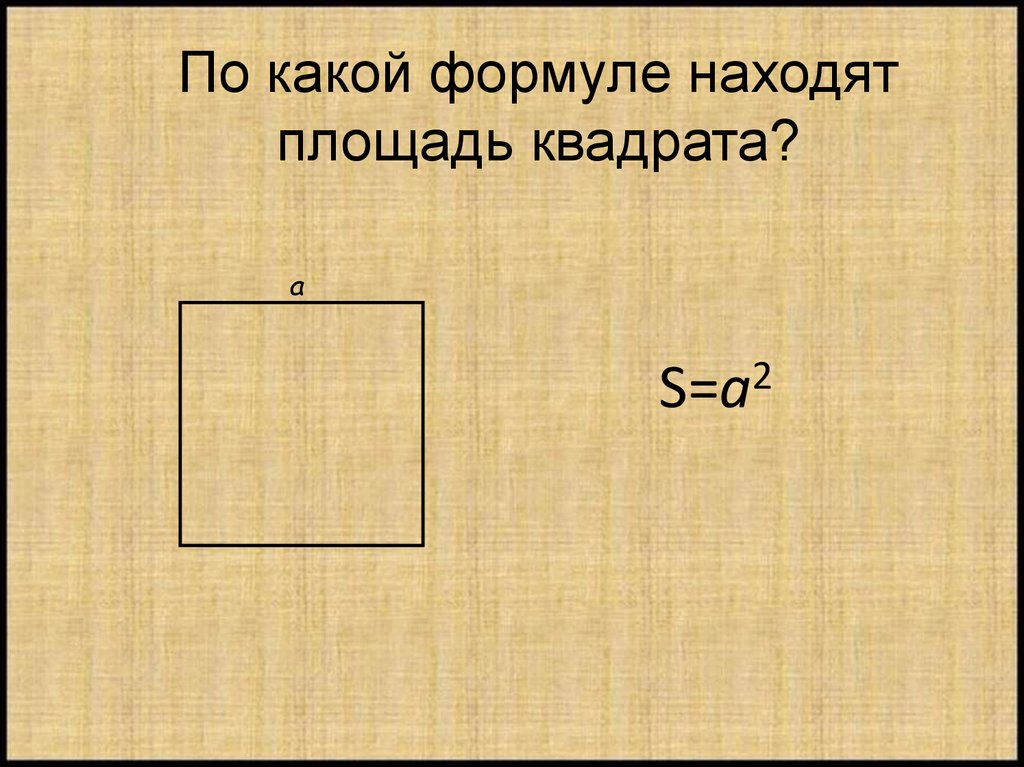
По стороне
В геометрии площадь всегда обозначается как S, а маленькие латинские буквы (например, а и b) – это стороны простой фигуры.
В основе вычисления площади любого прямоугольника по стороне лежит простая формула: S = ab , но в случае с квадратом формулу преобразовывают в S = а² , так как две стороны одинаковы по длине.
Отсюда следует утверждение, что площадь квадрата равна квадрату его стороны.
Пример 1: Дан квадрат, сторона которого равна 5 см. Чему равна площадь?
Решение: S = 5² = 25 см
Пример 2: Сторона фигуры 3 см. Найдите площадь.
Решение: S = 3² = 9 см
По диагонали
Еще один вариант найти площадь – это произвести вычисления относительно диагонали фигуры (d). Правда, для этого нужно сперва найти длину самой диагонали. Известно, что диагональ делит квадрат на два равнобедренных треугольника. А значит, вычисления можно провести по известной теореме Пифагора, где катетами будут выступать стороны квадрата, а гипотенузой – собственно диагональ.
А значит, вычисления можно провести по известной теореме Пифагора, где катетами будут выступать стороны квадрата, а гипотенузой – собственно диагональ.
Расчет площади по диагонали производится по принципу: площадь квадрата равна квадрату длины диагонали (вычисленной по теореме Пифагора) и поделенному на два.
Пример: Дан квадрат, диагональ которого составляет 10 см. Как вычислить площадь?
Решение: Согласно формуле, приведенной выше, вычисления производятся так: S = 10²/2 = 100/2 = 50 cм²
По периметру
Периметр – сумма всех длин сторон квадрата. Обозначается периметр латинской буквой Р. Беря во внимание определение квадрата, получаем универсальную формулу расчета периметра для равностороннего четырехугольника: Р = 4а . То есть, периметр квадрата равен длине стороны, помноженной на четыре.
Вычисления площади квадрата относительно суммы всех сторон необходимо в том случае, если в задаче задано только значение периметра.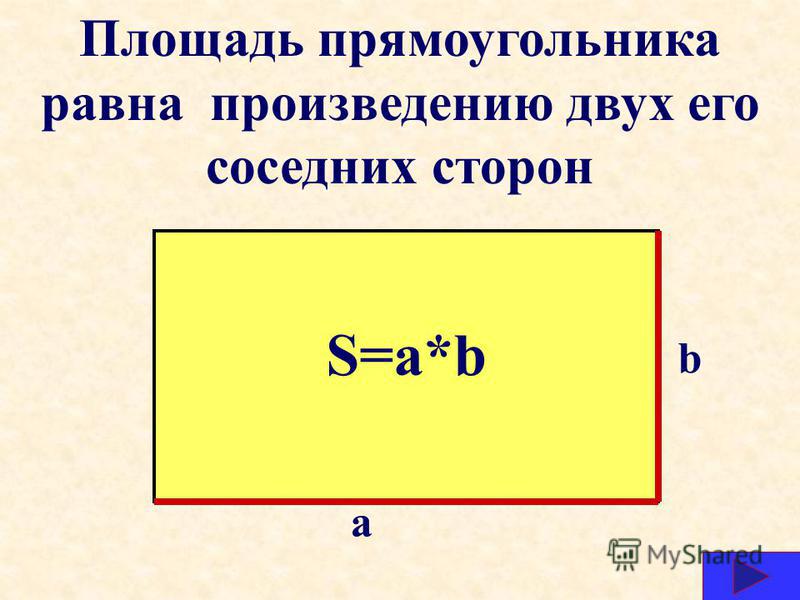 Зная формулу вычисления периметра, очень легко найти площадь.
Зная формулу вычисления периметра, очень легко найти площадь.
Если Р = 4а , то а = Р/4 . Далее уже нужно использовать формулу расчета площади по стороне.
Пример: Пусть будет дан квадрат с периметром 100 мм. Какова площадь?
Решение: Сторона квадрата будет равна 100/4 = 25 мм. Ну, а площадь квадрата дальше вычисляется по формуле, где площадь квадрата равна квадрату сторон. То есть, S = 25² = 625 мм²
Площадь квадрата вписанного в окружность
Этот вариант используется как следствие формулы, полученной ранее (расчет по диагонали). Согласно математическим данным, диаметр круга как раз и будет равен диагонали квадрата. Поэтому, чтобы оперативно рассчитать площадь равностороннего четырехугольника, достаточно будет знать диаметр круга. А далее используется уже известная формула: S = d²/2
Типовая задача: например, дана окружность с диагональю 8 см и в нее вписан квадрат. Какая площадь четырехугольника?
Правильное решение: S = 8²/2 = 64/2 = 32 cм²
Видео урок
youtube.com/embed/n2DuIBjJFIo» frameborder=»0″ allowfullscreen=»»>Формулы площадей квадрата и прямоугольника
Период изучения темы: Декабрь.
Слайд 2.
Цели: Изучить формулы площади прямоугольника и площади квадрата. Познакомиться со свойствами равных фигур. Научиться применять понятие площади. Формировать умения отвечать на вопросы. Закрепить умения использовать формулы при решении задач.
Слайд 3.
Оргмомент.
– Ребята, давайте проверим нашу готовность к уроку.
(У каждого должны быть: дневник, тетрадь, учебник, ручка, карандаш, линейка, тетрадный лист, ножницы).
Слайд 4.
Актуализация знаний.
– Какие изученные сведения нам сегодня пригодятся? (Понятия площади, стороны квадрата, единицы измерения площадей, действия сложения, вычитания, умножения, деления, степень числа).
– Что изучали на прошлом уроке? (Формулы).
– Какие? (Пути, периметра квадрата, периметра прямоугольника, учились определять стороны квадрата и прямоугольника, зная их площади).
– Что называют формулой? (Запись правила с помощью букв).
– А всякое ли правило можно записать формулой? (Нет, например, на уроках русского языка, там используют схемы).
Слайд 5.
Подведение к изучению нового материала.
– Какие формулы площади изучены нами на прошлом уроке? (Квадрата и прямоугольника).
– Какие действия надо выполнять, пользуясь этими формулами? (Находить степень числа, действия умножения, деления).
– Что можно найти с помощью указанных действий? (Делением – сторону прямоугольника или квадрата, сложением – периметр, вычитанием – сторону прямоугольника, умножением – площадь).
– Каким справочным материалом можно воспользоваться в классе? (Таблицами квадратов и кубов натуральных чисел – на переднем форзаце учебника).
Слайд 6.
Устно.
Вычислить (№ 382-а,б, стр. 63)16*5 : 8 * 19 + 6 |
100 – 19 : 3 + 23 * 4 |
196 |
200 |
Слайд 7.
Найти соответствия:
Слайд 8.
Вычислить:
Слайд 9.
Есть ли среди этих фигур прямоугольники? Как называются эти фигуры?
Слайд 10.
Изучение темы.
– Какова же тема сегодняшнего урока? Помогите, ребята, соберите разбежавшиеся буквы в слово! («Формулы площадейквадрата и прямоугольника»).
Слайд 11.
– А какие площади мы будем изучать? Найдите формулы.
– Но всегда ли сразу можно найти площадь фигуры? (Нет).
– Почему? (Не все фигуры имеют форму квадрата или прямоугольника).
– Подумайте, что для этого можно сделать? (Для этого фигуру удобно разделить на квадраты со стороной 1 см. Найти площадь одного квадрата, затем сложить полученные площади, или умножить площадь одного квадратика на количество таких квадратов).
Слайд 12.
– Оцените площадь такой фигуры? (7 см2).
Слайд 13.
– Возьмём несколько фигур (на партах у ребят комплекты раздаточного материала – готовых фигурок).
Найдите срединих равные.
Как?
Докажите. (Подсказка: а как – об этом написано в учебнике на странице 108, снизу 7 строка). Ребята работают в группе, находят пары равных фигур. В четырёх парах по две одинаковые фигуры и одна пара с разными фигурами, видят, где одинаковые, а где неодинаковые, и объясняют, почему. При этом повторяют буквы латинского алфавита и вспоминают произношение на английском языке.
(Подсказка: а как – об этом написано в учебнике на странице 108, снизу 7 строка). Ребята работают в группе, находят пары равных фигур. В четырёх парах по две одинаковые фигуры и одна пара с разными фигурами, видят, где одинаковые, а где неодинаковые, и объясняют, почему. При этом повторяют буквы латинского алфавита и вспоминают произношение на английском языке.
Слайд 14.
– А что будет, если мы разрежем фигуру на части? (Каждая часть станет меньше всей фигуры).
– А площадь останется такой же или изменится?Сравните. Проверьте. Докажите.(Дети разрезают данные им фигурки на части.Делают вывод, сравнивают с текстом учебника на странице 108, снизу 1 строка).
– А возможно ли найти площади фигур, полученных из прямоугольника? Длину и ширину, зная площадь прямоугольника?
– Какие фигуры получатся, если провести диагональ прямоугольника? (Треугольники).
– Что такое диагональ?(Отрезок, соединяющий противолежащие углы).
– Какие это треугольники? (Прямоугольные).
– А равны ли они между собой? (Да).
– Докажите, что они равны, не применяя вычислений? (Разрезать прямоугольник по диагонали, полученные треугольники наложить друг на друга, они совпадают).
Слайды 15, 16.
– Что же тогда можно сказать про площадь прямоугольного треугольника? (Площадь прямоугольного треугольника равна половине площади прямоугольника, из которого он получен). Ученики проверяют свой вывод на модели и по учебнику на странице 109.
Слайд 17.
Закрепление.
– Какие формулы изучили?
– Какие понятия? (стр. 108-109).
Слайд 18.
– Творческое задание. Из данных фигур получите прямоугольники (на столах у каждого учащегося лежит одна из фигур, можно добавить другие).
Слайд 19.
Решение с комментариями.
– Страница 109: устно № 709, 710, 711, 712.
– В тетради и у доски: № 717, 720.
– В тетрадях с комментариями: № 715, 719.
– Самостоятельно: № 716.
Слайд 20.
Запись домашнего задания.
П. 18, стр. 108-109 (учить), № 738, 740, КРО № 737 – с объяснением.
Слайд 21.
Рефлексия. Подведение итогов урока.
– Было ли интересно на уроке? Понятен ли материалурока? Чувствуете ли усталость, удовольствие от своей работы?
Самооценка.
– Оценки за урок: «5» – , «4» – , «3» – (с согласия учащихся выставляются в журнал).
Приложение.
Как вычислить квадратные футы с помощью математики
Обновлено 19 декабря 2020 г.
Автор: Лиза Мэлони
Если вы когда-либо измеряли длину, ширину или высоту чего-либо, вы измеряли в одном измерении. Как только вы объединяете любые два из этих измерений, вы говорите о концепции, называемой площадью, или о том, сколько места занимает фигура в двухмерном пространстве. Точное вычисление площади крайне неправильных форм может потребовать передовых математических методов, таких как исчисление. Но для более распространенных геометрических фигур, таких как круги, прямоугольники и треугольники, вы можете найти площадь с помощью нескольких простых формул.
Точное вычисление площади крайне неправильных форм может потребовать передовых математических методов, таких как исчисление. Но для более распространенных геометрических фигур, таких как круги, прямоугольники и треугольники, вы можете найти площадь с помощью нескольких простых формул.
Предупреждения
Прежде чем приступить к расчету площади, обратите внимание: все измерения должны выполняться в одних и тех же единицах измерения. Поэтому, если вы рассчитываете площадь в квадратных футах, все необходимые измерения должны быть указаны в футах. Если вы рассчитываете площадь в квадратных дюймах, все измерения должны быть указаны в дюймах и так далее.
Квадратные футы Формула для прямоугольников и квадратов
Если фигура, которую вы рассматриваете, является квадратом или прямоугольником, найти площадь так же просто, как умножить длину на ширину. В пересчете на футы эта формула пригодится для всего: от измерения площади газона до расчета размеров комнат в вашем доме.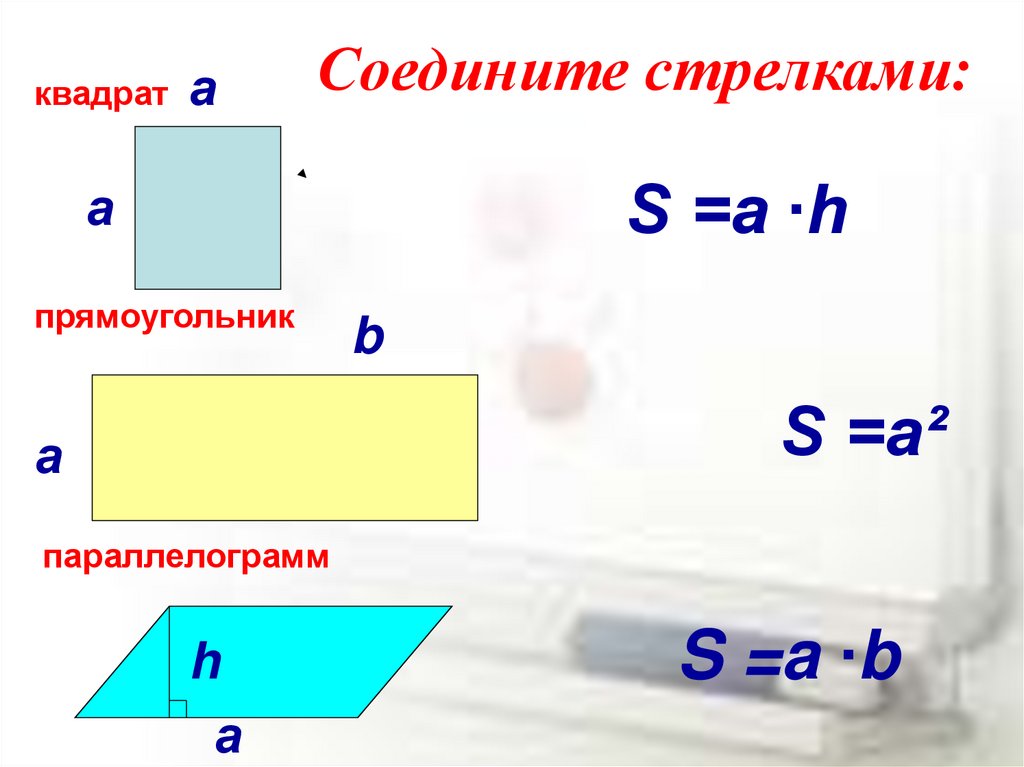 92
92
Если вы вычисляете площадь прямоугольника, вы должны использовать эту формулу. Если вы вычисляете площадь квадрата, у вас есть два варианта: либо использовать эту формулу, либо использовать свои знания о том, что все четыре стороны квадрата имеют одинаковую длину, чтобы составить еще более простую формулу:
Площадь квадрата = длина 2 , где длина — это длина любой стороны квадрата.
Вычисление квадратных футов параллелограмма
Нет необходимости вводить размеры параллелограмма в калькулятор площади квадратных футов; Вы можете вычислить площадь самостоятельно, умножив основание параллелограмма на его высоту.
Формула:
\text{ площадь} = \text{ основание} ×\text{ высота}
Пример: Какова площадь параллелограмма с основанием 6 футов и высотой 2 фута ? Подстановка данных в формулу дает:
6 \text{ футов} × 2 \text{ футов} = 12 \text{ футов}^2
Нахождение площади треугольника
Для треугольников также существует формула квадратных футов, и это всего на один шаг больше, чем нахождение площади параллелограмма.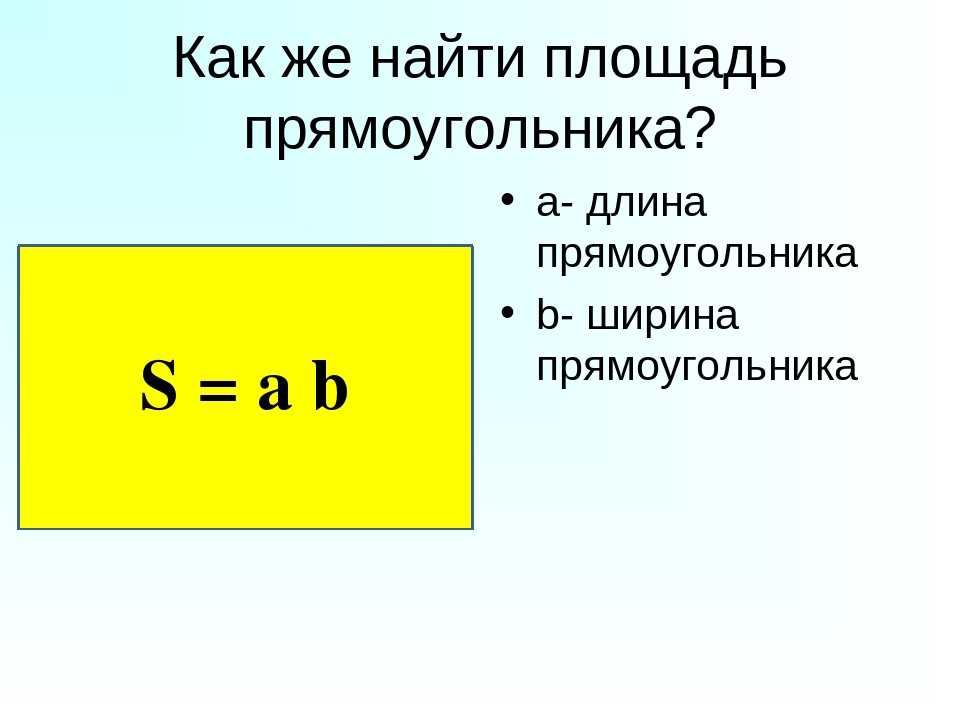
Формула:
\text{ площадь} = \frac{1}{2}\text{ основание} × \text{ высота}
Пример: Представьте, что вы столкнулись с треугольник с основанием 3 фута и высотой 6 футов. Какова его площадь? Применение этой информации к формуле дает вам:
92Итак, площадь вашего круга равна 12,56 фута в квадрате.
Площадь квадрата — введение, формула, примеры
Площадь квадрата определяется как количество квадратных единиц, необходимых для заполнения квадрата.
В общем, площадь определяется как область, занимаемая внутри границы плоского объекта или двумерной фигуры.
Измерение производится в квадратных единицах, стандартной единицей измерения являются квадратные метры (м2).
Для вычисления площади существуют предопределенные формулы для квадратов, прямоугольников, кругов, треугольников и т. д.
В этой статье вы узнаете о площади квадрата. Присоединяйтесь к онлайн-школе Safalta School и подготовьтесь к экзаменам на совет директоров под руководством наших опытных преподавателей.
Цифровой маркетингГрафический дизайнMS Excel (10 часов)Курс подготовки к собеседованиюПрограмма предпринимательстваНаписание контента Программа «Чемпион» (средний язык хинди) Группа биологии Программа чемпиона 12-го класса (средний английский язык) Группа математики Группа 12-го класса Программа чемпиона (средний английский язык) Группа биологии Программа чемпиона 10-го класса (средний язык хинди) Программа чемпиона 10-го класса (средний английский язык)
Бесплатные демонстрационные занятия
Зарегистрируйтесь здесь, чтобы получить бесплатные демонстрационные занятия
Выберите категориюНавыкиПравительствоАкадемические науки
Выберите курс
Пожалуйста, заполните имя
Пожалуйста, введите только 10-значный номер мобильного телефона
Пожалуйста, выберите курс
Пожалуйста, заполните адрес электронной почты
Что-то пошло не так!
Загрузите приложение и начните обучение
Источник: Safalta.com
Наша онлайн-школа призвана помочь учащимся подготовиться к экзаменам на совет директоров, обеспечив учащимся концептуальную ясность по всем предметам и возможность набрать максимальные баллы на экзаменах.
Что такое площадь?
Площадь — это пространство, занимаемое объектом. Это область, занятая любой формой. При измерении площади квадрата учитывают только длину его стороны. Все стороны квадрата равны, следовательно, его площадь равна квадрату стороны.
Точно так же мы можем найти площадь других фигур, таких как прямоугольник, параллелограмм, треугольник или любой многоугольник, исходя из его сторон.
Площадь поверхности рассчитывается на основе радиуса или расстояния ее внешней линии от оси для криволинейных объектов поверхности.
Пример: окружность
Формула площади квадрата
Прежде чем перейти к формуле площади квадрата, используемой для вычисления занимаемой области, давайте попробуем использовать миллиметровую бумагу. Требуется найти площадь стороны 5 см. Используя этот размер, начертите на миллиметровой бумаге квадрат размером 1 см × × 1 см. Квадрат покрывает 25 полных квадратов.
Таким образом, площадь квадрата равна 25 квадратных см, что можно записать как 5 см × 5 см, то есть сторона × сторона.
Из приведенного выше обсуждения можно сделать вывод, что формула может дать площадь квадрата:
Площадь квадрата = сторона × сторона
Следовательно, площадь квадрата = сторона2 квадратных единиц
и периметр квадрата = 4 × единицы стороны
Здесь приведены некоторые списки преобразования единиц измерения для справки. Некоторые преобразования единиц измерения-
- 1 м = 100 см
- 1 кв. м = 10 000 кв. см
- 1 км = 1000 м
- 1 кв. км = 1 000 000 кв. м
Площадь квадрата Примеры
Пример 1. Найдите площадь буфера обмена, сторона которого равна 1 см.
Решение:
Сторона буфера обмена = 120 см = 1,2 м
Площадь буфера обмена = сторона × сторона
= 120 см × 120 см
= 14400 кв. См
= 1,44 С. Св. м
Пример 2. Сторона квадратной стены равна 75 м. Какова стоимость покраски в размере 5000 руб. 3 на кв.м?
Сторона квадратной стены равна 75 м. Какова стоимость покраски в размере 5000 руб. 3 на кв.м?
Раствор :
Сторона стены = 75 м
Площадь стены = сторона × сторона = 75 м × 75 м = 5625 кв.м
За 1 кв.м стоимость покраски = рупий 3
Таким образом, для 5625 кв.м стоимость покраски = руб. 3 × 5625 = 16875
Пример 3 : Пол двора длиной 50 м и шириной 40 м должен быть покрыт квадратной плиткой. Сторона каждой плитки равна 2 м. Найдите количество плиток, необходимое для покрытия пола.
Решение :
Длина этажа = 50 м
Ширина этажа = 40 м
Площадь пола = длина × ширина = 50 м × 40 м = 2000 кв. м
3 Сторона одной плитки = 2 мПлощадь одной плитки = сторона × сторона = 2 м × 2 м = 4 кв. м
Необходимое количество плиток = площадь пола/площадь плитки = 2000/4 = 500 плиток
Как известно, квадрат — это двумерная фигура с четырьмя сторонами.