Формулы объемов: Формулы объема и программы для расчета объема

Решение задач на объем шара и его частей 11 класс онлайн-подготовка на Ростелеком Лицей

Повторение

 

Рассмотрим решение различных задач на объем шара и его частей. Напомним формулу объема шара:

 

Рис. 1 Формулы объёмов шара и сегмента

, а также объема сегмента: . (См. Рис. 1.)

На самом деле формулу объема сегмента помнить не обязательно, т. к. ее можно выводить с помощью интеграла, если вы помните.

 

Задача 1

 

 

Диаметр Луны составляет приблизительно четверть диаметра Земли. Какую часть объема Земли составляет объем Луны, если считать их шарами? (См. Рис. 2.)

 

Рис. 2 Земля и Луна

Решение. Раз диаметры отличаются в  раза, то и радиусы в  раза, то есть  (см. Рис. 3).

Рис. 3 Радиусы

Мы увидели, что если измерения некоторой фигуры изменить в  раз, то объем данной фигуры изменится в  раз. В данном случае измерение увеличили в  раза, значит, объем увеличился в  раза.

Ответ: .

 

Задача 2

 

 

Во сколько раз увеличится масса металлического шарика, если увеличить его радиус в два раза? Предполагается, что оба шарика сплошные и состоят из одинакового материала.

 

Рис. 4 Иллюстрация к задаче 2

Решение

По определению , тогда .

Раз материалы одинаковые (плотности шаров равны), то . При этом , а тогда по формуле . То есть , а значит, и массы отличаются в  раз.

Ответ: в  раз.

Важное следствие: если измерения фигур изменить в  раз, то не только объем, а и масса данной фигуры изменится в  раз при условии, что объекты однородны и состоят из одного и того же самого материала.

 

Задача 3

 

 

 

 

Рис. 5 Три сплошных металлических шарика и полученный новый
Радиусы трех сплошных металлических шариков равны ,  и  см соответственно. Эти шарики расплавили и из получившегося металла отлили новый сплошной шар. Чему будет равен его радиус? (См. Рис. 5.)

Решение. Раз масса не изменилась, а плотность одинаковая, то . Сокращаем на  и получаем, что объем нового шара будет равен сумме объемов исходных. Имеем: 

Сократим на :

 cм.

Ответ:  см.

 

Задача 4

 

 

Сколько кубометров земли потребуется для устройства клумбы, имеющей форму шарового сегмента с радиусом основания  м и высотой  см? (См. Рис. 6.)

 

Рис. 6 Шаровой сегмент

Решение

  м,  см  м. Как мы знаем, по формуле:

.

 

Рис. 7 Иллюстрация к обозначению переменных
Найдем радиус шара. Пусть он равен . Тогда имеем прямоугольный треугольник  ( – центр шара,  – центр сечения,  – точка на границе сечения), , ; . (См. Рис. 7.)

По теореме Пифагора:

м.

Осталось подставить это в формулу:

.

Ответ:.

 

Задача 5

 

 

Найти радиус шара, если известно, что его объем равен объему цилиндра с осевым сечением, имеющим форму квадрата со стороной .

 

Рис. 8 Иллюстрация условия задачи 5

Решение. Рассмотрим цилиндр из условия.
, . Значит,
(см. Рис. 9).

Рис. 9 Цилиндр из условия

С другой стороны, .

Приравнивая, имеем:

Ответ: .

 

Заключение

 

 

Сегодня мы решили ряд задач, которые используют формулы объема шара и объем сегмента, увидели, как эти формулы работают на практике, и выяснили связь между объемом и массой.

 

 

Список литературы

1. Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.

2. А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002. В.Ф. Бутузов, Ю.А. Глазков. Рабочая тетрадь по геометрии 11 класс.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт fxyz.ru (Источник)

2. Интернет-сайт math34.ru (Источник)

3. Интернет-сайт «Математика? Легко!» (Источник)

 

Домашнее задание

1. Шар радиуса  пересечен плоскостью на расстоянии  от центра. Найдите площадь сечения.

2. Металлический шар радиуса  переплавили в конус, высота которого – . Найдите отношение площади боковой поверхности конуса к площади его основания.

3. Радиусы трех шаров равны , и . Найдите радиус шара, объем которого равен сумме объемов данных шаров.

 

Презентации формулы объемов многогранников и тел вращения. Тела вращения Объёмы тел вращения

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №4»

Подготовила:

учитель математики

Федина Любовь Ивановна.

г. Исилькуль 2014г

Тема урока » Объемы многогранников и тел вращения»

Цели:

Обобщить и систематизировать знания учащихся по теме урока;

Закрепить вычислительные и начертательные навыки учащихся;

Развить мышление, логические способности, умение работать с геометрическим материалом, читать чертежи, работать по ним;

Воспитать чувство ответственности, сплоченности, сознательной дисциплины, умения работать в группе;

Привить интерес к изучаемому предмету.

Тип урока: урок-обобщение

Технология: личностно-ориентированная, проблемно-исследовательская, критического мышления.

Форма проведения:

Оборудование: линейка, ручка, карандаш, листочки с заданиями,
фигуры конусов, цилиндров, призм и пирамид, чертежи геометрических тел на листах формата А4 + скотч, раздаточный материал

План урока.

Организационный момент. Сообщение темы и цели урока.

а) Верно или неверно;

б)Кластер по теме « Объемы тел»;

г) Вычисление объемов моделей многогранников.

Решение стереометрических задач.

Итог урока.

Домашнее задание.

Ход урока.

Не бойся, что не знаешь

-бойся, что не научишься.

Организационный момент. Сообщение темы и цели урока.

— Здравствуйте, тема нашего урока « Объемы многогранников и тел вращения».

Подумайте и постарайтесь сформулировать цель урока: (учащиеся высказывают предполагаемые формулировки цели урока, в конце кто- то один делает общий вывод).

Актуализация знаний учащихся.

а)- Перед вами вопросы презентации «Верно или неверно?» , ответьте на них с помощью знаков «+» и «-» .

Презентация (Слайд с1-4)

1. Объем любого многогранника можно вычислить по формуле: V =S осн H .

2. Неверно, что S шара = 4πR 2 .

3. Верно ли, что если объем куба равен 64 см 3 , то сторона равна 8 см.

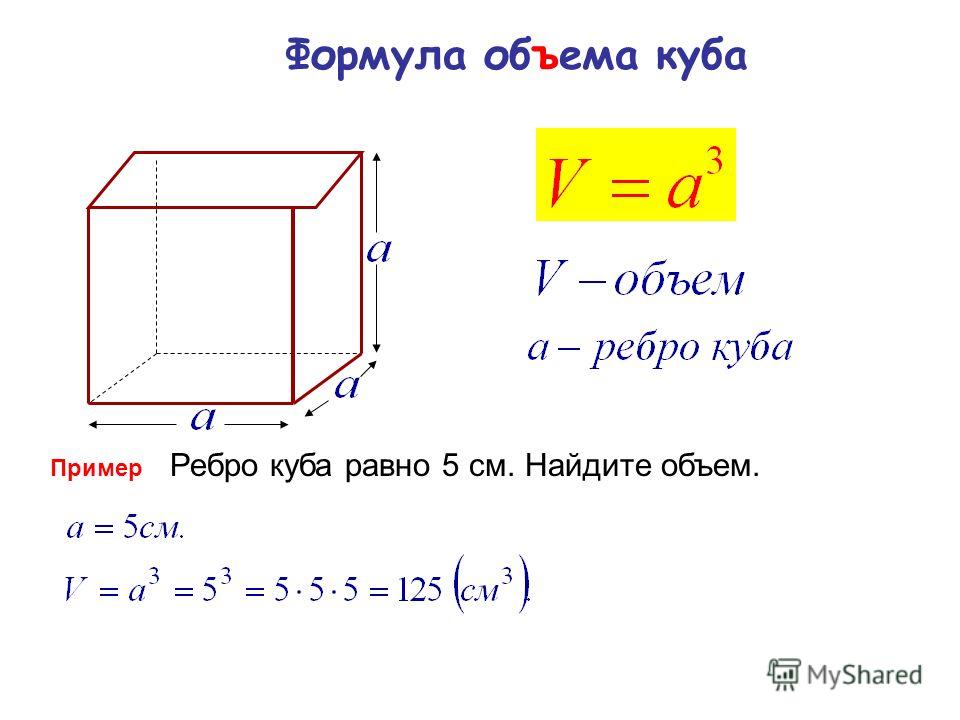
4. Верно ли, что если сторона куба равна 5 см, то объем равен 125 см 3 .

5. Верно ли, что объем конуса и пирамиды можно вычислить по формуле:

V = S осн H .

6.Неверно, что высота прямой призмы равна ее боковому ребру.

7. Верно ли, что все грани правильной пирамиды равносторонние треугольники?

8.Верно ли, что если в прямоугольный параллелепипед вписан шар, то параллелепипед-куб.

9.Верно ли, что образующая цилиндра больше его высоты?

10.Может ли осевое сечение цилиндра быть трапецией?

11.Верно ли, что объём цилиндра меньше объёма любой описанной около него призмы?

12.

Верно ли, что если осевые сечения двух цилиндров – равные прямоугольники, то объёмы цилиндров тоже равны?

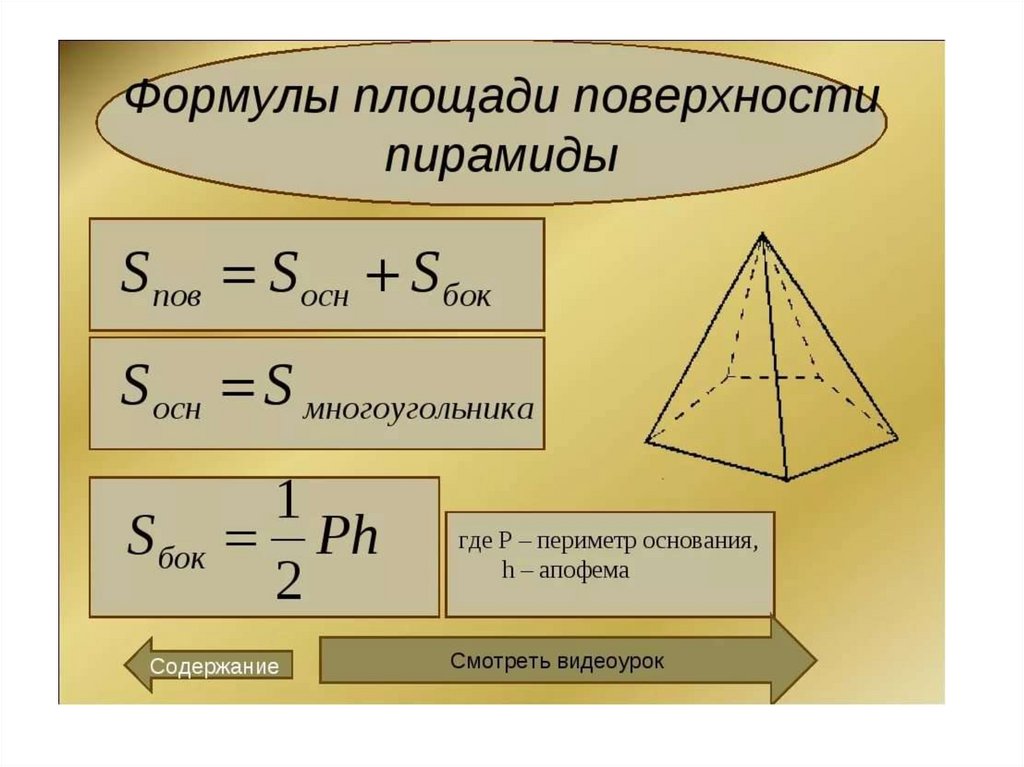
13.Неверно, что осевое сечение цилиндра – квадрат.

14. Верно ли, что многогранник называют правильным, если в основании лежит правильный многоугольник .

15.Верно ли, что если в цилиндр вписан конус, V конуса= V цилиндра

Проверьте ваши ответы и напишите, какие вопросы у вас вызвали затруднения.

б) Заполните кластер по теме « Объемы тел».

Геометрические тела

Многогранники

Тела вращения

призма

пирамида

конус

цилиндр

шар

V = S осн H .

V= π R 3

V =S осн H .

в) Решение задач из презентации по теме «Объёмы»;

-А теперь переходим к следующему этапу урока:

— Устное решение задач по готовым чертежам.

Презентация (слайды 5 — 9)

Слайд 5:

1. Объем параллелепипеда равен 6. Найдите объем треугольной пирамиды АВСДА 1 В 1 . (ответ. 3)

Слайд 6:

2.Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 10. (ответ.30)

Слайд 7:

3. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота

которого равны 1. Найдите объем параллелепипеда. (ответ.4)

Слайд 8:

4.Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V / π . (ответ.25)

Слайд 9:

5.Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V / π . (ответ.300)

г) Вычисление объемов моделей многогранников.

Перед вами на столах модели фигур.

Ваша задача:

Произведите необходимые измерения и вычислите объемы данных фигур.

Проверьте полученные результаты (ответы могут быть приблизительно равны).

3. Решение стереометрических задач.

Перед вами на столах лежат конверты с задачами, разной степени сложности. Оцените свои знания и выберите по две задачи из конверта и решите их самостоятельно.

У доски работают ученики, занимающиеся на «4» и «5».

(Чертежи фигур даны на половине ватмана. Учащиеся берут чертеж, на нем достраивают недостающие условия и решают задачу) )

5. Образующая и радиусы большего и меньшего основания усечённого конуса равны соответственно 13 см, 11 см, 6 см. Вычислите объём этого конуса. (ответ: V = 892 см 3)

6.Найдите объём правильной пирамиды, если боковое ребро равно 3см, а сторона основания – 4см. (ответ. Ответ: см 3)

7.Основание пирамиды – квадрат. Сторона основания равна 20 дм, а её высота равна 21 дм. Найдите объём пирамиды. (Ответ : V =2800 дм 3)

8. Диагональ осевого сечения цилиндра 13 см, высота 5 см. Найдите объём цилиндра. (Ответ : см 3)

9. Диагональ осевого сечения цилиндра 10 см, высота 8 см. Найдите объём цилиндра. (ответ.72π см 3)

10. Образующая и радиусы большего и меньшего основания усечённого конуса равны соответственно 13 см, 11 см, 6 см. Вычислите объём этого конуса. (ответ.892 см 3)

«5»

5.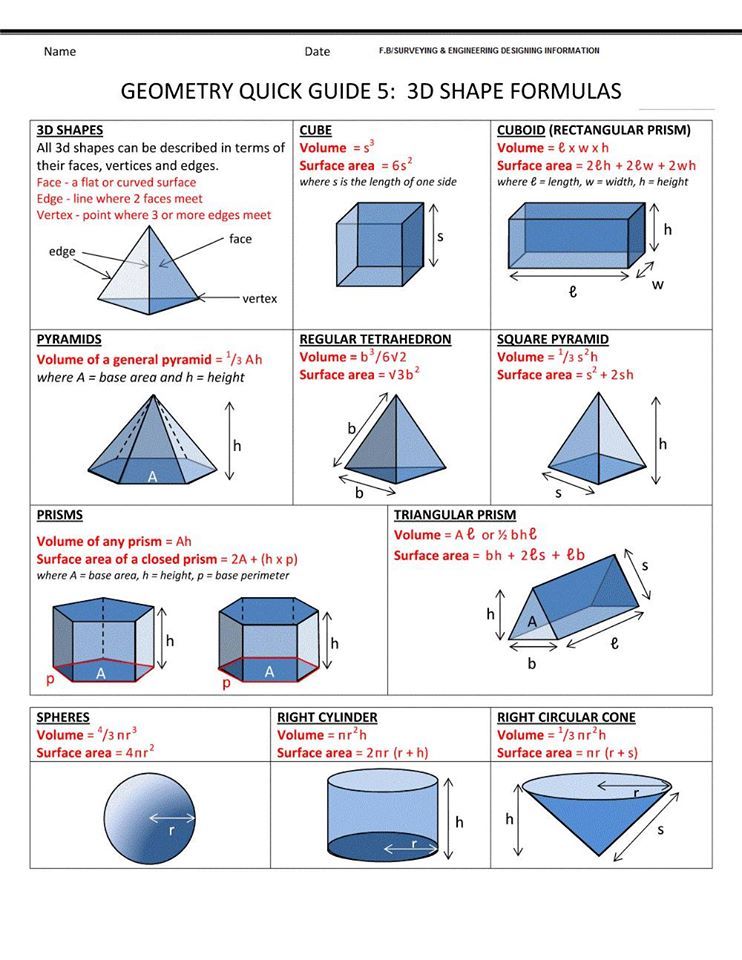 В цилиндр вписана правильная четырехугольная призма. Найдите отношение объемов призмы и цилиндра. (ответ. 2/π).

6.Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза? (ответ.3)

4.Итог урока.

А теперь настало время подвести итоги урока и записать домашнее задание.

Итак, на листочках ответьте на вопросы:

Я сегодня понял(а)_______________ .

Я сегодня узнал (а)______________.

Я хотел(а) бы спросить___________ .

Домашнее задание. Выберите из конверта.

Тетради сдать.

Cлайд 1

Объёмы и поверхности тел вращения Учитель математики МОУ СОШ №8 х. Шунтук Майкопскского района Республики Адыгея Грюнер Наталья Андреевна

Cлайд 2

Cлайд 3

оглавление 1.Виды тел вращения 2.Определения тел вращения: а)цилиндр б)конус в)шар 3.Сечения тел вращения: а)цилиндр б)конус в)шар 4.Объёмы тел вращения 5. Площади поверхностей тел вращения Завершить работу

Cлайд 4

ВИДЫ ТЕЛ ВРАЩЕНИЯ Цилиндр-тело, которое описывает прямоугольник при вращении его около стороны как оси Конус-тело, которое получено при вращении прямоугольного треугольника вокруг его катета как оси Шар-тело полученное при вращении полукруга вокруг его диаметра как оси

Cлайд 5

ОПРЕДЕЛЕНИЕ ЦИЛИНДРА Цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки,соединяющие соответствующие точки окружностей кругов,образующими цилиндра.

Cлайд 6

ОПРЕДЕЛЕНИЕ КОНУСА Конусом называется тело,которое состоит из круга-основания конуса,точки, не лежащей в плоскости этого круга,вершины конуса и всех отрезков,соединяющих вершину конуса с точками основания.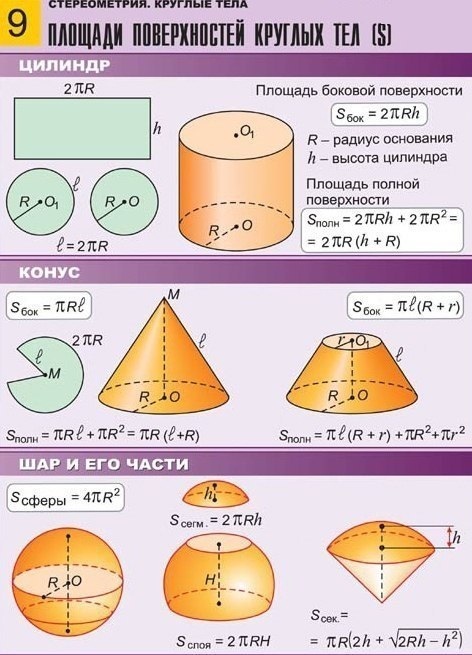

Cлайд 7

СЕЧЕНИЯ ЦИЛИНДРА Сечение цилиндра плоскостью,параллельной его оси,представляет прямоугольник. Осевое сечение-сечение цилиндра плоскостью,проходящей через его ось Сечение цилиндра плоскостью, параллельной основаниям, представляет собой круг.

Cлайд 8

ОПРЕДЕЛЕНИЕ ШАРА Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии,не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние радиусом шара.

Cлайд 9

СЕЧЕНИЕ КОНУСА Сечение конуса плоскостью,проходящей через его вершину, представляет собой равнобедренный треугольник. Осевое сечение конуса-это сечение, проходящее через его ось. Сечение конуса плоскостью, параллельной его основаниям, представляет собой круг с центром на оси конуса.

Cлайд 10

СЕЧЕНИЯ ШАРА Сечение шара плоскостью есть круг.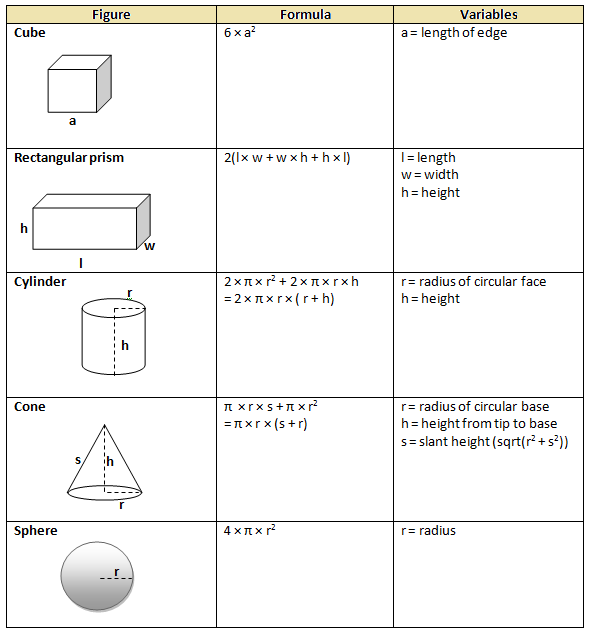 Центр этого шара есть основание перпендикуляра,опущенного из центра шара на секущую плоскость. Сечение шара диаметральной плоскостью называется большим кругом.

Cлайд 11

ОБЪЁМЫ ТЕЛ ВРАЩЕНИЯ фигура формула правило цилиндр V=S*H Объём цилиндра равен произведению площади основания на высоту. конус V=1/3*S*H Объём конуса равен одной трети произведения площади основания на высоту. шар V=4/3*П*R3 Объём шара Теорема. Объём шара радиуса R равен. Шаровой сегмент Шаровой сегмент. Объём шарового сегмента. Шаровой сектор V=2/3*П*R2*Н Шаровой сегмент. Объём шарового сегмента.

Cлайд 12

ПЛОЩАДИ ПОВЕРХНОСТЕЙ ТЕЛ ВРАЩЕНИЯ фигура правило Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту. Площадь боковой поверхности конуса равна половине произведения длины окружности основания на длину образующей. Площадь поверхности сферы вычисляется по формуле S=4*П*R*R

Cлайд 13

Объём шара Теорема. Объём шара радиуса R равен. Доказательство. Рассмотрим шар радиуса R с центром в точке О и выберем ось Ох произвольным образом (рис.). Сечение шара плоскостью, перпендикулярной к оси Ох и проходя щей через точку М этой оси, является кругом с центром в точке М. Обозначим радиус этого круга через r, а его площадь через S(х), где х — абсцисса точки М. Выразим S(х) через х и R. Из прямоугольного треугольника ОМС находим: (2.6.1) Так как, то (2.6.2) Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т. е. Для всех х,удовлетворяющих условию. Применяя основную формулу для вычисления объемов тел при, получим Теорема доказана.

Cлайд 14

Шаровой сегмент. Объём шарового сегмента. Шаровым сегментом называется часть шара, отсеченная от него плоскостью. Всякая плоскость, пересекающая шар, разбивает его на два сегмента. Объема сегмента

Cлайд 15

Шаровой сектор. Объём шарового сектора. Шаровой сектор, тело, которое получается из шарового сегмента и конуса. Объём сектора V=2/3ПR2H

Cлайд 16

Задача № 1. Цистерна имеет форму цилиндра,к основаниям которой присоединены равные шаровые сегменты. Радиус цилиндра равен 1,5 м, а высота сегмента равна 0,5 м. Какой длины должна быть образующая цилиндра, чтобы вместимость цистерны равнялась 50 м3?

«Цилиндр геометрия 11 класс» — 3.Ось цилиндра. 2. 3.Получение цилиндра. 4. Радиус основания. Геометрия 11 класс. 2.Понятие цилиндрической поверхности. 1.Разработка урока 2.Материалы к уроку. 4. Сечение плоскостью, перпендикулярной к оси. Теоретический материал Задачи. Геометрия 11 класс Тема: Цилиндр. 1.Примеры цилиндров. 1.

«Урок Объём цилиндра» — Цилиндрическая поверхность. Устные упражнения по теме. B. Осевое сечение — ……………. Н. D1. Любые осевые сечения цилиндра ….. между собой. План урока. A1. D. A. Прямой цилиндр.

«Поверхность цилиндра» — Film by: A. Shevchenko R. Trushenkov. «Понятие цилиндра». L1. Образующие. Осевое сечение. L. Algebra & Geometria Entertainment. Ось цилиндра. Основания цилиндра.

«Цилиндр конус шар» — Определение цилиндра. Виды тел вращения. Объёмы тел вращения. Объёмы и поверхности тел вращения. Определение шара. Сечение шара диаметральной плоскостью называется большим кругом. Объём шарового сегмента. Объём шарового сектора. Оглавление. Определение конуса. Сечения цилиндра. Сечения шара. Дано: Доказательство.

«Объём цилиндра» — Цилиндры из жизни. Объём цилиндра Объём конуса. Цилиндры-башни. Объём конуса. Цилиндр: история. Объём цилиндра равен произведению площади основания на высоту. Объём цилиндра. Конусы огромного размера. Объём усечённого конуса. Конус: история. Ведро – пример усечённого конуса. Водовзводная башня (Москва) Собственный дом архитектора К.Мельникова (Москва) Замок Сфорца (Милан).

Объёмы и поверхности тел вращения

Учитель математики МОУ СОШ №8

х. Шунтук Майкопскского района Республики Адыгея

Грюнер Наталья Андреевна

900igr.net

1.Виды тел вращения 2. Определения тел вращения: а)цилиндр

3.Сечения тел вращения:

а)цилиндр

4.Объёмы тел вращения 5.Площади поверхностей тел вращения

Завершить работу

ВИДЫ ТЕЛ ВРАЩЕНИЯ

Цилиндр-тело, которое описывает прямоугольник при вращении его около стороны как оси

Конус-тело, которое получено при вращении прямоугольного треугольника вокруг его катета как оси

Шар-тело полученное при вращении полукруга вокруг его диаметра как оси

ОПРЕДЕЛЕНИЕ ЦИЛИНДРА

Цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.

Круги называются основаниями цилиндра, а отрезки,соединяющие соответствующие точки окружностей кругов,образующими цилиндра.

ОПРЕДЕЛЕНИЕ КОНУСА

Конусом называется тело,которое состоит из круга-основания конуса,точки, не лежащей в плоскости этого круга,вершины конуса и всех отрезков,соединяющих вершину конуса с точками основания.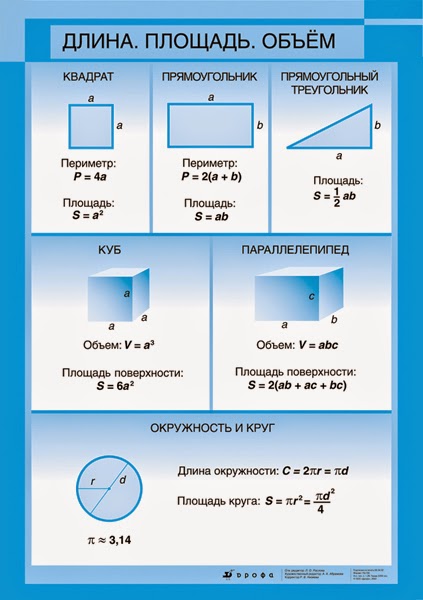

СЕЧЕНИЯ ЦИЛИНДРА

Сечение цилиндра плоскостью,параллельной его оси,представляет прямоугольник.

Осевое сечение-сечение цилиндра плоскостью,проходящей через его ось

Сечение цилиндра плоскостью, параллельной основаниям, представляет собой круг.

ОПРЕДЕЛЕНИЕ ШАРА

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии,не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние радиусом шара.

СЕЧЕНИЕ КОНУСА

Сечение конуса плоскостью,проходящей через его вершину, представляет собой равнобедренный треугольник.

Осевое сечение конуса-это сечение, проходящее через его ось.

Сечение конуса плоскостью, параллельной его основаниям, представляет собой круг с центром на оси конуса.

СЕЧЕНИЯ ШАРА

Сечение шара плоскостью есть круг. Центр этого шара есть основание перпендикуляра,опущенного из центра шара на секущую плоскость.

Сечение шара диаметральной плоскостью называется большим кругом.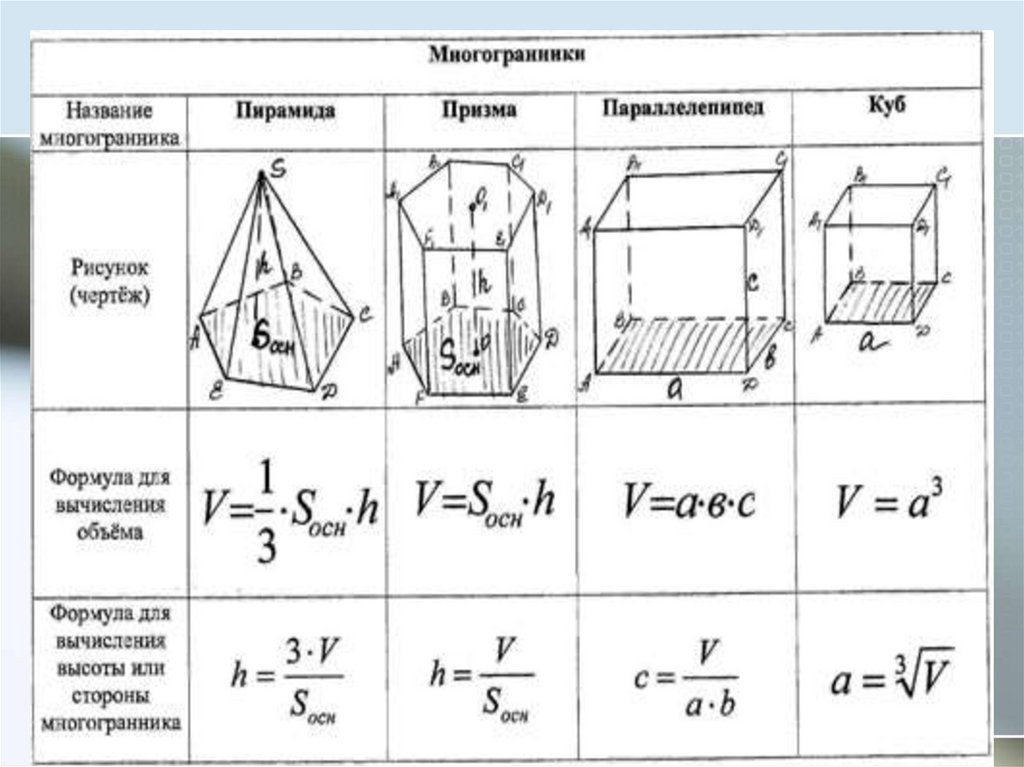

ОБЪЁМЫ ТЕЛ ВРАЩЕНИЯ

Объём цилиндра равен произведению площади основания на высоту.

Шаровой сегмент

Объём конуса равен одной трети произведения площади основания на высоту.

Объём шара Теорема. Объём шара радиуса R равен.

V=2/3 *П* R 2 *Н

Шаровой сегмент. Объём шарового сегмента.

ПЛОЩАДИ ПОВЕРХНОСТЕЙ ТЕЛ ВРАЩЕНИЯ

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

Площадь боковой поверхности конуса равна половине произведения длины окружности основания на длину образующей.

Площадь поверхности сферы вычисляется по формуле S=4* П *R*R

Объём шара Теорема. Объём шара радиуса R равен .

Доказательство. Рассмотрим шар радиуса R с центром в точке О и выберем ось Ох произвольным образом (рис.). Сечение шара плоскостью, перпендикулярной к оси Ох и проходя­щей через точку М этой оси, является кругом с центром в точке М.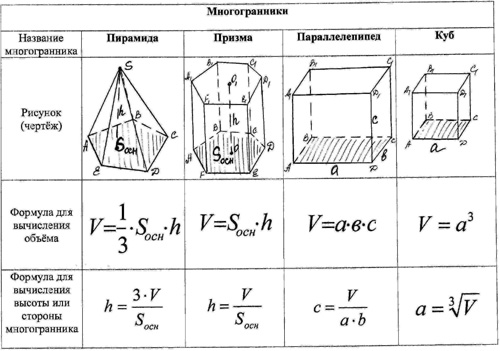 Обозначим радиус этого круга через r, а его площадь через S(х), где х — абсцисса точки М. Выразим S(х) через х и R. Из прямоугольного треугольника ОМС находим:

Так как , то (2.6.2)

Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т. е. Для всех х, удовлетворяющих условию. Применяя основную формулу для вычисления объемов тел при

, получим

Теорема доказана.

Шаровой сегмент. Объём шарового сегмента.

• Шаровым сегментом называется часть шара, отсеченная от него плоскостью. Всякая плоскость, пересекающая шар, разбивает его на два сегмента.
• Объема сегмента

Шаровой сектор. Объём шарового сектора.

• Шаровой сектор, тело, которое получается из шарового сегмента и конуса.

• Объём сектора

• V=2/3 П R 2 H

Задача № 1.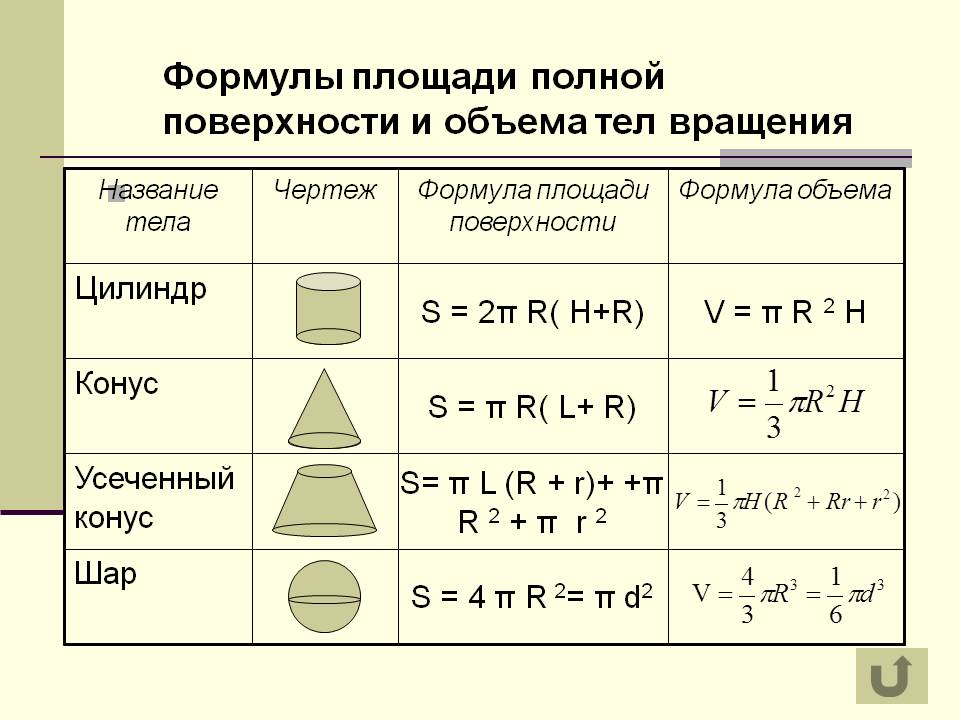

• Цистерна имеет форму цилиндра,к основаниям которой присоединены равные шаровые сегменты. Радиус цилиндра равен 1,5 м, а высота сегмента равна 0,5 м. Какой длины должна быть образующая цилиндра, чтобы вместимость цистерны равнялась 50 м3?

Шаровые сегменты.

ответ:~6,78.

Задача № 2.

• О- центр шара.
• О 1 -центр круга сечения шара. Найти объём и площадь поверхности шара.

Дано: шар сечение с центром О 1 . R сеч. =6см. Угол ОАВ=30 0 . V шара =? S сферы = ?

• Решение :

V=4/3 П R 2 S=4 П R 2

В ∆ ОО 1 А : угол О 1 =90 0 ,О 1 А=6,

угол ОАВ=30 0 . tg 30 0 =ОО 1 / О 1 А ОО 1 =О 1 А* tg30 0 . ОО 1 =6*√3 ÷ 3 =2 √3

ОА= R=OO 1 ( по св-ву катета леж.против угла 30 0 ).

ОА=2√3 ÷2 =√3

V=4 П(√3) 2 ÷ 3=(4*3,14*3) ÷ 3=12,56

S= 4П(√3) 2 =4*3,14*3=37,68

Ответ :V=12 ,56; S=37 ,68.

Задача № 3

Полуцилиндрический свод подвала имеет 6м. длины и 5,8м. в диаметре.Найдите полную поверхность подвала.

Дано: Цилиндр.АВСД-осевое сечение. АД=6м. D= 5,8м. S п.под.= ?

• Решение:

• S п.под. =(S п ÷ 2)+ S АВСД
• S п ÷ 2= (2П Rh+2 П R 2)÷2=2(П Rh+ П R 2)÷2= П Rh+ П R 2
• R=d÷2=5 ,8 ÷ 2=2,9 м.
• S п ÷ 2=3,14*2,9+3,14*(2,9) 2 =

54,636+26,4074=81,0434

АВСД-прямоуг.(по опр.осев.сеч.)

S АВСД= АВ*АД=5,8*6=34,8м 2

S п. под. =34,8+81,0434≈116м 2 .

Ответ:S п.под. ≈116м 2 .

Volume Formulas — GeeksforGeeks

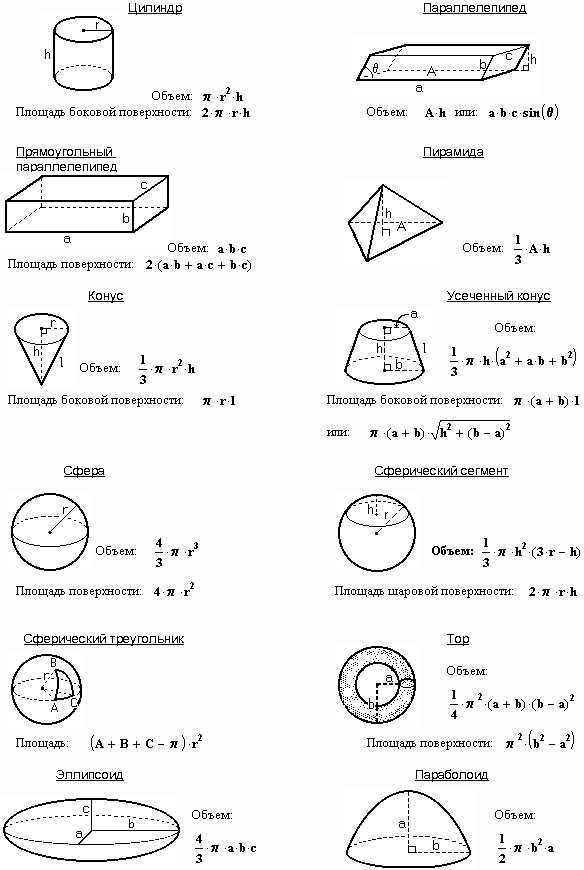
Измерение — это раздел математики, который занимается изучением измерения геометрической фигуры. Он включает в себя различные параметры, такие как длина, ширина, высота, площадь и объем. Он в целом разделен на две части: 2D и 3D измерения на основе фигур. Двухмерное измерение касается двухмерных фигур, таких как квадраты, прямоугольники и треугольники. Обычно они имеют длину, ширину, высоту и площадь. Трехмерное измерение — это изучение трехмерных фигур, таких как конус, призма и т. д. Оно имеет все параметры двухмерных форм и некоторые дополнительные параметры, такие как объем, толщина и т. д.

Объем 

Определяется как объем пространства, занимаемый трехмерным объектом в твердых телах, включая куб, прямоугольный параллелепипед, конус, цилиндр, призму и т. д. Он представлен символом (V), а единицы измерения кубические метры или кубические сантиметры (cc).

Объем куба

Куб — это трехмерное тело, все стороны которого равны.

Рассмотрим куб со стороной а.

Куб

 Объем куба 

V = a ³  

, где a — сторона куба.

Объем куба по диагонали

Объем куба

V= (√3 * d ³ )/9

9 где длина диагонали

3

3 куб.

Пример: Каков будет объем куба, если его сторона равна 2 метрам?

Ответ:

Данное тело является кубом, поэтому V=a ³

Длина стороны равна 2 метрам

Следовательно, v=2*2*2

= 8 м ³

Пример: Что будет объем куба, если его диагональ равна 9 м?

Ответ:

Данное тело является кубом, поэтому V = (√3 * d ³ )/9

Длина диагонали 9 метров

 3*9*9*9 *9/9

                    =140,29m ³

Объем прямоугольного параллелепипеда

Прямоугольный параллелепипед представляет собой трехмерное тело, имеющее длину, ширину и высоту.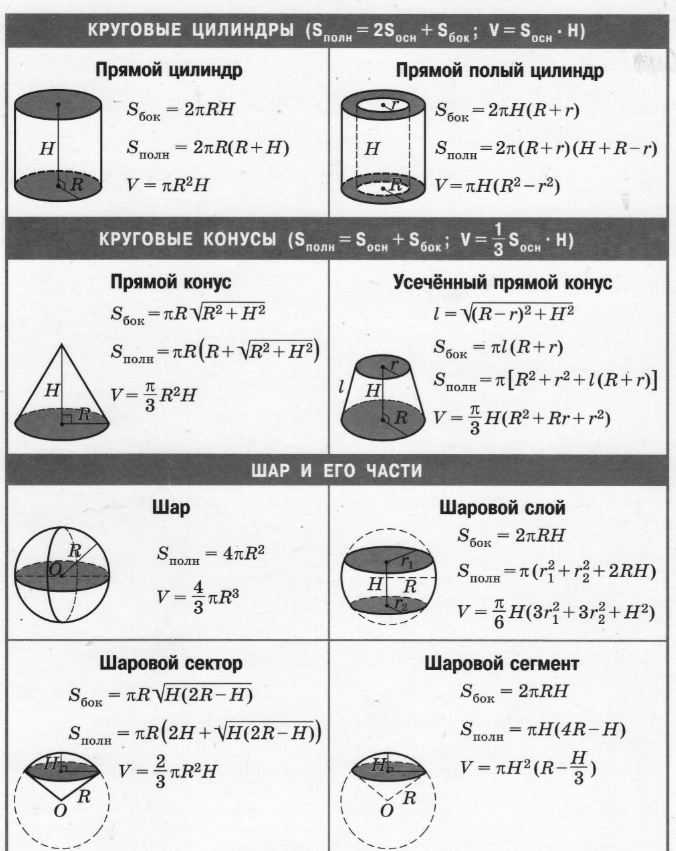

Рассмотрим прямоугольный параллелепипед высоты h, длины l и ширины b.

Cuboid

Объем кубоидного

V = L*B*H

, где, L = длина

B = Шета

H = Высота

H = Высота

H = высота

H = Высота

9003

H = Высота

9003

H = высота

9003

H = Высота Пример: Каков будет объем прямоугольного параллелепипеда длины 10 высоты 10 ширины 20.

Ответ:

Объем кубоида составляет v = L*B*H

= 10*10*20

= 2000 M ³

Объем Cone

. Конус представляет собой трехмерное тело с круглым основанием и заостренной головкой.

Рассмотрим конус высотой h и радиусом основания r.

Конус

Объем конуса

V = πr ² H/3

Где, R = Radius

H = высота

Пример: конус с радиусом 30 м и высотой 50 м. с водой. Какое количество воды хранится в нем.

Ответ:

Радиус конуса r = 30m

Высота конуса составляет h = 50m

Объем v = πr ² H/3

= 3.14*30*30 *50/3

                                     =47 100 м ³

Объем цилиндра

Цилиндр представляет собой трехмерное тело с двумя гранями в виде окружностей и некоторой высотой.

Рассмотрим цилиндр с радиусом основания r и высотой h.

Цилиндр

Объем цилиндра составляет

V = Hπr ²

, где, H = высота

R = Radius

900

Пример: Резервуар для воды имеет высоту 20 метров и диаметр 10 метров. Сколько воды мы можем вместить в этот резервуар?

Ответ: 

Резервуар для воды представляет собой цилиндр, поэтому его объем равен πr ² ч.

Высота h=20 м

Диаметр d=100м подразумевает r=d/2=5м.

поэтому количество воды, которое он содержит, равно объему

поэтому v =3,14*5*5*20

                 =1 570 м ³

Объем сферы

Сфера представляет собой трехмерную версию окружности и имеет только радиус.

Рассмотрим сферу радиуса r.

Sphere

Объем сферы составляет

V = 4/3πr ³

, где R = радиус сферы

Пример: Spherical Balloon с Radius 10M 10м 10м 10м 10м. заполняется водой. Какое количество воды хранится в нем.

Ответ:

Радиус R = 10 м

Объем сферы V = 4/3πr3

= 4*3,14*10*10*10/3

= 4186,6 M ³

Примеры вопросов

Вопрос 1: Каков будет объем куба, если его сторона равна 5 метрам?

Ответ: 

Данное тело является кубом, поэтому V=a ³

Длина стороны равна 5 метрам

Следовательно, v=5*5*5

                 на 100 метров, сколько воды мы можем вместить в этот резервуар?

Ответ:  

Резервуар для воды представляет собой цилиндр, поэтому его объем равен πr ² ч.

Высота h=20 м

Диаметр d =100 подразумевает r =d/2 = 50,

поэтому количество воды, которое он содержит, равно объему 

поэтому v =3,14*50*50*20

                 =157 000 м ³

^{90 наполнен водой. Какое количество воды хранится в нем.}

Ответ:

Радиус r = 50 м

Объем сферы V = 4/3πr ³

= 523,333 M ³

Вопрос 4: Конус радиусом 20 м и высотой 100 м заполнен водой. Какое количество воды хранится в нем.

Ответ:

Радиус конуса r = 20 м

Высота конуса составляет = 100 м

Объем v = πr ² H/3

= 3,14*20** 20*100/3

                         =41 866 м ³

Вопрос 5: Каков будет объем прямоугольного параллелепипеда длиной 10 м высотой 50 м шириной 40 м.

Ответ:

Объем кубоида составляет v = L*B*H

= 10*50*40

= 20 000 м ³

Вопрос 6: Что будет объем куба, если его диагональ 18 м?

Ответ:

Данное тело является кубом, поэтому V= (√3 * d ³ )/9

Длина диагонали 18 м

Следовательно, V =√3*18*18*18/9

                   =1 122,36 м ³

Вопрос 7.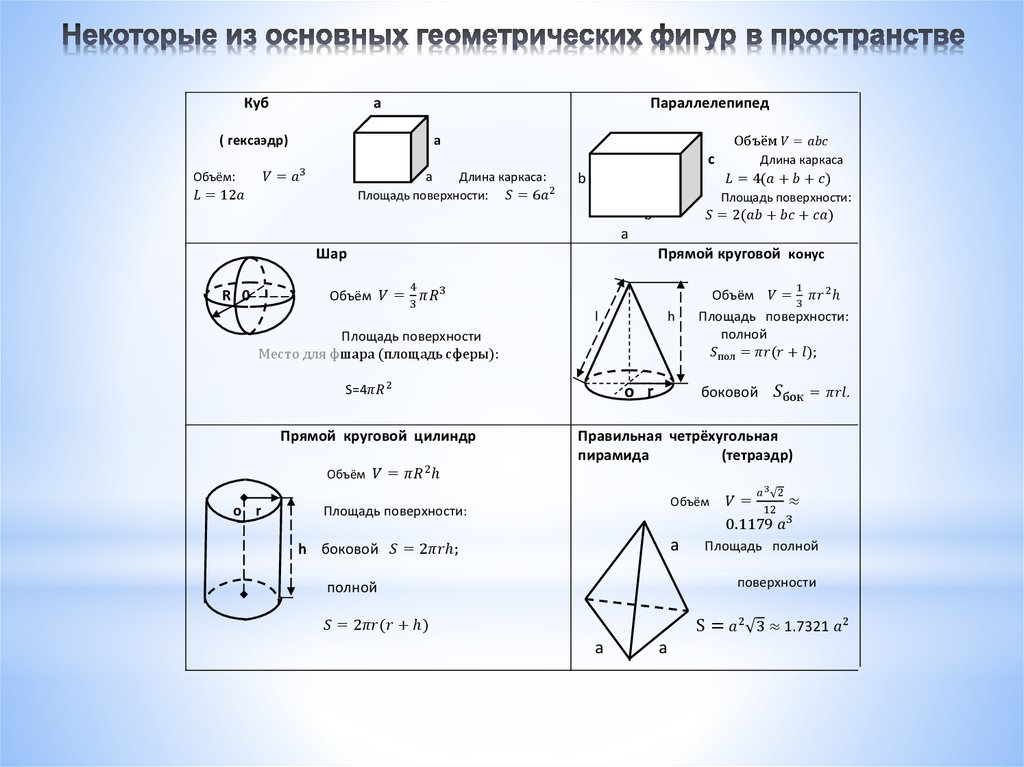 Каков будет объем куба, если его сторона равна 010 м 90 60?

Ответ:

Данное твердое вещество — это куб, поэтому V = A ³

Длина боковой стороны составляет 60 метров

Следовательно V = 60*60*60

= 216 000 м ^3.

Точность расчетных формул общего объема печени до резекции печени

Сохранить цитату в файл

Формат: Резюме (текст) PubMedPMIDAbstract (текст) CSV

Добавить в коллекции

• Создать новую коллекцию
• Добавить в существующую коллекцию

Назовите свою коллекцию:

Имя должно содержать менее 100 символов

Выберите коллекцию:

Невозможно загрузить вашу коллекцию из-за ошибки
Повторите попытку

Добавить в мою библиографию

• Моя библиография

Не удалось загрузить делегатов из-за ошибки
Повторите попытку

Ваш сохраненный поиск

Название сохраненного поиска:

Условия поиска:

Тестовые условия поиска

Электронное письмо: (изменить)

Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый рабочий день

Который день? воскресеньепонедельниквторниксредачетвергпятницасуббота

Формат отчета: РезюмеРезюме (текст)АбстрактАбстракт (текст)PubMed

Отправить максимум: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.

Отправить, даже если нет новых результатов

Необязательный текст в электронном письме:

Создайте файл для внешнего программного обеспечения для управления цитированием

Полнотекстовые ссылки

Эльзевир Наука

Полнотекстовые ссылки

. 2019 сен; 166 (3): 247-253.

doi: 10.1016/j.surg.2019.05.003. Epub 2019 14 июня.

Пим Б. Олтхоф ¹ , Рональд ван Дам ² , Элио Йовин ³ , Рикардо Роблес Кампос ⁴ , Эдуардо де Сантибаньес ⁵ , Карл Олдхафер ⁶ , Массимо Малаго ⁷ , Эдди К. Абдалла ⁸ , Эрик Шадде ⁹

Принадлежности

• ¹ Хирургическое отделение Reinier de Graaf Gasthuis, Делфт, Нидерланды; Кафедра хирургии, Академический медицинский центр, Амстердамский университет, Амстердам, Нидерланды. Электронный адрес: [email protected].
• ² Кафедра хирургии, Медицинский центр Маастрихтского университета, Маастрихт, Нидерланды, и Университетская клиника Аахена, Ахен, Германия.
• ³ Отделение хирургии, больница C.A. Pizzardi Maggiore, Болонья, Италия.
• ⁴ Хирургическое отделение университетской больницы Вирхен де ла Арриксака, Мурсия, Испания.
• ⁵ Хирургическое отделение Итальянской больницы, Буэнос-Айрес, Аргентина.
• ⁶ Отделение общей, висцеральной и онкологической хирургии, клиника Asklepios Klinik Barmbek, Гамбург, Германия.
• ⁷ Отделение HPB и хирургии трансплантации печени, Royal Free Hospital, Университетский колледж Лондона, Лондон, Великобритания.
• ⁸ Отделение гепато-панкреато-билиарной хирургии, Институт рака больницы Нортсайд, Атланта, Джорджия.
• ⁹ Институт физиологии, Центр интегративной физиологии человека, Цюрихский университет, Цюрих, Швейцария; Хирургическое отделение Кантональной больницы Винтертур, Винтертур, Швейцария; Отделение хирургии, Медицинский центр Университета Раш, Чикаго, Иллинойс.

• PMID: 31204072
• DOI: 10.1016/j.surg.2019.05.003

Пим Б. Олтхоф и соавт. Хирургия. 2019 Сентябрь

. 2019 сен; 166 (3): 247-253.

doi: 10.1016/j.surg.2019.05.003. Epub 2019 14 июня.

Авторы

Пим Б. Олтхоф ¹ , Рональд ван Дам ² , Элио Йовин ³ , Рикардо Роблес Кампос ⁴ , Эдуардо де Сантибаньес ⁵ , Карл Олдхафер ⁶ , Массимо Малаго ⁷ , Эдди К.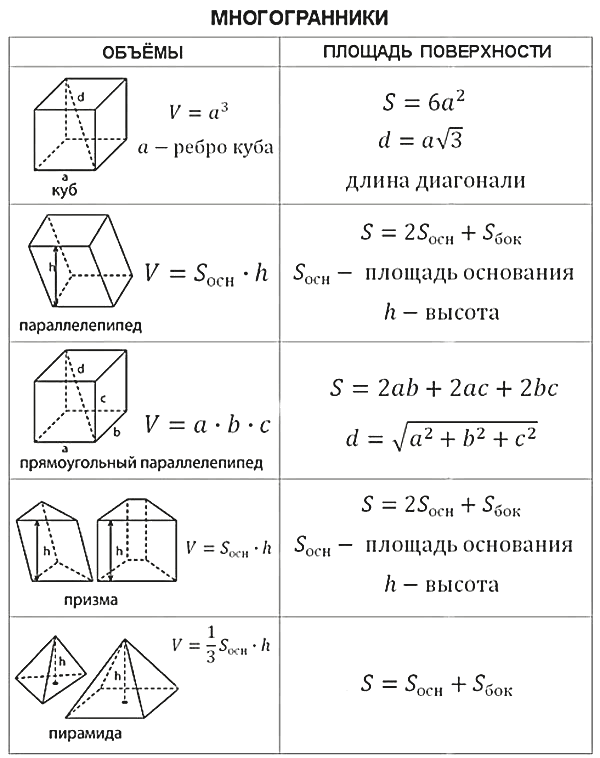 Абдалла ⁸ , Эрик Шадде ⁹

Принадлежности

• ¹ Хирургическое отделение Reinier de Graaf Gasthuis, Делфт, Нидерланды; Кафедра хирургии, Академический медицинский центр, Амстердамский университет, Амстердам, Нидерланды. Электронный адрес: [email protected].
• ² Кафедра хирургии, Медицинский центр Маастрихтского университета, Маастрихт, Нидерланды, и Университетская клиника Аахена, Ахен, Германия.
• ³ Отделение хирургии, больница C. A. Pizzardi Maggiore, Болонья, Италия.
• ⁴ Хирургическое отделение университетской больницы Вирхен де ла Арриксака, Мурсия, Испания.
• ⁵ Хирургическое отделение Итальянской больницы, Буэнос-Айрес, Аргентина.
• ⁶ Отделение общей, висцеральной и онкологической хирургии, клиника Asklepios Klinik Barmbek, Гамбург, Германия.
• ⁷ Отделение HPB и хирургии трансплантации печени, Royal Free Hospital, Университетский колледж Лондона, Лондон, Великобритания.
• ⁸ Отделение гепато-панкреато-билиарной хирургии, Институт рака больницы Нортсайд, Атланта, Джорджия.
• ⁹ Институт физиологии, Центр интегративной физиологии человека, Цюрихский университет, Цюрих, Швейцария; Хирургическое отделение Кантональной больницы Винтертур, Винтертур, Швейцария; Отделение хирургии, Медицинский центр Университета Раш, Чикаго, Иллинойс.

• PMID: 31204072
• DOI: 10.1016/ж.сург.2019.05.003

Абстрактный

Задний план: Будущий объем остаточной печени используется для прогнозирования риска печеночной недостаточности у пациентов, которым предстоит обширная резекция печени. Формулы для оценки общего объема печени на основе биометрических данных широко используются для расчета будущего объема остаточной печени; однако остается неясным, какая формула является наиболее точной. В этом исследовании оценивались опубликованные оценочные формулы общего объема печени, чтобы определить, какая формула лучше всего предсказывает фактический будущий объем остатка печени на основе измерений у большого числа пациентов, перенесших ассоциированную перегородку печени и перевязку воротной вены для поэтапной гепатэктомии.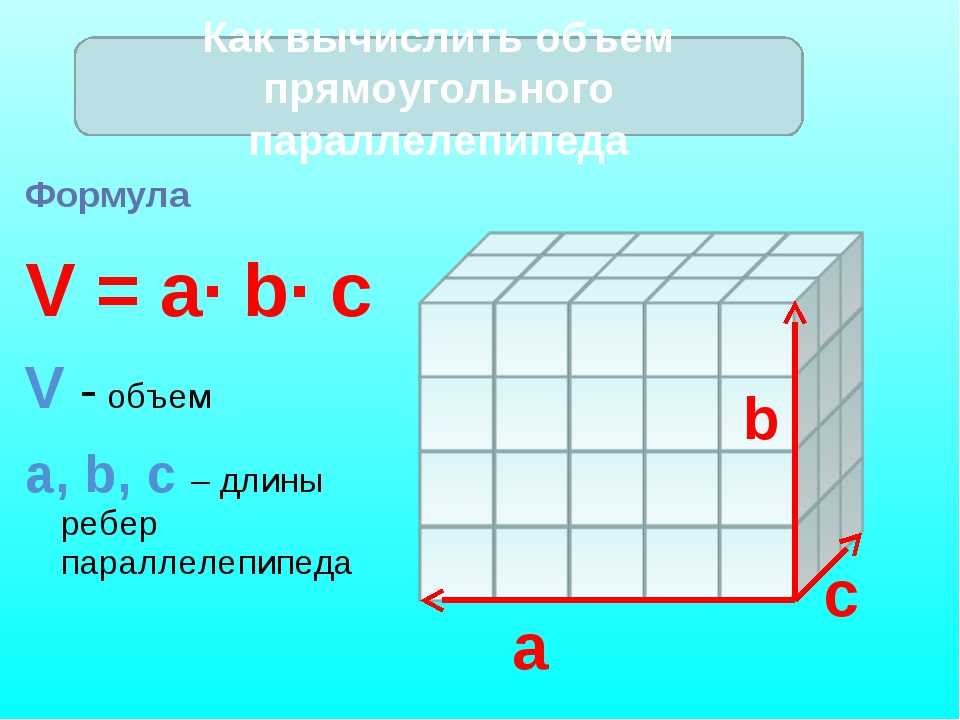

Методы: В это исследование были включены все пациенты с полными данными об объеме печени в соответствующей перегородке печени и перевязке воротной вены для поэтапной гепатэктомии. Оценочный общий объем печени и предполагаемый будущий объем остатка печени были рассчитаны по 16 опубликованным формулам. Медианное завышение или занижение по сравнению с фактически измеренными объемами определяли для оценки общего объема печени и будущего остаточного объема печени. Долю пациентов с заниженным или завышенным будущим объемом остатка печени для каждой формулы сравнивали друг с другом, используя 25% отсечение для каждой формулы.

Результаты: Среди 529 исследованных пациентов формулы варьировались от 19% занижения до 63% завышения оценки общего объема печени. Оценка будущего объема остатка печени приводит к недооценке на 10% и завышению на 5% среди формул.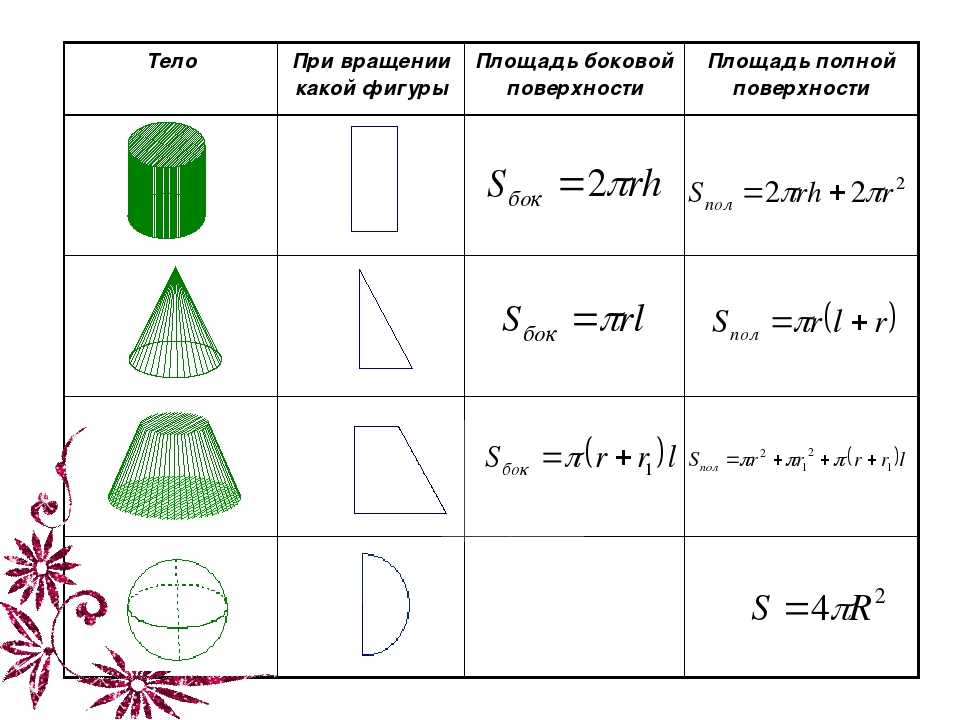 Из всех изученных формул формула Vauthey1 была наиболее точной, приводя к недооценке будущего объема остаточной печени у 20% и завышению будущего объема остаточной печени у 6% пациентов.

Заключение: Валидация 16 опубликованных формул общего объема печени в многоцентровой международной когорте из 529 пациентов, перенесших поэтапную гепатэктомию, показала, что формула Воти (оценочный общий объем печени = 18,51 × масса тела + 191,8) обеспечивает наиболее точный прогноз фактического объема остаточной печени в будущем. .

Copyright © 2019 Elsevier Inc. Все права защищены.

Похожие статьи

• Влияние полноты расщепления на будущую гипертрофию остатка печени при ассоциировании перегородки печени и перевязки воротной вены для поэтапной гепатэктомии (ALPPS) при гепатоцеллюлярной карциноме: полная-ALPPS по сравнению с частичной-ALPPS.

  Чан ACY, Чок К., Дай JWC, Ло CM. Чан Эйси и др. Хирургия. 2017 февраль; 161(2):357-364. doi: 10.1016/j.surg.2016.07.029. Epub 2016 3 сентября. Хирургия. 2017. PMID: 27596751

• Анализ эффективности эмболизации воротной вены у пациентов с обширным злокачественным новообразованием печени и очень низким будущим объемом остатка печени, включая сравнение с ассоциированной перегородкой печени с перевязкой воротной вены для поэтапной гепатэктомии.

  Шиндо Дж., Воти Дж. Н., Зиммитти Г., Керли С. А., Хуанг С. И., Махваш А., Гупта С., Уоллес М. Д., Алоя Т. А. Шиндо Дж. и др. J Am Coll Surg. 2013 июль; 217(1):126-33; обсуждение 133-4. doi: 10.1016/j.jamcollsurg.2013.03.004. Epub 2013 28 апр. J Am Coll Surg. 2013. PMID: 23632095 Бесплатная статья ЧВК.

• Неоадъювантная химиотерапия не влияет на будущий рост остатка печени и результаты ассоциированной перегородки печени и лигирования воротной вены для поэтапной гепатэктомии.

  Хассельгрен К., Малаго М., Вьяс С., Кампос Р.Р., Брусадин Р., Линекер М., Петровски Х., Клавьен П.А., Мачадо М.А., Эрнандес-Алехандро Р., Ванис К., Вальтер Л., Сандстрём П., Бьернссон Б. Хассельгрен К. и соавт. Хирургия. 2017 Май; 161(5):1255-1265. doi: 10.1016/j.surg.2016.11.033. Epub 2017 9 января. Хирургия. 2017. PMID: 28081953

• Будущая остаточная функция печени как прогностический фактор реакции гипертрофии после эмболизации воротной вены.

  Чеслак К.П., Хуисман Ф., Байс Т., Беннинк Р.Дж., ван Лиенден К.П., Верхей Дж., Бесселинк М.Г., Буш ОРЦ, ван Гулик ТМ. Чеслак К.П. и др. Хирургия. 2017 июль; 162(1):37-47. doi: 10.1016/j.surg.2016.12.031. Epub 2017 30 марта. Хирургия. 2017. PMID: 28365007

• Объединение перегородки печени и перевязки воротной вены для поэтапной гепатэктомии (ALPPS): новая стратегия повышения резектабельности в хирургии печени.

  Чжан GQ, Чжан ZW, Лау WY, Чен XP. Чжан Г.К. и др. Int J Surg. 2014;12(5):437-41. doi: 10.1016/j.ijsu.2014.03.009. Epub 2014 2 апр. Int J Surg. 2014. PMID: 24704086 Рассмотрение.

Посмотреть все похожие статьи

Цитируется

• Текущие данные о постгепатэктомической печеночной недостаточности: всесторонний обзор.

  Спаррелид Э., Олтхоф П.Б., Дасари Б.В.М., Эрдманн Д.И., Сантол Дж., Старлингер П., Гилг С. Спаррелид Э. и др. Открытый БЖС. 2022 ноябрь 2;6(6):zrac142. дои: 10.1093/bjsopen/zrac142. Открытый БЖС. 2022. PMID: 36415029 Бесплатная статья ЧВК. Рассмотрение.

• Метод глубокого обучения nnU-Net для сегментации паренхимы и определения объема печени по изображениям компьютерной томографии.

  Петтит Р.В., Марлатт Б.Б., Корр С.Дж., Хавелка Дж., Рана А. Петтит Р.В. и др. Энн Сург Оупен. 2022 июнь;3(2):e155. doi: 10.1097/as9.0000000000000155. Epub 2022 30 марта. Энн Сург Оупен. 2022. PMID: 36275876 Бесплатная статья ЧВК.

• Разработка и внутренняя валидация шкалы комплексной предоперационной оценки риска ALPPS (CAPRA): подходит ли пациент для связывания перегородки печени и лигирования воротной вены для поэтапной гепатэктомии (ALPPS)?

  Капобьянко И., Олдхафер К.Дж., Фард-Агайе М.Х., Роблес-Кампос Р., Брусадин Р., Петровски Х., Линекер М., Мехраби А., Хоффманн К., Ли Дж., Хойманн А., Эрнандес-Алехандро Р., Тун-Абрахам М.Э., Джовин Э., Серенари М., Бьорнссон Б., Сандстрем П., Алиханов Р., Ефанов М., Муйесан П., Шлегель А., ван Гулик Т.М., Олтхоф П.Б., Ставру Г.А., Серна-Игита Л.М., Кенигсрайнер А., Надалин С. Капобьянко I и др. Гепатобилиарный Surg Nutr. 2022 Февраль;11(1):52-66. дои: 10.21037/hbsn-21-396. Гепатобилиарный Surg Nutr. 2022. PMID: 35284531 Бесплатная статья ЧВК.

• ^99m Гепатобилиарная сцинтиграфия с Tc-меброфенином и объемные показатели перед подготовкой печени: корреляции и расхождения у пациентов без цирроза.

  Гиу Б., Дешайес Э., Панаро Ф., Санглиер Ф., Кусумано С., Эррерро А., Сгарбура О., Молинари Н., Кене Ф., Кассинотто К. Гуйу Б. и др. Энн Трансл Мед. 2021 май;9(9):795. doi: 10.21037/атм-20-7372. Энн Трансл Мед. 2021. PMID: 34268408 Бесплатная статья ЧВК.

• Количественная магнитно-резонансная томография предсказывает индивидуальную будущую работу печени после резекции печени по поводу рака.

  Mole DJ, Fallowfield JA, Sherif AE, Kendall T, Semple S, Kelly M, Ridgway G, Connell JJ, McGonigle J, Banerjee R, Brady JM, Zheng X, Hughes M, Neyton L, McClintock J, Tucker G, Нейлон Х.

  No related posts.