2). Формулы радиусов окружности
а). равносторонний треугольник б). прямоугольный треугольник
.
в). разносторонний треугольник
13
1). Свойство медианы в прямоугольном треугольнике:
медиана в прямоугольном треугольнике равна половине гипотенузы.
CM = AB или CM = AM = MB
2). Свойство высоты в равнобедренном прямоугольном треугольнике:
высота в равнобедренном прямоугольном треугольнике равна половине гипотенузы.
( т. к. высота в равнобедренном треугольнике является и медианой)
3). Свойство биссектрисы треугольника:
биссектриса треугольника делит противоположенную сторону на
отрезки,
пропорциональные боковым сторонам.
Если , то
14
4). Свойство площадей треугольников с равными углами:
Площади треугольников с равными углами относятся как произведение прилежащих сторон.
Если , то
5). Свойство площадей треугольников с одинаковыми высотами:
площади треугольников с одинаковыми высотами относятся как основания.
Если , то
6). Свойство медианы треугольника:
медиана треугольника делит его на два равновеликих.
Если BM –медиана, то =
7). Свойство точки пересечения медиан:
медианы точкой пересечения делятся в отношении 2:1, считая от вершины.
8). Свойство треугольников, образованных при пересечении трех медиан треугольника: треугольники,
образованные при пересечении
трех медиан в треугольнике — равновелики.
Если — медианы, то
9). Свойство прямой, проведенной параллельно стороне треугольника:
прямая, параллельная стороне треугольника, отсекает треугольник, подобный данному.
B
P K
C
A
Если PK║ AC, то Δ PBK Δ ABC и
Четырехугольники
1. Свойства фигур.
1). Параллелограмм.
Определение: параллелограмм – четырехугольник, у которого стороны попарно параллельны.
Свойство: а). противоположенные стороны и углы равны
б). диагонали в точке пересечения делятся пополам.
в). углы, прилежащие к одной стороне, в сумме дают 180°
AB = CD, BC = AD,
A = C, B = D,
AO = OC, BO = OD,
A + D = 180°, A + B = 180°
2). Прямоугольник.
Прямоугольник.
Определение: прямоугольник – это параллелограмм, у которого все углы прямые.
Свойство: диагонали равны.
AC = BD.
3). Ромб
Определение: ромб – это параллелограмм, у которого все стороны равны.
Свойства: а). диагонали перпендикулярны,
б). диагонали являются биссектрисами углов.
AC BD,
4). Квадрат.
Определение: квадрат – это параллелограмм, у которого все углы прямые и все стороны равны.
Свойства: диагонали равны,
точкой пересечения делятся пополам,
перпендикулярны,
делят
углы пополам.
AC = BD, AC BD, AO = OC, BO = OD,
5). Трапеция.
Определение: трапеция — это четырехугольник, у которого две стороны параллельны, а две — нет.
равнобедренная трапеция – у которой боковые стороны равны.
Свойство равнобедренной трапеции: а). диагонали равны
б). углы при основании равны.
B C
A D
Е сли AB = CD, то AC = BD и A = B.
Свойство средней линии трапеции: средняя линия трапеции параллельна основаниям и равна их полу сумме.
MN – средняя линия трапеции
MN ║ BC║ AD
MN =
c++ — Поиск рациональной универсальной формулы для нахождения координат центров окружностей, вписанных в квадрат
Универсальной формулы для размещения центров окружностей нет, это открытая проблема.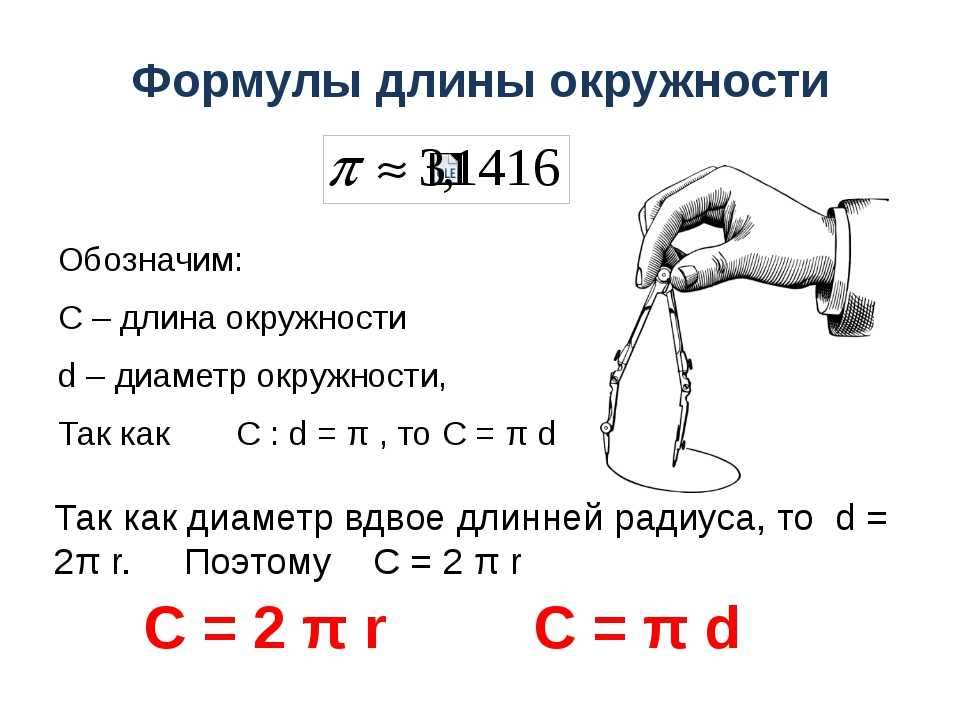
Вы поставили задачу так: определить какое максимальное количество окружностей радиуса r можно поместить в квадрат размера a без пересечений. Оказывается что ответ зависит только от отношения r/a. Не умаляя общности положим a = 1: вписываем окружности в единичный квадрат.
Обозначим максимальное число окружностей через m(r). Это монотонно убывающая целочисленная функция. Чтобы её задать достаточно вычислить r(n) = max{r|m(r) = n}. Именно в такой формулировке этой задачей занимаются математики. Значения r(n), n <= 20 можно найти в этой статье.
r(n) можно вычислить приближенно. Один из подходов такой: бросаем n случайных точек в единичный квадрат. Затем начинаем двигать их случайным образом в цикле. Перед движением точки вычисляется минимум из расстояний от неё до сторон квадрата и половинок расстояний до других точек. Такой же минимум вычисляется после движения. Если новый минимум меньше старого движение отменяется. Это грубый аналог броуновского движения под действием внешней силы: точки отталкиваются друг от друга и от сторон квадрата.
Если новый минимум меньше старого движение отменяется. Это грубый аналог броуновского движения под действием внешней силы: точки отталкиваются друг от друга и от сторон квадрата.
Хотя это прототип, он способен получить 17 из 20 конфигураций из статьи за несколько минут. Чтобы получить более серьёзные результаты нужно оптимизировать математическую модель и программу.
Прототип на Python:
import itertools
import matplotlib.pyplot as plt
import random
import sys
def cycle(a):
return a + a[:1]
def dist(a, b):
return ((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2) ** 0.5
def get_radius(centers, i, cc):
def gen():
yield cc[0]
yield 1 - cc[0]
yield cc[1]
yield 1 - cc[1]
for j, c in enumerate(centers):
if j != i:
yield dist(cc, c) / 2
return min(gen())
def get_common_radius(centers):
def gen():
for c in centers:
yield c[0]
yield 1 - c[0]
yield c[1]
yield 1 - c[1]
for i, j in itertools. combinations(range(len(centers)), 2):
yield dist(centers[i], centers[j]) / 2
return min(gen())
def plot_circles(centers):
radius = get_common_radius(centers)
poly = ((0, 0), (1, 0), (1, 1), (0, 1))
circles = [plt.Circle(c, radius, fill=False) for c in centers]
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
for c in circles:
ax.add_artist(c)
plt.plot(*zip(*cycle(poly)))
plt.show()
def shake(centers, step, r):
for i, c in enumerate(centers):
radius = get_radius(centers, i, c)
new_c = tuple(v + step * (2 * r.random() - 1) for v in c)
new_radius = get_radius(centers, i, new_c)
if radius < new_radius:
centers[i] = new_c
def main():
n = int(sys.argv[1])
r = random.Random()
centers = [(r.random(), r.random()) for _ in range(n)]
for p in range(0, 10):
step = 0.5 ** p
for _ in range(10 * 2 ** p):
shake(centers, step, r)
plot_circles(centers)
main()
combinations(range(len(centers)), 2):
yield dist(centers[i], centers[j]) / 2
return min(gen())
def plot_circles(centers):
radius = get_common_radius(centers)
poly = ((0, 0), (1, 0), (1, 1), (0, 1))
circles = [plt.Circle(c, radius, fill=False) for c in centers]
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
for c in circles:
ax.add_artist(c)
plt.plot(*zip(*cycle(poly)))
plt.show()
def shake(centers, step, r):
for i, c in enumerate(centers):
radius = get_radius(centers, i, c)
new_c = tuple(v + step * (2 * r.random() - 1) for v in c)
new_radius = get_radius(centers, i, new_c)
if radius < new_radius:
centers[i] = new_c
def main():
n = int(sys.argv[1])
r = random.Random()
centers = [(r.random(), r.random()) for _ in range(n)]
for p in range(0, 10):
step = 0.5 ** p
for _ in range(10 * 2 ** p):
shake(centers, step, r)
plot_circles(centers)
main()
Калькулятор формул круга
Автор Luis Hoyos
Отзыв от Wojciech Sas, PhD
Последнее обновление: 02 февраля 2023 г. Пример
Пример
Калькулятор формулы круга позволяет легко выполнять вычисления круга. Продолжайте читать, чтобы узнать такие вещи, как:
- Формула для расчета диаметра круга по его радиусу или наоборот.
- По какой формуле вычисляется длина окружности.
- Какова формула площади круга.
Формулы окружности
Хотя использование калькулятора формул окружности является самым быстрым способом вычисления окружностей, очень важно знать формулы , чтобы лучше понять процесс.
Формула для расчета диаметра круга по его радиусу и наоборот
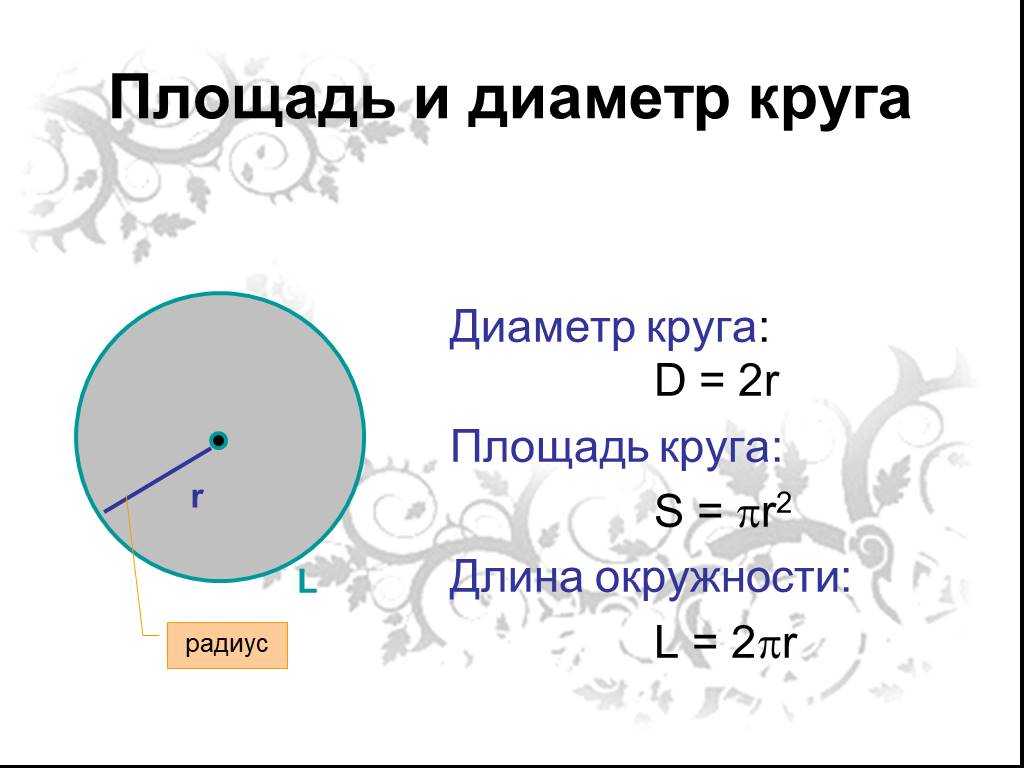
Формула диаметра круга является самой простой из уравнений и говорит, что диаметр ( d ) равен удвоенному радиусу ( r ) :
d = 2r
r = r /2
Формулы вычисления длины окружности и площади круга более сложны. Посмотрите на уравнения в следующих разделах.
Посмотрите на уравнения в следующих разделах.
Формула для вычисления длины окружности
Формула для вычисления длины окружности ( c ) можно выразить через радиус, диаметр и площадь ( A ):
Мы можем выразить формулу для вычисления площади круга через радиус, диаметр и длину окружности: Предположим, у вас есть круг радиусом 3 см. Если вы хотите рассчитать его площадь и окружность, вы можете сделать это, выполнив следующие действия: Теперь, когда вы знаете, как рассчитать формулу длины окружности и площади круга, взгляните 👀 на другие калькуляторы: π (пи) умножить на радиус p половина = πr. 1,825 в . Формула диаметра круга гласит, что диаметр в два раза больше радиуса. Чтобы найти радиус, просто разделите диаметр на два: Luis Hoyos Radius (r) Diameter (d) Circumference (c) Area (A) Check out 23 similar 2d geometry calculators 📏 AreaArea of a rectangleArea of crescent… 20 еще Площадь окружности Диаметр окружности Длина окружности Прежде чем мы перейдем к различным формулам для круга. Давайте быстро определим, что такое круг на самом деле и почему это важно. Открытый справочник по математике определяет круг как; «Линия, образующая замкнутый контур, каждая точка которого находится на фиксированном расстоянии от центральной точки». Однако, если бы вы поискали вокруг, вы бы обнаружили различные исследования и определения, которые затрудняют понимание того, как точно определить круг. Мы разбираем различные определения в нашей статье Что такое круг? Мы можем упростить приведенное выше определение круга до; Окружность представляет собой набор точек, равных по радиусу (радиусу) от фиксированной точки (центральной точки) на плоскости. Теперь, когда у нас есть заданное определение круга, давайте быстро определим переменные, участвующие в формулах круга. Площадь круга (переменная: A ) — площадь внутри круга. Окружность (переменная: C ) — это периметр круга. Пи (переменная: π ) — это расстояние от центра круга до любой точки на окружности. Радиус (переменная: r ) — это расстояние от центра окружности до любой точки на окружности. Диаметр (переменная: d ) — это расстояние, проходящее через центр окружности, от любой точки окружности до другой противоположной точки окружности, или, другими словами, равно удвоенному радиусу окружности. . С этим фундаментальным пониманием мы теперь можем решать различные формулы круга. Формула площади круга может быть выражена следующим образом: А = π г 2 Определение площади круга — полезный инструмент для измерения пространства внутри окружности круга. Разобьем уравнение и определим переменные. Площадь круга представлена как A . С другой стороны уравнения имеем π (Пи), умноженное на r 2 (радиус) в квадрате. Обычная мнемоника для запоминания этой формулы, которую вы выучили в школе: "Пирог квадратной формы" . Пример того, как найти радиус ( r ) в области формулы круга, можно найти в нашем уроке Основы алгебры - 5. Формулы и буквенные уравнения. Формула диаметра круга может быть выражена следующим образом: Д = 2 р Как упоминалось выше, диаметр круга просто в два раза больше длины радиуса круга. Это самое длинное расстояние между двумя точками на окружности. Формула длины окружности может быть выражена следующим образом: С = 2 π г Длину окружности можно найти, умножив в 2 раза π умножить на радиус r . Окружность так же важна, как и площадь уравнения окружности в реальной жизни. Представьте, что вы стоите на краю круглого катка, вы можете прокатиться от края к центру катка, чтобы найти радиус, и, продолжая движение к противоположному краю, вы можете найти диаметр. Теперь мы можем перейти к более сложным формулам окружности. Окружность, центр (0, 0), радиус r . Окружность с центром (0, 0) и радиусом r имеет уравнение: х 2 + у 2 = r 2 Это означает, что любая точка ( x , y ) на окружности даст квадрат радиуса при подстановке в уравнение окружности. Окружность, центр ( h , k ), радиус r . Окружность с центром ( h , k ) и радиусом r имеет уравнение: ( x − h ) 2 + ( y − k ) 2 = r 28 Эти формулы являются прямым следствием формулы Пифагора для длины гипотенузы прямоугольного треугольника. Загрузить миллиметровку Эскиз окружности x 2 + y 2 = 4. Сначала найдите центр и радиус. Ответить Уравнение имеет вид x 2 + y 2 = r 2 , поэтому у нас есть круг с центром (0, 0) и радиусом `r=sqrt4=2`. Окружность, центр (0, 0), радиус 2. Нарисуйте круг ( x − 2) 2 + ( y − 3) 2 = 16 Сначала найдите центр и радиус. Ответить Уравнение имеет вид ( x − h ) 2 + ( y − k ) 2 = r 8 , 3) и радиус `r=sqrt(16)=4`. Окружность, центр (2, 3), радиус 4. Нарисуйте круг ( x + 4) 2 + ( y − 5) 2 = 36 Ответить Уравнение имеет вид ( x − h ) 2 + ( y − k ) 2 = r 4 8 9. У нас есть круг с центром в точке (−4, 5) и радиусом `r=sqrt(36)=6`. Окружность, центр (−4, 5), радиус 6. Будьте осторожны с положительным и отрицательным и - ценности в этой работе! Уравнение, которое можно записать в следующем виде (с константами D , E , F ), представляет собой окружность : х 2 + у 2 + Dx + Ey + F = 0 Это называется общей формой круга . Найти центр и радиус окружности x 2 + у 2 + 8 x + 6 у = 0 Нарисуйте круг. Ответить Пожалуйста, пересмотрите Завершение
Квадрат сначала... Наша цель - привести уравнение к виду: ( 92` Теперь это в нужном нам формате, и мы можем определить центр и радиус круга. Таким образом, центр круга равен (−4, −3), а радиус равен 5
единицы измерения. Окружность, центр (−4, −3), радиус 5. Обратите внимание, что окружность проходит через (0, 0). Это логично, так как: c = 2πr
c = πd
c = 2√(049) для вычисления площади круга A = πr²
A = πd²/4
A = c²/(4π) Как использовать формулу площади и длины окружности? Пример
A = π × (3 см)² = 28,2743 см² .
c = 2π × (3 см) = 18,8496 см .
18,8496 см для площади и окружности. Другие полезные инструменты, такие как калькулятор формулы окружности
Часто задаваемые вопросы
Какова формула периметра полукруга?
 Формула периметра полукруга — это та же формула для длины окружности, разделенная на два. Это приводит к произведению π (пи) и радиуса.
Формула периметра полукруга — это та же формула для длины окружности, разделенная на два. Это приводит к произведению π (пи) и радиуса. Каков радиус круга диаметром 3,65 дюйма?
r = 3,65 дюйма / 2 = 1,825 дюйма . 3. Круг | Площадь круга
Формулы окружности:
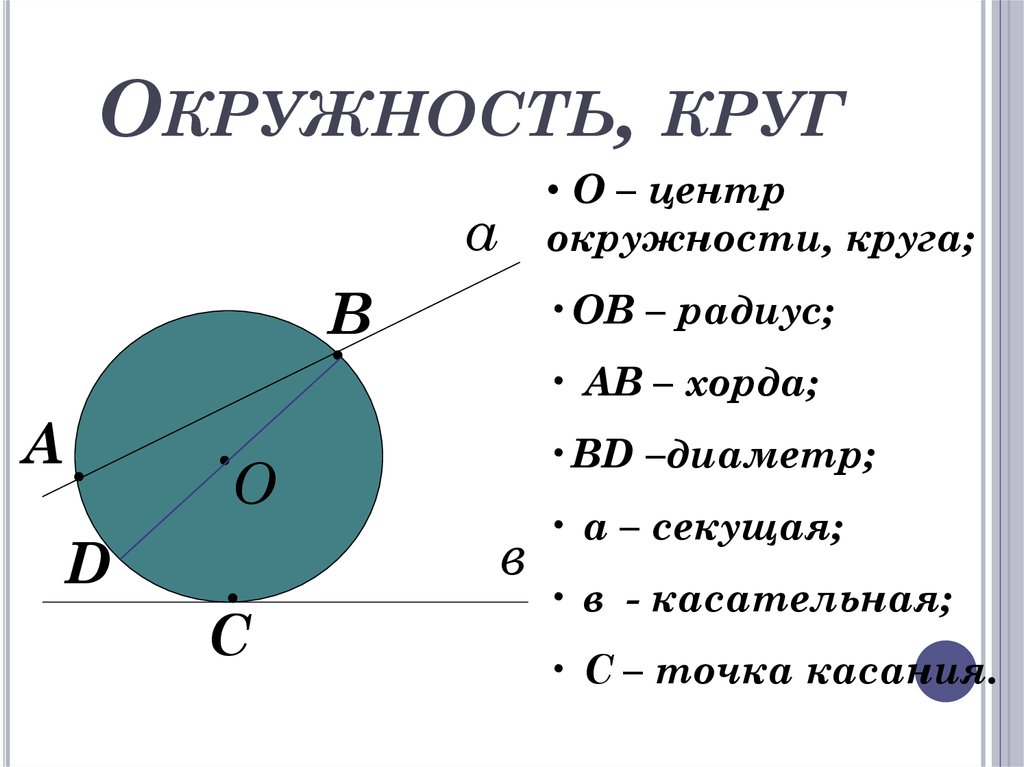

а. Формулы круга
Площадь круга
 Повторите это несколько раз, чтобы убедиться, что вы можете быстро вспомнить его, чтобы вычислить площадь круга в следующем тесте!
Повторите это несколько раз, чтобы убедиться, что вы можете быстро вспомнить его, чтобы вычислить площадь круга в следующем тесте! Диаметр круга
Окружность круга
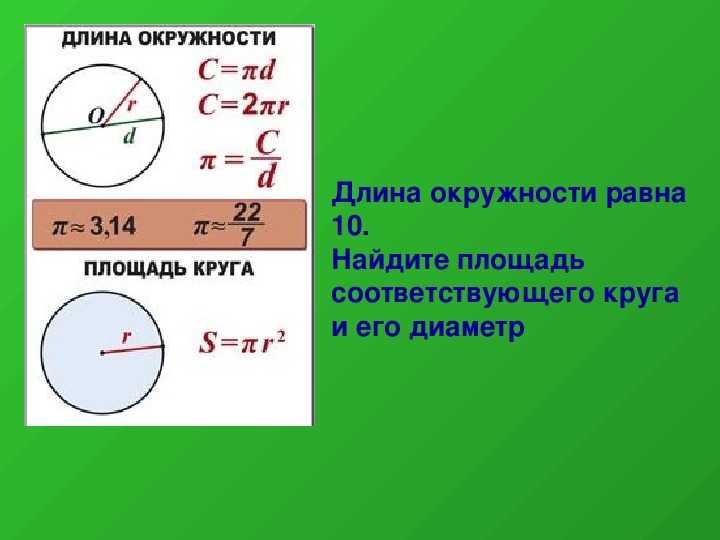 Теперь, зная, что число Пи есть константа π = 3,14, вы можете решить все формулы круга и найти площадь, диаметр и длину катка.
Теперь, зная, что число Пи есть константа π = 3,14, вы можете решить все формулы круга и найти площадь, диаметр и длину катка. Центр в начале координат
xy(0, 0)(r, 0)rОткрыть изображение на новой странице Центр не в начале координат
xy(h, k)rОткрыть изображение на новой странице
Нужна миллиметровка?
Значок миллиметровки Пример 1
Пример 2
Пример 3
б. Общая форма круга
Пример 4

Нет необходимости расширять это, так как это наиболее полезная форма уравнения.
2. Определите центр и радиус, а затем нарисуйте окружность:
3 х 2 + 3 у 2 - 12 х + 4 = 0
Ответить
Мы завершаем квадрат , как мы это делали в предыдущем примере выше.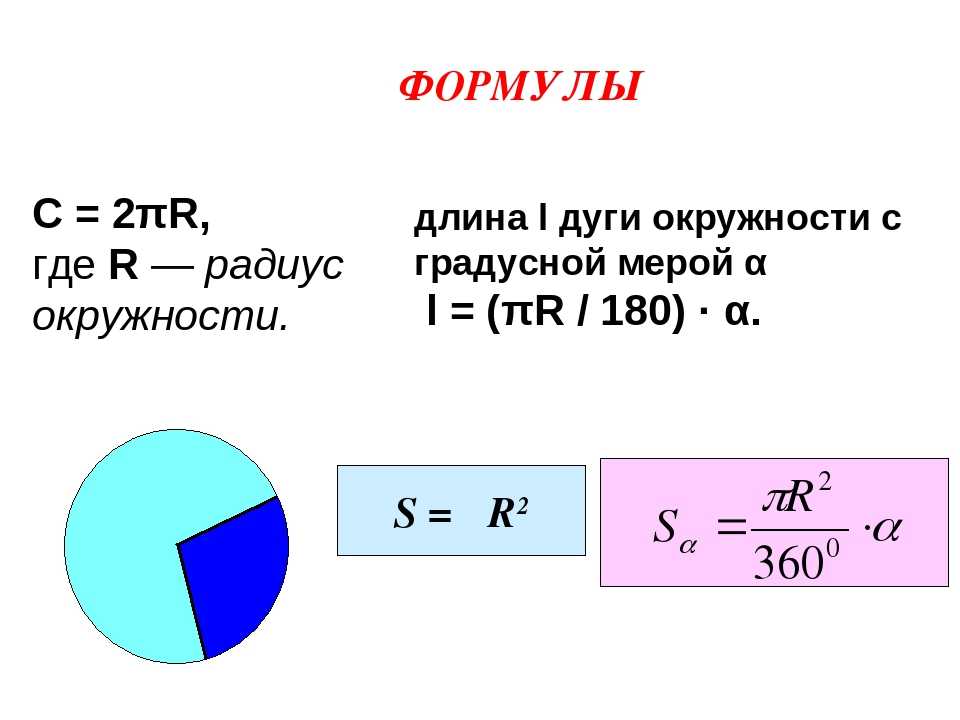

 combinations(range(len(centers)), 2):
yield dist(centers[i], centers[j]) / 2
return min(gen())
def plot_circles(centers):
radius = get_common_radius(centers)
poly = ((0, 0), (1, 0), (1, 1), (0, 1))
circles = [plt.Circle(c, radius, fill=False) for c in centers]
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
for c in circles:
ax.add_artist(c)
plt.plot(*zip(*cycle(poly)))
plt.show()
def shake(centers, step, r):
for i, c in enumerate(centers):
radius = get_radius(centers, i, c)
new_c = tuple(v + step * (2 * r.random() - 1) for v in c)
new_radius = get_radius(centers, i, new_c)
if radius < new_radius:
centers[i] = new_c
def main():
n = int(sys.argv[1])
r = random.Random()
centers = [(r.random(), r.random()) for _ in range(n)]
for p in range(0, 10):
step = 0.5 ** p
for _ in range(10 * 2 ** p):
shake(centers, step, r)
plot_circles(centers)
main()
combinations(range(len(centers)), 2):
yield dist(centers[i], centers[j]) / 2
return min(gen())
def plot_circles(centers):
radius = get_common_radius(centers)
poly = ((0, 0), (1, 0), (1, 1), (0, 1))
circles = [plt.Circle(c, radius, fill=False) for c in centers]
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
for c in circles:
ax.add_artist(c)
plt.plot(*zip(*cycle(poly)))
plt.show()
def shake(centers, step, r):
for i, c in enumerate(centers):
radius = get_radius(centers, i, c)
new_c = tuple(v + step * (2 * r.random() - 1) for v in c)
new_radius = get_radius(centers, i, new_c)
if radius < new_radius:
centers[i] = new_c
def main():
n = int(sys.argv[1])
r = random.Random()
centers = [(r.random(), r.random()) for _ in range(n)]
for p in range(0, 10):
step = 0.5 ** p
for _ in range(10 * 2 ** p):
shake(centers, step, r)
plot_circles(centers)
main()